Cos2A cos 4a sin 4a: Упростите выражение cos^2a-cos^4a+sin^4a — ответ на Uchi.ru

Содержание

Если \\[\\sin 4A — \\cos 2A = \\cos 4A — \\sin 2A\\] (где, \\[0 A \\dfrac{\\pi }{4}\\] ) тогда значение \\[\\tan 4A\\] равно A) \\[1\\]B) \\[\\dfrac{1}{{\\sqrt 3 }}\\]C) \\[ \\sqrt 3 \\]D) \\[\\dfrac{{\\left( {\\sqrt 3 — 1} \\right)}}{{\\left( {\\sqrt 3 + 1} \ \right)}}\\]E) \\[\\dfrac {{\\left( {\\sqrt 3 + 1} \\right)}}{{\\left( {\\sqrt 3

Подсказка: Здесь, в этом вопросе, мы должны найти точное значение данного уравнения тригонометрической функции.Для этого сначала мы должны упростить данное уравнение, используя формулу суммы в произведение тригонометрии, т. е. \[\sin x + \ sin y = 2 \ sin \ left ( {\ dfrac {{x + y}} {2}} \ right) \ cos \ left ( {\ dfrac {{x — y}} {2}} \ right) \ ] и \[\ cos x + \ cos y = 2 \ cos \ left ( {\ dfrac {{x + y}} {2}} \ right) \ cos \ left ( {\ dfrac {{x — y}} {2}} \right)\] то по определению и стандартным значениям углов тригонометрических соотношений получаем искомое значение.0005

Полный пошаговый ответ:
Функция угла, выраженная как отношение двух сторон прямоугольного треугольника, содержащего этот угол; синус, косинус, тангенс, котангенс, секанс или косеканс, известный как тригонометрическая функция.
Рассмотрим данное уравнение:
\[\sin 4A — \cos 2A = \cos 4A — \sin 2A\]
Переставляя данное уравнение, мы имеем
\[ \Rightarrow \,\,\,\,\sin 4A + \sin 2A = \cos 4A + \cos 2A\] ———(1)
Теперь применим сумму к формуле произведения тригонометрии, т. е. \[\sin x + \sin y = 2 \sin \left( {\dfrac{{x + y}}{2}} \right)\cos \left( {\dfrac{{x — y}}{2}} \right)\] В LHS и
\[\cos x + \cos y = 2\cos \left( {\dfrac{{x + y}}{2}} \right)\cos \left({\dfrac{{x — y}}{ 2}} \right)\] в RHS, тогда
Здесь \[x = 4A\] и \[y = 2A\]
При подстановке значений \[x\] и \[y\] в формулу, тогда уравнение (1) принимает вид
\[ \Rightarrow \,\,\,\,2\sin \left( {\dfrac{{4A + 2A}}{2}} \right)\cos \left( {\dfrac{ {4A — 2A}}{2}} \right) = 2\cos \left( {\dfrac{{4A + 2A}}{2}} \right)\cos \left({\dfrac{{4A — 2A }}{2}} \right)\]
\[ \Rightarrow \,\,\,\,2\sin \left( {\dfrac{{6A}}{2}} \right)\cos \left( {\dfrac{{2A}}{2}} \right) = 2\cos \left( {\dfrac{{6A}}{2}} \right)\cos \left({\dfrac{{2A}} {2}} \справа)\]
При упрощении получаем
\[ \Rightarrow \,\,\,\,2\sin \left( {3A} \right)\cos \left( A \right) = 2\cos \left( {3A} \right)\cos \left( A \right)\]
Разделим обе части на \[\cos \left( A \right)\], тогда получим
\[ \Rightarrow \,\,\,\,2 \sin \left( {3A} \right) = 2\cos \left( {3A} \right)\]
Разделить обе стороны на \[\cos \left( {3A} \right)\], затем
\ [ \Rightarrow \,\,\,\,\dfrac{{2\sin \left( {3A} \right)}}{{2\operatorname{Cos} \left( {3A} \right)}} = 1 \]
При упрощении получаем
\[ \Rightarrow \,\,\,\,\dfrac{{\sin\left({3A}\right)}}{{\operatorname{Cos} \left({3A}\right)}} = 1 \] ——(2)
Согласно определению тригонометрического соотношения, тангенс — это отношение между синусом и косинусом, т.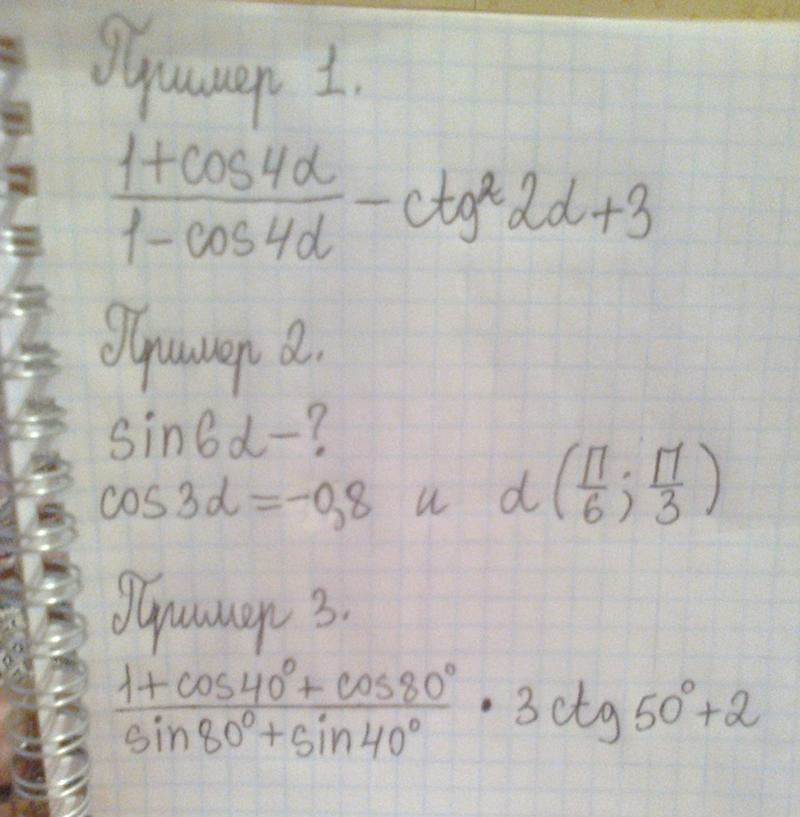 е. \[\dfrac {{\sin \theta}}{{\cos \theta}} = \ tan \theta \], тогда уравнение (2) принимает вид
\[ \Rightarrow \,\,\,\,\tan 3A = 1\] ——(3)
Учитывая диапазоны углов \[A\] из \[0 < A < \dfrac{\pi }{4}\], затем
\[3A = \dfrac{\pi }{4}\]
Обе стороны разделить на 3, затем 9\ circ } = \ tan \ left ( {\ dfrac {\ pi} {3}} \ right) = \ sqrt 3 \].
\[\следовательно \,\,\,\tan \left( {\dfrac{\pi }{3}} \right) = \sqrt 3 \]
Следовательно, искомое значение равно \[\sqrt 3 \ ].

Примечание:
При решении задач по тригонометрии необходимо знать определения и таблицу стандартных углов всех шести тригонометрических отношений синуса, косинуса, тангенса, секанса, косеканса и котангенса. Помните стандартные формулы, такие как тригонометрические тождества, двойные и половинные углы, тождество суммы и разности и т. д.

Многочисленные углы — Flip Ebook Pages 1-50

General

Опционально

Математика

класс 10

GOM

Binod Kasula

[Электронная почта защищена]

SIN (A + B) = SINA. .cosB + cosA.sinB
sin(A + A) = sinA.cosA + cosA.sinA
sin2A = 2sinA.cosA
sin2B = 2sinB.cosB
sin(A + B) = sinA.cosB + cosA.sinB
sin (B + B) = sinB.cosB + cosB.sinB
sin2B = 2sinB.cosB
cos2A
cos(A + B) = cosA.cosB — sinA.sinB
cos(A + A) = cosA.cosA — sinA.sinA
cos2A = cos2A — sin2A
cos2B = cos2B — sin2B
sin2A = 2sinA.cosA
cos2A= cos2A — sin2A
Формула cos2A через sinA
= cosA
cos2A — sin2A
или, cos2A = 1- sin2A — sin2A
или, cos2A = 1 — 2sin2A

[email protected]

Формула cos2A через cosA.

cos2A = cos2A — sin2A

или, cos2A = cos2A — (1 — cos2A)

или, cos2A = cos2A — 1 + cos2A

COS2A = 2COS2A — 1

COS2A = 1-2SIN2A

или, 2SIN2A = 1 — COS2A

или SIN2A = 1 — COS2A
2

COS2A = 2COS2A — 1

или, COS2A +1 = 2COS2A

.
5A

a — 1

или 2cos2a = 1 + cos2a

cos2a = 1 + cos2a
2

[Электронная почта защищена]

1. Sin2a = 2sina.cosa

2.cos2a = cos2a — sin2a

3.cos2a = = cos2a = cos2a — sin2a

3.cos2a =. 2cos2A — 1

4. cos2A = 1 — 2sin2A

5. 2sin2A = 1 — cos2A

6.2cos2A = 1 + cos2A

7. sin2A = 1 — cos2A
2

8.cos2A = 1 + cos2A
2

tanA + tanB
tan (A+B). + tanA
tan(A+A) = 1 — tanA.tanA

2tanA
9. tan2A = 1 -tan2A

cotB.cotA — 1
cot(A + B) = cotB + cotA

cotA.cotA — 1
cot(A + A) = cotA + cotA

cot2A — 1
10.cot2A = 2cotA

[email protected]

Формула sin2A через tanA.

sin2A = 2sinA.cosA

sin2A = 2sinA.cosA . cosA

cosA

sin2A = 2 sinA .cos2A
.cosA

1
sin2A = 2 tanA. Sec2a

1
SIN2A = 2 TANA .1+ TAN2A

2TANA
SIN2A = 1+ TAN2A

Формула SIN2A с точки зрения COTA

Формула Cos2a в термине Tana

Formul cotA

[электронная почта защищена]

cos2A = cos2A — sin2A

или, cos2A =(cos2A — sin2A). cos2A

cos2A

cos2A sin2A 1
или, cos2A = (cos2A — cos2A) . sec2A

или cos2A = (1 — tan2A) . 1
1 + TAN2A

 COS2A = 1 — TAN2A
1 + TAN2A

1 — TAN2A
Формула COS2A в термин TANA составляет 1 + TAN2A

[Электронное письмо защищено]

1. SIN2A = 2SINA .cosA
2tanA

2. sin2A = 1 + tan2A
2cotA

3. sin2A = 1 + cot2A
4. sin3A = 3sinA — 4sin3A
5. cos3a = 4cos3a — 3cosa
6. cos2a = cos2a — sin2a
7. cos2a = 2cos2a — 1
8. cos2a = 1 — 2sin2a
9. 2cos2a = 1 + cos2a
10. 2sin2a = 1 — cos2a

66. 1 — TAN2A
11. COS2A = 1 + TAN2A

COT2A — 1
12. COS2A = COT2A + 1
13. COS3A = 4COS3A — 3COSA

[Электронное письмо защищено]

2TANA
14. — tan2A

cot2A — 1
15. cot2A = 2cotA

3tanA — tan3A
16. tan3A= 1- 3 tan2A

COT3A — 3COTA
17. COT3A = 3COT2A — 1

18. Докажите, что TAN2A = 1- COS2A
1+ COS2A

19. Докажите, что COT2A = 1+ COS2A
1 — COS2A

. — 1
cos2A = cot2A + 1

или cos2A ( cot2A + 1 ) = cot2A — 1

или cos2A . cot2A + cos2A = cot2A — 1

или, 1 + cos2A = cot2A — cos2A . cot2A

или, 1 + cos2A = cot2A( 1 — cos2A)

или, cot2A = 1+ cos2A
1 — cos2A

[email protected]

18. Докажите, что tan2A = 1- cos2A
1 + cos2A

имеем

1 — tan2A
cos2A = 1 + tan2A

или

или cos2A + cos2A. tan2A = 1 — tan2A

или cos2A. tan2a + tan2a = 1 — cos2a

или, tan2a (cos2a + 1) = 1 — cos2a

или, tan2a = 1 — cos2a
1 + cos2a

[электронное письмо защищено]

4
1. Если cosA = 5, найдите значения sin2A, cos2A и tan2A.

найти значение sinA.

sinA = 1 — cos2A

4
здесь, cosA = 5

sinA = 1-cos2A = 2 16 25-16 93
1- 25 = 25 = 25 = 5  =

имеем, sin2A = 2sinA . cosA

3 4 24
или, sin2A = 2.5 .5 = 25

4 22
135 97
снова, cos2A = cos2A — sin2A = — 5 = 25 — 25 = 25

24
sin2A 25 24
здесь, снова for, tan2A = cos2A = 7 = 7

0006 Упражнение: A

4
1. Если sinA = 5, то найти cos2A, sin2A и tan2A.

1
2. Если sinA = 2, то найти sin3A и cos3A.

[email protected]

2.Докажите, что 1- cos2A = 2cos2(90 — A)
LHS

1- cos2A
= 2sin2A
= 2cos2(90 — A) Доказано.

2. Докажите, что 1+ cos2A = 2sin2(90 — A)
LHS, 1+ cos2A
= 2cos2A
= 2sin2(90-A) RHS, доказано. здесь cosA= sin(90 — A)
Докажите, что 1 + sin2A = 2cos2(45 — A)

3. Докажите, что 1 — sin2A = 2sin2(45 — A)
LHS , 1 — sin2A
= 1 — cos(90 — 2A)
= 1 — cos2(45-A)
= 2sin2(45-A) RHS доказано

[email protected]

4. Докажите, что 1 + sin2A = 2cos2(45 — A)

LHS, 1 + sin2A

= 1 + cos(90 -2A)