| 5.1.1.8. Примеры вычисления производных |
Высшая математика > 5. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| gif»> | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Производная степенной функции с натуральным показателем. Производная суммы, произведения и частного двух функций
Бурковская Нина Дмитриевна.
Уральский технологический колледж «Сервис», г.Уральск, ЗКО,РК
Преподаватель математики.
Тема программы:Производная – 23 часа
Тема урока: Производная степенной функции с натуральным показателем. Производная суммы, произведения и частного двух функций.
Цель урока:Изучить правила нахождения производной функции, уметь вычислять производную
Тип урока: Изучение новой темы, формирование зун.
Методы ведения: лекция
Оборудование урока презентация
ХОД УРОКА:
Организационный момент – 1 – 2 мин.
Приветствие учащихся.
Отметить отсутствующих.
II. Опрос по домашнему заданию
III. Объяснение нового материала. Краткий конспект.
1. Производная суммы функций равна сумме производных.
(u + v)¢ = u¢ + .
2. .Производная произведения равна сумме произведений производной первой функции на вторую функцию и производной второй функции на первую функцию.
(uv)¢ = u¢v + v¢u
3. Постоянный множитель можно выносить за знак производной.
(сu)¢ = cu¢ .
4.Производная частного двух функций равна дроби, числитель которой есть разность между произведениями производной числителя на знаменатель и производной знаменателя на числитель, а знаменатель есть квадрат знаменателя, если производные
числителя и знаменателя существуют.
5. Производная степенной функции у = хn равна произведению показателя функции на аргумент в степени на единицу меньшей.
у = хn , у¢ = nxn-1
ПРИМЕР №1 Найти производную функции у = х2 + 10.
Решение. у¢ = (х2 + 10)¢ = (х
ПРИМЕР№ 2. Найти производную функции у = (5х — 8) · х2 .
Решение. Выше мы уже находили производные функций :
у1 = 5х — 8, у1¢ = 5 ; у2 = х2 , у2¢ = 2х.
у¢ = ((5х — 8) ·х2)¢ = (5х — 8)¢ · х2 + (х2)¢ · (5х — 8) =
= 5· х2 + 2х· (5х — 8) = 5х2 + 10х2 — 16х = 15х2 — 16х .
ПРИМЕР № 3. Найти производную функции у = 3х2 .
Решение. Постоянный множитель можно выносить за знак производной. у¢ = (3х2)¢ = 3 · (х2)¢ = 3 · 2х = 6х.
у¢ = (3х2)¢ = 3 · (х2)¢ = 3 · 2х = 6х.
ПРИМЕР№ 4
Найти производную функции у =
Решение.
= .
ПРИМЕР №5.
Найти производные функций у = х20 , z = 5x4 .
Решение. у¢ = 20х19, z’ = 5· 4х3= 20х3 .
Формула (xn)¢ = nxn-1 верна не только для целых положительных х, но для любого рационального показателя.
ПРИМЕР№6.
Найти производные функций у = , z = ,
Решение.y = = х-1 . у¢ = -1 х-1-1 = — х-2 = .
z = = . z¢ = ==
z¢ = ==
Закрепление нового материала: № 175
Задание на дом §14 №176
Литература: А.Е. Абылкасымова и др. Алгебра и начала анализа 10, 11
классы.
Дидактический материал по алгебре и начала анализа для 10, 11 класов.
{2x}\) Скачать публикацию в формате PDF| Форма перехвата наклона: уравнение с выводом и примерами | |
| Decimal фракции: операции, типы с решаемыми примерами | 9|
| Векторное пространство с определением, аксиомами, свойствами и примерами решения | |
| Пифагорейские тройки: изучите понятие, типы, набор различных значений и примеры решения. |
Силовое правило
Степень означает показатель степени, такой как 2 x 2
Степенное правило, одно из наиболее часто используемых производных правил, гласит:
Производная от x n равна nx (n−1)
Пример: Какова производная x
2 ?Для x 2 мы используем правило степени с n = 2:
| Производная от x 2 | = | 2x (2−1) |
| = | 2x 1 | |
| = | 2x |
Ответ: производная от x 2 равна 2x
«Производная от» может быть показана этой маленькой «тире»: ’
Используя эту метку, мы можем написать Power Rule следующим образом:
f’(x n ) = nx (n−1)
Пример: Какова производная x
3 ?f’(x 3 ) = 3x 3−1 = 3x 2
«Производная от» также может быть показана д дх
Пример: что такое
д дх (1/х) ?1/x равно x −1
Использование степенного правила с n = −1 :
д дх х n = nx n−1
д дх х -1 = -1х -1-1 = -х -2
Как запомнить
«умножить на мощность
затем уменьшить мощность на 1″
Короткий стол
Вот Power Rule с примерами значений.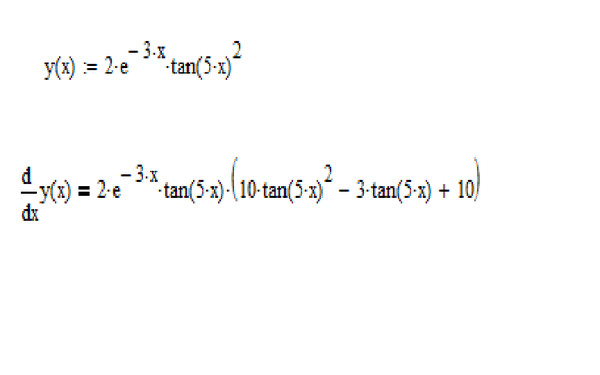




 Рекомендуем ее
запомнить
Рекомендуем ее
запомнить