По теореме Виета решим квадратное уравнение:
а1=1;а2=3-не удовлетворяет условию
При sinx=1: х=arcsin(1)=90
Знаешь ответ? Добавь его сюда!
Последние вопросы
- Физика
21 минут назад
Оценить число молекул воздуха в земной атмосфере, если давление воздуха вблизи поверхности Земли на уровне моря равно 760 мм рт.ст., молярная масса воздуха 29 г/моль. Радиус Земли 6400 км. Ускорение свободного падения считать постоянным и равным 9,8 м/с2 .
- Математика
1 час назад
умоляю помогите
- Математика
3 часа назад
Помогите пожалуйста от этой оценки зависит годовая оценка
- Информатика
11 часов назад
3 вариант
- Информатика
11 часов назад
Помогите
- Физика
14 часов назад
Реохорд. x+1 y(0)=2; y'(0)=1.
x+1 y(0)=2; y'(0)=1. - Математика
15 часов назад
1. Случайная величина распределена равномерно на отрезке [−2; 5]. Найти математическое ожидание и дисперсию. Что вероятнее: в результате ис- пытания случайная величина окажется в интервале (2,5; 3) или вне его?
- Математика
15 часов назад
1. В цехе работают 8 мужчин и 12 женщин. По табельным номерам отбира- ют 6 человек. Какова вероятность того, что среди них будут только 2 женщины? - Физика
15 часов назад
определи фокусное расстояние лупы с точностью до сантиметра если её оптическая сила равна d 5.3 дптр.
- Алгебра
17 часов назад
-6x^2+x+2>0.
 Решение квадратных неравенств
Решение квадратных неравенств - Физика
17 часов назад
2.3. Блок укреплен на вершине двух наклонных плоскостей, составляющих с горизонтом углы а = 30° и (3 = 45°. Гири равной массы
(т
х = т2 = 2 кг) соединены нитью, перекинутой через блок. Считая нить и блок невесомыми, принимая коэффициенты трения гирь о наклонные плоскости равными f1= f2= =0,1 и пренебрегая трением в блоке, определите: 1) ускорение, с которым движутся гири; 2) силу натяжения нити. [1) 0,24 м/с2; 2) 12 Н]
- История
22 часов назад
ПЖ помогите КТО ЭТО Я НЕЗНАЮ
- Алгебра
22 часов назад
Негр и мексиканец падают с небоскрёба.
 Кто упадёт первым?
Кто упадёт первым? - Математика
1 день назад
В машине сидят негр и мексиканец. Кто за рулём?
Довідкові матеріали до НМТ з математики
Advertisement
Download to read offlineEducation
Довідкові матеріали до НМТ з математики
Advertisement
Advertisement
Advertisement
Довідкові матеріали до НМТ з математики
- 2
Таблиця квадратів від 10 до 49
АЛГЕБРА І ПОЧАТКИ АНАЛІЗУ
ДОВІДКОВІ МАТЕРІАЛИ
Одиниці
Десятки
0
100
1
400
2
900
3
1600
4
1
121
441
961
1681
2
144
484
1024
1764
3
169
529
1089
1849
4
196
576
1156
1936
5
225
625
1225
2025
6
256
676
1296
2116
7
289
729
1369
2209
8 9
324 361
784 841
1444 1521
2304 2401
Формули скороченого множення Квадратне рівняння
Модуль числа
Степені Логарифми
Арифметична прогресія
Теорія ймовірностей Комбінаторика
Геометрична прогресія
a2
– b2
= (a – b)(a + b)
(a + b)2
= a2
+ 2ab + b2
(a – b)2
= a2
– 2ab + b2
ax2
+ bx + c = 0, a ≠ 0
D = b2
– 4ac – дискримінант
x1 =
–b – D
—
2a
, x2 =
–b + D
—
2a
, якщо D > 0
x1 = x2 =
–b
—
2а , якщо D = 0
ax2
+ bx + c = a(x – x1)(x – x2)
a1
= а, аn
= a ⋅ a .
 .. ⋅ a
n разів
для a ∈ R, n ∈ N, n 2
a0
= 1, де а ≠ 0 a2
= а
a–n
=
1
—
аn для а ≠ 0, n ∈ N
a
m
—
n
= am
n
, а > 0, m ∈ Z, n ∈ N, n 2
ax
⋅ ay
= ax + y аx
—
аy = ax – y
(ax
)y
= ax ⋅ y
(ab)x
= ax
⋅ bx
(a
–
b)
x
=
аx
—
bx
a > 0, а ≠ 1, b > 0, c > 0, k ≠ 0
alogab
= b logаа = 1 logа1 = 0
logа(b ⋅ c) = logаb + logаc
logа
b
–
c = logаb – logаc
logаbn
= n ⋅ logаb
logаk b = 1
–
k
⋅ logаb
an = a1 + d(n – 1) Sn =
a1 + аn
—
2
⋅ n
Pn = 1 ⋅ 2 ⋅ 3 ⋅ … ⋅ n = n! C
k
n =
n!
—
k! ⋅ (n – k)!
Ak
n =
n!
—
(n – k)!
P(A) =
k
–
n
bn = b1 ⋅ qn – 1
Sn =
b1(qn
– 1)
—
q – 1
, (q ≠ 1)
a =
a, якщо а 0,
–a, якщо а < 0
.. ⋅ a
n разів
для a ∈ R, n ∈ N, n 2
a0
= 1, де а ≠ 0 a2
= а
a–n
=
1
—
аn для а ≠ 0, n ∈ N
a
m
—
n
= am
n
, а > 0, m ∈ Z, n ∈ N, n 2
ax
⋅ ay
= ax + y аx
—
аy = ax – y
(ax
)y
= ax ⋅ y
(ab)x
= ax
⋅ bx
(a
–
b)
x
=
аx
—
bx
a > 0, а ≠ 1, b > 0, c > 0, k ≠ 0
alogab
= b logаа = 1 logа1 = 0
logа(b ⋅ c) = logаb + logаc
logа
b
–
c = logаb – logаc
logаbn
= n ⋅ logаb
logаk b = 1
–
k
⋅ logаb
an = a1 + d(n – 1) Sn =
a1 + аn
—
2
⋅ n
Pn = 1 ⋅ 2 ⋅ 3 ⋅ … ⋅ n = n! C
k
n =
n!
—
k! ⋅ (n – k)!
Ak
n =
n!
—
(n – k)!
P(A) =
k
–
n
bn = b1 ⋅ qn – 1
Sn =
b1(qn
– 1)
—
q – 1
, (q ≠ 1)
a =
a, якщо а 0,
–a, якщо а < 0 - 23 Похідна функції Тригонометрія Таблиця значень тригонометричних функцій деяких кутів Первісна функції та визначений інтеграл С, – сталі (С)′ = 0 х′ = 1 (х )′ = x–1 ( x)′ = 1 – 2 x (ex )′ = ex (ln x)′ = 1 – x (sin x)′ = cos x (cos x)′ = –sin x (tg x)′ = 1 – cos2x (u + v)′ = u′ + v′ (u – v)′ = u′ – v′ (uv)′ = u′v + uv′ (Cu)′ = Cu′ (u – v)′ = u′v – uv′ – v2 sin = y cos = x sin2 + cos2 = 1 tg = sin – cos 1 + tg2 = 1 – cos2 sin2 = 2sin cos cos2 = cos2 – sin2 sin(90o + ) = cos sin(180o – ) = sin cos(90o + ) = –sin cos(180o – ) = –cos tg(90o + ) = – 1 – tg tg(180o – ) = –tg a ∫ b f(x)dx = F(x)a b = F(b) – F(a) – формула Ньютона-Лейбніца 0 –1 –1 1 1 y x M(x, y) x y tg α cos α sin α рад град 0o 0 α 0 1 0 0 0 30o π – 6 1 – 2 1 – 2 2 — 2 1 — 3 2 — 2 3 — 2 3 — 2 45 o π – 4 1 3 60 o π – 3 90 o 180 o 270 o 360 o π – 2 π 3π — 2 2π 1 0 0 –1 –1 0 0 1 не існує не існує Загальний вигляд первісних F(x) + C, C – довільна стала Функція f(x) 0 C x + 1 — + C + 1 ln x + C x + C sin x –cos x + C cos x sin x + C tg x + C 1 — cos2 x 1 ex ex + C 1 – x x , ≠ –1
- 24 Кінець зошита ГЕОМЕТРІЯ Довільний трикутник Паралелограм Пряма призма Циліндр Конус Куля, сфера Правильна піраміда Прямокутник Ромб Трапеція Прямокутний трикутник Координати та вектори Трикутники Чотирикутники Коло Об’ємні фігури та тіла Круг S = ab sinγ S = aha V = Sосн ⋅ H Sб = Pосн ⋅ H V = 1 – 3 Sосн ⋅ H Sб = 1 – 2 Pосн ⋅ m V = πR2 H Sб = 2πRH V = 1 – 3 πR2 H Sб = πRL V = 4 – 3 πR3 S = 4πR2 L = 2πR (x – x0)2 + (y – y0)2 = R2 S = πR2 S = 1 – 2 d1d2, d1, d2 – діагоналі ромба S = a + b — 2 ⋅ h, a і b – основи трапеції S = ab p = a + b + c — 2 + β + γ = 180о a2 = b2 + c2 – 2bc cos a — sin = b — sinβ = c — sinγ = 2R R – радіус кола, описаного навколо трикутника ABC a2 + b2 = c2 (теорема Піфагора) b – c = cos a – c = sin a – b = tg c a b C A B β γ ha α c a b α a b γ ha a b d1 d2 a b h R M(x0, y0) H M(x0, y0, z0) A(x1, y1, z1) B(x2, y2, z2) H m H R R H L R R S = 1 – 2 a ⋅ ha S = 1 – 2 b ⋅ c ⋅ sin S = p(p – a)(p – b)(p – c) x0 = x1 + x2 — 2 y0 = y1 + y2 — 2 z0 = z1 + z2 — 2 AB(x2 – x1, y2 – y1, z2 – z1) AB= (x2 – x1)2 + (y2 – y1)2 + (z2 – z1)2 a ⋅ b = a1b1 + a2b2 + a3b3 a ⋅ b = a⋅bcosφ φ a(a1, a2, a3) b(b1, b2, b3)
Advertisement
Формула Cos2x: вывод, применение и пример вопроса с решением
Формула Cos2X является одним из основных тригонометрических тождеств, используемых для определения значения тригонометрической функции косинуса для двойных углов.
Cos2x Формула в тригонометрии может быть выражена через различные тригонометрические функции, такие как синус, косинус и тангенс. Это также известно как тождество двойного угла функции косинуса. Идентичность cos2x помогает представить косинус составного угла 2x в терминах синуса, а также тригонометрические функции косинуса только в терминах функции косинуса, только функции синуса и только функции тангенса. 92 раза?
Идентичность формулы cos2x в тригонометрии может быть выражена различными способами. Cos2x представлен множеством тригонометрических функций, включая, среди прочего, синус, косинус и тангенс. Формула cos2x относится к категории тригонометрических тождеств двойного угла, поскольку рассматриваемый угол является делителем 2 или удвоенным по отношению к x. Идентичность cos2x в нескольких альтернативных формах показана ниже:
- cos2x = cos2x — sin2x
- cos2x = 2cos2x — 1
- cos2x = 1 — 2sin2x
- cos2x = (1 — tan2x)/(1 + tan2x)
Cos2x, также называемый тождеством функции косинуса с двойным углом, является одним из многих важных тригонометрических тождеств, используемых для нахождения значения тригонометрической функции косинуса для двойных углов. Cos2x выражается через различные тригонометрические функции, и каждая из его формул используется для упрощения сложных тригонометрических выражений и решения задач интегрирования. Это тригонометрическая функция двойного угла, которая помогает узнать значение cos при удвоении угла x.
Cos2x выражается через различные тригонометрические функции, и каждая из его формул используется для упрощения сложных тригонометрических выражений и решения задач интегрирования. Это тригонометрическая функция двойного угла, которая помогает узнать значение cos при удвоении угла x.
Формула cos2x может быть выражена в четырех различных формах. Значение косинуса составного угла «2x» представлено только с точки зрения функции синуса, только с точки зрения функции косинуса, с точки зрения тригонометрических функций синуса и косинуса и только с точки зрения функции тангенса. Ниже показаны некоторые способы получения формулы Cos2x:
Вывод формулы Cos2x с использованием формулы сложения углов Формулу Cos2x можно получить, используя формулу сложения углов для функции косинуса. Угол 2x также можно записать как 2x = x + x. Кроме того, мы уже знаем, что cos (a + b) = cos a x cos b — sin a x sin b. Это можно использовать для подтверждения идентичности cos2x. Используя формулу сложения углов для функции косинуса, мы можем заменить a = x и b = x в формуле для cos (a + b).
Используя формулу сложения углов для функции косинуса, мы можем заменить a = x и b = x в формуле для cos (a + b).
cos2x = cos (x + x)
= cos x x cos x — sin x x sin x
= cos2x — sin2x
Таким образом, мы имеем cos2x = cos2x — sin2x
Вывод формулы Cos2x через Sin xТеперь, когда мы установили cos2x = cos2x — sin2x, мы выведем формулу для cos2x только через синус функция. Мы можем использовать тождество тригонометрии cos2x + sin2x = 1, чтобы вывести формулу cos2x через sin x. Имеем
cos2x = cos2x — sin2x
= (1 — sin2x) — sin2x [Так как cos2x + sin2x = 1 ⇒ cos2x = 1 — sin2x]
= 1 — sin2x — sin2x
= 1 — 2sin2x
Следовательно, с точки зрения sin x мы имеем cos2x = 1 — 2sin2x.
Деривация формулы COS2X в терминах COS X, как мы получили COS2X = 1 — 2SIN2X, мы получим COS2X с точки зрения COS X, т.е. — sin2x и cos2x + sin2x = 1, чтобы доказать, что cos2x = 2cos2x — 1, мы имеем,
cos2x = cos2x — sin2x
= cos2x — (1 — cos2x) [Так как cos2x + sin2x = 1 ⇒ sin2x = 1 — cos2x ]
= cos2x — 1 + cos2x
= 2cos2x — 1
Следовательно, через cos x имеем cos2x = 2cos2x — 1.
Использование уголка Формула сложения, мы получили cos2x = cos2x — sin2x. Теперь мы выведем cos2x через tan x, используя несколько тригонометрических тождеств и тригонометрических формул, таких как cos2x = cos2x — sin2x, cos2x + sin2x = 1 и tan x = sin x/cos x.
Мы это уже знаем,
cos2x = cos2x — sin2x
= (cos2x — sin2x)/1
= (cos2x — sin2x)/(cos2x + sin2x) [Как cos2x + sin2x = 1]
Деление числителя и знаменателя (cos2x — sin2x)/( cos2x + sin2x) на cos2x.
(cos2x — sin2x)/(cos2x + sin2x) = (cos2x/cos2x — sin2x/cos2x)/( cos2x/cos2x + sin2x/cos2x)
= (1 — tan2x)/(1 + tan2x) [Поскольку tan x = sin x / cos x]
Таким образом, в терминах тангенса x мы имеем cos2x = (1 — tan2x)/(1 + tan2x)
92x = (cos2x + 1)/2
⇒ cos2x = (cos2x + 1)/2
Как применить идентификатор Cos2x? Формула cos2x используется для решения различных математических задач. Рассмотрим пример, демонстрирующий применение формулы cos2x.
Рассмотрим пример, демонстрирующий применение формулы cos2x.
Например: мы определим значение cos 120°, используя тождество cos2x. Уже известно, что cos2x = cos2x — sin2x и sin 60° = √3/2, cos 60° = 1/2. Поскольку 2x = 120°, x = 60°. Следовательно, имеем
cos 120° = cos260° — sin260°
= (1/2)2 — (√3/2)2
= 1/4 — 3/4
= -1/2
Решенные примеры с использованием формулы Cos2x
Понять формулу cos2x, учитывая решенные примеры показывают, как можно использовать формулу cos 2x
Пример 1 : Найдите тождество тройного угла функции косинуса, используя формулу cos2x
Решение: тождество тройного угла функции косинуса равно cos 3x = 4 cos3x – 3 cos x
cos 3x = cos (2x + x) = cos2x cos x – sin 2x sin x
= (2cos2x – 1) cos x – 2 sin x cos x sin x [Поскольку cos2x = 2cos2x – 1 и sin2x = 2 sin x cos x]
= 2 cos3x – cos x – 2 sin2x cos x
= 2 cos3x – cos x – 2 cos x (1 – cos2x) [Поскольку cos2x + sin2x = 1 ⇒ sin2x = 1 – cos2x]
= 2 cos3x – cos x – 2 cos x + 2 cos3x
= 4 cos3x – 3 потому что х.
Пример 2: Решить Sin x = 12/13, найти Cos 2x
Решение: Как мы знаем, Cos2x = 1 –2Sin2x
= 1 – 2 (12/13)2
= 1 – 2 (144/169)
= 1 –288/169
= 169 – 288/169
= -119/169
Формула двойного угла для косинуса 9000 1
Тригонометрическое соотношение – это отношение длины любых двух сторон прямоугольного треугольника. Эти соотношения можно использовать для вычисления сторон прямоугольного треугольника, а также углов, образующихся между ними. Отношение косинусов рассчитывается путем вычисления отношения длины прилежащей стороны угла к длине гипотенузы. Обозначается аббревиатурой cos.
Если θ — угол между основанием и гипотенузой прямоугольного треугольника, то
cos θ = Основание/Гипотенуза = BC/AC
Cos Формула двойного угла
В тригонометрии cos 2x — это тождество двойного угла. Поскольку функция cos является обратной функцией секущей, ее также можно представить как cos 2x = 1/sec 2x. Это важное тригонометрическое тождество, которое можно использовать для решения различных задач тригонометрии и интегрирования. Значение cos 2x повторяется через каждые π радиан, cos 2x = cos (2x + π). Он имеет значительно более узкий график, чем cos x. Это тригонометрическая функция, которая возвращает значение функции cos двойного угла.
Это важное тригонометрическое тождество, которое можно использовать для решения различных задач тригонометрии и интегрирования. Значение cos 2x повторяется через каждые π радиан, cos 2x = cos (2x + π). Он имеет значительно более узкий график, чем cos x. Это тригонометрическая функция, которая возвращает значение функции cos двойного угла.
cos 2x = cos 2 x – sin 2 x
Приведенную выше формулу можно еще больше упростить, используя тождество синуса и косинуса.
Подставляя sin 2 x = 1 – cos 2 x, формула принимает вид 002 cos 2x = 2 cos 2 x – 1
Подставляя cos 2 x = 1 – sin 2 x, формула принимает следующий вид:
cos 2x = (1 – sin 2 x) – sin 2 x
cos 2x = 1 – 2 sin 2 x
Производная
Примеры задачФормулу для cos 2x можно получить, используя формулу суммы углов для функция косинуса.
Мы уже знаем, cos (A + B) = cos A cos B – sin A sin B
Чтобы вычислить значение косинуса двойного угла, угол A должен быть равен углу B.
Полагая A = B, мы получить,
cos (A + A) = cos A cos A – sin A sin A
cos 2A = cos 2 A – sin 2 A
Отсюда выводится формула соотношения двойного угла косинуса.
Задача 1. Если cos x = 3/5, найдите значение cos 2x по формуле.
Решение:
Имеем, cos x = 3/5.
Очевидно, sin x = 4/5.
Используя формулу получаем,
cos 2x = cos 2 x – sin 2 x
= (3/5) 2 – (4/5) 2
= 9/25 – 16/25
= -7/25
Задача 2. Если cos х = 12/ 13, найдите значение cos 2x по формуле.
Решение:
Имеем, cos x = 12/13.
Очевидно, sin x = 5/13.
Используя формулу получаем,
cos 2x = cos 2 x – sin 2 x
= (12/13) 2 – (5/13) 2 90 226
= 144/169 – 25/169
= 119/169
Задача 3. Если sin x = 3/5, найдите значение cos 2x по формуле.
Решение:
Итак, sin x = 3/5.
Очевидно, что cos x = 4/5.
Используя формулу получаем,
cos 2x = cos 2 x – sin 2 x= (4/5) 2 – (3/5) 2
= 16/25 – 9/25
= 7/25
Задача 4. Если tan x = 12/5, найдите значение cos 2x по формуле.
Решение:
Имеем tan x = 12/5.
Очевидно, что sin x = 12/13 и cos x = 5/13.
Используя формулу получаем,
cos 2x = cos 2 x – sin 2 x
= (5/13) 2 – (12/13) 2 90 226
= 25/169 – 144/169
= -119/169
Задача 5. Если sec x = 17/8, найдите значение cos 2x по формуле.
Если sec x = 17/8, найдите значение cos 2x по формуле.
Решение:
Имеем, сек х = 17/8.
Очевидно, что cos x = 8/17 и sin x = 15/17.
Используя формулу получаем,
cos 2x = cos 2 x – sin 2 x
= (8/17) 2 – (15/17) 2 90 226
= 64/289 – 225/289
= -161/225
Задача 6. Если cot x = 15/8, найдите значение cos 2x по формуле.
Решение:
Имеем, кроватка х = 15/8.
Очевидно, что cos x = 15/17 и sin x = 8/17.
Используя формулу получаем,
cos 2x = cos 2 x – sin 2 x
= (15/17) 2 – (8/17) 2 90 226
= 225/289 – 64/289
= 161/225
Задача 7. Если cos 2 x = 5/8, найдите значение cos 2x по формуле.
Решение:
Имеем
cos 2 x = 5/8
Используя формулу получаем,
cos 2x = 2 cos 2 x – 1
= 2 (5/8) – 1
= 5/4 – 1
= 1/4 9000 3
Задача 8.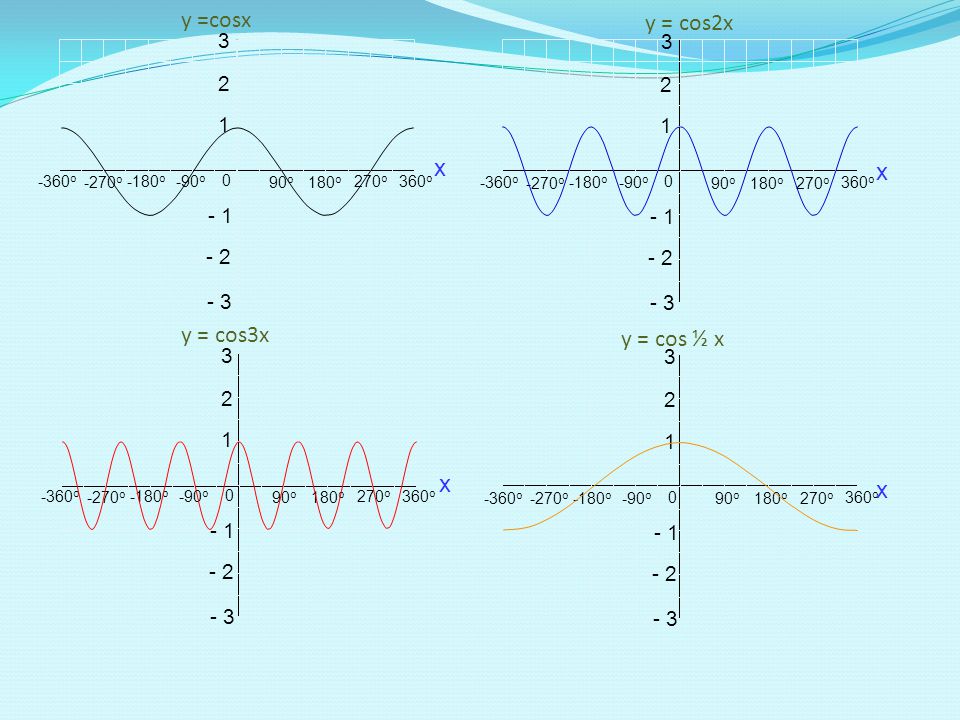

 x+1 y(0)=2; y'(0)=1.
x+1 y(0)=2; y'(0)=1.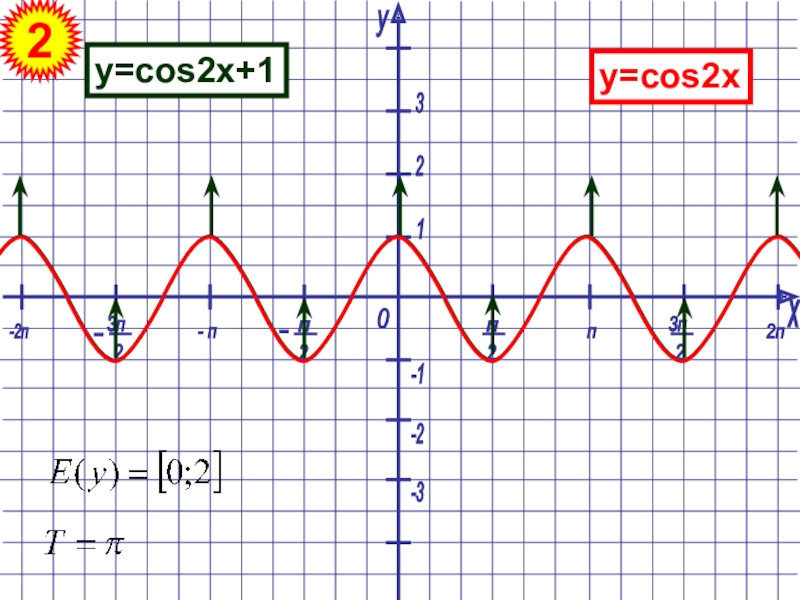 Решение квадратных неравенств
Решение квадратных неравенств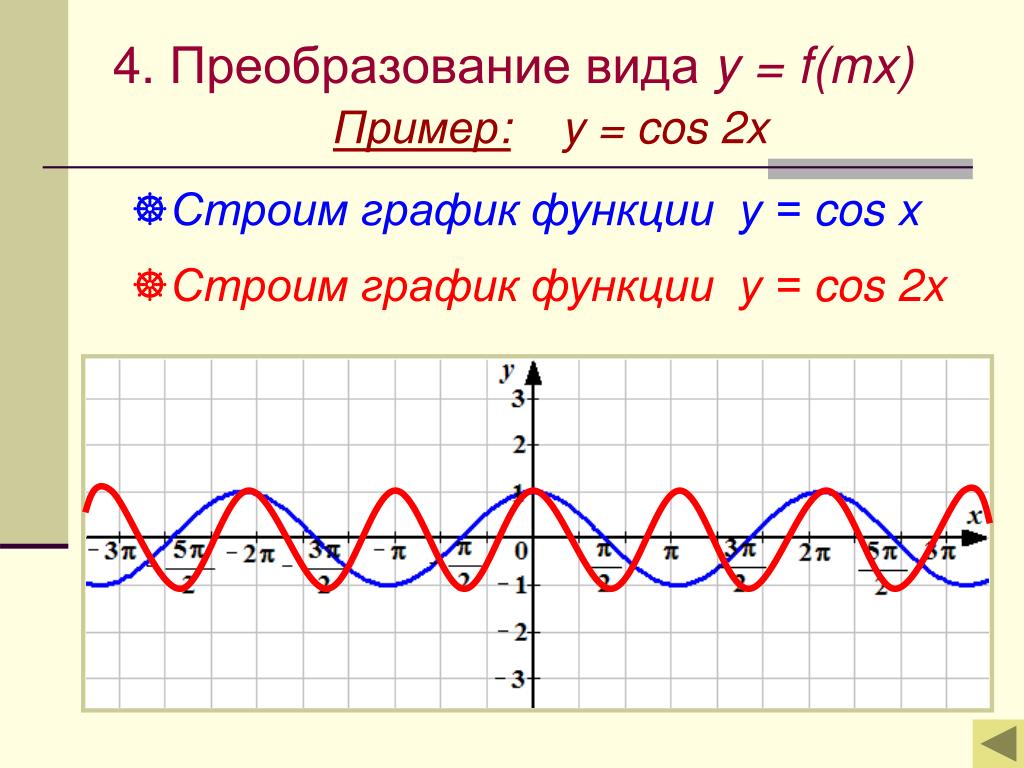 Кто упадёт первым?
Кто упадёт первым? .. ⋅ a
n разів
для a ∈ R, n ∈ N, n 2
a0
= 1, де а ≠ 0 a2
= а
a–n
=
1
—
аn для а ≠ 0, n ∈ N
a
m
—
n
= am
n
, а > 0, m ∈ Z, n ∈ N, n 2
ax
⋅ ay
= ax + y аx
—
аy = ax – y
(ax
)y
= ax ⋅ y
(ab)x
= ax
⋅ bx
(a
–
b)
x
=
аx
—
bx
a > 0, а ≠ 1, b > 0, c > 0, k ≠ 0
alogab
= b logаа = 1 logа1 = 0
logа(b ⋅ c) = logаb + logаc
logа
b
–
c = logаb – logаc
logаbn
= n ⋅ logаb
logаk b = 1
–
k
⋅ logаb
an = a1 + d(n – 1) Sn =
a1 + аn
—
2
⋅ n
Pn = 1 ⋅ 2 ⋅ 3 ⋅ … ⋅ n = n! C
k
n =
n!
—
k! ⋅ (n – k)!
Ak
n =
n!
—
(n – k)!
P(A) =
k
–
n
bn = b1 ⋅ qn – 1
Sn =
b1(qn
– 1)
—
q – 1
, (q ≠ 1)
a =
a, якщо а 0,
–a, якщо а < 0
.. ⋅ a
n разів
для a ∈ R, n ∈ N, n 2
a0
= 1, де а ≠ 0 a2
= а
a–n
=
1
—
аn для а ≠ 0, n ∈ N
a
m
—
n
= am
n
, а > 0, m ∈ Z, n ∈ N, n 2
ax
⋅ ay
= ax + y аx
—
аy = ax – y
(ax
)y
= ax ⋅ y
(ab)x
= ax
⋅ bx
(a
–
b)
x
=
аx
—
bx
a > 0, а ≠ 1, b > 0, c > 0, k ≠ 0
alogab
= b logаа = 1 logа1 = 0
logа(b ⋅ c) = logаb + logаc
logа
b
–
c = logаb – logаc
logаbn
= n ⋅ logаb
logаk b = 1
–
k
⋅ logаb
an = a1 + d(n – 1) Sn =
a1 + аn
—
2
⋅ n
Pn = 1 ⋅ 2 ⋅ 3 ⋅ … ⋅ n = n! C
k
n =
n!
—
k! ⋅ (n – k)!
Ak
n =
n!
—
(n – k)!
P(A) =
k
–
n
bn = b1 ⋅ qn – 1
Sn =
b1(qn
– 1)
—
q – 1
, (q ≠ 1)
a =
a, якщо а 0,
–a, якщо а < 0
