Ctg cos sin: Основные тригонометрические тождества sin, cos, tg, ctg

найдите sin a cos a ctg a если tg a 16 — Учеба и наука

Ответы

17. 03.21

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Решено

Начертите треугольник АВС.

Постройте вектор: 1) АС+СВ 2)ВА-ВС 3)АС+АВ

Здравствуйте! Прошу помощи! Алеша сказал: «У Змея Горыныча больше трех голов». Добрыня сказал: » У Змея больше 4-х голов». Илья сказал:»У Змея больше

Периметр правильного треугольника, вписанного в окружность, равен 6√3 дм. Найдите периметр правильного шестиугольника описанного около той же окружности.

На окружности с центром в точке О по порядку отмечены 4 точки: D, H, L, P. Найди вторую сторону получившегося четырехугольника, если угол D=90

Вычислите длину дуги окружности с радиусом 4см,если ее градусная мера равна 120 градусов.Чему равна площадь соответствующего данной дуге

Пользуйтесь нашим приложением

Мэтуэй | Популярные задачи

92-4*-1+2 92

1	Найти том	сфера (5)	
2	Найти площадь	круг (5)	
3	Найдите площадь поверхности	сфера (5)	
4	Найти площадь	круг (7)	
5	Найти площадь	круг (2)	
6	Найти площадь	круг (4)	
7	Найти площадь	круг (6)	
8	Найти том	сфера (4)	
9	Найти площадь	круг (3)	
10 9(1/2)
11	Найти простую факторизацию	741
12	Найти том	сфера (3)	
13	Оценить	3 квадратный корень из 8*3 квадратный корень из 10
14	Найти площадь	круг (10)	
15	Найти площадь	круг (8)	
16	Найдите площадь поверхности	сфера (6)	
17	Найти простую факторизацию	1162
18	Найти площадь	круг (1)	
19	Найдите окружность	круг (5)	
20	Найти том	сфера (2)	
21	Найти том	сфера (6)	
22	Найдите площадь поверхности	сфера (4)	
23	Найти том	сфера (7)	
24	Оценить	квадратный корень из -121
25	Найти простую факторизацию	513
26	Оценка	квадратный корень из 3/16* квадратный корень из 3/9
27	Найти том	коробка (2)(2)(2)	
28	Найдите окружность	круг (6)	
29	Найдите окружность	круг (3)	
30	Найдите площадь поверхности	сфера (2)	
31	Оценить	2 1/2÷22000000
32	Найдите Том	коробка (5)(5)(5)	
33	Найти том	коробка (10)(10)(10)	
34	Найдите окружность	круг (4)	
35	Преобразование в проценты	1,7
36	Оценить	(5/6)÷(4/1)
37	Оценить	3/5+3/5
38	Оценить	ф(-2)	92
40	Найти площадь	круг (12)	
41	Найти том	коробка (3)(3)(3)	
42	Найти том	коробка (4)(4)(4)
45	Найти простую факторизацию	228
46	Оценить	0+0
47	Найти площадь	круг (9)	
48	Найдите окружность	круг (8)	
49	Найдите окружность	круг (7)	
50	Найти том	сфера (10)	
51	Найдите площадь поверхности	сфера (10)	
52	Найдите площадь поверхности	сфера (7)	
53	Определить, является простым или составным	5
60	Преобразование в упрощенную дробь	2 1/4
61	Найдите площадь поверхности	сфера (12)	
62	Найти том	сфера (1)	
63	Найдите окружность	круг (2)	
64	Найти том	коробка (12)(12)(12)	
65	Добавить	2+2=
66	Найдите площадь поверхности	коробка (3)(3)(3)	
67	Оценить	корень пятой степени из 6* корень шестой из 7
68	Оценить	7/40+17/50
69	Найти простую факторизацию	1617
70	Оценить	27-(квадратный корень из 89)/32
71	Оценить	9÷4
72	Оценка 92
74	Оценить	1-(1-15/16)
75	Преобразование в упрощенную дробь	8
76	Оценка	656-521	9-2
79	Оценить	4-(6)/-5
80	Оценить	3-3*6+2
81	Найдите площадь поверхности	коробка (5)(5)(5)	
82	Найдите площадь поверхности	сфера (8)	
83	Найти площадь	круг (14)	
84	Преобразование в десятичное число	5 ноября
85 9-2
88	Оценить	1/2*3*9
89	Оценить	4/4-17/-4
90	Оценить	11. 02+17.19
91	Оценить	3/5+3/10
92	Оценить	4/5*3/8
93	Оценить	6/(2(2+1))
94	Упростить	квадратный корень из 144
95	Преобразование в упрощенную дробь	725%
96	Преобразование в упрощенную дробь	6 1/4
97	Оценить	7/10-2/5
98	Оценить	6÷3
99	Оценить	5+4
100	Оценить	квадратный корень из 12- квадратный корень из 192

Funkcje trygonometryczne zmiennej rzeczywistej — baza wiedzy

W 1 klasie są omawiane funkcje trygonometryczne kąta skierowanego.
Прзыпомний к загадке:

Wtedy:
1) sinα =
2) cosα =
3) tgα = , gdzie x≠0
4) ctgα = , gdzie y≠0
Wiadomo że dziedziną funkcji sinus i cosinus są liczby rzeczywiste, a funkcji tangens liczby rzeczywiste z wyjątkiem π/2 +kπ , k. Wynika to z wykresów tych funkcji.

Podstawowe tożsamości trygonometryczne:

Przykład 1.

Wiedząc, że tgα = — i α, obliczymy sinα, cosα, ctgα.

Zacznijmy od obliczenia ctgα:

Wiadomo że ctgα = , zatem ctgα =-

Następnie obliczymy sinα oraz cosα:

 

Korzystając z własności 1) oraz 2), tworzymy układ równań i rozwiązujemy go:
 

12 sinα = -5 cosα /:12

 /144

169  = 144 /:169

 oraz α, затем cosα < 0

Одп. Szukane wartości: , , ctgα = — .

Пшедставмы взоры redukcyjne, umożliwią nam one rozwiązywanie równań jak i później nierówności тригонометрический.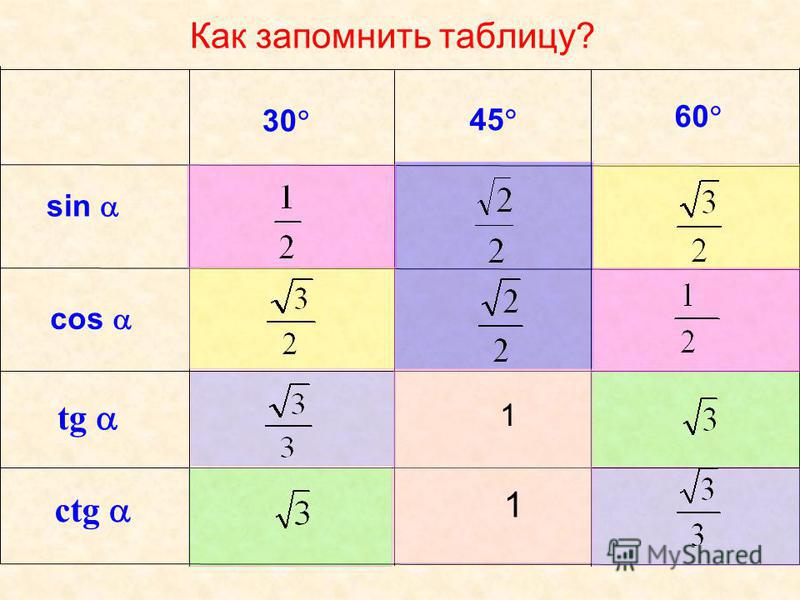 Są to wzory umożliwiające zapisanie większych na pierwszy rzut oka trudnych wartości funkcji trygonometrycznych za pomocą mniejszych argumentsów o znanych nam wartościach.

Na co należy zwrócić uwagę korzystając z wzorów redukcyjnych?

Znane wartości kątowe. Zawsze próbujemy do nich sprowadzić wyrażenie.

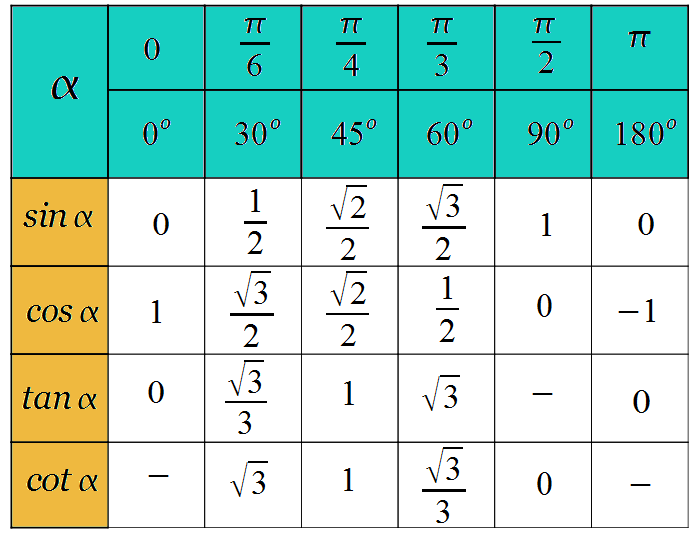
х	0
синх	0				1
cosx	1				0
тгх	0		1		Не истек
КТГХ	Не истек		1		0

Znak wyrażenia. Залежи на od ćwiartki w której znajduję się dana wartość.

Чвяртка	я	II	III	IV
синх	+	+	—	—
cosx	+	—	—	+
тгх	+	—	+	—
ктх	+	—	+	—

Uwaga: Przydatna w zapamiętywaniu znaku funkcji trygonometrycznych jest rymowanka „w pierwszej wszystkie są dodatnie, w othertylko sinus, w trzeciej tangens i cotangens a w czwartej косинус.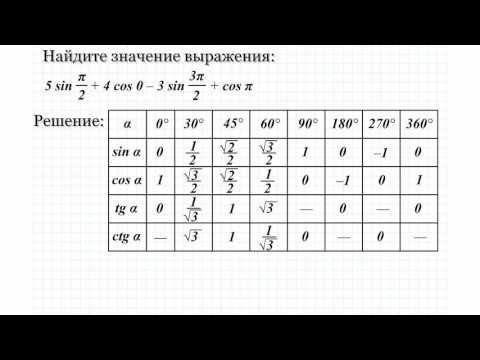

3. Jeżeli we wzorze znajduje się nieparzysta wielokrotność   + α lub   , to funkcja zmienia się na кофе Oznacza to że sinus zmienia się na cosinus, a tangens zmienia się na котангенс. С инным выпадку функця позостае без змян.

 

                            

Przykład 2.

Obliczymy wartość wyrażeń:
а)                                 б)

 

Rozwiązanie:

   

(Шутка к И.В. Чвяртке, затем cosα > 0)

1

(Шутка к III Чвяртке, затем тга > 0 )

   =

Ad б.

) = sin() = sin(π —

) = ctg() = — 
2.   + 1

 

Оконечная функция тригонометрический

Пршипомниумы определение funkcji okresowej:
Funkcje nazywamy okresową wtedy i tylko wtedy, gdy istnieje taka liczba T różna od zera, że ​​dla każdej liczby x należącej do dziedziny funkcji f liczba x + T наложение дзедзины на их функции или заходы в руны f(x + T) = f(x), gdzie T jest okresem funkcji f. Jeśli istnieje najmniejszy okres dodatni funkcji, nazywamy go okresem podstawowym(zasadniczym).

Окрес подставных функций sinus oraz cosinus jest liczba 2π, zapisujemy to: T0= 2π , затем

sin(2π +x) = sinx или раз cos(2π + x) = cosx             , x

Okresem podstawowym funkcji tangens oraz cotangens jest π, zapisujemy to : T0= π , zatem

tg(π + x ) = tgx , x —

ctg(π + x ) = ctgx , x —

Przykłic 5 подставной funkcji:

f(x) = sin(5x)                      b)cos(

Rozwiązanie:

T0 – okres podstawowy funkcji f, zatem:

f(x + T0) = sin[5(x + T0)]= sin(5x + 5T0)

Funkcja f jest okresowa zatem zachodzi równość: f(x + T0) = f(x), otrzymujemy

sin(5x + 5T0) = sin5x,

wprowadzam zmienną α = 5x, więc sin(α +5T0) = sinα

Okresemm funkcji sinus jest 2π, zatem 5T0 = 2π, więc T0 =

Odp: Okresem podstawowym funkcji f(x) = sin(5x) jest liczba .

Парзистоць и nieparzystość funkcji trygonometrycznych

Warunek parzystość функции: f(-x) = f(x)
Warunek nieparzystości funkcji: f(-x) = -f(x)
Jest to prawdziwe jeśli x oraz -x należą do tej samej dziedziny.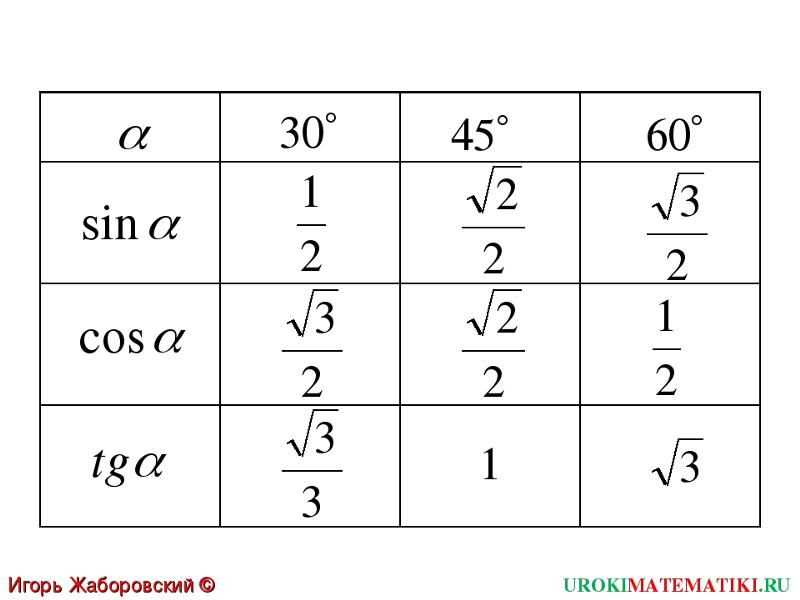
Warto zauważyć, że:
funkcja y = cos x jest funkcją parzystą, dla x ∈ R, ponieważ cos(x) = cos(-x)
posostałe funkcje są funkcjami nieparzystymi.

Zbiór wartości funkcji trygonometrycznych

Zbiorem wartości funkcji;
sinus oraz cosinus jest przedział liczb <-1,1>
tangens oraz cotangens jest zbiór liczb rzeczywistych.

Przykład 4

Wyznaczmy zbiór wartości функция f(x) =

Wiadomo że, -1≤ cos2x ≤1 ,

Musimy przekształcić nierówność w sposób równoważy tak abyśmy pośrodku otrzymali naszą zadaną функция.

-1≤ cos2x  ≤1 /

-≤ cos2x  ≤/-3

—3 ≤ cos2x — 3  ≤- 3

Odp: Zbiorem wartości jest przedział liczbowy <--3, -3>.

Zadania do zrobienia

1. Wyznacz pozostałe wartości funkcji trygonometrycznych kąta , , jeśli:

а) cos =

 

909:50 б) тг =

 

опр. а) lub

 

                б) lub

 

2.