100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
Единое национальное тестирование
История Казахстана
Онлайн тесты и шпаргалки по истории Казахстана
Далее
Всемирная история
Онлайн тесты и шпаргалки по Всемирной истории.
Далее
Математика
Онлайн тесты и шпаргалки по математике.
Далее
Химия
Онлайн тесты и шпаргалки по химии.
Далее
Физика
Онлайн тесты и шпаргалки по физике.
Далее
Биология
Онлайн тесты и шпаргалки по биологии.
Далее
География
Онлайн тесты и шпаргалки по географии.
Далее
Русский язык
Онлайн тесты и шпаргалки по русскому языку.
Далее
Готовые работы
ДИПЛОМНЫЕ РАБОТЫ
Многое уже позади и теперь ты — выпускник, если, конечно, вовремя напишешь дипломную работу.
Но жизнь — такая штука, что только сейчас тебе становится понятно, что, перестав быть студентом, ты потеряешь все студенческие
радости, многие из которых, ты так и не попробовал, всё откладывая и откладывая на потом. И теперь, вместо того, чтобы навёрстывать упущенное, ты корпишь над дипломной работой? Есть отличный выход: скачать нужную тебе дипломную
работу с нашего сайта — и у тебя мигом появится масса свободного времени!
Дипломные работы успешно защищены в ведущих Университетах РК.
Стоимость работы от 20 000 тенге
Перейти
КУРСОВЫЕ РАБОТЫ
Курсовой проект — это первая серьезная практическая работа. Именно с написания курсовой начинается подготовка к разработке дипломных проектов. Если студент научиться правильно излагать содержание темы в курсовом проекте
и грамотно его оформлять, то в последующем у него не возникнет проблем ни с написанием отчетов, ни с составлением дипломных работ, ни с выполнением других практических заданий.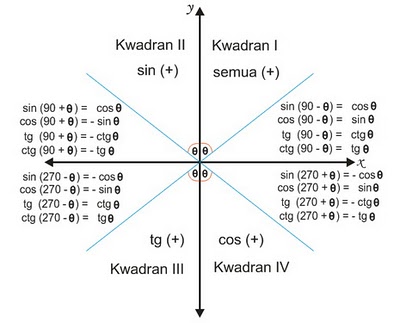
Стоимость работы от 2 500 тенге
Перейти
МАГИСТЕРСКИЕ ДИССЕРТАЦИИ
В настоящее время в высших учебных заведениях Казахстана и стран СНГ очень распространена ступень высшего профессионального образования, которая следует после бакалавриата — магистратура. В магистратуре обучаются с
целью получения диплома магистра, признаваемого в большинстве стран мира больше, чем диплом бакалавра, а также признаётся зарубежными работодателями. Итогом обучения в магистратуре является защита магистерской диссертации.
Стоимость работы от 35 000 тенге
Перейти
ОТЧЕТЫ ПО ПРАКТИКЕ
После прохождения любого типа студенческой практики (учебной, производственной, преддипломной) требуется составить отчёт.
Этот документ будет подтверждением практической работы студента и основой формирования оценки
за практику. Обычно, чтобы составить отчёт по практике, требуется собрать и проанализировать информацию о предприятии, рассмотреть структуру и распорядок работы организации, в которой проходится практика, составить календарный
план и описать свою практическую деятельность.
Перейти
Пропустить новости сайта
Новости сайта
Пропустить Навигация Пропустить Меню блога
- Просмотр всех записей
Назад
Вы не вошли в систему (Вход)
Котангенс | это… Что такое Котангенс?
Рис. 1
Графики тригонометрических функций: синуса, косинуса, тангенса, секанса, косеканса, котангенса
Тригонометрические функции — вид элементарных функций.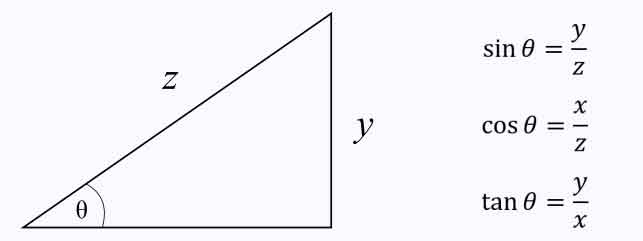
Содержание
|
4 Определение тригонометрических функций через рядыСпособы определения
Геометрическое определение
Рис. 2
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически. Пусть дана декартова система координат на плоскости и построена окружность радиуса R с центром в начале координат O. Будем измерять углы как повороты от положительного направления оси абсцисс до луча OB. Направление против часовой стрелки считается положительным, по часовой стрелке отрицательным.
Абсциссу точки В обозначим xB, ординату обозначим yB (см. рисунок.)
- Синусом называется отношение
- Косинусом называется отношение
- Тангенс определяется как
- Котангенс определяется как
- Секанс определяется как
- Косеканс определяется как
Рис. 3.
Тригонометрические функции угла α в тригонометрической окружности с радиусом, равным единице.
Ясно, что значения тригонометрических функций не зависят от величины радиуса окружности R в силу свойств подобных фигур. Часто этот радиус принимают равным величине единичного отрезка, тогда синус равен просто ординате
Если α — действительное число, то синусом α в математическом анализе называется синус угла, радианная мера которого равна α, аналогично для прочих тригонометрических функций.
Определение тригонометрических функций для острых углов
Рис. 4.
Тригонометрические функции острого угла
Во многих учебниках элементарной геометрии до настоящего времени тригонометрические функции острого угла определяются как отношения сторон прямоугольного треугольника. Пусть OAB — треугольник с углом α. Тогда:
- Синусом α называется отношение AB/OB (противолежащего катета к гипотенузе)
- Косинусом α называется отношение ОА/OB (прилежащего катета к гипотенузе)
- Тангенсом α называется отношение AB/OA (отношение противолежащего катета к прилежащему)
- Котангенсом α называется отношение ОА/AB (отношение прилежащего катета к противолежащему)
- Секансом α называется отношение ОB/OA (гипотенузы к прилежащему катету)
- Косекансом α называется отношение ОB/AB (гипотенузы к противолежащему катету)
Построив систему координат с началом в точке O, направлением оси абсцисс вдоль OA и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее.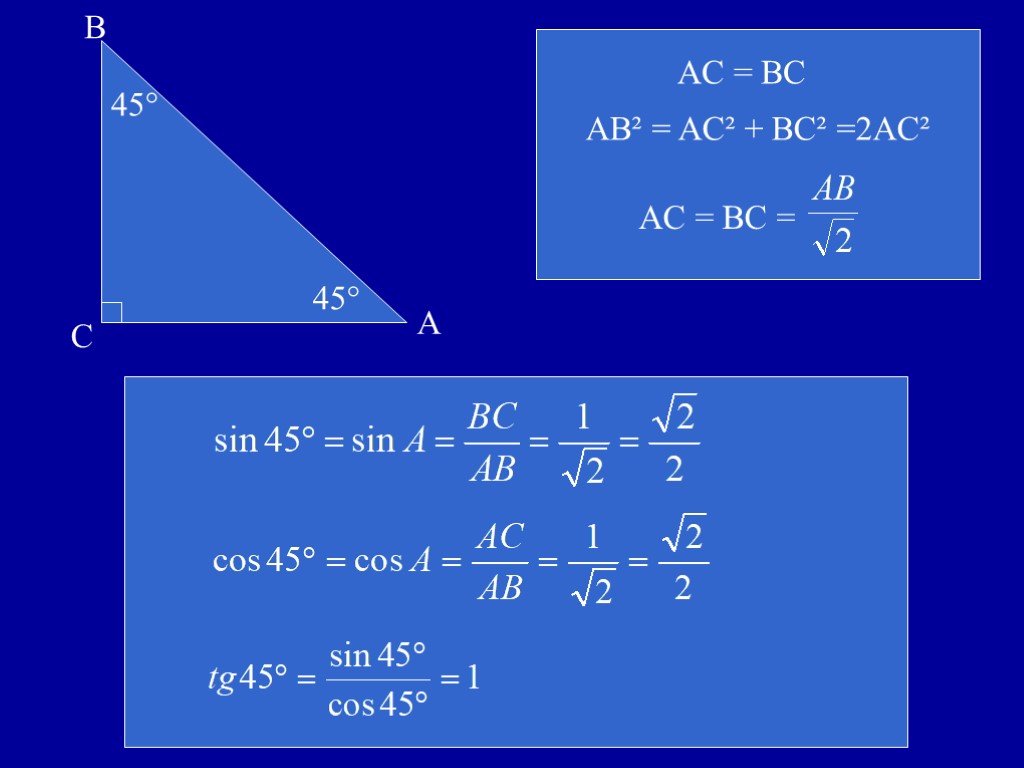
Данное определение имеет некоторое педагогическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач про тупоугольные треугольники (см. Теорема синусов, Теорема косинусов).
Определение тригонометрических функций как решений дифференциальных уравнений
Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решение дифференциального уравнения
с начальными условиями cos(0) = sin'(0) = 1, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:
Определение тригонометрических функций как решений функциональных уравнений
Функции косинус и синус можно определить как непрерывные решения (f и g соответственно) системы функциональных уравнений:
Определение тригонометрических функций через ряды
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу и что производная косинуса равна минус синусу.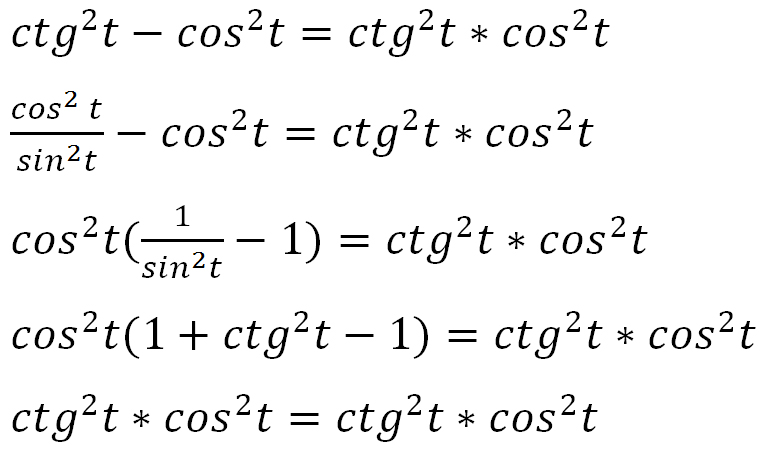
Пользуясь этими формулами, а также уравнениями и можно найти разложения в ряд Тейлора и других тригонометрических функций:
- где Bn — числа Бернулли.
- где En — числа Эйлера.
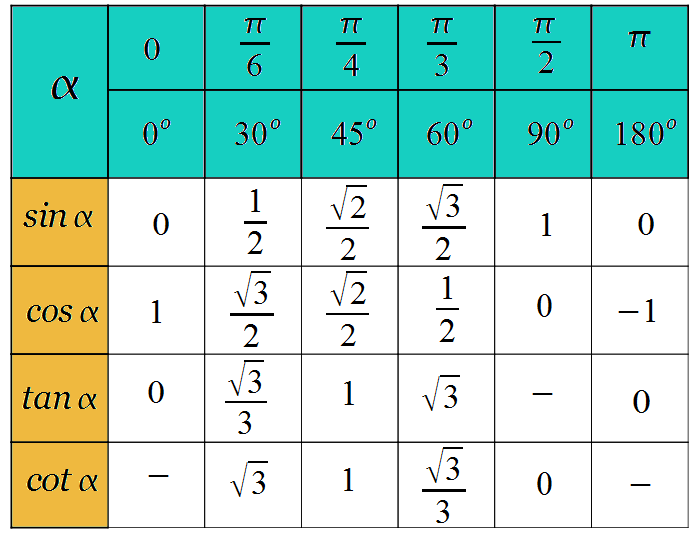
Значения тригонометрических функций для некоторых углов
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице.
Значения косинуса и синуса на окружности.
| 0°(0 рад) | 30° (π/6) | 45° (π/4) | 60° (π/3) | 90° (π/2) | 180° (π) | 270° (3π/2) | 360° (2π) | |
|---|---|---|---|---|---|---|---|---|
Значения тригонометрических функций нестандартных углов
Свойства тригонометрических функций
Простейшие тождества
Так как синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
Деля это уравнение на квадрат косинуса и синуса соответственно имеем далее:
Чётность
Косинус и секанс — чётные.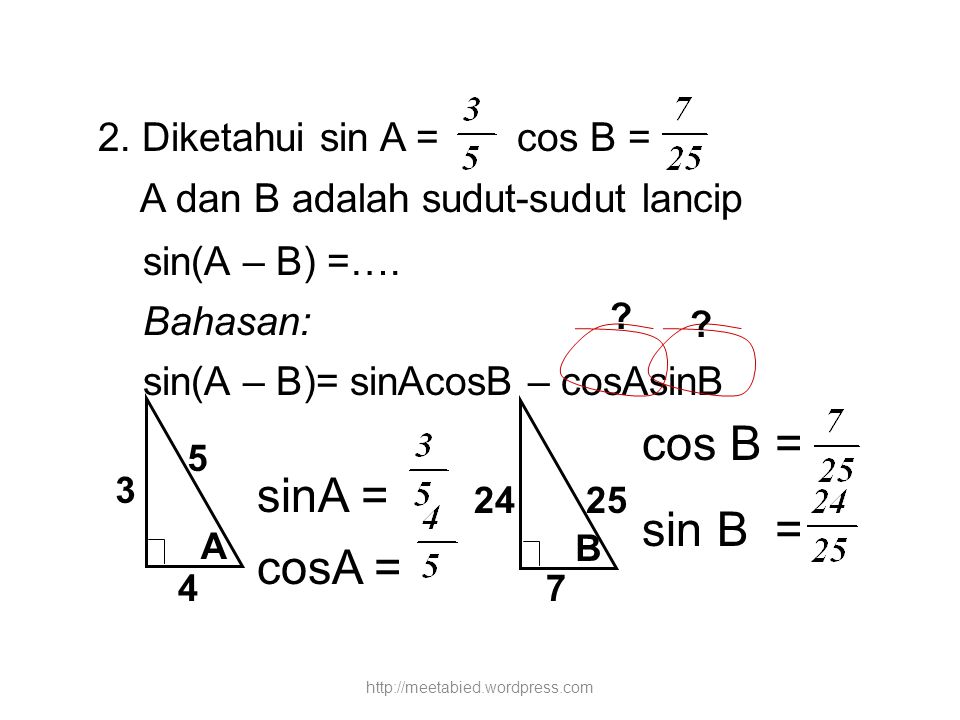
Остальные четыре функции — нечётные, то есть:
Периодичность
Функции y = sin α, y = cos α, y = sec α, y = cosec α — периодические с периодом 2π. Функции: y = tg α, y = ctg α — c периодом π
Формулы приведения
Здесь f — любая тригонометрическая функция, g — соответствующая ей другая функция из пары (то есть косинус для синуса, синус для косинуса и аналогично для остальных функций). Нужный знак в правой части равенства определяется следующим образом: предположим что угол α находится в первой четверти, тогда определяем знаки значений функций в левой и правой части равенства и в случае их несовпадения перед правой частью пишем знак -, например:
Формулы сложения
Другие тригонометрические тождества.
Однопараметрическое представление
Все тригонометрические функции можно выразить через тангенс половинного угла.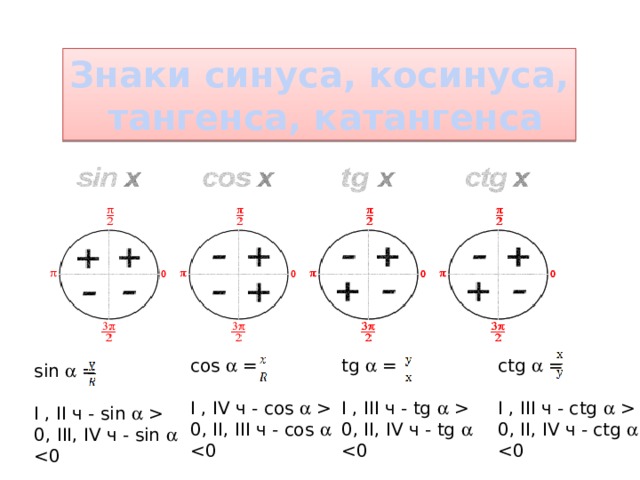
Производные и интегралы
Все тригонометрические функции непрерывно дифференцируемы на всей области определения:
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом:
- См. также Список интегралов от тригонометрических функций
История
Линия синуса у индийских математиков первоначально называлась «арха-джива» («полутетива»), затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские переводчики не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали арабскими буквами и стали называть линию синуса «джиба». Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса «джайб», что буквально обозначает «впадина», «пазуха».
При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus, имеющим то же значение.
Современное обозначение синуса sin и косинуса cos введено Леонардом Эйлером в XVIII веке.
Термины «тангенс» (от лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке (1561—1656) в его книге «Геометрия круглого» (Geometria rotundi, 1583)
Сам термин тригонометрические функции введён Клюгелем в 1770.
См. также
- Гиперболические функции
- Обратные тригонометрические функции
- Редко используемые тригонометрические функции
- Эллиптические функции
- Теорема косинусов
- Теорема синусов
- Тригонометрические формулы
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Функция Гудермана связывает тригонометрические функции и гиперболические функции без привлечения комплексных чисел.
Ссылки
- GonioLab: Проясненная Единичная Окружность, Тригонометрические и Гиперболические функции (Java Web Start)
- Weisstein, Eric W. Тригонометрические функции на сайте Wolfram MathWorld.(англ.)
- Онлайн калькулятор: вычисление значений тригонометрических функций
Что такое синус, косинус, тангенс и котангенс / 5-Minute Crafts
В математике тригонометрические функции используются для определения острых углов прямоугольного треугольника. Для этого вычисляются отношения его сторон, катетов и гипотенузы.
Гипотенуза — самая длинная сторона прямоугольного треугольника, противоположная прямому углу. Катеты — это две другие стороны, которые вместе составляют угол 90°. Катет, расположенный рядом с острым углом, который необходимо вычислить, называется смежной ножкой, тот, который расположен напротив, называется противоположной ножкой.
Тригонометрические функции используются во многих научных областях. Например, в астрономии для вычисления местоположения небесных тел или в геодезии — для вычисления длин, площадей и относительных углов между объектами.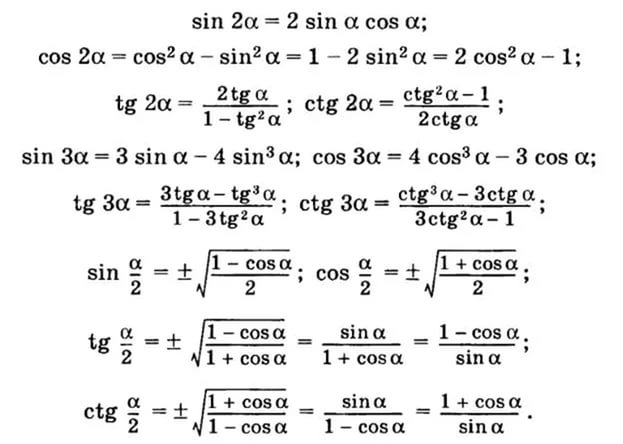
5-Minute Crafts хочет рассказать вам о наиболее часто используемых тригонометрических функциях (синус, косинус и тангенс) и их обратных функциях (косеканс, секанс и котангенс).
1. Синус
Синус острого угла прямоугольного треугольника равен отношению противолежащего катета к гипотенузе. Для треугольника AOB формула sin α = AB / OB .
2. Косинус
Косинус острого угла прямоугольного треугольника равен отношению прилежащего катета к гипотенузе. Для треугольника AOB используется формула , потому что α = OA / OB .
3. Тангенс
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему. Для треугольника AOB формула такова: tg α = AB / OA .
Тангенс — это производная функция, которую также можно вычислить путем деления синуса на косинус. Формула тг α = sin α / cos α .
4. Котангенс
Котангенс острого угла прямоугольного треугольника равен отношению прилежащего катета к противолежащему. Для треугольника AOB используется формула ctg α = OA / AB .
Котангенс — производная функция, которую также можно вычислить путем деления косинуса на синус. Формула: ctg α = cos α / sin α .
5. Секанс
Секанс острого угла прямоугольного треугольника равен отношению гипотенузы к прилежащему катету. Для треугольника АОВ формула сек α = ОВ/ОА .
Секанс — это производная функция, которую также можно вычислить путем деления единицы на косинус острого угла. Формула: сек α = 1 / cos α .
6. Косеканс
Косеканс острого угла прямоугольного треугольника равен отношению гипотенузы к противолежащему катету.
Для треугольника AOB формула cosec α = OB / AB .
Косеканс — это производная функция, которую также можно вычислить путем деления единицы на синус острого угла. Формула: cosec α = 1 / sin α .
5-Minute Crafts/Tech/What Sine, Cosine, Tangent, and Cotangent Are All About
Share This Article
Online calculator: Trigonometric functions
Study Math Geometry
Этот онлайн-калькулятор вычисляет значения элементарных тригонометрических функций, таких как sin, cos, tg, ctg, sec, cosec для угла, который может быть задан в градусах, радианах или градах.
Элементарные функции Тригонометрические функции представляют собой набор элементарных функций, связывающих углы треугольника с длинами сторон треугольника. Их также называют круговыми функциями. Смотрите картинку.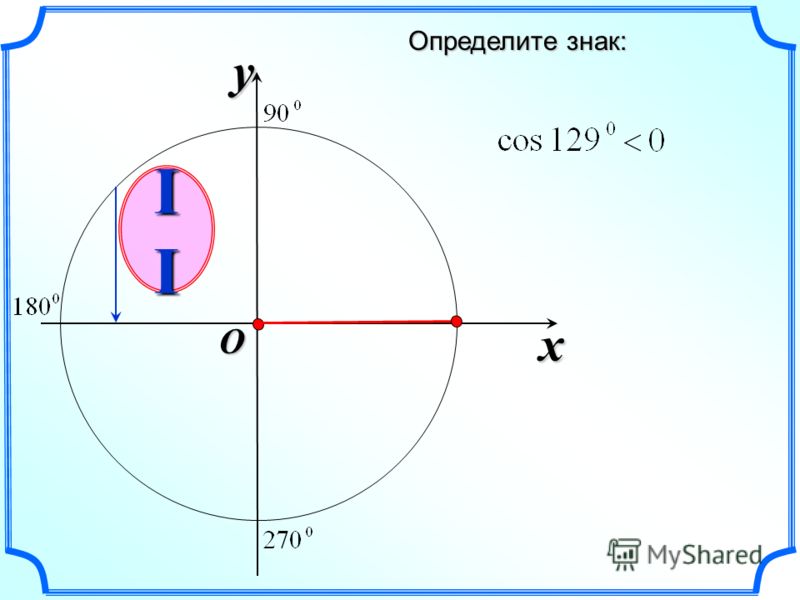
The trigonometric functions are:
sin — sine
cos — cosine
tg — tangent
ctg — cotangent
sec — secant
cosec — cosecant
versin — versine ( с синусоидой)
Vercos — Vercosine (Versed Cosine)
Haversin — Haversed Sine
Exsec — Exsecant
Excsc — Excosecant
— Получите эти функции, введите значение на угла в -alles результатов. Угол может быть введен в градусах, радианах, градах, минутах или секундах.
Тригонометрические функции
Единицы
Градусы
Радианы
Минуты
Секунды
Точность вычислений
Число знаков после запятой: 10
Файл очень большой.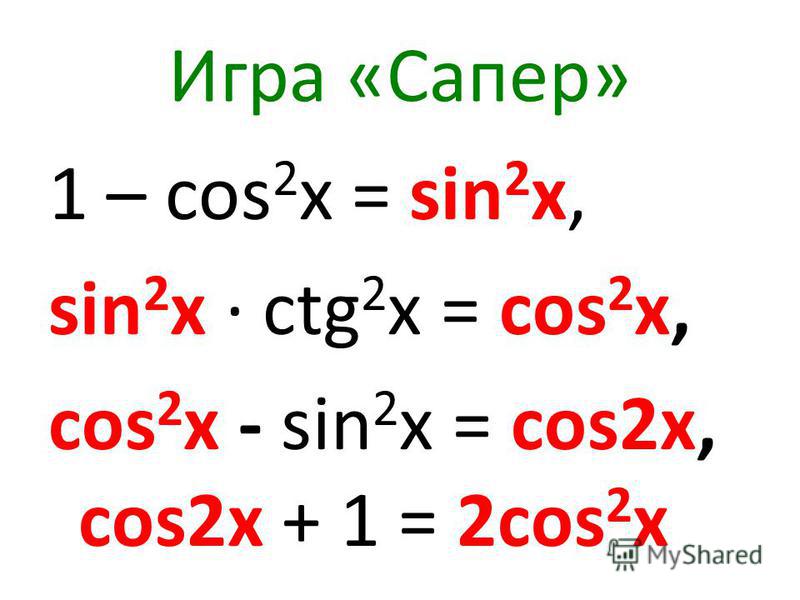
Во время загрузки и создания может происходить замедление работы браузера.
Ну, немного школьной теории.
Синус угла ( sin ) есть отношение длины противоположной стороны к длине гипотенузы.
Косинус угла (cos) есть отношение длины прилежащей стороны к длине гипотенузы.
Все остальные функции выражаются через синус и косинус следующим образом:
Тангенс:
(отношение длины противолежащей стороны к длине прилежащей стороны)
Котангенс:
(отношение длины прилежащей стороны к длине противолежащей стороны)
Секанс:
( отношение длины гипотенузы к длине прилежащего катета)
Косеканс:
(отношение длины гипотенузы к длине противолежащего катета)
Прочие тригонометрические функции:
Обратный синус:
Покрытый синус:
Наборный синус:
Exsecant:
Excosecant:
URL, скопированный в буфер обмена
Аналогичные калькуляторы
- • Математический калькулятор
- • Проблемы с лимитом решания.
