Ctg формулы: определение, формула, таблица, график, свойства

Содержание

формулы cos, sin, tg, ctg

Основные формулы тригонометрии — это формулы, устанавливающие связи между основными тригонометрическими функциями. Синус, косинус, тангенс и котангенс связаны между собой множеством соотношений. Ниже приведем основные тригонометрические формулы, а для удобства сгруппируем их по назначению. С использованием данных формул можно решить практически любую задачу из стандартного курса тригонометрии. Сразу отметим, что ниже приведены лишь сами формулы, а не их вывод, которому будут посвящены отдельные статьи.

Основные тождества тригонометрии

Тригонометрические тождества дают связь между синусом, косинусом, тангенсом и котангенсом одного угла, позволяя выразить одну функцию через другую.

Тригонометрические тождества

sin2a+cos2a=1tgα=sinαcosα, ctgα=cosαsinαtgα·ctgα=1tg2α+1=1cos2α, ctg2α+1=1sin2α

Эти тождества напрямую вытекают из определений единичной окружности, синуса (sin), косинуса (cos), тангенса (tg) и котангенса (ctg).

Формулы приведения

Формулы приведения позволяют переходить от работы с произвольными и сколь угодно большими углами к работе с углами в пределах от 0 до 90 градусов.

Формулы приведения

sinα+2πz=sinα, cosα+2πz=cosαtgα+2πz=tgα, ctgα+2πz=ctgαsin-α+2πz=-sinα, cos-α+2πz=cosαtg-α+2πz=-tgα, ctg-α+2πz=-ctgαsinπ2+α+2πz=cosα, cosπ2+α+2πz=-sinαtgπ2+α+2πz=-ctgα, ctgπ2+α+2πz=-tgαsinπ2-α+2πz=cosα, cosπ2-α+2πz=sinαtgπ2-α+2πz=ctgα, ctgπ2-α+2πz=tgαsinπ+α+2πz=-sinα, cosπ+α+2πz=-cosαtgπ+α+2πz=tgα, ctgπ+α+2πz=ctgαsinπ-α+2πz=sinα, cosπ-α+2πz=-cosαtgπ-α+2πz=-tgα, ctgπ-α+2πz=-ctgαsin3π2+α+2πz=-cosα, cos3π2+α+2πz=sinαtg3π2+α+2πz=-ctgα, ctg3π2+α+2πz=-tgαsin3π2-α+2πz=-cosα, cos3π2-α+2πz=-sinαtg3π2-α+2πz=ctgα, ctg3π2-α+2πz=tgα

Формулы приведения являются следствием периодичности тригонометрических функций.

Тригонометрические формулы сложения

Формулы сложения в тригонометрии позволяют выразить тригонометрическую функцию суммы или разности углов через тригонометрические функции этих углов.

Тригонометрические формулы сложения

sinα±β=sinα·cosβ±cosα·sinβcosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβtgα±β=tgα±tgβ1±tgα·tgβctgα±β=-1±ctgα·ctgβctgα±ctgβ

На основе формул сложения выводятся тригонометрические формулы кратного угла.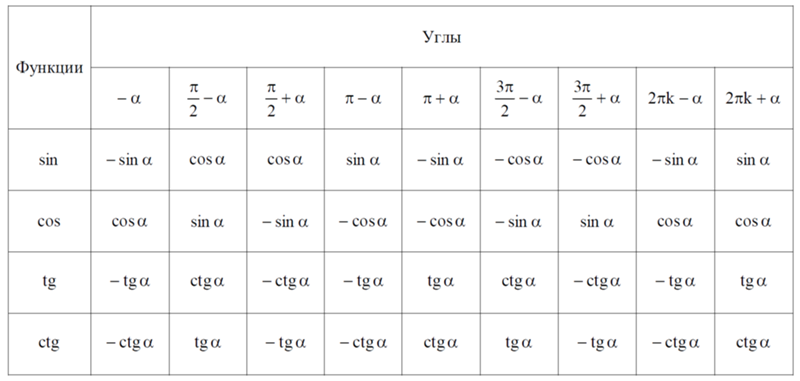

Формулы кратного угла: двойного, тройного и т.д.

Формулы двойного и тройного угла

sin2α=2·sinα·cosαcos2α=cos2α-sin2α, cos2α=1-2sin2α, cos2α=2cos2α-1tg2α=2·tgα1-tg2α сtg2α=сtg2α-12·сtgα sin3α=3sinα·cos2α-sin3α, sin3α=3sinα-4sin3αcos3α=cos3α-3sin2α·cosα, cos3α=-3cosα+4cos3αtg3α=3tgα-tg3α1-3tg2αctg3α=ctg3α-3ctgα3ctg2α-1

Формулы половинного угла

Формулы половинного угла в тригонометрии являются следствием формул двойного угла и выражают соотношения между основными функциями половинного угла и косинусом целого угла.

Формулы половинного угла

sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα

Формулы понижения степени

sin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8

Часто при расчетах действовать с громоздктми степенями неудобно. Формулы понижения степени позволяют понизить степень тригонометрической функции со сколь угодно большой до первой. Приведем их общий вид:

Общий вид формул понижения степени

для четных n

sinnα=Cn2n2n+12n-1∑k=0n2-1(-1)n2-k·Ckn·cos((n-2k)α)cosnα=Cn2n2n+12n-1∑k=0n2-1Ckn·cos((n-2k)α)

для нечетных n

sinnα=12n-1∑k=0n-12(-1)n-12-k·Ckn·sin((n-2k)α)cosnα=12n-1∑k=0n-12Ckn·cos((n-2k)α)

Сумма и разность тригонометрических функций

Разность и сумму тригонометрических функций можно представить в виде произведения. Разложение на множители разностей синусов и косинусов очень удобно применять при решении тригонометрических уравнений и упрощении выражений.

Сумма и разность тригонометрических функций

sinα+sinβ=2sinα+β2·cosα-β2sinα-sinβ=2sinα-β2·cosα+β2cosα+cosβ=2cosα+β2·cosα-β2cosα-cosβ=-2sinα+β2·sinα-β2, cosα-cosβ=2sinα+β2·sinβ-α2

Произведение тригонометрических функций

Если формулы суммы и разности функций позволяют перейти к их произведению, то формулы произведения тригонометрических функций осуществляют обратный переход — от произведения к сумме. Рассматриваются формулы произведения синусов, косинусов и синуса на косинус.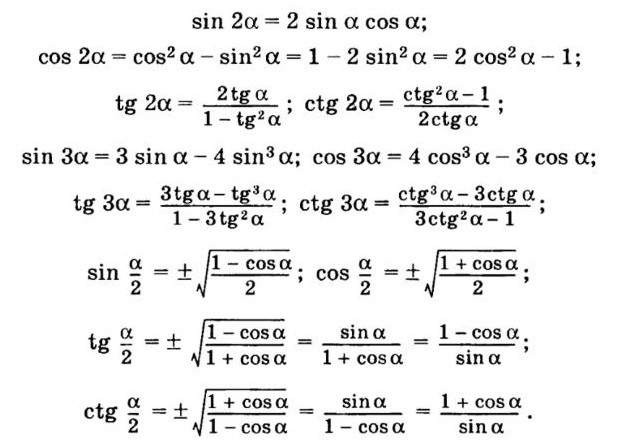

Формулы произведения тригонометрических функций

sinα·sinβ=12·(cos(α-β)-cos(α+β))cosα·cosβ=12·(cos(α-β)+cos(α+β))sinα·cosβ=12·(sin(α-β)+sin(α+β))

Универсальная тригонометрическая подстановка

Все основные тригонометрические функции — синус, косинус, тангенс и котангенс, — могут быть выражены через тангенс половинного угла.

Универсальная тригонометрическая подстановка

sinα=2tgα21+tg2α2cosα=1-tg2α21+tg2α2tgα=2tgα21-tg2α2ctgα=1-tg2α22tgα2

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р.

Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

формулы cos, sin, tg, ctg

Основные тождества тригонометрии

Тригонометрические тождества

sin2a+cos2a=1tgα=sinαcosα, ctgα=cosαsinαtgα·ctgα=1tg2α+1=1cos2α, ctg2α+1=1sin2α

Формулы приведения

Формулы приведения являются следствием периодичности тригонометрических функций.

Тригонометрические формулы сложения

sinα±β=sinα·cosβ±cosα·sinβcosα+β=cosα·cosβ-sinα·sinβcosα-β=cosα·cosβ+sinα·sinβtgα±β=tgα±tgβ1±tgα·tgβctgα±β=-1±ctgα·ctgβctgα±ctgβ

На основе формул сложения выводятся тригонометрические формулы кратного угла.

Формулы кратного угла: двойного, тройного и т.д.

Формулы двойного и тройного угла

Формулы половинного угла

sin2α2=1-cosα2cos2α2=1+cosα2tg2α2=1-cosα1+cosαctg2α2=1+cosα1-cosα

Формулы понижения степени

sin2α=1-cos2α2cos2α=1+cos2α2sin3α=3sinα-sin3α4cos3α=3cosα+cos3α4sin4α=3-4cos2α+cos4α8cos4α=3+4cos2α+cos4α8

Общий вид формул понижения степени

для четных n

sinnα=Cn2n2n+12n-1∑k=0n2-1(-1)n2-k·Ckn·cos((n-2k)α)cosnα=Cn2n2n+12n-1∑k=0n2-1Ckn·cos((n-2k)α)

для нечетных n

sinnα=12n-1∑k=0n-12(-1)n-12-k·Ckn·sin((n-2k)α)cosnα=12n-1∑k=0n-12Ckn·cos((n-2k)α)

Сумма и разность тригонометрических функций

sinα+sinβ=2sinα+β2·cosα-β2sinα-sinβ=2sinα-β2·cosα+β2cosα+cosβ=2cosα+β2·cosα-β2cosα-cosβ=-2sinα+β2·sinα-β2, cosα-cosβ=2sinα+β2·sinβ-α2

Произведение тригонометрических функций

Формулы произведения тригонометрических функций

sinα·sinβ=12·(cos(α-β)-cos(α+β))cosα·cosβ=12·(cos(α-β)+cos(α+β))sinα·cosβ=12·(sin(α-β)+sin(α+β))

Универсальная тригонометрическая подстановка

sinα=2tgα21+tg2α2cosα=1-tg2α21+tg2α2tgα=2tgα21-tg2α2ctgα=1-tg2α22tgα2

Решение задач от 1 дня / от 150 р. Курсовая работа от 5 дней / от 1800 р.

Реферат от 1 дня / от 700 р.

Автор: Ирина Мальцевская

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Тригонометрические функции тангенс и котангенс tg и ctg. Свойства. Основные формулы, формулы кратных и половинных аргументов, сложения, преобразования суммы в произведение, преобразования произведения в сумму

Раздел недели: Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.

Поиск на сайте DPVA

Поставщики оборудования

Полезные ссылки

О проекте

Обратная связь

Ответы на вопросы.

Оглавление

Таблицы DPVA.ru — Инженерный Справочник

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Тригонометрические функции тангенс и котангенс tg и ctg. Свойства. Основные формулы, формулы кратных и половинных аргументов, сложения, преобразования суммы в произведение, преобразования произведения в сумму

Тригонометрические функции тангенс и котангенс tg и ctg.

Свойства. Основные формулы,
формулы кратных и половинных аргументов, сложения, преобразования суммы в произведение,
преобразования произведения в сумму.

Тригонометрические функции тангенс и котангенс tg и ctg. Свойства:

Свойства
Область определения:
Область значений:
Четность:
Наименьший положительный период:
Координаты точек пересечения графика с осью:
Ox Oy
Промежутки, на которых функция принимает (промежутки знакопостоянства):
Положительные значения Отрицательные значения
Экстремумы:
Промежутки монотонности:
Асимптоты:

Основные формулы. Тригонометрические функции тангенс и котангенс tg и ctg:

Формулы кратных и половинных аргументов. Тригонометрические функции тангенс и котангенс tg и ctg.

Формулы сложения. Тригонометрические функции тангенс и котангенс tg и ctg.

Формулы преобразования суммы в произведение. Тригонометрические функции тангенс и котангенс tg и ctg.

Формулы преобразования произведения в сумму. Тригонометрические функции тангенс и котангенс tg и ctg.

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Дополнительная информация от Инженерного cправочника DPVA, а именно — другие подразделы данного раздела:

Поиск в инженерном справочнике DPVA. Введите свой запрос:

Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.

Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers

Консультации и техническая
поддержка сайта: Zavarka Team

Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.

{2}(\alpha) $$
$$ \operatorname{tg}(\alpha)=\frac{\sin (\alpha)}{\cos (\alpha)}=\frac{1}{\operatorname{ctg}(\alpha)} $$

Формулы суммы и разности (16 шт)

$$ \sin (\alpha+\beta)=\sin (\alpha) \cdot \cos (\beta)+\cos (\alpha) \cdot \sin (\beta) $$
$$ \sin (\alpha-\beta)=\sin (\alpha) \cdot \cos (\beta)-\cos (\alpha) \cdot \sin (\beta) $$
$$ \cos (\alpha+\beta)=\cos (\alpha) \cdot \cos (\beta)-\sin (\alpha) \cdot \sin (\beta) $$
$$ \cos (\alpha-\beta)=\cos (\alpha) \cdot \cos (\beta)+\sin (\alpha) \cdot \sin (\beta) $$
$$ \operatorname{tg}(\alpha+\beta)=\frac{\operatorname{tg}(\alpha)+\operatorname{tg}(\beta)}{1-\operatorname{tg}(\alpha) \cdot \operatorname{tg}(\beta)} \operatorname{tg}(\alpha-\beta)=\frac{\operatorname{tg}(\alpha)-\operatorname{tg}(\beta)}{1+\operatorname{tg}(\alpha) \cdot \operatorname{tg}(\beta)} $$
$$ \operatorname{ctg}(\alpha+\beta)=\frac{\operatorname{ctg}(\alpha) \cdot \operatorname{ctg}(\beta)-1}{\operatorname{ctg}(\alpha)-\operatorname{ctg}(\beta)} \operatorname{ctg}(\alpha+\beta)=\frac{\operatorname{ctg}(\alpha) \cdot \operatorname{ctg}(\beta)-1}{\operatorname{ctg}(\alpha)-\operatorname{ctg}(\beta)} $$
$$ \sin (\alpha)+\sin (\beta)=2 \cdot \sin \left(\frac{\alpha+\beta}{2}\right) \cdot \cos \left(\frac{\alpha-\beta}{2}\right) $$
$$ \sin (\alpha)-\sin (\beta)=2 \cdot \cos \left(\frac{\alpha+\beta}{2}\right) \cdot \sin \left(\frac{\alpha-\beta}{2}\right) $$
$$ \cos (\alpha)+\cos (\beta)=2 \cdot \cos \left(\frac{\alpha+\beta}{2}\right) \cdot \cos \left(\frac{\alpha-\beta}{2}\right) $$
$$ \cos (\alpha)-\cos (\beta)=-2 \cdot \sin \left(\frac{\alpha+\beta}{2}\right) \cdot \sin \left(\frac{\alpha-\beta}{2}\right) $$
$$ \operatorname{tg}(\alpha)+\operatorname{tg}(\beta)=\frac{\sin (\alpha+\beta)}{\cos (\alpha) \cdot \cos (\beta)} \operatorname{tg}(\alpha)-\operatorname{tg}(\beta)=\frac{\sin (\alpha-\beta)}{\cos (\alpha) \cdot \cos (\beta)} $$
$$ \operatorname{ctg}(\alpha)+\operatorname{ctg}(\beta)=\frac{\sin (\beta+\alpha)}{\sin (\alpha) \cdot \sin (\beta)} \quad \operatorname{ctg}(\alpha)-\operatorname{ctg}(\beta)=\frac{\sin (\beta-\alpha)}{\sin (\alpha) \cdot \sin (\beta)} $$

Формулы понижения степени (10 шт)

$$ \sin ^{2}(\alpha)=\frac{1-\cos (2 \alpha)}{2} \quad \cos ^{2}(\alpha)=\frac{1+\cos (2 \alpha)}{2} $$
$$ \operatorname{tg}^{2}(\alpha)=\frac{1-\cos (2 \alpha)}{1+\cos (2 \alpha)} \quad \operatorname{ctg}^{2}(\alpha)=\frac{1+\cos (2 \alpha)}{1-\cos (2 \alpha)} $$
$$ \cos ^{3}(\alpha)=\frac{1}{4}(3 \cdot \cos (\alpha)+\cos (3 \alpha)) $$
$$ \sin ^{3}(\alpha)=\frac{1}{4}(3 \cdot \sin (\alpha)-\sin (3 \alpha)) $$
$$ \cos ^{4}(\alpha)-\sin ^{4}(\alpha)=\cos (2 \alpha) $$
$$ \cos ^{4}(\alpha)+\sin ^{4}(\alpha)=1-\frac{\sin ^{2}(2 \alpha)}{2} $$
$$ \cos ^{6}(\alpha)+\sin ^{6}(\alpha)=1-\frac{3}{4} \sin ^{2}(2 \alpha) $$
$$ \cos ^{6}(\alpha)-\sin ^{6}(\alpha)=\cos (2 \alpha) \cdot\left[1-\frac{1}{4} \sin ^{2}(2 \alpha)\right] $$

Формулы для функций кратных аргументов (11 шт)

$$ \sin (2 \alpha)=2 \cdot \sin (\alpha) \cdot \cos (\alpha) $$
$$ \cos (2 \alpha)=\cos ^{2}(\alpha)-\sin ^{2}(\alpha)=2 \cdot \cos ^{2}(\alpha)-1=1-2 \cdot \sin ^{2}(\alpha) $$
$$ \operatorname{tg}(2 \alpha)=\frac{2 \cdot \operatorname{tg}(\alpha)}{1-\operatorname{tg}^{2}(\alpha)} \quad \operatorname{ctg}(2 \alpha)=\frac{\operatorname{ctg}^{2}(\alpha)-1}{2 \cdot \operatorname{ctg}(\alpha)} $$
$$ \sin (3 \alpha)=3 \cdot \sin (\alpha)-4 \cdot \sin ^{3}(\alpha) $$
$$ \cos (3 \cdot \alpha)=4 \cdot \cos ^{3}(\alpha)-3 \cdot \cos (\alpha) $$
$$ \operatorname{tg}(3 \alpha)=\frac{3 \cdot \operatorname{tg}(\alpha)-\operatorname{tg}^{3}(\alpha)}{1-3 \cdot \operatorname{tg}^{2}(\alpha)}=\operatorname{tg}(\alpha) \cdot \operatorname{tg}\left(\frac{\pi}{3}+\alpha\right) \cdot \operatorname{tg}\left(\frac{\pi}{3}-\alpha\right) $$
$$ \operatorname{ctg}(3 \cdot \alpha)=\frac{3 \cdot \operatorname{ctg}(\alpha)-\operatorname{ctg}^{3}(\alpha)}{1-3 \cdot \operatorname{ctg}^{2}(\alpha)} $$

Формулы произведения функций (6 шт)

$$ \sin (\alpha) \cdot \sin (\beta)=\frac{1}{2}(\cos (\alpha-\beta)-\cos (\alpha+\beta)) $$
$$ \cos (\alpha) \cdot \cos (\beta)=\frac{1}{2}(\cos (\alpha-\beta)+\cos (\alpha+\beta)) $$
$$ \sin (\alpha) \cdot \cos (\beta)=\frac{1}{2}(\sin (\alpha-\beta)+\sin (\alpha+\beta)) $$
$$ \operatorname{tg}(\alpha) \cdot \operatorname{tg}(\beta)=\frac{\operatorname{tg}(\alpha)+\operatorname{tg}(\beta)}{\operatorname{ctg}(\alpha)+\operatorname{ctg}(\beta)} \quad \operatorname{ctg}(\alpha) \cdot \operatorname{ctg}(\beta)=\frac{\operatorname{ctg}(\alpha)+\operatorname{ctg}(\beta)}{\operatorname{tg}(\alpha)+\operatorname{tg}(\beta)} $$
$$ \operatorname{ctg}(\alpha) \cdot \operatorname{tg}(\beta)=\frac{\operatorname{ctg}(\alpha)+\operatorname{tg}(\beta)}{\operatorname{tg}(\alpha)+\operatorname{ctg}(\beta)} $$

Формулы, связывающие все тригонометрические функции с тангенсом половинного угла (3 шт)

$$ \sin (\alpha)=\frac{2 \cdot \operatorname{tg}\left(\frac{\alpha}{2}\right)}{1+\operatorname{tg}^{2}\left(\frac{\alpha}{2}\right)} \quad \cos (\alpha)=\frac{1-\operatorname{tg}^{2}\left(\frac{\alpha}{2}\right)}{1+\operatorname{tg}^{2}\left(\frac{\alpha}{2}\right)} \quad \operatorname{tg}(\alpha)=\frac{2 \cdot \operatorname{tg}\left(\frac{\alpha}{2}\right)}{1-\operatorname{tg}^{2}\left(\frac{\alpha}{2}\right)} $$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Тригонометрические формулы

Тригонометрические формулы — часто встречающиеся математические выражения для тригонометрических функций, которые выполняются при всех значениях аргумента.

Навигация Тригонометрические функции Основные тригонометрические формулы Тригонометрические функции суммы и разности углов Тригонометрические функции двойного угла Формулы тройного угла Формулы понижения степени Формулы преобразования суммы и разности тригонометрических функций в произведение Формулы преобразования произведений функций Универсальная тригонометрическая подстановка

Тригонометрические функции

sin α, cos α

tg α =	sin α	, α ≠	π	+ πn, n є Z
	cos α		2

ctg α =	cos α	, α ≠ π + πn, n є Z
	sin α

sec α =	1	, α ≠	π	+ πn, n є Z
	cos α		2

cosec α =	1	, α ≠ π + πn, n є Z
	sin α

Основные тригонометрические формулы

sin² α + cos² α = 1

tg α · ctg α = 1

1 + tg² α =	1
	cos² α

1 + ctg² α =	1
	sin² α

Тригонометрические функции суммы и разности углов

sin(α + β) = sin α · cos β + cos α · sin β

sin(α – β) = sin α · cos β – cos α · sin β

cos(α + β) = cos α · cos β – sin α · sin β

cos(α – β) = cos α · cos β + sin α · sin β

tg(α + β) =	tg α + tg β
	1 – tgα · tg β

tg(α – β) =	tg α – tg β
	1 + tgα · tg β

ctg(α + β) =	ctgα · ctg β — 1
	ctg β + ctg α

ctg(α — β) =	ctgα · ctg β + 1
	ctg β — ctg α

Тригонометрические функции двойного угла

sin 2α = 2 sin α · cos α

cos 2α = cos² α — sin² α

tg 2α =	2 tg α
	1 — tg² α

ctg 2α =	ctg² α — 1
	2 ctg α

Формулы тройного угла

sin 3α = 3 sin α — 4 sin³ α

cos 3α = 4 cos³ α — 3 cos α

tg 3α =	3 tg α — tg³ α
	1 — 3 tg² α

ctg 3α =	3 ctg α — ctg³ α
	1 — 3 ctg² α

Формулы понижения степени

sin² α =	1 — cos 2α
	2

cos² α =	1 + cos 2α
	2

sin³ α =	3 sin α — sin 3α
	4

cos³ α =	3 cos α + cos 3α
	4

Формулы преобразования суммы и разности тригонометрических функций в произведение

sin α + sin β = 2 sin	α + β	cos	α — β
	2		2

sin α — sin β = 2 sin	α — β	cos	α + β
	2		2

cos α + cos β = 2 cos	α + β	cos	α — β
	2		2

cos α — cos β = -2 sin	α + β	sin	α — β
	2		2

tg α + tg β =	sin(α + β)
	cos α · cos β

tg α — tg β =	sin(α — β)
	cos α · cos β

ctg α + ctg β =	sin(α + β)
	sin α · sin β

ctg α — ctg β =	sin(β — α)
	sin α · sin β

a sin α + b cos α = r sin (α + φ),

где r² = a² + b², sin φ =	b	, tg φ =	b
	r		a

Формулы преобразования произведений функций

sin α · sin β =	1	(cos(α — β) — cos(α + β))
	2

sin α · cos β =	1	(sin(α + β) + sin(α — β))
	2

cos α · cos β =	1	(cos(α + β) + cos(α — β))
	2

Универсальная тригонометрическая подстановка

sin α =	2 tg (α/2)
	1 + tg² (α/2)

cos α =	1 — tg² (α/2)
	1 + tg² (α/2)

tg α =	2 tg (α/2)
	1 — tg² (α/2)

ctg α =	1 — tg² (α/2)
	2 tg (α/2)

Формулы сокращенного умножения (a ± b)² Формулы и свойства степеней aⁿ Формулы и свойства корней ⁿ√a Формулы и свойства логарифмов log_a b Формулы и свойства арифметической прогрессии a_n Формулы и свойства геометрической прогрессии b_n Тригонометрические формулы sin x cos x Обратные тригонометрические формулы arcsin x Таблица производных ddx Таблица интегралов ∫x dx

Всі таблиці та формули

Тригонометрия | Математические формулы | Indigomath Математика

Синус и косинус

Найти

Известно, что:

a =

Вычислить ‘a’

Тангенс

Найти

Известно, что:

a =

Вычислить ‘a’

Котангенс

Найти

Известно, что:

a =

Вычислить ‘a’

Произведение тангенса и котангенса

Найти

Известно, что:

a =

Вычислить ‘a’

Тангенс и косинус

Найти

Известно, что:

a =

Вычислить ‘a’

Котангенс и синус

Найти

Известно, что:

a =

Вычислить ‘a’

Синус суммы углов

Найти

Известно, что:

ab =

Вычислить ‘a’

Синус разницы углов

Найти

Известно, что:

ab =

Вычислить ‘a’

Косинус суммы углов

Найти

Известно, что:

ab =

Вычислить ‘a’

Косинус разницы углов

Найти

Известно, что:

ab =

Вычислить ‘a’

Тангенс суммы углов

Найти

Известно, что:

ab =

Вычислить ‘a’

Тангенс разницы углов

Найти

Известно, что:

ab =

Вычислить ‘a’

Синус двойного угла

Найти

Известно, что:

a =

Вычислить ‘a’

Косинус двойного угла

Найти

Известно, что:

a =

Вычислить ‘a’

Косинус двойного угла

Найти

Известно, что:

a =

Вычислить ‘a’

Косинус двойного угла

Найти

Известно, что:

a =

Вычислить ‘a’

Тангенс двойного угла

Найти

Известно, что:

a =

Вычислить ‘a’

Котангенс двойного угла

Найти

Известно, что:

a =

Вычислить ‘a’

Котангенс двойного угла

Найти

Известно, что:

a =

Вычислить ‘a’

Сумма синусов

Найти

Известно, что:

ab =

Вычислить ‘a’

Разница синусов

Найти

Известно, что:

ab =

Вычислить ‘a’

Сумма косинусов

Найти

Известно, что:

ab =

Вычислить ‘a’

Разница косинусов

Найти

Известно, что:

ab =

Вычислить ‘a’

Произведение синуса и косинуса

Найти

Известно, что:

ab =

Вычислить ‘a’

Произведение синусов

Найти

Известно, что:

ab =

Вычислить ‘a’

Произведение косинусов

Найти

Известно, что:

ab =

Вычислить ‘a’

Понижение степени синуса

Найти

Известно, что:

a =

Вычислить ‘a’

Понижение степени косинуса

Найти

Известно, что:

a =

Вычислить ‘a’

Тригонометрия | Математические формулы | Математика

Синус и косинус

Находить

Известно, что:

а =

Вычислить а

Тангенс

Находить

Известно, что:

а =

Вычислить а

Котангенс

Находить

Известно, что:

а =

Вычислить а

Произведение тангенса и котангенса

Находить

Известно, что:

а =

Вычислить а

Тангенс и косинус

Находить

Известно, что:

а =

Вычислить а

Котангенс и синус

Находить

Известно, что:

а =

Вычислить «а»

Синус суммы углов

Находить

Известно, что:

аб =

Вычислить «а»

Синус разности углов

Находить

Известно, что:

аб =

Вычислить а

Косинус суммы углов

Находить

Известно, что:

аб =

Вычислить а

Косинус разности углов

Находить

Известно, что:

аб =

Вычислить а

Тангенс суммы углов

Находить

Известно, что:

аб =

Вычислить «а»

Тангенс разности углов

Находить

Известно, что:

аб =

Вычислить а

Синус двойного угла

Находить

Известно, что:

а =

Вычислить а

Косинус двойного угла

Находить

Известно, что:

а =

Вычислить а

Косинус двойного угла

Находить

Известно, что:

а =

Вычислить а

Косинус двойного угла

Находить

Известно, что:

а =

Вычислить а

Тангенс двойного угла

Находить

Известно, что:

а =

Вычислить а

Котангенс двойного угла

Находить

Известно, что:

а =

Вычислить а

Котангенс двойного угла

Находить

Известно, что:

а =

Вычислить «а»

Сумма синусов (сумма к произведению)

Находить

Известно, что:

аб =

Вычислить «а»

Разность синусов (разность с произведением)

Находить

Известно, что:

аб =

Вычислить «а»

Сумма косинусов (сумма к произведению)

Находить

Известно, что:

аб =

Вычислить «а»

Разность косинусов (разность произведения)

Находить

Известно, что:

аб =

Вычислить а

Произведение синуса и косинуса

Находить

Известно, что:

аб =

Вычислить «а»

Произведение синусов

Находить

Известно, что:

аб =

Вычислить «а»

Произведение косинусов

Находить

Известно, что:

аб =

Рассчитать «а»

Снижение мощности для синуса

Находить

Известно, что:

а =

Рассчитать «а»

Снижение мощности для косинуса

Находить

Известно, что:

а = 92{\alpha}=1\] Формулы тангенса и котангенса: \[\begin{split}&\text{tg}{\alpha}=\frac{\sin{\alpha}}{\cos{\alpha }}\\\\\\\\&\text{ctg}{\alpha}=\frac{\cos{\alpha}}{\sin{\alpha}}\\\\\\\\&\text {tg}{\alpha}\cdot \text{ctg}{\alpha=1}\\\\\end{split}\] Тригонометрические формулы сложения: \[\begin{split}&\\&\sin {\ left ( \ alpha + \ beta \ right)} = \ sin {\ alpha} \ cos {\ beta} + \ sin {\ beta} \ cos {\ alpha} \\\\\\\\&\ sin {\ left ( \ alpha — \ beta \ right)} = \ sin {\ alpha} \ cos {\ beta} — \ sin {\ beta} \ cos {\ alpha} \\\\\\\\&\ cos {\ left ( \ alpha + \ beta \ right)} = \ cos {\ alpha} \ cos {\ beta} — \ sin {\ alpha} \ sin {\ beta} \\\\\\\\\&\ cos {\ left ( \ alpha — \ beta \ right)} = \ cos {\ alpha} \ cos {\ beta} + \ sin {\ alpha} \ sin {\ beta} \\\\\\\\\&\ text {tg}{\left (\alpha +\beta \right)}=\frac{\text{tg}{\alpha}+\text{tg}{\beta}}{1-\text{tg}{\ альфа }\ \text{tg}{\beta}}\\\\\\\\&\text{tg}{\left ( \alpha -\beta \right )}=\frac{\text{tg}{ \alpha }-\text{tg}{\beta}}{1+\text{tg}{\alpha }\ \text{tg}{\beta }}\\\\\\\\&\text{ctg {\ левый t (\alpha +\beta \right)}=\frac{\text{ctg}{\alpha}\ \text{ctg}{\beta}-1}{\text{ctg}{\beta}+\text {ctg}{\alpha}}\\\\\\\\&\text{ctg}{\left (\alpha -\beta \right)}=\frac{\text{ctg}{\alpha}\ \ text{ctg}{\beta}+1}{\text{ctg}{\beta}-\text{ctg}{\alpha }}\\\\\end{split}\] 9\circ -\alpha \right )}=-\text{ctg}{\alpha }\end{split}\]

Сумма тождеств: \[\begin{split}&\\&\sin{ \alpha}+\sin{\beta}=2\sin{\frac{\alpha +\beta}}{2}}\cos{\frac{\alpha -\beta}}{2}}\\\\\\ \\&\sin{\alpha}-\sin{\beta}=2\cos{\frac{\alpha+\beta}{2}}\sin{\frac{\alpha-\beta}{2}} \\\\\\\\&\ соз {\ альфа} + \ соз {\ бета} = 2 \ соз {\ гидроразрыва {\ альфа + \ бета} {2}} \ соз {\ гидроразрыва {\ альфа — \ бета {2}} \\\\\\\\&\cos{\alpha} -\cos{\beta}=-2\sin{\frac{\alpha +\beta}}{2}}\sin{ \frac{\alpha -\beta} {2}}\\\\\\\\&\text{tg}{\alpha}+\text{tg}{\beta}=\frac{\sin{\left ( \alpha +\beta \right )}}{\cos{\alpha}\cos{\beta}}\\\\\\\\&\text{tg}{\alpha}-\text{tg}{ \beta}=\frac{\sin{\left (\alpha -\beta \right)}}{\cos{\alpha}\cos{\beta}}\\\\\\\\&\text{ctg }{\alpha}+\text{ctg}{\beta}=\frac{\sin{\left (\beta +\alpha \right)}}}{\sin{\alpha}\sin{\beta}}\ \\\\\\\&\text{ctg}{\alpha}-\text{ctg}{\beta}=\frac{\sin{\left (\beta -\alpha \right)}}{\sin {\ альфа} \ грех {\ бета}} \\\\\\\\&\ соз {\ а lpha} + \ sin {\ alpha} = \ sqrt {2} \ sin {\ left ( 45 ^ \ circ + \ alpha \ right )} = \ sqrt {2} \ cos {\ left ( 45 ^ \ circ — \ альфа \ справа)} \\\\\\\\&\cos{\alpha}-\sin{\alpha}=\sqrt{2}\cos{\left (45^\circ +\alpha \right)} =\sqrt{2}\sin{\left ( 45^\circ -\alpha \right )}\\\\\end{split}\] Идентификаторы продукта: \[\begin{split}&\\&\sin{\alpha}\sin{\beta}=\frac{1}{2}\left [\cos{\left (\alpha -\ бета \ справа ) — \ соз {\ влево ( \ альфа + \ бета \ справа )}} \ справа ] \\\\\\& \ соз {\ альфа} \ соз {\ бета} = \ гидроразрыва {1} { 2}\left [\cos{\left (\alpha -\beta\right)+\cos{\left (\alpha +\beta \right)}} \right]\\\\\\&\sin{\ альфа} \ cos {\ бета} = \ гидроразрыва {1} {2} \ влево [ \ грех {\ влево ( \ альфа — \ бета \ вправо) + \ грех {\ влево ( \ альфа + \ бета \ вправо)} } \right ]\\\\\\\end{split}\] Другие формулы: 92{\alpha}=\cos{\left (\alpha +\beta\right)}\cos{\left (\alpha -\beta \right)}\\\\\end{split}\]

тема

Геометрия

Следующая тема

Предел последовательности

Как я могу определить, какие из моих продуктов вносят наибольший или наименьший вклад в мои глобальные продажи?

Узнайте, как использовать Contribution to Growth (CTG) для анализа эффективности продаж.

Знание того, какие из ваших продуктов способствуют вашему росту в наименьшей или наибольшей степени, — лучший способ контролировать эффективность продаж на Amazon.

Независимо от того, продаете ли вы несколько продуктов нескольких брендов на разных торговых площадках Amazon или просто имеете небольшой ассортимент товаров в одной категории, знание того, когда, где и как использовать вклад C в Growth , может стать первым шагом в правильное направление для вашего бизнес-анализа.

Для простоты CTG на Amazon предназначен для сравнения эффективности продаж различных продуктов или групп продуктов. Это делается путем выбора двух разных диапазонов дат и просмотра того, какие продукты работали лучше или хуже в течение одного периода по сравнению с другим. CTG обычно рассчитывается в процентах (также в базисных пунктах), чтобы установить, какую долю роста (или снижения) произвел каждый продукт или группа продуктов по сравнению с другими.

Простое сравнение двух продуктов за два разных периода

Ниже приведен пример простого сравнительного расчета.

Представьте себе, что вы сравниваете два продукта:

A BAR of SOAP
A Бутылка Shampoo

-й сор. в декабре 2019 г.

Бутылка шампуня была продана на сумму 2000 долларов США в ноябре 2019 г.по сравнению с продажами на 200 долларов в декабре 2019 года.

Давайте разберемся.

ноябрь 2019 г.
Общая продажа составила $ 3000
Бар мыла Продажи = $ 1000 (33% от общего количества)
бутылка Shampoo Sales = 32323232323232323 гг. Декабрь 2019 г.
Общий объем продаж составил 1000 долларов США
Кусок мыла объем продаж = 800 долларов США (80% от общей суммы)
Бутылка шампуня продаж = $200 (20% от общей суммы)

Таким образом, если мы проведем простые сравнительные расчеты между декабрем 2019 года и ноябрем 2019 года, мы увидим, что:

Продажи мыла упали на -20%

Продажи бутылки шампуня снизились на -90% на самом деле хочу перейти на более глубокий уровень анализа. В конце концов, мы хотим понять, какой именно продукт больше всего способствовал общему снижению продаж. Для этого нам нужно сделать расчет CTG для каждого продукта:

Для куска мыла нам нужно сделать следующий расчет:

[ кусок мыла общий объем продаж ноябрь 2019 года МИНУС кусок мыла общий объем продаж декабрь 2019 года]

3 7
DIVIDED Общий объем продаж, ноябрь 2019 г. МИНУС Общий объем продаж, декабрь 2019 г.]
Если результат больше 0, мы умножаем его на -1, а затем на 100, чтобы сформулировать процентное соотношение
Кусок мыла Расчет CTG равен
(1000 - 800) / (3000 - 1000) = 0,1 * -1 * 100 = -10%

Установив, что CTG для куска мыла составляет -10%, мы можем с уверенностью сказать, что расчет CTG для бутылки шампуня составляет -90%.
Это кажется банальным при сравнении двух продуктов, однако внутри Seelk Studio мы автоматизировали расчет CTG, чтобы обрабатывать любое количество сравнений продуктов (или даже групп продуктов). Вы можете легко сравнить CTG сотен и тысяч различных продуктов 🤩!
Ознакомьтесь с приведенным ниже примером.
Нужна помощь с вкладом в рост? Свяжитесь с экспертами Seelk по Amazon, чтобы лучше пилотировать и разрабатывать стратегию своего бизнеса на Amazon.
Небольшое напоминание: основы CTG просты:
Мы хотим сравнить эффективность продаж наших продуктов за два разных периода, чтобы увидеть, какие продукты вносят наибольший или наименьший вклад в переход от одного периода к другому.
Расчет CTG может работать с отдельными продуктами, однако он также работает при сравнении групп продуктов, например, марок производителя.
В качестве примера мы выбрали Muki , вымышленного шведского фармацевтического производителя и продавца Amazon. У них есть пять разных брендов:
Чтобы создать основу для нашего расчета CTG, мы спросили себя:

Какой из этих пяти брендов в наибольшей степени способствовал росту за последний квартал по сравнению с предыдущим кварталом?
В данном случае мы сравниваем Q4 2019 с Q3 2019.
Как рассчитать CTG в Seelk Studio?
Хорошие новости 🤓: панель бизнес-аналитики (BI) Seelk Studio автоматически рассчитает для вас ваш CTG. Чтобы рассчитать CTG для «Пользовательских брендов» Muki, мы сделали следующие три простых шага:
1. Выберите группу
Выберите «Пользовательские бренды» Muki в раскрывающемся списке «Группировать по» в верхней части интерфейса BI
.
2. Сравните два периода дат
Откройте средство выбора даты в правом верхнем углу интерфейса BI, включите и режим 9.0317 и используя месяцев и выбирая октябрь 2019 года → ноябрь 2019 года для нашего периода A и Prev. Период для B Период (по умолчанию июль 2019 г. → сентябрь 2019 г.). Не забудьте нажать Применить 👍 !
3. Заказ по CTG
Чтобы увидеть расчет CTG для «Пользовательских брендов», прокрутите вниз до таблицы данных и щелкните столбец «[A] vs [B] CTG (%)», чтобы заказать его из либо по возрастанию, либо по убыванию — в зависимости от того, хотите ли вы сначала увидеть своих проигравших или победителей 🧐.
Мы увидели следующее:
Как видите, бренд Muki Eson внес наибольший вклад в рост, а Runner занял второе место. Из этого можно извлечь все типы анализа, но самый быстрый способ получить представление о том, где происходит реальный рост продаж, — это погрузиться немного глубже на уровень продукта.
В Seelk Studio мы сделали глубокий анализ от анализа бренда до анализа на уровне продукта одним щелчком мыши.
В приведенном выше примере мы хотим определить, какие продукты относятся к марке Резина (марка Muki, которая внесла наименьший вклад в рост). Сделать это можно просто:
Таблица данных внутри BI Dashboard Seelk Studio автоматически рассчитает ваш CTG при сравнении двух периодов.
Таким образом, независимо от того, сравниваете ли вы годовые данные или просто два уникальных диапазона дат, столбец «A vs B CTG %» всегда будет доступен для заказа.
Это относится к любому параметру вашего Каталога — настраиваемым атрибутам, маркплетам (странам) или ASIN.
Интеграл от cot x — формула, доказательство, примеры l Интегрирование от cot x
Перед тем как узнать, что такое интеграл от cot x, давайте вспомним несколько фактов о функции cot (или) котангенса. В прямоугольном треугольнике, если х — один из острых углов, то ctg х — это отношение прилежащей стороны х к противолежащей стороне х. Таким образом, это можно записать как (cos x)/(sin x) как cos x = (смежный)/(гипотенуза) и sin x = (противоположный)/(гипотенуза). Воспользуемся этими фактами, чтобы найти интеграл от ctg x.
Давайте изучим интеграл формулы cot x вместе с его доказательством и примерами.
1. Чему равен интеграл от Cot x dx?
2. Интеграл Cot x Доказательство заменой
3. Определенный интеграл от Cot x dx
4. FAQ по Integral of Cot x
Чему равен интеграл от Cot x dx?
Интеграл от cot x dx равен ln |sin x| + C. Он представлен как ∫ кроватка x dx, поэтому ∫ кроватка x dx = ln |sin x| + C , где «C» — постоянная интегрирования. Здесь
‘∫’ — это символ интегрирования.
cot x — подынтегральная функция.
dx означает, что интегрирование производится по x.
Мы используем метод интегрирования методом подстановки, чтобы доказать эту интеграцию формулы cot x. Мы увидим это в следующем разделе.
Интеграл Cot x Доказательство заменой
Вот вывод формулы интеграла от ctg x с помощью интегрирования методом подстановки. Для этого напомним, что ctg x = cos x/sin x. Тогда ∫ кроватка x dx становится
∫ кроватка x dx = ∫ (cos x)/(sin x) dx
Подставьте sin x = u. Тогда cos x dx = du. Тогда приведенный выше интеграл принимает вид
= ∫ (1/u) du
= ln |u| + C (Поскольку ∫ 1/x dx = ln|x| + C)
Замените u = sin x здесь,
= ln |sin x| + C
Таким образом, ∫ cot x dx = ln |sin x| + C.
Отсюда доказано.
Определенный интеграл от Cot x dx
Определенный интеграл от cot x dx является интегралом с нижними и верхними границами. Для его оценки подставляем верхний и нижний пределы в значение интеграла ctg x dx и вычитаем их в том же порядке. Мы будем работать над некоторыми определенными интегралами от ctg x dx.
Интеграл от Cot x От 0 до пи/2 9{\pi/2}\) cot x dx = ln √2
Следовательно, интеграл от cot x от π/4 до π/2 равен ln √2.
Важные замечания по интегралу от Cot x dx:
∫ cot x dx = ln |sin x| + С
Так как sin x и csc x обратны друг другу,
∫ кроватка x dx = ln |csc x| ^-1 + C = — ln |csc x| + С
∫ кроватка ² x dx = — csc x + C as d/dx(csc x) = -cot ² x + C
Темы, относящиеся к интегралу от Cot x dx:
Формулы интегрирования
Интеграл греха x
Интеграл сек x
Интегральный калькулятор
Расчетный калькулятор
Часто задаваемые вопросы по Integral of Cot x
Чему равен интеграл от Cot x?
Интеграл от кроватки x равен ln |sin x| + C. Математически это обозначается как ∫ cot x dx = ln |sin x| + C.
Равна ли производная от Cot x интегралу от Cot x?
Нет, производная от кроватки x равна -csc ² x, а интеграл от кроватки x равен ln |sin x| + C. т. е.
d/dx(cot x) = -csc ² x
∫ раскладушка x dx = ln |sin x| + С
Чему равен интеграл от Cot x от 0 до Pi?
Мы знаем, что ∫ cot x dx = ln |sin x| + C. Подставляя пределы, ln |sin π| — пер |sin 0| = расходится (поскольку 0 НЕ находится в области логарифмической функции).
Чему равен интеграл от Cot x Sec x?
∫ кроватка x sec x dx = ∫(cos x)/(sin x) · (1/cos x) dx = ∫ 1/sin x dx = ∫ csc x dx = — ln |csc x + кроватка x| + C.
Как вывести интеграл от формулы Cot x?
Чтобы вывести формулу для ∫ cot x dx, запишем cot x как (cos x)/(sin x). Тогда интеграл принимает вид ∫ (cos x)/(sin x) dx. Предположим, что sin x = u, тогда cos x dx = du. Тогда интеграл принимает вид ∫ (1/u) du = ln |u| + C (или) ln |sin x) + C.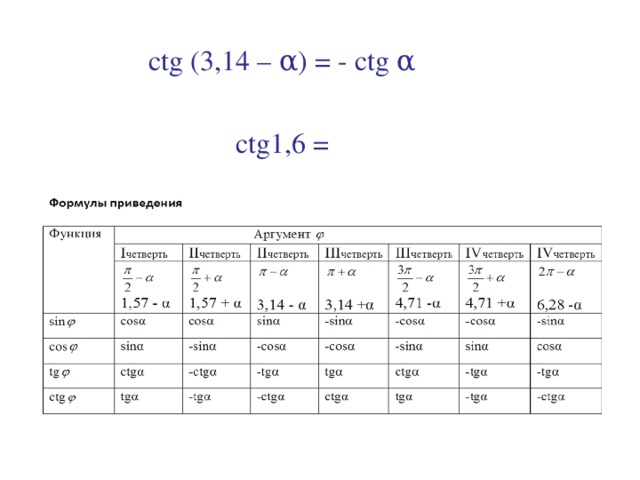 2x?
Мы знаем, что производная csc x равна -cot ² x. Таким образом, производная от -csc x равна cot ² x. Поскольку интегрирование представляет собой процесс, обратный дифференцированию, ∫ cot ² x dx = -csc x + C.
Чему равен интеграл от Cot x Csc
² x dx?
Предположим, что кроватка x = u, тогда -csc ² x dx = du. Тогда данный интеграл принимает вид ∫ -u du = -u ² /2 + C = -cot ² x/2 + C.
Математические функции — NumPy v1.23 Manual
Тригонометрические функции
sin (x, /[ out, where, casting, order, …])
Тригонометрический синус, поэлементный.
cos (x, /[ out, where, casting, order, …])
Поэлементный косинус.
tan (x, /[ out, where, casting, order, . ..])
Вычислить тангенс поэлементно.
arcsin (x, /[ out, where, casting, order, …])
Арксинус, поэлементный.
arccos (x, /[ out, where, casting, order, …])
Тригонометрический арккосинус, поэлементный.
arctan (x, /[ out, where, casting, order, …])
Тригонометрический арктангенс, поэлементный.
гипот (x1, x2, /[ out, where, casting, …])
Зная катеты прямоугольного треугольника, верните его гипотенузу.
arctan2 (x1, x2, /[ out, where, casting, …])
Поэлементный арктангенс x1/x2 правильный выбор квадранта.
градусов (x, /[ out, where, casting, order, …])
Преобразование углов из радианов в градусы.
радианы (x, /[ out, where, casting, order, …])
Преобразование углов из градусов в радианы.
развернуть (p[ дисконт, ось, точка])
Разверните, взяв дополнение больших дельт относительно периода.
deg2rad (x, /[ из, где, кастинг, заказ, …])
Преобразование углов из градусов в радианы.
rad2deg (x, /[ out, where, casting, order, …])
Преобразование углов из радианов в градусы.
Гиперболические функции
sinh (x, /[ out, where, casting, order, …])
Гиперболический синус, поэлементный.
cosh (x, /[ out, where, casting, order, …])
Гиперболический косинус, поэлементный.
tanh (x, /[ out, where, casting, order, …])
Поэлементное вычисление гиперболического тангенса.
arcsinh (x, /[ out, where, casting, order, …])
Обратный гиперболический синус поэлементно.
arccosh (x, /[ out, where, casting, order, …])
Арктический гиперболический косинус, поэлементный.
arctanh (x, /[ out, where, casting, order, …])
Поэлементный аркгиперболический тангенс.
Округление
около (a[ десятичные, выход])
Равномерное округление до заданного числа десятичных знаков.
round_ (a[ десятичные, out])
Округление массива до заданного числа знаков после запятой.
rint (x, /[ out, where, casting, order, …])
Округление элементов массива до ближайшего целого числа.
исправить (x[ out])
Округлить до ближайшего целого числа в сторону нуля.
этаж (x, /[ аут, где, литье, заказ, …])
Вернуть пол ввода поэлементно.
ceil (x, /[ out, where, casting, order, …])
Вернуть потолок ввода поэлементно.
trunc (x, /[ out, where, casting, order, …])
Возвращает усеченное значение ввода поэлементно.
Суммы, произведения, разности
prod (a[ ось, dtype, out, keepdims, …])
Возвращает произведение элементов массива по заданной оси.
сумма (a[ ось, dtype, выход, keepdims, …])
Сумма элементов массива по заданной оси.
nanprod (a[ ось, dtype, выход, keepdims, …])
Возвращает произведение элементов массива по заданной оси, рассматривая не числа (NaN) как единицы.
nansum (a[ ось, dtype, out, keepdims, …])
Возвращает сумму элементов массива по заданной оси, рассматривая Not a Numbers (NaNs) как ноль.
cumprod (a[ ось, dtype, выход])
Возвращает совокупное произведение элементов по заданной оси.
общая сумма (a[ ось, dtype, выход])
Возвращает совокупную сумму элементов по заданной оси.
nancumprod (a[ ось, dtype, выход])
Возвращает кумулятивное произведение элементов массива по заданной оси, рассматривая Not a Numbers (NaNs) как единое целое.
nancumsum (a[ ось, dtype, выход])
Возвращает кумулятивную сумму элементов массива по заданной оси, рассматривая Not a Numbers (NaNs) как ноль.
diff (a[ n, ось, начало, добавление])
Вычислить n-ю дискретную разность по заданной оси.
ediff1d (ary[ to_end, to_begin])
Различия между последовательными элементами массива.
градиент (f, *varargs[ ось, edge_order])
Возвращает градиент N-мерного массива.
крест (a, b[ осьa, осьb, осьc, ось])
Возвращает векторное произведение двух (массивов) векторов.
ловушка (y[ x, dx, ось])
Проинтегрируйте вдоль заданной оси, используя составное правило трапеций.
Экспоненты и логарифмы
exp (x, /[ out, where, casting, order, …])
Вычислить экспоненту всех элементов входного массива.
expm1 (x, /[ out, where, casting, order, …])
Вычислить exp(x) - 1 для всех элементов массива.
exp2 (x, /[ out, where, casting, order, …])
Вычислить 2**p для всех p во входном массиве.
журнал (x, /[ out, where, casting, order, …])
Натуральный логарифм, поэлементно.
log10 (x, /[ out, where, casting, order, …])
Возвращает логарифм по основанию 10 входного массива поэлементно.
log2 (x, /[ out, where, casting, order, . ..])
Логарифм по основанию 2 числа x .
log1p (x, /[ out, where, casting, order, …])
Возвращает натуральный логарифм единицы плюс входной массив поэлементно.
logaddexp (x1, x2, /[ out, where, casting, …])
Логарифм суммы возведений в степень входных данных.
logaddexp2 (x1, x2, /[ out, where, casting, …])
Логарифм суммы возведений в степень входных данных по основанию 2.
Другие специальные функции
i0 (х)
Модифицированная функция Бесселя первого рода, порядок 0.
синк (х)
Вернуть нормализованную функцию sinc.
Подпрограммы с плавающей запятой
знаковый бит (x, /[ out, where, casting, order, . ..])
Возвращает поэлементно True, если установлен знаковый бит (меньше нуля).
копия (x1, x2, /[ out, where, casting, …])
Изменить знак x1 на знак x2 поэлементно.
frexp (x[ out1, out2], / [[ out, where, …])
Разложите элементы x на мантисса и двойки в степени.
ldexp (x1, x2, /[ out, where, casting, …])
Возвращает x1 * 2**x2 поэлементно.
nextafter (x1, x2, /[ out, where, casting, …])
Возвращает следующее значение с плавающей запятой после x1 в сторону x2, поэлементно.
интервал (x, /[ out, where, casting, order, …])
Возвращает расстояние между x и ближайшим соседним числом.
Рациональные подпрограммы
lcm (x1, x2, /[ out, where, casting, order, . ..])
Возвращает наименьшее общее кратное числа |x1| и |x2|
gcd (x1, x2, /[ out, where, casting, order, …])
Возвращает наибольший общий делитель числа |x1| и |x2|
Арифметические операции
добавить (x1, x2, /[ out, where, casting, order, …])
Добавить аргументы поэлементно.
обратное (x, /[ out, where, casting, …])
Возвращает обратную величину аргумента, поэлементно.
положительный (x, /[ out, where, casting, order, …])
Числовое положительное, поэлементное.
отрицательный (x, /[ out, where, casting, order, …])
Числовое отрицательное число, поэлементно.
умножить (x1, x2, /[ out, где, приведение, …])
Поэлементное умножение аргументов.
разделить (x1, x2, /[ out, where, casting, …])
Разделить аргументы поэлементно.
мощность (x1, x2, /[ out, where, casting, …])
Элементы первого массива возведены в степени из второго массива, поэлементно.
вычесть (x1, x2, /[ out, where, casting, …])
Вычитание аргументов поэлементно.
true_divide (x1, x2, /[ выход, где, …])
Разделить аргументы поэлементно.
floor_divide (x1, x2, /[ выход, где, …])
Возвращает наибольшее целое число, меньшее или равное делению входных данных.
float_power (x1, x2, /[ выход, где, . ..])
Элементы первого массива возведены в степени из второго массива, поэлементно.
fmod (x1, x2, /[ out, where, casting, …])
Возвращает поэлементный остаток от деления.
mod (x1, x2, /[ out, where, casting, order, …])
Возвращает поэлементный остаток от деления.
modf (x[ out1, out2], / [[ out, where, …])
Возвращает дробную и целую части массива поэлементно.
остаток (x1, x2, /[ out, where, casting, …])
Возвращает поэлементный остаток от деления.
divmod (x1, x2[ out1, out2], / [[ out, …])
Возвращает поэлементно частное и остаток одновременно.
Обработка комплексных чисел
угол (z[ град])
Возвращает угол сложного аргумента.
реальный (вал)
Возвращает действительную часть сложного аргумента.
изображение (вал)
Возвращает мнимую часть сложного аргумента.
conj (x, /[ out, where, casting, order, …])
Вернуть комплексно-сопряженное число поэлементно.
сопряжение (x, /[ out, where, casting, …])
Вернуть комплексно-сопряженное число поэлементно.
Поиск экстремумов
максимум (x1, x2, /[ out, where, casting, …])
Поэлементный максимум элементов массива.
fmax (x1, x2, /[ out, where, casting, …])
Поэлементный максимум элементов массива.
amax (a[ ось, выход, keepdims, начальный, где])
Возвращает максимум массива или максимум по оси.
nanmax (a[ ось, выход, keepdims, начальный, где])
Возвращает максимум массива или максимум вдоль оси, игнорируя любые значения NaN.
минимум (x1, x2, /[ out, where, casting, …])
Поэлементный минимум элементов массива.
fmin (x1, x2, /[ out, where, casting, …])
Поэлементный минимум элементов массива.
амин (a[ ось, выход, keepdims, начальный, где])
Возвращает минимум массива или минимум вдоль оси.
нанмин (a[ ось, выход, keepdims, инициал, где])
Возвращает минимум массива или минимум вдоль оси, игнорируя любые значения NaN.
Разное
свертка (а, v[ режим])
Возвращает дискретную линейную свертку двух одномерных последовательностей.
зажим (a, a_min, a_max[ out])
Обрезать (ограничить) значения в массиве.
sqrt (x, /[ out, where, casting, order, …])
Возвращает неотрицательный квадратный корень массива поэлементно.
cbrt (x, /[ out, where, casting, order, …])
Возвращает кубический корень массива поэлементно.
квадрат (x, /[ out, where, casting, order, …])
Возвращает поэлементный квадрат ввода.
абсолютный (x, /[ out, where, casting, order, …])
Поэлементное вычисление абсолютного значения.
fabs (x, /[ out, where, casting, order, …])
Вычислить абсолютные значения поэлементно.
знак (x, /[ out, where, casting, order, …])
Возвращает поэлементное указание знака числа.
heaviside (x1, x2, /[ out, где, casting, …])
Вычисление ступенчатой функции Хевисайда.
nan_to_num (x[ копировать, nan, posinf, neginf])
Заменить NaN на ноль и бесконечность на большие конечные числа (поведение по умолчанию) или на числа, заданные пользователем с помощью nan , posinf и/или neginf ключевых слов.
real_if_close (a[ tol])
Если ввод комплексный, все мнимые части близки к нулю, вернуть действительные части.
вставка (x, xp, fp[ лево, право, точка])
Одномерная линейная интерполяция для монотонно возрастающих точек выборки.
Часто задаваемые вопросы о кормлении смесью: Начало работы (для родителей)
Планируете ли вы кормить ребенка смесью с самого начала, хотите дополнить грудное молоко смесью или переходите с грудного молока на смесь, у вас, вероятно, возникнут вопросы.
Вот ответы на некоторые распространенные вопросы о искусственном вскармливании.
Какие расходные материалы мне нужны?
Начните с основ:
формула
вода (водопроводная вода подойдет, но используйте бутилированную, если вы беспокоитесь о безопасности воды)
бутылки
соски
Держите под рукой салфетки для отрыжки и ершик для бутылочек/сосок.
Стерилизатор для бутылочек не нужен, но стерилизуйте бутылочки и соски, прокипятив их в течение 5 минут перед первым использованием.
Какую бутылку следует использовать?
Бутылки бывают разных форм и размеров. Они могут быть изготовлены из стекла, пластика, силикона или нержавеющей стали. Вот некоторые отличия:
Пластиковые бутылки теперь «не содержат бисфенола-А» — это означает, что они не содержат химический бисфенол А (БФА). Это химическое вещество может быть вредным и содержится в некоторых видах пластика, но запрещено в детских бутылочках. Несколько лет назад в некоторых пластиковых детских бутылочках был BPA, но сейчас его нет.
Стеклянные бутылки. Разбитые стеклянные бутылки могут нанести травму, но силиконовые втулки облегчают их захват и предотвращают поломки.
Силиконовые бутылки и бутылки из нержавеющей стали — более новые варианты. Они небьющиеся, но, как правило, дороже, чем пластиковые или стеклянные.
Некоторым детям лучше подходят бутылочки определенной формы, бутылочки с вентиляцией или бутылочки с вкладышем внутри. Возможно, вам придется попробовать несколько видов, прежде чем вы найдете то, что лучше всего подходит для вас и вашего ребенка.
Чтобы пережить первую неделю или около того, убедитесь, что у вас достаточно смеси, воды, бутылочек и сосок.
Со временем вы, возможно, захотите купить больше или другие виды бутылок. Вы также можете найти, что стоит приобрести другие принадлежности, такие как сушилка для бутылок или специальная корзина для посудомоечной машины.
Какой тип соски следует использовать?
Соски могут быть изготовлены из силикона (прозрачные) или латекса (коричневые) самых разных форм. Разновидности включают стандартные или традиционные соски, ортодонтические соски, соски с широким основанием и соски с плоским верхом. Используйте любой тип, который предпочитает ваш ребенок.
Соски также часто имеют разное количество, «стадии» или «скорости потока», чтобы отразить размер отверстия соска, который влияет на поток (т. е. медленный, средний или быстрый) смеси или грудного молока. Отверстия становятся больше по мере того, как дети становятся старше и готовы справляться с более быстрым потоком молока. Слишком быстрые потоки могут вызвать рвотные позывы у детей младшего возраста, поскольку они дают им больше молока, чем они могут усвоить. Более медленный поток может раздражать некоторых детей, заставлять их сосать сильнее и заглатывать слишком много воздуха.
Начинайте кормить новорожденного с соски с самым медленным потоком. Когда ваш ребенок подрастет, вы можете увеличить поток, если хотите. Некоторые дети в младенчестве могут довольствоваться использованием соски одного и того же вида и размера. Если ваш ребенок кажется суетливым или расстроенным из-за соски, попробуйте другой вид (например, с большим отверстием), чтобы увидеть, есть ли разница.
Как часто нужно менять соски?
Это зависит от того, насколько соски, которые вы используете, выдерживают чистку и повседневное использование. Регулярно проверяйте их на наличие признаков износа и заменяйте примерно каждые 2 месяца или чаще, если заметите разрывы или повреждения.
Какой тип формулы следует использовать?
В настоящее время доступно множество различных формул. Спросите своего врача, какой вид лучше всего подходит для вашего ребенка.
Не пытайтесь самостоятельно приготовить формулу дома. Онлайн-рецепты могут выглядеть здоровыми и обещать полноценные питательные вещества, но в них может быть слишком мало или слишком много важных питательных веществ, что может вызвать серьезные проблемы со здоровьем у вашего ребенка.
Существует множество различных марок детских смесей, и все, что производится в Соединенных Штатах (торговые марки, торговые марки и дженерики), должно соответствовать строгим стандартам питания и безопасности.
Типы смесей включают:
смеси на основе коровьего молока. Большинство смесей производится из коровьего молока. В эти смеси добавлено железо, в котором нуждаются дети. Используйте только обогащенную железом формулу, если ваш врач не советует вам этого делать.
смеси на основе сои. Предназначены для детей, рожденных с врожденной недостаточностью лактазы или галактоземией. Этот тип смеси также используется родителями, которые не хотят, чтобы их дети питались животным белком. Дайте только обогащенную железом соевую смесь, если только ваш врач не сказал иначе. (Многие дети с аллергией на коровье молоко также имеют аллергию на белок в соевых смесях, поэтому смеси на основе сои обычно не помогают при аллергии на молочный белок.)
гипоаллергенные смеси для детей, которые не переносят коровье молоко или соевые смеси, например, для детей с аллергией на молочные или соевые белки. Белки в гипоаллергенных смесях расщепляются, поэтому их легче усваивать.
специализированные формулы. Предназначены для недоношенных детей.
Как приготовить молочную смесь?
Формула выпускается в трех основных формах:
порошки , которые требуют смешивания с водой и стоят меньше всего
концентраты , представляющие собой жидкости, требующие разбавления водой
готовые к употреблению (или готовые к употреблению) жидкости, которые можно разливать прямо в бутылочки. Это самые дорогие, но удобные, если вы путешествуете или не можете добраться до источника чистой воды.
При приготовлении смеси внимательно следуйте указаниям на этикетке. Не добавляйте больше воды, чем указано.
Какую бы смесь вы ни выбрали, проверяйте срок годности на всех банках и бутылочках со смесью и не используйте смесь из протекающих, помятых или иным образом поврежденных контейнеров. Не разбавляйте формулу водой — это опасно, так как уменьшает количество питательных веществ в каждой бутылочке.
Формула может быть дорогой. Как я могу сэкономить деньги?
Поищите лучшие предложения на выбранную вами смесь:
Воспользуйтесь преимуществами бесплатных образцов и купонов, отправленных вам в первые несколько месяцев после рождения вашего ребенка.
Вырежьте купоны и зарегистрируйтесь в онлайн-клубах купонов и приложениях, которые позволяют распечатывать и сохранять купоны.
Зарегистрируйтесь в клубах производителей смесей и в специальных программах (по почте или через Интернет), которые могут предлагать скидки, купоны и/или бесплатные смеси и другие продукты.
No related posts.