Онлайн урок: Сложение и вычитание десятичных дробей по предмету Математика 5 класс
Десятичные дроби используют в самых различных сферах деятельности человека.
Они значительно упрощают вычисления и измерения.
Десятичные дроби удобны при решении профессиональных и бытовых задач.
Важным преимуществом десятичных дробей является то, что математические действия, производимые с ними, схожи по своей сути с арифметическими действиями, которые можно совершать с натуральными числами.
Десятичные дроби можно сравнивать, складывать, вычитать, умножать и делить, возводить в степень.
На данном уроке рассмотрим правила сложения и вычитания десятичных дробей.
Узнаем, как складывать и вычитать десятичные дроби столбиком.
Выясним, как на координатной прямой можно отметить десятичную дробь, не переводя ее в обыкновенную дробь.
Рассмотрим пример решения составной текстовой задачи на сложение и вычитание десятичных дробей арифметическим и алгебраическим способом.
Разберем простую арифметическую задачу.
На детский праздник купили 2,250 кг шоколадных конфет и 3,550 кг карамели.
Сколько всего конфет купили на детский праздник?
Решение:
Кратко запишем условие задачи.
Чтобы найти ответ на поставленный вопрос (найти общее количество конфет), необходимо сложить шоколадные конфеты и карамель вместе.
Схематически изобразим условие задачи.
Сложим десятичные дроби 2,250 и 3,550.
Сложение десятичных дробей можно свести к сложению смешанных чисел, которые соответствуют этим дробям.
Десятичной дроби 2,250 соответствует смешанное число \(\mathbf{2\frac{250}{1000}}\).
Десятичной дроби 3,550 соответствует смешанное число \(\mathbf{3\frac{550}{1000}}\).
Нам известно, как найти сумму двух смешанных чисел.
Сложим целые части отдельно, дробные- отдельно.
\(\mathbf{2\frac{250}{1000} + 3\frac{550}{1000} = 2 + \frac{250}{1000} + 3 + \frac{550}{1000} = (2 + 3) + (\frac{250}{1000} + \frac{550}{1000}) =}\)
\(\mathbf{= 5 + \frac{800}{1000} = 5\frac{800}{1000}}\) (кг) всего конфет купили для детского праздника.
Ответ: \(\mathbf{5\frac{800}{1000} = 5,800}\) (кг).
Такой же ответ можно получить, не обращая десятичные дроби в смешанные числа.
Выясним, как и по каким правилам складывают десятичные дроби.
Так как запись десятичных дробей основана на позиционной системе счисления, в которой значение каждого числового знака зависит от позиции (от места) в числе, десятичные дроби удобно складывать поразрядно.
В связи с этим, чтобы сложить дроби, записанные в десятичной форме, необходимо убедиться, что в числах одинаковое количество разрядов после запятой.
Сложение десятичных дробей практически не отличается от сложения натуральных чисел, удобнее всего выполнять операцию сложения в столбик, записывая соответствующие разряды друг под другом.
Чтобы сложить две десятичные дроби столбиком, необходимо соблюдать следующие правила:
- Уравнять в слагаемых количество цифр после запятой, дописав нужное количество нулей к одной из дробей.
- Записать слагаемые друг под другом так, чтобы разряды второго слагаемого располагались строго под соответствующими разрядами первого слагаемого, а запятая под запятой.
- Сложить поразрядно числа, не обращая внимание на запятую так же, как выполняется сложение столбиком натуральных чисел.
- Поставить в полученной сумме запятую под запятыми слагаемых.
Используя данный алгоритм сложения десятичных дробей, решим задачу про конфеты, рассмотренную в начале нашего урока.
Вспомним условие задачи.
2,250 кг шоколадных конфет
3,550 кг карамельных конфет
Общее количество конфет- ? кг
Решение:
Найдем общее количество конфет, купленных на праздник, сложив две десятичные дроби 2,250 и 3,550.
Количество десятичных знаков в данных дробях одинаково, поэтому сразу запишем дроби в столбик так, чтобы одноименные разряды находились друг под другом, запятая под запятой (целая часть под целой частью, дробная под дробной).
Выполним сложение дробей по правилам сложения столбиком натуральных чисел, не обращая внимание на десятичные запятые.
Сложим цифры поразрядно.
Поставим десятичную запятую в полученный результат суммы под запятыми, которые стоят в слагаемых (по правилу: «запятая под запятой»).
В итоге операция сложения двух десятичных дробей выглядит так:
2,250 + 3,550 = 5,800 (кг) конфет купили для детского праздника
Ответ: 5,800 (кг).
При сложении десятичных дробей получился результат такой же, как при сложении смешанных чисел, которые этим дробям соответствуют.
Как видите, операция сложения десятичных дробей мало отличается от сложения натуральных чисел, важно только верно расположить разряды и десятичные запятые слагаемых.
Встречаются случаи, когда приходится складывать десятичные дроби, в которых различное количество десятичных знаков.
Если после запятой в одном из слагаемых десятичных знаков меньше, чем в другом, количество знаков нужно уравнять, недостающие разряды следует заменить нулем.
После этого десятичные дроби складывают.
Рассмотрим поясняющий пример.
Найдем сумму десятичных дробей 0,434 и 0,28.
В первой десятичной дроби 0,434 после запятой три десятичных знака (разряд десятых, сотых, тысячных).
Во второй десятичной дроби 0,28 после запятой два десятичных знака (разряд десятых и сотых, отсутствует разряд тысячных).
Уравняем количество десятичных знаков.
Допишем нуль справа от десятичной запятой после самой правой ненулевой цифры (в разряде тысячных).
В итоге получим десятичную дробь 0,280, равную дроби 0,28.
Столбиком запишем дроби 0,434 и 0,280 так чтобы одноименные разряды и десятичные запятые находились строго друг под другом.
Далее выполним сложение дробей по правилам сложения столбиком натуральных чисел, не обращая внимание на десятичные запятые.
Сложим цифры поразрядно.
При сложении сотых получается двузначное число 11, поэтому единицу запишем под чертой, а свободный десяток перенесем в старший разряд.
Поставим десятичную запятую в полученный результат суммы под запятыми, которые стоят в слагаемых (по правилу: «запятая под запятой»).
В итоге операция сложения двух десятичных дробей 0,434 и 0,280 будет выглядеть так:
Сложение десятичной дроби и натурального числа.
Иногда приходится находить сумму десятичной дроби и натурального числа.
По сути, чтобы сложить натуральное число с десятичной дробью, необходимо это натуральное число и целую часть десятичной дроби сложить, а дробную часть оставить без изменений.
При сложении десятичной дроби и натурального числа в конце натурального числа можно поставить десятичную запятую и приписать столько нулей, сколько содержится десятичных знаков в дроби.
Данные действия не изменят значение натурального числа.
Рассмотрим поясняющий пример, решим простую задачу на сложение.
С первого участка собрали 60 т зерна, а со второго на 16,8 т больше.
Сколько тонн зерна собрали со второго участка?
Решение:
Запишем кратко условие задачи.
Из условия задачи известно, что со второго участка собрали зерна больше, чем с первого, т.е. получается со второго поля убрали столько же, сколько и с первого, да еще 16,8 т.
Схематично изобразим условие задачи.
Такая задача, в которой одно число увеличивают на какое-нибудь другое число (задача на увеличение на некоторое количество единиц), решается всегда сложением.
Сложим натуральное число
Для этого прибавим к целой части десятичной дроби натуральное число, а дробную часть оставим прежней.
Целая часть десятичной дроби 16,8 равна 16, прибавим к ней 60, получим число 76, поставим запятую и припишем дробную часть заданной десятичной дроби.
16,8 + 60 = 76,8 (т) зерна собрали со второго участка.
Ответ: 76,8 (т).
У меня есть дополнительная информация к этой части урока!
Закрыть
На нашем простом примере рассмотрим, как сложить натуральное число с десятичной дробью столбиком.
Сложим натуральное число 60 с десятичной дробью 16,8.
Число 60
можно представить в виде десятичной дроби, в которой дробная часть равна нулю.Для этого после числа 60 нужно поставить десятичную запятую и приписать необходимое количество нулей.
В нашем случае допишем всего один нуль, так как во втором слагаемом, т. е. в десятичной дроби 16,8, присутствует только один десятичный знак.
е. в десятичной дроби 16,8, присутствует только один десятичный знак.
В результате получим десятичную дробь 60, 0, равную натуральному числу 60.
Запишем дроби в столбик так, чтобы одноименные разряды находились друг под другом, запятая под запятой (целая часть под целой частью, дробная под дробной).
Далее выполним сложение дробей по правилам сложения столбиком натуральных чисел, не обращая внимание на десятичные запятые.
Сложим цифры поразрядно.
Поставим десятичную запятую в полученный результат суммы под запятыми, которые стоят в слагаемых (по правилу: «запятая под запятой»).
В итоге сумма натурального числа и десятичной дроби будет выглядеть следующим образом:
Сложение десятичных дробей с обыкновенной дробью (смешанным числом).
- Сложение десятичных дробей с обыкновенной дробью (смешанным числом) можно свести к сложению обыкновенных дробей (смешанных чисел).

Для этого десятичную дробь необходимо представить в виде обыкновенной дроби.
- Сложение десятичных дробей с обыкновенной дробью (смешанным числом) можно свести к сложению десятичных дробей, представив обыкновенную дробь (смешанное число) в виде десятичной дроби.
Для примера сложим смешанное число и десятичную дробь.
Найдите сумму \(\mathbf{1\frac{2}{10} + 0,5}\).
Первый способ.
Переведем десятичную дробь в обыкновенную.
\(\mathbf{0,5 = \frac{5}{10}}\)
Теперь сумму смешанного числа \(\mathbf{1\frac{2}{10}}\) и обыкновенной дроби \(\mathbf{\frac{5}{10}}\) найдем по правилу сложения смешанного числа и обыкновенной дроби.
Сложим смешанное число и правильную дробь, найдем только сумму дробной части смешанного числа и этой дроби, целую же часть смешанного числа при этом оставим без изменений.
\(\mathbf{1\frac{2}{10} + \frac{5}{10} = 1 + \frac{2}{10} + \frac{5}{10} = 1 + (\frac{2}{10} + \frac{5}{10}) = 1 + \frac{7}{10} = 1\frac{7}{10}}\)
Переведем смешанное число \(\mathbf{1\frac{7}{10}}\) в десятичную дробь.
\(\mathbf{1\frac{7}{10} = 1,7}\)
Ответ: 1,7.
Второй способ.
Представим смешанное число в виде десятичной дроби.
\(\mathbf{1\frac{2}{10} = 1,2}\)
Теперь сумму десятичной дроби 1,2 и десятичной дроби 0,5 найдем по правилу сложения десятичных дробей.
Сумму чисел 1,2 и 0,5 запишем столбиком, располагая соответствующие разряды друг под другом, запятая под запятой.
Ответ: 1,7.
Вычисляя сумму первым и вторым способом, получили одинаковые ответы, следовательно, рассмотренные нами способы нахождения суммы десятичной дроби и обыкновенной дроби (смешанного числа) равноправны.
У меня есть дополнительная информация к этой части урока!
Закрыть
Десятичную дробь легко отметить на координатном луче, не переводя ее в смешанное число.
Для этого нужно разложить по разрядам десятичную дробь.
Рассмотрим пример.
Отметим на координатном луче число 1,25 (одна целая двадцать пять сотых).
Разложим заданное число по разрядам.
1,25 = 1 + 0,2 + 0,05
Изобразим горизонтальный координатный луч, направленный вправо, с началом отсчета в точке О(0) и единичным отрезком ОЕ, равным 1 единице.
Отложим один единичный отрезок от начала координат, получим одну целую единицу.
Чтобы отметить дробь 0,2, второй единичный отрезок разделим на десять долей, каждая такая доля будет равна \(\mathbf{\frac{1}{10} = 0,1}\).
От точки с координатой 1 отложим вправо две доли единичного отрезка ОЕ, получим точку 1,2.
Далее, чтобы отметить сотые доли, разделим долю единичного отрезка, следующую за точкой с координатой 1,2 на десять частей, каждая такая часть будет равна \(\mathbf{\frac{1}{100} = 0,01}\).
Отложим от числа 1,2 пять сотых долей, получим число 1,25.
Пройти тест
Закрыть тест
Пройти тест и получить оценку можно после входа или регистрации
Вход Регистрация
Рассмотрим правила вычитания десятичных дробей.
Так как десятичная дробь- это десятичная запись обыкновенной дроби, вычитание двух десятичных дробей можно свести к разности соответствующих обыкновенных дробей.
Рассмотрим пример вычисления десятичных дробей.
Задача
Провод длинной 15,45 м разрезали на две части.
Длина первой части провода 5,20 м.
Какова длина второй части провода?
Решение:
Кратко запишем условие задачи.
Две части провода вместе представляют собой целый провод.
Длина первой части провода- это известное слагаемое.
Длина второй части провода- это неизвестное слагаемое.
Схематически изобразим условие задачи.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Найдем разность двух десятичных дробей 15,45 и 5,2.
Представим заданные десятичные дроби в виде смешанных чисел.
Десятичной дроби 15,45 соответствует смешанное число \(\mathbf{15\frac{45}{100}}\).
Десятичной дроби 5,2 соответствует смешанное число \(\mathbf{5\frac{2}{10}}\).
Приведем дроби к общему знаменателю.
Десятичная дробь 15,45 содержит два десятичных знака (разряд десятых и разряд сотых).
Десятичная дробь 5,2 содержит один десятичный знак (разряд десятых).
Чтобы уравнять количество знаков после запятой, запишем нуль в дроби 5,2 после разряда десятых.
Получим число 5,20, равное 5,2.
Десятичная дробь 5,20 соответствует смешанному числу \(\mathbf{5\frac{20}{100}}\).
После того, как мы уравняли знаменатели дробных частей смешанных чисел, можно приступать к вычитанию.
\(\mathbf{15\frac{45}{100} — 5\frac{20}{100} = (15 + \frac{45}{100}) — (5 + \frac{20}{100}) = (15 — 5) + (\frac{45}{100} — \frac{20}{100}) = 10\frac{25}{100}}\)
Переведем смешанное число \(\mathbf{10\frac{25}{100}}\) в десятичную дробь.
\(\mathbf{10\frac{25}{100} = 10,25}\) (м) длина второй части провода
Ответ: 10,25 (м).
Такой же ответ можно получить, не переводя десятичные дроби в смешанные числа.
Так же как при сложении, десятичные дроби удобно вычитать в столбик.
Операция вычитания десятичных дробей столбиком очень похожа на вычитание натуральных чисел аналогичным способом.
Выполняя вычитание десятичных дробей столбиком, необходимо соблюдать несложные правила:
- Уравнять количество десятичных знаков в уменьшаемом и вычитаемом (если это требуется), дописав необходимое количество нулей к одной из дробей.

- Вычитаемое записать под уменьшаемым в столбик так, чтобы соответствующие их разряды находились строго друг под другом, запятая под запятой.
- Выполнить вычитание столбиком так, как вычитают натуральные числа (не обращая внимание на запятые).
- В полученной разности поставить запятую так, чтобы она находилась строго под запятыми уменьшаемого и вычитаемого.
Воспользуемся данным алгоритмом при решении задачи.
Вспомним задачу про провод, рассмотренную выше.
Кратко запишем условие задачи.
Две части провода вместе представляют собой целый провод.
Длина первой части провода- это известное слагаемое.
Длина второй части провода- это неизвестное слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Найдем разность двух десятичных дробей 15,45 и 5,2.
Уравняем количество знаков в уменьшаемом и вычитаемом, для этого в дробную часть десятичной дроби 5,2 в разряд сотых запишем нуль.
Получим число 5,20, равное 5,2.
Запишем уменьшаемое 15,45 и вычитаемое 5,20 столбиком так, чтобы соответствующие их разряды находились строго друг под другом, запятая под запятой (целая часть под целой частью, дробная под дробной).
Вычтем дроби, не обращая внимание на десятичные запятые.
В полученной разности запятую поставим строго под запятыми, стоящими в уменьшаемом и вычитаемом.
Вычитание десятичных дробей столбиком будет выглядеть так:
В итоге получаем:
15,45 – 5,20 = 10,25 (м) длина второй части провода.
Ответ: 10,25 (м).
При вычитании десятичных дробей получился результат такой же, как при вычитании смешанных чисел, которые этим дробям соответствуют.
Операция вычитания десятичных дробей практически не отличается от вычитания натуральных чисел, важно только верно расположить разряды и десятичные запятые уменьшаемого и вычитаемого.
Вычитание десятичной дроби из натурального числа.
Вычитание десятичной дроби из натурального числа удобней выполнять в столбик.
Натуральное число в таком случае лучше представить в виде десятичной дроби, заменив дробную часть нулями.
Рассмотрим пример.
Периметр треугольника равен 34 см.
Сумма двух его сторон равна 23,1 см.
Найдите длину его третьей стороны.
Сделаем условный рисунок.
Пусть a, b, c— стороны треугольника, Р— это периметр треугольника- сумма длин трех его сторон.
Представим натуральное число 34 в виде десятичной дроби.
Вычитаемая дробь имеет один знак в дробной части, поэтому после натурального числа 34 поставим десятичную запятую, а после нее запишем один нуль, получим число 34,0 (тридцать четыре целых ноль десятых).
Выполним вычитание десятичных дробей 34,0 и 23,1 столбиком.
Так как из нуля единица не вычитается, займем десяток единиц из старшего разряда, при этом в нем на один десяток единиц станет меньше.
В итоге получаем:
c = 34 – 23,1 = 10,9 (см)- длина третьей стороны треугольника.
Ответ: с = 10,9 (см).
Вычитание натурального числа из десятичной дроби.
Чтобы вычесть натуральное число из десятичной дроби, необходимо это натуральное число вычесть из целой части уменьшаемой десятичной дроби, при этом дробную часть десятичной дроби необходимо оставить без изменений.
Пример.
Решим уравнение 59,3 – х = 18.
Найдем значение неизвестного х, при котором данное уравнение обратиться в верное равенство.
В заданном уравнении неизвестное является вычитаемым.
Чтобы найти вычитаемое (х), необходимо из уменьшаемого вычесть разность.
59,3 – х = 18
х = 59,3 – 18
Вычтем из десятичной дроби натуральное число по правилу: из целой части десятичной дроби 59,3 вычтем число 18, получим число 41, а дробную часть оставим без изменений.
х = 41,3
Проверка:
В исходное уравнение 59,3 – х = 18 вместо неизвестного х подставим найденное число х = 41,3.
59,3 – 41,3 = 18
Выполним вычитание столбиком двух десятичных дробей 59,3 и 41,3.
Вычитаемое запишем под уменьшаемым так, чтобы одноименные их разряды стояли строго друг под другом, запятая вычитаемого под запятой уменьшаемого.
Поразрядно выполним вычитание, в полученной разности поставим десятичную запятую так, чтобы она находилась под запятыми уменьшаемого и вычитаемого.
18,0 = 18 (получили верное равенство, значит корень уравнения найден верно).
Ответ: х = 41,3.
Вычитание десятичной дроби из обыкновенной (смешанного числа) и наоборот.
Первый способ.
Вычитание десятичной дроби из обыкновенной (смешанного числа) и обыкновенной (смешанного числа) из десятичной можно свести к разности двух обыкновенных дробей (к разности двух смешанных чисел).
Для этого десятичную дробь нужно представить в виде обыкновенной дроби (смешанного числа) и выполнить вычитание двух обыкновенных дробей (смешанных чисел).
Второй способ.
Вычитание десятичной дроби из обыкновенной (смешанного числа) и обыкновенной (смешанного числа) из десятичной можно свести к разности двух десятичных дробей.
Для этого обыкновенную дробь (смешанное число) нужно представить в виде десятичной дроби и выполнить вычитание двух десятичных дробей.
Рассмотрим пример.
Найдите значение выражения \(\mathbf{27\frac{35}{100} — 6,11}\).
Решение №1.
Переведем десятичную дробь 6,11 в смешанное число.
\(\mathbf{6,11 = 6\frac{11}{100}}\)
Подставим в исходное выражение вместо десятичной дроби 6,11 полученное смешанное число \(\mathbf{6\frac{11}{100}}\).
Найдем разность двух смешанных чисел.
\(\mathbf{27\frac{35}{100} — 6\frac{11}{100} = (27 — 6) + (\frac{35}{100} — \frac{11}{100}) = 21 + \frac{24}{100} = 21\frac{24}{100}}\)
Решение №2.
Представим смешанное число \(\mathbf{27\frac{35}{100}}\) в виде десятичной дроби.
\(\mathbf{27\frac{35}{100} = 27,35}\)
Подставим в исходное выражение вместо смешанного числа \(\mathbf{27\frac{35}{100}}\) соответствующую ему десятичную дробь 27,35.
Найдем разность двух десятичных дробей: 27,35 – 6,11.
Выполним вычитание столбиком.
Вычитаемое запишем под уменьшаемым так, чтобы одноименные их разряды стояли строго друг под другом, запятая вычитаемого под запятой уменьшаемого.
Поразрядно выполним вычитание, в полученной разности поставим десятичную запятую так, чтобы она находилась под запятыми уменьшаемого и вычитаемого.
В результате получили десятичную дробь 21,24.
Находя значение выражения \(\mathbf{27\frac{35}{100} — 6,11}\) первым и вторым способом, получили один и тот же ответ, что доказывает равенство этих двух способов вычисления.
Пройти тест
Закрыть тест
Пройти тест и получить оценку можно после входа или регистрации
Вход Регистрация
Математические операции сложения и вычитания часто приходятся использовать при решении уравнений и различных задач.
Для одной и той же задачи может существовать несколько верных способов ее решения.
Выбрав верную логику рассуждения, можно значительно упростить и ускорить процесс решения текстовой задачи.
Попробуем решить составную текстовую задачу на сложение и вычитание десятичных дробей арифметическим и алгебраическим способом.
При решении задач тем и другим способом необходимо учитывать и соблюдать основные свойства и правила математических операций, применять известные правила упрощения и преобразования выражений.
Задача.
В трехкомнатной квартире, площадью 51,5 м2, первая комната имеет площадь 10,5 м2, площадь второй комнаты на 12,3 м2 больше площади первой.
Какова площадь третьей комнаты?
Решим данную задачу арифметическим способом (составлением выражения).
Запишем кратко условие задачи.
Площадь первой комнаты- 10,5 м2
Площадь второй комнаты- 10,5 + 12,3 м2
Площадь третьей комнаты- ? м2
Общая площадь квартиры- 51,5 м2.
Чтобы найти площадь третьей комнаты, необходимо из общей площади трехкомнатной квартиры вычесть площадь первой и второй комнаты.
Составим выражение:
Найдем значение полученного выражения.
Данное выражение содержатся сразу несколько арифметических операций и скобки.
Определим порядок действий в данном выражении, используя правила, которые определяют порядок выполнения действий в математических выражениях.
1) Это выражение содержит скобки, следовательно, первым делом выполним действия в них.
Найдем сумму двух десятичных дробей 10,5 и 12,3 столбиком.
Количество десятичных знаков в десятичных дробях одинаково, поэтому сразу запишем дроби в столбик так, чтобы одноименные разряды находились друг под другом, запятая под запятой (целая часть под целой частью, дробная под дробной).
Поразрядно выполним сложение, в полученной сумме поставим десятичную запятую так, чтобы она находилась под запятыми слагаемых.
Оставшиеся за скобками действия- это действия первой ступени (сложение и вычитание), они выполняются по порядку следования слева направо.
2) Найдем разность десятичных дробей 51,5 и 10,5.
Вычитаемое запишем под уменьшаемым так, чтобы одноименные их разряды стояли строго друг под другом, запятая вычитаемого под запятой уменьшаемого.
Поразрядно выполним вычитание, в полученной разности поставим десятичную запятую так, чтобы она находилась под запятыми уменьшаемого и вычитаемого.
3) Найдем разность значений, которые были получены во втором и первом действии, т.е. из десятичной дроби 41,0 вычтем десятичную дробь 22,8.
В результате получим:
51,5 – 10,5 – (10,5 + 12,3) = 18,2 (м2) площадь третьей комнаты.
Ответ: 18,2 (м2).
Эту же задачу можно решить арифметическим способом, но по действиям.
Запишем кратко условие задачи.
Площадь третьей комнаты- ? м2
Общая площадь квартиры- 51,5 м2.
В этом случае решение заданной задачи будет состоять из следующих этапов:
- Найдем площадь второй комнаты (данное действие мы выполняли, решая задачу первым способом).
- Сложив результат, полученный в первом действии, с площадью первой комнаты, определим общую площадь двух комнат- первой и второй вместе.
- Из площади всей трехкомнатной квартиры вычтем общую площадь первой и второй комнат.
1. 10,5 + 12,3 = 22,8 (м2) площадь второй комнаты.
2. Чтобы высчитать площадь второй комнаты, выполним сложение двух десятичных дробей столбиком:
10,5 + 22,8 = 33,3 (м2) площадь первой и второй комнат вместе.
3. Чтобы высчитать площадь третьей комнаты, выполним вычитание двух десятичных дробей столбиком:
51,5 – 33,3 = 18,2 (м2) площадь третьей комнаты.
Ответ: 18,2 (м2).
Решим задачу алгебраическим способом.
Кратко запишем условие задачи.
Площадь первой комнаты- 10,5 м2
Площадь второй комнаты- 10,5 + 12,3 м2
Пусть х м2 площадь третьей комнаты
Зная, что площадь всей квартиры равна 51,5 м2, составим уравнение.
10,5 + (10,5 + 12,3) + х = 51,5
Упростим уравнение: выполним действие в скобках, т.е. найдем сумму чисел 10,5 и 12,3, полученный результат сложим с первым слагаемым. (данные действия мы уже выполняли, решая задачу арифметическим способом).
10,5 + (10,5 + 12,3) = 10,5 + 22,8 = 33,3
В итоге получаем, что целое выражение 10,5 + (10,5 + 12,3) тождественно равно 33,3.
Подставим в исходное уравнение вместо суммы трех десятичных дробей результат их суммы: 33,3.
Получим простое уравнение с неизвестным слагаемым.
33,3 + х = 51,5
х = 51,5 – 33,3
х = 18,2 (м2) площадь третьей комнаты.
Ответ: 18,2 (м2).
Все три способа решения задачи равноправны и дают одинаковый результат.
Пройти тест
Закрыть тест
Пройти тест и получить оценку можно после входа или регистрации
Вход Регистрация
Пройти тест
Свойства дробей — общие формулы, правила и примеры для 5 класса » Kupuk.net
Использование дробных чисел позволило рассчитывать величины и проводить измерения в тех случаях, когда невозможно получить результат в виде целого. Любые действия над выражениями в математике выполняют с помощью правил и теорем, простейшие из которых изучают в 4−5 классах. Общие свойства и формулы для дробей довольно простые, но чтобы в них разобраться, следует самостоятельно прорешать несколько примеров и запомнить простые алгоритмы.
Общие свойства и формулы для дробей довольно простые, но чтобы в них разобраться, следует самостоятельно прорешать несколько примеров и запомнить простые алгоритмы.
Общие сведения
Дробь — это число, образуемое из равных долей единицы. Чтобы разобраться в сути выражения, следует понять, что означают слова «целое» и «часть». Пусть есть плитка шоколадки. Она разделена на десять частей. Если взять один кусочек, можно сказать, что в руках находится одна часть из десяти. Отломать второй — получится два куска опять же из десяти.
Эти кусочки и являются долями. То есть тем, из чего состоит целая часть. При этом их размеры должны быть одинаковыми. В рассматриваемой шоколадке их десять. Если её поделить пополам, то это действие будет сродни удалению пяти долей. На математическом языке это действие будет записано как 5 / 10. Целую же шоколадку можно представить так: 10 / 10.
Наклонная черта обозначает деление. В верхней части записывают число, определяющее, сколько долей было забрано от целого, значение которого указывается в нижней строке. В математике принято для краткости число, стоящее над чертой, называть числителем (делимым), а под ней знаменателем (делителем).
В математике принято для краткости число, стоящее над чертой, называть числителем (делимым), а под ней знаменателем (делителем).
В зависимости от значений отношения, существующие дробные выражения разделяют на три типа:
- правильные — делимое по количеству меньше делителя;
- неправильные — значение числителя больше, чем знаменателя;
- смешанные — состоят из целой части и неправильного выражения;
- многоэтажные — в числителе или знаменателе стоят дробные числа, например, (7/8) / 2.
Существуют и так называемые десятичные дроби. Их исторически выделили из-за простоты выражения. При этом в записи используется не черта, а запятая. Она отделяет единицы от десятичных значений. Например, 1,2; 0,2; 3,56. Это просто иные записи обыкновенных дробных выражений. Так: 1,2 = 12 / 10; 0,2 = 2 /10; 3,56 = 356 / 100.
Пожалуй, понятие смешанной дроби требует дополнительного объяснения. Записывают её так: x (y / z), где: x — целое число; y / z — дробное отношение. По сути, между двумя частями стоит знак плюс, который не указывают. Поэтому выражение x (y / z) можно переписать как x (y / z) = x + (y / z). Например, 3 (4/5) = 3 + (4 / 5).
По сути, между двумя частями стоит знак плюс, который не указывают. Поэтому выражение x (y / z) можно переписать как x (y / z) = x + (y / z). Например, 3 (4/5) = 3 + (4 / 5).
Так как дроби это числа, то с ними можно выполнять любые арифметические операции. Но их можно не только складывать, вычитать, умножать, делить, но и возводить в степень, дифференцировать, брать логарифм. Для выполнения этих действий нужно знать правила и свойства дробей, которым и обучают на уроках математики в школе.
Главное правило
Основное свойство дроби заключается в том, что если числитель и знаменатель умножить на одно и то же число, то результат действия от этого не изменится. Это правило справедливо и для операции деления. Доказать это утверждение довольно просто.
Пусть есть два равных выражения a / b и m / n. Они будут равными, если у них одинаковые числители и знаменатели. Значит: a * n = b * m. Например, 3 / 5 = 6 / 10, так как 3 * 10 = 5 * 6. Из этого следует, что одинаковыми будут по величине и выражения a / b = (m * c) / n * c), ведь равенство a * (n * c) = b * (m * c) также справедливо. Утверждать о верности последнего выражения можно на основании сочетательного и переместительного свойства умножения.
Они будут равными, если у них одинаковые числители и знаменатели. Значит: a * n = b * m. Например, 3 / 5 = 6 / 10, так как 3 * 10 = 5 * 6. Из этого следует, что одинаковыми будут по величине и выражения a / b = (m * c) / n * c), ведь равенство a * (n * c) = b * (m * c) также справедливо. Утверждать о верности последнего выражения можно на основании сочетательного и переместительного свойства умножения.
Эти правила гласят следующее:
- для любых натуральных чисел верно равенство a * b = b * a;
- результат перемножения трёх и более аргументов не поменяется, если группу членов заменить произведением a · b · c = (a · b) · c = a · (b · c).
Таким образом, можно записать: a / b = a * c / b * c. Это равенство и соответствует основному свойству дроби. В 5 классе после доказательства правильности утверждения, ученикам предлагается подумать над следствием, вытекающим из правила. На самом деле оно простое и порядка 90 процентов учеников называют его. Звучит оно так: если в дробном выражении делимое и делитель разделить на одно и то же число, значение выражения не изменится.
Звучит оно так: если в дробном выражении делимое и делитель разделить на одно и то же число, значение выражения не изменится.
Эти правила очень важны. Благодаря им исходное равенство можно при необходимости привести к простому виду. Использование следствия иногда называют сокращением дроби. Например, пусть есть простое для понимания отношение: 60 / 30. Если выполнить деление, то в ответе получится цифра два. Но изначально числитель и знаменатель можно сократить на десять, то есть разделить на это число: 60 / 30 = 6 / 3 = 2. Результат не поменялся. Более того, можно упростить и 6 / 3, выполнив деление на три: 6 / 3 = 2 / 1 = 2. Ответ снова совпадает.
Для общего же случая нужно отметить, что сокращение возможно лишь тогда, когда делимое и делитель не являются взаимно простыми числами. Если это не так, то дробь считается несократимой. Например, 1 / 2; 4 / 5. Использование основного свойства заключается в приведении исходного выражения к несократимому: 18 / 30 = 3 / 5 (после сокращения на шесть).
Нужно отметить, что на рассмотренных правилах построены практически все алгоритмы, связанные с выполнением математических действий над дробями.
Действия с дробями
Перед тем как приступить к изучению алгоритмов выполнения арифметических операций над дробями, нужно научиться преобразовывать смешанное отношение в неправильное число и находить наименьший общий знаменатель.
Для преобразования необходимо целое умножить на делитель дробной части, а затем полученное число сложить с её делимым. Затем результат прибавления занести в числитель, а знаменатель записать без изменения. При этом целое число можно представить как неправильную дробь, если добавить к ней знаменатель, равняющийся единице. Например, 9 (3 / 4) = ((9 * 4) + 3) / 4 = 39 / 4. Это операция обратимая, то есть преобразование можно выполнить и в обратную сторону.
Если в выражениях, над которыми необходимо выполнить сложение или вычитание, стоят одинаковые по значению делители, то говорят, что они приведённые. То есть чтобы выполнить арифметическую операцию, нужно найти общее кратное для всех знаменателей. Для его определения существуют несколько методов. Самый простой, но далеко не рациональный, простое перемножение делителей.
То есть чтобы выполнить арифметическую операцию, нужно найти общее кратное для всех знаменателей. Для его определения существуют несколько методов. Самый простой, но далеко не рациональный, простое перемножение делителей.
Другой заключается в выявлении наименьшего числа среди всех знаменателей, умножения его на два с последующей пробой деления полученного результата на оставшиеся делители без остатка. Если это невозможно, меньший знаменатель умножают на три. Это действие повторяют до тех пор, пока не найдётся число, делящееся на все делители без остатка.
Алгоритмы выполнения операций над дробными выражениями следующие:
 Математическая формула будет следующей: (a / b): (c / d) = (a * d) / (b * c).
Математическая формула будет следующей: (a / b): (c / d) = (a * d) / (b * c).Решение задач
Несмотря на то что свойства дробей несложны, для лучшего их понимания нужно прорешать несколько простых примеров. Обычно хватает решить около шести заданий, чтобы получить необходимые навыки. Вот несколько наиболее интересных типовых примеров для самостоятельной работы:
 Его нахождение будет выглядеть следующим образом: 3 / 5 + 12 / 16 = 3 /5 + 3 / 4 = ((3 * 4) + (3 * 5)) / 20 = (12 + 15) / 20 = 27 /20. Получилось неправильное выражение. Согласно правилу преобразования, его нужно представить, как смешанную дробь: 27 /20 = ((1 * 20) + 7) / 20 = (1 * 20) / 20 + 7 / 20 = 1 + 7 / 20 = 1 (7/20). Так как в расчёте целая часть равняется единице, а в сравниваемой — двойке, то можно утверждать, что (3 / 5 + 12 / 16) меньше 2 (4/5).
Его нахождение будет выглядеть следующим образом: 3 / 5 + 12 / 16 = 3 /5 + 3 / 4 = ((3 * 4) + (3 * 5)) / 20 = (12 + 15) / 20 = 27 /20. Получилось неправильное выражение. Согласно правилу преобразования, его нужно представить, как смешанную дробь: 27 /20 = ((1 * 20) + 7) / 20 = (1 * 20) / 20 + 7 / 20 = 1 + 7 / 20 = 1 (7/20). Так как в расчёте целая часть равняется единице, а в сравниваемой — двойке, то можно утверждать, что (3 / 5 + 12 / 16) меньше 2 (4/5).
Таким образом, использование свойств требует логического мышления и знания формул выполнения действий.
На этапе обучения их можно даже выписать в отдельную таблицу и пользоваться ей при решении, пока действия не дойдут до автоматизма. При этом полученный результат удобно проверять на онлайн-калькуляторах, которых в интернете можно насчитать более двух десятков. Это обычные сайты, выполняющие различные расчёты в режиме реального времени.
Основное свойство алгебраической дроби 8 класс онлайн-подготовка на Ростелеком Лицей
Основное свойство обыкновенной дроби
Вспомним основное свойство обыкновенной дроби: значение дроби не изменится, если ее числитель и знаменатель одновременно умножить или разделить на одно и то же отличное от нуля число. Напомним, что деление числителя и знаменателя дроби на одно и то же отличное от нуля число называется сокращением.
Например: , при этом значение дробей не изменяется. Однако зачастую при применении данного свойства многие допускают стандартные ошибки:
1) — в приведенном примере допущена ошибка деления только одного слагаемого из числителя на 2, а не всего числителя. Правильная последовательность действий выглядит таким образом: или .
2) — здесь мы видим похожую ошибку, однако, кроме этого еще в результате деления получен 0, а не 1, что является еще более частой и грубой ошибкой.
Теперь необходимо перейти к рассмотрению алгебраической дроби. Вспомним это понятие из предыдущего урока.
Определение. Рациональная (алгебраическая) дробь – дробное выражение вида , где – многочлены. – числитель, – знаменатель.
Алгебраические дроби являются, в некотором смысле, обобщением обыкновенных дробей и над ними можно проводить те же операции, что и над обыкновенными дробями.
Основное свойство алгебраической дроби
Основное свойство алгебраической дроби – и числитель, и знаменатель дроби можно умножать и делить на один и тот же многочлен (одночлен) или число, отличное от нуля. Это будет тождественное преобразование алгебраической дроби. Вспомним, что как и ранее, деление числителя и знаменателя дроби на одно и то же отличное от нуля выражение называется сокращением.
Основное свойство алгебраической дроби позволяет сокращать дроби и приводить их к наименьшему общему знаменателю.
Примеры сокращения обыкновенных дробей
Для сокращения обыкновенных дробей мы прибегали к основной теореме арифметики, разлагали и числитель, и знаменатель на простые множители.
Определение. Простое число – натуральное число, которое делится только на единицу и само себя. Все остальные натуральные числа называются составными. 1 не является ни простым, ни составным числом.
Пример 1. а), где множители, на которые разложены числители и знаменатели указанных дробей, являются простыми числами.
Ответ. ; .
Примеры сокращения алгебраических дробей
Следовательно, для сокращения дробей необходимо предварительно разложить на множители числитель и знаменатель дроби, а затем разделить их на общие множители. Т.е. следует владеть методами разложения многочленов на множители.
Пример 2. Сократить дробь а), б) , в) .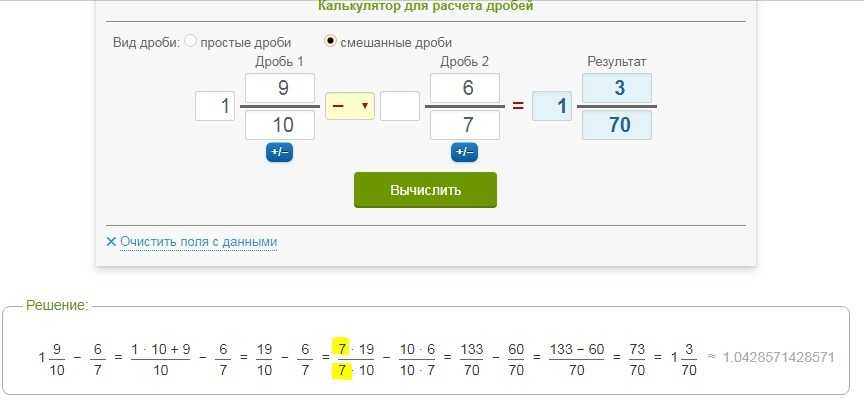
Решение. а) . Необходимо заметить, что в числителе находится полный квадрат, а в знаменателе разность квадратов. После сокращения необходимо указать, что , во избежание деления на ноль.
б) . В знаменателе выносится общий числовой множитель, что полезно делать практически в любом случае, когда это возможно. Аналогично с предыдущим примером указываем, что .
в) . В знаменателе выносим за скобки минус (или, формально, ). Не забываем, что при сокращении .
Ответ. ;; .
Теперь приведём пример на приведение к общему знаменателю, делается это аналогично с обыкновенными дробями.
Приведение обыкновенных дробей к общему знаменателю
Пример 3. Привести к общему знаменателю дроби и .
Решение. Для нахождения наименьшего общего знаменателя необходимо найти наименьшее общее кратное (НОК) двух знаменателей, т.е. НОК(3;5). Иными словами, найти наименьшее число, которое делится на 3 и на 5 одновременно. Очевидно, что это число 15, записать это можно таким образом: НОК(3;5)=15 – это и будет общий знаменатель указанных дробей.
Очевидно, что это число 15, записать это можно таким образом: НОК(3;5)=15 – это и будет общий знаменатель указанных дробей.
Чтобы преобразовать знаменатель 3 в 15, его необходимо умножить на 5, а для преобразования 5 в 15, его необходимо умножить на 3. По основному свойству алгебраической дроби следует умножить на те же числа и соответствующие числители указанных дробей.
и .
Ответ.; .
Пример 4. Привести к общему знаменателю дроби и .
Решение. Проведем аналогичные предыдущему примеру действия. Наименьшее общее кратное знаменателей НОК(12;18)=36. Приведем к этому знаменателю обе дроби:
и .
Ответ.; .
Сокращение сложных обыкновенных дробей
Теперь рассмотрим примеры, демонстрирующие применение техники сокращения дробей для их упрощения в более сложных случаях.
Пример 5. Вычислить значение дроби: а) , б) , в) .
а) . При сокращении пользуемся правилом деления степеней .
б) .
в) .
Сокращение сложных алгебраических дробей
После того, как мы повторили использование основного свойства обыкновенной дроби, можно перейти к рассмотрению алгебраических дробей.
Пример 6. Упростить дробь и вычислить при заданных значениях переменных: а) ; , б) ;
Решение. При подходе к решению возможен следующий вариант – сразу же подставить значения переменных и начать расчет дроби, но в таком случае решение сильно усложняется и необходимое на его решение время увеличивается, не говоря уже об опасности ошибиться в сложных вычислениях. Поэтому удобно сначала упростить выражение в буквенном виде, а затем уже подставить значения переменных.
а) . При сокращении на множитель необходимо проверить, не обращается ли он в ноль в указанных значениях переменных. При подстановке получаем , что дает возможность сокращения на данный множитель.
б) . В знаменателе выносим минус, как мы это уже делали в примере 2. При сокращении на снова проверяем не делим ли мы на ноль: .
При сокращении на снова проверяем не делим ли мы на ноль: .
Ответ. ; .
Приведение алгебраических дробей к общему знаменателю
Пример 7. Привести к общему знаменателю дроби а) и , б) и , в) и .
Решение. а) В данном случае подойдем к решению следующим образом: не будем пользоваться понятием НОК, как во втором примере, а просто умножим знаменатель первой дроби на знаменатель второй и наоборот – это позволит привести дроби к одинаковому знаменателю. Конечно же, не забываем при этом умножать и числители дробей на такие же выражения.
. В числителе раскрыли скобки, а в знаменателе воспользовались формулой разности квадратов.
. Аналогичные действия.
Видно, что такой способ позволяет умножить знаменатель и числитель одной дроби на тот элемент из знаменателя второй дроби, которого не хватает. С другой дробью проводятся аналогичные действия, и знаменатели приводятся к общему.
б) Проделаем аналогичные с предыдущим пунктом действия:
. Умножим числитель и знаменатель на тот элемент знаменателя второй дроби, которого не хватало (в данном случае на весь знаменатель).
Умножим числитель и знаменатель на тот элемент знаменателя второй дроби, которого не хватало (в данном случае на весь знаменатель).
. Аналогично.
в) . В данном случае мы умножили на 3 (множитель который присутствует в знаменателе второй дроби и отсутствует в первой).
.
Ответ. а) ; , б) ; , в) ; .
На данном уроке мы изучили основное свойство алгебраической дроби и рассмотрели основные задачи с его использованием. На следующем уроке мы более подробно разберем приведение дробей к общему знаменателю с использованием формул сокращенного умножения и метода группировки при разложении на множители.
Список литературы
- Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений.
 – М.: Просвещение, 2006.
– М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- ЕГЭ по математике (Источник).
- Фестиваль педагогических идей «Открытый урок» (Источник).
- Математика в школе: поурочные планы (Источник).
Домашнее задание
- №20, 22, 23, 26, 27, 29. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
- Сократить дробь: а) , б) , в) , г) .
- Привести дробь к знаменателю .
Действия с дробями: правила, приёмы, примеры
- Основное свойство дроби
- Сокращение дробей
- Приведение дробей к общему знаменателю
- Сложение и вычитание дробей
- Умножение и деление дробей
- Свойства пропорции
- Представление рациональной дроби в виде суммы простейших дробей
Условимся считать, что под «действиями с дробями» на нашем уроке будут пониматься
действия с обыкновенными дробями. Обыкновенная дробь — это дробь, обладающая такими атрибутами, как
числитель, дробная черта и знаменатель. Это отличает обыкновенную дробь от десятичной, которая получается
из обыкновенной путём приведения знаменателя к числу, кратному 10.
Обыкновенная дробь — это дробь, обладающая такими атрибутами, как
числитель, дробная черта и знаменатель. Это отличает обыкновенную дробь от десятичной, которая получается
из обыкновенной путём приведения знаменателя к числу, кратному 10.
Десятичная дробь записывается с запятой, отделяющей целую часть от дробной. У нас пойдёт речь о действиях с обыкновенными дробями, так как именно они вызывают наибольшие затруднения у студентов, позабывших основы этой темы, пройденной в первой половине школьного курса математики. Вместе с тем при преобразованиях выражений в высшей математике используются в основном именно действия с обыкновенными дробями. Одни сокращения дробей чего стоят! Десятичные же дроби особых затруднений не вызывают. Итак, вперёд!
Две дроби и называются равными, если .
Например, , так как
Равными также являются дроби и (так как ), и (так как ).
Очевидно, равными являются и дроби
и . Это означает,
что если числитель и знаменатель данной дроби умножить или разделить на одно и то же натуральное число,
то получится дробь, равная данной: .
Это означает,
что если числитель и знаменатель данной дроби умножить или разделить на одно и то же натуральное число,
то получится дробь, равная данной: .
Это свойство называется основным свойством дроби.
Основное свойство дроби можно использовать для перемены знаков у числителя и знаменателя дроби. Если числитель и знаменатель дроби умножить на -1, то получим . Это означает, что значение дроби не изменится, если одновременно изменить знаки у числителя и знаменателя. Если же изменить знак только у числителя или только у знаменателя, то и дробь изменит свой знак:
;
.
Пользуясь основным свойством дроби, можно заменить данную дробь другой дробью, равной данной, но с меньшим числителем и знаменателем. Такую замену называют сокращением дроби.
Пусть, например, дана дробь . Числа 36 и 48 имеют наибольший общий делитель 12. Тогда
.
В общем случае сокращение дроби возможно всегда, если числитель и знаменатель не
являются взаимно простыми числами. Если числитель и знаменатель — взаимно простые числа, то дробь
называется несократимой.
Если числитель и знаменатель — взаимно простые числа, то дробь
называется несократимой.
Забыли, что такое простые и составные числа и чем они различаются? Сейчас узнаем заново.
Простым называется число, которое делится (нацело) на само себя и на единицу. Составным числом называется число, которое делится на само себя, единицу и минимум ещё на одно натуральное число.
Вот первые 25 простых чисел в порядке их возрастания:
2; 3; 5; 7; 11; 13; 17; 19; 23; 29; 31; 37; 41; 43; 47; 53; 59; 61; 67; 71; 73; 79; 83; 89; 97.
А вот все составные числа, не превышающие 50, также в порядке их возрастания:
4; 6; 8; 9; 10; 12; 14; 15; 16; 18; 20; 21; 22; 24; 25; 26; 27; 28; 30; 32; 33; 34; 35; 36; 38; 39; 40; 42; 44; 45; 46; 48; 49; 50.
На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и
наименьшего общего кратного двух чисел.
Итак, сократить дробь — это значит разделить числитель и знаменатель дроби на общий множитель. Всё вышесказанное применимо и к дробным выражениям, содержащим переменные.
Пример 1. Сократить дробь
.
Решение. Для разложения числителя на множители, представив предварительно одночлен — 5xy в виде суммы — 2xy — 3xy, получим
Для разложения знаменателя на множители используем формулу разности квадратов:
.
В результате
.
Далее, изменяя знаки в числителе и знаменателе дроби, получим
Пусть даны две дроби и
. Они имеют разные
знаменатели: 5 и 7. Пользуясь основным свойством дроби, можно заменить эти дроби другими, равными им,
причём такими, что у полученных дробей будут одинаковые знаменатели. Умножив числитель и знаменатель
дроби на 7, получим
Умножив числитель и знаменатель
дроби на 7, получим
.
Умножив числитель и знаменатель дроби на 5, получим
.
Итак, дроби приведены к общему знаменателю:
.
Но это не единственное решение поставленной задачи: например, данные дроби можно привести также к общему знаменателю 70:
,
и вообще к любому знаменателю, делящемуся одновременно на 5 и 7.
Рассмотрим ещё один пример: приведём к общему знаменателю дроби и . Рассуждая, как в предыдущем примере, получим
,
.
Но в данном случае можно привести дроби к общему знаменателю, меньшему, чем произведение знаменателей этих дробей. Найдём наименьшее общее кратное чисел 24 и 30: НОК(24, 30) = 120.
Так как 120:4=5, то чтобы записать дробь
со знаменателем 120, надо и числитель, и знаменатель умножить на 5, это число называется дополнительным
множителем. Значит .
Значит .
Далее, получаем 120:30=4. Умножив числитель и знаменатель дроби на дополнительный множитель 4, получим .
Итак, данные дроби приведены к общему знаменателю.
Наименьшее общее кратное знаменателей этих дробей является наименьшим возможным общим знаменателем.
На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и наименьшего общего кратного двух чисел.
Для дробных выражений, в которые входят переменные, общим знаменателем является многочлен, который делится на знаменатель каждой дроби.
Пример 2. Найти общий знаменатель дробей и .
Решение. Общим знаменателем данных дробей является многочлен
,
так как он делится и на ,
и на .
Однако этот многочлен не единственный, который может быть общим знаменателем данных дробей.
Им может быть также многочлен ,
и многочлен , и
многочлен и т. д.
Обычно берут такой общий знаменатель, что любой другой общий знаменатель делится на выбранный без
остатка. Такой знаменатель называется наименьшим общим знаменателем.
д.
Обычно берут такой общий знаменатель, что любой другой общий знаменатель делится на выбранный без
остатка. Такой знаменатель называется наименьшим общим знаменателем.
В нашем примере наименьший общий знаменатель равен . Получили:
;
.
Нам удалось привести дроби к наименьшему общему знаменателю. Это произошло путём умножения числителя и знаменателя первой дроби на , а числителя и знаменателя второй дроби — на . Многочлены и называются дополнительными множителями, соответственно для первой и для второй дроби.
Сложение дробей определяется следующим образом:
.
Например,
.
Если b = d, то
.
Это значит, что для сложения дробей с одинаковым знаменателем достаточно сложить числители, а знаменатель оставить прежним. Например,
.
Если же складываются дроби с разными знаменателями, то обычно приводят дроби к наименьшему общему знаменателю, а потом складывают числители. Например,
.
На сайте есть калькулятор онлайн для вычисления наибольшего общего делителя и наименьшего общего кратного двух чисел.
Теперь рассмотрим пример сложения дробных выражений с переменными.
Пример 3. Преобразовать в одну дробь выражение
.
Решение. Найдём наименьший общий знаменатель. Для этого сначала разложим знаменатели на множители:
1) ;
2) ;
3) .
Наименьший общий знаменатель:
Дополнительные множители, на которые умножаются числители дробей:
1) 6;
2) ;
3) .
Результат этого умножения:
.
Далее, раскрывая скобки и выполняя тождественные преобразования, получаем
.
Произведение двух дробей и равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей, т. е. .
Например,
.
При делении дроби на дробь числитель делимого умножается на знаменатель делителя, а знаменатель делимого — на числитель делителя, т. е. .
Например,
.
1. Произведение крайних членов пропорции равно произведению её средних членов, т. е. если , то .
2. Из пропорции вытекают следующие пропорции: , , , то есть в пропорции можно менять местами крайние и средние члены или те и другие одновременно.
3. Чтобы найти неизвестный средний (крайний) член пропорции, нужно
произведение крайних (средних) членов пропорции разделить на известный средний (крайний)
член пропорции:
и
.
В высшей математике это действие с дробями чаще всего применяется при интегрировании рациональных функций. Поэтому оно подробно разобрано в уроке Интегрирование рациональных функций и метод неопределённых коэффициентов.
| Назад | Листать | Вперёд>>> |
Нет времени вникать в решение? Можно заказать работу!
К началу страницы
Другие темы в блоке «Школьная математика»
Действия со степенями и корнями
Решение квадратных уравнений
Решение дробных уравнений с преобразованием в квадратное уравнение
Решение четырехэтажных дробей. Дроби. Умножение и деление дробей
Инструкция
Принято разделять обыкновенные и десятичные дроби , знакомство с которыми начинается еще в средней школе. В настоящее нет такой области знаний, где не применялось бы это . Даже в мы говорим первая 17 века, и все сразу , что имеются ввиду 1600-1625 года. Также часто приходится сталкиваться с элементарными действиями над , а также их преобразованием из одного вида в другой.
Также часто приходится сталкиваться с элементарными действиями над , а также их преобразованием из одного вида в другой.
Приведение дробей к общему знаменателю является, пожалуй, наиболее важным действием над . Это основа проведения абсолютно всех вычислений. Итак, допустим есть две дроби a/b и c/d. Тогда, для того чтобы привести их к общему знаменателю, нужно найти наименьшее общее кратное (М) чисел b и d, и далее умножить числитель первой дроби на (М/b), а числитель второй на (M/d).
Сравнение дробей, еще одна немаловажная задача. Для того чтобы это сделать, приведите заданные простые дроби к общему знаменателю и потом сравните числители, чей числитель окажется больше, та дробь и больше.
Для того чтобы выполнить сложение или вычитание обыкновенных дробей, нужно привести их к общему знаменателю, а после произвести нужное математическое с этих дробей. Знаменатель же остается без изменения. Допустим нужно из a/b вычесть c/d. Для этого требуется найти наименьшее общее кратное M чисел b и d, и после вычесть из одного числителя другой, не меняя при этом знаменатель: (a*(M/b)-(c*(M/d))/M
Достаточно просто умножить одну дробь на другую, для этого следует просто перемножить их числители и знаменатели:
(a/b)*(c/d)=(a*c)/(b*d)Чтобы разделить одну дробь на другую, нужно дробь делимого умножить на дробь обратную делителю. (a/b)/(c/d)=(a*d)/(b*c)
(a/b)/(c/d)=(a*d)/(b*c)
Стоить напомнить, что для того чтобы получить обратную дробь, нужно числитель и знаменатель поменять местами.
Дробные выражения сложны для понимания ребёнком. У большинства возникают сложности, связанные с . При изучении темы «сложение дробей с целыми числами», ребёнок впадает в ступор, затрудняясь решить задание. Во многих примерах перед тем как выполнить действие нужно произвести ряд вычислений. Например, преобразовать дроби или перевести неправильную дробь в правильную.
Объясним ребёнку наглядно. Возьмём три яблока, два из которых будут целыми, а третье разрежем на 4 части. От разрезанного яблока отделим одну дольку, а остальные три положим рядом с двумя целыми фруктами. Получим ¼ яблока в одной стороне и 2 ¾ — в другой. Если мы их соединим, то получим целых три яблока. Попробуем уменьшить 2 ¾ яблока на ¼, то есть уберём ещё одну дольку, получим 2 2/4 яблока.
Рассмотрим подробнее действия с дробями, в составе которых присутствуют целые числа:
Для начала вспомним правило вычисления для дробных выражений с общим знаменателем:
На первый взгляд всё легко и просто. Но это касается только выражений, не требующих преобразования.
Но это касается только выражений, не требующих преобразования.
Как найти значение выражения где знаменатели разные
В некоторых заданиях необходимо найти значение выражения, где знаменатели разные. Рассмотрим конкретный случай:
3 2/7+6 1/3
Найдём значение данного выражения, для этого найдём для двух дробей общий знаменатель.
Для чисел 7 и 3 – это 21. Целые части оставляем прежними, а дробные – приводим к 21, для этого первую дробь умножаем на 3, вторую – на 7, получаем:
6/21+7/21, не забываем, что целые части не подлежат преобразованию. В итоге получаем две дроби с одним знаменателям и вычисляем их сумму:
3 6/21+6 7/21=9 15/21
Что если в результате сложения получается неправильная дробь, которая уже имеет целую часть:
2 1/3+3 2/3
В данном случае складываем целые части и дробные, получаем:
5 3/3, как известно, 3/3 – это единица, значит 2 1/3+3 2/3=5 3/3=5+1=6
С нахождением суммы всё понятно, разберём вычитание:
Из всего сказанного вытекает правило действий над смешанными числами, которое звучит так:
- Если же от дробного выражения необходимо вычесть целое число, не нужно представлять второе число в виде дроби, достаточно произвести действие только над целыми частями.

Попробуем самостоятельно вычислить значение выражений:
Разберём подробнее пример под буквой «м»:
4 5/11-2 8/11, числитель первой дроби меньше, чем второй. Для этого занимаем одно целое число у первой дроби, получаем,
3 5/11+11/11=3 целых 16/11, отнимаем от первой дроби вторую:
3 16/11-2 8/11=1 целая 8/11
- Будьте внимательны при выполнении задания, не забывайте преобразовывать неправильные дроби в смешанные, выделяя целую часть. Для этого необходимо значение числителя разделить на значение знаменателя, то что получилось, встаёт на место целой части, остаток – будет числителем, например:
19/4=4 ¾, проверим: 4*4+3=19, в знаменателе 4 остаётся без изменений.
Подведём итог:
Перед тем как приступить к выполнению задания, связанного с дробями, необходимо проанализировать, что это за выражение, какие преобразования нужно совершить над дробью, чтобы решение было правильным. Ищите более рациональные способ решения. Не идите сложными путями. Распланируйте все действия, решайте сначала в черновом варианте, затем переносите в школьную тетрадь.
Не идите сложными путями. Распланируйте все действия, решайте сначала в черновом варианте, затем переносите в школьную тетрадь.
Чтобы не произошло путаницы при решении дробных выражений, необходимо руководствоваться правилом последовательности. Решайте всё внимательно, не торопясь.
Практически каждый пятиклассник после первого знакомства с обыкновенными дробями находится в небольшом шоке. Мало того, что нужно еще понять суть дроби, так с ними еще придется выполнять арифметические действия. После этого маленькие ученики будут систематически допрашивать своего учителя, разузнавать когда же эти дроби кончатся.
Чтобы избежать подобных ситуаций, достаточно всего лишь как можно проще объяснить детям эту нелегкую тему, а лучше в игровой форме.
Суть дроби
Перед тем, как узнать что такое дробь, ребенок должен познакомиться с понятием доля . Здесь лучше всего подойдет ассоциативный метод.
Представьте целый торт, который поделили на несколько равных частей, допустим на четыре. Тогда каждый кусочек торта, можно назвать долей. Если взять один из четырех кусков торта, то он будет одной четвертой долей.
Тогда каждый кусочек торта, можно назвать долей. Если взять один из четырех кусков торта, то он будет одной четвертой долей.
Доли бывают разные, потому что, целое можно поделить на совершенно разное количество частей. Чем больше долей в целом, тем они меньше, и наоборот.
Чтобы доли можно было обозначить, придумали такое математическое понятие, как обыкновенная дробь . Дробь позволит нам записать столько долей, сколько потребуется.
Составными частями дроби являются числитель и знаменатель, которые разделены дробной чертой либо наклонной чертой. Многие дети не понимают их смысла, поэтому и суть дроби им не понятна. Дробная черта обозначает деление, здесь нет ничего сложного.
Знаменатель принято записывать снизу, под дробной чертой или справа от накл.черты. Он показывает количество долей целого. Числитель, он записывается сверху над дробной чертой или слева от накл.черты, определяет сколько долей взяли.К примеру дробь 4/7. В данном случае 7-это знаменатель, показывает, что есть всего 7 долей, а числитель 4 указывает на то, что из семи долей взяли четыре.
Основные доли и их запись в дробях:
Помимо обыкновеной, существует еще и десятичная дробь.
Действия с дробями 5 класс
В пятом классе учатся выполнять все арифметические действия с дробями.
Все действия с дробями выполняются по правилам, и надеяться на то, что не выучив правило все получится само сабой не стоит. Поэтому не стоит пренебрегать устной частью домашнего задания по математике.
Мы уже поняли, что запись десятичной и обыкновенной дроби различны, следовательно и арифметические действия будут выполняться по-разному. Действия с обыкновенными дробями зависят от тех чисел, которые стоят в знаменателе, а в десятичной-после запятой справа.
Для дробей, у которых знаменатели одинаковые, алгоритм сложения и вычитания очень прост. Действия выполняем только с числителями.
Для дробей с разными знаменателями нужно найти Наименьший Общий Знаменатель (НОЗ). Это то число, которое будет делиться без остатка на все знаменатели, и будет наименьшим из таких чисел, если их несколько.
Для сложения либо вычитания десятичных дробей, нужно записать их в столбик, запятая под запятой, и уравнить количество десятичных знаков если это требуется.
Чтобы перемножить обыкновенные дроби просто найди произведение числителей и знаменателей. Очень простое правило.
Деление выполняется по следующему алгоритму:
- Делимое записать без изменения
- Деление превратить в умножение
- Делитель перевернуть (записать обратную дробь делителю)
- Выполнить умножение
Сложение дробей, объяснение
Давайте более подробно разберем, как складывать обыкновенные и десятичные дроби.
Как видно на изображении выше, у дроби одна третья и две третьих общий знаменатель три. Значит требуется сложить только числители единицу и два, а знаменатель оставить без изменения. В итоге получается сумма три третьих. Такой ответ, когда числитель и знаменатель дроби равны, можно записать как 1, так как 3:3 = 1.
Требуется найти сумму дробей две третьих и две девятых. В этом случае знаменатели различны, 3 и 9. Чтобы выполнить сложение, нужно подобрать общий. Есть очень простой способ. Выбираем наибольший знаменатель, это 9. Проверяем делится ли он на 3. Так как 9:3 = 3 без остатка, следовательно 9 подходит как общий знаменатель.
Следующим шагом находим дополнительные множители для каждого числителя. Для этого общий знаменатель 9 делим поочередно на знаменатель каждой дроби, полученные числа и будут допол. множ. Для первой дроби: 9:3 = 3, дописываем к числителю первой дроби 3. Для второй дроби: 9:9 = 1, единицу можно не дописывать, так как при умножении на нее получится то же самое число.
Теперь умножаем числители на их дополнительные множители и складываем результаты. Полученная сумма дробь восемь девятых.
Сложение десятичных дробей выполняется по тому же правилу, что и сложение натуральных чисел. В столбик, разряд записывается под разрядом. Единственное отличие в том, что в десятичных дробях нужно правильно поставить запятую в результате. Для этого дроби записываются запятая под запятой, и в сумме требуется лишь снести запятую вниз.
Для этого дроби записываются запятая под запятой, и в сумме требуется лишь снести запятую вниз.
Найдем сумму дробей 38, 251 и 1, 56. Чтобы было удобнее выполнять действия, мы уровняли количество десятичных знаков справа, добавив 0.
Складываем дроби не обращая внимания на запятую. А в полученной сумме просто опускаем запятую вниз. Ответ: 39, 811.
Вычитание дробей, объяснение
Чтобы найти разность дробей две третьих и одна третья, нужно вычислить разность числителей 2-1 = 1, а знаменатель оставить без изменения. В ответе получаем разность одну третью.
Найдем разность дробей пять шестых и семь десятых. Находим общий знаменатель. Используем способ подбора, из 6 и 10 наибольший 10. Проверяем: 10: 6 без остатка не делится. Добавляем еще 10, получается 20:6, тоже без остатка не делится. Снова увеличиваем на 10, получили 30:6 = 5. Общий знаменатель 30. Так же НОЗ можно найти по таблице умножения.
Находим дополнительные множители. 30:6 = 5 — для первой дроби. 30:10 = 3 — для второй. Перемножаем числители и их доп.множ. Получаем уменьшаемое 25/30 и вычитаемое 21/30. Далее выполняем вычитание числителей, а знаменатель оставляем без изменения.
30:10 = 3 — для второй. Перемножаем числители и их доп.множ. Получаем уменьшаемое 25/30 и вычитаемое 21/30. Далее выполняем вычитание числителей, а знаменатель оставляем без изменения.
В результате получилась разность 4/30. Дробь сократимая. Разделим ее на 2. В ответе 2/15.
Деление десятичных дробей 5 класс
В этой теме рассматривается два варианта действий:
Умножение десятичных дробей 5 класс
Вспомните, как вы умножаете натуральные числа, точно таким же способом и находят произведение десятичных дробей. Сначала разберемся, как умножить десятичную дробь на натуральное число. Для этого:
При умножении десятичной дроби на десятичную, действуем точно также.
Смешанные дроби 5 класс
Пятиклашки любят называть такие дроби не смешанные, а >, наверное так легче запомнить. Смешанные дроби называются так от того, что они получились путем соединения целого натурального числа и обыкновенной дроби.
Смешанная дробь состоит из целой и дробной части.
При чтении таких дробей сначала называют целую часть, затем дробную: одна целая две третьих, две целых одна пятая, три целых две пятых, четыре целых три четвертых.
Как же они получаются, эти смешанные дроби? Все довольно просто. Когда мы получаем в ответе неправильную дробь (дробь у которой числитель больше знаменателя), мы ее должны всегда переводить в смешанную. Достаточно разделить числитель на знаменатель. Это действие называется выделением целой части:
Перевести смешанную дробь обратно в неправильную тоже несложно:
Примеры с десятичными дробями 5 класс с объяснением
Много вопросов у детей вызывают примеры на несколько действий. Разберем пару таких примеров.
(0,4 · 8,25 — 2,025) : 0,5 =
Первым действием находим произведение чисел 8,25 и 0,4. Выполняем умножение по правилу. В ответе отсчитываем справа налево три знака и ставим запятую.
Второе действие находится там же в скобках, это разность. От 3,300 вычитаем 2,025. Записываем действие в столбик, запятая под запятой.
От 3,300 вычитаем 2,025. Записываем действие в столбик, запятая под запятой.
Третье действие-деление. Полученную разность во втором действии делим на 0,5. Запятая переносится на один знак. Результат 2,55.
Ответ: 2,55.
(0, 93 + 0, 07) : (0, 93 — 0, 805) =
Первое действие сумма в скобках.Складываем в столбик, помним, что запятая под запятой. Получаем ответ 1,00.
Второе действие разность из второй скобки. Так как у уменьшаемого меньше знаков после запятой, чем у вычитаемого, добавляем недостающий. Результат вычитания 0 ,125.
Третьим действие делим сумму на разность. Запятая переносится на три знака. Получилось деление 1000 на 125.
Ответ: 8 .
Примеры с обыкновенными дробями с разными знаменателями 5 класс с объяснением
В первом примере находим сумму дробей 5/8 и 3/7. Общим знаменателем будет число 56. Находим дополнительные множ., разделим 56:8 = 7 и 56:7 = 8. Дописываем их к первой и второй дроби соответственно. Перемножаем числители и их множители, получаем сумму дробей 35/56 и 24/56. Получили сумму 59/56. Дробь неправильная, переводим ее в смешанное число.Остальные примеры решаются аналогично.
Перемножаем числители и их множители, получаем сумму дробей 35/56 и 24/56. Получили сумму 59/56. Дробь неправильная, переводим ее в смешанное число.Остальные примеры решаются аналогично.
Примеры с дробями 5 класс для тренировки
Для удобства переведите смешанные дроби в неправильные и выполняйте действия.
Как научить ребенка легко решать дроби с помощью лего
С помощью такого конструктора можно не только хорошо развивать воображение ребенка, но и объяснить наглядно в игровой форме, что такое доля и дробь.
На картинке ниже показано, что одна часть с восемью кружками это целое. Значит, взяв пазл с четырьмя кружками, получается половина, или 1/2. На картинке наглядно показано, как решать примеры с лего, если считать кружки на деталях.
Вы можете построить башенки из определенного количества частей и подписать каждую из них, как на картинке ниже. Например возьмем башенку из семи частей. Каждая часть зеленого конструктора будет 1/7. Если вы к одной такой части добавите еще две, то получится 3/7. Наглядное объяснение примера 1/7+2/7 = 3/7.
Если вы к одной такой части добавите еще две, то получится 3/7. Наглядное объяснение примера 1/7+2/7 = 3/7.
Чтобы получать пятерки по математике не забывайте учить правила и отрабатывать их на практике.
Удобный и простой онлайн калькулятор дробей с подробным решением может:
- Складывать, вычитать, умножать и делить дроби онлайн,
- Получать готовое решение дробей картинкой и удобно его переносить.
Результат решения дробей будет тут…
0
1
2
3
4
5
6
7
8
9
Знак дроби «/»
+
—
*
:
_cтереть
Очистить
У нашего онлайн калькулятора дробей быстрый ввод . Чтобы получить решение дробей, к примеру , просто напишите 1/2+2/7 в калькулятор и нажмите кнопку «Решать дроби «.
Калькулятор напишет вам подробное решение дробей и выдаст удобную для копирования картинку .
Знаки используемые для записи в калькуляторе
Набирать пример для решения вы можете как, с клавиатуры, так и используя кнопки.
Возможности онлайн калькулятора дробей
Калькулятор дробей может выполнить операции только с 2-мя простыми дробями. Они могут быть как правильными(числитель меньше знаменателя), так и неправильными(числитель больше знаменателя). Числа в числителе и знаменатели не могут быть отрицательными и больше 999.Наш онлайн калькулятор решает дроби и приводит ответ к правильному виду — сокращает дробь и выделяет целую часть, если потребуется.
Если вам нужно решить отрицательные дроби, просто воспользуйтесь свойствами минуса.
При перемножении и делении отрицательных дробей минус на минус дает плюс. То есть произведение и делении отрицательных дробей, равно произведению и делению таких же положительных. Если одна дробь при перемножении или делении отрицательная, то просто уберите минус, а потом добавьте его к ответу.
При сложении отрицательных дробей, результат будет таким же как если бы вы складывали такие же положительные дроби. Если вы прибавляете одну отрицательную дробь, то это тоже самое, что вычесть такую же положительную.
При вычитании отрицательных дробей, результат будет таким же, как если бы поменяли их местами и сделали положительными. То есть минус на минус в данном случае дает плюс, а от перестановки слагаемых сумма не меняется. Этими же правилами мы пользуемся при вычитании дробей одна из которых отрицательная.
Для решения смешанных дробей (дробей, в которых выделена целая часть) просто загоните целую часть в дробь. Для этого умножьте целую часть на знаменатель и прибавьте к числителю.
Если вам нужно решить онлайн 3 и более дроби, то решать их следует по очереди. Сначала посчитайте первые 2 дроби, потом с полученным ответом прорешайте следующую дробь и так далее. Выполняйте операции по очереди по 2 дроби, и в итоге вы получите верный ответ.
В статье покажем, как решать дроби на простых понятных примерах. Разберемся, что такое дробь и рассмотрим решение дробей !
Понятие дроби вводится в курс математики начиная с 6 класса средней школы.
Дроби имеют вид: ±X/Y, где Y — знаменатель, он сообщает на сколько частей разделили целое, а X — числитель, он сообщает, сколько таких частей взяли. Для наглядности возьмем пример с тортом:
Для наглядности возьмем пример с тортом:
В первом случае торт разрезали поровну и взяли одну половину, т.е. 1/2. Во втором случае торт разрезали на 7 частей, из которых взяли 4 части, т.е. 4/7.
Если часть от деления одного числа на другое не является целым числом, ее записывают в виде дроби.
Например, выражение 4:2 = 2 дает целое число, а вот 4:7 нацело не делится, поэтому такое выражение записывается в виде дроби 4/7.
Иными словами дробь — это выражение, которое обозначает деление двух чисел или выражений, и которое записывается с помощью дробной черты.
Если числитель меньше знаменателя — дробь является правильной, если наоборот — неправильной. В состав дроби может входить целое число.
Например, 5 целых 3/4.
Данная запись означает, что для того, чтобы получить целую 6 не хватает одной части от четырех.
Если вы хотите запомнить, как решать дроби за 6 класс , вам надо понять, что решение дробей , в основном, сводится к понимаю нескольких простых вещей.
- Дробь по сути это выражение доли. То есть числовое выражение того, какую часть составляет данное значение от одного целого. К примеру дробь 3/5 выражает, что, если мы поделили что то целое на 5 частей и количество долей или частей это этого целого — три.
- Дробь может быть меньше 1, например 1/2(или по сути половина), тогда она правильная. Если дробь больше 1, к примеру 3/2(три половины или один с половиной), то она неправильная и для упрощения решения, нам лучше выделить целую часть 3/2= 1 целая 1/2.
- Дроби это такие же числа, как 1, 3, 10, и даже 100, только числа это не целые а дробные. С ними можно выполнять все те же операции, что с числами. Считать дроби не сложнее, и далее на конкретных примерах мы это покажем.
Как решать дроби. Примеры.
К дробям применимы самые разные арифметические операции.
Приведение дроби к общему знаменателю
Например, необходимо сравнить дроби 3/4 и 4/5.
Чтобы решить задачу, сначала найдем наименьший общий знаменатель, т. е. наименьшее число, которое делится без остатка на каждый из знаменателей дробей
е. наименьшее число, которое делится без остатка на каждый из знаменателей дробей
Наименьший общий знаменатель(4,5) = 20
Затем знаменатель обоих дробей приводится к наименьшему общему знаменателю
Ответ: 15/20
Сложение и вычитание дробей
Если необходимо посчитать сумму двух дробей, их сначала приводят к общему знаменателю, затем складывают числители, при этом знаменатель останется без изменений. Разность дробей считается аналогичным образом, различие лишь в том, что числители вычитаются.
Например, необходимо найти сумму дробей 1/2 и 1/3
Теперь найдем разность дробей 1/2 и 1/4
Умножение и деление дробей
Тут решение дробей несложное, здесь все достаточно просто:
- Умножение — числители и знаменатели дробей перемножаются между собой;
- Деление — сперва получаем дробь, обратную второй дроби, т.е. меняем местами ее числитель и знаменатель, после чего полученные дроби перемножаем.
Например:
На этом о том, как решать дроби , всё. Если у вас остались какие то вопросы по решению дробей , что то непонятно, то пишите в комментарии и мы обязательно вам ответим.
Если у вас остались какие то вопросы по решению дробей , что то непонятно, то пишите в комментарии и мы обязательно вам ответим.
Если вы учитель, то возможно скачать презентацию для начальной школы (http://school-box.ru/nachalnaya-shkola/prezentazii-po-matematike.html) будет вам кстати.
Вычисление приближенной правильной дроби
|
|
|
||||||||||||||||||||||||||||
Калькулятор перекрестного умножения
Создано Maciej Kowalski, кандидатом наук
Отредактировано Стивеном Вудингом
Последнее обновление: 06 апреля 2022 г.
- Решение x с дробями : использование калькулятора перекрестного умножения
- Часто задаваемые вопросы
Добро пожаловать в Omni калькулятор перекрестного умножения , где мы будем решать x с дробями. Выражения, которые мы рассматриваем здесь, часто называют пропорциями, и есть простой алгоритмический способ работы с ними: перекрестно умножить дроби . Фактически, независимо от того, какое из четырех значений неизвестно, как только мы пересечем умножение и деление, , мы обязательно получим наш результат , без каких-либо условий.
Но прежде чем мы зайдем вперед, давайте немного замедлимся и научимся выполнять перекрестное умножение легко и просто .
Решение x с дробями
Обычно мы используем перекрестное умножение, когда у нас есть уравнений с одной переменной, включая дроби . Например, он включает выражения вида:
Обратите внимание, что мы можем иметь отрицательные числа или десятичные дроби в числителях или знаменателях. Кроме того, в последнем примере
Кроме того, в последнем примере x находится за пределами дроби , но мы можем легко получить ее внутри, следуя основным правилам умножения дроби:
| х | = | * | = |
| = |
Такие уравнения, даже если они выглядят причудливо, должны подчиняться тем же правилам, что и любые другие . В частности, мы можем складывать или вычитать любое число, и мы можем умножать или делить на любое ненулевое значение, если мы делаем это по обе стороны от знака равенства . Для наших целей последняя пара арифметических операций оказывается решающей: мы умножим и разделим , чтобы найти значение
В частности, мы можем складывать или вычитать любое число, и мы можем умножать или делить на любое ненулевое значение, если мы делаем это по обе стороны от знака равенства . Для наших целей последняя пара арифметических операций оказывается решающей: мы умножим и разделим , чтобы найти значение x .
Как скрещивать дроби
Подсказка кроется в названии « скрестить умножение ». Мы возьмем произведение значений в перекрестном шаблоне :
левый числитель * правый знаменатель = правый числитель * левый знаменатель .
А если бы мы использовали символы, появляющиеся в калькуляторе перекрестного умножения Омни, т.е. возьмем уравнение:
мы получим:
A * D = B * C . Фактически, это все, что есть для решения x с дробями. В конце концов, как только мы перекрестим умножение, у нас больше не будет дробей, поэтому мы можем обратиться к другим известным методам работы с уравнениями. Например, если мы хотим найти
Например, если мы хотим найти A из приведенной выше формулы, достаточно разделить обе части на D :
(A * D) / D = (B * C) / D .| = |
|
Обратите внимание, что какая бы буква нам ни понадобилась (т. е. какой бы ни был числитель или знаменатель), процедура останется той же: перекрестно умножить и разделить. Разница лишь в том, на что мы делим на втором шаге. Для точности делим на:
-
Dпри поискеA; -
Cпри поискеB; -
Bпри поискеC; и -
Aпри поискеD.
Кроме того, вспомним, что мы всегда можем поменять местами стороны уравнения . Поэтому мы всегда можем изменить формулу:
левый числитель * правый знаменатель = правый числитель * левый знаменатель ,
на:
правый числитель * левый знаменатель = левый числитель * правый знаменатель .
Однако обратите внимание, что пары остаются теми же : нам нужно сохранить схему перекрестного умножения.
Хорошо, инструкции по перекрестному умножению кажутся достаточно простыми, не так ли? Пора перейти от символов и теории к числам и практиковать . И, чтобы убить двух зайцев одним выстрелом, мы воспользуемся возможностью , чтобы наш калькулятор умножения крестов сиял .
Пример: использование калькулятора перекрестного умножения
Предположим, что вы строите модель самолета . После нескольких часов кропотливой склейки самолет готов: он будет великолепно смотреться на полке, чтобы все могли им восхищаться. Но теперь, когда часть DIY закончена, почему бы нам не узнать что-нибудь об этом? Давайте посчитаем , насколько велик реальный эквивалент .
Но теперь, когда часть DIY закончена, почему бы нам не узнать что-нибудь об этом? Давайте посчитаем , насколько велик реальный эквивалент .
На коробке написано, что модель выполнена на 1:100 9Масштаб 0022. Вы берете линейку и проверяете, что ваше творение имеет длину 3,5 дюймов . Хотите верьте, хотите нет, но это все, что нам нужно, чтобы найти ответ. Хитрость в заключается в хорошем понимании того, как работает масштабирование : единица измерения на коробке пропорциональна соотношению модельной и реальной длин. В нашем случае это означает, что 3,5 дюймов по отношению к фактической длине самолета, что 1 по отношению к 100 :
, где x обозначает искомое значение. Однако, прежде чем мы бросимся решать ее самостоятельно, давайте посмотрим насколько легко решается задача с калькулятором перекрестного умножения Omni под рукой .
В верхней части нашего инструмента мы видим формулу:
и четыре переменных поля, соответствующие буквам. Как показывает калькулятор перекрестного умножения, достаточно ввести три значений, поэтому мы вернемся к нашей задаче и напишем:
-
А = 3,5,С = 1иД = 100.
В тот момент, когда мы введем третье число, , инструмент выдаст ответ . Обратите внимание, как он также предоставляет пошаговое объяснение внизу: то же самое, что мы дадим прямо сейчас.
Начнем с того, чему научил нас предыдущий раздел: мы перекрестно умножим дроби :
х * 1 = 3,5 * 100 x = 350 Обычно нам нужно разделить результат на число, стоящее перед x . Однако в нашем случае это число оказалось 1 , , поэтому не нужно.
Мы получили ответ! Реальный самолет имеет длину 350 дюймов. Что ж, нам, вероятно, следует перейти от калькулятора перекрестного умножения к преобразователю длины, чтобы получить более разумный ответ , вам не кажется?
Часто задаваемые вопросы
Как найти x с помощью дробей?
Чтобы решить для x с дробями , вам нужно:
- Преобразовать обе части в частные.
- Крест умножьте дробей.
- Упростите два выражения.
- Разделите на то, что находится перед
x. - Наслаждайтесь , решив
xс дробями.
Как скрестить дроби?
Чтобы скрестить дроби , вам необходимо:
- Убедитесь, что у вас есть только дроби с каждой стороны.
- Умножьте числитель первого на знаменатель второго.

- Умножьте числитель второго на знаменатель первого.
- Объединить шагов 2-3 в уравнение.
- При необходимости решить полученное уравнение базовыми методами.
- Наслаждайтесь игрой , перемножив дроби крестом.
Почему перекрестное умножение работает?
Перекрестное умножение, по сути, простое умножение дважды .
Во-первых, мы умножаем обе части на знаменатель левой части , что оставляет только числитель слева (согласно правилам упрощения дробей), и умножает правый числитель (согласно правилам умножения дробей). Затем мы умножаем обе части на знаменатель правой части , что дает произведение слева и убивает знаменатель справа.
В общем, поскольку мы всегда можем умножить обе части уравнения на ненулевое число, перекрестное умножение действительно работает .
Как работает перекрестное умножение?
Чтобы использовать перекрестное умножение , вам необходимо:
- Убедитесь, что у вас есть только дробь с каждой стороны.

- Умножьте числитель первого на знаменатель второго.
- Умножьте числитель второго на знаменатель первого.
- Объединить шагов 2-3 в уравнение.
- При необходимости решить полученное уравнение базовыми методами.
- Наслаждайтесь , используя перекрестное умножение.
Как сравнивать дроби с помощью перекрестного умножения?
Чтобы сравнить дроби с помощью перекрестного умножения , вам необходимо:
- Убедитесь, что у вас есть только дробь с каждой стороны.
- Умножьте числитель первого на знаменатель второго.
- Умножьте числитель второго на знаменатель первого.
- Сравните значения из шагов 2 и 3.
- Если на шаге 2 было:
- Меньше , то первая дробь меньше; или
- Больше , тогда первая дробь больше.

- Если один из множителей был отрицательным, изменить отношение на его противоположное.
- Наслаждайтесь игрой , сравнив дроби с помощью перекрестного умножения.
Как решить пропорции с помощью перекрестного умножения?
Чтобы решить пропорции с помощью перекрестного умножения , вам необходимо:
- Убедитесь, что у вас есть только дроби с каждой стороны.
- Умножьте числитель первого на знаменатель второго.
- Умножьте числитель второго на знаменатель первого.
- Объединить шагов 2-3 в уравнение.
- Решите полученное уравнение базовыми методами.
- Наслаждайтесь игрой , решив пропорцию с помощью перекрестного умножения.
Мацей Ковальский, кандидат наук
Введите любые три цифры:
Хотите узнать больше о пропорциональности? Если это так, проверьте калькулятор коэффициента дальше!
Ознакомьтесь с 60 похожими арифметическими калькуляторами ➗
Абсолютное значениеСложениеАссоциативное свойство… Еще 57
Алгебра Игры - Математические игры для детей
Баскетбол
Алгебраические выражения - найдите значение переменных.
Играть здесь >>>
Автогонки
Автогонки на алгебраических выражениях онлайн
Играть здесь >>>
Крокодил игра
Игра "Решение алгебраических выражений" для детей.
Играть здесь >>>
Пиратская игра
Пиратская игра с алгебраическими выражениями для решения.
Играйте здесь >>>
Veiz Game
Алгебраические выражения - Найдите значение переменных
Играйте здесь >>
Snakes & Ladders
FUNAKERS и LADSERS -LADSERS и LADDERS и LADDERS
. алгебраические выражения
Играть здесь >>>
Колесо Фортуны
Вращайте колесо и решайте алгебраические выражения.
Играть здесь >>>
Пиратские сокровища
Остров пиратских сокровищ игра на алгебраических выражениях.
Играть здесь >>>
Баскетбол
Сравнение дробей баскетбольная математическая игра.
Играть здесь >>>
Автомобильные гонки
Сравнение двух фракций автомобильных гонок онлайн.
Играть здесь >>>
Крокодил игра
Крокодил и лягушка настольная игра на сравнение дробей.
Играть здесь >>>
Пиратская игра
Больше, меньше, равно - математическая пиратская игра на дроби.
Играть здесь >>>
Игра-викторина
Игра "Узнай, как сравнить две дроби". .
Играть здесь >>>
Змеи и лестницы
Интерактивные онлайн-змеи и лестницы - сравнение дробей.
Играть здесь >>>
Колесо Фортуны
Решите задачи на сравнение дробей в игре "Вращение колеса".
Играть здесь >>>
Пиратские сокровища
Сравните две дроби, <, >, = математическая пиратская игра онлайн.
Играть здесь >>>
Баскетбол
Преобразование десятичных дробей в дроби математическая игра.
Играть здесь >>>
Автомобильная гонка
Как преобразовать десятичную дробь в автомобильную раллийную игру.
Играть здесь >>>
Крокодил игра
Изучите процесс преобразования десятичной дроби в дробь.
Играйте здесь >>>
Pirate Game
Pirate Game при преобразовании десятичных десятиц в фракции ..
Играйте здесь >>>
Quiz Game
Алгебра. дробить.
Играть здесь >>>
Змеи и лестницы
Как преобразовать дроби в десятичные - змейки и лестницы.
Играйте здесь >>>
Wheel of Fortune
Преобразование десятичных десятиц в калькулятор фракций. диаграмма.
Играть здесь >>>
Баскетбол
преобразование дробей в десятичные игры в баскетбол.
Играть здесь >>>
Автомобильная гонка
Преобразование дробей в десятичные автомобильные ралли игры онлайн.
Играть здесь >>>
Крокодил игра
как преобразовать дроби в десятичные настольная игра.
Играть здесь >>>
Пиратская игра
Пиратская игра учит переводить дроби в десятичные.
Играть здесь >>>
Викторина
Преобразование дробей в десятичные калькулятор онлайн игра-викторина.
Играйте здесь >>>
Змеи и лестницы
Преобразование дробей в десятичные дроби с помощью змей и лестниц.
Играть здесь >>>
Колесо Фортуны
Таблица для перевода дробей в десятичные игры Wheel Spin.
Играть здесь >>>
Пиратские сокровища
Преобразование дробей в десятичные игры - игра пиратские сокровища.
Играть здесь >>>
Баскетбол
Как найти дроби числа игра в баскетбол для детей.
Играть здесь >>>
Автомобильные гонки
Найдите дроби чисел в математической игре автомобильных гонок онлайн.
Играть здесь >>>
Крокодил игра
Найди части целого числа крокодил настольная игра викторина.
Играть здесь >>>
Пиратская игра
Как находить дроби в числовом ряду в пиратской игре.
Играть здесь >>>
Игра-викторина
Интерактивная викторина, обучающая детей находить дроби чисел.
Играть здесь >>>
Змеи и лестницы
Математическая игра змеи и лестницы на нахождение частей чисел.
Играть здесь >>>
Колесо фортуны
Колесо фортуны игра с задачами на нахождение дробей.
Играть здесь >>>
Сокровище пиратов
Что такое дробь числа - пиратская игра для школьников.
Играть здесь >>>
Баскетбол
Умножение дробей игра с алгеброй.
Играть здесь >>>
Автомобильная гонка
Автомобильная игра с задачами по алгебре. Гоночная игра MCQ.
Играть здесь >>>
Крокодил игра
Умножение дробей игры для алгебры 1 - Крокодил настольная игра.
Играть здесь >>>
Пиратская игра
Умножай на дроби пиратская игра онлайн.
Играть здесь >>>
Игра-викторина
Игра-викторина "Умножение дробей".
Играть здесь >>>
Змеи и лестницы
Умножение с калькулятором дробей игра для детей онлайн.
Играть здесь >>>
Колесо Фортуны
Умножение дробей на целочисленное колесо вращения.
Играть здесь >>>
Сокровища пиратов
Пример умножения дробей - Игры Остров пиратских сокровищ.
Играть здесь >>>
Баскетбол
Найдите проценты от числа игра в баскетбол с мячом с викториной.
Играть здесь >>>
Автомобильные гонки
Как вычислить процентное соотношение чисел автомобильные ралли игры для детей.
Играть здесь >>>
Крокодил игра
Проценты от целых чисел настольная игра крокодил.
Играть здесь >>>
Пиратская игра
Найти процент от другого числа обзора пиратской игры.
Играть здесь >>>
Игра-викторина
Процентная игра с числовой формулой с викториной MCQ.
Играть здесь >>>
Змеи и лестницы
Решите уравнения с процентами в математической викторине.
Играть здесь >>>
Колесо Фортуны
Проценты от целых чисел в онлайн игре колесо фортуны.
Играть здесь >>>
Сокровища пиратов
Найти проценты онлайн пиратская игра для школьников.
Играйте здесь >>>
Баскетбол
Дополнение до алгебры - Игровое обучение - Баскебол
Играйте здесь >>>
CAR Race
Game. решать.
Играть здесь >>>
Игра "Крокодил"
Решение задач по алгебре с поиском пропущенных переменных в игре "Крокодил".
Играть здесь >>>
Пиратская игра
Алгебра сложения шаблонов - решение пиратской игры.
Играть здесь >>>
Игра-викторина
Электронная обучающая игра с добавлением и поиском неизвестных переменных.
Играть здесь >>>
Змеи и лестницы
Методы сложения алгебры, изученные в игре.
Играть здесь >>>
Колесо Фортуны
Игровые викторины на сложение в линейных уравнениях.
Играть здесь >>>
Сокровища пиратов
Предварительно алгебраические задачи на сложение в пиратской игре.
Играть здесь >>>
Баскетбол
Баскетбольная игра умножения матриц линейной алгебры.
Играть здесь >>>
Автомобильные гонки
Игра на умножение алгебры - формула один.
Играть здесь >>>
Крокодил игра
Линейная алгебра умножение крокодил игра для обзора.
Играть здесь >>>
Пиратская игра
Алгебра перекрестное умножение - Интерактивная пиратская игра.
Играть здесь >>>
Игра-викторина
Викторина на умножение по алгебре с MCQ и переменными.
Играть здесь >>>
Змеи и лестницы
Игра змей и лестниц на алгебраическое умножение.
Играть здесь >>>
Колесо Фортуны
Колесо фортуны игра на умножение алгебры.
Играть здесь >>>
Сокровище пиратов
Пират Карибского моря игра на умножение алгебры.
Играть здесь >>>
Баскетбол
Баскетбол игра онлайн бесплатно на задачи вычитания алгебры.
Играть здесь >>>
Автомобильные гонки
Автомобильные гонки для ПК, посвященные задачам на вычитание по алгебре.
Играть здесь >>>
Игра Крокодил
Игра Крокодил на алгебраическом вычитании с пропущенными значениями.
Играть здесь >>>
Пиратская игра
Пиратская игра на вычитание в линейных уравнениях.
Играть здесь >>>
Игра-викторина
Интерактивная викторина по алгебре с вычитанием.
Играть здесь >>>
Змеи и лестницы
Змеи и лестницы настольная игра онлайн с алгебраическим вычитанием.
Играть здесь >>>
Колесо фортуны
Колесо фортуны Игра с задачами на вычитание по алгебре.
Играть здесь >>>
Сокровище пиратов
Алгебра 1 игра на вычитание с пиратской настольной игрой.
Играть здесь >>>
Баскетбол
Математическая баскетбольная игра «Упрощение дробей» - обучение на основе игры.
Играть здесь >>>
Автомобильные гонки
Автомобильные гонки игра онлайн о том, как упростить дробь.
Играть здесь >>>
Крокодил игра
Крокодил игровое поле на упрощении дробей.
Играть здесь >>>
Пиратская игра
Сократи дробь до минимума математическая пиратская игра.
Играть здесь >>>
Игра-викторина
Интерактивная онлайн-викторина на уменьшение дроби до наименьшего.
Играть здесь >>>
Змеи и лестницы
Упростите дробь с помощью множителей числителя и знаменателя.
Играть здесь >>>
Колесо Фортуны
Обучение алгебре на основе игры с упрощением дробей.
Играть здесь >>>
Сокровище пиратов
Пиратская игра сегодня для студентов, чтобы повторить упрощение фракций.
Играть здесь >>>
Баскетбол
Вычитание дробей Электронная обучающая игра для школьников.
Играть здесь >>>
Автомобильная гонка
Гонки на автомобилях игра на вычитание дробей.
Играть здесь >>>
Крокодил игра
Вычитание дробей крокодил настольная игра для веселого обучения.
Играть здесь >>>
Пиратская игра
Пиратские воды игра с вычитанием дробей mcq's.
Играть здесь >>>
Игра-викторина
Интерактивная забавная викторина на тему джунглей по вычитанию дробей.
Играть здесь >>>
Змеи и лестницы
Змеи и лестницы онлайн игра на вычитание дробей.
Играть здесь >>>
Колесо Фортуны
Крути колесо игровое шоу онлайн на вычитание дробей.
Играть здесь >>>
Сокровище пиратов
Математическая пиратская настольная игра для школьников на вычитание дробей..
Играть здесь >>>
АЛГЕБРА ИГРЫ - УРАВНЕНИЯ С ОПРЕДЕЛЕННОЙ ПЕРЕМЕННОЙ Y = 1
Баскетбольная алгебра игра с определяемой переменной y = 1 алгебраическая игра с определяемой переменной y = 1
алгебраическая игра «прогулка по доске» с определяемой переменной y = 1
футбол алгебраическая игра с определяемой переменной y = 1
АЛГЕБРА ИГРЫ — УРАВНЕНИЯ С ОПРЕДЕЛЯЕМОЙ ПЕРЕМЕННОЙ Y = 6
Алгебра игра в баскетбол с определяемой переменной y = 6
Алгебра игра En Garde с определяемой переменной y = 6
Алгебра игра Walk the Plank с определяемой переменной y = 6
Футбольная алгебра игра с определяемой переменной y = 6
АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ ИГРЫ
Алгебраические выражения в дуэльной игре
Алгебраические выражения в футболе
Алгебраические выражения в баскетболе
Алгебраические выражения в игре «ходьба по доске»
Pre - Algebra с добавлением игр
Pre - Algebra Adding En Garde Duel Game
Pre - Algebra с добавлением футбольной игры
Pre - Algebra Diving Addian Walk The Plank Game
Pre - Game Division Division
Pre - -
Игра в баскетбол
0003
Предварительное алгебраическое умножение в дуэльной игре
Предварительное алгебраическое умножение игра прогулка по доске
Предварительное алгебраическое умножение в баскетбол
Предварительное алгебраическое умножение в футбол
Предварительное алгебраическое вычитание 9000
Вычитание, игра в баскетбол,
0003Отрицательный показатель степени — правила, дроби, решение, вычисление
Отрицательный показатель степени определяется как мультипликативное значение, обратное основанию, возведенное в степень, противоположную знаку данной степени. Проще говоря, мы пишем обратное число, а затем решаем его как положительные показатели. Например, (2/3) -2 можно записать как (3/2) 2 . Мы знаем, что показатель степени относится к тому, сколько раз число умножается само на себя. Например, 3 2 = 3 × 3. В случае положительных степеней мы легко умножаем число (основание) само на себя, но в случае отрицательных степеней мы умножаем обратное число само на себя. Например, 3 -2 = 1/3 × 1/3.
Проще говоря, мы пишем обратное число, а затем решаем его как положительные показатели. Например, (2/3) -2 можно записать как (3/2) 2 . Мы знаем, что показатель степени относится к тому, сколько раз число умножается само на себя. Например, 3 2 = 3 × 3. В случае положительных степеней мы легко умножаем число (основание) само на себя, но в случае отрицательных степеней мы умножаем обратное число само на себя. Например, 3 -2 = 1/3 × 1/3.
Давайте узнаем больше об отрицательных показателях вместе с соответствующими правилами и решим больше примеров.
| 1. | Что такое отрицательные показатели? |
| 2. | Числа и выражения с отрицательными показателями |
| 3. | Правила отрицательного экспонента |
| 4. | Почему дроби с отрицательными показателями степени? |
5. | Отрицательные степени дроби |
| 6. | Умножение отрицательных показателей |
| 7. | Как решать отрицательные показатели? |
| 8. | Часто задаваемые вопросы об отрицательных показателях |
Что такое отрицательные показатели?
Мы знаем, что показатель степени числа говорит нам, во сколько раз мы должны умножить основание. Например, в 8 2 8 — основание, а 2 — показатель степени. Мы знаем, что 8 2 = 8 × 8. Отрицательная экспонента говорит нам, сколько раз мы должны умножить обратную величину основания. Рассмотрим 8 -2 , здесь основание равно 8, и у нас есть отрицательный показатель степени (-2). 8 -2 выражается как 1/8 × 1/8 = 1/8 2 .
Числа и выражения с отрицательными показателями
Вот несколько примеров, которые выражают отрицательные показатели с помощью переменных и чисел. Обратите внимание на приведенную ниже таблицу, чтобы увидеть, как число/выражение с отрицательным показателем степени записывается в его обратной форме и как изменяется знак степени.
Обратите внимание на приведенную ниже таблицу, чтобы увидеть, как число/выражение с отрицательным показателем степени записывается в его обратной форме и как изменяется знак степени.
| Отрицательная экспонента | Результат |
|---|---|
| 2 -1 | 1/2 |
| 3 -2 | 1/3 2 = 1/9 |
| x -3 | 1/х 3 |
| (2 + 4x) -2 | 1/(2 + 4x) 2 |
| (х 2 + у 2 ) -3 | 1/(х 2 + у 2 ) 3 |
Правила отрицательного экспонента
У нас есть набор правил или законов для отрицательных показателей, которые облегчают процесс упрощения. Ниже приведены основные правила решения отрицательных показателей.
- Правило 1: Правило отрицательного показателя степени гласит, что для основания 'a' с отрицательным показателем степени -n возьмите обратное основание (которое равно 1/a) и умножьте его само на себя n раз.
т. е. a (-n) = 1/a × 1/a × ... n раз = 1/a n - Правило 2: Правило остается тем же, даже если в знаменателе есть отрицательный показатель степени.
т. е. 1/a (-n) = a × a × ... .n раз = a n
Давайте применим эти правила и посмотрим, как они работают с числами.
Пример 1: Решить: 2 -2 + 3 -2
Решение:
- Используйте правило отрицательного порядка a -n = 1/a n
- 2 -2 + 3 -2 = 1/2 2 + 1/3 2 = 1/4 + 1/9
- Возьмите наименьшее общее кратное (НОК): (9 + 4)/36 = 13/36
Следовательно, 2 -2 + 3 -2 = 13/36
Решение:
- Используйте второе правило с отрицательным показателем в знаменателе: 1/a -n =a n
- 1/4 -2 + 1/2 -3 = 4 2 + 2 3 =16 + 8 = 24
Следовательно, 1/4 -2 + 1/2 -3 = 24.
Отрицательные показатели представляют собой дроби
Отрицательная экспонента приводит нас к обратному числу. Другими словами, -n = 1/a n и 5 -3 становится 1/5 3 = 1/125. Вот как отрицательные показатели превращают числа в дроби. Давайте возьмем другой пример, чтобы увидеть, как отрицательные показатели превращаются в дроби.
Пример: Выразите 2 -1 и 4 -2 в виде дробей.
Решение:
2 -1 можно записать как 1/2, а 4 -2 можно записать как 1/4 2 . Следовательно, отрицательные показатели превращаются в дроби при изменении знака их показателя.
Отрицательные показатели степени дроби
Иногда у нас может быть отрицательная дробная экспонента, например 4 -3/2 . Мы можем применить то же правило a -n = 1/a n , чтобы выразить это через положительный показатель степени. т. е. 4 -3/2 = 1/4 3/2 . Кроме того, мы можем упростить это, используя правила экспоненты.
т. е. 4 -3/2 = 1/4 3/2 . Кроме того, мы можем упростить это, используя правила экспоненты.
4 -3/2 = 1/4 3/2
= 1 / (2 2 ) 3/2
= 1 / 2 3
= 1/8
Умножение отрицательных показателей
Умножение отрицательных показателей такое же, как умножение любого другого числа. Как мы уже обсуждали, отрицательные показатели степени могут быть выражены в виде дробей, поэтому их можно легко решить после преобразования в дроби. После этого преобразования мы умножаем отрицательные показатели, используя то же правило умножения, которое мы применяем для умножения положительных показателей. Давайте разберемся с умножением отрицательных показателей на следующем примере. 9{3} \раз 4}\)
Как решать отрицательные показатели?
Чтобы решить выражения с отрицательными показателями, сначала преобразуйте их в положительные показатели, используя одно из следующих правил, и упростите:
- a -n = 1/a n
- 1/a -n = a n
Пример : Решите: (7 3 ) × (3 9{4}}\)

Важные примечания об отрицательных показателях степени:
- Степень или степень означает, сколько раз нужно умножить основание само на себя.
a м = a × a × a ….. m раз
a -m = 1/a × 1/a × 1/a ….. m раз - a -n также известен как мультипликативная инверсия n .
- Если a -m = a -n , то m = n.
- Отношение между показателем степени (положительные степени) и отрицательным показателем (отрицательной степенью) выражается как x = 1/a -x
☛ Похожие темы:
- Калькулятор отрицательных показателей
- Калькулятор правил экспоненты
- Калькулятор экспоненты
Примеры отрицательных показателей
Пример 1: Найдите решение данного выражения (3 2 + 4 2 ) -2 .

Решение:
Данное выражение:
(3 2 + 4 2 ) -2 = (9 + 16) -2
- = (25) -2
= 1/25 2 (по правилу отрицательной степени)
= 1/625.
Следовательно, (3 2 + 4 2 ) -2 = 1/625Ответ: 1/625
Пример 2: Найдите значение x в 27/3 -x = 3 6
Решение:
Здесь у нас есть отрицательные показатели степени с переменными.
27/3 -x = 3 6
3 3 /3 -x = 3 6
3 3 × 3 x = 3 6
3 (3 + x) = 3 6Если основания одинаковые, то степени должны быть равны, поэтому 3 + x = 6. Решая это, x = 3.
Ответ: x = 3
Пример 3: Упростите следующее, используя правила отрицательной степени: (2/3) -2 + (5) -1
Решение:
Используя правила отрицательной степени, мы можем написать (2 /3) -2 как (3/2) 2 и (5) -1 как 1/5.
 Итак, мы можем упростить данное выражение как
Итак, мы можем упростить данное выражение как
= (3/2) 2 + 1/5
= 9/4 + 1/5
После взятия LCM получаем, (45+4)/20
49/20
Следовательно, (2/3) 91 562 -2 91 563 + (5) 91 562 -1 91 563 упрощается до 49/20.Ответ: 49/20.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами.
Часто задаваемые вопросы об отрицательных показателях
Что означают отрицательные показатели?
Отрицательные показатели степени означают отрицательные числа, которые присутствуют вместо показателей степени. Например, в числе 2 -8 , -8 - отрицательная степень основания 2.
Приводят ли отрицательные степени к отрицательным числам?
Нет, отрицательные показатели степени не обязательно должны давать отрицательные числа. Например, 2 -3 = 1/8, что является положительным числом.
Например, 2 -3 = 1/8, что является положительным числом.
Как рассчитать отрицательные показатели?
Отрицательные показатели рассчитываются с использованием тех же законов показателей, которые используются для вычисления положительных показателей. Например, чтобы решить: 3 -3 + 1/2 -4 , сначала мы преобразуем их в обратную форму: 1/3 3 + 2 4 , затем упростите 1/27 + 16. Взяв НОК, [1+ (16 × 27)]/27 = 433/27.
Каково правило для отрицательных показателей?
При работе с отрицательными показателями полезны два основных правила:
- a -n = 1/a n
- 1/a -n = a n
Как решать дроби с отрицательными показателями?
Дроби с отрицательными показателями можно решить, взяв обратную дробь. Затем найдите значение числа, взяв положительное значение данного отрицательного показателя степени. Например, (3/4) -2 = (4/3) 2 = 4 2 /3 2 . Это приводит к 16/9, что является окончательным ответом.
Это приводит к 16/9, что является окончательным ответом.
Как делить отрицательные показатели?
Деление степеней с одинаковым основанием приводит к вычитанию степеней. Например, чтобы решить y 5 ÷ y -3 = y 5-(-3) = y 8 . Это также можно упростить альтернативным способом. т. е. y 5 ÷ y -3 = y 5 /y -3 , сначала мы меняем отрицательный показатель степени (y -3 ) в положительную, написав ее обратную. Получается: у 5 × у 3 = у (5+3) = у 8 .
Как умножать отрицательные показатели?
При умножении отрицательных степеней сначала нам нужно преобразовать их в положительные степени, записав соответствующие числа в обратной форме. Как только они преобразуются в положительные, мы умножаем их, используя те же правила, что и для умножения положительных показателей. Например, у -5 × y -2 = 1/год 5 × 1/год 2 = 1/год (5+2) = 1/год 7
Почему отрицательные экспоненты?
Когда нам нужно изменить отрицательную степень на положительную, мы должны написать обратную величину данного числа. Итак, отрицательный знак степени косвенно означает обратную величину данного числа, точно так же, как положительный показатель степени означает многократное умножение основания.
Итак, отрицательный знак степени косвенно означает обратную величину данного числа, точно так же, как положительный показатель степени означает многократное умножение основания.
Сколько будет 10 в отрицательной степени числа 2?
10 в отрицательной степени 2 представляется как 10 -2 , что равно (1/10 2 ) = 1/100.
Предварительный алгебраический калькулятор | Пошаговый калькулятор
1.2k
АКЦИИ
Независимо от того, во что верит или хочет верить большинство людей, математика на самом деле удивительна. Он знакомит вас со всем, от физики до естествознания и геологии. Изучите математику достаточно хорошо, и вы сможете расшифровать тайны Вселенной в кратчайшие сроки.
Кроме того, математика является важным навыком, который необходимо приобрести, независимо от того, какую карьеру вы собираетесь выбрать, будь то инженерия, программирование или биохимия.
Конечно, в математике все понимать не нужно. Вы не должны решить специальную теорию относительности Эйнштейна или что-то в этом роде, но вам нужно понять основы.
Вы не должны решить специальную теорию относительности Эйнштейна или что-то в этом роде, но вам нужно понять основы.
Подводя итог, скажу, что вам нужно понимать принципы математики, если вы хотите преуспеть в жизни. Не позволяйте никому убеждать вас в обратном.
По сути, важность математики привела к очаровательному изобретению, называемому калькулятором. Проблема в том, что калькуляторы немного просты и не специализированы, а это означает, что вам понадобится некоторое время, чтобы привыкнуть к различным функциям и тому, что делает каждая кнопка. Это привело к необходимости в более специализированных инструментах, таких как калькулятор для предварительной алгебры. НО, поскольку производители в основном ищут прибыль, эта идея показалась идиотской и невыгодной, поэтому такого инструмента не найти. Вы не найдете его легко, т.
Поскольку мы живем в то время, когда технологии и Интернет распространены повсеместно, было создано несколько онлайн-инструментов, чтобы решить эту проблему, что привело к созданию калькулятора предварительной алгебры.
Этот бесплатный онлайн-калькулятор для предварительной алгебры разработан с учетом функциональности, простоты использования и точности, что делает его любимым приложением для многих студентов, изучающих алгебру по всему миру.
Используйте этот инструмент правильно, и вы обязательно начнете плодотворное математическое путешествие, которое откроет бесчисленные карьерные возможности для вас (или ваших детей, если вы используете этот инструмент, чтобы помочь им в математике)
Поскольку вы здесь, вы, вероятно, уже знаете, что такое предалгебра. Но, если у вас все еще есть смутное представление об этой концепции, предварительная алгебра — это первый урок математики, который вы посещаете в старшей школе. Другими словами, это основа, на которой вы будете строить свои математические знания и опыт.
На подготовительных занятиях по алгебре вы изучите множество дополнительных предметов, таких как целые числа, уравнения, неравенства, графики и функции, проценты и вероятности. Список, конечно, можно продолжить, но это основные пункты, и они охватываются нашим предварительным алгебраическим справочным калькулятором.
Список, конечно, можно продолжить, но это основные пункты, и они охватываются нашим предварительным алгебраическим справочным калькулятором.
SolveMathProblems хочет сделать такой важный образовательный шаг приятным занятием.
Как упоминалось выше, предварительная алгебра является важным шагом в вашей образовательной жизни. Обычно этому учат в старшей школе, но многие дети могут начать изучать его раньше, например, одаренные дети и дети, обучающиеся на дому. К счастью, наш калькулятор предварительных алгебраических уравнений подойдет вам независимо от того, к какой категории вы принадлежите.
Как следует из названия, основной целью этого класса является подготовка учащихся к алгебре и высшей математике. Другими словами, если учащийся не сможет заложить прочную основу в начальной алгебре, он/она, вероятно, сочтет математику верхнего уровня более сложной, чем она есть на самом деле. По сути, многие ученики не воспринимают предварительную алгебру всерьез, поэтому позже они находят математику слишком сложной и сложной, что в конечном итоге приводит к эпидемии «я ненавижу математику».
Предварительная алгебра охватывает множество понятий, большинство из которых поддерживаются нашим онлайн-калькулятором предварительной алгебры. Эти понятия включают целые числа, сложение, вычитание, умножение, деление, простые числа, задачи со словами, точки, линии, объем, дроби, вероятности и т. д. или мост к настоящей математике, но это далеко не так. Почему? Потому что вы не хотите погружаться в сложную математику, пока мучаетесь с простыми дробями и десятичными знаками.
Математика — это целый процесс, к которому нужно относиться серьезно. Дело не в вашем возрасте или прохождении занятий; речь идет о том, чтобы научиться решать большие задачи, разделяя их на более мелкие, что возвращает нас к предалгебре.
Каждое новое понятие, которое вы изучаете во время образовательного курса, основано на простых понятиях, что показывает огромную роль, которую играет предварительная алгебра, и, следовательно, большую помощь, которую может оказать наш онлайн-калькулятор для предварительной алгебры.
Независимо от того, пытаетесь ли вы преуспеть в своем классе алгебры, боретесь с непосильной домашней работой, которую дал вам учитель, или хотите освоить основы математики; изучение предварительной алгебры является важным шагом в вашей образовательной жизни.
Попытка пройтись по основам приведет лишь к накоплению слабых мест позже, так что не торопитесь и закрепите свои математические знания на надежном фундаменте, правильно изучив предварительную алгебру с помощью следующего продуктивного подхода.
Начните свое путешествие с изучения чисел и их свойств
Если вы только начинаете изучать предварительную алгебру, вы, вероятно, знакомы с основными понятиями, операциями и функциями, такими как сложение и вычитание, умножение и деление. Теперь пришло время заняться более сложными вещами.
Некоторые расширенные числовые свойства и операции, которые вам необходимо освоить в качестве студента, изучающего алгебру, включают, помимо прочего, десятичные дроби, квадратные корни, целые числа и отрицательные числа.
Хотя для некоторых из вас они могут показаться базовыми, хорошее знание этих операций и свойств может на самом деле улучшить ваши навыки и оказаться бесценным активом в будущем.
Медленно переходите к соотношениям и пропорциям
Основные соотношения описывают, как одна сумма соотносится с другой, а пропорции сравнивают соотношения. Студенты знакомы с обоими, но если вы хотите по-настоящему освоить предварительную алгебру, знакомства будет недостаточно, вам нужно полностью овладеть этими понятиями.
Как? Практика, конечно.
Один из лучших способов сделать это — использовать наш предварительный алгебраический калькулятор для решения задач и выявления ошибок, о которых вы не знали. Делайте это последовательно, и отношения и пропорции станут для вас куском пирога в кратчайшие сроки.
Изучение факторинга
Факторинг — это важный навык, который необходимо освоить в алгебре, поскольку он может очень помочь в задачах, содержащих экспоненты, упрощение и другие темы. Начните с базового факторинга, разбивая небольшие числа, а затем продвигайтесь вперед, изучая более сложные темы факторинга, такие как выполнение простой факторизации числа и нахождение наибольшего общего делителя двух чисел. Если все это кажется вам слишком сложным, вы можете воспользоваться нашим факторинговым калькулятором, который покажет вам, как выполнять операции факторинга шаг за шагом.
Начните с базового факторинга, разбивая небольшие числа, а затем продвигайтесь вперед, изучая более сложные темы факторинга, такие как выполнение простой факторизации числа и нахождение наибольшего общего делителя двух чисел. Если все это кажется вам слишком сложным, вы можете воспользоваться нашим факторинговым калькулятором, который покажет вам, как выполнять операции факторинга шаг за шагом.
Понимание дробей
Хотя дроби могут показаться вам элементарной математикой, их овладение может оказаться большим подспорьем для ваших будущих занятий. Вы можете развивать свои знания о дробях, работая над задачами, требующими обращения с дробями путем сложения, вычитания, деления и умножения.
Если вы столкнетесь с трудностями при решении какой-либо задачи, вы можете прибегнуть к калькулятору упрощенных дробей Mathway, так как он может упростить алгебраические дроби и помочь вам лучше понять вопросы, над которыми вы работаете.
Итак, вот оно. По сути, это лучший план успеха в предварительной алгебре, поэтому убедитесь, что вы правильно описали каждый шаг. Что бы вы ни делали, всегда помните золотое правило; практика делает совершенным.
Что бы вы ни делали, всегда помните золотое правило; практика делает совершенным.
Вы, наверное, начинаете ненавидеть меня за то, что я повторяю это миллион раз, но я действительно не могу не подчеркнуть: практика делает совершенным. Любой математический предмет поначалу может показаться сложным, но с каждой решаемой задачей вы становитесь на шаг ближе к тому, чтобы стать мастером в этой области.
Предварительная алгебра — действительно классный предмет, и вы можете найти отличное применение ее различным функциям, уравнениям и свойствам повсюду вокруг вас.
Итак, сложно ли учить предварительную алгебру? Нет, это не так, пока вам нравится то, что вы делаете, а не практиковать это ради оценки в классе, которую вы собираетесь получить.
Кроме того, первый шаг к прогрессу — это действие, поэтому перестаньте быть ленивым учеником, возьмите тетрадь и рабочую тетрадь по алгебре и начните решать задачи. Если вы когда-нибудь застрянете, помните, что наш предварительный алгебраический калькулятор всегда будет здесь, чтобы помочь вам преодолеть любые препятствия, которые могут встретиться на вашем пути.
Независимо от того, пытаетесь ли вы решить предварительный экзамен по алгебре с помощью калькулятора или ищете бесплатный калькулятор для 7-го класса с переменными и выражениями, который поможет вам с домашним заданием, вы обязательно найдете применение этому онлайн-инструменту.
Вам следует использовать калькулятор для предварительной алгебры, если:
- Вы ищете калькулятор для предварительной алгебры с шагами
Нет смысла отрицать это; большинству людей наплевать на процесс, их волнует только результат, который они могут показать своему учителю. Но есть исключение для тех, кто хочет понять, как получить этот результат, что вызывает потребность в калькуляторе, который не только решает задачу или уравнение, но и показывает, как вы можете сделать это самостоятельно.
Это именно то, что делает наш калькулятор предварительной алгебры, предоставляя вам уникальный опыт обучения, шаг за шагом. Итак, если вам нужен предварительный алгебраический калькулятор, который показывает работу, вы находитесь в правильном месте.
- Вам нужен калькулятор, которым можно пользоваться где угодно
Устали везде носить с собой калькулятор? Хотите эффективно использовать свой ноутбук, планшет или смартфон? Ваша собака сломала ваш научный калькулятор, оставив вас без инструмента для решения домашнего задания? Если вы можете относиться к любому из них, поиск онлайн-калькулятора до алгебры становится необходимостью.
Как следует из названия, это онлайн-инструмент, а это означает, что все, что вам нужно, это сигнал Wi-Fi или мобильное подключение для передачи данных, и вы готовы к своей оценке.
Хотите еще больше хороших новостей? Не нужно искать ссылку для скачивания калькулятора предварительной алгебры, так как этот онлайн-калькулятор для предварительной алгебры не требует загрузки и установки, поэтому вам не нужно беспокоиться о емкости памяти вашего устройства, сосредоточившись на домашнем задании.
- Вам не нужен предварительный алгебраический калькулятор; вы хотите ЛУЧШИЙ калькулятор для предварительной алгебры
Посмотрим правде в глаза. Научные калькуляторы не были созданы для предварительной алгебры. Они были созданы для более продвинутых вещей. Конечно, они могут делать и то, и другое, но найти более специализированный инструмент может быть намного лучше. Итак, если вы когда-нибудь задавались вопросом, как выполнить предварительную алгебру на калькуляторе, этот инструмент — решение, которое вы ищете.
Научные калькуляторы не были созданы для предварительной алгебры. Они были созданы для более продвинутых вещей. Конечно, они могут делать и то, и другое, но найти более специализированный инструмент может быть намного лучше. Итак, если вы когда-нибудь задавались вопросом, как выполнить предварительную алгебру на калькуляторе, этот инструмент — решение, которое вы ищете.
- Вам понадобится калькулятор предварительных алгебраических уравнений, чтобы проверить домашнее задание
SolveMathProblems — это веб-сайт, который отвечает на математические задачи, а наш предварительный алгебраический калькулятор — отличный инструмент, который вы можете использовать, чтобы проверить ответы на домашние задания и убедиться, что они соответствуют действительности.
Излишне говорить, что не нужно просто вводить свою проблему, щелкать ответ и записывать решение. Вы только обманываете себя таким образом.
Хотя идея давать правильное домашнее задание без каких-либо усилий может показаться привлекательной, на самом деле это плохой ход, поскольку чем больше вы это делаете, тем ленивее и глупее становитесь.
Вместо этого вам следует поработать над домашним заданием, не торопясь попытаться решить его правильно, а затем использовать этот предварительный алгебраический калькулятор, чтобы проверить свои ответы.
Вы получили правильные ответы с первого раза? Идеальный! Пришло время больше практики!
Вы допустили ошибки? Нет проблем, проверяйте свои ошибки и работайте над устранением слабых мест.
Таким образом, вы будете учиться, оттачивать свои навыки и одновременно исправлять домашнюю работу.
- Вам нужен калькулятор упрощающих выражений до алгебры
К сожалению, стандартные калькуляторы (за исключением некоторых дорогостоящих) не показывают шаги, необходимые для решения конкретной проблемы, и они не запрограммированы на облегчение вашей жизни за счет упрощения пути к решению. С другой стороны, приложение SolveMathPorblems не является стандартным калькулятором.
Что делает этот мощный инструмент, так это то, что он берет проблему, которую вы ему подаете, а затем упрощает выражение, тем самым показывая вам, как получить решение самым простым способом.
Другими словами, этот предварительный алгебраический калькулятор отвечает на ваши вопросы, не забивая вам голову еще более сложными вопросами о том, как он получил решение. Удобно, да?
Потому что кому захочется постоянно носить с собой калькулятор?
Онлайн-калькулятор предварительной алгебры — это удобный инструмент, к которому вы можете получить доступ в любое время и в любом месте — не нужно носить с собой громоздкий калькулятор и подвергаться издевательствам за то, что он выглядит как ботаник.
Всякий раз, когда вам нужно решить задачу по алгебре, вы можете просто достать свой телефон, планшет или ноутбук, открыть приложение-калькулятор помощи по алгебре и начать работать над ним. Если это не удобно, то я не знаю, что тогда.
Кроме того, будучи онлайн-инструментом, наше приложение совместимо с любым устройством, будь то смартфон, планшет или ноутбук, если оно подключено к Интернету.
Потому что за знания не нужно платить, особенно когда речь идет об основных навыках, которые должен понимать каждый, таких как математика и предварительная алгебра.
И SolveMathProblems, и Mathway увлечены математикой и предварительной алгеброй, и мы хотели бы, чтобы она стала любимым предметом изучения во всем мире. Вот почему мы представляем этот бесплатный калькулятор предварительной алгебры с бесплатными шагами.
Итак, если вы ищете бесплатный онлайн-калькулятор предварительной алгебры, вы только что сорвали джекпот. Перестаньте спрашивать себя «какой калькулятор мне купить для предварительной алгебры?». Вам не нужно ничего покупать, если у вас есть доступ к приложению SMP.
Проще говоря, вы можете сделать многое, поэтому не позволяйте тому факту, что это онлайн-инструмент, ввести вас в заблуждение, думая, что он не способен на то, что может любой другой калькулятор, и даже больше.
Вы можете использовать калькулятор математической подготовки к алгебре как:
- Лаборатория калькулятора предварительной алгебры
- Предварительная алгебра Y = X Калькулятор
- Предварительный алгебраический калькулятор для T-диаграмм
- Калькулятор предварительной алгебры
- Калькулятор алгебры для дошкольников
- Pre Алгебра Подобные цифры Калькулятор Масштабный коэффициент и X
- Калькулятор словесных задач по алгебре
- Калькулятор похожих фигур для предварительной алгебры
- Калькулятор двухэтапных уравнений для предварительного алгебраического решения
- Калькулятор поиска значения X Предварительная алгебра
- Калькулятор распределительных свойств до алгебры
Другими словами, приложение SolveMathProblems — это калькулятор предварительной алгебры, нет, лучший калькулятор предварительной алгебры для различных целей, независимо от того, на каком уровне вы находитесь. Это просто ваш билет к успешному путешествию по алгебре, поэтому обязательно воспользуйтесь этой возможностью и опробуйте приложение. Вам нечего терять, но все приобретете.
Это просто ваш билет к успешному путешествию по алгебре, поэтому обязательно воспользуйтесь этой возможностью и опробуйте приложение. Вам нечего терять, но все приобретете.
Если вы посмотрите на интерфейс научного калькулятора SolveMathProblems для предварительной алгебры, вы заметите, что он содержит много символов, некоторые из которых существуют в обычных калькуляторах, а другие уникальны для этого инструмента.
К этим символам относятся скобки, абсолютное значение, дроби, экспоненты, квадратные корни, меньше или равно, треугольник, трапеция, цилиндр, прямоугольная пирамида и знак деления, среди прочих.
Такое разнообразие символов делает этот предварительный алгебраический калькулятор одновременно лучшим графическим калькулятором для алгебры 2 и предварительного расчета и лучшим графическим калькулятором для предварительной алгебры.
Будучи многофункциональным калькулятором, этот инструмент можно использовать для выполнения домашних заданий, работы в колледже, проверки ответов и тестирования. Так что, если у вас есть свободное время и вы хотите улучшить свои предварительные алгебраические навыки, просто возьмите свой смартфон, откройте эту веб-страницу и поработайте над некоторыми задачами.
Так что, если у вас есть свободное время и вы хотите улучшить свои предварительные алгебраические навыки, просто возьмите свой смартфон, откройте эту веб-страницу и поработайте над некоторыми задачами.
Вы можете заниматься дома, в автобусе, в путешествии, где угодно! Даже если у вас нет под рукой задач для решения, вы можете воспользоваться одним из доступных примеров.
Вы когда-нибудь читали книгу «Как использовать калькулятор для предварительной алгебры для чайников»? Я уверен, что нет, потому что его не существует. Но не волнуйтесь, больше не нужно прокручивать результаты поиска Google в калькуляторе предварительной алгебры, пытаясь понять, как правильно решить домашнее задание. Сегодня, благодаря сложному онлайн-инструменту Mathway, использование онлайн-калькулятора для предварительной алгебры никогда не было проще. Вы должны просто:
- Напишите свою проблему, используя один из предоставленных примеров или доступные символы.
- Нажмите кнопку «Показать», чтобы проверить задачу в стандартном математическом формате, к которому вы привыкли.
 Если у вас возникнут какие-либо проблемы, вы можете нажать на ? Кнопка рядом с полем «Ввести проблему».
Если у вас возникнут какие-либо проблемы, вы можете нажать на ? Кнопка рядом с полем «Ввести проблему». - Калькулятор автоматически выберет тип задачи в зависимости от того, что вы написали. В вероятном случае неправильного выбора вы можете самостоятельно выбрать правильный тип из раскрывающегося списка «Выбрать тему».
- Нажмите «Ответить» и подождите, пока произойдет волшебство.
- Проверьте ответ и сравните его со своим решением. Если вы допустили ошибку, обязательно запишите ее, чтобы продолжить работу над ней. Если вам нужно проверить пошаговое решение, вы можете зарегистрироваться в Mathway.
Легко.
Хотя нам бы хотелось, чтобы мы были теми, кто разработал этот великолепный инструмент, на самом деле это плод творческого ума Mathway, хотя мы реализовали его на нашем сайте, чтобы облегчить доступ к нему для наших пользователей по всему миру.
Если вы хотите разблокировать все возможности калькулятора, вам нужно будет пройти предварительный процесс регистрации калькулятора алгебры Mathway.
Не беспокойтесь, так как это коротко и просто, но сначала обязательно получите одобрение родителей, если вы несовершеннолетний.
В общем, если вы застряли в сложном уравнении, которое хотите решить, чтобы доказать своему учителю, что вы действительно так умны, как утверждаете, пришло время получить надежное бесплатное приложение для калькулятора по алгебре.
Вышеупомянутый инструмент не только удобен и удобен для пользователя, но также может работать как калькулятор экспоненциальных уравнений, приложение для решения математических задач и даже калькулятор фундаментальной теоремы алгебры.
По сути, это приложение мечты любого студента, изучающего алгебру. Чего ты ждешь? Это та помощь по алгебре, которую ты искал, иди решай задачки, юный Эйнштейн!
Наш калькулятор предварительной алгебры поможет вам не только проверить домашнюю работу, но и даст дополнительную практику для подготовки к тестам и контрольным.
Чем больше вы практикуетесь, тем лучше вы будете подготовлены. Калькулятор даст вам дополнительные задачи, чтобы попробовать. Найдите тему, которую вы хотите просмотреть, в разделе Examples калькулятора. Проблема будет отображаться в поле. (Если это трудно понять, это потому, что это написано в нотации калькулятора. Нажмите кнопку Показать , чтобы просмотреть задачу в стандартном математическом формате.) Выберите тему сообщает калькулятору, что делать с задачей; просто убедитесь, что это соответствует указаниям для типа задачи, которую вы хотите попрактиковать. Решите задачу и проверьте свой ответ с помощью калькулятора. Если вы ответите правильно, то поймете, что вы на правильном пути. Если нет, вам нужно вернуться к своей работе, чтобы найти свои ошибки. Если вы не можете его найти, попросите помощи у родителей или друзей или зарегистрируйтесь на Mathway. Mathway покажет вам, как решать задачу шаг за шагом, чтобы вы могли найти свою ошибку и посмотреть, как правильно решить задачу.
Калькулятор даст вам дополнительные задачи, чтобы попробовать. Найдите тему, которую вы хотите просмотреть, в разделе Examples калькулятора. Проблема будет отображаться в поле. (Если это трудно понять, это потому, что это написано в нотации калькулятора. Нажмите кнопку Показать , чтобы просмотреть задачу в стандартном математическом формате.) Выберите тему сообщает калькулятору, что делать с задачей; просто убедитесь, что это соответствует указаниям для типа задачи, которую вы хотите попрактиковать. Решите задачу и проверьте свой ответ с помощью калькулятора. Если вы ответите правильно, то поймете, что вы на правильном пути. Если нет, вам нужно вернуться к своей работе, чтобы найти свои ошибки. Если вы не можете его найти, попросите помощи у родителей или друзей или зарегистрируйтесь на Mathway. Mathway покажет вам, как решать задачу шаг за шагом, чтобы вы могли найти свою ошибку и посмотреть, как правильно решить задачу.
Учителя назначают домашнее задание, чтобы вы научились правильно решать задачи. Чтобы проверить домашнее задание, просто введите задачу и нажмите . Ответьте , чтобы убедиться, что вы правы. Если вы ответите правильно, это будет здорово! Однако, если вы ошибаетесь, не просто записывайте правильный ответ. Если вы это сделаете, вы обманываете себя, потому что на самом деле не знаете, как решить проблему, и не будете знать, что делать на предстоящем тесте. Вам нужно понять, какую ошибку вы совершили, чтобы не повторять ее снова. Так что вернитесь и проверьте свою работу, и если вы не можете найти свою ошибку, попросите кого-нибудь о помощи. Или попросите своих родителей записать вас на Mathway, где вы шаг за шагом покажете, как решить проблему. Mathway намного дешевле, чем репетиторство, и будет выгодным вложением, поскольку вы можете использовать его, чтобы учиться и проверять домашнюю работу до конца года.
Чтобы проверить домашнее задание, просто введите задачу и нажмите . Ответьте , чтобы убедиться, что вы правы. Если вы ответите правильно, это будет здорово! Однако, если вы ошибаетесь, не просто записывайте правильный ответ. Если вы это сделаете, вы обманываете себя, потому что на самом деле не знаете, как решить проблему, и не будете знать, что делать на предстоящем тесте. Вам нужно понять, какую ошибку вы совершили, чтобы не повторять ее снова. Так что вернитесь и проверьте свою работу, и если вы не можете найти свою ошибку, попросите кого-нибудь о помощи. Или попросите своих родителей записать вас на Mathway, где вы шаг за шагом покажете, как решить проблему. Mathway намного дешевле, чем репетиторство, и будет выгодным вложением, поскольку вы можете использовать его, чтобы учиться и проверять домашнюю работу до конца года.
1. Вы можете ввести задачу, используя пример или символы.
2. Нажмите кнопку Показать рядом с Math Format . Это покажет вашу задачу в обычном математическом формате, к которому вы привыкли. Если это выглядит неправильно и вам нужна дополнительная помощь, щелкните значок ? Поле рядом с полем Введите проблему .
Это покажет вашу задачу в обычном математическом формате, к которому вы привыкли. Если это выглядит неправильно и вам нужна дополнительная помощь, щелкните значок ? Поле рядом с полем Введите проблему .
3. Раскрывающийся список Select Topic будет заполнен наиболее распространенным типом проблемы, но если вы хотите, чтобы калькулятор делал что-то другое, просто выберите правильный вариант из раскрывающегося списка.
4. Щелкните Ответ , чтобы просмотреть ответ.
5. Если вы допустили ошибку, вам нужно выяснить, что вы сделали не так. Чтобы увидеть шаги, зарегистрируйтесь в Mathway.
На примере:
Прокрутите темы, чтобы найти тип задач, которые вы хотите проверить или попрактиковаться. Это предоставит пример в калькуляторе, чтобы вы могли увидеть, как он отформатирован. Затем вы можете изменить числа или переменные, чтобы они соответствовали проблеме, которую вы пытаетесь проверить.
Круглые скобки — Они указывают на умножение или на то, что сначала нужно выполнить внутреннюю операцию.
Скобки – Используйте скобки, если вам нужна скобка внутри скобки – Скобки выходят наружу, как показано в этом примере: [3 + 2(10 -1)] ÷ 7.
Абсолютное значение – Абсолютное значение value говорит, насколько далеко число от нуля. Это всегда одно и то же число, но положительное. Например, |3| равно 3 и |-3| также 3.
(2) для 5 2 . Помните, что показатель степени говорит, сколько раз основание умножается само на себя.
Квадратные корни – введите подкоренное число (число внутри символа квадратного корня) внутри скобок. Квадратные корни находят, какое число, умноженное на себя, равняется подкоренному. Например, квадратный корень из 49 равен 7, потому что 7 * 7 = 49.
Например, квадратный корень из 49 равен 7, потому что 7 * 7 = 49.
Другие корни — Введите индекс после символа √ и подкоренной дроби в скобках. Например, используйте √3:(8) для . Помните, что другой индекс означает, что ответ должен быть умножен сам на себя столько раз, чтобы получить подкоренное число. В нашем примере 2 * 2 * 2 = 8, поэтому ответом будет 2, потому что 2 умножить на 9.0103 3 (индекс) умножить на 8.
Примечание. Если индекс не указан, предполагается, что он равен двум и называется просто квадратным корнем.
Координаты — Введите координату, как обычно, например (1,5).
Точка/наклон – Используйте эту кнопку, если вы знаете одну координату и наклон (м) линии. Затем вы можете либо найти уравнение линии, либо посмотреть график линии. Введите координату в скобках и наклон после m= . Например, линия с наклоном ½ и координатой (3,5) будет выглядеть так: (3,5),m=1/2.
Например, линия с наклоном ½ и координатой (3,5) будет выглядеть так: (3,5),m=1/2.
Научное обозначение – В скобках введите число, а затем показатель степени. Например, 2,6 x 10 будет выглядеть так: sci[2.6,8]. Помните, что отрицательные показатели используются для чисел меньше нуля.
Больше или равно . Если вам нужно использовать только знак больше чем ( > ), просто введите его с клавиатуры. (Нажмите shift, затем точку.)
Меньше или равно — Если вам нужно использовать только знак «меньше» (<), просто введите его с клавиатуры. (Нажмите Shift, затем запятую.)
Прямоугольник – В скобках введите длину и ширину прямоугольника. Калькулятор может дать вам периметр или площадь. Помните, что периметр — это расстояние вокруг внешней стороны фигуры (например, забор вокруг двора), а эта площадь — площадь поверхности, которую покрывает фигура (например, ковровое покрытие в комнате).
Круг — введите радиус в поле скобки. Радиус - это расстояние от центра к краям. Если вам известен диаметр (расстояние по всей окружности), разделите его на два, чтобы найти радиус. Затем калькулятор может вычислить площадь или длину окружности. Окружность означает расстояние вокруг внешней стороны круга. Формула площади круга равна ², а длина окружности равна .
Треугольник – Введите основание и высоту в скобках. Помните, что высота треугольника составляет прямой угол с основанием — это не одна из сторон, если у вас нет прямоугольного треугольника. Площадь треугольника находится по формуле A = ½bh .
Параллелограмм – Параллелограмм имеет две пары параллельных сторон. Введите основание и высоту в скобках. Помните, что высота параллелограмма составляет прямой угол с основанием. Формула площади параллелограмма равна 9. 0103 А = чч .
0103 А = чч .
Трапеция – Трапеция имеет только один набор параллельных сторон. В скобках введите одно из оснований, затем высоту, а затем другое основание. *Обратите внимание, что высота должна быть посередине. Основаниями являются две параллельные стороны трапеции, а высота образует прямой угол с обоими основаниями. Формула площади трапеции такова.
Прямоугольные призмы – Прямоугольная призма – это официальное название коробки. Введите длину, ширину и высоту в скобках. Затем вы можете найти объем или площадь поверхности. Объем — это количество пространства внутри фигуры (например, количество воды, которое поместится в бассейн). Площадь поверхности — это площадь всех внешних поверхностей (например, сколько упаковочной бумаги потребуется, чтобы обернуть коробку).
Цилиндр – Сначала введите высоту, затем радиус. Помните, что радиус — это расстояние от центра круга до внешней стороны круга. Формула объема цилиндра такова.
Помните, что радиус — это расстояние от центра круга до внешней стороны круга. Формула объема цилиндра такова.
Конус – Сначала введите высоту, затем радиус. Помните, что радиус — это расстояние от центра круга до внешней стороны круга. Формула объема конуса такова.
Прямоугольная пирамида – Сначала введите высоту, затем длину и ширину основания. Формула объема прямоугольной пирамиды такова.
Сфера – Введите радиус сферы в скобках. Помните, что радиус — это расстояние от центра сферы до внешней стороны. Если вам дан диаметр (расстояние до конца), вы должны разделить его на 2, чтобы найти радиус. Формула объема шара такова. Площадь поверхности можно найти по формуле .
Знак деления – Для умножения используйте кнопку со звездочкой на клавиатуре. (Нажмите Shift, затем 8).
Пи — Пи — это уникальное число, которое описывает соотношение между длиной окружности и диаметром каждого круга. Пи примерно равно 3,14.
- Будьте внимательны в классе. Очень важно слушать и задавать вопросы в классе. Если вы пропустите инструкцию, которую дает ваш учитель, вам придется разобраться с этим позже. Мало того, что это займет намного больше времени, так еще и будет труднее научиться самостоятельно. Так что не поддавайтесь искушению писать заметки своим друзьям или рисовать во время урока и слушайте! Вы будете рады, что сделали это.
- Серьезно отнеситесь к домашнему заданию. Домашнее задание по математике разработано, чтобы дать вам возможность попрактиковаться в том, что вы узнали в классе. Ваши тесты и викторины будут содержать задачи, очень похожие на те, что указаны в вашем домашнем задании, поэтому, если вы знаете, как делать домашнее задание, вы будете знать, как работать с ним в тесте.
 Однако, если вы не знаете, как делать домашнее задание, у вас будут проблемы. Так что делайте все возможное. Если вы столкнулись с проблемами, которые не можете решить, попросите кого-нибудь о помощи или запишите вопрос, который вы зададите учителю, когда будете выполнять домашнюю работу в классе на следующий день.
Однако, если вы не знаете, как делать домашнее задание, у вас будут проблемы. Так что делайте все возможное. Если вы столкнулись с проблемами, которые не можете решить, попросите кого-нибудь о помощи или запишите вопрос, который вы зададите учителю, когда будете выполнять домашнюю работу в классе на следующий день. - Учитесь на своих ошибках. Вы будете делать ошибки в математике — это часть процесса. Важно, чтобы вы учились на своих ошибках, чтобы не совершать их снова и снова. Всякий раз, когда вы неправильно решаете проблему, вам нужно вернуться и выяснить, где вы ошиблись. Если вы не можете найти свою ошибку, обратитесь за помощью к другу, родителю или учителю. Или, если ваши родители запишут вас в Mathway, вы сможете увидеть шаги для каждой задачи и найти там свою ошибку.
Дроби в выражениях и уравнениях: правила
Алгебраические выражения в математике состоят из констант и переменных , связанных алгебраическими операциями (сложения, вычитания, умножения и деления). Дробь — это деление двух выражений: например, это дроби выражений, содержащих константы и/или переменные.
Дробь — это деление двух выражений: например, это дроби выражений, содержащих константы и/или переменные.
Уравнение — это математическое выражение, состоящее из символ равенства между двумя алгебраическими выражениями . Например, это уравнение.
Решить уравнение означает найти значение переменной, при котором выражения в левой и правой частях равны ; это значение называется решением уравнения. Например, решение уравнения: если вы подставите это значение с обеих сторон уравнения, вы получите .
В этой статье речь идет о наличии дроби в выражениях и уравнениях ; такие уравнения называются (что неудивительно) дробными уравнениями.
Первый шаг в работе с дробными уравнениями состоит в исключении из них дробей . Давайте погрузимся и посмотрим, как этого добиться!
Что такое термины, коэффициенты, переменные и константы?
- Термины являются строительными блоками алгебраических выражений: в выражении каждый термин отделяется знаком плюс (+) или минус (-).
 В уравнении 3x и 4 — члены выражения в левой части; а 10 — член выражения в правой части.
В уравнении 3x и 4 — члены выражения в левой части; а 10 — член выражения в правой части. - Коэффициенты — это значения, которые умножают переменные в выражении или уравнении. При заданном выражении коэффициент – это число, на которое умножается х, т.е.
- Переменные — это буквы в выражениях и уравнениях, которые используются для представления неизвестных величин. Когда у вас есть выражение, заданное как , x и y идентифицируются как переменные.
- Константы — это числа в выражениях и уравнениях, которые не изменяются. Например, в уравнении 4 является константой.
Рисунок 1. Термины алгебры, siyavula.com
Как решать выражения с дробями: пошаговые примеры
Если вы имеете дело с дробями в выражениях, проще всего складывать и вычитать их, когда они общий знаменатель . Это означает, что мы найдем эквивалентную долю участвующих дробей, найдя наименьший общий делитель (LCD) для знаменателей терминов.
Упрощение
Решение:
Здесь мы найдем общий знаменатель для двух членов, чтобы их можно было сложить. Во-первых, нам нужно будет найти LCD для знаменателей двух дробей, 5 и 4. Наименьший общий делитель для обоих чисел будет 20. Теперь мы найдем эквивалентную дробь для обоих.
Если знаменатель первой дроби теперь должен быть равен 20, это означает, что мы, вероятно, умножили первоначальный знаменатель, 5, на 4. Это означает, что нам придется умножить числитель также на 4, чтобы получить эквивалентную дробь.
Проделаем то же самое для второй дроби. 20 в знаменателе также означает, что мы должны были умножить 4 (в знаменателе) на 5, чтобы получить 20 в качестве нового знаменателя эквивалентной дроби. Это означает, что нам придется умножить числитель также на 5.
Теперь у нас есть новое выражение:
Это становится намного проще решить, поскольку все, что нам нужно сделать, это сложить числители и сохранить знаменатели.
Так как дальше это не может быть упрощено, мы остановимся на этом.
Решите выражения с дробями с помощью F
актуализации и G группировкиМогут быть более сложные задачи, где нам, возможно, придется использовать пару методов, таких как факторизация и группировка . В этих ситуациях нужно быть очень осторожным в отношении того, что конкретно представляет собой термин и когда разделяются его компоненты. Давайте посмотрим на пример ниже:
Упростить
Решение:
Поскольку мы ничего не можем отменить в текущем выражении, мы можем разложить на множители, чтобы посмотреть, что мы можем сделать из ситуации. Сначала мы сгруппируем одинаковые термины в числителе, переставив их так, чтобы термины, содержащие x , были близки друг к другу, а термины, содержащие b , также были близки.
Теперь разложим на множители. Общий множитель первых двух членов числителя равен х. Это можно исключить. Общий множитель в последних двух членах числителя равен 9.0103 -b , и это тоже можно вынести за скобки.
Общий множитель первых двух членов числителя равен х. Это можно исключить. Общий множитель в последних двух членах числителя равен 9.0103 -b , и это тоже можно вынести за скобки.
Вся идея разложения здесь на множители заключается в построении общей скобки, чтобы одну из них можно было убрать. Здесь имеем и . Учитывая коммутативность сложения, обе скобки совпадают.
Это оставит нас с:
Теперь мы немедленно разложим знаменатель на множители. Поскольку x кажутся общими в обоих терминах, это то, что будет исключено.
Теперь мы остались в ситуации, когда мы можем свободно отменить. в знаменателе сократится в числителе. Это верно, если отличается от .
Это самая простая форма, которую мы можем получить из этого выражения.
Как решать уравнения с дробями: пошаговые примеры
Как упоминалось ранее, при работе с уравнениями с дробями следует обращать внимание на то, чтобы сначала исключить дробь . Вы должны умножить все члены в обеих частях уравнения на знаменатель дроби.
Вы должны умножить все члены в обеих частях уравнения на знаменатель дроби.
Если бы нам дали уравнение , мы сначала умножили бы уравнение (технически это также каждый член уравнения) на 2.
Решение:
После умножения на 2 дробь сократится.
Теперь мы изменим уравнение, чтобы поставить одинаковые члены в разные стороны уравнения.
Разделите обе части на 10
Чтобы убедиться, что это действительно решение уравнения, вам нужно подставить значение x обратно в исходное уравнение:
Решить
Решение:
Члены уравнения с двумя дробями с одинаковым знаменателем будут умножены на знаменатель, как упоминалось ранее.
Подобные термины теперь будут сгруппированы с этой точки.
Разделите обе части на 4
Чтобы вычислить это, вам нужно подставить значение x обратно в исходное уравнение.
Решите
Решение:
Наш пример сильно отличается от обычного. Поскольку у нас есть две дроби с разными знаменателями, мы найдем НОК для обеих и умножим их на уравнение. LCM равно 4, поэтому
Теперь мы расширим то, что в скобках:
Групповые термины:
3: разделить обе стороны на 3
3.0003
Чтобы оценить это, вам нужно подставить значение x обратно в исходное уравнение.
Дроби в выражениях и уравнениях – основные выводы
- Левая и правая части уравнения должны оставаться равными при работе с ними.
- Первый шаг при работе с дробными уравнениями — исключить из них дроби.
- Если у вас есть уравнение с двумя дробями и разными знаменателями, найдите НОК для обоих чисел.
Перекрестное умножение дробей (видео и практические вопросы)
vimeo.com/video/363921769?app_id=122963" frameborder="0" allow="autoplay; fullscreen" allowfullscreen="">TranscriptFAQsTractice
Привет, ребята! Добро пожаловать в это видео о том, как скрестить дробей .
При умножении дробей название намекает на то, как это делается на самом деле.
Вы буквально умножаете на . Допустим, у вас есть две дроби, которые равны друг другу. Допустим, \(\frac{a}{b}=\frac{c}{d}\).
Чтобы их умножить, нужно умножить числитель первой дроби на знаменатель второй дроби, а затем записать это число. Затем вы умножаете числитель второй дроби на число в знаменателе первой дроби и записываете это число.
Причина, по которой мы скрещиваем умножение дробей, состоит в том, чтобы сравнивать их. Перекрестное умножение дробей говорит нам, равны ли две дроби или какая из них больше. Это особенно полезно, когда вы работаете с более крупными дробями, которые вы не знаете, как уменьшить.
Как скрестить-умножить
Скрестить-умножить дроби – Пример 1
Найдите, какая из двух дробей наибольшая.
\(\frac{4}{26}=\frac{7}{32}\)
Итак, когда мы умножаем это, когда мы приравниваем его, а затем перемножаем эти две дроби вместе, мы получаем 128. Итак, \(4\times 32=128\). И когда мы перемножим эти два числа, мы получим \(7\times 26=182\). Итак, мы знаем, что \(\frac{7}{32}\) больше, чем \(\frac{4}{26}\), потому что 182 больше, чем 128.
Мы всегда должны помнить, что число, которое мы умноженная на наш числитель, представляет соответствующую дробь. Таким образом, это число (128) представляет эту дробь \((\frac{4}{26})\), а это число (182) представляет эту дробь \((\frac{7}{32})\). Я упоминаю об этом, потому что может быть немного запутанно видеть, как числа, взятые из двух разных дробей, умножаются вместе, но произведение представляет только одну из дробей, а не другую. 128 идет слева, чтобы представить \(\frac{4}{26}\), а \(7\times 26=182\) идет справа, чтобы представить эту дробь вот здесь \((\frac{7} {32})\).
Перемножение дробей помогает нам узнать, равны ли числа, а если нет, то какое из них больше, а какое меньше. Но это не единственное его использование. Перемножение дробей может помочь нам найти неизвестные переменные в дробях.
Перекрестное умножение дробей — Пример 2
Допустим, у нас есть две дроби \(\frac{9}{16}=\frac{x}{27}\). Мы можем перекрестно умножить в любое время, когда у нас есть дробь, которая установлена равной другой дроби. Теперь, чтобы скрестить умножение, мы делаем то же самое, что и в нашем последнем примере. Мы берем числитель одной стороны и умножаем его на знаменатель другой стороны, и делаем то же самое с числителем другой стороны. В этом случае мы умножаем \(9\умножить на 27\) и \(16\умножить на х\). Это даст нам \(243=16x\). Теперь все, что нам нужно сделать, чтобы получить x сам по себе, это разделить обе части на 16. Это сокращается, и мы получаем \(x=\frac{243}{16}\), и вы можете упростить это еще больше. Теперь мы сделали бы то же самое, даже если \(x\) стоит в нашем знаменателе, это не имеет значения.
Я надеюсь, что это видео о перекрестном умножении дробей было полезным для вас.
Увидимся в следующий раз!
Сложение и вычитание дробей | Умножение и деление дробей
Часто задаваемые вопросы
Q
Как скрестить дроби?
A
Перекрестное умножение дробей путем умножения знаменателя одной дроби на числитель другой дроби и последующего сравнения двух значений. Дробь с большим значением является большей дробью.
*Примечание: Будьте осторожны, всегда переходите от знаменателя к числителю! Если привести числитель к знаменателю, получится не та дробь, как та, что больше.
Пример. Какая дробь больше: \(\frac{4}{5}\) или \(\frac{3}{8}\)?
\(\frac{4}{5}\) больше, чем \(\frac{3}{8}\).
Q
Когда вы скрещиваете дроби?
A
Перемножить дроби, если вы хотите определить, больше ли одна дробь другой, или если вы ищете недостающий числитель или знаменатель в эквивалентных дробях.
Q
Как скрещивать дроби с разными знаменателями?
A
Почти все перемножаемые дроби будут иметь разные знаменатели. Это никак не влияет на процесс. Перекрестное умножение как обычно.
Q
Почему работает перекрестное умножение дробей?
A
Перемножение дробей, чтобы определить, больше ли одна, работает, потому что это быстрый способ приведения дробей к общему знаменателю и сравнения дробей.
пр. Что больше: \(\frac{7}{9}\) или \(\frac{8}{12}\)?
Перекрестное умножение:
84>72, поэтому \(\frac{7}{9}\)>\(\frac{8}{12}\)
Преобразовать и сравнить:
\(\frac{7}{9 }×\frac{12}{12}=\frac{84}{108}\)
\(\frac{8}{12}×\frac{9}{9}=\frac{72}{108} \)
84>72, поэтому \(\frac{7}{9}>\frac{8}{12}\)
Перемножение дробей для нахождения отсутствующего числителя или знаменателя для эквивалентных дробей работает, потому что это сокращение для перестановка, чтобы изолировать переменную.
пр. Найдите x: \(\frac{3}{7}=\frac{2}{x}\)
Перемножение:
\(\frac{3}{7}=\frac{2}{x}\)
3x=14
\(x=\frac{14}{3}\)
Перестановка:
\ (\frac{3}{7}=\frac{2}{x}\)
\(\frac{3}{7}\) x=2
\(x=2×\frac{7}{3) }\)
\(x=\frac{14}{3}\)
Q
Можете ли вы перекрестить умножение при сложении дробей?
A
Нет, при сложении дробей нельзя умножать крест. Перекрестное умножение только тогда, когда вам нужно определить, больше ли одна дробь другой, или если вы пытаетесь найти недостающий числитель или знаменатель в эквивалентных дробях.
Q
Как скрестить дроби с переменными?
A
Перемножить дроби с переменными, перемножив противоположные числители и знаменатели эквивалентных дробей, приравняв значения друг к другу и найдя переменную.
пр. \(\frac{4}{5}=\frac{x}{20}\)
4×20=5x
80=5x
16=x
Практические вопросы
Вопрос №1:
Какая дробь больше: \(\frac{17}{29{30}}{17}\rightarrow\frac{3}{5}>\frac{6}{17}\text{, потому что }51\)>\(30\)
Следовательно, \(\frac{3 }{8}\)
Скрыть ответ
Вопрос № 3:
Найдите отсутствующую переменную.
\(\frac{18}{21}=\frac{x}{63}\)
\(x=6\)
\(x=27\)
\(x=54\)
\(x=85\)
Показать ответ
Ответ:
Правильный ответ: \(x=54\). Чтобы решить эту проблему, начните с перекрестного умножения.
\(18\times63=21x\)
\(1,134=21x\)
Затем разделите на 21 с обеих сторон.
\(54=x\)
Скрыть ответ
Вопрос №4:
Найдите отсутствующую переменную.
\(\frac{7}{y}=\frac{42}{72}\)
\(y=9\)
\(y=12\)
\(y=229\)
\(y=432\)
Показать ответ
Ответ:
Правильный ответ: \(y=12\). Чтобы решить эту проблему, начните с перекрестного умножения.
\(7\times72=42г\)
\(504=42y\)
Затем разделите на 42 с обеих сторон.


