0.625 как дробь [Конвертер десятичных дробей в дробные]
0.625 в виде дроби равно 625/1000 или же 5/8
Шаги по преобразованию 0.625 в дробь:
Запишите 0.625 как
0.625/1
Умножьте числитель и знаменатель на 10 для каждой цифры после десятичной точки:
0.625/1
=
0.625 x 1000/1 x 1000
=
625/1000
Чтобы уменьшить дробь, мы находим наибольший общий фактор (GCF) для 625 а также 1000. Фактор — это просто число, которое делится на другое число без остатка.
Факторы 625 находятся: 1 5 25 125 625
Факторы 1000 находятся: 1 2 4 5 8 10 20 25 40 50 100 125 200 250 500 1000
Наибольший общий фактор (GCF) для обоих 625 а также 1000 является: 125
Теперь, чтобы уменьшить дробь, мы разделим числитель и знаменатель на значение GCF.
625/1000
=
625 ÷ 125/1000 ÷ 125
=
5/8
В качестве примечания, целая часть целого числа: пусто
Десятичная часть: . 625
= 625/1000
625
= 625/1000
Полная простая разбивка на фракции:
625/1000
= 125/200
= 25/40
= 5/8
Прокрутите вниз, чтобы настроить точку точности, позволяющую разбить 0.625 на определенное количество цифр. На странице также есть 2-3D графические изображения 0.625 в виде дроби, различные типы фракций, и какой тип фракции 0.625 когда преобразован.
Графическое представление 0.625 как дробь
Круговая диаграмма представление дробной части 0.625
2D диаграмма3D диаграмма
Введите десятичное значение:
Уровень точности для 0.625
Уровень точности — это количество цифр, до которых нужно округлить. Выберите точку с более низкой точностью ниже, чтобы разбить десятичную дробь 0.625 вниз в дробной форме. Точка точности по умолчанию — 5.
Если последняя конечная цифра — «5», вы можете использовать параметры «округлить половину вверх» и «округлить половину вниз», чтобы округлить эту цифру в большую или меньшую сторону при изменении точки точности.
Например, 0,875 с точностью 2, округленная половина вверх = 88/100, округленная половина вниз = 87/100.
выберите точку точности:
1 2 3 4 5 6 7 8 9
округлить до половины округлить до половины
62500/100000
= 6250/10000
= 625/1000
= 125/200
= 25/40
= 5/8
Числитель и знаменатель для 0.625 как дробь
0.625 = 0 625/1000
числитель / знаменатель = 625/1000
Является 625/1000 cмешанное, целое число или правильная дробь?
Смешанное число состоит из целого числа (целые числа не имеют дробной или десятичной части) и правильной дробной части (дроби, где числитель (верхнее число) меньше знаменателя (нижнее число). В этом случае целое числовое значение empty и правильное значение дроби 625/1000.
Можно ли все десятичные дроби преобразовать в дробь?
Не все десятичные дроби можно преобразовать в дроби.
Завершающие десятичные дроби имеют ограниченное количество цифр после десятичной точки.
Пример: 7860.40 = 7860 40/100
Повторяющиеся десятичные дроби имеют одно или несколько повторяющихся чисел после десятичной точки, которые продолжаются бесконечно.
Пример: 4481.3333 = 4481 3333/10000 = 333/1000 = 33/100 = 1/3 (rounded)
Иррациональные десятичные дроби продолжаются вечно и никогда не образуют повторяющегося рисунка. Этот тип десятичной дроби не может быть выражен дробью.
Пример: 0.189481563…..
Дробь в десятичную
Вы также можете увидеть обратное преобразование, т.е. как дробь 625/1000преобразуется в десятичную дробь.
Обратная связь
Вы нашли 0.625 дробную страницу полезной? да Нет
Сообщение: (мы ценим ваши отзывы, которые помогают улучшить наши страницы с десятичными дробями)
0.
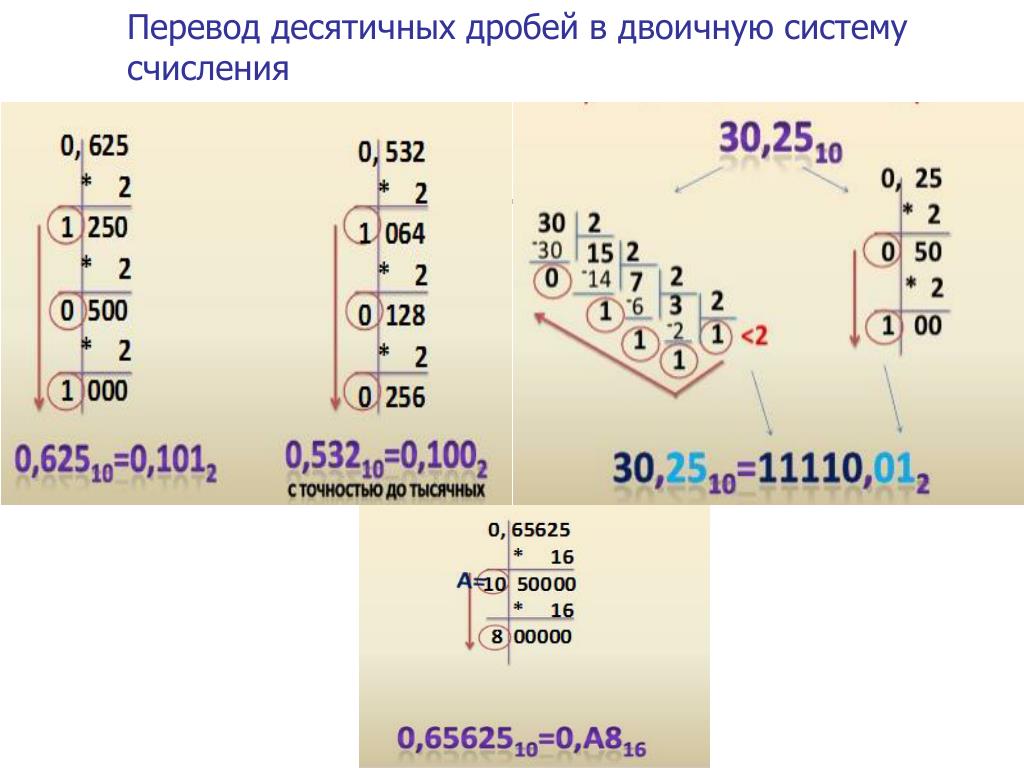
Перевод десятичных чисел в дробь: онлайн калькулятор
Говоря сухим математическим языком, дробь — это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.
Представление дробей
Существует минимум две формы записи одного дробного числа: в десятичной форме или в виде обыкновенной дроби. В десятичной форме числа выглядят как 0,5; 0,25 или 1,375. Любое из этих значений мы может представить в виде обыкновенной дроби:
- 0,5 = 1/2;
- 0,25 = 1/4;
- 1,375 = 11/8.
И если 0,5 и 0,25 мы без проблем конвертируем из обыкновенной дроби в десятичную и обратно, то в случае с числом 1,375 все неочевидно. Как быстро преобразовать любое десятичное число в дробь? Существует три простых способа.
Избавляемся от запятой
Самый простой алгоритм подразумевает умножение числа на 10 до тех пор, пока из числителя не исчезнет запятая. Такое преобразование осуществляется в три шага:
Шаг 1: Для начала десятичное число запишем в виде дроби «число/1», то есть мы получим 0,5/1; 0,25/1 и 1,375/1.
Шаг 2: После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая:
- 0,5/1 = 5/10;
- 0,25/1 = 2,5/10 = 25/100;
- 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.
Шаг 3: Сокращаем полученные дроби до удобоваримого вида:
- 5/10 = 1 × 5 / 2 × 5 = 1/2;
- 25/100 = 1 × 25 / 4 × 25 = 1/4;
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8.
Число 1,375 пришлось три раза умножать на 10, что уже не очень удобно, а что нам придется делать в случае, если понадобится преобразовать число 0,000625? В этой ситуации используем следующий способ преобразования дробей.
Избавляемся от запятой еще проще
Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс. И вновь мы выполняем три шага.
Шаг 1: Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n.
Шаг 2: Теперь нам достаточно представить дробь в виде C/10n, где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:
- для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/103 = 1375/1000;
- для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/106 = 625/1000000.
По сути, 10n – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить.
Шаг 3: Сокращаем нули и получаем итоговый результат:
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
- 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.
Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.
Преобразование на слух
Для тех, кто умеет правильно читать десятичные дроби, проще всего их преобразовать на слух. Если вы читаете 0,025 не как «ноль, ноль, двадцать пять», а как «25 тысячных», то у вас не будет никаких проблем с конвертацией десятичных чисел в обыкновенные дроби.
0,025 = 25/1000 = 1/40
Таким образом, правильное прочтение десятичного числа позволяет сразу же записать ее как обыкновенную дробь и сократить в случае необходимости.
Примеры использования дробей в повседневной жизни
На первый взгляд обыкновенные дроби практически не используются в быту или на работе и трудно представить ситуацию, когда вам понадобится перевести десятичную дробь в обычную за пределами школьных задач. Рассмотрим пару примеров.
Рассмотрим пару примеров.
Работа
Итак, вы работаете в кондитерском магазине и продаете халву на развес. Для простоты реализации продукта вы разделяете халву на килограммовые брикеты, однако мало кто из покупателей готов приобрести целый килограмм. Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию.
0,4 = 4/10 = 2/5
Быт
К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % — это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем:
0,12 = 12/100 = 3/25
Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет.
Заключение
Дроби широко используются в повседневной жизни, поэтому если вам часто необходимо преобразовывать десятичные значения в обыкновенные дроби, вам пригодится онлайн-калькулятор, при помощи которого можно мгновенно получить результат в виде уже сокращенной дроби.
Как из дроби сделать число с запятой. Действия с дробями
Говоря сухим математическим языком, дробь — это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.
Представление дробей
Существует минимум две формы записи одного дробного числа: в десятичной форме или в виде обыкновенной дроби. В десятичной форме числа выглядят как 0,5; 0,25 или 1,375. Любое из этих значений мы может представить в виде обыкновенной дроби:
- 0,5 = 1/2;
- 0,25 = 1/4;
- 1,375 = 11/8.
И если 0,5 и 0,25 мы без проблем конвертируем из обыкновенной дроби в десятичную и обратно, то в случае с числом 1,375 все неочевидно. Как быстро преобразовать любое десятичное число в дробь? Существует три простых способа.
Избавляемся от запятой
Самый простой алгоритм подразумевает умножение числа на 10 до тех пор, пока из числителя не исчезнет запятая. Такое преобразование осуществляется в три шага:
Такое преобразование осуществляется в три шага:
Шаг 2 : После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая:
- 0,5/1 = 5/10;
- 0,25/1 = 2,5/10 = 25/100;
- 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.
Шаг 3 : Сокращаем полученные дроби до удобоваримого вида:
- 5/10 = 1 × 5 / 2 × 5 = 1/2;
- 25/100 = 1 × 25 / 4 × 25 = 1/4;
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8.
Число 1,375 пришлось три раза умножать на 10, что уже не очень удобно, а что нам придется делать в случае, если понадобится преобразовать число 0,000625? В этой ситуации используем следующий способ преобразования дробей.
Избавляемся от запятой еще проще
Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс.
Шаг 1 : Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n.
Шаг 2 : Теперь нам достаточно представить дробь в виде C/10 n , где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:
- для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/10 3 = 1375/1000;
- для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/10 6 = 625/1000000.
По сути, 10 n – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить.
Шаг 3 : Сокращаем нули и получаем итоговый результат:
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
- 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.
Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.
В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.
Преобразование на слух
Для тех, кто умеет правильно читать десятичные дроби, проще всего их преобразовать на слух. Если вы читаете 0,025 не как «ноль, ноль, двадцать пять», а как «25 тысячных», то у вас не будет никаких проблем с конвертацией десятичных чисел в обыкновенные дроби.
0,025 = 25/1000 = 1/40
Таким образом, правильное прочтение десятичного числа позволяет сразу же записать ее как обыкновенную дробь и сократить в случае необходимости.
Примеры использования дробей в повседневной жизни
На первый взгляд обыкновенные дроби практически не используются в быту или на работе и трудно представить ситуацию, когда вам понадобится перевести десятичную дробь в обычную за пределами школьных задач. Рассмотрим пару примеров.
Работа
Итак, вы работаете в кондитерском магазине и продаете халву на развес. Для простоты реализации продукта вы разделяете халву на килограммовые брикеты, однако мало кто из покупателей готов приобрести целый килограмм. Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию.
Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию.
0,4 = 4/10 = 2/5
Быт
К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % — это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем:
0,12 = 12/100 = 3/25
Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет.
Заключение
Дроби широко используются в повседневной жизни, поэтому если вам часто необходимо преобразовывать десятичные значения в обыкновенные дроби, вам пригодится онлайн-калькулятор, при помощи которого можно мгновенно получить результат в виде уже сокращенной дроби.
Пытаясь решить математические задачи с дробями, школьник понимает, что ему недостаточно одного только желания решить эти задачи. Также необходимы и знания по вычислениям с дробными числами. В некоторых задачах все начальные данные подаются в условии в дробном виде. В других же часть их может быть дробями, а часть — целыми числами. Чтобы производить какие-то вычисления с этими заданными значениями, надо сначала привести их к единому виду, то есть целые числа перевести в дробные, а потом уже заниматься вычислениями. Вообще способ, как целое число перевести в дробь, очень прост. Для этого надо в числителе итоговой дроби написать само заданное число, а в ее знаменателе — единичку. То есть если надо перевести в дробь число 12, то полученная дробь будет 12/1.
В некоторых задачах все начальные данные подаются в условии в дробном виде. В других же часть их может быть дробями, а часть — целыми числами. Чтобы производить какие-то вычисления с этими заданными значениями, надо сначала привести их к единому виду, то есть целые числа перевести в дробные, а потом уже заниматься вычислениями. Вообще способ, как целое число перевести в дробь, очень прост. Для этого надо в числителе итоговой дроби написать само заданное число, а в ее знаменателе — единичку. То есть если надо перевести в дробь число 12, то полученная дробь будет 12/1.
Такие модификации помогают приводить дроби к общему знаменателю. Это нужно для того, чтобы получить возможность проводить вычитание или сложение дробных чисел. При их умножении и делении общий знаменатель не требуется. Можно рассмотреть на примере, как перевести число в дробь и потом произвести сложение двух дробных чисел. Допустим надо сложить число 12 и дробное число 3/4. Первое слагаемое (число 12) приводится к виду 12/1.
В результате умножения получится: 12/1=48/4. Если 48 разделить на 4, то получается 12, значит дробь приведена к правильному знаменателю. Таким образом можно заодно и понять, как дробь перевести в целое число. Это касается только неправильных дробей, потому что у них числитель больше, чем знаменатель. В таком случае числитель делится на знаменатель и, если не получается остатка, будет целое число. С остатком же дробь так и остается дробью, но с выделенной целой частью. Теперь относительно приведения к общему знаменателю на рассмотренном примере. Если бы у первого слагаемого знаменатель был бы равен какому-нибудь другому числу, кроме 1, числитель и знаменатель первого числа надо бы было умножить на знаменатель второго, а числитель и знаменатель второго — на знаменатель первого.
Оба слагаемых приведены к их общему знаменателю и готовы к сложению. Получается, что в данной задаче нужно сложить два числа: 48/4 и 3/4. При сложении двух дробей с одинаковым знаменателем суммировать нужно только их верхние части, то есть числители. Знаменатель суммы останется без изменения. В этом примере должно получиться 48/4+3/4=(48+3) /4=51/4. Это и будет результат сложения. Но в математике принято неправильные дроби приводить к правильным. Выше рассматривалось, как превратить дробь в число, но в этом примере не получится целое число из дроби 51/4, так как число 51 не делится без остатка на число 4. Поэтому нужно выделить целую часть данной дроби и ее дробную часть. Целой частью будет то число, которое получается при делении нацело первого же меньшего, чем 51, числа.
То есть то, которое можно разделить на 4 без остатка. Первое число перед числом 51, которое нацело делится на 4, будет число 48. Разделив 48 на 4, получается число 12. Значит целой частью искомой дроби будет 12. Осталось только найти дробную часть числа. Знаменатель дробной части остается тем же, то есть 4 в данном случае. Чтобы найти числитель дробной части, надо от исходного числителя вычесть то число, которое делилось на знаменатель без остатка. В рассматриваемом примере требуется для этого вычесть из числа 51 число 48. То есть числитель дробной части равен 3. Результатом сложения будет 12 целых и 3/4. То же самое делается и при вычитании дробей. Допустим надо из целого числа 12 вычесть дробное число 3/4. Для этого целое число 12 переводится в дробное 12/1, а затем приводится к общему знаменателю со вторым числом — 48/4.
Осталось только найти дробную часть числа. Знаменатель дробной части остается тем же, то есть 4 в данном случае. Чтобы найти числитель дробной части, надо от исходного числителя вычесть то число, которое делилось на знаменатель без остатка. В рассматриваемом примере требуется для этого вычесть из числа 51 число 48. То есть числитель дробной части равен 3. Результатом сложения будет 12 целых и 3/4. То же самое делается и при вычитании дробей. Допустим надо из целого числа 12 вычесть дробное число 3/4. Для этого целое число 12 переводится в дробное 12/1, а затем приводится к общему знаменателю со вторым числом — 48/4.
При вычитании точно так же знаменатель обеих дробей остается без изменения, а с их числителями и проводят вычитание. То есть от числителя первой дроби вычитают числитель второй. В данном примере это будет 48/4-3/4=(48-3) /4=45/4. И опять получилась неправильная дробь, которую надо привести к правильной. Для выделения целой части определяют первое до 45 число, которое делится на 4 без остатка. Это будет 44. Если число 44 разделить на 4, получится 11. Значит целая часть итоговой дроби равна 11. В дробной части также знаменатель оставляют без изменения а из числителя исходной неправильной дроби вычитают то число, которое делилось на знаменатель без остатка. То есть надо из 45 вычесть 44. Значит числитель в дробной части равен 1 и 12-3/4=11 и 1/4.
Это будет 44. Если число 44 разделить на 4, получится 11. Значит целая часть итоговой дроби равна 11. В дробной части также знаменатель оставляют без изменения а из числителя исходной неправильной дроби вычитают то число, которое делилось на знаменатель без остатка. То есть надо из 45 вычесть 44. Значит числитель в дробной части равен 1 и 12-3/4=11 и 1/4.
Если дано одно число целое и одно дробное, но его знаменатель равен 10, то проще второе число перевести в десятичную дробь, а потом производить вычисления. Например надо сложить целое число 12 и дробное число 3/10. Если число 3/10 записать в виде десятичной дроби, получится 0,3. Теперь значительно легче к 12 прибавить 0,3 и получить 2,3, чем приводить дроби к общему знаменателю, производить вычисления, а затем выделять целую и дробную части из неправильной дроби. Даже самые простые задачки с дробными числами предполагают, что школьник (или студент) знает, как перевести целое число в дробь. Эти правила слишком просты и легко запоминаются. Зато с помощью них очень просто проводить вычисления дробных чисел.
Зато с помощью них очень просто проводить вычисления дробных чисел.
В самом начале нужно все-таки узнать, что такое дробь и каких видов она бывает. А бывает она трех видов. И первый из них это обыкновенная дробь, например ½, 3/7,3/432 и т. д. Эти числа также можно записывать при помощи горизонтальной черточки. И первое, и второе будет одинаково верно. Цифра сверху называется числительным, а снизу знаменателем. Есть даже поговорка, для тех людей, кто постоянно путает эти два названия. Она звучит так: «Зззззапомни! Зззззнаменатель — внизззззу! ». Это поможет не запутаться. Обыкновенная дробь это всего лишь два числа, которые делятся друг на друга. Черточка в них и обозначает знак деления. Ее можно заменить знаком двоеточие. Если стоит вопрос «как дробь перевести в число», то это очень просто. Следует всего лишь числитель поделить на знаменатель. И все. Дробь переведена.
Второй вид дробей называется десятичным. Это ряд цифр с запятой. К примеру, 0,5, 3,5 и т. д. Назвали их десятичными, только потому, что после запетой первая цифра обозначает «десятки», вторая в десять раз больше «сотни» и так далее. А первые цифра до запятой, называются целыми. Например, число 2,4 звучит так, двенадцать целых и двести тридцать четыре тысячных. Такие дроби появляются в основном из-за того, что поделив два числа без остатка не получается. И большинство обыкновенных дробей, во время того как их будут переводить в числа, в конечном итоге имеют вид десятичной дроби. Например, одна вторая ровняется ноль целым пяти десятым.
А первые цифра до запятой, называются целыми. Например, число 2,4 звучит так, двенадцать целых и двести тридцать четыре тысячных. Такие дроби появляются в основном из-за того, что поделив два числа без остатка не получается. И большинство обыкновенных дробей, во время того как их будут переводить в числа, в конечном итоге имеют вид десятичной дроби. Например, одна вторая ровняется ноль целым пяти десятым.
И заключительный третий вид. Это смешанные числа. Пример этого можно привести такой, как 2½. Звучит так, две целых и одна вторая. В старших классов такой вид дробей уже не используются. Их наверняка необходимо будет приводить или в обыкновенный вид дроби, или в десятичный. Сделать это так же легко. Просто целое число нужно умножить на знаменатель и, полученное обозначение, сложить с числительным. Возьмем наш пример 2½. Два умножается на два, получается четыре. Четыре плюс один, равно пяти. И дробь формой 2½ образуется в 5/2. А пять, поделив на два можно получить десятичную дробь. 2½=5/2=2,5. Уже стало понятно, как переводить дроби в числа. Следует всего лишь разделить числитель на знаменатель. Если числа большие можно воспользоваться калькулятором.
2½=5/2=2,5. Уже стало понятно, как переводить дроби в числа. Следует всего лишь разделить числитель на знаменатель. Если числа большие можно воспользоваться калькулятором.
Если на нем получается не целые числа и после запятой идет очень много цифр, то тогда данное значение можно округлить. Округляется все очень просто. Сначала следует определиться, к какой цифре нужно округлить. Следует рассмотреть пример. Человеку нужно округлить число ноль целых, девять тысяч семьсот пятьдесят шесть десятитысячных или в цифровом значении 0,6. Округление необходимо сделать до сотых. Это означает, что в данный момент до семи сотых. После цифры семь в дроби идет пять. Теперь нужно использовать правила для округления. Цифры больше пяти округляются в большую сторону, а меньшие – в меньшую. В примере у человека — пять, она стоит на пограничье, но считается, что округление происходит в большую сторону. Значит, все цифры после семерки убираем и к ней прибавляем единицу. Получается 0,8.
Также возникают ситуации, когда человеку необходимо быстро перевести обыкновенную дробь в число, а калькулятора рядом нет. Для этого стоит применить деление столбиком. Первым делом следует на листке написать рядом друг с другом числитель и знаменатель. Между ними ставится уголок деления, он похож на букву «Т», только лежащую на боку. Для примера можно взять дробь десять шестых. И так, десять следует поделить на шесть. Сколько шестерок может вместиться в десятке, только одна. Единица записывается под уголком. Десять отнять шесть получится четыре. Сколько шестерок будет в четверке, несколько. Значит, в ответе после единицы ставится запятая, а четверка умножается на десять. В сорока шесть шестерок. В ответе дописывается шестерка, а от сорока отнимается тридцать шесть. Получается опять четыре.
Для этого стоит применить деление столбиком. Первым делом следует на листке написать рядом друг с другом числитель и знаменатель. Между ними ставится уголок деления, он похож на букву «Т», только лежащую на боку. Для примера можно взять дробь десять шестых. И так, десять следует поделить на шесть. Сколько шестерок может вместиться в десятке, только одна. Единица записывается под уголком. Десять отнять шесть получится четыре. Сколько шестерок будет в четверке, несколько. Значит, в ответе после единицы ставится запятая, а четверка умножается на десять. В сорока шесть шестерок. В ответе дописывается шестерка, а от сорока отнимается тридцать шесть. Получается опять четыре.
В данном примере произошло зацикливание, если продолжить делать все точно также получится ответ 1,6(6) Цифру шесть продолжается для бесконечности, но применив правило округления, можно привести получение число к 1,7. Что намного удобней. Из этого можно сделать вывод, что не все обыкновенные дроби можно перевести в десятичные. В некоторых происходит зацикливание. Но зато любую десятичную дробь можно перевести в простую. Здесь поможет элементарное правило, как слышится, так и пишется. Например, число 1,5, слышится, как одна целых двадцать пять сотых. Так и нужно записать, одна целая, двадцать пять поделить на сто. Одна целая это сто, а значит, простая дробь будет сто двадцать пять на сто (125/100) . Все также просто и понятно.
В некоторых происходит зацикливание. Но зато любую десятичную дробь можно перевести в простую. Здесь поможет элементарное правило, как слышится, так и пишется. Например, число 1,5, слышится, как одна целых двадцать пять сотых. Так и нужно записать, одна целая, двадцать пять поделить на сто. Одна целая это сто, а значит, простая дробь будет сто двадцать пять на сто (125/100) . Все также просто и понятно.
Вот и было разобраны самые основные правила и преобразования, которые связанны с дробями. Все они несложные, но знать их следует. В повседневную жизнь уже давно вошли дроби, особенно десятичные. Это хорошо видно на ценниках в магазинах. Круглые цены уже давно не кто не пишет, а с дробями цена кажется визуально на много дешевле. Также одна из теорий гласит, что человечество отвернулось от римских цифр и приняла в оборот арабские, только потому, что в римских не было дробей. И многие ученые соглашаются с этим предположением. Ведь с дробями можно вести подсчеты более точней. А в наш век космических технологий, точность в расчетах нужна как никогда. Так что изучать дроби в школе по математики жизненно необходимо для понимания многих наук и технических достижений.
Так что изучать дроби в школе по математики жизненно необходимо для понимания многих наук и технических достижений.
Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления.
В таких случаях говорят, что выполнено деление с остатком , и решение записывают в таком виде:
497: 4 = 124 (1 остаток).
Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое , 4 — делитель . Результат деления при делении с остатком называют неполным частным . В нашем случае это число 124. И, наконец, последний компонент, которого нет в обычном делении, — остаток . В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело . Считают, что при таком делении остаток равен нулю. В нашем случае остаток равен 1.
Остаток всегда меньше делителя.
Проверку при делении можно сделать умножением. Если, например, имеется равенство 64: 32 = 2, то проверку можно сделать
так: 64 = 32 * 2.
Если, например, имеется равенство 64: 32 = 2, то проверку можно сделать
так: 64 = 32 * 2.
Часто в случаях, когда выполняется деление с остатком, удобно использовать равенство
а = b * n + r ,
где а — делимое, b — делитель, n — неполное частное, r — остаток.
Частное от деления натуральных чисел можно записать в виде дроби.
Числитель дроби — это делимое, а знаменатель — делитель.
Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление . Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».
Частное от деления натуральных чисел m и n можно записать в виде дроби \(\frac{m}{n} \), где числитель m — делимое, а
знаменатель п — делитель:
\(m:n = \frac{m}{n} \)
Верны следующие правила:
Чтобы получить дробь \(\frac{m}{n} \), надо единицу разделить на n равных частей (долей) и взять m таких частей.
Чтобы получить дробь \(\frac{m}{n} \), надо число m разделить на число n.
Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.
Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.
Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a \cdot n}{b \cdot n} \)
Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится:
\(\large \frac{a}{b} = \frac{a: m}{b: m} \)
Это свойство называют основным свойством дроби .
Два последних преобразования называют сокращением дроби .
Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю .
Правильные и неправильные дроби.
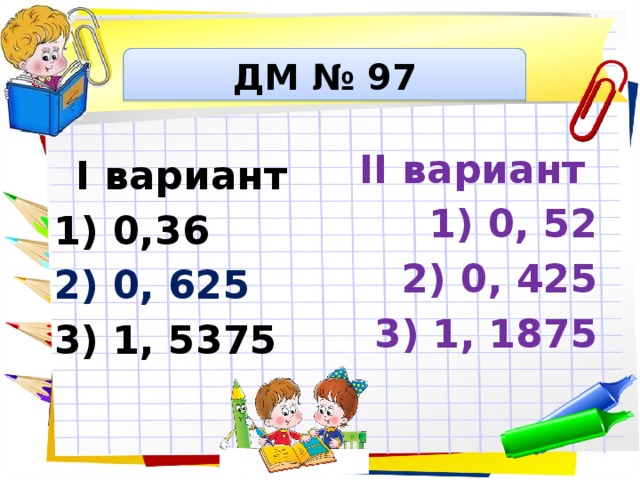 Смешанные числа
Смешанные числаВы уже знаете, что дробь можно получить, если разделить целое на равные части и взять несколько таких частей. Например, дробь \(\frac{3}{4} \) означает три четвёртых доли единицы. Во многих задачах предыдущего параграфа обыкновенные дроби использовались для обозначения части целого. Здравый смысл подсказывает, что часть всегда должна быть меньше целого, но как тогда быть с такими дробями, как, например, \(\frac{5}{5} \) или \(\frac{8}{5} \)? Ясно, что это уже не часть единицы. Наверное, поэтому такие дроби, у которых числитель больше знаменателя или равен ему, называют неправильными дробями . Остальные дроби, т. е. дроби, у которых числитель меньше знаменателя, называют правильными дробями .
Как вы знаете, любую обыкновенную дробь, и правильную, и неправильную, можно рассматривать как результат деления числителя на
знаменатель. Поэтому в математике, в отличие от обычного языка, термин «неправильная дробь» означает не то, что мы что-то сделали
неправильно, а только то, что у этой дроби числитель больше знаменателя или равен ему.
Если число состоит из целой части и дроби, то такие дроби называются смешанными .
Например:
\(5:3 = 1\frac{2}{3} \) : 1 — целая часть, а \(\frac{2}{3} \) — дробная часть.
Если числитель дроби \(\frac{a}{b} \) делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её числитель
разделить на это число:
\(\large \frac{a}{b} : n = \frac{a:n}{b} \)
Если числитель дроби \(\frac{a}{b} \) не делится на натуральное число n, то, чтобы разделить эту дробь на n, надо её
знаменатель умножить на это число:
\(\large \frac{a}{b} : n = \frac{a}{bn} \)
Заметим, что второе правило справедливо и в том случае, когда числитель делится на n. Поэтому мы можем его применять тогда, когда трудно с первого взгляда определить, делится числитель дроби на n или нет.
Действия с дробями. Сложение дробей.
С дробными числами, как и с натуральными числами, можно выполнять арифметические действия. Рассмотрим сначала сложение дробей.
Легко сложить дроби с одинаковыми знаменателями. Найдем, например, сумму \(\frac{2}{7} \) и \(\frac{3}{7} \).
Легко понять, что \(\frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Найдем, например, сумму \(\frac{2}{7} \) и \(\frac{3}{7} \).
Легко понять, что \(\frac{2}{7} + \frac{2}{7} = \frac{5}{7} \)
Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить прежним.
Используя буквы, правило сложения дробей с одинаковыми знаменателями можно записать так:
\(\large \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c} \)
Если требуется сложить дроби с разными знаменателями, то их предварительно следует привести к общему знаменателю. Например:
\(\large \frac{2}{3}+\frac{4}{5} = \frac{2\cdot 5}{3\cdot 5}+\frac{4\cdot 3}{5\cdot 3} = \frac{10}{15}+\frac{12}{15} = \frac{10+12}{15} = \frac{22}{15} \)
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства сложения.
Сложение смешанных дробей
Такие записи, как \(2\frac{2}{3} \), называют смешанными дробями . При этом число 2 называют целой частью смешанной
дроби, а число \(\frac{2}{3} \) — ее дробной частью . Запись \(2\frac{2}{3} \) читают так: «две и две трети».
Запись \(2\frac{2}{3} \) читают так: «две и две трети».
При делении числа 8 на число 3 можно получить два ответа: \(\frac{8}{3} \) и \(2\frac{2}{3} \). Они выражают одно и то же дробное число, т.е \(\frac{8}{3} = 2 \frac{2}{3} \)
Таким образом, неправильная дробь \(\frac{8}{3} \) представлена в виде смешанной дроби \(2\frac{2}{3} \). В таких случаях говорят, что из неправильной дроби выделили целую часть .
Вычитание дробей (дробных чисел)
Вычитание дробных чисел, как и натуральных, определяется на основе действия сложения: вычесть из одного числа другое — это значит
найти такое число, которое при сложении со вторым дает первое. Например:
\(\frac{8}{9}-\frac{1}{9} = \frac{7}{9} \) так как \(\frac{7}{9}+\frac{1}{9} = \frac{8}{9} \)
Правило вычитания дробей с одинаковыми знаменателями похоже на правило сложения таких дробей:
чтобы найти разность дробей с одинаковыми знаменателями, надо из числителя первой дроби вычесть числитель второй, а знаменатель
оставить прежним.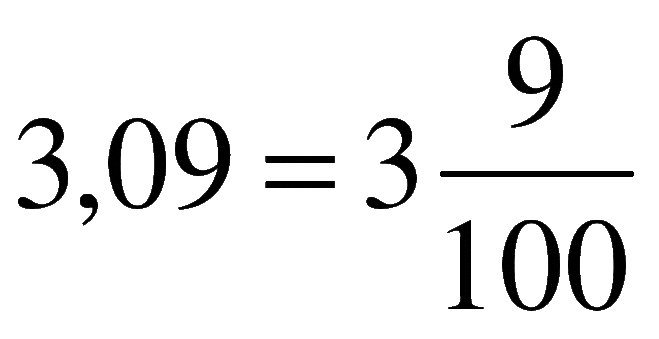
С помощью букв это правило записывается так:
\(\large \frac{a}{c}-\frac{b}{c} = \frac{a-b}{c} \)
Умножение дробей
Чтобы умножить дробь на дробь, нужно перемножить их числители и знаменатели и первое произведение записать числителем, а второе — знаменателем.
С помощью букв правило умножения дробей можно записать так:
\(\large \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d} \)
Пользуясь сформулированным правилом, молено умножать дробь на натуральное число, на смешанную дробь, а также перемножать смешанные дроби. Для этого нужно натуральное число записать в виде дроби со знаменателем 1, смешанную дробь — в виде неправильной дроби.
Результат умножения надо упрощать (если это возможно), сокращая дробь и выделяя целую часть неправильной дроби.
Для дробей, как и для натуральных чисел, справедливы переместительное и сочетательное свойства умножения, а также распределительное свойство умножения относительно сложения.
Деление дробей
Возьмем дробь \(\frac{2}{3} \) и «перевернем» ее, поменяв местами числитель и знаменатель. Получим дробь \(\frac{3}{2} \).
Эту дробь называют обратной дроби \(\frac{2}{3} \).
Получим дробь \(\frac{3}{2} \).
Эту дробь называют обратной дроби \(\frac{2}{3} \).
Если мы теперь «перевернем» дробь \(\frac{3}{2} \), то получим исходную дробь \(\frac{2}{3} \). Поэтому такие дроби, как \(\frac{2}{3} \) и \(\frac{3}{2} \) называют взаимно обратными .
Взаимно обратными являются, например, дроби \(\frac{6}{5} \) и \(\frac{5}{6} \), \(\frac{7}{18} \) и \(\frac{18}{7} \).
С помощью букв взаимно обратные дроби можно записать так: \(\frac{a}{b} \) и \(\frac{b}{a} \)
Понятно, что произведение взаимно обратных дробей равно 1 . Например: \(\frac{2}{3} \cdot \frac{3}{2} =1 \)
Используя взаимно обратные дроби, можно деление дробей свести к умножению.
Правило деления дроби на дробь:
чтобы разделить одну дробь на другую, нужно делимое умножить на дробь, обратную делителю.
Используя буквы, правило деления дробей можно записать так:
\(\large \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} \)
Если делимое или делитель является натуральным числом или смешанной дробью, то, для того чтобы воспользоваться правилом деления
дробей, его надо предварительно представить в виде неправильной дроби.
Урок 5. разложение обыкновенной дроби в конечную десятичную дробь — Алгебра — 7 класс
Нахождение дроби
Выберите правильный ответ.
Найдите несократимую дробь, равную $\frac{26}{91}$ .
$\frac{2}{7}$ | |
$\frac{2}{3}$ | |
$\frac{7}{2}$ | |
$\frac{3}{8}$ |
Дроби
Выберите правильный ответ.
Дробь $\frac{7}{15}$ перевести в конечную десятичную можно нельзя .
Перевод дробей
Установите соответствия между обыкновенными и десятичными дробями.
$\frac{3}{20}$
$\frac{7}{25}$
$\frac{4}{5}$
$0,15$
$0,28$
Рациональные числа
Впишите нужные подписи, используя слова «можно» и «нельзя».
Какие дроби можно перевести в конечные десятичные, какие – нельзя?
$\frac{14}{25}$
$\frac{13}{16}$
$\frac{5}{34}$
$\frac{14}{45}$
Определение
Вставьте в текст нужные слова.
Чтобы представить дробь в виде , нужно и числитель, и знаменатель на одно и то же число так, чтобы в знаменателе получилось 10, 100, 1000 и т. д.
д.
составных
умножить
упрощенной
десятичной
обыкновенную
простую
разделить
Обыкновенные дроби
Выделите цветом правильный ответ.
Представьте обыкновенную дробь $\frac{15}{16}$ в виде десятичной.
0,9255
0,8745
0,7825
0,9375
Зеленый
Представление обыкновенной дроби
Подчеркните правильный ответ или ответы.
Несократимую обыкновенную дробь можно представить в виде десятичной.
Если знаменатель делится на числитель.
Если знаменатель не делится на числитель.
Если знаменатель имеет простой делитель только 5.
Если знаменатель имеет простой делитель только 2.
Если знаменатель не имеет простых делителей, кроме 2 или 5.
Рациональное число
Заполните пропуски в тексте.
Знаменатель дроби $\frac{17}{625}$ имеет простой делитель .
Приведение дробей
Заполните пропуски в таблице.
| Десятичная дробь | Обыкновенная дробь |
|---|---|
| $0,125$ | |
| $0,6$ | |
| $0,725$ |
$\frac{3}{5}$
$\frac{29}{40}$
$\frac{1}{8}$
Деление уголком
Выберите правильные ответы.
Найдите дроби, которые нельзя записать в виде конечной десятичной дроби.
$\frac{101}{40}$
$\frac{229}{200}$
$\frac{785}{300}$
$\frac{80}{60}$
Дроби
Выберите правильный ответ.
Обыкновенная несократимая дробь $\frac{27}{40}$ равна десятичной дроби 0,6 0,6750 0,675 0,67
Деление
Подчеркните правильный ответ.
С помощью деления уголком представьте дробь $\frac{128}{625}$ в виде десятичной дроби.
0,2046
0,2048
0,204
0,314
Единицы измерения
Выделите цветом правильный ответ.
Дробь $\frac{651}{2000}$, представленная в виде конечной десятичной, равна…
$3,075$
$3,25$
$0,3725$
$0,3255$
Бирюзовый
Рациональные числа
Впишите недостающую цифру.
Какую цифру нужно записать вместо звёздочки так, чтобы дробь можно было перевести в конечную десятичную $\frac{13}{32 * }$?
Сбросить ответы Сохранить и перейти к следующему
Перевод десятичных чисел в дробь и наоборот — онлайн калькулятор. Перевод обыкновенных дробей в десятичные дроби
Большое количество учащихся, и не только, задаются вопросом, как перевести дробь в число. Чтобы это сделать, имеется несколько достаточно простых и понятных способов. Выбор конкретного способа зависит от предпочтений решающего.
Выбор конкретного способа зависит от предпочтений решающего.
В первую очередь нужно знать, как дроби записываются. А записываются они следующим образом:
- Обыкновенная. Пишется с числителем и знаменателем через наклонную или столбиком (1/2).
- Десятичная. Пишется через запятую (1,0, 2,5 и так далее).
Перед тем как приступить к решению, нужно знать, что такое неправильная дробь, ведь она встречается достаточно часто. Она имеет числитель больше знаменателя, например, 15/6. Неправильную дробь также можно решать такими способами, без каких-либо усилий и затрат времени.
Смешанное число — это когда в результате выходит целое число и дробная часть, к примеру 52/3.
Любое натуральное число можно записать дробью с совершенно разными натуральными знаменателями, например:1= 2/2=3/3 = и т.д.
Перевести можно еще и с помощью калькулятора, но не все они имеют такую функцию. Существует специальный инженерный калькулятор, где есть такая функция, но не всегда есть возможность его использовать, особенно в школе. Поэтому лучше разобраться в данной теме.
Поэтому лучше разобраться в данной теме.
Первым делом стоит обратить внимание на то, какая дробь. Если ее можно с легкостью множить до 10 на одинаковые с числителем значения, то можно воспользоваться первым способом. Например: обыкновенная ½ умножаете в числителе и знаменателе на 5 и получаете 5/10, которое можно записать как 0,5.
Данное правило основано на том, что десятичная всегда имеет в знаменателе круглое значение, такое как 10,100,1000 и так далее.
Из этого выходит, что если множить числитель и знаменатель, то нужно добиваться получения в знаменателе именно такого значения в результате умножения, независимо от того, что выходит в числителе.
Стоит помнить, что некоторые дроби нельзя перевести, для этого необходимо перед началом решения проверить ее.
Например: 1,3333, где цифра 3 повторяется до бесконечности, причем калькулятор тоже не избавит от нее. Решением такой проблемы может быть только округление таким образом, чтобы получилось целое число, если это возможно. Если такой возможности не имеется, то следует вернуться в начало примера и проверить правильность решения задачи, возможно, была допущена ошибка.
Если такой возможности не имеется, то следует вернуться в начало примера и проверить правильность решения задачи, возможно, была допущена ошибка.
Рисунок 1-3. Перевод дробей путем умножения.
Рассмотрим для закрепления описанной информации следующий пример перевода:
- Например, необходимо перевести 6/20 в десятичную. Первым делом ее следует проверить, как показано на рисунке 1.
- Только после того как убедились, что можно разложить, как в данном случае на 2 и 5, нужно приступать к самому переводу.
- Наиболее простым вариантом будет умножить знаменатель, получив результат 100, является 5, так как 20х5=100.
- Следуя примеру на рисунке 2, в итоге получится 0,3.
Можно закрепить результат и еще раз все просмотреть по рисунку 3. Для того чтобы полностью разобраться в теме и больше не прибегать к изучению этого материала. Эти знания помогут не только ребенку, но и взрослому человеку.
Перевод путем деления
Второй вариант перевода дробей является немного сложней, но более популярным. Таким методом в основном пользуются в школах учителя для объяснения. В целом, он намного проще объясняется и быстрее понимается.
Таким методом в основном пользуются в школах учителя для объяснения. В целом, он намного проще объясняется и быстрее понимается.
Стоит помнить, что для правильного преобразования простой дроби необходимо ее числитель поделить на знаменатель. Ведь если задуматься, то решение это и есть процесс деления.
Для того чтобы понять это простое правило, нужно рассмотреть следующий пример решения:
- Возьмем 78/200, которую нужно перевести в десятичную. Для этого следует 78 разделить на 200, то есть числитель на знаменатель.
- Но перед тем как начать, стоит провести проверку, как показано на рисунке 4.
- После того как убедились, что ее можно решить, следует приступать к процессу. Для этого стоит разделить числитель на знаменатель в столбик или уголком, как показано на рисунке 5. В начальных классах школ учат такому делению, и трудностей с этим не должно возникнуть.
На рисунке 6 показаны примеры наиболее распространенных примеров, их просто можно запомнить, чтобы при необходимости не тратить время для решения. Ведь в школе на каждую контрольную или самостоятельную работы дается мало времени для решения, поэтому не стоит тратить его на то, что можно выучить и просто помнить.
Ведь в школе на каждую контрольную или самостоятельную работы дается мало времени для решения, поэтому не стоит тратить его на то, что можно выучить и просто помнить.
Перевод процентов
Переводить проценты в десятичное число тоже достаточно легко. Этому начинают учить в 5 классе, а в некоторых школах еще раньше. Но если ваш ребенок на уроке математики не понял эту тему, можно наглядно ему еще раз объяснить. Для начала следует выучить определения понятия, что такое процент.
Процент — это одна сотая часть от какого-либо числа, другими словами, абсолютная произвольная. Например, от 100 это будет 1 и так далее.
На рисунке 7 показан наглядный пример перевода процентов.
Чтобы перевести процент, надо всего лишь убрать значок %, а затем разделить его на 100.
Еще 1 пример показан на рисунке 8.
Если надо провести обратную «конвертацию», необходимо все сделать с точностью до наоборот. Другими словами, число необходимо умножить на сто и после приписать значок процентов.
А для того чтобы обычную перевести в проценты, также можно использовать этот пример. Только изначально следует перевести дробь в число и только потом в проценты.
Исходя из описанного выше, можно легко понять принцип перевода. С помощью этих способов можно ребенку объяснять тему, если он ее не понял или не присутствовал на уроке в момент ее прохождения.
И никогда не будет необходимости нанимать репетитора, чтобы он объяснил ребенку, как перевести дробь в число или процент.
Простые дроби не всегда удобны в обращении. В отчет или в ведомость их не вставишь, да и современные компьютерные программы не всегда дружат с такими числами. Перевести простую дробь в (или в десятичную дробь) не составит труда.
Вам понадобится
- листок бумаги, ручка, калькулятор
Инструкция
Перевести дробь в число — значит разделить числитель на знаменатель. Числитель — это верхняя часть дроби, знаменатель — нижняя. Если под рукой есть калькулятор, то нажмите на кнопки, и задача выполнена. В результате у вас получится либо целое число, либо десятичная дробь. Десятичная дробь может получится с длинным остатком после запятой. В этом случае дробь нужно округлить до определенного, нужного вам разряда, используя правила округления (цифры до 5 округляются в меньшую сторону, от 5 включительно и более — в большую сторону).
В результате у вас получится либо целое число, либо десятичная дробь. Десятичная дробь может получится с длинным остатком после запятой. В этом случае дробь нужно округлить до определенного, нужного вам разряда, используя правила округления (цифры до 5 округляются в меньшую сторону, от 5 включительно и более — в большую сторону).
Если калькулятора под рукой не оказалось, но придется делить в столбик. Напишите числитель дроби рядом со знаменателем, между ними уголочек, означающий деление. К примеру, переведите в число дробь 10/6. Для начала 10 разделите на 6. Получится 1. Запишите результат по уголком. Перемножьте 1 на 6, получится 6. Вычтите 6 из 10. Получится остаток 4. Остаток нужно снова разделить на 6. Допишите к 4 цифру 0, и разделите 40 на 6. Получится 6. Запишите 6 в результат, после запятой. Перемножьте 6 на 6. Получится 36. Вычтите 36 из 40. Получится вновь остаток 4. Далее можно не продолжать, поскольку становится очевидным, что результатом будет число 1,66(6). Округлите данную дробь до того разряда, который вам необходим. Например, 1,67. Это и есть окончательный результат.
Например, 1,67. Это и есть окончательный результат.
Дробь может быть преобразована в целое число либо в десятичную дробь. Неправильная дробь, числитель которой больше знаменателя и делится на него без остатка, переводится в целое число, например: 20/5. Делим 20 на 5 и получаем число 4. Если дробь правильная, то есть числитель меньше знаменателя, то тогда преобразовать ее в число (десятичную дробь). Больше информации о дробях вы сможете почерпнуть из нашего раздела — .
Способы преобразования дроби в число
- Первый способ, как перевести дробь в число годится для дроби, которую можно преобразовать в число, являющееся десятичной дробью. Сначала выясним, можно ли перевести заданную дробь в дробь десятичную. Для этого обратим внимание на знаменатель (цифра, которая под чертой или справа от наклонной). Если знаменатель можно разложить на множители (в нашем примере — 2 и 5), которые могут повторяться, то данную дробь реально преобразовать в конечную десятичную дробь. Например: 11/40 =11/(2∙2∙2∙5).
 Данная обыкновенная дробь переведется в число (десятичную дробь) с конечным количеством знаков после запятой. А вот дробь 17/60 =17/(5∙2∙2∙3) переведется в число с бесконечным количеством знаков после запятой. То есть при точном вычислении числового значения довольно трудно определить конечный знак после запятой, поскольку таких знаков бесконечное множество. Поэтому для решения задач обычно требуется округлить значение до сотых или тысячных. Дальше — необходимо умножить и числитель, и знаменатель на такое число, чтобы в знаменателе получились цифры 10, 100, 1000 и т. д. Например: 11/40 =(11∙25)/(40∙25) =275/1000 =0,275
Данная обыкновенная дробь переведется в число (десятичную дробь) с конечным количеством знаков после запятой. А вот дробь 17/60 =17/(5∙2∙2∙3) переведется в число с бесконечным количеством знаков после запятой. То есть при точном вычислении числового значения довольно трудно определить конечный знак после запятой, поскольку таких знаков бесконечное множество. Поэтому для решения задач обычно требуется округлить значение до сотых или тысячных. Дальше — необходимо умножить и числитель, и знаменатель на такое число, чтобы в знаменателе получились цифры 10, 100, 1000 и т. д. Например: 11/40 =(11∙25)/(40∙25) =275/1000 =0,275 - Второй способ, как перевести дробь в число — более простой: необходимо числитель поделить на знаменатель. Для применения этого способа просто произведем деление, а полученное число и будет той искомой десятичной дробью. Например, надо перевести дробь 2/15 в число. Делим 2 на 15. Получаем 0, 1333… — бесконечная дробь. Записываем так: 0,13(3). Если дробь неправильная, то есть числитель больше знаменателя (например, 345/100), то в результате преобразования ее в число получится целое числовое значение или десятичная дробь с целой дробной частью.
 В нашем примере это будет 3,45. Чтобы преобразовать смешанную дробь такого вида, как 3 2 / 7 , в число, то нужно сначала превратить ее в неправильную дробь: (3∙7+2)/7 =23/7. Далее делим 23 на 7 и получаем число 3,2857143, которое сокращаем до 3,29.
В нашем примере это будет 3,45. Чтобы преобразовать смешанную дробь такого вида, как 3 2 / 7 , в число, то нужно сначала превратить ее в неправильную дробь: (3∙7+2)/7 =23/7. Далее делим 23 на 7 и получаем число 3,2857143, которое сокращаем до 3,29.
Самый простой способ по переводу дроби в число — это использование калькулятора или иного вычислительного прибора. Укажем сначала числитель дроби, потом нажмем кнопку со значком «разделить» и набираем знаменатель. После нажатия клавиши «=» мы получаем искомое число.
Говоря сухим математическим языком, дробь — это число, которое представляется в виде части от единицы. Дроби широко используются в жизни человека: при помощи дробных чисел мы указываем пропорции в кулинарных рецептах, выставляем десятичные оценки на соревнованиях или используем их для подсчета скидок в магазинах.
Представление дробей
Существует минимум две формы записи одного дробного числа: в десятичной форме или в виде обыкновенной дроби. В десятичной форме числа выглядят как 0,5; 0,25 или 1,375. Любое из этих значений мы может представить в виде обыкновенной дроби:
Любое из этих значений мы может представить в виде обыкновенной дроби:
- 0,5 = 1/2;
- 0,25 = 1/4;
- 1,375 = 11/8.
И если 0,5 и 0,25 мы без проблем конвертируем из обыкновенной дроби в десятичную и обратно, то в случае с числом 1,375 все неочевидно. Как быстро преобразовать любое десятичное число в дробь? Существует три простых способа.
Избавляемся от запятой
Самый простой алгоритм подразумевает умножение числа на 10 до тех пор, пока из числителя не исчезнет запятая. Такое преобразование осуществляется в три шага:
Шаг 1 : Для начала десятичное число запишем в виде дроби «число/1», то есть мы получим 0,5/1; 0,25/1 и 1,375/1.
Шаг 2 : После этого умножим числитель и знаменатель новых дробей до тех пор, пока из числителей не исчезнет запятая:
- 0,5/1 = 5/10;
- 0,25/1 = 2,5/10 = 25/100;
- 1,375/1 = 13,75/10 = 137,5/100 = 1375/1000.
Шаг 3 : Сокращаем полученные дроби до удобоваримого вида:
- 5/10 = 1 × 5 / 2 × 5 = 1/2;
- 25/100 = 1 × 25 / 4 × 25 = 1/4;
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8.

Число 1,375 пришлось три раза умножать на 10, что уже не очень удобно, а что нам придется делать в случае, если понадобится преобразовать число 0,000625? В этой ситуации используем следующий способ преобразования дробей.
Избавляемся от запятой еще проще
Первый способ детально описывает алгоритм «удаления» запятой из десятичной дроби, однако мы можем упростить этот процесс. И вновь мы выполняем три шага.
Шаг 1 : Считаем, сколько цифр стоит после запятой. К примеру, у числа 1,375 таких цифр три, а у 0,000625 — шесть. Это количество мы обозначим буквой n.
Шаг 2 : Теперь нам достаточно представить дробь в виде C/10 n , где C – это значимые цифры дроби (без нулей, если они есть), а n – количество цифр после запятой. К примеру:
- для числа 1,375 C = 1375, n = 3, итоговая дробь согласно формуле 1375/10 3 = 1375/1000;
- для числа 0,000625 C = 625, n = 6, итоговая дробь согласно формуле 625/10 6 = 625/1000000.
По сути, 10 n – это 1 с количеством нулей, равным n, поэтому вам не нужно заморачиваться с возведением десятки в степень — достаточно указать 1 с n нулей. После этого столь богатую на нули дробь желательно сократить.
После этого столь богатую на нули дробь желательно сократить.
Шаг 3 : Сокращаем нули и получаем итоговый результат:
- 1375/1000 = 11 × 125 / 8 × 125 = 11/8;
- 625/1000000 = 1 × 625/ 1600 × 625 = 1/1600.
Дробь 11/8 — это неправильная дробь, так как числитель у нее больше знаменателя, а значит, мы можем выделить целую часть. В этой ситуации мы вычитаем из 11/8 целую часть 8/8 и получаем остаток 3/8, следовательно, дробь выглядит как 1 и 3/8.
Преобразование на слух
Для тех, кто умеет правильно читать десятичные дроби, проще всего их преобразовать на слух. Если вы читаете 0,025 не как «ноль, ноль, двадцать пять», а как «25 тысячных», то у вас не будет никаких проблем с конвертацией десятичных чисел в обыкновенные дроби.
0,025 = 25/1000 = 1/40
Таким образом, правильное прочтение десятичного числа позволяет сразу же записать ее как обыкновенную дробь и сократить в случае необходимости.
Примеры использования дробей в повседневной жизни
На первый взгляд обыкновенные дроби практически не используются в быту или на работе и трудно представить ситуацию, когда вам понадобится перевести десятичную дробь в обычную за пределами школьных задач. Рассмотрим пару примеров.
Рассмотрим пару примеров.
Работа
Итак, вы работаете в кондитерском магазине и продаете халву на развес. Для простоты реализации продукта вы разделяете халву на килограммовые брикеты, однако мало кто из покупателей готов приобрести целый килограмм. Поэтому вам приходится каждый раз разделять лакомство на кусочки. И если очередной покупатель попросит у вас 0,4 кг халвы, вы без проблем продадите ему нужную порцию.
0,4 = 4/10 = 2/5
Быт
К примеру, необходимо сделать 12 % раствор для покраски модели в нужный вам оттенок. Для этого нужно смешать краску и растворитель, но как правильно это сделать? 12 % — это десятичная дробь 0,12. Преобразовываем число в обыкновенную дробь и получаем:
0,12 = 12/100 = 3/25
Зная дроби, вы сможете правильно смешать компоненты и получить нужный цвет.
Заключение
Дроби широко используются в повседневной жизни, поэтому если вам часто необходимо преобразовывать десятичные значения в обыкновенные дроби, вам пригодится онлайн-калькулятор, при помощи которого можно мгновенно получить результат в виде уже сокращенной дроби.
Вот, казалось бы, перевод десятичной дроби в обычную — элементарная тема, но многие ученики её не понимают! Поэтому сегодня мы подробно рассмотрим сразу несколько алгоритмов, с помощью которых вы разберётесь с любыми дробями буквально за секунду.
Напомню, что существует как минимум две формы записи одной и той же дроби: обыкновенная и десятичная. Десятичные дроби — это всевозможные конструкции вида 0,75; 1,33; и даже −7,41. А вот примеры обыкновенных дробей, которые выражают те же самые числа:
Сейчас разберёмся: как от десятичной записи перейти к обычной? И самое главное: как сделать это максимально быстро?
Основной алгоритм
На самом деле существует как минимум два алгоритма. И мы сейчас рассмотрим оба. Начнём с первого — самого простого и понятного.
Чтобы перевести десятичную дробь в обыкновенную, необходимо выполнить три шага:
Важное замечание по поводу отрицательных чисел. Если в исходном примере перед десятичной дробью стоит знак «минус», то и на выходе перед обыкновенной дробью тоже должен стоять «минус». {3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.
{3}}=1000$. Во-вторых, если убрать из десятичной записи запятую, то мы получим вот это: 0,004 → 0004. Вспомним, что нули слева надо убрать, поэтому по факту у нас число 4. Дальше всё просто: делим, сокращаем и получаем ответ.
Наконец, последний пример:
Особенность этой дроби — наличие целой части. Поэтому на выходе у нас получается неправильная дробь 47/25. Можно, конечно, попытаться разделить 47 на 25 с остатком и таким образом вновь выделить целую часть. Но зачем усложнять себе жизнь, если это можно сделать ещё на этапе преобразований? Что ж, разберёмся.
Что делать с целой частью
На самом деле всё очень просто: если мы хотим получить правильную дробь, то необходимо убрать из неё целую часть на время преобразований, а затем, когда получим результат, вновь дописать её справа перед дробной чертой.
Например, рассмотрим то же самое число: 1,88. Забьём на единицу (целую часть) и посмотрим на дробь 0,88. Она легко преобразуется:
Затем вспоминаем про «утерянную» единицу и дописываем её спереди:
\[\frac{22}{25}\to 1\frac{22}{25}\]
Вот и всё! Ответ получился тем же самым, что и после выделения целой части в прошлый раз. Ещё парочка примеров:
Ещё парочка примеров:
\[\begin{align}& 2,15\to 0,15=\frac{15}{100}=\frac{3}{20}\to 2\frac{3}{20}; \\& 13,8\to 0,8=\frac{8}{10}=\frac{4}{5}\to 13\frac{4}{5}. \\\end{align}\]
В этом и состоит прелесть математики: каким бы путём вы не пошли, если все вычисления выполнены правильно, ответ всегда будет одним и тем же.:)
В заключение хотел бы рассмотреть ещё один приём, который многим помогает.
Преобразования «на слух»
Давайте задумаемся о том, что вообще такое десятичная дробь. Точнее, как мы её читаем. Например, число 0,64 — мы читаем его как «ноль целых, 64 сотых», правильно? Ну, или просто «64 сотых». Ключевое слово здесь — «сотых», т.е. число 100.
А что насчёт 0,004? Это же «ноль целых, 4 тысячных» или просто «четыре тысячных». Так или иначе, ключевое слово — «тысячных», т.е. 1000.
Ну и что в этом такого? А то, что именно эти числа в итоге «всплывают» в знаменателях на втором этапе алгоритма. Т.е. 0,004 — это «четыре тысячных» или «4 разделить на 1000»:
Попробуйте потренироваться сами — это очень просто. Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому
Главное — правильно прочесть исходную дробь. Например, 2,5 — это «2 целых, 5 десятых», поэтому
А какое-нибудь 1,125 — это «1 целая, 125 тысячных», поэтому
В последнем примере, конечно, кто-то возразит, мол, не всякому ученику очевидно, что 1000 делится на 125. Но здесь нужно помнить, что 1000 = 10 3 , а 10 = 2 ∙ 5, поэтому
\[\begin{align}& 1000=10\cdot 10\cdot 10=2\cdot 5\cdot 2\cdot 5\cdot 2\cdot 5= \\& =2\cdot 2\cdot 2\cdot 5\cdot 5\cdot 5=8\cdot 125\end{align}\]
Таким образом, любая степень десятки раскладывается лишь на множители 2 и 5 — именно эти множители нужно искать и в числителе, чтобы в итоге всё сократилось.
На этом урок окончен. Переходим к более сложной обратной операции — см. «
Легко вычислить 0,625 как дробь в простейшей форме
Ниже мы рассмотрим, как вычислить 0,625 как дробь , что даст вам 5/8 как простейшую форму 0,625.
«В математике искусство задавать вопросы более ценно, чем решать задачи».
— Георг Кантор
Следовательно, самая простая форма дроби, полученной из десятичной дроби 0,625, — 5/8. Как же мы дошли до этого числа? Давайте внимательно рассмотрим получение дробей из десятичных и последующее выражение этих дробей в их простейшей форме.
Преобразование десятичных дробей в дроби
Фото: Clker-Free-Vector-Images via Pixabay, CC0
Предположим, у вас есть десятичная дробь, но вам нужна дробь. В частности, скажем, что у вас есть десятичное число 0,625, и вы хотите превратить его в дробь. Чтобы сделать это, вы должны знать некоторые вещи о связи между десятичными дробями и дробями.
Десятичные дроби представляют часть целого числа. Первый столбец после запятой называется десятыми, второй столбец — разряд сотен, а третий столбец — тысячными десятичными знаками. Число 1,10, единица с двумя знаками после запятой, может рассматриваться как 1 и одна десятая.
Обратите внимание, что десятичные дроби тесно связаны с процентами. 1,00 — это всего лишь 100%, и чтобы получить любое число после запятой в процентах, все, что вам нужно сделать, — это переместить запятую на два знака вправо. Таким образом, 0,12 станет 12%.
1,00 — это всего лишь 100%, и чтобы получить любое число после запятой в процентах, все, что вам нужно сделать, — это переместить запятую на два знака вправо. Таким образом, 0,12 станет 12%.
Что касается преобразования десятичной дроби в дробь, то это тоже очень просто. Вы просто берете десятичную дробь и размещаете под ней соответствующее количество столбцов. Допустим, у вас есть десятичное число 0,412. 2 находится в тысячном столбце, поэтому мы можем просто сказать, что это эквивалентно 412/1000. (Это тоже 41,2%.)
Приведение дроби к простейшей форме
412/1000 немного громоздко. Если говорить о дроби, то она может быть намного меньше. Как нам найти наименьшую дробь, которая могла бы представлять десятичную дробь? Нахождение этой наименьшей дроби называется преобразованием числа в его наименьшее значение или уменьшением. Чтобы представить дробь в наименьшем виде, нам нужно найти то, что называется наибольшим общим делителем (иногда называемым наибольшим общим делителем).
«Если бы у меня было 60 минут на решение проблемы, я бы потратил 55 минут на ее определение и 5 минут на решение». — Альберт Эйнштейн
Для дроби 412/1000 мы хотим найти наибольшее число, которое равномерно делится как на числитель, так и на знаменатель. В этом случае наибольшее число, которое равномерно входит и в 412, и в 1000, равно 4. Теперь все, что нам нужно сделать, это разделить обе части числа на 4. Это дает нам 103/250.
Как вычислить 0,625 в виде дроби (Фото: Мои собственные)
Возвращаясь к нашему исходному примеру 0,625, мы должны найти наибольший общий делитель для 625/1000. В данном случае искомое число — 125. 125 делится на 625 пять раз, а на 1000 — восемь раз. Это означает, что простейшая форма 625/1000 — ⅝.
В приведенных выше примерах мы уже знали наибольший общий делитель, но на самом деле, чтобы найти это число, обычно приходится выполнять некоторые математические действия. Как проще всего найти GCF? Найти GCF можно, перечислив простые числа каждого числа, а затем умножив общие простые множители.
Список простых чисел:
Возьмем, к примеру, дробь 18/24. Простые множители — это числа, которые можно умножить только на единицу и на себя. Простые делители числа 18 — это два и три, наименьшие числа, которые можно умножить, чтобы получить 18 (2 x 3 x 3 = 18). Между тем, простые множители числа 24 также равны 2 и 3 (2 х 2 х 2 х 3 = 24). Умножение 2 и 3 вместе дает нам 6, которые мы делим на 18/24. Это аккуратно сокращается до ¾.
Рассмотрим еще один пример.
Фото: My Own
Найдем наибольший общий делитель 168/210. Простые делители числа 168 равны 2, 3 и 7 (2 х 2 х 2 х 3 х 7 = 168). Простые делители числа 210 равны 2, 3, 5 и 7 (2 х 3 х 5 х 7 = 210). Умножение общих множителей — 2, 3, 7 — вместе дает нам 42. Разделение 42 на числитель и знаменатель 168/210 дает нам ⅘.
Есть несколько других способов найти наибольший общий множитель. Альтернативный способ найти GCF состоит в том, чтобы просто перечислить все факторы и выбрать наибольший фактор, общий для двух чисел.
Список множителей числа:
Например, если ваша дробь 64/96, их перечисление дает следующие множители:
Факторы для 64: 1, 2, 4, 5, 16, 32 и 64.
Множители для 96 в конечном итоге будут следующими: 1, 2, 3, 4, 6, 7, 12, 16, 24, 32, 48 и 96.
Теперь давайте определим общие множители: 1, 2 , 4, 8, 16, 32.
Теперь мы знаем, что 32 — это наибольший общий множитель, который мы можем разделить на 64/96, чтобы получить ⅔.
Разделение числа на более мелкие части:
Еще одним методом нахождения наибольшего общего делителя является метод деления. Вы можете разделить два числа на все меньшие и меньшие куски. Каждый раз, когда два числа имеют общие делители, делите их до тех пор, пока не получите числа, которые уже нельзя разделить. Например, давайте найдем GCF 144/280.
Фото: My Own
Увеличив число 280 и 144 на 2, вы получите:
140 и 72. 140 и 72 имеют больше общих множителей, поэтому мы можем разделить это дальше. Попробуем снова разделить на два. Это дает нам:
Попробуем снова разделить на два. Это дает нам:
70 и 36. 70 и 36 все еще имеют общие множители между собой, поэтому их можно разделить дальше. Давайте снова разделим их на два:
35 и 18. Эти два числа не имеют общих делителей, кроме 1, поэтому на этом нам нужно остановиться. Теперь мы можем перемножить числа, которые мы разделили на 2 х 2 х 2 = 8. Разделим 8 на 144/280 и получим 18/35.
«Математика — это не числа, уравнения, вычисления или алгоритмы: это понимание». — Уильям Пол Терстон
Подведение итогов:
Помните, что десятичные дроби легко превратить в дроби. Вы делаете это, просто сдвигая десятичную запятую вправо, пока не достигнете нуля, а затем смотрите, сколько столбцов вам пришлось переместить запятую. Если последнее число находится в столбце тысяч, поставьте 1000 в качестве знаменателя.
Чтобы представить дробь в ее простейшей форме, вам нужно найти наибольший общий делитель (или наибольший общий делитель). Существует несколько различных методов нахождения GCF:
Существует несколько различных методов нахождения GCF:
Вы можете перечислить простые числа каждого числа, а затем перемножить общие простые множители. Более длинный способ сделать это — перечислить все делители числа и выбрать наибольший общий делитель двух чисел.
Вы также можете продолжать делить числа на общие множители до тех пор, пока они не перестанут иметь между собой общие множители и не примут простейшую форму. Затем вы будете умножать числа, на которые вы разделили.
Калькулятор дробей
Этот калькулятор выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т. е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта одновременно является знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1,45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример | ||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 | ||||||||||||||||||||||||||||||||||||||
| — | minus sign | subtraction | 1 1/2 — 2/3 | ||||||||||||||||||||||||||||||||||||||
| * | asterisk | multiplication | 2/3 * 3/4 | ||||||||||||||||||||||||||||||||||||||
| × | times sign | multiplication | 2/3 × 5/6 | ||||||||||||||||||||||||||||||||||||||
| : | division sign | division 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • сокращение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
more math problems »
Что такое 0,625 как дробь? (Преобразовать 0,625 в дробь) Хотите преобразовать 0,625 в дробь? Если это так, вы находитесь в правильном месте! В этом пошаговом руководстве мы точно покажем вам, что представляет собой дробная форма числа 0,625, и покажем, как именно его рассчитать, чтобы вы могли преобразовать любое десятичное число в дробь. Хотите быстро узнать или показать учащимся, как преобразовать 0,625 в дробь? Включи это очень быстрое и веселое видео прямо сейчас! Существует много причин, по которым вам может понадобиться преобразовать десятичную дробь в дробь. Самая распространенная причина в том, что ваш учитель сказал вам! Но помимо этого, десятичная форма дроби позволяет очень легко сравнивать две дроби, не задумываясь об этом. Прежде чем мы начнем, краткий обзор. Число над дробной чертой является числителем, а число под дробной чертой — знаменателем. Если вы много работали с дробями, вы, вероятно, уже знаете это, но никогда не помешает перепроверить! Итак, первое, что нужно сделать, это показать вам, что любое число может быть дробью, если вы используете 1 в качестве знаменателя. Взгляните: 0,625 / 1 Что мы действительно хотим сделать, так это полностью избавиться от десятичных знаков, чтобы числитель в нашей дроби был целым числом. Чтобы получить целую дробь, нам нужно умножить и числитель, и знаменатель на 10, если после запятой стоит одно число , 100, если есть два числа, 1000, если это три числа и 10,000, если это… ну, вы поняли идею! В нашем случае 625 состоит из 3 цифр, поэтому нам нужно умножить числитель и знаменатель на 1000. Теперь нам просто нужно выполнить это умножение, чтобы получить целую дробь: 0,625 x 1000 / 1 х 1000 знак равно 625 / 1000 Следующий шаг — упростить эту дробь, а для этого нам нужно найти наибольший общий делитель (НОД). Это иногда также известно как:
GCF может быть немного сложно вычислить вручную, но вы можете использовать наш удобный калькулятор GCF, чтобы вычислить его. В случае 625 и 1000 наибольший общий делитель равен 125. 625/125 / 1000/125 знак равно 5 / 8 Вот и все! Всего за несколько коротких шагов мы выяснили, что такое 0,625 как дробь. Полный ответ для вашего удовольствия ниже: 5/8 Надеемся, что это руководство помогло вам понять, как преобразовать десятичное число в дробь. Теперь вы можете пойти дальше и конвертировать десятичные дроби в дроби столько, сколько пожелает ваше маленькое сердце! Процитируйте, дайте ссылку или ссылку на эту страницуЕсли вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
Предустановленный список десятичных дробейНиже приведены ссылки на некоторые предустановленные десятичные вычисления, которые обычно ищут: Что такое 0,25 как дробь? Что такое 0,50 как дробь? Что такое 0,75 как дробь? Что такое 0,100 как дробь? Что такое 0,125 как дробь? Что такое 0,150 в виде дроби? Что такое 0,175 в виде дроби? Что такое 0,200 в виде дроби? Что такое 0,225 в виде дроби? Что такое 0,250 как дробь? Что такое 0,275 в виде дроби? Что такое 0,300 в виде дроби? Что такое 0,325 как дробь? Что такое 0,350 как дробь? Что такое 0,375 как дробь? Что такое 0,400 как дробь? Что такое 0,425 как дробь? Что такое 0,450 как дробь? Что такое 0,475 как дробь? Что такое 0,500 в виде дроби? Что такое 0,525 в виде дроби? Что такое 0,550 как дробь? Что такое 0,575 в виде дроби? Что такое 0,600 в виде дроби? Что такое 0,625 в виде дроби? Что такое 0,650 в виде дроби? Что такое 0,675 в виде дроби? Что такое 0,700 как дробь? Что такое 0,725 как дробь? Что такое 0,750 как дробь? Что такое 0,775 в виде дроби? Что такое 0,800 как дробь? Что такое 0,825 как дробь? Что такое 0,850 как дробь? Что такое 0,875 в виде дроби? Что такое 0,900 как дробь? Что такое 0,925 как дробь? Что такое 0,950 как дробь? Что такое 0,975 как дробь? Что такое 0,1000 в виде дроби? Чему равно число 1,25 в виде дроби? Что такое 1,50 как дробь? Чему равно 1,75 в виде дроби? Что такое 1,100 как дробь? Чему равно число 1,125 в виде дроби? Что такое 1,150 как дробь? Чему равно 1,175 в виде дроби? Что такое 1. Чему равно число 1,225 в виде дроби? Что такое 1,250 как дробь? Что такое 1,275 как дробь? Что такое 1.300 как дробь? Чему равно число 1,325 в виде дроби? Что такое 1,350 как дробь? Что такое 1,375 как дробь? Что такое 1.400 как дробь? Чему равно число 1,425 в виде дроби? Что такое 1,450 как дробь? Чему равно 1,475 в виде дроби? Что такое 1.500 как дробь? Чему равно число 1,525 в виде дроби? Что такое 1,550 как дробь? Чему равно число 1,575 в виде дроби? Что такое 1.600 как дробь? Чему равно число 1,625 в виде дроби? Что такое 1,650 как дробь? Что такое 1,675 как дробь? Что такое 1.700 как дробь? Что такое 1,725 как дробь? Что такое 1,750 как дробь? Что такое 1,775 как дробь? Что такое 1.800 как дробь? Чему равно число 1,825 в виде дроби? Что такое 1,850 как дробь? Чему равно 1,875 в виде дроби? Что такое 1. Чему равно число 1,925 в виде дроби? Что такое 1,950 как дробь? Что такое 1,975 как дробь? Чему равно 1,1000 в виде дроби? Чему равно число 2,25 в виде дроби? Чему равно 2,50 в виде дроби? Чему равно число 2,75 в виде дроби? Что такое 2,100 как дробь? Чему равно число 2,125 в виде дроби? Что такое 2,150 как дробь? Чему равно число 2,175 в виде дроби? Что такое 2.200 как дробь? Чему равно число 2,225 в виде дроби? Что такое 2,250 как дробь? Чему равно число 2,275 в виде дроби? Что такое 2.300 как дробь? Чему равно число 2,325 в виде дроби? Что такое 2,350 как дробь? Чему равно число 2,375 в виде дроби? Что такое 2.400 как дробь? Чему равно число 2,425 в виде дроби? Что такое 2,450 как дробь? Чему равно число 2,475 в виде дроби? Что такое 2.500 как дробь? Чему равно число 2,525 в виде дроби? Что такое 2,550 как дробь? Чему равно число 2,575 в виде дроби? Что такое 2. Чему равно число 2,625 в виде дроби? Что такое 2,650 как дробь? Чему равно число 2,675 в виде дроби? Что такое 2.700 как дробь? Чему равно число 2,725 в виде дроби? Что такое 2,750 как дробь? Чему равно число 2,775 в виде дроби? Что такое 2.800 как дробь? Чему равно число 2,825 в виде дроби? Что такое 2,850 как дробь? Чему равно число 2,875 в виде дроби? Что такое 2.900 как дробь? Чему равно число 2,925 в виде дроби? Что такое 2,950 как дробь? Чему равно число 2,975 в виде дроби? Что такое 2,1000 как дробь? Чему равно число 3,25 в виде дроби? Что такое 3,50 как дробь? Чему равно число 3,75 в виде дроби? Что такое 3,100 как дробь? Чему равно число 3,125 в виде дроби? Чему равно число 3,150 в виде дроби? Чему равно число 3,175 в виде дроби? Что такое 3.200 как дробь? Чему равно число 3,225 в виде дроби? Что такое 3,250 как дробь? Чему равно число 3,275 в виде дроби? Что такое 3. Чему равно число 3,325 в виде дроби? Чему равно 3,350 в виде дроби? Чему равно число 3,375 в виде дроби? Что такое 3,400 как дробь? Чему равно число 3,425 в виде дроби? Чему равно число 3,450 в виде дроби? Чему равно число 3,475 в виде дроби? Что такое 3.500 как дробь? Чему равно число 3,525 в виде дроби? Чему равно 3,550 в виде дроби? Чему равно число 3,575 в виде дроби? Что такое 3,600 как дробь? Чему равно число 3,625 в виде дроби? Чему равно число 3,650 в виде дроби? Чему равно число 3,675 в виде дроби? Что такое 3,700 в виде дроби? Чему равно число 3,725 в виде дроби? Чему равно 3,750 в виде дроби? Чему равно число 3,775 в виде дроби? Что такое 3.800 как дробь? Чему равно число 3,825 в виде дроби? Чему равно 3,850 в виде дроби? Чему равно число 3,875 в виде дроби? Что такое 3,900 как дробь? Чему равно число 3,925 в виде дроби? Чему равно 3,950 в виде дроби? Чему равно число 3,975 в виде дроби? Что такое 3,1000 в виде дроби? Чему равно число 4,25 в виде дроби? Что такое 4,50 как дробь? Чему равно число 4,75 в виде дроби? Что такое 4,100 как дробь? Чему равно число 4,125 в виде дроби? Что такое 4,150 как дробь? Чему равно число 4,175 в виде дроби? Что такое 4. Чему равно число 4,225 в виде дроби? Что такое 4,250 как дробь? Чему равно число 4,275 в виде дроби? Что такое 4.300 как дробь? Чему равно число 4,325 в виде дроби? Чему равно 4,350 в виде дроби? Чему равно число 4,375 в виде дроби? Что такое 4.400 как дробь? Чему равно число 4,425 в виде дроби? Чему равно число 4,450 в виде дроби? Чему равно число 4,475 в виде дроби? Что такое 4.500 как дробь? Чему равно число 4,525 в виде дроби? Что такое 4,550 как дробь? Чему равно число 4,575 в виде дроби? Что такое 4.600 как дробь? Чему равно число 4,625 в виде дроби? Что такое 4,650 как дробь? Чему равно число 4,675 в виде дроби? Что такое 4.700 как дробь? Чему равно число 4,725 в виде дроби? Чему равно число 4,750 в виде дроби? Чему равно число 4,775 в виде дроби? Что такое 4. Чему равно число 4,825 в виде дроби? Чему равно число 4,850 в виде дроби? Чему равно число 4,875 в виде дроби? Что такое 4,900 как дробь? Чему равно число 4,925 в виде дроби? Что такое 4,950 как дробь? Чему равно число 4,975 в виде дроби? Что такое 4,1000 как дробь? Что такое 5,25 как дробь? Что такое 5,50 как дробь? Что такое 5,75 как дробь? Что такое 5,100 как дробь? Что такое 5,125 как дробь? Что такое 5,150 как дробь? Чему равно число 5,175 в виде дроби? Что такое 5.200 как дробь? Что такое 5,225 как дробь? Что такое 5,250 как дробь? Что такое 5,275 как дробь? Что такое 5.300 как дробь? Что такое 5,325 как дробь? Что такое 5,350 как дробь? Что такое 5,375 как дробь? Что такое 5.400 как дробь? Что такое 5,425 как дробь? Что такое 5,450 как дробь? Что такое 5,475 как дробь? Что такое 5. Чему равно число 5,525 в виде дроби? Что такое 5,550 как дробь? Что такое 5,575 как дробь? Что такое 5.600 как дробь? Что такое 5,625 как дробь? Что такое 5,650 как дробь? Что такое 5,675 как дробь? Что такое 5.700 как дробь? Что такое 5,725 как дробь? Что такое 5,750 как дробь? Чему равно число 5,775 в виде дроби? Что такое 5.800 как дробь? Что такое 5,825 как дробь? Что такое 5,850 как дробь? Что такое 5,875 как дробь? Что такое 5,900 как дробь? Что такое 5,925 как дробь? Что такое 5,950 как дробь? Что такое 5,975 как дробь? Что такое 5,1000 как дробь? Чему равно 6,25 в виде дроби? Что такое 6,50 как дробь? Что такое 6,75 как дробь? Что такое 6,100 как дробь? Чему равно число 6,125 в виде дроби? Что такое 6,150 как дробь? Чему равно 6,175 в виде дроби? Что такое 6. Чему равно число 6,225 в виде дроби? Что такое 6,250 как дробь? Чему равно 6,275 в виде дроби? Что такое 6.300 как дробь? Чему равно 6,325 в виде дроби? Что такое 6,350 как дробь? Чему равно число 6,375 в виде дроби? Что такое 6.400 как дробь? Чему равно число 6,425 в виде дроби? Что такое 6,450 как дробь? Чему равно число 6,475 в виде дроби? Что такое 6.500 как дробь? Чему равно число 6,525 в виде дроби? Что такое 6,550 как дробь? Чему равно число 6,575 в виде дроби? Что такое 6.600 как дробь? Чему равно 6,625 в виде дроби? Что такое 6,650 как дробь? Чему равно 6,675 в виде дроби? Что такое 6.700 как дробь? Чему равно число 6,725 в виде дроби? Что такое 6,750 как дробь? Чему равно 6,775 в виде дроби? Что такое 6.800 как дробь? Чему равно 6,825 в виде дроби? Что такое 6,850 как дробь? Чему равно число 6,875 в виде дроби? Что такое 6. Чему равно 6,925 в виде дроби? Что такое 6,950 как дробь? Чему равно 6,975 в виде дроби? Чему равно 6,1000 в виде дроби? Чему равно 7,25 в виде дроби? Что такое 7,50 как дробь? Что такое 7,75 как дробь? Что такое 7,100 как дробь? Что такое 7,125 как дробь? Что такое 7,150 как дробь? Чему равно 7,175 в виде дроби? Что такое 7.200 как дробь? Что такое 7,225 как дробь? Что такое 7,250 как дробь? Чему равно 7,275 в виде дроби? Что такое 7.300 как дробь? Чему равно число 7,325 в виде дроби? Что такое 7,350 как дробь? Чему равно 7,375 в виде дроби? Что такое 7.400 как дробь? Что такое 7,425 как дробь? Что такое 7,450 как дробь? Чему равно число 7,475 в виде дроби? Что такое 7.500 как дробь? Что такое 7,525 как дробь? Что такое 7,550 как дробь? Чему равно 7,575 в виде дроби? Что такое 7. Чему равно число 7,625 в виде дроби? Что такое 7,650 как дробь? Чему равно 7,675 в виде дроби? Что такое 7.700 как дробь? Что такое 7,725 как дробь? Что такое 7,750 как дробь? Чему равно 7,775 в виде дроби? Что такое 7.800 как дробь? Что такое 7,825 как дробь? Что такое 7,850 как дробь? Чему равно 7,875 в виде дроби? Что такое 7.900 как дробь? Чему равно число 7,925 в виде дроби? Что такое 7,950 как дробь? Чему равно число 7,975 в виде дроби? Что такое 7,1000 как дробь? Что такое 8,25 как дробь? Что такое 8,50 как дробь? Что такое 8,75 как дробь? Что такое 8,100 как дробь? Чему равно число 8,125 в виде дроби? Что такое 8,150 как дробь? Чему равно число 8,175 в виде дроби? Что такое 8.200 как дробь? Чему равно число 8,225 в виде дроби? Что такое 8,250 как дробь? Чему равно число 8,275 в виде дроби? Что такое 8. Что такое 8,325 как дробь? Что такое 8,350 как дробь? Чему равно число 8,375 в виде дроби? Что такое 8.400 как дробь? Чему равно число 8,425 в виде дроби? Что такое 8,450 как дробь? Чему равно число 8,475 в виде дроби? Что такое 8.500 как дробь? Чему равно число 8,525 в виде дроби? Что такое 8,550 как дробь? Чему равно число 8,575 в виде дроби? Что такое 8.600 как дробь? Чему равно число 8,625 в виде дроби? Что такое 8,650 как дробь? Чему равно число 8,675 в виде дроби? Что такое 8.700 как дробь? Что такое 8,725 как дробь? Что такое 8,750 как дробь? Чему равно число 8,775 в виде дроби? Что такое 8.800 как дробь? Чему равно число 8,825 в виде дроби? Что такое 8,850 как дробь? Чему равно число 8,875 в виде дроби? Что такое 8.900 как дробь? Что такое 8,925 как дробь? Что такое 8,950 как дробь? Чему равно число 8,975 в виде дроби? Что такое 8,1000 как дробь? Что такое 9,25 как дробь? Что такое 9,50 как дробь? Что такое 9,75 как дробь? Что такое 9. Чему равно число 9,125 в виде дроби? Что такое 9,150 как дробь? Что такое 9,175 как дробь? Что такое 9.200 как дробь? Что такое 9,225 как дробь? Что такое 9,250 как дробь? Что такое 9,275 как дробь? Что такое 9.300 как дробь? Что такое 9,325 как дробь? Что такое 9,350 как дробь? Что такое 9,375 как дробь? Что такое 9.400 как дробь? Что такое 9,425 как дробь? Что такое 9,450 как дробь? Что такое 9,475 как дробь? Что такое 9.500 как дробь? Что такое 9,525 как дробь? Что такое 9,550 как дробь? Что такое 9,575 как дробь? Что такое 9.600 как дробь? Что такое 9,625 как дробь? Что такое 9,650 как дробь? Что такое 9,675 как дробь? Что такое 9.700 как дробь? Что такое 9,725 как дробь? Что такое 9,750 как дробь? Что такое 9,775 как дробь? Что такое 9. Что такое 9,825 как дробь? Что такое 9,850 как дробь? Что такое 9,875 как дробь? Что такое 9.900 как дробь? Что такое 9,925 как дробь? Что такое 9,950 как дробь? Что такое 9,975 как дробь? Что такое 9,1000 как дробь? Случайные вычисления десятичных чисел в дробиЕсли вы действительно любите преобразование десятичных чисел в дроби и просто не можете насытиться, вот несколько случайных вычислений для вас: Что такое 94,932 как дробь? Чему равно 20,979 в виде дроби? Чему равно число 47,923 в виде дроби? Чему равно число 57,175 в виде дроби? Чему равно число 88,387 в виде дроби? Чему равно число 37,749 в виде дроби? Чему равно 54,98 в виде дроби? Что такое 81,210 в виде дроби? Чему равно число 86,801 в виде дроби? Чему равно число 81,198 в виде дроби? Чему равно 65,916 в виде дроби? Чему равно число 14,117 в виде дроби? Что такое 99,322 в виде дроби? Чему равно число 95,423 в виде дроби? Чему равно 79,290 в виде дроби? Чему равно 20,589 в виде дроби? Чему равно 39,658 в виде дроби? Чему равно число 81,417 в виде дроби? Что такое 93,9 как дробь? Чему равно 66,359 в виде дроби? Чему равно число 49,606 в виде дроби? Чему равно 75,963 в виде дроби? Что такое 21,140 как дробь? Чему равно число 17,163 в виде дроби? Чему равно число 3,121 в виде дроби? Что такое 11,616 как дробь? Что такое 11,414 как дробь? Чему равно 40,324 в виде дроби? Чему равно 50,857 в виде дроби? Чему равно число 2,136 в виде дроби? Чему равно число 30,803 в виде дроби? Чему равно число 16,695 в виде дроби? Чему равно число 50,263 в виде дроби? Чему равно 66,808 в виде дроби? Чему равно 73,92 в виде дроби? Чему равно число 33,691 в виде дроби? Чему равно 59,291 в виде дроби? Чему равно 73,944 в виде дроби? Чему равно число 35,636 в виде дроби? Чему равно число 13,612 в виде дроби? Чему равно число 26,569 в виде дроби? Что такое 94,242 в виде дроби? Чему равно число 89,193 в виде дроби? Чему равно число 94,28 в виде дроби? Чему равно 41,73 в виде дроби? Чему равно число 63,155 в виде дроби? Что такое 13,506 как дробь? Чему равно число 31,736 в виде дроби? Чему равно 73,287 в виде дроби? Что такое 22. Чему равно 19,372 в виде дроби? Чему равно 77,606 в виде дроби? Чему равно число 26,647 в виде дроби? Чему равно 71,784 в виде дроби? Чему равно число 73,665 в виде дроби? Чему равно число 14,818 в виде дроби? Чему равно число 97,221 в виде дроби? Чему равно число 3,654 в виде дроби? Что такое 14,405 как дробь? Чему равно 61,170 в виде дроби? Чему равно 60,15 в виде дроби? Чему равно число 14,58 в виде дроби? Чему равно число 48,776 в виде дроби? Чему равно число 22,868 в виде дроби? Чему равно число 39,119 в виде дроби? Чему равно 77,48 в виде дроби? Чему равно число 87,867 в виде дроби? Чему равно число 37,888 в виде дроби? Чему равно число 74,928 в виде дроби? Чему равно число 45,229 в виде дроби? Чему равно число 36,181 в виде дроби? Чему равно число 94,482 в виде дроби? Чему равно число 36,412 в виде дроби? Чему равно 60,259 в виде дроби? Чему равно 55,839 в виде дроби? Чему равно 75,992 в виде дроби? Чему равно число 41,337 в виде дроби? Чему равно 48,192 в виде дроби? Чему равно 57,718 в виде дроби? Чему равно 59,773 в виде дроби? Чему равно 64,420 в виде дроби? Чему равно число 93,284 в виде дроби? Что такое 92,90 как дробь? Чему равно число 44,633 в виде дроби? Чему равно 74,502 в виде дроби? Чему равно число 95,32 в виде дроби? Что такое 19,545 как дробь? Чему равно число 92,835 в виде дроби? Чему равно 2,707 в виде дроби? Чему равно 75,428 в виде дроби? Чему равно число 85,597 в виде дроби? Чему равно число 17,885 в виде дроби? Чему равно 62,863 в виде дроби? Чему равно 6,192 в виде дроби? Чему равно 67,273 в виде дроби? Чему равно число 3,839 в виде дроби? Чему равно 78,791 в виде дроби? Чему равно число 67,179 в виде дроби? Чему равно число 3,504 в виде дроби? Чему равно 15,54 в виде дроби? Что такое 9,254 как дробь?
Что такое 625 как дробь? – Reviews Wiki Ответ: 0,625 в виде дроби равно 625/100, что можно сократить до 5/8 . Аналогично, что такое дробь? Таблица преобразования десятичной дроби в дробную
2 Что такое рулетка? . 625 | 15.875 | ||||||||||||||||||||||||||||||||||||||
| 41/64 | . 640625 | 16.272 | |||||||||||||||||||||||||||||||||||||||
| 21/32 | . 65625 | 16,669 | |||||||||||||||||||||||||||||||||||||||
| 43/64 | . 671875 | 17,066 |
Как упростить дроби? Вы можете упростить дробь , если числитель (верхнее число) и знаменатель (нижнее число) можно разделить на одно и то же число . Шесть двенадцатых можно упростить до половины, или 1 вместо 2, потому что оба числа делятся на 6. 6 входит в число 6 один раз, а 6 входит в число 12 дважды.
Во-вторых Как преобразовать десятичную дробь в дробь в простой форме? Десятичные числа можно записывать в виде дробей. Чтобы преобразовать десятичное число в дробь, поместите десятичное число над его разрядным значением . Например, в 0,6 шестерка находится на десятом месте, поэтому мы помещаем 6 на 10, чтобы получить эквивалентную дробь 6/10. При необходимости упростите дробь.
Чтобы преобразовать десятичное число в дробь, поместите десятичное число над его разрядным значением . Например, в 0,6 шестерка находится на десятом месте, поэтому мы помещаем 6 на 10, чтобы получить эквивалентную дробь 6/10. При необходимости упростите дробь.
Что упрощено?
— сделать менее сложным или сложным; сделать проще или проще: упростить проблему.
то Что такое дробь для детей? Дробь — это часть целого числа и способ разделить число на равные части. Он записывается как количество подсчитываемых равных частей, называемое числителем, над количеством частей в целом, называемое знаменателем. Эти числа разделены линией.
Это реальное число? действительное число, в математике количество, которое может быть выражено как бесконечное десятичное расширение . … Действительные числа включают положительные и отрицательные целые числа и дроби (или рациональные числа), а также иррациональные числа.
Что такое 0,75 на линейке?
Fraction, Decimal, and Millimeter Equivalent Measurements
| Fraction | Decimal | millimeters |
|---|---|---|
| 3 ⁄ 4 » | 0. 75 75 | 19.05 |
| 13 ⁄ 16 » | 0,8125 | 20,6375 |
| 7 ⁄ 8 » | 0.875 | 22.225 |
| 15 ⁄ 16 » | 0.9375 | 23.8125 |
• Feb 11, 2021
Где .0625 на линейке?
| ДЮЙМЫ | ДЕСЯТИЧНАЯ ЗАМЕТКА ДЮЙМА | МИЛЛИМЕТРЫ |
|---|---|---|
| 1/16 | . 0625 | 1.597500 |
| 1/13 | . 0769 | 1.953850 |
| 5/64 | . 078125 | 1.984375 |
| 1/12 | . 0833 | 2,116671 |
Что такое 0,1 дюйма в дробях?
Таблица преобразования дюймовых дробей – Эквиваленты десятичных и метрических дробей
| Fraction (inches) | Decimal (inches) | Metric (millimeters) |
|---|---|---|
| 61 / 64 » | 0.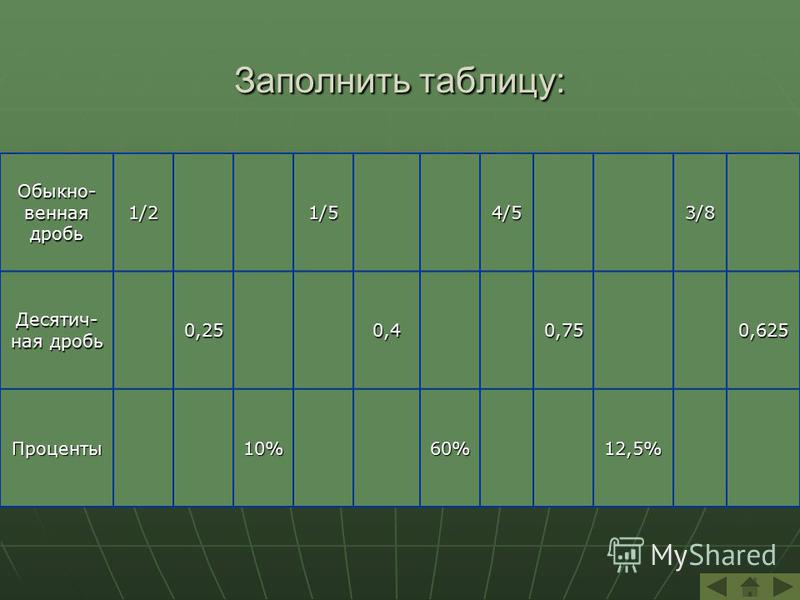 953125″ 953125″ | 24.209375 mm |
| 31 / 32 » | 0.96875″ | 24,60625 мм |
| 63 / 64″ | 0,984375″ | 25,003125 мм |
| 30106 « | 25,4 мм |
Как упростить число?
Что упрощено?
до .
Как упростить десятичные отношения?Чтобы упростить отношение десятичных дробей, мы удаляем десятичную точку и уменьшаем отношение до отношения целых чисел . Умножаем числитель и знаменатель отношения в дробной форме на 10, 100 , 1000 т. е. степень десяти, чтобы исключить десятичную дробь, тогда дробь упрощается до наименьшего значения. 0005
0005
Как превратить 0,5 в дробь?
Ответ: 0,5 в виде дроби записывается как 1/2 .
Как выглядит упрощенная дробь? Запись дроби в ее простейшей форме означает, что верхние и нижние числа больше не могут быть точно или без остатка разделены на одно и то же целое число (кроме числа 1) . Например, дробь 2/3 полностью сокращена.
Как сделать простейшую форму?
Как научить ребенка дробям?
com/embed/Y3A3bPmMNcg» frameborder=»0″ allowfullscreen=»allowfullscreen» data-original-w=»720″ data-original-h=»520″>Как учить дроби первоклассников?
Преобразование дроби в десятичную дробь
Преобразование дроби в десятичную дробьГлавная›Конвертация›Преобразование чисел›Дробь в десятичную
Калькулятор фракций Упрощение дробей Преобразователь дробей
От DecimalFractionPercent
До Десятичная дробьПроцент
Введите дробь
Десятичный результат
Расчет
Конвертер десятичных чисел в дроби ►
Как преобразовать дробь в десятичную
Метод №1
Разложить знаменатель на степень числа 10.
Пример №1
3/5 расширяется до 6/10 путем умножения числителя на 2 и знаменателя на 2:
| 3 | = | 3×2 | = | 6 | = | 0,6 |
| 5 | 5×2 | 10 |
Пример #2
3/4 расширяется до 75/100 путем умножения числителя на 25 и знаменателя на 25:
| 3 | = | 3×25 | = | 75 | = | 0,75 |
| 4 | 4×25 | 100 |
Пример #3
5/8 расширяется до 625/1000 путем умножения числителя на 125 и знаменателя на 125:
| 5 | = | 5×125 | = | 625 | = | 0,625 |
| 8 | 8×125 | 1000 |
Метод №2
- Используйте калькулятор, чтобы разделить числитель дроби на знаменатель.

- Для смешанных чисел добавьте целое число.
Пример №1
2/5 = 2÷5 = 0,4
Пример №2
1 2/5 = 1+2÷5 = 1,4 по знаменателю дроби.
Пример
Вычислить 3/4 путем деления 3 на 4 в длину:
| 0,75 | |
| 4 | 3 |
| 0 | |
| 30 | |
| 28 | |
| 20 | |
| 20 | |
| 0 |
Таблица перевода дроби в десятичную дробь
| Дробь | Десятичный |
|---|---|
| 1/2 | 0,5 |
| 1/3 | 0,33333333 |
| 2/3 | 0,66666667 |
| 1/4 | 0,25 |
| 2/4 | 0,5 |
| 3/4 | 0,75 |
| 1/5 | 0,2 |
| 2/5 | 0,4 |
| 3/5 | 0,6 |
| 4/5 | 0,8 |
| 1/6 | 0,16666667 |
| 2/6 | 0,33333333 |
| 3/6 | 0,5 |
| 4/6 | 0,66666667 |
| 5/6 | 0,83333333 |
| 1/7 | 0,14285714 |
| 2/7 | 0,28571429 |
| 3/7 | 0,42857143 |
| 4/7 | 0,57142858 |
| 5/7 | 0,71428571 |
| 6/7 | 0,85714286 |
| 1/8 | 0,125 |
| 2/8 | 0,25 |
| 3/8 | 0,375 |
| 4/8 | 0,5 |
| 5/8 | 0,625 |
| 6/8 | 0,75 |
| 7/8 | 0,875 |
| 1/9 | 0,11111111 |
| 2/9 | 0,22222222 |
| 3/9 | 0,33333333 |
| 4/9 | 0,44444444 |
| 5/9 | 0,55555556 |
| 6/9 | 0,66666667 |
| 7/9 | 0,77777778 |
| 8/9 | 0,88888889 |
| 1/10 | 0,1 |
| 2/10 | 0,2 |
| 3/10 | 0,3 |
| 4/10 | 0,4 |
| 5/10 | 0,5 |
| 6/10 | 0,6 |
| 7/10 | 0,7 |
| 8/10 | 0,8 |
| 9/10 | 0,9 |
| 1/11 | 0,009 |
| 2/11 | 0,18181818 |
| 3/11 | 0,27272727 |
| 4/11 | 0,36363636 |
| 5/11 | 0,45454545 |
| 6/11 | 0,54545454 |
| 7/11 | 0,63636363 |
| 8/11 | 0,72727272 |
| 9/11 | 0,81818181 |
| 10/11 | 0,091 |
Преобразование десятичной дроби в дробную ►
См.
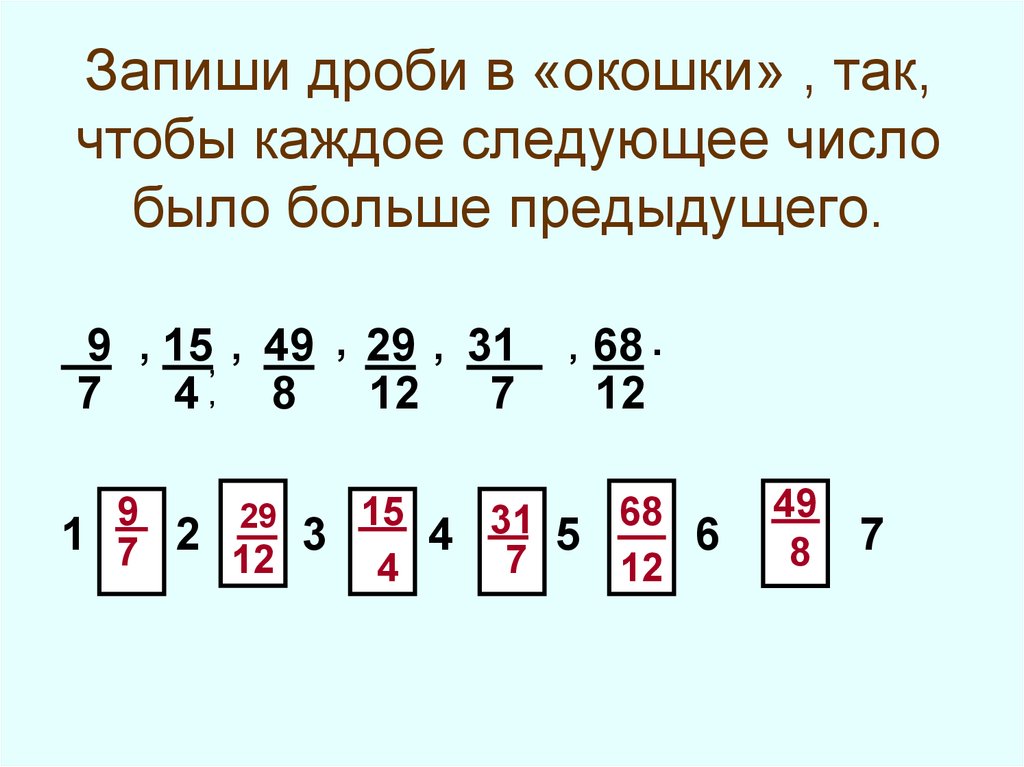

 Данная обыкновенная дробь переведется в число (десятичную дробь) с конечным количеством знаков после запятой. А вот дробь 17/60 =17/(5∙2∙2∙3) переведется в число с бесконечным количеством знаков после запятой. То есть при точном вычислении числового значения довольно трудно определить конечный знак после запятой, поскольку таких знаков бесконечное множество. Поэтому для решения задач обычно требуется округлить значение до сотых или тысячных. Дальше — необходимо умножить и числитель, и знаменатель на такое число, чтобы в знаменателе получились цифры 10, 100, 1000 и т. д. Например: 11/40 =(11∙25)/(40∙25) =275/1000 =0,275
Данная обыкновенная дробь переведется в число (десятичную дробь) с конечным количеством знаков после запятой. А вот дробь 17/60 =17/(5∙2∙2∙3) переведется в число с бесконечным количеством знаков после запятой. То есть при точном вычислении числового значения довольно трудно определить конечный знак после запятой, поскольку таких знаков бесконечное множество. Поэтому для решения задач обычно требуется округлить значение до сотых или тысячных. Дальше — необходимо умножить и числитель, и знаменатель на такое число, чтобы в знаменателе получились цифры 10, 100, 1000 и т. д. Например: 11/40 =(11∙25)/(40∙25) =275/1000 =0,275 В нашем примере это будет 3,45. Чтобы преобразовать смешанную дробь такого вида, как 3 2 / 7 , в число, то нужно сначала превратить ее в неправильную дробь: (3∙7+2)/7 =23/7. Далее делим 23 на 7 и получаем число 3,2857143, которое сокращаем до 3,29.
В нашем примере это будет 3,45. Чтобы преобразовать смешанную дробь такого вида, как 3 2 / 7 , в число, то нужно сначала превратить ее в неправильную дробь: (3∙7+2)/7 =23/7. Далее делим 23 на 7 и получаем число 3,2857143, которое сокращаем до 3,29.
 — Георг Кантор
— Георг Кантор Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  6 детей — девочки. Какую часть детей составляют девочки?
6 детей — девочки. Какую часть детей составляют девочки?
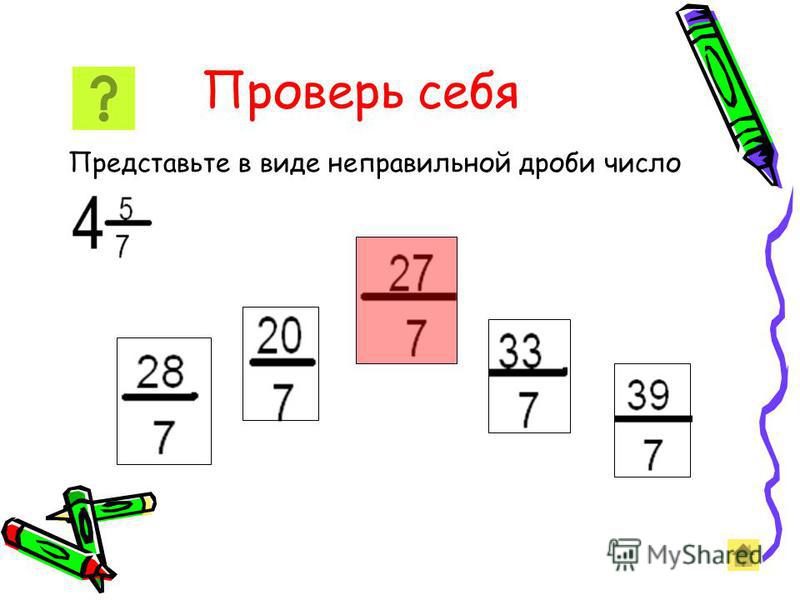 Пойдем!
Пойдем! Для этого нам нужно посчитать числа после запятой, что в данном случае равно 625.
Для этого нам нужно посчитать числа после запятой, что в данном случае равно 625. Это означает, что для упрощения дроби мы можем разделить числитель и знаменатель на 125 и получим:
Это означает, что для упрощения дроби мы можем разделить числитель и знаменатель на 125 и получим: VisualFractions.com . По состоянию на 17 сентября 2022 г. http://visualfractions.com/calculator/decimal-as-fraction/what-is-0-625-as-a-fraction/.
VisualFractions.com . По состоянию на 17 сентября 2022 г. http://visualfractions.com/calculator/decimal-as-fraction/what-is-0-625-as-a-fraction/. 200 как дробь?
200 как дробь? 900 как дробь?
900 как дробь? 600 как дробь?
600 как дробь? 300 как дробь?
300 как дробь? 200 как дробь?
200 как дробь? 800 как дробь?
800 как дробь? 500 как дробь?
500 как дробь? 200 как дробь?
200 как дробь? 900 как дробь?
900 как дробь? 600 как дробь?
600 как дробь? 300 как дробь?
300 как дробь? 100 как дробь?
100 как дробь? 800 как дробь?
800 как дробь? 500 как дробь?
500 как дробь? Преобразуем 0,625 в дробь.
Преобразуем 0,625 в дробь.