как найти, формула, через среднюю линию
Содержание:
- Основные свойства трапеции
-
Способы нахождений периметра
- По всем сторонам
- По сторонам равнобедренной трапеции
- Через среднюю линию
- Примеры решения задач
Содержание
- Основные свойства трапеции
- По всем сторонам
- По сторонам равнобедренной трапеции
- Через среднюю линию
- Примеры решения задач
Определения
Трапеция — это четырехугольник, у которого лишь одна пара противолежащих сторон параллельна.
Периметр трапеции — это сумма длин всех его сторон.
Основные свойства трапеции
- средняя линия трапеции параллельна ее основаниям, а также равна половине их суммы;
- биссектриса любого угла данного четырехугольника отсекает на его основании отрезок, равный боковой стороне;
- треугольники ABO и DCO (на картинке), образованные диагоналями фигуры и ее основаниями, подобны;
- треугольники OAB и OCD, образованные диагоналями трапеции и ее боковыми сторонами, имеют одинаковую площадь;
- если сумма длин оснований четырехугольника равна сумме его боковых ребер, то в фигуру можно вписать окружность;
- точки M и N середины диагоналей лежат на одной прямой со средней линией фигуры. Также отрезок MN равен полуразность оснований четырехугольника;
- середины оснований фигуры, точка пересечения ее диагоналей, а также точка пересечения продолжений ее боковых сторон лежат на одной прямой;
Свойства равнобедренной трапеции
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Если нет возможности написать самому, закажите тут.
- в равнобедренной трапеции углы при обоих ее основаниях одинаковы;
- диагонали равны;
- равнобедренную трапецию всегда можно вписать в окружность или описать окружность вокруг;
- если диагонали перпендикулярны, то высота фигуры равна полусумме ее оснований.
Способы нахождений периметра
Рассмотрим способы, с помощью которых можно найти сумму длин всех сторон данного четырехугольника.
По всем сторонам
Формула для нахождения периметра выглядит так:
P=a+b+c+d
где a, b, c, d — стороны трапеции.
По сторонам равнобедренной трапеции
Если нам известны ребра этого четырехугольника с одинаковыми боковыми сторонами, то находить ее P можно по следующей формуле:
\(P=2\times a+b+c\)
или
\(P=2\times c+a+b\)
Через среднюю линию
Так как средняя линия трапеции равна полусумме ее оснований, то формулу P можно выразить так:
\(P=2\times l+AB+CD\)
где l — средняя линия фигуры.
Примеры решения задач
Давайте рассмотрим наглядные примеры решения задач на нахождение суммы длин всех ребер этой фигуры.
Задача 1
Дана трапеция с боковыми сторонами 4 см и 5 см, а ее основания равны 7 см и 10 см. Найти периметр данного многоугольника.
Решение:
Нам пригодится самая первая формула для расчета:
P=a+b+c+d.
Подставляем значения и получаем:
P=4+7+5+10=26\;см.
Ответ: 26 см.
Задача 2
Известно, что у трапеции две боковые стороны равны 7 см, а ее основания равны 5 см и 8 см. Нужно найти P четырехугольника.
Решение:
Так как трапеция равнобедренная, удобнее всего будет использовать формулу:
\(P=2\times a+b+c\)
Таким образом, получается:
\(P=2\times 7+5+8=27\) см.
Ответ: 27 см.
Задача 3
Средняя линия l трапеции равна 6 см, а боковые стороны 5 см и 9 см. Вычислить P фигуры.
Вычислить P фигуры.
Решение:
Считать будем по формуле
\(P=2\times l+a+c\)
\(P=2\times 6+5+9=26\) см.
Ответ: 26 см.
Насколько полезной была для вас статья?
Рейтинг: 3.50 (Голосов: 4)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Периметр трапеции — справочник для студентов и школьников
Формула периметра произвольной трапеции ABCD (рис. 1), в которой \(\ A B=a, B C=b, C D=C, A D=d \), имеет вид:
\(\ P_{A B C D}=a+b+c+d \)
В случае, если трапеция ABCD – равнобокая (рис. 2), то есть \(\ A B=C D=a, B C=b, A D=C \) формула для периметра трапеции примет вид:
\(\ P_{A B C D}=2 a+b+c \)
Примеры решения задач
ПРИМЕР 1
Найти периметр равнобокой трапеции ABCD, стороны которой соответственно равны AB=CD=2 см, BC=3 см и AD=5 см. {2}}=\sqrt{16+9}=\sqrt{25}=5(\mathrm{см})
\)
{2}}=\sqrt{16+9}=\sqrt{25}=5(\mathrm{см})
\)
Периметр данной прямоугольной трапеции найдем по формуле
\(\ P_{A B C D}=a+b+c+d \)
В данном случае она примет вид:
\(\ P_{A B C D}=A B+B C+C D+A D \)
Подставляя длинны сторон трапеции в последнее равенство, получим
\(\ P_{A B C D}=4+6+5+9=24(\mathrm{см }) \)
\(\ P_{A B C D}=24 \mathrm{см} \)
Физика
166
Реклама и PR
31
Педагогика
80
Психология
72
Социология
7
Астрономия
9
Биология
30
Культурология
86
Экология
8
Право и юриспруденция
36
Политология
13
Экономика
49
Финансы
9
История
16
Философия8
Информатика
20
Право
35
Информационные технологии
6
Экономическая теория
7
Менеджент
719
Математика
338
Химия
20
Микро- и макроэкономика
1
Медицина
5
Государственное и муниципальное управление
2
География
542
Информационная безопасность
2
Аудит
11
Безопасность жизнедеятельности
3
Архитектура и строительство
Банковское дело
1
Рынок ценных бумаг
6
Менеджмент организации
2
Маркетинг
238
Кредит
3
Инвестиции
2
Журналистика
1
Конфликтология
15
Этика
9
Формулы дифференцирования Периметр окружности Периметр круга Периметр треугольника Площадь эллипса
Узнать цену работы
Узнай цену
своей работы
Имя
Выбрать тип работыЧасть дипломаДипломнаяКурсоваяКонтрольнаяРешение задачРефератНаучно — исследовательскаяОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерскаяНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация в ВАКПубликация в ScopusДиплом MBAПовышение оригинальностиКопирайтингДругое Принимаю Политику конфиденциальностиПодпишись на рассылку, чтобы не пропустить информацию об акциях
Формула периметра трапеции.
 Трапеция. Формулы, признаки и свойства трапеции
Трапеция. Формулы, признаки и свойства трапецииСодержание
- Принятые в формулах обозначения
- Найти периметр трапеции
- Основные свойства равнобедренной трапеции
- Формулы длин сторон равнобедренной трапеции:
- Формулы длины средней линии равнобедренной трапеции:
- Формулы определения длины высоты равнобедренной трапеции:
- В исходных данных: все стороны
- Периметр произвольной трапеции
- Вписанная окружность
- Решение задач о прямоугольной трапеции
- Задача Даны три стороны, одна из которых перпендикулярная боковая.
- Задача Даны оба основания и угол при основании
- Свойства и признаки равнобедренной трапеции
- Формула определения радиуса вписанной в трапецию окружности
- Формулы определения длин отрезков проходящих через трапецию:
- Определение периметра прямоугольной трапеции
- Известны: диагонали и углы между ними
- Высота трапеции через стороны
- В задаче даны: боковые стороны и углы при нижнем основании
- Высота равнобедренной трапеции через среднюю линию и площадь
Принятые в формулах обозначения
Во всех приведенных ниже математических записях верны такие прочтения букв.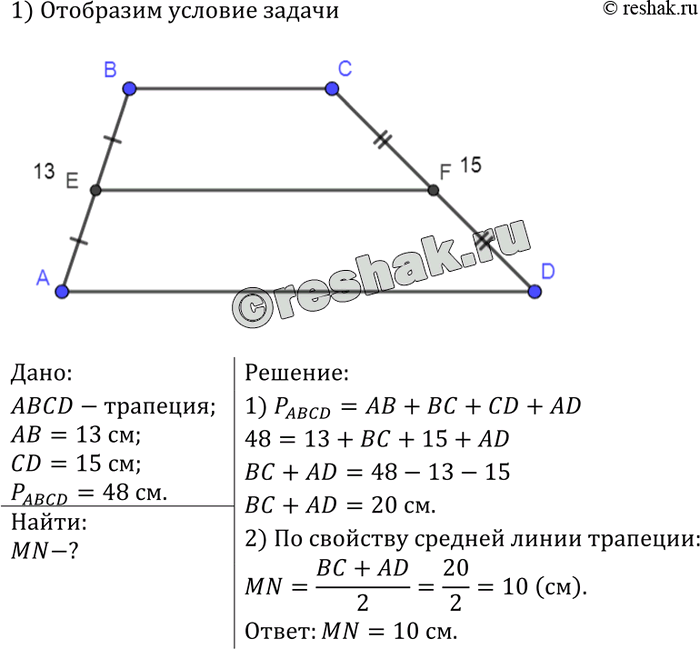
| произвольная трапеция | равнобедренная трапеция | название |
| а | а | нижнее основание |
| в | в | верхнее основание |
| с, d | с | боковые стороны |
| н | н | высота |
| m | m | средняя линия |
| d1, d2 | d1 | диагонали |
| s | s | площадь |
| α, β | α | углы при нижнем основании |
| γ, δ | γ, δ | углы на пересечении диагоналей |
Найти периметр трапеции
Введите данные:
| a = |
| b = |
| c = |
| d = |
Вводить можно числа или дроби (-2.4, 5/7, …).
Основные свойства равнобедренной трапеции
1. Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:
Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
2. Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:
AB = CD = m
3. Вокруг равнобедренной трапеции можно описать окружность
4. Если диагонали взаимно перпендикулярны, то высота равна полусумме оснований (средней лини):
h = m
5. Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты:
SABCD = h2
6. Если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции:
h2 = BC · AD
7. Сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции:
AC2 + BD2 = AB2 + CD2 + 2BC · AD
8.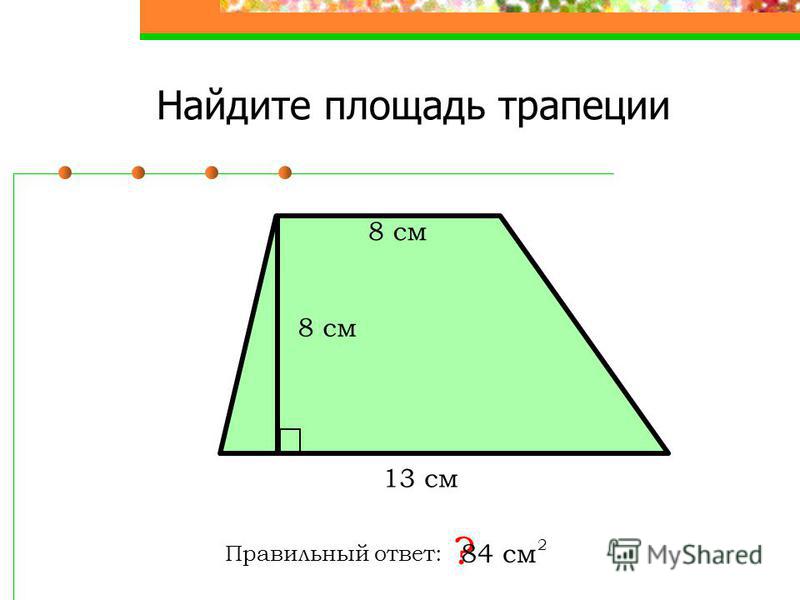 Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:
Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:
HF ┴ BC, HF ┴ AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) – равен полуразности оснований:
| AP = | BC + AD |
| 2 |
| PD = | AD – BC |
| 2 |
10. Также смотрите свойства трапеции
Формулы длин сторон равнобедренной трапеции:
1. Формулы длины сторон через другие стороны, высоту и угол:
a = b + 2h ctg α = b + 2c cos α
b = a – 2h ctg α = a – 2c cos α
| c = | h | = | a – b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d12 – c2 | b = | d12 – c2 | c = √d12 – ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | – b b = | 2S | – a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
| с = | S |
| m sin α |
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
| с = | 2S |
| (a + b) sin α |
Формулы длины средней линии равнобедренной трапеции:
1. Формула определения длины средней линии через основания, высоту и угол при основании:
m = a – h ctg α = b + h ctg α = a – √c2 – h2 = b + √c2 – h2
2. Формула средней линии трапеции через площадь и сторону:
| m = | S |
| c sin α |
Формулы определения длины высоты равнобедренной трапеции:
1.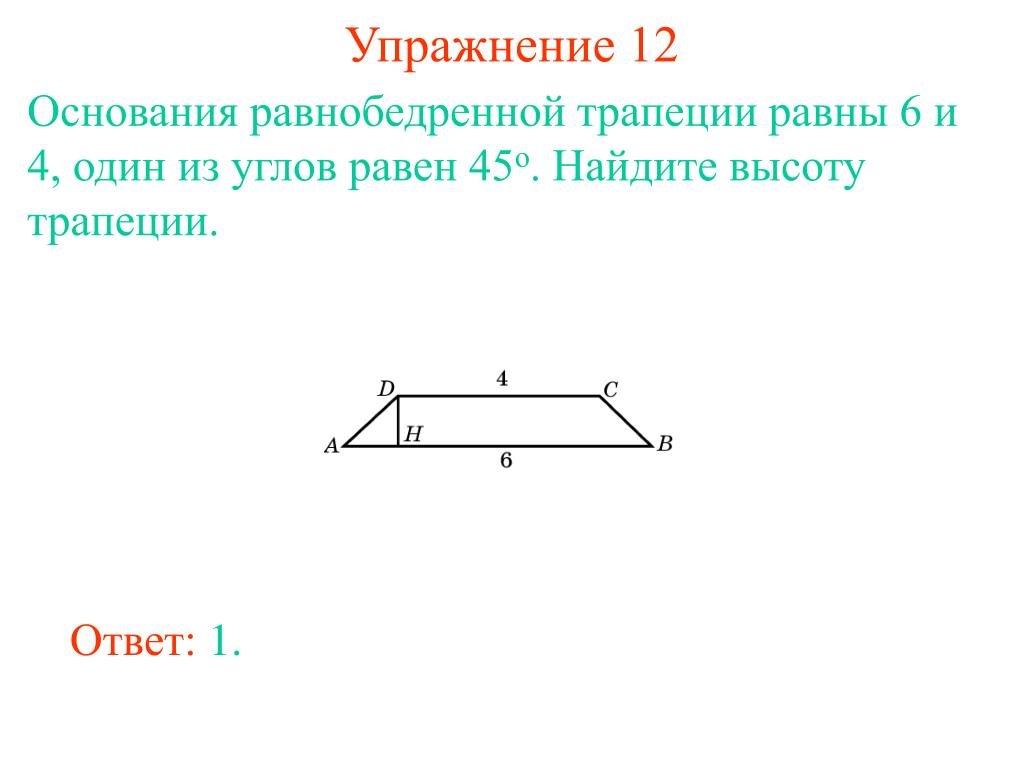 Формула высоты через стороны:
Формула высоты через стороны:
| h = | 1 | √4c2 – (a – b)2 |
| 2 |
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a – b | tg β | = c sin β |
| 2 |
В исходных данных: все стороны
Для того чтобы найти высоту трапеции в общем случае потребуется воспользоваться такой формулой:
н = √(с2 – (((а – в)2 + с2 – d2)/(2(а – в)))2). Номер 1.
Не самая короткая, но и встречается в задачах достаточно редко. Обычно можно воспользоваться другими данными.
Формула, которая подскажет, как найти высоту равнобедренной трапеции в той же ситуации, гораздо короче:
н = √(с2 – (а – в)2/4). Номер 2.
Периметр произвольной трапеции
Периметр произвольной трапеции, в которой AB=a, BC=b, CD=c, AD=d, имеет вид:
[ LARGE P_{ABCD} = a + b + c + d ]
где:
P – периметр трапеции
a, b, c, d – стороны трапеции
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и она делит боковую сторону точкой касания на два отрезка — и , то , то
Решение задач о прямоугольной трапеции
Прямоугольной называют трапецию, у которой углы при одной из боковых сторон равны 900.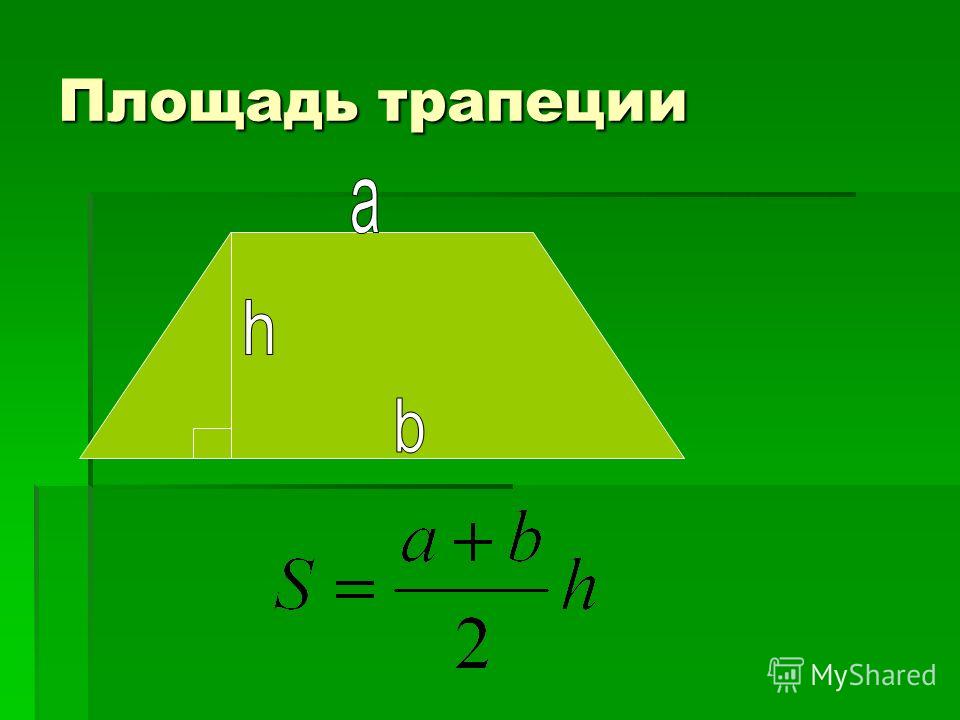 Рассмотрим пример, как найти боковую сторону трапеции, если известны три другие стороны.
Рассмотрим пример, как найти боковую сторону трапеции, если известны три другие стороны.
Задача Даны три стороны, одна из которых перпендикулярная боковая.
Допустим, нам дана прямоугольная трапеция АВСД, у которой АВ перпендикулярно ВС. Известно, что АВ = 12 см, ВС = 1 см, АД = 6 см. Необходимо найти большую боковую сторону.
Решение:
Из точки С опускаем проводим высоту СК и получаем прямоугольный треугольник СДК и прямоугольник АВСК. Поскольку у прямоугольника противоположные стороны равны СК = АВ = 12 см, а АК = ВС = 1 см.
Находим отрезок КД:
- КД = АД – АК = 6 – 1 = 5 (см)
Согласно теореме Пифагора:
- СД2=СК2+КД2=122+52=144+25=169
- СД = √169 = 13 (см)
Ответ: СД = 13 см
Задача Даны оба основания и угол при основании
Дана трапеция АВСД, у которой основания ВС и АД равны 6 и 10 см соответственно, угол ВАД – прямой, а СДА равен 45 градусов.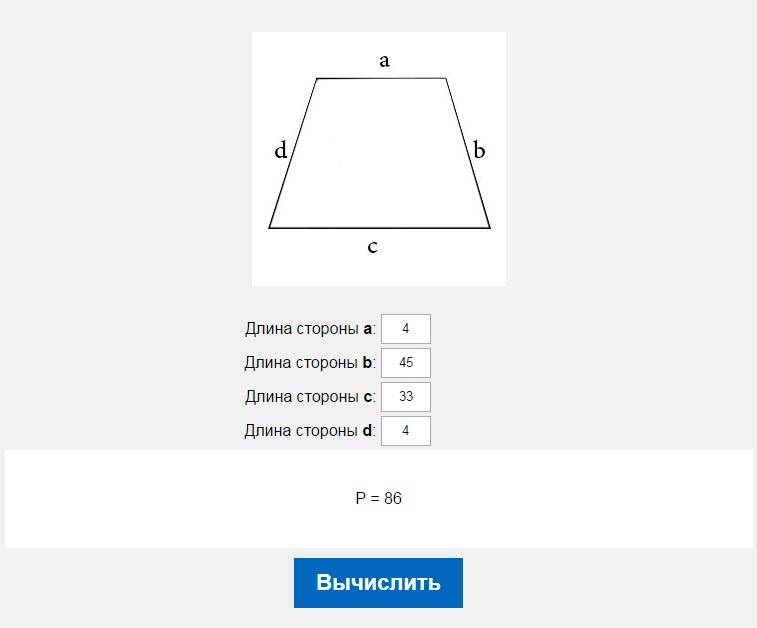 Найдите меньшую боковую сторону.
Найдите меньшую боковую сторону.
- Проводим высоту СК и получаем прямоугольный треугольник СКД и прямоугольник АВСК. Поскольку у прямоугольника противоположные стороны равны АК = ВС = 6 см.
- КД = АД – АК = 10 – 6 = 4 см
- cos 45 = √2/2 = КД / СД, отсюда СД = КД / cos 45
- Получаем СД = 4/√2/2 = 4√2 (см)
Ответ: СД = 4√2 см
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
| r = | h |
| 2 |
Формулы определения длин отрезков проходящих через трапецию:
1. Формула определения длин отрезков проходящих через трапецию:
Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Определение периметра прямоугольной трапеции
Периметр прямоугольной трапеции определяется по той же формуле, что и периметр равнобедренной, однако в этом случае формула имеет вид:
Периметр ABCD = АВ+ВС+СD+AD. Рассмотрим пример определения периметра прямоугольной трапеции. В данном примере сторона АВ = 5 см, ВС = 7см, AD = 10 см, длина стороны СD неизвестна.
- опустим высоту из вершины С, высота CH = AB = 5см;
- исходя из рисунка 3, AH = BC = 7 см;
- HD = AD – AH = 10 – 7 = 3 см;
- далее для нахождения периметра, необходимо определить длину стороны СD, являющейся в равнобедренном треугольнике СHD гипотенузой. Согласно теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, таким образом, длина стороны СD = 5,83 см: CD = = 5,83 см;
- подставляя полученные значения в формулу, получим периметр равный 27,83 см: Периметр ABCD = 5+7+5,83+10 = 27,83 см.

Итак, определить длину одной из сторон трапеции можно воспользовавшись теоремой Пифагора. Так же, для определения длины различных сторон трапеции могут помочь следующие формулы:
- формула расчета длины основания через среднюю линию;
- формулы длин сторон через высоту и угол при нижнем основании трапеции;
- формулы длин сторон трапеции через диагонали, высоту и угол между диагоналями;
- формулы длин сторон равнобедренной трапеции через площадь.
Как видно, для решения задач, связанных с расчетом длины сторон трапеции, существует более чем широкий спектр математических приемов, выбор которых обусловлен конкретной ситуацией.
Известны: диагонали и углы между ними
Обычно к этим данным присоединяются еще известные величины. Например, основания или средняя линия. Если даны основания, то для ответа на вопрос, как найти высоту трапеции, пригодится такая формула:
н = (d1* d2 * sin γ) / (а + в) или н = (d1* d2 * sin δ) / (а + в). 2} = sqrt{4 – (frac{4 + 4 — 8}{4}} = 2$ см.
2} = sqrt{4 – (frac{4 + 4 — 8}{4}} = 2$ см.
Проверим полученное значение с помощью онлайн-калькулятора. Результат совпадает, а значит, задача решена верно.
В задаче даны: боковые стороны и углы при нижнем основании
Принимают, что угол α прилежит к боковой стороне с обозначением «с», соответственно угол β к стороне d. Тогда формула для того, как найти высоту трапеции, в общем виде будет такой:
н = с * sin α= d * sin β. Номер 3.
Если фигура равнобедренная, то можно воспользоваться таким вариантом:
н = с * sin α= ((а – в) / 2) * tg α. Номер 4.
Высота равнобедренной трапеции через среднюю линию и площадь
Если известна площадь равнобедренной трапеции и длина её средней линии, то высоту можно рассчитать по формуле:
$h = frac{S}{m}$, где
$m$ — средняя линия трапеции;
$S$ — её площадь.
Рассмотрим на примере, как найти высоту равнобедренной трапеции, если известны основания.
Пример 2
Задача
Дана равнобедренная трапеция с основаниями $a$ и $d$, соответственно равными $3$ и $5$ см, и площадью, равной $8$ $см^2$. Найдите, чему равна высота трапеции.
Найдите, чему равна высота трапеции.
Решение:
Найдём среднюю линию трапеции:
$m = frac{a + d}{2} = frac{3 + 5}{2} = 4$ см.
Теперь сосчитаем высоту трапеции:
$h = frac{8}{4} = 2$ см.
Результаты совпадают с решением онлайн-калькулятора, а значит, ответ — верный.
Источники
- https://www.syl.ru/article/187872/mod_kak-nayti-vyisotu-trapetsii-formulyi-na-vse-sluchai-jizni
- https://ru.onlinemschool.com/math/assistance/figures_perimeter/trapezium/
- https://ru.onlinemschool.com/math/formula/trapezium_isosceles/
- https://calcsbox.com/post/formula-perimetra-trapecii.html
- https://egemaximum.ru/trapeciya-svojstva-trapecii/
- https://elhow.ru/ucheba/geometrija/planimetrija/kak-najti-bokovye-storony-trapecii
- https://ru.onlinemschool.com/math/formula/trapezium/
- http://kakumno.ru/najti-perimetr-trapecii.html
- https://spravochnick.ru/calculators/kak_nayti_vysotu_trapecii/
Задание 3.
 Периметр трапеции | Уроки математики и физики для школьников и родителей
Периметр трапеции | Уроки математики и физики для школьников и родителейЗадание 3. Периметр трапеции
Прежде чем приступить к решению примеров и задач, обязательно ознакомьтесь с теоретической частью урока
или
посмотритеВИДЕОУРОК
1. Средняя линия трапеции 24 см. Зная, что трапецию можно разрезать на ромб и равносторонний треугольник, вычислите её периметр.
а) 48 см;
б) 80 см;
в) 96 см;
г) 32 см.
2. Боковая сторона равнобедренной трапеции равна 6 см, средняя линия 10 см. Найдите периметр трапеции.
а) 32 см;
б) 36 см;
в) 30 см;
г) 34 см.
3. Найти периметр трапеции.
а) 135 см;
б) 130 см;
в) 138 см;
г) 132 см.
4. Найти периметр трапеции.
а) 22 м;
б) 18 м;
в) 20 м;
г) 24 м.
5. Найдите периметр трапеции ABCD,
AD = DС = 10 м,
ВС = 8 м,
угол С = 90°.
а) 29;
б) 32;
в) 35;
г) 34.
6. В равнобедренной трапеции основания равны 12 и 27, острый угол равен 60°. Найдите её периметр.
а) 71;
б) 66;
в) 64;
г) 69.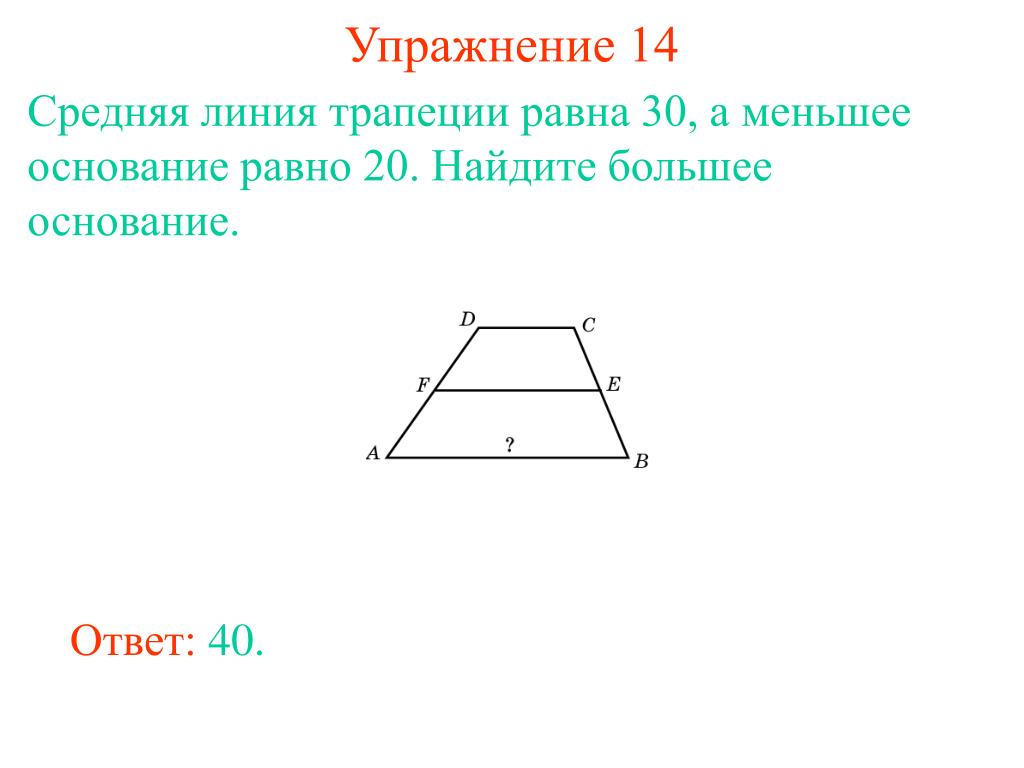
7. Вычислите периметр равнобедренной трапеции, если её меньшее основание равно 10 см, боковая сторона равна 8 см и угол между ними равен 135°.
а) 4(9 + 2√͞͞͞͞͞2) см;
б) 2(9 + 2√͞͞͞͞͞2) см;
в) 4(9 + √͞͞͞͞͞2) см;
г) (9 + 2√͞͞͞͞͞2) см.
8. Диагональ равнобедренной трапеции – биссектриса её острого угла и перпендикулярна боковой стороне. Найдите периметр трапеции, если её меньшее основание равно 6см.
а) 36 см;
б)
28 см;
в) 30 см;
г)
42 см.
9. Меньшая диагональ прямоугольной трапеции делит её тупой
угол пополам, а другую диагональ делит в отношении 5
: 2, считая от вершины острого
угла. Найдите периметр трапеции, если её меньшая боковая сторона равна 12 см.
Меньшая диагональ прямоугольной трапеции делит её тупой
угол пополам, а другую диагональ делит в отношении 5
: 2, считая от вершины острого
угла. Найдите периметр трапеции, если её меньшая боковая сторона равна 12 см.
а) 52 см;
б) 58 см;
в) 44 см;
г) 48 см.
10. Большая диагональ прямоугольной трапеции делит её острый угол пополам, а другую диагональ делит в отношении 5 : 8, считая от вершины тупого угла. Найдите периметр трапеции, если её меньшая боковая сторона равна 16 см.
а) 102 см;
б)
76 см;
в) 88 см;
г) 94 см.
11.
Диагональ равнобедренной трапеции делит пополам её тупой уго, а среднюю линию
трапеции на отрезки 4 см и 5 см.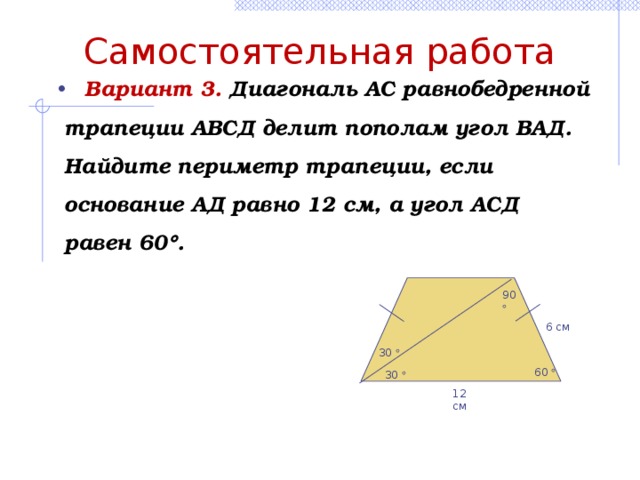 Найдите периметр трапеции.
Найдите периметр трапеции.
а) 38 см;
б) 36 см;
в) 42 см;
г) 34 см.
12. Периметр трапеции 72см, углы при большем основании по 60°. Диагональ делит среднюю линию на части, одна из которых на 8 см больше другой. Найдите длины оснований трапеций.
а) 10 см, 30 см;
б) 12 см, 28 см;
в) 13 см, 27 см;
г) 15 см, 25 см.
Следующее Предыдущее Главная страница
Подписаться на: Комментарии к сообщению (Atom)
Как найти сторону трапеции зная периметр. Как найти периметр трапеции
Инструкция
Если известны длины обоих оснований (a и b) и длина боковой стороны (c), то периметр (P) этой геометрической фигуры рассчитывается очень просто. Так как трапеция равнобедренна, то ее боковые стороны имеют одинаковую длину, а , что вам известны длины всех сторон — просто сложите их: P = a+b+2*c.
Так как трапеция равнобедренна, то ее боковые стороны имеют одинаковую длину, а , что вам известны длины всех сторон — просто сложите их: P = a+b+2*c.
Если длины обоих оснований неизвестны, но дана длина линии (l) и боковой стороны (c), то и этих данных достаточно для вычисления периметра (P). Средняя линия параллельна обоим основаниям и по длине равна их полусумме. Удвойте это и добавьте к нему тоже удвоенную длину боковой стороны — это и будет периметром равнобедренной трапеции: P = 2*l+2*c.
Если из условий задачи известны длины обоих оснований (a и b) и высота (h) равнобедренной трапеции, то с этих данных можно восстановить длину недостающей боковой стороны. Сделать это можно рассмотрев треугольник, в котором гипотенузой будет неизвестная сторона, а катетами — высота и короткий отрезок, который она отсекает от длинного основания трапеции. Длину этого отрезка можно вычислить, поделив пополам разность между длинами большего и меньшего оснований: (a-b)/2. Длина гипотенузы (боковой стороны трапеции), согласно теореме Пифагора, будет равна квадратному корню из суммы возведенных в длин обоих известных катетов. Замените в формуле из первого шага длину боковой стороны полученным выражением, и вы получите такую формулу периметра: P = a+b+2*√(h²+(a-b)²/4).
Замените в формуле из первого шага длину боковой стороны полученным выражением, и вы получите такую формулу периметра: P = a+b+2*√(h²+(a-b)²/4).
Если в задачи даны длины меньшего основания (b) и боковой стороны (c), а также высота равнобедренной трапеции (h), то рассматривая тот же вспомогательный треугольник, что и в предыдущем шаге, вам придется вычислять длину катета. Вновь воспользуйтесь теоремой Пифагора — искомая величина будет равна корню из разности между возведенной в квадрат длиной боковой стороны (гипотенузы) и высотой (): √(c²-h²). По этому неизвестного основания трапеции можно восстановить его длину — удвойте это выражение и добавьте к результату длину короткого основания: b+2*√(c²-h²). Подставьте это выражение в формулу из первого шага и найдите периметр равнобедренной трапеции: P = b+2*√(c²-h²)+b+2*c = 2*(√(c²-h²)+b+c).
Источники:
- периметр трапеции
Трапеция представляет собой четырехугольник с двумя параллельными сторонами. Эти стороны называются основаниями. Их конечные точки соединены отрезками, которые называются боковыми сторонами. У равнобедренной трапеции боковые стороны равны.
Их конечные точки соединены отрезками, которые называются боковыми сторонами. У равнобедренной трапеции боковые стороны равны.
Вам понадобится
- — равнобедренная трапеция;
- — длины оснований трапеции;
- — высота трапеции;
- — лист бумаги;
- — карандаш;
- — линейка.
Инструкция
Постройте согласно условиям задачи. Вам должны быть даны несколько параметров. Как , это оба и высота. Но возможны и другие условия — одно из оснований, его наклона к нему боковой стороны и высота. Обозначьте трапецию как АBCD, основания пусть будут a и b, высоту обозначьте как h, а боковые стороны — х. Поскольку трапеция равнобедренная, боковые стороны у нее равны.
Из вершин B и С проведите высоты к нижнему основанию. Точки обозначьте как M и N. К вас получилось два прямоугольных треугольника — AМВ и СND. Они равны, поскольку по условиям задачи равны их гипотенузы АВ и CD, а также катеты ВМ и СN. Соответственно, отрезки АМ и DN также равны между собой.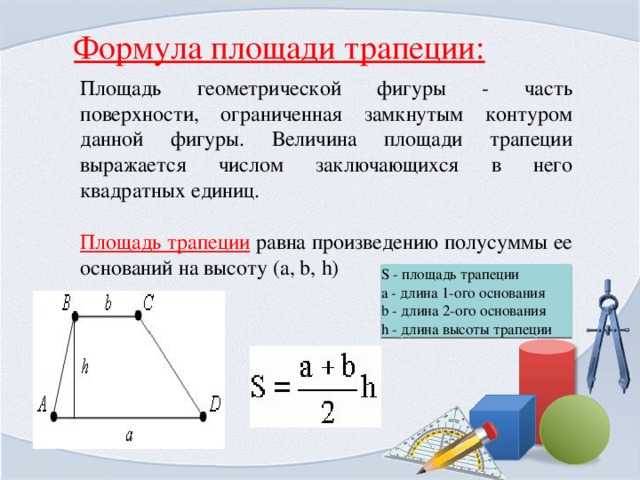 Обозначьте их длину как y.
Обозначьте их длину как y.
Для того, чтобы найти длину суммы этих отрезков, необходимо из длины основания a вычесть длину основания b. 2у=a-b. Соответственно, один такой отрезок будет оснований, деленной на 2. y=(a-b)/2.
Найдите длину боковой стороны трапеции, которая одновременно является и гипотенузой треугольника с известными вам катетами. Вычислите ее по теореме Пифагора. Она будет квадратному корню из суммы квадратов высоты и разности оснований, деленной на 2. То есть x=√y2+h3=√(a-b)2/4+h3.
Зная высоту и угол наклона боковой стороны к основанию, сделайте те же самые построения. Разность оснований в этом случае вычислять не нужно. Воспользуйтесь теоремой синусов. Гипотенуза равна длине катета, умноженной на синус противолежащего ему угла. В данном случае x=h*sinCDN или x=h*sinBAM.
Если вам дан угол наклона боковой стороны трапеции не к нижнему, а к верхнему основанию, найдите нужный угол, исходя из параллельных прямых. Вспомните одно из свойств трапеции, согласно которому углы между одним из оснований и боковыми сторонами равны.
Обратите внимание
Повторите свойства равнобедренной трапеции. Если разделить оба ее основания пополам и повести через эти точки линию, то она будет осью этой геометрической фигуры.
Если опустить высоту из одной вершины верхнего основания на нижнее, то на этом последнем получатся два отрезка. Например, в данном случае это отрезки АМ и DМ. Один из них равен полусумме оснований а и b, а другой — половине их разности.
Источники:
- в равнобедренной трапеции основания найти боковые стороны
Трапецией считают четырехугольник, имеющий лишь две параллельные стороны — они называются основаниями этой фигуры. Если при этом длины двух других — боковых — сторон одинаковы, трапеция называется равнобедренной или равнобокой. Линия, которая соединяет середины боковых сторон, называется средней линией трапеции и может быть рассчитана несколькими способами.
Инструкция
Если известны длины обоих оснований (А и В), для вычисления длины (L) используйте свойство этого элемента трапеции — она равна полусумме длин оснований: L = ½*(А+В). Например, с , имеющими длины 10см и 20см, средняя линия должна быть равна ½*(10+20) = 15см.
Например, с , имеющими длины 10см и 20см, средняя линия должна быть равна ½*(10+20) = 15см.
Средняя линия (L) вместе с высотой (h) равнобокой трапеции является сомножителем в формуле вычисления площади (S) этой фигуры. Если эти два параметра даны в исходных задачи, для вычисления длины средней линии делите площадь на высоту: L = S/h. Например, при площади в 75 см² равнобедренная трапеция высотой в 15см должна иметь среднюю длиной в 75/15 = 5см.
При известных периметре (Р) и длине боковой стороны (С) равнобедренной трапеции рассчитать среднюю линию (L) фигуры тоже несложно. Отнимите от периметра две длины боковых сторон, а оставшаяся величина будет суммой длин оснований — поделите ее пополам, и задача будет решена: L = (P-2*С)/2. Например, при периметре, равном 150см, и боковой длиной в 25см длина средней линии должна (150-2*25)/2 = 50см.
Зная длины периметра (P) и высоты (h), а также величину одного из острых углов (α) равнобедренной трапеции, тоже можно вычислить длину ее средней линии (L).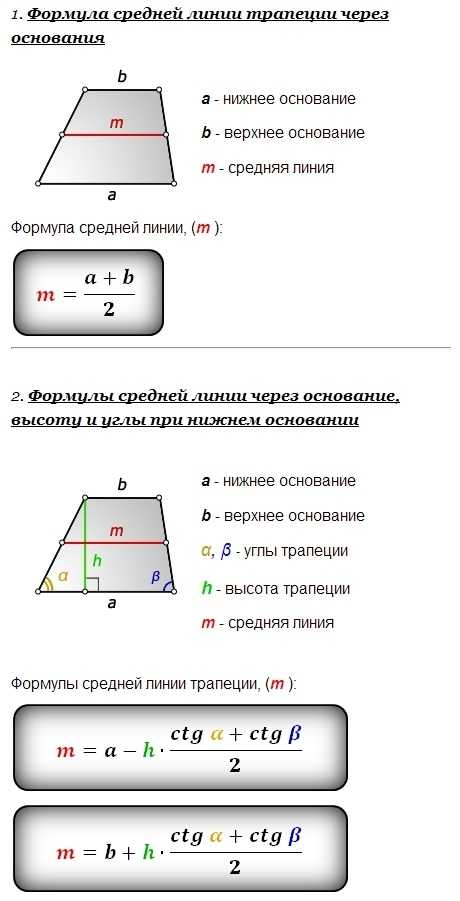 В треугольнике, составленном высотой, боковой стороной и частью основания, один из углов является прямым, а величина другого известна. Это позволит вычислить длину боковой стороны по теореме синусов — разделите высоту на синус известного угла: h/sin(α). Затем подставьте это выражение в формулу из предыдущего шага и вы получите равенство: L = (P-2*h/sin(α))/2 = P/2-h/sin(α). Например, если известный угол имеет величину в 30°, высота равна 10см, а периметр составляет 150см, длина средней линии должна быть рассчитана так: 150/2-10/sin(30°) = 75-20 = 55см.
В треугольнике, составленном высотой, боковой стороной и частью основания, один из углов является прямым, а величина другого известна. Это позволит вычислить длину боковой стороны по теореме синусов — разделите высоту на синус известного угла: h/sin(α). Затем подставьте это выражение в формулу из предыдущего шага и вы получите равенство: L = (P-2*h/sin(α))/2 = P/2-h/sin(α). Например, если известный угол имеет величину в 30°, высота равна 10см, а периметр составляет 150см, длина средней линии должна быть рассчитана так: 150/2-10/sin(30°) = 75-20 = 55см.
Периметр — это сумма всех сторон многоугольника. В правильных многоугольниках строго определенная зависимость между сторонами позволяет упростить нахождение периметра.
Инструкция
В произвольной фигуре, ограниченной разными отрезками ломаной линии, периметр определяется последовательным измерением сторон и суммированием результатов измерения. Для правильных многоугольников возможно вычислением по формулам, учитывающим связи между сторонами фигуры.
В произвольном треугольнике со сторонами а, b, с периметр Р вычисляется по формуле: Р=а+b+с. У равнобедренного треугольника две стороны равны между собой: а=b, и нахождения периметра упрощается до Р=2*а+с.
Если в равнобедренном треугольнике по условию даны размеры не всех сторон, то для нахождения периметра можно использовать другие известные параметры, например площадь треугольника, его углы, высоты, биссектрисы и медианы. Например, если известны только две равные стороны равнобедренного треугольника и любой из его углов, то третью сторону найдите по теореме синусов, из которой следует, что отношение стороны треугольника к синусу противолежащего угла есть величина постоянная для данного треугольника. Тогда неизвестная сторона может быть выражена через известную: a=b*SinА/SinВ, где А — угол против неизвестной стороны а, В — угол против известной стороны b.
Если известна площадь S равнобедренного треугольника и его основание b, то из формулы для определения площади треугольника S=b*h/2 найдите высоту h: h=2*S/b. Эта высота, опущенная на основание b, делит заданный равнобедренный треугольник на два равных прямоугольных треугольника. Боковые стороны a исходного равнобедренного гипотенузами прямоугольных треугольников. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов b и h. Тогда периметр P равнобедренного треугольника вычисляется по формуле:
Эта высота, опущенная на основание b, делит заданный равнобедренный треугольник на два равных прямоугольных треугольника. Боковые стороны a исходного равнобедренного гипотенузами прямоугольных треугольников. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов b и h. Тогда периметр P равнобедренного треугольника вычисляется по формуле:
P=b+2*√(b²/4) +4*S²/b²).
Трапецией называют четырехугольник, основания которого лежат на двух параллельных прямых, при этом две другие стороны параллельными не являются. Нахождение основания равнобедренной трапеции требуется как при сдаче теории и решении задач в учебных заведениях, так и в ряде профессий (инженерных, архитектурных, дизайнерских).
Инструкция
У равнобедренной (или равнобокой) трапеции непараллельные стороны как и углы, которые образуются при пересечении нижнего основания, равны.
Трапеция имеет два основания, и чтобы их найти, нужно сначала обозначить фигуру. Пусть дана равнобедренная ABCD с основаниями AD и BC.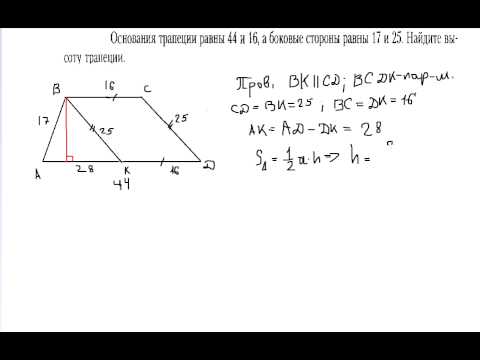 При этом известны все параметры, кроме оснований. Боковая сторона AB=CD=a, высота BH=h и площадь равна S.
При этом известны все параметры, кроме оснований. Боковая сторона AB=CD=a, высота BH=h и площадь равна S.
Для решения задачи об основании трапеции проще всего будет составить систему уравнений, чтобы через взаимосвязанные величины найти нужные основания.
Обозначьте отрезок BC за x, а AD за y, чтобы в дальнейшем было удобно обращаться с формулами и понимать их. Если не сделать этого сразу, можно запутаться.
Выпишите , которые пригодятся при решении поставленной задачи, используя известные данные. Формула площади равнобедренной трапеции: S=((AD+BC)*h)/2. Теорема Пифагора: a*a = h*h +AH*AH .
Вспомните свойство равнобедренной трапеции: высоты, выходящие из вершины трапеции, отсекают равные отрезки на большом основании. Отсюда следует, что два основания можно связать по формуле, вытекающей из этого свойства: AD=BC+2AH или y=x+2AH
Трапеция – четырехугольная геометрическая фигура, имеющая две параллельные стороны, которые называются основаниями, и две непараллельные боковые стороны.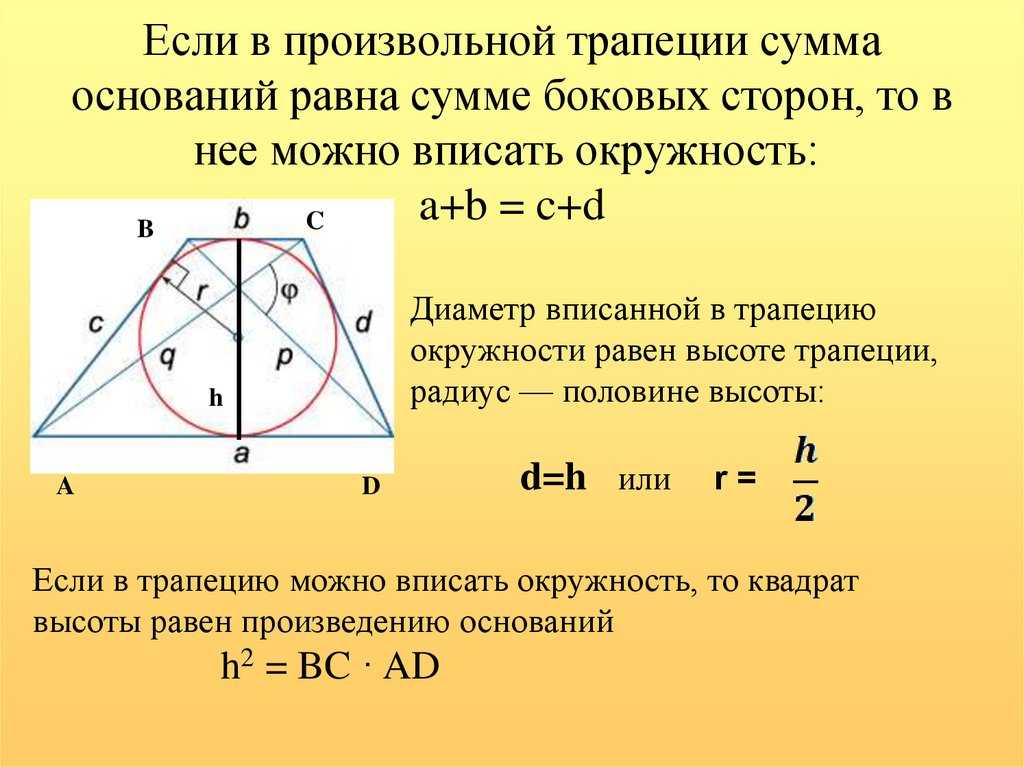 Если боковые стороны равны, то фигура называется равнобедренной трапецией. Прямоугольная трапеция – когда одна боковая сторона образует с основанием прямой угол. Для нахождения периметра трапеции можно воспользоваться одним из методов, в зависимости от исходных данных.
Если боковые стороны равны, то фигура называется равнобедренной трапецией. Прямоугольная трапеция – когда одна боковая сторона образует с основанием прямой угол. Для нахождения периметра трапеции можно воспользоваться одним из методов, в зависимости от исходных данных.
Как найти периметр трапеции, когда известна длина боковых сторон и оснований
В этом случае никаких затруднений нет. Воспользовавшись формулой P=a+b+c+d и подставив все известные данные, легко найдем периметр трапеции. Например: a=5, b=4, c=6, d=4. Используя формулу, получаем P=5+4+6+4=19
Данный метод нельзя использовать, если не известна длина хотя бы одной из сторон.
Как найти периметр трапеции, когда известна длина боковых сторон, верхнего основания и высоты
Разбиваем трапецию на два треугольника и прямоугольник.
Для того чтобы можно было воспользоваться формулой P=a+b+c+d, необходимо найти нижнее основание. Его можно представить как выражение k+a+n.
Далее воспользуемся теоремой Пифагора.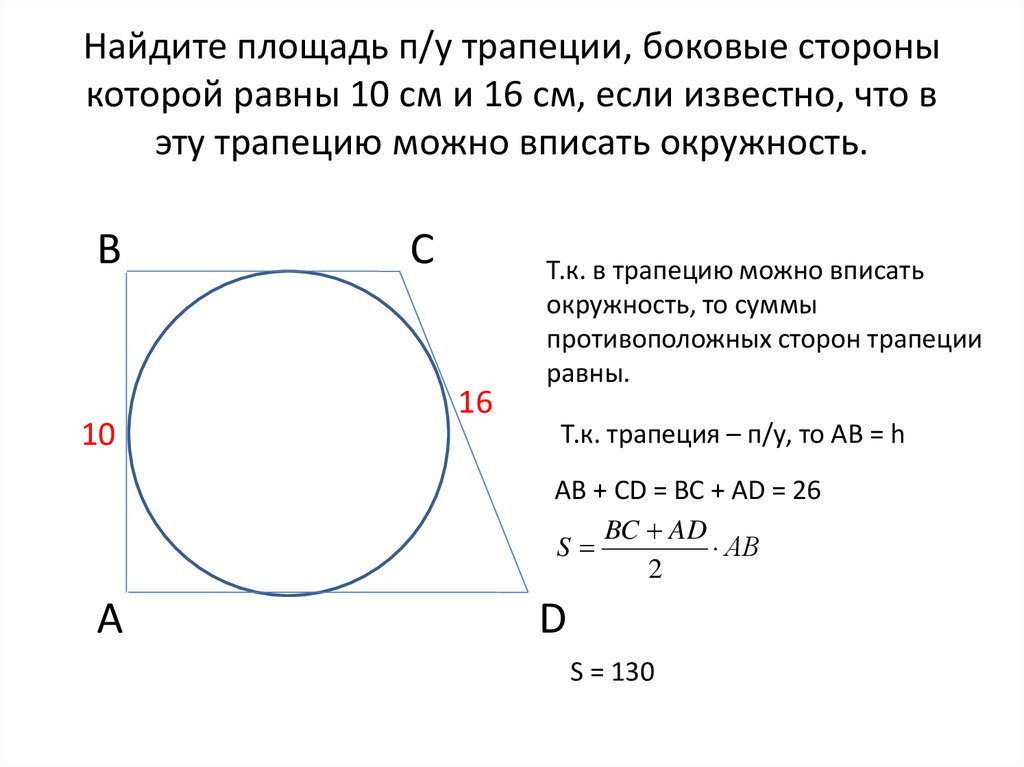 1/2. Далее по формуле P=a+2c+d высчитываем периметр.
1/2. Далее по формуле P=a+2c+d высчитываем периметр.
Как найти периметр трапеции, когда известны нижнее основание, боковые стороны и нижние углы
Рассмотрим пример, когда известны нижнее основание AD, боковые стороны AB и CD, а так же углы BAD и CDA.
Из вершин B и C проводим две высоты, которые образуют прямоугольник и два прямоугольных треугольника. В треугольнике ABK сторона AB является гипотенузой. Осталось найти катеты по формуле BK=AB*sin(BAK) и AK=AB*cos(BAK). Так как BK и CN – высоты, то они равны. По такой же формуле находим ND=CD*cos(CDN). Осталось вычислить BC=AD-AK-ND. Теперь необходимо сложить все стороны и ответ готов.
Как найти периметр трапеции, когда известна длина боковых сторон и средней линии
Средняя линия трапеции равна половине суммы длин ее оснований, т.е. f=(a+d)/2. Когда длина оснований неизвестна, но даны размеры боковых сторон и средней линии, периметр находится по формуле P=2*f+c+b.
Как видно, найти периметр трапеции не так уж и сложно.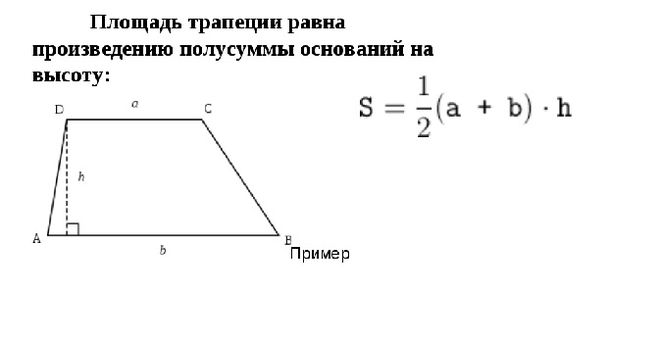 Приступая к решению задачи, нужно лишь определить, какие величины известны и каким методом можно воспользоваться. И тогда решить даже сложную задачу не составит труда.
Приступая к решению задачи, нужно лишь определить, какие величины известны и каким методом можно воспользоваться. И тогда решить даже сложную задачу не составит труда.
Трапеция — это такой четырехугольник, у которого 2 параллельных основания, а остальные стороны не параллельны друг другу. У прямоугольной трапеции один угол прямой, как вы уже наверняка догадались.
Шаг 1. Формула вычисления периметра прямоугольной трапеции
Периметр прямоугольной трапеции вычисляется с помощью суммирования длин всех сторон, что весьма логично. Тут она от остальных фигур ну ничем не отличается:
Шаг 2. Решение задач на тему определения периметра прямоугольной трапеции
Задача №1
Нужно найти периметр прямоугольной трапеции, когда даны длины всех сторон. Тут всё просто. Складываем все 4 значения , и готово. Это самый лёгкий вариант нахождения периметра. Остальные задачи в итоге всё равно сводятся к нему, но нужно рассмотреть и остальные варианты, интересно же!
Задача №2
Нужно найти периметр всё той же прямоугольной трапеции, но в этом случае мы знаем длину нижнего основания AD , которая равна a . Одна из боковых сторон CD , которая не перпендикулярна ему, равна d . Угол между этим основанием и стороной равен Альфа .
Одна из боковых сторон CD , которая не перпендикулярна ему, равна d . Угол между этим основанием и стороной равен Альфа .
Решение задачи №2
Катеты находятся по таким формулам: CE = CD*sin(ADC) , в свою очередь ED = CD*cos(ADC) . Верхнее основание вычисляется так: BC = AD — ED = a — CD*cos(ADC) = a — d*cos(Альфа) . Длина перпендикулярной стороны считается по формуле: AB = CE = d*sin(Альфа) . После этих действий вы будете обладать драгоценными знаниями о длине всех сторон трапеции.
Задача №3
Требуется найти периметр трапеции, когда даны длины его оснований. AD = a , BC=c . Также мы знаем длину перпендикулярной стороны AB , которая равна b . Острый угол при неперпендикулярной стороне равен Альфа .
Решение задачи №3
Для начала проведите высоту трапеции на большее основание, начало которой будет лежать в вершине С . После этого восхитительного действия мы получаем отрезок CE и делим трапецию на 2 фигуры: прямоугольник ABCE , а также треугольник ECD (прямоугольный). Гипотенузой треугольника в нашем случае будет известная нам сторона CD , один из катетов будет равен перпендикулярной боковой стороне нашей трапеции (опираемся на правило прямоугольника, по которому параллельные стороны равны). Длина другого отрезка будет равна разности оснований трапеции. И опять вроде всё просто.
Гипотенузой треугольника в нашем случае будет известная нам сторона CD , один из катетов будет равен перпендикулярной боковой стороне нашей трапеции (опираемся на правило прямоугольника, по которому параллельные стороны равны). Длина другого отрезка будет равна разности оснований трапеции. И опять вроде всё просто.
Для начала снова проводим перпендикуляр CE и так же получаем прямоугольник ABCE вместе с треугольником CED . Осталось найти длину гипотенузы того треугольника, который мы получили, мы с уверенностью можем сказать, что CD = AB/sin(ADC) = b/sin(Альфа) . Мы снова нашли все длины сторон. Осталось только их сложить. Надеемся, вы сможете сделать это без нас.
Каких только задачек нам не приходится решать, фантазия составителей учебников по математике поистине неистощима. Например, как найти периметр трапеции? Для начала разберемся, что же такое трапеция. Не стоит бояться этой фигуры. Это всего-навсего прямоугольник, у которого две стороны всегда параллельны друг другу и называются основаниями, а остальные называются боковыми, и они могут быть разными. Если боковые стороны трапеции равны, то она называется равнобедренной. Также есть понятие прямоугольной трапеции, у которой одна из боковых сторон соединена с основанием трапеции под прямым углом.
Если боковые стороны трапеции равны, то она называется равнобедренной. Также есть понятие прямоугольной трапеции, у которой одна из боковых сторон соединена с основанием трапеции под прямым углом.
Как находить периметр трапеции
Что такое периметр? Периметр — это сумма длин всех сторон прямоугольника, к коим трапеция также имеет непосредственное отношение. Все остальные задачи, где неизвестны некоторые величины, сводятся также к суммированию сторон после того, как все неизвестные будут найдены.
А, если все стороны равны? Если вам дана для решения задача, где даны все сторону трапеции a b c d, то их просто нужно сложить все вместе, полученный результат и будет периметром. Периметр прямоугольной трапеции. Предположим, что нам дана прямоугольная трапеция, где известно нижнее основание AD=a, неперпендикулярная сторона CD=d, а также угол Альфа.
Как решать? Проводим из вершины С высоту, которая сразу разделяет нашу трапецию на прямоугольник ABCE и треугольник ECD. Этот треугольник у нас прямой, мы знаем его гипотенузу CD, которая равна d. Теперь находим катеты треугольника по формуле CE = CD*sin(ADC) и ED = CD*cos(ADC). Теперь мы знаем практически все. ВС = АD-ЕD, а сторона АВ соответственно равна найденному ранее катету СЕ. Теперь осталось только сложить все найденные стороны, и ответ готов.
Теперь находим катеты треугольника по формуле CE = CD*sin(ADC) и ED = CD*cos(ADC). Теперь мы знаем практически все. ВС = АD-ЕD, а сторона АВ соответственно равна найденному ранее катету СЕ. Теперь осталось только сложить все найденные стороны, и ответ готов.
Периметр равнобедренной трапеции
- Известны боковые стороны и средняя линия. Как найти периметр равнобедренной трапеции, если вам известны лишь боковые равные стороны AB и CD и средняя линия EF? Средняя линия трапеции, как известно, параллельна основаниям, и к тому же равна полусумме этих оснований. И чтобы найти длину оснований, нам нужно лишь удвоить длину средней линии. Исходя из этих данных решение таково: Р=2EF+2AB
- Известны основания и высота. В задаче могут быть известны только длины оснований и высота трапеции. Высота образует прямоугольный треугольник, причем их получается два равных. Нижний катет находится очень просто: (АD-ВС)/2. Теперь нам известны оба катета, остается лишь найти гипотенузу, применив теорему Пифагора.
 Гипотенуза у нас равна корню из суммы квадратов катетов.
Гипотенуза у нас равна корню из суммы квадратов катетов. - Итак, мы нашли боковую сторону трапеции, их у нас две и они равны, основания нам известны изначально, поэтому нам теперь остается все только сложить, и мы получим искомый периметр. Таким образом, находить периметр трапеции совершенно несложно. Главное и первостепенное в этом деле, знать ее свойства, и тогда у вас никогда не будет проблем с решением задач по трапециям. Поэтому, прежде чем приниматься за вычисления, не помешает немного теории.
Найдите периметр трапеции. Здравствуйте! В этой публикации мы с вами рассмотрим решение типовых задачек входящих в состав экзамена по математике. Требуется вычислить периметр трапеции. Можно сказать, что это задания для устных вычислений, они просты. Перед решением рекомендую посмотреть статью « » . Рассмотрим задачи:
27834. В равнобедренной трапеции основания равны 12 и 27, острый угол равен 60 0 . Найдите ее периметр.
Для того, чтобы найти периметр нам необходимо вычислить боковую сторону. Из вершин меньшего основания опустим высоты:
Из вершин меньшего основания опустим высоты:
AD является гипотенузой в прямоугольном треугольнике ADF. Её мы можем вычислить воспользовавшись определением косинуса:
AF мы можем вычислить:
Следовательно:
Таким образом периметр равен 12+27+15+15=69.
*При решении задачи также можно было воспользоваться свойством катета лежащего против угла 30°. Посмотрите:
∠ADF равен 30°, катет AF равен половине гипотенузы AD. AF=7,5 следовательно AD будет равно 15.
27835. Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.
Ход решения очевиден! Давайте посмотрим на эскиз: AD и AE это часть периметра, DE=CB – противолежащие стороны параллелограмма. То есть
Остаётся прибавить DC и EB. В условии сказано, что DC=4. Так DC и EB являются противолежащими сторонами параллелограмма, то они равны:
Таким образом периметр равен 15+4+4=23.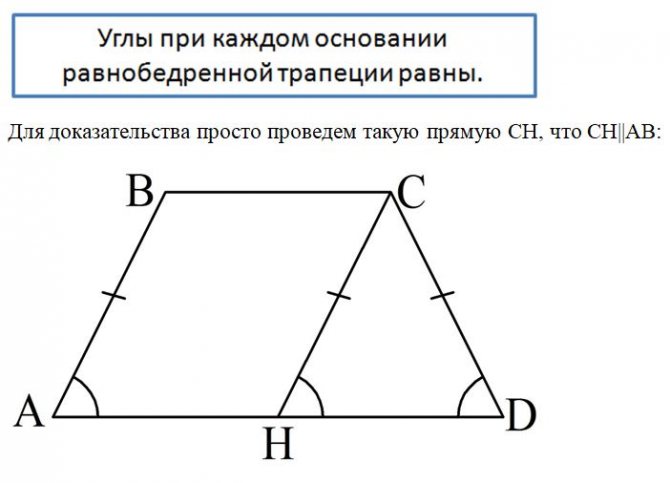
На этом всё, успеха вам!
С уважением, Александр Крутицких.
Как найти периметр прямоугольной трапеции
Как найти периметр прямоугольной трапеции
Трапеция – это такой четырехугольник, у которого 2 параллельных основания, а остальные стороны не параллельны друг другу. У прямоугольной трапеции один угол прямой, как вы уже наверняка догадались.
Шаг 1. Формула вычисления периметра прямоугольной трапеции
Периметр прямоугольной трапеции вычисляется с помощью суммирования длин всех сторон, что весьма логично. Тут она от остальных фигур ну ничем не отличается:
Шаг 2. Решение задач на тему определения периметра прямоугольной трапеции
Задача №1
Нужно найти периметр прямоугольной трапеции, когда даны длины всех сторон. Тут всё просто. Складываем все 4 значения, и готово. Это самый лёгкий вариант нахождения периметра. Остальные задачи в итоге всё равно сводятся к нему, но нужно рассмотреть и остальные варианты, интересно же!
Задача №2
Нужно найти периметр всё той же прямоугольной трапеции, но в этом случае мы знаем длину нижнего основания AD, которая равна a. Одна из боковых сторон CD, которая не перпендикулярна ему, равна d. Угол между этим основанием и стороной равен Альфа.
Одна из боковых сторон CD, которая не перпендикулярна ему, равна d. Угол между этим основанием и стороной равен Альфа.
Решение задачи №2
Катеты находятся по таким формулам: CE = CD*sin(ADC), в свою очередь ED = CD*cos(ADC). Верхнее основание вычисляется так: BC = AD — ED = a — CD*cos(ADC) = a — d*cos(Альфа). Длина перпендикулярной стороны считается по формуле: AB = CE = d*sin(Альфа). После этих действий вы будете обладать драгоценными знаниями о длине всех сторон трапеции.
Задача №3
Требуется найти периметр трапеции, когда даны длины его оснований. AD = a, BC=c. Также мы знаем длину перпендикулярной стороны AB, которая равна b. Острый угол при неперпендикулярной стороне равен Альфа.
Решение задачи №3
Для начала проведите высоту трапеции на большее основание, начало которой будет лежать в вершине С. После этого восхитительного действия мы получаем отрезок CE и делим трапецию на 2 фигуры: прямоугольник ABCE, а также треугольник ECD (прямоугольный). Гипотенузой треугольника в нашем случае будет известная нам сторона CD, один из катетов будет равен перпендикулярной боковой стороне нашей трапеции (опираемся на правило прямоугольника, по которому параллельные стороны равны). Длина другого отрезка будет равна разности оснований трапеции. И опять вроде всё просто.
После этого восхитительного действия мы получаем отрезок CE и делим трапецию на 2 фигуры: прямоугольник ABCE, а также треугольник ECD (прямоугольный). Гипотенузой треугольника в нашем случае будет известная нам сторона CD, один из катетов будет равен перпендикулярной боковой стороне нашей трапеции (опираемся на правило прямоугольника, по которому параллельные стороны равны). Длина другого отрезка будет равна разности оснований трапеции. И опять вроде всё просто.
Для начала снова проводим перпендикуляр CE и так же получаем прямоугольник ABCE вместе с треугольником CED. Осталось найти длину гипотенузы того треугольника, который мы получили, мы с уверенностью можем сказать, что CD = AB/sin(ADC) = b/sin(Альфа). Мы снова нашли все длины сторон. Осталось только их сложить. Надеемся, вы сможете сделать это без нас.
Надеемся, вы сможете сделать это без нас.
Периметр трапеции
Формула периметра произвольной трапеции (рис. 1), в которой , имеет вид:
В случае, если трапеция – равнобокая (рис. 2), то есть , формула для периметра трапеции примет вид:
Примеры решения задач
| Задание | Найти периметр равнобокой трапеции , стороны которой соответственно равны см, см и см. |
| Решение | Обозначим см, см и см. Для нахождения периметра заданной равнобокой трапеции воспользуемся формулой: |
Подставляя в неё исходные данные, получим
(см)
| Задание | Найти периметр прямоугольной трапеции, если её основания равны соответственно 9 дм и 6 дм, а меньшая боковая сторона равна 4 дм. |
| Решение | Сделаем рисунок (рис. 3). |
Обозначим . Опустим высоту из вершины :
Так как , то , то есть
Далее рассмотрим треугольник , он прямоугольный, – гипотенуза.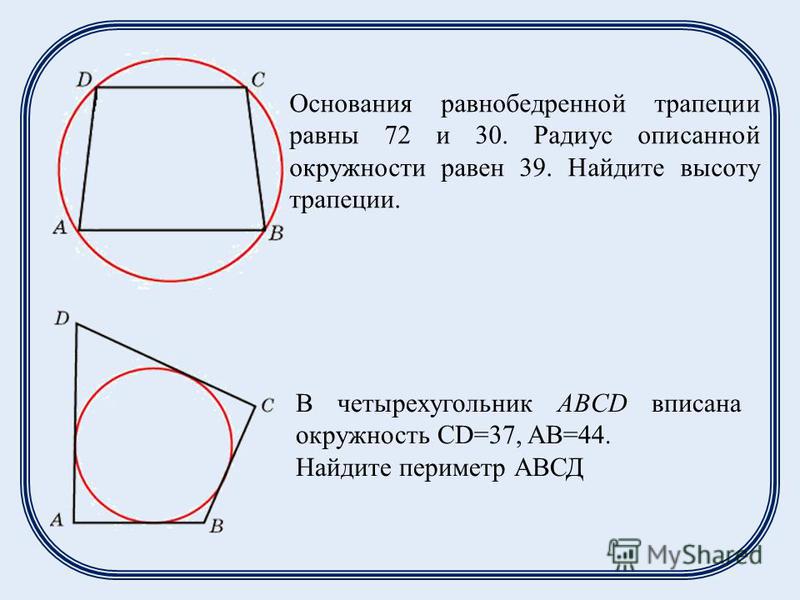 Найдем ее по теореме Пифагора:
Найдем ее по теореме Пифагора:
Подставляя в последнее равенство известные значения катетов, получим
(см)
Периметр данной прямоугольной трапеции найдем по формуле
В данном случае она примет вид:
Подставляя длинны сторон трапеции в последнее равенство, получим
(см)
Как найти периметр трапеции: равнобедренной, разносторонней, прямоугольной
Во всех приведенных ниже математических записях верны такие прочтения букв.
| произвольная трапеция | равнобедренная трапеция | название |
| а | а | нижнее основание |
| в | в | верхнее основание |
| с, d | с | боковые стороны |
| н | н | высота |
| m | m | средняя линия |
| d1, d2 | d1 | диагонали |
| s | s | площадь |
| α, β | α | углы при нижнем основании |
| γ, δ | γ, δ | углы на пересечении диагоналей |
Найти периметр трапеции
Введите данные:
| a = |
| b = |
| c = |
| d = |
Вводить можно числа или дроби (-2.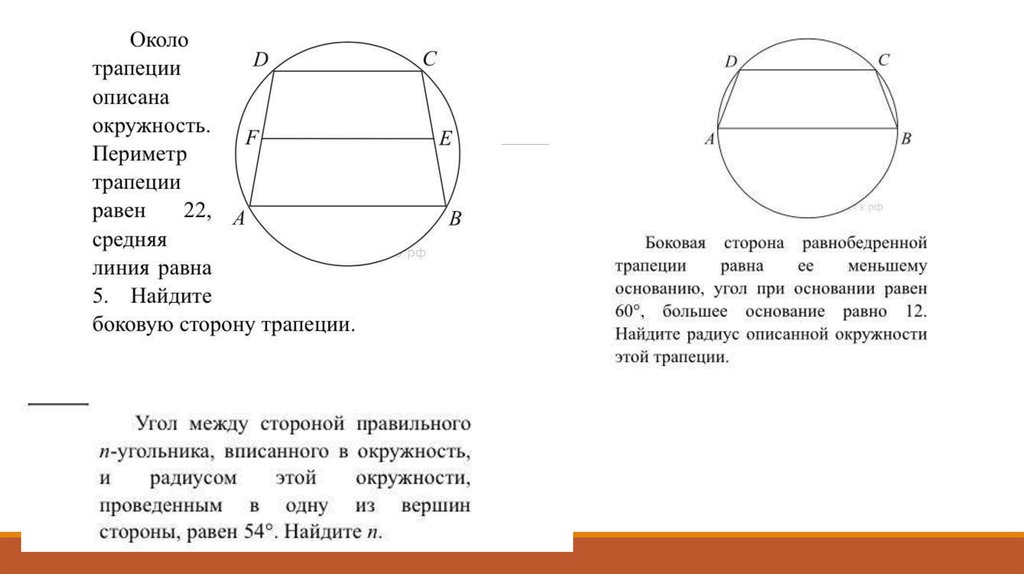 4, 5/7, …).
4, 5/7, …).
Основные свойства равнобедренной трапеции
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
AC 2 + BD 2 = AB 2 + CD 2 + 2BC · AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) – равен полуразности оснований:
| AP = | BC + AD |
| 2 |
| PD = | AD – BC |
| 2 |
Формулы длин сторон равнобедренной трапеции:
a = b + 2 h ctg α = b + 2 c cos α
b = a – 2 h ctg α = a – 2 c cos α
| c = | h | = | a – b |
| sin α | 2 cos α |
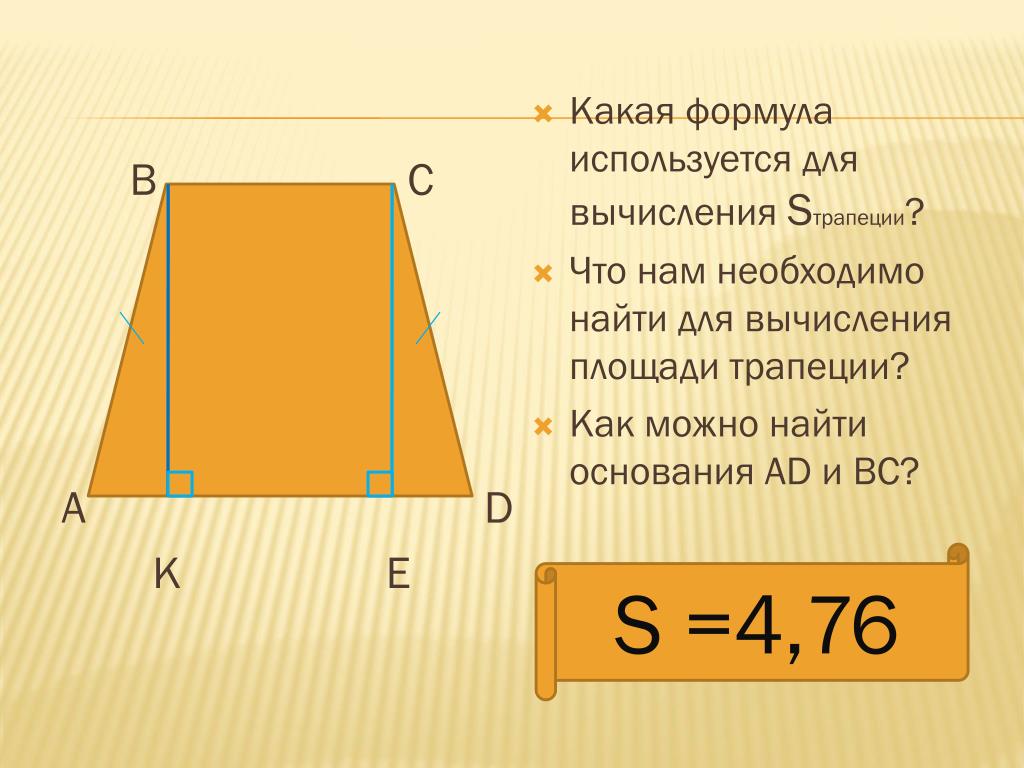
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d 1 2 – c 2 | b = | d 1 2 – c 2 | c = √ d 1 2 – ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | – b b = | 2S | – a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
| с = | S |
| m sin α |
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
| с = | 2S |
| ( a + b ) sin α |
Формулы длины средней линии равнобедренной трапеции:
m = a – h ctg α = b + h ctg α = a – √ c 2 – h 2 = b + √ c 2 – h 2
2. Формула средней линии трапеции через площадь и сторону:
| m = | S |
| c sin α |
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
| h = | 1 | √ 4 c 2 – ( a – b ) 2 |
| 2 |
2. Формула высоты через стороны и угол прилегающий к основе:
Формула высоты через стороны и угол прилегающий к основе:
| h = | a – b | tg β | = c sin β |
| 2 |
В исходных данных: все стороны
Для того чтобы найти высоту трапеции в общем случае потребуется воспользоваться такой формулой:
н = √(с 2 – (((а – в) 2 + с 2 – d 2 )/(2(а – в))) 2 ). Номер 1.
Не самая короткая, но и встречается в задачах достаточно редко. Обычно можно воспользоваться другими данными.
Формула, которая подскажет, как найти высоту равнобедренной трапеции в той же ситуации, гораздо короче:
Периметр произвольной трапеции
Периметр произвольной трапеции, в которой AB=a , BC=b , CD=c , AD=d , имеет вид:
[ LARGE P_ = a + b + c + d ]
где:
P – периметр трапеции
a, b, c, d – стороны трапеции
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и она делит боковую сторону точкой касания на два отрезка — и , то , то
Решение задач о прямоугольной трапеции
Прямоугольной называют трапецию, у которой углы при одной из боковых сторон равны 90 0 . Рассмотрим пример, как найти боковую сторону трапеции, если известны три другие стороны.
Рассмотрим пример, как найти боковую сторону трапеции, если известны три другие стороны.
Задача Даны три стороны, одна из которых перпендикулярная боковая.
Допустим, нам дана прямоугольная трапеция АВСД, у которой АВ перпендикулярно ВС. Известно, что АВ = 12 см, ВС = 1 см, АД = 6 см. Необходимо найти большую боковую сторону.
Из точки С опускаем проводим высоту СК и получаем прямоугольный треугольник СДК и прямоугольник АВСК. Поскольку у прямоугольника противоположные стороны равны СК = АВ = 12 см, а АК = ВС = 1 см.
Находим отрезок КД:
- КД = АД – АК = 6 – 1 = 5 (см)
Согласно теореме Пифагора:
- СД 2 =СК 2 +КД 2 =12 2 +5 2 =144+25=169
- СД = √169 = 13 (см)
Ответ: СД = 13 см
Задача Даны оба основания и угол при основании
Дана трапеция АВСД, у которой основания ВС и АД равны 6 и 10 см соответственно, угол ВАД – прямой, а СДА равен 45 градусов. Найдите меньшую боковую сторону.
- Проводим высоту СК и получаем прямоугольный треугольник СКД и прямоугольник АВСК.
 Поскольку у прямоугольника противоположные стороны равны АК = ВС = 6 см.
Поскольку у прямоугольника противоположные стороны равны АК = ВС = 6 см. - КД = АД – АК = 10 – 6 = 4 см
- cos 45 = √2/2 = КД / СД, отсюда СД = КД / cos 45
- Получаем СД = 4/√2/2 = 4√2 (см)
Ответ: СД = 4√2 см
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Формула определения радиуса вписанной в трапецию окружности
1. Формула радиуса вписанной окружности через высоту:
| r = | h |
| 2 |
Формулы определения длин отрезков проходящих через трапецию:
1.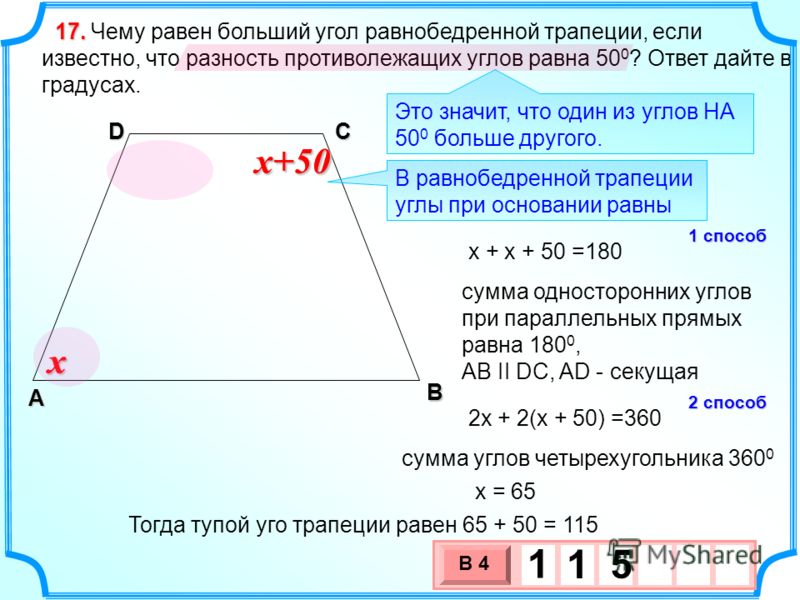 Формула определения длин отрезков проходящих через трапецию:
Формула определения длин отрезков проходящих через трапецию:
| KM = NL = | b | KN = ML = | a | TO = OQ = | a · b |
| 2 | 2 | a + b |
Определение периметра прямоугольной трапеции
Периметр прямоугольной трапеции определяется по той же формуле, что и периметр равнобедренной, однако в этом случае формула имеет вид:
Периметр ABCD = АВ+ВС+СD+AD. Рассмотрим пример определения периметра прямоугольной трапеции. В данном примере сторона АВ = 5 см, ВС = 7см, AD = 10 см, длина стороны СD неизвестна.
- опустим высоту из вершины С, высота CH = AB = 5см;
- исходя из рисунка 3, AH = BC = 7 см;
- HD = AD – AH = 10 – 7 = 3 см;
- далее для нахождения периметра, необходимо определить длину стороны СD, являющейся в равнобедренном треугольнике СHD гипотенузой. Согласно теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, таким образом, длина стороны СD = 5,83 см: CD = = 5,83 см;
- подставляя полученные значения в формулу, получим периметр равный 27,83 см: Периметр ABCD = 5+7+5,83+10 = 27,83 см.

Итак, определить длину одной из сторон трапеции можно воспользовавшись теоремой Пифагора. Так же, для определения длины различных сторон трапеции могут помочь следующие формулы:
- формула расчета длины основания через среднюю линию;
- формулы длин сторон через высоту и угол при нижнем основании трапеции;
- формулы длин сторон трапеции через диагонали, высоту и угол между диагоналями;
- формулы длин сторон равнобедренной трапеции через площадь.
Как видно, для решения задач, связанных с расчетом длины сторон трапеции, существует более чем широкий спектр математических приемов, выбор которых обусловлен конкретной ситуацией.
Известны: диагонали и углы между ними
Обычно к этим данным присоединяются еще известные величины. Например, основания или средняя линия. Если даны основания, то для ответа на вопрос, как найти высоту трапеции, пригодится такая формула:
Это для общего вида фигуры. Если дана равнобедренная, то запись преобразится так:
н = (d1 2 * sin γ) / (а + в) или н = (d1 2 * sin δ) / (а + в). Номер 6.
Номер 6.
Когда в задаче идет речь о средней линии трапеции, то формулы для поиска ее высоты становятся такими:
н = (d1 2 * sin γ) / 2m или н = (d1 2 * sin δ) / 2m. Номер 6а.
Как найти периметр и площадь трапеции (видео и практика)
TranscriptFAQsPractice
Привет, и добро пожаловать в это видео о нахождении площади и периметра трапеции!
Что такое трапеция?
Трапеция — это четырехсторонний многоугольник , или «четырехугольник», который имеет по крайней мере один набор параллельных сторон. В трапеции есть два типа сторон: катеты и основания. У трапеции два катета и два основания.
Мы можем сказать, какие стороны являются основаниями, потому что они параллельны друг другу.
Здесь мы видим, что верх и низ параллельны из-за совпадающих стрелок на этих сторонах.
Как найти периметр трапеции
Зная длины катетов и длины оснований, мы можем найти периметр трапеции. Периметр — это расстояние вокруг объекта. Например, если мы хотим построить забор вокруг двора в форме трапеции, нам нужно знать периметр двора, чтобы знать, сколько забора нужно купить.
Формула периметра трапеции
Формула периметра трапеции: \(P=b_1+b_2+l_1+l_2\).
Нам не нужно запоминать эту формулу, потому что, как и в случае с любым другим типом многоугольника, это просто причудливый способ сказать, что суммирует все стороны вместе !
Найдем периметр этой трапеции:
\(10+21+12+16=59 м\)
Вот и все! Переходим к область .
Как найти площадь трапеции
Вот трапеция на миллиметровой бумаге:
Помните, что площадь — это мера того, сколько квадратных единиц поместится внутри фигуры. Сколько квадратов внутри нашей трапеции?
Сколько квадратов внутри нашей трапеции?
Есть 24 полных квадрата плюс восемь полуквадратов, что означает, что площадь трапеции составляет 28 квадратных единиц. Но что, если у нас нет миллиметровой бумаги или трапеции подходящего размера? Вот почему нам нужна формула!
Формула площади трапеции
Формула для нахождения площади трапеции: \(A=h(\frac{b_1+b_2}{2})\).
Обратите внимание, что деление суммы оснований на два равно среднему значению этих длин. Поскольку наша примерная задача представлена на графике, мы можем видеть, что верхнее основание, которое мы назовем основанием 1, имеет длину три единицы. Наша нижняя база, база 2, имеет длину 11 единиц. Высота трапеции, то есть расстояние между основаниями, равна четырем единицам:
92\)
Такой же ответ мы получили, когда считали!
Давайте попробуем еще один:
Хорошо, это выглядит немного иначе, чем трапеция, которую мы только что сделали. Но мы можем сказать, что это трапеция, потому что у нее есть один набор из параллельных сторон . Мы можем использовать формулу, так что теперь нам просто нужно выяснить, какие числа куда идут. Параллельные стороны — это основания, поэтому мы можем установить основание один равным 6 сантиметрам, а основание два равным 3 сантиметрам. Внутри трапеции нет пунктирной или цветной линии, соединяющей основания, которая явно была бы высотой, но нижняя сторона соединяет основания и перпендикулярна им, как мы можем сказать по символу прямого угла. Так 4 сантиметра это высота, хоть и сбоку! Подключим все: 92\)
Но мы можем сказать, что это трапеция, потому что у нее есть один набор из параллельных сторон . Мы можем использовать формулу, так что теперь нам просто нужно выяснить, какие числа куда идут. Параллельные стороны — это основания, поэтому мы можем установить основание один равным 6 сантиметрам, а основание два равным 3 сантиметрам. Внутри трапеции нет пунктирной или цветной линии, соединяющей основания, которая явно была бы высотой, но нижняя сторона соединяет основания и перпендикулярна им, как мы можем сказать по символу прямого угла. Так 4 сантиметра это высота, хоть и сбоку! Подключим все: 92\)
Эта формула также работает для нахождения площади параллелограммов . Это потому, что все параллелограммы являются трапециями, поскольку у них есть хотя бы один набор параллельных сторон. На самом деле все параллелограммы имеют два множества.
Вот и все, что нужно для нахождения периметра и площади трапеций.
Спасибо за просмотр и удачной учебы!
Часто задаваемые вопросы
Q
Как найти площадь трапеции?
A
Каждая из двух параллельных сторон трапеции является основанием . Расстояние между основаниями (измеряемое перпендикулярно каждому) равно высоте . Чтобы найти площадь трапеции, мы умножаем среднюю длину двух оснований на высоту. В символах, если длины оснований равны \(a\) и \(b\), а высота равна \(h\) (см. диаграмму), то площадь \(A\) трапеции равна \ (A=\frac{(a+b)}{2}h\), что также можно записать как \(A=\frac{1}{2}(a+b)h\). 92\).
Расстояние между основаниями (измеряемое перпендикулярно каждому) равно высоте . Чтобы найти площадь трапеции, мы умножаем среднюю длину двух оснований на высоту. В символах, если длины оснований равны \(a\) и \(b\), а высота равна \(h\) (см. диаграмму), то площадь \(A\) трапеции равна \ (A=\frac{(a+b)}{2}h\), что также можно записать как \(A=\frac{1}{2}(a+b)h\). 92\).
Q
Почему работает формула площади трапеции?
A
Формула площади трапеции работает, потому что она получена из формулы площади параллелограмма. Трапеция внизу (со сплошными сторонами) имеет основания длины \(a\) и \(b\) и высоты \(h\). Предположим, мы делаем ее копию, поворачиваем ее наполовину и помещаем рядом с исходной трапецией так, чтобы стороны (непараллельные стороны) одинаковой длины совпадали (заштрихованная трапеция со штрихованными сторонами). Вместе эти фигуры образуют параллелограмм с длиной основания \(a+b\) и высотой \(h\). По стандартной формуле площадь этого параллелограмма равна \(\text{площадь}=\text{основание}×\text{высота}=(a+b)h\). Площадь исходной трапеции равна половине этой, а именно \(\frac{1}{2}(a+b)h\) или, что то же самое, \(\frac{(a+b)}{2}h \). Эта же процедура работает для каждой трапеции. 92\) и т. д. Обычно мы используем квадрат единицы, используемой для измерения оснований и высоты трапеции. Например, если мы измеряем основания и высоту в сантиметрах, мы обычно даем площадь в квадратных сантиметрах.
Площадь исходной трапеции равна половине этой, а именно \(\frac{1}{2}(a+b)h\) или, что то же самое, \(\frac{(a+b)}{2}h \). Эта же процедура работает для каждой трапеции. 92\) и т. д. Обычно мы используем квадрат единицы, используемой для измерения оснований и высоты трапеции. Например, если мы измеряем основания и высоту в сантиметрах, мы обычно даем площадь в квадратных сантиметрах.
Q
Как найти периметр трапеции?
A
Периметр фигуры — это расстояние вокруг нее. Найдем периметр трапеции, сложив длины ее четырех сторон.
Q
Как найти периметр трапеции по теореме Пифагора?
A
Если мы не знаем длины всех четырех сторон трапеции, иногда у нас достаточно другой информации, чтобы найти длины недостающих сторон по теореме Пифагора. Например, у трапеции на схеме основания равны 2 см и 9 см, высота 4 см, а более длинное основание выступает за более короткое основание на 3 см слева и 4 см справа. Это делает стороны \(c\) и \(d\) гипотенузами прямоугольных треугольников со сторонами, длина которых нам известна.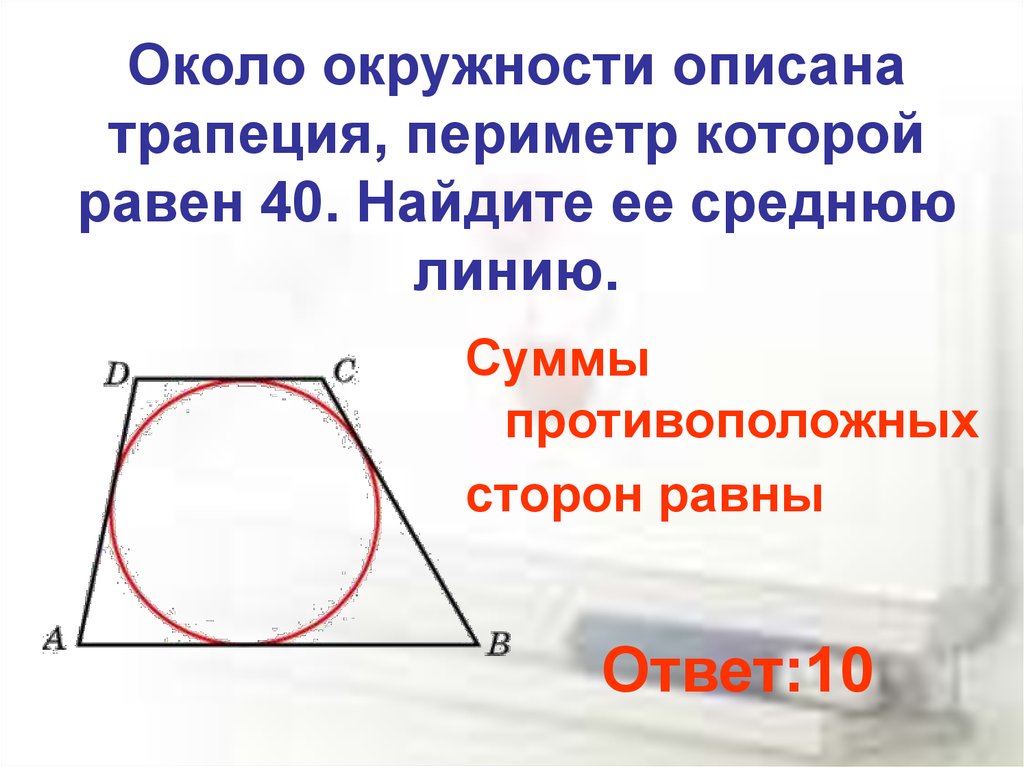 2=92=16+16=32\), поэтому \(d=\sqrt{32}=\sqrt{16\cdot2}=\sqrt{16}\cdot \sqrt{2}=4\sqrt{2} ≈5,7 \текст{см}\). Теперь мы можем найти периметр \(P\) трапеции, сложив четыре стороны: \(P=9+5+2+4sqrt{2}=16+4\sqrt{2}≈16+5,7 =21,7\текст{см}\). Это один из примеров нахождения периметра трапеции по теореме Пифагора.
2=92=16+16=32\), поэтому \(d=\sqrt{32}=\sqrt{16\cdot2}=\sqrt{16}\cdot \sqrt{2}=4\sqrt{2} ≈5,7 \текст{см}\). Теперь мы можем найти периметр \(P\) трапеции, сложив четыре стороны: \(P=9+5+2+4sqrt{2}=16+4\sqrt{2}≈16+5,7 =21,7\текст{см}\). Это один из примеров нахождения периметра трапеции по теореме Пифагора.
Q
Как найти площадь трапеции без высоты?
A
Если мы не знаем высоту трапеции, иногда у нас достаточно другой информации, чтобы найти высоту по теореме Пифагора. Например, у трапеции на схеме основания равны 2 см и 92\). Это пример нахождения площади трапеции без высоты.
Практические вопросы
Вопрос №1:
Каков периметр этой трапеции?
74 в
86 в
142 в
300 в
Показать ответ
Ответ:
Правильный ответ — 74 дюйма. .
.
\(P=23+12+27+12=74\текст{in}\)
Скрыть ответ
Вопрос №2:
Какова площадь этой трапеции?
96 cm 2
81 cm 2
57 cm 2
41 cm 2
Show Answer
Answer:
The correct answer is 81 cm 2 . Формула площади трапеции:
\(A=\frac{1}{2}(b_1+b_2)h\)
Длина основания 1 равна 12 см. Длина основания 2 равна 15 см. Длина по высоте 6 см. 92\)
Скрыть ответ
Вопрос №3:
Каков периметр этой трапеции?
34 в
48 в
36 в
42 в
Показать ответ
Ответ:
Правильный ответ — 36 дюймов.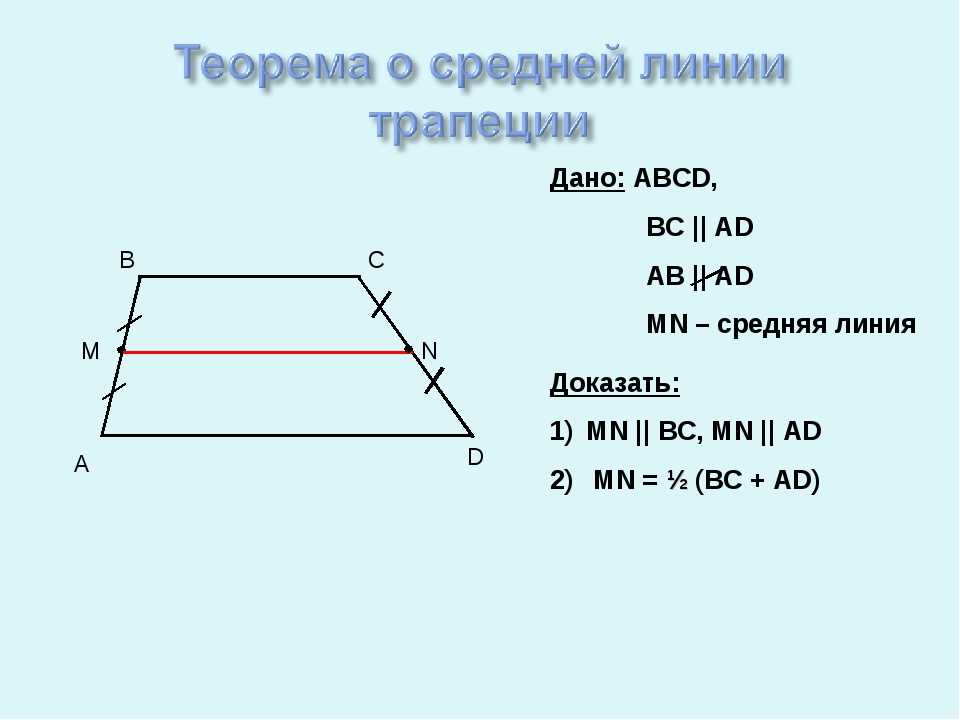 2\)
2\)
Скрыть ответ
Вопрос №5:
Каков периметр этой трапеции?
153 см
140 см
47 см
55 см
Показать Ответ
Ответ:
см. Правильный ответ. Чтобы найти периметр трапеции, сложите длины всех четырех сторон.\(P=15+8+20+12=55\text{ см}\)
Скрыть ответ
Вернуться к видео по геометрии
587523
Как найти периметр трапеции
Как найти периметр трапеции — Промежуточная геометрия—>
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство по ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- Алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительное исчисление
- Статистика
- Тригонометрия
репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский диалект
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочие
- Бухгалтерский учет
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Мы открыты в субботу и воскресенье!
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все промежуточные ресурсы по геометрии
8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Учитесь по концепции
Справка по промежуточной геометрии » Плоская геометрия » Четырехугольники » Трапеции » Как найти периметр трапеции
Найдите периметр следующей трапеции.
Возможные ответы:
Правильный ответ:
Объяснение:
Ответ: 50 футов. Чтобы найти периметр, нужно найти длину левой стороны. После некоторого вывода вы можете найти, что основание треугольника равно 6 футам. Затем, используя теорему Пифагора, или 3-4-5 прямоугольных треугольников, вы можете найти, что высота треугольника и прямоугольника составляет 8 футов.
Как только вы обнаружите, что последняя сторона равна 8 футам, вы можете добавить
, чтобы получить ответ 50 футов для периметра.
Сообщить об ошибке
Высота трапеции см, а длина см.
Найдите периметр трапеции с точностью до сотых.
Возможные ответы:
Правильный ответ:
Пояснение:
Используйте треугольник, образованный высотой трапеции, чтобы найти длины двух сторон трапеции и длину:
.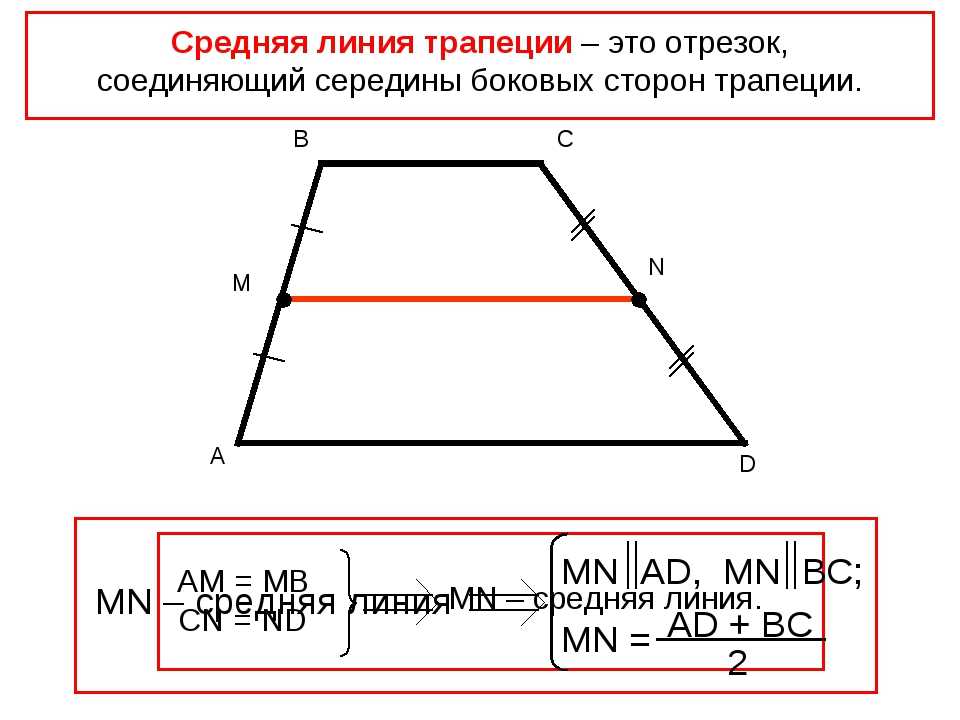 см.
см.
Это находит основание треугольника, которое можно дважды прибавить к , чтобы найти : см.
Теперь используйте тот же треугольник, чтобы найти длины сторон.
. см.
Наконец, сложите все длины вместе: см.
Сообщить об ошибке
Найдите периметр трапеции ниже.
Возможные ответы:
Правильный ответ:
Объяснение:
Затем мы можем использовать теорему Пифагора, чтобы найти правую часть нижнего основания. Затем мы можем использовать это значение для определения левой части.
Снова используя теорему Пифагора, мы можем вычислить, что левая сторона равна 20. Это означает, что теперь мы знаем все четыре стороны. Периметр — это просто сумма.
Сообщить об ошибке
У равнобедренной трапеции два основания параллельны друг другу.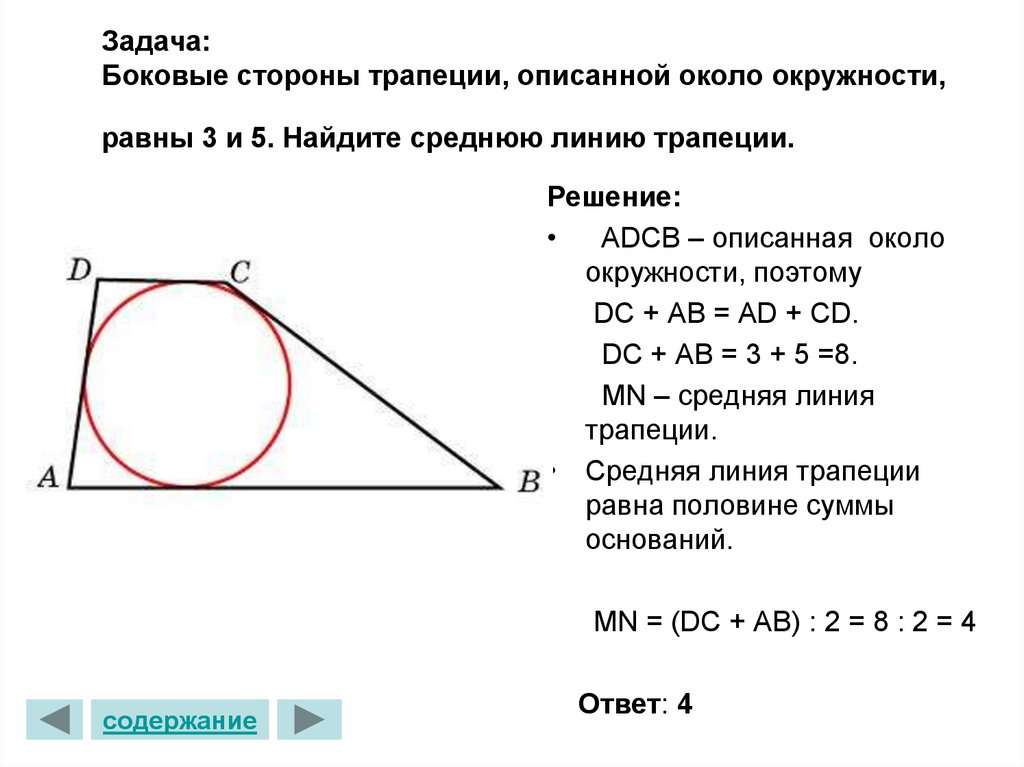 Большее основание в раз больше меньшего. Меньшее основание имеет длину в дюймах, а длина непараллельных сторон трапеции имеет длину в дюймах.
Большее основание в раз больше меньшего. Меньшее основание имеет длину в дюймах, а длина непараллельных сторон трапеции имеет длину в дюймах.
Каков периметр трапеции?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы найти периметр этой трапеции, сначала найдите длину большего основания. Затем найдите сумму всех сторон. Важно отметить, что поскольку это равнобедренная трапеция, обе непараллельные стороны будут иметь одинаковую длину.
Решение:
Меньшее основание равно дюймам. Таким образом, большее основание равно:
, где длина одной из непараллельных сторон равнобедренной трапеции.
Сообщить об ошибке
Имущество доктора Робинсона имеет форму равнобедренной трапеции. Доктор Робинсон дал подрядчику следующие размеры, чтобы подрядчик мог построить стену вокруг всего участка.
Измерения собственности:
Найдите периметр собственности доктора Робинсона.
Возможные ответы:
Правильный ответ:
Объяснение:
Измерения, которые д-р Робинсон дал подрядчику, включают длины двух основных сторон и одной из непараллельных сторон объекта. Поскольку собственность доктора Робинсона имеет форму равнобедренной трапеции, должны быть две непараллельные стороны одинаковой длины.
Решение:
Сообщить об ошибке
Уведомление об авторских правах
Посмотреть репетиторов
Боряна
Сертифицированный репетитор
Софийский университет им. Св. Климента Охридского, бакалавр гуманитарных наук, преподавание английского языка как второго (ESL).
Просмотр репетиторов
Sunmble
Сертифицированный репетитор
Женский колледж Пакистана, научный сотрудник, наука и технология. Кингстонский университет, магистр наук, биотехнология.
Кингстонский университет, магистр наук, биотехнология.
Посмотреть репетиторов
Карен
Сертифицированный репетитор
Главный кампус Университета Пердью, бакалавр искусств, специальное образование для детей младшего возраста.
Все ресурсы промежуточной геометрии
8 Диагностические тесты 250 практических тестов Вопрос дня Карточки Учитесь по концепции
Периметр трапеции — определение, формула и примеры
Периметр трапеции представляет собой сумму длин каждой стороны трапеции. Трапеция — это четырехугольник, у которого две стороны параллельны друг другу, а две непараллельные стороны называются соответственно основаниями и катетами. Давайте узнаем, как рассчитать периметр трапеции в этой статье.
| 1. | Каков периметр трапеции? |
| 2. | Формула периметра трапеции |
3. | Как найти периметр трапеции? |
| 4. | Часто задаваемые вопросы по периметру трапеции |
Что такое периметр трапеции?
периметр трапеции определяется как общая длина границы трапеции. Трапеция — это двумерная фигура (2D-форма) и неправильный многоугольник. Таким образом, периметр трапеции вычисляется путем сложения длин всех ее сторон. Периметр трапеции выражается в линейных единицах, таких как «дюймы», «футы», «метры» или «сантиметры» и т. д.
Формула периметра трапеции
Формула периметра трапеции простая, в которой добавляются длины всех 4-х сторон. Обратите внимание на приведенную ниже трапецию ABCD, в которой стороны AB и CD (основания) параллельны друг другу, а стороны AD и BC (ножки) непараллельны.
Периметр трапеции ABCD можно рассчитать по формуле Периметр (P) = AB + BC + CD + DA. Его также можно записать в виде суммы длин параллельных сторон и суммы длин непараллельных сторон, где AB и CD — параллельные стороны, а AD и BC — непараллельные стороны.
Как найти периметр трапеции?
Периметр трапеции можно найти, выполнив следующие шаги:
- Шаг 1: Напишите размеры всех сторон трапеции.
- Шаг 2: Добавьте длины всех сторон.
- Шаг 3: Как только значение периметра получено, запишите единицу измерения с полученным таким образом значением.
Пример: Найдите периметр трапеции, параллельные стороны которой равны 5 единицам и 7 единицам, а непараллельные стороны равны 3 единицам и 4 единицам.
Решение: Даны длины параллельных сторон 5 единиц и 7 единиц, а длины непараллельных сторон 3 единицы и 4 единицы.
Таким образом, периметр трапеции равен P = сумме длин всех сторон
⇒ P = (5 + 7 + 3 + 4)
Следовательно, P = 19 единиц.
∴ Периметр трапеции 19 единиц.
Периметр трапеции с отсутствующей стороной
Периметр трапеции можно рассчитать, даже если отсутствует сторона. В таких случаях мы используем заданные стороны трапеции и применяем теорему Пифагора и другие свойства, чтобы найти недостающую сторону, а затем можно вычислить периметр. Давайте разберемся в этом с помощью примера.
Давайте разберемся в этом с помощью примера.
Пример: Найдите периметр трапеции ABCD, если ее размеры заданы следующим образом: AB = 120 м, DE = 50 м, EF = 120 м, FC = 80 м, BF = 90 м.
Решение: Используя заданные размеры, мы можем найти недостающие стороны AD и BC.
- Шаг 1: Если взять треугольник BFC, то дано, что BF = 90 м и FC = 80 м. Мы видим, что треугольник BFC прямоугольный. Итак, мы можем вычислить значение BC, используя теорему Пифагора.
- Шаг 2: Согласно теореме Пифагора, BC 2 = BF 2 + FC 2 . Это означает, что БК 2 = 90 2 + 80 2 . Следовательно, БК 2 = 8100 + 6400 ⇒ БК = √14500 = 120,41 м
- Шаг 3: Поскольку BF = 90 м, AE также будет равно 90 м, поскольку AB параллельна DC. Теперь мы можем вычислить недостающую сторону AD трапеции.
- Шаг 4: Если взять прямоугольный треугольник ADE, мы знаем, что AE = 90 м, ДЭ = 50 м.
 Итак, после применения теоремы Пифагора мы получаем AD 2 = AE 2 + DE 2 . Это означает, что 2 = 90 2 + 50 2 . Следовательно, н.э. 2 = 8100 + 2500 ⇒ н.э. = √10600 = 102,9 м.
Итак, после применения теоремы Пифагора мы получаем AD 2 = AE 2 + DE 2 . Это означает, что 2 = 90 2 + 50 2 . Следовательно, н.э. 2 = 8100 + 2500 ⇒ н.э. = √10600 = 102,9 м. - Шаг 5: Теперь, когда мы знаем все стороны трапеции, мы можем найти ее периметр, сложив все 4 стороны. Это означает, что периметр трапеции ABCD = AB + BC + CD + DE ⇒ 120 + 120,41 + 250 + 102,9 = 59.3,31 м. Следовательно, периметр трапеции равен 593,31 м.
☛ Статьи по теме
- Формула трапеции
- Калькулятор периметра трапеции
- Формулы периметра
- Периметр многоугольника
- Периметр прямоугольника
- Периметр квадрата
- Периметр треугольника
- Разница между площадью и периметром
- Площадь трапеции
Примеры на периметре трапеции
Пример 1: Найдите периметр трапеции со сторонами 10 м, 6 м, 8 м и 9 м.

Решение: Размеры трапеции 10 м, 6 м, 8 м и 9 м. Таким образом, периметр трапеции можно рассчитать по формуле:
Периметр трапеции = (10 + 6 + 8 + 9) метров. Таким образом, периметр трапеции = 33 метра
∴ Периметр трапеции 33 метра.
Пример 2: Каков периметр трапеции, у которой сумма длин непараллельных сторон равна 12 единицам, а сумма параллельных сторон равна 8 единицам?
Решение: Учитывая, что сумма длин непараллельных сторон = 12 единиц, сумма параллельных сторон = 8 единиц.
Периметр трапеции = сумма длин параллельных сторон + сумма длин непараллельных сторон ⇒ P = 12 единиц + 8 единиц.
Таким образом, периметр (P) = 20 единиц
Следовательно, периметр трапеции равен 20 единицам.
Пример 3: Верно или неверно:
а.) Периметр трапеции вычисляется путем сложения длин всех ее сторон.

б.) Трапеция – это четырехугольник, у которого две стороны параллельны друг другу и две непараллельны.
Решение:
а.) Верно, периметр трапеции вычисляется путем сложения длин всех ее сторон.
б.) Верно, трапеция – это четырехугольник, у которого две стороны параллельны друг другу и две непараллельны.
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами Cuemath.
Запись на бесплатный пробный урок
Практические вопросы по периметру трапеции
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по периметру трапеции
Что такое периметр трапеции?
Общая длина границы трапеции называется периметром трапеции. Периметр трапеции зависит от длины всех ее сторон и выражается в линейных единицах.
Какая формула для периметра трапеции?
Формула периметра трапеции представляет собой сумму длин всех сторон трапеции. Для любой трапеции ABCD периметр трапеции ABCD выражается как P = AB + BC + CD + AD, где AB, CD — параллельные стороны (основания), а AD, BC — непараллельные стороны (катеты). Таким образом, периметр трапеции также можно записать как P = (сумма длин параллельных сторон) + (сумма длин непараллельных сторон).
Как найти периметр трапеции?
Периметр трапеции можно найти, выполнив следующие действия:
- Шаг 1: Найдите длины всех 4 сторон трапеции.
- Шаг 2: Сложите длины всех сторон трапеции, чтобы получить значение периметра трапеции.
- Шаг 3: Как только значение периметра трапеции получено, мы указываем единицу, которая должна быть помещена вместе с ней.
Как найти длину недостающей стороны, если известен периметр трапеции?
Мы можем найти недостающую длину стороны трапеции, если известен периметр.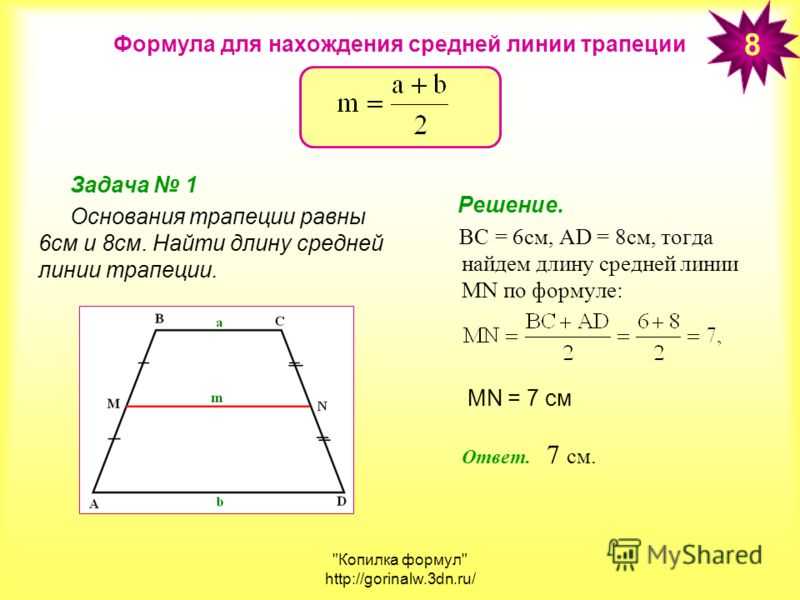 Давайте разберемся в этом на примере.
Давайте разберемся в этом на примере.
Пример: Если периметр трапеции равен 24 единицам, а остальные стороны равны: 5 единиц, 7 единиц, 4 единицы, найдем недостающую сторону.
- Шаг 1: Запишите данные размеры трапеции. Периметр = 24 единицы, Сторона 1 = 5 единиц, Сторона 2 = 7 единиц, Сторона 3 = 4 единицы.
- Шаг 2: Предположим, что недостающая длина стороны трапеции равна x единицам.
- Шаг 3: Сложите длины всех сторон трапеции и приравняйте значение к периметру трапеции. Здесь это будет записано как 24 = 5 + 7 + 4 + x .
- Шаг 4: Как только уравнение будет сформировано, решите «x», чтобы получить значение длины недостающей стороны трапеции. После решения для значения «x» мы получаем, x = 24 — 16 = 8 единиц. Следовательно, длина недостающей стороны равна 8 единицам.
Что произойдет с периметром трапеции, если все стороны трапеции удвоить?
Если длины всех сторон трапеции удвоить, то периметр также удвоится как P = (сумма длин параллельных сторон) + (сумма длин непараллельных сторон), а значение каждой стороны будет удвоится, тем самым удвоив значение периметра.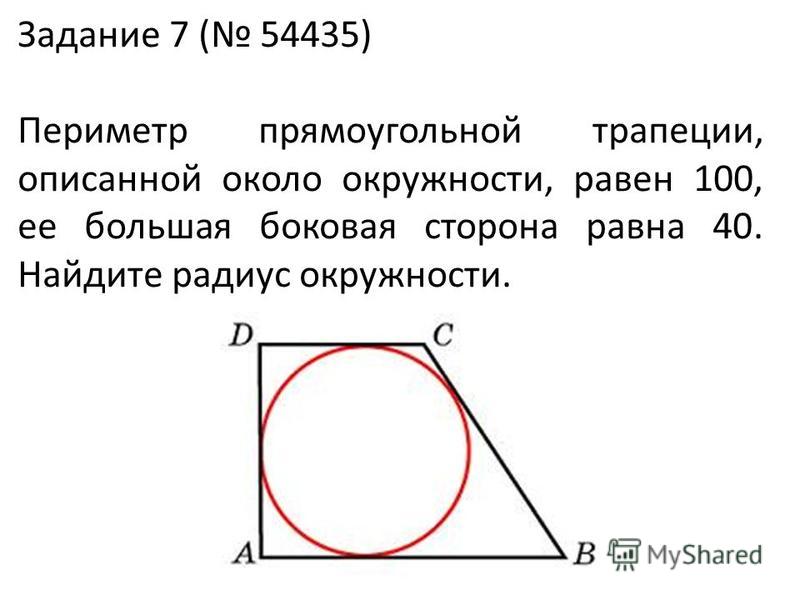
Как найти периметр равнобедренной трапеции?
Периметр равнобедренной трапеции можно вычислить так же, как мы находим периметр обычной трапеции. Однако у равнобедренной трапеции катеты одинаковой длины, поэтому найти периметр становится проще. В этом случае периметр можно рассчитать по формуле Периметр трапеции = a + b + 2c; где «а» и «b» — параллельные стороны, а с — катет трапеции. Поскольку две ноги равны по длине, мы представляем их как c + c = 2c в формуле.
Загрузить БЕСПЛАТНЫЕ учебные материалы
Рабочий лист по периметру
5.14: Площадь и периметр трапеций
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 4998
Площадь равна высоте, умноженной на среднее значение оснований; периметр это сумма сторон.
Трапеция представляет собой четырехугольник с одной парой параллельных сторон. Параллельные стороны называются основаниями, и мы будем называть длины оснований \(b_1\) и \(b_2\). Перпендикулярное расстояние между параллельными сторонами является высотой трапеции. Площадь трапеции равна \(A=\dfrac{1}{2}h(b_1+b_2)\), где \(h\) всегда перпендикулярна основаниям.
Рисунок \(\PageIndex{1}\)Что, если бы вам были даны трапеция, размеры двух ее оснований и высота? Как можно найти полное расстояние вокруг трапеции и количество места, которое она занимает? 92 \конец{выровнено}\)
Пример \(\PageIndex{5}\)
Найдите периметр и площадь трапеции.
Рисунок \(\PageIndex{6}\)Решение
Хотя длина второго основания нам не известна, мы можем найти его с помощью специальных прямоугольных треугольников. Оба треугольника на концах этой трапеции являются равнобедренными прямоугольными треугольниками, поэтому гипотенузы равны \(4\sqrt{2}\), а длина других катетов равна 4. 2 \end{выровнены}\)
2 \end{выровнены}\)
Обзор
Найдите площадь и периметр следующих фигур. Округлите ответы до сотых.
- Рисунок \(\PageIndex{7}\)
- Рисунок \(\PageIndex{8}\)
Найдите площади следующих трапеций.
- Трапеция с основаниями 3 и 7 дюймов и высотой 3 дюйма
- Трапеция с основаниями 6 и 8 дюймов и высотой 5 дюймов
- Трапеция с основаниями 10 дюймов и 26 дюймов и высотой 2 дюйма
- Трапеция с основаниями 15 и 12 дюймов и высотой 10 дюймов
- Трапеция с основаниями 4 и 23 дюйма и высотой 21 дюйм
- Трапеция с основаниями 9 дюймов и 4 дюйма и высотой 1 дюйм
- Трапеция с основаниями 12 и 8 дюймов и высотой 16 дюймов
- Трапеция с основаниями 26 дюймов и 14 дюймов и высотой 19 дюймов
Используйте данные цифры, чтобы ответить на вопросы.
Рисунок \(\PageIndex{9}\)- Каков периметр трапеции?
- Какова площадь трапеции?
- Каков периметр трапеции?
- Какова площадь трапеции?
- Каков периметр трапеции?
- Какова площадь трапеции?
Обзор (ответы)
Чтобы просмотреть ответы на обзор, откройте этот PDF-файл и найдите раздел 10.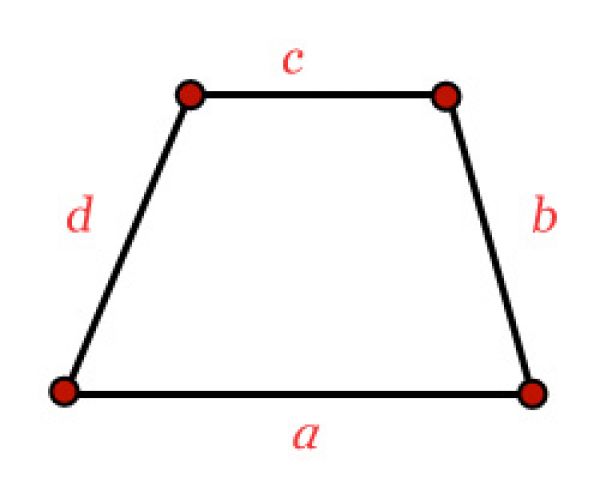 5.
5.
Словарь
| Срок | Определение |
|---|---|
| площадь | Количество места внутри фигуры. Площадь измеряется в квадратных единицах. |
| равнобедренная трапеция | Равнобедренная трапеция — это трапеция, у которой непараллельные стороны конгруэнтны. |
| средний сегмент (трапеции) | Отрезок, соединяющий середины непараллельных сторон. |
| периметр | Расстояние вокруг формы. К периметру любой фигуры должна быть привязана единица измерения. Если не указаны конкретные единицы измерения (футы, дюймы, сантиметры и т.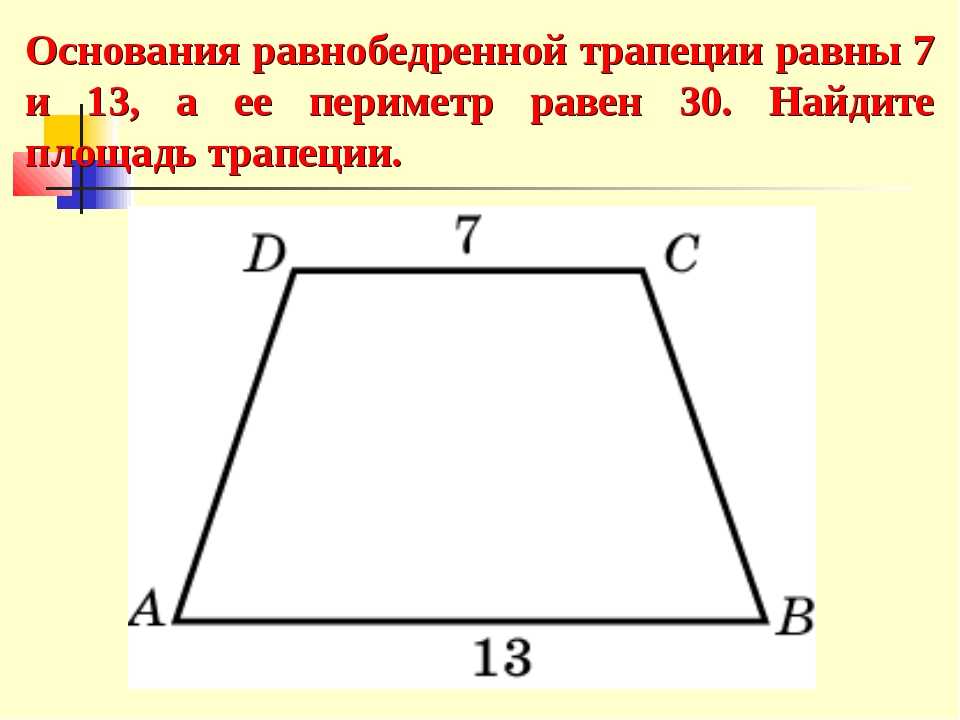 д.), напишите единицы. д.), напишите единицы. |
| трапеция | Четырехугольник, у которого ровно одна пара параллельных сторон. |
Дополнительные ресурсы
Интерактивный элемент
Видео: Примеры площади и периметра трапеций — основные положения
Упражнения: Площадь и периметр трапеций Вопросы для обсуждения
Учебные пособия: Треугольники и четырехугольники Периметр трапеций
Реальный мир: Периметр
Эта страница под названием 5.14: Площадь и периметр трапеций распространяется под лицензией CK-12 и была создана, изменена и/или курирована Фондом CK-12 через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts. ; подробная история редактирования доступна по запросу.
ПОД ЛИЦЕНЗИЕЙ
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- СК12
- Лицензия
- СК-12
- Программа ООР или издатель
- СК-12
- Показать оглавление
- нет
- Теги
- источник@https://www.
 ck12.org/c/geometry
ck12.org/c/geometry
- источник@https://www.
Как найти периметр трапеции?
Трапеция представляет собой плоскую замкнутую форму с четырьмя прямыми гранями и парой параллельных граней. Параллельные стороны трапеции называются основаниями, а непараллельные стороны – катетами. Трапеция также может иметь параллельные стороны. Параллельные плоскости могут быть горизонтальными, вертикальными или наклонными.
Трапеция
Трапеция — это многоугольник только с одной парой параллельных сторон. Эта параллельная сторона также называется параллельным основанием трапеции. Две другие стороны трапеции не параллельны и называются катетами трапеции. Одна школа математики утверждает, что у трапеции может быть пара параллельных сторон, а другая школа математики утверждает, что у трапеции может быть более одной пары параллельных сторон. Учитывая второе определение, параллелограмм также является трапецеидальным соответственно. Однако первое определение не считает параллелограмм трапецией.
Типы трапеций
Трапеции можно разделить на три категории:
- Прямоугольная трапеция: Прямоугольная трапеция — это трапеция, в которой пара прямых углов смежны друг с другом.
- Равнобедренная трапеция: Если непараллельные стороны или катеты трапеции имеют одинаковую длину, они называются равнобедренными трапециями.
- Несимметричная трапеция: Если стороны и углы трапеции не равны, мы называем ее разносторонней трапецией.
Периметр трапеции
Периметр трапеции равен сумме длин сторон трапеции. Формула периметра трапеции так же проста, как сумма длин ее четырех сторон. В приведенной ниже трапеции ABCD рассмотрим случай, когда стороны AB и CD (основание) параллельны друг другу, а стороны AD и BC (катетки) — нет. Периметр трапеции ABCD можно рассчитать по формуле периметр (P) = AB + BC + CD + DA. Его также можно выразить как сумму длин параллельных сторон и сумму длин непараллельных сторон. где стороны AB и CD параллельны, а стороны AD и BC непараллельны.
Его также можно выразить как сумму длин параллельных сторон и сумму длин непараллельных сторон. где стороны AB и CD параллельны, а стороны AD и BC непараллельны.
Как найти периметр трапеции?
Периметр трапеции можно рассчитать, выполнив следующие шаги:
Шаг 1 : Запишите размеры всех сторон трапеции.
Шаг 2: Добавьте длины всех сторон.
Шаг 3: После получения значения периметра запишите единицы измерения с этим значением.
Пример: Чему равен периметр трапеции, если непараллельные стороны имеют длину 10 единиц, а параллельные стороны — 5 единиц?
Решение:
Предположим, что сумма длин непараллельных сторон = 10 единицам, тогда сумма параллельных сторон = 5 единицам. Периметр трапеции = сумма длин параллельных сторон + сумма длин непараллельных сторон ⇒ P = 10 единиц + 5 единиц.
Итак, периметр (P) = 15 единиц.
Как найти периметр трапеции с отсутствующей стороной?
Периметр трапеции можно вычислить, даже если сторон недостаточно. В таких случаях вы можете использовать заданные стороны трапеции, применить теорему Пифагора и другие свойства, чтобы найти недостающие стороны, а затем вычислить периметр.
Пример: Найдите периметр трапеции PQRS с размерами PQ = 110 м, SV = 40 м, VU = 110 м, UR = 70 м, QU = 80 м.
Решение :
Используйте заданные размеры, чтобы найти отсутствующие поверхности PS и QR.
Шаг 1: Если мы возьмем △QUR, мы получим QU = 80 м и UR = 70 м. Мы видим, что △QUR — прямоугольный треугольник. Таким образом, мы можем использовать теорему Пифагора для вычисления значения QR.
Шаг 2: Согласно теореме Пифагора QR 2 = QU 2 + UR 2 . Это означает QR 2 = 80 2 + 70 2 .
Таким образом, QR 2 = 6400 + 4900 ⇒ QR = √11300 = 106,301 м.
Шаг 3: Поскольку QU = 80 м, PQ параллельно SR, поэтому PV также равно 80 м, поэтому теперь мы можем вычислить недостающую сторону PS трапеции.
Шаг 4: Берем прямоугольный треугольник △PSV, PV = 80 м, SV = 40 м, поэтому, применяя теорему Пифагора, получаем PS 2 = PV 2 + SV 2 . Это означает PS 2 = 80 2 + 40 2 . Итак, PS 2 = 6400 + 1600 ⇒ PS = √8000 = 89,44 м.
Шаг 5: Теперь, когда мы знаем все грани трапеции, мы можем сложить все четыре грани, чтобы найти периметр. Это означает, что периметр трапеции равен PQRS = PQ + QR + RS + SP ⇒ 110 + 106,301 + 220 + 89,44 = 525,741 м.
Примеры вопросов
Вопрос 1: Приведите две основные формулы трапеций.
Ответ:
Периметр трапеции = сумма всех сторон трапеции = a + b + c +d
Площадь трапеции = A = [(a + b)/2] × h.
Где a , b , c , d длины четырех сторон трапеции.
Вопрос 2: Трапеция/трапеция считается четырехугольником?
Ответ:
Четырехугольник — это замкнутая фигура, имеющая четыре стороны. В результате трапеции иногда называют четырехугольниками. Некоторые люди описывают трапецию как четырехугольник только с одним набором параллельных сторон и удаляют параллелограмм из определения. Другие определяют трапецию как четырехугольник по крайней мере с одной парой параллельных сторон, что делает параллелограмм особым типом трапеции. Трапеции бывают разных размеров углов.
Вопрос 3: Чем трапеция отличается от трапеции?
Ответ:
Трапеция — это четырехугольник с парой параллельных сторон, обращенных друг к другу, трапеция — это также четырехугольник с одной из параллельных сторон, противоположных друг другу.
Итак, два термина трапеция и трапеция одинаковы, но имеют разное написание в разных странах.
В американском английском это trapezium, а в британском английском — trapezium.
Вопрос 4: Назовите три свойства трапеции.
Ответ:
- Если трапеция равнобедренная, то ее основание и диагональ равны.
- Пересечение диагоналей лежит на той же линии, что и середины двух противоположных сторон.
- Противоположные стороны равнобедренной трапеции равны.
Вопрос 5. Равны ли диагонали трапеции? Объяснять.
Ответ:
Трапеции бывают трех типов: равнобедренные, многоцелевые и прямые. Для равнобедренной трапеции диагонали одинаковы, потому что непараллельные стороны или катеты трапеции имеют одинаковую длину. У разносторонней и прямой трапеции диагонали не равны.
Вопрос 6: Если периметр трапеции равен 60 единицам, а три стороны равны 10 единицам, 25 единицам и 12 единицам соответственно, используйте формулу трапеции, чтобы найти размер четвертой стороны.
Решение:
- Дан периметр трапеции = 60 единиц
- Дана длина стороны 1 трапеции = 10 единиц трапеция = 12 единиц
Пусть d единиц — длина четвертой стороны трапеции,
Используя формулу трапеции, периметр трапеции = сумма всех сторон трапеции
60 = 10 + 25 + 12 +d
60 = 47 + д
д = 13 единиц.
Периметр трапеции – формулы и примеры
Периметр трапеции равен общему расстоянию вокруг пределов трапеции. Это означает, что периметр трапеции получается сложением длин всех сторон. Напомним, что трапеция — это двумерная геометрическая фигура и тип четырехугольника, который имеет две параллельные стороны и две непараллельные стороны. Расстояние по перпендикуляру между его параллельными сторонами называется высотой.
Здесь мы узнаем о формуле для вычисления периметра трапеции. Также мы рассмотрим несколько примеров, в которых будем применять эту формулу.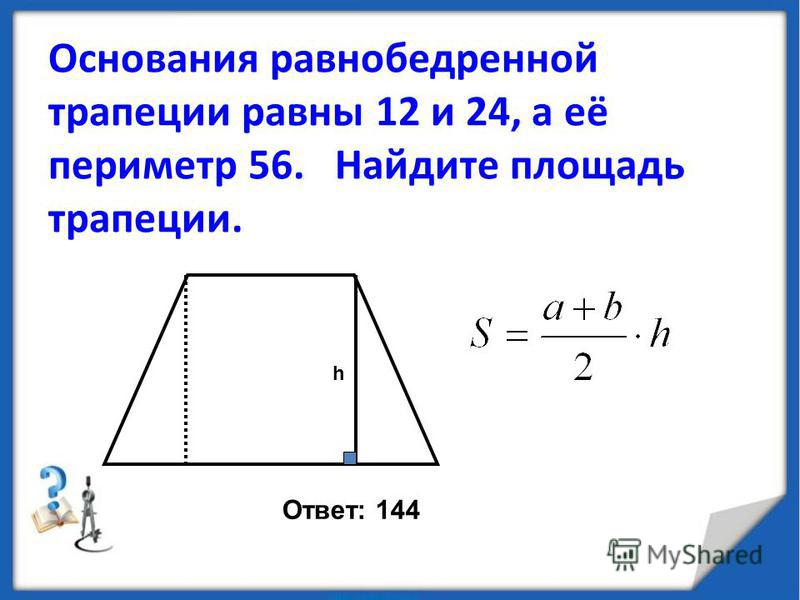
ГЕОМЕТРИЯ
Актуально для …
Изучение периметра трапеции на примерах.
См. примеры
Содержание
ГЕОМЕТРИЯ
Актуально для …
Изучение периметра трапеции на примерах.
См. примеры
Формула периметра трапеции
Периметр трапеции находится путем сложения длин всех ее сторон. Таким образом, формула для периметра трапеции имеет вид:
| $латекс p=a+b+c+d$ |
где « a, b, c, d » представляют собой длины сторон трапеции.
Периметр равнобедренной трапеции
Если и b представляет длины параллельных сторон, а c представляет длины боковых сторон равнобедренной трапеции, тогда периметр будет равен:
Периметр трапеции – Примеры с ответами
В следующих примерах мы используем формулу для периметра трапеции, чтобы получить ответ. Каждый пример имеет свое решение, но рекомендуется попробовать решить упражнения самостоятельно, прежде чем смотреть ответ.
Каждый пример имеет свое решение, но рекомендуется попробовать решить упражнения самостоятельно, прежде чем смотреть ответ.
Длина сторон трапеции 6 см, 8 см, 5 см и 7 см. Каков его периметр?
Решение
Используя $latex a, ~b, ~c, ~d$ для представления длин сторон трапеции, мы имеем:
$latex p=a+b+c+d$
$ латекс p=6+8+5+7$
$латекс p=26$
Периметр трапеции 26см.
ПРИМЕР 2Длина сторон трапеции 12 м, 14 м, 7 м и 9 м.м. Каков его периметр?
Решение
Опять же, мы можем использовать $latex a, ~b, ~c, ~d$ для представления длин сторон трапеции. Подставив эти значения в формулу периметра, мы получим:
$латекс p=a+b+c+d$
$латекс p=12+14+7+9$
$латекс p=42$
периметр трапеции 42 метра.
ПРИМЕР 3У равнобедренной трапеции две параллельные стороны равны 11 м и 13 м. Если боковые стороны трапеции равны 9м, каков его периметр?
Решение
Мы можем использовать $latex a, ~b$ для представления длины параллельных сторон и c для представления длины боковых сторон.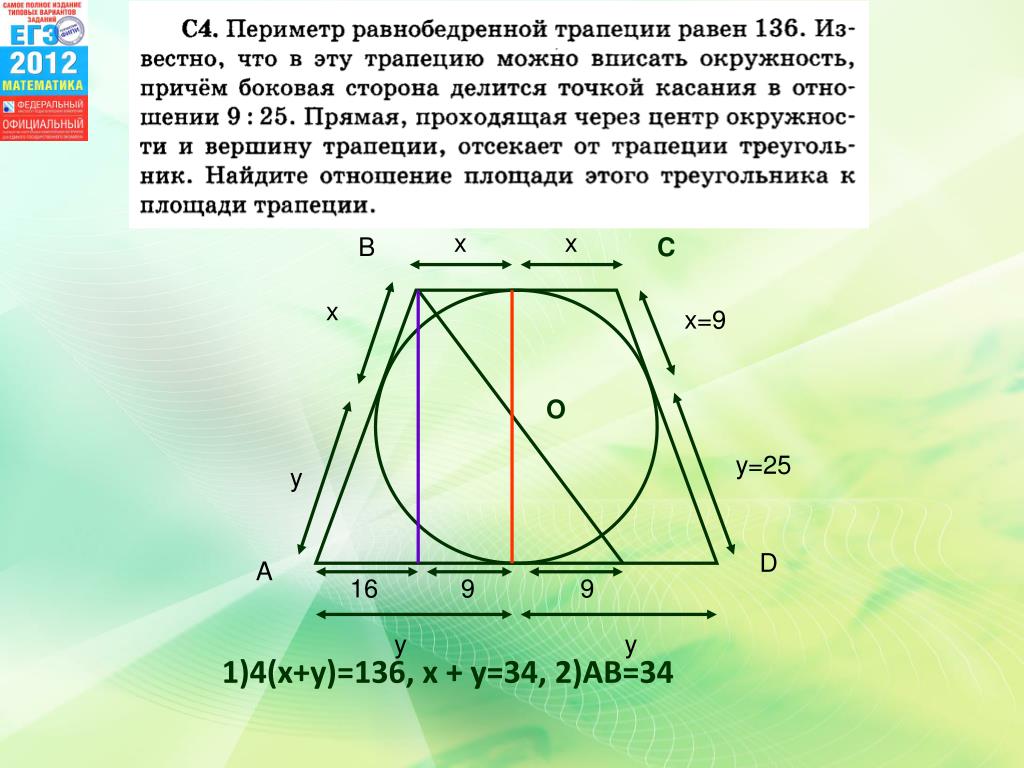 Таким образом, мы имеем:
Таким образом, мы имеем:
$латекс p=a+b+2c$
$латекс p=11+13+2(9)$
$латекс p=24+18$
$латекс p=42$
Периметр трапеции 42 м.
Начните прямо сейчас: изучите наши дополнительные ресурсы по математике
ПРИМЕР 4Если периметр трапеции равен 86 м, а три стороны равны 21 м, 23 м и 25 м, то какова длина четвертой стороны?
Решение
В данном случае ищем длину одной из сторон трапеции. Мы можем представить эту сторону с помощью d . Поэтому мы подставляем данные значения и находим d :
$латекс p=a+b+c+d$
$латекс 86=21+23+25+d$
$латекс d=86 -21-23-25$
$латекс d=17$
Длина четвертой стороны 17 м.
ПРИМЕР 5Если периметр равнобедренной трапеции равен 64 см, а длины ее параллельных сторон равны 13 см и 17 см, какова длина одной из ее боковых сторон?
Решение
Мы можем представить длину боковых сторон как c . Поэтому мы подставляем данные значения в формулу и находим c :
Поэтому мы подставляем данные значения в формулу и находим c :
$latex p=a+b+2c$
$latex 64=13+17+2c$
$латекс 64=30+2c$
$латекс 34=2c$
$латекс c=17$
Длина одной из боковых сторон 17 см.
Периметр трапеции – практические задачи
Примените на практике то, что вы узнали о периметре трапеции, со следующими задачами. Решите задачи и выберите свой ответ. Проверьте выбранный ответ, чтобы убедиться, что вы выбрали правильный.
Чему равен периметр трапеции со сторонами 7м, 8м, 9мм, а 10м?
Выберите ответ
$латекс p=31$ м
$латекс p=32$ м
$латекс p=33$ м
$latex p=34$ m
Чему равен периметр трапеции с параллельными сторонами 12 м и 13 м и боковыми сторонами 15 м?
Выберите ответ
$латекс p=50$ м
$латекс p=53$ м
$латекс p=55$ м
$латекс р=57$ м
Трапеция имеет периметр 65 м и стороны 14 м, 15 м и 16 м.



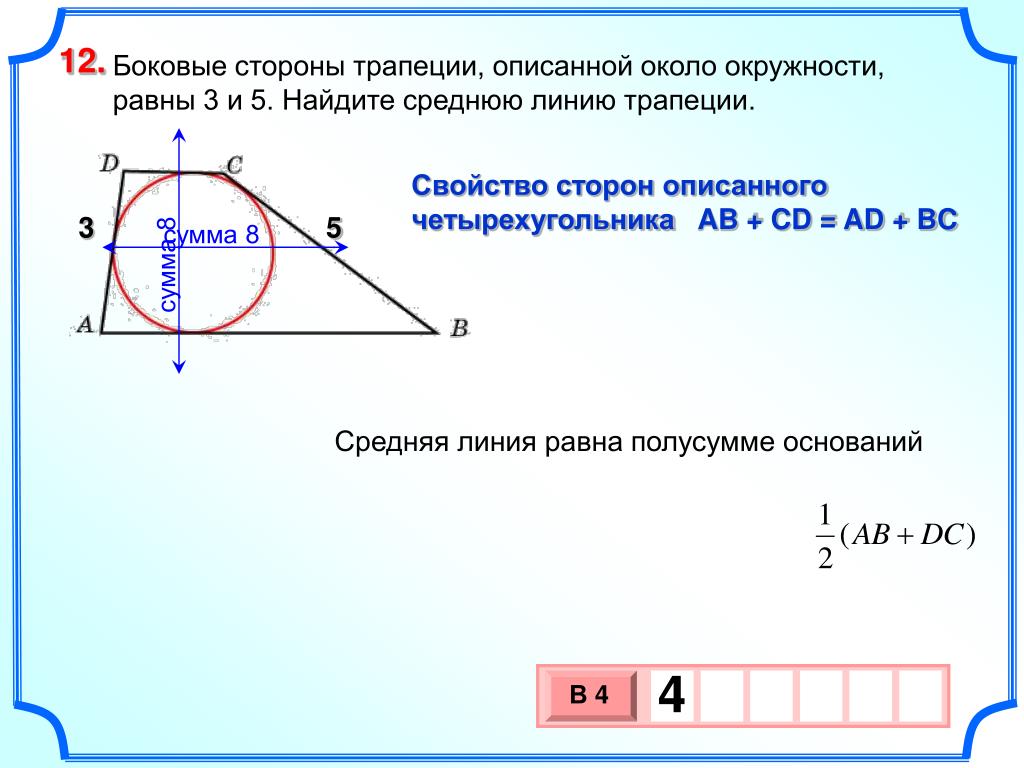 Гипотенуза у нас равна корню из суммы квадратов катетов.
Гипотенуза у нас равна корню из суммы квадратов катетов.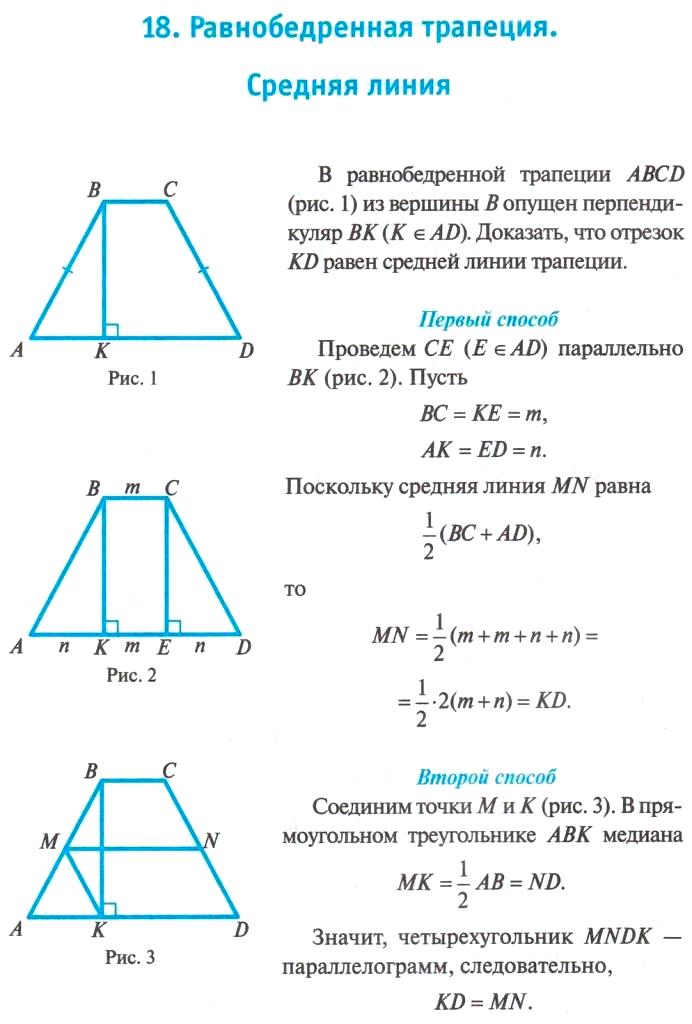 Поскольку у прямоугольника противоположные стороны равны АК = ВС = 6 см.
Поскольку у прямоугольника противоположные стороны равны АК = ВС = 6 см.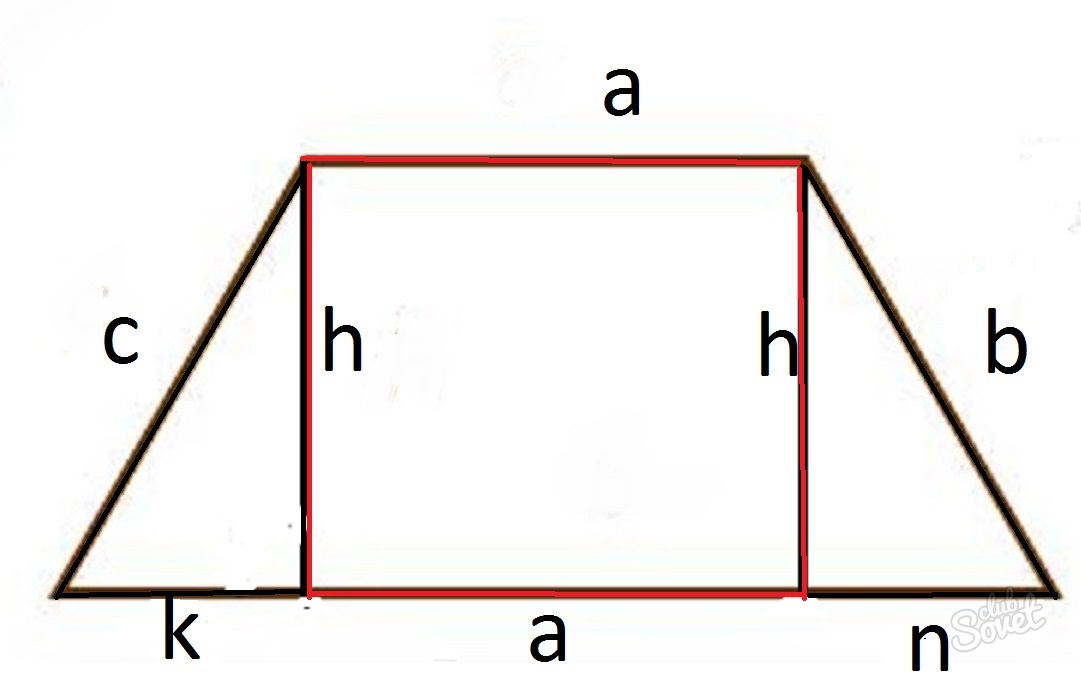
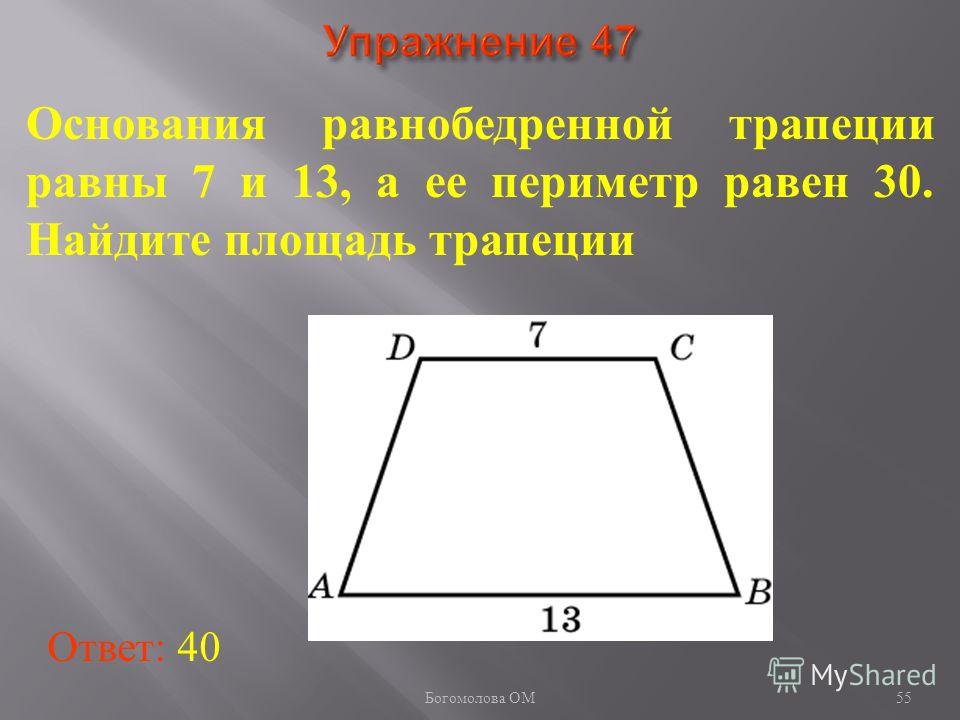 Итак, после применения теоремы Пифагора мы получаем AD 2 = AE 2 + DE 2 . Это означает, что 2 = 90 2 + 50 2 . Следовательно, н.э. 2 = 8100 + 2500 ⇒ н.э. = √10600 = 102,9 м.
Итак, после применения теоремы Пифагора мы получаем AD 2 = AE 2 + DE 2 . Это означает, что 2 = 90 2 + 50 2 . Следовательно, н.э. 2 = 8100 + 2500 ⇒ н.э. = √10600 = 102,9 м.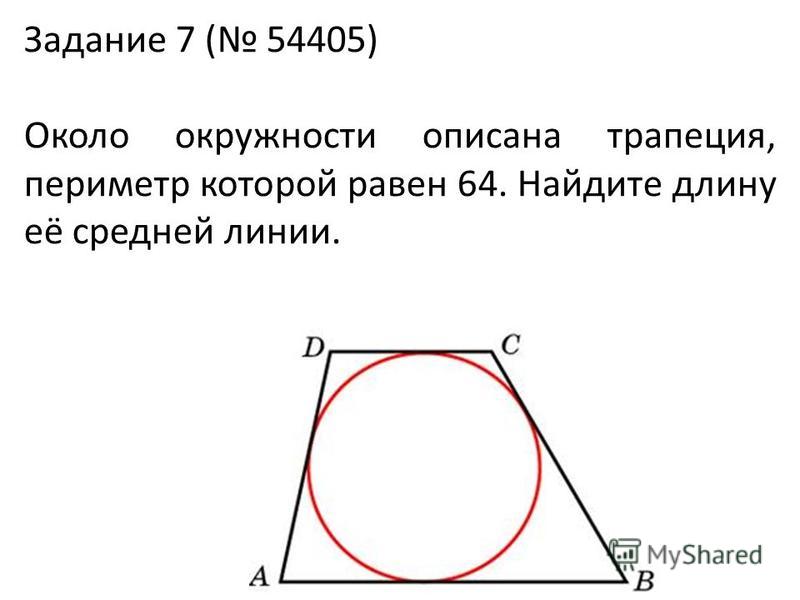
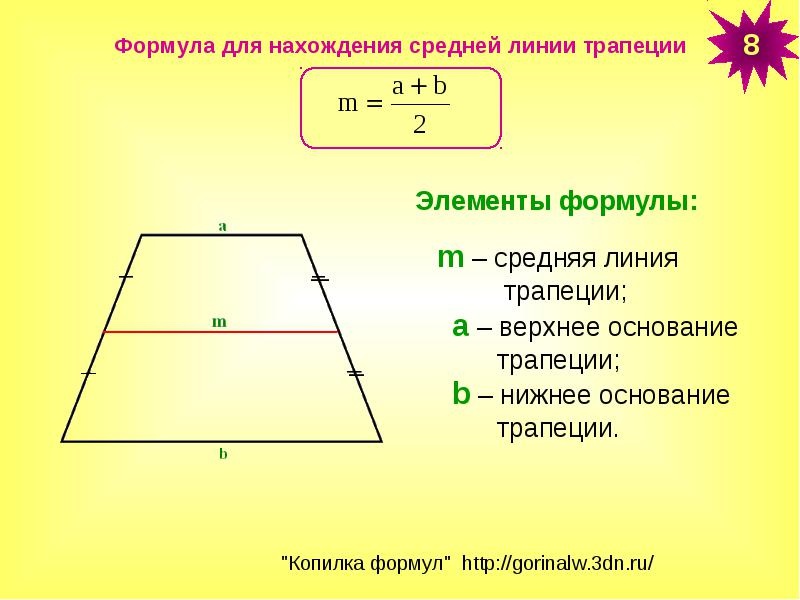
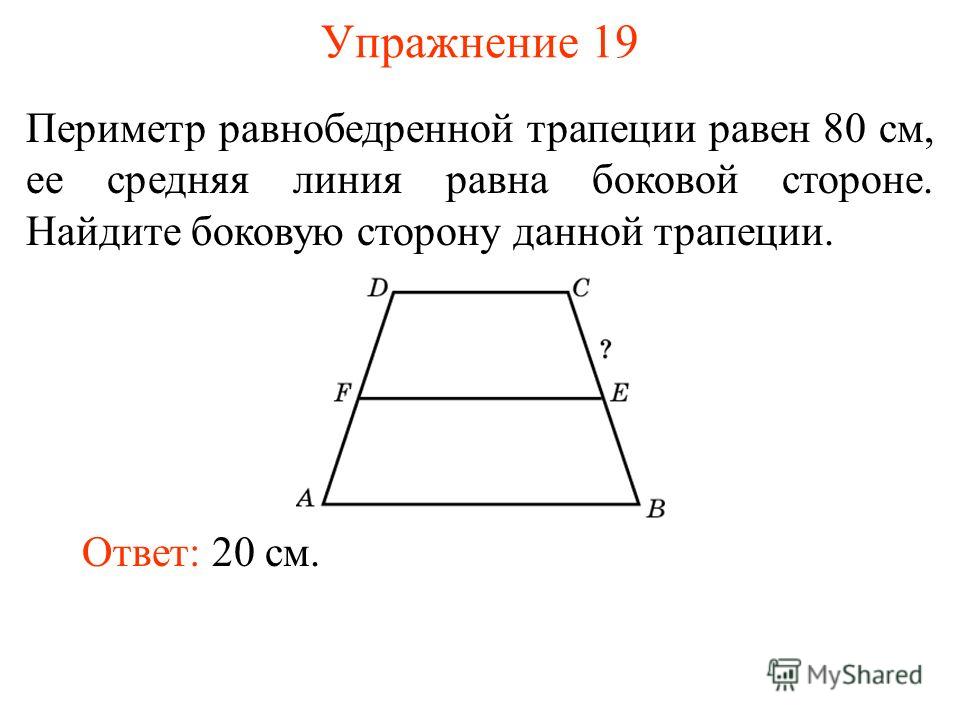 ck12.org/c/geometry
ck12.org/c/geometry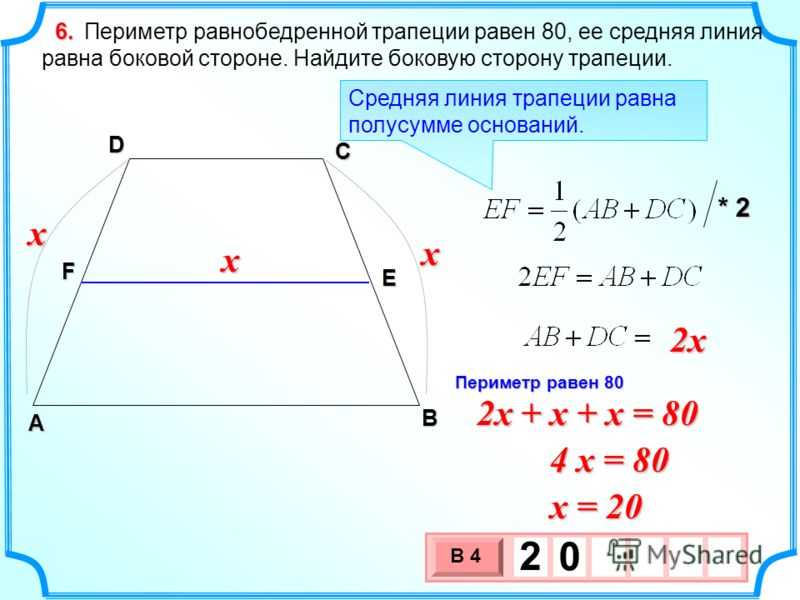
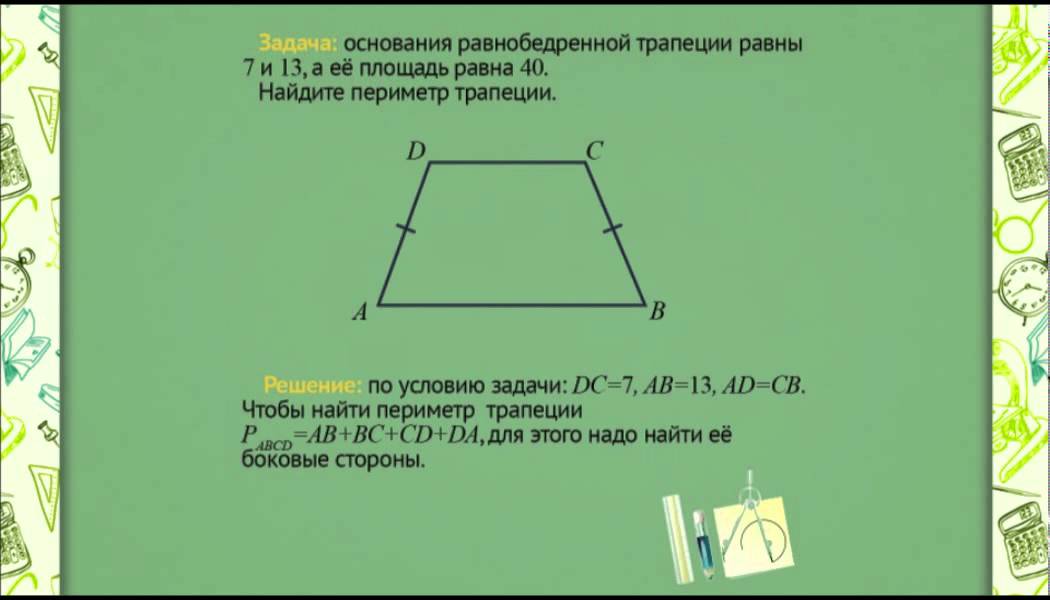 Таким образом, QR 2 = 6400 + 4900 ⇒ QR = √11300 = 106,301 м.
Таким образом, QR 2 = 6400 + 4900 ⇒ QR = √11300 = 106,301 м.
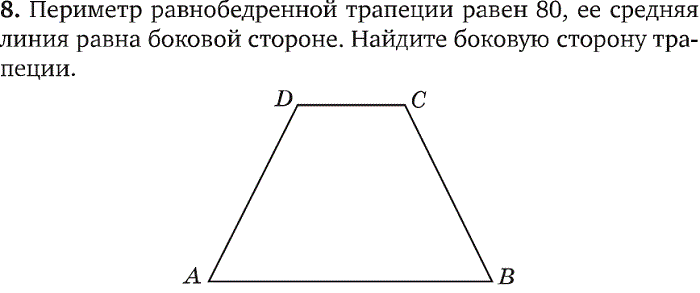 В американском английском это trapezium, а в британском английском — trapezium.
В американском английском это trapezium, а в британском английском — trapezium.