тригонометрической, множество функций, порядок нахождения
Содержание:
- Что такое функция в алгебре
-
Виды функций
- Линейная
- Обратная пропорциональность
- Квадратичная (квадратная)
- Степенная
- Показательная
- Логарифмическая
- Тригонометрические
-
Типы функций
- Важные свойства
-
Методы нахождения
- Перебор значений
- Графический метод
- Учет непрерывности и монотонности
- Производная, min и max
- Пример решения
- Что такое функция в алгебре
-
Виды функций
- Линейная
- Обратная пропорциональность
- Квадратичная (квадратная)
- Степенная
- Показательная
- Логарифмическая
- Тригонометрические
-
Типы функций
- Важные свойства
-
Методы нахождения
- Перебор значений
- Графический метод
- Учет непрерывности и монотонности
- Производная, min и max
- Пример решения
Что такое функция в алгебре
Определение
Функция в алгебре — некое математическое выражение y=f(x), где каждому значению переменной x соответствует одно значение переменной y.
Из этого следует, что решений у функции может быть много. Для обозначения совокупностей таких решений вводятся особые термины.
Определние
Множество значений функции y=f(x) — совокупность значений переменной y, которые она принимает при переборе всех значений переменной x на заданном отрезке X.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определение
Областью значений функции y=f(x) называется такое множество значений, которые функция y принимает при переборе всех значений аргумента x из области определения. Область значений обозначается как E(f).
Определение
Область допустимых значений (область определения) функции — такое множество всех значений переменных, при которых функция имеет смысл, то есть решается.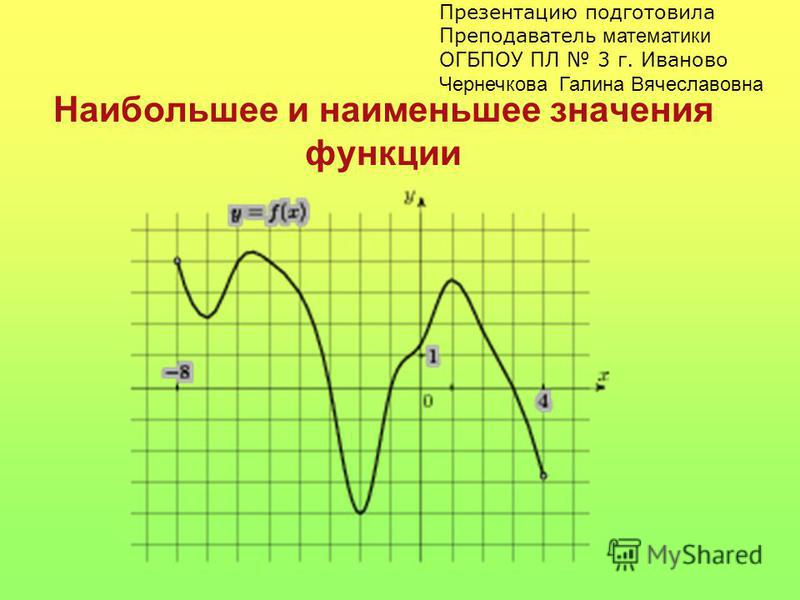 {\mathrm x}\)
{\mathrm x}\)
Для показательной функции существует одно определяющее условие: \(\mathrm a>0\). В связи с этим область ее значений включает в себя все положительные числа:
\(\mathrm E(\mathrm f)=(0;\;+\infty) \)
Логарифмическая
\(\mathrm y=\log_{\mathrm a}\left(\mathrm x\right)\)
По своим свойствам логарифмическая функция обратна показательной. Для данных функций область определения и область значений меняются местами соответственно. ОЗ логарифмической функции включает в себя все действительные числа:
\(\mathrm E(\mathrm f)=(-\infty;\;+\infty)\)
Тригонометрические
Рассмотрим четыре базовые тригонометрические функции:
- синус;
- косинус;
- тангенс;
- котангенс.
Первые две периодически повторяются в промежутке между -1 и 1:
\(\mathrm E(\mathrm f)=(-1;\;1)\)
Область значения тангенса и котангенса включает в себя все действительные числа:
\(\mathrm E(\mathrm f)=(-\infty;\;+\infty)\)
Типы функций
При определении области значений функции необходимо учитывать ее фундаментальные особенности. Обозначенная выше классификация — не единственная. У математических функций есть некоторые параметры, которые влияют как на саму область значений, так и на выбор методики ее нахождения.
Обозначенная выше классификация — не единственная. У математических функций есть некоторые параметры, которые влияют как на саму область значений, так и на выбор методики ее нахождения.
Важные свойства
К наиболее важным для поиска области значений функции относят следующие ее свойства:
- Непрерывность. Непрерывной называется функция, на графике которой нет «точек разрыва». Таким точкам соответствуют значения переменной, при которых функция не имеет смысла, то есть — исключенные из области определения.
- Монотонность. Монотонной называется функция, которая не возрастает или не убывает на всей области определения.
- Четность. Четной называется функция, не меняющая своего значения при смене знака переменной. То есть, f(-x)=f(x). Соответственно, нечетная функция меняет значение. Выделяют также функции общего вида, которые не симметричны относительно центра или оси координат.

- Периодичность. Периодическая функция повторяет свои значения через определенные равные интервалы значений переменной.
Методы нахождения
Поиск области значений функции несколько сложнее, чем определение ОДЗ. В зависимости от вида и типа функции, а также условий задачи для этого могут применяться различные методы.
Перебор значений
Самый простой и ограниченный способ. При его помощи можно находить область значений на небольшом промежутке целых чисел \(x\in(a;\;b)\). В таком случае заданные значения переменной поочередно подставляются в уравнение и вычисляются значения функции, соответствующие им.
Графический метод
Как ясно из названия способа, для его реализации необходимо построить график исследуемой функции. По внешнему виду кривой уже можно делать некоторые выводы. Если линия графика соответствует одному из видов элементарных функций, например, является параболой, то в качестве области значений берется промежуток, соответствующий данному графику.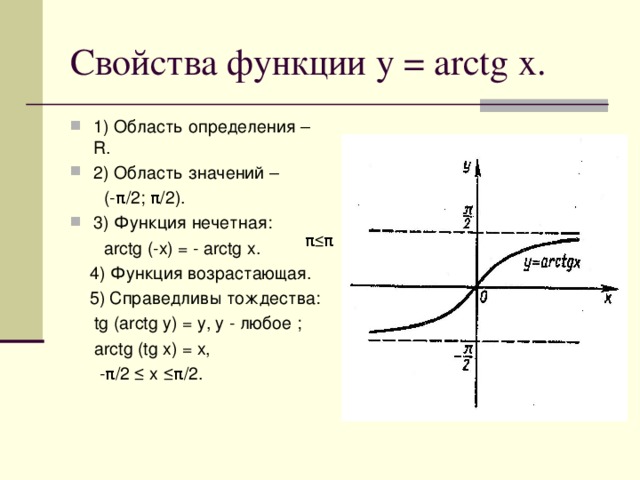
Рисунок 1. Значение непрерывности и монотонности функции для области определения
На графике видно, что функция монотонно убывает на промежутке \(\lbrack-4;\;0\rbrack\) и монотонно возрастает на промежутке\( \lbrack0;\;4\rbrack\). Исходя из этого и непрерывности функции, можно экстраполировать данную закономерность на всю область определения. Так как минимальное значение данной функции равняется нулю, область значений будет следующей:
\(\mathrm E(\mathrm f)=\lbrack0;\;+\infty)\)
Производная, min и max
Описанные выше способы подходят не для всех ситуаций. В общем случае, задача по определению области значений функции всегда сводится к нахождению ее минимального и максимального значения или точек экстремума.
Определение
Согласно теореме Ферма, в точках локального экстремума производная исследуемой функции равняется нулю.
Важно понимать, что сами локальный экстремум не обязательно является максимумом или минимумом для функции в целом. Такие точки называются критическими или стационарными. Поэтому, кроме самих точек необходимо определять промежутки возрастания и убывания:
- если при переходе через критическую точку производная функции меняет знак с (+) на (-), то эта точка является максимумом;
- если при переходе через критическую точку производная меняет знак с (-) на (+), то такая точка является минимумом;
- если при переходе знак производной не меняется, то экстремума в данной точке нет.
Кроме того, экстремумы функции можно определять по второй производной. Предположим, при исследовании функции обнаружилась некая критическая точка x_1. Для нее справедливы следующие неравенства:
Если \(f»(x_1)>0\), то \(x_1\) — точка минимума. 2-5\) следующая:
2-5\) следующая:
\(E(y)=\lbrack-6;\;+\infty).\)
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Поиск по содержимому
Область значения функции с примерами решения
Содержание:
- Области, значений некоторых функций
- Пример с решением
Областью (множеством) значений функции называется множество для каждого элемента у которого найдётся хотя бы одно значение аргумента такое, что
Область значений функции обозначается или
Области, значений некоторых функцийОбласть значений линейной функции есть множество всех действительных чисел если и множество, состоящее из одного значения если
По этой ссылке вы найдёте полный курс лекций по высшей математике:
| Высшая математика: лекции, формулы, теоремы, примеры задач с решением |
Пример с решением
Область значений функции состоит из единственного числа 3.
Область значений квадратичной функции определяется ординатой вершины параболы и направлением её ветвей:
- — если то ветви параболы направлены вверх, и
- — если то ветви параболы направлены вниз, и
С каждым уравнением (неравенством, системой) связаны конструирующие их аналитические выражения. Последние в свою очередь могут задавать функции одной или нескольких переменных. С этой точки зрения, например, уравнение мы можем рассматривать как задачу о нахождении значений аргумента при которых равны значения функций и
Такие, казалось бы, тривиальные рассуждения нередко дают возможность найти результативный путь решения многих задач. Кратко основную идею можно сформулировать так: ключ решения — свойства функций.
Возможно вам будут полезны данные страницы:
Прямые и плоскости в пространстве |
Решение кубических уравнений |
Формулы приведения |
Найти значение выражения |
По существу, в немалом числе ранее решенных примеров мы использовали свойства функций. Но при этом, выделяя идею решения, иначе расставляли акценты. В настоящем параграфе будем отдавать предпочтение функциональному подходу, суть которого достаточно ясно раскрывается на следующем простом примере. Требуется решить неравенство С одной стороны, используя свойства числовых неравенств (возведение обеих частей в четную степень), можно показать, что неравенство равносильно
Но при этом, выделяя идею решения, иначе расставляли акценты. В настоящем параграфе будем отдавать предпочтение функциональному подходу, суть которого достаточно ясно раскрывается на следующем простом примере. Требуется решить неравенство С одной стороны, используя свойства числовых неравенств (возведение обеих частей в четную степень), можно показать, что неравенство равносильно
С другой стороны, функциональный взгляд позволяет рассуждать так: перепишем исходное неравенство в виде
Далее, учитывая характер монотонности функции получаем
Прежде чем непосредственно приступить к изучению вопроса, отметим, что пункты этого параграфа, за малым исключением, соответствуют стандартной схеме исследования функции.
И последнее. Мы посчитали нецелесообразным посвящать отдельный пункт области определения функции, что понятно, так как, работая с уравнением,неравенством, системой, почти всегда приходится учитывать их области определения.
А, Область значения функции. Вначале обратимся к задачам, в условии которых непосредственно содержится требование поиска области значения функции.
Вначале обратимся к задачам, в условии которых непосредственно содержится требование поиска области значения функции.
Пример 1.
Найти все целые при которых множество значений функции не пересекается с
промежутком
Решение:
Имеем
Очевидно Отсюда
Следовательно, область определения функции — промежуток
Полученный промежуток не должен иметь общих точек с лучом
Понятно, что для этого достаточно потребовать
Отсюда или
Ответ,
Пример 2.
При каких область значений функции не содержит ни одного целого четного числа ?
Решение:
Для нахождения области определения данной функции удобно воспользоваться известным приемом. Рассмотрим равенство как уравнение с параметрами и переменной Теперь поставим следующую задачу: найти все значения параметра при которых найдется такое что указанное уравнение имеет хотя бы одно решение.
Так как то переходим к равносильному уравнению Отсюда Проверка показывает, что при это уравнение не имеет решений. Следовательно, Ясно, что это уравнение имеет решение, если С учетом
Следовательно, Ясно, что это уравнение имеет решение, если С учетом
получаем Значит, область знчения данной функции — промежуток Полученный интервал не
содержит ни одного четного числа, если он полностью «помещается» в отрезке где Для выполнения этого условия достаточно потребовать
Перепишем эту систему в таком виде:
Понятно, что она имеет решения, если
Отсюда возможны два случая: Без труда устанавливаем, что в первом случае во втором
Ответ,
Пример 3.
Найти все значения параметра для которых отрезок принадлежит области значений функции
Решение:
Пусть — одно из значений данной функции. Переформулируем условие задачи: найти все такие, что для
любого уравнение имеет решения. Прежде всего заметим, что при не корень этого уравнения. Теперь запишем систему, равносильную рассматриваемому уравнению:
Отсюда так как Следовательно, при условие выполняется «автоматически».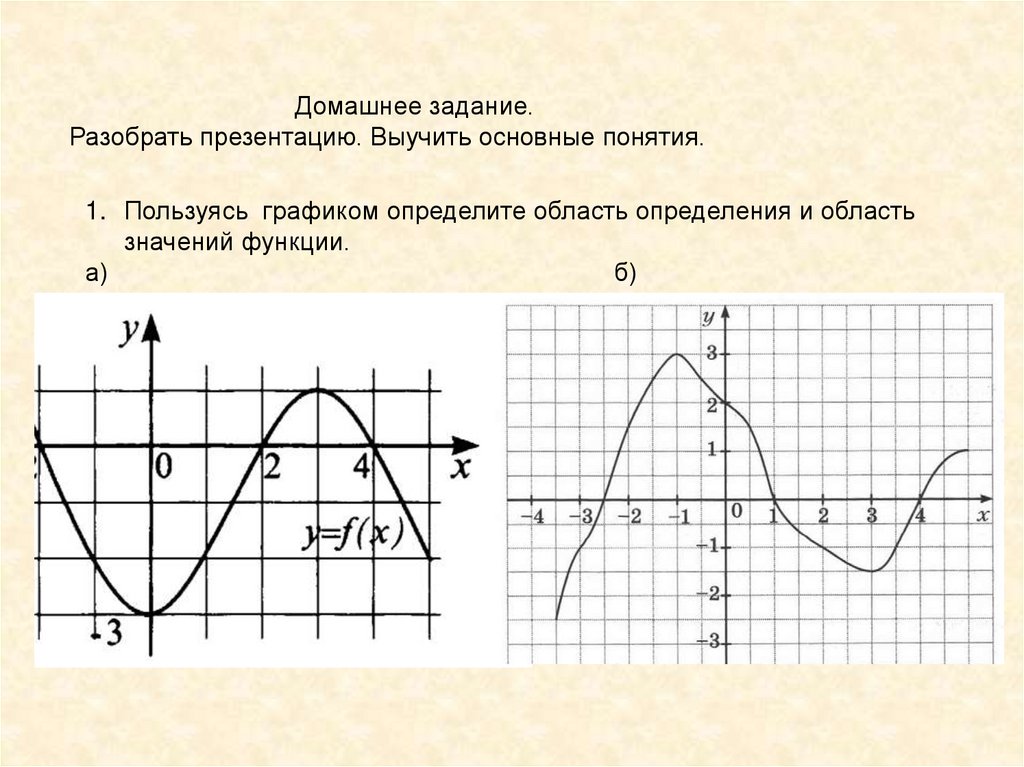 Осталось выяснить, при каких система
Осталось выяснить, при каких система
имеет решения. Понятно, что дискриминант квадратного уравнения системы должен быть неотрицательным, т.е.
Получаем Пусть Тогда Рассмотрим квадратичную функцию
на отрезке Для неотрицательности дискриминанта достаточно потребовать, чтобы не превосходило наименьшего значения функции на отрезке
Так как рассматриваемая функция на указанном отрезке возрастает то Итак
Ответ,
Условие следующих двух задач не содержит прямой подсказки использовать область значения функции. Такая необходимость возникает в ходе решения.
Пример 4. При каких значениях найдутся такие что числа будут являться последовательными членами геометрической прогрессии?
Решение:
По свойству членов геометрической прогрессии
Пусть Рассмотрим функцию в области определения Имеем
так как Заметим, что и в силу непрерывности функции ее область значений в указанной области определения — это промежуток Следовательно, найдутся такие Отсюда
Ответ.
Пример 5. Решить систему
Решение:
Напрашивается замена где
Имеем
Отсюда легко получить
Тогда
Учитывая области значений функций записываем систему, определяющую область допустимых значений параметра
Отсюда При таких имеем
Ответ. Если при других решений нет.
В последнем примере идея замены довольно прозрачна. Однако подобная ситуация встречается отнюдь не всегда.
Ниже рассмотрим тип задач, в которых область значений функций помогает найти далеко не очевидную замену. Вначале изложим суть вопроса в общем виде. Пусть в задаче фигурирует переменная область допустимых значений которой множество Если существует такая функция с той же областью значений то при необходимости возможно провести замену
Подобные замены порой существенно упрощают решение. Поясним сказанное на примере. Пусть из условия задачи следует, что переменная пробегает все значения из отрезка и только эти. 2
2
Понятие функции. Область определения функции. Множество значений функции
| Справочник по математике | Элементы математического анализа | Функции |
Содержание
| Понятие функции. Область определения функции. Множество значений функции |
| Примеры решения задач |
Понятие функции. Область определения функции. Множество значений функции
ОПРЕДЕЛЕНИЕ. Пусть X – некоторое множество чисел. Говорят, что на множестве X задана числовая функция, если указано правило, с помощью которого каждому числу x из множества X ставится в соответствие некоторое число.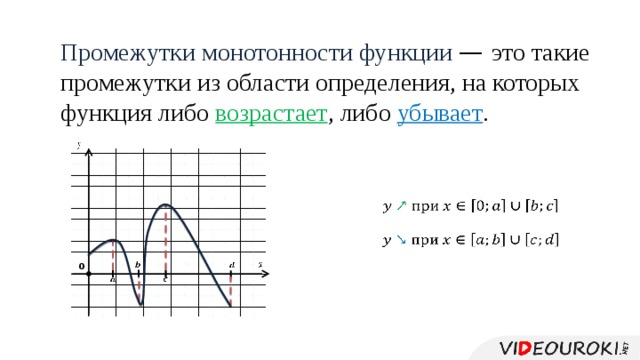
Это принято обозначать так:
y = f (x),
причем в этой записи x называют аргументом функции или независимой переменной, а y называют значением функции, соответствующим аргументу x .
Множество X называют областью определения функции f и обозначают D ( f ) . Множество Y всех возможных значений функции y = f (x) называют множеством значений функции f и обозначают E ( f ) (рис. 1).
Рис.1
Примеры решения задач
Часто в задачах известна формула, задающая функцию f , и требуется найти наиболее широкое множество чисел, к которым данную формулу можно применить. В этом случае указанная задача формулируется так: «Найти область определения функции y = f (x)». В некоторых задачах требуется найти не только область определения функции, но и множество ее значений.
В некоторых задачах требуется найти не только область определения функции, но и множество ее значений.
ЗАДАЧА 1. Найти область определения функции
РЕШЕНИЕ. Указанная функцию представляет собой результат, полученный при делении числа x4 на число (3 + x) . Поскольку единственным ограничением является запрет деления на число 0 , то число (3 + x) не может равняться 0 , то есть .
ОТВЕТ. .
ЗАДАЧА 2. Найти область определения функции
РЕШЕНИЕ. Поскольку квадратный корень можно извлекать только из неотрицательных чисел, то область определения данной функции задается неравенством
которое эквивалентно неравенству
и может быть записано в виде
.
Решая это неравенство с помощью метода интервалов, получим
ОТВЕТ.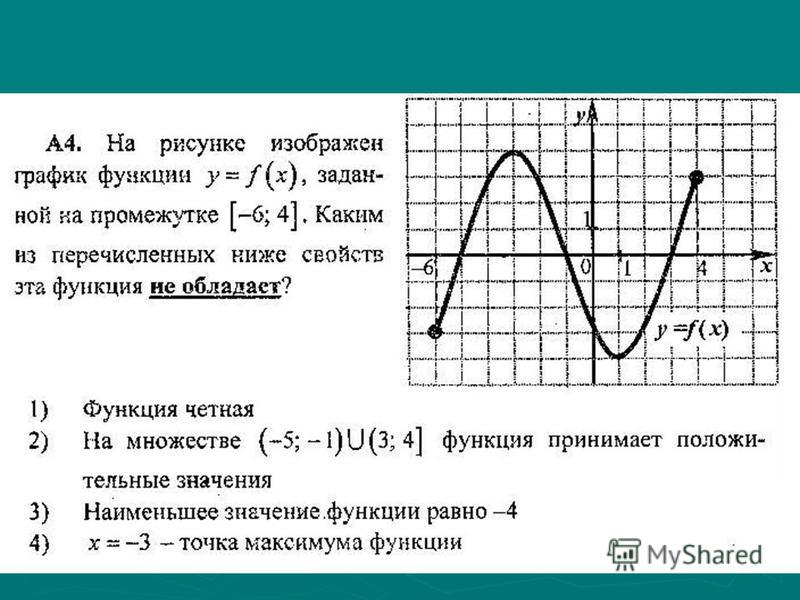 .
.
ЗАДАЧА 3. Найти область определения функции
РЕШЕНИЕ. Исходя из определений логарифма и квадратного корня, область определения данной функции задается следующей системой неравенств
| (1) |
Решая второе неравенство системы с помощью метода интервалов,
получим
Таким образом, система (1) эквивалентна системе
Решением этой системы является интервал
ОТВЕТ. .
ЗАДАЧА 4 . Найти множество значений функции
y = 3sin x + 4cos x
РЕШЕНИЕ. Воспользовавшись формулой дополнительного угла (вспомогательного аргумента), получим
y = 5 sin (x + φ) ,
где
Поскольку множеством значений функции y = sin (x + φ) является отрезок [–1, 1], то множеством значений функции y = 5 sin (x +φ) будет отрезок [–5, 5].
ОТВЕТ. .
ЗАДАЧА 5 . Найти множество значений функции
y = x2 + 6x + 8
РЕШЕНИЕ. Поскольку
и для каждого числа существуют решения уравнения
x2 + 6x + 8 = y ,
определяемые формулой
то множеством значений функции y = x2 + 6x + 8 будет множество .
ОТВЕТ. .
Тема урока «Множество значений функции в задачах ЕГЭ. Область значений функции (множество значений функции). Необходимые понятия и примеры нахождения
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.

- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
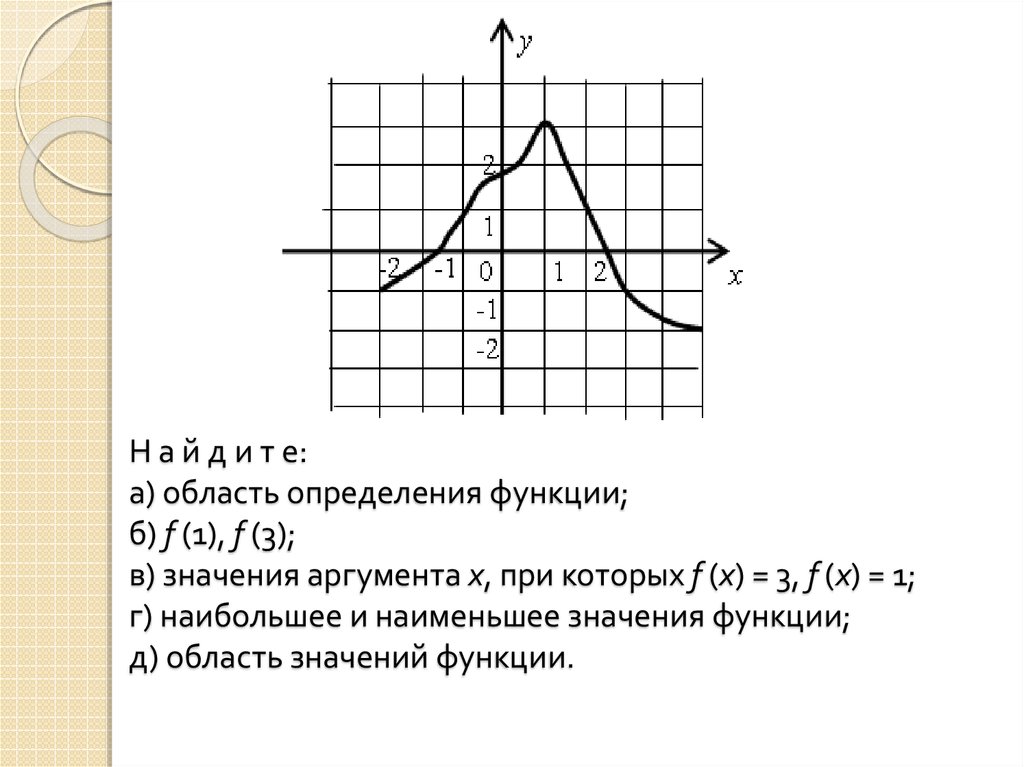
Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции
- область значений функции
- нули функции
- промежутки возрастания и убывания
- точки максимума и минимума
- наибольшее и наименьшее значение функции на отрезке.

Уточним терминологию:
Абсцисса — это координата точки по горизонтали.
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось .
Ось ординат — вертикальная ось, или ось .
Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается .
Другими словами, мы сами выбираем , подставляем в формулу функции и получаем .
Область определения функции — множество тех (и только тех) значений аргумента , при которых функция существует.
Обозначается: или .
На нашем рисунке область определения функции — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок — от самого нижнего до самого верхнего значения .
Нули функции — точки, где значение функции равно нулю, то есть .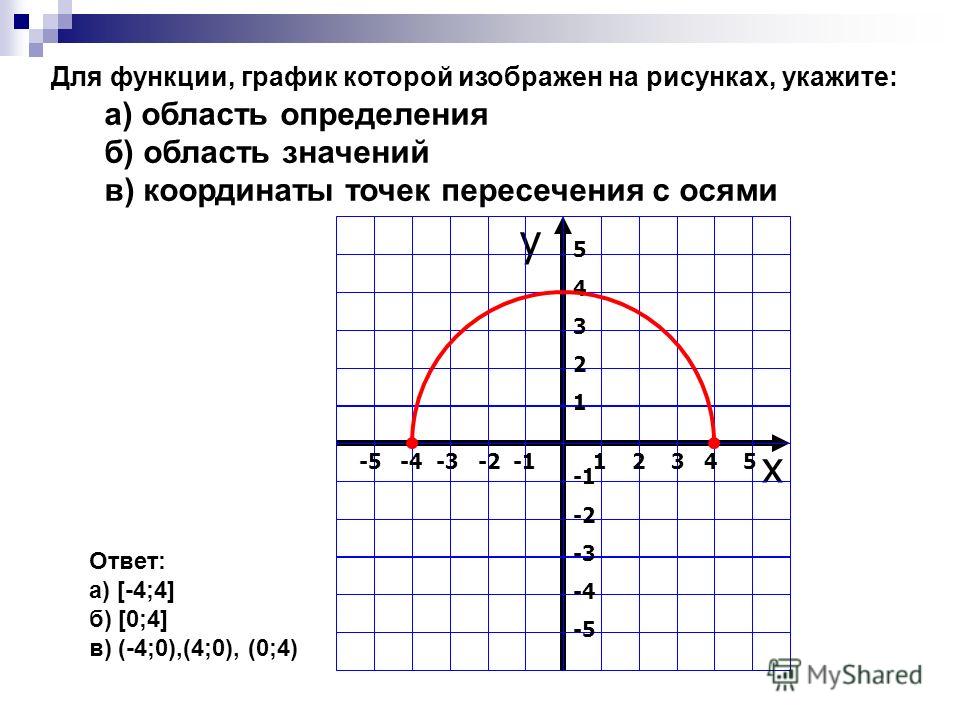 На нашем рисунке это точки и .
На нашем рисунке это точки и .
Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.
Функция возрастает
Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.
Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Для убывающей функции большему значению соответствует меньшее значение . График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .
Определим, что такое точки максимума и минимума функции .
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше , чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».
На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции . В нашем случае это и .
А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке .
Можно сказать, что экстремумы функции равны и .
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ САХАЛИНСКОЙ ОБЛАСТИ
ГБПОУ «СТРОИТЕЛЬНЫЙ ТЕХНИКУМ»
Практические работы
По дисциплине «Математика»
Раздел: « Функции, их свойства и графики».
Тема: Функции. Область определения и множество значений функции. Четные и нечетные функции.
(дидактический материал)
Составила:
Преподаватель
Казанцева Н. А.
А.
Южно-сахалинск-2017
Практические работы по математике по разделу « и методические указания по их выполнению предназначены для студентов ГБПОУ «Сахалинский строительный техникум»
Составител ь : Казанцева Н. А., преподаватель математики
Материал содержит практические работы по математике « Функции, их свойства и графики» и указания по их выполнению. Методические указания составлены в соответствии с рабочей программой по математике и предназначены для студентов Сахалинского строительного техникума , обучающихся по программам общего образования.
1)Практическое занятие №1. Функции. Область определения и множество значений функции.………………………………………………………………4
2)Практическое занятие №2 . Четные и нечетные функции……………….6
Практическое занятие №1
Функции. Область определения и множество значений функции.
Цели: закрепить умения и навыки решения задач по теме: «Область определения и множество значений функции.
Оборудование:
Указание. Сначала следует повторить теоретический материал по теме: «Область определения и множество значений функции», после чего можно приступать к выполнению практической части.
Методические указания:
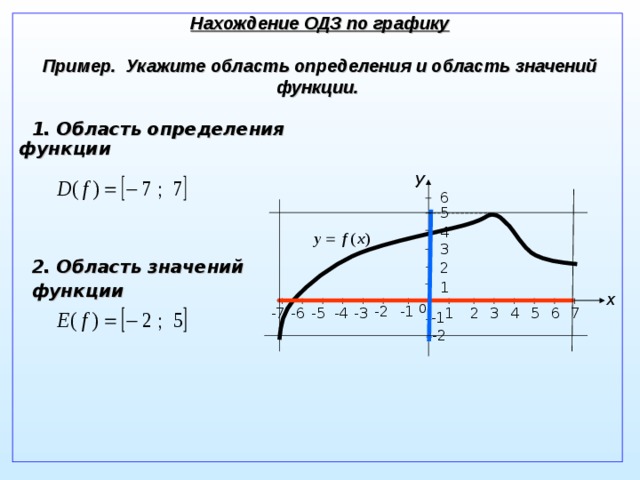
Определение : Область определения функции – это множество всех значений аргумента х, на котором задается функция (или множество х при которых функция имеет смысл).
Обозначение: D (у), D ( f )- область определения функции.
Правило: Для нахождения о бласти определения функции по графику необходимо график спроектировать на ОХ.
Определение: Область значения функции – это множество у, при которых функция имеет смысл.
Обозначение: Е(у), Е(f )- область значения функции.
Правило: Для нахождения о бласти значения функции по графику необходимо график спроектировать на ОУ.
№ 1.Найдите значения функции:
a ) f (x ) = 4 x + в точках 2;20 ;
б) f (x ) = 2 · cos (x ) в точках; 0;
в) f (x ) = в точках 1;0; 2;
г) f (x ) = 6 sin 4 x в точках; 0;
е)
f
(x
) = 2 9
x
+ 10 в точках 2; 0; 5.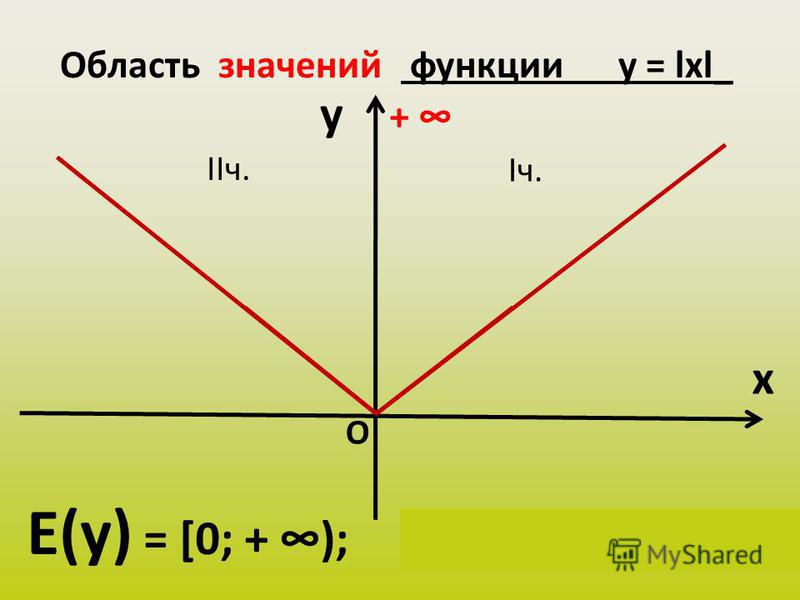
№ 2.Найдите область определения функции:
a) f(x) = ; б ) f(x) = ; в ) f(x) = ;
г) f (x ) = ; д) f (x ) = ; е) f (x ) = 6 x +1;
ж) f (x ) = ; з) f (x ) = .
№3. Найдите область значений функции:
а) f (x ) = 2+3 x ; б) f (x ) = 2 7 x + 3.
№ 4.Найдите область определения и область значения функции, график которой изображен на рисунке:
Практическое занятие №2
Четные и нечетные функции.
Цели: закрепить умения и навыки решения задач по теме: «Четные и нечетные функции».
Оборудование: тетрадь для практических работ, ручка, методические рекомендации по выполнению работы
Указание. Сначала следует повторить теоретический материал по теме: «Четные и нечетные функции», после чего можно приступать к выполнению практической части.
Не забывайте о правильном оформлении решения.
Методические указания:
К важнейшим свойствам функций относится четность и нечетность.
Определение: Функция называется нечетной меняет свое значение на противоположное,
т.е. f (х )= f (х ) .
График нечетной функции симметричен относительно начала координат (0;0).
Примеры : нечетными функциями являются у=х, у= , у= sin х и др.
Например, график у= действительно обладает симметричностью относительно начала координат (см. рис.1):
Рис.1. Г рафик у= (кубическая парабола)
Определение: Функция называется четной , если при изменении знака аргумента, она не меняет свое значение, т.е. f (х )= f (х ) .
График четной функции симметричен относительно оси ОУ.
Примеры : четными функциями являются функции у= , у= ,
у= cos x и др.
Например, покажем симметричность графика у= относительно оси ОУ:
Рис.2. Г рафик у=
Задания для практической работы:
№1. Исследуйте функцию на четность или нечетность аналитическим путем:
1) f (х ) = 2 х 3 – 3; 2) f (х ) = 5 х 2 + 3;
3) g (х ) = – + ; 4) g (х ) = –2 х 3 + 3;
5) у(х)= 7хс tg x ; 6) у(х)= + cos x ;
7)
t
(х)=
tg
x
3; 8)
t
(х)= +
sin
x
.
№2. Исследуйте функцию на четность или нечетность аналитическим путем:
1) f (х ) = ; 2) f (х ) = 6 + · sin 2 x · cos x ;
3) f (х ) = ; 4) f (х ) = 2 + · cos 2 x · sin x ;
5) f (х ) = ; 6) f (х ) = 3 + · sin 4 x · cos x ;
7) f (х ) = ; 8) f (х ) = 3 + · cos 4 x · sin x .
№3. Исследуйте функцию на четность или нечетность по графику:
№4. Проверьте, является ли четной или нечетной функция?
Функция y=f(x) — это такая зависимость переменной y от переменной x , когда каждому допустимому значению переменной x соответствует единственное значение переменной y .
Областью определения функции D(f) называют множество всех допустимых значений переменной x .
Область значений функции E(f) — множество всех допустимых значений переменной y .
График функции y=f(x)
— множество точек плоскости, координаты которых удовлетворяют данной функциональной зависимости, то есть точек, вида M
(x; f(x))
.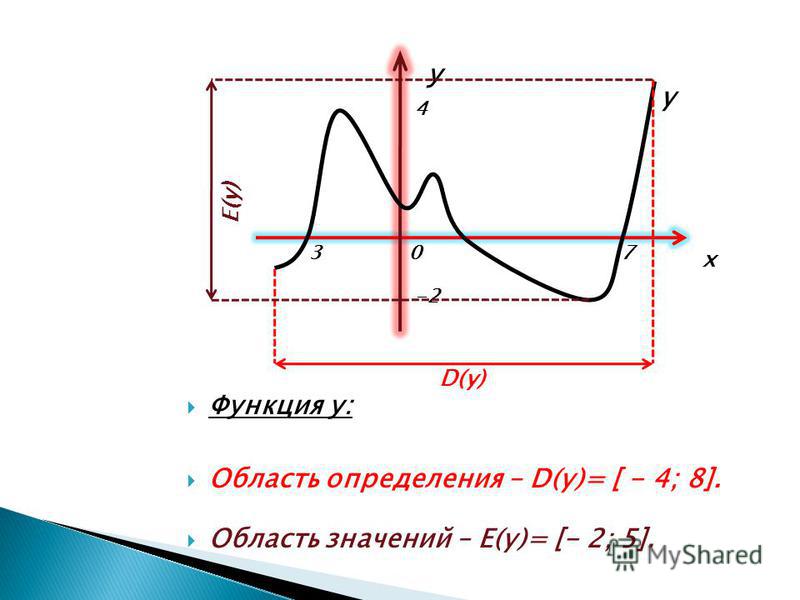 График функции представляет собой некоторую линию на плоскости.
График функции представляет собой некоторую линию на плоскости.
Если b=0 , то функция примет вид y=kx и будет называться прямой пропорциональностью .
D(f) : x \in R;\enspace E(f) : y \in R
График линейной функции — прямая.
Угловой коэффициент k прямой y=kx+b вычисляется по следующей формуле:
k= tg \alpha , где \alpha — угол наклона прямой к положительному направлению оси Ox .
1) Функция монотонно возрастает при k > 0 .
Например: y=x+1
2) Функция монотонно убывает при k
Например: y=-x+1
3) Если k=0 , то придавая b произвольные значения, получим семейство прямых параллельных оси Ox .
Например: y=-1
Обратная пропорциональность
Обратной пропорциональностью называется функция вида y=\frac {k}{x} , где k — отличное от нуля, действительное число
D(f) : x \in \left \{ R/x \neq 0 \right \}; \: E(f) : y \in \left \{R/y \neq 0 \right \} .
Графиком функции y=\frac {k}{x}
является гипербола.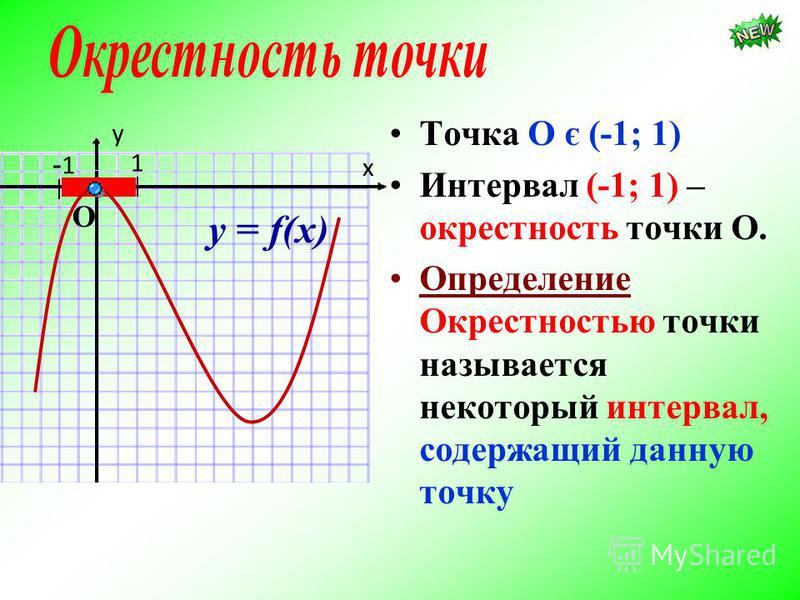 2
. D(f) : x \in R; \: E(f) : y \in
; основной период функции T=2 \pi
2
. D(f) : x \in R; \: E(f) : y \in
; основной период функции T=2 \pi
Инструкция
Вспомните, что функция — это такая зависимость переменной Y от переменной Х, при которой каждому значению переменной X соответствует единственное значение переменной Y.
Переменная X является независимой переменной или аргументом. Переменная Y — зависимая переменная. Считается также, что переменная Y является функцией от переменной X. Значения функции равны значениям зависимой переменной.
Для наглядности записывайте выражения. Если зависимость переменной Y от переменной X является функцией, то это записывают так: y=f(x). (Читают: у равно f от х.) Символом f(x) обозначьте значение функции, соответствующее значению аргумента, равному х.
Исследование функции на четность или нечетность — один из шагов общего алгоритма исследования функции, необходимого для построения графика функции и изучения её свойств. В этом шаге необходимо определить, является ли функция четной или нечетной. Если про функцию нельзя сказать, что она является четной или нечетной, то говорят, что это функция общего вида.
Если про функцию нельзя сказать, что она является четной или нечетной, то говорят, что это функция общего вида.
Инструкция
Подставьте аргумента x аргумент (-x) и посмотрите, что получилось в итоге. Сравните с изначальной функцией y(x). Если y(-x)=y(x), имеем четную функцию. Если y(-x)=-y(x), имеем нечетную функцию. Если y(-x) не равняется y(x) и не равняется -y(x), имеем функцию общего вида.
Все операции с функцией можно производить только в том множестве, где она определена. Поэтому при исследовании функции и построения ее графика первую роль играет нахождение области определения.
Инструкция
Если функция имеет вид y=g(x)/f(x), решите f(x)≠0, потому что знаменатель дроби не может быть равен нулю. Например, y=(x+2)/(x−4), x−4≠0. То есть областью определения будет множество (-∞; 4)∪(4; +∞).
Когда при определении функции присутствует корень четной , решите неравенство, где значение будет больше или равно нуля. Корень четной степени может быть взят только из неотрицательного числа. Например, y=√(x−2), x−2≥0. Тогда областью определения является множество , то есть если y=arcsin(f(x)) или y=arccos(f(x)), нужно решить двойное неравенство -1≤f(x)≤1. Например, y=arccos(x+2), -1≤x+2≤1. Областью определения будет отрезок [-3; -1].
Например, y=√(x−2), x−2≥0. Тогда областью определения является множество , то есть если y=arcsin(f(x)) или y=arccos(f(x)), нужно решить двойное неравенство -1≤f(x)≤1. Например, y=arccos(x+2), -1≤x+2≤1. Областью определения будет отрезок [-3; -1].
Наконец, если задана комбинация различных функций, то область определения представляет собой пересечение областей определения всех этих функций. Например, y=sin(2*x)+x/√(x+2)+arcsin(x−6)+lg(x−6). Сначала найдите область определения всех слагаемых. Sin(2*x) определен на всей числовой прямой. Для функции x/√(x+2) решите неравенство x+2>0 и область определения будет (-2; +∞). Область определения функции arcsin(x−6) задается двойным неравенством -1≤x-6≤1, то есть получается отрезок . Для логарифма имеет место неравенство x−6>0, а это есть интервал (6; +∞). Таким образом, областью определения функции будет множество (-∞; +∞)∩(-2; +∞)∩∩(6; +∞), то есть (6; 7].
Видео по теме
Источники:
- область определения функции с логарифмом
Функция — это понятие, отражающее связь между элементами множеств или другими словами это «закон», по которому каждому элементу одного множества (называемому областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
1.Понятие функции. 2.Свойства функций. 3.Основные элементарные функции.
|
|||||||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 9 | |||||||||||||||||||||||||||||
1. Понятие функции Понятие «функция» является одним из основных понятий в математике. Под функцией понимают некий закон, по которому одна переменная величина зависит от другой.
|
|||||||||||||||||||||||||||||
2. Cвойства функций 1. 2.Монотонность. Функция называется возрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции, т.е. при x1< (>) x2, f(x1) < (>) f(x2). 3.Периодичность. Если значение функции f(x) повторяется через определенный период Т, то функция называется периодической с периодом Т ≠ 0 , т.е. f(x + T) = f(x). В противном случае непериодической. 4. Ограниченность. Функция f (x) называется ограниченной на промежутке Х, если существует такое положительное число М > 0 , что для любого x, принадлежащего промежутку Х, | f (x) | < M.
|
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
3. Основные элементарные функцииСтепенная функция у = х |
|
||||||||||||||||||||||||||||
| у = х² область определения (-∞,∞) |
|
||||||||||||||||||||||||||||
| у = х³ область определения (-∞,∞) |
|
||||||||||||||||||||||||||||
| у = 1/х область определения (-∞,0)U(0,∞) |
|
||||||||||||||||||||||||||||
| у = 1/х² область определения (-∞,0)U(0,∞) |
|
||||||||||||||||||||||||||||
|
область определения [0,∞) |
|
||||||||||||||||||||||||||||
|
область определения (-∞,∞) |
|
||||||||||||||||||||||||||||
Показательная функция у = а ͯ (a>0 a≠1) область определения (-∞,∞) |
|
||||||||||||||||||||||||||||
Логарифмическая функция у = log ₐ x (a>0 a≠1) область определения (0,∞) |
|
||||||||||||||||||||||||||||
Тригонометрические функции y = sin x область определения (-∞; ∞) |
|
||||||||||||||||||||||||||||
y = cos x область определения (-∞; ∞) |
|
||||||||||||||||||||||||||||
y = tg x область определения |
|
||||||||||||||||||||||||||||
y = ctg x область определения |
|
||||||||||||||||||||||||||||
y = arcsin x область определения [-1; 1] |
|
||||||||||||||||||||||||||||
y = arccos x область определения [-1; 1] |
|
||||||||||||||||||||||||||||
y = arctg x область определения (-∞; ∞) |
|
||||||||||||||||||||||||||||
y = arcctg x область определения (-∞; ∞) |
|||||||||||||||||||||||||||||
Пример 1.
Найти область определения функции. |
|||||||||||||||||||||||||||||
Пример 2Выяснить четность или нечетность функции. |
График функции y=x³+2sin x |
||||||||||||||||||||||||||||
Пример 3 |
|||||||||||||||||||||||||||||
| 1 2 3 4 5 6 7 8 9 | |||||||||||||||||||||||||||||
.
 Какова область действия переменных в JavaScript?
Какова область действия переменных в JavaScript?TLDR
JavaScript имеет лексическую (также называемую статической) область видимости и замыкания. Это означает, что вы можете определить область действия идентификатора, просмотрев исходный код.
Четыре области действия:
- Глобальная — видна всем
- Функция — видна внутри функции (и ее подфункций и блоков)
- Блок — виден внутри блока (и его подблоков)
- Модуль — виден внутри модуля
Вне особых случаев глобальной области и области модуля переменные объявляются с использованием var (область функции), let (область действия блока) и const (область действия блока). Большинство других форм объявления идентификатора имеют блочную область видимости в строгом режиме.
Обзор
Область действия — это область кодовой базы, в которой действует идентификатор.
Лексическая среда — это сопоставление между именами идентификаторов и связанными с ними значениями.
Область действия формируется из связанной вложенности лексических сред, причем каждый уровень вложенности соответствует лексической среде родительского контекста выполнения.
Эти связанные лексические среды образуют «цепочку» области видимости. Разрешение идентификатора — это процесс поиска в этой цепочке совпадающего идентификатора.
Разрешение идентификатора происходит только в одном направлении: наружу. Таким образом, внешнее лексическое окружение не может «видеть» внутреннее лексическое окружение.
Существует три важных фактора, определяющих область действия идентификатора в JavaScript:
- Как был объявлен идентификатор
- Где был объявлен идентификатор
- Независимо от того, находитесь ли вы в строгом или нестрогом режиме
Некоторые из способов объявления идентификаторов:
-
var,letиconst - Параметры функции
- Параметр блока захвата
- Объявления функций
- Именованные функциональные выражения
- Неявно определенные свойства глобального объекта (т.
 е. отсутствуют
е. отсутствуют varв нестрогом режиме) -
импортвыписки -
оценка
Некоторые идентификаторы местоположений могут быть объявлены:
- Глобальный контекст
- Функциональный блок
- Рядовой блок
- Верхняя часть управляющей структуры (например, цикл, if, while и т. д.)
- Корпус конструкции управления
- Модули
Стили объявлений
var
Идентификаторы, объявленные с использованием var , имеют область действия , за исключением случаев, когда они объявлены непосредственно в глобальном контексте, и в этом случае они добавляются как свойства глобального объекта и имеют глобальную область действия. Существуют отдельные правила их использования в функциях eval .
let и const
Идентификаторы, объявленные с использованием let и const имеют область действия блока , за исключением случаев, когда они объявлены непосредственно в глобальном контексте, и в этом случае они имеют глобальную область действия.
Примечание: let , const и var все подняты. Это означает, что их логическая позиция определения является вершиной их охватывающей области (блока или функции). Однако переменные, объявленные с использованием let и const , не могут быть прочитаны или назначены до тех пор, пока управление не пройдет точку объявления в исходном коде. Промежуточный период известен как временная мертвая зона.
функция f() {
функция г() {
console.log(x)
}
пусть х = 1
грамм()
}
f() // 1, потому что x поднимается, несмотря на то, что он объявлен с помощью `let`! Имена параметров функций
Имена параметров функций ограничиваются телом функции. Обратите внимание, что в этом есть небольшая сложность. Функции, объявленные как аргументы по умолчанию, закрываются по списку параметров, а не по телу функции.
Объявления функций
Объявления функций имеют блочную область в строгом режиме и область действия в нестрогом режиме. Примечание: нестрогий режим — это сложный набор эмерджентных правил, основанных на причудливых исторических реализациях различных браузеров.
Примечание: нестрогий режим — это сложный набор эмерджентных правил, основанных на причудливых исторических реализациях различных браузеров.
Выражения именованных функций
Выражения именованных функций ограничены самими собой (например, с целью рекурсии).
Неявно определенные свойства глобального объекта
В нестрогом режиме неявно определенные свойства глобального объекта имеют глобальную область действия, поскольку глобальный объект находится на вершине цепочки областей действия. В строгом режиме это запрещено.
eval
В строках eval переменные объявлены с использованием var будет помещен в текущую область или, если eval используется косвенно, как свойства глобального объекта.
Примеры
Следующее вызовет ошибку ReferenceError, так как имена x , y и z не имеют значения вне функции f .
функция f() {
переменная х = 1
пусть у = 1
постоянная г = 1
}
console. log(typeof x) // не определено (потому что var имеет область действия!)
console.log(typeof y) // не определено (поскольку тело функции представляет собой блок)
console.log(typeof z) // не определено (поскольку тело функции представляет собой блок)
log(typeof x) // не определено (потому что var имеет область действия!)
console.log(typeof y) // не определено (поскольку тело функции представляет собой блок)
console.log(typeof z) // не определено (поскольку тело функции представляет собой блок) Следующее вызовет ошибку ReferenceError для y и z , но не для x , поскольку видимость x не ограничена блоком. Блоки, определяющие тела структур управления, например , если , для и , пока , ведут себя аналогично.
{
переменная х = 1
пусть у = 1
постоянная г = 1
}
console.log(x) // 1
console.log(typeof y) // не определено, потому что `y` имеет блочную область видимости
console.log(typeof z) // не определено, потому что `z` имеет область блока В дальнейшем x видны вне цикла, потому что var имеет область действия:
for(var x = 0; x < 5; ++x) {}
console.log(x) // 5 (обратите внимание, что это вне цикла!) . ..из-за такого поведения вам нужно быть осторожным при закрытии переменных, объявленных с помощью
..из-за такого поведения вам нужно быть осторожным при закрытии переменных, объявленных с помощью var в циклах. Здесь объявлен только один экземпляр переменной x , и он логически находится вне цикла.
Следующие отпечатки 5 , пять раз, а затем печатает 5 в шестой раз для console.log вне цикла:
for(var x = 0; x < 5; ++x) {
setTimeout(() => console.log(x)) // закрывается по `x`, который логически расположен в верхней части охватывающей области, над циклом
}
console.log(x) // примечание: виден вне цикла Следующее выводит undefined , потому что x является блочным. Обратные вызовы запускаются один за другим асинхронно. Новое поведение для пусть переменных означает, что каждая анонимная функция закрывается по другой переменной с именем x (в отличие от var ), поэтому печатаются целые числа от 0 до 4 . :
:
for(let x = 0; х < 5; ++х) {
setTimeout(() => console.log(x)) // объявления `let` повторно объявляются для каждой итерации, поэтому замыкания захватывают разные переменные
}
console.log(typeof x) // undefined Следующее НЕ будет выдавать ReferenceError , так как видимость x не ограничена блоком; однако он напечатает undefined , потому что переменная не была инициализирована (из-за оператора if ).
если(ложь) {
переменная х = 1
}
console.log(x) // здесь `x` был объявлен, но не инициализирован Переменная, объявленная в начале цикла for с использованием let , ограничена телом цикла:
for (пусть х = 0; х < 10; ++х) {}
console.log(typeof x) // не определено, потому что `x` имеет блочную область видимости Следующее вызовет ошибку ReferenceError , поскольку видимость x ограничена блоком:
if(false) {
пусть х = 1
}
console. log(typeof x) // не определено, потому что `x` имеет блочную область видимости
log(typeof x) // не определено, потому что `x` имеет блочную область видимости Переменные, объявленные с использованием var , let или const , относятся к модулям:
// module1.js
переменная х = 0
функция экспорта f() {}
//module2.js
импортировать f из 'module1.js'
console.log(x) // выдает ReferenceError
Следующее будет объявлять свойство глобального объекта, поскольку переменные, объявленные с использованием var в глобальном контексте, добавляются как свойства к глобальному объекту:
var x = 1
console.log(window.hasOwnProperty('x')) // true let и const в глобальном контексте не добавляют свойства к глобальному объекту, но по-прежнему имеют глобальную область действия:
let x = 1
console.log(window.hasOwnProperty('x')) // false Параметры функции можно считать объявленными в теле функции:
функция f(x) {}
console.log(typeof x) // не определено, потому что `x` ограничен функцией Параметры блока catch ограничены телом блока catch:
try {} catch(e) {}
console. log(typeof e) // не определено, потому что область действия `e` ограничена блоком catch
log(typeof e) // не определено, потому что область действия `e` ограничена блоком catch Выражения именованных функций ограничены только самим выражением:
(function foo() { console.log(foo) }) ()
console.log(typeof foo) // не определено, потому что `foo` ограничено собственным выражением В нестрогом режиме неявно определенные свойства глобального объекта имеют глобальную область действия. В строгом режиме вы получаете ошибку.
x = 1 // неявно определенное свойство глобального объекта (без "var"!)
console.log(x) // 1
console.log(window.hasOwnProperty('x')) // true В нестрогом режиме объявления функций имеют область действия. В строгом режиме они имеют блочную область действия.
'использовать строго'
{
функция foo() {}
}
console.log(typeof foo) // не определено, потому что `foo` имеет блочную область видимости Принцип работы
Область действия определяется как лексическая область кода, в которой действует идентификатор.
В JavaScript каждый объект-функция имеет скрытую ссылку [[Environment]] , которая является ссылкой на лексическое окружение контекста выполнения (фрейм стека), в котором он был создан.
При вызове функции вызывается скрытый метод [[Call]] . Этот метод создает новый контекст выполнения и устанавливает связь между новым контекстом выполнения и лексическим окружением объекта-функции. Это делается путем копирования [[Environment]] значение объекта-функции во внешнее поле ссылки на лексическое окружение нового контекста выполнения.
Обратите внимание, что эта связь между новым контекстом выполнения и лексическим окружением функционального объекта называется замыканием.
Таким образом, в JavaScript область действия реализуется через лексические окружения, связанные друг с другом в «цепочку» внешними ссылками. Эта цепочка лексических окружений называется цепочкой области действия, и разрешение идентификатора происходит путем поиска по цепочке соответствующего идентификатора.
Узнайте больше.
Scope Rules in Functions — Learning Python [Книга]
Теперь, когда мы приступили к написанию собственных функций, нам нужно чтобы получить более формальное представление о том, что означают имена в Python. Когда ты использовать имя в программе, Python создает, изменяет или ищет имя в том, что известно как пространство имен — место, где живут имена. Как мы видели, имена в Python Spring возникают, когда им присваивается значение. Потому что имена не объявлены заранее, Python использует присваивание имя, чтобы связать его с определенным пространством имен. Помимо упаковки код, функции добавляют дополнительный слой пространства имен к ваши программы — по умолчанию имена, назначенные внутри функции, связанный с пространством имен этой функции, и никаким другим.
Вот как это работает. Прежде чем вы начали писать функции,
весь код был написан на верхнем уровне модуля, поэтому имена
либо жили в самом модуле, либо были встроены в Python
предопределяет (например, открыть ). [29] Функции обеспечивают вложенность
пространство имен (иногда называемое
а scope ), который локализует используемые ими имена, например
что имена внутри функции не будут конфликтовать с именами снаружи
(в модуле или другой функции). Обычно мы говорим, что функции определяют локальная область , а модули определяют глобальная область . Эти две области связаны как
следующим образом:
[29] Функции обеспечивают вложенность
пространство имен (иногда называемое
а scope ), который локализует используемые ими имена, например
что имена внутри функции не будут конфликтовать с именами снаружи
(в модуле или другой функции). Обычно мы говорим, что функции определяют локальная область , а модули определяют глобальная область . Эти две области связаны как
следующим образом:
- Охватывающий модуль представляет собой глобальную область действия
Каждый модуль представляет собой глобальную область действия — пространство имен, в котором переменные создается (назначается) на верхнем уровне файла модуля live.
- Каждый вызов функции — это новая локальная область
Каждый раз, когда вы вызываете функцию, вы создаете новую локальную область — пространство имен, в котором обычно живут имена, созданные внутри функции.
- Назначаемые имена являются локальными, если они не объявлены глобальными
По умолчанию все имена, назначенные внутри определения функции, поместить в локальную область (пространство имен, связанное с функцией вызов).
 Если вам нужно присвоить имя, которое находится на верхнем уровне
модуль, содержащий функцию, вы можете сделать это, объявив его в
Если вам нужно присвоить имя, которое находится на верхнем уровне
модуль, содержащий функцию, вы можете сделать это, объявив его в глобальный операторвнутри функции.- Все остальные имена являются глобальными или встроенными
Имена, которым не присвоено значение в определении функции, считаются быть глобальными (в пространстве имен объемлющего модуля) или встроенными (в модуле предопределенных имен Python предоставляет).
Разрешение имени: Правило LGB
Если предыдущий раздел звучит запутанно, на самом деле он сводится к трем простые правила:
Ссылки на имена ищут не более трех областей: локальную, затем глобальную, затем встроенный.
При назначении имен создаются или изменяются локальные имена по умолчанию.
«Глобальные» объявления сопоставляют присвоенные имена объем модуля.
Другими словами, все имена, назначенные внутри функции
9Оператор 0019 def по умолчанию является локальным; функции могут
использовать глобальные переменные, но они должны объявить глобальные переменные, чтобы изменить их. Разрешение имен Python иногда называют Правило LGB , после имен областей действия:
Разрешение имен Python иногда называют Правило LGB , после имен областей действия:
Когда вы используете неполное имя внутри функции, Python ищет три области действия — локальная (L), затем глобальная (G) и затем встроенный (B) — и останавливается на первом месте, где встречается имя.
Когда вы назначаете имя в функции (вместо того, чтобы просто ссылаться на нее в выражении), Python всегда создает или изменяет имя в локальная область, если только она не объявлена глобальной в этом функция.
Вне функции (т. е. на верхнем уровне модуля или на интерактивная подсказка), локальная область такая же, как global — пространство имен модуля.
Рисунок 4.1 иллюстрирует возможности Python.
три
масштабы. В качестве предварительного просмотра мы также хотели бы, чтобы вы знали, что эти
правила применяются только к простым именам (например, spam ).
В следующих двух главах мы увидим, что правила для
полные имена (например, object. , называемые атрибуты ) живут в конкретном объекте и т.д.
работать по-разному. spam
spam
Рис. 4-1. Правило поиска области LGB
Пример
Давайте посмотрим на ан пример, который демонстрирует идеи масштаба. Допустим, мы пишем следующее код в файле модуля:
# глобальная область
X = 99 # X и функция назначены в модуле: глобальный
def func(Y): # Y и Z назначены в function: locals
# локальная область
Z = X + Y # X не присваивается, поэтому это глобальная
вернуть Z
func(1) # функция в модуле: result=100 Этот модуль и содержащиеся в нем функции используют ряд имен для заниматься своими делами. Используя правила области действия Python, мы можем классифицировать следующие имена:
- Глобальные имена:
X,func Xявляется глобальным, потому что он назначается в верхний уровень файла модуля; на него можно сослаться внутри функционировать, не будучи объявленным глобальным.
функцияесть глобальный по той же причине;по умолчаниюзаявление присваивает функциональному объекту имяfuncв верхний уровень модуля.- Местные названия:
Y,Z YиZявляются локальными для функции (и существуют только во время выполнения функции), потому что они оба присвоили значение в определении функции;Zв силу утверждения=, иY, потому что аргументы всегда передаются задание (подробнее об этом через минуту).
Весь смысл этой схемы сегрегации имен в том, что местные
переменные служат временными именами, которые вам нужны только во время работы функции.
Бег. Например, аргумент Y и
результат сложения Z существует только внутри функции;
они не мешают закрывающему модулю
пространство имен (или любую другую функцию, если на то пошло). Местный/глобальный
различие также облегчает понимание функции; большинство из
имена, которые она использует, появляются в самой функции, а не в каком-то произвольном месте.
разместить в модуле. [30]
Местный/глобальный
различие также облегчает понимание функции; большинство из
имена, которые она использует, появляются в самой функции, а не в каком-то произвольном месте.
разместить в модуле. [30]
The global Statement
The global утверждение
это единственное, что
что-то вроде объявления в Python. Он сообщает Python, что
функция планирует изменить глобальные имена — имена, которые живут в
ограничивающая область видимости модуля (пространство имен). Мы говорили о глобальный уже мимоходом; как итог:
globalозначает «имя на верхнем уровне файл модуля».Глобальные имена должны быть объявлены, только если они назначены в функция.
Глобальные имена могут использоваться в функции без объявления.
Оператор global — это просто ключевое слово. глобальный , за которым следует одно или несколько имен, разделенных
запятые. Все перечисленные имена будут сопоставлены с прилагаемым
область действия модуля при назначении или ссылке внутри функции
тело. Например:
Все перечисленные имена будут сопоставлены с прилагаемым
область действия модуля при назначении или ссылке внутри функции
тело. Например:
y, z = 1, 2 # глобальные переменные в модуле
определение all_global():
global x # объявляем присвоенные глобальные значения
x = y + z # нет необходимости объявлять y,z: правило 9 области 30131 Здесь x , y и
z - все глобальные внутри функции
all_global . и и
z являются глобальными, поскольку они не назначены в
функция; x является глобальным, потому что мы так сказали: мы
перечислил его в операторе global , чтобы сопоставить его с
область модуля явно. Без
глобальный здесь, x будет
считается местным в силу назначения. Заметь
и и z не декларируются
Глобальный; Правило поиска Python LGB находит их в модуле
автоматически. Также обратите внимание, что x может не существовать. в охватывающем модуле перед запуском функции; если нет, то
назначение в функции создает
в охватывающем модуле перед запуском функции; если нет, то
назначение в функции создает x в
модуль.
[29] Помните,
код, набранный в интерактивной командной строке, действительно вводится в
встроенный модуль называется __ main __, поэтому
интерактивно созданные имена также живут в модуле. Есть больше
о модулях в главе 5.
[30] Внимательный читатель может заметить
что из-за правила LGB имена в локальной области могут переопределять
одноименные переменные в глобальной и встроенной области видимости, а также
глобальные имена могут переопределять встроенные. Функция может, например,
создайте локальную переменную с именем open , но она будет
скрыть встроенную функцию под названием открыть , которая живет
во встроенной (внешней) области.
Получите Learning Python прямо сейчас с обучающей платформой O’Reilly.
члена O’Reilly проходят онлайн-обучение в режиме реального времени, а также получают книги, видео и цифровой контент почти от 200 издателей.
Начать бесплатную пробную версию
Разрешение имен в коде — настоящий Python Он определяет видимость переменной в коде. Область действия имени или переменной зависит от места в вашем коде, где вы создаете эту переменную. Концепция области Python обычно представлена с использованием правила, известного как
Правило LEGB . Буквы в аббревиатуре LEGB означают локальные, объемлющие, глобальные и встроенные области . Это суммирует не только уровни области действия Python, но и последовательность шагов, которые Python следует при разрешении имен в программе.
В этом руководстве вы узнаете:
- Что такое области и как они работают в Python
- Почему важно знать об области Python
- Что за Правило LEGB и как Python использует его для разрешения имен
- Как изменить стандартное поведение области Python с использованием
глобальногоинелокального - Какие инструменты, связанные с областью действия, предлагает Python и как их можно использовать
Обладая этими знаниями, вы можете воспользоваться преимуществами областей видимости Python для написания более надежных и удобных в сопровождении программ. Использование области Python поможет вам избежать или свести к минимуму ошибки, связанные с конфликтом имен, а также с неправильным использованием глобальных имен в ваших программах.
Использование области Python поможет вам избежать или свести к минимуму ошибки, связанные с конфликтом имен, а также с неправильным использованием глобальных имен в ваших программах.
Вы получите максимальную отдачу от этого руководства, если знакомы с понятиями Python среднего уровня, такими как классы, функции, внутренние функции, переменные, исключения, включения, встроенные функции и стандартные структуры данных.
Бесплатный бонус: 5 Thoughts On Python Mastery, бесплатный курс для Python-разработчиков, который показывает вам дорожную карту и образ мышления, которые вам понадобятся, чтобы вывести свои навыки Python на новый уровень.
Понимание области применения
В программировании область действия имени определяет область программы, в которой вы можете получить однозначный доступ к этому имени, например, к переменным, функциям, объектам и т. д. Имя будет видно и доступно только коду в его области действия. Некоторые языки программирования используют область видимости для предотвращения конфликтов имен и непредсказуемого поведения. Чаще всего вы различаете два основных диапазона:
Некоторые языки программирования используют область видимости для предотвращения конфликтов имен и непредсказуемого поведения. Чаще всего вы различаете два основных диапазона:
-
Глобальная область: Имена, которые вы определяете в этой области, доступны для всего вашего кода.
-
Локальная область: Имена, которые вы определяете в этой области, доступны или видны только коду в этой области.
Scope появился потому, что ранние языки программирования (например, BASIC) имели только глобальных имени . С таким именем любая часть программы могла изменить любую переменную в любое время, так что обслуживание и отладка больших программ могли стать настоящим кошмаром. Чтобы работать с глобальными именами, вам нужно одновременно помнить весь код, чтобы знать, каково значение данного имени в любое время. Это был важный побочный эффект отсутствия прицелов.
Некоторые языки, такие как Python, используют область действия , чтобы избежать подобных проблем. Когда вы используете язык, который реализует область действия, у вас нет возможности получить доступ ко всем переменным в программе во всех местах этой программы. В этом случае ваша возможность доступа к данному имени будет зависеть от того, где вы определили это имя.
Когда вы используете язык, который реализует область действия, у вас нет возможности получить доступ ко всем переменным в программе во всех местах этой программы. В этом случае ваша возможность доступа к данному имени будет зависеть от того, где вы определили это имя.
Примечание: Вы будете использовать термин имя для обозначения идентификаторов переменных, констант, функций, классов или любых других объектов, которым можно присвоить имя.
Имена в ваших программах будут иметь область действия блока кода, в котором вы их определяете. Когда вы можете получить доступ к значению данного имени из какого-либо места в вашем коде, вы скажете, что это имя в области . Если вы не можете получить доступ к имени, вы скажете, что имя выходит за рамки .
Удалить рекламу
Имена и области видимости в Python
Поскольку Python является языком с динамической типизацией, переменные в Python появляются, когда вы впервые присваиваете им значение. С другой стороны, функции и классы доступны после того, как вы определите их с помощью
С другой стороны, функции и классы доступны после того, как вы определите их с помощью def или class соответственно. Наконец, модули существуют после их импорта. Подводя итог, вы можете создавать имена Python с помощью одной из следующих операций:
| Эксплуатация | Заявление|
|---|---|
| Задания | х = значение |
| Импортные операции | модуль импорта или из имени импорта модуля |
| Описание функций | функция my_func(): ... |
| Определения аргументов в контексте функций | определение my_func(arg1, arg2,... argN): ... |
| Определения классов | класс MyClass: ... |
Все эти операции создают или, в случае присваивания, обновляют новые имена Python, поскольку все они присваивают имя переменной, константе, функции, классу, экземпляру, модулю или другому объекту Python.
Примечание: Существует важное различие между операциями присваивания и операциями ссылки или доступа . Когда вы ссылаетесь на имя, вы просто извлекаете его содержимое или значение. Когда вы назначаете имя, вы либо создаете это имя, либо изменяете его.
Python использует расположение присвоения имени или определения, чтобы связать его с определенной областью. Другими словами, то, где вы назначаете или определяете имя в своем коде, определяет область действия или видимость этого имени.
Например, если вы присваиваете значение имени внутри функции, то это имя будет иметь локальную область Python . Напротив, если вы присвоите значение имени за пределами всех функций, скажем, на верхнем уровне модуля, то это имя будет иметь глобальную область Python .
Область действия Python и пространство имен
В Python концепция области тесно связана с концепцией пространства имен. Как вы уже узнали, область действия Python определяет, где в вашей программе отображается имя. Области Python реализованы в виде словарей, которые сопоставляют имена объектам. Эти словари обычно называются пространства имен . Это конкретные механизмы, которые Python использует для хранения имен. Они хранятся в специальном атрибуте с именем
Как вы уже узнали, область действия Python определяет, где в вашей программе отображается имя. Области Python реализованы в виде словарей, которые сопоставляют имена объектам. Эти словари обычно называются пространства имен . Это конкретные механизмы, которые Python использует для хранения имен. Они хранятся в специальном атрибуте с именем .__dict__ .
Имена на верхнем уровне модуля хранятся в пространстве имен модуля. Другими словами, они хранятся в атрибуте модуля .__dict__ . Взгляните на следующий код:
>>>
>>> импорт системы >>> sys.__dict__.keys() dict_keys(['__name__', '__doc__', '__package__',..., 'argv', 'ps1', 'ps2'])
После импорта sys вы можете использовать .keys() для проверки ключей sys.__dict__ . Это возвращает список со всеми именами, определенными на верхнем уровне модуля. В этом случае можно сказать, что . содержит пространство имен  __dict__
__dict__ sys и является конкретным представлением области модуля.
Примечание: Вывод некоторых примеров в этом руководстве был сокращен ( ... ) для экономии места. Вывод может варьироваться в зависимости от вашей платформы, версии Python или даже от того, как долго вы используете текущий интерактивный сеанс Python.
В качестве еще одного примера предположим, что вам нужно использовать имя ps1 , которое определено в sys . Если вы знаете, как .__dict__ и пространства имен работают в Python, то вы можете ссылаться на ps1 как минимум двумя разными способами:
- Использование записи через точку в имени модуля в форме
module.name - Использование операции подписки на
.__dict__в формеmodule.__dict__['name']
Взгляните на следующий код:
>>>
>>> sys.ps1 '>>> ' >>> sys.__dict__['ps1'] '>>> '
После того, как вы импортировали sys , вы можете получить доступ к ps1 , используя запись через точку на sys . Вы также можете получить доступ к ps1 , используя поиск ключа по словарю с помощью ключа 'ps1' . Оба действия возвращают один и тот же результат: '>>> ' .
Примечание: ps1 — это строка, определяющая основную подсказку интерпретатора Python. ps1 определяется, только если интерпретатор находится в интерактивном режиме и его начальное значение равно '>>> ' .
Всякий раз, когда вы используете имя, такое как имя переменной или функции, Python выполняет поиск по различным уровням области видимости (или пространствам имен), чтобы определить, существует ли это имя или нет. Если имя существует, то вы всегда получите первое его вхождение. В противном случае вы получите ошибку. Вы познакомитесь с этим механизмом поиска в следующем разделе.
Вы познакомитесь с этим механизмом поиска в следующем разделе.
Удаление рекламы
Использование правила LEGB для Python Scope
Python разрешает имена с помощью так называемого правила LEGB , которое названо в честь области Python для имен. Буквы в LEGB означают Local, Enclosing, Global и Built-in. Вот краткий обзор того, что означают эти термины:
Локальная область (или функция) — это блок кода или тело любой функции Python или
лямбда-выражения. Эта область Python содержит имена, которые вы определяете внутри функции. Эти имена будут видны только из кода функции. Создается при вызове функции, , а не при определении функции, поэтому у вас будет столько же различных локальных областей видимости, сколько и вызовов функций. Это верно, даже если вы вызываете одну и ту же функцию несколько раз или рекурсивно. Каждый вызов приведет к созданию новой локальной области видимости.
Охватывающая (или нелокальная) область — это специальная область, которая существует только для вложенных функций. Если локальная область является внутренней или вложенной функцией, то объемлющая область является областью действия внешней или объемлющей функции. Эта область содержит имена, которые вы определяете во внешней функции. Имена во внешней области видны из кода внутренней и внешней функций.
Глобальная область (или модуль) — это самая верхняя область в программе, скрипте или модуле Python. Эта область Python содержит все имена, которые вы определяете на верхнем уровне программы или модуля. Имена в этой области Python видны отовсюду в вашем коде.
Встроенная область — это специальная область Python, которая создается или загружается всякий раз, когда вы запускаете сценарий или открываете интерактивный сеанс. Эта область содержит имена, такие как ключевые слова, функции, исключения и другие атрибуты, встроенные в Python.
 Имена в этой области Python также доступны из любого места в вашем коде. Он автоматически загружается Python при запуске программы или скрипта.
Имена в этой области Python также доступны из любого места в вашем коде. Он автоматически загружается Python при запуске программы или скрипта.
Правило LEGB — это своего рода процедура поиска имен, которая определяет порядок, в котором Python ищет имена. Например, если вы ссылаетесь на заданное имя, Python будет искать это имя последовательно в локальной, объемлющей, глобальной и встроенной области видимости. Если имя существует, вы получите первое его вхождение. В противном случае вы получите ошибку.
Примечание: Обратите внимание, что поиск в локальной и включающей областях Python выполняется только в том случае, если вы используете имя внутри функции (локальная область) или вложенной или внутренней функции (локальная и включающая область).
Таким образом, при использовании вложенных функций имена разрешаются путем предварительной проверки локальной области видимости или локальной области действия самой внутренней функции. Затем Python просматривает все охватывающие области видимости внешних функций, начиная с самой внутренней и заканчивая самой внешней областью.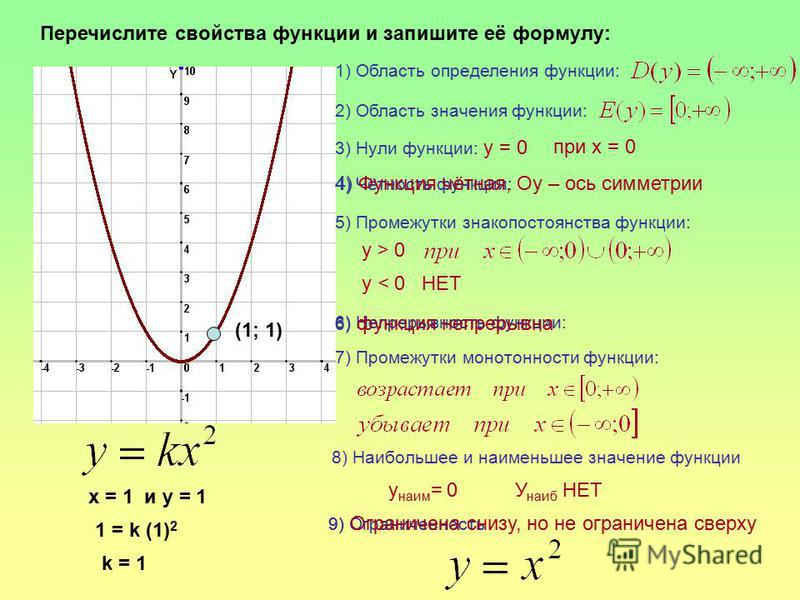 Если совпадений не найдено, Python просматривает глобальную и встроенную области видимости. Если он не может найти имя, вы получите сообщение об ошибке.
Если совпадений не найдено, Python просматривает глобальную и встроенную области видимости. Если он не может найти имя, вы получите сообщение об ошибке.
В любой момент выполнения у вас будет максимум четыре активных области Python — локальная, объемлющая, глобальная и встроенная — в зависимости от того, где вы находитесь в коде. С другой стороны, у вас всегда будет как минимум две активные области: глобальная и встроенная. Эти два прицела всегда будут доступны для вас.
Функции: локальная область
Локальная область или область функции — это область Python, созданная при вызовах функций. Каждый раз, когда вы вызываете функцию, вы также создаете новую локальную область видимости. С другой стороны, вы можете рассматривать каждый оператор def и выражение lambda как план для новых локальных областей. Эти локальные области видимости будут возникать всякий раз, когда вы вызываете функцию под рукой.
По умолчанию параметры и имена, которые вы назначаете внутри функции, существуют только внутри функции или локальной области, связанной с вызовом функции.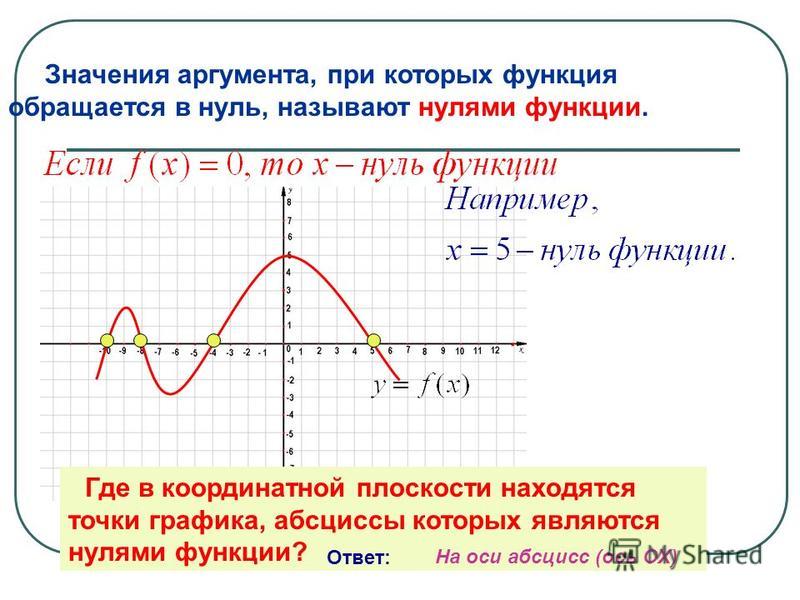 Когда функция возвращается, локальная область видимости уничтожается, а имена забываются. Вот как это работает:
Когда функция возвращается, локальная область видимости уничтожается, а имена забываются. Вот как это работает:
>>>
>>> квадрат по умолчанию (основание):
... результат = база ** 2
... print(f'Квадрат {основания} равен: {результат}')
...
>>> квадрат(10)
Квадрат 10 это: 100
>>> результат # недоступен из-за пределов Square()
Traceback (последний последний вызов):
Файл "", строка 1, в
результат
NameError: имя «результат» не определено
>>> base # Недоступно из-за пределов Square()
Traceback (последний последний вызов):
Файл "", строка 1, в
база
NameError: имя «база» не определено
>>> квадрат(20)
Квадрат 20 это: 400
Square() — это функция, которая вычисляет квадрат заданного числа, по основанию . Когда вы вызываете функцию, Python создает локальную область, содержащую имена base (аргумент) и result (локальная переменная). После первого вызова square() , base содержит значение 10 , а результат содержит значение 100 . Во второй раз локальные имена не будут помнить значения, которые были в них сохранены при первом вызове функции. Обратите внимание, что
Во второй раз локальные имена не будут помнить значения, которые были в них сохранены при первом вызове функции. Обратите внимание, что база теперь содержит значение 20 , а результат содержит 400 .
Примечание: Если вы попытаетесь получить доступ к результату или base после вызова функции, вы получите NameError , потому что они существуют только в локальной области видимости, созданной вызовом Square() . Всякий раз, когда вы пытаетесь получить доступ к имени, которое не определено ни в одной области Python, вы получите NameError . Сообщение об ошибке будет содержать имя, которое не удалось найти.
Поскольку вы не можете получить доступ к локальным именам из операторов, находящихся вне функции, разные функции могут определять объекты с одним и тем же именем. Посмотрите этот пример:
>>>
>>> куб по определению (база): ... результат = база ** 3 ... print(f'Куб {базы} равен: {результат}') ... >>> куб(30) Куб 30 это: 27000
Обратите внимание, что вы определяете cube() , используя ту же переменную и параметр, которые вы использовали в Square() . Однако, поскольку cube() не может видеть имена внутри локальной области видимости Square() и наоборот, обе функции работают, как и ожидалось, без каких-либо конфликтов имен.
Вы можете избежать конфликтов имен в своих программах, правильно используя локальную область видимости Python. Это также делает функции более автономными и создает программные модули, которые можно обслуживать. Кроме того, поскольку вы не можете изменять локальные имена из удаленных мест в своем коде, ваши программы будет легче отлаживать, читать и изменять.
Вы можете просмотреть имена и параметры функции, используя .__code__ , который является атрибутом, содержащим информацию о внутреннем коде функции. Взгляните на код ниже:
Взгляните на код ниже:
>>>
>>> Square.__code__.co_varnames («база», «результат») >>> Square.__code__.co_argcount 1 >>> Square.__code__.co_consts (Нет, 2, 'Квадрат ',' равен: ') >>> Square.__code__.co_name 'площадь'
В этом примере кода вы проверяете .__code__ на квадрате() . Это специальный атрибут, который содержит информацию о коде функции Python. В этом случае вы видите, что .co_varnames содержит кортеж, содержащий имена, которые вы определили внутри Square() .
Удаление рекламы
Вложенные функции: закрывающая область действия
Охватывающая или нелокальная область наблюдается, когда вы вкладываете функции в другие функции. Охватывающая область была добавлена в Python 2.2. Он принимает форму локальной области видимости любой объемлющей функции. Имена, которые вы определяете в охватывающей области Python, обычно известны как 9. 0103 нелокальные имена . Рассмотрим следующий код:
0103 нелокальные имена . Рассмотрим следующий код:
>>>
>>> определение external_func():
... # Этот блок является локальной областью видимости external_func()
... var = 100 # Нелокальная переменная
... # Это также объемлющая область inner_func()
... определение внутренней_функции():
... # Этот блок является локальной областью видимости inner_func()
... print(f"Печать переменной из inner_func(): {var}")
...
... внутренняя_функция()
... print(f"Печать var из external_func(): {var}")
...
>>> внешняя_функция()
Печать var из inner_func(): 100
Печать var из external_func(): 100
>>> внутренняя_функция()
Traceback (последний последний вызов):
Файл "", строка 1, в
NameError: имя 'inner_func' не определено
Когда вы вызываете external_func() , вы также создаете локальную область. Локальная область действия external_func() одновременно является охватывающей областью действия inner_func() . Изнутри
Изнутри inner_func() эта область не является ни глобальной, ни локальной. Это специальный прицел, который находится между этими двумя прицелами и известен как объемлющий прицел .
Примечание: В каком-то смысле inner_func() — это временная функция, которая оживает только во время выполнения закрывающей ее функции, внешняя_функция() . Обратите внимание, что inner_func() виден только коду external_func() .
Все имена, которые вы создаете в охватывающей области видимости, видны изнутри inner_func() , за исключением тех, которые созданы после вызова inner_func() . Вот новая версия external_fun() , которая показывает эту точку:
>>>
>>> определение external_func():
... переменная = 100
... определение внутренней_функции():
... print(f"Печать переменной из inner_func(): {var}")
. .. print(f"Печать other_var из inner_func(): {another_var}")
...
... внутренняя_функция()
... Another_var = 200 # Это определяется после вызова inner_func()
... print(f"Печать var из external_func(): {var}")
...
>>> внешняя_функция()
Печать var из inner_func(): 100
Traceback (последний последний вызов):
Файл "
.. print(f"Печать other_var из inner_func(): {another_var}")
...
... внутренняя_функция()
... Another_var = 200 # Это определяется после вызова inner_func()
... print(f"Печать var из external_func(): {var}")
...
>>> внешняя_функция()
Печать var из inner_func(): 100
Traceback (последний последний вызов):
Файл "", строка 1, в
внешняя_функция()
Файл "", строка 7, в external_func
внутренняя_функция()
Файл "", строка 5, в inner_func
print(f"Печать other_var из inner_func(): {another_var}")
NameError: ссылка на свободную переменную 'another_var' перед назначением во вложении
сфера
Когда вы вызываете external_func() , код переходит к точке, в которой вы вызываете inner_func() . Последний оператор inner_func() пытается получить доступ к other_var . На данный момент other_var еще не определено, поэтому Python выдает NameError , потому что не может найти имя, которое вы пытаетесь использовать.
И последнее, но не менее важное: вы не можете изменять имена в охватывающей области внутри вложенной функции, если вы не объявите их как нелокальный во вложенной функции. Вы узнаете, как использовать нелокальный позже в этом руководстве.
Модули: глобальный охват
С того момента, как вы запускаете программу Python, вы находитесь в глобальной области действия Python. Внутри Python превращает основной скрипт вашей программы в модуль с именем __main__ для выполнения основной программы. Пространство имен этого модуля является основной глобальной областью вашей программы.
Примечание: В Python понятия глобальной области действия и глобальных имен тесно связаны с файлами модулей. Например, если вы определяете имя на верхнем уровне любого модуля Python, то это имя считается глобальным для модуля. Вот почему этот вид прицела также называется 9.0103 объем модуля .
Если вы работаете в интерактивном сеансе Python, вы заметите, что '__main__' также является именем его основного модуля. Чтобы проверить это, откройте интерактивный сеанс и введите следующее:
Чтобы проверить это, откройте интерактивный сеанс и введите следующее:
>>>
>>> __имя__ '__главный__'
Всякий раз, когда вы запускаете программу Python или интерактивный сеанс, как в приведенном выше коде, интерпретатор выполняет код в модуле или сценарии, который служит точкой входа в вашу программу. Этот модуль или скрипт загружается со специальным именем, __основной__ . С этого момента вы можете сказать, что ваша основная глобальная область видимости — это область __main__ .
Чтобы проверить имена в вашей основной глобальной области, вы можете использовать dir() . Если вы вызовете dir() без аргументов, вы получите список имен, которые находятся в вашей текущей глобальной области видимости. Взгляните на этот код:
>>>
>>> директор() ['__аннотации__', '__builtins__',..., '__package__', '__spec__'] >>> var = 100 # Назначить var на верхний уровень __main__ >>> директор() ['__аннотации__', '__builtins__',..., '__package__', '__spec__', 'var']
Когда вы вызываете dir() без аргументов, вы получаете список имен, доступных в вашей основной глобальной области Python. Обратите внимание, что если вы назначите новое имя (например, var здесь) на верхнем уровне модуля (которое здесь __main__ ), то это имя будет добавлено в список, возвращаемый dir() .
Примечание: Подробнее о dir() вы узнаете позже в этом руководстве.
Для каждого выполнения программы существует только одна глобальная область Python. Эта область видимости существует до тех пор, пока программа не завершится и все ее имена не будут забыты. В противном случае при следующем запуске программы имена запомнят свои значения из предыдущего запуска.
Вы можете получить доступ или сослаться на значение любого глобального имени из любого места вашего кода. Сюда входят функции и классы. Вот пример, поясняющий эти моменты:
>>>
>>> переменная = 100 >>> Функция функции(): ... return var # Вы можете получить доступ к var из func() ... >>> функция() 100 >>> var # Остается без изменений 100
Внутри func() вы можете свободно обращаться или ссылаться на значение var . Это не влияет на ваше глобальное имя var , но показывает, что var можно свободно получить из func() . С другой стороны, вы не можете назначать глобальные имена внутри функций, если вы явно не объявите их как глобальные имена с помощью оператора global , который вы увидите позже.
Всякий раз, когда вы присваиваете значение имени в Python, может произойти одно из двух:
- Вы создаете новое имя
- Вы обновляете существующее имя
Конкретное поведение будет зависеть от области Python, в которой вы назначаете имя. Если вы попытаетесь присвоить значение глобальному имени внутри функции, то вы создадите это имя в локальной области видимости функции, затеняя или переопределяя глобальное имя. Это означает, что вы не сможете изменить большинство переменных, которые были определены вне функции, изнутри функции.
Это означает, что вы не сможете изменить большинство переменных, которые были определены вне функции, изнутри функции.
Если вы будете следовать этой логике, то поймете, что следующий код не будет работать так, как вы ожидаете:
>>>
>>> var = 100 # Глобальная переменная >>> определение приращения(): ... var = var + 1 # Попытаться обновить глобальную переменную ... >>> приращение() Traceback (последний последний вызов): Файл "", строка 1, в приращение() Файл " ", строка 2, приращение вар = вар + 1 UnboundLocalError: ссылка на локальную переменную 'var' перед назначением
В рамках increment() вы пытаетесь увеличить глобальную переменную, вар . Поскольку var не объявлен global внутри increment() , Python создает внутри функции новую локальную переменную с тем же именем, var . В процессе Python понимает, что вы пытаетесь использовать локальную переменную var перед ее первым назначением ( var + 1 ), поэтому выдает ошибку UnboundLocalError .
Вот еще пример:
>>>
>>> var = 100 # Глобальная переменная >>> Функция функции(): ... print(var) # Ссылка на глобальную переменную var ... var = 200 # Определить новую локальную переменную с тем же именем, var ... >>> функция() Traceback (последний последний вызов): Файл "", строка 1, в функция() Файл " ", строка 2, в функции печать (вар) UnboundLocalError: ссылка на локальную переменную 'var' перед назначением
Вероятно, вы ожидаете, что сможете распечатать глобальную переменную var и обновить var позже, но снова получите UnboundLocalError . Здесь происходит то, что когда вы запускаете тело func() , Python решает, что var является локальной переменной, потому что она назначена в пределах области действия функции. Это не ошибка, а дизайнерский выбор. Python предполагает, что имена, назначенные в теле функции, являются локальными для этой функции.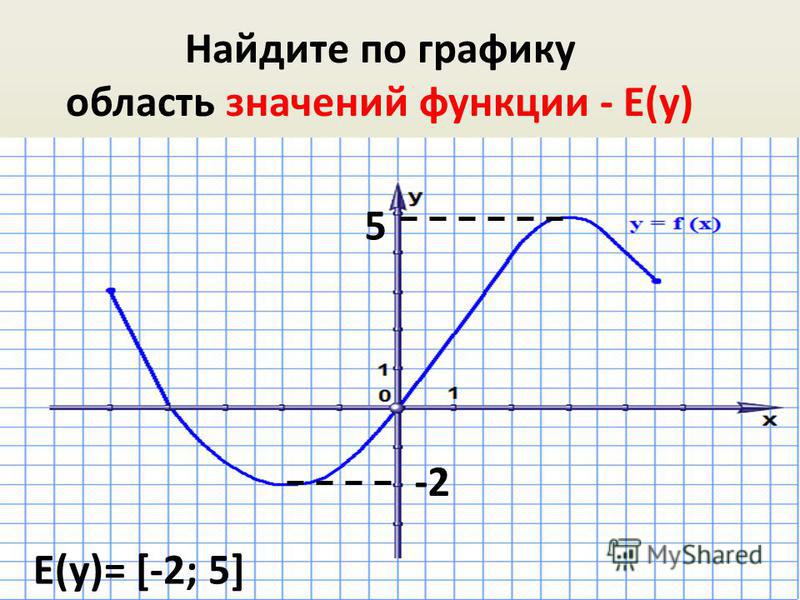
Примечание. Глобальные имена можно обновлять или изменять из любого места в вашей глобальной области Python. Кроме того, оператор global можно использовать для изменения глобальных имен практически из любого места вашего кода, как вы увидите в операторе global .
Изменение глобальных имен обычно считается плохой практикой программирования, поскольку это может привести к следующему коду:
- Сложность отладки: Почти любой оператор в программе может изменить значение глобального имени.
- Трудно понять: Вам необходимо знать обо всех операторах, которые обращаются к глобальным именам и изменяют их.
- Повторное использование невозможно: Код зависит от глобальных имен, специфичных для конкретной программы.
Хорошая практика программирования рекомендует использовать локальные имена, а не глобальные имена. Вот несколько советов:
- Напишите автономные функции, которые полагаются на локальные имена, а не на глобальные.

- Попробуйте использовать уникальные имена объектов, независимо от того, в какой области вы находитесь.
- Избегайте модификаций глобального имени в ваших программах.
- Избегайте межмодульных модификаций имени .
- Используйте глобальные имена как константы, которые не изменяются во время выполнения вашей программы.
До этого момента вы рассмотрели три области видимости Python. Посмотрите следующий пример, чтобы узнать, где они расположены в вашем коде и как Python ищет в них имена:
>>>
>>> # Эта область является глобальной или модульной областью >>> число = 100 >>> определение external_func(): ... # Этот блок является локальной областью видимости external_func() ... # Это также объемлющая область inner_func() ... определение внутренней_функции(): ... # Этот блок является локальной областью действия inner_func() ... печать (число) ... ... внутренняя_функция() ... >>> внешняя_функция() 100
Когда вы вызываете external_func() , вы получаете 100 напечатано на вашем экране. Но как Python ищет имя по номеру в этом случае? Следуя правилу LEGB, вы будете искать номер в следующих местах:
- Внутри
inner_func(): Это локальная область видимости, нономертам не существует. - Внутри
external_func(): Это объемлющая область видимости, ночислотам также не определено. - В составе модуля: Это глобальная область видимости, и вы найдете там
число, так что вы можете вывестичислона экран.
Если число не определено внутри глобальной области, тогда Python продолжает поиск, просматривая встроенную область. Это последний компонент правила LEGB, как вы увидите в следующем разделе.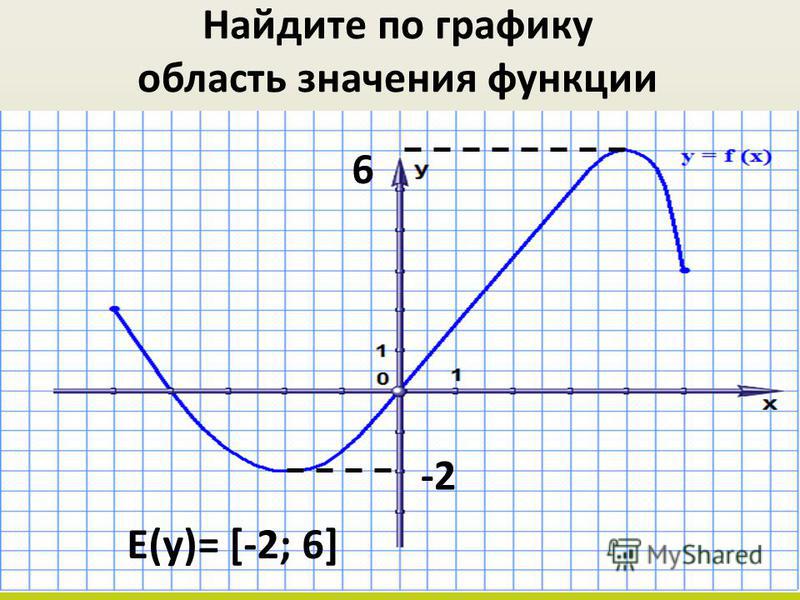
Удалить рекламу
Встроенные функции : Встроенная область видимости Встроенная область — это специальная область Python, реализованная в виде стандартного библиотечного модуля с именем 9.0019 встроенных функций в Python 3.x. Все встроенные объекты Python находятся в этом модуле. Они автоматически загружаются во встроенную область видимости при запуске интерпретатора Python. Python ищет встроенных функций в последнюю очередь в своем поиске LEGB, поэтому вы получаете все имена, которые он определяет, бесплатно. Это означает, что вы можете использовать их без импорта какого-либо модуля.
Обратите внимание, что имена в встроенных функциях всегда загружаются в вашу глобальную область Python со специальным именем __builtins__ , как вы можете видеть в следующем коде:
>>>
>>> директор() ['__аннотации__', '__builtins__',..., '__package__', '__spec__'] >>> директория(__builtins__) ['ArithmeticError', 'AssertionError',..., 'tuple', 'type', 'vars', 'zip']
В выводе первого вызова dir() видно, что __builtins__ всегда присутствует в глобальной области Python. Если вы проверите __builtins__ , используя dir() , то вы получите полный список встроенных имен Python.
Встроенная область видимости содержит более 150 имен в текущей глобальной области Python. Например, в Python 3.8 вы можете узнать точное количество имен следующим образом:
>>>
>>> len(dir(__builtins__)) 152
При вызове len() вы получаете количество элементов в списке , возвращенном dir() . Это возвращает 152 имени, которые включают исключения, функции, типы, специальные атрибуты и другие встроенные объекты Python.
Несмотря на то, что вы можете получить доступ ко всем этим встроенным объектам Python бесплатно (без импорта чего-либо), вы также можете явно импортировать встроенных функций и обращаться к именам с использованием записи через точку. Вот как это работает:
Вот как это работает:
>>>
>>> import builtins # Импорт встроенных модулей как обычный модуль >>> директория (встроенная) ['ArithmeticError', 'AssertionError',..., 'tuple', 'type', 'vars', 'zip'] >>> встроенная.сумма([1, 2, 3, 4, 5]) 15 >>> встроенные.max([1, 5, 8, 7, 3]) 8 >>> встроенный.sorted([1, 5, 8, 7, 3]) [1, 3, 5, 7, 8] >>> встроенный.pow(10, 2) 100
Вы можете импортировать встроенных модулей так же, как и любой другой модуль Python. С этого момента вы можете получить доступ ко всем именам в встроенных функциях , используя поиск атрибутов с точками или полные имена. Это может быть очень полезно, если вы хотите убедиться, что у вас не будет конфликта имен, если какое-либо из ваших глобальных имен переопределит любое встроенное имя.
Вы можете переопределить или переопределить любое встроенное имя в вашей глобальной области. Если вы это сделаете, имейте в виду, что это повлияет на весь ваш код. Взгляните на следующий пример:
Взгляните на следующий пример:
>>>
>>> abs(-15) # Стандартное использование встроенной функции 15 >>> abs = 20 # Переопределить встроенное имя в глобальной области видимости >>> абс (-15) Traceback (последний последний вызов): Файл "", строка 1, в TypeError: объект 'int' не может быть вызван
Если вы переопределяете или переназначаете abs , исходный встроенный abs() затрагивается во всем вашем коде. Теперь предположим, что вам нужно вызвать исходный abs() и вы забываете, что переназначили имя. В этом случае, когда вы снова вызовете abs() , вы получите TypeError , потому что abs теперь содержит ссылку на целое число, которое нельзя вызвать.
Примечание: Случайное или непреднамеренное переопределение или переопределение встроенных имен в вашей глобальной области видимости может стать источником опасных и трудно обнаруживаемых ошибок. Лучше постараться избежать такой практики.
Лучше постараться избежать такой практики.
Если вы экспериментируете с каким-то кодом и случайно переназначили встроенное имя в интерактивной подсказке, вы можете либо перезапустить сеанс, либо запустить del name , чтобы удалить переопределение из вашей глобальной области Python. Таким образом, вы восстанавливаете исходное имя во встроенной области. Если вы вернетесь к примеру abs() , вы можете сделать что-то вроде этого:
>>>
>>> del abs # Удалить переопределенный abs из вашей глобальной области видимости >>> abs(-15) # Восстановить исходный abs() 15
Когда вы удаляете пользовательское имя abs , вы удаляете имя из своей глобальной области. Это позволяет вам получить доступ к исходным abs() снова во встроенной области видимости.
Чтобы обойти такую ситуацию, вы можете явно импортировать встроенных функций , а затем использовать полные имена, как в следующем фрагменте кода:
>>>
>>> импортировать встроенные функции >>> встроенные файлы.abs(-15) 15
После явного импорта встроенных модулей имя модуля становится доступным в вашей глобальной области Python. С этого момента вы можете использовать полные имена, чтобы однозначно получать нужные вам имена из встроенных , точно так же, как вы сделали с встроенных.abs() в приведенном выше примере.
В качестве краткого обзора некоторые последствия области действия Python показаны в следующей таблице:
| Действие | Глобальный код | Местный код | Код вложенной функции |
|---|---|---|---|
| Имена доступа или ссылки, находящиеся в глобальной области видимости | Да | Да | Да |
| Изменить или обновить имена, находящиеся в глобальной области | Да | Нет (если не объявлено global ) | Нет (если не объявлено global ) |
| Доступ или ссылки на имена, находящиеся в локальной области | № | Да (своя локальная область), Нет (другая локальная область) | Да (своя локальная область), Нет (другая локальная область) |
| Переопределить имена во встроенной области | Да | Да (во время выполнения функции) | Да (во время выполнения функции) |
| Имена доступа или ссылки, которые находятся в окружающей их области | н/д | н/д | Да |
| Изменить или обновить имена, находящиеся в своей области действия | н/д | н/д | Нет (если не объявлен нелокальный ) |
Кроме того, код в разных областях может использовать одно и то же имя для разных объектов. Таким образом, вы можете использовать локальную переменную с именем
Таким образом, вы можете использовать локальную переменную с именем spam , а также глобальная переменная с тем же именем, spam . Однако это считается плохой практикой программирования.
Удаление рекламы
Изменение поведения области действия Python
Итак, вы узнали, как работают области Python и как они ограничивают видимость переменных, функций, классов и других объектов Python определенными частями вашего кода. Теперь вы знаете, что вы можете получить доступ к 90 103 глобальным именам 90 104 или ссылаться на них из любого места вашего кода, но их можно изменить или обновить из глобальной области Python.
Вы также знаете, что вы можете получить доступ к локальным именам только из локальной области Python, в которой они были созданы, или из вложенной функции, но вы не можете получить к ним доступ из глобальной области Python или из других локальных областей.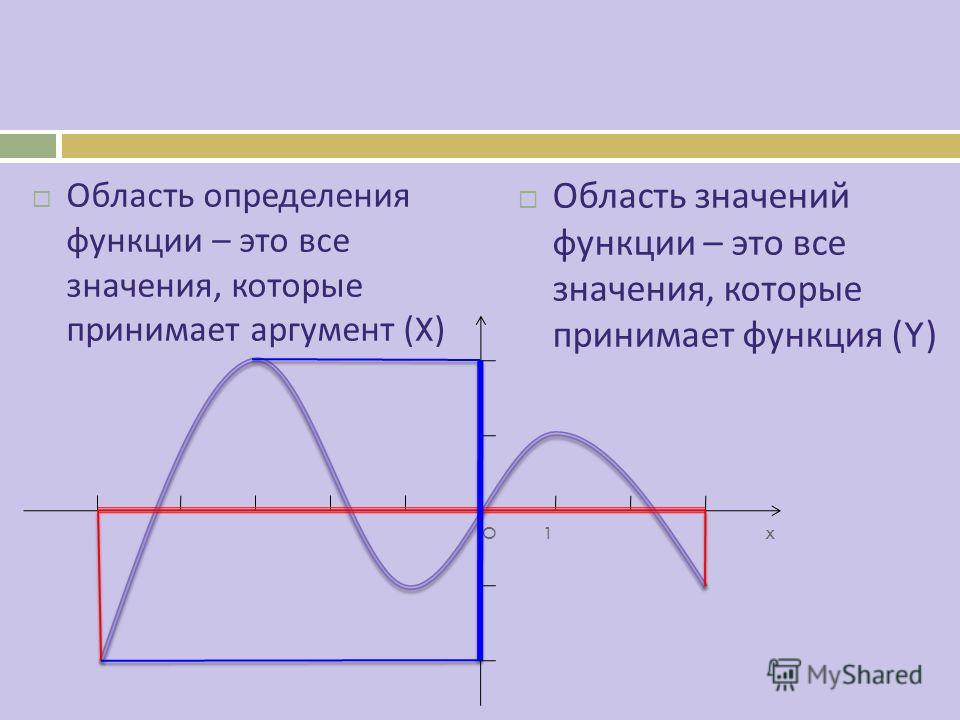 Кроме того, вы узнали, что к 90 103 нелокальным именам 90 104 можно получить доступ из вложенных функций, но их нельзя изменить или обновить оттуда.
Кроме того, вы узнали, что к 90 103 нелокальным именам 90 104 можно получить доступ из вложенных функций, но их нельзя изменить или обновить оттуда.
Несмотря на то, что области Python по умолчанию следуют этим общим правилам, существуют способы изменить это стандартное поведение. Python предоставляет два ключевых слова, которые позволяют изменять содержимое глобальных и нелокальных имен. Эти два ключевых слова:
-
глобальный -
нелокальный
В следующих двух разделах вы узнаете, как использовать эти ключевые слова Python для изменения стандартного поведения областей Python.
глобальное заявление Вы уже знаете, что когда вы пытаетесь присвоить значение глобальному имени внутри функции, вы создаете новое локальное имя в области действия функции. Чтобы изменить это поведение, вы можете использовать глобальный оператор .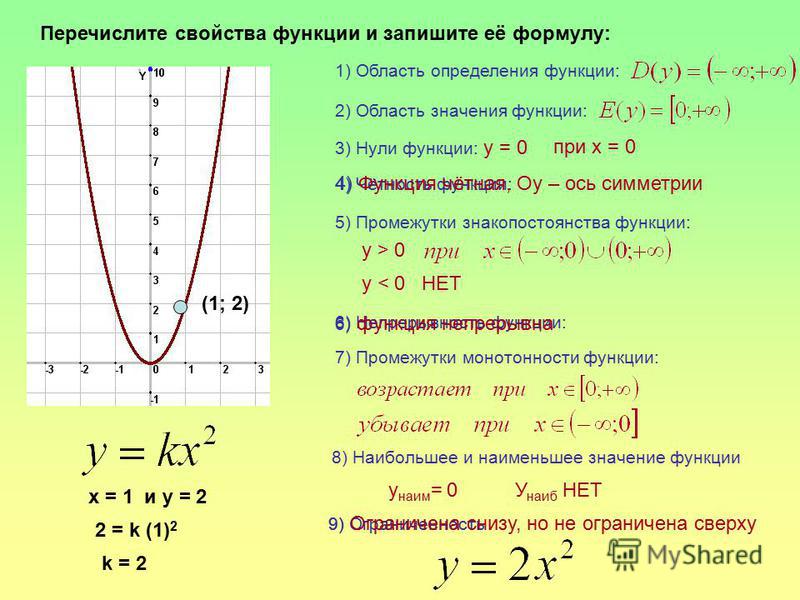 С помощью этого оператора вы можете определить список имен, которые будут рассматриваться как глобальные имена.
С помощью этого оператора вы можете определить список имен, которые будут рассматриваться как глобальные имена.
Оператор состоит из глобального ключевого слова , за которым следует одно или несколько имен, разделенных запятыми. Вы также можете использовать несколько операторов global с именем (или списком имен). Все имена, перечисленные в операторе global , будут сопоставлены с глобальной или модульной областью, в которой вы их определяете.
Вот пример, когда вы пытаетесь обновить глобальную переменную из функции:
>>>
>>> counter = 0 # Глобальное имя >>> определение update_counter(): ... counter = counter + 1 # Ошибка при попытке обновить счетчик ... >>> update_counter() Traceback (последний последний вызов): Файл "", строка 1, в Файл " ", строка 2, в update_counter UnboundLocalError: ссылка на локальную переменную 'counter' перед назначением
При попытке назначить счетчик внутри update_counter() , Python предполагает, что счетчик является локальным для update_counter() , и выдает UnboundLocalError , потому что вы пытаетесь получить доступ к имени, которое еще не определено.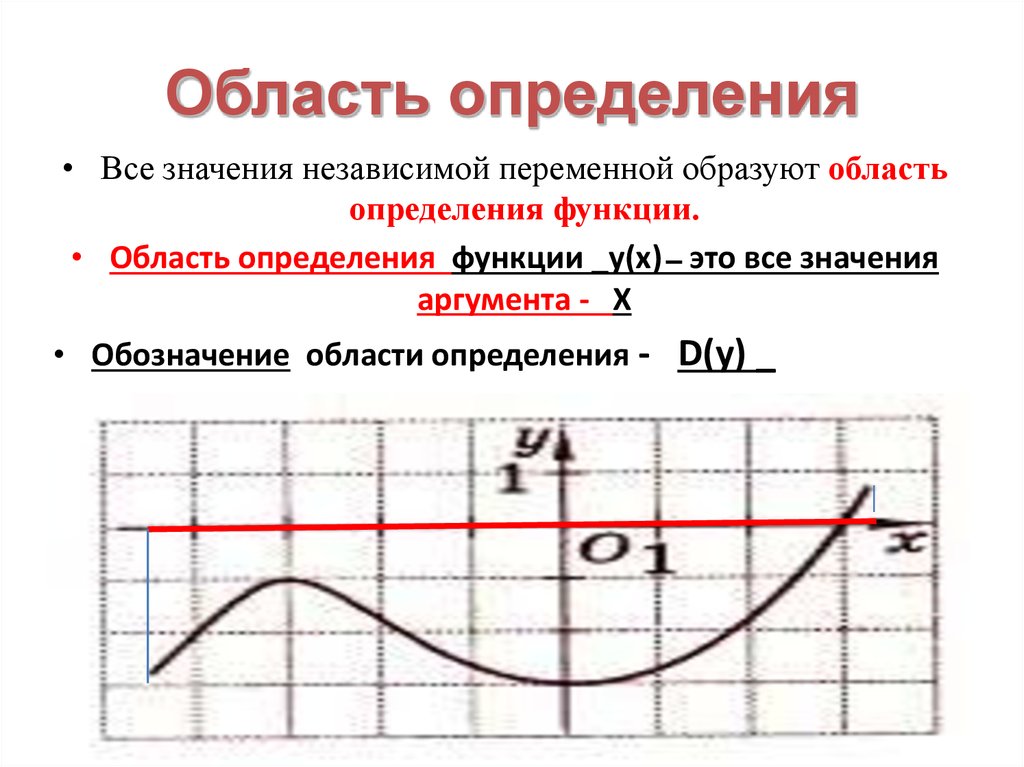
Если вы хотите, чтобы этот код работал так, как вы ожидаете здесь, вы можете использовать глобальную инструкцию следующим образом:
>>>
>>> counter = 0 # Глобальное имя >>> определение update_counter(): ... глобальный счетчик # Объявить счетчик как глобальный ... counter = counter + 1 # Успешно обновить счетчик ... >>> update_counter() >>> счетчик 1 >>> update_counter() >>> счетчик 2 >>> update_counter() >>> счетчик 3
В этой новой версии update_counter() вы добавляете оператор global counter в тело функции непосредственно перед попыткой изменить counter . С помощью этого крошечного изменения вы сопоставляете имя счетчика в области функции с тем же именем в глобальной области или области модуля. С этого момента вы можете свободно изменять счетчик внутри update_counter() . Все изменения отразятся в глобальной переменной.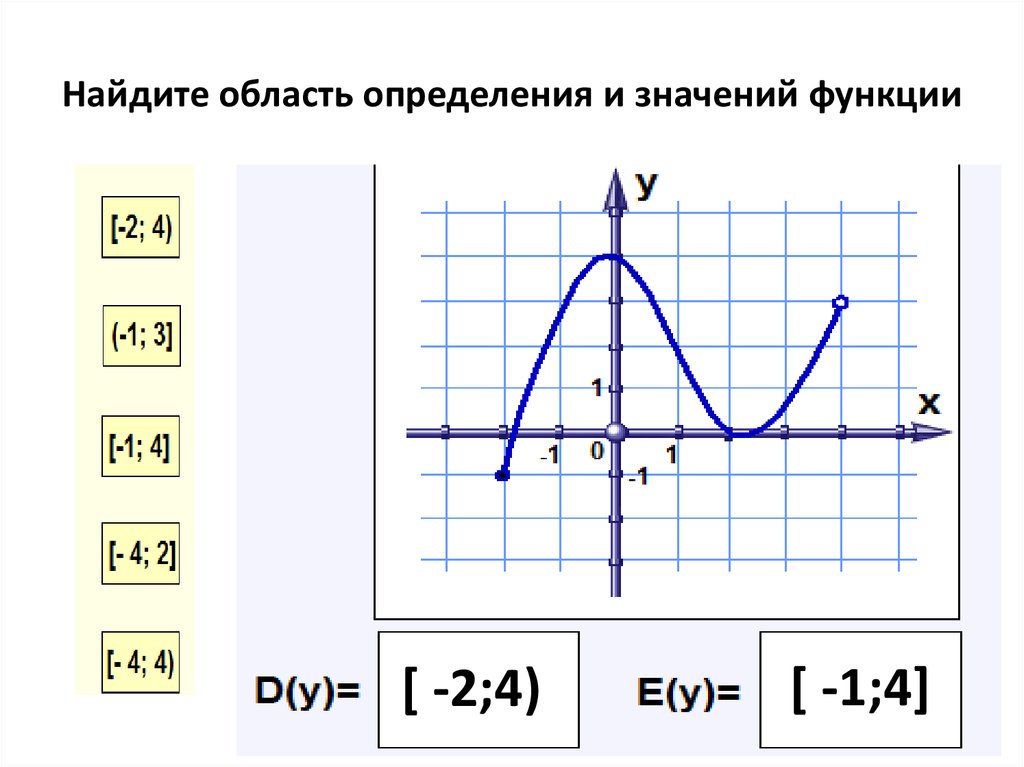
С помощью оператора global counter вы говорите Python искать в глобальной области видимости имя counter . Таким образом, выражение counter = counter + 1 не создает новое имя в области видимости функции, а обновляет его в глобальной области видимости.
Примечание: Использование global в целом считается плохой практикой. Если вы обнаружите, что используете global для решения проблем, подобных приведенной выше, остановитесь и подумайте, есть ли лучший способ написать свой код.
Например, вы можете попробовать написать автономную функцию, которая опирается на локальные имена, а не на глобальные, следующим образом:
>>>
>>> global_counter = 0 # Глобальное имя >>> def update_counter (счетчик): ... return counter + 1 # Доверять локальному имени ... >>> global_counter = update_counter(global_counter) >>> глобальный_счетчик 1 >>> global_counter = update_counter(global_counter) >>> глобальный_счетчик 2 >>> global_counter = update_counter(global_counter) >>> глобальный_счетчик 3
Эта реализация update_counter() определяет счетчик как параметр и возвращает его значение, увеличенное на 1 единиц при каждом вызове функции. Таким образом, результат
Таким образом, результат update_counter() зависит от счетчика , который вы используете в качестве входных данных, а не от изменений, которые другие функции (или фрагменты кода) могут выполнять в глобальной переменной global_counter .
Вы также можете использовать оператор global для создания ленивых глобальных имен, объявив их внутри функции. Взгляните на следующий код:
>>>
>>> def create_lazy_name(): ... global lazy # Создать глобальное имя, lazy ... ленивый = 100 ... вернуться ленивым ... >>> create_lazy_name() 100 >>> lazy # Имя теперь доступно в глобальной области видимости 100 >>> директор() ['__аннотации__', '__builtins__',..., 'create_lazy_name', 'ленивый']
Когда вы вызываете create_lazy_name() , вы также создаете глобальную переменную с именем lazy . Обратите внимание, что после вызова функции имя lazy доступен в глобальной области Python.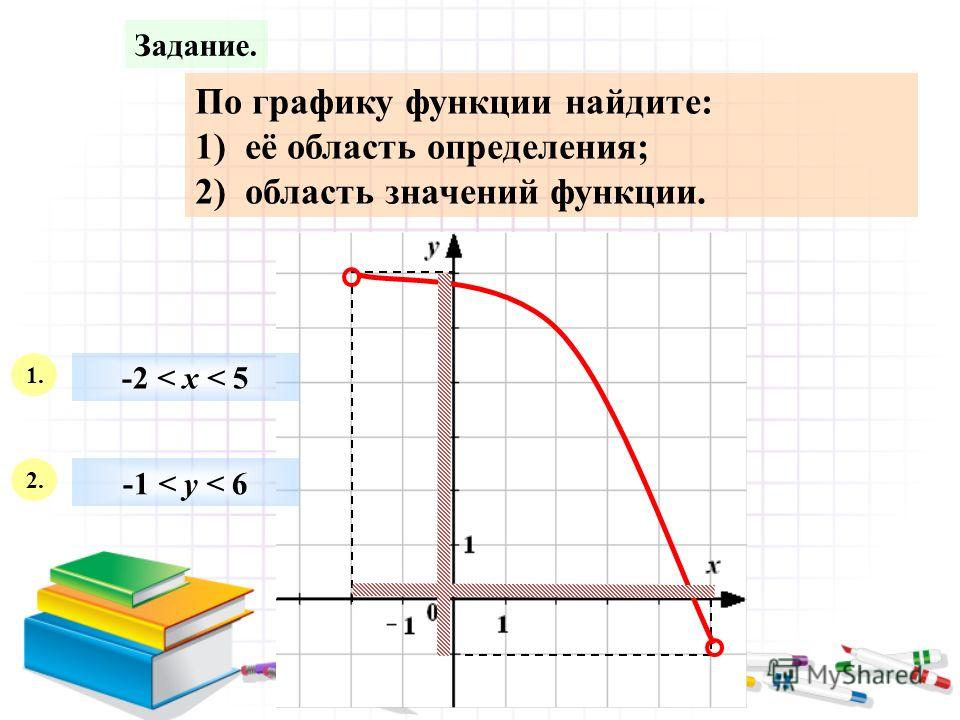 Если вы проверите глобальное пространство имен с помощью
Если вы проверите глобальное пространство имен с помощью dir() , то увидите, что lazy стоит последним в списке.
Примечание: Несмотря на то, что вы можете использовать оператор global для создания ленивых глобальных имен, это может быть опасной практикой, которая может привести к ошибкам в коде. Поэтому лучше избегать подобных вещей в своем коде.
Например, предположим, что вы пытаетесь получить доступ к одному из этих ленивых имен, но по какой-то причине ваш код еще не вызвал функцию, создающую это имя. В этом случае вы получите NameError и ваша программа выйдет из строя.
Наконец, стоит отметить, что вы можете использовать global внутри любой функции или вложенной функции, и перечисленные имена всегда будут сопоставлены с именами в глобальной области Python.
Также обратите внимание, что хотя использование оператора global на верхнем уровне модуля допустимо, это не имеет большого смысла, поскольку любое имя, назначенное в глобальной области видимости, уже является глобальным именем по определению. Взгляните на следующий код:
Взгляните на следующий код:
>>>
>>> имя = 100 >>> директор() ['__аннотации__', '__встроенные__',..., '__spec__', 'имя'] >>> глобальное имя >>> директор() ['__аннотации__', '__встроенные__',..., '__spec__', 'имя']
Использование оператора global , такого как global name , ничего не меняет в вашей текущей глобальной области видимости, как вы можете видеть в выводе dir() . Имя переменной является глобальной переменной независимо от того, используете ли вы глобальный или нет.
Удалить рекламу
нелокальный Заявление Аналогично глобальным именам, к нелокальным именам можно получить доступ из внутренних функций, но они не могут быть назначены или обновлены. Если вы хотите изменить их, вам нужно использовать оператор nonlocal . С помощью оператора nonlocal вы можете определить список имен, которые будут рассматриваться как нелокальные.
Оператор nonlocal состоит из нелокальное ключевое слово , за которым следует одно или несколько имен, разделенных запятыми. Эти имена будут ссылаться на те же имена в окружающей области Python. В следующем примере показано, как можно использовать nonlocal для изменения переменной, определенной во внешней или нелокальной области:
>>>
>>> функция функции(): ... var = 100 # Нелокальная переменная ... определение вложенное(): ... nonlocal var # Объявить var как нелокальный ... переменная += 100 ... ... вложенный () ... печать (вар) ... >>> функция() 200
С помощью оператора nonlocal var вы сообщаете Python, что будете изменять var внутри nested() . Затем вы увеличиваете var , используя расширенную операцию присваивания. Это изменение отражено в нелокальном имени var , которое теперь имеет значение 200 .
В отличие от global , вы не можете использовать nonlocal вне вложенной или закрытой функции. Чтобы быть более точным, вы не можете использовать оператор nonlocal либо в глобальной, либо в локальной области. Вот пример:
>>>
>>> nonlocal my_var # Попробуйте использовать нелокальный в глобальной области видимости Файл "", строка 1 SyntaxError: нелокальное объявление не разрешено на уровне модуля >>> Функция функции(): ... nonlocal var # Попробуйте использовать nonlocal в локальной области видимости ... печать (вар) ... Файл " ", строка 2 SyntaxError: не найдена привязка для нелокального 'var'
Здесь вы сначала пытаетесь использовать нелокальный оператор в глобальной области Python. Поскольку nonlocal работает только внутри внутренней или вложенной функции, вы получаете SyntaxError , говорящую вам, что вы не можете использовать nonlocal в области модуля. Обратите внимание, что
Обратите внимание, что nonlocal также не работает внутри локальной области видимости.
Примечание: Для получения более подробной информации об операторе nonlocal см. PEP 3104 — Доступ к именам во внешних областях.
В отличие от global , вы не можете использовать nonlocal для создания ленивых нелокальных имен. Имена должны уже существовать в окружающей области Python, если вы хотите использовать их как нелокальные имена. Это означает, что вы не можете создавать нелокальные имена, объявляя их в операторе nonlocal во вложенной функции. Взгляните на следующий пример кода:
>>>
>>> функция функции(): ... определение вложенное(): ... nonlocal lazy_var # Попробуйте создать нелокальное ленивое имя ... Файл "", строка 3 SyntaxError: привязка для нелокального 'lazy_var' не найдена
В этом примере, когда вы пытаетесь определить нелокальное имя, используя nonlocal lazy_var , Python немедленно выдает SyntaxError , потому что lazy_var не существует в охватывающей области nested() .
Использование закрывающих областей в качестве замыканий
Замыкания — это особый случай использования объемлющей области Python. Когда вы обрабатываете вложенную функцию как данные, операторы, составляющие эту функцию, упаковываются вместе со средой, в которой они выполняются. Полученный объект называется замыканием. Другими словами, замыкание — это внутренняя или вложенная функция, несущая информацию о включающей ее области видимости, даже если эта область действия завершила свое выполнение.
Примечание: Вы также можете назвать функцию такого типа factory , factory function , или, если быть более точным, фабрика замыканий , чтобы указать, что функция создает и возвращает замыкания (внутренняя функция). , а не классы или экземпляры.
Замыкания позволяют сохранять информацию о состоянии между вызовами функций. Это может быть полезно, когда вы хотите написать код, основанный на концепции ленивых или отложенных вычислений.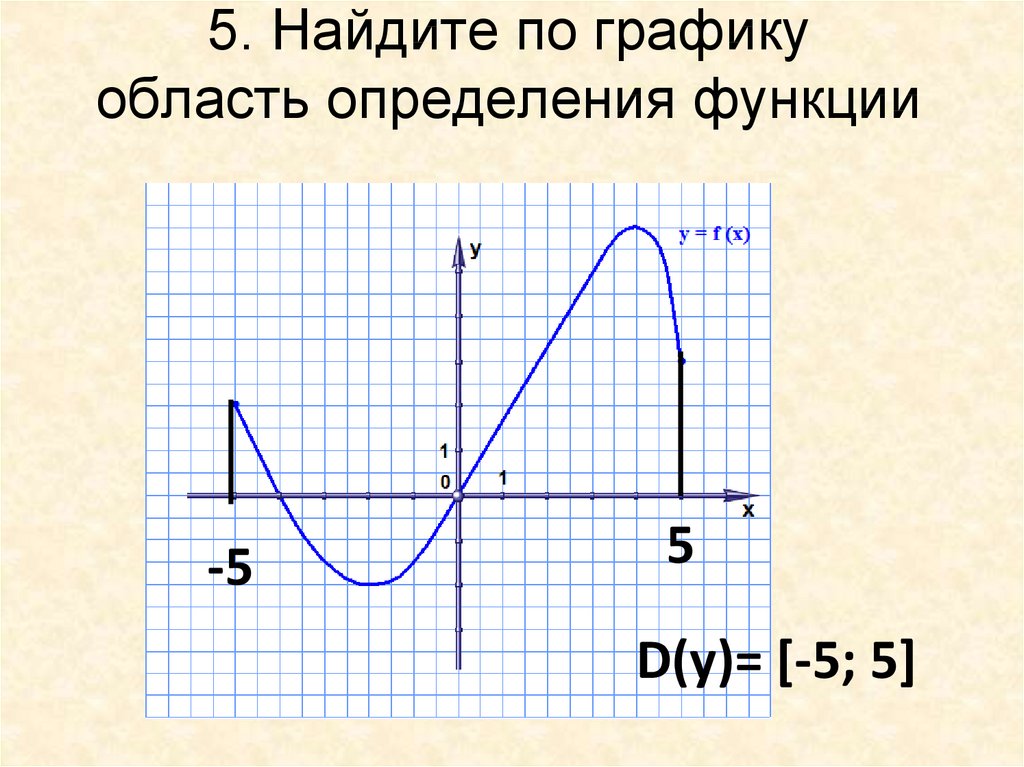 Взгляните на следующий код для примера того, как работают замыкания и как вы можете использовать их преимущества в Python:
Взгляните на следующий код для примера того, как работают замыкания и как вы можете использовать их преимущества в Python:
>>>
>>> def power_factory(exp): ... сила защиты (базовая): ... вернуть базу ** exp ... вернуть мощность ... >>> квадрат = power_factory(2) >>> квадрат(10) 100 >>> куб = power_factory(3) >>> куб(10) 1000 >>> куб(5) 125 >>> квадрат(15) 225
Ваша функция фабрики закрытия power_factory() принимает аргумент с именем exp . Вы можете использовать эту функцию для создания замыканий, которые выполняют различные силовые операции. Это работает, потому что каждый вызов power_factory() получает собственный набор информации о состоянии. Другими словами, он получает значение exp .
Примечание: Переменные типа exp называются свободными переменными . Это переменные, которые используются в блоке кода, но не определены там.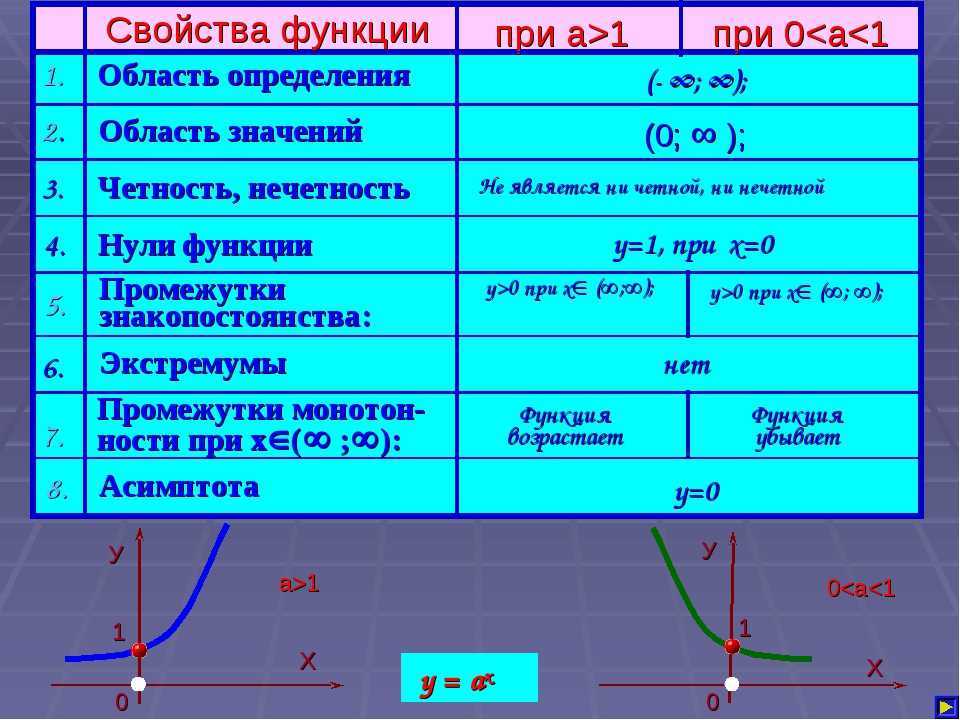 Свободные переменные — это механизм, который замыкания используют для сохранения информации о состоянии между вызовами.
Свободные переменные — это механизм, который замыкания используют для сохранения информации о состоянии между вызовами.
В приведенном выше примере внутренняя функция power() сначала назначается квадрат . В этом случае функция запоминает, что exp равно 2 . Во втором примере вы вызываете power_factory() , используя 3 в качестве аргумента. Таким образом, куб содержит функциональный объект, который запоминает, что exp равно 3 . Обратите внимание, что вы можете свободно повторно использовать квадрат и куб , потому что они не забывают соответствующую информацию о состоянии.
В качестве последнего примера использования замыканий предположим, что вам нужно вычислить среднее значение некоторых выборочных данных. Вы собираете данные через поток последовательных измерений анализируемого параметра. В этом случае вы можете использовать фабрику замыканий для создания замыкания, которое запоминает предыдущие измерения в образце. Взгляните на следующий код:
Взгляните на следующий код:
>>>
>>> среднее значение по умолчанию(): ... образец = [] ... def _mean (число): ... пример.дополнение(число) ... вернуть сумму (выборка) / len (выборка) ... вернуть _среднее ... >>> текущее_среднее = среднее() >>> текущее_среднее (10) 10,0 >>> текущее_среднее (15) 12,5 >>> текущее_среднее (12) 12.333333333333334 >>> текущее_среднее (11) 12,0 >>> текущее_среднее (13) 12.2
Замыкание, созданное в приведенном выше коде, запоминает информацию о состоянии выборка между вызовами current_mean . Таким образом, вы можете решить проблему элегантным и питоническим способом.
Обратите внимание: если ваш поток данных становится слишком большим, эта функция может стать проблемой с точки зрения использования памяти. Это потому, что с каждым вызовом current_mean sample будет содержать все больший и больший список значений. Взгляните на следующий код для альтернативной реализации с использованием nonlocal :
>>>
>>> среднее значение(): ... всего = 0 ... длина = 0 ... def _mean (число): ... нелокальная сумма, длина ... всего += число ... длина += 1 ... вернуть общее количество/длину ... вернуть _среднее ... >>> текущее_среднее = среднее() >>> текущее_среднее (10) 10,0 >>> текущее_среднее (15) 12,5 >>> текущее_среднее (12) 12.333333333333334 >>> текущее_среднее (11) 12,0 >>> текущее_среднее (13) 12.2
Несмотря на то, что это решение более подробное, у вас больше нет бесконечно растущего списка. Теперь у вас есть единственное значение для всего и длина . Эта реализация намного эффективнее с точки зрения потребления памяти, чем предыдущее решение.
Наконец, вы можете найти несколько примеров использования замыканий в стандартной библиотеке Python. Например, functools предоставляет функцию с именем partial() , которая использует метод замыкания для создания новых функциональных объектов, которые можно вызывать с использованием предопределенных аргументов. Вот пример:
Вот пример:
>>>
>>> из functools частичного импорта >>> сила защиты (exp, base): ... вернуть базу ** exp ... >>> квадрат = частичная (мощность, 2) >>> квадрат(10) 100
Вы используете частичное для создания функционального объекта, который запоминает информацию о состоянии, где exp=2 . Затем вы вызываете этот объект для выполнения операции питания и получения конечного результата.
Удалить рекламу
Приведение имен в соответствие с
импортом Когда вы пишете программу на Python, вы обычно организуете код в несколько модулей. Чтобы ваша программа работала, вам нужно перенести имена из этих отдельных модулей в ваш модуль __main__ . Для этого вам нужно явно импортировать модули или имена. Это единственный способ использовать эти имена в вашей основной глобальной области Python.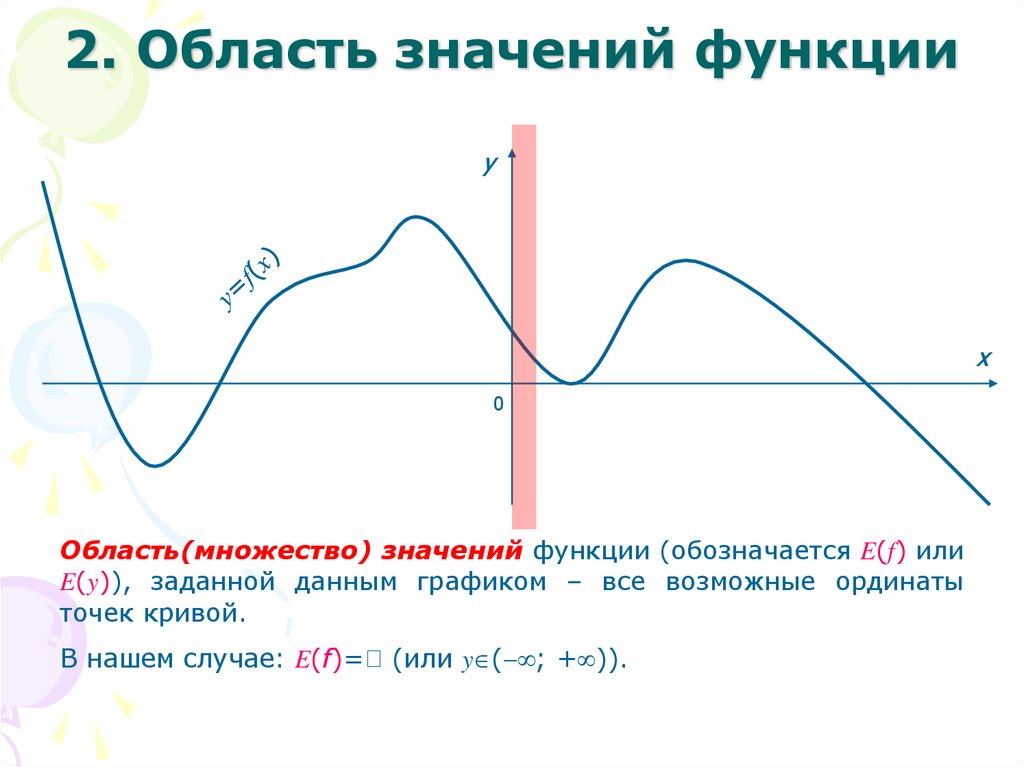
Взгляните на следующий код в качестве примера того, что происходит, когда вы импортируете некоторые стандартные модули и имена:
>>>
>>> директор() ['__аннотации__', '__builtins__',..., '__spec__'] >>> импорт систем >>> директор() ['__аннотации__', '__builtins__',..., '__spec__', 'sys'] >>> импортировать ОС >>> директор() ['__аннотации__', '__builtins__',..., '__spec__', 'os', 'sys'] >>> из functools частично импортировать >>> директор() ['__annotations__', '__builtins__',..., '__spec__', 'os', 'partial', 'sys']
Вы сначала импортируете sys и os из стандартной библиотеки Python. Вызвав dir() без аргументов, вы увидите, что эти модули теперь доступны для вас как имена в вашей текущей глобальной области видимости. Таким образом, вы можете использовать запись через точку, чтобы получить доступ к именам, определенным в sys и os .
В последней операции import используется форма from .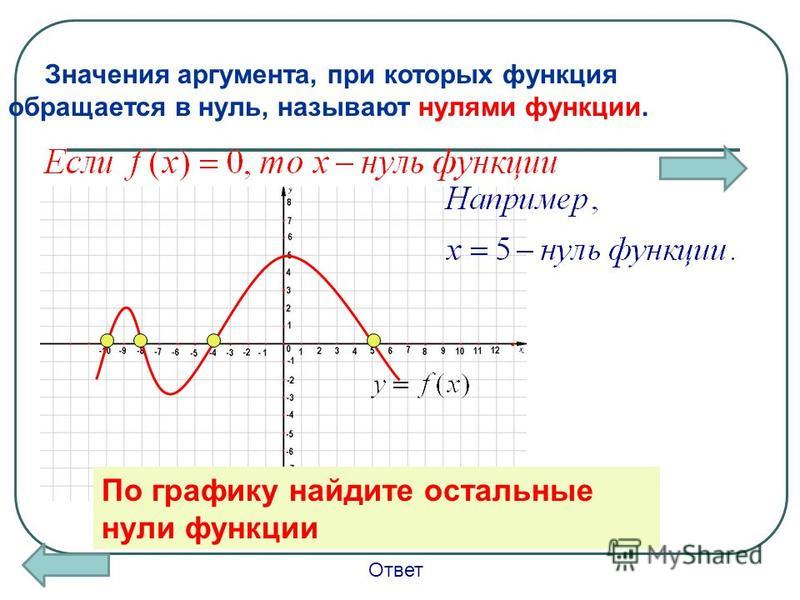 Таким образом, вы можете использовать импортированное имя непосредственно в коде. Другими словами, вам не нужно явно использовать запись через точку.
Таким образом, вы можете использовать импортированное имя непосредственно в коде. Другими словами, вам не нужно явно использовать запись через точку.
Обнаружение необычных областей Python
Вы обнаружите некоторые структуры Python, в которых разрешение имен не соответствует правилу LEGB для областей действия Python. Эти структуры включают в себя:
- Понимание
- Блоки исключений
- Классы и экземпляры
В следующих нескольких разделах вы узнаете, как область действия Python работает с этими тремя структурами. Обладая этими знаниями, вы сможете избежать тонких ошибок, связанных с использованием имен в подобных структурах Python.
Область действия переменных понимания
Первая структура, которую вы рассмотрим, — это понимание . Понимание — это компактный способ обработки всех или части элементов коллекции или последовательности. Вы можете использовать включения для создания списков, словарей и наборов.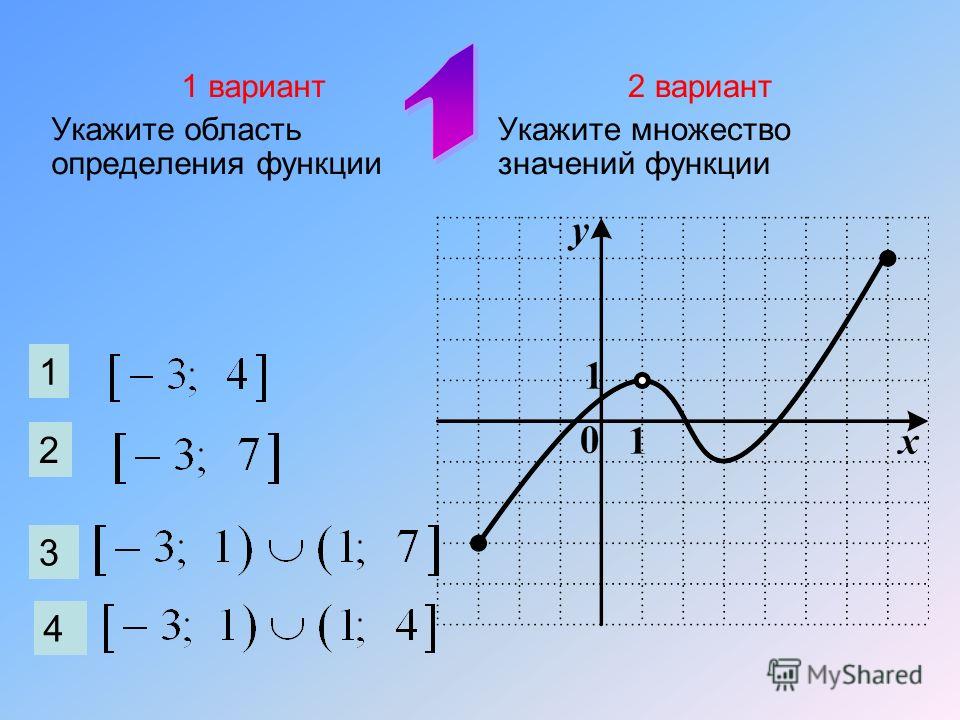
Включения состоят из пары скобок ( [] ) или фигурных скобок ( {} ), содержащих выражение, за которым следует одно или несколько предложений для предложений, а затем ноль или единица , если пункт на пункт для пункта .
Предложение for во включении работает аналогично традиционному циклу for . Переменная цикла в понимании является локальной по отношению к структуре. Проверьте следующий код:
>>>
>>> [элемент для элемента в диапазоне (5)] [0, 1, 2, 3, 4] >>> item # Попытаться получить доступ к переменной понимания Traceback (последний последний вызов): Файл "", строка 1, в вещь NameError: имя «элемент» не определено
После того, как вы запустите понимание списка, переменная элемент будет забыта, и вы больше не сможете получить доступ к ее значению. Маловероятно, что вам нужно использовать эту переменную вне понимания, но независимо от этого Python гарантирует, что ее значение больше не будет доступно после завершения понимания.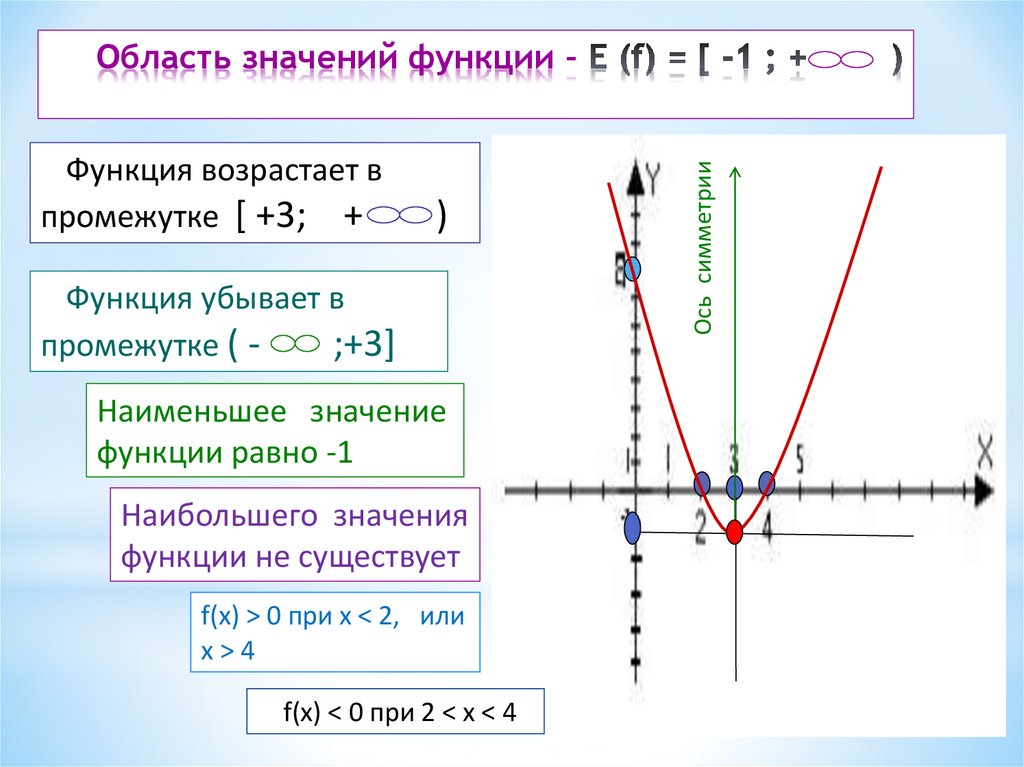
Обратите внимание, что это относится только к включениям. Когда дело доходит до обычных циклов для , переменная цикла содержит последнее значение, обработанное циклом:
>>>
>>> для элемента в диапазоне (5): ... печать (элемент) ... 0 1 2 3 4 >>> item # Доступ к переменной цикла 4
Вы можете свободно обращаться к переменной цикла элемента после завершения цикла. Здесь переменная цикла содержит последнее значение, обработанное циклом, в данном примере это 4 .
Удалить рекламу
Область действия переменных исключений
Еще один нетипичный случай области действия Python, с которым вы столкнетесь, — это случай с переменная исключения . Переменная исключения — это переменная, которая содержит ссылку на исключение, вызванное инструкцией try . В Python 3.x такие переменные являются локальными для блока , кроме , и забываются, когда блок заканчивается. Проверьте следующий код:
Проверьте следующий код:
>>>
>>> лст = [1, 2, 3] >>> попробуйте: ... лист[4] ... кроме IndexError как ошибка: ... # Переменная err является локальной для этого блока ... # Здесь с ошибкой можно делать что угодно ... печать (ошибка) ... индекс списка вне допустимого диапазона >>> err # Выходит за рамки Traceback (последний последний вызов): Файл "", строка 1, в ошибаться NameError: имя «ошибка» не определено
err содержит ссылку на исключение, вызванное предложением try . Вы можете использовать err только внутри блока кода пункта , кроме . Таким образом, вы можете сказать, что область Python для переменной исключения является локальной для блока кода , кроме . Также обратите внимание, что если вы попытаетесь получить доступ к err из-за пределов блока , кроме , вы получите NameError . Это потому, что после завершения блока , кроме , имя больше не существует.
Чтобы обойти это поведение, вы можете определить вспомогательную переменную из оператора try , а затем назначить исключение для этой переменной внутри блока , кроме . Посмотрите на следующий пример:
>>>
>>> лст = [1, 2, 3] >>> пример = Нет >>> попробуйте: ... лист[4] ... кроме IndexError как ошибка: ... экс = ошибка ... печать (ошибка) ... индекс списка вне допустимого диапазона >>> err # Выходит за рамки Traceback (последний последний вызов): Файл "", строка 1, в NameError: имя «ошибка» не определено >>> ex # Содержит ссылку на исключение индекс списка вне допустимого диапазона
Вы используете ex в качестве вспомогательной переменной для хранения ссылки на исключение, вызванное предложением try . Это может быть полезно, когда вам нужно что-то сделать с объектом исключения после завершения блока кода. Обратите внимание, что если исключение не возникает, то ex остается None .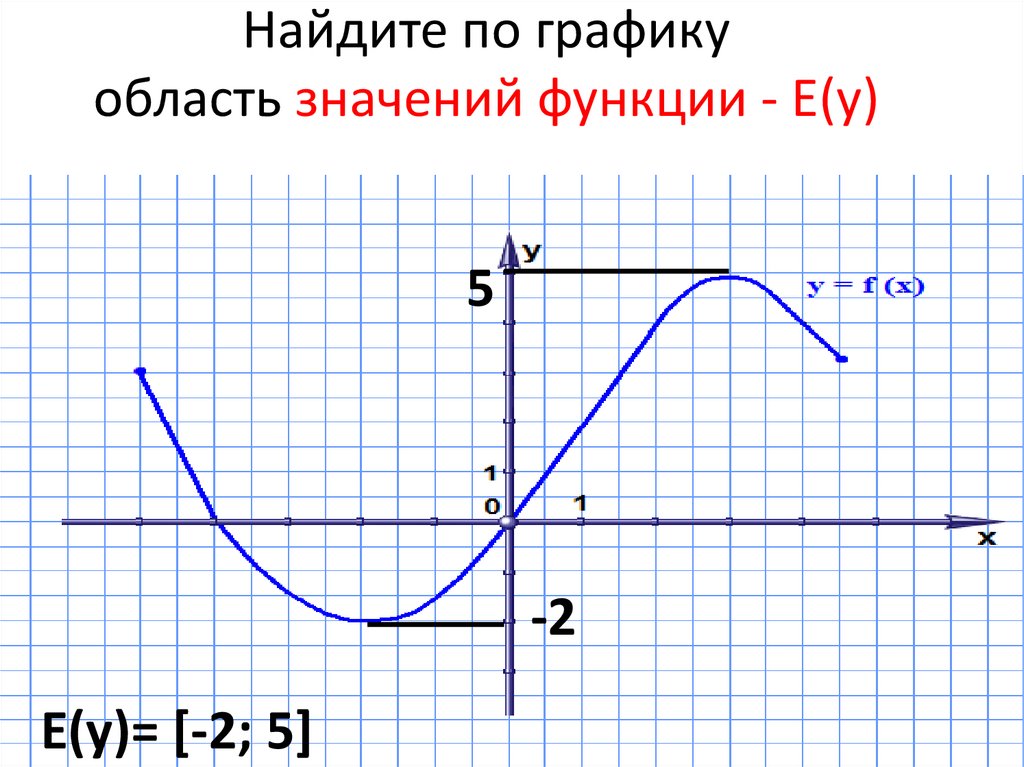
Область действия атрибутов класса и экземпляра
Когда вы определяете класс, вы создаете новую локальную область Python. Имена, назначенные на верхнем уровне класса, живут в этой локальной области. Имена, которые вы присвоили внутри 9Оператор 0019 класса не конфликтует с другими именами. Можно сказать, что эти имена следуют правилу LEGB, где блок класса представляет уровень L .
В отличие от функций, локальная область класса создается не во время вызова, а во время выполнения. Каждый объект класса имеет свой собственный атрибут .__dict__ , который содержит область действия класса или пространство имен, в котором живут все атрибуты класса . Проверьте этот код:
>>>
>>> класс А: ... атрибут = 100 ... >>> A.__dict__.keys() dict_keys(['__module__', 'attr', '__dict__', '__weakref__', '__doc__'])
Когда вы проверите ключи .__dict__ , вы увидите, что attr находится в списке вместе с другими специальными именами. Этот словарь представляет локальную область видимости класса. Имена в этой области видны всем экземплярам класса и самому классу.
Этот словарь представляет локальную область видимости класса. Имена в этой области видны всем экземплярам класса и самому классу.
Чтобы получить доступ к атрибуту класса извне класса, вам нужно использовать запись через точку следующим образом:
>>>
>>> класс А: ... атрибут = 100 ... print(attr) # Прямой доступ к атрибутам класса ... 100 >>> A.attr # Доступ к атрибуту класса извне класса 100 >>> attr # Не определен вне A Traceback (последний последний вызов): Файл "", строка 1, в атрибут NameError: имя 'attr' не определено
Внутри локальной области действия A вы можете получить прямой доступ к атрибутам класса, точно так же, как вы делали это в операторе print(attr) . Чтобы получить доступ к любому атрибуту класса после выполнения блока кода класса, вам нужно будет использовать точечную нотацию или ссылку на атрибут, как вы сделали с A.attr . В противном случае вы получите NameError , потому что атрибут attr является локальным для блока класса.
С другой стороны, если вы попытаетесь получить доступ к атрибуту, который не определен внутри класса, вы получите Ошибка атрибута . Посмотрите на следующий пример:
>>>
>>> A.undefined # Попытка получить доступ к неопределенному атрибуту класса Traceback (последний последний вызов): Файл "", строка 1, в А.не определено AttributeError: объект типа «A» не имеет атрибута «undefined»
В этом примере вы пытаетесь получить доступ к атрибуту undefined . Поскольку этот атрибут не существует в A , вы получаете AttributeError сообщает вам, что A не имеет атрибута с именем undefined .
Вы также можете получить доступ к любому атрибуту класса, используя экземпляр класса следующим образом:
>>>
>>> объект = А() >>> obj.attr 100
Когда у вас есть экземпляр, вы можете получить доступ к атрибутам класса, используя запись через точку, как вы сделали здесь с obj. . Атрибуты класса специфичны для объекта класса, но вы можете получить к ним доступ из любых экземпляров класса. Стоит отметить, что атрибуты класса являются общими для всех экземпляров класса. Если вы измените атрибут класса, то изменения будут видны во всех экземплярах класса.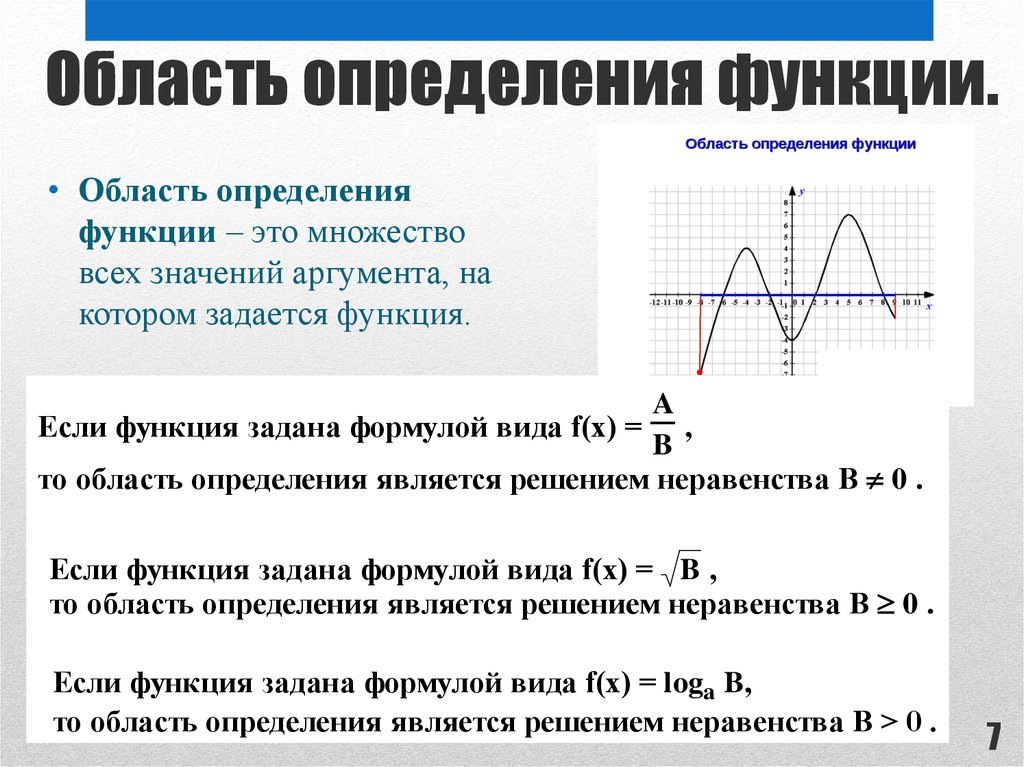 attr
attr
Примечание: Думайте о записи через точку, как если бы вы говорили Python: «Ищите атрибут с именем attr в obj . Если найдешь, то верни мне».
Всякий раз, когда вы вызываете класс, вы создаете новый экземпляр этого класса. Экземпляры имеют собственный атрибут .__dict__ , который содержит имена в локальной области или пространстве имен экземпляра. Эти имена обычно называются атрибутами экземпляра и являются локальными и специфическими для каждого экземпляра. Это означает, что если вы измените атрибут экземпляра, изменения будут видны только этому конкретному экземпляру.
Чтобы создать, обновить или получить доступ к любому атрибуту экземпляра внутри класса, вам нужно использовать self вместе с записью через точку. Здесь
Здесь self — это специальный атрибут, представляющий текущий экземпляр. С другой стороны, чтобы обновить или получить доступ к любому атрибуту экземпляра извне класса, вам нужно создать экземпляр, а затем использовать точечную нотацию. Вот как это работает:
>>>
>>> класс А:
... def __init__(self, var):
... self.var = var # Создать новый атрибут экземпляра
... self.var *= 2 # Обновить атрибут экземпляра
...
>>> объект = А(100)
>>> обж.__дикт__
{'вар': 200}
>>> obj.var
200
Класс A принимает аргумент с именем var , который автоматически удваивается внутри .__init__() с помощью операции присваивания self.var *= 2 . Обратите внимание, что когда вы проверяете .__dict__ на obj , вы получаете словарь, содержащий все атрибуты экземпляра. В этом случае словарь содержит только имя var , значение которого теперь равно 200 .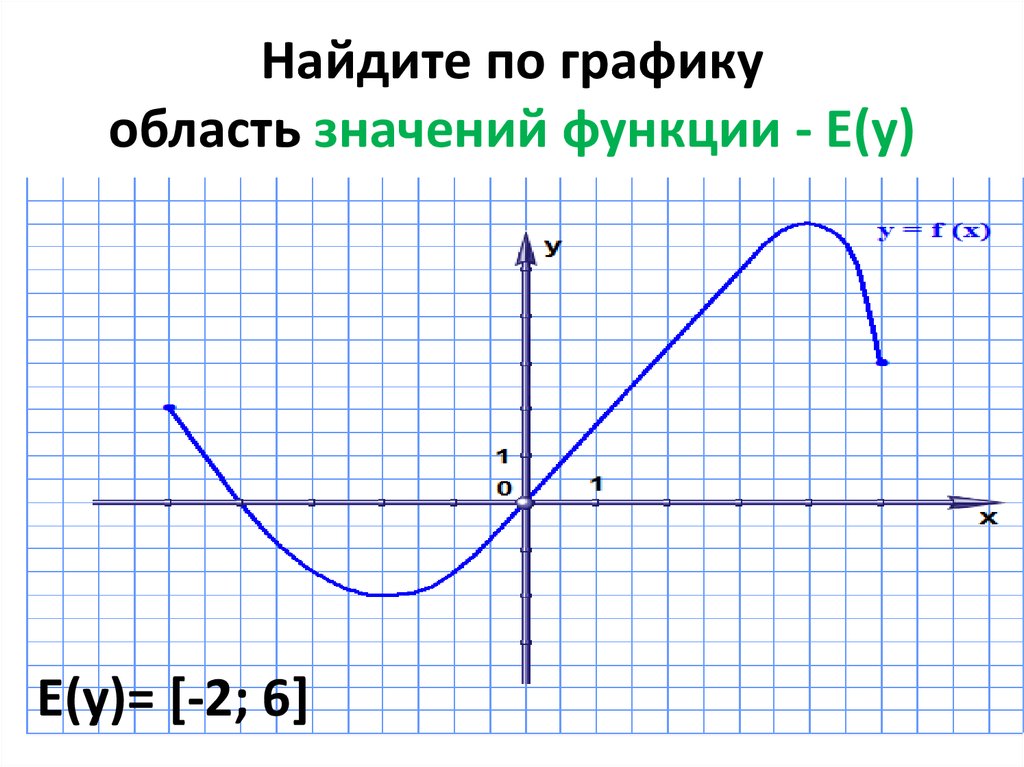
Несмотря на то, что атрибуты экземпляра можно создавать в любом методе класса, рекомендуется создавать и инициализировать их внутри .__init__() . Взгляните на эту новую версию A :
>>>
>>> класс А: ... def __init__(self, var): ... self.var = var ... ... определение дубликат_вар (я): ... вернуть self.var * 2 ... >>> объект = А(100) >>> obj.var 100 >>> obj.duplicate_var() 200 >>> А.вар Traceback (последний последний вызов): Файл "", строка 1, в А.вар AttributeError: объект типа «A» не имеет атрибута «var»
Здесь вы модифицируете A , чтобы добавить новый метод с именем Дублировать_var() . Затем вы создаете экземпляр A , передавая 100 инициализатору класса. После этого теперь вы можете вызвать Duplica_var() на obj , чтобы дублировать значение, хранящееся в self.var .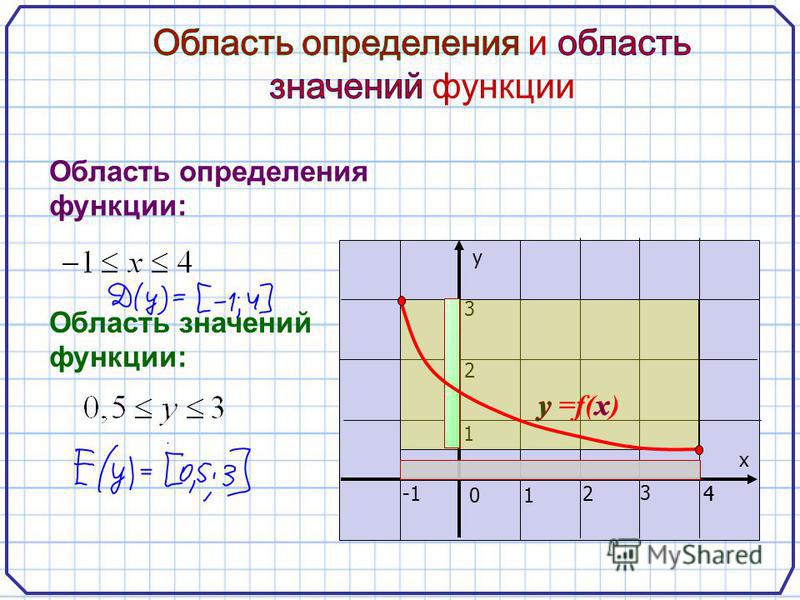 Наконец, если вы попытаетесь получить доступ к
Наконец, если вы попытаетесь получить доступ к var , используя объект класса вместо экземпляра, вы получите AttributeError , потому что атрибуты экземпляра не могут быть доступны с использованием объектов класса.
В общем, когда вы пишете объектно-ориентированный код на Python и пытаетесь получить доступ к атрибуту, ваша программа выполняет следующие шаги:
- Сначала проверьте локальную область или пространство имен экземпляра .
- Если атрибут там не найден, проверьте класс локальную область или пространство имен.
- Если имя не существует и в пространстве имен класса, вы получите
AttributeError.
Это основной механизм, с помощью которого Python разрешает имена в классах и экземплярах.
Хотя классы определяют локальную область видимости или пространство имен класса, они не создают охватывающую область для методов. Следовательно, когда вы реализуете класс, ссылки на атрибуты и методы должны выполняться с использованием записи через точку:
.
>>>
>>> класс А: ... переменная = 100 ... def print_var(self): ... print(var) # Попытаться получить прямой доступ к атрибуту класса ... >>> А().print_var() Traceback (последний последний вызов): Файл "", строка 1, в A().print_var() Файл " ", строка 4, в print_var печать (вар) NameError: имя 'var' не определено
Поскольку классы не создают охватывающую область для методов, вы не можете получить доступ к var напрямую из print_var() , как вы пытаетесь сделать здесь. Чтобы получить доступ к атрибутам класса из любого метода, вам нужно использовать запись через точку. Чтобы устранить проблему в этом примере, измените оператор print(var) внутри print_var() на print(A.var) и посмотрите, что произойдет.
Вы можете заменить атрибут класса атрибутом экземпляра, что изменит общее поведение вашего класса. Однако вы можете получить однозначный доступ к обоим атрибутам, используя запись через точку, как в следующем примере:
>>>
>>> класс А: ... переменная = 100 ... защита __init__(я): ... селф.вар = 200 ... ... def access_attr(self): ... # Используйте точечную нотацию для доступа к атрибутам класса и экземпляра ... print(f'Атрибут экземпляра: {self.var}') ... print(f'Атрибут класса: {A.var}') ... >>> объект = А() >>> obj.access_attr() Атрибут экземпляра: 200 Атрибут класса: 100 >>> A.var # Доступ к атрибутам класса 100 >>> A().var # Доступ к атрибутам экземпляра 200 >>> A.__dict__.keys() dict_keys(['__module__', 'var', '__init__',..., '__getattribute__']) >>> A().__dict__.keys() dict_keys(['var'])
Вышеупомянутый класс имеет атрибут экземпляра и атрибут класса с тем же именем var . Вы можете использовать следующий код для доступа к каждому из них:
- Экземпляр: Используйте
self.varдля доступа к этому атрибуту. - Класс: Используйте
A.varдля доступа к этому атрибуту.
Поскольку в обоих случаях используется запись через точку, проблем с конфликтами имен не возникает.
Примечание: В общем, хорошая практика ООП рекомендует не дублировать атрибуты класса атрибутами экземпляра, которые имеют другие обязанности или выполняют другие действия. Это может привести к незаметным и трудно обнаруживаемым ошибкам.
Наконец, обратите внимание, что класс .__dict__ и экземпляр .__dict__ — совершенно разные и независимые словари. Вот почему атрибуты класса доступны сразу после запуска или импорта модуля, в котором был определен класс. Напротив, атрибуты экземпляра оживают только после создания объекта или экземпляра.
Удалить рекламу
Заключение
Область переменной или имени определяет ее видимость во всем коде. В Python область действия реализована как локальная, объемлющая, глобальная или встроенная. Когда вы используете переменную или имя, Python последовательно выполняет поиск в этих областях, чтобы разрешить их. Если имя не найдено, вы получите сообщение об ошибке. Это общий механизм, который Python использует для разрешения имен и известен как 9.0103 Правило LEGB .
Если имя не найдено, вы получите сообщение об ошибке. Это общий механизм, который Python использует для разрешения имен и известен как 9.0103 Правило LEGB .
Теперь вы можете:
- Воспользуйтесь преимуществами области Python, чтобы избежать или свести к минимуму ошибки, связанные с конфликтом имен
- Правильно используйте глобальные и локальные имена в своих программах для повышения удобства сопровождения кода
- Используйте последовательную стратегию для доступа, изменения или обновления имен во всем вашем коде Python
Кроме того, вы рассказали о некоторых инструментах и методах, связанных с областью действия, которые предлагает Python, и о том, как вы можете использовать их для сбора информации об именах, находящихся в заданной области, или для изменения стандартного поведения области Python. Конечно, эта тема выходит за рамки этого руководства, так что продолжайте заниматься разрешением имен в Python!
Сравнение функций области видимости Kotlin — блог LogRocket
Язык программирования Kotlin, разработанный для виртуальной машины Java (JVM), сочетает в себе функции объектно-ориентированного и функционального программирования, а также другие парадигмы программирования. Kotlin, используемый в разработке для Android, предоставляет уникальную функцию, известную как функции области действия, однако многие разработчики сталкиваются с некоторыми трудностями при работе с этими функциями.
Kotlin, используемый в разработке для Android, предоставляет уникальную функцию, известную как функции области действия, однако многие разработчики сталкиваются с некоторыми трудностями при работе с этими функциями.
Как разработчик мобильных приложений Android, важно иметь полное представление об этой концепции, которая является важной частью разработки приложений. Красота Kotlin заключается в уникальных функциях, которые делают его подходящим как для фронтенд-, так и для бэкэнд-разработки. В этом уроке мы рассмотрим следующее:
- Что такое функции области видимости?
-
пустьфункция -
с функцией -
запускфункция -
применитьфункцию -
такжефункция - Когда и как использовать функции области видимости Kotlin
- Сравнение функций области Kotlin с обычными функциями
- Преимущества использования функций области видимости
Чтобы следовать этому руководству, вам потребуется следующее:
- Базовые знания языка программирования Kotlin
- IntelliJ IDE или Android Studio установлены
Начнем!
Что такое функции области видимости?
В Kotlin функции области используются для выполнения блока кода в области действия объекта. Как правило, вы можете использовать функции области видимости, чтобы обернуть переменную или набор логики и вернуть объектный литерал в качестве результата. Поэтому мы можем получить доступ к этим объектам без их имен. В Kotlin есть пять типов функций области видимости:
Как правило, вы можете использовать функции области видимости, чтобы обернуть переменную или набор логики и вернуть объектный литерал в качестве результата. Поэтому мы можем получить доступ к этим объектам без их имен. В Kotlin есть пять типов функций области видимости: пусть , с , запустите , примените , а также . Давайте рассмотрим эти примеры и их уникальные варианты использования.
Существует много общего между этими пятью функциями области действия, основанными на их схожих операциях, однако они различаются тем, возвращают ли они лямбда-результат или объект контекста. Они также различаются в зависимости от того, ссылаетесь ли вы на объект контекста с помощью ключевого слова this или it .
пусть функция Функция let имеет множество применений, но обычно она используется для предотвращения возникновения NullPointerException . Функция
Функция let возвращает лямбда-результат, а объектом контекста является идентификатор it . Рассмотрим следующий пример:
весело главное (){
val имя: Строка? = ноль
println(имя!!.перевернутое)
println(имя.длина)
}
В приведенном выше фрагменте кода мы присвоили значение null для имя переменная. Затем мы напечатали обратное и длину строки, включив оператор утверждения NotNull (!!) , чтобы подтвердить, что значение не равно null , потому что у нас есть имя строки, допускающее значение NULL. Поскольку мы вызываем функцию для значения null , это приводит к исключению NullPointerException . Однако мы можем предотвратить это, используя функцию let со следующим кодом:
веселье главное (){
val имя: Строка? = ноль
имя?.пусть{
println(это.перевернутое)
println(it.length)
}
}
Мы помещаем наш код внутрь лямбда-выражения функции let и заменяем имя объекта контекста идентификатором it . Чтобы предотвратить
Чтобы предотвратить NullPointerException , мы включаем оператор безопасного вызова , ( ?.) сразу после нашего объекта name .
Оператор безопасного вызова ставит условие и указывает нашей программе выполнять код, только если имя объект NotNull . В этом примере нам не нужно использовать утверждение NotNull (!!) .
Более 200 000 разработчиков используют LogRocket для улучшения цифрового взаимодействия
Подробнее →
Далее мы назначим строковое значение «Я люблю Kotlin» нашей переменной name . Затем мы возвращаем это строковое значение, сохраняя наше лямбда-значение в переменной с именем lengthOfString :
веселье главное (){
val имя: Строка? = "Я люблю Котлин!!"
val lengthOfString = имя?.let{
println(это.перевернутое)
println(it. length)
}
println (длина строки)
}
length)
}
println (длина строки)
}
с функцией Функция с имеет возвращаемый тип в качестве лямбда-результата, а объект контекста — это ключевое слово this , которое относится к самому объекту. Давайте рассмотрим пример в фрагменте кода ниже:
класс Человек{
var firstName: String = "Елена Уилсон"
переменный возраст: Int = 28
}
веселая главная () {
вал человек = человек ()
println(человек.имя)
println(человек.возраст)
}
В приведенном выше фрагменте кода мы создали класс Person и присвоили ему некоторые свойства: firstName и age . Затем в нашей основной функции мы распечатали значения, используя println , который используется для вывода cli .
Давайте представим, что у нас есть более двадцати свойств в классе Person , что привело бы к многократному повторению кода. Мы можем исправить это, используя функцию с и передав объект person в лямбда-выражении с использованием ключевого слова this :
н){
println(это. имя)
println(этот.возраст)
}
имя)
println(этот.возраст)
}
Объект контекста здесь относится к объекту person , над которым выполняется операция. Возвращаемое значение функции с является лямбда-результатом. Представьте, что мы решили добавить десять лет к age и сохранить значение в переменной с именем personInfo , которая имеет тип integer 9.0020 :
val человек = человек()
val personInfo : String = with (человек){
println(это.имя)
println(этот.возраст)
возраст + 10
«Я люблю игру в футбол»
}
println (информация о человеке)
}
Полученное значение равно «Я люблю игру в футбол» . Таким образом, функция с возвращает лямбда-функцию и использует ключевое слово this в качестве объекта контекста.
запуск функция Функция run возвращает лямбда-результат, и мы обращаемся к объекту контекста с помощью это ключевое слово . Функция
Функция run представляет собой комбинацию функций с и let . Давайте рассмотрим пример в фрагменте кода ниже:
веселье главное {
val человек: Человек? = Человек()
val bio = человек?.run {
println(имя)
println(возраст)
"ЛогРакета рулит!!!"
}
println (био)
}
Предполагая, что мы решили присвоить нулевое значение объекту person , мы должны предотвратить возникновение NullPointerException . Мы можем добиться этого, вызвав запустить функцию с объектом person . Далее мы вернем лямбда-функцию bio .
применить функцию применить — это функция более высокого порядка. Функция apply возвращает объект контекста, а объект контекста возвращает this . Рассмотрим следующий пример:
val автомобиль = Автомобиль()
вар carName: Строка = ""
вар carColor: Строка = ""
веселье главное {
val car = Car (). применить {
carName = "Ламборгини"
carColor = "темно-синий"
}
}
с (машиной) {
println(имя_автомобиля)
println(carColor)
}
применить {
carName = "Ламборгини"
carColor = "темно-синий"
}
}
с (машиной) {
println(имя_автомобиля)
println(carColor)
}
также функция Функция и аналогична предыдущим функциям тем, что она используется для выполнения операции над конкретным объектом после его инициализации. Функция and возвращает объект контекста, и на объект контекста можно ссылаться с помощью идентификатора it . Давайте обратимся к фрагменту кода ниже для более подробной информации:
веселье main(){
val numberList: mutableList = mutableListOf(1,2,4,5)
номерСписок.также{
println("Список элементов: $numberList")
номерСписок.добавить(6)
println("Список элементов после добавления элемента: $numberList")
номерСписок.удалить(4)
println("Список элементов после удаления элемента: $numberList")
}
}
Из приведенного выше кода мы создали объект numbersList с пятью целочисленными значениями и выполнили некоторые операции над объектом numbersList . Затем мы использовали функцию
Затем мы использовали функцию и . Обратите внимание, что в функции также мы можем обратиться к numberList , используя идентификатор it , как показано во фрагменте кода ниже:
веселье main(){
val numberList: mutableList = mutableListOf(1,2,4,5)
valmultiNumbers = numberList.also {
println("Список элементов: $it")
это.добавить(6)
println("Список элементов после добавления элемента: $it")
это.удалить(4)
println("Список элементов после удаления элемента: $it")
}
println("Исходные числа: $numberList")
println("Несколько чисел: $multipleNumbers)
}
Другой способ реализации функции и — использование ключевых слов it и и , как показано в приведенном ниже фрагменте кода. Мы используем функцию и , чтобы изменить значение переменной firstName , назначив ей Eden Peter :
веселье главное {
val человек = человек (). применить {
firstName = "Эден Эленвоке"
возраст = 22
}
с (человеком) {
println(имя)
println(возраст)
}
человек.также{
it.firstName = "Иден Питер"
println("Мое новое имя: + ${it.firstName}")
}
}
применить {
firstName = "Эден Эленвоке"
возраст = 22
}
с (человеком) {
println(имя)
println(возраст)
}
человек.также{
it.firstName = "Иден Питер"
println("Мое новое имя: + ${it.firstName}")
}
}
Когда и как использовать функции области видимости Kotlin
Использование функций области действия в нужном месте поначалу может показаться немного сложным, но это во многом зависит от того, чего мы хотим достичь с помощью проекта. Давайте сошлемся на сводку ниже как на руководство, чтобы сообщить нам, какую функцию области видимости использовать для каждого уникального варианта использования:
-
применить: вы хотите настроить или инициализировать объект -
с: вы хотите работать с ненулевым объектом -
let: вы хотите выполнить лямбда-функцию для объекта, допускающего значение NULL, и избежатьNullPointException -
run: вы хотите работать с объектом, допускающим значение NULL, выполнить лямбда-выражение и избежатьNullPointerException. Это комбинация
Это комбинация си, пустьимеет функции . -
также: Вы хотите выполнить некоторые дополнительные операции с объектами и настройки
Сравнение функций области Kotlin с обычными функциями
Давайте сравним функцию области действия и обычную функцию на нескольких примерах. Давайте рассмотрим обычную функцию, используя класс с именем Student с тремя атрибутами: studentName , studentNumber и studentAge , как показано ниже:
Ученик класса {
var studentName : Строка? = ноль
var studentNumber : Строка? = ноль
var studentAge : Int? = ноль
}
С помощью приведенного ниже фрагмента кода мы создаем экземпляр нашего класса и присваиваем ему значения:
val студент = Студент () student.studentName = "Питер Айделойе" студент.НомерСтудента = 08012345678 студент.studentAge = 28
Использование функции области видимости может помочь нам достичь тех же результатов, что и выше, более простым и понятным способом с меньшим количеством кода. Давайте сравним наше выражение выше с функцией
Давайте сравним наше выражение выше с функцией области действия во фрагменте кода ниже:
val person = Student().apply{
studentName = "Питер Айделойе"
номер студента = 08012345678
студенческий возраст = 28
}
В приведенном выше фрагменте кода мы создаем экземпляр объекта Student и вызываем функцию apply . Затем мы назначаем свойства studentName , studentNumber и studentAge в лямбда-выражении.
Когда мы сравниваем функцию области действия и нормальную функцию в приведенных выше примерах, мы замечаем, что мы успешно устранили повторение кода, где имя объекта студента повторялось несколько раз. Использование функции области видимости делает наш код более кратким и читаемым, и мы инициализировали наши свойства без использования студент имя объекта.
Преимущества использования функций области видимости
Из примеров в разделе сравнения функций выше мы пришли к пониманию некоторых преимуществ использования функций области видимости:
- Сокращенный шаблонный код
- Более краткий и точный код
- Уменьшенное повторение кода
- Улучшенная читаемость кода
Для дальнейшего чтения вы также можете ознакомиться с официальной документацией Kotlin.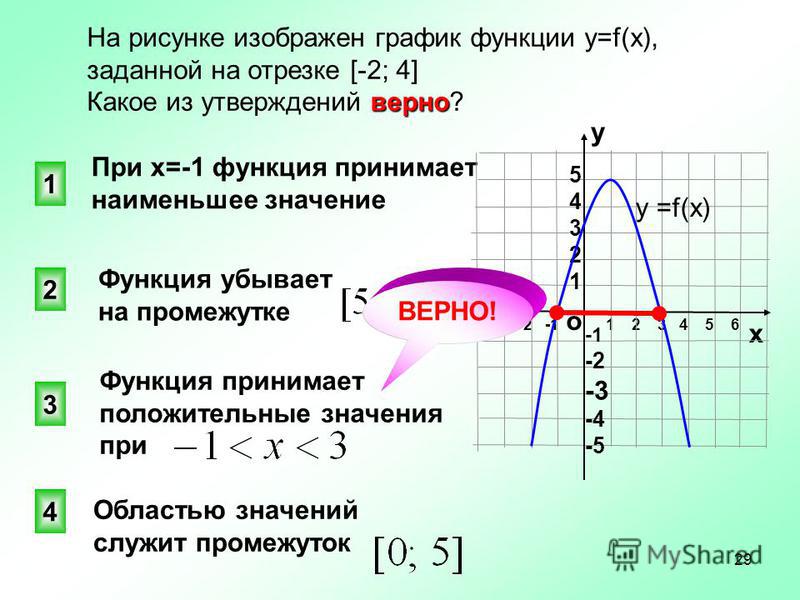
Вывод
В этой статье мы представили пять функций области видимости в Kotlin. Мы также рассмотрели несколько уникальных вариантов использования с примерами, проанализировав, когда использовать каждую функцию области видимости. Мы сравнили функции области действия с обычными функциями и, наконец, рассмотрели преимущества использования функций области видимости.
По мере роста популярности Android-разработки и увеличения количества Android-устройств на рынке знание языка программирования Kotlin становится все более важным. Я надеюсь, что эта статья была полезной, и, пожалуйста, не стесняйтесь оставлять комментарии, если у вас есть какие-либо вопросы. Удачного кодирования!
LogRocket: полная видимость ваших веб-приложений и мобильных приложений
LogRocket — это решение для мониторинга внешних приложений, которое позволяет воспроизводить проблемы, как если бы они возникли в вашем собственном браузере. Вместо того, чтобы гадать, почему возникают ошибки, или запрашивать у пользователей скриншоты и дампы журналов, LogRocket позволяет вам воспроизвести сеанс, чтобы быстро понять, что пошло не так.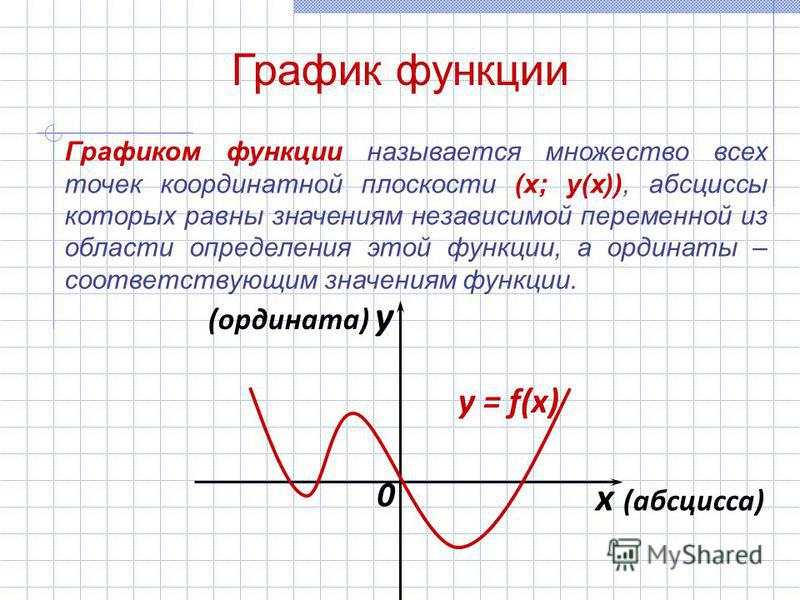 Он отлично работает с любым приложением, независимо от фреймворка, и имеет плагины для регистрации дополнительного контекста из Redux, Vuex и @ngrx/store.
Он отлично работает с любым приложением, независимо от фреймворка, и имеет плагины для регистрации дополнительного контекста из Redux, Vuex и @ngrx/store.
Помимо регистрации действий и состояния Redux, LogRocket записывает журналы консоли, ошибки JavaScript, трассировки стека, сетевые запросы/ответы с заголовками и телами, метаданные браузера и пользовательские журналы. Он также использует DOM для записи HTML и CSS на странице, воссоздавая идеальные до пикселя видео даже для самых сложных одностраничных и мобильных приложений.
Попробуйте бесплатно.
Функции области действия Kotlin
Когда мы используем лямбда-выражение для вызова методов объекта, создается временная область. В статье мы обсудим понятие функций области видимости. Scope Functions — это название этих функций. Объекты этих функций доступны, не зная их имен.
Какие типы функций области видимости существуют в Kotlin?
Функции области действия делают наш код более разборчивым, кратким и простым, что является важными атрибутами языка программирования Kotlin.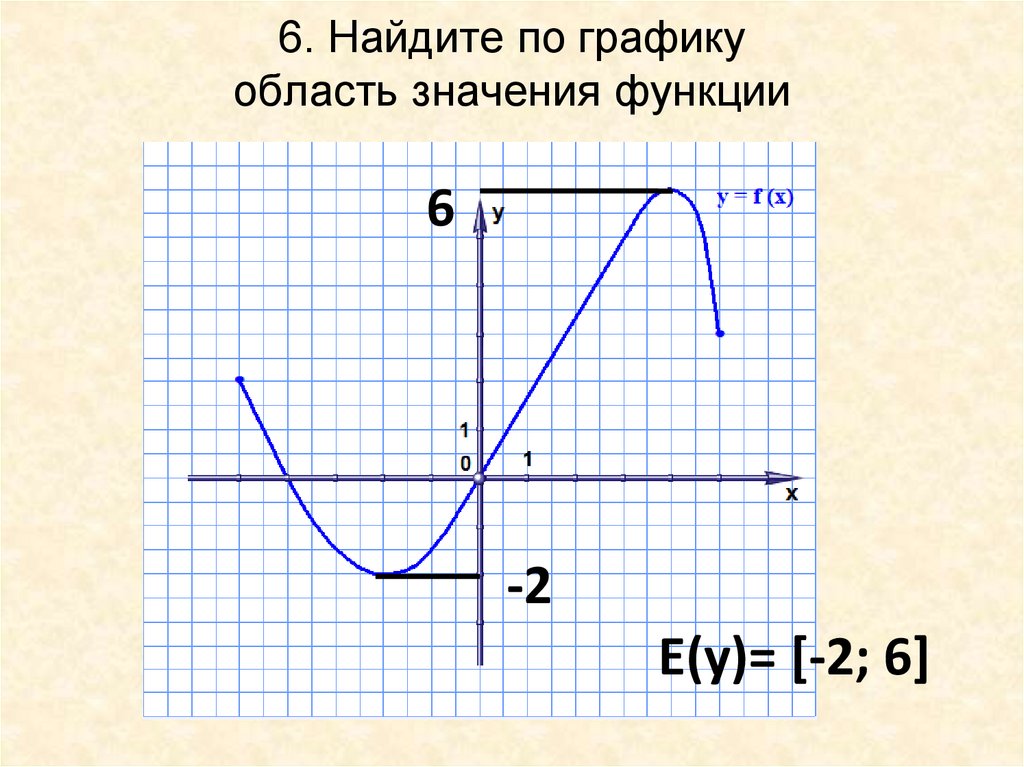 Когда мы не используем функцию области видимости, нам приходится вводить имя объекта каждый раз, когда мы хотим сослаться на член класса. Но мы можем ссылаться на члены без указания имени объекта при использовании функции области видимости. В целом у нас есть пять функций области видимости, и все они очень похожи с небольшими отличиями.
Когда мы не используем функцию области видимости, нам приходится вводить имя объекта каждый раз, когда мы хотим сослаться на член класса. Но мы можем ссылаться на члены без указания имени объекта при использовании функции области видимости. В целом у нас есть пять функций области видимости, и все они очень похожи с небольшими отличиями.
- пусть
- запустить
- применить
- с
- также
Как использовать функции области видимости Kotlin?
Чтобы понять основы использования различных функций области действия в языке Kotlin, вам следует взглянуть на следующие примеры:
Пример № 1. Использование функции области видимости «Let» в Kotlin
Функция Let часто используется для выполнения блока кода только с ненулевыми значениями. Мы должны использовать оператор безопасности «?». на ненулевой объект. Давайте используем функцию let в приведенном ниже коде.
У нас есть основная функция.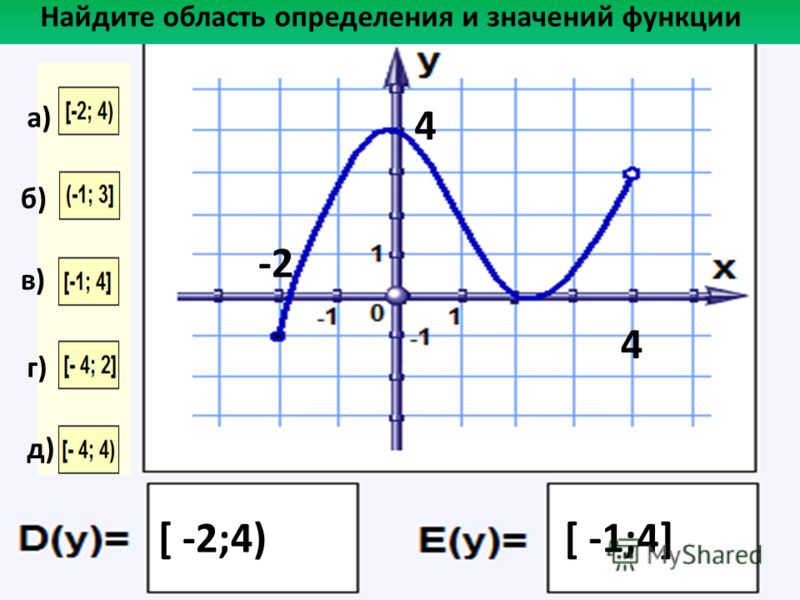 В главном функциональном блоке у нас есть переменная с ключевым словом «val», определенная как «str1». Переменная «str1», установленная со свойством типа Int и оператором безопасности null, используется для проверки того, является ли значение нулевым или нет. Поскольку мы инициализировали переменную «str1» целочисленным значением, которое не равно нулю. Затем мы должны использовать функцию let для «str1». В функциональном блоке let мы передали ключевое слово «it» в качестве параметра функции println, которая действует как объект контекста. После этого у нас есть еще одна переменная, определенная как «str2» и имеющая свойство типа String. Здесь также используется оператор безопасности null для проверки допустимости значений NULL. «str2» объявляется со строковым значением. Теперь используйте функцию let, которая вернет значения «str2», поскольку она не равна нулю. Здесь мы просто передали «str2» функции println.
В главном функциональном блоке у нас есть переменная с ключевым словом «val», определенная как «str1». Переменная «str1», установленная со свойством типа Int и оператором безопасности null, используется для проверки того, является ли значение нулевым или нет. Поскольку мы инициализировали переменную «str1» целочисленным значением, которое не равно нулю. Затем мы должны использовать функцию let для «str1». В функциональном блоке let мы передали ключевое слово «it» в качестве параметра функции println, которая действует как объект контекста. После этого у нас есть еще одна переменная, определенная как «str2» и имеющая свойство типа String. Здесь также используется оператор безопасности null для проверки допустимости значений NULL. «str2» объявляется со строковым значением. Теперь используйте функцию let, которая вернет значения «str2», поскольку она не равна нулю. Здесь мы просто передали «str2» функции println.
Результат использования функции let отображается на экране ниже.
Пример № 2: Использование функции области применения «Применить» в Kotlin
Функция применения используется для работы с членами объекта-получателя в первую очередь для их инициализации. Функция применения к блокам кода, которые возвращают сам объект, и ключевое слово «это» здесь является объектом контекста.
Функция применения к блокам кода, которые возвращают сам объект, и ключевое слово «это» здесь является объектом контекста.
В приведенном выше коде мы создали класс «Сотрудник», в котором мы определили переменные lateinit. Переменная lateinit — это переменная, которая инициализируется с опозданием. У нас есть три переменные lateinit для класса «Сотрудник»: «empName», «empContact» и «empDept», и мы устанавливаем свойство типа String для этих определенных переменных. Затем мы должны вызвать основную функцию, в которой мы использовали функцию применения. В функции применения у нас есть ключевое слово «this», используемое с переменной «empName». Ключевое слово this служит ссылкой на объект и содержит строку в качестве значения инициализации. Мы также инициализировали переменные «empContact» и «empDept» с определенными значениями. Ключевое слово this работает так же, как и другая переменная, объявленная в коде. Через функцию println мы получим напечатанные значения.
Результат применения функции отображается на экране терминала.
Пример № 3: Использование функции области видимости «With» в Kotlin
При вызове функций на объектах контекста без выдачи лямбда-результата рекомендуется использовать функцию «with».
У нас есть класс «Человек», в котором мы определили переменные lateinit. Переменным присваиваются имена «Имя» и «Возраст» и задается свойство Тип строки. Затем у нас есть основная функция, в которой мы создали объект с именем «p1». Объект «p1» вызывает функцию применения. В функции применения мы инициализировали переменные «Имя» и «Возраст» значениями. После этого мы вызвали функцию with и передали ей в качестве параметра объект p1. Обратите внимание, что мы не использовали «${Name}» и «${Age}» в функции println, потому что это было бы избыточно, поскольку блок кода распознает, что «Name» и «Age» используются в этом контексте о Объект «p1».
На экране терминала ниже вывод распечатывается.
Пример № 4: Использование функции «Выполнить» в Kotlin
Функция «Выполнить» идентична функциям «let» и «with». Когда объектная лямбда включает в себя как инициализацию объекта, так и обработку возвращаемого значения, тогда полезна функция «запустить».
В приведенном выше коде у нас есть класс под названием «Учителя», в котором мы определили переменные как «имя», «телефон» и «тема». Затем в основной функции у нас есть объект «учитель», который использует функцию применения. Обратите внимание, что мы не использовали имя объекта для обращения к членам класса и инициализации их значениями. После этого мы вызвали функцию запуска, которая известна как функция запуска без расширения, поскольку ей не передается объект-получатель.
Выходные данные функции запуска без расширения показаны на изображении ниже.
Пример № 5: Использование функции области действия «Также» в Kotlin
Функция «также» сравнима с функцией «пусть», за исключением того, что она относится к контексту объекта как «это», а не «это».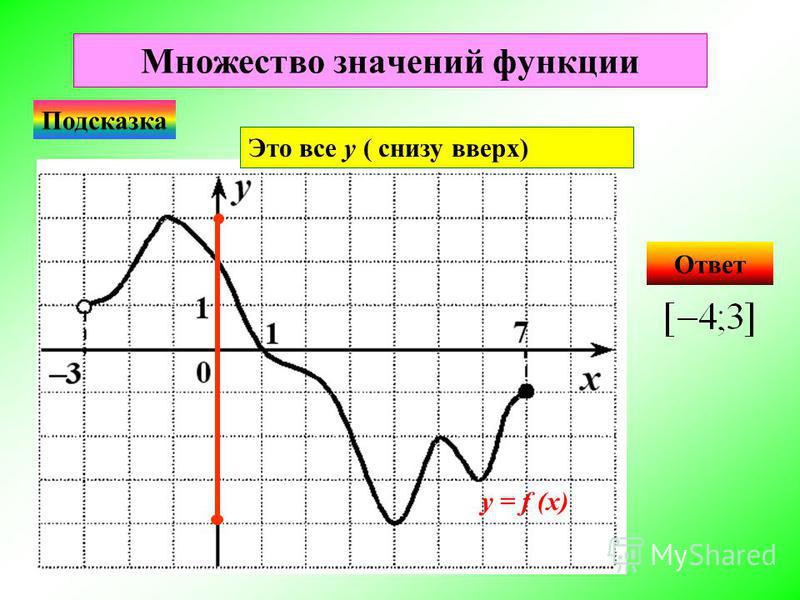 ” и обеспечивает нулевую проверку безопасности.
” и обеспечивает нулевую проверку безопасности.
В приведенном выше коде у нас есть основная функция, в которой мы объявляем переменную как «val» с именем «myList». Переменная «myList» содержит список значений с помощью функции mutableListOf. Мы вызвали функцию «также» для переменной «myList». В блоке «также» мы использовали ключевое слово «it» с функцией добавления и передали ему значение. Затем мы должны снова использовать ключевое слово «it» с функцией удаления и передать значение, которое мы хотим удалить. Через функцию println мы увидим обновленные значения списка.
Вывод ниже показывает, что список был обновлен.
Заключение
Мы подробно рассмотрели функции области видимости на основе результатов, продемонстрированных в предыдущем примере. Все эти иллюстрации просты и работают в Ubuntu 20.04, и они помогут вам научиться использовать функции области видимости.
Давайте также применим run с функциями области видимости Kotlin
Функции области видимости
В Kotlin функции области видимости позволяют выполнять функцию, т. е. блок кода, в контексте объекта. Затем объект становится доступным в этой временной области без использования имени. Несмотря на то, что все, что вы делаете с функциями области видимости, можно обойтись и без них, они позволяют по-разному структурировать ваш код. Их использование может повысить читабельность и сделать ваш код более лаконичным.
е. блок кода, в контексте объекта. Затем объект становится доступным в этой временной области без использования имени. Несмотря на то, что все, что вы делаете с функциями области видимости, можно обойтись и без них, они позволяют по-разному структурировать ваш код. Их использование может повысить читабельность и сделать ваш код более лаконичным.
Стандартная библиотека Kotlin предлагает четыре различных типа функций области видимости, которые можно классифицировать по способу обращения к объекту контекста и возвращаемому значению. Функция области действия либо обращается к объекту контекста как к аргументу функции , либо к получателю функции . Возвращаемое значение функции области действия — это либо результат функции , либо объект контекста .
Доступные функции: пусть , также , применить , запустить и с . В следующей таблице приведены характеристики каждой функции в зависимости от способа доступа к объекту контекста и типа возвращаемого значения, как описано выше.
let Запустить , с также Применить . В то время как все остальные функции области реализованы как функции расширения, с является обычной функцией. Теперь, когда я упомянул такие понятия, как приемники функций и функции расширения, имеет смысл кратко объяснить их, прежде чем мы перейдем к подробному описанию функций области видимости. Если вы уже знакомы с приемниками функций и функциями расширения в Kotlin, вы можете пропустить следующий раздел.
Аргументы функций, функции расширения, приемники
Kotlin позволяет рассматривать функции как значения. Это означает, что вы можете передавать функции в качестве аргументов другим функциям. С помощью оператора :: вы можете преобразовать метод в значение функции. Для повышения удобочитаемости последний аргумент функции можно поместить вне списка аргументов.
Для повышения удобочитаемости последний аргумент функции можно поместить вне списка аргументов.
В следующем примере показано, как это сделать путем определения функции более высокого порядка комбинирования , которая принимает аргумент функции ф . Мы вызываем его с помощью метода plus из класса Int и с литералом анонимной функции как внутри, так и вне списка аргументов:
// Применяем аргумент функции f к целым числам a и b
весело объединить (a: Int, b: Int, f: (Int, Int) -> Int): Int = f (a, b)
// Использование метода plus в качестве значения функции
объединить (1, 2, Int :: плюс)
// Передача литерала функции
объединить (1, 2, { а, б ->
знач х = а + б
х + 100
})
// Передача вне списка аргументов
объединить (1, 2) { а, б ->
знач х = а + б
х + 100
}
Функции расширения – это способ расширить существующие классы или интерфейсы, которыми вы не обязательно можете управлять. Определение функции расширения для класса позволяет вызывать этот метод для экземпляров этого класса, как если бы он был частью исходного определения класса.
В следующем примере определяется функция расширения для Int , возвращающая абсолютное значение:
fun Int.abs() = if (this < 0) -this else this
(-5).abs() // 5
Функциональные литералы с Receiver подобны функциям расширения, так как объект приемника доступен внутри функции через this . Следующий фрагмент кода определяет функцию расширения из предыдущего, но на этот раз как литерал функции с получателем:
val abs: Int.() -> Int = { if (this < 0) -this else this }
(-5).abs() // 5
Обычный вариант использования литералов функций с приемниками – безопасные по типу конструкторы. Теперь, когда мы рассмотрели основы, давайте рассмотрим пять функций области видимости по отдельности.
Let, also apply, run, with
Let
Функция области видимости let делает объект контекста доступным в качестве аргумента функции и возвращает результат функции. Типичным вариантом использования является применение к значениям безопасных для нуля преобразований.
знач. x: Целое? = ноль
// null-безопасное преобразование без let
val y1 = если (x != ноль) x + 1 иначе ноль
val y2 = если (y1 != ноль) y1/2 иначе ноль
// null-безопасное преобразование с let
val z1 = x?.let { it + 1 }
val z2 = z1?.let { it / 2 }
Также
Функция apply scope делает объект контекста доступным в качестве аргумента функции и возвращает объект контекста. Это можно использовать, когда вы вычисляете возвращаемое значение внутри функции, а затем хотите применить к нему некоторый побочный эффект, прежде чем вернуть его.
// присвоить, распечатать, вернуть
весело вычислитьNormal(): Строка {
вал результат = "результат"
println(результат)
вернуть результат
}
// возвращаем и также печатаем
весело вычислить также(): String =
"результат".также(::println)
Применить
Функция области применения делает объект контекста доступным в качестве получателя и возвращает объект контекста. Это делает его очень полезным для «специальных разработчиков» изменяемых объектов, таких как Java Beans.
Это делает его очень полезным для «специальных разработчиков» изменяемых объектов, таких как Java Beans.
// Java Bean, представляющий человека
открытый класс PersonBean {
частная строка firstName;
частная строка фамилия;
public void setFirstName (строка firstName) {
this.firstName = имя;
}
публичная строка getFirstName () {
вернуть имя;
}
public void setLastName (String lastName) {
this.lastName = фамилия;
}
публичная строка getLastName () {
вернуть фамилию;
}
}
// Инициализация традиционным способом
val p1 = PersonBean()
p1.firstName = "Фрэнк"
p1.lastName = "Рознер"
// Инициализация с помощью применения
val p2 = PersonBean (). применить {
имя = "Фрэнк"
фамилия = "Рознер"
}
Выполнить и с
Функция области видимости запуска делает объект контекста доступным в качестве получателя и возвращает результат функции. Его можно использовать как с ресивером, так и без него. При использовании его без приемника вы можете вычислить выражение, используя локальные переменные. Используя приемник,
При использовании его без приемника вы можете вычислить выражение, используя локальные переменные. Используя приемник, run можно вызывать для любого объекта, например объект связи.
// результат вычисления как результат блока
val результат = запустить {
значение х = 5
значение у = х + 3
у - 4
}
// вычисляем результат с приемником
вал результат2 = "текст".выполнить {
val хвост = подстрока (1)
хвост.toUpperCase()
}
Функция с работает точно так же, как run , но реализована как обычная функция, а не функция расширения.
val результат3 = с ("текст") {
val хвост = подстрока (1)
хвост.toUpperCase()
}
Резюме
В этом посте мы узнали о функциях области видимости пусть , также , применить , запустить и с . Они различаются способом обращения к объекту контекста и возвращаемым значением. В сочетании с концепциями аргументов функций, функций расширения и приемников функции области видимости представляют собой полезный инструмент для создания более читаемого кода.

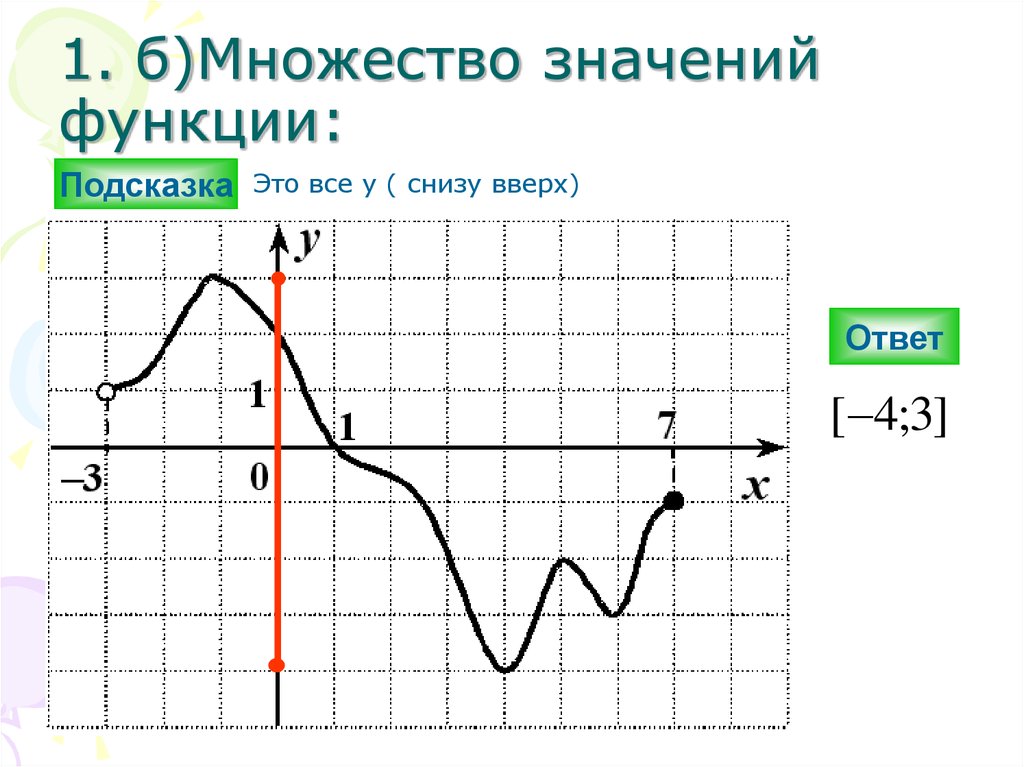
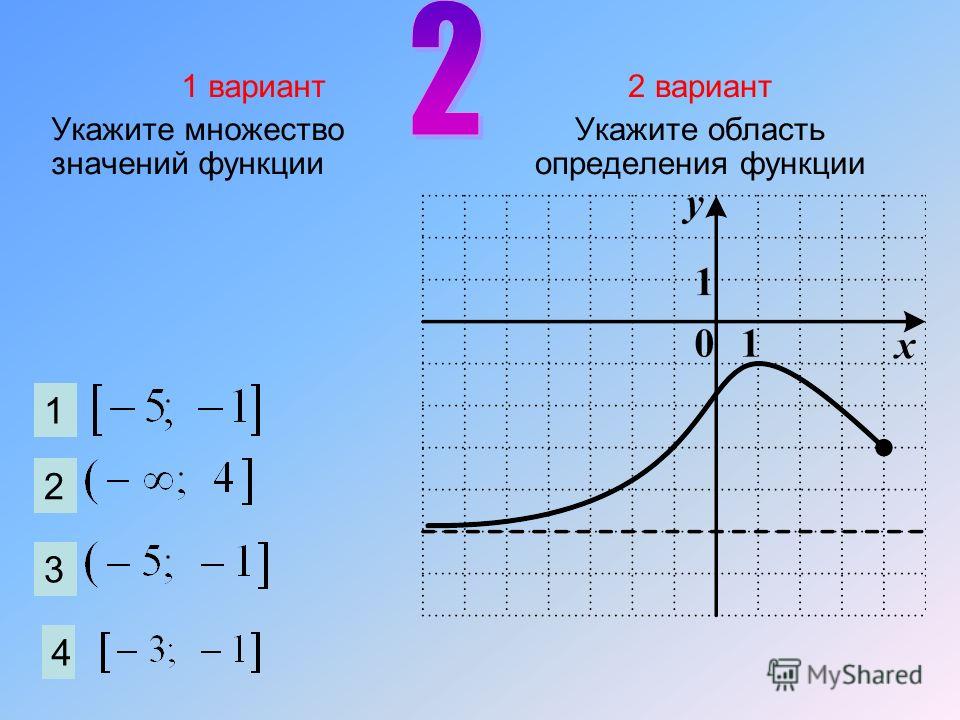
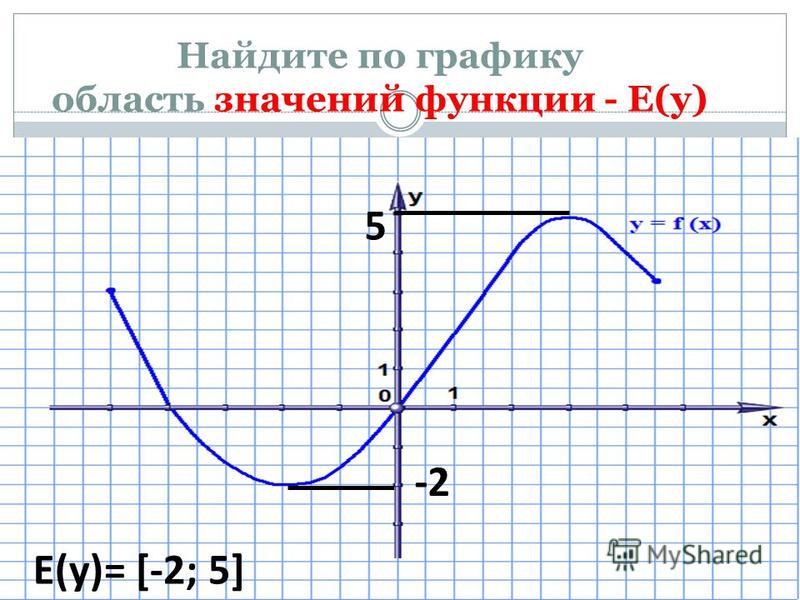
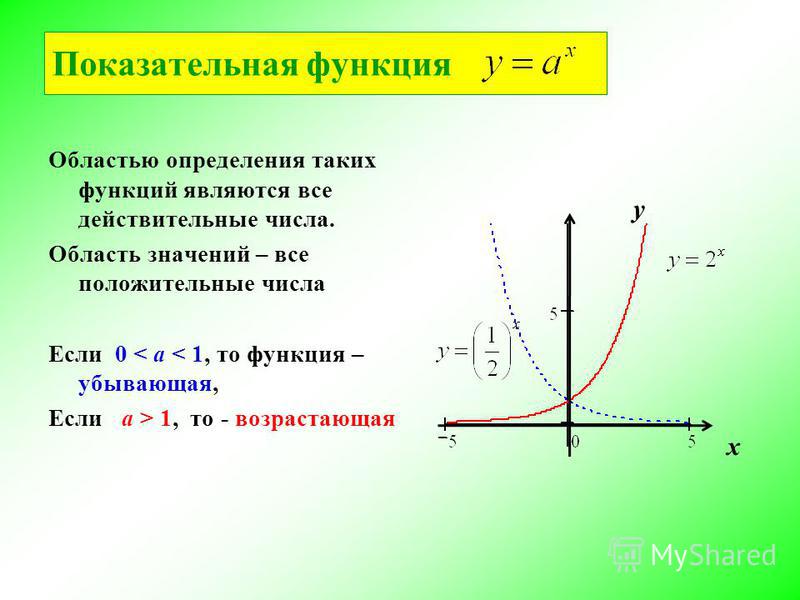
 Согласно определению, если каждому значению переменной х множества Х ставится в соответствие одно определенное значение переменной у множества Y, то такое соответствие называется функцией. Исходя из этого, можно дать другую формулировку: однозначное соответствие двух переменных величин на множестве действительных чисел R называется функцией.
Согласно определению, если каждому значению переменной х множества Х ставится в соответствие одно определенное значение переменной у множества Y, то такое соответствие называется функцией. Исходя из этого, можно дать другую формулировку: однозначное соответствие двух переменных величин на множестве действительных чисел R называется функцией. Четность и нечетность. Функция f(x) называется четной, если ее значения симметричны относительно оси OY, т.е. f(-x) = f(x). Функция f(x) называется нечетной, если ее значение изменяется на противоположное при изменении переменной х на -х , т.е. f(-x) = -f(x). В противном случае функция называется функцией общего вида.
Четность и нечетность. Функция f(x) называется четной, если ее значения симметричны относительно оси OY, т.е. f(-x) = f(x). Функция f(x) называется нечетной, если ее значение изменяется на противоположное при изменении переменной х на -х , т.е. f(-x) = -f(x). В противном случае функция называется функцией общего вида. В противном случае функция называется неограниченной.
В противном случае функция называется неограниченной.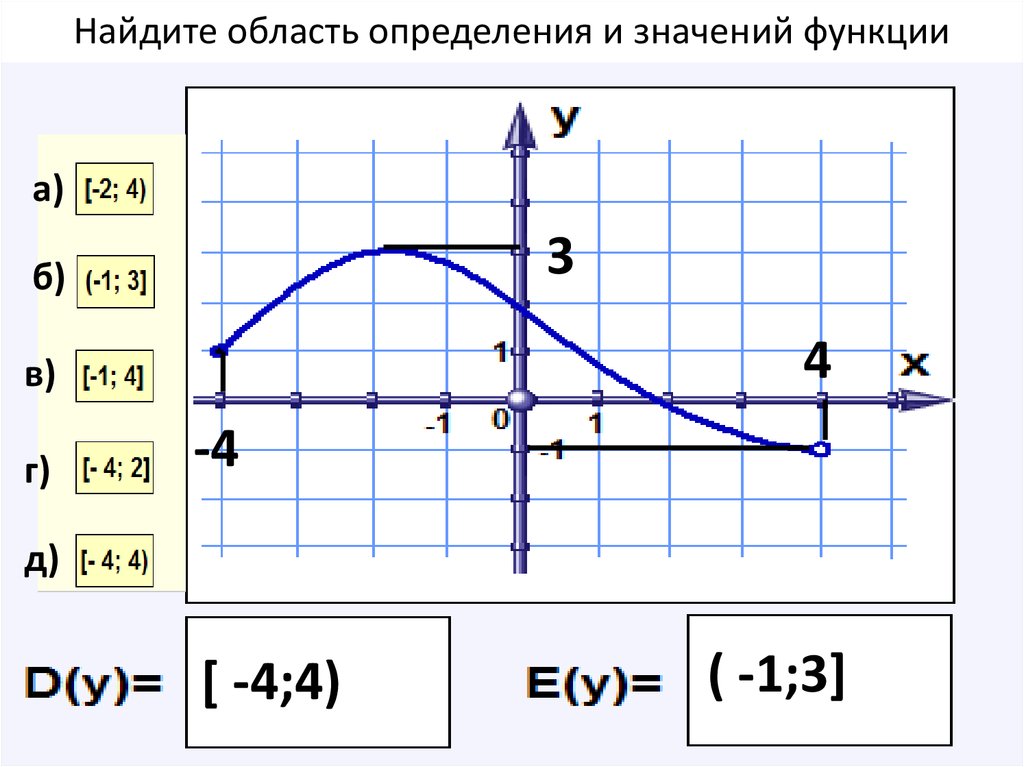 2000 руб / 120 мин — студенты.
2000 руб / 120 мин — студенты. е. отсутствуют
е. отсутствуют  log(typeof x) // не определено (потому что var имеет область действия!)
console.log(typeof y) // не определено (поскольку тело функции представляет собой блок)
console.log(typeof z) // не определено (поскольку тело функции представляет собой блок)
log(typeof x) // не определено (потому что var имеет область действия!)
console.log(typeof y) // не определено (поскольку тело функции представляет собой блок)
console.log(typeof z) // не определено (поскольку тело функции представляет собой блок)  log(typeof x) // не определено, потому что `x` имеет блочную область видимости
log(typeof x) // не определено, потому что `x` имеет блочную область видимости 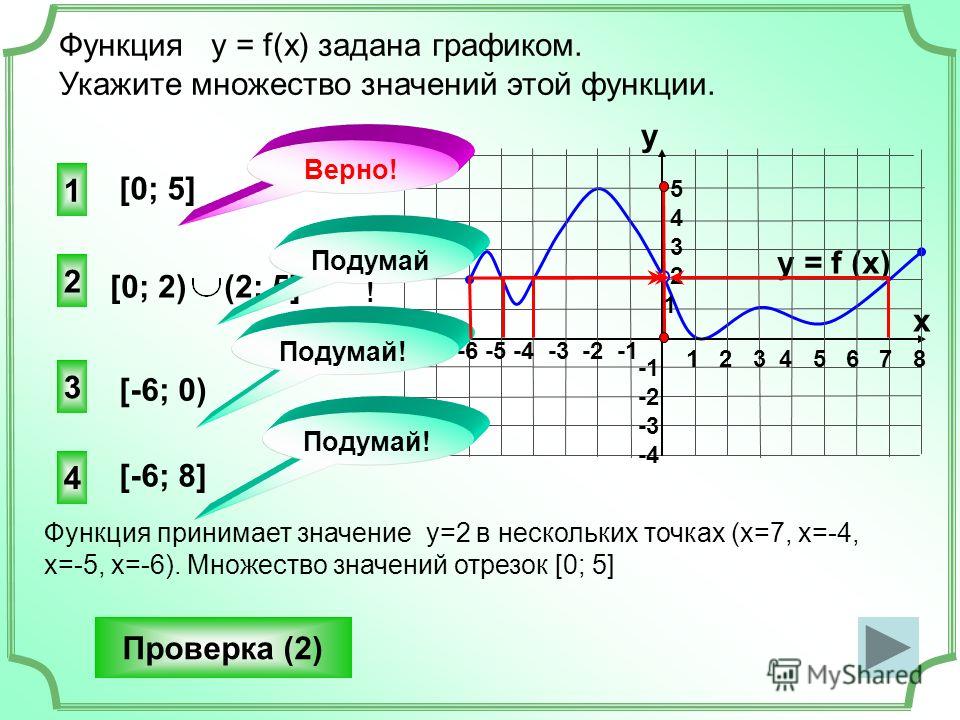 log(typeof e) // не определено, потому что область действия `e` ограничена блоком catch
log(typeof e) // не определено, потому что область действия `e` ограничена блоком catch  Если вам нужно присвоить имя, которое находится на верхнем уровне
модуль, содержащий функцию, вы можете сделать это, объявив его в
Если вам нужно присвоить имя, которое находится на верхнем уровне
модуль, содержащий функцию, вы можете сделать это, объявив его в 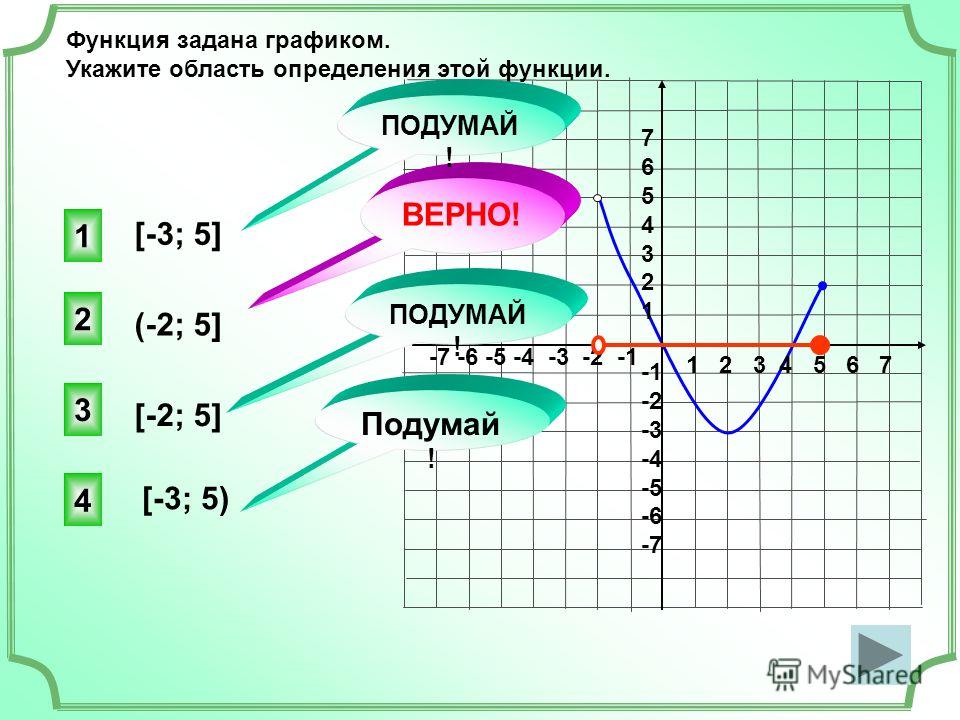
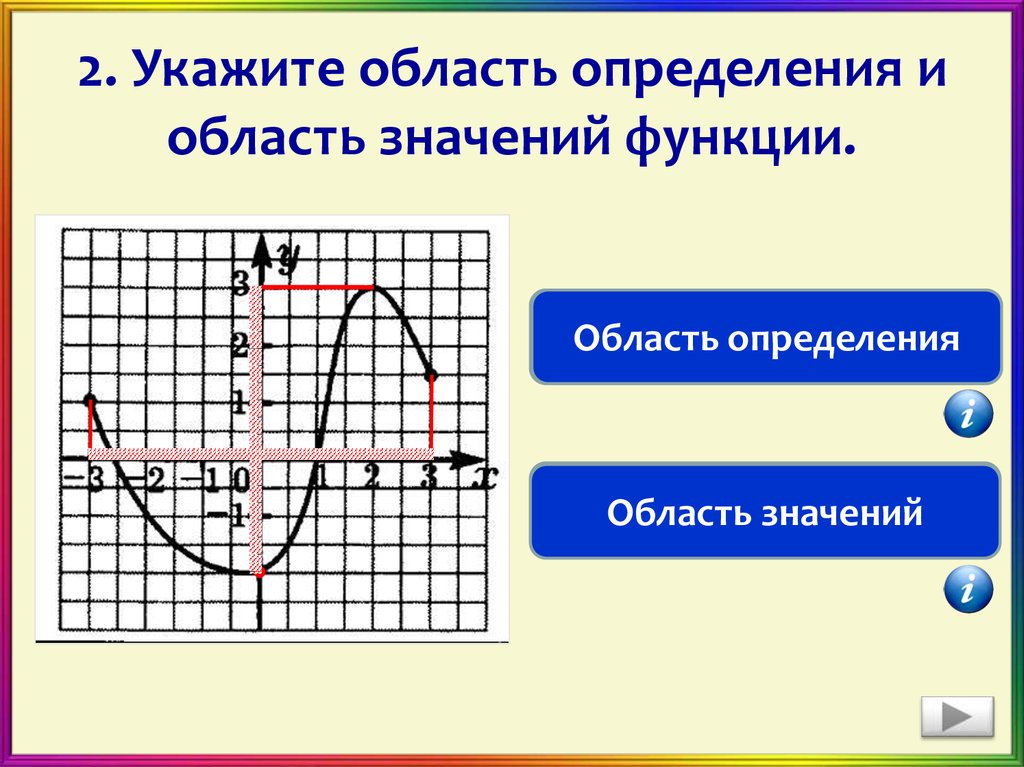 в охватывающем модуле перед запуском функции; если нет, то
назначение в функции создает
в охватывающем модуле перед запуском функции; если нет, то
назначение в функции создает 
 ps1
'>>> '
>>> sys.__dict__['ps1']
'>>> '
ps1
'>>> '
>>> sys.__dict__['ps1']
'>>> '

 Имена в этой области Python также доступны из любого места в вашем коде. Он автоматически загружается Python при запуске программы или скрипта.
Имена в этой области Python также доступны из любого места в вашем коде. Он автоматически загружается Python при запуске программы или скрипта. .. результат = база ** 3
... print(f'Куб {базы} равен: {результат}')
...
>>> куб(30)
Куб 30 это: 27000
.. результат = база ** 3
... print(f'Куб {базы} равен: {результат}')
...
>>> куб(30)
Куб 30 это: 27000
 .. print(f"Печать other_var из inner_func(): {another_var}")
...
... внутренняя_функция()
... Another_var = 200 # Это определяется после вызова inner_func()
... print(f"Печать var из external_func(): {var}")
...
>>> внешняя_функция()
Печать var из inner_func(): 100
Traceback (последний последний вызов):
Файл "
.. print(f"Печать other_var из inner_func(): {another_var}")
...
... внутренняя_функция()
... Another_var = 200 # Это определяется после вызова inner_func()
... print(f"Печать var из external_func(): {var}")
...
>>> внешняя_функция()
Печать var из inner_func(): 100
Traceback (последний последний вызов):
Файл "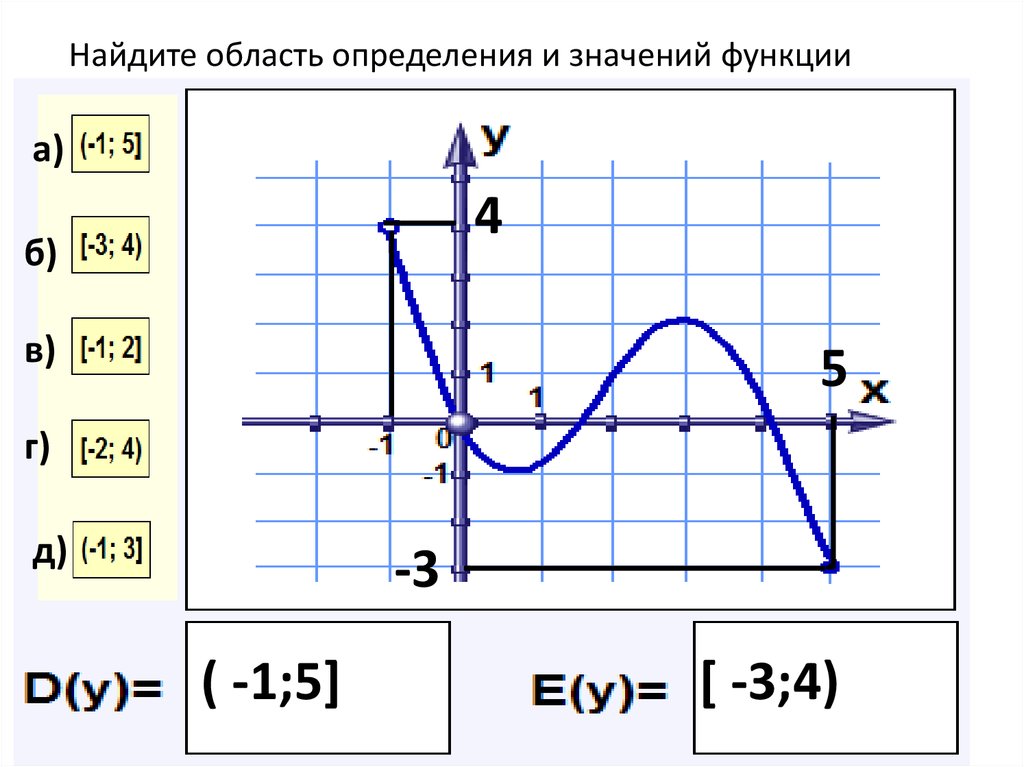 .., '__package__', '__spec__', 'var']
.., '__package__', '__spec__', 'var']
 .. return var # Вы можете получить доступ к var из func()
...
>>> функция()
100
>>> var # Остается без изменений
100
.. return var # Вы можете получить доступ к var из func()
...
>>> функция()
100
>>> var # Остается без изменений
100
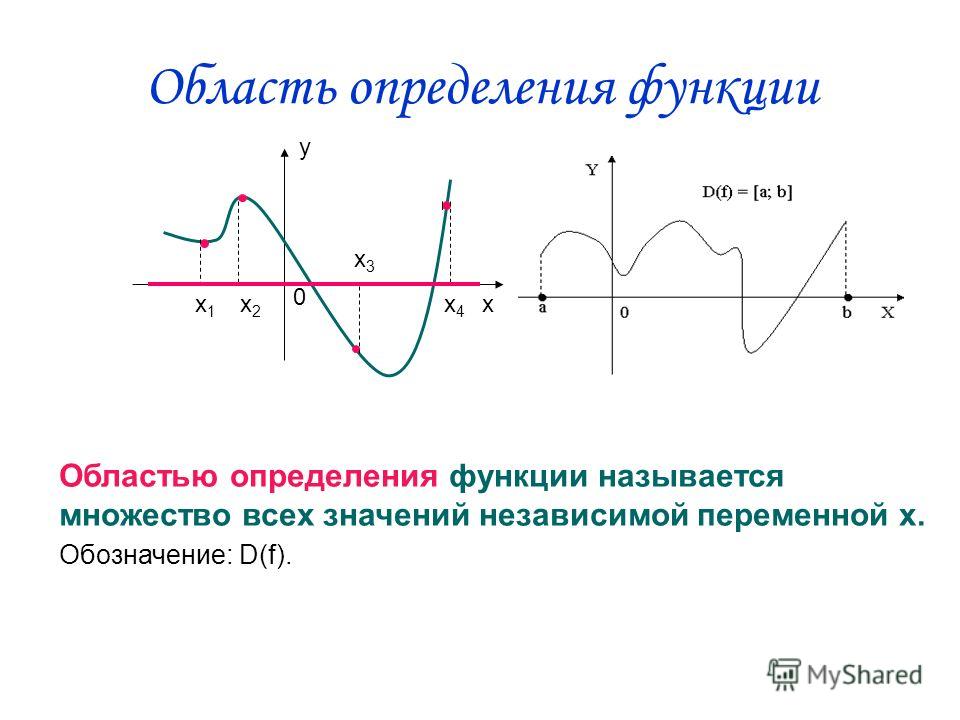
 .. печать (число)
...
... внутренняя_функция()
...
>>> внешняя_функция()
100
.. печать (число)
...
... внутренняя_функция()
...
>>> внешняя_функция()
100
 .., '__package__', '__spec__']
>>> директория(__builtins__)
['ArithmeticError', 'AssertionError',..., 'tuple', 'type', 'vars', 'zip']
.., '__package__', '__spec__']
>>> директория(__builtins__)
['ArithmeticError', 'AssertionError',..., 'tuple', 'type', 'vars', 'zip']
 abs(-15)
15
abs(-15)
15
 .. всего = 0
... длина = 0
... def _mean (число):
... нелокальная сумма, длина
... всего += число
... длина += 1
... вернуть общее количество/длину
... вернуть _среднее
...
>>> текущее_среднее = среднее()
>>> текущее_среднее (10)
10,0
>>> текущее_среднее (15)
12,5
>>> текущее_среднее (12)
12.333333333333334
>>> текущее_среднее (11)
12,0
>>> текущее_среднее (13)
12.2
.. всего = 0
... длина = 0
... def _mean (число):
... нелокальная сумма, длина
... всего += число
... длина += 1
... вернуть общее количество/длину
... вернуть _среднее
...
>>> текущее_среднее = среднее()
>>> текущее_среднее (10)
10,0
>>> текущее_среднее (15)
12,5
>>> текущее_среднее (12)
12.333333333333334
>>> текущее_среднее (11)
12,0
>>> текущее_среднее (13)
12.2
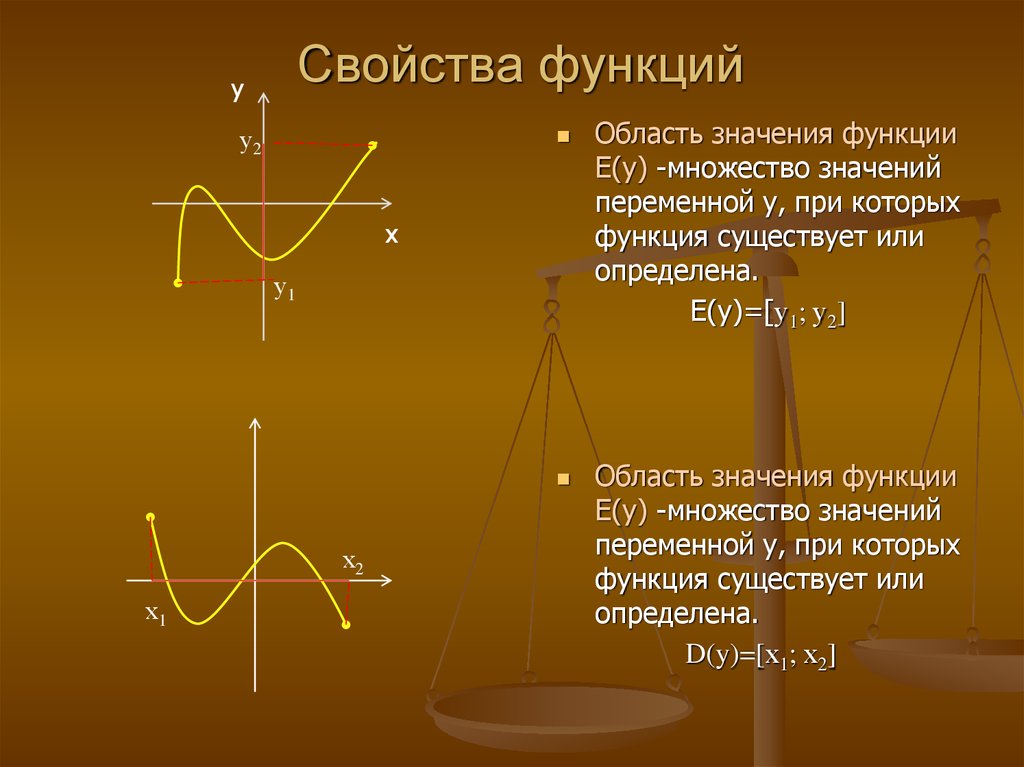 .. переменная = 100
... защита __init__(я):
... селф.вар = 200
...
... def access_attr(self):
... # Используйте точечную нотацию для доступа к атрибутам класса и экземпляра
... print(f'Атрибут экземпляра: {self.var}')
... print(f'Атрибут класса: {A.var}')
...
>>> объект = А()
>>> obj.access_attr()
Атрибут экземпляра: 200
Атрибут класса: 100
>>> A.var # Доступ к атрибутам класса
100
>>> A().var # Доступ к атрибутам экземпляра
200
>>> A.__dict__.keys()
dict_keys(['__module__', 'var', '__init__',..., '__getattribute__'])
>>> A().__dict__.keys()
dict_keys(['var'])
.. переменная = 100
... защита __init__(я):
... селф.вар = 200
...
... def access_attr(self):
... # Используйте точечную нотацию для доступа к атрибутам класса и экземпляра
... print(f'Атрибут экземпляра: {self.var}')
... print(f'Атрибут класса: {A.var}')
...
>>> объект = А()
>>> obj.access_attr()
Атрибут экземпляра: 200
Атрибут класса: 100
>>> A.var # Доступ к атрибутам класса
100
>>> A().var # Доступ к атрибутам экземпляра
200
>>> A.__dict__.keys()
dict_keys(['__module__', 'var', '__init__',..., '__getattribute__'])
>>> A().__dict__.keys()
dict_keys(['var'])
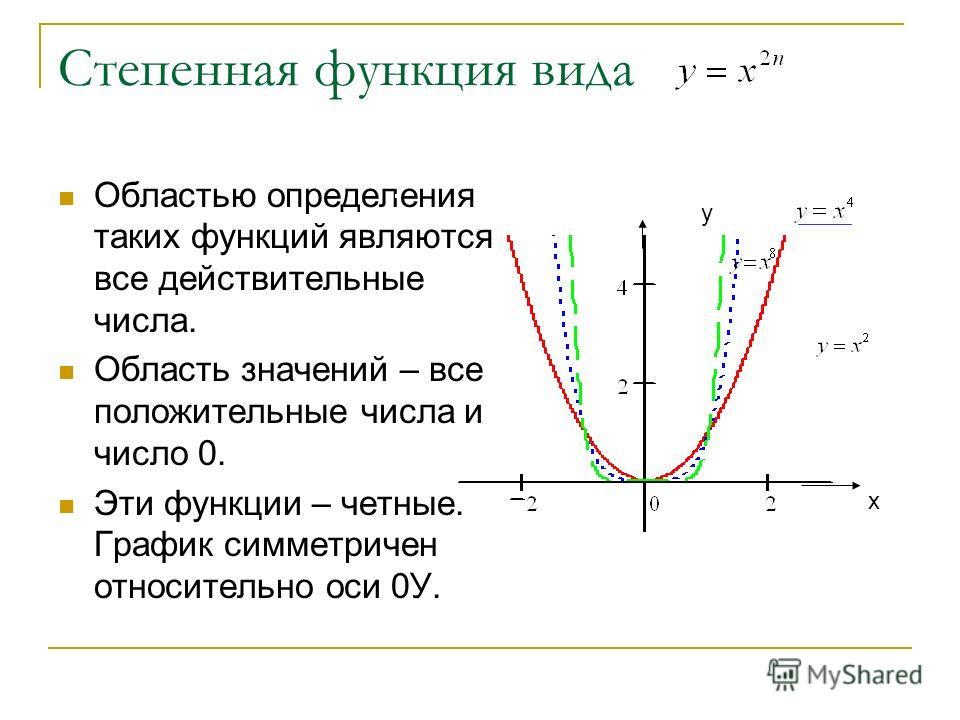 length)
}
println (длина строки)
}
length)
}
println (длина строки)
}
 имя)
println(этот.возраст)
}
имя)
println(этот.возраст)
}
 применить {
carName = "Ламборгини"
carColor = "темно-синий"
}
}
с (машиной) {
println(имя_автомобиля)
println(carColor)
}
применить {
carName = "Ламборгини"
carColor = "темно-синий"
}
}
с (машиной) {
println(имя_автомобиля)
println(carColor)
}
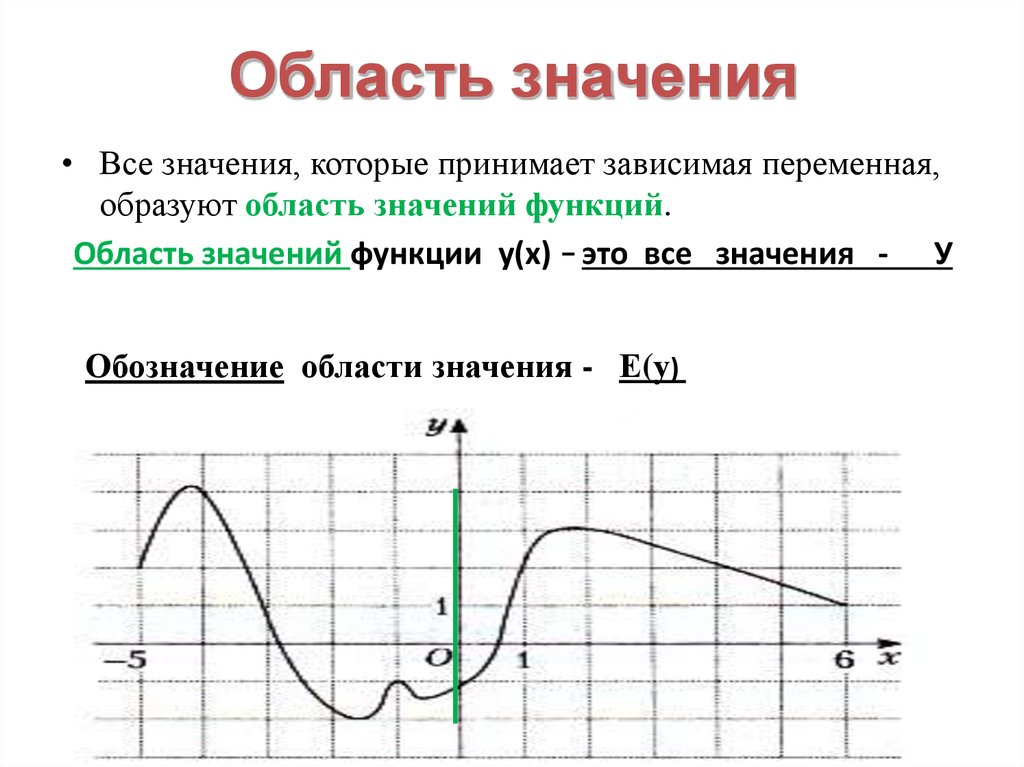 применить {
firstName = "Эден Эленвоке"
возраст = 22
}
с (человеком) {
println(имя)
println(возраст)
}
человек.также{
it.firstName = "Иден Питер"
println("Мое новое имя: + ${it.firstName}")
}
}
применить {
firstName = "Эден Эленвоке"
возраст = 22
}
с (человеком) {
println(имя)
println(возраст)
}
человек.также{
it.firstName = "Иден Питер"
println("Мое новое имя: + ${it.firstName}")
}
}
 Это комбинация
Это комбинация