404 Cтраница не найдена
Мы используем файлы cookies для улучшения работы сайта МГТУ и большего удобства его использования. Более подробную информацию об использовании файлов cookies можно найти здесь. Продолжая пользоваться сайтом, вы подтверждаете, что были проинформированы об использовании файлов cookies сайтом ФГБОУ ВО «МГТУ» и согласны с нашими правилами обработки персональных данных.
Размер:
AAA
Изображения Вкл. Выкл.
Обычная версия сайта
К сожалению запрашиваемая страница не найдена.
Но вы можете воспользоваться поиском или картой сайта ниже
|
|
Педагогический (научно-педагогический) составПодготовка к ЕГЭ 2016 года(Математика, Русский язык, Физика): 2014
Все тригонометрические формулы
Все формулы по тригонометрии
Основные тригонометрические тождества
sin2x + cos2x = 1
| tgx | = | sinx |
| cosx |
| ctgx | = | cosx |
| sinx |
tgx ctgx = 1
| tg2x + 1 | = | 1 |
| cos2x |
| ctg2x + 1 | = | 1 |
| sin2x |
Формулы двойного аргумента
sin2x = 2sinx cosx
| sin2x | = | 2tgx | = | 2ctgx | = | 2 |
| 1 + tg2x | 1 + ctg2x | tgx + ctgx |
cos2x = cos2x — sin2x = 2cos2x — 1 = 1 — 2sin2x
| cos2x | = | 1 — tg2x | = | ctg2x — 1 | = | ctgx — tgx |
| 1 + tg2x | ctg2x + 1 | ctgx + tgx |
| tg2x | = | 2tgx | = | 2ctgx | = | 2 |
| 1 — tg2x | ctg2x — 1 | ctgx — tgx |
| ctg2x | = | ctg2x — 1 | = | ctgx — tgx |
| 2ctgx | 2 |
Формулы тройного аргумента
sin3x = 3sinx — 4sin3x
cos3x = 4cos3x — 3cosx
| tg3x | = | 3tgx — tg3x1 |
| 1 — 3tg2x |
| ctg3x | = | ctg3x — 3ctgx |
| 3ctg2x — 1 |
Формулы половинного аргумента
| sin2 | x | = | 1 — cosx |
| 2 | 2 |
| cos2 | x | = | 1 + cosx |
| 2 | 2 |
| tg2 | x | = | 1 — cosx |
| 2 | 1 + cosx |
| ctg2 | x | = | 1 + cosx |
| 2 | 1 — cosx |
| tg | x | = | 1 — cosx | = | sinx |
| 2 | sinx | 1 + cosx |
| ctg | x | = | 1 + cosx | = | sinx |
| 2 | sinx | 1 — cosx |
Формулы квадратов тригонометрических функций
| sin2x | = | 1 — cos2x |
| 2 |
| cos2x | = | 1 + cos2x |
| 2 |
| tg2x | = | 1 — cos2x |
| 1 + cos2x |
| ctg2x | = | 1 + cos2x |
| 1 — cos2x |
| sin2 | x | = | 1 — cosx |
| 2 | 2 |
| cos2 | x | = | 1 + cosx |
| 2 | 2 |
| tg2 | x | = | 1 — cosx |
| 2 | 1 + cosx |
| ctg2 | x | = | 1 + cosx |
| 2 | 1 — cosx |
Формулы кубов тригонометрических функций
| sin3x | = | 3sinx — sin3x |
| 4 |
| cos3x | = | 3cosx + cos3x |
| 4 |
| tg3x | = | 3sinx — sin3x |
| 3cosx + cos3x |
| ctg3x | = | 3cosx + cos3x |
| 3sinx — sin3x |
Формулы тригонометрических функций в четвертой степени
| sin4x | = | 3 — 4cos2x + cos4x |
| 8 |
| cos4x | = | 3 + 4cos2x + cos4x |
| 8 |
Формулы сложения аргументов
sin(α + β) = sinα cosβ + cosα sinβ
cos(α + β) = cosα cosβ — sinα sinβ
| tg(α + β) | = | tgα + tgβ |
| 1 — tgα tgβ |
| ctg(α + β) | = | ctgα ctgβ — 1 |
| ctgα + ctgβ |
sin(α — β) = sinα cosβ — cosα sinβ
cos(α — β) = cosα cosβ + sinα sinβ
| tg(α — β) | = | tgα — tgβ |
| 1 + tgα tgβ |
| ctg(α — β) | = | ctgα ctgβ + 1 |
| ctgα — ctgβ |
Формулы суммы тригонометрических функций
| sinα + sinβ | = 2sin | α + β | ∙ cos | α — β |
| 2 | 2 |
| cosα + cosβ | = 2cos | α + β | ∙ cos | α — β |
| 2 | 2 |
(sinα + cosα)2 = 1 + sin2α
| tgα + tgβ1 | = | sin(α + β) |
| cosα cosβ |
| ctgα + ctgβ | = | sin(α + β) |
| sinα sinβ |
Формулы разности тригонометрических функций
| sinα — sinβ | = 2sin | α — β | ∙ cos | α + β |
| 2 | 2 |
| cosα — cosβ | = -2sin | α + β | ∙ sin | α — β |
| 2 | 2 |
(sinα — cosα)2 = 1 — sin2α
| tgα — tgβ | = | sin(α — β) |
| cosα cosβ |
| ctgα — ctgβ | = – | sin(α — β) |
| sinα sinβ |
Формулы произведения тригонометрических функций
| sinα ∙ sinβ | = | cos(α — β) — cos(α + β) |
| 2 |
| sinα ∙ cosβ | = | sin(α — β) + sin(α + β) |
| 2 |
| cosα ∙ cosβ | = | cos(α — β) + cos(α + β) |
| 2 |
| tgα ∙ tgβ | = | cos(α — β) — cos(α + β) | = | tgα + tgβ |
| cos(α — β) + cos(α + β) | ctgα + ctgβ |
| ctgα ∙ ctgβ | = | cos(α — β) + cos(α + β) | = | ctgα + ctgβ |
| cos(α — β) — cos(α + β) | tgα + tgβ |
| tgα ∙ ctgβ | = | sin(α — β) + sin(α + β) |
| sin(α + β) — sin(α — β) |
Изменение структуры ЕГЭ 2015
Изменения в КИМах ЕГЭ 2015 года Новости ЕГЭ Справка о планируемых изменениях в КИМ ЕГЭ 2015 года.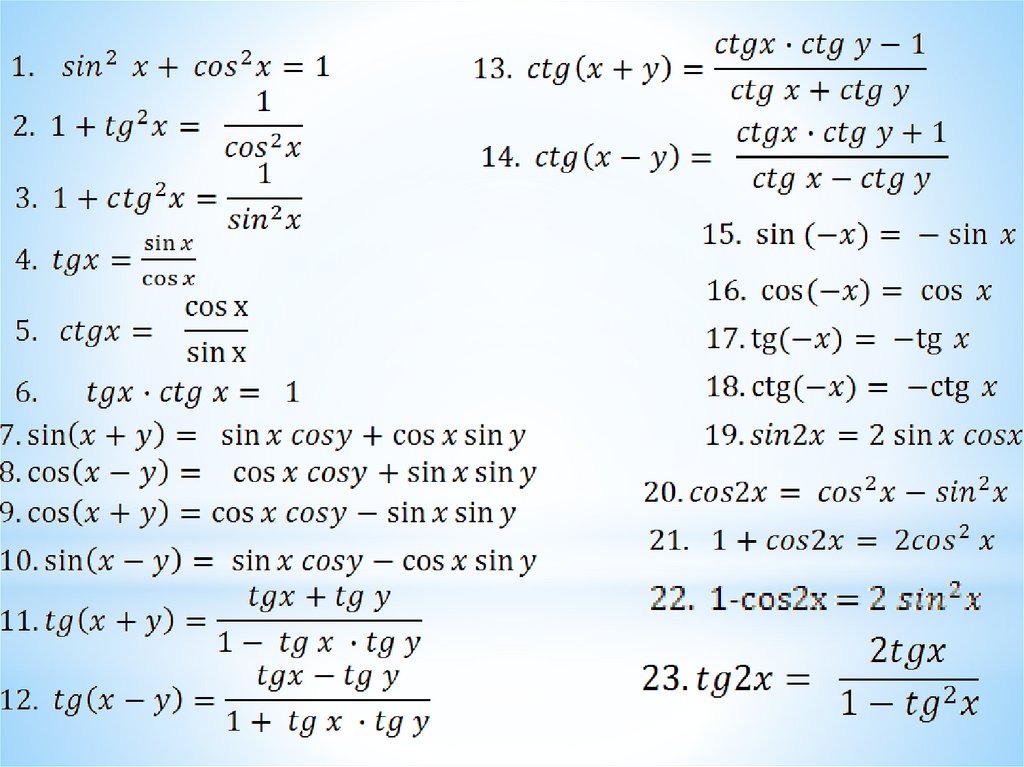
Официальные данные ФИПИ.
1. Изменена структура варианта КИМ: каждый вариант состоит из двух частей (часть 1 — задания с кратким ответом, часть 2 — задания с развернутым ответом).
2. Задания в варианте КИМ представлены в режиме сквозной нумерации без буквенных обозначений А, В, С.
3. Изменена форма записи ответа в заданиях с выбором одного ответа: как и в заданиях с кратким ответом, записывается цифрой номер правильного ответа (а не крестик).
4. По большинству учебных предметов сокращено количество заданий с выбором одного ответа. 5. На основе анализа статистических данных о результатах экзамена и качестве КИМ в ряде предметов исключены некоторые линии заданий, изменена форма ряда заданий.
6. На постоянной основе ведется работа по совершенствованию критериев оценивания заданий с развернутым ответом.
Русский язык, физика, математика егэ 2015
Этот сайт, посвященный сдаче ЕГЭ в 2015, точно поможет Вам.
Здесь публикуются решения сложнейших задач части С по математике и физике. Решение спорных и непростых задач части А и В по тем же предметам. А также, правила русского языка, которые помогут Вам сдать ЕГЭ по Русскому языку на результат, приближенный к заветным 100 баллам.
Физика/Математика/Русский язык ЕГЭ 2015 год.
Трапеция. ЕГЭ В10
Формула для вычисления площади трапеции
1) Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h).
S — площадь трапеции
a — длина 1-ого основания
b — длина 2-ого основания
h — длина высоты трапеци
Математика ЕГЭ 2015 Базовый уровень
Демонстрационный материал предназначен для того, чтобы дать представление о структуре будущих контрольных измерительных материалов, количестве заданий, их форме и уровне сложности.
Единый государственный экзамен (ЕГЭ) по математике с 2015 года будет разделен на базовый и профильный уровни.
Демо вариант ЕГЭ 2015 по математике базового уровня с ответами.
Задача по физике. Часть С
Катушку радиуса г = 3,0 см с числом витков n = 1000 помещают в однородное магнитное поле (ось катушки направлена вдоль линий поля). Индукция поля изменяется с постоянной скоростьюΔB/Δt = 10 мТл/с. Какой заряд qбудет на конденсаторе, подключенном к концам катушки? Емкость конденсатора С = 20мкФ.
Правда про ЕГЭ 2015
Уважаемые учителя, учащиеся выпускных классов и родители!
Уведомляем вас, что в связи с прекращением в 2009 году работы Экспертного совета ФИПИ, все последующие годы, включая текущий, 2014 год, ФИПИ не регламентирует и не грифует выпускаемые различными издательствами пособия по подготовке к ЕГЭ и ОГЭ.
ФИПИ не указывает на возможность или необходимость использования при подготовке к экзаменам каких-либо пособий, разработанных с участием или без участия авторских коллективов ФИПИ.
Математика С2 ЕГЭ 2015
Основанием прямого параллелепипеда является ромб ABCD, сторона которого равна а угол ВАD равен. Найдите расстояние от точки А до прямой , если известно, что боковое ребро данного параллелепипеда равно 8.
Решение.
Опустим из точки A перпендикуляр AE на прямую и проведем в плоскости грани прямую EF, параллельную прямой . Так как , то и , а, значит, прямая AF является проекцией прямой AE на плоскость ABC. Поскольку , то , а, следовательно, и согласно теореме о трех перпендикулярах.
Далее находим:
1) из : ;
2) из : .
Ответ: 10.
Следующие Предыдущие Главная страница
Подписаться на: Сообщения (Atom)
CHCX — Котировка акций CTGX Mining Inc — PINX
ПИНКС: CHCX
Последние цены закрытия обновлены по состоянию на
07 апреля 2022 г.
, 9:30 по восточному поясному времени
| USD
- Последнее закрытие 0,0002
- Сектор Основные материалы
- Промышленность Прочие промышленные металлы и горнодобывающая промышленность
- Инвестиционный стиль
- Дневной диапазон < 0,01 – < 0,01
- Годовой диапазон < 0,01 – < 0,01
- Рыночная капитализация 5 006,8624
- Объем / в среднем 1038,0 / 1 037,5
- Цена / Продажи 0,00
- Цена / Книга 0,00
- Форвард Div 3,33%
- Трейлинг Div-
1-звездочная цена
Investor
5-звездочная цена
инвестор
4.
ship
ИНВЕСТОР
О количественных рейтингах
Morningstar Количественные рейтинги акций (обозначенные на этой странице как) генерируются с использованием алгоритма, который сравнивает компании, не охваченные аналитиками, с сопоставимые компании, которые получают рейтинги, основанные аналитиками. Компании с рейтингами формально не покрываются аналитиками Morningstar, но статистически сопоставлены с компаниями, оцененными аналитиками, что позволяет нашим моделям рассчитать количественный ров, справедливая стоимость и рейтинг неопределенности. Нажмите здесь, чтобы узнать больше о том, как использовать эти рейтинги.
Откройте наш полный анализ с Morningstar Investor
Профиль компании CHCX
Описание деятельности
CTGX Mining Inc — международная компания, занимающаяся разработкой полезных ископаемых и полезных ископаемых с заботой об окружающей среде.
Он владеет добычей полезных ископаемых как в Мексике, так и в Колумбии, сосредоточенных на больших запасах редкоземельных элементов, золота, серебряного лития и других ценных руд.
Сектор Основные материалы
Промышленность Прочие промышленные металлы и горнодобывающая промышленность
Служащие —
Часто задаваемые вопросы по акциям CTGX Mining Inc.
Нет. В настоящее время CHCX не имеет форвардной дивидендной доходности.
Доходность по дивидендам позволяет инвесторам, особенно тем, кто заинтересован в акциях, приносящих дивиденды,
сравнить взаимосвязь между ценой акции и тем, как она вознаграждает акционеров в виде дивидендов.
Формула расчета дивидендной доходности заключается в делении годового дивиденда, выплачиваемого на акцию, на цену акции.
Узнайте больше о дивидендной доходности.
Рыночная капитализация CHCX составляет 5 006,86.
Рыночная капитализация рассчитывается путем умножения цены акций компании на общее количество акций.
Он часто используется для измерения размера компании. В ячейке Morningstar Style Box имена с большой заглавной буквы составляют
крупнейшие 70% акций США, компании со средней капитализацией составляют крупнейшие 70–90%, а компании с малой капитализацией составляют оставшиеся 10% компаний.
Узнайте больше о рыночной капитализации.
Бета-версию CHCX можно найти в разделе «Торговая информация» вверху этой страницы.
Бета-коэффициент акции измеряет, насколько тесно ее движение цены было связано с динамикой рынка в целом.
Сравнивать Историческая производительность CHCX по сравнению с конкурентами в отрасли и рынком в целом.
pro-matematica.ro
формула pentru tangentă și cotangentă
1.
Определения, свойства: 92 x} \), \( \displaystyle \forall x \in \mathbb{R} — \{ n \pi | n \in \mathbb{Z} \}\)
\( \displaystyle \text {tg}( \frac{ \pi}{2} — x) = \text {ctg} x \), \( \displaystyle \forall x \in \mathbb{R} — \{ \frac{\pi}{2} + n \pi | n \in \mathbb{Z} \}\)
\( \displaystyle \text {ctg}( \frac{ \pi}{2} — x) = \text {tg} x \), \( \displaystyle \forall x \in \mathbb{R} — \{ n \pi | n \in \mathbb{Z} \}\)
2. Функция тангенса и котангенса солнечного периода и основного периода \( \pi \ ):
\( \displaystyle \text {tg}(x + k \pi) = \text {tg} x \), \( \displaystyle \forall x \in \mathbb{R} — \{ \frac{\pi} {2} + n \pi | n \in \mathbb{Z} \}\), \( \forall k \in \mathbb{Z} \)
\( \displaystyle \text {ctg}(x + k \ pi) = \text {ctg} x \), \( \displaystyle \forall x \in \mathbb{R} — \{ n \pi | n \in \mathbb{Z} \}\), \( \forall k \in \mathbb{Z} \)
3. Функция тангенса и котангенса солнца не влияет:
\( \displaystyle \text {tg} (-x) = — \text {tg} x \), \( \displaystyle \forall x \in \mathbb{R} — \{ \frac{\pi}{2} + n \pi | n \in \mathbb{Z} \}\)
\( \displaystyle \text {ctg} (-x) = — \text {ctg} x \), \( \displaystyle \forall x \in \mathbb{R} — \{ n \pi | n \in \ mathbb{Z} \}\)
4.
Tangenta și cotangenta sumei și diferenței:
\( \displaystyle \text {tg} (a+b) = \frac{\text {tg} a + \text {tg} b}{1 — \text {tg} a \text {tg} b} \)
\( \displaystyle \text {tg} (a-b) = \frac{\text {tg} a — \text {tg} b }{1 + \text {tg} a \text {tg} b} \)
\( \displaystyle \text {ctg} (a+b) = \frac{\text {ctg} a \text {ctg} b — 1}{\text {ctg} а + \text {ctg} b} \) 92 a — 1}{2 \text {ctg} a} \)
6. Tangenta și cotangenta jumătății argumentsului:
\( \displaystyle \text {tg} \frac{a}{2} = \frac{\sin a}{1 + \cos a} = \frac{1 — \cos a}{\sin a} \)
\( \displaystyle \text {ctg} \frac{a}{2} = \frac{a}{2} = \frac{\sin a}{1 — \cos a} = \frac{1 + \cos a}{\sin a} \)
\( \displaystyle | \text {tg} \frac{a}{2} | = \sqrt { \frac{1 — \cos a}{1 + \cos a} } \)
\( \displaystyle | \text {ctg} \frac{a}{2} | = \sqrt { \frac{1 + \cos а}{1 — \cos а} } \)
8. Преобразование области сумелор в продукт:
\( \displaystyle \text {tg} p + \text {tg} q = \frac{ \sin(p+q)}{\cos p \cos q} \)
\ ( \displaystyle \text {tg} p — \text {tg} q = \frac{ \sin(p-q)}{\cos p \cos q} \)
\( \displaystyle \text {ctg} p + \text {ctg} q = \frac{ \sin(p+q)}{\sin p \sin q} \)
\( \displaystyle \text {ctg} p — \text {ctg} q = \frac{ \sin (p-q)}{\sin p \sin q} \)
9.