Целые и рациональные числа. Действительные числа
ТЕМА
1.1
ЦЕЛЫЕ и РАЦИОНАЛЬНЫЕ
ЧИСЛА.
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА.
2. Содержание:
СОДЕРЖАНИЕ:1.
2.
3.
4.
5.
Натуральные числа.
Целые числа.
Рациональные числа
Действительные числа
Преобразование выражений с
действительными числами.
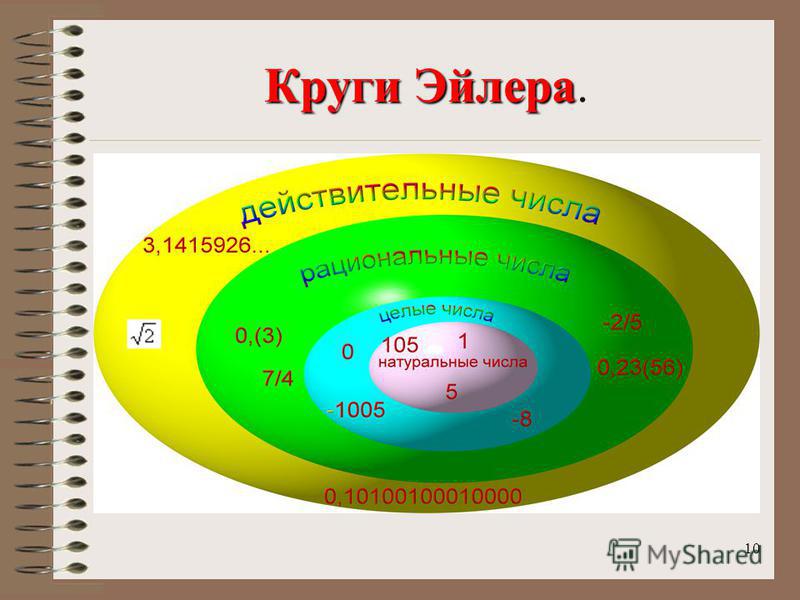
3. Знакомьтесь:
ЗНАКОМЬТЕСЬ:Натуральные
числа
Целые
числа
Рациональные
числа
Действительные
числа
N
Z
Q
R
Для счета предметов используются числа , которые
называются натуральными. Для обозначения
множества натуральных чисел употребляется
буква N -первая буква латинского слова Naturalis,
«естественный», «натуральный»
Натуральные числа, числа им противоположные
и число нуль, образуют множество целых чисел,
которое обозначается Z — первой буквой
немецкого слова Zahl — «число».
Натуральные числа
1, 2, 3, 4, 5, 6…
n — натуральное
n∈ N
Сумма и произведение натуральных
чисел есть число натуральное.

6. Целые числа
ЦЕЛЫЕЧИСЛА
Целыми числами называют множество
натуральных чисел, им противоположных и
число нуль.
Z=(1,2,3,4,5,6,7,8…
-1,-2,-3,-4,-5,-6,-7,-8…, 0)
Целые числа замкнуты относительны
суммы, произведения и разности.
Целые числа
…-3;-2;-1;0,1, 2, 3,…
m — целое
m Z
Сумма, произведение и разность
целых чисел есть число целое.
Отрицательные числа ввели
в математический обиход
Михаэль Штифель (1487—1567)
в книге «Полная арифметика» (1544),
и Никола Шюке (1445—1500)его работа была обнаружена в 1848
году.
Числа,
им противоположные
-6
-5
-4
-3
-2
-1
Натуральные числа
1 2 3 4 5 6
Z
Целые
m
Множество чисел, которое можно представить в виде
,
n Q
называется множеством рациональных чисел и обозначаетсяпервой буквой французского слова Quotient
— «отношение».
11. Рациональные числа
РАЦИОНАЛЬНЫЕЧИСЛА
Целые и дробные числа составляют множество
рациональных чисел.
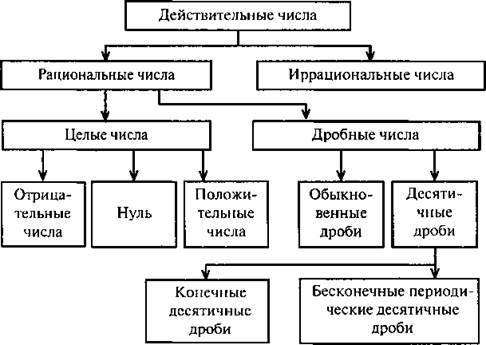
Q=(целые числа, дробные числа)
Рациональные числа замкнуты относительно
суммы, разности, произведения и частного (
исключая деления на нуль)
Рациональное число (лат. ratio —
отношение, деление, дробь) — число,
представляемое обыкновенной дробью , где
числитель m — целое число, а знаменатель n
— натуральное число. Такую дробь следует
понимать как результат деления m на n, даже
если нацело разделить не удаётся. В реальной
жизни рациональные числа используются для
счёта частей некоторых целых, но делимых
объектов, например, тортов или других
продуктов, разрезаемых на несколько частей
Целые числа
Дробные числа
2/7
2
5
7,1
3,2
0,(2)
0,1
1
0
-4
9
58
10
Q
Рациональные
Выполнить действия
Ответы
Вычислите:
.
3,5
ответ
Дроби естественно возникли при решении
задач о разделе имущества, измерении
земельных участков, исчислении времени.
Дробные числа
1
1
23 1
;
;
.

;
8 123
2
67
3
1
1
;
;
;
16 16 4
34 5
; ;
1 1
1
21
;
;
5
100
1
;
3600
Сумма, произведение и частное
дробных чисел есть число дробное.
Десятичные дроби в XV веке
ввел самаркандский ученый
ал — Каши.
Ничего, не зная об открытии ал – Коши,
десятичные дроби открыл второй раз,
приблизительно через 150 лет, после него,
фламандский ученый математик и инженер
Симон Стевин в труде «Децималь» (1585 г).
Множество рациональных чисел
Множество рациональных чисел обозначается и
может быть записано в виде: Q=m:n
Нужно понимать, что численно равные дроби
такие как, например, 3/4 и 9/12 , входят в это
множество как одно число.
Поскольку делением числителя и знаменателя
дроби на их наибольший общий делитель можно
получить единственное несократимое
представление рационального числа, то можно
говорить об их множестве как о множестве
несократимых дробей со взаимно простыми целым
числителем и натуральным знаменателем:
Рациональные числа
r — рациональное
r Q
Сумма, произведение, разность и
частное рациональных чисел есть
число рациональное.

Замените данные рациональные числа
десятичными дробями.
1
2
0,5
1
0,2
5
1
1
0,125
0 ,333…
8
3
1
0,25
4
2
0,4
5
3
0,375
8
2
0 ,666…
3
3
0,75
4
3
0,6
5
5
0,625
8
1
0 ,1666..
6
Чтобы обратить чисто периодическую дробь
в обыкновенную, нужно в числителе обыкновенной
дроби поставить число,
образованное из цифр, стоящих в периоде,
а в знаменателе – написать цифру 9 столько раз,
сколько цифр в периоде.
0,(2)=
2
1 цифра
9
0,(81)=
81
2 цифры
99
9
11
Чтобы обратить смешанную периодическую дробь
в обыкновенную, нужно в числителе обыкновенной дроби
поставить число, равное разности числа, образованного
цифрами, стоящими после запятой до начала второго
периода, и числа, образованного из цифр, стоящих после
запятой до начала первого периода;
а в знаменателе написать цифру 9 столько раз, сколько
цифр в периоде, и со столькими нулями, сколько цифр
между запятой и началом периода.
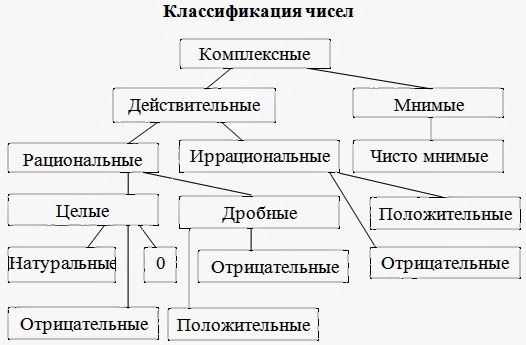
0,4(6)=
46
1 цифра
1 цифра
90
42 7
90 15
24. Рациональные числа как бесконечные десятичные дроби
РАЦИОНАЛЬНЫЕ ЧИСЛА КАКБЕСКОНЕЧНЫЕ ДЕСЯТИЧНЫЕ ДРОБИ
Для всех рациональных чисел можно использовать
один и тот же способ записи. Рассмотрим
1. Целое число 5
5,000
2. Обыкновенную дробь
0, 3(18)
3. Десятичную дробь 8,377
8,3(7)
25. Пример. Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь.
ПРИМЕР. ЗАПИСАТЬ В ВИДЕ ОБЫКНОВЕННОЙДРОБИ БЕСКОНЕЧНУЮ ДЕСЯТИЧНУЮ
ПЕРИОДИЧЕСКУЮ ДРОБЬ.
Положим, что х=1,(23), т.е. 1,232323…
100х=123,2323…
100х=123,2323…
х=1,2323…
99х=122
х=
Итак: 1,(23)=
122
99
Положим х=1,5(23)=1,52323…
Сначала умножим на 10.
Получим 15,2323.., а потом ещё на 100
1000х=1523,2323…
10х= 5,232323…
990х=1508
х=
Итак: 1,5(23)=
1508
999
1508
999
27. Иррациональные числа
ИРРАЦИОНАЛЬНЫЕ ЧИСЛАБесконечная
непериодическая дробь
называется иррациональным
числом.

Например:
Множество иррациональных чисел
обоначается J.
28. Действительные числа
ДЕЙСТВИТЕЛЬНЫЕЧИСЛА
R=(рациональные числа, иррациональные числа)
Действительные числа не обладают свойством
замкнутости — не всякое уравнение имеет корни.
29. Задания для самопроверки
ЗАДАНИЯ ДЛЯ САМОПРОВЕРКИКакие дроби называются десятичными
Действия с обыкновенными и десятичными
дробями
Какие числа называются действительными?
Действия с действительными числами.
Проверь себя
72
8
8
1) 1, (72) 1
1 1
99
11
11
912 9
903
301
2) 2,9(12) 2
2
2
990
990
495
128 12
116
29
3) 1,12(8) 1
1
1
900
900
225
Самостоятельная работа
1. Записать в виде десятичной дроби
а) 5
б) 53
99
12
2.Представьте в виде обыкновенной дроби
а) 2,3(82)
б) 2,(14)
в) 1,6(1)
ТЕМА.1 ЦЕЛЫЕ и РАЦИОНАЛЬНЫЕ ЧИСЛА. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА.
 Преподаватель
Гобова презентация, доклад, проект
Преподаватель
Гобова презентация, доклад, проектТЕМА.1
ЦЕЛЫЕ и РАЦИОНАЛЬНЫЕ ЧИСЛА.
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА.
Преподаватель
Содержание:
Натуральные числа.
Целые числа.
Рациональные числа
Действительные числа
Преобразование выражений с действительными числами.
Для счета предметов используются числа , которые называются натуральными. Для обозначения множества натуральных чисел употребляется буква N -первая буква латинского слова Naturalis, «естественный», «натуральный»
Натуральные числа
1, 2, 3, 4, 5, 6…
Целые числа
Целыми числами называют множество натуральных чисел, им противоположных и число нуль.
-1,-2,-3,-4,-5,-6,-7,-8…, 0)
Целые числа замкнуты относительны суммы, произведения и разности.
Целые числа
…-3;-2;-1;0,1, 2, 3,…
m — целое
Отрицательные числа ввели
в математический обиход
Михаэль Штифель (1487—1567)
в книге «Полная арифметика» (1544),
и Никола Шюке (1445—1500)-
его работа была обнаружена в 1848 году.
Рациональные числа
Целые и дробные числа составляют множество рациональных чисел.
Q=(целые числа, дробные числа)
Рациональные числа замкнуты относительно суммы, разности, произведения и частного (исключая деления на нуль)
Рациональное число (лат. ratio — отношение, деление, дробь) — число, представляемое обыкновенной дробью , где числитель m — целое число, а знаменатель n — натуральное число.
Выполнить действия Ответы
Вычислите:
.
ответ
3,5
Дробные числа
Ничего, не зная об открытии ал – Коши,
десятичные дроби открыл второй раз,
приблизительно через 150 лет, после него,
фламандский ученый математик и инженер
Множество рациональных чисел
Множество рациональных чисел обозначается и может быть записано в виде: Q=m:n
Нужно понимать, что численно равные дроби
такие как, например, 3/4 и 9/12 , входят в это множество как одно число.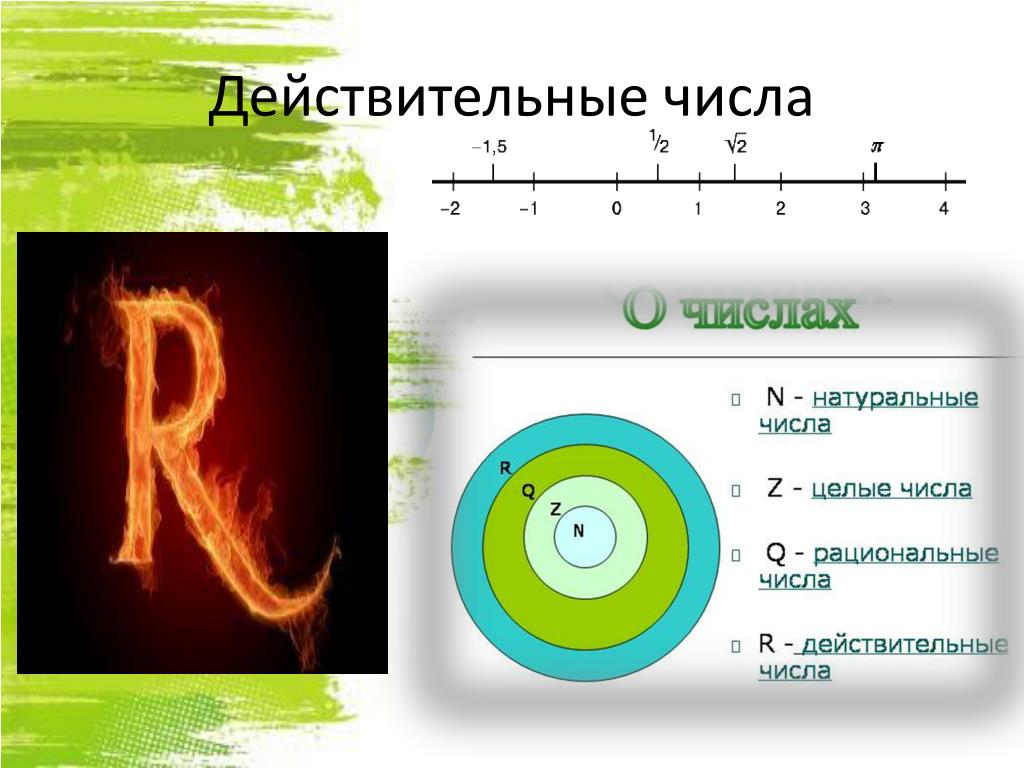
Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:
Рациональные числа
Замените данные рациональные числа
десятичными дробями.
0,(2)=
2
9
1 цифра
0,(81)=
81
2 цифры
99
Чтобы обратить смешанную периодическую дробь
в обыкновенную, нужно в числителе обыкновенной дроби
поставить число, равное разности числа, образованного цифрами, стоящими после запятой до начала второго периода, и числа, образованного из цифр, стоящих после запятой до начала первого периода;
а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и со столькими нулями, сколько цифр между запятой и началом периода.
0,4(6)=
4
6
4
1 цифра
9
1 цифра
0
Домашнее задание
Записать в виде обыкновенной дроби бесконечную десятичную периодическую дробь.
1,5(23)=
0,3(18)=
8,3(7) =
1,(72)=
2,9(12)=
1,12(8)=
Вариант 1
1. Записать в виде
а) б)
2.Представьте в виде
а) 15,(3)
б) 2,(14)
в) 1,6(1)
Вариант 2
бесконечной дроби
а) б)
обыкновенной дроби
а) 7,(2)
б) 23,(25)
в) 3,9(12)
Самостоятельная работа
Скачать презентацию
Классификация действительных чисел / наука | Thpanorama
Основной классификация действительных чисел Он делится на натуральные числа, целые числа, рациональные числа и иррациональные числа.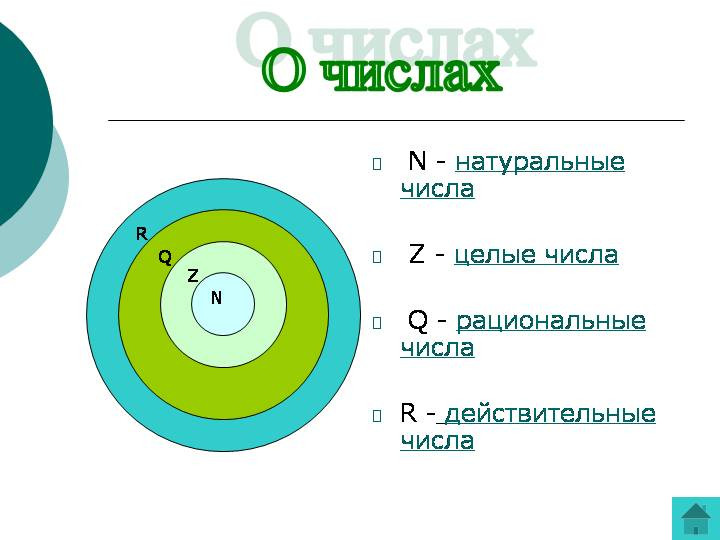 Действительные числа обозначены буквой R.
Действительные числа обозначены буквой R.
Существует множество способов построения или описания различных действительных чисел — от простых до более сложных, в зависимости от математической работы, которую вы хотите выполнить..
Натуральные числаЭто числа, которые используются для подсчета, например, «в стекле четыре цветка».
Некоторые определения начинают натуральные числа с 0, в то время как другие определения начинаются с 1. Для подсчета используются натуральные числа: 1,2,3,4,5,6,7,8,9,10 … и т. Д .; они используются как порядковые или кардинальные числа.
Натуральные числа — это базы, на основе которых можно построить множество других наборов чисел: целые числа, рациональные числа, действительные числа и комплексные числа среди других..
Эти цепочки расширений составляют натуральные числа, канонически идентифицированные в других системах счисления..
Свойства натуральных чисел, такие как делимость и распределение первичных чисел, изучаются в теории чисел.
Проблемы, связанные с подсчетом и упорядочением, такие как перечисления и разбиения, изучаются в комбинаторном.
На обычном языке, как и в начальных школах, натуральные числа можно назвать счетными числами, чтобы исключить отрицательные целые числа и ноль..
У них есть несколько свойств, таких как: сложение, умножение, вычитание, деление и т. Д..
Целые числаЦелые числа — это те числа, которые можно записать без дробной составляющей. Например: 21, 4, 0, -76 и т. Д. С другой стороны, числа типа 8.58 или √2 не являются целыми числами.
Можно сказать, что целые числа являются полными числами вместе с отрицательными числами натуральных чисел. Они используются, чтобы выразить причитающиеся деньги, глубины относительно уровня моря или отрицательную температуру, чтобы назвать несколько применений.
Набор целых чисел состоит из нуля (0), натуральных положительных чисел (1,2,3 …) и отрицательных целых чисел (-1, -2, -3 …). Обычно это называется ZZ или жирным шрифтом Z (Z).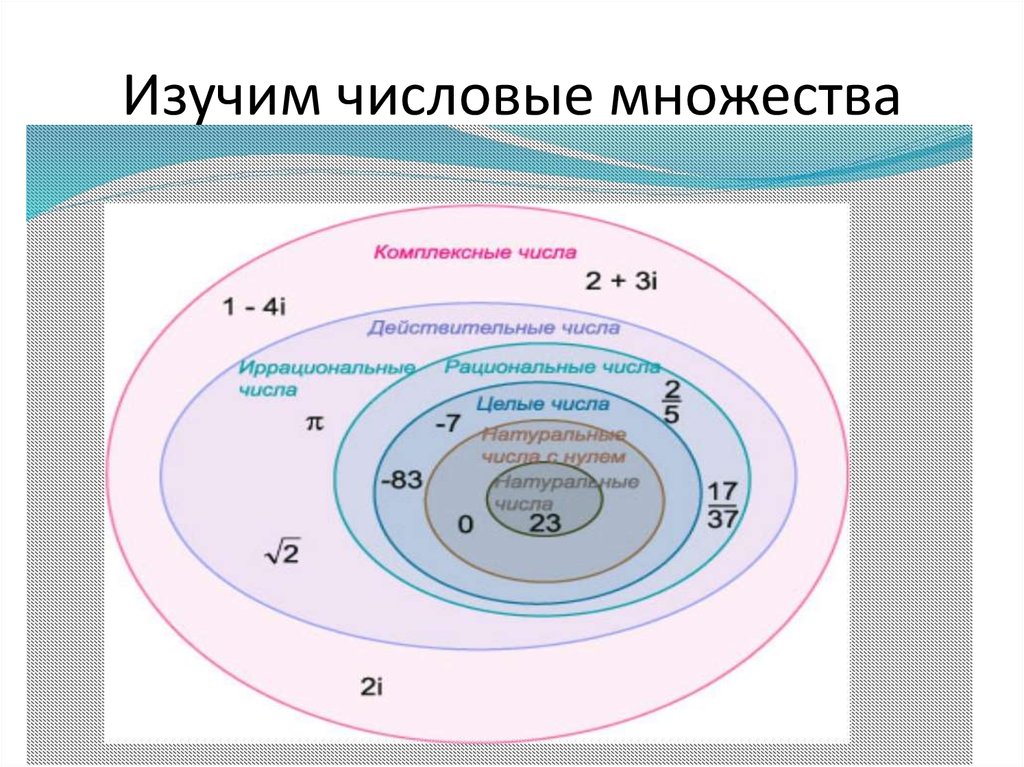
Z является подмножеством группы рациональных чисел Q, которые, в свою очередь, образуют группу действительных чисел R. Как и натуральные числа, Z является бесконечной группой учета.
Целые числа образуют наименьшую группу и наименьший набор натуральных чисел. В теории алгебраических чисел целые числа иногда называют иррациональными целыми, чтобы отличать их от алгебраических целых чисел..
Рациональные числаРациональное число — это любое число, которое может быть выражено как компонент или дробь двух целых чисел p / q, числителя p и знаменателя q. Поскольку q может быть равно 1, каждое целое число является рациональным числом.
Множество рациональных чисел, часто называемых «рациональными», обозначается через Q.
Десятичное разложение рационального числа всегда заканчивается после конечного числа цифр или когда одна и та же конечная последовательность цифр повторяется снова и снова.
Кроме того, любое повторное или конечное десятичное число представляет собой рациональное число. Эти утверждения верны не только для базы 10, но и для любой другой базы целых чисел.
Эти утверждения верны не только для базы 10, но и для любой другой базы целых чисел.
Вещественное число, которое не рационально, называется иррациональным. Иррациональные числа включают √2, a π и e, например. Поскольку весь набор пригодных для вычисления чисел является счетным, а группа действительных чисел не счетной, можно сказать, что почти все действительные числа иррациональны.
Рациональные числа могут быть формально определены как классы эквивалентностей пар целых чисел (p, q), так что q ≠ 0 или эквивалентное отношение, определенное (p1, q1) (p2, q2), только если p1, q2 = p2q1.
Рациональные числа вместе с сложением и умножением образуют поля, которые составляют целые числа и содержатся в любой ветви, содержащей целые числа..
Иррациональные числаИррациональные числа — это все действительные числа, которые не являются рациональными числами; Иррациональные числа не могут быть выражены в виде дробей. Рациональные числа — это числа, состоящие из долей целых чисел. .
.
Как следствие доказательства Кантора, что все действительные числа неисчислимы и что рациональные числа исчисляются, можно сделать вывод, что почти все действительные числа иррациональны.
Когда радиус длины двух отрезков линии является иррациональным числом, можно сказать, что эти отрезки линии несоизмеримы; это означает, что не существует достаточной длины, чтобы каждый из них мог быть «измерен» с определенным кратным целым числом.
К числу иррациональных чисел относятся радиус π от окружности круга до его диаметра, число Эйлера (e), золотое число (φ) и квадратный корень из двух; Более того, все квадратные корни натуральных чисел иррациональны. Единственным исключением из этого правила являются идеальные квадраты.
Можно видеть, что когда иррациональные числа выражаются позиционно в системе счисления (например, в десятичных числах), они не заканчиваются и не повторяются.
Это означает, что они не содержат последовательность цифр, повторение, с помощью которого производится линия представления.
Например: десятичное представление числа π начинается с 3.14159265358979, но не существует конечного числа цифр, которые могут точно представлять π, и при этом они не могут повторяться.
Доказательство того, что десятичное расширение рационального числа должно заканчиваться или повторяться, отличается от доказательства того, что десятичное расширение должно быть рациональным числом; хотя эти тесты являются базовыми и довольно длинными, они требуют некоторой работы.
Обычно математики, как правило, не используют понятие «окончание или повторение» для определения понятия рационального числа..
Иррациональные числа также могут быть обработаны через непрерывные дроби.
ссылки- Классификация действительных чисел. Получено с chilimath.com.
- Натуральное число Получено с wikipedia.org.
- Классификация чисел. Восстановлено с ditutor.com.
- Получено с wikipedia.org.
- Иррациональное число Получено с wikipedia.org.

Разница между действительными числами и целыми числами [Обновлено в 2022 г.]
Последнее обновление: 21 сентября 2022 г. / Автор Piyush Yadav / Факт проверен / 5 минут
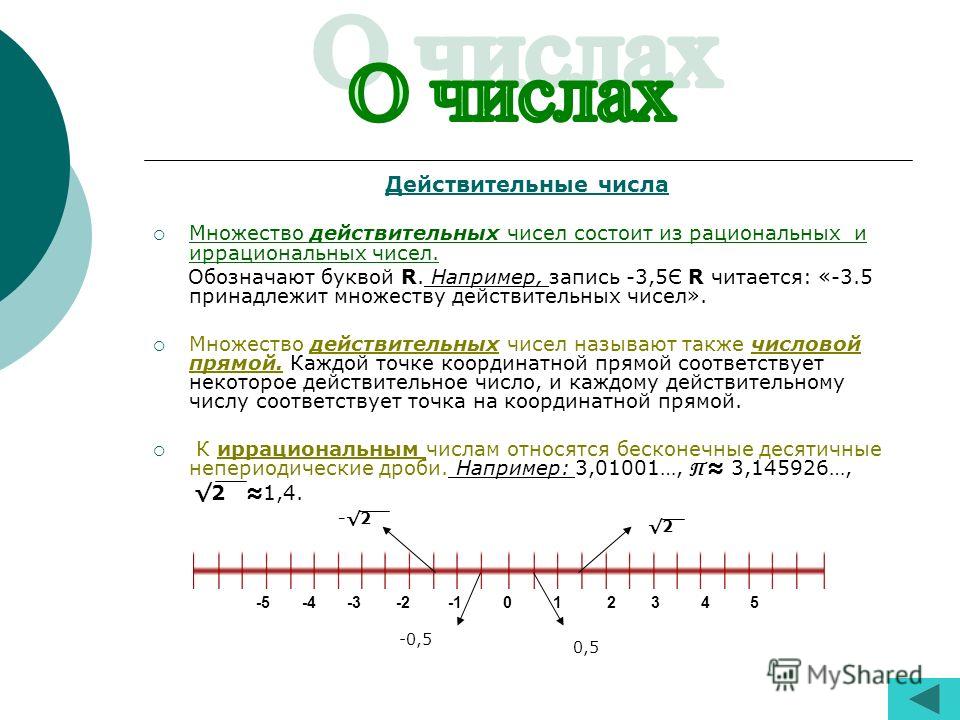
Числа могут быть двух типов, действительные и мнимые. Действительная система счисления разветвляется на другие системы счисления.
Вещественные числа можно разделить на рациональные и иррациональные числа. Целые числа и дроби относятся к рациональным числам.
Множество целых чисел состоит из целых чисел и их отрицательных значений. Целые числа представляют собой множество натуральных чисел и нуля.
Вещественные числа и целые числаОсновное различие между действительными числами и целыми числами заключается в том, что первые представляют собой более общую и широкую классификацию чисел. Однако целые числа, имеющие больше ограничений, являются подмножеством действительных чисел.
Целые числа, рациональные числа, иррациональные числа, натуральные числа и целые числа могут быть классифицированы как действительные числа, тогда как только целые числа и их отрицательные значения относятся к целочисленной системе счисления.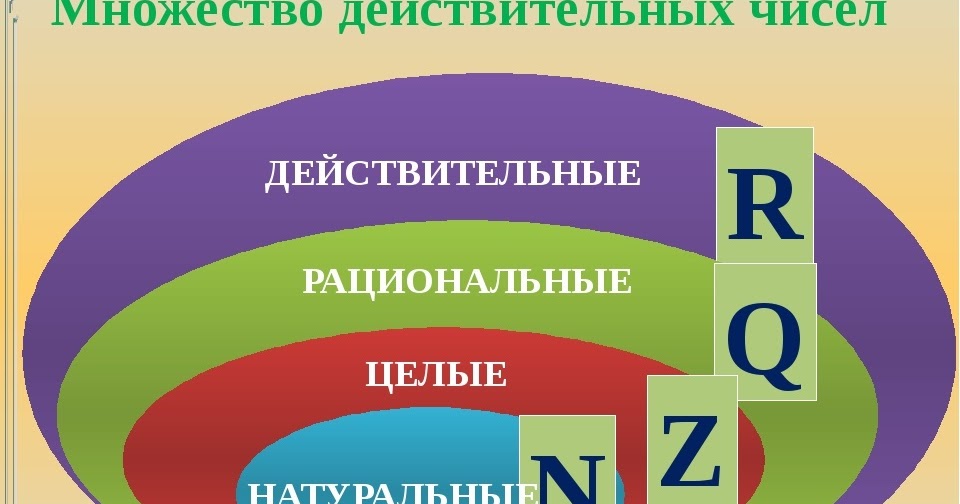
Следовательно, действительные числа включают дробные или десятичные числа. С другой стороны, целые числа — это строго целые числа (и их отрицательные значения). Целые числа не включают дроби или десятичные дроби.
Таблица сравнения между реальными числами и целыми числами (в табличной форме)
| Параметр сравнения | Реальные номера | Целевые целые. натуральные числа и целые числа классифицируются как действительные числа. | Только целые числа и их отрицательные числа классифицируются как целые числа. |
|---|---|---|---|
| Встречаемость дробей или десятичных знаков. | Дробные или десятичные числа являются действительными числами. | Целое число не может быть дробным или десятичным числом. | |
| Представление на числовой прямой | Любая точка на числовой прямой является действительным числом. | Целые числа и их отрицательные числа в числовой строке являются целыми числами. | |
| Счетность | Действительные числа образуют несчетное бесконечное множество. | Целые числа образуют счетное бесконечное множество. | |
| Обозначение | Набор всех действительных чисел представлен буквой «R» или «ℝ». | Набор всех целых чисел представлен буквой «Z». | |
| Происхождение | Термин «реальный» был придуман Рене Декартом в 17 веке для описания корней многочлена, которые не были мнимыми. Они назывались «реальными» только потому, что они не были «мнимыми». | В 1563 году Арбермут Холст изобрел целочисленную систему счисления, чтобы помочь ему в эксперименте с кроликами и слонами. Слово «целое число» происходит от латинского слова 16-го века «целое число», означающего «целое». или «неповрежденный». |
Что такое действительные числа?
Действительные числа являются неотъемлемой частью вселенной чисел. Их роль в развитии математики, несомненно, жизненно важна.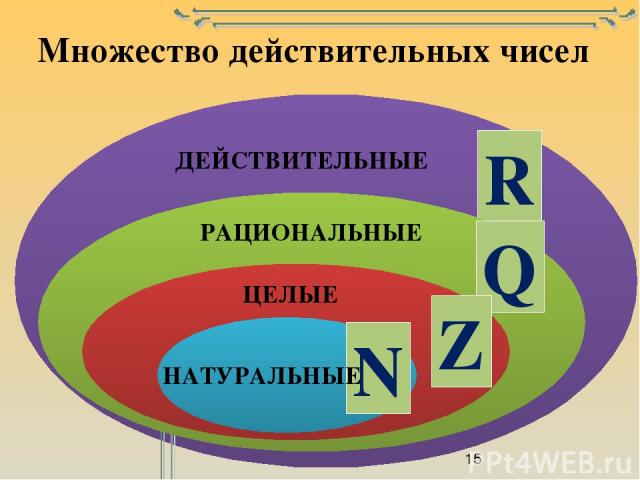
Любое число (кроме воображаемого), которое приходит вам на ум, является действительным числом.
Будь то положительное, отрицательное, дробное, иррациональное или даже 0.
Вещественное число и, следовательно, его подмножества (целые числа, рациональные числа, иррациональные числа, натуральные числа и целые числа) могут быть представлены в строке действительных чисел.
Чтобы отличить их от мнимых чисел, Декарт ввел термин «действительные» как средство описания корней многочлена.
Допускается дробное значение. Эта характеристика отличает их от целых чисел.
Действительные числа образуют неисчислимую бесконечность. Если мы возьмем две точки на числовой прямой, скажем, 0 и 1, между этими двумя точками существует бесконечное число действительных чисел.
Символы «R» или «ℝ» используются для представления набора всех действительных чисел.
Что такое целые числа?
Целочисленная система счисления является подмножеством вещественной системы счисления. Это означает, что все целые числа являются действительными числами; однако обратное неверно.
Это означает, что все целые числа являются действительными числами; однако обратное неверно.
Целыми считаются только целые числа и их отрицательные значения. Целые числа включают в себя счетные числа, такие как 0,1,2,3… и так далее.
Исключение дробных или десятичных значений делает эту систему уникальной и полезной. Действительные числа имеют интересную историю своего происхождения.
В 1563 году Арбермут Холст проводил эксперимент с кроликами и слонами.
Чтобы помочь ему в этом эксперименте, он изобрел эту систему счисления. Слово «Целое» происходит от латинского слова «целое» 16 -го -го века, означающего «целое» или «целое».
Этот факт еще больше усиливает недробный характер этой системы.
В отличие от действительных чисел, целые числа составляют набор исчисляемых бесконечных чисел. Если мы возьмем две точки на прямой с действительными числами, скажем, 0 и 1, между двумя точками не будет целых чисел.
Буква «Z» используется для обозначения набора всех целых чисел.
Основные различия между Действительные числа и целые числа
- Целые числа, рациональные числа, иррациональные числа, натуральные числа и целые числа классифицируются как действительные числа. Только целые числа и их отрицательные числа классифицируются как целые числа.
- Дроби и десятичные дроби могут быть включены в вещественные числа, но не в целые числа.
- Мы можем использовать числовую прямую, чтобы различать две системы счисления. Любая точка, которую вы укажете на этой линии, будет действительным числом. Целые числа и их отрицательные значения на числовой прямой — это целые числа.
- Обе эти системы счисления являются бесконечными множествами в природе. Однако действительные числа образуют неисчисляемое бесконечное множество, а целые числа образуют счетное бесконечное множество.
- Набор всех действительных чисел представлен буквой «R» или «ℝ». Набор всех целых чисел представлен буквой «Z».

Заключение
Целые числа помогают нам в повседневном использовании математики в нашей жизни. Например, положительные и отрицательные значения отображают прибыли и убытки в бизнес-операциях.
Слово «действительный» используется для обозначения того, что действительные числа — это числа, которые не являются мнимыми. Они вместе с мнимыми числами образуют комплексные числа.
Целые числа, рациональные числа, иррациональные числа, натуральные числа и целые числа классифицируются как действительные числа. Только целые числа и их отрицательные числа классифицируются как целые числа.
Исключение дробных чисел из целых чисел делает их отличными от действительных чисел. Вещественные числа допускают дроби и десятичные дроби.
Ссылки
- https://londmathsoc.onlinelibrary.wiley.com/doi/abs/10.1112/S002461150301428X
- https://eebweb.arizona.edu/Faculty/Dornhaus/%ellistGels/papers %20numbers%20counting%20cognition.
 pdf
pdf
Найдите «Спроси любую разницу» в Google. Оцените этот пост!
[Всего: 0]
Один запрос?
Я приложил столько усилий, чтобы написать этот пост в блоге, чтобы он был вам полезен. Это будет очень полезно для меня, если вы подумаете о том, чтобы поделиться им в социальных сетях или со своими друзьями/семьей. SHARING IS ♥️
Содержание
сообщите об этом объявлении
определение — Учитывая действительные числа: определить целые числа?
Есть несколько способов интерпретировать этот вопрос.
Наивным путем было бы просто дать какое-то определение множеству целых чисел. Это не очень сложно, мы можем распознать $1$ в действительных числах, потому что это единственное число $x$ такое, что $r\cdot x=r$ для всех $r\in\mathbb R$.
Теперь рассмотрим множество, полученное повторным добавлением $1$ к самому себе или вычитанием $1$ из самого себя. А именно $\{0,1,-1,1+1,-1-1,1+1+1,-1-1-1,\ldots\}$. Можно показать, что это множество действительно является целым числом. Каждое целое число является конечной суммой $1$ или аддитивной инверсией такого множества.
Можно показать, что это множество действительно является целым числом. Каждое целое число является конечной суммой $1$ или аддитивной инверсией такого множества.
Можно также определить, как это сделал Безымянный, что является индуктивным множеством, затем определить $\mathbb N$ как наименьшее индуктивное множество, а $\mathbb Z$ как наименьшее множество, содержащее $\mathbb N$ и замкнутое относительно сложение и вычитание.
Однако этот вопрос также можно интерпретировать, задав вопрос: « Можно ли определить первый порядок множества $\mathbb Z$ в $\mathbb R$ на языке упорядоченных полей? «, а именно, если вы живете внутри действительных чисел , существует ли в языке $0,1,+,\cdot,<$ формула, удовлетворяющая только целым числам?
Ответ на этот вопрос отрицательный. Целые числа не определимы в первом порядке в $\mathbb R$. Это нетривиальный результат в теории моделей. Но это важно отметить, потому что это совершенно правильная интерпретация вопроса, и она приводит к совершенно другому ответу, чем приведенный выше.
В частности, это помогает понять определимость первого порядка по сравнению с определимостью второго порядка, а также внутреннюю и внешнюю определимость.
Я добавляю еще кое-что к ответу из-за недавнего комментария ОП к исходному вопросу. Я чувствую, что необходимо некоторое разъяснение моего ответа здесь.
Сначала нам нужно понять, что означает « определяет » с точки зрения логики. Это означает, что существует язык, в котором действительные числа интерпретируют язык согласованным образом, и существует формула с одной свободной переменной, которая истинна тогда и только тогда, когда мы подставляем в нее целое число.
Например, мы не можем определить $\mathbb R$ в $\mathbb C$, если у нас есть только $0,1,+,\times$, но мы можем сделать это, если у нас также есть карта сопряжения в нашем словаре — как показано в вопросе.
Наивно говоря, когда мы подходим к математике, мы можем думать, что нам доступно все, что в какой-то степени верно.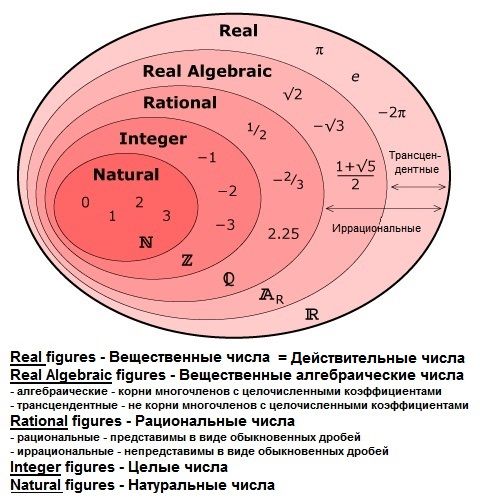
В этом вопросе не указан язык, что дает основания полагать, что речь идет о реальных числах на языке упорядоченных полей. Так что в нашем языке у нас есть только $0,1,+,\times,<$ (и равенство, у нас всегда есть равенство). В этом языке мы не можем определить целые числа внутри действительных чисел с помощью формулы первого порядка.
Ах, но что такое формула первого порядка? Ну, вообще в формуле мы можем иметь переменные, которые являются объектами нашей структуры (в данном случае, действительные числа), и мы можем иметь задает действительных чисел, и мы можем иметь наборов наборов действительных чисел
 Итак, переменные в логике первого порядка — это элементы вселенной, что в нашем случае означает просто вещественные числа. Логика второго порядка также позволила бы нам проводить количественную оценку наборов (действительных чисел), но не наборов наборов действительных чисел и так далее.
Итак, переменные в логике первого порядка — это элементы вселенной, что в нашем случае означает просто вещественные числа. Логика второго порядка также позволила бы нам проводить количественную оценку наборов (действительных чисел), но не наборов наборов действительных чисел и так далее.Так, например, мы можем написать определение для $2$, используя формулу первого порядка, т.е. $х=1+1$. Существует единственный элемент, удовлетворяющий этому свойству, и это $2$. И мы можем написать определение индуктивный набор с использованием формулы второго порядка, $0\in A\land\forall x(x\in A\rightarrow x+1\in A)$.
Но, как оказалось, мы не можем выразить свойство быть индуктивным множеством (и, конечно, мы не можем выразить свойство быть минимальным индуктивным множеством) в логике первого порядка, когда мы ограничиваемся только действительными числами как упорядоченным поле . Доказательство, как я заметил, нетривиально.
Комментарий, на который я ссылался, гласит:
@WillieWong Я не знаю поля реальных чисел: для меня реальные числа образуют линию.
— Виртлинк
Что дает еще один способ интерпретировать этот подход. Мы можем рассматривать действительные числа просто как упорядоченный набор. Мы игнорируем тот факт, что это поле, и просто смотрим на порядок.
Но у этого языка еще меньше выразительных возможностей, чем у упорядоченного поля, например, мы не можем даже определить сложение и умножение. На самом деле мы даже не можем определить $0$ и $1$ на этом языке. У нас есть только заказ, с которым можно работать, и с ним действительно не так много работы.
Гораздо проще показать, что просто как упорядоченное множество все результаты о неопределимости сохраняются, я не буду вдаваться в это, а просто отмечу, что определимость «невосприимчива к автоморфизмам», и $\mathbb R$ имеет множество автоморфизмов, которые сохраняют порядок и перемещают каждый элемент.
Далее довольно быстро натыкаешься на философию математики. Каковы реальные цифры? Это наборы? Являются ли они какой-либо структурой, интерпретирующей конкретный язык определенным образом? Мы строим целые числа из действительных чисел или мы строим действительные числа из целых чисел? (Конечно, сначала мы должны построить рациональные числа. )
)
Это интересные вопросы, но по существу спорные, если кто-то просто хочет говорить об определимости первого порядка в том или ином языке. Но если подойти к этому «наивным» способом, который допускает количественную оценку более высокого порядка и использование любой функции, о которой мы знаем, тогда ответ становится довольно простым (хотя можно столкнуться с цикличностью, если не быть достаточно осторожным).
Надеюсь, это объясняет, среди прочего, почему я начал свой ответ с » Есть несколько способов интерпретировать этот вопрос «. Мы просто можем видеть действительные числа как различную структуру в разных языках, и мы можем разрешить или не разрешить формулам использовать наборы действительных чисел. В каждой из этих интерпретаций вопроса мы может быть другой ответ и разные причины, чтобы этот ответ был верным! )
Но подождите, это еще не все!
- Истинное определение реальных чисел
- FO-определимость целых чисел в (Q, +, <)
- Что такое определимость в логике первого порядка?
Вот простое доказательство того, что должно быть несколько уровней бесконечности : ScienceAlert
Никруб/Shutterstock. com
com
Бесконечность — мощная концепция. Философы, художники, богословы, ученые и люди всех слоев общества боролись с идеями бесконечного и вечного на протяжении всей истории.
Бесконечность также является чрезвычайно важным понятием в математике. Бесконечность проявляется почти сразу же при работе с бесконечно большими множествами — наборами чисел, которые продолжаются вечно, как натуральные или счетные числа: 1, 2, 3, 4, 5 и так далее.
Однако не все бесконечные наборы одинаковы. На самом деле существует множество различных размеров или уровней бесконечности; некоторые бесконечные множества намного больше, чем другие бесконечные множества.
Теория бесконечных множеств была разработана в конце XIX в.19 века гениальным математиком Георгом Кантором. Многие идеи и теоремы Кантора лежат в основе современной математики. Одним из самых крутых нововведений Кантора был способ сравнивать размеры бесконечных множеств и использовать эту идею, чтобы показать, что бесконечностей много.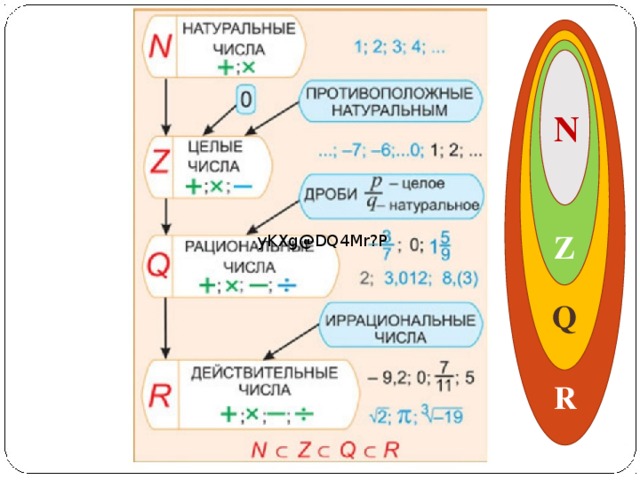
Чтобы увидеть, как работает теория Кантора, мы начнем с утверждения, что два множества имеют одинаковый размер, если мы можем установить взаимно однозначное соответствие или спарить элементы двух множеств. Мы можем начать с малого — множества {a, b, c} и {1, 2, 3} имеют одинаковый размер, так как я могу спарить их элементы:
Это немного сложно для сравнения двух таких небольших конечных множеств — очевидно, что они оба состоят из трех элементов и, следовательно, имеют одинаковый размер. Однако, когда мы смотрим на бесконечные множества, мы не можем просто смотреть на множества и подсчитывать количество элементов, поскольку множества продолжаются вечно. Таким образом, это более формальное определение будет очень полезным.
Счетно бесконечные множества
Наш базовый уровень бесконечности будет исходить из нашего самого основного бесконечного множества: ранее упомянутых натуральных чисел. Множество того же размера, что и натуральные числа, которое можно поставить в однозначное соответствие с натуральными числами, называется счетно бесконечным множеством.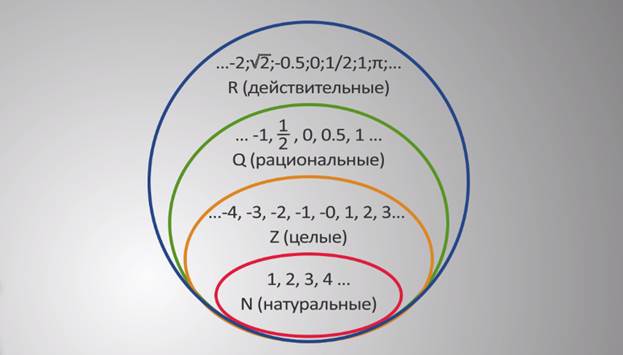
Удивительное количество бесконечных множеств на самом деле счетно. На первый взгляд набор целых чисел, состоящий из натуральных чисел, их эквивалентов в виде отрицательных чисел и нуля, выглядит так, как будто он должен быть больше, чем натуральные числа. В конце концов, к каждому из наших натуральных чисел, таких как 2 или 10, мы просто добавили отрицательное число, -2 или -10. Но целые числа счетны — мы можем найти способ присвоить каждому натуральному числу ровно одно целое число, прыгая туда-сюда между положительными и отрицательными числами:
Если мы продолжим шаблон, предложенный выше, мы закончим тем, что присвоим ровно одно целое число каждому натуральному числу, причем каждое целое число будет присвоено натуральному числу, что даст нам вид пары один к одному, что означает, что два набора одинаковы. размер.
Это немного странно, поскольку натуральные числа являются подмножеством целых чисел — каждое натуральное число также является целым числом. Но даже несмотря на то, что натуральные числа полностью содержатся в целых числах, эти два набора на самом деле имеют одинаковый размер.
Но даже несмотря на то, что натуральные числа полностью содержатся в целых числах, эти два набора на самом деле имеют одинаковый размер.
Рациональные числа — это числа, которые можно записать в виде дроби или отношения двух целых чисел: 1/2, -5/4, 3 (которое можно записать как 3/1) и т.п. Это еще одно бесконечное множество, которое выглядит так, как будто оно должно быть больше, чем натуральные числа — между любыми двумя натуральными числами у нас бесконечно много дробей.
Но, как и в случае с целыми числами, мы все еще можем составить пару один к одному, сопоставив каждому рациональному числу ровно одно натуральное число. Начните с создания сетки рациональных чисел: в каждой строке есть определенное натуральное число в нижней части дроби — знаменатели первой строки — все единицы, а 2-й строки — все двойки. Каждый столбец имеет определенное число в верхней части дроби — числители первого столбца все 1, а второго столбца все двойки. Эта сетка покрывает все положительные рациональные числа, поскольку любое отношение двух положительных целых чисел будет отображаться где-то в сетке:
Мы получаем соответствие между рациональными и натуральными числами, двигаясь зигзагом по сетке и считая. Дроби, такие как 2/2 и 4/6, которые являются просто альтернативными представлениями чисел, которые мы уже видели (2/2 совпадает с 1/1, а 4/6 совпадает с 2/3), пропускаются:
Дроби, такие как 2/2 и 4/6, которые являются просто альтернативными представлениями чисел, которые мы уже видели (2/2 совпадает с 1/1, а 4/6 совпадает с 2/3), пропускаются:
Итак, первое рациональное число 1/1, второе 2/1, третье 1/2, четвертое 1/3, мы пропускаем 2/2, так как оно просто сводится к 1/1, пятое это 3/1 и так далее.
Продолжая в том же духе, каждому рациональному числу будет присвоено уникальное натуральное число, показывая, что, как и целые числа, рациональные числа также являются счетно бесконечным множеством.
Несмотря на то, что мы добавили все эти дроби и отрицательные числа к нашему первоначальному базовому набору натуральных чисел, мы все еще находимся на нашем первом, базовом уровне бесконечности.
Несчетно бесконечные множества
Теперь рассмотрим действительные числа. Действительные числа — это набор чисел, которые можно записать с помощью некоторого десятичного расширения. Действительные числа включают в себя рациональные числа — любую часть двух целых чисел можно разделить и превратить в десятичную.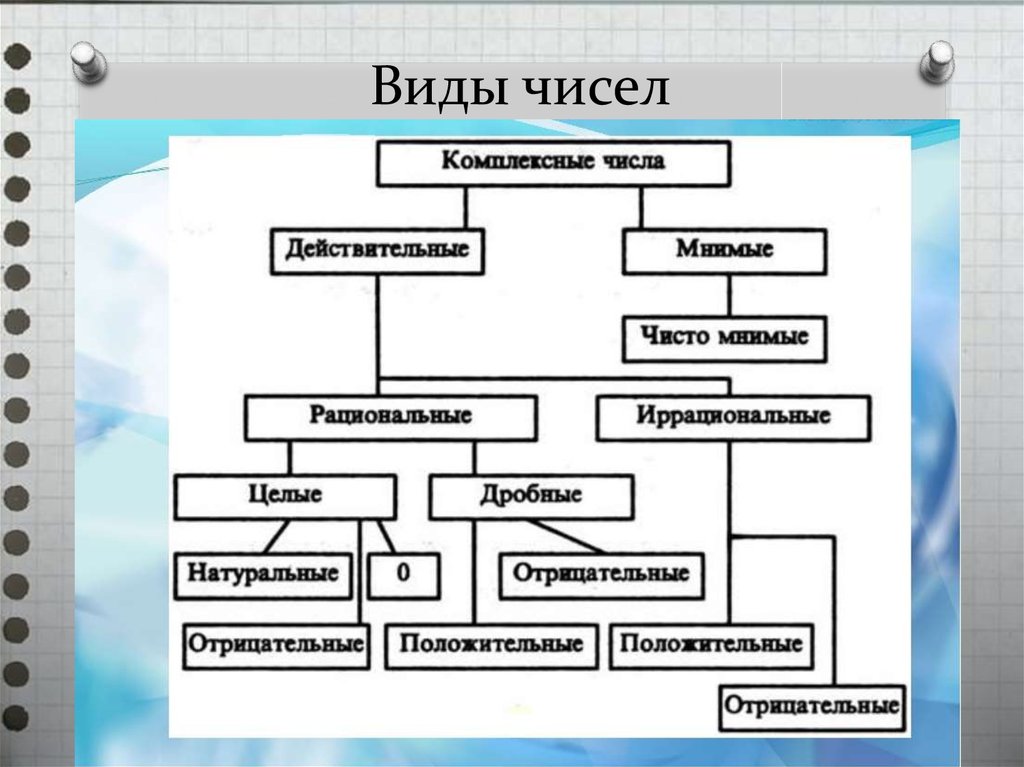 1/2 = 0,5 и 1/3 = 0,3333…, причем последнее продолжается с тройками навсегда. Действительные числа также включают иррациональные числа или десятичные дроби, которые продолжаются вечно, не устанавливаясь в повторяющийся шаблон или окончание. π иррационально — его десятичное расширение начинается со знакомого 3,14159.… но продолжается вечно, его цифры бешено мечутся.
1/2 = 0,5 и 1/3 = 0,3333…, причем последнее продолжается с тройками навсегда. Действительные числа также включают иррациональные числа или десятичные дроби, которые продолжаются вечно, не устанавливаясь в повторяющийся шаблон или окончание. π иррационально — его десятичное расширение начинается со знакомого 3,14159.… но продолжается вечно, его цифры бешено мечутся.
Мы смогли придумать умные соответствия с натуральными числами для целых и рациональных чисел, показав, что все они счетно бесконечны и имеют один и тот же размер. Учитывая это, мы можем подумать, что можем сделать что-то подобное с реальными числами.
Однако это невозможно. Действительные числа представляют собой неисчислимо бесконечное множество — на самом деле действительных чисел гораздо больше, чем натуральных чисел, и нет никакого способа выровнять действительные и натуральные числа так, чтобы мы приписывали каждому натуральному числу ровно одно действительное число.
Чтобы убедиться в этом, воспользуемся чрезвычайно мощной математической техникой: доказательством от противного. Мы начнем с выдвижения гипотезы о том, что верно обратное нашему утверждению — что действительные числа счетно бесконечны, и, таким образом, есть способ выровнять все действительные числа с натуральными во взаимно однозначном соответствии. Мы увидим, что не имеет значения, как именно выглядит это соответствие, поэтому предположим, что первые несколько пар в соответствии следующие:
Мы начнем с выдвижения гипотезы о том, что верно обратное нашему утверждению — что действительные числа счетно бесконечны, и, таким образом, есть способ выровнять все действительные числа с натуральными во взаимно однозначном соответствии. Мы увидим, что не имеет значения, как именно выглядит это соответствие, поэтому предположим, что первые несколько пар в соответствии следующие:
Наше большое предположение состоит в том, что каждое действительное число появляется где-то в этом списке. Теперь мы собираемся показать, что это на самом деле неправильно, создав новое число, которое не отображается в списке.
Для каждого натурального числа n мы смотрим на соответствующее действительное число в списке и берем цифру на n позиций справа от десятичной точки действительного числа. Итак, возьмем первую цифру первого числа, вторую цифру второго числа, третью цифру третьего числа и так далее:
Из нашего первого действительного числа мы получаем 5, наше второе число 3 и наше третье число 1.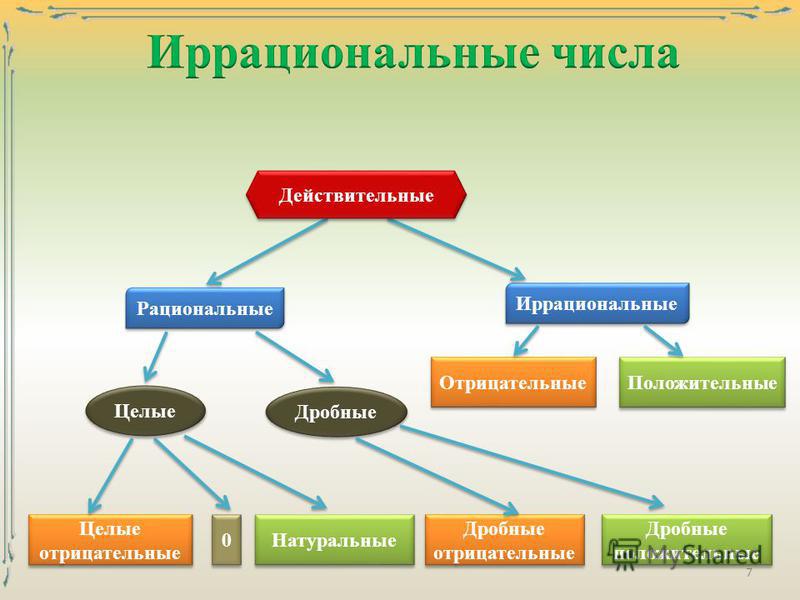 Мы делаем новое число, беря каждую из этих цифр и добавляя к ним 1 (переворачивая 0 если моя исходная цифра 9), что дает нам число 0,64207…, продолжая для всех других чисел в нашем списке.
Мы делаем новое число, беря каждую из этих цифр и добавляя к ним 1 (переворачивая 0 если моя исходная цифра 9), что дает нам число 0,64207…, продолжая для всех других чисел в нашем списке.
Это новое «диагональное» число определенно является действительным числом — оно имеет десятичное расширение. Но оно отличается от всех чисел в списке: его первая цифра отличается от первой цифры нашего первого числа, его вторая цифра отличается от второй цифры нашего второго числа и так далее.
Мы создали новый реальный номер, которого нет в нашем списке. Это противоречит нашему основному предположению, что каждое действительное число появляется где-то в соответствии.
Итак…
Ранее мы упоминали, что детали переписки не имеют значения. Это потому, что независимо от того, какое выравнивание мы пытаемся провести между действительными числами и натуральными числами, мы можем проделать тот же диагональный трюк, что и выше, создав число, которое не отображается в соответствии.


 pdf
pdf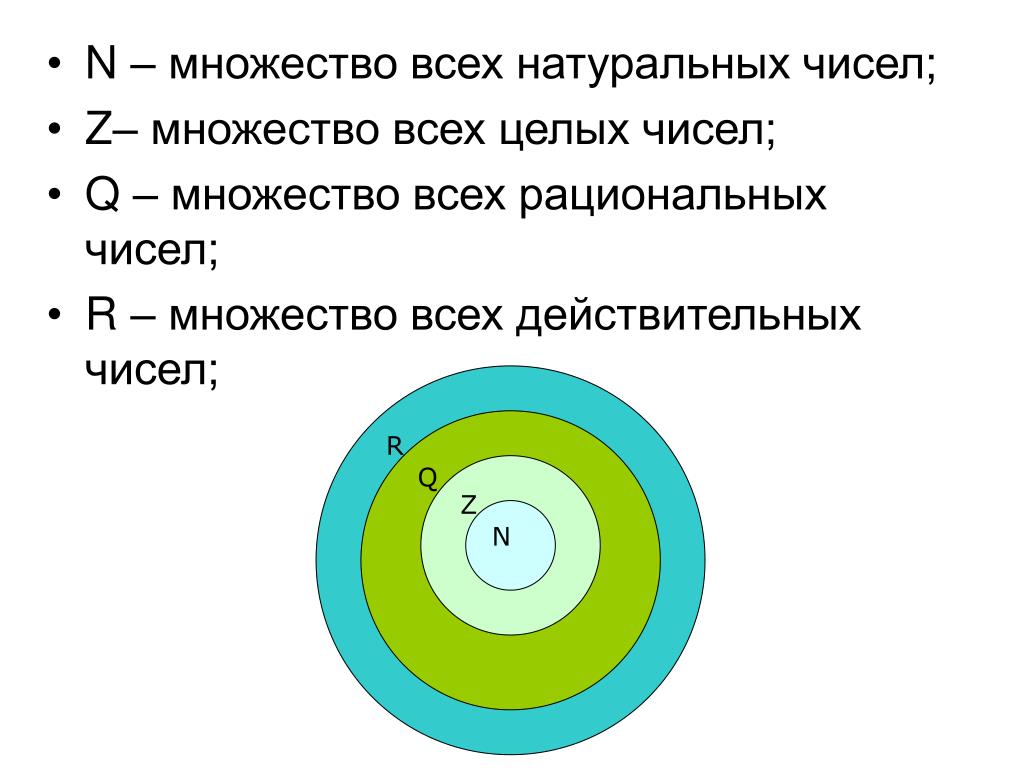 — Виртлинк
— Виртлинк