Центр круга точка о длина его радиуса 9 см: Центр круга — точка О, длина его радиуса 9 см. Где расположена точка А, если ОА=9 см?

Длина окружности. Площадь круга (Вольфсон Г.И.) 6 класс онлайн-подготовка на Ростелеком Лицей

Введение

 

Как вы знаете, многие предметы имеют форму круга. Чем это обусловлено?

 

Возьмем, к примеру, колесо. Понятно, что круглое колесо катится гораздо лучше, чем, например, квадратное. Или, скажем, стакан круглой формы удобнее держать в руке, чем стакан прямоугольной формы. Поэтому в какой-то момент человечество стало использовать круглые предметы. Но если вы используете круглые предметы, нужно научиться их измерять. Например, вам нужно знать длину окружности стакана, чтобы понять, сколько материала пойдет на его изготовление, или вам нужно знать площадь колеса, чтобы, например, определять, какой должен быть объем исходных материалов, чтобы его сделать.

Поэтому сегодня мы обсудим, как же учились находить длину окружности и площадь круга, и решим некоторые задачи, связанные с этим.

 

Окружность и круг

 

 

Вначале вспомним, что такое окружность и круг.

 

Окружность – множество всех точек на плоскости, равноудаленных от данной точки.

Т. е. есть некоторая точка, мы задаем какое-то расстояние – радиус окружности – и берем все точки, которые находятся от исходной на данном расстоянии (см. Рис. 1).

Рис. 1. Окружность

А теперь вспомним еще два важных понятия (см. Рис. 2).

Хордой называется такой отрезок, которые соединяет любые две точки, лежащие на окружности.

Диаметр – это такая хорда, которая проходит через центр окружности. Соответственно, как следствие, нетрудно догадаться, что диаметр равен двум радиусам.

Рис. 2. Хорда и диаметр

Круг – это все точки на плоскости, которые лежат внутри окружности, а также сама окружность (см. Рис. 3).

Рис. 3. Круг

 

Длина окружности

 

 

Теперь, когда мы вспомнили все важные определения, мы можем подумать, как же нам измерить длину окружности.

 

Один из способов, который был предложен, таков: возьмем, например, стакан, у которого дно будет круглой формы, и обмотаем нитку вокруг дна этого стакана. Теперь мы можем сделать засечку там, где конец нитки совпал с ее началом, затем размотать эту нитку и замерить ее длину линейкой. Естественно, измерение будет не совсем точным, оно будет зависеть от точности наших прикладываний, от точности линейки и т. п. Тем не менее мы примерно сможем измерить длину окружности (см. Рис. 4).

Рис. 4. Способ измерения длины окружности

Конечно же, чем дальше человечество продвигалось по своим научным взысканиям, тем более точно оно могло измерить эту самую длину окружности.

Еще в древности люди заметили, что если вы увеличите радиус окружности, например в два раза, то и длина этой окружности увеличится в два раза. Если уменьшить радиус в три раза, то и длина уменьшится в три раза. Иначе говоря: длина окружности и ее радиус пропорциональны друг другу. То есть их отношение – это постоянное число (см. Рис. 5).

Рис. 5. Иллюстрация пропорциональности длины окружности и радиуса

Так как отношение длины окружности к радиусу – постоянное число, то и отношение длины к диаметру – постоянное число.

Итак, пусть длина окружности , а диаметр окружности – . Так как отношение длины к диаметру всегда постоянное, то его можно примерно посчитать. Проделав это, вы примерно получите число  Так как число, которое равно отношению длины окружности к ее диаметру, не могли посчитать точно, его обозначили специальной буквой, буквой  (буква греческого алфавита).

На самом деле сейчас, когда в использование вошли мощные компьютеры, можно посчитать и тысячу, и даже миллионы знаков после запятой у числа . Это сделано, чтобы можно было более точно посчитать длину окружности. Для практических нужд нам достаточно знать первые несколько знаков: 3,14.

Кстати, есть специальные правила, которые позволяют запоминать число . Одно из правил – стихотворение:

Если очень постараться,

То запомнишь все как есть.

Три, четырнадцать, пятнадцать,

Девяносто два и шесть.

Есть и другое довольно забавное правило, которое тоже позволяет запомнить первые несколько знаков от числа .

Это я знаю и помню прекрасно:

Пи многие знаки мне лишни, напрасны

 

Если посчитать количество букв в каждом слове, мы получим число 3,14159265358.

Таким образом, мы выписали еще более длинный ряд. На самом деле есть стихотворения еще более длинные, которые позволяют запоминать число π. Некоторые даже проводят соответствующее чемпионаты, есть, например, чемпионат мира по тому, кто больше запомнит знаков у числа π.

Вернемся к нашей теме.

Используя эту формулу, мы можем посчитать длину любой окружности практически точно, потому что диаметр мы можем просто измерить линейкой, и если мы умножим его число π, то мы получим длину. С другой стороны, число π мы знаем не совсем точно, но для наших приблизительных вычислений достаточно взять его с точностью до сотых или до тысячных, после чего, перемножив, получить искомое число длины. Не забывайте: если вы подставите вместо числа π, например, 3,14, или 3,1415, то длина у вас получится приблизительной, так что знак равенства в этом случае поставить не можем, а можем поставить лишь знак примерного равенства . Если же вы хотите точное равенство, то оставляйте в ответе букву π, это и будет правильным ответом.

Рассмотрим конкретные примеры, на которых это работает.

 

Примеры на вычисление длины окружности

 

 

Пример 1

 

Дана окружность с радиусом 2 сантиметра. Чему равна ее длина?

Решение:

Ответ: 12,56 см.

Как видите, тут мы использовали знак приблизительного равенства.

 

Пример 2

Диаметр окружности равен 3 см, чему равна длина этой окружности?

Решение:

Ответ: 9,42 см.

Можно было записать ответ в виде: .

В этом случае мы можем поставить знак равенства, ведь значение абсолютно точное.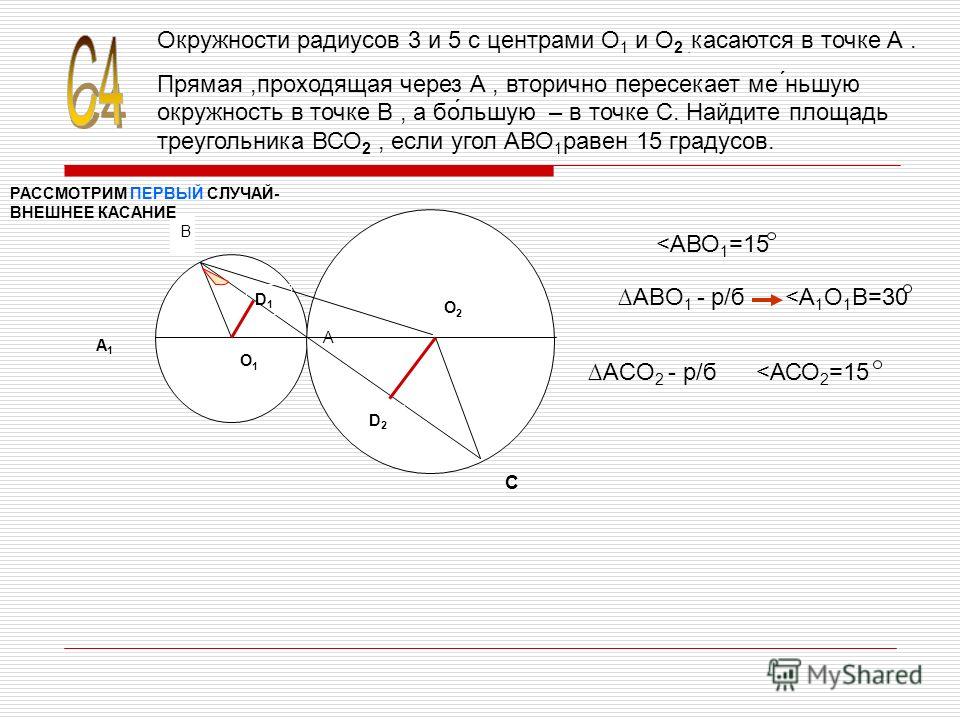 Другой вопрос, что для практических целей оно не совсем удобно. Но так как математика – точная наука, то точным ответом будет .

Между прочим, формулу  можно преобразовать. Если вспомнить, что диаметр – это удвоенный радиус, мы можем записать формулу в виде

Или:

.

 

Площадь круга

 

 

Разберемся, как наши предки искали площадь круга. Есть один метод для вычисления приблизительной площади.

 

Рассмотрим круг, заметим, что площадь этого круга, меньше, чем площадь квадрата, который описывает этот круг. Причем площадь этого квадрата мы легко можем посчитать – это квадрат его стороны.

С другой стороны, мы можем немного приблизить нашу фигуру к кругу, если вырезать квадратные уголки со сторон вершин квадрата. Остается фигура, которая по площади ближе к кругу. Аналогичным образом мы можем продолжать до бесконечности (см. Рис. 6).

Рис. 6. Приблизительное вычисление площади круга

Естественно, что точно так же мы можем сделать, если мы нарисуем квадрат внутри круга, после чего добавим такие прямоугольники со всех сторон и т. д., пока мы сколь угодно близко не приблизимся к площади искомого круга (см. Рис. 7).

Рис. 7. Приблизительное вычисление площади круга

Площадь круга мы можем оценить как сверху (площадь круга будем меньше, чем площадь фигуры, которая описывает круг), так и снизу (площадь круга больше, чем площадь фигуры, вписанной в эту окружность). Соответственно, если прямоугольников, которыми мы измеряем, будет довольно много, то мы сможем приблизительно оценить площадь круга.

В девятом классе вы докажете формулу, что на самом деле площадь круга  вычисляется так: .

 

Примеры на вычисление площади круга

 

 

Пример 1

 

Найдите площадь круга, если его радиус равен 1 см.

Решение:

Можно записать ответ в виде  либо же подставить число π и получить приблизительное значение.

Ответ: .

 

Пример 2

Найдите площадь круга, если диаметр круга равен 4 см.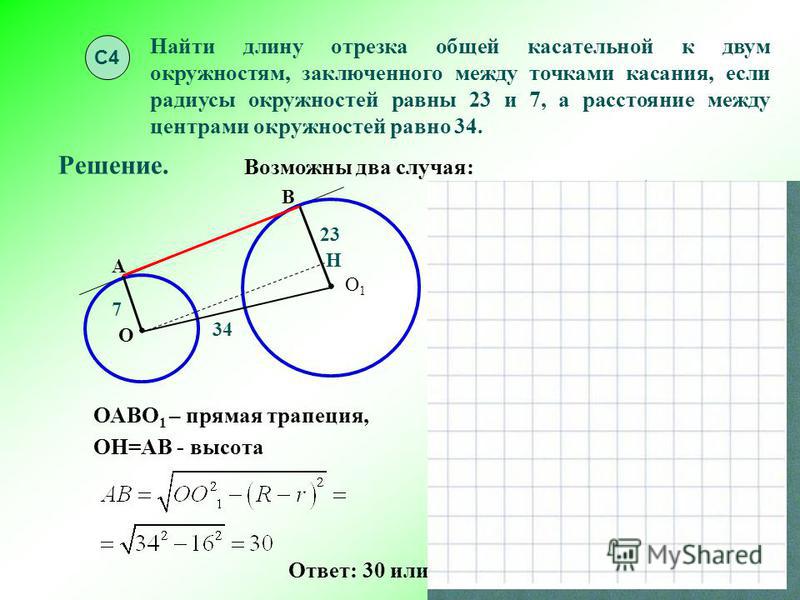

Решение:

,

Или же можем записать этот ответ точно, через π.

Ответ:  .

 

Заключение

 

 

Сегодня мы вспомнили, что такое окружность и что такое круг. Поняли, как люди научились считать длину окружности и площадь круга хотя бы приблизительно. Узнали, по каким формулам можно найти длину окружности и площадь круга, и научились этими формулами пользоваться.

 

Обратите внимание, что можно решать и обратные задачи, то есть находить радиус (диаметр) по заданной длине окружности или площади круга.

 

Список литературы

1. Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.

2. Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.

3. Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.

4. Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. – М.: ЗШ МИФИ, 2011.

5. Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – М.: ЗШ МИФИ, 2011.

6. Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт «Школьный помощник» (Источник)

2. Интернет-сайт math-prosto.ru (Источник)

3. Интернет-сайт «ЯКласс» (Источник)

 

Домашнее задание

1. Чему равна длина окружности, если ее радиус равен 31 дм, 200 см, 3200 мм. ()?

2. Окружность арены во всех цирках мира имеет длину 40,8 м. Найдите диаметр и площадь арены.

3. Останкинская телебашня в Москве опирается на площадку, имеющую форму кольца. Диаметр наружной окружности – 63 м, а внутренней – 14 м. Вычислить площадь фундамента башни.

 

Длина окружности. Площадь круга и кругового сектора 9 класс онлайн-подготовка на Ростелеком Лицей

Тема 35.

Длина окружности. Площадь круга и кругового сектора.

Чтобы получить наглядное представление о длине окружности, представим себе, что окружность сделана их тонкой нерастяжимой нити. Если мы разрежем нить в какой-нибудь точке А и распрямим ее, то получим отрезок AA₁, длина которого и есть длина окружности

Периметр любого правильного вписанного в окружность многоугольника является приближенным значением длины окружности. Чем больше число сторон такого многоугольника, тем точнее приближенное значение, так как многоугольник при увеличении числа сторон все ближе и ближе «прилегает» к окружности

Точное значение длины окружности – это предел, к которому стремится периметр правильного вписанного в окружность многоугольника при неограниченном увеличении числа его сторон.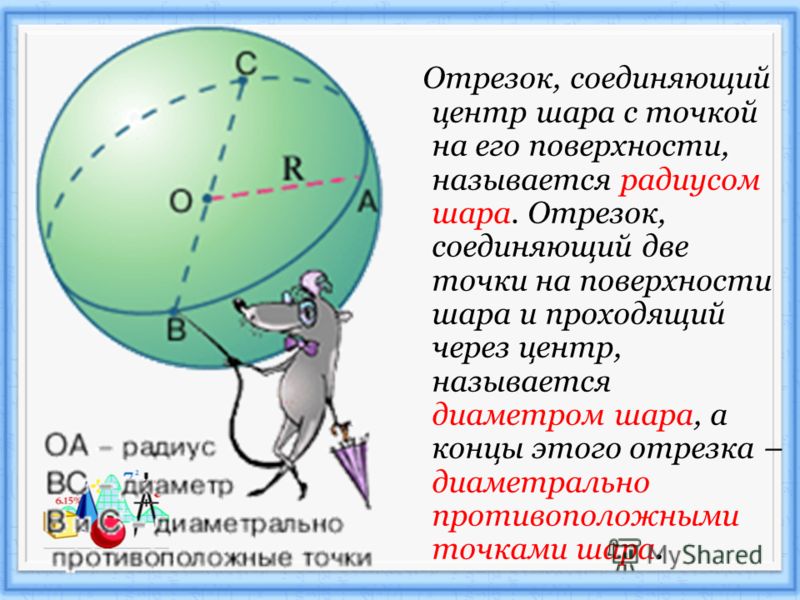

Выведем формулу, выражающую длину окружности через ее радиус.

Пусть С и С’ — длины окружностей радиусов R и R’

Впишем в каждую из них правильный n-угольник и обозначим через P_n и P’_n их периметры, а через a_n и a’_n их стороны. Используя формулу

an=2Rsin⁡180°n

Pn=n⋅an

Pn=n⋅2Rsin⁡180°n

P’n=n⋅a’n=n⋅2R’sin⁡180°n

PnPn’=2R2R’

Это равенство справедливо при любом значений n. Будем теперь неограниченно увеличивать число n. Так как Pn→C,Pn’→C’ при n→∞,то предел отношения PnPn’ равен CC’. С другой стороны, этот предел равен 2R2R’. То есть, CC’=2R2R’.Из этого равенства следует, что С2R = С’2R’ , т.е. отношение длины окружности к ее диаметру есть одно и то же число для всех окружностей. Это число принято обозначать греческой буквой

π (читается «пи»).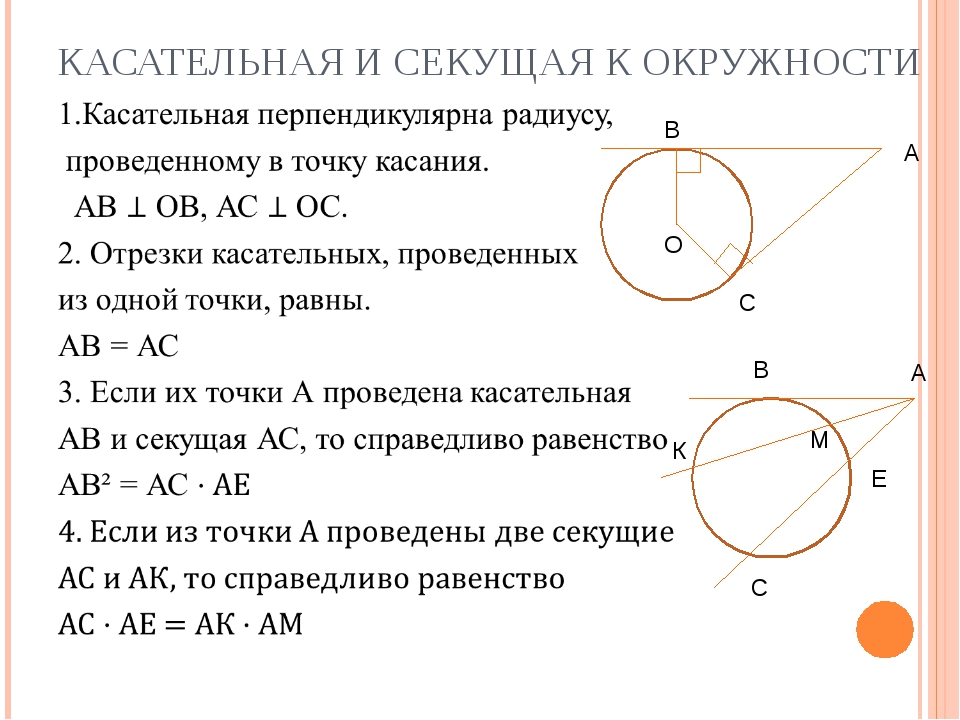

Из равенства С2R = π получаем формулу для вычисления длины окружности радиуса R: C=2πR

Доказано, что π является бесконечной непериодической десятичной дробью, т.е. иррациональным числом. Рациональное число 227 является приближенным значением числа π с точностью 0,002. При решении задач обычно пользуются приближенным значением π с точностью до 0,01: π = 3,14.

Выведем теперь формулу для вычисления длины 1 дуги окружности с градусной мерой α. Так как длина всей окружности равна 2πR, то длина дуги в 1° равна

2πR360°=πR180.

Поэтому длина 1 выражается формулой

l=πR180°∙α

Кругом называется часть плоскости, ограниченная окружностью. Круг радиуса R c центром О содержит точку О и все точки плоскости, находящиеся от точки O на расстоянии, не большем R.

S=πR² – площадь круга.

Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.

Площадь S кругового сектора радиуса R, ограниченного дугой с градусной мерой α. Так как площадь всего круга равна πR², то площадь кругового сектора, ограниченного дугой в 1°, равна πR2360°. Поэтому площадьSвыражается формулой

S=πR2360°·α.

Круговым сегментом или просто сегментом называется часть круга, ограниченная дугой и хордой, соединяющей концы этой дуги.

Если градусная мера дуги меньше 180°, то площадь кругового сегмента можно найти вычитая из площади сектора площадь равнобедренного треугольника, сторонами которого являются два радиуса и хорда сегмента.

Рассмотрим пример.

Из круга, радиус которого 10 см, вырезан сектор с дугой 60°. Найдем площадь оставшейся части.

Данную задачу можно решить двумя способами: из площади круга вычесть площадь кругового сектора, ограниченного дугой 60°, или найти как площадь кругового сектора, ограниченного дугой в 300°. Воспользуемся формулой

S=πR2360°·α

S=π∙102360°·300°=100π6∙5=500π6≈262 см²

Ответ: 262 см²

Как найти уравнение окружности

Все математические ресурсы ACT

14 Диагностические тесты 767 практических тестов Вопрос дня Карточки Learn by Concept

← Предыдущая 1 2 3 Следующая →

ACT Math Help » Алгебра » Координатная плоскость » Круги » Как найти уравнение окружности

В стандартной координатной плоскости каковы радиус и центр окружности?

Возможные ответы:

Правильный ответ:

Объяснение:

При нахождении центра и радиуса круга центр равен , а радиус равен . Обратите внимание, что они не отрицательны, хотя в уравнении перед ними стоят отрицательные знаки. Это становится важным при работе с действительными числами. Также обратите внимание на квадрат .

В нашем круге применяются те же принципы, что и в предыдущем, поэтому он является нашим центром. Обратите внимание, как поменялись местами знаки чисел. Это относится ко всем кругам из-за отрицательного значения в основном уравнении выше.

Чтобы найти радиус окружности, нужно взять число, которому равно уравнение, и извлечь из него квадратный корень. Это связано с упомянутым выше квадратом. . Используйте наименьшее общее кратное 27, чтобы найти, что три тройки составляют 27. Вычтите две тройки, так как квадратный корень из числа, умноженного на самого себя, равен самому себе. Это оставляет один 3 под радикалом. Поэтому наш радиус равен .

Центр: Радиус:

Сообщить об ошибке

Какова площадь круга в стандартной координатной плоскости?

Возможные ответы:

Правильный ответ:

Объяснение:

Общее уравнение окружности  .

Согласно вопросу, . Таким образом, .

Общее уравнение площади круга.

Когда мы подставляем 13 вместо , наша площадь становится равной .

Сообщить об ошибке

Окружность в стандартной координатной плоскости касается оси X в точке (3,0) и оси Y в точке (0,3). Что такое уравнение окружности?

Возможные ответы:

Правильный ответ:

Объяснение:

Формула уравнения окружности: (x – h) ² + (y – k) ² = r ² , где (h, k) представляет собой координаты центра круг, а r представляет радиус круга.

Если окружность касается оси x в точке (3,0), это означает, что она касается оси x в этой точке. Если окружность касается оси y в точке (0,3), это означает, что она касается оси y в этой точке. Зная эти две точки, мы можем определить центр и радиус окружности.

Центр круга должен быть равноудален от любой из точек на окружности. Это означает, что и (0,3), и (3,0) находятся на одинаковом расстоянии от центра. Если мы нарисуем эти точки на координатной плоскости, станет очевидным, что центр окружности должен быть (3,3). Эта точка находится ровно в трех единицах от каждой из заданных точек, что указывает на то, что радиус окружности равен 3,9.0005

Когда мы вводим эту информацию в формулу для окружности, мы получаем (x – 3) ² + (y – 3) ² = 9.

Сообщить об ошибке

Найти уравнение окружности с координаты центра  и радиус .

Возможные ответы:

Правильный ответ:

Объяснение:

Уравнение окружности

Центр равен  или, записанному по-другому . Заменив  для  и  для , наша формула становится

Наконец, формула круга 

Сообщить об ошибке

На плоскости xy, какова площадь круга со следующим уравнением:

Возможные ответы:

16 ответ:

Объяснение:

Уравнение стандартной формы окружности , где – центр окружности,  – радиус. Таким образом, поскольку у нас уже есть стандартное уравнение формы окружности, мы можем игнорировать  и , поскольку все, что нам нужно, это .

Площадь круга равна , что равно .

Сообщить об ошибке

Окружность имеет центр в точке (5,5) и радиус 2. Если формат уравнения для окружности (x-A)

2 + (y-B) ² =C, что такое С?

Возможные ответы:

Правильный ответ:

4

Пояснение:

Центр окружности находится в точке (5,5) и имеет радиус 2. Следовательно, уравнение (x-5) ² +(y-5) ² =2 ² , или (x-5) ² +(y-5) ² =4.

Сообщить об ошибке

Если центр окружности находится в точке (0,4), а диаметр окружности равен 6, каково уравнение этой окружности?

Возможные ответы:

(x-4) ² + Y ² =

(x-4) ² + y ² = 36

x ² + y ^{= 36}

x ² + y ^{+ y + y}

. 2 = 9

х ² + (у-4) ² = 36

x ² + (Y-4) ² = 9

Правильный ответ:

x ² + (Y-4) ² = 9005

6 + (Y-4) ² = 9 0005

14 + (Y-4) Объяснение:

Формула уравнения окружности:

(x-h) ² + (y-k) ² = r ²

Где (h,k) — центр окружности.

h = 0 и k = 4

и диаметр = 6, поэтому радиус = 3

(x-0) ² + (y-4) ² = 3 ²

x ² + (y-4) ² = 9

Сообщить об ошибке

5 9000 – 4) ² + (y + 3) ² = 29. Окружность A сдвинута вверх на пять единиц и влево на шесть единиц. Затем его радиус удваивается. Какое новое уравнение для окружности A?

Возможные ответы:

(x + 2) ² + (y – 2) ² = 116

(x + 2) ²  + (у – 2) ²  = 58

(х – 10) ² + (у + 8) ² = 116

(х + 6 у + 2) ^{2 ) 2 = 58}

(x — 10) ² + (y + 8) ² = 58

Правильный ответ:

(x + 2) ² + (Y — 2) ² = 116

Объяснение:

Общее уравнение окружности: (x – h) ² + (y – k) ² = r ² , где (h, k) представляет собой положение центра круга, а r представляет собой длину его радиуса.

Окружность A сначала имеет уравнение (x – 4) ²  + (y + 3) ²  = 29. Это означает, что ее центр должен находиться в точке (4, –3), а ее радиус равен √ 29.

Затем нам сообщают, что окружность А сдвинулась вверх на пять единиц, а затем влево на шесть единиц. Это означает, что координата y центра увеличится на пять, а координата x центра уменьшится на 6. Таким образом, новый центр будет расположен в точке (4 – 6, –3 + 5), или ( –2, 2).

Затем нам сообщают, что радиус круга A удвоился, что означает, что его новый радиус равен 2√29.

Теперь, когда у нас есть новый центр и радиус окружности A, мы можем написать ее общее уравнение, используя (x – h) ² + (y – k) ² = r ² . 11

(x + 2) ² + (y – 2) ² = 116.

Ответ: (x + 2) ² + (y – 2) ² = 116.

Сообщить об ошибке

Какое из следующих уравнений описывает все точки (x, y) на координатной плоскости, которые находятся на расстоянии пяти единиц от точки (– 3, 6)?

Возможные ответы:

у + 6 = 5 – (х – 3) ²

(х – 3) ²  + (у + 6) ^{2 0 5 9 0 0 0 = 0 0 0 = 0 ) 2  – (у + 6) 2  = 25}

(х + 3) ²  + (у – 6) ² = 25

(x — 3) ² + (y + 6) ² = 25

Правильный ответ:

(x + 3) ² + (y — 6) ² = 25

Объяснение:

Мы пытаемся найти уравнение для всех точек, находящихся на одинаковом расстоянии (5 единиц) от (–3, 6). Геометрическое место всех точек, равноудаленных от одной точки, представляет собой окружность. Другими словами, нам нужно найти уравнение окружности. Центр круга будет (–3, 6), а радиус, который является расстоянием от (–3,6), будет равен 5. 

Стандартная форма окружности приведена ниже:

(x – h) ² + (y – k) ² = r ² , где центр расположен в точках (h, k) и r это длина радиуса.

В этом случае h будет равно –3, k будет равно 6, а r будет равно 5.

(x + 3) ²  + (y – 6) ² = 25

Ответ: (x + 3) ²  + (y – 6) ²  = 25.

Сообщить об ошибке

Уравнение для окружности радиусом 12 с центром на пересечении двух прямых:

y ₁ = 4 x + 5 3

4 и 5 3

4

у ₂ = 5 х + 44?

Возможные ответы:

Ни один из других ответов

(x + 41) ² + (y + 161) ² = 144

(x — 22) ² + (Y — 3

(x — 22) ² + (Y — 3. ) ² = 12

(x — 41) ² + (y — 161) ² = 144

(x — 3) ² + (Y — 44) ² = 144

. Правильный ответ:

(x + 41) ²  + (y + 161) ² = 144

Объяснение:

Для начала определим точку пересечения этих двух прямых, установив равенства между собой:

4 x + 3 = 5 x + 44; 3 = х + 44; –41 = x

Чтобы найти координату y , подставьте в одно из уравнений. Возьмем y ₁ :

y = 4 * –41 + 3 = –164 + 3 = –161

Таким образом, центр нашей окружности: (–41, –161).

Теперь вспомните, что общая форма для круга с центром в точке ( x ₀ , y ₀ ) такова:

( x —

80443) ² + ( Y — Y ₀ ) ² = R ²

Для наших данных это означает, что наше уравнение:

( x 9000 + 41) 41). ² + ( Y + 161) ² = 12 ² или ( x + 41) ² + ( Y + 161) ² = 144

. Отчет о ошибке

4 ^{. ← Назад 1 2 3 Далее →}

Уведомление об авторских правах

Все математические ресурсы ACT

14 диагностических тестов 767 практических тестов Вопрос дня Карточки Learn by Concept

Математическая задача: Окружности — вопрос № 1485, геометрия, линия, планиметрия

В окружности радиусом 7,5 см построены две параллельные хорды, длина которых 9 см и 12 см. Вычислите расстояние этих хорд (если есть два возможных решения, напишите оба).

Правильный ответ:

x = 10,5 см
y = 1,5 см

Пошаговое объяснение:

r2=7,52=x12​+(9/2)2 r2=7,52=x22​+(12/2)2 x1=6 см x2=4,5 см x=x1+x2=10,5 см

y=∣x1−x2​∣=1,5 см

Нашли ошибку или неточность? Не стесняйтесь

, напишите нам

. Спасибо!

Советы для связанных онлайн-калькуляторов

Вы хотите преобразовать единицы длины?
Теорема Пифагора является основой для калькулятора прямоугольного треугольника.

You need to know the following knowledge to solve this word math problem:

• geometry
• line
• planimetrics
• Pythagorean theorem
• circle
• The right triangle altitude theorem
• chord

Единицы физических величин:

• длина

Уровень задачи:

• практика для 14-летних
• старшая школа

 

Рекомендуем посмотреть это обучающее видео по этой математической задаче: видео1   видео2

• Две хорды
  В окружности радиусом 8,5 см построены две параллельные хорды, длины которых 9 см и 12 см. Найдите расстояние хорд в окружности.
• Решения 45511
  Две параллельные хорды окружности радиусом 6 см имеют длины 6 см и 10 см. Вычислите их расстояние друг от друга. Найдите оба решения.
• Определить 6415
  Определить расстояние между двумя параллельными хордами длиной 7 см и 11 см в окружности радиусом 7 см
• Две параллельные хорды
  В окружности диаметром 70 см проведены две параллельные хорды так, что центр окружности лежит между хордами. Вычислите расстояние между этими хордами, если длина одной из них 42 см, а второй 56 см.
• Две хорды
  Две параллельные хорды проведены по окружности радиусом r = 26 см. Одна хорда имеет длину t1 = 48 см, а вторая — длину t2 = 20 см, при этом центр лежит между ними. Вычислите расстояние между двумя хордами.
• Две параллельные хорды
  Две параллельные хорды окружности имеют одинаковую длину 6 см и находятся на расстоянии 8 см друг от друга. Вычислите радиус окружности.
• Центры хорд
  Круг диаметром 17 см, верхняя хорда /CD/ = 10,2 см и нижняя хорда /EF/ = 7,5 см. Середины хорд H, G таковы, что /EH/ = 1/2 /EF/ и /CG/ = 1/2 /CD/. Определите расстояние между G и H, если CD II EF (параллельно).
• Сад
  В саду два противоположных параллельных забора. Их расстояние составляет 33,1 м. Длина этих двух заборов составляет 75,5 м и 49 м..4 метра. Вычислите площадь этого сада.
• Рассчитать 65014
  Радиус окружности 5,5 см. Высота составляет 2,3 см, что является расстоянием по хорде. Как мы можем вычислить длину строки?
• Шестиугольник 5
  Расстояние между параллельными сторонами правильного шестиугольника составляет 61 см. Вычислите длину радиуса окружности, описанной в этом шестиугольнике.
• Отрезок треугольника
  В треугольнике ABC со стороной /AB/ = 24 см построен средний отрезок /DE/ = 18 см, параллельный стороне AB на расстоянии 1 см от AB. Вычислите высоту треугольника ABC относительно стороны AB.
• Концентрические окружности
  В окружности диаметром 13 см построена хорда длиной 1 см. Вычислите радиус концентрической окружности, касающейся этой хорды.

  No related posts.