Цифры верные в широком смысле: Верные цифры числа это | govorun-otveti.ru

Содержание

1.3. Запись приближенных значений величин. Верные знаки

Приближенные значения величин обычно записывают в виде десятичных дробей с конечным числом цифр.

Значащими цифрами в записи десятичной дроби называются все цифры, начиная с первой ненулевой слева. Например, в дроби 0,00102030004 значащими цифрами (подчеркнуты) являются все цифры, начиная с третьей после запятой.

Цифра в записи приближенного значения числовой величиныx называется верной в широком (строгом) смысле слова, если абсолютная погрешность приближенного значения не превышает единицы (половины единицы) разряда, в котором стоит эта цифра.

Все цифры верные в строгом смысле слова, очевидно, будут верными и в широком смысле. Рассмотрим несколько примеров.

Пример 1

Пусть ,= 0,000007899.Требуется найти верные цифры в записив широком и строгом смысле слова и подчеркнуть их одинарной и двойной линией соответственно.

Проверяя для каждой цифры в записитребование, сформулированное в определении верных цифр, получим, что цифры 0, 1, 2, 3 и 4 будут верными в широком и строгом смысле слова одновременно. Цифра 5 будет верной в широком смысле слова, но не будет верной в строгом смысле слова:.

Отметим, что в разрядах, в которых в записи стоят незначащие нули, в записи стоят верные цифры в широком смысле слова.

Пример 2

Пусть теперь ,=0,000007899. Требуется найти верные цифры в записив широком и строгом смысле слова.

Абсолютная погрешность нам неизвестна, а известна лишь ее оценка . Если оценка абсолютной погрешностиприближенного значения не превышает единицы (половины единицы) разряда, в котором стоит цифра (в записи ), то эта цифра, очевидно, также будет верной в широком (строгом) смысле слова . Проверяя для каждой цифры в записи

это требование, получим часть верных цифр: .

Но, поскольку мы проверяем заведомо более жесткое требование, чемэто, среди неподчеркнутых цифр также могут оказаться верные, если погрешность окажется намного меньше своей оценки.

Отметим, что в тех разрядах, в которых в записи стоят незначащие нули, в записистоят верные цифры в широком смысле слова.

Пример 3

Пусть, =0,123456789, =0,123457899. В записи точного и приближенного значений подчеркнуты совпадающие цифры. Непосредственная проверка для каждой цифры в записи требования, сформулированного в определении верных цифр, показывает, что все подчеркнутые (совпадающие) цифры являются верными в широком смысле слова, а неподчеркнутые – неверными.

Но такое совпадение верных цифр (в широком смысле слова) в записи с соответствующими цифрами в записииногда нарушается. Это связано с тем, что некоторые вещественные числа могут записываться в десятичной системе двумя различными способами, например 1=1,0000.

..=0,9999… .

Пример 4

Пусть =1,0000…,=0,9999. В записи точного и приближенного значений нет ни одной совпадающей цифры. Непосредственная проверка для каждой цифры в записитребования, сформулированного в определении верных цифр, показывает, что цифры в записиявляются верными в широком смысле слова. В то же время если записатьдругим способом=0,9999…, то все верные цифры в записибудут совпадать с соответствующими цифрами в записи точного значения.

Рассмотренные примеры позволяют сформулировать некоторые свойства верных цифр.

Свойства верных цифр:

В тех десятичных разрядах, где в записи (или) стоят незначащие нули, в записидолжны стоять верные цифры в широком смысле слова (докажите это самостоятельно).
Верные цифры в записи приближенного значения всегда совпадают с соответствующими цифрами в записи точного значения, если выбрать необходимую форму его записи в виде десятичной дроби

Установим теперь связь между величинами абсолютной и относительной погрешностей приближенного значения и количеством верных цифр в его записи. Пусть абсолютная погрешность приближенного значения равна. Определим количество верных цифр в широком смысле слова в записипосле запятой. Запишемв общем виде, указывая только разряды и не указывая конкретных цифр, и подчеркнем разряды, в которых будут располагаться верные цифры в широком смысле слова:

Итак, если абсолютная погрешность приближенного значения равна

, то после десятичной запятой в записи будетn верных знаков.

Пусть теперь относительная погрешность приближенного значения равна. Установим общее количество верных знаков в записи. Для этого представимв показательной форме:. Здесь– вещественное число, называемое мантиссой, ар – целое число, называемое порядком . А для того, чтобы такое представление дроби было однозначным потребуем, чтобы

. (1.3.1)

Точное значение величины также запишем в показательной форме, причем с тем же порядкомp: . Для мантиссы точного значенияне будет выполняться условие (1.3.1). Значенияиестественно считать точным и приближенным значениями мантиссы величиныx. Тогда ипредставляют собой абсолютную и относительную погрешности приближенного значения мантиссы. Соответствующие цифры в записиидолжны совпадать попарно.Поэтому и количество верных цифр в записи ибудет одинаковым. Далее определяем количество верных цифр в записи. Запишем относительную погрешность

Отсюда

и, согласно формуле (1.3.1), для абсолютной погрешности получается оценка

(1.3.2)

Запишем в общем виде

Из формулы (1.3.1) следует, что первая цифра после десятичной запятой в записи должна быть отлична от нуля. Поэтому все цифры в записипосле запятой являются значащими. Из формулы (1.3.2) следует, что в записи мантиссы должно быть не меньшеn и не больше (n+1) верной цифры после десятичной запятой, причем все они являются значащими. Итак, в мантиссе имеется или

n или (n+1) верная значащая цифра. Поэтому общее количество верных значащих цифр в записи также будет равно либоn, либо (n+1).

Таким образом, мы показали, что если относительная погрешность приближенного значения равна , то общее количество верных значащих цифр в записи равно либо n, либо (n+1).

Верные и значащие цифры. Запись приближенных значений — Студопедия.Нет

Цифра числа называется верной (в широком смысле), если ее абсолютная погрешность не превосходит единицы разряда, вкотором стоит эта цифра.

Пример. Х=6,328 Х=0,0007 X<0,001 следовательно цифра 8-верная

Пример: А). Пусть 0 = 2,91385, В числе а верны в широком смысле цифры 2, 9, 1.

Б) Возьмем в качестве приближения к числу = 3,141592… число = 3,142. Тогда (рис.) откуда следует, что в приближенном значении = 3,142 все цифры являются верными.

В) Вычислим на 8-разрядном МК частное точных чисел 3,2 и 2,3, получим ответ: 1,3913043. Ответ содержит ошибку, поскольку

Рис. 1. Приближение числа

разрядная сетка МК не вместила всех цифр результата и все разряды начиная с восьмого были опущены. (В том, что ответ неточен, легко убедиться, проверив деление умножением: 1,3913043 2,3 = 3,9999998.) Не зная истинного значения допущенной ошибки, вычислитель в подобной ситуации всегда может быть уверен, что ее величина не превышает единицы самого младшего из изображенных на индикаторе разряда результата. Следовательно, в полученном результате все цифры верны.

Первая отброшенная (неверная) цифра часто называется сомнительной.

Говорят, что приближенное данное записано правильно, если в его записи все цифры верные. Если число записано правильно, то по одной только его записи в виде десятичной дроби можно судить о точности этого числа. Пусть, например, записано приближенное число

а = 16,784, в котором все цифры верны.

Из того, что верна последняя цифра 4, которая стоит в разряде тысячных, следует, что абсолютная погрешность значения а не превышает 0,001. Это значит, что можно принять т.е. а = 16,784±0,001.

Очевидно, что правильная запись приближенных данных не только допускает, но и обязывает выписывать нули в последних разрядах, если эти нули являются выражением верных цифр. Например, в записи = 109,070 нуль в конце означает, что цифра в разряде тысячных верна и она равна нулю. Предельной абсолютной погрешностью значения , как следует из записи, можно считать Для сравнения можно заметить, что значение с = 109,07 является менее точным, так как из его записи приходится принять, что

Значащими цифрами в записи числа называются все цифры в его десятичном изображении, отличные от нуля, и нули, если они расположены между значащими цифрами или стоят в конце для выражения верных знаков.

Пример а) 0,2409 — четыре значащие цифры; б) 24,09 — четыре значащие цифры; в) 100,700 — шесть значащих цифр.

Выдача числовых значений в ЭВМ, как правило, устроена таким образом, что нули в конце записи числа, даже если они верные, не сообщаются. Это означает, что если, например, ЭВМ показывает результат 247,064 и в то же время известно, что в этом результате верными должны быть восемь значащих цифр, то полученный ответ следует дополнить нулями: 247,06400.

В процессе вычислений часто происходит округление чисел, т.е. замена чисел их значениями с меньшим количеством значащих цифр. При округлении возникает погрешность, называемая погрешностью округления. Пусть

х -данное число, а х₁ — результат округления. Погрешность округления определяется как модуль разности прежнего и нового значений числа:

(5)

В отдельных случаях вместо ∆_окр приходится использовать его верхнюю оценку.

Задание 1.Округляя точные числа до трех значащих цифр, определить абсолютную и относительную погрешности полученных приближенных чисел.

Дано:

Найти:

Решение:

— приближенное значение числа A

Абсолютная погрешность:

Относительная погрешность:

Ответ: ;

Задание 2.Определить абсолютную погрешность приближенных чисел aпо их относительной погрешностиd.

Дано: a = 4,872; d = 5%.

Найти:

Решение:

Абсолютная погрешность:

Ответ:

Задание 3. Решить задачу.

При измерении длины с точностью до 5 м получено км, а при определении другой длины с точностью до 0.5 см, получено метров. Какое измерение по своему качеству лучше?

Дано: Км, М, М, См

Сравнить: и

Решение: Итак, по 1-му измерению, результат Км = М с точностью до М
( — абсолютная погрешность величины ).

Тогда относительная погрешность: %

По 2-му измерению, результат Км с точностью до См = М ( — абсолютная погрешность величины ).

Тогда относительная погрешность: %

Так как , то измерение можно считать по качеству лучше, чем .

Ответ: измерение по качеству лучше, чем .

Задание 4. а) Определить количество верных знаков в числе , если известна его предельная абсолютная погрешность

Дано:

Найти:

Решение:

По определению, n первые значащие цифры являются верными в узком смысле, если абсолютная погрешность этого числа не превышает половины единицы разряда младшей цифры, считая слева направо.

Абсолютная погрешность: , поэтому значащие цифры 8 и 4 числа 0,00842 верны в узком смысле.

Ответ: число X имеет две верных цифры в узком смысле (8 и 4), то есть

б) Определить количество верных знаков в числе , если известна его предельная относительная погрешность .

Дано: %

Найти:

Решение:

Предельная абсолютная погрешность:

Только первая значащая цифра 1 числа A верна в узком смысле.

Ответ: число A имеет одну верную цифру в узком смысле (1), то есть

Дано: %

Найти:

Решение:

Предельная абсолютная погрешность:

Только первая значащая цифра 1 числа A верна в узком смысле.

Ответ: число A имеет одну верную цифру в узком смысле (1), то есть

Задание 5.Найти предельные относительные погрешности, допускаемые при взятии вместо чисел 3.1, 3.14, 3.1416:

а) считая, что у них все записанные знаки являются верными;

б) зная, что

Провести сравнения погрешностей и сделать необходимые выводы.

Дано: , ,

Найти:

Решение:

А) :

Если считать, что все записанные знаки являются верными в узком смысле, то абсолютная погрешность:

Предельная абсолютная погрешность:

Тогда предельная относительная погрешность:

Если считать, что все записанные знаки являются верными в узком смысле, то абсолютная погрешность:

Предельная абсолютная погрешность:

Тогда предельная относительная погрешность:

Если считать, что все записанные знаки являются верными в узком смысле, то абсолютная погрешность:

Предельная абсолютная погрешность:

Тогда предельная относительная погрешность:

б) Пусть (прервем запись числа на 7-м знаке после запятой и считаем полученное число точным значением числа ).

Тогда абсолютная погрешность первого представления числа : .

Относительная погрешность: %

Абсолютная погрешность второго представления числа : .

Относительная погрешность: %

Абсолютная погрешность третьего представления числа : %.

Относительная погрешность: %

Выводы:

1) Можно заметить, что , то есть ;

, то есть ;

, то есть

Иными словами, для трех чисел их «истинная» относительная погрешность ограничена предельной относительной погрешностью, определенной из условия верности знаков чисел. Причем, для каждого числа две оценки отличаются меньше, чем на порядок. Значит, предположение о верности всех знаков чисел Обосновано.

2) Сравнение относительных погрешностей чисел :

показывает,

Что числа Перечислены

В порядке увеличения точности представления числа ,

То есть точнее , точнее .

Ответ: а)

б)

Задание 6.Найти сумму приближенных чисел , , считая в них все знаки верными, т. е. что абсолютная погрешность каждого слагаемого не превосходит половины единицы младшего разряда этого слагаемого. Определить абсолютную и относительную погрешности суммы.

Дано: , ,

Найти:

Решение:

1) Считаем, что в числах , , все знаки верны в узком смысле, то есть

Число с наибольшей абсолютной погрешностью .

2) Остальные числа округлим, сохраняя один запасный десятичный знак по сравнению с ранее выделенным наименее точным слагаемым :

, абсолютная погрешность округления

3) Сложим все эти числа, учитывая все сохраненные знаки:

4) Полученный результат округлим на один знак (формально):

, абсолютная погрешность округления

5) Полную абсолютную погрешность суммы будем складывать из трех компонентов:

A) суммы предельных абсолютных погрешностей исходных чисел;

B) абсолютной величины суммы ошибок округления слагаемых;

C) заключительной погрешности округления результата.

— абсолютная погрешность суммы.

% — относительная погрешность суммы.

Ответ: ; %.

Задание 7.Найти предельную абсолютную и относительную погрешности при вычислении объема прямого кругового цилиндра, если значения его высоты и радиуса основания имеют все верные знаки.

Дано: ,

Найти:

Решение:

Примем

1) Так как в числах и все числа верны, то их абсолютные погрешности:

Число с наибольшей абсолютной погрешностью .

Число R округлим, сохраняя один запасный десятичный знак по сравнению с ранее выделенным наименее точным слагаемым :

, абсолютная погрешность округления (округления не требуется)

2) перемножим числа, учитывая все сохраненные знаки:

3) Полученный результат округляем, сохраняя столько значащих цифр, сколько верных цифр имеется в числе H, то есть 2 значащих цифры:

;

Абсолютная погрешность округления

4) Полную абсолютную погрешность произведения будем складывать из двух слагаемых:

A) предельной абсолютной погрешности произведения до его округления;

B) заключительной погрешности округления произведения.

Абсолютную погрешность произведения до округления вычислим на основе предварительно найденной относительной погрешности произведения округленных сомножителей:

Полная абсолютная погрешность

Теперь перейдем к искомому объему.

(Здесь полученный результат округляем до трех значащих цифр).

— предельная абсолютная погрешность объема.

% — предельная относительная погрешность объема.

Ответ: , , %

Задание 8.Привести пример потери точности при вычитании двух близких чисел.

Решение:

Пусть и — два близких числа; примем, что у них одинаковое число знаков после запятой.

Считаем, что все знаки в числах и верны в узком смысле. Тогда абсолютные погрешности:

Относительные погрешности:

Так как , то

Абсолютная погрешность результата:

Относительная погрешность результата: %

При вычитании двух близких чисел и относительная погрешность возросла на 3 порядка!

Значащие и верные цифры.

Правило округления

Определение численных методов. Погрешности.

Прикладная математика – математическая наука, целью которой является решение прикладных задач: изучение явлений природы, получение их математического описания (математической модели) и его исследование.

Примеры мат.моделей: модель абсолютно твердого тела, модель звездного неба, модель человеческого организма, модели экономических, химических задач и т. д.

Каждая математическая модель содержит некоторые допущения (чем-то пренебрегают).

Основные требования, предъявляемые математическим моделям: 1) адекватность рассматриваемому явлению, 2) сравнительная простота и доступность, 3) необходимость правильной оценки области применения.

Определение. Создание математической модели процесса или явления называется математическим моделированием.

Для решения математических задач используются группы методов: аналитические, графические, численные.

1) Аналитические методы.

Особенность методов состоит в использовании детерминированной информации, строгой алгоритмизации действий и однозначности установленной функциональной зависимости. Для решения задач используются символьные вычисления — это преобразования и работа с математическими равенствами и формулами как с последовательностью символов. Разработкой и реализацией аналитических методов решения математических задач на компьютере занимается компьютерная алгебра, в которой предполагается, что исходные данные, как и результаты решения, сформулированы в аналитическом (символьном) виде. Аналитические решения чаще удаётся получить для наиболее грубых (простых) моделей, реже — для более точных. Аналитические методы основываются на фундаментальной теории математического анализа, функционального анализа, интегральных и дифференциальных исчислений, разработанной группой выдающихся отечественных ученых — А.Н. Колмогоровым, С.В. Фоминым, Л. В. Канторовичем и др.

Недостаток – не всегда можно получить точное решение: многие решения не всегда выражаются в известных функциях или точных методов нахождения решений попросту не существует.

2) Графические методы.

Графические методы считаются весьма важным и эффективным орудием современной науки, они надежно вошли в методику научных исследований.

Недостаток – невысокая точность полученного решения, невозможность построить графики.

3) Численные методы.

Численные методы – раздел прикладной математики.

Определение. Численные (вычислительные) методы — методы решения математических задач в численном виде, иначе, это методы решения задач, сводящиеся к арифметическим и некоторым логическим действиям над числами, при этом результат также получается в виде числовых значений.

Численные методы появились в связи с тем, что искомые решения не всегда выражаются в привычных для нас элементарных или других известных функциях, то есть аналитическим и численным методами отыскать их невозможно. С появлением численных методов появилось решение, но его отыскание было затруднено громоздкими арифметическими операциями над числами, что привело к созданию ЭВМ.

За математическими выражениями в численных методах стоят приближённые численные значения, так как исходные данные в задаче, так и её решения представляются в виде числа или набора чисел. Результат вычислений — также приближенное число. Существуют методы, при помощи которых можно получить и точное решение, например, метод Гаусса для решения систем линейных алгебраических уравнений.

Определение. Численный метод называется сходящимся, если получаемое численное решение задачи очень близко к истинному решению.

Существует достаточно большое количество численных методов, обладающих своими достоинствами и недостатками, которые зависят, прежде всего, от свойств функций, значение которых ищется. Одним из сравнительных показателей качества метода является количество значений функции, которое нужно вычислить для решения задачи с заданной погрешностью. Чем это число меньше, тем при прочих равных условиях эффективнее метод.

Численные методы позволяют получить частные численные решения многих задач, даже сложных математических моделей. К тому же при решении большинства практических задач точное решение не всегда является необходимым.

Как было сказано выше – результатом вычислений с помощью численных методов является приближенные числа.

Определение. Математические действия над приближенными числами называются приближенными вычислениями.

Поэтому главным вопросом является вопрос о погрешности вычислений.

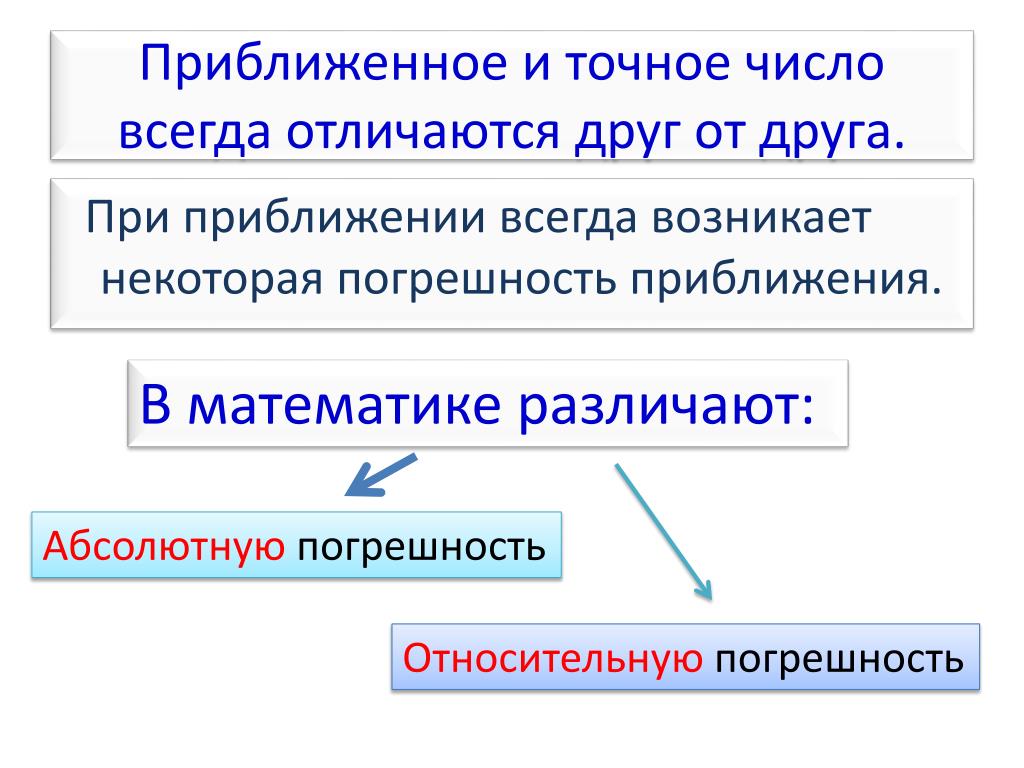
Определение.Погрешность – отклонение точного значения от приближенного.

Источники погрешности – 1)несоответствие математической модели изучаемому явлению, 2) погрешность исходных данных, 3) погрешность метода решения, 4) ошибки округления исходных данных.

Классификация погрешностей – а) неустранимая (источники 1 и 2), b) погрешность метода (источник 3), c) погрешность округления (источник 4)

Пусть а – точное неизвестное числовое значение величины, а^*известное приближенное числовое значение этой величины (приближенное число).

Определение. Число называется абсолютной погрешностью округления.

Абсолютная погрешность не полностью характеризует точность измерения. Качество измерения более характеризуется относительной погрешностью.

Определение. Относительной погрешностью называется .

Относительная погрешность безразмерна, часто выражается в процентах.

Любое приближенное число а^* может быть представлено в виде:

, где m – величина разряда или разряд, а — цифра числа. Например, 38, 57 =

Определяющим точность вычисления является не число десятичных знаков, а число значащих цифр результата.

Определение. Значащими цифрами числа называются все цифры в его записи, начиная с первой ненулевой слева.

Например, 25, 047 – 5 значащих цифр, 0,00250 – 3 значащие цифры.

Определение. Значащая цифра приближенного числа а^*называется верной в широком смысле, если абсолютная погрешность не превосходит единицы десятичного разряда, в котором стоит : , и верной в узком смысле, если . n – число верных цифр в числе. Остальные цифры называются сомнительными.

Пример. Сколько верных цифр содержит число ?

Решение. m = 1, так как

В широком смысле:

, с другой стороны , отсюда 2 – n = -2, то есть n = 4. Верные в широком смысле цифры – 8, 5, 2, 6.

В узком смысле:

, с другой стороны , отсюда 2 – n = -1, то есть n = 3. Верные в широком смысле цифры – 8, 5, 2.

Числа 23,56 и 23,5600 как приближенные различны.

Если число записано без указания его абсолютной погрешности, то выписаны только верные цифры.

Употребляя запись надо помнить правило: выписывать с одной или двумя значащими цифрами, а младший разряд в а^* должен соответствовать младшему разряду в .

— правильно, и — неправильно.

Определение. Число цифр после запятой от первой цифры до последней верной цифры называется числом верных цифр после запятой.

В основе процессов округления числа лежит идея минимальной разности числа а и его округленного значения а^*.

Правило округления (правило четной цифры): если в старшем из отбрасываемых разрядов стоит цифра меньше 5, то содержимое сохраняемых разрядов числа не изменяется. В противном случае в младший сохраняемый разряд добавляется 1 с тем же знаком, что и у самого числа. При этом, если первая слева из отброшенных цифр равна 5, и за ней не следуют отличные от нуля цифры, то последняя оставшаяся цифра усиливается, если она нечетная, и остается без изменений, если она четная.

, , , , .

Абсолютная погрешность округления не превосходит половины единицы разряда, определяемого последней оставленной значащей цифрой.

Дата добавления: 2016-06-15; просмотров: 16557; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Лекции по математике для студентов 1 курса СПО

Лекция 1. 1

Дествительные числа.

I. Множество натуральных чисел – это множество чисел, которыми пользуются при счете предметов.

Всякому натуральному числу соответствует точка на числовой прямой.

Задание: Назовите самое маленькое натуральное число. Существует ли самое большое натуральное число?

II. Множество целых чисел – это множество, состоящее из натуральных чисел, им противоположных чисел и нуля.

Всякому целому числу соответствует точка на числовой прямой.

Задания:

1. Существуют ли самое маленькое и самое большое целое число?

2. Верно ли утверждение:

a. любое натуральное число является целым;

b. любое целое число является натуральным?

III. Множество рациональных чисел – это множество несократимых дробей вида

Всякому рациональному числу соответствует точка на числовой прямой.

Свойство рациональных чисел: Всякое рациональное число можно представить в виде бесконечной периодической десятичной дроби.

Обратно: всякая бесконечная периодическая десятичная дробь является рациональным числом.

Правило перевода периодических дробей в обыкновенные:

Чисто периодические дроби

Смешанные периодические дроби

Чистая периодическая дробь равна обыкновенной дроби, в числителе которой записан период, а в знаменателе – столько девяток, сколько цифр периоде.

Пример: .

Смешанная периодическая дробь равна обыкновенной дроби, в числителе которой записана разность между числом до второго периода и числом до первого периода, а в знаменателе – число, составленное из стольких девяток, сколько цифр в периоде и стольких нулей, сколько цифр между запятой и периодом.

Пример: .

для чисто периодической дроби: в числителе пишется число, стоящее в периоде, а в знаменателе столько «9», сколько цифр в периоде, целая часть остается без изменения.

для смешанной периодической дроби: в числителе разность между числом, стоящим после запятой, и числом, стоящим после запятой до периода, а в знаменателе столько «9», сколько цифр в периоде, со столькими «0», сколько цифр после запятой до периода

Задания:

1. Докажите, что числа являются рациональными и отметьте эти числа на числовой прямой.

2. Верно ли утверждение:

а) всякое натуральное число является рациональным;

б) всякое целое число является рациональным;

в) верно ли утверждение: Всякое рациональное число является целым?

3. Представьте рациональные числа в виде бесконечных периодических десятичных дробей.

4. Переведите периодические дроби в обыкновенные. Проверьте результат перевода.

IV. Множество иррациональных чисел – это множество чисел, которые нельзя представить в виде несократимых дробей

Всякому иррациональному числу соответствует точка на числовой прямой.

Свойство иррациональных чисел: Всякое иррациональное число представимо в виде бесконечной десятичной непериодической дроби.

Пример: π ≈ 3,1415926535897932384626433832795…;

…

Задание: Докажите, что числа , , являются иррациональными.

V. Множество действительных (вещественных) чисел – это объединение множеств рациональных и иррациональных чисел.

Каждому действительному числу соответствует точка на числовой прямой.

Обратно: каждой точке на числовой прямой соответствует определенное действительное число.

Следовательно, между множеством действительных чисел и множеством точек на числовой прямой существует взаимно-однозначное соответствие.

Задания:

1. Верно ли утверждение:

а) всякое целое число является действительным;

б) всякое рациональное число является вещественным;

в) всякое иррациональное число является вещественным;

г) всякое действительное число является рациональным;

д) всякое вещественное число является целым?

2. Даны числа: .
Выпишите: а) натуральные числа; б) целые числа; в) рациональные числа; г) иррациональные числа.

Лекция 1.2 Абсолютная погрешность приближенного значения числа.

Модуль числа – это само число, если оно неотрицательно, и число, ему противоположное, если оно отрицательно.

Примеры: .

С геометрической точки зрения модуль числа – это расстояние от этого числа до начала отсчета.

Вывод: модуль числа отрицательным быть не может!

Приближенные вычисления

Приближенное число есть такое число, которое отличается от точного на погрешность (ошибку), допущенную в соответствии с условиями данной задачи, и заменяет точное число в расчетной формуле.

Обозначим буквой a₀ точное число, а буквой a его приближенное значение, тогда a₀ ≈ a.

Абсолютная погрешность приближенного значения числа – это модуль разности между точным и приближенным значением этого числа, т.е. .

Так как точное число чаще всего неизвестно, то можно указать положительное число ∆а, удовлетворяющее неравенству .

Число ∆а называется границей абсолютной погрешности.

1. Даны приближенные значения числа х = 2/3; а₁= 0,6; а₂ = 0,66;

а₃ = 0,67. Какое из этих трех приближений является лучшим?

;

а₃ = 0,67 – лучшее приближение

2. Длина детали х (см) заключена в границах 33 ≤ х ≤ 34. Найти границу абсолютной погрешности измерения детали.

○ Примем за приближенное значение длины детали среднее арифметическое границ:

а = (33 + 34)/2 = 33,5 (см). Тогда граница абсолютной погрешности приближенного значения длины детали не превзойдет 0,5 (см).

Величину Δа можно найти и как полуразность верхней и нижней границ, т. е. Δа = (34 — 33)/2 = 0,5 (см). Длина детали х, найденная с точностью до Δа = 0,5 см, заключена между приближенными значениями числа х:

33,5 — 0,5 ≤ x ≤ 33,5 + 0,5; x = 33,5 ± 0,5 (см).

3. Найдите абсолютную погрешность округления до единиц следующих чисел:

1) 0,8; 2) 7,6; 3) 19,3; 4) 563,58.

4. Граница абсолютной погрешности приближенного значения 386 числа х равна 0,5. Укажите границы, в которых заключено число х.

5. Найдите границу абсолютной погрешности измерений, полученных в виде неравенства 37 < x < 38.

5. Амперметр дает точность ±0,02 А. При измерении силы тока получили 10,63 А. Укажите границы этого числа.

6. Атомная масса водорода — 1,0082 ± 0,0005, а меди — 63,44 ± 0,15. Укажите границы приближенных значений этих чисел.

8. Площадь квадрата равна 24,5 ± 0,3 (см²). Найдите границы измерения площади квадрата.

Задание:

1. Записать числа в виде двойного неравенства:

а) а = 347,50; ∆а = 0,0047;

б) а_{0 =}7,269 ± 0,0004.

2. Докажите, что число 1,7 является приближенным значением числа 1, 739 с точностью до 0,05.

3. Точное значение числа х неизвестно, а известно лишь, что
0,68 < х< 0,72. Найдите точность приближения h.

4. Вычислите приближенное значение величины х, равное среднему арифметическому границ, и укажите точность этого приближения, если: а) 3,6 ≤ х ≤ 4,2; б) 0,12 ≤ х ≤ 0,14.

Лекция 1.3 Верные цифры числа. Запись приближенного значения числа.

Верные и значащие цифры числа.

Цифра т приближенного числа а называется верной в широком смысле, если граница абсолютной погрешности числа а не превосходит единицы того разряда, в котором записывается цифра т.

Цифра т приближенного числа а называется верной в строгом смысле, если граница абсолютной погрешности числа а не превосходит половины единицы того разряда, в котором записана цифра т.

В числах, полученных в результате измерений или вычислений и используемых при расчетах в качестве исходных данных, а также в десятичной записи приближенного значения числа, все цифры

должны быть верными.

Наиболее употребительна такая запись приближенного числа (например, в математических таблицах), при которой цифры верны в строгом смысле.

Граница абсолютной погрешности Δа находится непосредственно

по записи приближенного значения а числа х.

Цифры в записи приближенного числа, о которых не известно, являются ли они верными, называются сомнительными.

Значащими цифрами приближенного числа называются все его верные цифры, кроме нулей, стоящих перед первой цифрой (слева направо), отличной от нуля.

Округление чисел. При округлении числа а его заменяют числом a₁

с меньшим количеством значащих цифр. Абсолютная величина разности |а – а₁| называется погрешностью округления

При округлении числа до т значащих цифр отбрасывают все цифры, стоящие правее т-й значащей цифры, или при сохранении разрядов заменяют их нулями. При этом если первая слева из отброшенных

цифр больше или равна 5, то последнюю оставшуюся цифру увеличивают на единицу.

При применении этого правила погрешность округления не превосходит половины единицы десятичного разряда, определяемого последней оставленной значащей цифрой.

Округление приближенных значений чисел с сохранением в записи только верных цифр производится до разряда, в котором записана первая справа верная цифра.

9. Найти границу абсолютной погрешности приближенного значения 0,1968 числа х, все цифры которого верны в строгом смысле.

○ Граница абсолютной погрешности этого числа равна 0,00005, т. е. половине

единицы последнего разряда, сохраняемого в записи.●

10. Указать верные цифры (в широком смысле) следующих чисел:

1) 3,73 ± 0,056; 2) 3,627 ± 0,0008; 3) 4,732 ± 0,06; 4) 561 274 ± 500.

○ 1) Граница погрешности Δа = 0,056 не превосходит единицы разряда десятых

(неравенство 0,056 < 0,1 верное). Следовательно, верными являются цифры 3 и 7.

2) Так как Δа = 0,0008 < 0,001, то все цифры приближенного числа 3,627 верны.

3) Поскольку Δа = 0,06 < 0,1, верными являются цифры 4 и 7.

4) Так как Δа = 500 < 1000, то верны цифры 5, 6 и 1.●

11. За приближенное значение числа 26,7 взято число 27. Являются

ли цифры числа 27 верными?

○ Так как |26,7 — 27| = 0,3 < 1, то цифры 2 и 7 — верные в строгом смысле.●

12. Приближенное значение числа 9,587 ± 0,03 округлить до первого справа верного разряда.

○ Первая справа верная цифра находится в разряде десятых, поэтому число 9,587

округляем до десятых: 9,587 ≈ 9,6. Новое значение границы погрешности Δа равно

сумме границы погрешности 0,03 и погрешности округления 0,013, т. е. Δа = 0,03 +

+ 0,013 = 0,043 < 0,1. Число 9,6 является приближенным значением числа 9,587 с точ-

ностью до 0,1. Цифры 9 и 6 верные.●

13. Укажите верные цифры (в широком смысле) следующих чисел:

1) 0,028 ± 0,004; 2) 0,463 ± 0,0008; 3) 0,078 ± 0,002; 4) 12,78 ± 0,0005;

5) 375 ± 20.

14. Назовите верные цифры числа π ≈ 3,14, считая π ≈ 3,1416.

15. За приближенное значение числа 999,82 взято число 1000. Укажите верные цифры числа 1000.

16. Сохраните только верные цифры в записи следующих приближенных значений чисел:

1) 280 ± 10; 2) 8900 ± 100; 3) 530 000 ± 100; 4) 5740 ± 10.

17. Округлите до первого справа верного разряда приближенные значения данных чисел:

1) 0,3281 ± 0,05; 2) 2,0637 ± 0,0025; 3) 14,0367 ± 0,8;

4) 24,734 ± 0,06.

18. Округлите приближенные значения данных чисел до первого справа верного разряда и запишите эти числа в стандартном виде:

1) 12 378 ± 25; 2) 15 763 ± 50; 3) 8724 ± 25; 4) 812 ± 6.

19. Укажите границу погрешности приближения, если в записи приближенных значений данных чисел все цифры верные (в широком смысле): 1) x ≈ 0,56; 2) х ≈ 84,3; 3) х ≈ 5,10; 4) х ≈ 4,100.

Лекция 1.4 Относительная погрешность приближенного значения числа

Относительная погрешность приближенного значения числа – это отношение абсолютной погрешности этого числа к самому числу, т.е. или в процентах .

Так как в большинстве случаев истинное значение величины a₀ неизвестно, то на практике относительную погрешность оценивают некоторым числом , большим этой погрешности.

В качестве можно взять отношение или любое число, большее этого отношения, но достаточно близкое к нему, т. е. .

Число называется границей относительной погрешности.

Качество измерений или вычислений тем лучше, чем меньше граница относительной погрешности.

Зависимость относительной погрешности от числа значащих цифр

иллюстрируется табл. 1.1

число	Наименьшее число	Наибольшее число	Граница абсолютной погрешности	Относительная погрешность наибольшего числа	Относительная погрешность наименьшего числа
Однозначное	1	9	0,5	0,056=5,6%	0,5=50%
Двузначное	10	99	0,5	0,005=0,5%	0,05=5%
Трехзначное	100	999	0,5	0,0005=0,05%	0,005=0,5%
Четырехзначное	1000	9999	0,5	0,00005=0,005%	0,0005=0,05%

Из табл. 1.1 ясно, что три верные значащие цифры обеспечивают точность результата (относительную погрешность) от 0,05 до 0,5 %. В технических и других расчетах, не требующих особо высокой точности, достаточно бывает обеспечить точность результата порядка десятых долей процента. Поэтому в технических расчетах принято выполнять вычисления с тремя значащими цифрами.

Пример: Пусть а₀ = 42,1 ± 0,2. Вычислить в процентах границу относительной погрешности приближенного значения величины а.

Решение: Имеем а = 42,1; h = 0,2. Следовательно, .

Задания:

1. Округлите число 123 до десятков и найдите абсолютную и относительную погрешность округления.

2. Округлите число 8, 2478 до сотых и найдите абсолютную и относительную погрешность округления.

3. Найдите относительную погрешность приближенных чисел:

а) 35,148 ± 0,00074;

б) 0,012 ± 0,001;

в) 17,2 ± 0,25.

4. Установите, какое равенство точнее: .

5. Найдите верхнюю и нижнюю границы, если приближенное значение числа и относительная погрешность в процентах соответственно равны:

а) 18 и 1%;

б) 0,6 и 15%.

Лекция 1.5

Действия над приближенными значениями числа

Сложение приближенных значений чисел

Граница абсолютной погрешности суммы приближенных значений

чисел равна сумме границ абсолютных погрешностей этих чисел:

Δ(a + b) = Δa + Δb, (2.1)

где а и b — приближенные значения чисел; Δa и Δb — границы абсо-

лютных погрешностей соответствующих приближений.

Граница относительной погрешности суммы вычисляется по фор-

муле

( )

a b

+ a b

_ = _ +

. (2. 2)

1. Найти сумму S приближенных значений чисел 6,8 ± 0,05; 4,3 ± 0,05

и 3,575 ± 0,0005.

○ Имеем

S = 6,8 + 4,3 + 3,575 = 14,675; ΔS = 0,05 + 0,05 + 0,0005 = 0,1005.

Граница абсолютной погрешности заключена в пределах 0,05 < 0,1005 < 0,5.

В приближенном значении суммы верными являются лишь две цифры (в разрядах

десятков и единиц). Полученный результат округлим до единиц: S = 14,675 ≈ 15.●

2. Найдите сумму приближенных значений чисел 6,54 ± 0,005;

16,022 ± 0,0005 и 1,9646 ± 0,00005.

3. Вычислите сумму a = 5 + 11, взяв приближенные значения кор-

ней с точностью до 0,001. Найдите а, Δа и εa.

4. Вычислите сумму a = 3 + 5 + 7 с четырьмя значащими циф-

рами. Найдите а, Δa и εa.

5. Электрическая цепь состоит из трех последовательно соединен-

ных проводников с сопротивлениями r1 = 4,8 ± 0,05 (Ом), r2 = 6,25 ±

± 0,005 (Ом) и r3 = 7,725 ± 0,0005 (Ом). Вычислите общее сопротивление

цепи по формуле R = r₁ + r₂ + r₃. Найдите R, ΔR и ε_R.

Вычитание приближенных значений чисел

Граница абсолютной погрешности разности двух приближенных

значений чисел равна сумме границ их абсолютных погрешностей:

Δ(a — b) = Δa + Δb. (2.3)

Граница относительной погрешности разности вычисляется по фор-

муле

a b

− a b

_ = _ + _

−

. (2.4)

6. Вычислить разность двух приближенных значений чисел а = 5,863 ±

± 0,0005 и b = 2,746 ± 0,0005. Найти Δ(а — b) и εa–b.

○ По формуле (2.3) вычисляем границу абсолютной погрешности разности а — b:

Δ(а — b) = 0,0005 + 0,0005 = 0,001.

В приближенном значении разности цифра в разряде тысячных не может быть

верной, так как Δ(а — b) > 0,0005. Итак, а — b = 3,117 ≈ 3,12. Абсолютная погрешность

разности 0,001. В приближенном числе 3,12 все цифры верные.

По формуле (2.4) находим относительную погрешность разности:

εа–b = 0,001/3,12 = 0,00032 ≈ 0,03 %.●

7. Вычислите разность чисел 8,72 и 2,6532, границы абсолютной

погрешности которых соответственно равны 0,005 и 0,00005.

8. Вычислите разность a = 13 − 5 с четырьмя значащимицифрами.

Найдите Δa и εa.

Лекция 1.6. Комплексные числа

Определение 1. Число, квадрат которого равен -1, называется мнимой единицей и обозначается буквой i. i² = -1.

Следовательно, .

Определение 2. Числа вида a + bi, где a и b – действительные числа, i – мнимая единица, называются комплексными.

Данная форма записи комплексного числа называется алгебраической.

Число а является действительной частью комплексного числа, bi – его мнимой частью, число b называется коэффициентом при мнимой части.

Если b = 0, то комплексное число a + bi = a + 0i = a, то есть является действительным числом.

Вывод: действительные числа являются частным случаем комплексных чисел.

Если а = 0, то комплексное число a + bi = bi и называется чисто мнимым.

Сложение, вычитание и умножение комплексных чисел выполняется по правилам соответствующих действий над многочленами.

Задания:

1. Выполните сложение, вычитание и умножение комплексных чисел:

а) z₁ = 3+5i и z₂ = 7–2i;

б) z₁ = -2+3i и z₂ = 7–4i;

в) z₁ = 3–2i и z₂ = 7–i;

г) z₁ = 1–i и z₂ = 1+i;

д) z₁ = 3–9i и z₂ = 5+2i.

Определение 3. Два комплексных числа называются сопряженными, если они отличаются друг от друга только знаками перед мнимой частью (a + bi и a – bi).

Произведение двух сопряженных комплексных чисел всегда равно действительному числу (проверьте!).

Для деления одного комплексного числа на другое необходимо умножить делимое и делитель на комплексное число, сопряженное делителю.

Примеры действий с комплексными числами

Даны два комплексных числа z₁ = 3+5i и z₂ = 7–2i. Выполнить их сложение, вычитание, умножение и деление.

I. Сложение

Раскрываем скобки, применяем переместительный и сочетательный законы сложения и правило приведения подобных слагаемых.

II. Вычитание

Применяем те же правила, что и при сложении, но не забываем, что если перед раскрываемой скобкой стоит знак «минус», то у всех слагаемых в скобке знак меняется на противоположный.

III. Умножение

Используем правило умножения многочленов: каждое слагаемое в первой скобке умножаем на каждое слагаемое во второй скобке.

Не забываем, что i² = -1.

IV. Деление

Число, сопряженное делителю , – это число 7+2i. Домножаем числитель и знаменатель дроби на число 7+2i и выполняем необходимые преобразования: в числителе перемножаем два комплексных числа по предыдущему правилу, а в знаменателе используем разность квадратов .

Задания:

1. Выполните деление комплексных чисел:

а) ;

б) ;

в) ;

г) .

2. Выполните указанные действия с комплексными числами:

а) ;

б) ;

в) ;

г) ;

д) .

3. Решите квадратные уравнения с отрицательными дискриминантами:

а)

б)

в)

Вычислительные методы

Лабораторная работа №1

Методы оценки погрешностей

I. Описание работы

Тема: Методы оценки погрешностей приближенных величин.

Задание 1. Округляя точные числа до трех значащих цифр, определить абсолютную и относительную погрешности полученных приближенных чисел.

Дано:

Найти:

Решение:

— приближенное значение числа A

Абсолютная погрешность:

Относительная погрешность:

Ответ: ;

Задание 2. Определить абсолютную погрешность приближенных чисел по их относительной погрешности .

Дано:

Найти:

Решение:

Абсолютная погрешность:

Ответ:

Задание 3. Решить задачу.

Дано: Км, М, М, См

Сравнить: и

Решение: Итак, по 1-му измерению, результат Км = М с точностью до М ( — абсолютная погрешность величины ).

Тогда относительная погрешность: %

По 2-му измерению, результат Км с точностью до См =М ( — абсолютная погрешность величины ).

Тогда относительная погрешность: %

Так как , то измерение можно считать по качеству лучше, чем .

Ответ: измерение по качеству лучше, чем .

Дано:

Найти:

Решение:

Абсолютная погрешность: , поэтому значащие цифры 8 и 4 числа 0,00842 верны в узком смысле.

Ответ: число X имеет две верных цифры в узком смысле (8 и 4), то есть

Б) Определить количество верных знаков в числе , если известна его предельная относительная погрешность .

Дано: %

Найти:

Решение:

Предельная абсолютная погрешность:

Только первая значащая цифра 1 числа A верна в узком смысле.

Ответ: число A имеет одну верную цифру в узком смысле (1), то есть

Задание 5. Найти предельные относительные погрешности, допускаемые при взятии вместо чисел 3.1, 3.14, 3.1416:

А) считая, что у них все записанные знаки являются верными;

Б) зная, что

Провести сравнения погрешностей и сделать необходимые выводы.

Дано: , ,

Найти:

Решение:

А) :

Если считать, что все записанные знаки являются верными в узком смысле, то абсолютная погрешность:

Предельная абсолютная погрешность:

Тогда предельная относительная погрешность:

Если считать, что все записанные знаки являются верными в узком смысле, то абсолютная погрешность:

Предельная абсолютная погрешность:

Тогда предельная относительная погрешность:

Если считать, что все записанные знаки являются верными в узком смысле, то абсолютная погрешность:

Предельная абсолютная погрешность:

Тогда предельная относительная погрешность:

Б) Пусть (прервем запись числа на 7-м знаке после запятой и считаем полученное число точным значением числа ).

Тогда абсолютная погрешность первого представления числа : .

Относительная погрешность: %

Абсолютная погрешность второго представления числа : .

Относительная погрешность: %

Абсолютная погрешность третьего представления числа : %.

Относительная погрешность: %

Выводы:

1) Можно заметить, что , то есть ;

, то есть ;

, то есть

2) Сравнение относительных погрешностей чисел :

показывает,

Что числа Перечислены

В порядке увеличения точности представления числа ,

То есть точнее , точнее .

Ответ: а)

б)

Задание 6. Найти сумму приближенных чисел , , считая в них все знаки верными, т. е. что абсолютная погрешность каждого слагаемого не превосходит половины единицы младшего разряда этого слагаемого. Определить абсолютную и относительную погрешности суммы.

Дано: , ,

Найти:

Решение:

1) Считаем, что в числах , , все знаки верны в узком смысле, то есть

Число с наибольшей абсолютной погрешностью .

, абсолютная погрешность округления

3) Сложим все эти числа, учитывая все сохраненные знаки:

4) Полученный результат округлим на один знак (формально):

, абсолютная погрешность округления

5) Полную абсолютную погрешность суммы будем складывать из трех компонентов:

A) суммы предельных абсолютных погрешностей исходных чисел;

B) абсолютной величины суммы ошибок округления слагаемых;

C) заключительной погрешности округления результата.

— абсолютная погрешность суммы.

% — относительная погрешность суммы.

Ответ: ; %.

Задание 7. Найти предельную абсолютную и относительную погрешности при вычислении объема прямого кругового цилиндра, если значения его высоты и радиуса основания имеют все верные знаки.

Дано: ,

Найти:

Решение:

Примем

1) Так как в числах и все числа верны, то их абсолютные погрешности:

Число с наибольшей абсолютной погрешностью .

, абсолютная погрешность округления (округления не требуется)

2) перемножим числа, учитывая все сохраненные знаки:

;

Абсолютная погрешность округления

4) Полную абсолютную погрешность произведения будем складывать из двух слагаемых:

A) предельной абсолютной погрешности произведения до его округления;

B) заключительной погрешности округления произведения.

Полная абсолютная погрешность

Теперь перейдем к искомому объему.

(Здесь полученный результат округляем до трех значащих цифр).

— предельная абсолютная погрешность объема.

% — предельная относительная погрешность объема.

Ответ: , , %

Задание 8. Привести пример потери точности при вычитании двух близких чисел.

Решение:

Пусть и — два близких числа; примем, что у них одинаковое число знаков после запятой.

Считаем, что все знаки в числах и верны в узком смысле. Тогда абсолютные погрешности:

Относительные погрешности:

Так как , то

Абсолютная погрешность результата:

Относительная погрешность результата: %

При вычитании двух близких чисел и относительная погрешность возросла на 3 порядка!

Лабораторная работа №2

Метод Гаусса

I. Описание работы

Тема: Решение системы линейных неоднородных алгебраических уравнений методом Гаусса (схема единственного деления).

Задание. Решить систему трех уравнений с тремя неизвестными с точностью искомых неизвестных до .

Промежуточные вычисления вести с двумя запасными знаками.

Решение:

Исходные данные и все результаты вычислений запишем в таблицу 1.

Прямой ход

1. Записываем коэффициенты данной системы в трех строках и четырех столбцах раздела 1 таблицы 1.

2. Суммируем все коэффициенты по строке и записываем сумму в столбце (столбец контроля), например .

3. Делим все числа, стоящие в первой строке, на и результаты записываем в 4-й строке раздела 1.

4. Вычисляем и делаем проверку, если вычисления ведутся с 6 и более знаками после запятой, то числа и не должны отличаться более, чем на единицу последнего разряда:

5. По формулам вычисляем коэффициенты :

Результаты записываем в первые две строки раздела:

6. Делаем проверку. Сумма элементов каждой строки не должна отличаться от более, чем на 1-2 единицы последнего разряда. Заметим, что ,

7. Делим все элементы 1 строки раздела 2 на и результаты записываем в 3 строке раздела 2.

8. Делаем проверку:

9. По формулам вычисляем :

Результаты записываем в 1 строку раздела 3.

10. Делаем проверку:

11. Делим все элементы 1 строки раздела 3 на и результаты записываем в следующей (второй) строке этого раздела.

12. Делаем проверку:

Обратный ход

1. В разделе 4 записываем единицы

2. Записываем .

3. Для вычисления и используем лишь строки разделов, содержащие 1.

4. Вычислим по формуле: .

5. Вычислим по формуле:

6. Аналогично проводим обратный ход в контрольной системе. Записываем ,

вычисляем и с заменой и на и соответственно:

Делаем обычную проверку по строкам – должно быть , с точностью до 1-2 единиц последнего разряда.

Действительно:

Заполним таблицу 1 результатами вычислений:

Таблица 1

Раз Дел
1	1 2 3
2	2 3
3	3
4		1 1 1	1	1

Округлим полученное решение до , по требованию задачи:

Окончательную проверку точности полученного решения системы выполним подстановкой этого решения в систему. Должно получиться приближенное тождество с точностью до .

Ответ:

< Предыдущая		Следующая >

Пример выполнения задания — Студопедия

Поделись

Задача

1.Определить, какое равенство точнее 9/11 или = 4.24?

Решение. Находим значения данных выражений с большим числом десятичных знаков: a₁ = 9/11 = 0.8181818…, a₂ = = 4.2426… . Затем вычисляем предельные абсолютные погрешности, округляя их с избытком:

Δa₁ = |0.181818 – 0.818| ≤ 0.00019, Δa₂ = |4.2426 – 4.24| ≤ 0.0027.

Предельные относительные погрешности составляют

δa₁ = = 0.00024 = 0.024 %;

δa₂ = = 0.00064 = 0.064 %.

Так как δa₁ < δa₂, то равенство 9/11 = 0. 818 является более точным.

2.Округлить сомнительные цифры числа 72.353(±0.026), оставив верные знаки в узком смысле.

Решение. Пусть 72.353(±0.026) = a. Согласно условию, погрешность Δa = 0.026 < 0.05; это означает, что в числе 72.353 верными в узком смысле являются цифры 7, 2, 3. По правилам округления найдём приближённое значение числа, сохранив десятые доли:

a₁ = 72.4; Δa₁ = Δa + Δ_OKP = 0.026 + 0.047 = 0.073.

Полученная погрешность больше 0.05; значит, нужно уменьшить число цифр в приближённом числе до двух:

a₂ = 72; Δa₂ = Δa + Δ_OKP = 0.026 + 0.353 = 0.379.

Так как Δa₂ < 0.5, то обе оставшиеся цифры верны в узком смысле.

Округлить сомнительные цифры числа 2.3544; δ = 0.2 %, оставив верные знаки в широком смысле.

Решение. Пусть a = 2.3544; δa = 0.2 %; тогда Δa = a·δa = 0.00471. В данном числе верными в широком смысле являются три цифры, поэтому округляем его, сохраняя эти три цифры:

a₁ = 2.35; Δa₁ = 0.0044 + 0.00471 = 0.00911 < 0.01.

Значит, в округлённом числе 2.35 все три цифры верны в широком смысле.

3.Найти предельные абсолютные и относительные погрешности числа 0.4357, если они имеют только верные цифры в узком смысле.

Решение. Так как все четыре цифры числа a = 0.4357 верны в узком смысле, то абсолютная погрешность Δa = 0.00005, а относительная погрешность

Δa = 1/(2·4·10³) = 0.000125 = 0.0125 %

Найти предельные абсолютные и относительные погрешности числа 12.384, если они имеют только верные цифры в широком смысле.

Решение. Так как все пять цифр числа a = 12.384 верны в широком смысле, то Δa = 0. 001, δa = 1/10⁴ = 0.0001 = 0.01 %

ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2. Изучение численных методов решения уравнений (3 ч)

Цель работы – дать студенту возможность изучить алгоритмы и методы нахождения корней нелинейных уравнений.

Теоретические сведения.

Задача нахождения корней линейных уравнений вида встречается в различных областях научных исследований (здесь – некоторая непрерывная функция). Нелинейные уравнения можно разделить на два класса – алгебраические и трансцендентные. Алгебраическими уравнениями называются уравнения, содержащие только алгебраические функции (целые, рациональные, иррациональные). В частности, многочлен является целой алгебраической функцией. Уравнения, содержащие другие функции (тригонометрические, показательные, логарифмические и др.), называются трансцендентными.

Методы решения нелинейных уравнений делятся на прямые и итерационные. Прямые методы позволяют записать корни в виде некоторого конечного соотношения (формулы).

Однако встречающиеся на практике уравнения не удаётся решить такими простыми методами. Для их решения используются итерационные методы, т. е. методы последовательных приближений.

Метод половинного деления

В методе половинного деления (дихотомии, бисекции) заданный отрезок [a, b] разделим пополам (рисунок 2) и положим x₀ = (a + b)/2.Из двух полученных отрезков [a; х₀] и [x₀; b] выбираем тот, на концах которого функция f (x) имеет противоположные знаки. Полученный отрезок снова делим пополам и приводим те же рассуждения. Процесс продолжаем до тех пор, пока длина отрезка, на концах которого функция имеет противоположные знаки, не будет меньше заданного ε, любую точку отрезка с точностью ε можно принять за корень уравнения f (x) = 0.

Таким образом, если x₀ и x₁ таковы, что f (x₀)·f (x₁) < 0, то полагаем x₂ = (x₀ + x₁)/2 и вычисляем f (x₂). Если f (x₂) = 0, то корень найден. В противном случае из отрезков [х₀; х₂] и [х₂; х₁] выбирам тот, на концах которого f принимает значения разных знаков, и проделываем аналогичную операцию. Процесс продолжаем до получения требуемой точности.

Рисунок 2 – Метод половинного деления (дихотомии)

Пример 1. Составить программу для нахождения корней методом половинного деления для функции f (x) = x² + 1.7x + 1.7 по схеме алгоритма.

2\): (i) Эквивалентно коэффициенту детерминации линейной регрессии ненаблюдаемого значения генотипа на наблюдаемый фенотип; (ii) Это также квадрат корреляции между предсказанным значением фенотипа и значением генотипа; и (iii) Он представляет собой долю дифференциала отбора ($S$), которая может быть реализована как реакция на отбор ($R$) (Falconer and Mackay, 2005).

Есть две основные причины, по которым наследуемость на основе среднего начального значения представляет интерес в селекции растений (Schmidt et al., 2019).2С\] Где:

$\Delta G$ — генетическая выгода
$S$ — среднее фенотипическое значение выбранных генотипов, выраженное как отклонение от среднего по популяции.

Обычные проблемы

На практике большинство испытаний проводится в рамках многосредовых испытаний (МЕТ), в которых представлены несбалансированные данные, поскольку не все сорта испытываются в каждой среде или просто когда данные о делянке утеряны или когда количество повторов в каждом месте варьируется между генотипами (Schmidt et al. др., 2019б). Однако стандартный метод оценки наследуемости неявно предполагает сбалансированные данные, независимые эффекты генотипа и однородные дисперсии.

Как рассчитать наследуемость?

Согласно Schmidt et al. (2019a), компоненты дисперсии можно рассчитать двумя способами:

1) Двухэтапный подход

При двухэтапном подходе на первом этапе каждый эксперимент анализируется индивидуально в соответствии с их планом эксперимента (решетка, CRBD и т. д.) (Zystro et al., 2018). А для среды второго этапа обозначается взаимодействие по годам. Этот подход предполагает единую дисперсию взаимодействия генотипа и окружающей среды (GxE), даже если в течение нескольких лет тестировались несколько местоположений (Buntaran et al., 2020). 9{СИНИЙ}}{2}}\)

Функция наследуемости в упаковке

Для расчета стандартной наследуемости в экспериментах MET количество местоположений и повторений следует включить вручную в функцию h3cal() . В случае разности числа повторений в каждом эксперименте берут максимальное значение (часто делается на практике) (Schmidt et al., 2019b).

Для удаления выбросов реализована функция Метода 4, использованного для Bernal-Vasquez et al. (2016): Бонферрони-Холм использует повторно масштабированный MAD для стандартизации остатков (BH-MADR).

Загрузка пакетов

функция h3cal

 dt Картофель
 час <- h3cal(данные = dt
            , черта = "стебельdw"
            , gen. name = "гено"
            , отв.п = 5
            , fixed.model = "0 + (1|блок) + гено"
            , random.model = "1 + (1|блок) + (1|гено)"
            , означает = ИСТИНА
            , plot_diag = ИСТИНА
            , выбросы.rm = ИСТИНА
            )

Информация о модели

 час$модель %>% сводка()
## Линейная смешанная модель, подобранная REML ['lmerMod']
## Формула: Stemdw ~ 1 + (1 | блок) + (1 | geno)
## Данные: dt.rm
## Веса: веса
##
## Критерий REML при сходимости: 796.1
##
## Масштабированные остатки:
## Мин. 1 кв. Медиана 3 кв. Макс.
## -2,38440 -0,64247 -0,08589 0,57452 2,84508
##
## Случайные эффекты:
## Группы Имя Отклонение Стандартное отклонение.
## гено (перехват) 19,960 4,4677
## блок (Перехват) 0,110 0,3316
## Остаток 9,411 3,0677
## Количество наблюдений: 148, групп: гено, 15; блок, 5
##
## Фиксированные эффекты:
## Оценить стандарт. Значение ошибки t
## (Пересечение) 12,51 1,19 10,51

Компоненты дисперсии

 hr$tabsmr %>% kable(caption = "Таблица компонентов отклонения")

Таблица 2: Таблица компонентов отклонения
0 стержень	5	15	1	1	12,59867	4,749994	2,818	22. 302	19.	9.410932	21.84221	0,8	0,8	0,95	0,73

Лучшие линейные несмещенные оценщики (BLUE)

 hr$blues %>% kable(caption = "BLUEs")

Таблица 3: СИНИЕ
Г01	15.73200	1.030325	119.7830	13.63	17.77201
Г02	10.12100	1.030325	119.7830	8.0809903	12.16101
Г03	9.69500	1.030325	119. 7830	7,6549903	11.73501
Г04	15.17700	1.030325	119.7830	13.1369903	17.21701
Г05	12.87106	1.086433	122,5189	10.7204483	15.02167
Г06	22.30200	1.030325	119.7830	20.2619903	24.34201
Г07	2,81800	1.030325	119.7830	0,7779903	4.85801
Г08	10. 42300	1.030325	119.7830	8.3829903	12.46301
Г09	15.66800	1.030325	119.7830	13.6279903	17.70801
G10	9.24200	1.030325	119.7830	7.2019903	11.28201
G11	6.42500	1.030325	119.7830	4.3849903	8.46501
G12	16.11100	1.030325	119.7830	14.0709903	18. 15101
Г13	14.62900	1.030325	119.7830	12.5889903	16.66901
G14	16.29700	1.030325	119.7830	14.2569903	18.33701
Г15	11.46900	1.030325	119.7830	9.4289903	13.50901

Лучшие линейные несмещенные предикторы (BLUP)

 hr$blups %>% kable(caption = "BLUPs")

Таблица 4: BLUP
Г01	15.587018
Г02	10.228658
Г03	9,821839
Г04	15. 057007
Г05	12.843686
Г06	20.631268
Г07	3.254483
Г08	10.517060
Г09	15.525899
G10	9.389236
G11	6.699074
G12	15.3
Г13	14.533681
G14	16.126578
Г15	11.515963

Выбросы

 hr$outliers$fixed %>% kable(caption = "Модель с фиксированными выбросами")

Таблица 5: Фиксированные выбросы модели
68	IV	Г05	80,65	60. 36709	18.84505	0	68	0	0	ВЫБРОС

 hr$outliers$random %>% kable(caption = "Модель случайных выбросов")

Таблица 6: Модель случайных выбросов
68	IV	Г05	80,65	61.39925	18.886677	0,0000000	68	0,0000000000	0,0000000	ВЫБРОС
100	IV	Г06	33,52	12.02340	3,698449	0,0002169	100	0,0002169207	0,0323212	ВЫБРОС

Сравнение: h3cal и asreml

https://inkaverse. com/articles/extra/stagewise.html

Берналь-Васкес, А.-М., Х.-Ф. Утц и Х.-П. Пьефо. 2016. Методы обнаружения выбросов для обобщенных решеток: пример перехода от ANOVA к REML. Теоретическая и прикладная генетика 129(4): 787–804. doi: 10.1007/s00122-016-2666-6.

Bolker, B. 2021. Средняя дисперсия разницы BLUE или BLUP в lme4. Переполнение стека. https://stackoverflow.com/questions/38697477/mean-variance-of-a-difference-of-blues-or-blups-in-lme4 (по состоянию на 21 мая 2021 г.).

Бунтаран, Х., Х.-П. Пьефо, П. Шмидт, Дж. Райден, М. Холлинг и др. 2020. Перекрестная проверка поэтапного анализа смешанной модели шведских сортоиспытаний с озимой пшеницей и яровым ячменем. Crop Science 60 (5): 2221–2240. doi: 10.1002/csc2.20177.

Фальконер Д.С. и Т.Ф. Маккей. 2005. Введение в количественную генетику (Пирсон Прентис Холл, редактор). Четвертый.

Шмидт П., Дж. Хартунг, Дж. Бенневиц и Х.-П. Пьефо. 2019а. Наследуемость в селекции растений на основе различий генотипов. Генетика 212 (4): 991–1008. doi: 10.1534/genetics.119.302134.

Шмидт П., Дж. Хартунг, Дж. Рат и Х.-П. Пьефо. 2019б. Оценка наследуемости в широком смысле с помощью несбалансированных данных испытаний сельскохозяйственных сортов. Crop Science 59 (2): 525–536. doi: 10.2135/cropsci2018.06.0376.

Зистро, Дж., М. Колли и Дж. Доусон. 2018. Альтернативные экспериментальные схемы селекции растений. Обзоры селекции растений. John Wiley & Sons, Ltd. с. 87–117

в широком смысле – французский перевод – Linguee

Эти мероприятия должны способствовать или быть в состоянии способствовать активному участию молодых граждан в общественной жизни и жизни общества, как

[…]

а также на разработку и внедрение Сообщества

[…] по с , по по широкий смысл , в т ч е область молодежи.

eur-lex.europa.eu

Ces activits doivent notamment contributor, ou pouvoir contributor, la участие активно де jeunes citoyens la vie publique et la socit ainsi qu’au

[…]

Развитие и деятельность по сотрудничеству

[…] Commun AU TAIRE DANS LE DO MA INE DE LA JE UNESS E U SEA U SEA .

eur-lex.europa.eu

Если мы тал ки н г в а широкий смысл a b ou акцизный […]

пошлины на моторное топливо и другие товары, затем снижение ставок акцизов

[…]

поможет экономике расти и быть более конкурентоспособной.

europarl.europa.eu

S’ag is sant, au sens большой, d es d roit s d’accises […]

sur les carburants et autres produits, une rduction des taux d’accises

[…]

Favoriserait la croissance conomique et une plus grande comptitivit.

europarl.europa.eu

Если взять e i t in a широкий смысл a n d вы добавляете […]

креветок, и вы добавляете другие акции, которые есть, сэр, честно говоря, я не могу предположить.

www2.parl.gc.ca

Si vous le pr en ez dan s u n sens large e t q ue vo us [. ..]

les crevettes, les autres stocks qui son t dans l a nature, monsieur, je ne pourrais

[…]

mme pas me risquer avancer un chiffre.

www2.parl.gc.ca

Они определены как в e d в a в широком смысле a s a ny процедуры […]

при проведении Евросистемой сделки с одним или несколькими контрагентами без проведения торгов.

ecb.europa.eu

Elles recouvrent d’une

[…] manir e gnrale t oute pr ocdu re dans la 16 2 quell0652 Евросистема […]

выполнить одну транзакцию по

[. ..]

quelques contreparties sans recourir aux appels d’offres.

ecb.europa.eu

То есть, SERV IC E S в A Широкий смысл Sense 0652 er, чем Интернет […]

Конкретно службы, хотя эта технология может стать частью конечного решения.

daccess-ods.un.org

Autrement dit, il s’agit

[…] de se rv льды au sen s большой d u ter me et

2n […]

уникальность веб-услуг, а также учетная запись

[…]

que cette dernire technologie fait partie intgrante de la solution offerte.

daccess-ods. un.org

daccess-ods.un.org

This type of media ti o n — in a broad sense — i s p art of criminal […]

процедура.

unodc.org

Тип Ce de md ia tion — au se ns большой — fait par 2 ti 906 […]

процедура покупки.

unodc.org

Термин «доли покупки и продажи»

[…] быть ниже до o d in a broad sense a n d includes orders, […]

котировки и признаки интереса.

eur-lex. europa.eu

eur-lex.europa.eu

L’expression intrts acheteurs et vendeurs

[…] doit s’e nt endre au se ns большой, c omm e i nclua nt les ordres , […]

prix e t указания d’intrt.

eur-lex.europa.eu

Действует,

[…] устойчивость iss ue s , in a широкий смысл , a стр. […]

к окружающей среде и природным ресурсам, но и к другим видам капитала.

office.sciences-po.fr

Вопросы по номеру

[…] soutena bi lit au sens большой va len ten e и далее и другие [. ..]

Защита окружающей среды и природных ресурсов,

[…]

Почтовый ящик для других типов капитала.

office.sciences-po.fr

В a широкий смысл , t […]

отвечает за предоставление МАГАТЭ информации и доступ к объектам в соответствии со статьей

[…]

соглашение о гарантиях и ДП.

ccsn.gc.ca

De f aon gnrale , le SN […]

AIEA des renseignements et l’accs aux Installations, соответствие l’accord relatif

[…]

Дополнительные гарантии и дополнительный протокол.

ccsn.gc.ca

Кроме специального узкого понятия этики как части философии, которое дает

[. ..]

теоретическое объяснение и интерпретация

[…] of moral it y , in a broad sense e t hi cs, is commonly […]

понимается как знание

[…]

фундаментальные ценности человеческого существования.

unesdoc.unesco.org

Outre la notion restreinte et spcifique de l’thique comme domaine philosophique qui permet une

[…]

Подробное объяснение и интерпретация

[…] боевой дух, l’ thiq ue (a u sens g n ra l du te rme) […]

communment dsigne comme la connaissance

[. ..]

фундаментальные ценности человеческого существования.

unesdoc.unesco.org

Важность приглашения представителей

[…] от гражданского общества т.е. т у в a в широком смысле т o […]

местные процессы планирования уже подчеркнуты.

aedh.eu

Il importe d’associer des reprsentants de la

[…] общество c ivile au se ns большое au x p roc essus d e планировка […]

национальных и местных, cela и dj t soulign.

aedh.eu

Срок

[…] Предприятие было US E D в A Широкий смысл Широкий смысл . 0652 над производством […]

единицы, использующие рабочую силу, принадлежат и управляются одним человеком

[…]

лица, работающие за свой счет в качестве самозанятых лиц, самостоятельно или с помощью неоплачиваемых семейных работников.

daccess-ods.un.org

U tili s dans so n sens g n ral , le т эрме предприятие […]

Извлечение производственных единиц, которыми пользуются работники основного производства

[…]

et quiont un propritaire unique qui en assure la gestion pour son propre en tant que travailleur indpendant, seul ou avec l’aide de travailleurs familiaux non rmunrs.

daccess-ods.un.org

Во-вторых, многие из этих инструментов были

[. ..]

не разработан из

[…] perspective of measuring people’s capabili ti e s in a broad sense , b ut for the purpose of assessing educational [.. .]

политик, обычно

[…]

требовали сосредоточиться на более узком наборе измеримых компетенций.

oree.org

Ванная комната, без выходных

[…] pas t l abor s dans l ‘ide d e mesurer les capacits des pers on nes, au sens large du terme, май с и ле […]

но d’valuer les politiques

[…]

ducatives qui, en rgle gnrale, requraient de se concentrer sur un plus petit nombre de comptences mesurables.

oree.org

The MSITS identifies four different modes of trad in g , in a broad sense , b et единицы, проживающие в разных странах.

daccess-ods.un.org

Le Manuel des statistiques du comme rc e international d es services dfinit quatre modes gnraux de commerce en tre entits rsidan t dans d iffrents pays.

daccess-ods.un.org

В этом контексте

[…] criteria of accessibility, unders to o d in a broad sense ( t ra nsport, IT and communications, services [. ..]

общего интереса), становятся первостепенными.

arcatlantique.org

Dans ce c ontexte, le critre d’accessibilit ente nd u dan s u n sens large (tr ans port, t echnologie [ …]

информация и информация

[…]

связь, услуги d’intrts gnraux) est de ce fait primordial.

arcatlantique.org

Аналогичным образом проект конвенции, касающийся

[…]

к Европейскому патентному закону, определенному

[…] the patentabi li t y in a broad sense b y s pecifying that [. ..]

применимо ко всем новым

[…]

Изобретение, относящееся к продуктам или процессам в любой области, в том числе к разновидностям растений или породам животных и к по существу биологическим процессам получения растений или животных.

aippi.org

De mme, le projet de Convention relatif un

[…]

droit europen des brevets dfinit la

[…] breve ta bili t a u sens big en pr ci sant qu ‘elle […]

аппликация всех новых изобретений

[…]

родственников продуктов или продуктов, происходящих из доменов, и включает в себя различные виды животных или животных рас и биологических продуктов, необходимых для получения животных или животных.

aippi. org

aippi.org

Свобода здесь консе IV E D в A Широкий смысл , широкий смысл , .

и негативные свободы.

www2.ohchr.org

La libert est p рост ici dans un sen s большой r эко уврант ла ф ой […]

свободы позитивы и нгативы.

www2.ohchr.org

Законодательство об охране авторских прав должно предусматривать специальную систему для промышленных образцов

[…]

и модели, определяемые как промышленные

[…] статьи учитывают er e d в a широкий смысл , т [. ..]

включая, в частности, предметы художественного мастерства.

aippi.org

Законодательство о праве на авторское право на разработку и внедрение специального режима для дизайнеров и промышленных моделей

[…]

dfinis comme des objets

[…] industriels con si dr s dans un sens large, c’e st— di re englobant […]

без примечаний к ремесленным предметам.

aippi.org

в A Широкий смысл , T T T .

dfo-mpo.gc.ca

De fao n grale, le prochain dfi устойчив к воздействию [. ..]

цветов.

dfo-mpo.gc.ca

Fre ed o m in a широкий смысл е м бр асы оба отсутствие […]

принуждения и ограничений, а также право на выражение убеждений и обычаев.

www2.parl.gc.ca

L a libe rt au sen s большой c om порт e l’ […]

принуждение и противодействие, а также право манифестации, связанные с принуждением и практикой.

www2.parl.gc.ca

На наш взгляд, необходимо также законодательно закрепить

[…] individual’s right to fre ed o m in a broad sense , w hi ch is true freedom.

europarl.europa.eu

Il s’agit, notre avis, d’introduire galeme nt dans la lgislation le droit la libert de

[…] l’indi vi du au se ns large, l equ el co ns t it ue l e sens m me де ла Либерт.

europarl.europa.eu

С учетом вышеизложенного делегаты сочли, что это

[…]

необходимо определить общий

[…] linguistic po li c y in a broad sense a nd , in p a рт икулярный, [. ..]

определить рамки своего политического

[…]

и техническое управление, а также определить инструменты управления.

unesdoc.unesco.org

Au vu de ce qui prcde, les dlgus ont jug

[…]

ncessaire de dfinir une politique

[…] лингвистический co mmune au se ns большой, e n p art iculi er de dfinir […]

le cadre de sa gestion politique

[…]

и т. д. Техника и др d’identifier des outils de gestion cet effet.

unesdoc.unesco.org

Комиссия в свою очередь должна быть сформирована

[…]

сети команд избранных мирян, которые работают вместе в

[. ..] marriage prepara ti o n in a broad sense a n d not only in the […]

курсы.

pcf.va

La Commission devrait tre, son tour, forme d’un rseau

[…]

d’quipes de lacs choisis pour ce faire, qui colaboreraient la

[…] prpar at ion dans son sen s big, et non seul courent em em

pcf.va

Глубокое восхищение индийской культурой

[…] провел здесь и помог нашему родственнику io n s в a широкий смысл .

lalettrediplomatique.fr

lalettrediplomatique. fr

D an s un sen s плюс большой, l’ восхищение po ur la культура […]

indienne y est profondment enracine et cela a favouris nos отношения.

lalettrediplomatique.fr

Показать, что мы можем сделать консервацию в

[…]

способ улучшить благосостояние людей (in

[…] Их мнение IO N ) в A Широкий Sense Sense Sense . Только

— у них на лицах улыбки?

cepf.net

Montrer que nous sommes accepts d’amliorer le quotidien des gens ( dans l eurs

[. ..] мнения) et dans u n sens g nra l, et pas seulement […]

leur revenu, n’ont-ils

[…]

pas des sourires sur leurs visages ?

cepf.net

1 — In a broad sense , a currency […] Область

может быть определена как сосуществование якорной валюты и ряда спутниковых валют.

banquecentrale.eu

1 — A используйте ns большой, u ne zon e mon t aire se […]

dfinit Principlement par la coexistence d’une monnaie доминирующий et de plusieurs monnaies спутников.

banquecentrale. eu

banquecentrale.eu

Нововведение учтено по C I P в a широкий смысл .

cordis.europa.eu

DANS L E CA DR E DU CIP, L’NVINATION EST PR ISE EN COMPTE AU AU AU AU .

cordis.europa.eu

В а в широком смысле , w привет […]

согласен, что некоторые реформы были необходимы в свете многочисленных публичных проявлений злоупотреблений,

[…]

многие теперь спрашивают: «Не слишком ли далеко зашло регулирование управления?»

D ‘une faon g nrale , les n омбре [. ..]

rapports public d’abus ont convaincu la plupart des gens de la ncessit de Certaines

[…]

rformes mais nombreux sont ceux qui aujourd’hui se required si la rglementation relative la gouvernance des entreprises n’est pas en voie d’aller trop loin.

powercorporation.com

Метод непараметрической регрессии для соглашения в широком смысле

Список журналов
Рукописи авторов HHS
PMC5440120

J Непараметр Стат. Авторская рукопись; доступно в PMC 2017 17 июня. 2017; 29(2): 280–300.

Опубликовано онлайн 2017 март 17. DOI: 10. 1080/10485252.2017.1303058

PMCID: PMC5440120

NIHMSID: NIHMS827801

PMID: 28546735 9000 9009

. непрерывное измерение часто представляет интерес в исследованиях психического здоровья. С этой целью Пэн, Ли, Го и Манатунга (2011) представили концепцию соглашения в широком смысле (BSA) и разработали непараметрическую оценку и вывод для показателя BSA. В этой работе мы предлагаем основу непараметрической регрессии для BSA, которая обеспечивает надежный инструмент для дальнейшего исследования неоднородности населения в BSA. Мы разрабатываем процедуры вывода, включая оценку функции регрессии и проверку гипотез. Обширные симуляционные исследования демонстрируют удовлетворительную производительность предложенного метода. Мы также применяем новый метод к недавнему исследованию Grady Trauma Study и обнаруживаем интересное влияние тяжести депрессии на соответствие между самооценкой симптомов и клиническим диагнозом у пациентов с посттравматическим стрессовым расстройством (PSTD).

Ключевые слова: Широкое соглашение, Складной нож, Непараметрическая регрессия, U-статистика

Классификация субъектов AMS: Первичный: 62G08, Вторичный: 62G20

В последние годы наблюдается огромный интерес к улучшению оценки и диагностики расстройств психического здоровья (Gillespie et al., 2009). Например, посттравматическое стрессовое расстройство (ПТСР) представляет собой сложное гетерогенное расстройство и является одним из наиболее распространенных расстройств психического здоровья среди ветеранов боевых действий (Kessler, Sonnega, Bromet, Hughes и Nelson 19).95). Шкала ПТСР, проводимая клиницистом (CAPS), в настоящее время является наилучшим доступным стандартом для диагностики посттравматического стрессового расстройства (да или нет), но требует значительного времени и усилий клиницистов и обученных клинических исследователей, которые имеют практические знания о посттравматическом стрессовом расстройстве (Фоа, Риггс, Данку, и Ротбаум, 1993; Фоа и Толин, 2000). Интервью по шкале симптомов посттравматического стрессового расстройства (PSS) представляет собой альтернативную самооценку тяжести посттравматического стрессового расстройства, которая требует гораздо меньше времени для оценки, чем CAPS, и обеспечивает непрерывную оценку, указывающую на тяжесть посттравматического стрессового расстройства (Foa et al. 19).93). Изучение соответствия между диагнозом CAPS и PSS может привести к повышению полезности этих инструментов. Например, если есть хорошая согласованность между диагнозами PSS и CAPS, PSS может использоваться как менее дорогостоящий суррогат CAPS с достаточной надежностью или достоверностью. Решение такой проблемы невозможно с помощью традиционных методов согласования (Cohen, 1960, 1968; Fleiss et al., 1971; Kraemer, 1980; Lin, 1989 и др.), поскольку они обычно требуют проведения измерений в одном масштабе.

Структура соглашения в широком смысле (BSA), представленная Peng et al. (2011), специально разработан для характеристики соответствия между непрерывным измерением и порядковым измерением. Например, показатель BSA, предложенный Peng et al. (2011) может показать способность интерпретации PSS в соответствии с CAPS-диагностикой посттравматического стрессового расстройства. Мера BSA масштабируется от -1 до 1 по своему определению и легко интерпретируется. Показатель BSA, равный 1, соответствует идеальному сценарию BSA, где существует определенный способ дискретизации PSS для получения согласованного однозначного соответствия с диагнозом CAPS. Пэн и др. (2011) предложили непараметрическую оценку и процедуры вывода на основе складного ножа для их меры BSA. Их методы в первую очередь ориентированы на одновыборочный случай.

Расстройства психического здоровья, такие как посттравматическое стрессовое расстройство, обычно подвержены большой гетерогенности популяции, что проявляется в высокой изменчивости фенотипов заболевания. Таким образом, во многих исследованиях психического здоровья оценщик, предложенный Peng et al. (2011) может дать хорошее общее обобщение BSA, но может пострадать от потери точности из-за потенциальных вариаций BSA среди разных субпопуляций. Модель гетерогенности BSA, если она существует, также может представлять большой научный интерес. Например, в недавнем исследовании Grady Trauma Study (Gillespie et al. 2009), далее именуемое исследованием посттравматического стресса, 8091 субъект, подвергшийся травме, был набран в залах ожидания первичной медицинской помощи больницы Грейди, медицинского учреждения в центральной части города. Данные, собранные у этих субъектов, включают несколько клинических оценок, таких как CAPS, PSS, и другую информацию, такую как оценка депрессивного расстройства, измеренная с помощью опросника депрессии Бека (BDI) (Beck, Ward, Mendelson, Mock, and Erbaugh, 1961). В исследовательском анализе мы оценили показатель BSA между диагнозами PSS и CAPS для четырех подгрупп, стратифицированных по шкале депрессии BDI, и получили соответствующие доверительные интервалы; видеть . Показано, что показатель BSA может значительно различаться в разных группах BDI. Результаты показывают, что может быть хорошая согласованность между диагнозами PSS и CAPS у пациентов с посттравматическим стрессовым расстройством без симптомов депрессии или с небольшими симптомами депрессии, но это не так для тех, кто страдает тяжелой депрессией. Такая неоднородная модель BSA может помочь в понимании этих инструментов, но ее нельзя раскрыть с помощью простого исследования BSA с одной выборкой.

Открыть в отдельном окне

Оценка BSA между диагнозами PSS и CAPS по показателю BDI и соответствующим 95% доверительным интервалам.

Вдохновленные примером посттравматического стресса, мы предлагаем расширить текущую структуру BSA, разработав надежный инструмент регрессии для BSA. Как показано в примере с посттравматическим стрессовым расстройством, характер изменения BSA с ковариантой может быть нелинейным. Поэтому мы изучаем метод непараметрической регрессии BSA, чтобы учесть нелинейные ковариатные эффекты. Есть некоторые важные тонкости в формулировании непараметрической регрессионной модели для BSA и разработке ее оценки. То есть, в отличие от обычных показателей ассоциации или согласия (например, коэффициента корреляции, коэффициента Каппа), показатель BSA в случае одной выборки не определяется при распределении измерений от одной единицы/субъекта. Вместо этого он строится на основе сравнения данных от нескольких единиц/субъектов. Когда исследуемая популяция может быть гетерогенной, необходимо соответствующим образом адаптировать концепцию BSA. Например, одной из сложных задач является выявление сопоставимых единиц/субъектов при определении показателя BSA с учетом неоднородности населения. Это создает некоторые концептуальные сложности для моделирования, оценки и вывода BSA в условиях регрессии.

В Разделе 2 мы сначала рассматриваем существующую структуру BSA, после чего вводим показатель BSA с поправкой на ковариацию и нашу формулировку непараметрической регрессионной модели. В разделе 3 мы предлагаем непараметрическую оценку функции регрессии в предложенной модели, которая использует идею ядерной регрессии в контексте регрессии BSA. Мы изучаем асимптотические свойства предложенной оценки и разрабатываем процедуры вывода, включая оценку дисперсии, доверительные интервалы и проверку гипотез. В разделе 4 мы представляем исследования моделирования, которые демонстрируют хорошую производительность предложенного метода на конечной выборке. Применение наших методов к исследованию ПТСР представлено в разделе 5. Мы завершаем эту статью несколькими замечаниями в разделе 6.

2.1. Обзор согласия в широком смысле

Концепция согласия в широком смысле (BSA) расширяет парадигму классических исследований согласия, которые касаются только измерений в одном и том же масштабе. Пусть X и Y будут непрерывными и порядковыми измерениями общего признака у одного и того же субъекта. Пусть 𝒟 _X и 𝒟 _Y будут доменом X и Y соответственно. По определению Peng et al. (2011), X и Y находятся в полном согласии (или несоответствии) в широком смысле тогда и только тогда, когда существует возрастающая (или убывающая) ступенчатая функция Ψ от 𝒟 _X до 𝒟 _Y такая, что Y = Ψ( X ) с вероятностью 1. Это определение подразумевает, что при наличии полного совпадения (несогласия) можно определить набор точек отсечения для непрерывного X , так что дискретизированное X имеет точное однозначное согласованное (или несогласное) соответствие с порядковым номером Д .

Пэн и др. (2011) ввел меру, характеризующую соответствие в широком смысле между непрерывным измерением и порядковым измерением. Ключевая идея, лежащая в основе Peng et al. (2011) мера BSA заключается в количественной оценке отклонения от идеального согласия в широком смысле с использованием расстояния между наблюдаемыми рангами в X и рангами, ожидаемыми при идеальном BSA, для группы случайно выбранных наблюдений, по одному из каждой категории . Y . То есть, предположим, что порядковый номер Y принимает значения 1 < … < L . Let X̌ _[ _L _] Обозначайте случайно выбранный x , данный y = L ( L = 1, 2,… L ( L = 1, 2,… L . Обозначите ранги { X̌ _[1], X̌ _[2],…, X̌ _[ _L ] _{777727177727272727272727272727272727727727727271727271271727727727127127127127127127127127.}

._{7127127127127127127127127127127127127127127127127127._{27. _{7. , Р _[2] , …, R _[ _L _] ). Мера BSA между X и Y (Пенг и др., 2011) определяется как
ρbsa(X,Y)=1-E{∑l=1L(l-R[l])2}EX⊥Y{ ∑l=1L(l-R[l])2},
(1)
, где E (·) обозначает математическое ожидание, а E _X _⊥ Y 9011 ожидание при независимости между X и Y . Когда X и Y независимы, ρ _bsa ( X , Y ) = 0. Peng et al. (2011) показали, что
EX⊥Y{∑l=1L(l-R[l])2} равно константе C _L ≡ ( L ³ − L )/6, а −1 ≤ ρ 6 bsa ( X , Y ) ≤ 1 с ρ _bsa ( X , Y ) = 1 (или −1), что соответствует идеальному сценарию согласия (несогласия) в широком смысле. Пэн и др. (2011) предложили непараметрическую оценку ρ _bsa ( X , Y ). Они установили теоретические свойства своей оценки и соответственно разработали процедуры вывода для ρ _bsa ( X , Y ).
2.2. Предлагаемая структура регрессии для показателя BSA
Пусть Z обозначает вектор независимых переменных. Наблюдаемые данные состоят из n случайных выборок ( X , Y , Z ), обозначаемый {( X _i , Y _i , Z _i ) : i = 1, 2, …, } .
Сначала мы вводим концепцию согласованности в широком смысле с поправкой на ковариацию в качестве основы предлагаемой модели регрессии. В частности, мы определяем согласованность в широком смысле с поправкой на ковариацию (BSA) как l=1L(l-R[l])2∣Z},
(2)
, где E (·| Z ) обозначает условное ожидание, заданное Z и E _X _⊥ _Y _| _Z (·| Z ) обозначает условное математическое ожидание, заданное Z при независимости между X и Y , заданное Z .
Показатель BSA с поправкой на ковариацию, определенный в (2), легко интерпретировать. Интуитивно, ρ _bsa ( X , Y | Z ) можно рассматривать как показатель BSA для подгруппы с общим значением Z . Как и его нескорректированный аналог ρ _BSA ( x , Y ), ρ _BSA ( x , Y | Z ). bsa ( X , Y | Z ) ≤ 1. Большая звездная величина ρ _bsa ( X , Y | Z = z ) предполагает высокую вероятность интерпретации непрерывного измерения X в соответствии с порядковой шкалой Y для субпопуляции1, характеризуемой Z я .
Основываясь на концепции BSA с поправкой на ковариацию, естественный подход к формулированию модели регрессии для BSA состоит в том, чтобы указать ρ _bsa ( X , Y | Z ) как функцию Z (т. е. функция регрессии). То есть мы предполагаем
ρ _BSA ( x , Y ∣ Z = Z ) = M ( Z ),
), где
,
,
,
,
,
),
(),
(
),
),
),
(
). m ( z ) — функция гладкой регрессии, функциональная форма которой не определена. Модель (3) представляет собой непараметрическую модель, которая позволяет надежно и гибко исследовать неоднородность в BSA. Оценка функции регрессии m (·) может помочь выявить, как BSA между X и Y меняется с Z . Он также может предоставить более точную меру для описания выравнивания между X и Y с учетом ковариаты Z .
Не ограничивая общности и для простоты изложения, в дальнейшем мы сосредоточимся на случае, когда Z — одна непрерывная ковариата. Включение дискретных ковариат в модель (3) эквивалентно проведению стратифицированного анализа только с непрерывными ковариатами. Расширение наших предложений в разделе 2.3 для включения нескольких непрерывных ковариат является довольно простым и отмечено в разделе 6.
3.1. Оценка функции регрессии
В этом подразделе мы предлагаем непараметрическую оценку m (·), основанную на соответствующей адаптации метода ядерной регрессии (Надарая, 1965; Уотсон, 1964) в контексте регрессии BSA.
Чтобы применить метод ядерной регрессии для получения непараметрической оценки m (·), мы сначала отметим, что
EX⊥Y∣Z{∑l=1L(l-R[l])2∣Z}=CL. Это можно показать по линиям Peng et al. (2011). Учитывая этот результат, модель (3) можно переписать в виде
1-E{∑l=1L(l-R[l])2∣Z}CL=m(z).
Это означает, что для оценки м ( z ) нам нужно только получить оценку
E{∑l=1L(l-R[l])2∣Z=z}. Участие ранговой статистики R _[ _l _] ( l = 1, …, L ) в
E{∑l=1L(l-R[l])2∣Z=z} влечет за собой сравнение нескольких распределений, а именно распределений X при заданном Y = l ( l = 1, …, L ), когда Z = Z . В условиях одной выборки Peng et al. (2011) приняли идею стратифицированной повторной выборки и рассмотрели все возможные группы L наблюдений ( X , Y ) с различными значениями Y . Чтобы обобщить эту стратегию на случай регрессии, мы предлагаем далее использовать идею ядерной регрессии, с помощью которой мы заимствуем информацию из наблюдений со значениями ковариации, близкими к Z = z , чтобы построить оценку для м ( z ).
Более конкретно, пусть S⃗ = (1, 2, …, L ). Не ограничивая общности, сначала упорядочим наблюдаемые данные следующим образом:
(Y1=1,X1,Z1),…,(Yn1=1,Xn1,Zn1),(Yn1+1=2,Xn1+1,Zn1+1),…,(Yn1+n2=2,Xn1 +n2,Zn1+n2),⋮…⋮(Y∑l=1L-1nl+1=L,X∑l=1L-1nl+1,Z∑l=1L-1nl+1),…,(Y∑ l=1Lnl=L,X∑l=1Lnl,Z∑l=1Lnl)}
(4)
где n _l обозначает количество наблюдений с Г = л и
∑l=1Lnl=n. Определять
X∼s,ts=X∑l=1s-1nl+ts, где 1 ≤ t _с ≤ n _с (1 ≤ с ≤ L ). Let Z̃ _{s , t _s} denote the sample covariate associated with X̃ _{s , t _s} . Для х ⃗ = ( х ₁ , х ₂,…, x _L ) ′, мы определяем R⃗ ( X⃗ ) = ( R _[1], R _[2],… … R [2] ,… … R [2] ,… R [2] , R [2] , R [2] , R _[2],, R _[2],, R _L _] ), где
r[l]≡∑j=1LI(x[l]≥x[j]) обозначает ранг x _l среди { x ₁ , x ₂ , …, 9001 _л }. Предлагаем оценить
E{∑l=1L(l-R[l])2∣Z=z} по
Gn,hn(z)=∑j1=1n1…∑jL=1nL{khn(Z∼1,j1-z)×… ×khn(Z∼L,jL-z)‖S→-R→(X∼1,j1,…,X∼L,jL)‖2}∑j1=1n1…∑jL=1nL{khn(Z∼1 ,j1-z)×…×khn(Z~L,jL-z)},
где || · || – евклидова норма в ℛ ^L , h – параметр сглаживания (полоса пропускания), а
kh(z)=hn-1k(hn-1z). Здесь k (·) — неотрицательная симметричная непрерывная ядерная функция, удовлетворяющая условию ∫ || к ( z )|| dz < ∞ and ∫ k ( z ) dz = 1. By the definition above, G _{n , h _n} ( z ) may be рассматривается как средневзвешенное значение случайных выборок || S⃗ − R⃗ ( X̃ _{1, j ₁} , …, X̃ _{L , j _L} )|| ² с Z ∈ [ z − h _n , z + h _n ]. Когда пропускная способность h _n → 0 при увеличении n , мы ожидаем G _{n , h _{n 9(z)=1-Gn,hn(s)CL.}}
(5)
Мы можем показать, что || S⃗ − R⃗ ( X̃ _{1, j ₁} , …, X̃ _{L , j _L} )|| ² ≤ 2 C _L (Peng et al. 2011), и, следовательно, −1 ≤ m̂ ( z ) ≤ 1.
3.2. Асимптотические свойства
Сначала введем необходимые обозначения и условия регулярности. Пусть p _l = P ( Y = l ). Пусть f ₍ _X _, _Z _{) |} _Д ₌ _l ( x , z ) обозначают условную совместную плотность X и Z при заданном Y = l . Аналогично, мы принимаем обозначение в виде f _V ( v ) для обозначения функции плотности случайной величины V . Позволять
{(Xˇ[l],Zˇ[l])}l=1n — независимые пары случайных величин, где _] ) соответствует плотности соединения f ₍ _X _, _Z _)| _Д ₌ _л ( x , z ). Определить V _i = ( X _i , Y _i , Z _i ) T. Позволять
σn2(z)=nVar[ξn,1(z,V1)], где ξ _n _,1 ( z , V ₁ ) определено в (8) приложения А.
Определить
m*(z1,z2,…,zL)=E[∑l=1L(l-R[l])2∣Zˇ[1]=z1,Zˇ[2]=z2,…,Zˇ[L ]=zL].
By the definition of ρ _bsa ( X , Y | Z ), under model (3), we have m _* ( z , z , …, z ) = C _L {1 − м ( z )}.
Примем следующие условия регулярности:
C1
p _l > 0 для l = 1, …, L .
C2
lim _n _→∞ h _n → 0 и
limn→∞nhnL=∞.
C3
F _{ž _{[ L ]}} ( Z ), Longer Lawner = 1, . .., L. ). производные второго порядка.
С4
м _* ( з ₁ , Z ₂,…, Z _L ) — это ограниченная непрерывная функция ( Z ₁, Z ₂,…, Z , 2 ,…, Z 2 ,…, Z 2 ,…, Z 2 ,…, Z , 2 . непрерывные частные производные первого и второго порядка.
C5
limn→∞hn2nhnL=λ, 0 ≤ λ < ∞.
C6
lim _n _→∞ σ _n ( z8 ) =(z)-m(z)]+λCL-1{∏l=1LfZˇ[l](z)}-1B(z)→dN(0,σ2(z)),
, где B ( z ) определено в Приложении A (см. лемму 1).
Для доказательства теорем 1 и 2 основная идея состоит в том, чтобы m̂ ( z ) аппроксимировать U-статистикой, А). Используя теорию U-статистики и стандартные аргументы ядерной регрессии, мы устанавливаем согласованность m̂ ( z ). Для асимптотического распределения 9(z)-m(z)] с соответствующей поправкой на разницу между m̂ ^[1] ( z ) и m̂ ( z ). Подробные доказательства теорем 1 и 2 приведены в Приложении A.
Как предложил один рецензент, можно улучшить скорость сходимости m̂ ( z ), наложив предположения о гладкости более высокого порядка на m _* ( ·) и f _{Ž _{[ l ]}} (·) и использование другого выбора полосы пропускания и ядра более высокого порядка. Такое асимптотическое уточнение является многообещающим и заслуживает дальнейших исследований
3.3. Выбор полосы пропускания
Выбор параметра сглаживания (полосы пропускания) ч является важной практической задачей. Типичная стратегия состоит в том, чтобы определить целевую функцию, которая измеряет производительность оценки с заданной полосой пропускания, а затем выбрать полосу пропускания, которая дает оптимальное значение целевой функции. По сравнению с обычными регрессионными моделями, дизайн целевой функции оценки производительности менее прост в настройке регрессии BSA. Это потому, что { R _[1] , …, R _[( _L _)] } с Z = z 900, непосредственно не наблюдается
To assess the performance of a given bandwidth, we utilize the fact that ρ _bsa ( X , Y ) = E { ρ _bsa ( X , Y | Z )}. По этому факту мы сначала оцениваем нескорректированную меру BSA 9∗∗(h)∣.
(6)
На практике рекомендуется начинать с начальной полосы пропускания h ₀ , а затем искать в сетке на интервале [ h ₀ /3, 3 h 0 _{] найти оптимальную полосу пропускания h _opt , определенную в (6). Рекомендуемая начальная пропускная способность: ч ₀ = ( σ̂ ² / n ) ^1/ ^L 42}
, где 429269,0017 σ̂ — оценка стандартного отклонения для ρ̂ _bsa ( X , Y ) (Пенг и др. , 2011). Такой выбор ч ₀ мотивирован нашими результатами по асимптотической среднеквадратической ошибке (AMISE) м̂ (·). В Приложении B мы показываем, что AMISE минимизируется при ширине полосы, которая имеет тот же порядок, что и описанная выше ч ₀.
3.4. Вывод
Учитывая сложную аналитическую форму числа σ ² ( z ), мы предлагаем оценить асимптотическую дисперсию m̂ ( z ) методом складного ножа. That is, let m̂ ⁻ ⁱ ( z ) denote the proposed estimator of m ( z ) obtained from the data excluding ( X _i , Y _i , Z _и ). Оценщик дисперсии складного ножа m̂ ( 9(z))],
, где z ₁₋ _α _/2 обозначает 100 (1 − α /2)-й процентиль N 0, N 0,). (z(1))). 9н-1Дн,хн. Мы можем показать, что при нулевой гипотезе H ₀ предельное распределение T _n равно
хд-12. Следовательно, можно отклонить нулевую гипотезу, когда T _n больше 100 (1 − α )-го процентиля
хд-12.
Мы провели симуляционные исследования, чтобы оценить производительность предложенных методов на конечной выборке. Мы рассмотрели две установки моделирования. В обеих установках мы устанавливаем L = 3 и генерируем Y из полиномиального распределения с вероятностью (1/3, 1/3, 1/3) и Z из равномерного распределения, Unif (0, 1). В установке (I) мы сгенерировали X , учитывая Y = 1 и Z = z из Unif (0, 1), X , учитывая Y = 007 и Z . z из Unif (1 − 0,5 z , 1 + 0,5 z ), и X с учетом Y = 3 и Z = z из Unif (1, 2). В установке (II) мы сгенерировали X , учитывая Y = 1 и Z = z из Unif (0, 1), X , учитывая Y = 07 и Z . z из Unif (0,5, 1,5) и X с учетом Y = 3 и Z = z из Unif (1, 2). Путем некоторых алгебраических преобразований мы можем показать, что m ( z ) = 1 − z /8 при установке (I) и м ( z ) = 0,875 при установке (II).
Мы применили предложенный метод для оценки м ( z ) как для установки (I), так и для установки (II), приняв функцию ядра Гаусса (второго порядка). Предложенные процедуры выбора полосы пропускания на основе (6) дали полосы пропускания h = 0,20 и 0,15 для n = 100 и 200 соответственно. В представлено m̂ ( z ) для z = 0,1, 0,3, 0,5, 0,7 и 0,9, соответствующие эмпирические стандартные отклонения, оценки среднего стандартного отклонения на основе складного ножа и эмпирические вероятности охвата 95% доверительных интервалов на основе 500 смоделированных наборов данных размером n = 100 и 200. Из , мы видим, что m̂ ( z ) практически беспристрастен. Расчетные стандартные отклонения, основанные на методе складного ножа, хорошо согласуются с эмпирическими стандартными отклонениями. Величина эмпирических стандартных отклонений предполагает довольно хорошую эффективность оценки m̂ ( z ) при размере выборки 100. Как и ожидалось, стандартные отклонения уменьшаются по мере увеличения размера выборки. 95% доверительные интервалы имеют вероятности охвата, близкие к номинальному уровню.
Таблица 1
Результаты моделирования на м² ( z ): эмпирические систематические ошибки (EmpBias), эмпирическое стандартное отклонение (EmpSD), оценочное стандартное отклонение (EstSD) и эмпирические вероятности охвата 95% доверительного интервала (Cov95).
0,95 9007 7 8 0092 920 4004278 0. 875 0,0278 0,000 0,0278 0,000,0,0278 0,000,0,0278 0,000 0. 4278 0.5 Setup n z m ( z ) EmpBias EmpSD EstSD Cov95
(I) 100 0. 1 0.988 0.011 0.015 0.015 0.93
0.3 0.963 0.003 0.017 0.017 0.92
0.5 0.938 0.001 0. 021 0.022 0.94
0.7 0.913 −0.003 0.026 0.027 0.92
0.9 0.888 −0.013 0.034 0.037 0. 89
200 0.1 0.988 0.014 0.011 0.011 0.95
0.3 0.963 0.003 0.012 0.013 0.97
0. 5 0.938 −0.002 0.015 0.017 0.96
0.7 0,913 −0,006 0,017 0,021 0,97
0,9 0,888 –0,0,0,0987 0,888 о0087 0,93
(II) 100 0. 1 0.875 0.000 0.038 0.040 0.94
0.3 0.875 0.000 0.031 0.033 0.94
0,5 0,875 0,000 0,030 0,031 −0.001 0.031 0.032 0.94
0.9 0.875 −0.001 0.037 0.040 0.94
200 0.1 0.875 0.001 0,024 0,026 0,97
0,3 0,875 0,000 0,020 0,020 0,020 0,020 0,020 0.875 −0.003 0.021 0.021 0.95
0.7 0.875 −0.001 0.021 0.022 0.96
0.9 0.875 0. 003 0,023 0,027 0,95
Открыть в отдельном окне
0017 м ( z ) над z . For both setups, we let z ⁽¹⁾ = 0.20, z ⁽²⁾ = 0.40, z ⁽³⁾ = 0.60, and z ⁽⁴⁾ = 0.80 , которые соответственно являются 20-м, 40-м, 60-м и 80-м квантилем Z . В , мы сообщаем об эмпирических коэффициентах отклонения H ₀ . Обратите внимание, что м ( z ) является постоянной функцией в настройке (II). Таким образом, эмпирические показатели отказа при установке (II) соответствуют эмпирическим размерам предлагаемого теста.
Таблица 2
Результаты моделирования эмпирических коэффициентов отклонения теста постоянства.
Setup Sample Size (n) Rejection Rate
(I) 100 0.41
200 0.77
(II) 100 0,04
200 0,05
Открыть в отдельном окне
Представленные результаты демонстрируют удовлетворительное выполнение предложенного теста на постоянство для м ( z ). В установке (II) эмпирические размеры довольно близки к номинальному уровню 0,05. При установке (I) эмпирические коэффициенты отклонения составляют 41% и 77% для n = 100 и 200 соответственно. Этот результат демонстрирует хорошую мощность предложенного теста постоянства.
The Grady Trauma Study — перекрестное исследование, первоначально предназначенное для определения относительного вклада генетических и связанных с травмой факторов риска развития посттравматического стрессового расстройства (ПТСР) у сильно травмированного гражданского городского населения с низким социально-экономическим статусом, преимущественно африканского происхождения. Американские мужчины и женщины. Участникам этого исследования было предложено заполнить опросники из 17 пунктов шкалы самоотчета о симптомах посттравматического стрессового расстройства (PSS-SR), самоотчета о симптомах посттравматического стрессового расстройства, во время ожидания в приемных отделениях первичной медико-санитарной помощи или акушерско-гинекологических клиниках Грейди. Мемориальный госпиталь в Атланте, Джорджия, США. Шкала посттравматического стресса (CAPS) из 17 пунктов, применяемая клиницистами (Foa and Tolin 2000; Foa et al. 19).93)) вводили обученные клиницисты для подгруппы участников исследования, которые согласились на более тщательную оценку диагноза посттравматического стрессового расстройства. Тяжесть клинической депрессии у участников исследования также измерялась с помощью анкеты самоотчетов из 21 пункта, измеряющей BDI (Beck et al., 1961).
Категориальный диагноз посттравматического стрессового расстройства на основе CAPS (т. е. посттравматическое стрессовое расстройство в сравнении с отсутствием посттравматического стрессового расстройства) является наилучшей доступной психиатрической диагностикой посттравматического стрессового расстройства. Однако администрирование CAPS занимает много времени и требует специально обученного персонала. Поэтому представляется практически привлекательным исследовать, как более простые и менее дорогостоящие самооценки PSS могут служить потенциальной заменой CAPS, принимая во внимание характеристики субъекта, измеренные в этом исследовании. Одной из характеристик, представляющих особый интерес, является тяжесть депрессии, измеряемая по сумме баллов BDI. Это связано с тем, что посттравматическое стрессовое расстройство часто сочетается с большим депрессивным расстройством (БДР) (Breslau, Davis, Andreski, and Peterson 19).91; Кесслер и др. 1995, 2005). В результате пациенты с посттравматическим стрессовым расстройством могут иметь очень вариабельные фенотипы в области депрессии. Например, баллы BDI в нашем наборе данных колеблются от 0 до 48, отражая широкий диапазон тяжести депрессии от отсутствия или незначительных симптомов депрессии до тяжелых симптомов депрессии. Поправка на неоднородность населения, полученная с помощью баллов BDI, при оценке согласованности между CAPS и PSS приведет к более точному представлению о полезности PSS в качестве потенциального суррогата CAPS.
Руководствуясь этими соображениями, мы провели анализ для оценки BSA между порядковым диагнозом посттравматического стрессового расстройства, основанным на CAPS, и непрерывной оценкой PSS, а также того, как она зависит от общей оценки BDI. В наш анализ были включены 956 субъектов исследования Grady Trauma Study, у которых была полная информация о диагнозе CAPS (ПТСР в сравнении с отсутствием ПТСР), общих баллах PSS (0–51) и общих баллах BDI (0–63). Без поправки на баллы BDI предполагаемый BSA между диагнозом CAPS и баллом PSS составляет 0,617 со стандартной ошибкой, 0,034 и 95% доверительный интервал (0,550, 0,684).
Чтобы изучить, как BSA между диагнозом CAPS и BDI может меняться в зависимости от оценки BDI, мы сначала рассчитали оценки BSA отдельно для четырех групп субъектов, определенных оценкой BDI (т. е. 0 ≤ BDI < 10, 10 ≤ BDI < 20, 20 ≤ BDI < 30, BDI ≥ 30). На рисунке показаны оценки BSA и соответствующие 95% доверительные интервалы для этих четырех групп BDI. Показано, что оценка BSA между диагнозом на основе CAPS и оценкой PSS довольно высока для группы с низким показателем BDI (т. е. 0 ≥ BDI < 10), около 0,63, в то время как оценки BSA намного ниже для групп с высоким BDI. Например, для группы с показателем BDI от 20 до 30 расчетный BSA составляет всего около 0,25.
Мы применили предложенный метод непараметрической регрессии, чтобы исследовать, как BSA между диагнозом CAPS и PSS изменяется с оценкой BDI. В мы наносим оценки для м ( z ) с z = 0, 1, …, 40 вместе с соответствующими 95% доверительными интервалами. Полоса пропускания, выбранная предложенной процедурой, составляет ч = 6 в этом примере. демонстрирует общую тенденцию к снижению BSA по мере увеличения показателя BDI, что согласуется с исследовательским анализом в . В также приведены оценки для m ( z ) с z = 1, 5, 10, 15, 25, 40 и соответствующими стандартными ошибками и 95% доверительными интервалами. И то, и другое предполагает значительное несоответствие (или несоответствие) между диагнозом CAPS и баллами PSS у субъектов с симптомами тяжелой депрессии. Некоторые подтверждающие описательные данные также представлены в , где представлены диаграммы показателей PSS отдельно для субъектов с диагнозом посттравматического стрессового расстройства и без посттравматического стресса (на основе CAPS), стратифицированных по показателям BDI. Показано, что субъекты с симптомами тяжелой депрессии (например, BDI ≥ 30) имеют довольно схожие самооценки PSS в группе с диагнозом посттравматического стрессового расстройства и в группе без диагноза посттравматического стресса. Это говорит о том, что ПСШ гораздо менее показательно для диагноза КАФС у субъектов с тяжелыми симптомами депрессии, чем у лиц с легкими симптомами депрессии. Это интересное открытие не может быть обнаружено с помощью нескорректированного анализа BSA.
Открыть в отдельном окне
Расчетная функция регрессии BSA относительно показателя BDI (сплошная линия) и соответствующих точечных 95% доверительных интервалов (пунктирные линии).
Открыть в отдельном окне
Диаграммы PSS, соответствующие диагнозу CAPS, стратифицированные по шкале BDI. Таблица 30009
z
BDI m̂ ( z ) SE 95% CI
1 0. 62 0.073 (0.48, 0.76)
5 0.58 0.059 (0.46, 0.70)
10 0.54 0.052 (0.44, 0.64 )
15 0.51 0.048 (0. 42, 0.60)
25 0.40 0.060 (0.28, 0.52)
40 0.35 0.118 (0.12, 0.58)
Open in отдельное окно
Мы также применили наши предложения в разделе 3.4, чтобы оценить, является ли интересующий BSA постоянным по сравнению с показателем BDI. Ставим z ⁽¹⁾, z ⁽²⁾, z ⁽³⁾ и z ⁽⁴⁾ как 20-й, 40-й, 60-й и 80-й процентили наблюдаемых показателей BDI, которые равны 4, 8, 14 и 22 соответственно. Мы получили тестовую статистику T _n = 7,99, которая дает значение p = 0,046. Этот результат предполагает, что BSA между диагнозом CAPS и PSS может меняться в зависимости от оценки BDI. Практический вывод заключается в том, что PSS может служить разумной заменой CAPS у пациентов с посттравматическим стрессовым расстройством с низкими симптомами депрессии. Однако диагнозы PSS и CAPS могут быть плохо согласованы у субъектов с тяжелой депрессией. Эти результаты дают гораздо более точное представление о взаимосвязи между CAPS и PSS по сравнению с результатами простого одновыборочного исследования BSA.
В этой статье мы предложили метод непараметрической регрессии для согласования в широком смысле (BSA). Мы адаптировали метод ядерной регрессии в контексте BSA и подробно обосновали наши предложения. Новый метод предоставляет надежный инструмент для изучения неоднородности населения в соответствии между порядковым измерением и непрерывным измерением, что может дать полезную научную информацию.
Для простоты представления мы представляем новую структуру регрессии BSA в случае с одной единственной непрерывной ковариантой. Наши предложения можно легко обобщить на ситуации с несколькими непрерывными ковариатами, например, приняв ядерную функцию многомерного произведения. При работе с несколькими ковариатами новый метод, учитывая его гибкость моделирования, может потребовать большого размера выборки для получения достаточно точной оценки. Многообещающее практическое использование предложенного метода состоит в том, чтобы исследовать соответствующую функциональную форму эффекта непрерывной ковариаты на интересующий BSA. Полученные результаты могут помочь в разработке более ограничительной модели регрессии для BSA, которая обеспечивает лучшую интерпретируемость и эффективность оценки.
Это исследование поддерживается грантом Национального института здравоохранения США 5R01 MH079448-06. Авторы благодарят доктора Таню Йованович за предоставление набора данных из исследования посттравматического стрессового расстройства и стимулирующие обсуждения.
Notation
Define V̌ _[ _l _] = ( X̌ _[ _l _] , Y̌ _[ _l _] = л , Ž _[ _л _]) ^Т . Пусть X̌ = ( X̌ _[1], X̌ _[2],… X̌ _[ _{L ₇7}7777779276766676766767676767666EN 67676767676767676767676767676767676676767676676767667676666). = ( ž _[1], ž _[2],…, ž _[ _L _]) _]) _]) _]) _]) _]) _L _]7 _{] )0018, и ž = ( ž _[1],…, ž _[ _L _]) 677 _]) 68677}. затем
fZˇ(zˇ)=∏l=1L{fZˇ[l](zˇ[l])}. Обратите внимание, что
R[l]=∑j=1LI(Xˇ[l]≥Xˇ[j]). Let Θ _L denote the sample space of R⃗ = ( R _[1] , …, R _[ _L _] ) which consists of L ! перестановки {1, 2, …, L } и ω _N _, _L = {( J ₁, J _{2 ₁, J 9277 2} 1 , J 9276 2 1 , J 9277 2 1 , J _71,, J 2 ₁. _l ≤ n , j ₁ , …, j _L все различны}. Пусть γ _L = 1/( L ! C _L ).
Пусть H _f (·) обозначает гессиан функции f и
ν2=(∫u12k(u1)du10…00∫u12k(u2)du2…0⋮⋮…⋮00…∫uL2k(uL)duL).
For ( m ₁ , …, m _L ) ∈ Ω _n _, _L , define
ψhn(z,Vm1,…,VmL)= I{(Ym1,…,YmL)∈ΘL}×[{khn(Zm1-z)×…×khn(ZmL-z)}×∑l′=1L{Yml′-∑r=1LI(Xml′≥Xmr )}2],ϕhn(z,Vm1,…,VmL)=[I{(Ym1,…,YmL)∈ΘL}{khn(Zm1-z)×…×khn(ZmL-z)}],
и
g(z,V1,…,VL)=1-ψhn(z,V1,…,VL)γL[∏l=1L{fZˇ[l](z)}]-1(∏l=1Lpl) -1.
Define W _{h _n} ( z ) = Σ _{( m ₁ ,…, m _L )∈Ω _n , L} [ ϕ _{h _n} ( z , V _{m ₁} , …, V _{m _L} )],
Mn,L(z)=(nL)Whn(z)CL,Tn,hn=Whn(z)/(nL), 9[2](z)={(nL)-1∑(m1,…,mL)∈Ωn,Lψhn(z,Vm1,…,VmL)}×[Mn,L(z)-γL{∏l=1LfZˇ [l](z)}(∏l=1Lpl)].
In addition, let g ₁ ( z , v ₁ ) = E [ g ( z , v ₁ , V ₂ ,…, V _L )], ζ _{H _N, 1} ( Z ) = VAR [ G69776777777777777777677777677767777677776767777777767777677776777767677767776777767776767. 9 29176) = .0018 , V ₁ )], g̃ ₁ ( z , V ₁ ) = g ₁ ( z , V ₁ ) − E [ G ( Z , V ₁, V ₂,…, V _L )] и ϕ 9277 L )] и ϕ 9277 L )] и ϕ 9277 L )] и ϕ _). ( z , v ₁ ) = E { ϕ _{H _N} ( Z , V ₁, V _{2 _{,…, V _{2 9277,… . .., V _{2 9277,… ... V ₂,… 9277 V V _{2 9277,… 9277 V V _{2 _{,… V _{. h _n} ( z , V ₁ ) = ϕ _{1, h _n} ( z , V ₁ ) − E { ϕ _{ч _n} ( z , V ₁ , …, V _L )}.}}}}}}}
Технические леммы и доказательства
Лемма 1
В условиях C 2 – C 4,
E[ψhn(z,V1,…,VL)]=aL(z)+hn2L!(∏ =1Lpl)B(z)+O(hn3),
где
aL(z)=L!(∏l=1Lpl){∏l=1LfZˇ[l](z)}CL{1-m(z)} и
B(z)=B1(z)+12{∏l=1LfZˇ[l](z)}B2(z)+12m∗(z)B3(z) с B ₁ ( z ) = [∇ м _* ( z )] ^T ν ₂ ∇ f _ž ( z ), B ₂ ( z ) = trace{ H _{m _*} ( z ) ν ₂ }, and B ₃ ( z ) = trace{ H _{f _Ž} ( z ) ν ₂ }.
Доказательство леммы 1
Во-первых, имеем
E[ψhn(z,V1,…,VL)]=E[I{(Y1,…,YL)∈ΘL}×{khn(Z1-z)×…×khn(ZL -z)}×{∑l′=1L{Yl′-∑r=1LI(Xl′≥Xr)}2}]=P{(Y1,…,YL)∈ΘL}×E[{khn(Z1- z)×…×khn(ZL-z)}×{∑l′=1L{Yl′-∑r=1LI(Xl′≥Xr)}2}∣(Y1,…,YL)∈ΘL]=L! (∏l=1Lpl)E[{khn(Z1-z)×…×khn(ZL-z)}×{∑l′=1L{Yl′-∑r=1LI(Xl′≥Xr)}2}∣ Y1=1,…,YL=L].
By the definition of ( Ž _[1] , Ž _[2] , …, Ž _[ _L _] ) ^T , the conditional distribution of ( Z ₁ , …, Z _L ) ^T given ( Y ₁ = 1, …, Y _L = L ) совпадает с распределением ( Ž _[1] , …, Ž _[ _L _{] 9,28018 T 9,208017 9. Следовательно,}
E[ψhn(z,V1,…,VL)]=L!(∏l=1Lpl)×E[{khn(Zˇ[1]-z)×…×khn(Zˇ[L]-z )}×∑l=1L{l-∑r=1LI(Xˇ[l]≥Xˇ[r])}2]=L!(∏l=1Lpl)×E[{khn(Zˇ[1]-z) ×…×khn(Zˇ[L]-z)}×∑l=1L(l-R[l])2]=L!(∏l=1Lpl)×E[{khn(Zˇ[1]-z)×… ×khn(Zˇ[L]-z)}×E{∑l=1L(l-R[l])2∣Zˇ[1],…,Zˇ[L]}]=L!(∏l=1Lpl)×E [{(1/hn)k((Zˇ[1]-z)/hn)×…×(1/hn)k((Zˇ[L]-z)/hn)}×m∗(Zˇ[1] ,…,Zˇ[L])].
For j = 1, 2, …, L , let ( Ž _[ _j _] − z )/ h _n = u _j и u = ( u ₁ , …, u _L ) ^T . Применяя разложение Тейлора в окрестности z = ( х ₁ = z , …, х _L = z ) ^T , получаем
E[ψhn(z,V1,…,VL)]=L!(∏l=1Lpl)×∫{k(u1)×…×k(uL) }×m∗(z+hnu)fZˇ(z+hnu)du1…duL=L!(∏l=1Lpl)×∫{k(u1)×…×k(uL)}×{m∗(z)+ hnuT∇m∗(Zˇ)∣Zˇ=z+hn22uTHm∗(Zˇ)∣Zˇ=zu+O(hn3)}×{fZˇ(z)+hnuT∇fZˇ(Zˇ)∣Zˇ=z+hn22uTHfZˇ(Zˇ)∣ Zˇ=zu+O(hn3)}du1…duL=L!(∏l=1Lpl){m∗(z)fZˇ(z)}+L!(∏l=1Lpl)hn2∫[∇m∗(z) ]TuuT[∇fZˇ(z)]{k(u1)×…×k(uL)}du1…duL+L!(∏l=1Lpl)hn22fZˇ(z)∫uTHm∗(z)u{k(u1) ×…×k(uL)}du1…duL+L!(∏l=1Lpl)hn22m∗(z)∫uTHfZˇ(z)u{k(u1)×…×k(uL)}du1…duL+O( hn3)
С ∫ K ( U _L ) DU _L = 1 и ∫ U _L K ( L _L ) DU 9277 L _{L _{7777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777777. 9277 1, 2,…, L , мы имеем}}
∫ ⋯ ∫ ∫ U ₁ U ₂ { K ( U 1 ) × × 9276 1 ) × × 1 ) × × 9276 1 )… u 1 )… U 1 927) × U 1 927). _L )} d u ₁ d u ₂ … d u _L = ∫ u ₁ k ( u ₁ ) d u ₁ × ∫ u ₂ K ( U ₂) D U ₂ = 0
и
∫U12 {K (U1) ×… × k (ul) x2 x2 x2 x2 x2 x2 {2 x2 {12 {u (u1) × du13 ∫ (у1)ду1.
Эти результаты ведут к дальнейшему упрощению E [ ψ _h ( z , V ₁ , …, V _L )] после стандартных алгебраических действий:
E[ψhn(z,V1,…,VL)]=L!(∏l=1Lpl)[CL{1-m(z)}{∏l=1LfZˇ[l](z)}]+hn2L! (∏l=1Lpl)[B1(z)+12B2(z){∏l=1LfZˇ[l](z)}+12m∗(z)B3(z)]+O(hn3).
Следовательно,
E[ψhn(z,V1,…,VL)]=aL(z)+hn2L!(∏l=1Lpl)B(z)+O(hn3).
Лемма 2
При условиях C 2 и C 4,
E[ϕhn(z,V1,…,VL)]=L!(∏l=1Lpl){∏l=1LfZˇ[l] (z)}+O(hn2). 9[1](z)]=L2nζhn,1+O(1n2hn2L)=L2nζhn,1+o(1nhnL).
Вычисление ζ _{h _n ,1} дает, что
ζhn,1=Var[g1(z,V1)]≤Var[g(z,V1)]≤Var[g(z,V1)][g(z,V1)][g(z,V1)][g(z,V1)][g(z,V1)][g(z,V1)][g(z,V1)][g(z,V1)][ Следствие 3.2(i) из Shao (2003)]=[γLfZˇ-1(z)(∏l=1Lpl)-1]2Var[ψhn(z,V1,…,VL)]≤[γLfZˇ-1(z)( ∏l=1Lpl)-1]2E[ψhn(z,V1,…,VL)]2=L!(∏l=1Lpl)[γLfZˇ-1(z)(∏l=1Lpl)-1]2×E [{khn(Zˇ[1]-z)×…×khn(Zˇ[L]-z)}2×{∑l=1L{l-R[l]}2}2]≤[1L!CL2fZˇ-2(z )(∏l=1Lpl)-1]{L2(L-1)4}E[{khn(Zˇ[1]-z)×…×khn(Zˇ[L]-z)}2]=[1L! CL2fZˇ-2(z)(∏l=1Lpl)-1{L2(L-1)4}]×1hnL{fZˇ(z)κL2+O(hn2)}=1hnL[1L!CL2fZˇ-1(z)( ∏l=1Lpl)-1κL2{L2(L-1)4}]+O(hn2hnL)=1hnL[36(L-1)2L!(L+1)2fZˇ-1(z)(∏l=1Lpl) -1κL2]+O(hn2hnL), 9[1](z)-m(z)=n-1∑i=1nLg∼1(z,Vi)-hn2CL-1{∏l=1LfZˇ[l](z)}-1B(z)+O( hn3)+op(1nhnL)
(10)
Applying similar arguments to T _{n , h _n} ( z ) and using Lemma 2, we obtain
Tn ,hn(z)-L!(∏l=1Lpl){∏l=1LfZˇ[l](z)}=Ln∑i=1nϕ∼1,hn(z,Vi)+O(hn2)+op(1nhnL ).
(11)
Обратите внимание, что
Mn,L(z)-γL{∏l=1LfZˇ[l](z)}(∏l=1Lpl)=(nL)Whn(z)CL-γL{∏ l=1LfZˇ[l](z)}(∏l=1Lpl)=-CL-1{∏l=1LfZˇ[l](z)}L!{∏l=1Lpl}1{Whn(z)/(nL )}×[Th,hn(z)-L!(∏l=1Lpl){∏l=1LfZˇ[l](z)}]
(12)
Повторяя линии в доказательстве леммы 3, мы можем показать, что
Var[Whn(z)/(nL)]=O(1/nhnL). Это вместе с леммой 2 означает, что
Whn(z)(nL)=L!(∏l=1Lpl){∏l=1LfZˇ[l](z)}+O(hn2)+Op(1nhnL)
(13)
В силу (10), (12), (13) и условия C 2 имеем
Mn,L(z)-γL{∏l=1LfZˇ[l](z)} (∏l=1Lpl)=-1CL[L!(∏l=1Lpl){∏l=1LfZˇ[l](z)}]2×1n∑i=1nLϕ∼1,hn(z,Vi)+O( hn2)+Op(1nhnL).
(14)
Кроме того, при условии C2 из леммы 1 и леммы 2 следует 9[2](z)=∑i=1nξn,i-hn2nhnLCL-1{∏l=1LfZˇ[l](z)}-1B(z)+op(1).
Это завершает доказательство леммы 4.
Лемма 5
При условиях )2L!(L+1)2[∏l=1LfZˇ[l](z)]-1(∏l=1Lpl)-1κL2]+2{LaL(z)CL[{∏l=1LfZˇ[l]( z)}L!(∏l=1Lpl)]2}2L!(∏l=1Lpl)[∏l=1LfZˇ[l](z)]-1κL2+O(hn).
Доказательство леммы 5
Легко видеть, что0018 , В ₁ )} ²
=E[Lg∼1(z,V1)hnL+LaL(z)CL[{∏l=1LfZˇ[l](z)}L!(∏ l=1Lpl)]2ϕ∼1,hn(z,V1)hnL]2≤2L2hnLE{g∼1(z,V1)}2+2hnL{LaL(z)CL[{∏l=1LfZˇ[l](z )}L!(∏l=1Lpl)]2}2E{ϕ∼1,hn(z,V1)}2
Далее, следуя строкам, аналогичным приведенным в доказательстве леммы 3, получаем
E{g ∼1(z,V1)}2=Var[g1(z,V1)]≤Var[g(z,V1,V2…,VL)]≤E[g(z,V1,V2…,VL)]2 ≤1hnL[36(L-1)2L!(L+1)2fZˇ-1(z)(∏l=1Lpl)-1κL2]+O(hn2hnL)
и
E{ϕ∼1,hn(z ,V1)}2=Var[ϕ1,hn(z,V1)]≤Var[ϕhn(z,V1,…,VL)]≤E[ϕhn(z,V1,…,VL)]2≤1hnL[L !(∏l=1Lpl)fZˇ-1(z)κL2+O(hn)],
where κ _L is defined in Lemma 3. These results complete the proof of Lemma 5 and further imply that E { ξ _n _, _i ( z , В ₁ )} ² < ∞.
Доказательство теоремы 1
Сначала из (13) получаем, что
Mn,L(z)-γL{∏l=1LfZˇ[l](z)}(∏l=1Lpl)→p0. Тогда из (15) и применения теоремы Слуцкого следует, что
9[1](z)]=m(z)+O(hn2). Применяя теорему Слуцкого, получаем m̂ ^[1] ( z ) → _p m ( z ). Объединение этого результата с (17) приводит к m̂ ( z ) → _p m ( z ).
Доказательство теоремы 2
Поскольку лемма 5 подразумевает, что E [{ ξ _N _{, 1} ( Z , V 1 _{) at 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286, 9286. применить вариант центральной предельной теоремы Линдеберга (например, следствие 1.3 Шао (2003)) для оценки
∑i=1nξn,i(z,Vi). Это при условии 9(z)]≈h5[CL-1{∏l=1LfZˇ[l](z)}-1B(z)]2+σ2(z)nhL.}
AMSE — это точечная мера точности, а глобальная мера точности — асимптотическая среднеквадратическая ошибка (AMISE), определенная формулой AMISE = ∫ AMSE [ m̂ ( z )] dz . Асимптотически оптимальная пропускная способность функции ядерной регрессии часто получается путем минимизации AMISE (Ruppert, Sheather, and Wand 1995). Обратите внимание, что
ddhAMISE=0 подразумевает, что
h _opt = ( L / A ) ^{1/ L +4} [∫ σ ² ( z ) d z ] ^{1/ L +4} ( 1/ n ) ^{1/ L +4} ,
(19)
где
A=4CL-2∫[{∏l=1LfZˇ[l](z)}-1B(z)}-1B(z)} ]2дз.
Таким образом, оптимальная ширина полосы h _opt имеет порядок O ({∫ σ ² ( z ) dz / n } ^1/ ^L ⁺⁴ ). Мотивировано этим результатом, мы предлагаем выбрать начальное значение для нашего поиска полосы пропускания как H ₀ = ( σ̂ ² / N ) ^{1 /} 9 444444444444444444444444444444444444444444444444444444444444444444444444444444444SINS 686868686868686868686868686868686868686868686868686868^{. где σ̂ — расчетное стандартное отклонение для нескорректированной оценки BSA (Пенг и др., 2011).}
Бек А.Т., Уорд Ч., Мендельсон М.М., Мок Дж.Дж., Эрбо Дж.Дж. Инвентарь для измерения депрессии. Архив общей психиатрии. 1961;4:561–571. http://dx.doi.org/10.1001/archpsyc.1961.01710120031004. [PubMed] [Google Scholar]
Бреслау Н., Дэвис Г., Андрески П., Петерсон Э. Травматические события и посттравматическое стрессовое расстройство у городского населения молодых людей. Архив общей психиатрии. 1991; 48: 216–222. http://dx.doi.org/10.1001/archpsyc.1991.01810270028003. [PubMed] [Google Scholar]
Коэн Дж. Коэффициент согласия для номинальных шкал. Педагогическое и психологическое измерение. 1960; 20: 37–46. http://dx.doi.org/10.1177/001316446002000104. [Академия Google]
Коэн Дж. Взвешенная каппа: Положение о соглашении о номинальной шкале для масштабируемого несогласия или частичного кредита. Психологический вестник. 1968 г. http://personalityproject.org/r/src/contrib/psych/html/kappa.html. [PubMed]
Fleiss J, et al. Измерение согласования номинальной шкалы между многими оценщиками. Психологический вестник. 1971; 76: 378–382. [Google Scholar]
Фоа Э.Б., Толин Д.Ф. Сравнение версии интервью по шкале симптомов посттравматического стрессового расстройства и шкалы посттравматического стрессового расстройства, разработанной врачом. Журнал травматического стресса. 2000; 13: 181–19.1. http://dx.doi.org/10.1023/A:10077813. [PubMed] [Google Scholar]
Foa EB, Riggs DS, Dancu CV, Rothbaum BO. Надежность и валидность краткого инструмента для оценки посттравматического стрессового расстройства. Журнал травматического стресса. 1993; 6: 459–473. http://dx.doi.org/10.1002/jts.24405. [Google Scholar]
Гиллеспи С.Ф., Брэдли Б., Мерсер К., Смит А.К., Конни К., Гапен М., Вайс Т., Шварц А.С., Кубеллс Д.Ф., Ресслер К.Дж. Воздействие травм и связанные со стрессом расстройства у пациентов первичной медико-санитарной помощи в центральной части города. Общебольничная психиатрия. 2009 г.;31:504–14. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Кесслер Р., Соннега А., Бромет Э., Хьюз М., Нельсон С. Посттравматическое стрессовое расстройство в национальном обзоре сопутствующих заболеваний. Архив общей психиатрии. 1995; 52: 1048–1060. http://dx.doi.org/10.1001/archpsyc.1995.03
0066012. [PubMed] [Google Scholar]
Кесслер Р., Берглунд П., Демлер О., Джин Р., Мерикангас К., Уолтерс Э. Распространенность расстройств dsm-iv в течение жизни и возраст начала заболевания в репликации национального обследования сопутствующих заболеваний. Архив общей психиатрии. 2005;62:593–602. http://dx.doi.org/10.1001/archpsyc.62.6.593. [PubMed] [Google Scholar]
Kraemer HC. Расширение коэффициента Каппа. Биометрия. 1980; 36: 207–216. http://www.jstor.org/stable/2529972. [PubMed] [Google Scholar]
Лин ЛИК. Коэффициент корреляции соответствия для оценки воспроизводимости. Биометрия. 1989; 45: 255–268. http://www.jstor.org/stable/2532051. [PubMed] [Google Scholar]
Надарая Е.А. О непараметрических оценках функций плотности и кривых регрессии. Теория вероятностей и ее приложения. 1965;10:186–190. http://dx.doi.org/10.1137/1110024. [Google Scholar]
Пэн Л., Ли Р., Го Ю., Манатунга А. Методика оценки согласованности в широком смысле между порядковыми и непрерывными измерениями. J Amer Statist Assoc. 2011; 106:1592–1601. http://dx.doi.org/10.1198/jasa.2011.tm10483. [Бесплатная статья PMC] [PubMed] [Google Scholar]
Ruppert D, Sheather SJ, Wand MP. Эффективный селектор пропускной способности для локальной регрессии методом наименьших квадратов. J Amer Statist Assoc. 1995; 90: 1257–1270. http://links.jstor.org/sici?sici=0162-1459(199512)90:432<1257:AEBSFL>2.0.CO;2-0&origin=MSN. [Google Scholar]
Шао Дж. Спрингер Тексты в статистике. 2. Спрингер-Верлаг; Нью-Йорк: 2003. Математическая статистика. http://dx.doi.org/10.1007/b97553. [Google Scholar]
Watson GS. Гладкий регрессионный анализ. Санхи: Индийский статистический журнал, серия A (1961–2002) 1964; 26: 359–372. http://www.jstor.org/stable/25049340. [Академия Google]
Что является лучшим доказательством и как его найти
Почему научные данные лучше, чем только мнение экспертов?
В широком смысле доказательством исследования может быть любое систематическое наблюдение, направленное на установление фактов и получение выводов. Все, что не соответствует этому определению, обычно классифицируется как «экспертное мнение», в основу которого входят опыт работы с пациентами, понимание биологии, знание доклинических исследований, а также результаты исследований. Использование мнения экспертов в качестве единственной основы для принятия решений оказалось проблематичным, потому что на практике врачи часто слишком быстро вводят новые методы лечения, прежде чем они продемонстрировали свою эффективность, или слишком медленно внедряют проверенные методы лечения.
Однако клинический опыт имеет ключевое значение для интерпретации и применения данных исследований на практике, а также для формулирования рекомендаций, например, в контексте клинических руководств. Другими словами, данные исследований необходимы, но недостаточны для принятия правильных решений в отношении здоровья.
Какие исследования надежнее?
Не все доказательства одинаково надежны.
План любого исследования, качественного или количественного, при котором данные собираются от отдельных лиц или групп людей, обычно называется первичным исследованием. Существует много типов планов первичного исследования, но для каждого типа вопросов о здоровье есть один, который дает более достоверную информацию.
При принятии решения о лечении существует консенсус в отношении того, что наиболее надежным первичным исследованием является рандомизированное контролируемое исследование (РКИ). В этом типе исследования пациентам случайным образом назначают либо тестируемое лечение, либо сравнительное лечение (иногда называемое контрольным лечением). Случайный действительно означает случайный. Решение о включении кого-либо в ту или иную группу принимается как подбрасывание монеты: орел попадает в одну группу, решка — в другую.
Контрольное лечение может быть другим типом лечения или фиктивным лечением, которое не должно иметь никакого эффекта (плацебо). Затем исследователи сравнивают эффекты различных методов лечения.
Крупные рандомизированные испытания дороги и требуют времени. Кроме того, иногда может быть неэтично проводить исследование, в котором некоторым людям случайным образом было назначено не проходить лечение. Например, было бы неправильно давать кислород одним детям с приступом астмы и не давать его другим. В подобных случаях лучшим выбором могут быть другие планы первичного исследования.
Лабораторные исследования представляют собой еще один вид исследований. В газетах часто появляются сообщения об исследованиях, показывающих, как лекарство излечивает рак у мышей. Но то, что лечение работает на животных в лабораторных экспериментах, не означает, что оно будет работать и на людях. Фактически, большинство лекарств, которые, как было доказано, излечивают рак у мышей, не действуют на людей.
Очень редко мы не можем основывать свои решения о здоровье на результатах исследований. Иногда исследования не проводились, потому что врачи привыкли лечить состояние таким образом, который, казалось бы, работал. Это часто верно для лечения сломанных костей и операций. Но то, что нет исследований по лечению, не означает, что оно не работает. Это просто означает, что никто не может сказать наверняка.
Почему нам не следует читать исследования
Чтобы определить и обобщить все, что мы знаем о том или ином вмешательстве в здравоохранение, требуются огромные усилия. Количество данных резко возросло. По самым скромным подсчетам, ежегодно издается более 35 000 медицинских журналов и почти 20 миллионов исследовательских статей. С другой стороны, до половины существующих данных могут не публиковаться.
Как за всем этим уследить? И как вы можете сказать, хорошее исследование или нет? Каждое первичное исследование — это только часть головоломки, на которую могут уйти годы. Редко какое-либо одно исследование отвечает на вопросы врача или пациента.
Несмотря на то, что читать большое количество исследований нецелесообразно, высококачественные первичные исследования, особенно РКИ, составляют основу того, что мы знаем, и являются лучшим способом расширения знаний. Любые усилия по поддержке или содействию проведению надежных, прозрачных и независимых испытаний, которые полностью и ясно публикуются, заслуживают одобрения. Важным проектом в этом отношении является инициатива «Все испытания».
Почему мы должны читать систематические обзоры
В большинстве случаев одно исследование не дает нам достаточно информации. Наилучшие ответы находятся путем объединения результатов многих исследований.
Систематический обзор — это тип исследования, в котором рассматриваются результаты всех качественных исследований. Он объединяет результаты этих отдельных исследований в одно резюме. Это дает оценку рисков и преимуществ лечения. Иногда эти обзоры включают статистический анализ, называемый метаанализом, который объединяет результаты нескольких исследований для получения лечебного эффекта.
Систематические обзоры все чаще используются для принятия решений, потому что они снижают вероятность того, что вас введут в заблуждение, взглянув на одну часть головоломки. Будучи систематическими, они также более прозрачны и стали золотым стандартом для синтеза постоянно расширяющейся и противоречивой биомедицинской литературы.
Систематические обзоры не являются надежными. Их результаты настолько хороши, насколько хороши исследования, которые они включают, и методы, которые они используют. Но в лучших обзорах четко указывается, являются ли включенные в них исследования качественными или нет.
Три причины, по которым нам не следует читать (большинство) систематических обзоров
Во-первых, число систематических обзоров со временем увеличилось. С 11 в день в 2010 г. [1] они резко выросли до 40 и более в день в 2015 г. [2] Некоторые описывают, что это производство достигло масштабов эпидемии, когда подавляющее большинство подготовленных систематических обзоров и метаанализов не нужны. вводящие в заблуждение и/или противоречивые. [3][4] Таким образом, поиск более одного систематического обзора по вопросу является скорее правилом, чем исключением, и нет ничего необычного в том, чтобы найти несколько десятков самых горячих вопросов.
Во-вторых, большинство систематических обзоров посвящены узкому вопросу. Их трудно поместить в контекст всех доступных альтернатив для отдельного случая. Чтение нескольких обзоров для оценки всех альтернатив нецелесообразно, даже более того, если мы считаем, что их обычно трудно читать среднему клиницисту, которому приходится решать несколько вопросов каждый день. [5]
В-третьих, систематические обзоры не говорят вам, что делать или что рекомендуется для данного пациента или ситуации. Действительно, хорошие систематические обзоры явно избегают рекомендаций.
Таким образом, несмотря на то, что систематические обзоры играют ключевую роль в любом процессе принятия решений на основе фактических данных, большинство из них некачественные или устаревшие, и они редко предоставляют всю информацию, необходимую для принятия решений в реальном мире.
Как найти наилучшие имеющиеся доказательства?
Принимая во внимание огромное количество доступной информации, мы можем быстро отказаться от периодического просмотра наших любимых журналов как средства поиска наилучших доступных доказательств.
Традиционный подход к поиску доказательств заключается в использовании основных баз данных, таких как PubMed или EMBASE. Они представляют собой всеобъемлющие источники, включающие миллионы релевантных, но также и нерелевантных статей. Несмотря на то, что в прошлом они были предпочтительным подходом к поиску доказательств, информационная перегрузка сделала их непрактичными, и большинству клиницистов не удалось бы найти таким образом наилучшие доступные доказательства, как бы они ни старались.
Другой популярный подход — просто поиск в Google. К сожалению, из-за отсутствия прозрачности Google не является надежным способом отфильтровывать текущие наилучшие доказательства из необоснованных или не контролируемых научными исследованиями источников. [6]
Три альтернативы доступа к лучшим доказательствам?
Альтернатива 1. Выберите лучший систематический обзор
Овладение искусством определения, оценки и применения высококачественных систематических обзоров на практике может быть очень полезным. Это непросто, но после освоения дает более широкую картину: что известно, а что неизвестно.
Лучший единый источник систематических обзоров высочайшего качества производится международной организацией Cochrane Collaboration, названной в честь известного исследователя. [4] Доступ к ним можно получить в Кокрановской библиотеке.
К сожалению, Кокрановские обзоры не охватывают все существующие вопросы или не всегда актуальны. Кроме того, могут быть некокрановские обзоры, которые превосходят Кокрановские обзоры.
Существует множество ресурсов, облегчающих доступ к систематическим обзорам (и другим ресурсам), например, база данных Trip, PubMed Health, ACCESSSS или Epistemonikos.
База данных Epistemonikos является инновационной как для одновременного поиска по нескольким ресурсам, так и для индексирования и связывания соответствующих доказательств. Например, Epistemonikos связывает систематические обзоры и включенные в них исследования и, таким образом, позволяет группировать систематические обзоры на основе общих первичных исследований. Epistemonikos также уникален тем, что предлагает заметный многоязычный пользовательский интерфейс, многоязычный поиск и перевод рефератов на более чем 9 языков.[6] Эта база данных включает в себя несколько инструментов для сравнения систематических обзоров, в том числе матрицу доказательств, динамическую таблицу, показывающую все систематические обзоры и первичные исследования, включенные в эти обзоры.
Кроме того, Epistemonikos стал партнером Cochrane, и в 2017 году будет запущен комбинированный поиск как в Cochrane Library, так и в Epistemonikos.
Альтернатива 2- Ознакомьтесь с заслуживающими доверия рекомендациями
Хотя систематические обзоры могут обеспечить обобщение пользы и вреда вмешательств, они не объединяют эти факторы с ценностями и предпочтениями пациентов или соображениями о ресурсах, чтобы предложить рекомендуемый курс действий. Кроме того, чтобы полностью ответить на вопросы, клиницисты должны будут интегрировать информацию из нескольких систематических обзоров, охватывающих все соответствующие альтернативы и исходы. Большинство клиницистов, скорее всего, предпочтут руководство, а не интерпретацию систематических обзоров самостоятельно.
Надежные руководства, особенно если они разработаны в соответствии с высокими стандартами, такими как подход «Оценка, разработка и оценка рекомендаций» (GRADE), предлагают систематическое и прозрачное руководство по переходу от фактических данных к рекомендациям. [7]
Многие веб-сайты, посвященные руководствам, позиционируют себя как «основанные на фактических данных», но лишь немногие из них содержат явные ссылки на результаты исследований. [8] Если в них нет встроенных ссылок на соответствующие результаты исследований, отклоните их. Если они есть, вы можете оценить силу приверженности доказательствам в поддержку вывода, проверяя, основаны ли утверждения на высококачественных или низкокачественных доказательствах, используя альтернативу 1, описанную выше.
К сожалению, большинство руководств имеют серьезные ограничения или устарели. [9], [10] Упражнение по поиску и оценке наилучшего руководства требует много времени. Это особенно сложно для специалистов широкого профиля, занимающихся вопросами, связанными с различными состояниями или заболеваниями.
Альтернатива 3- Использование инструментов для оказания медицинской помощи
Инструменты для оказания медицинской помощи, такие как BMJ Best Practice, были разработаны в ответ на реальную потребность в обобщении постоянно расширяющейся биомедицинской литературы по постоянно увеличение числа альтернатив для принятия обоснованных решений. На этом конкурентном рынке более успешными оказались продукты с инновационными, удобными для пользователя интерфейсами, которые улучшают поиск, синтез, организацию и применение научно обоснованного контента во многих различных областях клинической практики.
Однако та же самая невозможность наверстать упущенное с новыми данными без ущерба для качества, которая влияет на рекомендации, также влияет на инструменты для оказания медицинской помощи. Клиницисты должны ознакомиться с информационным ресурсом по месту оказания медицинской помощи, к которому они хотят или могут получить доступ, и изучить встроенные ссылки на соответствующие результаты исследований. Клиницисты могут легко оценить силу приверженности доказательствам, проверяя, основаны ли утверждения на доказательствах высокого или низкого качества, используя альтернативу 1, описанную выше. Полнота, использование подхода GRADE и независимость — это другие характеристики, которые следует учитывать при выборе информационных сводок по месту оказания медицинской помощи.
Полный список этих ресурсов можно найти в исследовании Kwag et al.
Будущее
Поиск наилучших доступных доказательств является более сложной задачей, чем это было на заре движения за доказательную базу, и основной причиной является экспоненциальный рост «доказательной» информации в любой из разновидностей, описанных выше. .
Однако, проявив немного терпения и практики, занятой клиницист обнаружит, что доказательная практика стала намного проще, чем 5 или 10 лет назад. Мы вступаем в стадию обмена информацией между различными системами, технологии используются во благо, а различные игроки начинают создавать альянсы.
Первопроходцам наверняка понравятся первые эксперименты с живыми систематическими обзорами (высококачественные, актуальные онлайн-резюмы исследований в области здравоохранения, которые обновляются по мере появления новых исследований), руководствами по жизни, быстрыми обзорами, связанными с быстрыми рекомендациями. , просто чтобы упомянуть несколько. [13], [14], [15]
Маловероятно, что картина бесчисленных исследований и обзоров низкого качества изменится в обозримом будущем. Однако не будет сюрпризом, если через 3-5 лет отделение зёрен от плевел станет тривиальной задачей. Возможно, обещание доказательной медицины о более эффективном и безопасном медицинском вмешательстве, приводящем к лучшим результатам для здоровья пациентов, может быть выполнено.
Автор: Габриэль Рада
Конкурирующие интересы: Габриэль Рада является соучредителем и председателем базы данных Epistemonikos, частью команды, которая основала и поддерживает PDQ-Evidence, а также редактором Cochrane Collaboration.
Связанные блоги
Живые систематические обзоры: получение данных в режиме реального времени для принятия решений в области здравоохранения
Подробнее
Ссылки
день: как мы будем идти в ногу? ПЛОС Мед. 2010 сен 21;7(9):e1000326. doi: 10.1371/journal.pmed.1000326
База данных Epistemonikos [фильтр = систематический обзор; год=2015]. Бесплатная, реляционная, совместная, многоязычная база данных медицинских данных. https://www.epistemonikos.org/en/search?&q=*&classification=systematic-review&year_start=2015&year_end=2015&fl=14542 По состоянию на 5 января 2017 г.
Иоаннидис JP. Массовое производство избыточных, вводящих в заблуждение и противоречивых систематических обзоров и метаанализов. Milbank Q. 9 сентября 2016 г.4(3):485-514. дои: 10.1111/1468-0009.12210.
Пейдж М.Дж., Шамсир Л., Альтман Д.Г. и др. Эпидемиология и отчетные характеристики систематических обзоров биомедицинских исследований: перекрестное исследование. ПЛОС Мед. 2016;13(5):e1002028.
Дель Фиол Г., Уоркман Т.Е., Горман П.Н. Клинические вопросы, поднятые клиницистами в пунктах оказания медицинской помощи: систематический обзор. JAMA Стажер Мед. 2014 май; 174(5):710-8. doi: 10.1001/jamainternmed.2014.368.
Агорицас Т., Вандвик П., Нойманн И., Рохверг Б., Яшке Р., Хейворд Р. и соавт. Глава 5: поиск наилучших текущих доказательств. В: Руководства пользователя медицинской литературы: руководство по доказательной клинической практике. Чикаго: MacGraw-Hill, 2014.
Guyatt GH, Oxman AD, Vist GE, et al. УРОВЕНЬ: Формирующийся консенсус в отношении оценки качества доказательств и силы рекомендаций. БМЖ. 2008;336(7650):924-926. doi: 10.1136/bmj.39489.470347
Нойманн И., Сантессо Н., Акл Э.А., Ринд Д.М., Вандвик П.О., Алонсо-Коэльо П., Агорицас Т., Мустафа Р.А., Александр П.Е., Шюнеманн Х., Гайятт Г.Х. Руководство для медицинских работников по интерпретации и использованию рекомендаций в руководствах, разработанных с использованием подхода GRADE. Дж. Клин Эпидемиол. 2016 апр;72:45-55. doi: 10.1016/j.jclinepi.2015.11.017
Alonso-Coello P, Irfan A, Solà I, Gich I, Delgado-Noguera M, Rigau D, Tort S, Bonfill X, Burgers J, Schunemann H. Качество рекомендаций по клинической практике за последние два десятилетия: систематический обзор руководящих оценочных исследований. Квалифицированное здравоохранение Saf. 2010 дек;19(6):e58. doi: 10.1136/qshc.2010.042077
Мартинес Гарсия Л., Санабрия А.Дж., Гарсия Альварес Э., Трухильо-Мартин М.М., Этксеандия-Икобальцета И., Коцева А., Ригау Д., Луро-Гонсалес А., Барахас-Нава Л., Диас Дель Кампо П., Эстрада М.Д., Сола И., Грасиа Дж., Сальседо-Фернандес Ф., Лоусон Дж., Хейнс Р.Б., Алонсо-Коэльо П.; Рабочая группа по обновлению руководящих принципов. Обоснованность рекомендаций клинических руководств: анализ выживаемости. CMAJ. 2014 4 ноября; 186(16):1211-9. doi: 10.1503/cmaj.140547
Kwag KH, González-Lorenzo M, Banzi R, Bonovas S, Moja L. Предоставление врачам высококачественной информации: обновленная оценка информационных сводок по месту оказания помощи в Интернете. J Med Internet Res. 2016 19 января; 18 (1): e15. doi: 10.2196/jmir.5234
Banzi R, Cinquini M, Liberati A, Moschetti I, Pecoraro V, Tagliabue L, Moja L. Скорость обновления онлайн-резюме на основе фактических данных по месту оказания медицинской помощи: проспективный когортный анализ. БМЖ. 2011 23 сентября; 343: d5856. дои: 10.1136/bmj.d5856
Эллиот Дж. Х., Тернер Т., Клавизи О., Томас Дж., Хиггинс Дж. П., Мавергеймс С., Груэн Р. Л. Живые систематические обзоры: новая возможность сократить разрыв между фактическими данными и практикой. ПЛОС Мед. 18 февраля 2014 г .; 11 (2): e1001603. doi: 10.1371/journal.pmed.1001603
Вандвик П.О., Брандт Л., Алонсо-Коэльо П., Тревик С., Акл Э.А., Кристиансен А., Фог-Хин А., Агорицас Т., Монтори В.М., Гайятт Г. Создание клинических рекомендаций, которым мы можем доверять, использовать и делиться: новый эпоха близка. Грудь. 2013 авг; 144 (2): 381-9. doi: 10.1378/сундук.13-0746
Вандвик П.О., Отто К.М., Семенюк Р.А., Багур Р., Гайатт Г.Х., Литвин Л., Уитлок Р., Вартдал Т., Бригер Д., Аертгертс Б., Прайс С., Форутан Ф., Шапиро М., Мерц Р., Спенсер Ф.А. Транскатетерная или хирургическая замена аортального клапана у пациентов с тяжелым симптоматическим аортальным стенозом с хирургическим риском от низкого до среднего: руководство по клинической практике. БМЖ. 2016 Сентябрь 28;354:i5085. дои: 10.1136/bmj.i5085

Широкая денежная масса Определение
По
Даниэль Либерто
Полная биография
Даниэль Либерто — журналист с более чем 10-летним опытом работы в таких изданиях, как Financial Times, The Independent и Investors Chronicle. Он получил степень магистра журналистики в Лондонском колледже коммуникаций. Даниэль является экспертом в области корпоративных финансов и инвестиций в акционерный капитал, а также в производстве подкастов и видео.
Узнайте о нашем
редакционная политика
Обновлено 30 ноября 2020 г.
Рассмотрено
Майкл Дж. Бойл
Рассмотрено
Майкл Дж. Бойл
Полная биография
Майкл Бойл — опытный специалист в области финансов, более 10 лет занимающийся финансовым планированием, деривативами, акциями, фиксированным доходом, управлением проектами и аналитикой.
Узнайте о нашем
Совет финансового контроля
Факт проверен
Майкл Логан
Факт проверен
Майкл Логан
Полная биография
Майкл Логан — опытный писатель, продюсер и руководитель редакции. Как журналист, он широко освещал деловые и технические новости в США и Азии. Он создал мультимедийный контент, который собрал миллиарды просмотров по всему миру.
Узнайте о нашем
редакционная политика
Что такое широкие деньги?
Широкая денежная масса – это категория для измерения количества денег, обращающихся в экономике. Он определяется как наиболее всеобъемлющий метод расчета денежной массы в данной стране и включает ограниченные деньги наряду с другими активами, которые можно легко конвертировать в наличные деньги для покупки товаров и услуг.
Ключевые выводы
Широкая денежная масса — наиболее гибкий метод измерения денежной массы в экономике, учета денежных средств и других активов, легко конвертируемых в валюту.
Формула расчета денежной массы варьируется от страны к стране, поэтому термин «широкая денежная масса» всегда определяется во избежание неправильного толкования.
Центральные банки, как правило, следят за ростом денежной массы, чтобы прогнозировать инфляцию.
Понимание широких денег
Поскольку наличные деньги можно обменять на многие виды финансовых инструментов, для экономистов непростая задача определить, сколько денег циркулирует в экономике. Денежная масса измеряется по-разному. Экономисты используют заглавную букву «М», за которой следует число, для обозначения измерения, которое они используют в данном контексте.
Формула расчета денежной массы варьируется от страны к стране. Широкая денежная масса — это самая широкая мера, охватывающая узкие деньги (например, наличные и чековые депозиты), а также менее ликвидные активы, такие как депозитные сертификаты, иностранная валюта, счета денежного рынка, рыночные ценные бумаги, казначейские векселя и все остальное, что можно легко конвертировать. в наличные деньги (но не включая акции компании).
Пример широких денег
В Соединенных Штатах наиболее распространенными показателями денежной массы являются M1 и M2. В марте 2006 года Федеральная резервная система прекратила публикацию статистики M3.
Эти показатели различаются в зависимости от ликвидности включенных счетов. M0 обычно включает только наиболее ликвидные инструменты, такие как монеты и банкноты в обращении. На другом конце шкалы находится M3, который относится к категории самого широкого измерения денег.
Разные страны определяют свои измерения денег немного по-разному. В академической среде термин «широкие деньги» используется во избежание неправильного толкования. В большинстве случаев широкие деньги означают то же, что и М3, тогда как М0 и М1 обычно относятся к узким деньгам.
Федеральная резервная система отслеживает денежную массу M1 и M2. M1 определяется как валюта в руках населения, дорожные чеки, депозиты до востребования и чековые депозиты. M2 включает сберегательные счета M1 плюс, взаимные фонды денежного рынка и срочные депозиты до $100 000.
Преимущества широких денег
Расширение объема денежной массы в обращении дает несколько преимуществ. Прежде всего, это помогает политикам лучше понимать потенциальные инфляционные тенденции. Центральные банки часто рассматривают широкую денежную массу наряду с узкой денежной массой для определения денежно-кредитной политики.
Экономисты обнаружили тесную связь между денежной массой, инфляцией и процентными ставками. Центральные банки, такие как Федеральная резервная система, используют более низкие процентные ставки для увеличения денежной массы, когда целью является стимулирование экономики. И наоборот, в условиях инфляции процентные ставки повышаются, а денежная масса уменьшается, что приводит к снижению цен.
Проще говоря, если денег больше, экономика имеет тенденцию к ускорению, потому что у предприятий есть легкий доступ к финансированию. Если в системе меньше денег, экономика замедляется, и цены могут упасть или остановиться. В этом контексте широкая денежная масса является одним из показателей, которые центральные банки используют для определения того, какие интервенции, если таковые имеются, они могли бы ввести, чтобы повлиять на экономику.
Источники статей
Investopedia требует, чтобы авторы использовали первоисточники для поддержки своей работы. К ним относятся официальные документы, правительственные данные, оригинальные отчеты и интервью с отраслевыми экспертами. Мы также при необходимости ссылаемся на оригинальные исследования других авторитетных издателей. Вы можете узнать больше о стандартах, которым мы следуем при создании точного и беспристрастного контента, в нашем
редакционная политика.
Федеральный резервный банк Нью-Йорка. «Денежная масса». По состоянию на 1 ноября 2020 г.
Curriculum Definition
Термин учебный план относится к урокам и академическому содержанию, преподаваемым в школе или в рамках определенного курса или программы. В словарях учебная программа часто определяется как курсы, предлагаемые школой, но редко используется в таком общем смысле в школах. В зависимости от того, насколько широко педагоги определяют или используют этот термин, учебная программа обычно относится к знаниям и навыкам, которые, как ожидается, получат учащиеся, включая стандарты обучения или цели обучения, которым они должны соответствовать; разделы и уроки, которые преподают учителя; задания и проекты, данные студентам; книги, материалы, видео, презентации и материалы для чтения, используемые в курсе; а также тесты, оценки и другие методы, используемые для оценки обучения учащихся. Например, учебная программа отдельного учителя может представлять собой конкретные стандарты обучения, уроки, задания и материалы, используемые для организации и преподавания определенного курса.
Когда термины учебная программа или учебная программа используются в образовательном контексте без оговорок, конкретных примеров или дополнительных объяснений, может быть трудно точно определить, к чему относятся эти термины, главным образом потому, что они могут применяться все или только некоторые из составных частей школьной академической программы или курсов.
Во многих случаях учителя разрабатывают свои собственные учебные программы, часто уточняя и улучшая их на протяжении многих лет, хотя учителя также часто адаптируют уроки и программы, созданные другими учителями, используют шаблоны учебных программ и руководства для структурирования своих уроков и курсов, или приобрести готовые учебные программы у частных лиц и компаний. В некоторых случаях школы приобретают комплексные пакеты учебных программ для всех классов — часто по определенной предметной области, такой как математика, — которые учителя должны использовать или которым должны следовать. Учебная программа может также включать в себя академические требования школы для выпуска, такие как курсы, которые учащиеся должны пройти и сдать, количество кредитов, которые учащиеся должны заполнить, и другие требования, такие как завершение завершающего проекта или определенное количество часов общественных работ. Вообще говоря, учебная программа в школах принимает множество различных форм — слишком много, чтобы всесторонне перечислить их здесь.
Важно отметить, что, хотя учебная программа охватывает широкий спектр потенциальных образовательных и учебных практик, преподаватели часто имеют в виду очень точное техническое значение, когда они используют этот термин. Большинство учителей тратят много времени на обдумывание, изучение, обсуждение и анализ учебной программы, и многие преподаватели приобрели профессиональный опыт в разработке учебных программ, т. е. они знают, как структурировать, организовывать и проводить уроки таким образом, чтобы облегчить или ускорить обучение. Непреподавателям некоторые учебные материалы могут показаться простыми или прямолинейными (например, список обязательной литературы), но они могут отражать глубокое и сложное понимание академической дисциплины и наиболее эффективных стратегий приобретения знаний и управления классом.
Связанное обсуждение см. в скрытом учебном плане.
Реформа
Поскольку учебная программа является одним из основополагающих элементов эффективного школьного обучения и преподавания, она часто является объектом реформ, большинство из которых в целом направлены либо на то, чтобы обязать, либо поощрять большую стандартизацию и согласованность учебных программ в разных штатах, школах, классах. , предметные области и курсы. Ниже приведены несколько репрезентативных примеров того, как учебная программа направлена на совершенствование или используется для повышения эффективности школы и повышения эффективности учителей:
Требования стандартов: Когда новые стандарты обучения принимаются на уровне штата, округа или школы, учителя обычно изменяют то, что они преподают, и приводят свою учебную программу в «соответствие» требованиям к обучению, изложенным в новых стандартах. Хотя техническое согласование учебного плана со стандартами не обязательно означает, что учителя преподают в соответствии со стандартами — или, что более важно, что учащиеся действительно оправдывают ожидания в отношении обучения — стандарты обучения остаются механизмом, с помощью которого лица, определяющие политику, и школьные руководители попытаться улучшить учебный план и качество преподавания. Например, инициатива Common Core State Standards представляет собой национальную попытку повлиять на разработку учебных программ и качество преподавания в школах путем принятия штатами новых стандартов обучения.
Требования к оцениванию: Еще одной стратегией реформ, которая косвенно влияет на учебную программу, является оценивание, поскольку методы, используемые для измерения успеваемости учащихся, заставляют учителей преподавать содержание и навыки, которые в конечном итоге будут оцениваться. Наиболее часто обсуждаемыми примерами являются стандартизированное тестирование и тестирование с высокими ставками, которые могут привести к явлению, неофициально называемому «обучение тесту». Поскольку федеральная политика и политика штата требуют, чтобы учащиеся сдавали стандартные тесты на определенных уровнях обучения, а нормативные штрафы или негативная огласка могут быть результатом плохой успеваемости учащихся (в случае с тестами с высокими ставками), учителя, следовательно, вынуждены преподавать таким образом, чтобы могут улучшить успеваемость учащихся по стандартизированным тестам, например, путем обучения содержанию, которое может быть проверено, или путем обучения студентов конкретным методам сдачи теста. В то время как стандартизированные тесты являются одним из способов использования оценивания для улучшения реформы учебной программы, школы могут также использовать рубрики и многие другие стратегии для повышения качества обучения посредством модификации стратегий оценивания, требований и ожиданий.
Согласование учебной программы: Школы могут попытаться улучшить качество учебной программы, приведя преподавательскую деятельность и ожидания курса в «согласование» со стандартами обучения и другими школьными курсами — практика, иногда называемая «сопоставлением учебной программы». Основная идея состоит в том, чтобы создать более последовательную и последовательную учебную программу, убедившись, что учителя преподают наиболее важный контент и устраняют пробелы в обучении, которые могут существовать между последовательными курсами и уровнями обучения. Например, учителя могут пересматривать свою программу по математике, чтобы убедиться, что то, чему учащиеся фактически учат на каждом курсе алгебры I, предлагаемом в школе, не только отражает ожидаемые стандарты обучения для этой предметной области и уровня обучения, но и готовит учащихся к алгебре II. и геометрия. Если учебная программа не согласована, учащимся может преподаваться существенно различающийся контент в каждом курсе алгебры I, например, а учащиеся, изучающие разные курсы алгебры I, могут закончить курсы, подготовленные к алгебре II неодинаково. Более подробное обсуждение см. в согласованной учебной программе.
Философия учебной программы: Структура и цели любой учебной программы отражают образовательную философию — преднамеренно или непреднамеренно — педагогов, разработавших ее. Следовательно, реформа учебного плана может произойти путем принятия другой философии или модели обучения школой или педагогом. Школы, которые следуют модели экспедиционного обучения, например, используют различные подходы к обучению, обычно известные как обучение на основе проектов, которое включает в себя связанные стратегии, такие как обучение на основе сообщества и аутентичное обучение. В школах экспедиционного обучения учащиеся выполняют многогранные проекты, называемые «экспедициями», которые требуют от учителей разработки и структурирования учебной программы способами, которые сильно отличаются от более традиционных подходов, обычно используемых в школах.
Пакеты учебных программ: В некоторых случаях школы принимают решение приобрести или принять пакет учебных программ, разработанный сторонней организацией. Одним из хорошо известных и часто используемых вариантов для американских государственных школ является Международный бакалавриат, который предлагает учебные программы для начальных школ, средних школ и старших классов. Округа могут приобрести все три программы, или отдельная школа может приобрести только одну, и программы могут быть предложены всем или только некоторым учащимся школы. Когда школы принимают пакет учебных программ, учителя часто проходят специальную подготовку, чтобы гарантировать, что учебная программа эффективно реализуется и преподается. Во многих случаях пакеты учебных программ покупаются или принимаются, потому что они воспринимаются как более качественные или престижные, чем существующие варианты учебных программ, предлагаемые школой или самостоятельно разработанные учителями.
Учебные ресурсы: Ресурсы, которые школы предоставляют учителям, также могут существенно повлиять на учебную программу. Например, если школьный округ или школа приобретают определенный набор учебников и требуют, чтобы учителя использовали их, эти учебники неизбежно повлияют на то, что преподается и как учителя преподают. Покупки технологий — еще один пример ресурсов, которые потенциально могут повлиять на учебную программу. Если всем учащимся выдать ноутбуки, а все классы оборудовать интерактивными досками, например, учителя могут внести существенные изменения в то, что они преподают, и в то, как они преподают, чтобы воспользоваться преимуществами этих новых технологий (более подробное обсуждение этого примера см. -к одному). Однако в большинстве случаев новые ресурсы учебной программы требуют от школ вложений в профессиональное развитие, которое помогает учителям эффективно использовать новые ресурсы, учитывая, что простое предоставление новых ресурсов без инвестиций в образование и подготовку учителей может не привести к желаемым улучшениям. Кроме того, тип профессионального развития, предоставляемого учителям, также может иметь большое влияние на разработку и разработку учебных программ.
Стандартизация учебной программы: Штаты, округа и школы также могут попытаться улучшить качество и эффективность преподавания, потребовав или просто поощряя учителей использовать либо стандартизированную учебную программу, либо общие процессы разработки учебной программы. Хотя стратегии, используемые для продвижения более стандартизированных учебных программ, могут широко варьироваться от штата к штату или от школы к школе, общая цель состоит в том, чтобы повысить качество преподавания за счет большей согласованности учебных программ. Считается, что успеваемость в школе, скорее всего, улучшится, если методы преподавания и требования к обучению будут основаны на здравых принципах и последовательно применяются во всем штате, округе или школе. Стандарты учебной программы также могут быть созданы или предложены влиятельными образовательными организациями, такими как, например, Национальная ассоциация учителей естественных наук или Национальный совет учителей математики, с целью формирования ожиданий от обучения и преподавания в рамках определенных академических дисциплин.
Составление учебных программ: Часто называемое «сценарными учебными планами», составление учебных планов представляет собой наиболее предписывающую форму стандартизированной, предварительно составленной учебной программы, поскольку обычно требуется, чтобы учителя не только следовали определенной последовательности заранее подготовленных уроков, но и фактически читали вслух из учебный сценарий в классе. Хотя профессиональная автономия и творческий потенциал отдельных учителей могут быть значительно ограничены при использовании такой системы учебных программ, общее обоснование заключается в том, что качество преподавания может быть обеспечено или улучшено или, по крайней мере, сохранено во всей школе или системе образования, если учителя будут следовать четкому плану. обучающий сценарий. Хотя не каждый учитель по своей природе может быть превосходным учителем, все учителя могут, по крайней мере, получить качественный учебный план, которому они должны следовать.No related posts.}}}

1.3. Запись приближенных значений величин. Верные знаки

Верные и значащие цифры. Запись приближенных значений — Студопедия.Нет

Значащие и верные цифры.

Лекции по математике для студентов 1 курса СПО

Вычислительные методы

Пример выполнения задания — Студопедия

Обычные проблемы

Как рассчитать наследуемость?

1) Двухэтапный подход

Функция наследуемости в упаковке

Загрузка пакетов

функция h3cal

Информация о модели

Компоненты дисперсии

Лучшие линейные несмещенные оценщики (BLUE)

Лучшие линейные несмещенные предикторы (BLUP)

Выбросы

Сравнение: h3cal и asreml

в широком смысле – французский перевод – Linguee

Метод непараметрической регрессии для соглашения в широком смысле

2.1. Обзор согласия в широком смысле

2.2. Предлагаемая структура регрессии для показателя BSA

3.1. Оценка функции регрессии

3.2. Асимптотические свойства

3.3. Выбор полосы пропускания

3.4. Вывод

Таблица 1

Таблица 2

Notation

Технические леммы и доказательства

Лемма 1

Доказательство леммы 1

Лемма 2

Лемма 5

Доказательство леммы 5

Доказательство теоремы 1

Доказательство теоремы 2

Что является лучшим доказательством и как его найти

Почему научные данные лучше, чем только мнение экспертов?

Какие исследования надежнее?

Почему нам не следует читать исследования

Почему мы должны читать систематические обзоры

Три причины, по которым нам не следует читать (большинство) систематических обзоров

Как найти наилучшие имеющиеся доказательства?

Три альтернативы доступа к лучшим доказательствам?

Будущее

Связанные блоги

Ссылки

Широкая денежная масса Определение

Что такое широкие деньги?

Ключевые выводы

Понимание широких денег

Пример широких денег

Преимущества широких денег

Curriculum Definition

Реформа

Добавить комментарий Отменить ответ

`Добавить комментарий Отменить ответ`