Циклоид что такое: ЦИКЛОИДА | это… Что такое ЦИКЛОИДА?

что значит быть циклоидом — T&P

Человеческие характеры очень разнообразны, но среди них, тем не менее, можно выделить типичные «рисунки». Для описания некоторых подобных паттернов в психологии существует понятие «акцентуация». Так называют сумму наиболее ярко очерченных свойств характера, которые еще находятся в пределах клинической нормы, но делают человека уязвимым к психологическим нагрузкам определенного типа. Циклоидная акцентуация — один из ее вариантов. T&P рассказывают о том, что отличает циклоида от циклотимика, каковы плюсы и минусы этого типа и что делать, если у вас такой характер.

Акцентуация характера — это не болезнь. Несмотря на то, что некоторые названия вариантов акцентуации: эпилептоид, истероид, шизоид и другие, — образованы от названий психических заболеваний, любой человек с акцентуацией здоров и нормален. У эпилептоида нет эпилепсии, а шизоид не болеет шизофренией (иначе они стали бы эпилептиком и шизофреником). У людей с акцентуацией лишь обострены определенные черты характера. Создатель этого понятия, немецкий психиатр Карл Леонгард, к примеру, писал, что «население Берлина — это на 50% акцентуированные личности и на 50% — стандартный тип людей». Тем не менее, в некоторых неблагоприятных обстоятельствах акцентуация может превратиться в болезнь, «добрав» патологичности.

Составители Энциклопедического словаря по психологии и педагогике (2013) пишут об этом понятии так: «Акцентуации характера отличаются от психопатий отсутствием одновременного проявления свойственной последним триады признаков: стабильность характера во времени, тотальности его проявлений во всех ситуациях, социальной дезадаптации». Иначе говоря, эпилептоид не всегда стремится маниакально поддерживать порядок, а истероид не в любой ситуации жаждет оказаться в центре всеобщего внимания.

В российской психологии акцентуация характера остается популярным понятием, однако общепринятой классификации на сегодняшний день не существует. Современные версии типологии опираются на работы Карла Леонгарда, монографию советского психиатра Андрея Личко и другие исследования. Работы Личко позволили глубже понять причины появления и этиологию неврозов, поскольку психиатр выдвинул концепцию так называемого «места наименьшего сопротивления», или «слабого звена» в характере.

«Введение понятия “места наименьшего сопротивления” характера, а также описание этих мест применительно к каждому типу — важный вклад в психологическую теорию характера, — пишет в своей монографии российский психолог, специалист в области экспериментальной психологии и нейро-лингвистического программирования, профессор МГУ Юлия Гиппенрейтер. — Он имеет также неоценимое практическое значение. Слабые места каждого характера надо знать, чтобы избегать неправильных шагов, излишних нагрузок и осложнений в семье и на работе, при воспитании детей, организации собственной жизни и т. п.»

Вдоль по радуге в грозу: плюсы и минусы циклоидной акцентуации

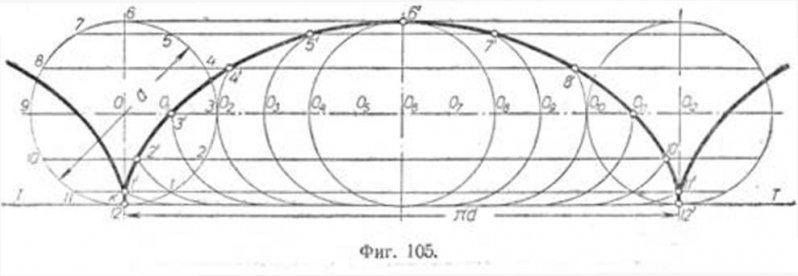
Название циклоидной акцентуации характера дала геометрическая кривая — циклоида, или рулетта, как называли ее раньше. Эту кривую рисует катящаяся окружность.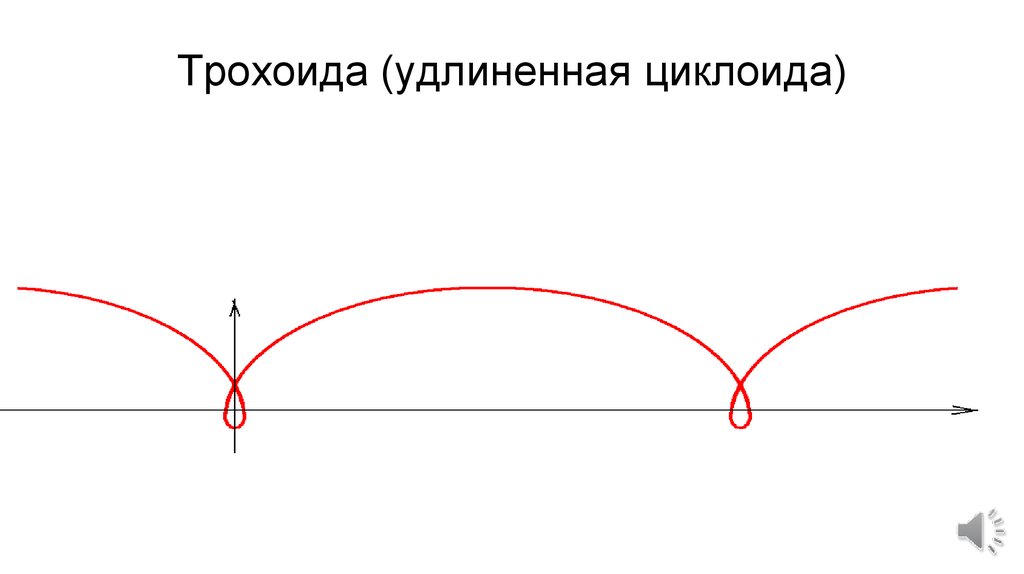 Паскаль писал о ней так: «Рулетта является линией столь обычной, что после прямой и окружности нет более часто встречающейся линии; она так часто вычерчивается перед глазами каждого, что надо удивляться тому, как не рассмотрели ее древние… ибо это не что иное, как путь, описываемый в воздухе гвоздем колеса».

На плоскости циклоида выглядит как бесконечная последовательность арок, которые упираются своим основанием в горизонталь. Окружность «катится» по этой горизонтали, и точка у нее на боку описывает полукруг, то оказываясь в высшей точке, то падая к подножию. Именно так повышается и падает настроение у человека с циклоидной акцентуацией характера. У циклоида нет циклотимии — психического аффективного расстройства, при котором эмоциональное состояние человека колеблется между депрессией и гипертимией (или даже гипоманией). Циклотимик страдает от резких скачков настроения и работоспособности, которые мешают ему вести привычный образ жизни, — в то время как циклоид просто живет как на качелях, которые постоянно описывают полукруг, поднимая его высоко над землей и вновь опуская к исходной точке.

«Диаметр» циклоиды, по которой скользит настроение такого человека, может быть разным: от мягких беспричинных перепадов между «не очень» и «в порядке» до настоящих прыжков от счастья до глубокой тоски и обратно. При этом для окружающих такой человек, как правило, остается отличным деловым партнером, внимательным другом и нежным возлюбленным. Он не склонен к конфликтам (исключая моменты самых глубоких падений), ведет себя естественно и добродушно, спокойно относится ко многим обстоятельствам, которые у других людей вызывают массу негативных чувств. В темпераменте циклоида есть теплота и мягкость, ему присущи юмор и озорство. Он не расстается с этими качествами даже в моменты грусти, хотя становится обходительным одиночкой, не выказывая враждебности к другим.

© Tsto Helsinki

Существенный плюс циклоидной акцентуации характера заключается в том, что она делает человека гибким и адаптивным, способствуя развитию способностей к эмпатии. Циклоид легко настраиватеся на любую волну, поскольку эмоциональные «качели» априори обеспечивают ему широкий психологический диапазон. Такой человек остро чувствует радость жизни и ее печаль. Это помогает в развитии творческих навыков и подчас позволяет «превратить» циклоидную акцентуацию в карьеру писателя, художника или журналиста.

При этом сами скачки настроения, особенно во взрослом возрасте, не ощущаются ярко. Человек с циклоидной акцентуацией характера скорее назовет это «градиентом» — от светлой грусти до развернутой тоски — и от легкого желания улыбнуться до бодрости, радости и склонности к гедонизму. Разного рода удовольствия, оттенки чувств и нюансы обстоятельств доступны и знакомы таким людям. Они знают о них очень много — и много могут о них рассказать, обеспечив собеседнику, слушателю или читателю с другим складом характера шанс научиться радоваться повседневности.

Эмоциональные градиенты циклоидной акцентуации, с другой стороны, создают специфический ритм жизни: скачет работоспособность, эмоциональность, общительность, самооценка, общий уровень энергии, творческие способности. И в этом случае, конечно, нужно приспособить к акцентуации свой график жизни: например, выбирать проектную работу с ее рывками и паузами, — или свободный график. В последнем случае стоит помнить, что в фазе подъема все обычно получается, складывается и приносит плоды само по себе, — а вот в фазе спада может быть трудно. В нижней точке кривой циклоид становится уязвимым, страдает от недостатка жизненных сил и веры в себя.

И это пройдет: если вы циклоид

Человеку с циклоидной акцентуацией характера необходимо помнить, что спады его настроения возникают сами по себе — и исчезают так же. Негативное состояние просто «проходит», и главная задача заключается в том, чтобы до начала нового взлета не наделать ошибок, перессорившись с окружающими, бросив институт или недописанную книгу.

Более серьезная опасность для циклоида заключается в том, что в неблагоприятных обстоятельствах такая акцентуация может превратиться в биполярное расстройство, циклотимию или маниакально-депрессивный психоз. Особенно внимательно относиться к своим «перепадам» следует тем, у кого в семье уже были случаи одного из этих психических заболеваний. И все-таки, даже если семейный анамнез налицо, болезни можно избежать, — ведь она развивается как правило не сама по себе, а на фоне длительного и интенсивного стресса.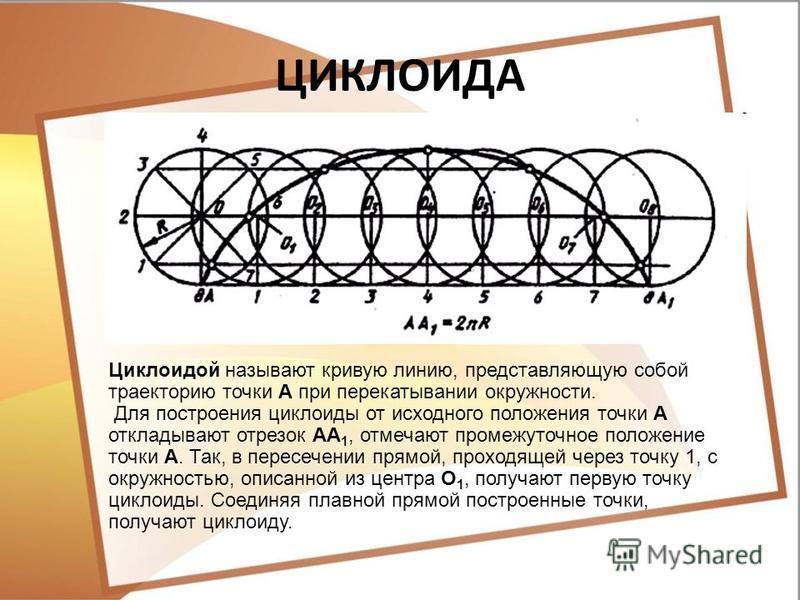 Именно от него циклоиду нужно беречь себя, избегая по-настоящему стрессогенных обстоятельств или смягчая их по мере сил.

Гвоздь колеса: если рядом циклоид

Люди с циклоидной акцентуацией характера хорошо переносят многие неприятные моменты межличностных отношений, однако и у них есть «ахиллесова пята». Они не терпят монотонных действий в работе и рутинности в личных отношениях. В погоне за разнообразием и приключениями такие люди подчас могут совершать настоящие маленькие безумства, — но, вероятно, будут рады, если их близкие решат поучаствовать в затее.

В негативной фазе самооценку циклоида легко травмировать, поскольку в эти моменты он склонен себя недооценивать. У него мало сил, нет веры в себя, он бросает начатое, отказывается от прошлых целей. Вот почему в фазе падения человеку с циклоидной акцентуацией важно помочь быть последовательным и поддержать его, чтобы он не потерял достижения и бонусы, заработанные на подъеме.

Циклоида / Этюды // Математические этюды

Циклоида / Этюды // Математические этюды

Математические этюды

К списку

Пом­ните оран­же­вые пластмас­со­вые ката­фоты — све­то­от­ража­тели, при­креп­ляющи­еся к спи­цам вело­сипед­ного колеса? При­крепим ката­фот к самому ободу колеса и про­сле­дим за его тра­ек­то­рией. Полу­чен­ные кри­вые при­над­лежат семейству цик­лоид.

Колесо при этом назы­ва­ется про­из­во­дящим кругом (или окруж­но­стью) цик­ло­иды.

Но давайте вер­нёмся в наш век и пере­ся­дем на более современ­ную тех­нику. На пути байка попался каму­шек, кото­рый застрял в про­тек­торе колеса. Про­вер­нувшись несколько кругов с коле­сом, куда поле­тит камень, когда выско­чит из про­тек­тора? Про­тив направ­ле­ния движе­ния мотоцикла или по направ­ле­нию?

Как известно, сво­бод­ное движе­ние тела начи­на­ется по каса­тель­ной к той тра­ек­то­рии, по кото­рой оно двига­лось. Каса­тель­ная к цик­ло­иде все­гда направ­лена по направ­ле­нию движе­ния и про­хо­дит через верх­нюю точку про­из­во­дящей окруж­но­сти. По направ­ле­нию движе­ния поле­тит и наш каму­шек.

Пом­ните, как Вы ката­лись в дет­стве по лужам на вело­сипеде без зад­него крыла? Мок­рая полоска на вашей спине явля­ется житейским под­твер­жде­нием только что полу­чен­ного результата.

Век XVII — это век цик­ло­иды. Лучшие учё­ные изу­чали её уди­ви­тель­ные свойства.

Какая тра­ек­то­рия при­ве­дёт тело, движуще­еся под действием силы тяже­сти, из одной точки в другую за крат­чайшее время? Это была одна из пер­вых задач той науки, кото­рая сей­час носит назва­ние вари­аци­он­ное исчис­ле­ние.

Мини­ми­зи­ро­вать (или мак­си­ми­зи­ро­вать) можно раз­ные вещи — длину пути, ско­рость, время. В задаче о бра­хи­сто­хроне мини­ми­зи­ру­ется именно время (что под­чёр­ки­ва­ется самим назва­нием: греч. βράχιστος — наименьший, χρόνος — время).

Пер­вое, что при­хо­дит на ум, — это прямо­ли­ней­ная тра­ек­то­рия. Давайте также рас­смот­рим пере­вёр­ну­тую цик­ло­иду с точ­кой воз­врата в верх­ней из задан­ных точек. И, сле­дуя за Гали­лео Гали­леем, — чет­вер­тинку окруж­но­сти, соеди­няющую наши точки.

Сде­лаем боб­слей­ные трассы с рас­смот­рен­ными профи­лями и про­сле­дим, какой из бобов при­е­дет пер­вым.

Исто­рия боб­слея берёт своё начало в Швейца­рии. В 1924 году во фран­цуз­ском городе Шамони про­хо­дят пер­вые зим­ние Олимпийские игры. На них уже про­во­дятся сорев­но­ва­ния по боб­слею для экипажей двоек и чет­вё­рок. Един­ствен­ный год, когда на Олимпийских играх экипаж боба состоял из пяти чело­век, был 1928. С тех пор в боб­слее все­гда сорев­нуются муж­ские экипажи двойки и чет­вёрки. В пра­ви­лах боб­слея много инте­рес­ного. Конечно же, суще­ствует огра­ни­че­ния на вес боба и команды, но суще­ствуют даже огра­ни­че­ния на мате­ри­алы, кото­рые можно исполь­зо­вать в конь­ках боба (перед­няя пара их подвижна и свя­зана с рулём, зад­няя закреп­лена жёстко). Напри­мер, радий не может исполь­зо­ваться при изго­тов­ле­нии конь­ков.

Дадим старт нашим чет­вёр­кам. Какой же боб пер­вым при­е­дет к финишу? Боб зелё­ного цвета, выступающий за команду Матема­ти­че­ских этю­дов и катившийся по цик­ло­и­даль­ной горке, при­хо­дит пер­вым!

Почему же Гали­лео Гали­лей рас­смат­ри­вал чет­вер­тинку окруж­но­сти и счи­тал, что это наи­лучшая в смысле времени тра­ек­то­рия спуска? Он впи­сы­вал в неё лома­ные и заме­тил, что при уве­ли­че­нии числа зве­ньев время спуска уменьша­ется.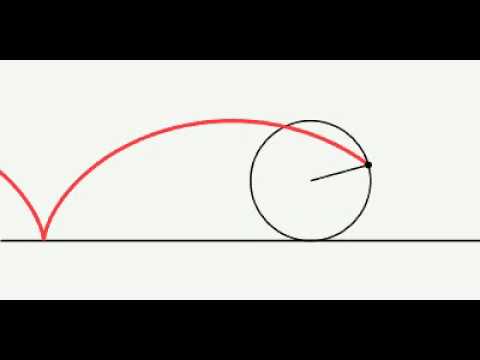 Отсюда Гали­лей есте­ствен­ным обра­зом перешёл к окруж­но­сти, но сде­лал невер­ный вывод, что эта тра­ек­то­рия наи­лучшая среди всех возмож­ных. Как мы видели, наи­лучшей тра­ек­то­рией явля­ется цик­ло­ида.

Через две дан­ные точки можно про­ве­сти един­ствен­ную цик­ло­иду с усло­вием, что в верх­ней точке нахо­дится точка воз­врата цик­ло­иды. И даже когда цик­ло­иде при­хо­дится под­ниматься, чтобы пройти через вто­рую точку, она всё равно будет кри­вой наи­ско­рейшего спуска!

Ещё одна кра­си­вая задача, свя­зан­ная с цик­ло­и­дой, — задача о тау­то­хроне. В пере­воде с гре­че­ского ταύτίς озна­чает «тот же самый», χρόνος, как мы уже знаем — «время».

Сде­лаем три оди­на­ко­вые горки с профи­лем в виде цик­ло­иды, так, чтобы концы горок совпа­дали и рас­по­лага­лись в вершине цик­ло­иды. Поста­вим три боба на раз­ные высоты и дадим отмашку. Уди­ви­тель­нейший факт — все бобы при­едут вниз одно­временно!

Зимой Вы можете постро­ить во дворе горку изо льда и про­ве­рить это свойство вжи­вую.

Задача о тау­то­хроне состоит в нахож­де­нии такой кри­вой, что, начи­ная с любого началь­ного положе­ния, время спуска в задан­ную точку будет оди­на­ко­вым.

Хри­стиан Гюйгенс дока­зал, что един­ствен­ной тау­то­хро­ной явля­ется цик­ло­ида.

Конечно же, Гюйгенса не инте­ре­со­вал спуск по ледя­ным гор­кам. В то время учё­ные не имели такой рос­коши заниматься нау­ками из любви к искус­ству. Задачи, кото­рые изу­ча­лись, исхо­дили из жизни и запро­сов тех­ники того времени. В XVII веке совершаются уже даль­ние мор­ские пла­ва­ния. Широту моряки умели опре­де­лять уже доста­точно точно, но уди­ви­тельно, что долготу не умели опре­де­лять совсем. И один из пред­лагавшихся спо­со­бов изме­ре­ния широты был осно­ван на нали­чии точ­ных хро­номет­ров.

Пер­вым, кто задумал делать маят­ни­ко­вые часы, кото­рые были бы точны, был Гали­лео Гали­лей. Однако в тот момент, когда он начи­нает их реа­ли­зо­вы­вать, он уже стар, он слеп, и за оставшийся год своей жизни учё­ный не успе­вает сде­лать часы.

Он завещает это сыну, однако тот мед­лит и начи­нает заниматься маят­ни­ком тоже лишь перед смер­тью и не успе­вает реа­ли­зо­вать замы­сел. Сле­дующей зна­ко­вой фигу­рой был Хри­стиан Гюйгенс.

Он заме­тил, что период коле­ба­ния обыч­ного маят­ника, рас­смат­ри­вавшегося Гали­леем, зави­сит от изна­чаль­ного положе­ния, т.е. от ампли­туды. Задумавшись о том, какова должна быть тра­ек­то­рия движе­ния груза, чтобы время каче­ния по ней не зави­село от ампли­туды, он решает задачу о тау­то­хроне. Но как заста­вить груз двигаться по цик­ло­иде? Пере­водя тео­ре­ти­че­ские иссле­до­ва­ния в прак­ти­че­скую плос­кость, Гюйгенс делает «щёчки», на кото­рые нама­ты­ва­ется веревка маят­ника, и решает ещё несколько матема­ти­че­ских задач. Он дока­зы­вает, что «щёчки» должны иметь профиль той же самой цик­ло­иды, тем самым пока­зы­вая, что эво­лю­той цик­ло­иды явля­ется цик­ло­ида с теми же парамет­рами.

Кроме того, пред­ложен­ная Гюйген­сом кон­струкция цик­ло­и­даль­ного маят­ника поз­во­ляет посчи­тать длину цик­ло­иды. Если синюю ниточку, длина кото­рой равна четырём ради­у­сам про­из­во­дящего круга, мак­симально откло­нить, то её конец будет в точке пере­се­че­ния «щёчки» и цик­ло­иды-тра­ек­то­рии, т.е. в вершине цик­ло­иды-«щёчки». Так как это поло­вина длины арки цик­ло­иды, то пол­ная длина равна восьми ради­у­сам про­из­во­дящего круга.

Хри­стиан Гюйгенс сде­лал цик­ло­и­даль­ный маят­ник, и часы с ним про­хо­дили испыта­ния в мор­ских путеше­ствиях, но не при­жи­лись. Впро­чем, так же, как и часы с обыч­ным маят­ни­ком для этих целей.

Отчего же, однако, до сих пор суще­ствуют часо­вые меха­низмы с обык­но­вен­ным маят­ни­ком? Если при­гля­деться, то при малых откло­не­ниях, как у крас­ного маят­ника, «щёчки» цик­ло­и­даль­ного маят­ника почти не ока­зы­вают вли­я­ния. Соот­вет­ственно, движе­ние по цик­ло­иде и по окруж­но­сти при малых откло­не­ниях почти совпа­дают.

Лите­ра­тура

Берман Г. Н. Цик­ло­ида. — М. : Наука, 1980.

Гин­ди­кин С. Г. Рас­сказы о физи­ках и матема­ти­ках. — М. : МЦНМО, 2006.

Другие этюды раздела «Замечательные кривые»

  Цепная линия  Винтовая линия

Математические этюды

Праздник циклоиды. Недавно я обнаружил новую форму — … | Рай Салливан

Недавно я открыл для себя новую форму — циклоиду. Никогда об этом не слышал? Теперь у вас есть шанс учиться вместе со мной и удивляться.

[ПРИМЕЧАНИЕ: этот пост не такой длинный, как кажется. Там много картинок.]

Не так уж часто можно обнаружить новую форму. Я думаю, что большинство из нас полагает, что наши знания о формах уже давно исчерпаны. Мы знаем наши квадраты, круги и треугольники из начальной школы, а позже в старшей школе добавили параболы, эллипсы и синусоиды. Но никто не изучает новую форму в свои 30, верно? Неправильный!

Недавно я обнаружил новую интересную форму: циклоиду. Да, вы правильно прочитали — новая форма. В этом блоге я стремился представить себя (и горстку моих читателей) этой форме. В итоге получилось намного веселее (и зануднее), чем я ожидал. 🧠 🤙

Что такое циклоида?

Согласно Википедии, циклоида определяется как «кривая, описываемая точкой на окружности, когда она катится по прямой без проскальзывания». Возможно, это проще представить с помощью следующей анимированной гифки:

Они видят, как я катаюсь… Циклоид. Магистерский.

Циклоида — это красная кривая, описываемая точкой за пределами круга, когда она катится по линии. Вот именно — это циклоида. Просто, верно? Опять неправильно.

История циклоиды

Циклоиду иногда называют «Еленой геометров», потому что за многие годы она вызвала так много споров среди математиков. Один спор вокруг того, кто открыл форму. Самый древний цитируемый кандидат — биограф Пифагора Ямвлих (ок. 245 г. н.э. — ок. 325 г. н.э.). Среди других упоминается множество эрудитов, включая немца Николая Кузанского (1401–1464), француза Шарля де Бовеля (1475–1566), итальянца Галилео Галилея (1564–1642) и француза Марина Мерсенна (1588–1648). Никто точно не знает, кто заслуживает признания.

Ямвлих: греческий философ, икона моды на тоги и (возможно) первооткрыватель циклоиды. Циклоидная известность, по-видимому, не дает вам мраморного бюста. Источник: Википедия.

Я полагаю, что большинство людей, как и я, слышали только о Галилее, который, как оказалось, был первым человеком, серьезно изучившим циклоиды и давшим им свое имя. Он зашел так далеко, что построил модели циклоид из листового металла, пытаясь понять площадь под кривой циклоиды. Вероятно, ему было бы полезно исчисление. Евангелисте Торричелли (1608–1647), изобретшему ртутный барометр, приписывают правильное вычисление площади под одной дугой циклоиды BTW.

Со временем циклоиды привлекли внимание известных математиков, включая Рене Декарта (1596–1650), Пьера де Ферма (1607–1626), Блеза Паскаля (1623–1662), Исаака Ньютона (1642–1726), Готфрида Лейбница. (1646–1716), Гийом де л’Опиталь (1661–1704), Иоганн Бернулли (1667–1748), Леонард Эйлер (1707–1783) и Жозеф Луи Лагранж (1736–1813). Это, безусловно, имена, которые я узнаю.

Видимо, им нравилось создавать конкурсы и задачи, связанные с циклоидами, которые заканчивались драками и обзыванием. Например, Паскаль организовал соревнование по вычислению (1) центра тяжести, (2) площади и (3) объема циклоиды с испанским золотом в качестве приза. Трое судей посчитали, что никто не выиграл, что звучит не очень весело. Кристофер Рен (1632–1723), знаменитый проектировщик собора Святого Павла в Лондоне, представил доказательство для определения длины циклоиды во время конкурса, что на самом деле не входило в число вопросов конкурса, но все же довольно круто. Судьи конкурса утверждали, что он уже решил эту задачу много лет назад, но так и не записал ее. Это привело к публичным дракам. Еще менее весело. (Рен опубликовал свою работу и получил признание FWIW.)

Еще одна математическая задача была предложена Бернулли в 1696 году и закончилась мелочностью, но об этом мы еще услышим позже.

Знакомство с циклоидами с помощью математики

Теперь, когда мы познакомились с историей циклоидов, вы можете задать себе те же вопросы геометрии, что и наши мертвые друзья-математики Галилей и Рен: какова площадь под циклоидой? Какова длина пути циклоиды? Другими словами, расскажи мне об этой форме, чувак.

У нас (к счастью) есть математика (и YouTube), чтобы помочь нам.

Существуют параметрические уравнения, отображающие путь циклоиды относительно времени (t) по мере того, как круг катится вперед по осям x и y. Я нашел этот вывод YouTube особенно полезным для визуализации его синусоидальной природы. Имеется два уравнения, поскольку положения x и y не зависят друг от друга:

• x(t) = r(t−sin(t))
• y(t) = r(1−cos(t))

Чтобы увидеть эти уравнения в действии, давайте представим, что t = π. В этот момент x(π) = r(π−sin(π)). Поскольку sin(π) = 0, то x(π) = πr. Это половина пути вращения круга, поскольку длина окружности, по которой будет вращаться круг, равна 2πr. Высота будет y(π) = r(1−cos(π)). Поскольку cos(π) = -1, то r(1-(-1))=2 и y(π) = 2r. Это имеет смысл, так как наша точка на окружности будет в самой высокой точке на полпути к рулону, на два полных радиуса выше линии.

Теперь, когда у нас есть уравнения, мы можем использовать вычисления, чтобы найти площадь и длину циклоиды. Да, я поставил перед собой задачу посчитать (не без помощи YouTube и Google). У меня были воспоминания о тригонометрии и исчислении AP с половинными тождествами углов и интегралами. Вот моя работа, со вкусом выполненная маркерами разных цветов:

Как и в большинстве случаев, связанных с кругами, решения просты. Площадь под циклоидой равна 3πr². Удивительно, но Галилей очень близко подошел к соотношению 3:1 между площадью циклоиды (3πr²) и площадью круга (πr²), используя суперстаромодный метод листового металла, упомянутый ранее. Длина циклоиды всего 8r. Это ответ, который Рен получил ранее. Никаких π или чего-то еще в этом решении.

Честно говоря, это красивые ответы. 😘

Циклоиды в физике

Полезны ли циклоиды помимо их элегантности? Встречаются ли они где-нибудь в природе? Хотя циклоиды не достигают высот некоторых своих геометрических родственников, они все же поражают воображение своим появлением в мире природы.

Вернемся к математическому заданию Бернулли 1696 года. Вот как он поставил свою задачу перед ведущими математиками того времени:

Я, Иоганн Бернулли, обращаюсь к самым блестящим математикам мира. Нет ничего более привлекательного для интеллигентных людей, чем честная, сложная проблема, возможное решение которой принесет славу и останется памятником на века. Следуя примеру Паскаля, Ферма и др., я надеюсь получить благодарность всего научного сообщества, поставив перед лучшими математиками нашего времени задачу, которая проверит их методы и силу их интеллекта. Если кто-нибудь сообщит мне решение предложенной задачи, я публично объявлю его достойным похвалы.

Этот человек не боялся говорить о крупной игре — хотя все «Я публично объявлю его достойным похвалы» кажется менее интересным, чем испанское золото, и более чем сексистским. Затем Бернулли задал свой вопрос:

Если даны две точки А и В на вертикальной плоскости, какую кривую описывает точка, на которую действует только сила тяжести, которая начинается в А и достигает В за кратчайшее время.

Другими словами, если шарик перемещается из более высокой точки в более низкую по кривой (при условии, что точки не расположены непосредственно друг под другом), какой путь должен пройти шарик, чтобы завершить путешествие за кратчайшее время ? Это предполагает, что шарик движется в плоскости без трения с однородным гравитационным полем.

Приз Бернулли в виде «похвалы» еще более забавен, учитывая, что он неправильно вывел правильное решение этой задачи, а затем заимствовал правильный вывод у своего брата. Угу.

Бернулли дал шесть месяцев на то, чтобы люди представили решения, но никто этого не сделал. Лейбниц выступал за продление срока представления на полтора года. Именно в этот продолжительный период Исаак Ньютон услышал об этой проблеме. Сообщается, что он нашел вызов в письме Иоганна Бернулли в 16:00. когда он вернулся домой с Королевского монетного двора 29 января, 1697. Он не спал всю ночь и на следующий день анонимно отправил правильное решение. Решение было, по-видимому, настолько хорошим и настолько явно принадлежало Ньютону, что Бернулли определил его как человека, «узнавающего льва по следу его когтя». 🐅

Решение Ньютона за один вечер превзошло две недели, которые понадобились Бернулли для решения задачи. Затем, в манере математического микрофона, Ньютон добавил в свое письмо немного пикантности: «Я не люблю, когда иностранцы ругают меня [пристают] и дразнят меня математическими вещами…» Ньютон никогда не был известен как самый приятный человек. Дикий.

Ньютон, самый проницательный циклоидный математик. Источник: Какая культура.

Это самое быстрое решение, найденное Ньютоном и Бернулли, называется брахистохронной кривой, что в переводе с греческого означает «кратчайшее время». Как вы могли догадаться по теме этого блога, кривая брахистохроны является частью пути циклоиды. Ниже видео, которое я нашел в Instagram, показывающее эту кривую в действии. Так же я столкнулся с циклоидами:

Кривая брахистохроны в действии.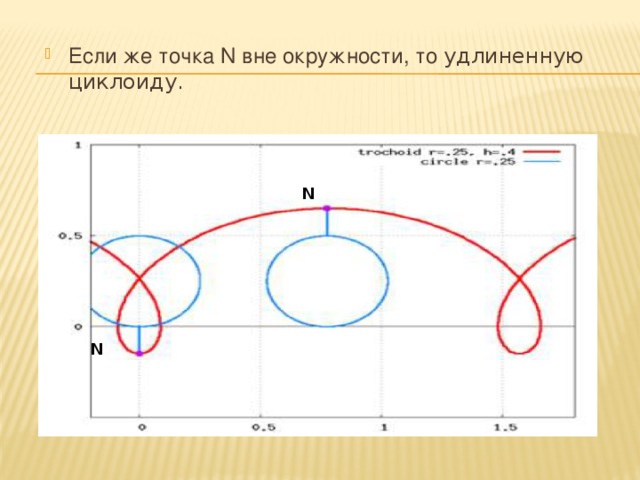 Это всегда самый быстрый путь для объекта, перемещающегося между двумя точками на разной высоте из-за гравитации. Кривая брахистохроны находится посередине на верхнем изображении, а красная кривая — на втором.

Это невероятно круто. Всегда интересно видеть силу форм в природе.

Еще одна забавная кривая, которая является частью репертуара циклоиды, — это кривая таутохрона, что в переводе с греческого означает «одно и то же время». Вы можете поместить шарик в любое место на этой кривой, и ему потребуется столько же времени, чтобы скатиться на дно. Он также основан на половине циклоиды. Вот эта кривая в действии:

Таутохронная кривая, еще одна удивительная циклоидальная форма. Неважно, куда вы поместите цветной шар на этой кривой, все они одновременно покатятся вниз.

Есть еще нечто, называемое циклоидальным маятником. Представьте, что вы поместили конец маятника в точку встречи двух перевернутых циклоид. Если вы раскачаете маятник, струна будет изгибаться против циклоид на всем своем пути. Форма конца следов маятника — ЕЩЕ ОДИН ЧЕРТОВЫЙ ЦИКЛОИД. 🤯

Циклоидный маятник между двумя циклоидами, создающий еще одну циклоиду.

Есть множество вариаций, которые вы можете сделать с циклоидами катящегося круга. Вы можете перекатывать круг вперед, но вместо этого отслеживать точку внутри или снаружи периметра круга, чтобы создать более завитые или плоские кривые. Визуализация каждого представлена ​​на изображении ниже:

Вариации циклоидной кривой из ResearchGate.

Вы также можете накатывать круги и фигуры на другие круги и фигуры, чтобы расширить семейство циклоидов, как мы увидим позже.

Наконец-то можно создать циклоиду в физике прямо сейчас, бросив что-нибудь с любой высоты. Движение объекта к земле будет прямой линией вниз. Поскольку земля (круг) немного вращается на пути вниз, путь, по которому будет двигаться падающий объект, будет очень слегка перевернутой циклоидой (хотя и очень маленькой)!²

Мы, циклоиды в литературе

Циклоиды, должно быть, были в моде, потому что они время от времени появлялись в литературе в предыдущие века. Хотя я не буду документировать все случаи, вот один из классического романа Германа Мелвилла 1851 года «Моби Дик »: косвенно бросается в глаза тот замечательный факт, что в геометрии все тела, скользящие по циклоиде , например, мой мыльный камень спустится из любой точки в одно и то же время.

Циклоиды в архитектуре

Теперь, когда мы все согласились, что циклоиды невероятно круты, я начал задаваться вопросом, пропускал ли я циклоиды где-нибудь еще в повседневной жизни.

Архитектура полна геометрических форм. Многие из наиболее известных типов арок основаны на кругах (римская арка), эллипсе (полуэллиптическая арка), параболах (параболическая арка) и контактных сетях (цепная арка). Существует множество примеров каждого из них, но я привел несколько наиболее известных из них ниже:

Триумфальная арка в Париже, Франция, представляет собой полукруглую арку, также известную как римская арка. Мост Кью через реку Темзу в Лондоне, Великобритания, представляет собой полуэллиптическую арку. Полуэллиптические арки особенно хороши для создания более широких пролетов арок для таких вещей, как движение лодок и поездов. Мост Биксби-Крик на американском маршруте 1 в Биг-Суре, Калифорния, представляет собой параболическую арку. Фото: Alamy. The Gateway Arch в Сент-Луисе, штат Мичиган, представляет собой цепную арку. Цепные арки являются самыми прочными из всех форм арок, учитывая их равномерное распределение веса.

Циклоида очень похожа на арку. Так используются ли циклоидные арки в архитектуре? Согласно моим интернет-исследованиям, они есть, но редко. Есть два ярких примера, которые постоянно появляются (в основном из-за их включения в Википедию, посвященную циклоидам).

Первый — это крыша Художественного музея Кимбелла в Форт-Уэрте, штат Техас. Многочисленные арки этой крыши представляют собой серию циклоидов с небольшим пространством между ними. Это дает успокаивающий вид колеса катящегося. Я копаю это. Отличный выбор для художественного музея.

Циклоидные арки в Художественном музее Кимбелла в Форт-Уэрте, штат Техас.

Второй пример циклоидной арки в архитектурном дизайне заставил меня задуматься. На фасаде Центра Хопкинса в Дартмутском колледже в Ганновере, штат Нью-Хэмпшир, есть циклоидные арки. Дартмут — это место, где я учился на бакалавриате, поэтому я буквально видел эту форму каждый день в течение 4 лет. Может поэтому меня так тянет?

Циклоидные арки на фасаде Центра Хопкинса в Дартмутском колледже в Ганновере, Нью-Хэмпшир.

Оказывается, в 2016 году наш журнал для выпускников назвал циклоидные арки Хопа одной из 101 причины полюбить Дартмут. Я не мог удержаться и обратился за дополнительной информацией. Пока ничего существенного в ответ не услышал :

Циклоиды в искусстве и досуге

Вы, наверное, тоже играли с циклоидами в детстве. Игрушка Hasbro Spirograph, которая производится с середины 1960-х годов, основана на модифицированной форме циклоидов, называемых гипоциклоидами. Вместо того, чтобы катить круг по линии, гипоциклоида представляет собой «особую плоскую кривую, образованную следом фиксированной точки на маленьком круге, который катится внутри большего круга».

Игрушка спирограф. Источник: Википедия.

Двумя особыми формами гипоциклоиды являются дельтовидная и астроидная. Вы можете сделать эти формы, ввернув круг внутри другого большого круга с трехкратным и четырехкратным радиусом соответственно:

Дельтовидная (слева) и астроидная (справа) — две особые формы гипоциклоиды.

Вероятно, вы уже видели форму астроида. В логотипе футбольной команды Pittsburgh Steelers три астроида разного цвета. Циклоиды продолжают бить меня близко к дому.

Логотип Pittsburgh Steelers состоит из 3 астроидов, которые представляют собой особый тип гипоциклоиды.

Если вы находите эти формы успокаивающими, есть ряд художников, которые создают циклоидные рисунки, подобные показанному ниже, включая в свой дизайн несколько вращающихся кругов разных размеров:

Циклоидная художественная машина, которую я нашел на Pinterest.Циклоидная графика для продажи на Kickstarter.

Циклоиды в оптике

Вы также можете катить круги снаружи других кругов и отслеживать их путь, чтобы получить дополнительные производные циклоиды. Одним из частных случаев этой категории является кардиоида. Это форма, созданная путем отслеживания точки на краю круга, катящегося по снаружи другого круга с таким же радиусом. Путь этой циклоиды имеет ровно один пик, как показано ниже, и напоминает сердце (отсюда и название):

Кардиоида — еще один особый класс циклоид.

Кардиоиды постоянно появляются в природе, особенно в каустиках, созданных из двух круглых поверхностей. В оптике каустика определяется как «оболочка световых лучей, отраженных или преломленных искривленной поверхностью или объектом, или проекция этой оболочки лучей на другую поверхность. Каустика — это кривая или поверхность, к которой касается каждый световой луч, определяющая границу огибающей лучей как кривую концентрированного света».

Мы видим кардиоиды в каустике, созданной множеством круглых объектов, от кофейных чашек до часов.

Кардиоида в каустике кофейной чашки. Кардиоида в каустике часов.

Следите за этой формой, когда в следующий раз будете садиться за чашку чая утром! ☕️

Граница центральной области множества Мандельброта (известного фрактальной геометрией и теорией хаоса) также является точной кардиоидой. Я действительно не понимаю, как и почему, но это кардиоида, которая выглядит иначе. Шум. 👍

Центральная область первого периода множества Мандельброта является точной кардиоидой.

Циклоидные формы не ограничиваются только кругами. Вы также можете накатывать некруглые формы на другие фигуры и знакомиться с целым рядом новых форм, называемых циклогонами. Например, вот циклогон для качения треугольника и квадрата по прямой:

Одна арка циклогона, образованная равносторонним треугольником, катящимся по прямой без проскальзывания. Источник: Википедия. Одна арка циклогона, образованная квадратом, катящимся по прямой без проскальзывания. Источник: Википедия.

Циклоиды в космосе

Наблюдение за явлением циклоиды не ограничивается микромасштабом вращающихся колес, часов, чашек и спирографов. Они также видны на планетарном уровне. Поскольку спутник Юпитера Европа (меньший круг) вращается вокруг большой планеты (больший круг), гравитационные силы (линия), действующие на поверхность Луны, имеют циклоидальный характер. Циклоидная форма видна на растрескивающихся ледяных поверхностях Европы на спутниковых снимках. Трещина соответствует орбитальному пути Луны вокруг Юпитера и возникающему в результате гравитационному давлению.

Поверхность спутника Юпитера Европы циклоидальной формы. Источник: Science.org. Образование циклоидальных трещин на Европе. Источник: Research Gate.

Резюме

Был ли это очередной гик-фестиваль поста в блоге? Безусловно. Но, надеюсь, вы узнали кое-что о новой форме, которую либо открываете для себя впервые, как я, либо узнаете о ней больше. На самом деле, поскольку циклоиды на самом деле представляют собой целую группу интересных форм, я в итоге узнал около 20 новых форм, начиная от брахистохронных кривых и заканчивая дельтоидами и циклогонами.

Насколько круто открывать новые формы, когда тебе за тридцать?

Заставляет меня смотреть на вселенную вокруг меня с большим любопытством и удивлением…

¹ Эли, Маор и Ойген Йост. «Искривленная математика и красивая геометрия». Американский ученый.

² Линч, Питер. «Изогнутая история циклоидов, от Галилея до велосипедных передач». Айриш Таймс . 17 сентября 2015 г.

циклоиды

циклоиды

---

Циклоиды, гипоциклоиды, эпициклоиды

Гипотрохоиды и эпитрохоиды

(расследование в движении с использованием GSP)

---

Когда колесо движется по прямой, геометрическое место любой точки на его Окружность будет знакомой кривой, известной как циклоида (щелкните фильм кнопка фильма).

Когда колесо катится внутри круга, точки на окружности кривых следа колеса, известных как гипоциклоиды, тогда как когда колесо катится вне круга эпициклоиды порождены точками на окружность колеса. Наконец, кривые, прочерченные точками внутри колеса называются гипотрохоидами и эпитрохоидами для качения колеса. внутри и снаружи круга соответственно.

 

---

Я заинтересован в этой статье, чтобы увидеть, как мы можем использовать блокнот Geometer’s Sketchpad (GSP) как инструмент для изучения свойств этих фигур. Я утверждаю, что учащиеся узнают гораздо больше о фигурах, написав сценарии GSP. привлечь их, чем они будут из лекции или демонстрации.

Позвольте мне описать, что, по моему мнению, может повлечь за собой обучение:

1. Понимание проблемы

GSP не имеет функции, с помощью которой вы можете сказать ему «крутить колесо». о круг. Тогда первая задача состоит в том, чтобы найти способ, которым это может быть достигнуто, и для этого студент должен будет по-настоящему понять проблема. То есть нам нужно как-то имитировать катящееся колесо. круг — поскольку катящееся колесо касается круга при вращении, кажется ясно, что, совершив один оборот, колесо должно было коснуться часть круга, равная окружности колеса.

На этом рисунке катящееся колесо имеет радиус одной трети окружности. а после одного оборота колеса «задела» треть круга. Также важно отметить, что радиус колеса прошел через 360 градусов, но угол между начальной точкой на окружность и эта точка касания 360/3 = 120 градусов!

2. Строительство

Теперь, когда мы поняли задачу, мы можем начать с построения. Ключом к построению является тот факт, что мы оба можем анимировать два аспекта. эскиза GSP одновременно и что мы можем быть уверены, что точка движется в одной анимации делает это с той же скоростью, что и точка в другой анимации (при условии, что мы выбрали одинаковую настройку (быстро/нормально/медленно)).

Основа конструкции следующая:

Для окружности с центром O и радиусом OA постройте точку T на окружности. круга. Колесо построено по радиусу OT с центром B’. Теперь проще всего было бы анимировать T вокруг центра круга O во время анимации. некоторая точка (S’) вокруг колеса — GSP этого не позволяет (поскольку колесо является результатом точки T, и вы не можете анимировать что-то, что является результат другой анимации) и мы должны ввести второй круг.

Отсюда построение: Дан OA и окружность (центр O, проходящая через А) построить еще одну прямую O’A’ = OA и некоторую точку B на отрезке О’А’. Колесо построено по радиусу OT так, что O’B = B’T, где T равно произвольная точка на окружности. S — произвольная точка на изображении колесо (центр окружности O’ и проходящий через B). Наконец, мы строим S’ так что угол BO’S = угол TB’S’ и если мы теперь анимируем T по кругу и S вокруг изображения колеса получаем искомую кривую, обводя точки’.

Эта конструкция обеспечивает основу для всех различных кривых, которые мы хотим расследовать……

ОДНАКО……..

У конструкции есть небольшая проблема с точностью (что, к сожалению, является функцией программного обеспечения). Есть определенные свойства из этих кривых, которые хорошо известны, а именно: В случае гипоциклоидов (и эпициклоиды), если R/r — отношение радиуса окружности к радиус колеса и R/r рационально, то R будет представлять число точек, а r указывает, сколько раз колесо должно перевернуться круг до завершения рисунка (на рисунках ниже R/r = 3, 4 и 2 соответственно)

Использование нашей конструкции, к сожалению, приводит к некоторым неточностям. .. (для обсуждения из этих неточностей нажмите здесь почитать переписку от разработчика)

Другая конструкция

Если мы вернемся к нашим первоначальным замечаниям, мы вспомним (а если это не было тогда очевидно — это должно быть после первой конструкции) что есть зависимость между углом, на который повернулось колесо, и угол окружности, по которой он прошел, можно определить по формуле: угол TBS = R/r * угол TOA (и для полной точности: угол TBS = — (R/r *угол ТОА)).

Использование этого метода явно решает проблему неточности, описанную ранее. К сожалению, однако, он вводит другое: в случае, когда R/r равно рационально и r не равно 1, получаем (в случае R/r = 3/2):

Обратите внимание, что локус неполный! Это легко понять, если рассмотреть что на самом деле происходит с нашей конструкцией:

В первом случае (при R/r = 3) при приближении угла TOA к 180 градусам — скажи на 179градусы угла TBS = — (3 * 179) = — 537 градусов, тогда как угол TOA проходит 180 градусов, чтобы сказать 181 градус GSP измеряет угол как — 179 градусов и ТБС = — (3 * — 179) = 537 градусов. К счастью, углы — (3 * 181) = 573 и 537 на самом деле одно и то же равнодействующее движение БС и на эскиз не влияет. Во втором случае (при R/r = 3/2) мы рассмотрим тот же сценарий, когда TOA изменится со 178 градусов на 182 (= — 178) градусов, TBS изменяется от — 267 градусов (- (3/2 * 178) = — 267) до (- (3/2 * -178) = 267 градусов и на этот раз 267 градусов и -267 градусов даю же результирующее движение БС и отсюда новая проблема!

СРАВНЕНИЕ КОНСТРУКЦИЙ

Каждая конструкция имеет некоторые преимущества и, следовательно, некоторую ценность. Величайший Преимущество второй конструкции в том, что мы можем построить гипоциклоиду как локус, который позволяет нам наблюдать влияние изменения R/r без приходится каждый раз анимировать кривую. Нажмите кнопку для QuickTime фильм, который иллюстрирует это замечание:

Одно важное замечание, которое вы должны были сделать, наблюдая за фильма была та же самая ошибка, которая вызывает проблему, когда r в R/r не 1 тоже вызывает затруднения в этой ситуации — сравните следующий ролик из фильм с соответствующей сценой, используя другую нашу конструкцию (R/r = 7/2 в каждом случае):

Так что остается выбор — использовать первую конструкцию, несмотря на ее врожденный недостаток (и повысить точность, внеся некоторые коррективы в фактические размеры R для каждого случая) ИЛИ используйте вторую конструкцию, которая технически ошибочен, но дает более точную иллюзию в пределах определенных параметры (R/r имеет r = 1).

3. Разведка

Теперь мы готовы исследовать свойства циклоидов, Гипоциклоиды, эпициклоиды, гипотрохоиды и эпитрохоиды

Для целей данной статьи я привожу только иллюстрации (как рисунки и видеоролики) и эскизы GSP (для того, чтобы читатель мог с ними поиграть).

 

ГИПОЦИКЛОИДЫ

Чтобы получить доступ к эскизу GSP, используемому для рисования этих гипоциклоид, щелкните значок GSP. кнопка:

Р/р = 2:

Диаметр колеса следов астроиды:
R/r = 4:R/r = 4/3

В случае R/r = 4/3 мы получаем точно такую ​​же гипоциклоиду, как и при R/r = 4 (хотя на схеме это не совсем ясно), но след диаметр колеса совсем другой!

 

ЭПИЦИКЛОИДЫ

Чтобы получить доступ к эскизу GSP, используемому для рисования этих эпициклоид, щелкните значок GSP. кнопка:

R/r = 1. Эта эпициклоида называется кардиоидой.

Кардиоида также может рассматриваться с использованием некоторых произвольных точек на окружность неподвижного круга как центры кругов, проходящих через пик кардиоиды, как на рисунке выше.