Цилиндр формула объема: Калькулятор объема цилиндра | «Караван»

3

Проверить ответ поможет калькулятор .

формула через диаметр и высоту

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Геометрия Нахождение объема цилиндра: формула и задачи

В данной публикации мы рассмотрим, как можно найти объем цилиндра и разберем примеры решения задач.

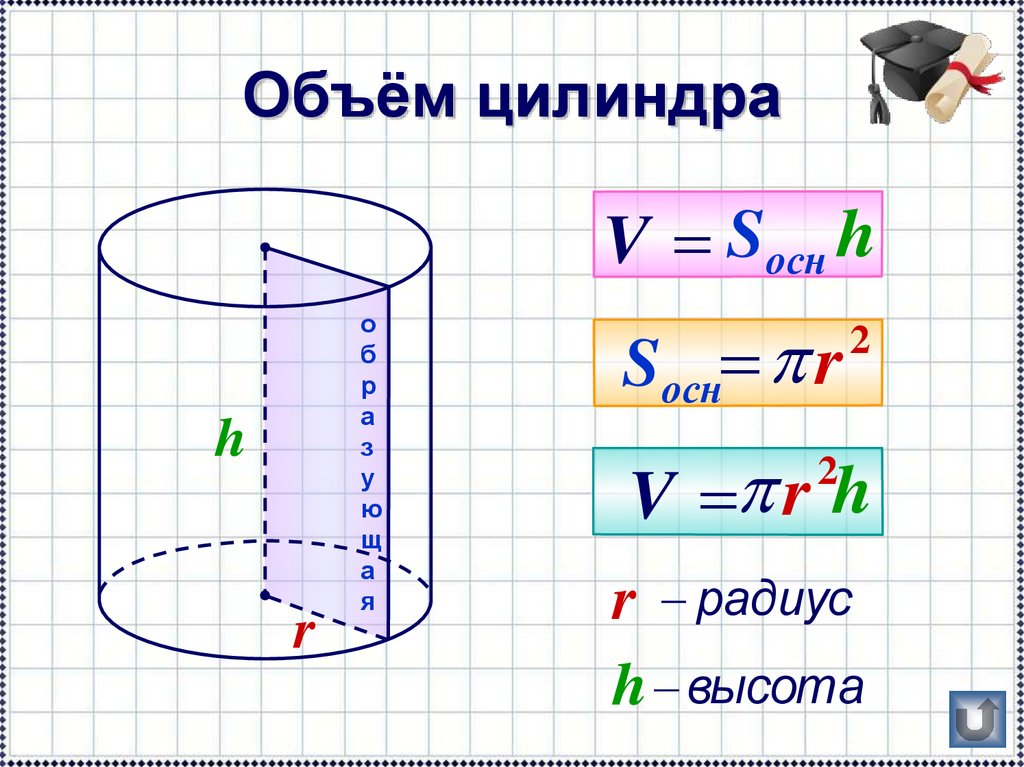
• Формула вычисления объема цилиндра
  • Через площадь основания и высоту
  • Через радиус основания и высоту
  • Через диаметр основания и высоту
• Примеры задач

Формула вычисления объема цилиндра

Через площадь основания и высоту

Объем (V) цилиндра равняется произведению его высоты и площади основания.

V = S ⋅ H

Через радиус основания и высоту

Как мы знаем, в качестве оснований цилиндра (равны между собой) выступает круг, площадь которого вычисляется так: S = π ⋅ R². Следовательно, формулу для вычисления объема цилиндра можно представить в виде:

V = π ⋅ R² ⋅ H

Примечание: в расчетах значение числа π округляется до 3,14.

Через диаметр основания и высоту

Как нам известно, диаметр круга равняется двум его радиусам: d = 2R. А значит, вычислить объем цилиндра можно следующим образом:

V = π ⋅ (^d/₂)² ⋅ H

Примеры задач

Задание 1
Найдите объем цилиндра, если дана площадь его основания – 78,5 см², а также, высота – 10 см.

Решение:
Применим первую формулу, подставив в нее известные значения:

V = 78,5 см² ⋅ 10 см = 785 см³.

Задание 2
Высота цилиндра равна 6 см, а его диаметр – 8 см. Найдите объем фигуры.

Решение:
Воспользовавшись третьей формулой, в которой участвует диаметр, получаем:
V = 3,14 ⋅ (8/2 см)² ⋅ 6 см = 301,44 см³.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Калькулятор круглого цилиндра

Форма круглого цилиндра

r = радиус
ч = высота
В = объем
L = площадь боковой поверхности
T = площадь верхней поверхности
B = площадь базовой поверхности
A = общая площадь поверхности
π = пи = 3,1415926535898
√ = квадратный корень

Калькулятор Использование

Этот онлайн-калькулятор рассчитает различные свойства цилиндра по двум известным значениям.

Он также рассчитает эти свойства с точки зрения PI π. Это правильный круглый цилиндр, верхняя и нижняя поверхности которого параллельны, но его обычно называют «цилиндром».

Единицы: Обратите внимание, что единицы измерения показаны для удобства, но не влияют на расчеты. Единицы используются для указания порядка результатов, таких как футы, футы ² или фут ³ . Например, если вы начинаете с мм и знаете r и h в мм, ваши расчеты дадут V в мм ³ , L в мм ² , T в мм ² , B в мм ² и A в мм ² .

Ниже приведены стандартные формулы для цилиндра. Расчеты основаны на алгебраических манипуляциях с этими стандартными формулами.

Формулы цилиндра через r и h:

• Рассчитать объем цилиндра:
  • В = πr ² ч
• Рассчитайте площадь боковой поверхности цилиндра (только кривизну снаружи)**:
  • Д = 2πrh
• Рассчитайте площадь верхней и нижней поверхности цилиндра (2 круги):
  • Т = В = πr ²
• Общая площадь поверхности закрытого цилиндра:
  • A = L + T + B = 2πrh + 2(πr ² ) = 2πr(h+r)

** Рассчитывается площадь только боковой поверхности наружной стенки цилиндра. Чтобы рассчитать общую площадь поверхности, вам нужно будет также рассчитать площадь верха и низа. Вы можете сделать это с помощью круговой калькулятор.

Расчеты цилиндров:

Используйте следующие дополнительные формулы вместе с формулами выше.

• По радиусу и высоте рассчитайте объем, площадь боковой поверхности и общую площадь поверхности.
  Вычислить V, L, A | Учитывая г, ч
  • используйте формулы выше
• По заданным радиусу и объему рассчитайте высоту, площадь боковой поверхности и общую площадь поверхности.
  Вычислить h, L, A | Учитывая г, В
  • ч = В / πr ²
• По заданным радиусу и площади боковой поверхности рассчитайте высоту, объем и общую площадь поверхности.
  Рассчитать h, V, A | Учитывая г, L
  • ч = л/2πr
• Зная высоту и площадь боковой поверхности, рассчитайте радиус, объем и общую площадь поверхности.
  Рассчитать r, V, A | Учитывая h, L
  • r = л/2πh
• Зная высоту и объем, рассчитайте радиус, площадь боковой поверхности и общую площадь поверхности.
  Вычислить r, L, A | Учитывая h, V
  • $r = √(В / πh)

Рассчитать

%PDF-1.5 % 1 0 объект > эндообъект 190 объект >поток приложение/pdf

Рассчитать

Adobe Illustrator CS32009-06-17T10:31:49-05:002009-06-17T10:31:49-05:002009-06-17T10:31:49-05:00

168256JPEG/9j/4AAQkQMAGSkZJRgABAgEASABIAAD9QGMAGSkZJRgABAgEASABIAAD9QGMAGASUGza lNA+0AAAAAABAASAAAAAAEA AQBIAAAAAQAB/+4ADkFkb2JlAGTAAAAAAAf/bAIQABgQEBAUEBgUFBgkGBQYJCwgGBggLDAoKCwoK DBAMDAwMDAwQDA4PEA8ODBMTFBQTExwbGxscHx8fHx8fHx8fHwEHBwcNDA0YEBAYGHURFRofHx8f Hx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8fHx8f/8AAEQgBAACoAwER AAIRAQMRAf/EAaIAAAAHAQEBAQEAAAAAAAAAAAQFAwIGAQAHCAkKCwEAAgIDAQEBAQEAAAAAAAAA AQACAwQFBgcICQoLEAACAQMDagQCBgcDBAIGAnMBAgMRBAAFIRIxQVEGE2EicYEUMpGhBxWxQiPB UtHhMxZi8CRygvElQzRTkqKyY3PCNUQnk6OzNhdUZHTD0uIIJoMJChgZhJRFRqS0VtNVKBry4/PE 1OT0ZXWFlaW1xdXl9WZ2hpamtsbW5vY3R1dnd4eXp7fh2+f3OEhYaHiImKi4yNjo+Ck5SVlpeYmZ qbnJ2en5KjpKWmp6ipqqusra6voRAAICAQIDBQUEBQYECAMDbQEAAhEDBCESMUEFURNhIgZxgZEy obHwFMHR4SNCFVJicvEzJDRDghaSUyWiY7LCB3PSNeJEgxdUkwgJChgZJjZFGidkdFU38qOzwygp 0+PzhJSktMTU5PRldYWVpbXF1eX1RlZmdoaWprbG1ub2R1dnd4eXp7fh2+f3OEhYaHiImKi4yNjo +DlJWWl5iZmpucnZ6fkqOkpaanqKmqq6ytrq+v/aAAwDAQACEQMRAD8A61/zkHq0tr5Nt9MhlWJ9 YvIrSV2bgEiaoEjE/DwWdoQ4b4SDQ7VxSHz9b6l5at47db7Qre7k0+6P6bOn6lqsv12xZgqPoqjU lFy0YjlM8lBGlBja0mOj6Mmqm5W10Owu2tYJL2aSx1bVpIEtko3L1m1Hi7KGAbiftbAZgZNRPjMY 1sHptL2XpRpoZc5neSVDhrz8vJTH+GLtIreHRYba4JImuh2PWOA6EUDXp47da1rXKRrpmhsHYz9м cGPjkTknGPIRri/G6vY2mgXMEOnQ+XPX1i7nWG0mGp6sI2D1QLx+uhefMijcqeIyY1k6AocRceXY Om4pTMpxxQjcrFSvu3HcnMn5frpWm+YT5h8r3Fo1jps89lfpfaoYxeFVW2QObuWCXlJIo4779dgR mRhyZOIiYdVr9NohhjPBORkTvGVXW/d+N3gepvbvqV29tT6s00hgoAo4FjxoBsNu2ZTpkLirsVdi rsVdirsVdirsVZT5NsdFuLDVpbmKyu9WgEH6PsdSuvqVu8bM31iT1BNa8pI6JxT1NwzGhpir0f8A wF+SlpaXlpeanIt7bWuoXMhnvIre8WZBZXFnaIjD0vU9KaSF6xtykElAOICKLVl/LD8kON1Z/wCK IQsd4n1fVX1O05zW4jn9SOOBUIj4MqfFICJSBwZA+K2x7yvpf5Vw65Npuox2l7Yi30aX9IXt9Kv7 68ns1v1jNtJaIEhiuZqqwZkMZLNQEYqr3X5Y/l9DaxRSaw9rqkunWl2Iri/05FWS5ihlqVl9E/EJ n9OJmXZeTyorKcVt6r/ziD/yhGs/9tM/9Q8eKlR/5yJ1G4m82aLpsNpHfGws5bx7OeG5uIJ0uS60 mitVeVkjms4i3EdG6jrgKh5jceW54nuI4L25UQ2y3GjyjTtbif15gBc6UhFtSLTKzzfu1FW2qdzi llXk7y/5MurTUL3zQL7TIInhW1ttJ03UViQyrI7KkT2kz+moQcetB9o1IrgjRiUiZ9Xp8ntFLHix 49Ptwxo2Bufmparp9kNVuIPLUc+oaSIHkgNzpWpCSNETnKWaS1SrgqxHEmvYV+HIT0sr9NcPm2ab TRAYXLOWOW7Jgfq7uvwqkBFatpD2Gq6beXE97byCYoNI1ekMqNyQgyWXBwAFJ9/EbmI0U4kGJFuT k9o9PnjOGWE+CXKquv7fvTHzN5p8xnyPrM+papc3V3qF5aG2huo72COP6uJ9RkCw3UcCU52cafux QAhajlTMzBjnGzI2S8/2lqsGXhjhhwQiOdDiPvr9b57zIdW7FXYqjdFh02bWLCHVJmt9NkuIkvp0 FWjgZwJXUeKpUjFXp+jeTPIV5qcl3rlxo+k2lpqFlDHYWmsLMl1Zy3SxzO1ZJ5AVicszrOnEL/dj rihVsPy+/KuLVYJLnWYZNOgvjBMkuq2Lie3+u2UUM/GH0pY0mtp7mRlB5R8ByYUNVbTF/wAt/wAm bWwghm1+1mvbp4RcXEOsW0wtVkvbOJlVhFAJG9E3D8zFxRa8lPwtitpW/kL8sLTRZ/MMF9Jqtrp4 0+8urQX9sxVLm5tlmspYYUS4Zlhnes0ZUchxoGBxW0QPJH5PRnUw2sW876TZXkMUq38SxXd7FZxS QOsZPqSepPcShGiYJ+4AZayYqqw/lj+S8dzdx3fmzlHHLbLatDqNh8UdzqNxbFy3puD6VokM7jtU 1oCKK2kdl+X35eTa15ds28y25tNQshcaxdSX9vbrbSUiLAFoZArq0jqIX3bjXmtfhVtHWnkf8pU0 x7460lzdJp8rNYT6hbIDdHTUuFlXisTkJczCJYASxdTuQrLitqEXlr8ptSjs4Pr6afNbaVYS30sd wkIa5uLZZLmUyXM1ys7QSbG3hiiep4ivGuKo7UvI35X3us3NPM7yWMNtOItSu9WspZGls5/qkMAi EQkZfq0Ymjb7LLxiUinLFbem/wDOIP8AyhGs/wDbTP8A1Dx4qXpPmz8qvJ3mrVF1PVrd5LtYlgJV /gZYyxQmNgycl9RgGpWhp0xQkv8A0L5+W3/LG/8AyS/6p4ptp/8AnHv8t2FBayKfEejX8YzitrP+ hd/y5/3zN/07/wDVHFbd/wBC7/lz/vmb/p3/AOqOK2up/OO/5YvbtBNZTSI5+IiUwkgUIUmARVWo rQ98VtD/APQsv5Qf9Wqb/pLuP+a8UW7/AKFl/KD/AKtU3/SXcf8ANeK27/oWX8oP+rVN/wBJdx/z Xitu/wChZfyg/wCrVN/0l3H/ADXitu/6Fl/KD/q1Tf8ASXcf814rbv8AoWX8oP8Aq1Tf9Jdx/wA1 4rbv+hZfyg/6tU3/AEl3H/NeK2jT+QP5cnSv0QYr/wDRIf1Rp/6QvPq/qfz+l6nDlv1piqC/6Fl/ KD/q1Tf9Jdx/zXitu/6Fl/KD/q1Tf9Jdx/zXitu/6Fl/KD/q1Tf9Jdx/zXitu/6Fl/KD/q1Tf9Jd x/zXitu/6Fl/KD/q1Tf9Jdx/zXitu/6Fl/KD/q1Tf9Jdx/zXitsx8leQfLHkuwnsPL1u9tbXMvry o8jykycQlauWI2UYqk9l+ZepXE8cTeU9UIUUvpIYywhkKLKIwsqwSMVjcFuSrvtH6mxKqrpP5lXd 9btLN5Q1+zKyxRlZbRRtP8SOAZFchFp6tF+Btt6VxVStfzSuJfqwm8m+YomuXQCljyWOOV2VHmJd OBULWRQCVr32OKtTfmpL6DNbeT/Mcs5VDHHJp7RKWkERCs3Jivh26OeJpwfwFVVT/lZd5CtyLvyh rwltprqKltaidJEtxzieNuUfL14yONBTnVamgYqok/mG5up7ZPLGu1hJWOd7LjDI31Z7j4WDs3H9 2I6lftsFFd6KpU35zQiaK3Xyb5pkunVGkt005S8Qkd0Qy/vuKBvTJBJ6fTRVMbH8xbm6v47JvKWv W8jOUkmmtUWBaKrBhL6hUqxegO3Rq0Ipiqhb/mfdytac/J3mCOO7jVt7P44pPWMLrMpYBQoo4bka ru023VWXH5qzR6PcahF5M8yPPEYUisWsKSyNPDJKpAV5KInp8JW/YZlFCTIqNsfzEkuZZY38ra/b egfTlkls1CepxqyoVkZpANxzQFDTZjVaqpZcfm+9vDcXU3k3zGljbQJcSSmyCsFaP1WBWR0X93Qq /wAWxxVEQfm3p9xJBHB5e12X6zYtqNuyWQZXiS0W74oyyEMzeosS0+h2fhriq6T81YOMj2/lfzDe JFLJBI1vYhgHiMav1kUn4pabd1b+U4qqXn5lvb2Ul0nlPzDP6ctxEIY7GsjLbSQoZFXnXjKJ+UVa cwj9KYqo3P5rw2ulzavc+WNeg0239b1pZrNYpAsXACT0XkEgRy9AWAPcjiGYKu/5Wsklz9XtfK2v 3D/uTzS0jCenPEZUkqZa8CFZA1OPMca4qibP8wb/AFLTNSuNP8ravBe2NvHcW9pqtu1ktyXHJoon QXJ5p0YcOvSoqQqoR/mZe/VYJpfKOuI5kiju4ltGdk9Z5o+cdP71UaAM/wBmiOrdTxxVDWX5wxX/ AKy2PlPzFLJAl0ZK2SCNZbPmHgaQSsvqM0fFUWpqRtiqf+UPOE3mFbhLjQtT0S5tFiMyalbmKN2l DEi3lqVlCcdzt1G2KvKbS9/L+x0qyvLrz35onvHlSRYXmnWaa5tCnqxhGiKkN9cSNv3hUoAA5CFs KrYvMv5Xal6LHzr5lt57Wzkgtb8vIJzAUacuHS3dpGeKGQguCfH94sfFVH65qPk+3N9LffmHr629 xc28izaZJLS1iubZ4IYjSKfkZJIJSfSQFXpVVI5YqqC4/Kudb/TZfOevTizmFzcwSzXlbf6gsvqo n7gFF/0STlx3DD4CpK4qk73n5bau0Mlv+Yfmk6jwe2068/0hyJpS12CixWi/G8fh5Bx5R0QbigCr 7i9/LqO5utOt/Pfmt7q5ktDqM9pO8RhaOH0lmLPBHUTIOTlOZagPhhVq+1v8rbVzAfzI803ktqsl tJYR3c0jkSSvFIzq0CtI0Z5dWJVQCB9nAqfahcfl+/mG/wBSm8669a39u99ay2qSzNHBRXvLgQRm 3kCgQQELw7AAfvKYVQTat+Wb2ssA8++Y57bVPq7QWxlupGSOSSaZUjL2xlKusUquHZmKDj/Liqw6 n+UttJDcWPnfXNOj1aF761tbZ7iKOWFw9lGEWS2+Hg8UnpgkOTQmqqnFVRFx+VV0l/cHz3rky6s1 493LbyXIjMKW8iHkDC/JI4VIQmqs6niNiqqpjpvmr8t202XT77X9e9LVnXU7SS/eeSURwJ9d/wBF АБХАКНИЭЛфснжШ5ВхВПтЭ8наХрсС6нпПнжжХкВк3к3qхб7ипхлРЗИХССЕМиК9вККООзНуВбАкДж f8q7hZ4UtvN2vW+nJay20lqLx2kLyDikySn7DRqAAOJG1RQliyqnP+TltIlqF82+ZYZbOIQwzx6g vqcQzM3xNE32+Q5U2oqj9nFURP8AlNYT6xe6tN5g1yS7uvrAgLXaEWYuRIpFn+6rFw9X4N/hovhi rVr+UtnaxXMEXmXzALWe2itIrY3/AO7txB6fGS3HD93L+63b3Pjiqofywf11lHm/zIKTmd4/r6lH q0bekQYjSMGLotNmYdGOKrLn8qbeeT1m8z+YEu1SeOO8S9USotxL6jBW9KlFBKKCKBe3JUZVVt5+ U8V1qf6RPmvzHHMoPoxpfKYomaoZ40eJwrFSV27EgbYqmXlzyF+gtWbUI/MeuagjxmJrDUbz63bb 0PMLInMMOOxD+PicVSSy/Pn8vpbP6zfyXujssaTTW99ZzrJFHK3GJ5PSWZQstKqeXT5iqqbSfmz5 AinFvLqZjnpCxie2ulZfrE31eMMDF8LGUcSrbr3piqCP54flmsoSTVWiR4lmjmktrlUaNoFueVfT +H91IrfFStaCpxVCp+b35QrFDbC7iSy1svJbkWkvo3byzSRTlkWMmvqRt6jSKAa1qcVRA/PP8tPT uZzqbrZ21rHfPdG3n4NBLKkClVCGSvqSqtCo9vstRVXg/OTyFJObSW8lttQS3srqexlglMsS6iIj ArmNXj5VuY1YqxVSwqcVUx+d35cfouPUn1KRIGVGkU21wzR84UuKScUZRSKQN136LU7Yqhm/Oz8u byy1gPJNcW+mwzNfQvbkrLFFMttME5fu3AMyV3oVf2biqjT+a35d6fpkRtrpvq0YMFra29pcLQww QzCIJ6arEBHcxAc+KgsFrUEBVCn89vy1Wf0ZNQmjdIhNPytLn92GkSFFNIyXLSScR6fIbHenVVF3 f5q/l3o1w2mNefVxZSraTJHbyrFAxaSJBsgVlMkDRj0+VD7b4qq6f+bfkLUrO+utN1E3f1C0kv5o FhmilMMYkJ4JOkXJj6D0Xr36b4qk+nf85BfltcxRG7uLzS7mZisdleWVx67cRViBAk6mnQ/F/Cqq bal+b/5f6cOVzqREST3FtPKsMzLFJaCQzchx5EAwMoKg1NKdRiqHT86viBthPNdTwepc3VpbxvbT M0r2bRh4Uxq6CN/XjKM7AHkOhqAqin/N38vklvIpNU4PYNbpcVguCAbpgkNCIzUM54mnQ9АйКОП+ dP5aJPLA2rsJILZL2YfVLyiQS24ukZm9Gg5QnlxrXtTltiqprH5weQNISSW+1Bkt4LlrK6nEE5SK ZGnQqaJVv3lnInwBt6diDiqHi/O38u5A7fX5FVbq1skZreb45b1WeAqApIDLGx+KhAG43Wqq/R/z r/LfVrOa6tNUPGCVYJongmWVWklEMRKcKgSMRxP30oaKst0fUotU0my1OKOSGK+t4rmOKYASIsyB wrhSwDANQ0J3xV5to/n7zJ9Wke48zeVL9GnMVvLBcSySEy3MaQqUiC1HpR3PQdQpqVV2KqEHnjzv bWJl1LzV5SgcpHqMsZuC08dpNPFIiosZcMjWzlFIDlmZeLGoOKqsnnvzpc2VtdWnmfydHNZkJqdZ 5zYyS3EYNtEs7bqzFJW4huQop3BpiqD1D8yPNMqMYPOHlHT/AK7bQw26yTTLLb3HpxtcTlJlqgDe t6frLxI9KoqW5KoiTzP5+0iK0h07U/JUek3TQ2+jfvLqKFumMVZd4FaJS0ksfGh50IHVhiqLvPPfn ArcT23mTySmm+s3oXb3k1Vt2l4xB/jMfqcI5amvEutKUBxVZZ+cfNN1d0/Tnlj1JPWk0+5uRcxTC KS4jijRVkWEOvqJJEwVuX93vU1JVL7j8zPOGjafA2teY/KkjSw/WHuLNr25JSWSZY2iWCOQFd4RH VSW4v9rqAqYjzt5jmcM3mTyRcSG0luNPT61JRbpJJVjlB9RmMIh3kZd6hqbYqiZvO3nOGaZ21ryh 9XjW6uFT6xdczbQt6QbkCwLQyK/rcVO4CfCTyCq2z8/a6+oaYzeYvLNxYXbl5442nSQ20kMRt3Xk zCGSSUmiTGnxBQWbCqUR+f8A81zHaT/pbyI0NwnKb/TZ19h5ZHHJxLIrDhCwqnLcN+ypbAq+z/MP zdcJf28vm3ykLn0IpYrq3ldrWJt2uFilZmDHBE0nFwx35fZ+EKuh/Mjz1OsSRa75PW6vVhNpHJ+ kRRhSGfmhEbpG05AiZ6fy77YVRr+fPN5hWVPMfk9bK9+sLZXf1qdnEjQubaML9hiJ42Vq/sinEsN wqnp/wCYHnB7C1R/MPlKS7uYqWU8kt1Gk8n1WBk5EiNVdprhGMaivBxQVGKqkPnLz8sTKPMXkub6 ТБК80кл3МзмкIeGaQx+kiLyZWkotOJ2O+KqV15x86zapqi23m7ytaejqMNvYWUzyAC2BmKrIZArP PP8AAjemxX4G4FWBqqjH80fmDeW9LHBrXleCWZES7ubeaSRPrES1YFt3lPxLNDJEq/um5MWoR8NV UmsvzL87HU47ybzN5MutCM3ozx20t563G3NbhowBKV2YVkZmjC8WpvuqzPRdY8w3vmy7htNd0XUt HinkNxZQyiW+ghC8EVRDwEdJQQ4k51oaMK8VVYppv5decTdaTPfaP5RS3t5fU9DSbaeGBNnZZW+K MybEqo3UFySp6gqjrbyJ5lYqdY8t+SZUkgWGZo7SUHlEyR20I9SNuUaRRgCvQ0VVolWCpdp3krzj b6BdWclr5LiE9xAI2tIJIIUu1kNvKtI40DPwJVOVSXZkYcDxwqip/wAvvM/qSvLoflLXrSN5fq63 Nkq3AVIqKqcYli5yTD4wxAWn2jypGFXyeXvPK6Lay31h5Ljto47uS79aGVrVTcRGKExkog4+nwik JPxJUeGFUw1b8v8AVJPqX6N0Xy1HALZINR064tFe2kMcwYKvG3EnEIWMfxAI3VX5VUKgtX8lee5D qAg0/wApG1Ekn6JmubV/UtbYPJJGD+5ZKkhlNQRz5nsuKoWy8v+c7aBNM+qeRv08hMMcXoyDjaP Az+isKJG9A7MFHT0utWqSVRmneR/PSavJHe6X5THl8yNHHFbWriYWKxyGG0ZGg4FBcMkh+Lryp1A AVQj8p+fkEkk9l5Qiu7qOa0s9Pls2SIF3mM3psvORhOkjSyAk8gOJRCztirem/l550i0eZLnSfJ8 esyQFVu7SxZKzwvAbZ3Z4mVhxWYt+6+FuHFSAcVbvvy582XtvaQzaN5QWj01BktJlMkPpRgrGwTm hMk121VYEVTfd6qqGjflh5qsLJIJdG8nT+teGe5jaxkKRW8sXGeGA8AzVaoQyVoh57gAYqmHlb8 xYLW0uI9H8mx6wBKL547e6SMiNhLZek4X1F4S1d+QO+60OKoG/8Ay486XljHbS6X5T9GKea4Syig uYIOa82tH5RKsoZXYl6NQh5OtRhVWuPIXnSZogNF8nJFayXctnH9UkZY2kUC2ejQsRKhhj5urAEE jj8CkhW18jeeDFEsuheSuRkVLxVs5wklqxKSoAyMQTDHDQGoqu/wgYqst/IPn2NYLmax8o3Wocpp ZPWsG4QSvAFR7d4445N5ERJOe5jVd64qiB5M8+xTWSW+m+U4bRbZPrKLayD0L2DmYpbNRFsoYQn94Tx47Yqhbf8AL7zzBHpyR6X5Pha3sUtrueKyZXLtec7iOP8Ac8RDJbM4KgCsjMaAEUVZr5N0O70+ wM2q6ZpFhrM0kj3L6NGVhcycOblpEjkLSGMFq+A3NK4qgl/KT8vU4enpAjCTPcKqTXCqJZfQ5txW QD4vqcNf9X3NVVCH8l/y0hhjgXR+UMMglijkubqRVYI0YADyt8IR2HH7PtiqyP8AJL8s0sJNPOjh 7ORw4iaaeq8YDbgCQOJCODN9pifiO/SiqoPyY/LMNK/6FUyTXSX0kpnuS5uYwwSQOZOQpzOwNO+K rv8AlTf5bfVry1Ojg29+qJdRtcXJDLHM1wtKy/D+9dm+GlakHY4qsufyX/LS6t1t7jR/WhT1iEe5 u2H+kSrPLWsu/KRA2+Kqn/Knfy35TsdGUtchxKTNch+9keRytZPhLNK4JWnwnj9nbFWrj8nPy3ub W8tZtHDQ380lzdj17kF5ZijOeQlDCphXYGg7dTirrz8nfy4vIXhudHEsUk0Vy6G4uaGWBp2jY0l7 G8l26Hlv0FFVe7/KzyJc31zqEunMt3dyGa6njurqIyMTKTz9OVKg/WZAV6UNOgFFVTyz+XfkjypO +oaHZfUGNubd3FxcPF6AczfYkkePZyW5UqKnfc4qyjFXYq7FXYq7FWgylioILDqO4rirldGLBWBK Hi4BrQ0BofoIOKt4q7FXYq7FXYqlPmDzLp2h3/q3PKaQlQttCY/VIblQ8ZHjFPgPf8cVRi6rpbKG F5AQ26n1E3rv44q3+k9N/wCWuH/kYv8AXFUDpHmrSNVubu2t3Ky2kphIkKASbkB4uLNyU8TTFU3x V2KuxV5J+aGq295qctvYaneJItq9nKttMY4IZWb+9QCqtLwZ42qOh61BGEIec2nlrR7O3vbezieC HUbY2d6qyykyQNKJmQs7M3xONyDXt02w0tsu/LvWx5Y1QrNc3DaNMsnq2pdpQs8rR/6QfULOaLFx 4qQACaCuClt7hBPPDPCk0LrJFIoaORTVWU7ggjAlfirsVYx+YepWlt5cuLaS+nsbu6AW0ks24XAdG DVUgqQu1HNRsadTiFeE6voGlatqc+oXyTTyyFVtxLcSuYIU4FIIyCg4qYxuRX3pkkWiHguV1e51u 1vLi11q6eWZ76OV6iSaP0ndYyTDXgAoqhC9gMVt775a80adr9oZbYlJ46fWLZ/tIT+tTTY/q6ZFK cYq7FXYqhtT06DubGayuC4hnAWT02KNQEGlR40ofbFUu0rRJtHkmSzpcW8qx8WuJW9QFAV4lgjcg FoFJNabdhiqY+pqX++If+Rzf9UsVd6mpf74h/wCRzf8AVLFUDrcWt3OmTRWtraSXHwvFHPK5ido2 DhHpF0YrSvbrv0xVjHljVrjzLb3mnalo3+HdYiR1ns7izY0jasYmguAyxSDl0KnCrLNG0KPShLxv Ly8aYIHN5cST0KAiqByQnKu/HbAqA8961LpPlyeWBilzcEW8DjYqz1JYHsQisR70whXieFDsVdir 0j8ptZlcXWjysWSNfrFqOoUFqSj2HJlI9ycBUPRcCXYq8D83a++pare6k/OSFCwto0BZvRjrwVVF d2G9B+0TkkPO7/WtWmmsbhZ1toEdneGISc5UVwFDrII+IZQwIYVGYufVRx7cy7nsvsTLq7MajEdT +hVsvMupDVaTA3NpdzhIoYoyGt1ZQFJ482cArudhuTtsMcGqjk25FHafYmbRgGVSgeo/S9A8t6zN o+s219GxCKwW4UftQsRzU/RuPcDMp073vIpdirsVUby9trOAz3D8IwQK0LGp8AoJxVRi1aymiWWL 1ZInAZJFhlKsD0IITcYql135mmiv7aG302e5tJG4XN0CEMZZ/SjpG9CayAq3IrQb74qmUV/JLEkq WcxSRQymsI2IqP8AdmKpVN5qnj1eOyGmSta+mz3F3zjrGV9UU9ME1B9Bt+X0HFU3/Sem/wDLXD/y MX+uKtWuq6XdzPBa3kFxNFvJFFIjstDQ8lUkjfbFWK/mzDI/lu3da8YbyN5COgBjkQV/2TjCEF5N hV2KuxVmn5TQufMdzMPsR2box93ljK/8QOAqHrOBLsVfOTQyQsyZARJETG4PUMpoQfeoySGJeaLO 4F8bniTC6gBhvQgU3zTa7GRPi6F9B9ldbi8DwiQJgnbvt3li0uGvhccSIkU1Y9CSKADHQ4yZ8XQJ 9qtZj8DwruZI27qZY0TzAwoKvL8CAdSzbAfec3L56+jsil2KuxVD3+nWWoW5tr2FZ4CQxjbpUbjF WI+afLXnO5ay0vynfRaBpUKxi4vzJJNOEBKGC3t2BiXjGAQxb2p3xVPofLSQwpCuoXbKnpVZ2jd2 AGX1g7O0ZYlnJLb07YqjINPlhhjhS9n4RqEWohrRRQf7rxVCt5diaR3N3PykqHNIdwfV2/u+n+kP irHdL8v+fNM8zSLcaiNb8r3LH0TPPJBe2YILUPprwuFqOIqQ3jXfFWU6foOl6fcz3NpE0c1yS07G SRgzMxckqzMK8iTWmKquqabbanp1xYXIrDcIUYjqPBh7qdxirw3XtA1DRL5rS8TY1MM4B4SL4qf1 jtkkJdiqpb289zOlvbxtLPKeMcaCrMfYYq9n8keWP0DpRWahv7kh7pgagU+yg9lB++uApZFgV2Kv L/zG8nXEN3NrdjGXtZjzvI1FTG/7UlB+y3VvA79MIKGAkAih4B6jCrgAooBQDt2xVnf5c+T57m8i 1m9jKWcB52iNsZJB9l6fyr1HiaYCr1PAl2KuxV2KsL1XzF+ZtrrmrQaf5Sh2PSIEibSrv9IQ2rzs Yg0qMrCUr+8qikhfuNQq6TzN+Zf1SaZPJaevFLPElr+k7cmVF9MQTJJxChXZ35K4DBVJ60VlUvi8 4/nAlv8A6R+X6zXEbhWMOqWaLKh9SrqrsfTpxj2LN9r2xVXuPNX5sieT0PI8bW5gtBCW1O25rczx h7kuPhDRWzExmlGcgFaqxKKtXnmb83YbWwFv5Ngu7swF9SZdQgjiEyBT6cIY8v3h5qpaoXYmtKFV nVs8slvFJNF6MzorSQlg3BiKleQ2NDtUYqqYq8/i1Tz/AH51DTNW8tWGqwQyzRw3cNxCkQKwzSQi W2klndXLLCv2wf3nLYLuqxW20PzW5tEvPy7iW5+ryyXvDWAiyTQQFgkCC4cok87Iis3L0x9qtag2 qb+WtX886MtvFcflzDpvrVjub9dWsyDIQREg5s8p9WQKqryNOXfAqdy+Y/zUkS8EHk+C3kge3Fq0 uoQzLcL6yrdFAvplR6XIxl+J7stfgxVbH5r/ADFNxCsHlu11O3QJDqD2t/BG0NzWD1VId3p6XOWq 7k8V6VxVUu/OPnqyvpTd+T0h0SK5dJNXbVbRVjs45lX65NHIE4KYS0vAMx24mla4ql8nnj81o9тм tF8i28pr/o8A1m0SYxK/F7khlqYjyWg4BgevXZVjepXmrXxOqDyDYy2kayx6hDDrlrbyQ3kU0iSR PLFIKHKOOLnIp3HLrVWGFUZJpXnKwvL/APRH5eWshW6li0i8utTWdBBEv7u4nhkkJ/fNTgqHku/K nEF21egaJrHmW61q/stU0P8AR9jDHBLY363UM4lMiD1Y3iUiRCknIK3HiwHbuFT7FXYq7FXYq7FX Yq7FXYq7FXYq7FXgV7pf5W3breWn5beY9QbVrprmV4kvEhYoWU3XIXPPAsJZDF0JO/whlYqojVfI /wCW0NhqdlZfl5r1w6RzxIxN0Q3pvcIGt3mnmAJcGRPg3EgahqRiqq9l+XRW20tfInmG+vBZPaMX hnglNtbIIYzKySxKnrmwj9M0UdxSrDCqZ6FYeStF1mHUtF8heYbbUYZJyknC4RWadnglJWS59F+f оI37yg4lHr4BV2l2PlX9OarL/gPWrVb+/j1K41A/WGWa7tZhcwP6TShkPq3LvRV9PqNyCqlUJp+i /lxdXMat5B8x2S3ckU5M8V4sIkeCVQ0iR3LqjUj9OSq/aZC3XkFUuvm/L/Woo7nWfyx81NdIr21F tb0yRwQSFoaSLPGSH9agCVIA4/YVTgVZrD/lZZ293rGo/lz5jhtC0NxdSvDPColkkW4BaN7qNFpL NQ8f2uQOwFVU7eLykuq32qX35fa8NUWfUIpJ7aOedJEpO/qR0mjB+sR3kgXilA7MgPwqSVZx5Q8l eTdHkfW9C0t9PudVhQzCU3CyCM0dImhnY+jw6CMKvH7NBSmBWT4q7FXYq7FXYq7FXYq7FXYq7FXY q7FXYq7FXYq7FXYq7FXYq7FXYq7FXYqwi1/OLyZPJbxl7mMzoXZvQaVIhQOBJJB6qV4Hk3EtwH95 wNcVW2f5y+Sr/Rr7VdOa7vYtOERuYYraVZAtwyrCV9QRo3qc1YKG5UO4G9FVOx/PP8s7z0PT1R1a 5l9G3VrW5+MtK8KP8MbBUdomoWp70xVWvfzk8i2+mxalDdS3tnJPaW7SW8L/AAG+RngZhIIyVYIa 8akdxirUH51/ltPrNrpEeq1ur14YrJ/RmEcstwEaONX4deMsbVNF+Ib9AKrX/OjyMl9bW/q3JtLq ON49TFvIbYNPJ6UMb7eqryvy41jp8Lb7HFVa3/OT8up9Nm1JNUYW1vEk89ba65qklz9UWiCLkx9f 4CFBPfpviqJtfzS8kX0GqyadqK3sujxu95axqyS1jWZjGgmESs9LWQ8a9BX7JBxVKdI/PX8v9WbS o7Ke5e41WeK3S3MDB4fXavipJv2VRnh51UtTkpNAa4qj9N/OD8uNSu7C0tdZU3OpqHsIpYbiAzKx lAZfVjTYm3cD3oOrLVVDp+dfkBbaCa7urmyNxH66RS2dy7LCbp7OOWQwxypGJZYjwDsG3FQCaYqz HTNQh2HTbXUIAyw3cSTxq9AwWRQwrQsO/YkYqicVdirsVdirsVdirsVdirsVeQ+SvPPnDVrHT7q0 1nypeJe3NdSnZ7u3uXU3EMAMcLxW7PJxPopzRat6e56FVGXXnbzUtjZf87V5Pt2Von1C7a7b4ofV d6xcm4D1bd7cVIpVnI24YqgpvPP5jQpfzNrflKU2NjJe3UVtJe3CRR2kwWWUiGN5FDfvEZCWYEDj 0bFVfRfPXna60mHU5fMPlBoLg+vKzzXMKxQuyOioJBFIv+jQ3D/vRXkP5QaKs5sfP/ki/Xla67Yy KXeJD9YjXm0QLP6fIjmoVSeS1FATXFWrvz75GtDym1yw9Q+ipSOeOSQidTJD8EZZ6OlXU0pxq3Tf FW5vP/keGNZZNf09YHLqtx9ZiMXONUZozKG4B+MqsEryI3ApXFV1t598kXMcEkOv6eRcrzgU3MSu w9JZj8DMGqInVyCKgGpxVo+ffJQvDZ/pyyMywzXMhE6FEit24StJID6acSG2Zgfhb+VqKq8vnDyl Dbi5l1uwjtz6NJnuoVQ/WU9SD4i1P3qDkn8w3GKpXN+Zn5Zywwrc+YNNCzsCsNxNGjKV/eK0kchD RgcahnAFaeIxVFxefvIn1lbJdf06O4Jjjht2uYo2f1I0kj9JWZfUVkkUqUqDXbFV1z5+8j28NzNL r+nhLO3S8ueN1C7JbyhDFKVVi3GT1U4GnxclpXkMVU/+Vi+RDJwGvWTD0vWMizI0YT0zN8UgPBT6 QL0Jrx36Yquh/MLLLFFINfsI/Wi9dIp7iOGUIIhOxeKUpIhWJg7BlBUdaYq6T8wfI6WUl5+nbJ7 eFo45TFMkrI8rKiKyIWcMWddqYqpn8y/y+Dsn+I9OoiGVpPrMXp8AQK+py4dem+9Gp9lqKtxfmN5 Il0+S/i1eCSGNZWeNOTT0gX1JaW4HrngnxmifZ36YqiZ/OvlCCdbaTWLM3TTLai2SZHm9ZpGiEfp IWflzidTttxav2TiqHtfzD8l3Wgtr1tq0M2mLavftInIyC2iYpJKYAPWCqylT8Gx2xVFWvnDy5da 7LoMN4Dq8NTJZtHIjAKKk1dVU7bih4HTFWEf4V/MyHT7EQWvltNZrEl3qSQEtGsc7yngTFGAixQ2 8afuyQwr2DAqh5Py281rqiXMujeTvQkFtDcRCymdI4YJZSTDGQAJPTFuo+ICqdPhXAqIsPJf5hQ6 6L57Dylb289xJHqQtLSRJLmxmPOUSM0bOZZHoxHPjUAmtKFVfP5E856hHKl9Fodq1+LP9JNaQQyL yVphemJLqylrzjnHD1mffkPhDHFUDB+Xvni01K4a10HyQbGEXQ0qaSylW6Acv9XWUxRRxooDhX4D cV7muKozU/Ifm671AmLSPKUFms6rDcC0Z7tbOEzLCn7yGSPmIWjTpRfj47EUVasvy58zWmm6Pbmy 8t3txbyx3GoNdWSLHHIsKwyfU47eCBQSsMZV3HJdxXgFUFUBZeQvzIgL89E8iswpLFJ9TnDCVwqO vwRpRFjLIjbtxADVqTgVMbL8vvMwkujqWk+VL2O9uYnuVayPJoDJG9wzMIlDyP8AvGUODRwGLENx RVCDyH+ZU9nbWlzb+VYYVnhmufq1rKKxWwjWK2QGNR6axGaEdGEZVa/aqq1e/lz50nBDaL5KuyJr p42vtPeXhE7j6tGgRIqUQfvCamtOuKq9t5F87teLqF7oXko3y286rKllO0kc8cHp2SpMyq3pBgvq bVC1C9qKr4fy08wNZact3BoJnnEcXmaGGxthBNbw3SSQwQ87V2McFuixxiT+RejfHiqybyB56S/u I7W38s/owzCb1XslW6viVZZX1ALAYjJIrEM0IWvJugNAqh9R8h/mFcyTpBofkm2jckJc/VZZJSnI pxkR4CpEluEjYctt6GlAFWVaN5PlF7qUWtaPoL6VcTCW2Fra/vn9Ir9X+sh0EbNEAQrDpt4VKqZT +QPIlxy+seW9Lm5tzf1LK3arVY1NUO9ZGP0nxxVUbyV5PYty0WxKyLIksf1eP03EvAPzj48HJESi rCtBTFVRfKHlNbz66uiWAvBKbj6yLWh2fWYszSc+PLmS7EtWu58cVXnyv5amMTwnSbL0pIjbyR/V4 uLQs/qGIjjQoX+Lj0rvirdv5Z8uW2pnVbbS7SDUinpG9igjSYpxVeJkVQxHGNR16ADFUyxVp2VEZ 2NFUEk+wxVgMv57fljHqQsG1VhIsYmuJGt540hV1R4/UMiIauJBQKDT9qmKpf5x86eW/MWi2b6L5 qutJVrm3jN9ZwXB/46NtKLdZU/cuUcfy/ErUPwsAyqsIfW7G40m6g0n8ydRvJNVdRCsMF2slqJrk RpLA13dwShRJa+lQyt9ogLWTcqy/XPJWvaPy1fWfPOr3mmxXVt6Nnbt9UkZpZ1j4SulxAkgcyEcU C9uK7BSqxVb8prF20vnvV4LR7ya5jkdJZIYobO/WF4FEd7I7xSNFQERV4uhPEMVdV6hD+aXl+XXL HRfQuFvb6Y24B+rkRSBrhaTcZmZKm0bjt8VVpXegVmOKuxVj/mrz95U8qGBdevTaNdJNJbj0ppes 26GSTeNHAIUVAJFe2KpVp/5x/l9exSuuotFJbxGe6gkgm5xoHijPIojoTyuY9lY/a+dFVD/leP5Z rf3unT6q0F/p/wBZ+u27W1wxjW0ZhKxaON46fu6ijVO3c0xVD6rBe/mLDDc+WfMl95aj0qd4LxoA jm49a3huEBCTcV4LKv215A1FBirEi0miX8mka15w1nUNY9d7H67G4gtlkmsXKH0kvQqFTcpIedKc FNFUF8Kofy5raaBcW2t6l521LWILSwXV76xnUxRmGa1iWGORp702/qyG6V41jJXkKfapVV7P5d1+ y1/SYtUsldLeV5Y1WUKHBhlaFuQVnA+JDtWvjQ7YFTLFXYq7FXYq7FXYq8e8ueYJSljFH+bFncxW rNcait1YxRySQCaORkd55g8BZeSLzqeLEqPhBCqd2pXUws0H5iWt7KVtbN5bV4wrTrdyXEfGOC5E YkmVfR4hauqkHl0CqB0zWbJPL+lXdz+YKXtp/oUdtI0EsMkjva3EZNwiTLdH6zvN+8PwmPkPEFV3 lUNdaM1jb+fpr4Sx3UMrywTRXckjWEIUwmeU3Aa23mIiNatRvjBJVQOleZ9MFrfaxa+fp5IdXZLe wnawvZYLeUXYf93FcNKtZFvEi3A7FaBeIVR6WcUWrjV7z8ykls7XUZJZbdJhFAgLh/qk3G5MYVRB Knxr8gCG5qvT45I5Y1kjYPG4DI6kFWUioII6g4FXYqwH8yp44tT0iFPOUvlLUr5JrfS2MJmtZZvU gkJmVyLcsEQoiyEV5njXpirHbnVZn0u9V/zYiFnO8Vpa3psoEWCSZ0eNxcRPFzV1tZ1STnxPI1Zi uFU5tbnW5vrdxF+ZlhdWhCWsCwWdm7RXb+k4HJJX9R3SKThFxr8Z68VwKgHvrO7vbNLbz7JayXjS a3apLDdIklhNLFqFCZZkX0Et7cx124KzDavHCqrqV1HPdPpVx59e31NYIbia+9Ce2gEFvci59WOW OWG0HOC9ihY8m5DiSCdgqjo53h2RfLt55vkbUNNijuWjltbiCMQWtisN00tyJE9VXa6Scl5yUanc VAVKobibRfL9vob+fbq5uk+tRz6mNPub2SdruKKS3ZZQ1wyiEXcZjZJKNUCtVOFWV+UvJuu6LqUl 7qXmS61gS26wG2m9VYg6rEPVVHmmVW5Rv0A2bepBZgrLcVdirsVdirsVSJvIfkZ52nby7pjTuyu8 ps7cuWTZWLcK1XscVVrXyf5StJHltdESLeSSSOd3itYUZpYeXpyEqoqyc24t1FTTFW08oeU0hWFN FsFhUxFYxawhQYAwhIAWn7sOwT+WppiqrD5a8uQLEsOlWcSwKUgCW8SHEaMRMqUX4QY1CED9kU6Y qhIPInke3AFv5d0yEBi4EdnbrRiyMW2TryiQ/NR4DFVWHyf5ShuJLmHRLCK5lkE0syWsKu0i1Idm C1LCvXFUztbW2tLaK1tYkt7W3RYoIIlCRpGg4qiKtAqqBQAYqqYqxHz15Y1zWb3Sp9Nj0q4itDMl 5b6vbrOrQ3AWKVYm9N3QtCZK0YBjxDVXlirHk8k+dzZWFrNonk6WC3ECSW0lrK4UwMv72N1iijqV knKKIVCMw3IJxVEQeQ/MVosAsdL8s2sHoM93pkVmEs3vxdJ6VwAsPq1Sz9VQeY+NulMVQ0n5fedZ GCodEghgluIrQLZ25ZbGWxaFLcA2rBU+ssWZR1jYgnqpKp1rHkW4vJpfqlrptpat6IS3FvbPsk7G 4qZbSX/em3SCNh+yV2rx+IKhF8oedP0eIpf0Pcag0bi51WS3iS5mmluVW4ZwtvJCY5rJArKIwxNF J25YVdpfk7zlb3mkTXR0mT6rawQ6kyRQj1preGQrIoWzRlU3CWrBVkUIIhTfbAqPtf8AlcBjtmux oAmSYC7WF7wxyQco6mPknJJOIkpUsoqK1pirMsVdirsVeCmD8nLC1RbPzj5g0YaXavFJJaPdoYUe U3UnrN9WkQNI1yvX7Z48atuSqhrOp/lfdajqsFx528y6Pd3c962r2AS5JeAzsh5CK3kQRjgFiJLU iPEGE/CFTSS/8grqSaZP5180reXep3WmpafW54/RuZeHEc4Y1Ajjqhh+Igc6MKcgpVp9c/Li1to2 vPPHmcCaa5ga+nmuQ63Jtwxi9NYAEZIrvnG0cYT/ACjRRirWlN+WkN3aQWPmTzFZTStFYRTRyuPV msp5VMTiOJyz3D2zu5K0pWhTmysquvj+V73c7T+d/MMk9+jxycZ7liIxfTBAgEFf3dzBJFGFqaeK kHFVSFfyyn0G0MPnPzE+mwpJ6nxXbNfi6dy0k0T2xNwXeZqMi9RT9nZVDWeuflRqFzFaDz75huXu CE9GeS5dCl9ELdVlZrXikctRLR2ADUB4Rtiq29/wJperHT7/AM8ecbWa0dopYPrs8qObZyklRBHK 61DxsQOJ4OjAUqQqmksnkHVptI0A+edauGZntUtZJbhWuQ7TWwSZ1hiDlZ7R/im5A0INQ6Yqlcet /lWfMFk8Hm7zK8ttbW1xbRRy3fpSWrgyEU9L1mRy6NIg/wAhVFEKqqpzeZfywljTUV84+ZvXS29S BfXlWRbYTtKZEkliCcZuIRqvXgFDUK1CqOu9Q8i2GmiJvPHmp2Kw25iNxMLpGuheFGYywoyyKEmL cjVfSQUqFBVQ1t5j/KabUIfqvnvzAknp2Vql19ЮW9Vp3NxBE7ywvKWb0XJ5/CA5UUrQKtyaz+We oW9rDN5/80XNvdosMVq0d1/pazStIpCCxDyBvQKVTbiCv7R5BV2o6t+Xn1f6pbeZ/Mt09sl1qsZt 7hudvDDG9g0iy3KIiR8ixT4qBviNFwq3Z3n5dQiae584+adMigmNvB9b1C59JPqkFtcsQFEqBCk6 L+/3ZmKgV44qjb1Py2CXdvfeb9ejttOuLS2mtJZ7koksc7JGYmEJb967EM0bfAONDHRaKoB/MHkE yW8DeePNUsahT+kRNJHHScfXi0oEEZokS/EfTpHGT04sVVQ6a/8AlHot/ZLL5+8xuL1bfUhM9zdO lwoLJCkzpCJW9QPQr/LGAaAUIV6H+WsvlG4k1y70DWb3Wp7i6SXUJ78ys8ReMPDDF6scP7kI1UpX r1xVCL5L/Nol+f5jbMnFQmi2a8X5huY5O/7I40PzxVu28nfmsLe4aXz4sV5dMXPHTIZo4a+iFSIO 6iiLE4rxHIvyIqMVRw8peeoLKSO085OL2SYzNdXNjFcAgmOiekZEVVpG4pHxHx7AUGKripJvnr67 dXN152nkFwgjihhsoIkh53AlV0VmkXmI6xESCG6kGlMVZfYx3cVlbxXk63N2kaLcXKJ6SySBQHdY +T8Azb8eRp44q2LO0F214IIxdtGIWueK+oY1YsqF6cuIZiQOlTiq6WGGZQkqLIoZXCuAwDIwdGoe 6soIPY4qoapqllpdjJe3rslvGUViiPKxaRxGirHGruxZ2AAUYqxa5/OL8urXT31G51RobKMxgzva 3ag+szonGsNWHKJwStaU3xVaPzP/ACx0i39JdQisbbmzFEtpo4w80S3rsQsQUc0uBIx8W3+KuKrr T84fy7u7k21vqbvMrrGw+qXgA5+oQxYwheFIXJevEU3OKoi4/NLyNbG7E+oSR/UYjcXBa1u6ejyR BIh9Kkis0qhSleXatDiqjL+b/wCXcVylu2rfHKA0Lrb3TRSq0y24aKVYjHIvqyKvJWIxVl0MEEKs sMaxKzNIwRQoLuSzMad2Y1JxVfirsVdirsVdirsVdirsVdirsVdirsVdiqjfNOtlcNAwSdYnMTFG kAcKeJ4L8Tb9hucVeMJ5x846ppcztqOiapplwJIo7XU7O8kRxF6XF5RBboGIlu4OR4KONfgRlbiV SPRbw6tbx2OoXPk1HHP0ni06WKOVYZbf6w08t5acCEbhKhFXmeIDKaMiqK1Aa1pEl7aXaeUYGgd0i iTR7x5E+rxRPcvHHHbN/cW08Qjejrx4hq7nFU5ubTS21G1n0W78kx3lvdPItjwtv30bzJHayvxja 4W5R5JgPTZQZGC71OKqEup2lxJYyT3nkWWdwt8h9Bk9SFDL+kiySCV43QSD0/jDFlfntyUKrLWe3 gthe6pd+RGlWR727uYoOSSaU08YrbShV5yxNE6inMchGG+I1xVmfld/zbur/AEy71G/0C78tskhm msPrDT3ETrWCZWZRFy2BPGi7nbpQKz3FXYq7FXYq7FXYq7FXYq7FXYq7FXYq7FVssUUsTxSoskUi lZI2AZWVhQgg7EEYqlcPlDynDH6cOiWEUfwfAlrCq/uihj2C/sGFOPhxXwGKrB5L8nB5XGg6cHmd 5Jm+qQVd5CrSMx4blyilietBiqpJ5U8rSXT3cmjWL3cjPJJcNbQmRnlT05GZyvIl0HFj3G2KrV8n +Ul48dEsBxmW6WlrDtOrFlmHw/3gZ2IbrUnFVi+SfJiSLIug6csiLIiOLSAELNy9RQeHR/Ubl41N euKuPkjyWYEtzoGmmCKMwRRG0g4LEz+oY1XhQKXHKnSu+Kpra2traW0Vrawpb20CiOGCJQkaIooq qqgBQB0AxVVxV2KuxV2KuxV2KuxV4Ik9vpmjRrJp/nrRrCzspHMdi7/V7aKK1NuAplSKjcbT1fiU cZHDfZY0KpjeG11HULaK50/zoXt7iOfRdegX1ZI21SFPVKuqGOOKKNeDVqBzfavRVKjFHdjUYtQs PPWr+XbmJ0l0+5Y3DPMD60iMqMeC/uViRQwZWZgQCaqqj4ILu6imuS/5i2ckVzZ280IkDKCsLxM9 sJEJlhB+KZ2UcjRhvtgVEyO80Gq6XfWfnj0rb6+kbkG6SeOOC3gUqSvFy5iLwrVgWMjE/FhVKrmH RLPT7a2t7L8xNE0vRzcFI7UmGKOFFExjaRnZmib7CfEdx1HXFVS5vby70+aWO1/Me1u3a2UwxtIp SFLWSL4DJGy8miXnL8Jb1yvx/tYFTXzBpml+Y/MMGpXdp500vUbdZtOgv7KFLf4C1w6yF4FduI4m NGPZl5VDFsVS9beNbRW0+z/MCxglF5c3aQhYJDJIsd2ziIKwaZ5m4KPh49Su32iq5JbP6nbRzab+ Юл9eafHdSWl5cQqbqM6laem7pK3BPVgWVlSnxI1e2BUV5d8w2Wn+bEjm0/zhcX1jp6PBY6gGuyUm uUtpplJnZ5AWkV2LRjiqE7CiYVZdF+bFrNbwXMHlnzDNBcS8FlSwqgirQXBb1OPpGh6HlTfjQqSF Qw/OaxeO2kt/K3mS6Fzai8Ig08SNFG8rxRiRVk5BpPSLpQGqUbpiqKuPzUWGCOU+UvMsnqRRzNHH prM6eqD8DAP9tafEq1pUYq3qH5g69FDdT2PlHUbiG2dY1WZZIZZD/pQkdI0inJRTbR0I+0JRtUAM qgB+bmp2q3Dat5L1qDjMILKG0hN1PcsXugSkZEPwrHZq5IJ/vB+zRmVRyfmZeCdEm8o66sUlra3K yR2bycXuSgaGQbcXi9T4xUkBWqBtyVQEP5vaqIopbvyH5ijUpxuEgtGmkS4UEuqKRHzh+h5Zagtt 8AriqJn/ADcitxardeV9dtZtRcxadDNaoGkcR+pxYLIxQ+258KkOFVZtp959dtI7n0Jrf1K/ubhP TlXixX4l3p0qPbFURirAl/KCxEzXLeZvMul6YEto7xtRb1EVIPIuQogQsfVL8mU/FuKVNVVbSfyt isNYtNUm80eYNTksjygt7+9SWANShYoIkqWWqnfoSMVZvirH/OfnbSvKOnw3+pxXEtvM7Rg2yK5U rE8tX5MlFb0+PLoCryotWCrFJPz+8lxafqF7LbXqLp3L1I+NsxlCSRxk28iztDLvITxWTlRGNPs8 lvWP89PK1xqX6NsdO1S9vFlSGaKO3jjaEytwRphPLCYwSy/aoRUAiu2KrB+ffk831zZmzv1ltbtb CYlLenqvNHCGFJySnKYEvSg+ZUMq9JxV2KuxV2KuxV2KsT89/mVoPkltPGrw3co1JpUtzaRCY8og rMCvJW3DVFAemKpTpf52eWtVtGvtO07UrjT1WVvroihSImG3luWUepMjFvTtztTYla0riq7yp+dv lLzPq9rpmnW94kt4xWCaZIVj2gNx8XGV3WqCgBWtfbfFXoGKuxV2KuxV2KuxVbI4jjZz0QFjTrQC УКВЭдГ863ВжЯХJqH5iTwLF/pWpWl9obtO8Jjh2BoXkV5xE31aTqHf4X+HddiqZax5ja10w6y/mu 81CBCLC5ubO0MKrcWM7XzN6RuLeMF4isTMqlWQEMaHZVA+VvPlpeaUhvvNl4sGltZwCa5tSvrS/V LqOT1GsrqaZ/WCeqfUcBWQcd+irvJfmWS/0650weadTkt4rC5ub/AFGe2DELJplm6Mlwt1cyq9v6 xkpC27cqmtHdVD3nn9fL51q9l8x6lKb2D1dOlW1SeFUiuY5udtDcXsgrKmoLDRwhqhHwlQmKoq11 G+b8xNO0+58x6xIbvVJ2tFWERWMirb29+beq3jB4lhcpX0iKnYLQ81XtWBXYq8z/ADd1o6Zquhov mO/8uT30V3FbXltbreWkbQtDcSTXcDOvJUijZQ3AqoZmYqMVYleeepf0FcTy/mFfLp189vbafeHR 0WRBdOGinQwvFPIhFlOn845/EDQVKpzpXnWXUre81Cy/MmO8sPUi0+AJoyxmO9lEci/HIVVgyQSg VAUczVvhXAqEfzVDc3encPNGoWCX8c3mCCR7d5YhZM6ajLbyendyf3MVq0HADkOThRxJGFVXVfNC STSWd15tvYQtvHPJr0VsUtitpcJdMIorW6R1laHUI4XVoTULVgaYqmg1u4ttZby/e+YLuT9Exeub /wBAC2K6dp6R3sbvDdfWpXdrsTFXqysu1eIbFUqttY1fTdDtdAtPMmp6rdcZhLqa20Mk1wuoJbta Sj63eCeNYnv0VNwSRxPQFlWdeUvJuu6LqUl7qXmS61gS26wG2m9VYg6rEPVVHmmVW5Rv0A2bepBZ grLcVdirsVdirsVdirsVdirsVdirsVdirsVY35stvP7TQ3HlO7sIzHBKj2WpLIYJZnki9N2aFTKA kaybKwqWFemKrbP/AJWX9Yh2z9DfV/Xhr6P1rn9X9Sb1/tbep6fo8O3LnXbjiqSPon5zDUJGTzBZ NYfWJWiVkjWT0C1v6SNS0IqqxzFt/i5cQV2dFV+qWP503FzG1nqGlWkX1WRZkj5gG4Mk3pNGZbe4 YUj9LkWqOVfhIHxKp1a2XnmPS44ri+t59RiuVma5FI0mgNwzPAyeg3pgQcVVlq1ep2qyqB0PTfzP sniF/qtrqayTxtdm5VF9OAgCVLc20FtVwQxUyCm4HapVS+40T85pLKWSPX7OHUJJDxt1WM2yRmWZ vgdrNpK+m8SAMG+yasSa4qnfl5/zIl1y8k1+PS4NBBmXTorQzG8IEpETz8uUW8YB+Bu+47BVk+Ku xV2KsJtfMH5opL6d35VgmVQR60N7DGrsRUMAzSMqrTiRuTWvbM+WHT1tM/IuEMue6MPtCNh8wefH ibn5TWKcTRxorajCYzE4cvLzVGYcCqDjwqeW3TIHDh/1Tp/NPyZDNm/mdf5w+f4HVCfp78zhMZv8 LwSWrNwSzN7FHOgJ2kaWskbBQvxKFr8QpWhyXg6eq4zffWzE5c/MQ+F/ain13z20twE8tCKO3LGE m6glNyArFVHxxejyIALNypX7J3pEYsO3r5+R2/WzOXLv6OXLcb/qUU8wfmMGt0k8qoxHp/WpUvYA jBlAf0wzclKMSd+VQPfYnDg39f2FHi5v5nd1Hx+Sra6/5/e2L3HlRYZkmjT0hfwP6kTBvUkUgAJx IWimpPT3wSw4b2n/ALerDLmI3hW/877Vseu/mCjXKS+WEn4XZjtpo7uCMPal2Cy8GZzVUCkgsKk9 sTiw7VPp3Hn3KMube4fxd45Xz+S2DXPzHSMrP5Zgnl48w63scCVAb93Qic8qqKHp8XsThOLB0mf9 Lf6l8TN/MB+Nfr/BTjQ9T8wXk0y6pox0uJVBgb6xFccyHcGvpn4aoEYbdyK7ZTlhCIHDLi+FN2Oc z9Ueh52m+UNrsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdirsVdi rsVdirsVdirsVdir/9k=

uuid:8F13353A475BDE118720C33913AD9C03uuid:4c306924-8e2b-4697-9283-153e5477411fuuid:8E13353A475BDE118720C33913AD9C03uuid:F346078CCB59DE11ABB386CC1B9A166C1FalseFalse612.