D 0 формула: Дискриминант. Формула дискриминанта.

Формула корней квадратного уравнения — презентация онлайн

Похожие презентации:

Элементы комбинаторики ( 9-11 классы)

Применение производной в науке и в жизни

Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»

Знакомство детей с математическими знаками и монетами

Тренажёр по математике «Собираем урожай». Счет в пределах 10

Методы обработки экспериментальных данных

Лекция 6. Корреляционный и регрессионный анализ

Решение задач обязательной части ОГЭ по геометрии

Дифференциальные уравнения

Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи

1. Формула корней квадратного уравнения

Найди «лишнее»
2 х 7 х 3 0;
2
5 х 7 0;
2
х 5х 1 0;
Найди «лишнее»
2
3 х 4 0;
2
х
7 х 5 х 0;
2
4 х 3х 1 0.
2
Найди «лишнее»
х 3х 5 0;
2
х 7 х 1 0;
2
у х 2 х 8;
2
Найди «лишнее»
х 7 х 9;
2
9 х 13х 4 0;
2
7 х 3х 4 0;
2
Найди «лишнее»
3х 8 х 11 0;
2
у 2 х 7 х 3;
2
2 х 9 0;
2
Составьте квадратные
уравнения, если известны их
коэффициенты:
1. а=3, b=8, c=2;
2
3х 8 х 2 0;
2. а=1, b=0, c= -1;
х 2 0;
2
3. а=5, b=0,5, c= -3;
2
5х 0,5х 3 0;
Простые уравнения люди научились решать
более трех тысяч лет назад в Древнем Египте,
Вавилоне и только 40 лет назад научились
решать квадратные уравнения. Одним из тех,
кто внес большой вклад в развития
математики, был французский математик Виет
(Виет первым стал обозначать буквами не
только неизвестные, но и данные величины.
Тем самым ему удалось внедрить в науку
великую мысль о возможности выполнять
алгебраические преобразования над
символами, т. е. ввести понятие
математической формулы. Этим он внес
решающий вклад в создание буквенной
алгебры, чем завершил развитие математики
эпохи Возрождения и подготовил почву для
появления результатов Ферма, Декарта,
Ньютона.

9. Дискриминант квадратного уравнения

Определение: Дискриминантом
квадратного уравнения ах2 + bх + с = 0
называется выражение b2 – 4ac.
Его обозначают буквой D, т.е. D= b2 – 4ac.
Возможны три случая:
D 0
D 0
D 0

10. Если D  0

Если D 0
В этом случае уравнение ах2 + bх + с = 0 имеет
два действительных корня:
x
1
b D
2a
и
x
2
b D
.
2a

11. Если D = 0

В этом случае уравнение ах2 + bх + с = 0
имеет один действительный корень:
x b2 a
0
x 2ba

12. Если D  0

Если D 0
Уравнение ах2 + bх + с = 0 не имеет
действительных корней.

13. Решение квадратного уравнения

ах2 + bх + с = 0.
D= b2 – 4ac
D 0
x
1, 2
b D
2a
D 0
D=0
x
b
2a
Нет
действительных
корней

14. Задания:

Решить уравнение 2×2- 5x + 2 = 0.
Решить уравнение 2×2- 3x + 5 = 0.
Решить уравнение x2- 2x + 1 = 0.

15. Решить уравнение 2×2- 5x + 2 = 0

Решить уравнение 2×2- 5x + 2 = 0
Здесь a = 2, b = -5, c = 2.
Имеем D = b2- 4ac = (-5)2- 4 2 2 = 9.
Так как D > 0, то уравнение имеет два корня.
Найдем их по формуле
5 3
1
x1
2 2
2
b D
x
,
2a
и
5 3
x2
2,
2 2
то есть x1 = 2 и x2 = 0,5 — корни заданного уравнения.

16. Решить уравнение 2×2- 3x + 5 = 0

Здесь a = 2, b = -3, c = 5.
Найдем дискриминант D = b2- 4ac=
= (-3)2- 4·2·5 = -31, т.к. D < 0, то
уравнение
не имеет действительных корней.

17. Решить уравнение x2- 2x + 1 = 0

Здесь a = 1, b = -2, c = 1.
Получаем D = b2- 4ac = (-2)2- 4·1·1= 0, поскольку D=0
b
x
;
2a
Получили один
корень х = 1.
2
x
1 .
2 1
№1. Решите
уравнения:
а) х2+7х-44=0;
б) 9у2+6у+1=0;
в) –2t2+8t+2=0;
г) а+3а2= -11.
д) х2-10х-39=0;
е) 4у2-4у+1=0;
ж) –3t2-12t+6=0;
3) 4а2+5= а.
№2. а)При каких
значениях х равны
значения многочленов:
(1-3х)(х+1) и (х-1)(х+1)?
Б)При каких
значениях х равны
значения
многочленов:
(2-х)(2х+1) и (х2)(х+2)?
Ответы
№1.
А)х=-11, х=4
Б)y=-1/3
В)t=2±√5
Г)нет решения
Д)х=-3, х=13
Е)у=1/2
Ж)t=-2±√6
З)нет решения
№2
А)х=1/2, х=-1
Б)х=2, х=-1

20. СПАСИБО ЗА ВНИМАНИЕ!

English     Русский Правила

Решение квадратных уравнений: формула корней, дискриминант, график

Sign in

Password recovery

Восстановите свой пароль

Ваш адрес электронной почты

MicroExcel.ru Математика Алгебра Решение квадратных уравнений

Квадратное уравнение – это математическое уравнение, которое в общем виде выглядит так:

ax² + bx + c = 0

Это многочлен второго порядка с 3 коэффициентами:

• a – старший (первый) коэф., не должен быть равен 0;
• b – средний (второй) коэф.;
• c – свободный элемент.

Решением квадратного уравнения является нахождение двух чисел (его корней) – x₁ и x₂.

• Формула для вычисления корней
• Решений квадратных уравнений
  • Пример 1
  • Пример 2
  • Пример 3
• График квадратичной функции

Формула для вычисления корней

Для нахождения корней квадратного уравнения используется формула:

Выражение внутри квадратного корня называется дискриминантом и обозначается буквой D (или Δ):

D = b² – 4ac

Таким образом, формула для вычисления корней может быть представлена разными способами:

1. Если D > 0, у уравнения есть 2 корня:

2. Если D = 0, уравнение имеет всего один корень:

3. Если D < 0, вещественных корней нет, но есть комплексные:

Решений квадратных уравнений

Пример 1

3x² + 5x + 2 = 0

Решение:

a = 3, b = 5, c = 2

x₁ = (-5 + 1) / 6 = -4/6 = -2/3
x₂ = (-5 – 1) / 6 = -6/6 = -1

Пример 2

3x² – 6x + 3 = 0

Решение:

a = 3, b = -6, c = 3

x₁ = x₂ = 1

Пример 3

x² + 2x + 5 = 0

Решение:

a = 1, b = 2, c = 5

В данном случае нет вещественных корней, а решением являются комплексные числа:

x₁ = -1 + 2i

x₂ = -1 – 2i

График квадратичной функции

Графиком квадратичной функции является парабола.

f(x) = ax² + bx + c

• Корни квадратного уравнения – это точки пересечения параболы с осью абцисс (X).
• Если корень один – парабола касается оси в одной точке, не пересекая ее.
• При отсутствии вещественных корней (наличии комплексных), график с осю X не соприкасается.

ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ

Таблица знаков зодиака

Нахождение площади трапеции: формула и примеры

Нахождение длины окружности: формула и задачи

Римские цифры: таблицы

Таблица синусов

Тригонометрическая функция: Тангенс угла (tg)

Нахождение площади ромба: формула и примеры

Нахождение объема цилиндра: формула и задачи

Тригонометрическая функция: Синус угла (sin)

Геометрическая фигура: треугольник

Нахождение объема шара: формула и задачи

Тригонометрическая функция: Косинус угла (cos)

Нахождение объема конуса: формула и задачи

Таблица сложения чисел

Нахождение площади квадрата: формула и примеры

Что такое тетраэдр: определение, виды, формулы площади и объема

Нахождение объема пирамиды: формула и задачи

Признаки подобия треугольников

Нахождение периметра прямоугольника: формула и задачи

Формула Герона для треугольника

Что такое средняя линия треугольника

Нахождение площади треугольника: формула и примеры

Нахождение площади поверхности конуса: формула и задачи

Что такое прямоугольник: определение, свойства, признаки, формулы

Разность кубов: формула и примеры

Степени натуральных чисел

Нахождение площади правильного шестиугольника: формула и примеры

Тригонометрические значения углов: sin, cos, tg, ctg

Нахождение периметра квадрата: формула и задачи

Теорема Фалеса: формулировка и пример решения задачи

Сумма кубов: формула и примеры

Нахождение объема куба: формула и задачи

Куб разности: формула и примеры

Нахождение площади шарового сегмента

Что такое окружность: определение, свойства, формулы

Дискриминанты и определение числа действительных корней квадратного уравнения

Что такое дискриминант?

Дискриминант — это значение, вычисляемое из квадратного уравнения. Он использует его для «различения» корней (или решений) квадратного уравнения.

Квадратное уравнение имеет вид: ax ²  + bx + c

Дискриминант, D = b ²  — 4ac

Примечание. Это выражение находится внутри квадратного корня из квадратной формулы

.

Есть три случая для дискриминанта;

Случай 1:

б ²  — 4ас > 0

Если дискриминант больше нуля, это означает, что квадратное уравнение имеет два действительных, различных  (разных) корня.

Пример

х ²  — 5х + 2 = 0

а = 1, б = -5, с = 2

Дискриминант, D = b ²  — 4ac

= (-5) ² — 4 * (1) * (2)

= 17

Таким образом, квадратное уравнение 9 имеет два действительных различных корня. 0005

х ²  — 5х + 2.

Случай 2:

б ²  — 4ac < 0

Если дискриминант больше нуля, это означает, что квадратное уравнение не имеет

действительных корней.

Пример

3x ²  + 2x + 1 = 0

а = 3, б = 2, с = 1

Дискриминант, D = b ²  — 4ac

= (2) ^{2 —}  4 * (3) * (1)

= — 8

Следовательно, у квадратного уравнения 3x ²  + 2x + 1,

нет действительных корней.

Случай 3:

б ²  — 4ас = 0

Если дискриминант равен нулю, это означает, что квадратное уравнение имеет  два действительных одинаковых корня .

Пример

х ²  + 2х + 1 = 0

а = 1, б = 2, с = 1

Дискриминант, D = b ²  — 4ac

= (2) ²   — 4 * (1) * (1)

= 0

Следовательно, у квадратного уравнения есть два действительных одинаковых корня x

2  + 2x + 1.

Сводка

Квадратное уравнение равно ax ²  + bx + c

Определитель D = b ²  — 4ac

D > 0 означает два действительных различных корня.

D = 0 означает два действительных одинаковых корня/

D < 0 означает отсутствие реальных корней.

А теперь попробуйте эти (осторожно со знаками минус)

Вопросы

Q1. х ²  — 7х + 2 = 0

Q2. — 3x ²  + 2x — 1 = 0

Q3. 9x ²  — 12x + 4 = 0

Q4. — х ²  + х + 1 = 0

Ответы

Q1. D = 41 означает два действительных различных корня.

Q2. D = -16 означает отсутствие действительных корней.

Q3. D = 0 означает два действительных одинаковых корня.

Q4. D = 5 означает два действительных различных корня.

Квадратичная формула.

Ее происхождение и применение

Квадратичная формула — одна из самых любимых математических формул учащихся. Его можно довольно легко запомнить. Студенты охотно используют его для решения квадратных уравнений вида ax ² + bx + c = 0. Однако не все знают, почему мы его используем и откуда берется квадратная формула.

Когда мы пытаемся определить точки пересечения по оси x параболы (графика квадратичной функции), представленной некоторым квадратным уравнением, мы решаем это уравнение. Квадратные уравнения могут иметь 1 решение, 2 решения или не иметь решений. Это означает, что соответствующая парабола имеет 1, 2 точки пересечения или вообще не имеет их. Иногда точки пересечения x не являются «хорошими» числами (иррациональными), и трудно использовать методы факторинга для решения уравнения для определения точек пересечения x. В этом случае можно использовать квадратичную формулу.

Рассмотрим, например, квадратичную функцию, заданную уравнением f(x) = 6x ² + x – 2 .

Когда мы хотим определить x-отрезки (корни, нули) графика вышеприведенной функции, нам нужно сделать уравнение равным 0 и решить для x(s): 6x ² + x – 2 = 0 .

Это уравнение факторизуемо и может быть решено с помощью одного из методов факторинга, например, декомпозиции. Результатом процесса является факторизованная форма (2x – 1)(3x + 2) = 0 .

Следовательно, парабола пересекла ось x в двух точках: (1/2, 0) и (-2/3, 0) .

Это было нетрудно понять.

Теперь, если функция задается уравнением f(x) = 4x ² – 6x + 1 , попробуйте построить ее график с помощью графического калькулятора. Он имеет два х-перехвата, но очень сложно определить их точные значения, глядя на график или используя любой из методов факторинга. В таком случае 9Необходимо использовать квадратную формулу 0025 .

Что такое квадратичная формула и как ее использовать

Квадратную формулу можно использовать, когда уравнение квадратичной функции задано в стандартной форме :

f(x) = ax ² + bx + c , где a и b — коэффициенты, c — постоянное значение (также y-отрезок (0, c )).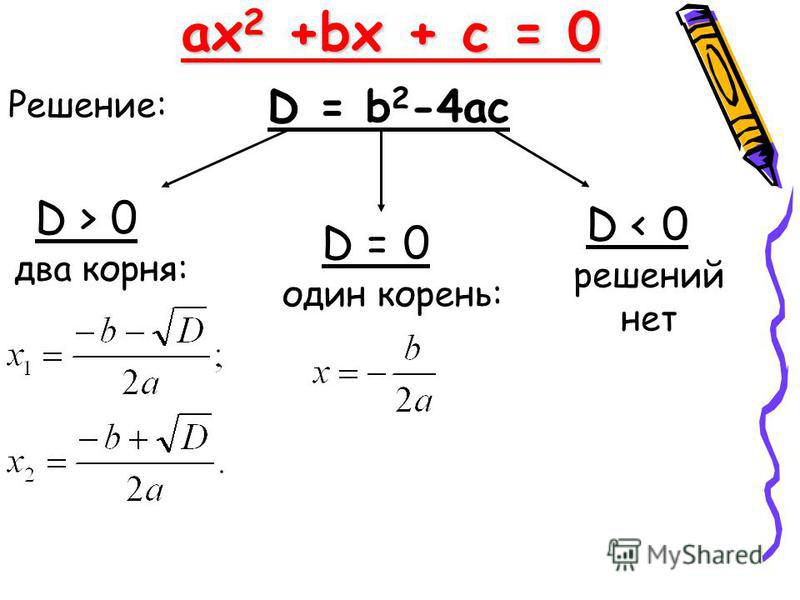

О чем следует помнить при использовании квадратичной формулы :

• Уравнение должно быть в стандартной форме, а должно быть равно 0 с одной стороны
• уравнение
• Знаки перед a , b и c в уравнении «привязаны» к ним
• Когда b отрицательно и возведено в квадрат под корнем квадратным – оно должно быть в скобках
• Сначала выполните все действия в числителе и только потом разделите на знаменатель
• В зависимости от задачи вам может понадобиться изложить решение(я) в приблизительной или точной форме. Решение (x) в точной форме содержит радикалы (если решение не является целым или рациональным числом).

Дискриминант

Квадратная формула является довольно полезным и простым инструментом для решения квадратных уравнений. Однако иногда бывает неприятно, когда вы настраиваете формулу и оцениваете ее половину только для того, чтобы обнаружить, что ее нельзя оценить дальше. Уравнение функции не имеет решений – парабола не имеет пересечений по оси x (см. диаграмму выше).

В этом случае на помощь приходит Дискриминант — выражение под квадратным корнем из квадратной формулы, предлагающее большую эффективность и ясность в отношении того, сколько решений можно ожидать, если таковые имеются.

Рассмотрим уравнение функции, которое мы уже рассмотрели выше, и определим, сколько у него пересечений по оси x и каких типов оно имеет: (х-перехваты)

Теперь воспользуемся полной квадратичной формулой для определения точного и приблизительного значений этих двух решений:

5

Есть несколько систем счисления, которые мы рассматриваем в математике.

Натуральные числа, целые числа, рациональные числа, иррациональные числа, действительные числа, комплексные числа и другие.

Система действительных чисел включает натуральные числа, целые числа, рациональные числа и иррациональные числа. Реальные числа — это числа, которые мы можем оценить и определить, зная известные нам методы, и они производят величины, соответствующие тому, что мы испытываем в реальной жизни.

Комплексная система счисления включает в себя все предыдущие системы счисления и мнимые числа, в которых мы рассматриваем значения, не определяющие количества, с которыми мы оперируем каждый день. Комплексная система счисления основана на значении i , что равно квадратному корню из отрицательного числа 1 (тогда как мы знаем, что в реальной системе счисления невозможно извлечь квадратный корень из отрицательного числа, поскольку никакое основание, положительное или отрицательное, при возведении в квадрат не даст отрицательного числа). стоимость).

Воображаемая единица

Следовательно, в комплексной системе счисления мы действительно можем вычислять квадратные корни из отрицательных чисел:

Важно помнить, что комплексная система счисления существует, и понимать, как она работает, потому что иногда выражение для Дискриминант может быть отрицательным, поэтому в итоге мы извлекаем квадратный корень из отрицательного числа.

И хотя уравнение функции в таком случае не будет иметь реальных решений, оно все же может иметь эти специальные сложные решения, основанные на i .

Происхождение и доказательство квадратичной формулы

Историки установили, что «квадратная» математика восходит к 1700 г. до н.э., когда вавилоняне работали с площадями и периметрами прямоугольников, пытаясь определить размеры.

Тогда древние греки пытались решать те же проблемы.

Однако и вавилоняне, и греки вычисляли свои решения геометрически, поскольку понятия алгебры и алгебраических обозначений еще не были разработаны.

Затем, в 825 году, известный персидский математик Мухаммад бин Муса аль-Хорезми использовал символы и понятие уравнения. Он создал метод решения квадратного уравнения, но предположил, что коэффициенты a , b и константа c в уравнении стандартной формы могут быть только положительными значениями. Таким образом, его уравнения всегда были равны c с одной стороны, а не 0.

В 1545 году европейский математик Джироламо Кардано рассмотрел вместе геометрический метод и метод аль-Хорезми и выяснил, как решать квадратные уравнения, которые допускали бы все действительные решения и даже мнимые числа. (это помогло дальнейшему развитию комплексной системы счисления).
В 1637 году Рене Декарт опубликовал «Геометрию», в которую была включена квадратичная формула в том виде, в каком мы ее используем сегодня.

Алгебраическое доказательство квадратичной формулы

( A -S будет уменьшено до 1 в результате)

(завершение квадрата)

2. Дискриминант) приводит к отрицательному значению, действительных решений нет, но мы все же можем определить сложные решения, как обсуждалось выше.

Применение квадратичной формулы в реальной жизни

Мяч бросают вверх с платформы над землей, и путь мяча можно смоделировать с помощью следующего уравнения

Где h(t) — высота в метрах, а t — время в секундах.

No related posts.