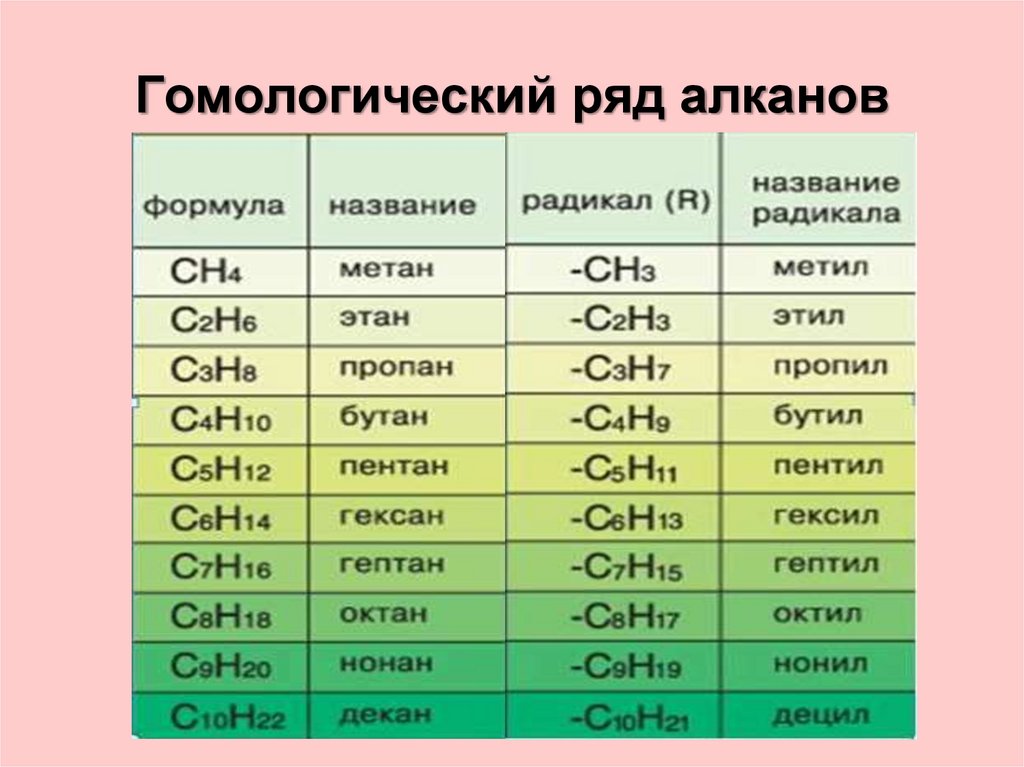
D1 формула: Внеклассный урок — Формулы корней квадратного уравнения. Дискриминант

alexxlab / / Разное

Внеклассный урок — Формулы корней квадратного уравнения. Дискриминант

 
Формулы корней квадратного уравнения. Дискриминант.
  

Формула №1:

         —b ± √D
x =  ————,  где D = b2 – 4ac.
             2a

Латинской буквой D обозначают дискриминант.

Дискриминант — это выражение, от которого зависит число корней данного уравнения.

Если D < 0, то уравнение не имеет корней.

Если D = 0, то уравнение имеет один корень.

Если D > 0, то уравнение имеет два корня.

Пример. Решим уравнение 12x2 + 7x + 1 = 0.

Сначала вычислим дискриминант.

Мы видим, что а = 12, b = 7, c = 1.

Итак:

D = b2 – 4ac = 72 – 4 · 12 · 1 = 49 – 48 = 1.

D > 0. Значит, уравнение имеет корни (причем два корня), а значит, можно вычислять дальше.

Чтобы найти корни, применим формулу корней квадратного уравнения:

         —b ± √D      -7 ± √1         -7 ± 1
x =  ———— = ———— = ————
             2a                24                 24

Находим оба значения x:

        -7 + 1        -6      -1          1
x1 = ——— = —— = — = – —
           24           24       4          4

 

         -7 – 1       -8       -1         1
x2 = ——— = —— = — = – — .
           24           24       3          3

 

                        1                   1
Ответ: x1 = – —,    x2 = – —
                        4                   3

 

Формула №2.

Из формулы №1 можно получить другую формулу, которой удобно пользоваться в случаях, когда второй коэффициент – четное число. В этом случае раскладываем его на множители, один из которых – множитель 2. То есть второй коэффициент представляем в виде 2k, где k – это половина изначально заданного числа. Тогда удобно пользоваться формулой:

      —k ± √D1
x = ————,   где D1 = k2 – ac
             a

Пример. Решим уравнение 5x2 – 16x + 3 = 0.

Записываем -16x в виде 2 · (-8x). Тогда k = -8,  a = 5,  c = 3. Мы уже можем найти дискриминант D1:

D1 = k2 – ac = (-8)2 – 5 · 3 = 64 – 15 = 49.

Теперь находим оба значения x:

      —k ± √D1       — (-8) ± √49      8 ± 7
x = ———— =  ————— = ———
             a                     5                  5

Отсюда:

          8 + 7       15
x1 = ——— =  — = 3
            5            5

 

         8 – 7         1
x2 = ——— =  — = 0,2
             5           5 

 

Ответ: x1 = 3; x2 = 0,2.

 

При решении квадратного уравнения по данным формулам целесообразно поступать следующим образом:

1) вычислить дискриминант и сравнить его с нулем;

2) если дискриминант положителен или равен нулю, то воспользоваться формулой корней; если дискриминант отрицателен, то записать, что корней нет.

 

—

MS Office 2007: Microsoft Excel

Сравнение числа

Введем в ячейку А1 формулу =7>5. Она вернет значение ИСТИНА. Скопируем содержимое А1 в А2 и исправим в А2 формулу: =3>5. Эта формула вернет значение ЛОЖЬ. Правые части обеих формул представ­ляют собой высказывания, т.е. утверждения, относительно которых можно заключить, верны они или нет.

Рассмотрим другой пример. Введем в ячейку А4 число 2, а в ячейку В4 формулу =А4>3. Формула возвращает значение ЛОЖЬ. Введем в А4 число 6. Формула возвращает значение ИСТИНА. В В4 записан предикат, т. е. высказывание с переменными (в данном случае переменная одна). В зависимости от значения переменных предикат может принимать значения ИСТИНА и ЛОЖЬ. В этом примере формула как бы дает ответ на вопрос: «Число (или результат вычислений по формуле), хранящееся в ячейке А4, превышает 3?» В зависимости от значения А4 ответ будет ДА (ИСТИНА) или НЕТ (ЛОЖЬ).

В формуле =А4>3 ее составные части (А4 и 3) можно считать арифметическими выражениями, только очень простыми. Более сложный пример: =(А4 А2-1)>(2 *А4+1). В этом выражении скобки можно опустить, потому что арифметические операции имеют более высокий приоритет, чем операции сравнения, но скобки придают формуле наглядность.

Операции сравнения можно свести в таблицу (Таблица 4).

Обратите внимание, что символ отношения «больше или равно» изображается двумя знаками: > и =. Причина в том, что на клавиатуре нет знака≥.

Высказывание и предикат имеют общее название — логическое вы­ражение. Имеются логические операции, которые позволяют строить сложные логические выражения. Эти операции реализованы в Excel как функции (НЕ, И, ИЛИ).

У логических функций аргументы могут принимать только два значения: ИСТИНА и ЛОЖЬ. Функция НЕ может иметь только один аргу­мент, а функции И и ИЛИ могут иметь два и более аргументов.

Задача 5.1.

В ячейке А1 (с именем z) запишите любое число. Выясните, при­надлежит ли оно отрезку [2, 5].

Решение задачи

Присвоим ячейке А1 имя z (ФормулыПрисвоить Имя). Введем в А1 число 3. Для того чтобы z принадлежал отрезку [2, 5], нужно, чтобы одновременно были истинны два предиката: z≥2 и z≤5.B ячейке В1 разместим формулу =И(z>=2;z<=5). Для ввода в формулу имени ячейки нажмите F3 для открытия списка имен. В ячейке В1 получим значение ИСТИНА.

Следует предостеречь от неверного ввода формулы: =2<=/<=5. Введите эту формулу в С1 и убедитесь, что возвращается ЛОЖЬ! Ко­варство этой, на первый взгляд, такой естественной формулы в том, что Excel ничего не сообщает о ее некорректности.

Задача 5.2.

В ячейке А1 (с именем z) записано число. Выяснить, принадлежит ли оно одному из лучей на числовой оси: (∞,2) или (5,∞).

Для того чтобы z принадлежал хотя бы одному из лучей, нужно, чтобы был истинным хотя бы один из предикатов: z < 2 или z > 5. В ячейке D1 поместите формулу =ИЛИ (z<2; z>5). А1 содержит число 3, поэтому формула возвращает ЛОЖЬ.

Задачу можно было решить иначе с учетом того обстоятельства, что на рабочем листе есть формула проверки принадлежности числа z отрезку [2, 5]. Упомянутые два луча составляют на числовой оси дополнение к этому отрезку. Введем в ячейку Е1 формулу =НЕ(В1). Убедитесь, вводя в ячейку А1 различные числа, что формулы в ячейках D1 и Е1 дают идентичные результаты.

На практике «в чистом виде» логические выражения, как правило, не используются. Логическое выражение используется в функции ЕСЛИ:

ЕСЛИ(лог_выражение, значение_если_истина, значение_если_ложь)

При вызове встроенной функции ЕСЛИ открывается диалоговое окно (рис. 88), имеющее три аргумента. В окне Лог_выражение записывается логическое выражение. Во втором аргументе Значение_если _истина записывается выражение, которое будет вычислено, если лог_выражение возвращает значение ИСТИНА, а в третьем аргументе — выражение, вычисляемое, если лог_выражение возвращает ЛОЖЬ.

Задача 5.3.

1. Введем в ячейку А2 формулу, которая возвращает z+1, если z >1, и z в противном случае: =ЕСЛИ (z>l; z + 1; z). (В Мастере функ­ций ЕСЛИ находится в категории «Логические», также как функции И, ИЛИ, НЕ).

2. Если z>60, то в ячейке В2 выводить сообщение «Превышено пороговое значение», в противном случае выводить z:

=ЕСЛИ(z>60;»Превышено пороговое значение»;z)

Обратите внимание, что текст в формулах вводится в кавычках.

3. Если z е [10,25], то возвращать z, если z < 10, то возвращать

если z > 25, то возвращать 25. Выражение для этого условия будет выглядеть примерно следующим образом (запишем формулу в С2):

=ЕСЛИ(z<10;10;ЕСЛИ(z<=2 5;z;25))

Теперь попробуйте менять значение z в ячейке А1, следя за тем, как меняются значения в ячейках с формулами.

Задача 5.4.

Построить график движения тела, брошенного под углом к горизонту, используя предыдущие результаты. Максимальная высота полета на графике должна быть отмечена кружком.

Исходные данные

Таблица зависимости высоты (hm) и дальности полета (Sm) от времени ™.

Решение задачи

На рис.88 представлена расчетная таблица в режиме отображения формул, а на рис.89 представлен график зависимости высоты (hm) от дальности полета (Sm) и таблица в режиме отображения данных, по которым построен график.

В диапазон G3:G24 вводятся значения времени ™ от 0 до 4,2, в колонку н — формулы для вычисления дальности полета (Sm), в колонку

I- формулы для вычисления высоты полета.

Выделив элементы этого ряда, с помощью диалогового окна Формат ряда данных, вызванного с помощью контекстного меню, можно изменить тип, цвет и размер маркера данного ряда.

Формулы в ячейках J3:J24 возвращают максимальное значение столбца I либо значение #Н/Д (нет данных). Полученные данные используются для того, чтобы отметить на графике максимальную высоту полета.

После выделения построенной диаграммы в нее добавляется новый ряд с помощью команды меню Конструктор — Данные-  Выбрать данные — Добавить ряд, значения которого содержатся в ячейках J3: J24.

Рост дивидендов (определение, формула) | Примеры расчета

Главная » Бухгалтерские ресурсы » Акционерный капитал » Рост дивидендов

Рост дивидендов — это существенное увеличение дивидендов, выплачиваемых компанией своим акционерам от одного периода к другому по сравнению с выплатой дивидендов за предыдущий период (как правило, рост рассчитывается каждый год).

Содержание
  • Что такое рост дивидендов?
    • Объяснение
    • Формула роста дивидендов
    • Как рассчитать? (Шаг за шагом объяснение)
    • Примеры
    • Рост дивидендов в зависимости от высокой доходности
    • Преимущества
    • Недостатки
    • Заключение
    • Рекомендуемые статьи

Обзор

. его акционер увеличивается в течение значительного периода, эта ставка дает процентное увеличение выплаты дивидендов за предстоящий период по сравнению с предыдущим периодом. Дивиденды компанииДивидендыДивиденды относятся к части прибыли от бизнеса, выплачиваемой акционерам в качестве благодарности за инвестиции в капитал компании. Читать далее, к ее акционерам относится доля ее прибыли, относящаяся к соответствующему периоду. Таким образом, рост дивидендов также является для анализатора способом определения результатов деятельности компании.