Контрольные работы по геометрии 10 класс | Материал по геометрии (10 класс):
КОНТРОЛЬНЫЕ РАБОТЫ ПО ГЕОМЕТРИИ
10 класс
Контрольная работа №1 по теме «Параллельность прямых и плоскостей».
Вариант I
1. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно.
а) Каково взаимное положение прямых ЕF и АВ?
б) Чему равен угол между прямыми ЕF и АВ, если ∠АВС = 150°? Поясните.
2. Дан пространственный четырехугольник ABCD, в котором диагонали АС и BD равны. Середины сторон этого четырехугольника соединены последовательно отрезками.
а) Выполните рисунок к задаче.
б) Докажите, что полученный четырехугольник есть ромб.
Вариант II
1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны AD, а K – середина стороны DC.
а) Каково взаимное положение прямых РK и АВ?
б) Чему равен угол между прямыми РK и АВ, если ∠АВС = 40° и ∠ВСА = 80°? Поясните.
2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно; Е∈ CD, K∈ DA, DE : EC = 1 : 2, DK : KA = 1 : 2.
а) Выполните рисунок к задаче.
б) Докажите, что четырехугольник MNEK есть трапеция.
Контрольная работа №2 по теме «Перпендикулярность прямых и плоскостей».
Вариант I
1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:
а) параллельными;
б) скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А2В2, если А1В1 = 12 см, В1О : ОВ2 = 3 : 4.
3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1.
Вариант II
1. Прямые a и b лежат в пересекающихся плоскостях α и β.
Могут ли эти прямые быть:
а) параллельными;
б) скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2. Через точку О, не лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках В1 и В2. Найдите длину отрезка А1В1, если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5.
3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K∈ DA, АK : KD = 1 : 3.
Контрольная работа №3 по теме «Многогранники»
Вариант I
1. Диагональ куба равна 6 см. Найдите:
а) ребро куба;
б) косинус угла между диагональю куба и плоскостью одной из его граней.
2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D.
а) Найдите расстояние от точки С до плоскости α.
б) Покажите на рисунке линейный угол двугранного угла DABM, М∈ α.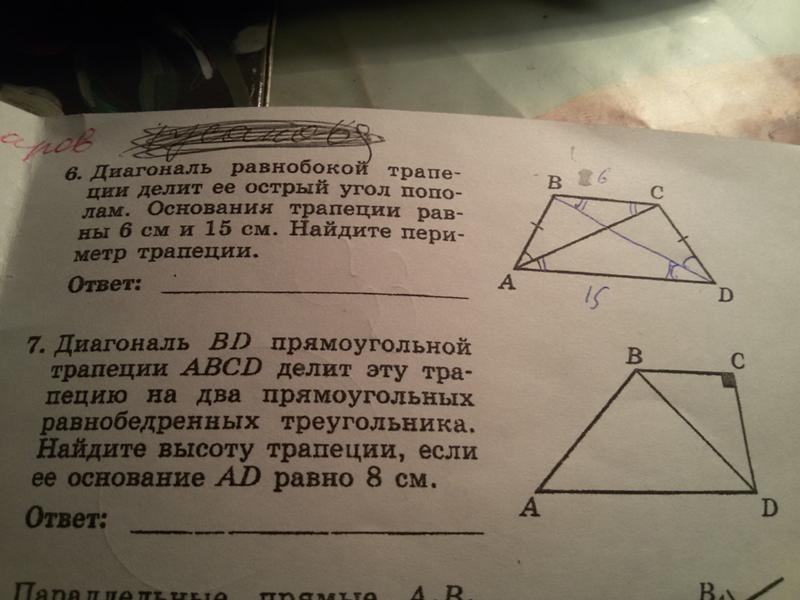
в) Найдите синус угла между плоскостью ромба и плоскостью α.
Вариант II
1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2 см, а его измерения относятся как 1 : 1 : 2. Найдите:
а) измерения параллелепипеда;
б) синус угла между диагональю параллелепипеда и плоскостью его основания.
2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии от точки В.
а) Найдите расстояние от точки С до плоскости α.
б) Покажите на рисунке линейный угол двугранного угла BADM, М ∈ α.
в) Найдите синус угла между плоскостью квадрата и плоскостью α.
Контрольная работа №4 по теме «Многогранники»
Вариант I
1. Основанием пирамиды DABC является правильный треугольник АВС, сторона которого равна а. Ребро DA перпендикулярно к плоскости АВС, а плоскость DBC составляет с плоскостью АВС угол в 30°. Найдите площадь боковой поверхности пирамиды.
2.
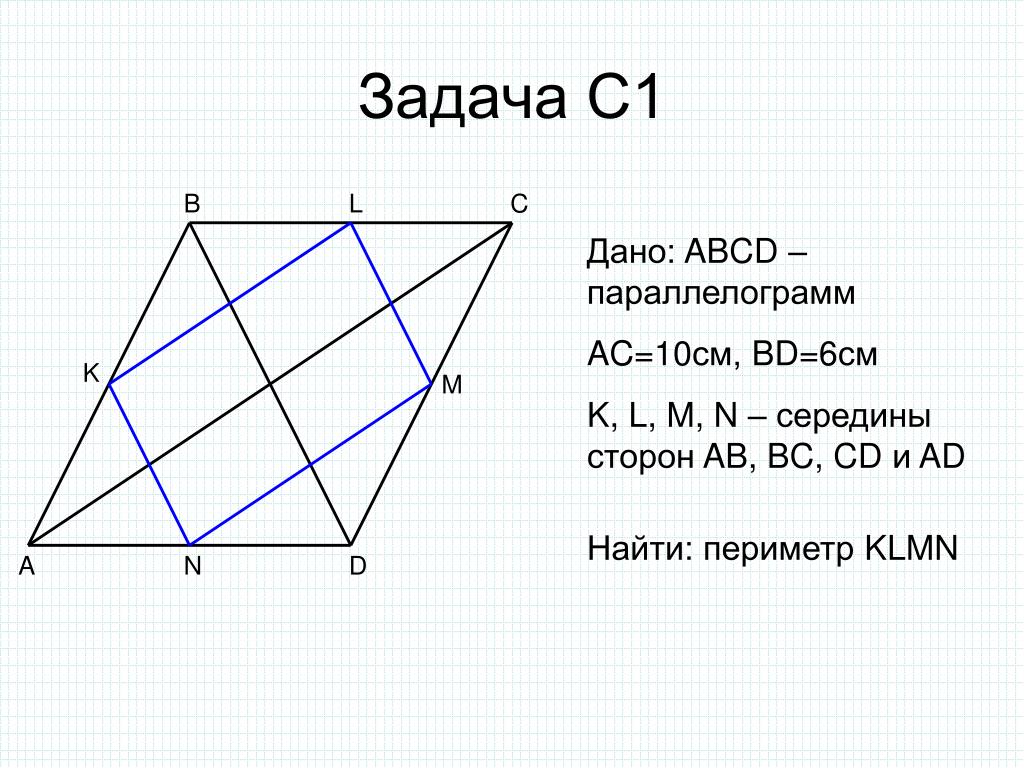Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите:
а) высоту ромба;
б) высоту параллелепипеда;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда.
Вариант II
1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.
2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны а и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
а) меньшую высоту параллелограмма;
б) угол между плоскостью АВС1 и плоскостью основания;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда.
Контрольная работа №5 по теме «Векторы»
Вариант I
1.
Дан параллелепипед ABCDA1B1C1D1. Изобразите на рисунке векторы, равные:
1) 1 + 1 + 1+ ;
2) .
2. В тетраэдре DABC М – точка пересечения медиан грани BDC, Е – середина АС. Разложите вектор по векторам , и .
3. Даны три неколлинеарных вектора , и . Найдите значения р и g, при которых векторы = +g + 8 и = +p + g коллинеарны.
4*. В тетраэдре DABC точки М и Н – середины соответственно ребер АD и ВС. Докажите, используя векторы, что прямые АВ, НМ и DC параллельны одной плоскости.
Вариант II
1. Дан параллелепипед ABCDA1B1C1D1. Изобразите на рисунке векторы, равные:
1) 1 + + 1+ ;
2) 1 .
2. В тетраэдре DABC точка Е – середина ребра AD, а М – точка пересечения медиан грани BDC. Разложите вектор по векторам , и .
3. Докажите, что векторы = + — , = — — и = — + компланарны.
4*. В тетраэдре DABC точки M и N – середины АВ и CD соответственно. Докажите, что середины отрезков МС, MD, NA и NB являются вершинами параллелограмма.
kontrolnye_10_geometrija
КОНТРОЛЬНЫЕ РАБОТЫ
ПО ГЕОМЕТРИИ
10 КЛАСС
УЧЕБНИК АТАНАСЯН Л.С.
Контрольная работа № 1
Тема: Параллельность прямых и плоскостей
Вариант I
1. Основание AD трапеции ABCD лежит в плоскости α. Через точки В и С проведены параллельные прямые, пересекающие плоскость α в точках Е и F соответственно.
а) Каково взаимное положение прямых ЕF и АВ?
б) Чему равен угол между прямыми ЕF и АВ, если АВС = 150°? Поясните.
2. Дан пространственный
четырехугольник ABCD,
в котором диагонали АС и BD равны. Середины сторон этого четырехугольника
соединены последовательно отрезками.
а) Выполните рисунок к задаче.
б) Докажите, что полученный четырехугольник есть ромб.
Контрольная работа № 1
Тема: Параллельность прямых и плоскостей
Вариант II
1. Треугольники АВС и АDC лежат в разных плоскостях и имеют общую сторону АС. Точка Р – середина стороны AD, а K – середина стороны DC.
а) Каково взаимное положение прямых РK и АВ?
б) Чему равен угол между прямыми РK и АВ, если АВС = 40° и ВСА = 80°? Поясните.
2. Дан пространственный четырехугольник АВСD, М и N – середины сторон АВ и ВС соответственно; Е CD, K DA, DE : EC = 1 : 2, DK : KA = 1 : 2.
а) Выполните рисунок
к задаче.
б) Докажите, что четырехугольник MNEK есть трапеция.
Контрольная работа № 2
Тема: Параллельность плоскостей. Тетраэдр и параллелепипед.
Вариант I
1. Прямые a и b лежат в параллельных плоскостях α и β. Могут ли эти прямые быть:
а) параллельными;
б) скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2. Через точку О, лежащую между параллельными плоскостями α и β, проведены прямые l и m. Прямая l пересекает плоскости α и β в точках А1 и А2 соответственно, прямая m – в точках
3. Изобразите параллелепипед ABCDA1B1C1D1 и постройте его сечение плоскостью, проходящей через точки M, N и K, являющиеся серединами ребер АВ, ВС и DD1.
Контрольная работа № 2
Тема: Параллельность плоскостей. Тетраэдр и параллелепипед.
Вариант II
1. Прямые a и b лежат в пересекающихся плоскостях α и β. Могут ли эти прямые быть:
а) параллельными;
б) скрещивающимися?
Сделайте рисунок для каждого возможного случая.
2. Через точку О,
не лежащую между параллельными
плоскостями α
и β,
проведены прямые l и m.
Прямая l пересекает плоскости α
и β
в точках А1 и А2 соответственно, прямая m – в точках В1 и В2.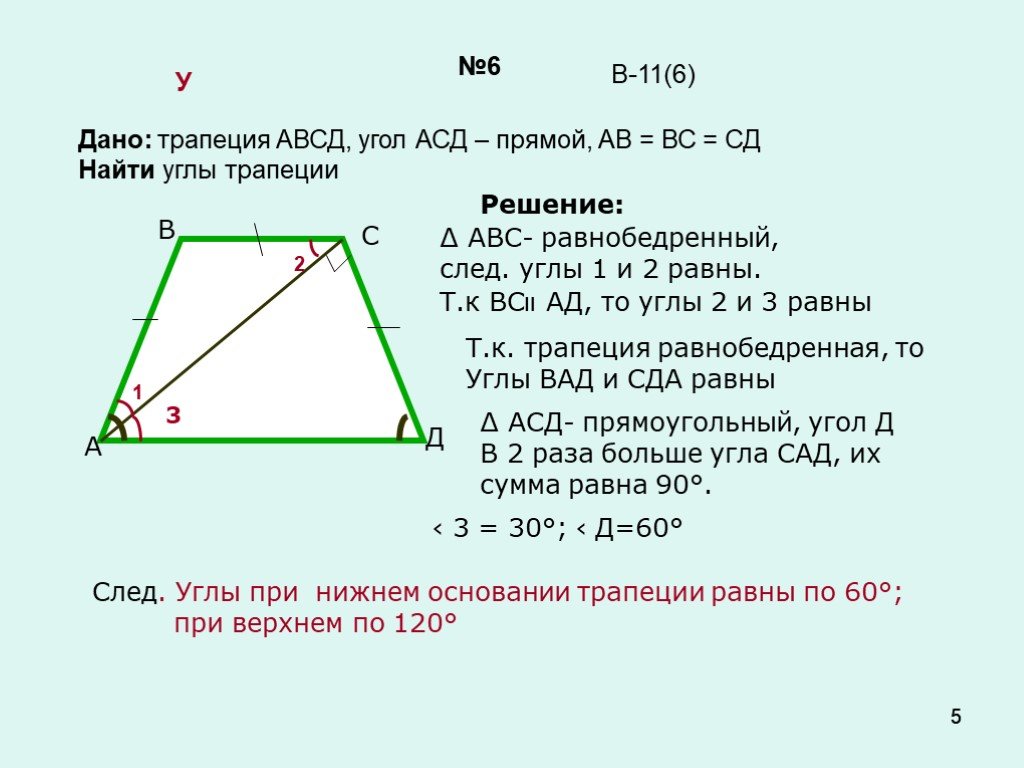
Найдите длину отрезка А1В1,
если А2В2 = 15 см, ОВ1 : ОВ2 = 3 : 5.
3. Изобразите тетраэдр DABC и постройте его сечение плоскостью, проходящей через точки M и N, являющиеся серединами ребер DC и BC, и точку K, такую, что K DA, АK : KD = 1 : 3.
Контрольная работа № 3
Тема: Перпендикулярность прямых и плоскостей
Вариант I
1. Диагональ куба равна 6 см. Найдите:
а) ребро куба;
б) косинус угла между диагональю куба и плоскостью одной из его граней.
2. Сторона АВ ромба ABCD равна a, один из углов равен 60°. Через сторону АВ проведена плоскость α на расстоянии от точки D.
а) Найдите расстояние
от точки С до плоскости α.
б) Покажите на рисунке линейный угол двугранного угла DABM, М α.
в) Найдите синус угла между плоскостью ромба и плоскостью α.
Контрольная работа № 3
Тема: Перпендикулярность прямых и плоскостей
Вариант II1. Основанием прямоугольного параллелепипеда служит квадрат; диагональ параллелепипеда равна 2 см, а его измерения относятся как 1 : 1 : 2. Найдите:
а) измерения параллелепипеда;
б) синус угла между диагональю параллелепипеда и плоскостью его основания.
2. Сторона квадрата ABCD равна а. Через сторону AD проведена плоскость α на расстоянии от точки В.
а) Найдите расстояние от точки С до плоскости α.
б) Покажите на
рисунке линейный угол двугранного
угла BADM, М α.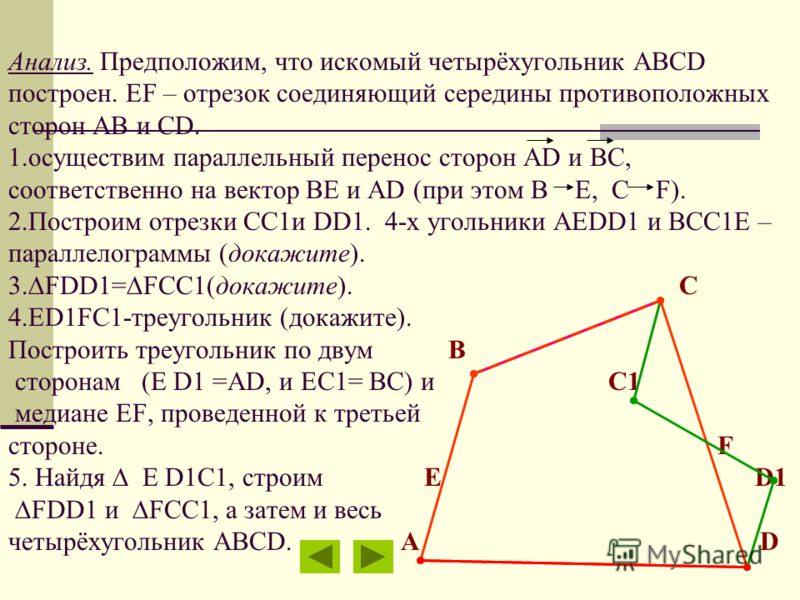
в) Найдите синус угла между плоскостью квадрата и плоскостью α.
Контрольная работа № 4
Тема: Многогранники
Вариант I
2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является ромб ABCD, сторона которого равна а и угол равен 60°. Плоскость AD1C1 составляет с плоскостью основания угол в 60°. Найдите:
а) высоту ромба;
б) высоту параллелепипеда;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности
параллелепипеда.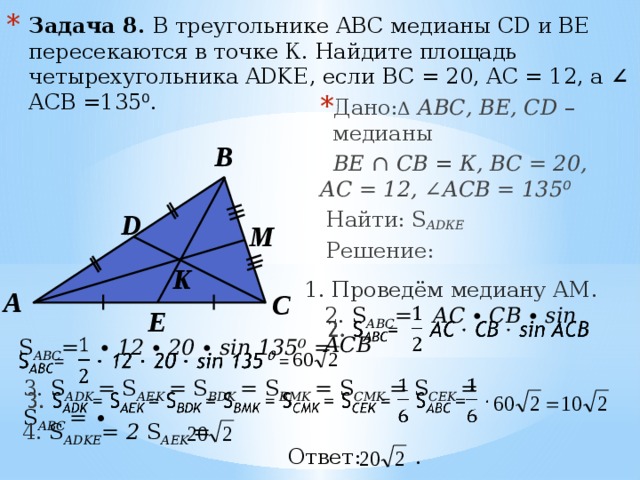
Контрольная работа № 4
Тема: Многогранники
Вариант II
1. Основанием пирамиды MABCD является квадрат ABCD, ребро MD перпендикулярно к плоскости основания, AD = DM = a. Найдите площадь поверхности пирамиды.
2. Основанием прямого параллелепипеда ABCDA1B1C1D1 является параллелограмм ABCD, стороны которого равны а и 2а, острый угол равен 45°. Высота параллелепипеда равна меньшей высоте параллелограмма. Найдите:
а) меньшую высоту параллелограмма;
б) угол между плоскостью АВС1 и плоскостью основания;
в) площадь боковой поверхности параллелепипеда;
г) площадь поверхности параллелепипеда.
геометрия — $ABCD$ является четырехугольником, а $P,Q$ являются серединами $CD, AB.
$…спросил
Изменено 5 лет, 6 месяцев назад
Просмотрено 330 раз
$\begingroup$
$ABCD$ — четырехугольник, а $P,Q$ — середины $CD, AB.$ $AP$ и $DQ$ пересекаются в точке $X, BP$ и $CQ$ пересекаются в точке $Y.$ Докажите, что $$ |ADX|+|BCY|=|PXQY|$$ (здесь $|N|$ означает площадь фигуры $N$)
Я совершенно не знаю, как решить эту проблему.
Будем признательны за любую помощь.
- геометрия
- площадь
- четырехугольник
$\endgroup$
4
$\begingroup$
Пусть S$_{N}$ будет площадью N.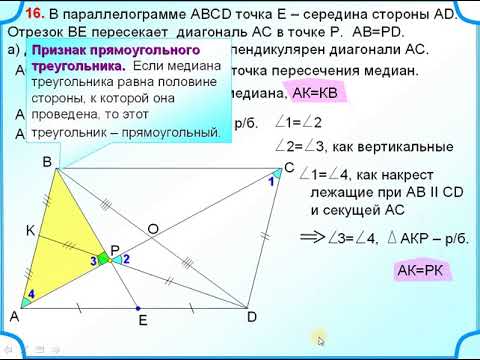
Сначала посмотрим на $_\треугольник$ABP: Q — середина $\Rightarrow$ PQ — медиана. Из PQ — медиана $\Rightarrow$ S$_{AQP}$ = S$_{BQP}$ $\Rightarrow$ S$_2$ + S$_3$ = S$_5$ + S$_8$ (1).
Теперь посмотрим на $_\triangle$DQC: P — середина $\Rightarrow$ QP — медиана. Из QP — медиана $\Rightarrow$ S$_{DPQ}$ = S$_{QPC}$ $\Rightarrow$ S$_4$ + S$_3$ = S$_7$ + S$_8$ (2).
Сложение уравнений (1) и (2) дает нам S$_2$ + S$_7$ = S$_4$ + S$_5$ (3).
Теперь рассмотрим $_\треугольник$ABC: CP — медиана (Q-середина) $\Rightarrow$ S$_{AQC}$ = S$_5$ + S$_6$ (4). В $_\triangle$CAD $\rightarrow$ AP — медиана $\Rightarrow$ S$_{ACP}$ = S$_1$ + S$_4$ (5).
Складывая (4) и (5), получаем S$_{AQCP}$ = S$_1$ + S$_4$ + S$_5$ + S$_6$ (6).
Теперь посмотрим на AQPC и DQBP:
S$_{AQCP}$ = S$_2$ + S$_3$ + S$_8$ + S$_7$ (7).
S$_{DQBP}$ = S$_5$ + S$_3$ + S$_8$ + S$_4$ (8).
Из (3), (7) и (8) $\Rightarrow$ S$_{AQCP}$ = S$_{DQBP}$ (9).
Из (9) и (6) получаем S$_{BQBP}$ = S$_1$ + S$_4$ + S$_5$ + S$_6$ или S$_5$ + S$_3$ + S$_8$ + S$_4$ = S$_1$ + S$_4$ + S$_5$ + S$_6$ $\Rightarrow$
$\Rightarrow$ S$_3$ + S$_8$ = S$_1$ + S$_6$ $\Rightarrow$ S$_{ADX}$ + S$_{BCY}$ = S$_{PXQY}$.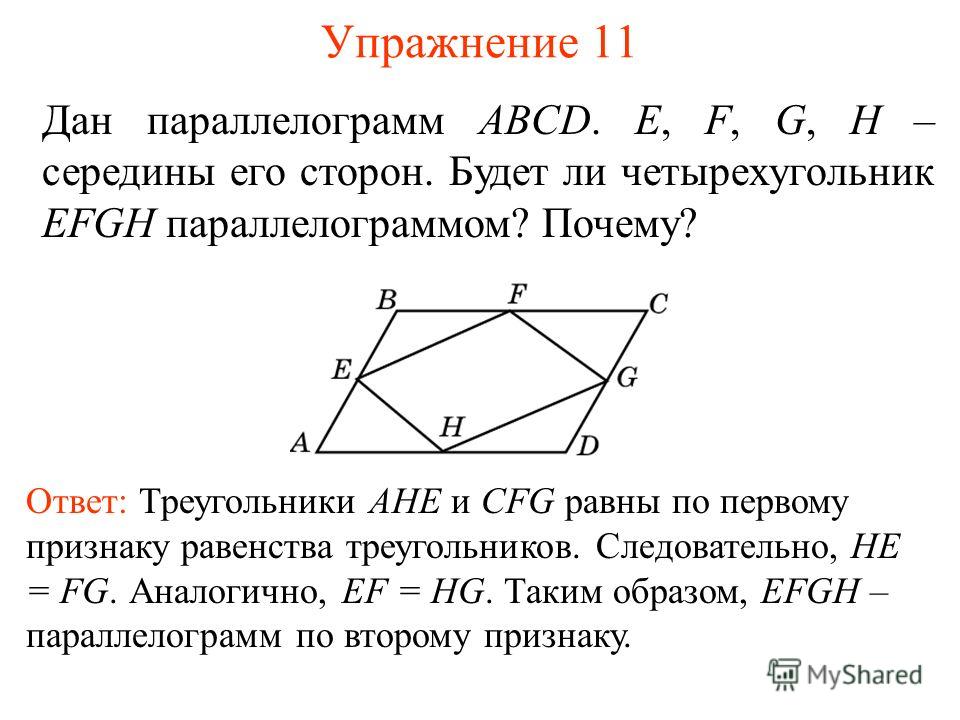
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Trang chủ — Diễn đàn Toán học
27-10-2022
Гуи бои bangbang1412 trong Toán học lý thú
Toan học như văn hóa và tri thức — математика как культура и знание toán học là một hoạt ộng tri thức, ược cho là một trong những hoạt ộng tinh tế nhất từng ược tạ ra bở nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh nh- Герман Гессе Пхак Хоа Чан Навоз Нхонг Хоут Донг Куа Как Ня Тоан Хок Мут Ках ан дю Тронг Игра в бисер. Có lẽ đó là nỗ lực văn học tốt nhất để bắt dù chỉ một cái nhìn thoáng qua những hoạt động nội tại totrong hợ hỻn. Người ta không phê phán một tác phẩm hư cấu bằng sự thiếu chính xác của nó, nhưng sẽc sự hự ể nói cái gì đ đ đ đ đ nghĩa về việc thế nà nói lЩ
Có kha nhiều cac nhà toán học thừa hưởng quan điể kiểu Plato về toán học. Điều này có nghĩa là họ họ có niềm tin rằng các ối tượng và xây dựng toán học có một kiểu tồn tại nào đ rong «thếi những ý nhrIng ‘ Như trong trường hợp của thiên ường thần thoại, những người khởi xướng niềm tin đ đ tỏ ra khá mập mờ về vị trí và tính nhất quan của thế giới plato ngoạ nhy nhất quan của thế giới ngo ngoo Một lý do thường được viện ra để củng cố góc nhìn Plato la sự hiệu quả của toán học trong việc mô hình hóa thế giới vật lít.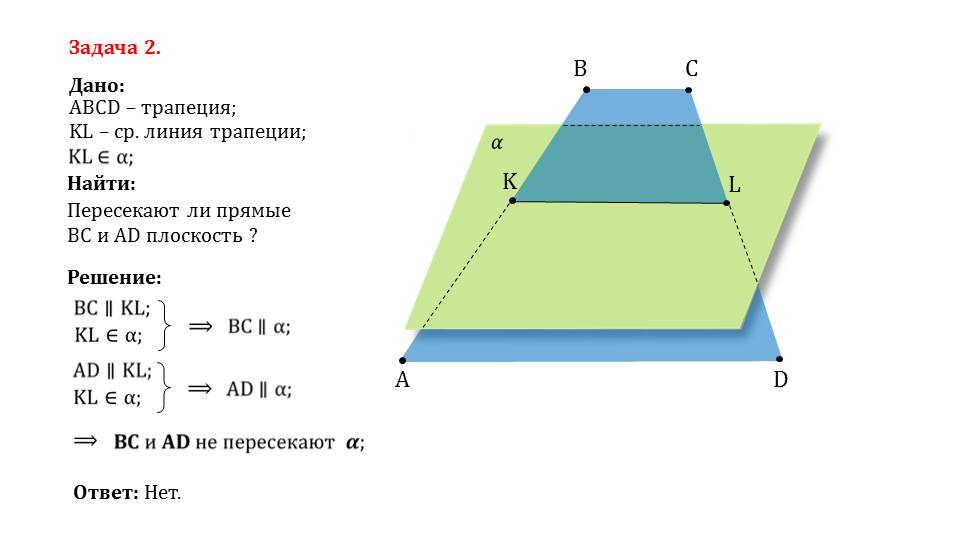
Không nghi ngờ gì những định luật Kepler cuối cùng cũng có thể được quan sát và thông hiểu bởi bất kì trí thông minh công nghệ nào sống trên một hình tinh bao quanh bởi lực hấp dẫn để quay quanh một ngôi sao (nhưng liệu một khám phá như vậy có tuân theo tiến trình mà chung ta biết, hành tinh có xoay quanh hai ngôi sao khong?). Tuy nhiên người ta khó có thể viện ra một…
Подробнее
21-10-2022
Гуи бои Nxb trong Tin tức — Vấn đề — Sự kiện
Mình dịch lại bai viết «Новаторские квантовые физики получают Нобелевскую премию по физике» trên quantmagazine. Bài viết gốc ở đây https://www.quantama…ysics-20221004/ Nếu có lỗi sai mọi người hay gửi tin nhắn cho minh. ————————————- cat nhà vật lý lượng tử then phong giành giải nobel vật lý các nhà vật lý alain aspect, john clauser và anton zeilinger đ giành no nobm no no zeilinger.
chứng minh bản chất lượng tử kỳ lạ sau xa của thực tại. Các thí nghiệm của họ đ đ cùng nhau thiết lập sự tồn tại của một hiện tượng lượng tử nơ ượ ượ ượ x kh kh n g g g g g g g g g g g g g g g gư gha ô gư gha ô gh ô gha gha gha gha gh gha gha gha gha gha gha gh gha gha gha gha gha gha gha gh gha ghag thể hình навоз được. Hiện tượng liên đới nằm ở trung tâm của một cuộc đụng độ nảy lửa vào những năm 1930 giữa những người Khổng lồ vật lý, Albert Einstein ở một bên, và một bên la Niels Bohr và Erwin Schrödinger về cách vứ trụ vận hanh ở cấp đᙙ cấp đᙙt. Эйнштейн олово rằng tất cả cac khía cạnh của thực tế nên có một sự tồn tại cụ thể và hoàn toàn có thể biết được. Tất cả cac vật thể — từ mặt trăng đến photon ánh sáng — phải có cac đặc tính được xac định chính xac có thể đophéng thám. Туй Нхьен, Бор, Шредингер ва Нхонг Нгои Унг Хой Кей Хок Лунг Той Сон Кхай Кхак Да Пхат Хиен Ранг Тхок Той Воч Кой Бан ла Кхунг; một hạt không có cac đặc tính nhất định cho đến thời điểm đo. Sự liên đới nổi lên Như một cách quyết định để phân biệt giữa hai phiên bản có thể có c.
..
Подробнее
09.01.2022
Гуи бои bangbang1412 trong Toán học hiện đại
Trong topic này mình muốn giới thiệu về K-lý thuyết Milnor (Milnor’s K-theory) và kết nối nó với một số lý thuyết đối đồng điều như đối đồng điều Galois, nhóm Bloch-Chow, đối đồng điều motivic. Về Mặt lịch Sử, Ban ầu k-lý thuyết ại số (алгебраический k-теория) chỉ ịnh nghĩa ược cho $ k_0, k_1, k_2 $ (grothendiec tạp rồi, về sau k-lý thuyết ại s chỉ ược ịnh nghĩa và nghiên cứu một cách có hệng từ sau quillen khi ô ưa ha ha ồ ồ ồ ồ ồ ồ ồ ồ ồ kh kh kha ọ kh kh kh hi hi hi hệ hệ hệ hệ hệ ọ ồ hệ hi hệ hệ hệ ọ ồ hệ hệ ngh nghy ô ư ư ư kha kh kh ha ư ư qu ượ ượ ượ ượ ị hệ h h gha ô Trước đ đt ịnh lý của matsumoto cho ta mô tả $ k_2 $ cụ thể dưới dạng phần tử sinh và quan hệ, milnor dựa trên ịnh nghĩa này ưa ra một ị ị n ọ ọ ọ ọ ọ ọ ị ọ ọ ọ ị ị kh kh kh kh kh kh kh kht hrết hrết hrết -lý thuyết milnor, nó chứa một phần thông tin của k-lý thuyết ại s s số (the nghĩa quillen + cổ điển) theo nghĩa sau khi tensor với $ \ так.
Ể thuận tiện cho người ọcc, mình sẽ ịnh nghĩa lại một số nhóm cổ điển $ k_0, k_1, k_2 $ và một số tính chất cơ bản (không chứng minh). Nhóm K_0 Cố định một vành $R$ (giao hoán có đơn vị). Nhắc lại rằng một модуль xạ ảnh la một hạng tử trực tiếp của một модуль tự do nào đó. Định nghĩa. Nhóm $K_0(R)$ được định nghia bởi công thức sau$$K_0(R) = \bigoplus \mathbb{Z}[P]/\sim,$$trong đó tổng trực tiếp lếy trån lớng cáp ấu $-модуль xạ ảnh hữu hạn sinh, quan hệ $\sim$ được cho bởi $[P] + [Q] = [P \oplus Q]$. Ta cũng có thể trang bị cho $K_0(R)$ một cấu t…
Подробнее
26-08-2022
Гуи бои bangbang1412 trong Toán học hiện đại
Gửi mọi người một самостоятельная заметка của minh về đối đồng điều động lực (мотивная когомология) phát triển bởi Voevodsky. Ối ồng điều ộng lực ược dự đoán tồn tại bởi beillinson, cụ thể, ô ro dự đoán tồn tại một phức $ \ mathbb {z} nta nta ntố ntố ntố ntố ntố ntố ntố w ntố w ntố ntố nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta nta net *,n}(X,\mathbb{Z})=\mathbb{H}_{Zar}^*(X,\mathbb{Z}(n))$ mà khi hạn chế tại một số bậc đặc biệt thu được K-lý thuyết Milnor, nhóm Bloch-Chow bậc cao và đồng thời có một dãy phổ hội tụ về K-lý thuyết Quillen sao cho sau khi tensor với $\mathbb{Q}$ dãy phổ này suy biến về $\gamma $-lọc của K-lý thuyết Quillen.
{\otimes q})$. Voevodsky sau đó đã được huy chương Fields vì chứng minh trọn vẹn giả thuyết Bloch-Kato bằng cách xây dựng một lớp đa tạha Rosdọa cựn trìn c. Với mình đ nhy là thành công ầu tiên hướng tới lý thuyết otive của grothendieck vì giả thuyế bloch-kato đ đ nối hai loại bấn biến: transcendental (nhómale). Đối đồng điều động lực tới nay có rất nhiều cách xây dựng, có thể kể đến: гиперкогомология Như trên Zarikis hoặc Nisnevich site. Như nhóm Bloch-Chow bậc cao. Như hom-set trong phạm trù мотив Hình Học $…
Подробнее
08.11.2022
Гуи бой Несбит trong Lịch sử toán học
[Nhan có bạn nhắc đến giả thuyết về cac số nguyên tố sinh đôi, xin chia sẻ một bài viết gần đay của GS. Vũ Hà Văn viết trên blog vào dịp Джеймс Мейнард nhận được Huy chương Fields năm nay. Giọng văn của giáo sư vẫn hài hước như mọi khi, đặc biệt là phần chốt hạ bằng hai câu thơ lục bát.
] Nhà toán học thứ hai được giải Fields năm nay là anh J. Maynard, vỡi những công trình về số nguyên tố . Số nguyên tố có lẽ la một trong nhung chủ đề lâu đời nhất và được chú ý tới nhất trong toán học. Cac nhà hiền triet Hy lập đáng kính đã nguyên cứu về nó, từ trước khi chúa Jesu ra đời. Rất có thể là trước cả khi Mỵ nương cưới Sơn tinh. Số nguyên tố la nhung số nguyên dương chỉ chia hết đươc cho chính nó. Ви до нхо 5; 6 không phải la số nguyên tố vì nó chia hết cho 2. Cac số nguyên tố nhỏ nhất la 2,3,5,7,11,13,17,19, 23,29, 31, 37….Số 1, thấp cổ be họng, không được vào hội. ТАКА РАЙНА ДЕЛА САУ XA HơN Là vì Một ịnh lý, xưa như quả ất, là tất cả các số nguyên dương ều có thể viết dưới dạng tích của một s nguyn thrết dướng tía nhan nhan nha nhan nhan nhan nhan nhan nhan th là nhân với 1 thì chả thêm vị gì, nên chàng đã bị loại. Từ thời Наполеон, người ta đã biết la có vô hạn số nguyên tố. Tức cái dãy 2,3,5…ở trên no sẽ kéo dài vô hạn. Một trong những câu hỏi nổi tiếng và trung tâm nhất của toán học, là cái sự kéo dai đó nó diễn ra như thế nào.
Chẳng hạn bạn thấy ở trên có tới 8 số nguyên tố giưã 1 và 20, nhưng giữa 21 và 40 chỉ còn 4 số. Tức tần suất xuất hiện của số nguyên tố ngày một giảm đi. Cũng như số lần …
Подробнее
15.07.2022
Гуи бой Несбит trong Thi HSG Quốc gia và Quốc tế
Kì thi lần này đội tuyển chúng ta xếp thứ 4, sau Trung Quốc, Hàn Quốc, và Mỹ. Đây la thành tích rất cao. Thành tích cá nhân của đội Việt Nam như sau: Em Ngô Quý Đăng là một trong 10 thí sinh giành được điểm tuyệt đối 42/42. Đây cũng là HCV thứ hai của em (HCV đầu tiên giành được năm 2020 lúc đang học lớp 10, rất tiếc la năm 2021 lại rng vÛt).
Подробнее
07.12.2022
Гои бои хоангвипмесси97 trong Thi HSG Quốc gia và Quốc tế
Ngày thi thứ nhấtBài 1: Ngân hàng Oslo có phát hành hai loại tiền xu: đồng vàng (kí hiệu bởi A) và đồng bạc (kí hiệu bởi B).
2 + x + k $ với $ x Biết rằng, hai cách xếp nhận được từ nhau qua phép quay và phép phản…
Подробнее
07.09.2022
Гои бои nmlinh26 trong Toán học hiện đại
Gửi cac thành viên trên diễn đàn ghi chú của minh về định lý phân loại mặt đóng, một định lý cơ bản của tô pô. Học sinh phổ thông có thể đọc được ghi chú này.https://drive.google…iew?usp=sharing
Подробнее
07.06.2022
Гуйбуи Э. Галуа trong Dành cho giáo viên các cấp
SKKN: Hướng dẫn học sinh giải bài toán tổ hợp tạo số bằng lập trình PASCAL
Подробнее
07.05.2022
Гуи бой Несбит trong Tin tức — Vấn đề — Sự kiện
Ngày 07.