選擇語言Bahasa Indonesia (Bahasa Indonesia)Bahasa Malaysia (Malay)Čeština (Czech)Dansk (Danish)Deutsch (German)English (English)Español (Spanish)繁體中文 (Chinese (Traditional))Français (French)한국어 (Korean)Italiano (Italian)简体中文 (Chinese (Simplified))Nederlands (Dutch)日本語 (Japanese)Norsk (Norwegian)Polski (Polish)Português (Portuguese)Română (Romanian)Русский (Russian)Svenska (Swedish)Tagalog (Tagalog)ภาษาไทย (Thai)Türkçe (Turkish)العربية (Arabic)
عفواً، لم نتمكن من العثور على الصفحة التي تبحث عنها. برجاء المحاولة مرة أخرى للصفحة السابقة أو الانتقال لـمركز المساعدة للمزيد من المعلومات
الإنتقال لموجزك الرئيسيOmlouváme se, nemůžeme najít stránku, kterou hledáte. Zkuste se vrátit zpátky na předchozí stránku, nebo se podívejte do našeho Centra nápovědy pro více informací
Přejít do informačního kanáluVi kan desværre ikke finde den side, du leder efter.
Gå tilbage til den forrige side, eller besøg Hjælp for at få flere oplysninger Gå til dit feedDie gewünschte Seite konnte leider nicht gefunden werden. Versuchen Sie, zur vorherigen Seite zurückzukehren, oder besuchen Sie unseren Hilfebereich, um mehr zu erfahren.
Zu Ihrem FeedUh oh, we can’t seem to find the page you’re looking for. Try going back to the previous page or see our Help Center for more information
Go to your feedVaya, parece que no podemos encontrar la página que buscas. Intenta volver a la página anterior o visita nuestro Centro de ayuda para más información.
Ir a tu feedNous ne trouvons pas la page que vous recherchez. Essayez de retourner à la page précédente ou consultez notre assistance clientèle pour plus d’informations
Ouvrez votre filMaaf, sepertinya kami tidak dapat menemukan halaman yang Anda cari.
Coba kembali ke halaman sebelumnya atau lihat Pusat Bantuan kami untuk informasi lebih lanjut Buka feed AndaNon abbiamo trovato la pagina che stai cercando. Prova a tornare alla pagina precedente o visita il nostro Centro assistenza per saperne di più.
Vai al tuo feed申し訳ありません。お探しのページが見つかりません。前のページに戻るか、ヘルプセンターで詳細をご確認ください
フィードに移動원하시는 페이지를 찾을 수 없습니다. 이전 페이지로 돌아가거나 고객센터에서 자세히 알아보세요.
홈으로 가기Harap maaf, kami tidak dapat menemui laman yang ingin anda cari. Cuba kembali ke laman sebelumnya atau lihat Pusat Bantuan kami untuk maklumat lanjut
Pergi ke suapanDe pagina waar u naar op zoek bent, kan niet worden gevonden. Probeer terug te gaan naar de vorige pagina of bezoek het Help Center voor meer informatie
Ga naar uw feedVi finner ikke siden du leter etter.
Gå tilbake til forrige side eller besøk vår brukerstøtte for mer informasjon Gå til din feedNie możemy znaleźć strony, której szukasz. Spróbuj wrócić do poprzedniej strony lub nasze Centrum pomocy, aby uzyskać więcej informacji
Przejdź do swojego kanałuA página que você está procurando não foi encontrada. Volte para a página anterior ou visite nossa Central de Ajuda para mais informações
Voltar para seu feedNe pare rău, nu găsim pagina pe care o căutaţi. Reveniţi la pagina anterioară sau consultaţi Centrul nostru de asistenţă pentru mai multe informaţii
Accesaţi fluxul dvs.Не удаётся найти искомую вами страницу. Вернитесь на предыдущую страницу или посетите страницу нашего справочного центра для получения дополнительной информации.
Перейти к лентеSidan du letar efter hittades inte.
Gå tillbaka till föregående sida eller besök vårt Hjälpcenter för mer information Gå till ditt nyhetsflödeขออภัย ดูเหมือนเราไม่พบหน้าที่คุณกำลังมองหาอยู่ ลองกลับไปที่หน้าเพจก่อน หรือดู ศูนย์ความช่วยเหลือ ของเราสำหรับข้อมูลเพิ่มเติม
ไปที่ฟีดของคุณNaku, mukhang hindi namin mahanap ang pahina na hinahanap mo. Subukang bumalik sa nakaraang pahina o tingnan ang aming Help Center para sa higit pang impormasyon
Pumunta sa iyong feedAradığınız sayfa bulunamadı. Önceki sayfaya geri dönün veya daha fazla bilgi için Yardım Merkezimizi görüntüleyin
Haber akışınıza gidin抱歉，无法找到页面。试试返回到前一页，或前往帮助中心了解更多信息
前往动态汇总我們好像找不到該頁面。請回到上一頁或前往說明中心來進一步瞭解
前往首頁動態Эффективная адаптация онлайн-модели с помощью добавочной симплексной таблицы
%PDF-1.4
%
134 0 объект
>/OCGs[137 0 R]>>/OutputIntents[131 0 R]/PageLabels 129 0 R/Pages 16 0 R/Тип/Каталог>>
эндообъект
136 0 объект
>/Шрифт>>>/Поля 141 0 R>>
эндообъект
133 0 объект
>поток
2017-01-21T19:42:11-08:00TeX2017-01-22T15:24:48-08:002017-01-22T15:24:48-08:00Это pdfTeX, версия 3.
14159265-2.6-1.40.17 (TeX Live 2016) kpathsea версия 6.2.2Acrobat Distiller 15.0 (Macintosh)FalseMachine Learning Methodsapplication/pdf
Симплексный метод — Промышленный инженер онлайн
Исследование операций
Брайан Салазар Лопес 13 мая 2020 г.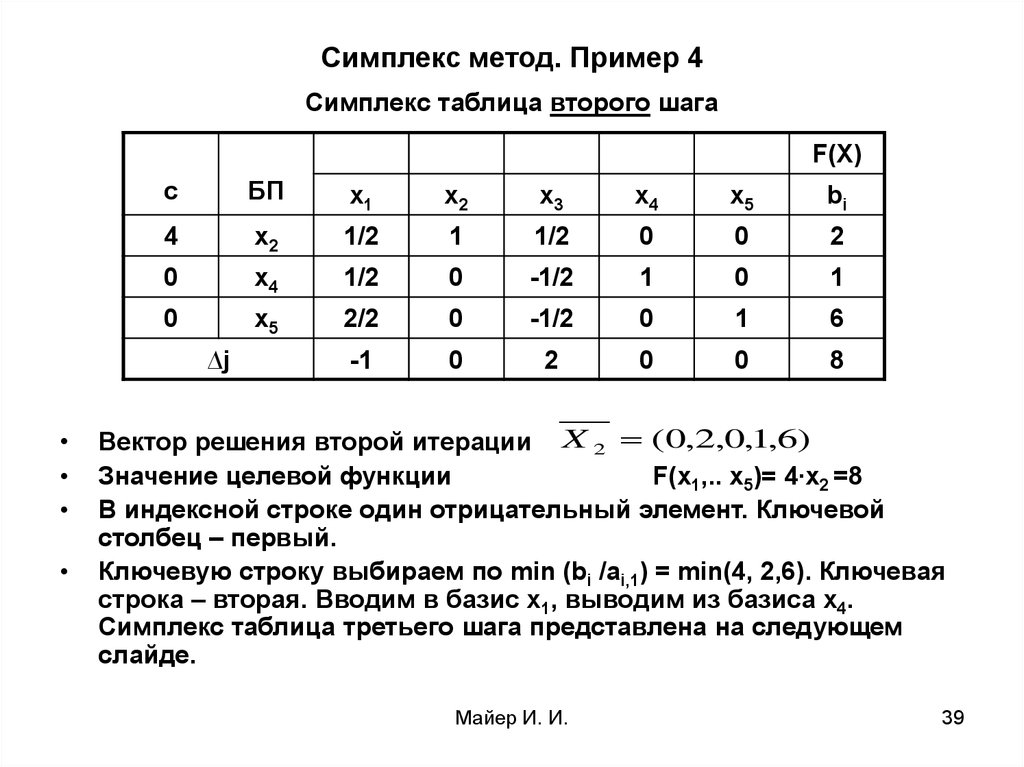
1945 6 минут чтения
Симплекс-метод — это аналитический метод решения задач линейного программирования , способный решать сложные модели, чем решенные с помощью графического метода.
Симплексный метод — это итерационный метод , улучшающий решение на каждом этапе. Математическая причина этого улучшения заключается в том, что метод состоит в обходе соседней вершины таким образом, чтобы она возрастала или уменьшалась (в зависимости от контекста целевой функции, является ли она максимальной или минимальной), учитывая, что количество вершин, которые многогранник решений конечен, всегда есть решение.
¿Что такое единичная матрица?
Матрица может быть определена как прямоугольное расположение элементов (или конечный список элементов), которые могут быть действительными числами или комплексными числами, расположенными в строках и столбцах.
Матрица идентичности, иногда двусмысленно называемая a, является квадратной (имеет такое же количество строк, как и такое же количество столбцов) порядка n, в которой все диагональные элементы равны единице (1) и все остальные компоненты равны нулю (0), это называется Идентичной матрицей или Идентичностью порядка «n» и обозначается:
Важность этой матричной теории в симплекс-методе является фундаментальной, учитывая, что алгоритм основан на указанной теории для самого решения проблемы.
Важные соображения при использовании симплекс-метода
Переменные запаса и излишкаСимплекс-метод работает на основе уравнений и начальных ограничений, которые являются моделью через линейное программирование, для этого вы должны преобразовать это неравенство в уравнениях с использованием некоторого типа переменных, называемых: Переменные резерва и излишка , которые связаны с ресурсом, на который ссылаются ограничения, и которые в окончательной таблице представляют собой «незатраты или излишки», на которые ссылаются многие резолюции операционных программ, эти переменные получают большую добавленную стоимость в анализ чувствительности и играют ключевую роль в создании базовой матрицы идентичности Simplex.
Эти переменные обычно обозначаются буквой «S» , они складываются, если ограничение «<= », и вычитаются, если ограничение «>=».
Например:
Искусственная переменная /
«М» метод: Искусственная переменная — это математический трюк, позволяющий превратить «>=» неравенства в уравнения, или когда равенства появляются в исходной задаче для решения, основная характеристика этих переменных заключается в том, что они не должны быть частью решения, учитывая, что они не представляют никакого ресурса.
Основной задачей этих переменных является формирование матрицы идентичности.
Эти переменные обозначаются буквой «A», всегда добавляются ограничения, их коэффициент равен M (поэтому метод называется M-методом, где M означает число, слишком большое и очень менее привлекательное для функции цели) , а знак в функции цели идет против самой себя, то есть в задачах на максимизацию знак минус (-), а в задачах на минимизацию знак плюс (+), повторяем с целью, что она значение решения равно нулю (0).
Пошагово: Симплексный метод
ПроблемаКомпания SAMAN Limited. Посвященный производству мебели, он расширил свое производство еще на две линии. Таким образом, в настоящее время производит столы, стулья, кровати и библиотеки. Для каждого стола требуется 2 прямоугольных элемента по 8 контактов и два квадратных элемента по 4 контакта. Для каждого стула требуется 1 прямоугольная деталь с 8 булавками и 2 квадратных детали с 4 булавками каждая; на каждую кровать требуется 1 квадратная деталь из 8 штифтов, 1 квадратная деталь из 4 штырей и 2 трапециевидных основания из 2 штырей в каждой; и, наконец, для каждой библиотеки требуется 2 прямоугольных элемента по 8 контактов в каждом, 2 трапециевидных основания по 2 контакта в каждом и 4 прямоугольных элемента по 2 контакта в каждом.
Стоимость изготовления каждого стола составляет 10 000 долларов США, а продается по 30 000 долларов США; стоимость изготовления каждого стула составляет 8000 долларов, а продается по 28000 долларов; стоимость изготовления каждой кровати составляет 20 000 долларов США, а продается по 40 000 долларов США; Стоимость изготовления каждой библиотеки составляет 40 000 долларов, а продается по 60 000 долларов. Главной целью Компании является максимизация прибыли.
Шаг 1: Моделирование посредством линейного программирования:
Переменные:
106 1 = Количество таблиц до производства (единицы)
x 2 = Количество стульев (единицы)
x 3 = Количество слоев для изготовления (UNITS)
3333333. Количество слоев. 4 = Quantity of libraries to manufacture (units)
Constraints:
2 X 1 + 1 X 2 + 1 X 3 + 2 X 4 <= 24
2 x 1 + 2 x 2 + 1 x 3 <= 20
2 x 3 + 2 2 x 3 + 2 2 x 3
<= 204 X 4 <= 16
Objective function:
Z MAX = 20000 X 1 + 20000 X 2 + 20000 Х 3 + 20000 X 4
Цель этого шага — назначить Slack Variable для каждого ресурса, учитывая, что все ограничения «<=».
2 X 1 + 1 X 2 + 1 X 3 + 2 X 4 + 1 S 1 + 0 S 2 + 0 S 3 + 0 S 4 = 24
2 X 1 + 2 x 2 + 1 x 3 + 0 x 4 + 0S 1 + 1 S 2 + 0 S 3 +
= 200 x 1 + 0 x 2 + 2 x 3 + 2 x 4 + 0 S 111079 9074
0 + 0 S0 X 1 + 0 X 2 + 0 X 3 + 4 X 4 + 0 S 1 + 0 S 2 + 0 S 3 + 1 S 4 = 16
Таким образом, мы можем увидеть матрицу идентичности (n = 4), сформированную переменными Slack, которые имеют только 1 коэффициент на соответствующем ресурсе.
; например, Slack Variable «S1» имеет только 1 коэффициент ограничения, соответствующего ресурсу 1.
The Objective Function does not suffer any kind of variations:
Z MAX = 20000 X 1 + 20000 X 2 + 20000 X 3 + 20000 X 4
Симплексный метод от исходного базового решения сделать все его итерации, это решение формируется с переменными коэффициента, отличного от нуля (0) на единичной матрице.
1 С 1 = 24
1 S 2 = 20
1 S 3 = 20
1 S 4 = 16
Solution (second term): В этой строке задается второе слагаемое решения, то есть правильным способом сделать это было бы задавать их упорядоченно, как в определении ограничений.
Cj : Эта строка ссылается на коэффициент каждой из этих переменных строки «Решение» в целевой функции.
Переменное решение: В этом столбце задается начальное базовое решение, а из этого столбца на каждой итерации включаются переменные, которые будут частью конечного решения.
Zj: В этой строке задается общий вклад, то есть сложение продуктов из срока и Cb.
Cj-Zj: В этой строке производится вычитание между строкой Cj и строкой Zj, это означает «Теневая цена» , то есть незаработанный доход для каждой единицы соответствующей переменной, которая не является частью решения.
Исходное решение:
Шаг 4: Сделайте необходимые итерацииЭто окончательный шаг симплекс-метода, который состоит в том, чтобы попытаться, пока многогранник движется от одной вершины к другой.
Процедура следующая:
1.
Чтобы оценить, какая переменная входит, какое оптимальное решение.
2. Тот факт, что переменная different является частью переменных решения, подразумевает ряд изменений в таблице Simplex. Изменение следующее:
- Прежде всего, не забудьте значение a , соответствующее переменным, входящим в
- Следующее, что нужно сделать, это начать заполнять остальную часть таблицы, строка за строкой.
- Повторите эту процедуру с двумя оставшимися рядами.
После того, как заданы значения матрицы, можно производить расчет до заполнения таблицы, соответствующей первой итерации.
На этом заканчивается первая итерация, этот шаг будет повторяться сколько угодно раз, и только будет завершен по следующим критериям.
| Развернуть | Свернуть | |
| Оптимальное решение | Когда все Cj – Zj <= 0 | Когда все Cj – Zj >= 0 |
- Продолжайте итерации, поэтому мы должны повторить предыдущие случаи:
В этой последней итерации мы можем наблюдать, что лозунг Cj-Zj <= 0, выполняется; для упражнения, целевой функцией которого является максимизация, таким образом, достигается оптимальный ответ.
x 1 = 0
x 2 = 7
x 3 = 6
x 4 = 6
x 4 = 6
x 4 = 6
x 4 = 6
x 4 = 6 x 4 = 6 x 4 = . 340000Тем не менее, когда симплекс-метод закончился, мы можем наблюдать единичную матрицу в прямоугольнике, определяемом переменными решения, тот факт, что в этом случае единичная матрица не показана, говорит нам о том, что существует другое оптимальное решение.
Способ достижения другого решения состоит в изменении порядка, в котором каждая из переменных попадает в основное решение, помните, что этот процесс был определен случайным образом из-за равенства Cj-Zj исходной таблицы.
Ниже приведен способ достижения другого решения.
Мы видим, что существует альтернативное оптимальное решение.
X 1 = 3 (Cantidad de mesas a producir = 3)
X 2 = 4 (Cantidad de Sillas a Productir = 4)
x 3 = 6 (Cantidad de Camas A Productir = 6)
x 4 = 4 (Cantidad de Biblioteca a ProductiR = 4 40107 = 4 (Cantidad de Bibliotec )
Con una utilidad de: $ 340000
Проблемы минимизации с помощью симплекс-метода
Для решения проблем минимизации существует два типа процедур: применимо к алгоритму, основанному на следующей математической логике: для любой функции f (x) любая точка, которая минимизирует f (x), также максимизирует a – f (x). Следовательно, следующая процедура умножает на отрицательный коэффициент (-1) всю целевую функцию.
Затем алгоритм решается как задача максимизации.