Пространственный четырехугольник рисунок (47 фото) » Рисунки для срисовки и не только
Пространственный четырехугольник
Скачать
Пространственный четырехугольник
Скачать
Пространственный четырехугольник АВСД
Скачать
Диагонали пространственного четырехугольника
Скачать
Пространственный четырехугольник ABCD
Пространственный четырехугольник АВСД
Пространственный четырехугольник
Скачать
Дан пространственный четырехугольник ABCD , M И N
Скачать
Пространственный четырёхугольник рисунок
Скачать
Пространственный четырехугольник
Скачать
Четырехугольник в пространстве
Пространственный четырехугольник ABCD
Скачать
Диагонали пространственного четырехугольника
Скачать
Параллелограмм Вариньона
Скачать
Развитие пространственного воображения
Скачать
Пространственный четырехугольник
Скачать
Пространственный четырёхугольник рисунок
Скачать
Пространственный четырехугольник
Скачать
Пространственный четырехугольн
Скачать
Сечение параллелепипеда пятиугольник
Скачать
Площадь четырехугольника Вариньона
Скачать
Пространственный четырёхугольник рисунок
Скачать
Дано: ABCD пространственный четырехугольник
Скачать
Пространственный четырёхугольник рисунок
Скачать
Четырехугольник фото
Скачать
Дано: ABCD пространственный четырехугольник
Скачать
Середины сторон ромба
Скачать
Четырёхугольник на плоскости
Скачать
Середины сторон равнобедренной трапеции
Скачать
Выпуклый и невыпуклый четырехугольник
Скачать
Выпуклом четырёхугольнике ABCD
Середины сторон произвольного четырехугольника
Скачать
Выпуклые четырехкгольниктк
Пространственный четырехугольник ABCD
Скачать
Пространственный четырехугольник
Пересечение треугольника и четырехугольника
Диагонали пространственного четырехугольника
Скачать
Бимедиана Вариньона
Скачать
Пространственный четырехугольник
Пространственный четырехугольник
Скачать
Параллелограмм Вариньона площадь
Доказательство середины сторон произвольного четырёхугольника
Скачать
Пространственный четырёхугольник рисунок
Скачать
Четырехугольник с равными сторонами
Скачать
Скачать
Скачать
10 класс.
Геометрия. Углы с сонаправленными сторонами. Угол между прямыми. — Углы с сонаправленными сторонами. Угол между прямыми.Комментарии преподавателяУглы с сонаправленными сторонами. Угол между двумя прямыми
Любая прямая, например ОО1 (Рис. 1.), рассекает плоскость на две полуплоскости. Если лучи ОА и О1А1 параллельны и лежат в одной полуплоскости, то они называются сонаправленными.
Лучи О2А2 и ОА не являются сонаправленными (Рис. 1.). Они параллельны, но не лежат в одной полуплоскости.
Рис. 1.
Если стороны двух углов сонаправленны, то такие углы равны.
Доказательство
Пусть нам даны параллельные лучи ОА и О1А1 и параллельные лучи ОВ и О1В1 (Рис. 2.). То есть, мы имеем два угла АОВ и А1О1В1, чьи стороны лежат на сонаправленных лучах. Докажем, что эти углы равны.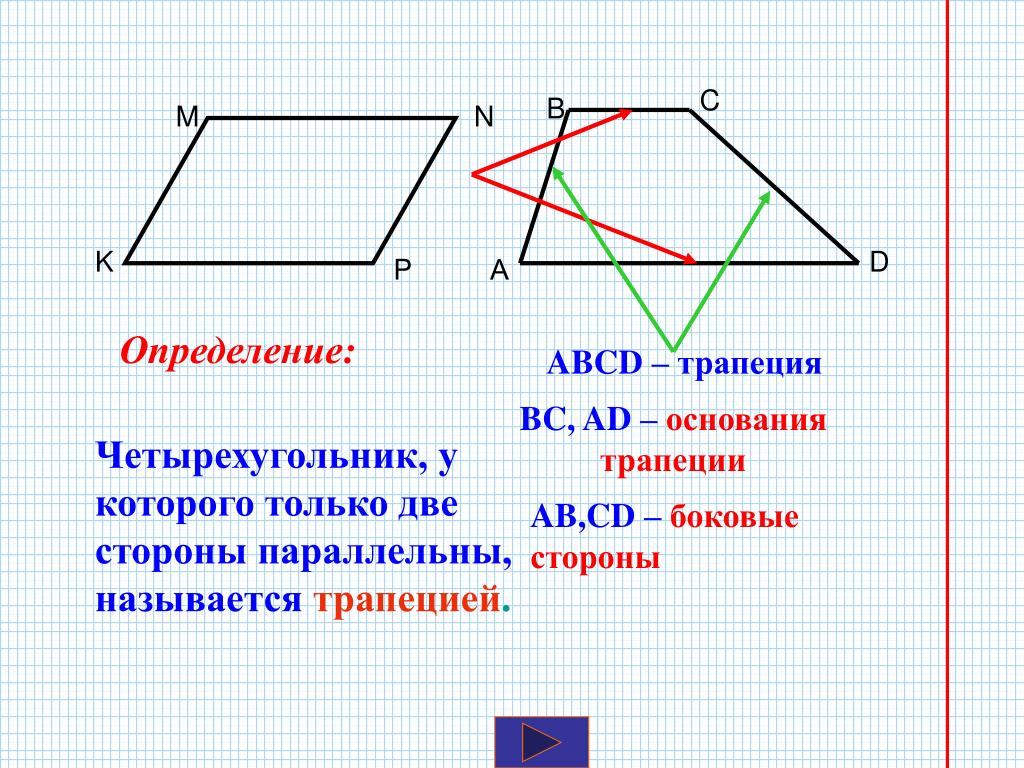
Рис. 2.
На стороне луча ОА и О1А1 выберем точки А и А1 так, чтобы отрезки ОА и О1А1 были равны. Аналогично, точки В и В1 выберем так, чтобы отрезки ОВ и О1В1 были равны.
Рассмотрим четырехугольник А1О1ОА (Рис. 3.). В этом четырехугольники стороны ОА и О1А1 параллельны и равны. По признаку параллелограмма, четырехугольник А1О1ОА является параллелограммом. Так как А1О1ОА – параллелограмм, то стороны ОО1 и АА1 параллельны и равны.
Рассмотрим четырехугольник В1О1ОВ. В этом четырехугольники стороны ОВ и О1В1 параллельны и равны. По признаку параллелограмма, четырехугольник В1О1ОВ является параллелограммом. Так как В1О1ОВ – параллелограмм, то стороны ОО1 и ВВ1 параллельны и равны.
Рис. 3.
И прямая АА1 параллельна прямой ОО1, и прямая ВВ1 параллельна прямой ОО1, значит прямые АА1 и ВВ1 параллельны.
Рассмотрим четырехугольник В1А1АВ. В этом четырехугольники стороны АА1 и ВВ1 параллельны и равны. По признаку параллелограмма, четырехугольник В1А1АВ является параллелограммом. Так как В1А1АВ – параллелограмм, то стороны АВ и А1В1 параллельны и равны.
Рассмотрим треугольники АОВ и А1О1В1. Стороны ОА и О1А1равны по построению. Стороны ОВ и О1В1 также равны по построению. А как мы доказали, и стороны АВ и А1В1 тоже равны. Значит, треугольники АОВ и А1О1В1равны по трем сторонам. В равных треугольниках против равных сторон лежат равные углы. Значит, углы АОВ и А1О1В1 равны, что и требовалось доказать.
1) Пересекающиеся прямые.
Если прямые пересекающиеся, то мы имеем четыре разных угла. Углом между двумя прямыми, называется наименьший из углов между двумя прямыми. Угол между пересекающимися прямыми а и b обозначим α (Рис.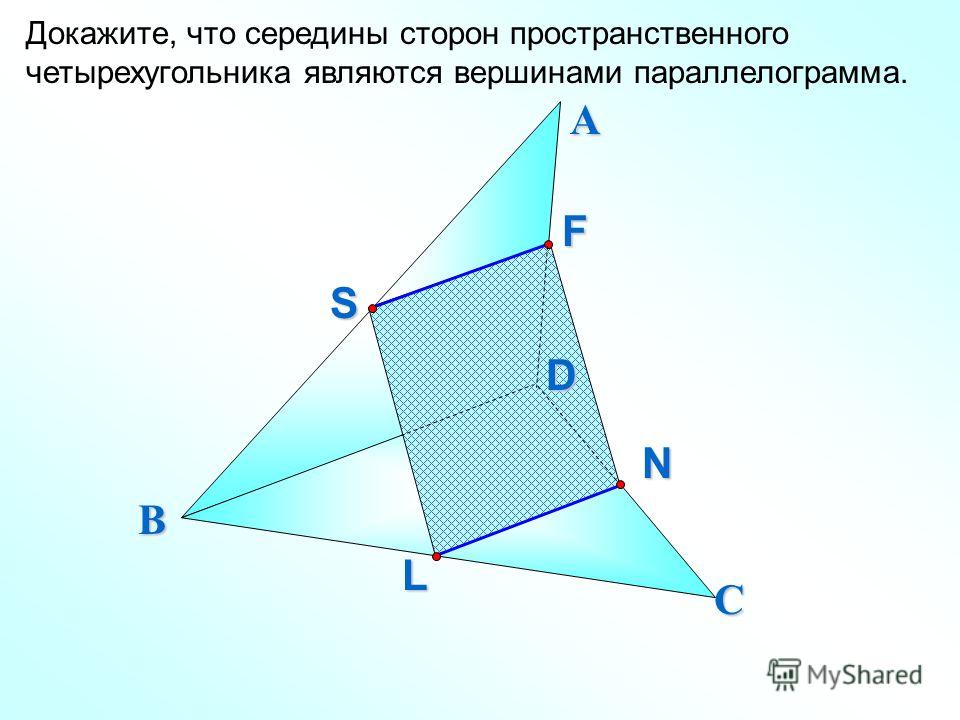
4.). Угол α такой, что .
Рис. 4. Угол между двумя пересекающимимся прямыми
2) Скрещивающиеся прямые
Пусть прямые а и b скрещивающиеся. Выберем произвольную точку О. Через точку О проведем прямую а1, параллельную прямой а, и прямую b1, параллельную прямой b (Рис. 5.). Прямые а1 и b1 пересекаются в точке О. Угол между двумя пересекающимися прямыми а1 и b1 , угол φ, и называется углом между скрещивающимися прямыми.
Рис. 5. Угол между двумя скрещивающимися прямыми
Зависит ли величина угла от выбранной точки О? Выберем точку О1. Через точку О1 проведем прямую а2, параллельную прямой а, и прямую b2, параллельную прямой b (Рис. 6.). Угол между пересекающимися прямымиа2 и b2 обозначим φ1. Тогда углы φ и φ1 — углы с сонаправленными сторонами.
Как мы доказали, такие углы равны между собой. Значит, величина угла между скрещивающимися прямыми не зависит от выбора точки О.
Рис. 6.
Прямые ОВ и СD параллельны, ОА и СD скрещиваются. Найдите угол между прямыми ОА и СD, если:
1) ∠АОВ = 40°.
Выберем точку С. Через нее проходи прямая СD. Проведем СА1 параллельно ОА (Рис. 7.). Тогда угол А1СD – угол между скрещивающимися прямыми ОА и СD. По теореме об углах с сонаправленными сторонами, угол А1СDравен углу АОВ, то есть 40°.
Рис. 7. Найти угол между двумя прямыми
2) ∠АОВ = 135°.
Сделаем то же самое построение (Рис. 8.). Тогда угол между скрещивающимися прямыми ОА и СD равен 45°, так как он наименьший из углов, которые получаются при пересечении прямых СD и СА1.
Рис. 8.
3) ∠АОВ = 90°.
Сделаем то же самое построение (Рис. 9.). Тогда все углы, которые получаются при пересечении прямых СD и СА1 равны 90°. Искомый угол равен 90°.
Рис. 9.
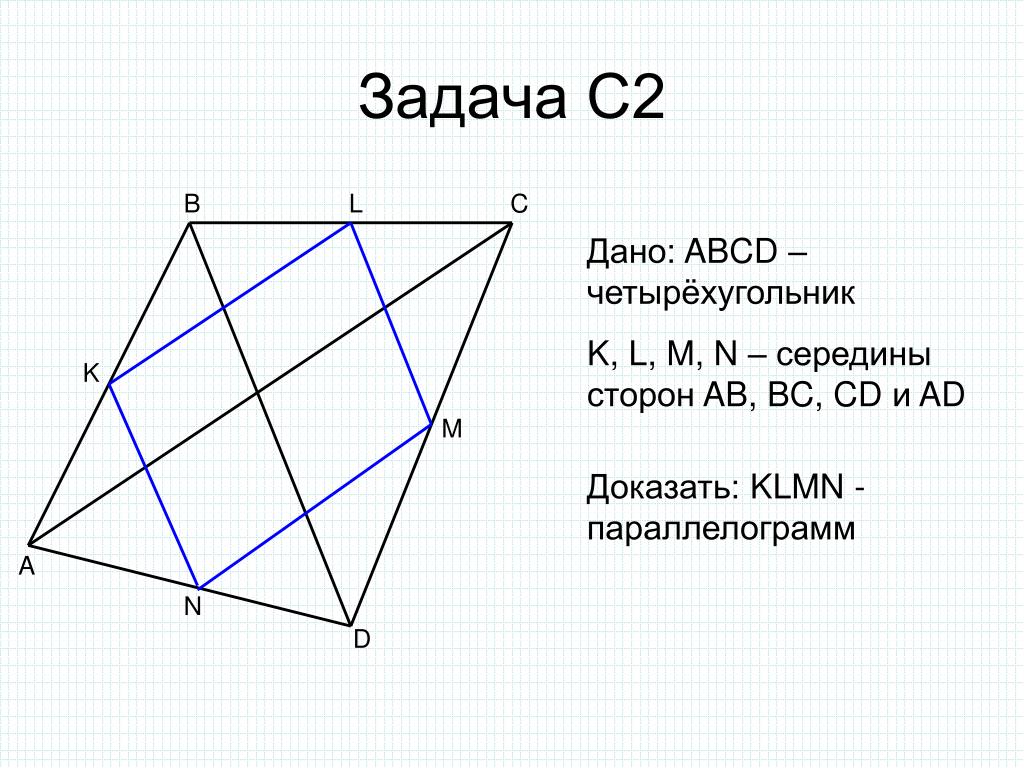
1) Докажите, что середины сторон пространственного четырехугольника являются вершинами параллелограмма.
Рис. 10.
Доказательство
Пусть нам дан пространственный четырехугольник ABCD. M, N, K, L – середины ребер BD, AD, AC, BC соответственно (Рис. 10.). Нужно доказать, что MNKL – параллелограмм.
Рассмотрим треугольник АВD. МN – средняя линия. По свойству средней линии, МN параллельна АВ и равняется ее половине.
Рассмотрим треугольник АВС. LК – средняя линия. По свойству средней линии, LК параллельна АВ и равняется ее половине.
И МN, и LК параллельны АВ.
Значит, МN параллельна LК по теореме о трех параллельных прямых.
Получаем, что в четырехугольнике MNKL – стороны МN и LК параллельны и равны, так как МN и LК равны половине АВ. Значит, по признаку параллелограмма, четырехугольник MNKL – параллелограмм, что и требовалось доказать.
2) Найдите угол между прямыми АВ и СD, если угол МNК = 135°.
Как мы уже доказали, МN параллельна прямой АВ. NК – средняя линия треугольника АСD, по свойству, NК параллельна DС. Значит, через точку N проходят две прямые МN и NК, которые параллельны скрещивающимся прямым АВ и DС соответственно. Значит, угол между прямыми МN и NК является углом между скрещивающимися прямыми АВ и DС. Нам дан тупой угол МNК = 135°. Угол между прямыми МN и NК – наименьший из углов, полученных при пересечении этих прямых, то есть 45°.
Итак, мы рассмотрели углы с сонаправленными сторонами и доказали их равенство. Рассмотрели углы между пересекающимися и скрещивающимися прямыми и решили несколько задач на нахождение угла между двумя прямыми. На следующем уроке мы продолжим решение задач и повторение теории.
ИСТОЧНИК
http://interneturok.ru/ru/school/geometry/10-klass/parallelnost-pryamyh-i-ploskostej/ugly-s-sonapravlennymi-storonami-ugol-mezhdu-pryamymi
https://www.youtube.com/watch?v=3MPNWBMgdfA
http://bigslide.ru/geometriya/12167-skreschivayuschiesya-pryamie-ugli-s-sonapravlennim.html
http://ppt4web.ru/images/288/15495/310/img8.jpg
http://mypresentation.ru/documents/1099e26ba41a0295f98a310078c25edf/img19.jpg
http://festival.1september.ru/articles/604596/presentation/18.jpg
глав-6-геометрия-тест-ответы — Googlesuche
AlleBilderVideosShoppingMapsNewsBücher
suchoptionen
[PDF] Test Review Answers.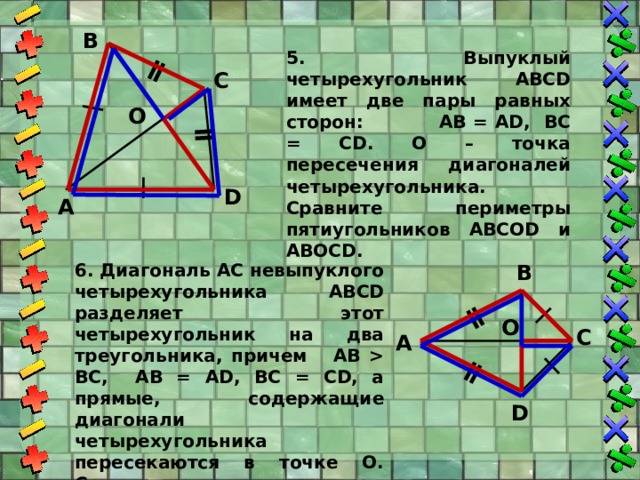
pdf — The Math CAB
Обзор теста главы 6. ДАТА. ПЕРИОД. СЧЕТ. 1. Чему равна сумма внутренних углов восьмиугольного ящика? 1. 1080. 2. Выпуклый пятиугольник имеет внутренние углы …
Изображение
Alle anzeigen
Alle anzeigen
[PDF] Тест по главе 6, форма 1
www.doralacademyprep.org › 2016/12/15 › ответы ch_ 6 обзор
15.12.2016 · Оценка. Глава 6. 49. Геометрия Гленко. 6. ОЦЕНКА. Впишите букву правильного ответа в пропуск справа от каждого вопроса.
[PDF] Тест по главам
portal.mywccc.org › Математика › Геометрия PH › Ресурсы
Тест по главам. Глава. 6. Глава. 6. Нарисуйте график каждого четырехугольника ABCD. Затем определите … 6. 7. Начертите два неконгруэнтных параллелограмма ABCD и EFGH такие, что.
[PDF] Глава 6 Ответы на тест по геометрии Pdf File Free — Nextbike
iframe.nextbike.de › file › lowpoly › FileName=Chapter+6+Geometry.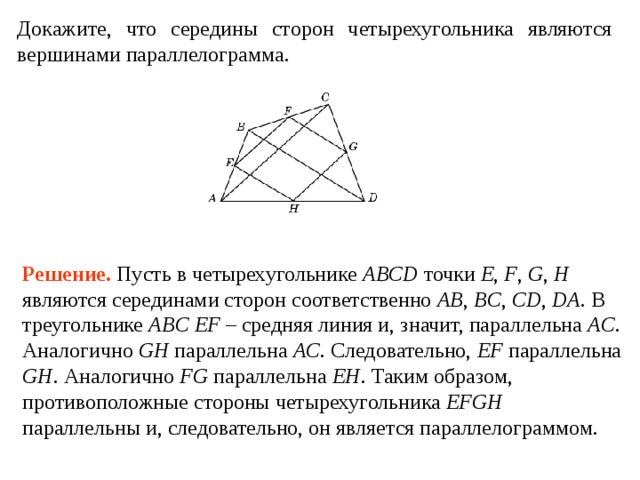
..
Вот почему мы даем сборники электронных книг в этот сайт. Вам будет очень легко увидеть руководство Глава 6 Ответы на тест по геометрии, как вам нравится. Путем поиска …
Тестовые карточки для главы 6 по геометрии — Quizlet
quizlet.com › Математика › Геометрия
Изучайте с помощью Quizlet и запоминайте карточки, содержащие такие термины, как «равноугольный многоугольник», «равносторонний многоугольник», «правильный многоугольник» и другие.
[PDF] Глава 6 Ответы
tarantamath.pbworks.com › file › fetch
Геометрия Глава 6. Ответы. 35. Глава 6 Ответы. Практика 6-1. 1. параллелограмм. 2. прямоугольник. 3. четырехугольник. 4. параллелограмм, четырехугольник.
[PDF] Тест по главе 6, форма 3
school.ckseattle.org › документы › 2019/12 › Ответы на тест 6, форма 3
Glencoe Geometry. Тест по главе 6, форма 3. БАЛЛ ______. 1. Сумма внутренних углов животного… Используйте формулу расстояния, чтобы обосновать свой ответ.