Как рассчитать диаметр исходя из длины окружности. Площадь круга
Одной линейкой здесь не обойтись, необходимо знать специальные формулы. Единственное, что от нас потребуется — это определить диаметр или радиус круга. В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.
Формулы, которые должен знать каждый
Еще в почти 4 000 лет назад, учёные выявили удивительное соотношение: если длину окружности разделить на ее диаметр, то получается одно и то же число, которое равно примерно 3,14. Это значение назвали именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:
Где P означает длину (периметр) окружности,
D — диаметр, П — число «Пи».
Длина окружности круга может также быть посчитана через ее радиус (r), который равен половине длины диаметра.
Как узнать диаметр окружности?
Представляет собой хорду, которая проходит через центр фигуры. При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.
Способ 1: вписываем прямоугольный треугольник в круг
Рассчитать длину окружности будет несложно, если мы найдем ее диаметр. Необходимо начертить в круге где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится.
Способ 2: вписываем любой треугольник
На стороне круга отмечаем три любые точки, соединяем их — получаем треугольник. Важно, чтобы центр окружности лежал в области треугольника, это можно сделать на глаз. Проводим к каждой стороне треугольника медианы, точка их пересечения совпадёт с центром окружности. А когда нам известен центр, можно с помощью линейки легко провести диаметр.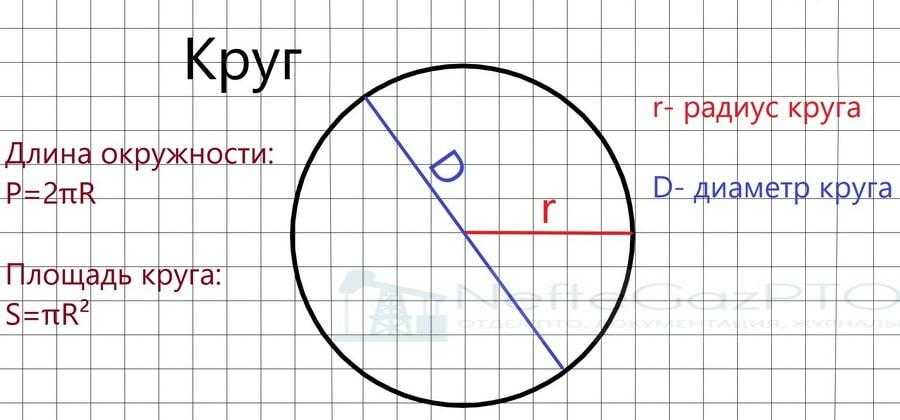
Данный способ очень похож на первый, но может применяться при отсутствии угольника или в тех случаях, когда нет возможности чертить на фигуре, например на тарелке. Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.
Пример задачи
- Ищем диаметр с помощью угольника, линейки и карандаша по способу № 1. Предположим, получилось 5 см.
- Зная диаметр, мы легко можем его вставить в нашу формулу: P = d П = 5*3,14 = 15,7В нашем случае получилось около 15,7. Теперь вы без особых проблем сможете объяснить, как рассчитать длину окружности.
Возьмем циркуль. Установим ножку циркуля с иглой в точку «O
», а ножку циркуля с
карандашом будем вращать вокруг этой точки.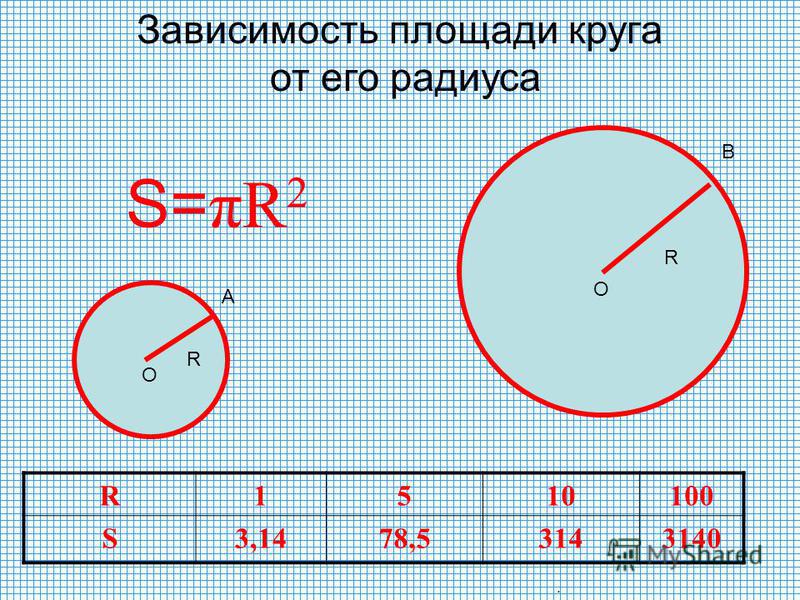 Таким образом, мы получим замкнутую
линию. Такую замкнутую линию называют — окружность .
Таким образом, мы получим замкнутую
линию. Такую замкнутую линию называют — окружность .
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Запомните!
Отношение длины окружности к её диаметру является одинаковым
для всех
окружностей и обозначается греческой буквой π
(«Пи»).
Число «Пи» относится к числам, точное значение которых записать невозможно
ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам
для наших вычислений достаточно использовать значение π
,
округленное до разряда сотых
π
≈ 3,14…
Теперь, зная, что такое число π
, мы
можем записать формулу длины окружности.
Запомните!
Длина окружности — это произведение числа π
и диаметра окружности.
Длина окружности обозначается буквой «С
» (читается как «Це»).
C = π
D
C = 2π
R
, так как D = 2R
Как найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Виленкин 6 класс. Номер 831
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2π R ≈ 2 · 3,14 · 24 ≈ 150,72 см
Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
Виленкин 6 класс. Номер 835
Условие задачи:
Определите диаметр окружности, если её длина равна 56,52 дм. (π ≈ 3,14 ).
Выразим из формулы длины окружности диаметр.
C = π
D
D = С / π
D = 56,52 / 3,14 = 18
дм
Хорда и дуга окружности
На рисунке ниже отметим на окружности две точки «A
» и «B
». Эти точки делят окружность
на две части, каждую из которых называют дугой .
Это синяя дуга «AB
» и черная дуга «AB
».
Точки «A
» и «B
» называют концами дуг .
Эти точки делят окружность
на две части, каждую из которых называют дугой .
Это синяя дуга «AB
» и черная дуга «AB
».
Точки «A
» и «B
» называют концами дуг .
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы , понятия и определения требуются для этого.
Вконтакте
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку . Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
- — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром.
 Её длину будем обозначать латинской буквой l.
Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Диаметр окружности.
Нахождение длины окружности и её площади
Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r . Таким образом, для ответа на вопрос, как найти диаметр круга, зная его радиус, достаточно последний умножить на два .
Формула длины окружности, выраженная через её радиус, имеет вид l = 2*П*r .
Внимание! Латинской буквой П (Пи) обозначается отношение длины окружности к её диаметру, и это есть непериодическая десятичная дробь.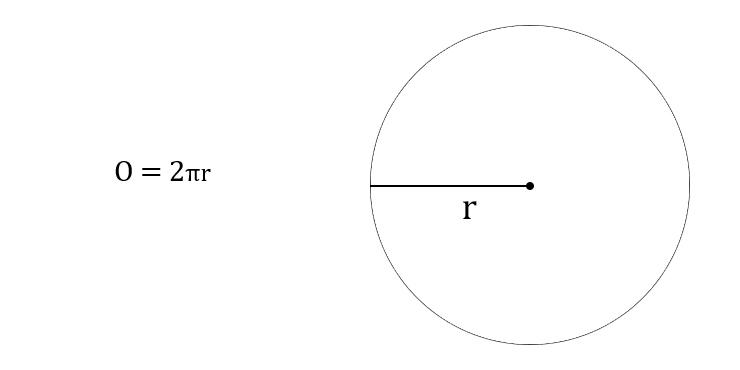 2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Длина окружности
Окружность — замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра. Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Описания фигуры
Кроме достаточно простого описательного определения существуют еще три математических характеристики окружности, которые уже сами по себе содержат ответ на вопрос, как найти длину окружности:
- Состоит из точек A и B и всех других, из которых AB можно увидеть под прямым углом. Диаметр данной фигуры равен длине рассматриваемого отрезка.
- Включает исключительно такие точки X, что отношение AX/BX неизменно и не равно единице. Если это условие не соблюдается, то это не окружность.
- Состоит из точек, для каждой из которых выполняется следующее равенство: сумма квадратов расстояний до двух других — это заданная величина, которая всегда больше половине длины отрезка между ними.

Терминология
Не у всех в школе был хороший учитель математики. Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия. Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Основные формулы
Из определений непосредственно следуют геометрические формулы, которые позволяют рассчитать основные характеристики окружности:
- Длина равна произведению числа π и диаметра. Формулу обычно записывают следующим образом: C = π*D.
- Радиус равен половине диаметра. Его также можно рассчитать, вычислив частное от деления длины окружности на удвоенное число π. Формула выглядит так: R = C/(2* π) = D/2.
- Диаметр равен частному от деления длины окружности на π или удвоенному радиусу.
 Формула является достаточно простой и выглядит так: D = C/π = 2*R.
Формула является достаточно простой и выглядит так: D = C/π = 2*R. - Площадь круга равна произведению числа π и квадрата радиуса. Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Как найти длину окружности по диаметру
Для простоты объяснения обозначим буквами необходимые для расчета характеристики фигуры. Пусть C — это искомая длина, D — ее диаметр, а число π приблизительно равно 3,14. Если у нас есть всего одна известная величина, то задачу можно считать решенной. Зачем это нужно в жизни? Предположим мы решили обнести круглый бассейн забором. Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Длина через радиус
Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из разных стран вовсе не обязательно знать язык друг друга. Предположим, что C — это длина окружности, r — ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство. Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка. Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Примеры задач
Мы уже рассмотрели несколько практических случаев полученных знаний о том, как узнать длину окружности. Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Решение примера
Для начала запишем, что нам дано: C = 26 см, π = 3,14. Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Не так страшен зверь, как его малюют
Вот мы и разобрались с такой непростой на первый взгляд задачей. Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
В процессе выполнения строительных работ в быту или на производстве может появиться необходимость в измерении диаметра трубы, которая уже вмонтирована в систему водоснабжения или канализации. Также знать данный параметр необходимо на стадии проектирования прокладки инженерных коммуникаций.
Отсюда возникает необходимость разобраться с тем, как определить диаметр трубы. Выбор конкретного способа выполнения измерений зависит от размеров объекта и от того, доступно ли расположение трубопровода.
Определение диаметра в бытовых условиях
До того, как замерить диаметр трубы, нужно приготовить следующие инструменты и устройства:
- рулетка или стандартная линейка;
- штангенциркуль;
- фотоаппарат — его задействуют при необходимости.
Если трубопровод доступен для проведения замеров, а торцы труб можно без проблем измерить, тогда достаточно иметь в распоряжении обычную линейку или рулетку. При этом следует учитывать, что используют такой метод, когда к точности предъявляются минимальные требования.
В этом случае выполняют измерение диаметра труб в такой последовательности:
- Подготовленные инструменты прикладывают к месту, где находится самая широкая часть торца изделия.
- Потом отсчитывают количество делений, соответствующих размеру диаметра.
Данный способ позволяет узнавать параметры трубопровода с точностью, составляющую несколько миллиметров.
Для измерения внешнего диаметра труб с небольшим сечением можно задействовать такой инструмент как штангенциркуль:
- Раздвигают его ножки и прикладывают к торцу изделия.

- Затем их нужно сдвинуть так, чтобы они оказались плотно прижатыми к наружной стороне стенок трубы.
- Ориентируясь на шкалу значений приспособления, узнают требуемый параметр.
Этот метод определения диаметра трубы дает довольно точные результаты, до десятых миллиметра.
Когда трубопровод недоступен для обмера и является частью уже функционирующей конструкции водоснабжения или газовой магистрали, поступают следующим образом: штангенциркуль прикладывают к трубе, к ее боковой поверхности. Таким способом обмеряют изделие в тех случаях, если у измерительного приспособления длина ножек превышает половину диаметра трубной продукции.
Нередко в бытовых условиях возникает необходимость узнать, как измерять диаметр трубы, имеющей большое сечение. Существует простой вариант, как это сделать: достаточно знать длину окружности изделия и константу π, равную 3,14.
Сначала при помощи рулетки или куска шнура обмеряют трубу в обхвате. Потом подставляют известные величины в формулу d=l:π, где:
Потом подставляют известные величины в формулу d=l:π, где:
d – определяемый диаметр;
l – длина измеренной окружности.
К примеру, обхват трубы составляет 62,8 сантиметра, тогда d = 62,8:3,14 =20 сантиметров или 200 миллиметров.
Бывают ситуации, когда проложенный трубопровод полностью недоступен. Тогда можно применить метод копирования. Суть его заключается в том, что к трубе прикладывают измерительный инструмент или небольшой по размеру предмет, у которого известны параметры.
К примеру, это может быть коробок спичек, длина которого равна 5 сантиметрам. Потом этот участок трубопровода фотографируют. Последующие вычисления выполняют по фотографии. На снимке измеряют видимую толщину изделия в миллиметрах. Потом нужно перевести все полученные величины в реальные параметры трубы с учетом масштаба произведенной фотосъемки.
Измерение диаметров в производственных условиях
На больших строящихся объектах трубы до начала проведения монтажа в обязательном порядке подвергают входному контролю.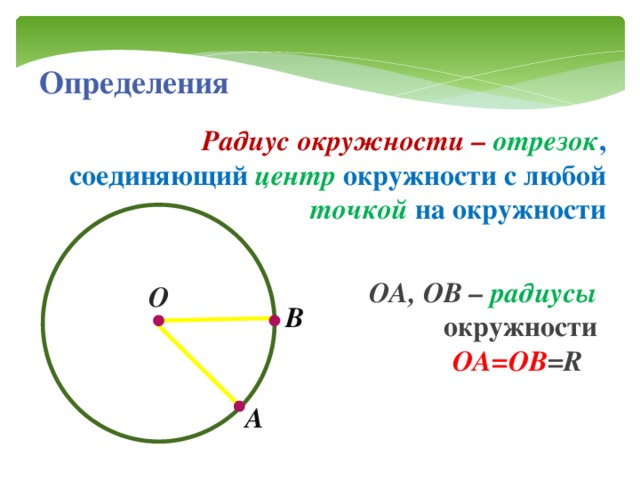 Прежде всего, проверяют сертификаты и маркировку, нанесенную на трубную продукцию.
Прежде всего, проверяют сертификаты и маркировку, нанесенную на трубную продукцию.
Документация должна содержать определенную информацию, касающуюся труб:
- номинальные размеры;
- номер и дата ТУ;
- марка металла или вид пластика;
- номер товарной партии;
- итоги проведенных испытаний;
- хим. анализ выплавки;
- тип термической обработки;
- результаты рентгеновской дефектоскопии.
Кроме этого, на поверхности всех изделий на расстоянии примерно 50 сантиметров от одного из торцов всегда наносят маркировку, содержащую:
- наименование производителя;
- номер плавки;
- номер изделия и его номинальные параметры;
- дату изготовления;
- эквивалент углерода.
Длины труб в производственных условиях определяют мерной проволокой. Также не возникает сложностей с тем, как измерить диаметр трубы рулеткой.
Для изделий первого класса допустимой величиной отклонения в одну или другую сторону от заявленной длины являются 15 миллиметров. Для второго класса –100 миллиметров.
Для второго класса –100 миллиметров.
У труб наружный диаметр сверяют, пользуясь формулой d = l:π-2Δр-0,2 мм, где кроме вышеописанных значений:
Δр – толщина материала рулетки;
0,2 миллиметра– припуск на прилегание инструмента к поверхности.
Допускается отклонение величины внешнего диаметра от заявленной производителем:
- для продукции с сечением не более 200 миллиметров–1,5 миллиметра;
- для больших труб – 0,7%.
В последнем случае для проверки трубной продукции пользуются ультразвуковыми измерительными приборами. Для определения толщины стенок задействуют штангенциркули, у которых деление на шкале соответствует 0,01 миллиметра. Минусовой допуск не должен превышать 5% номинальной толщины. При этом кривизна не может быть более 1,5 миллиметра на 1 погонный метр.
Из вышеописанной информации ясно, что несложно разобраться с тем, как определить диаметр трубы по длине окружности или при помощи несложных измерительных инструментов.
как найти длину окружности зная диаметр
Окружность — замкнутая кривая, все точки которой находятся на одинаковом расстоянии от центра. Эта фигура является плоской. Поэтому решение задачи, вопрос которой состоит в том, как найти длину окружности, является достаточно простым. Все имеющиеся способы, мы рассмотрим в сегодняшней статье.
Описания фигуры
Кроме достаточно простого описательного определения существуют еще три математических характеристики окружности, которые уже сами по себе содержат ответ на вопрос, как найти длину окружности:
- Состоит из точек A и B и всех других, из которых AB можно увидеть под прямым углом. Диаметр данной фигуры равен длине рассматриваемого отрезка.
- Включает исключительно такие точки X, что отношение AX/BX неизменно и не равно единице. Если это условие не соблюдается, то это не окружность.
- Состоит из точек, для каждой из которых выполняется следующее равенство: сумма квадратов расстояний до двух других — это заданная величина, которая всегда больше половине длины отрезка между ними.

Терминология
Не у всех в школе был хороший учитель математики. Поэтому ответ на вопрос, как найти длину окружности, осложняется еще и тем, что не все знают основные геометрические понятия. Радиус — отрезок, который соединяет центр фигуры с точкой на кривой. Особым случаем в тригонометрии является единичная окружность. Хорда — отрезок, который соединяет две точки кривой. Например, под это определение подпадает уже рассмотренный AB. Диаметр — это хорда, проходящая через центр. Число π равно длине единичной полуокружности.
Основные формулы
Из определений непосредственно следуют геометрические формулы, которые позволяют рассчитать основные характеристики окружности:
- Длина равна произведению числа π и диаметра. Формулу обычно записывают следующим образом: C = π*D.
- Радиус равен половине диаметра. Его также можно рассчитать, вычислив частное от деления длины окружности на удвоенное число π. Формула выглядит так: R = C/(2* π) = D/2.
- Диаметр равен частному от деления длины окружности на π или удвоенному радиусу.
 Формула является достаточно простой и выглядит так: D = C/π = 2*R.
Формула является достаточно простой и выглядит так: D = C/π = 2*R. - Площадь круга равна произведению числа π и квадрата радиуса. Аналогично в этой формуле можно использовать диаметр. В этом случае площадь будет равна частному от деления произведения числа π и квадрата диаметра на четыре. Формулу можно записать следующим образом: S = π*R 2 = π*D 2 /4.
Как найти длину окружности по диаметру
Для простоты объяснения обозначим буквами необходимые для расчета характеристики фигуры. Пусть C — это искомая длина, D — ее диаметр, а число π приблизительно равно 3,14. Если у нас есть всего одна известная величина, то задачу можно считать решенной. Зачем это нужно в жизни? Предположим мы решили обнести круглый бассейн забором. Как вычислить необходимое количество столбиков? И тут на помощь приходит умение, как вычислить длину окружности. Формула выглядит следующим образом: C = π D. В нашем примере диаметр определяется на основе радиуса бассейна и необходимого расстояния до забора. Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Например, предположим, что наш домашний искусственный водоем составляет 20 метров в ширину, а столбики мы собираемся ставить на десятиметровом расстоянии от него. Диаметр получившейся окружности равен 20 + 10*2 = 40 м. Длина — 3,14*40 = 125,6 метров. Нам понадобятся 25 столбиков, если промежуток между ними будет около 5 м.
Длина через радиус
Как всегда, начнем с присвоения характеристикам окружности букв. На самом деле они являются универсальными, поэтому математикам из разных стран вовсе не обязательно знать язык друг друга. Предположим, что C — это длина окружности, r — ее радиус, а π приблизительно равно 3,14. Формула выглядит в этом случае следующим образом: C = 2*π*r. Очевидно, что это абсолютно правильное равенство. Как мы уже разобрались диаметр окружности равен ее удвоенному радиусу, поэтому эта формула так и выглядит. В жизни этот способ тоже может часто пригодиться. Например, мы печем торт в специальной раздвижной форме. Чтобы он не испачкался, нам нужна декоративная обертка.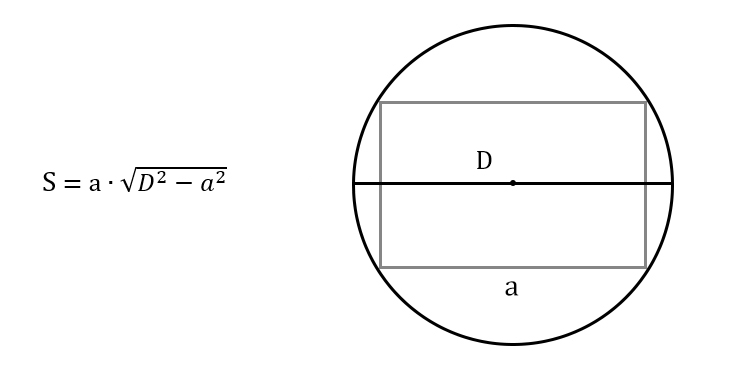 Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Но как вырезать круг нужного размера. Здесь на помощь и приходит математика. Те, кто знают, как узнать длину окружности, сразу скажут, что нужно умножить число π на удвоенный радиус формы. Если ее радиус равен 25 см, то длина будет составлять 157 сантиметров.
Примеры задач
Мы уже рассмотрели несколько практических случаев полученных знаний о том, как узнать длину окружности. Но зачастую нас заботят не они, а реальные математические задачи, которые содержатся в учебнике. Ведь за них учитель выставляет баллы! Поэтому давайте рассмотрим задачу повышенной сложности. Предположим, что длина окружности составляет 26 см. Как найти радиус такой фигуры?
Решение примера
Для начала запишем, что нам дано: C = 26 см, π = 3,14. Также вспомним формулу: C = 2* π*R. Из нее можно извлечь радиус окружности. Таким образом, R= C/2/π. Теперь приступим к непосредственному расчету. Сначала делим длину на два. Получаем 13. Теперь нужно разделить на значение числа π: 13/3,14 = 4,14 см. Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Важно не забыть записать ответ правильно, то есть с единицами измерения, иначе теряется весь практический смысл подобных задач. К тому же за подобную невнимательность можно получить оценку на один балл ниже. И как бы досадно ни было, придется мириться с таким положением вещей.
Не так страшен зверь, как его малюют
Вот мы и разобрались с такой непростой на первый взгляд задачей. Как оказалось, нужно просто понимать значение терминов и запомнить несколько легких формул. Математика — это не так страшно, нужно только приложить немного усилий. Так что геометрия ждет вас!
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы , понятия и определения требуются для этого.
Вконтакте
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку .
 Он обозначается латинской буквой r.
Он обозначается латинской буквой r. - Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
- — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Диаметр окружности.
Нахождение длины окружности и её площади
Если нам дан радиус окружности, то диаметр окружности описывает формула d = 2*r . 2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Длина окружности
Если в задаче известны такие величины, как длина окружности, ее радиус или площадь круга, который ограничен данной окружностью, то вычисление диаметра будет несложным. Существует несколько способов, которыми можно высчитать диаметр окружности. Они довольно просты и вовсе не вызывают никаких трудностей, как многим кажется на первый взгляд.
Как найти диаметр окружности – 1 способ
Когда дано значение радиуса окружности, то можно считать задачу наполовину решенной, поскольку радиус представляет собой расстояние от точки, которая лежит в любом месте на окружности, до центра этой самой окружности. Все, что нужно сделать для нахождения диаметра в этом случае, это умножить данную величину радиуса на 2. Такой способ вычисления объясняется тем, что радиус является половиной диаметра. Поэтому, если известно, чему равен радиус, то и значение половины искомой величины диаметра уже фактически найдено.
Как найти диаметр окружности – 2 способ
Если в задаче дано только значение длины окружности, то для нахождения величины диаметра нужно просто поделить ее на число, известное как π, приблизительное значение которого равно 3,14. То есть, если значение длины равняется 31,4, то разделив его на 3,14, получаем значение диаметра, которое равняется 10.
То есть, если значение длины равняется 31,4, то разделив его на 3,14, получаем значение диаметра, которое равняется 10.
Как найти диаметр окружности – 3 способ
Если в исходных данных приведено значение площади круга, то диаметр найти тоже просто. Все, что нужно сделать, это извлечь квадратный корень из данной величины и поделить полученный результат на число π. Это значит, что если значение площади равно 64, то при извлечении корня остается число 8. Если разделить полученную 8 на 3,14, то получим величину диаметра, которая равна примерно 2,5.
Как найти диаметр окружности – 4 способ
Внутри окружности нужно начертить при помощи линейки или угольника прямую горизонтальную линию от одной точки до другой. Пересечения этой прямой с линией окружностью пометьте буквами, например, А и В. Не имеет никакого значения, в какой из частей круга будет расположена эта прямая.
После этого нужно начертить еще две окружности. Но таким образом, чтобы точки А и В стали их центрами. Вновь образованные фигуры будут пересекаться в двух точках. Через них нужно провести еще одну прямую линию. После этого измеряем ее длину с помощью линейки. Значение измерения и будет равно длине диаметра, потому что последняя начерченная линия и есть сам диаметр.
Вновь образованные фигуры будут пересекаться в двух точках. Через них нужно провести еще одну прямую линию. После этого измеряем ее длину с помощью линейки. Значение измерения и будет равно длине диаметра, потому что последняя начерченная линия и есть сам диаметр.
Интересно, что еще очень далеко в прошлом для плетения корзин определенного размера прутики брали примерно в 3 раза длиннее. Ученые объяснили и доказали экспериментальным путем, что если длину любой окружности разделить на диаметр, то в результате получается почти одно и то же число.
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
Одной линейкой здесь не обойтись, необходимо знать специальные формулы. Единственное, что от нас потребуется — это определить диаметр или радиус круга. В некоторых задачах эти величины обозначены. Но что делать, если у нас нет ничего, кроме рисунка? Не беда. Диаметр и радиус можно вычислить с помощью обычной линейки. Теперь приступим к самому основному.
Формулы, которые должен знать каждый
Еще в почти 4 000 лет назад, учёные выявили удивительное соотношение: если длину окружности разделить на ее диаметр, то получается одно и то же число, которое равно примерно 3,14. Это значение назвали именно с этой буквы в древнегреческом языке начиналось слово «периметр» и «окружность». На основании того открытия, которое совершили древние ученые, можно рассчитать длину любой окружности:
Где P означает длину (периметр) окружности,
D — диаметр, П — число «Пи».
Длина окружности круга может также быть посчитана через ее радиус (r), который равен половине длины диаметра. Вот и вторая формула, которую нужно запомнить:
Вот и вторая формула, которую нужно запомнить:
Как узнать диаметр окружности?
Представляет собой хорду, которая проходит через центр фигуры. При этом она соединяет две наиболее удалённые точки в круге. Исходя из этого, можно самостоятельно прочертить диаметр (радиус) и измерить его длину с помощью линейки.
Способ 1: вписываем прямоугольный треугольник в круг
Рассчитать длину окружности будет несложно, если мы найдем ее диаметр. Необходимо начертить в круге где гипотенуза будет равна диаметру окружности. Для этого необходимо иметь под рукой линейку и угольник, иначе ничего не получится.
Способ 2: вписываем любой треугольник
На стороне круга отмечаем три любые точки, соединяем их — получаем треугольник. Важно, чтобы центр окружности лежал в области треугольника, это можно сделать на глаз. Проводим к каждой стороне треугольника медианы, точка их пересечения совпадёт с центром окружности. А когда нам известен центр, можно с помощью линейки легко провести диаметр.
Данный способ очень похож на первый, но может применяться при отсутствии угольника или в тех случаях, когда нет возможности чертить на фигуре, например на тарелке. Необходимо взять лист бумаги с прямыми углами. Прикладываем лист к кругу так, чтобы одна вершина его угла соприкасалась с краем круга. Далее отмечаем точками места, где стороны бумаги пересекаются с линией окружности. Соединяем эти точки с помощью карандаша и линейки. Если под рукой ничего нет, просто согните бумагу. Эта линия и будет равна длине диаметра.
Пример задачи
- Ищем диаметр с помощью угольника, линейки и карандаша по способу № 1. Предположим, получилось 5 см.
- Зная диаметр, мы легко можем его вставить в нашу формулу: P = d П = 5*3,14 = 15,7В нашем случае получилось около 15,7. Теперь вы без особых проблем сможете объяснить, как рассчитать длину окружности.
Чему равен радиус. Как найти радиус окружности. Вписанная и описанная окружность. Как найти радиус описанной окружности
Зачастую, когда школьник сдает выпускные экзамены в школе либо вступительные в какой-либо ВУЗ, ему необходимы определенные знания в области геометрии. Причем, задания бывают не такие уж сложные, просто нужно помнить базовые формулы, чтобы применить их в решении. Задачи, в которых необходимо найти радиус окружности, не являются исключением. В принципе, они достаточно просты в решении. В данной статье мы расскажем вам, как найти радиус окружности разными способами.
Причем, задания бывают не такие уж сложные, просто нужно помнить базовые формулы, чтобы применить их в решении. Задачи, в которых необходимо найти радиус окружности, не являются исключением. В принципе, они достаточно просты в решении. В данной статье мы расскажем вам, как найти радиус окружности разными способами.
Находим радиус окружности, исходя из формул
Когда вы получаете задание на контрольной или на экзамене, в котором надо найти радиус окружности, в первую очередь необходимо проанализировать имеющиеся данные. Потому что именно от них будет зависеть ход решения в целом. Так, например, найти рассматриваемую величину можно, используя такие параметры: длину окружности, ее площадь, диаметр и др. Мы рассмотрим самые простые и часто встречающиеся способы решения задач, в которых радиус окружности является неизвестным.
Все мы знаем, что радиусом окружности является длина от ее центра до какой-либо точки,которая расположена на самой окружности. В связи с этим, решения могут быть следующими:
- Когда вам в исходных данных задачи дан диаметр окружности, то решение здесь будет проще простого.
 Ведь нам известно, что диаметром является отрезок, который соединяет несколько точек на окружности, проходя при этом через ее центр. Из этого следует, что диаметр – это 2 радиуса. Тогда радиус мы находим по формуле: r=D/2, где r – это радиус окружности, а D, соответственно, ее диаметр. Например, диаметр по условию равен 32 см, тогда радиус мы вычисляем так: 32/2=16 см.
Ведь нам известно, что диаметром является отрезок, который соединяет несколько точек на окружности, проходя при этом через ее центр. Из этого следует, что диаметр – это 2 радиуса. Тогда радиус мы находим по формуле: r=D/2, где r – это радиус окружности, а D, соответственно, ее диаметр. Например, диаметр по условию равен 32 см, тогда радиус мы вычисляем так: 32/2=16 см. - Переходим к следующему способу решения. Допустим, вам в условии дана длина окружности. Выражаясь математическим языком, это так называемый периметр. Мы прекрасно знаем, что есть специальная формула нахождения длины окружности: P=2πr. Отсюда, мы можем вывести формулу радиуса: r=P/2π. Теперь рассмотрим это на примере. Допустим, по условию задачи вам дана длина окружности, равная 31,4 см, а π в математике – величина постоянная и всегда равна 3,14; тогда радиус находим следующим образом: 31,4/2*3,14=5 см.
- Теперь рассмотрим, как найти радиус окружности, если дана ее площадь. Формула площади окружности имеет такой вид: S=πr2.
 Отсюда находим формулу радиуса: r=√(S/π). Опять же рассмотрим все в цифровом исчислении. Пусть вам дана в условии задачи площадь, к примеру – 28,26 см2. Подставляем данные в выведенную нами формулу и получаем: √28,26/3,14=3 см.
Отсюда находим формулу радиуса: r=√(S/π). Опять же рассмотрим все в цифровом исчислении. Пусть вам дана в условии задачи площадь, к примеру – 28,26 см2. Подставляем данные в выведенную нами формулу и получаем: √28,26/3,14=3 см.
Теперь вам не составит труда решить любую задачу с нахождением радиуса окружности. Главное – четко проанализировать исходные данные, а потом применить подходящую формулу, и можете считать себя великим математиком.
Данный урок посвящён изучению окружности и круга. Также учитель научит отличать замкнутые и незамкнутые линии. Вы познакомитесь с основными свойствами окружности: центром, радиусом и диаметром. Выучите их определения. Научитесь определять радиус, если известен диаметр, и наоборот.
Если заполнить пространство внутри окружности, например начертить окружность с помощью циркуля на бумаге или картоне и вырезать, то получим круг (рис. 10).
Рис. 10. Круг
Круг — это часть плоскости, ограниченная окружностью.
Условие: Витя Верхоглядкин начертил в своей окружности (рис. 11) 11 диаметров. А когда пересчитал радиусы, получил 21. Правильно ли он сосчитал?
11) 11 диаметров. А когда пересчитал радиусы, получил 21. Правильно ли он сосчитал?
Рис. 11. Иллюстрация к задаче
Решение: радиусов должно быть в два раза больше, чем диаметров, поэтому:
Витя сосчитал неправильно.
Список литературы
- Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] — 2-е изд. — М.: Просвещение, 2012. — 112 с.: ил. — (Школа России).
- Рудницкая В.Н., Юдачёва Т.В. Математика, 3 класс. — М.: ВЕНТАНА-ГРАФ.
- Петерсон Л.Г. Математика, 3 класс. — М.: Ювента.
- Mypresentation.ru ().
- Sernam.ru ().
- School-assistant.ru ().
Домашнее задание
1. Математика. 3 класс. Учеб. для общеобразоват. учреждений с прил. на электрон. носителе. В 2 ч. Ч. 1 / [М.И. Моро, М.А. Бантова, Г.В. Бельтюкова и др.] — 2-е изд. — М.: Просвещение, 2012., ст. 94 № 1, ст. 95 № 3.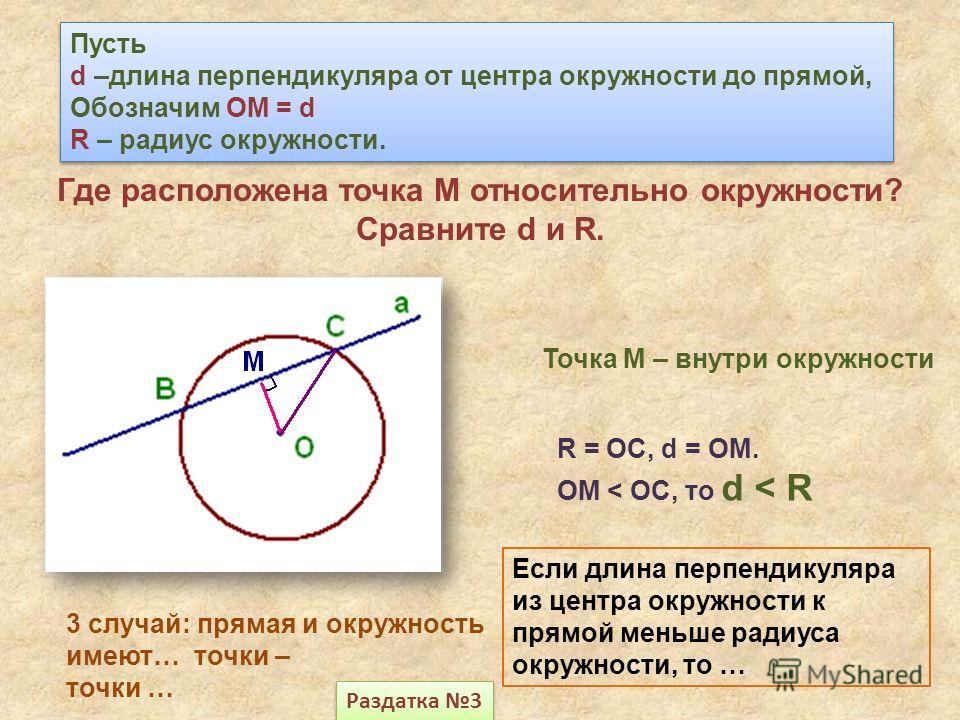
2. Разгадайте загадку.
Мы живём с братишкой дружно,
Нам так весело вдвоём,
Мы на лист поставим кружку (рис. 12),
Обведём карандашом.
Получилось то, что нужно —
Называется …
3. Необходимо определить диаметр окружности, если известно, что радиус равен 5 м.
4. * С помощью циркуля начертите две окружности с радиусами: а) 2 см и 5 см; б) 10 мм и 15 мм.
Окружность — геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки.
Данная точка (O) называется центром окружности .
Радиус окружности — это отрезок, соединяющий центр с какой-либо точкой окружности. Все радиусы имеют одну и ту же длину (по определению).
Хорда — отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром . Центр окружности является серединой любого диаметра.
Любые две точки окружности делят ее на две части. Каждая из этих частей называется дугой окружности . Дуга называется полуокружностью , если отрезок, соединяющий её концы, является диаметром.
Каждая из этих частей называется дугой окружности . Дуга называется полуокружностью , если отрезок, соединяющий её концы, является диаметром.
Длина единичной полуокружности обозначается через π .
Сумма градусных мер двух дуг окружности с общими концами равна 360º .
Часть плоскости, ограниченная окружностью, называется кругом .
Круговой сектор — часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Дуга, которая ограничивает сектор, называется дугой сектора .
Две окружности, имеющие общий центр, называются концентрическими .
Две окружности, пересекающиеся под прямым углом, называются ортогональными .
Взаимное расположение прямой и окружности
- Если расстояние от центра окружности до прямой меньше радиуса окружности (d), то прямая и окружность имеют две общие точки. В этом случае прямая называется секущей по отношению к окружности.
- Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют только одну общую точку.
 Такая прямая называется касательной к окружности , а их общая точка называется точкой касания прямой и окружности .
Такая прямая называется касательной к окружности , а их общая точка называется точкой касания прямой и окружности . - Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек .
Центральные и вписанные углы
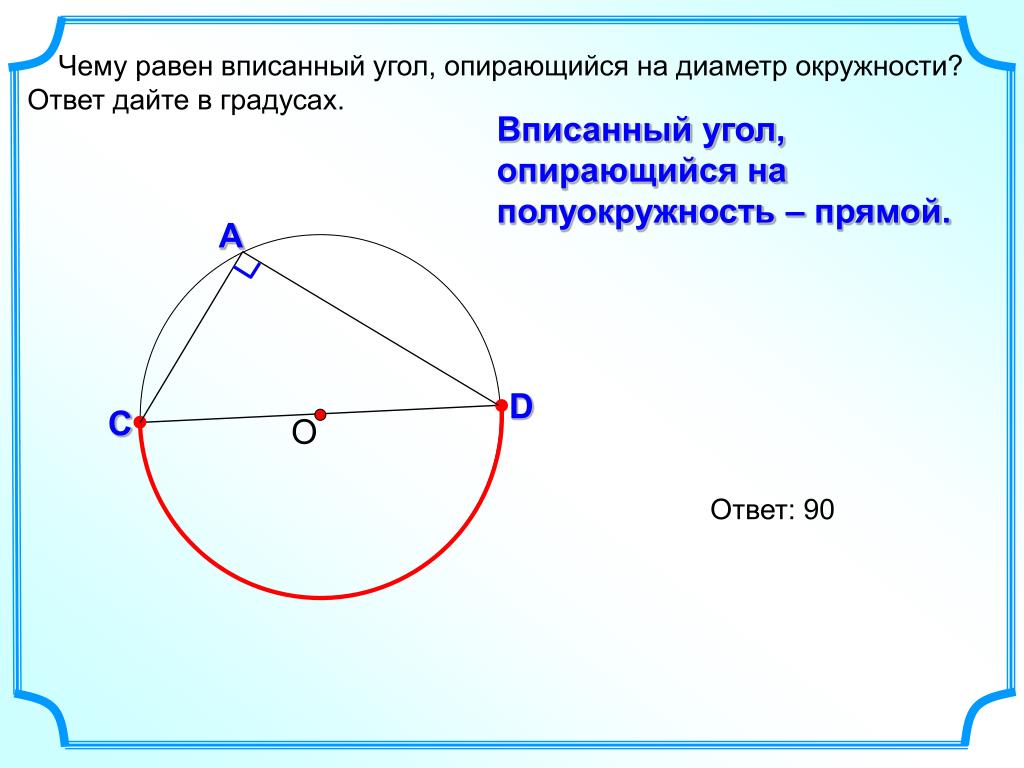
Центральный угол — это угол с вершиной в центре окружности.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают окружность.
Вписанный угол измеряется половиной дуги, на которую он опирается.
- Следствие 1.
Вписанные углы, опирающиеся на одну и ту же дугу, равны. - Следствие 2.
Вписанный угол, опирающийся на полуокружность — прямой.
Если две хорды окружности пересекаются, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
Основные формулы
- Длина окружности:
C = 2∙π∙R
- Длина дуги окружности:
R = С/(2∙π) = D/2
- Диаметр:
D = C/π = 2∙R
- Длина дуги окружности:
l = (π∙R) / 180∙α ,
где α — градусная мера длины дуги окружности)
- Площадь круга:
S = π∙R 2
- Площадь кругового сектора:
S = ((π∙R 2) / 360)∙α
Уравнение окружности
- В прямоугольной системе координат уравнение окружности радиуса r с центром в точке C (x о;y о) имеет вид:
(x — x о) 2 + (y — y о) 2 = r 2
- Уравнение окружности радиуса r с центром в начале координат имеет вид:
x 2 + y 2 = r 2
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы , понятия и определения требуются для этого.
Вконтакте
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку . Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
- — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Диаметр окружности. 2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Длина окружности
Как найти радиус окружности? Этот вопрос всегда актуален для школьников, изучающих планиметрию. Ниже мы рассмотрим несколько примеров того, как можно справиться с поставленной задачей.
В зависимости от условия задачи радиус окружности вы можете найти так.
Формула 1: R = Л / 2π, где Л — это а π — константа, равная 3,141…
Формула 2: R = √(S / π), где S — это величина площади круга.
Формула 1: R = В/2, где В — гипотенуза.
Формула 2: R = М*В, где В — гипотенуза, а М — медиана, проведенная к ней.
Как найти радиус окружности, если она описана вокруг правильного многоугольника
Формула: R = А / (2 * sin (360/(2*n))), где А — длина одной из сторон фигуры, а n — количество сторон в данной геометрической фигуре.
Как найти радиус вписанной окружности
Вписанной окружность называется тогда, когда она касается всех сторон многоугольника. Рассмотрим несколько примеров.
Формула 1: R = S / (Р/2), где — S и Р — площадь и периметр фигуры соответственно.
Формула 2: R = (Р/2 — А) * tg (а/2), где Р — периметр, А — длина одной из сторон, а — противолежащий этой стороне угол.
Как найти радиус окружности, если она вписана в прямоугольный треугольник
Формула 1:
Радиус окружности, которая вписана в ромб
Окружность можно вписать в любой ромб, как равносторонний, так и неравносторонний.
Формула 1: R = 2 * Н, где Н — это высота геометрической фигуры.
Формула 2: R = S / (А*2), где S — это а А — длина его стороны.
Формула 3: R = √((S * sin А)/4), где S — это площадь ромба, а sin А — синус острого угла данной геометрической фигуры.
Формула 4: R = В*Г/(√(В² + Г²), где В и Г — это длины диагоналей геометрической фигуры.
Формула 5: R = В*sin (А/2), где В — диагональ ромба, а А — это угол в вершинах, соединяющих диагональ.
Радиус окружности, которая вписана в треугольник
В том случае, если в условии задачи вам даны длины всех сторон фигуры, то сначала высчитайте (П), а затем полупериметр (п):
П = А+Б+В, где А, Б, В — длин сторон геометрической фигуры.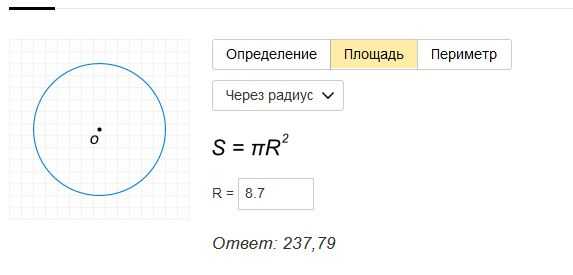
Формула 1: R = √((п-А)*(п-Б)*(п-В)/п).
А если, зная все те же три стороны, вам дана еще и то можете рассчитать искомый радиус следующим образом.
Формула 2: R = S * 2(А + Б + В)
Формула 3: R = S/п = S / (А+Б+В)/2), где — п — это полупериметр геометрической фигуры.
Формула 4: R = (п — А) * tg (А/2), где п — это полупериметр треугольника, А — одна из его сторон, а tg (А/2) — тангенс половины противолежащего этой стороне угла.
А ниже приведенная формула поможет отыскать радиус той окружности, которая вписана в
Формула 5: R =А * √3/6.
Радиус окружности, которая вписана в прямоугольный треугольник
Если в задаче даны длины катетов, а также гипотенуза, то радиус вписанной окружности узнается так.
Формула 1: R = (А+Б-С)/2, где А, Б — катеты, С — гипотенуза.
В том случае, если вам даны только два катета, самое время вспомнить теорему Пифагора, чтобы гипотенузу найти и воспользоваться вышеприведенной формулой.
С = √(А²+Б²).
Радиус окружности, которая вписана в квадрат
Окружность, которая вписана в квадрат, делит все его 4 стороны ровно пополам в точках касания.
Формула 1: R = А/2, где А — длина стороны квадрата.
Формула 2: R = S / (Р/2), где S и Р — площадь и периметр квадрата соответственно.
Как найти периметр окружности зная диаметр. Как найти и чему будет равна длина окружности. Основные формулы для вычислений
Часто звучит, как часть плоскости, которая ограничена окружностью. Окружность круга является плоской замкнутой кривой. Все точки, расположенные на кривой, удалены от центра круга на одинаковое расстояние. В круге его длина и периметр одинаковы. Соотношение длины любой окружности и ее диаметра постоянное и обозначается числом π = 3,1415 .
Определение периметра круга
Периметр круга радиуса r равен удвоенному произведению радиуса r на число π(~3.1415)
Формула периметра круга
Периметр круга радиуса \(r\) :
\[ \LARGE{P} = 2 \cdot \pi \cdot r \]
\[ \LARGE{P} = \pi \cdot d \]
\(P \) – периметр (длина окружности).
\(r \) – радиус.
\(d \)
– диаметр. 0}{n}}=\frac{2τ}{2τ»} \)
0}{n}}=\frac{2τ}{2τ»} \)
Получаем, что отношение \(\frac{ρ}{ρ»}=\frac{2τ}{2τ»} \) будет верным независимо от значения числа сторон вписанных правильных многоугольников. То есть
\(\lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{2τ}{2τ»} \)
С другой стороны, если бесконечно увеличивать число сторон вписанных правильных многоугольников (то есть \(n→∞ \) ), будем получать равенство:
\(lim_{n\to\infty}(\frac{ρ}{ρ»})=\frac{C}{C»} \)
Из последних двух равенств получим, что
\(\frac{C}{C»}=\frac{2τ}{2τ»} \)
\(\frac{C}{2τ}=\frac{C»}{2τ»} \)
Видим, что отношение длины окружности к его удвоенному радиусу всегда одно и тоже число, независимо от выбора окружности и ее параметров, то есть
\(\frac{C}{2τ}=const \)
Эту постоянную принять называть числом «пи» и обозначать \(π \) . Приближенно, это число будет равняться \(3,14 \) (точного значения этого числа нет, так как оно является иррациональным числом). Таким образом
\(\frac{C}{2τ}=π \)
Окончательно, получим, что длина окружности (периметр круга) определяется формулой
\(C=2πτ \)
В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Калькулятор круга — это сервис, специально разработанный для расчета геометрических размеров фигур онлайн. Благодаря данному сервису Вы без проблем сможете определить любой параметр фигуры, в основе которой лежит круг. Например: Вы знаете объем шара, а необходимо получить его площадь. Нет ничего проще! Выберите соответствующий параметр, введите числовое значение и нажмите кнопку рассчитать. Сервис не только выдает результаты вычислений, но и предоставляет формулы, по которым они были сделаны. При помощи нашего сервиса вы без труда рассчитаете радиус, диаметр, длину окружности (периметр круга), площадь круга и шара, объем шара.
Вычислить радиус
Задача на вычисление значения радиуса – одна из самых распространенных. Причина тому достаточно проста, ведь зная этот параметр, вы без особого труда сможете определить значение любого другого параметра круга или шара. Наш сайт построен именно на такой схеме. Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Вне зависимости от того, какой вы выбрали исходный параметр, первым делом вычисляется значение радиуса и на его основе строятся все последующие вычисления. Для большей точности вычислений, сайт использует число Пи с округлением до 10-го знака после запятой.
Рассчитать диаметр
Расчет диаметра – самый простой вид расчета из тех, что умеет выполнять наш калькулятор. Получить значение диаметра совсем нетрудно и вручную, для этого совсем не надо прибегать к помощи интернета. Диаметр равен значению радиуса умноженному на 2. Диаметр – важнейший параметр круга, который чрезвычайно часто используется в повседневной жизни. Уметь его правильно рассчитать и использовать должен абсолютно каждый. Воспользовавшись возможностями нашего сайта, вы вычислите диаметр с большой точностью за доли секунды.
Узнать длину окружности
Вы даже не представляете, как много вокруг нас круглых объектов и какую важную роль они играют в нашей жизни. Умение рассчитать длину окружности необходимо всем, от рядового водителя, до ведущего инженера-проектировщика. Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Формула для вычисления длинны окружности очень проста: D=2Pr. Расчет можно легко провести как на листке бумаги, так и при помощи данного интернет помощника. Преимущество последнего в том, что он проиллюстрирует все вычисления рисунками. И ко всему прочему, второй способ намного быстрее.
Вычислить площадь круга
Площадь круга – как и все перечисленные перечисленные в этой статье параметры является основой современной цивилизации. Уметь рассчитать и знать площадь круга полезно всем без исключения слоям населения. Трудно представить область науки и техники, в которой не надо было бы знать, площадь круга. Формула для вычисления опять же нетрудная: S=PR 2 . Эта формула и наш онлайн-калькулятор помогут Вам без лишних усилий узнать площадь любого круга. Наш сайт гарантирует высокую точность вычислений и их молниеносное выполнение.
Рассчитать площадь шара
Формула для расчета площади шара ничуть не сложнее формул, описанных в предыдущих пунктах. S=4Pr 2 . Этот нехитрый набор букв и цифр уже многие годы дает людям возможность достаточно точно вычислять площадь шара. Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Где это может быть применено? Да везде! Например, вы знаете, что площадь земного шара равна 510 100 000 километров квадратных. Перечислять, где может быть применено знание этой формулы перечислять бесполезно. Слишком широка область применения формулы для вычисления площади шара.
Вычислить объем шара
Для вычисления объема шара используют формулу V=4/3(Pr 3). Она была использована при создании нашего онлайн сервиса. Сайт сайт дает возможность рассчитать объем шара за считанные секунды, если вы Вам известен любой из следующих параметров: радиус, диаметр, длинна окружности, площадь круга или площадь шара. Так же вы можете применять его для обратного вычисления, например, чтобы зная объем шара, получить значение его радиуса или диаметра. Спасибо, что кратко ознакомились с возможностями нашего калькулятора круга. Надеемся, Вам у нас понравилось, и вы уже добавили сайт в закладки.
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы , понятия и определения требуются для этого.
Вконтакте
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку . Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
- — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Диаметр окружности. 2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Длина окружности
1. Сложнее найти длину окружности через диаметр , по этому сначала разберём этот вариант.
Пример: Найдите длину окружности диаметр которой равен 6 см . Мы используем приведённую выше формулу длины окружности, только сначала нам необходимо найти радиус. Для этого мы делим диаметр 6 см на 2 и получаем радиус окружности 3 см.
После этого всё предельно просто: Умножаем число Пи на 2 и на полученный радиус в 3 см.
2 * 3,14 * 3 см = 6,28 * 3см = 18,84 см.
2. А теперь ещё раз разберём простой вариант найдите длину окружности радиус равен 5 см
Решение: Радиус 5 см умножаем на 2 и умножаем на 3,14. Не пугайтесь, ведь перестановка местами множителей не влияет на результат, и формулу длины окружности можно применять в любой последовательности.
5см * 2 * 3,14 = 10 см * 3,14 = 31.4 см — это найденная длина окружности для радиуса 5 см!
Онлайн калькулятор длины окружности
Наш калькулятор длины окружности произведёт все эти не хитрые вычисления мгновенно и распишет решение в строку и с комментариями. Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Мы рассчитаем длину окружности для радиуса 3, 5, 6, 8 или 1 см, или диаметр равен 4, 10, 15, 20 дм, нашему калькулятору без разницы для какого значения радиуса найти длину окружности.
Все вычисления будут точными, оттестированными специалистами математиками. Результаты можно использовать в решении школьных задач по геометрии или математике, а также при рабочих расчётах в строительстве или в ремонте и отделке помещений, когда требуются точные вычисления по этой формуле.
Множество предметов в окружающем мире имеют круглую форму. Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом.
 При этом отрезок АВ – диаметр.
При этом отрезок АВ – диаметр. - Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.
Обратите внимание! Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Определение окружности
Формулы
Как вычислить длину окружности через радиус? Это делается по простой формуле:
где L – искомая величина,
π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность.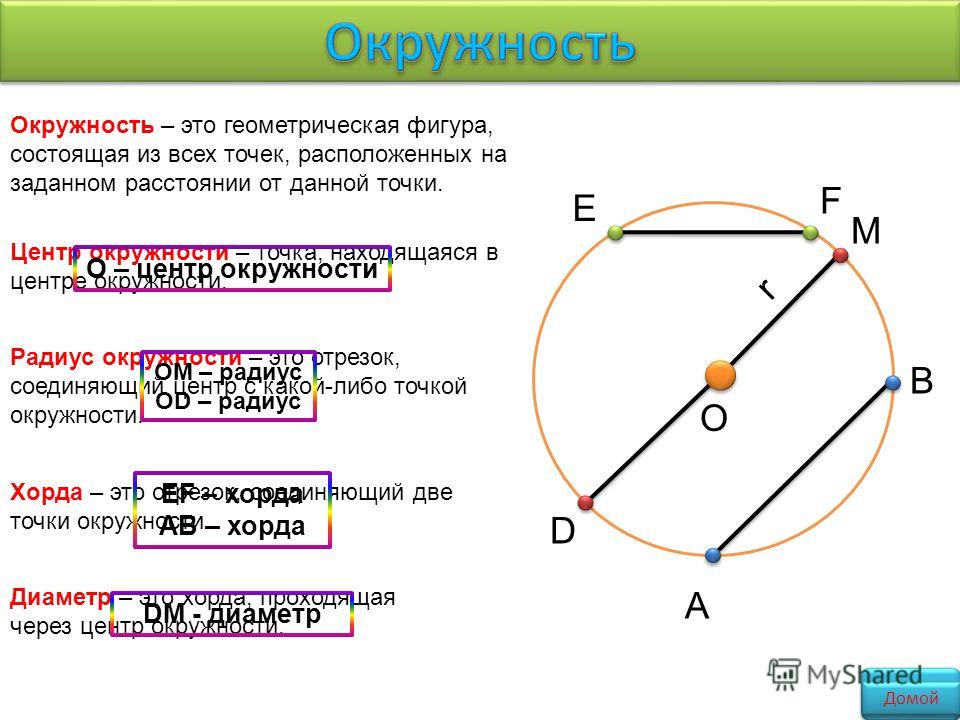 На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
L = 2πR = 2π√(S/π) = 2√(Sπ).
Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел. С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
Это интересно! Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.
Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр. У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой. Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Полезное видео: длина окружности
Практическое применение
Решать такую задачу чаще всего необходимо инженерам и архитекторам, но и в быту знание нужных формул тоже может пригодиться. Например, требуется обернуть бумажной полоской торт, испеченный в форме с поперечником 20 см. Тогда не составит труда найти длину этой полоски.
как найти длину окружности зная диаметр
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы , понятия и определения требуются для этого.
Вконтакте
Основные понятия и определения
- Радиус — это линия, соединяющая центр окружности и её произвольную точку . Он обозначается латинской буквой r.
- Хордой называется линия, соединяющая две произвольные точки лежащие на окружности .
- Диаметр — это линия, соединяющая два пункта окружности и проходящая через её центр . Он обозначается латинской буквой d.
- — это линия, состоящая из всех точек, находящихся на равном расстоянии от одной избранной точки, именуемой её центром. Её длину будем обозначать латинской буквой l.
Площадь круга — это вся территория, заключённая внутри окружности . Она измеряется в квадратных единицах и обозначается латинской буквой s.
Пользуясь нашими определениями, приходим к выводу, что диаметр круга равен его самой большой хорде.
Внимание! Из определения, что такое радиус круга можно узнать, что такое диаметр круга. Это два радиуса отложенные в противоположных направлениях!
Диаметр окружности. 2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
2 = 4*s/П . Для определения самого диаметра потребуется извлечь корень квадратный из правой части . Получится d = 2*sqrt(s/П).
Решение типовых заданий
- Узнаем, как найти диаметр, если дана длина окружности. Пусть она равняется 778,72 километра. Требуется найти d. d = 778,72/3,14 = 248 километров. Вспомним, что такое диаметр и сразу определим радиус, для этого определённое выше значение d разделим пополам. Получится r = 248/2 = 124 километра.
- Рассмотрим, как найти длину данной окружности, зная её радиус. Пусть r имеет значение 8 дм 7 см. Переведём это все в сантиметры, тогда r будет равняться 87 сантиметров. Воспользуемся формулой, как найти неизвестную длину круга. Тогда наше искомое будет равняться l = 2*3,14*87 = 546,36 см . Переведём наше полученное значение в целые числа метрических величин l = 546,36 см = 5 м 4 дм 6 см 3,6 мм.
- Пусть нам требуется определить площадь данной окружности по формуле через её известный диаметр.
 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.
Длина окружности
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π .
Определение длины окружности
Произвести расчёт окружности можно по следующей формуле:
L = π D = 2 π r
r — радиус окружности
D — диаметр окружности
L — длина окружности
π — 3.14
Задача:
Вычислить длину окружности , имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
L = π D = 2 π r
где L – длина окружности, π – 3,14 , r – радиус окружности, D – диаметр окружности.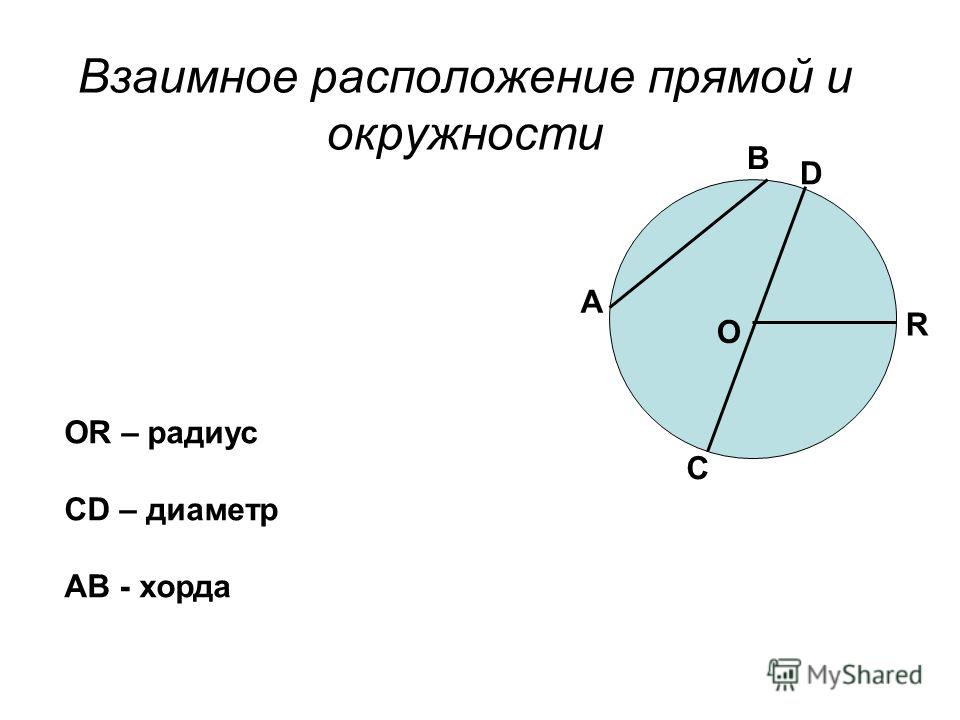
Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
L = 2 × 3,14 × 10 = 62,8 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом. Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства. Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.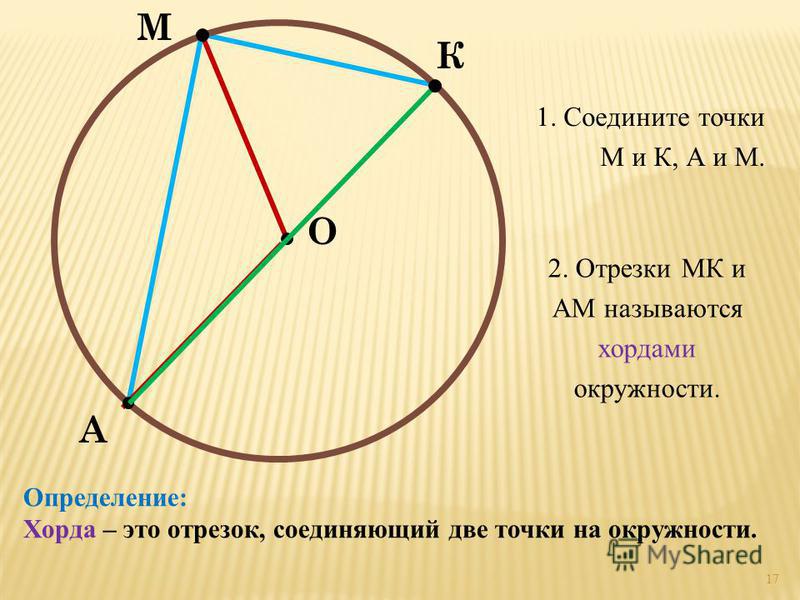
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов. Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами. Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике. Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.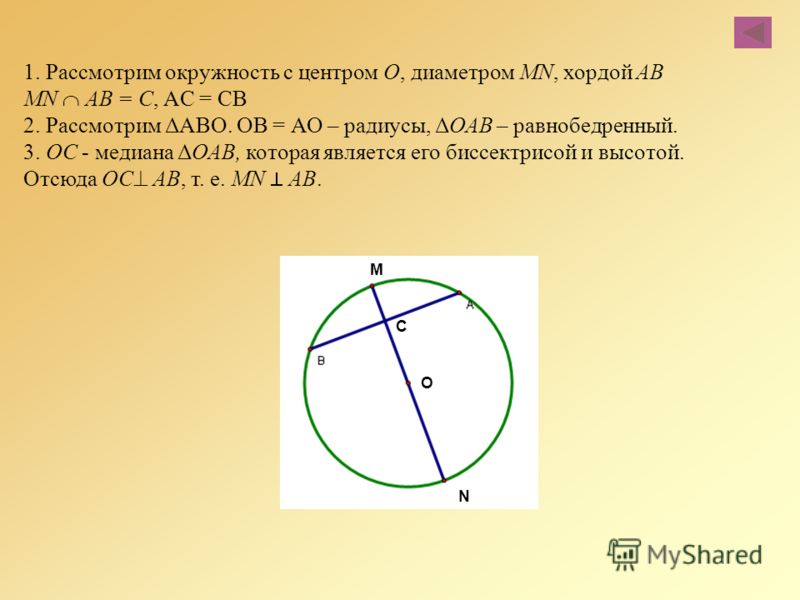
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля. Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента. Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам. Поскольку число π , необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Инструкция
Вспомните, что впервые математически вычислил это соотношение Архимед. Он правильные 96-тиугольники внутри окружности и вокруг нее. Периметр вписанного многоугольника принял за минимально возможную длину окружности, периметр описанной фигуры – за максимальный размер. По Архимеду соотношение длины окружности и диаметра равно 3,1419. Значительно позже это число «удлинил» до восьми знаков китайский математик Цзу Чунчжи. Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр (периферия). Сегодня компьютер легко вычисляет знаков числа Пи: 3,141592653589793238462643…
Периметр вписанного многоугольника принял за минимально возможную длину окружности, периметр описанной фигуры – за максимальный размер. По Архимеду соотношение длины окружности и диаметра равно 3,1419. Значительно позже это число «удлинил» до восьми знаков китайский математик Цзу Чунчжи. Его вычисления 900 лет оставались наиболее точными. Только в XVIII веке было посчитано сто знаков после запятой. А с 1706 года эта бесконечная десятичная дробь благодаря Уильяму Джонсу приобрела имя. Он обозначил ее первой буквой греческих слов периметр (периферия). Сегодня компьютер легко вычисляет знаков числа Пи: 3,141592653589793238462643…
Для расчетов число Пи сократите до 3,14. Получится, что для любой окружности ее длина, деленная на диаметр равна этому числу: L:d=3,14.
Выразите из этого утверждения формулу для нахождения диаметра. Получится, чтобы найти диаметр окружности надо длину окружности поделить на число Пи. Это выглядит так: d = L:3,14. Это универсальный способ найти диаметр, когда у окружности известна ее длина.
Итак, известна длина окружности, допустим, 15,7 см, разделите эту цифру на 3,14. Диаметр будет равен 5 см. Запишите это так: d = 15,7: 3,14 = 5 см.
Найдите диаметр по длине окружности, используя специальные таблицы для вычисления длины окружности . Эти таблицы включают в разные справочники. Например, они есть в «Четырехзначные математические таблицы» В.М. Брадиса.
Полезный совет
Запомните первые восемь цифр числа Пи с помощью стихотворения:
Нужно только постараться,
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть.
Источники:
- Число «Пи» рассчитано с рекордной точностью
- диаметр и длина окружности
- Как найти длину окружности?
Круг — это плоская геометрическая фигура, все точки которой находятся на одинаковом и отличном от нуля удалении от выбранной точки, которую называют центром окружности. Прямую, соединяющую любые две точки круга и проходящую через центр, называют его диаметром .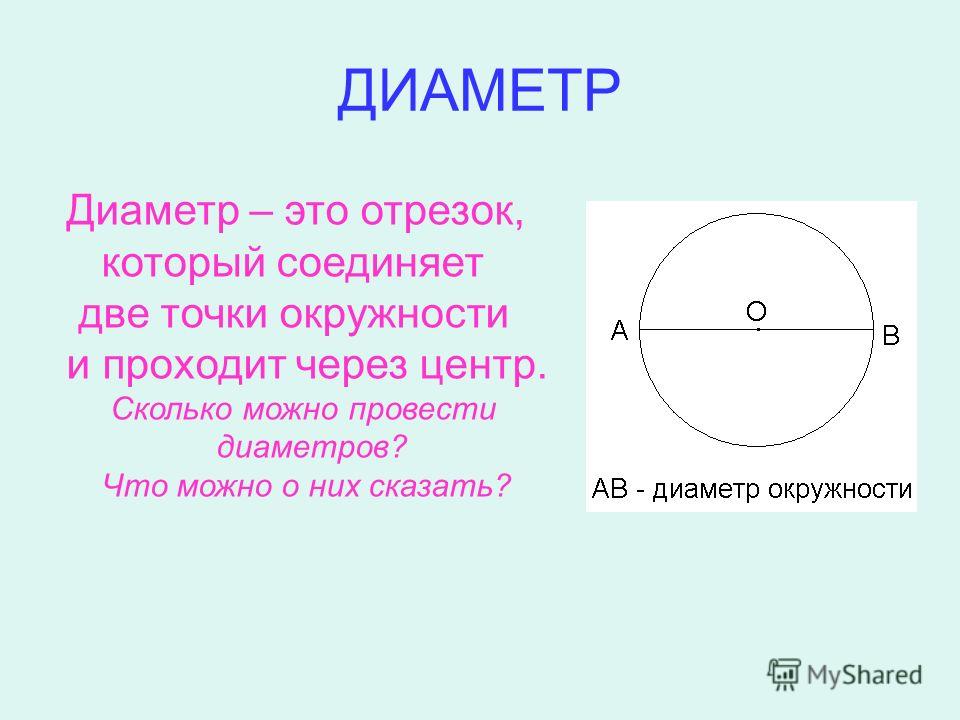 Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Суммарная длина всех границ двухмерной фигуры, которую обычно называют периметром, у круга чаще обозначается как «длина окружности». Зная длину окружности можно вычислить и ее диаметр.
Инструкция
Используйте для нахождения диаметра одно из основных свойств окружности, которое заключается в том, что соотношение длины ее периметра к диаметру одинаково для абсолютно всех окружностей. Конечно, постоянство не осталось не отмеченным математиками, и эта пропорция давно уже получила собственное — это число Пи (π — первая греческих слов «окружность » и «периметр»). Числовое этой определяется длиной окружности, у которой диаметр равен единице.
Делите известную длину окружности на число Пи, чтобы вычислить ее диаметр. Так как это число является « », то не имеет конечного значения — это дробь. Округляйте число Пи в соответствии с точностью результата, которую вам необходимо получить.
Видео по теме
Удивительное свойство окружности открыл нам древнегреческий ученый Архимед. Оно заключается в том, что отношение ее длины к длине диаметра одинаково для любой окружности . В своем труде «Об измерении круга» он вычислил его и обозначил числом «Пи». Оно иррационально, то есть его значение не может быть точно выражено. Для используется его величина, равная 3,14. Вы можете сами проверить утверждение Архимеда, сделав простые вычисления.
Оно заключается в том, что отношение ее длины к длине диаметра одинаково для любой окружности . В своем труде «Об измерении круга» он вычислил его и обозначил числом «Пи». Оно иррационально, то есть его значение не может быть точно выражено. Для используется его величина, равная 3,14. Вы можете сами проверить утверждение Архимеда, сделав простые вычисления.
Вам понадобится
- — циркуль;
- — линейка;
- — карандаш;
- — нитка.
Инструкция
Начертите на бумаге циркулем окружность произвольного диаметра. Проведите с помощью линейки и карандаша через ее центр отрезок, соединяющий две , находящиеся на линии окружности . Линейкой измерьте длину получившегося отрезка. Допустим, окружности в данном случае 7 сантиметрам.
Возьмите нитку и расположите ее по длине окружности . Измерьте получившуюся длину нитки. Пусть она будет равна 22 сантиметрам. Найдите отношение длины окружности к длине ее диаметра — 22 см: 7 см = 3,1428. … Округлите полученное число (3,14). Получилось знакомое число «Пи».
… Округлите полученное число (3,14). Получилось знакомое число «Пи».
Доказать это свойство окружности вы можете, используя чашку или стакан. Измерьте их диаметр линейкой. Обмотайте верх посуды ниткой, замерьте получившуюся длину. Поделив длину окружности чашки на длину ее диаметра, вы также получите число «Пи», убедившись в этом свойстве окружности , открытом Архимедом.
Используя это свойство, вы можете вычислить длину любой окружности по длине ее диаметра или по формулам:С = 2*п*R или С = D*п, где С — окружности , D — длина ее диаметра, R — длина ее радиуса.Для нахождения (плоскости, ограниченной линиями окружности ) используйте формулу S = π*R², если известен его радиус, либо формулу S = π*D²/4, если известен его диаметр.
Обратите внимание
А вы знаете, что четырнадцатого марта уже более двадцати лет отмечается День «Пи»? Это неофициальный праздник математиков, посвященный этому интересному числу, с которым в настоящее время связано множество формул, математических и физических аксиом.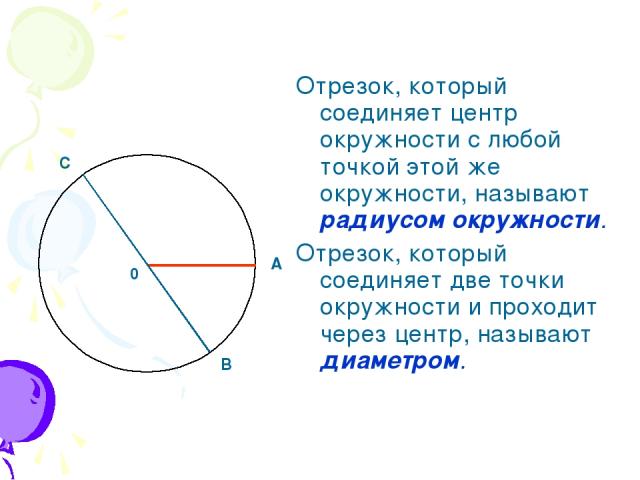 Придумал этот праздник американец Ларри Шоу, который обратил внимание, что в этот день (3.14 в системе записи дат в США) родился знаменитый ученый Эйнштейн.
Придумал этот праздник американец Ларри Шоу, который обратил внимание, что в этот день (3.14 в системе записи дат в США) родился знаменитый ученый Эйнштейн.
Источники:
- Архимед
Иногда около выпуклого многоугольника можно начертить таким образом, чтобы вершины всех углов лежали на ней. Такую окружность по отношению к многоугольнику надо называть описанной. Ее центр не обязательно должен находиться внутри периметра вписанной фигуры, но пользуясь свойствами описанной окружности , найти эту точку, как правило, не очень трудно.
Вам понадобится
- Линейка, карандаш, транспортир или угольник, циркуль.
Инструкция
Если многоугольник, около которого нужно описать окружность, начерчен на бумаге, для нахождения центр а круга достаточно линейки, карандаша и транспортира либо угольника. Измерьте длину любой из сторон фигуры, определите ее середину и поставьте в этом месте чертежа вспомогательную точку. С помощью угольника или транспортира проведите внутри многоугольника перпендикулярный этой стороне отрезок до пересечения с противоположной стороной.
С помощью угольника или транспортира проведите внутри многоугольника перпендикулярный этой стороне отрезок до пересечения с противоположной стороной.
Проделайте эту же операцию с любой другой стороной многоугольника. Пересечение двух построенных отрезков и будет искомой точкой. Это вытекает из основного свойства описанной окружности — ее центр в выпуклом многоугольнике с любым сторон всегда лежит в точке пересечения серединных перпендикуляров, проведенных к этим .
Для правильных многоугольников центр а вписанной окружности может быть намного проще. Например, если это квадрат, то начертите две диагонали — их пересечение и будет центр ом вписанной окружности . В многоугольнике с любым четным числом сторон достаточно соединить вспомогательными две пары лежащих друг напротив друга углов — центр описанной окружности должен совпадать с точкой их пересечения. В прямоугольном треугольнике для решения задачи просто определите середину самой длинной стороны фигуры — гипотенузы.
Если из условий неизвестно, можно ли в принципе описанную окружность для данного многоугольника, после определения предполагаемой точки центр а любым из описанных способов вы можете это выяснить. Отложите на циркуле расстояние между найденной точкой и любой из , установите в предполагаемый центр окружности и начертите круг — каждая вершина должна лежать на этой окружности . Если это не так, значит, не выполняется одно из свойств и описать окружность около данного многоугольника .
Определение диаметра может пригодиться не только для решения геометрических задач, но и помочь на практике. Например, зная диаметр горлышка банки, вы точно не ошибетесь в выборе крышки для нее. То же утверждение справедливо и для более габаритных окружностей.
Инструкция
Итак, введите обозначения величин. Пусть d – диаметр колодца, L – длина окружности, п – число Пи, значение которого приблизительно равно 3,14, R – радиус окружности. Длина окружности (L) известна. Предположим, что она равна 628 сантиметрам.
Предположим, что она равна 628 сантиметрам.
Далее для нахождения диаметра (d) воспользуйтесь формулой длины окружности: L=2пR, где R – неизвестная величина, L=628 см, а п=3,14. Теперь воспользуйтесь правилом нахождения неизвестного множителя: «Чтобы найти множитель, нужно произведение разделить на известный множитель». Получается: R=L/2п. Подставьте значения к формуле: R=628/2×3,14. Получается: R=628/6,28, R=100 см.
После того как радиус окружности найден (R=100 см), воспользуйтесь следующей формулой: диаметр окружности (d) равен двум радиусам окружности (2R). Получается: d=2R.
Теперь, чтобы найти диаметр, подставьте в формулу d=2R значения и вычислите результат. Так как радиус (R) известен, получается: d=2×100, d=200 см.
Источники:
- как по длине окружности определить диаметр
Длина окружности и диаметр являются взаимосвязанными геометрическими величинами. Это означает, что первую из них можно перевести во вторую без каких-либо дополнительных данных. Математической константой, через которую они связаны между собой, является число π.
Математической константой, через которую они связаны между собой, является число π.
Инструкция
Если окружность представлена в виде изображения на бумаге, а ее диаметр требуется определить приблизительно, измерьте его непосредственно. Если ее центр показан на чертеже, проведите через него линию. Если же центр не показан, найдите его при помощи циркуля. Для этого используйте угольник с углами в 90 и . Приложите его 90-градусным углом к окружности таким образом, чтобы ее касались оба катета, и обведите. Приложив затем к получившемуся прямому углу 45-градусный угол угольника, начертите . Она пройдет через центр окружности. Затем аналогичным образом начертите в другом месте окружности второй прямой угол и его биссектрису. Они пересекутся в центре. Это позволит измерить диаметр.
Для измерения диаметра предпочтительно использовать линейку, изготовленную из как можно более тонкого листового материала, либо портновский метр. При наличии только толстой линейки измерьте диаметр окружности при помощи циркуля, а затем, не изменяя его раствора, перенесите его на миллиметровую бумагу.
Также при отсутствии в условиях задачи числовых данных и при наличии только чертежа можно измерить длину окружности при помощи курвиметра, а диаметр затем рассчитать. Чтобы воспользоваться курвиметром, вначале вращением его колесика установите стрелку точно на нулевое деление. Затем отметьте на окружности точку и прижмите курвиметр к листу таким образом, чтобы штрих над колесиком указывал на эту точку. Проведите колесиком по линии окружности, пока штрих снова не окажется над этой точкой. Прочитайте показания. Они будут в , ограниченного ломаной линией. Если вписать в окружность правильный n-угольник со стороной b, то периметр такой фигуры Р равен произведению стороны b на число сторон n: Р=b*n. Сторона b может быть определена по формуле: b=2R*Sin (π/n), где R — радиус окружности, в которую вписали n-угольник.
При увеличении числа сторон периметр вписанного многоугольника будет все больше приближаться к L. Р= b*n=2n*R*Sin (π/n)=n*D*Sin (π/n). Зависимость между длиной окружности L и ее диаметром D постоянна. Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для вычисления диаметра
Отношение L/D=n*Sin (π/n) при стремлении числа сторон вписанного многоугольника к бесконечности стремится к числу π, постоянной величине, называемой «число пи» и выраженной бесконечной десятичной дробью. Для расчетов без применения вычислительной техники принимается значение π=3,14. Длина окружности и ее диаметр связаны формулой: L= πD. Для вычисления диаметра
Измерение окружности
О том, что наша планета имеет форму шара, ученым, занимающимся исследованиями в области геологии, было известно достаточно давно. Именно поэтому первые измерения величины окружности земной поверхности касались самой длинной параллели Земли — экватора. Эту величину, полагали ученые, можно считать правильной для любого другого способа измерения. Например, считалось, что если измерить окружность планеты по самому длинному
меридиану , полученная цифра будет точно такой же.Такое мнение существовало вплоть до XVIII века. Однако ученые ведущего научного учреждения того времени — Французской академии — придерживались мнения о том, что эта гипотеза неверна, и форма, которую имеет планета, не совсем правильна. Поэтому, по их мнению, длины окружности по самому длинному меридиану и по самой длинной параллели будут различаться.
Поэтому, по их мнению, длины окружности по самому длинному меридиану и по самой длинной параллели будут различаться.
В доказательство в 1735 и 1736 годах были предприняты две научные экспедиции, которые доказали истинность этого предположения. Впоследствии была установлена и величина различия между этими двумя — она составила 21,4 километра.
Длина окружности
В настоящее время длина окружности планеты Земля неоднократно измерена уже не посредством экстраполяции длины того или иного отрезка земной поверхности на ее полную величину, как это делалось раньше, а с применением современных высокоточных технологий. Благодаря этому удалось установить точную длину окружности по самому длинному меридиану и самой длинной параллели, а также уточнить величину различия между этими параметрами.Так, на сегодняшний день в научном сообществе в качестве официальной величины окружности планеты Земля по экватору, то есть наиболее длинной параллели, принято приводить цифру, составляющую 40075,70 километра.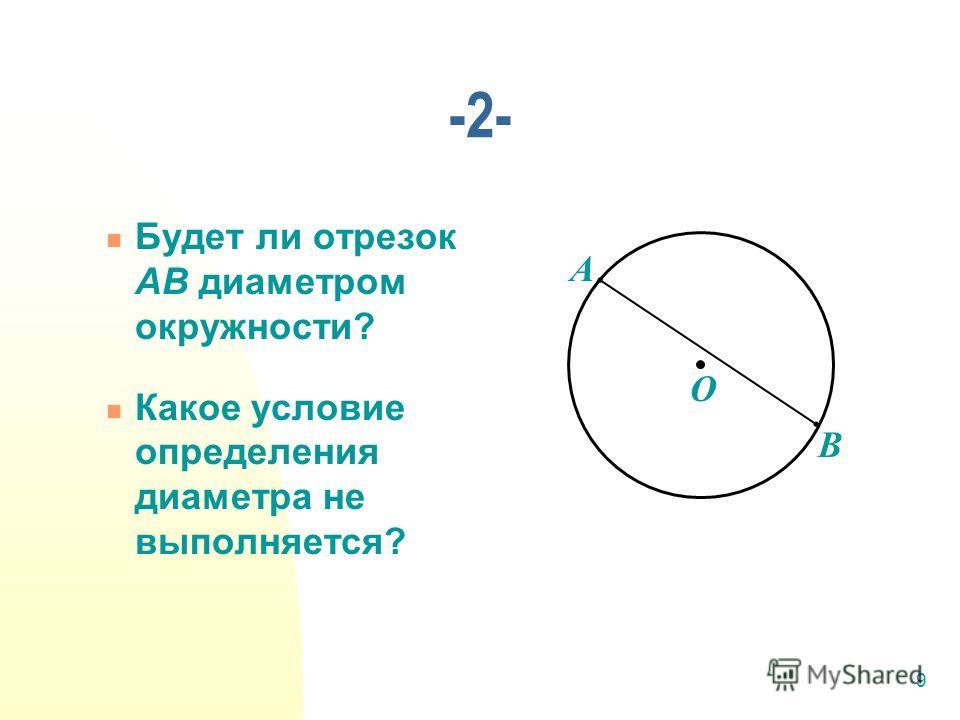 При этом аналогичный параметр, измеренный по самому длинному меридиану, то есть длина окружности, проходящей через земные полюсы, составляет 40008,55 километра.
При этом аналогичный параметр, измеренный по самому длинному меридиану, то есть длина окружности, проходящей через земные полюсы, составляет 40008,55 километра.
Таким образом, разница между длинами окружностей составляет 67,15 километра, и экватор является самой длинной окружностью нашей планеты. Кроме того, различие означает, что один градус географического меридиана несколько короче, чем один градус географической параллели.
- если известен диаметр окружности, то формула выглядит так L = ПD
- если известен радиус окружности, то формула имеет следующий вид L = 2Пr.
Формула длины окружности
Если воспользоваться Яндексом, то длину окружности можно посчитать в самом поисковом интерфейсе. Введите в Яндексе формула длины окружности , он вам выдаст формулу расчета и окошко для ввода значения. Дальше нужно будет нажать кнопку quot;Посчитатьquot;.
Окружность это такая геометрическая фигура, которая является совокупностью всех своих точек на плоскости, равноудаленных от ее центра, на расстояние, называемое радиусом.
Для того, чтобы вычислить длину окружности, обозначаемую обычно как L, надо радиус, обозначаемый как R, умножить на 2 и на число Пи. L=2ПиR. Пи — величина постоянная и равна 3,14.

Или можно взять удвоенный радиус, то есть диаметр (D) и тогда формула будет выглядеть так: L=ПиD.
Можно найти длину окружности не зная радиуса. Для этого нужно знать площадь круга.
Формула для расчета длины окружности по известной площади круга выглядит так:
L=2*корень квадратный пи*S
где S площадь круга.
Длина окружности
Можете скопировать себе на компьютер нижеприведенную табличку с основными формулами окружности и круга. Она вас, при решении геометрических задач, еще не раз выручит.
Здесь же присутствует формула длины окружности. Она имеет вид: L=2ПR
На сайте quot;Сборник формулquot;, можно посчитать длину окружности, введя имеющиеся у вас данные. Там же,
Решение уравнений:
Геометрическая прогрессия:
Комбинаторика:
Решить химическое уравнение
Известно, что независимо от длины окружности, ее отношение к диаметру является постоянным числом. Если известен диаметр окружности, то нужно эту величину умножить на число Пи (3,14).
Формула выглядит так:
Если известен радиус, то чтобы найти диаметр, умножаем его на два, а для нахождения длины окружности опять же на число Пи.
Окружностью в геометрии называют фигуру на плоскости, все точки, лежащие на окружности круга, удалены на равном расстоянии от центра окружности
Радиусом окружности называют в геометрии величину расстояния, отрезок от центра окружности до ее любой точки на окружности.
Длину окружности с радиусом вычисляют по формуле
Длина окружности L равно 2pi умножить на R.
Или выглядит формула так. Чтобы не путаться, запомните, что длина окружности это есть периметр круга.
r — это радиус
D — диаметр
Приблизительно 3,14
Но окружность — это не круг
Смотрите картинку, на которой видна разница между кругом и окружностью
Окружность это кривая, ограничивающая круг. Все ее точки находятся на равном от центра расстоянии. В формуле вычисления длины окружности используются значения радиуса или двойная величина радиуса — диаметр и число, всегда имеющее значение 3,14.
Формула, таким образом, выглядит так: L=d или L=2R , где L — значение длины окружности, получаемое умножением числа (3,14) на величину радиуса окружности или двойного диаметра.
Еще из средней школьной программы отчетливо помню формулу измерения длины окружности. Эта формула выглядит так- 2Пr, где r- это радиус окружности, которая равна половине диаметра, а число П неизменна и равна 3.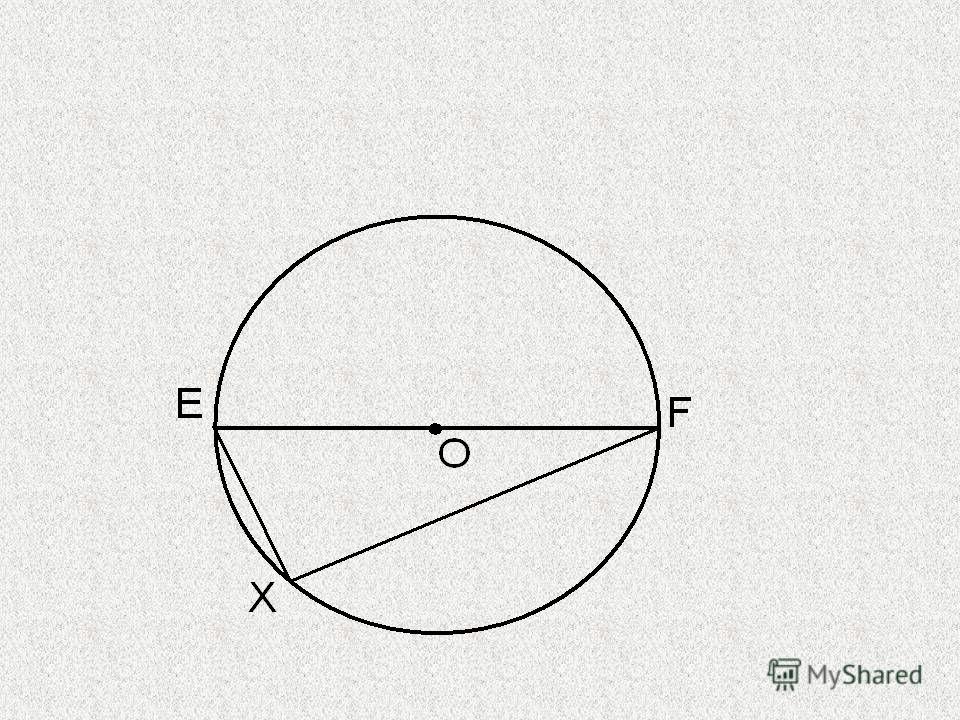 14.
14.
Формула длины окружности равна Пи умноженное на Диаметр или Пи умноженное на Радиус умноженный на 2.
Длину окружности можно найти одним из представленных способов:
Окружностью называют кривую линию, которая ограничивает собой круг. В геометрии фигуры плоские, поэтому определение относится к двухмерному изображению. Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
Предполагается, что все точки этой кривой удалены от центра круга на равное расстояние.
У окружности есть несколько характеристик, на основе которых производят расчеты, связанные с этой геометрической фигурой. В их число входит: диаметр, радиус, площадь и длина окружности. Эти характеристики взаимосвязаны, то есть для их вычисления достаточно информации хотя бы об одной из составляющих. Например, зная только радиус геометрической фигуры по формуле можно найти длину окружности, диаметр, и ее площадь.
- Радиус окружности – это отрезок внутри окружности, соединённый с ее центром.
- Диаметр – это отрезок внутри окружности, соединяющий ее точки и проходящий через центр. По сути, диаметр – это два радиуса. Именно так выглядит формула для его вычисления: D=2r.
- Есть еще одна составляющая окружности – хорда. Эта прямая, которая соединяет две точки окружности, но не всегда проходит через центр. Так вот ту хорду, которая через него проходит, тоже называют диаметром.

Как узнать длину окружности? Сейчас выясним.
Длина окружности: формула
Для обозначения этой характеристики выбрана латинская буква p. Еще Архимед доказал, что отношение длины окружности к ее диаметру является одним и тем же числом для всех окружностей: это число π, которое приблизительно равно 3,14159. Формула для вычисления π выглядит так: π = p/d. Согласно этой формуле, величина p равна πd, то есть длина окружности: p= πd. Поскольку d (диаметр) равен двум радиусам, то эту же формулу длины окружности можно записать как p=2πr.Рассмотрим применение формулы на примере простых задач:
Задача 1
У основания царь-колокола диаметр равен 6,6 метров. Какова длина окружности основания колокола?
- Итак, формула для вычисления окружности — p= πd
- Подставляем имеющееся значение в формулу: p=3,14*6,6= 20,724
Ответ: длина окружности основания колокола 20,7 метра.
Задача 2
Искусственный спутник Земли вращается на расстоянии 320 км от планеты. Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
Радиус Земли – 6370 км. Какова длина круговой орбиты спутника?
- 1.Вычислим радиус круговой орбиты спутника Земли: 6370+320=6690 (км)
- 2.Вычислим длину круговой орбиты спутника по формуле: P=2πr
- 3.P=2*3,14*6690=42013,2
Ответ: длина круговой орбиты спутника Земли 42013,2 км.
Способы измерения длины окружности
Вычисление длины окружности на практике используется не часто. Причиной тому приблизительное значение числа π. В быту для поиска длины круга используют специальный прибор – курвиметр. На окружности отмечают произвольную точку отсчета и ведут от нее прибор строго по линии, пока опять не дойдут до этой точки.
Как найти длину окружности? Нужно просто держать в голове незамысловатые формуля для вычислений.
Как рассчитать длину окружности по формулам через диаметр, равный двум радиусам
Окружность — это множество точек, которое располагается на одинаковом расстоянии от ее центра, представленного точкой. {circ}}
{circ}}
Диаметр, что перпендикулярен хорде, делит хорду и стянутые ею дуги пополам.
В случае, если хорды AB и CD окружности имеют пересечение в точке N, то произведения отрезков хорд, разделенные точкой N, равны между собой.
ANcdot NB = CN cdot ND
Касательная к окружности
- Касательной к окружности принято называть прямую, у которой имеется одна общая точка с окружностью.
- Если же у прямой есть две общие точки, ее называют секущей.
- Если провести радиус в точку касания, он будет перпендикулярен касательной к окружности.
Проведем две касательные из этой точки к нашей окружности. Получится, что отрезки касательных сравняются один с другим, а центр окружности расположится на биссектрисе угла с вершиной в этой точке.
AC = CB
Теперь к окружности из нашей точки проведем касательную и секущую. Получим, что квадрат длины отрезка касательной будет равен произведению всего отрезка секущей на его внешнюю часть. {circ}
{circ}
ight )
ight )
Вписанная окружность
- Вписанная окружность — это окружность, касающаяся сторон многоугольника.
- В точке, где пересекаются биссектрисы углов многоугольника, располагается ее центр.
- Окружность может быть вписанной не в каждый многоугольник.

- Площадь многоугольника с вписанной окружностью находится по формуле:
- S = pr,
- где:
- p — полупериметр многоугольника,
- r — радиус вписанной окружности.
- Отсюда следует, что радиус вписанной окружности равен:
- r = frac{S}{p}
Суммы длин противоположных сторон будут тождественны, если окружность вписана в выпуклый четырехугольник. И наоборот: в выпуклый четырехугольник вписывается окружность, если в нем суммы длин противоположных сторон тождественны.
AB + DC = AD + BC
В любой из треугольников возможно вписать окружность. Только одну единственную. В точке, где пересекаются биссектрисы внутренних углов фигуры, будет лежать центр этой вписанной окружности.
- Радиус вписанной окружности вычисляется по формуле:
- r = frac{S}{p},
- где p = frac{a + b + c}{2}
Описанная окружность
- Если окружность проходит через каждую вершину многоугольника, то такую окружность принято называть описанной около многоугольника.
 {circ}
{circ}
Около любого треугольника можно описать окружность, причем одну-единственную. Центр такой окружности будет расположен в точке, где пересекаются серединные перпендикуляры сторон треугольника.
- Радиус описанной окружности можно вычислить по формулам:
- R = frac{a}{2 sin A} = frac{b}{2 sin B} = frac{c}{2 sin C}
- R = frac{abc}{4 S}
- где:
- a, b, c — длины сторон треугольника,
- S — площадь треугольника.
Теорема Птолемея
- Под конец, рассмотрим теорему Птолемея.
- Теорема Птолемея гласит, что произведение диагоналей тождественно сумме произведений противоположных сторон вписанного четырехугольника.
- AC cdot BD = AB cdot CD + BC cdot AD
Источник: https://academyege.ru/page/okruzhnost-i-krug.html
Окружность
- Окружность — геометрическое место точек плоскости, расстояние от которых до центра окружности равно.
- Центр окръжности
- Радиус: расстояние от центра окружности до его границы.

Диаметр: наибольшее расстояние от одной границы окружности до другой. Диаметр равен двум радиусам.
$d = 2cdot r$
- Периметр (длина окружности): длина границы окружности.
Длина окружности $= pi cdot$ диаметр $= 2 cdot pi cdot$ радиус - Длина окружности $= pi cdot d = 2 cdot pi cdot r$
$pi$ — pi: число, равное 3,141592… или $approx frac{22}{7}$, то есть отношение $frac{ ext{длины окружности}}{ ext{диаметр}}$ любого окружности.
Дуга: изогнутая линия, которая является частью окружности.
Дуги окружности измеряется в градусах или радианах.
Например: 90° или $frac{pi}{2}$ — четверть круга,
180° или $pi$ — половина круга.
- Сумма всех дуг окружности составляет 360° или $2pi$
- Хорда: отрезок прямой, соединяющей две точки на окружности.
- Сектор: похож на часть пирога (клин).
 circ$
circ$Хорды
Источник: https://www.math20.com/ru/geometria/krugi.html
Площадь круга и его частей. Длина окружности и ее дуг
Справочник по математике Геометрия (Планиметрия) Окружность и круг Фигура Рисунок Определения и свойства Окружность Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности Дуга Часть окружности, расположенная между двумя точками окружности Круг Конечная часть плоскости, ограниченная окружностью Сектор Часть круга, ограниченная двумя радиусами Сегмент Часть круга, ограниченная хордой Правильный многоугольник Выпуклый многоугольник, у которого все стороны равны и все углы равны Около любого правильного многоугольника можно описать окружность Окружность Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности Дуга Часть окружности, расположенная между двумя точками окружности Круг Конечная часть плоскости, ограниченная окружностью Сектор Часть круга, ограниченная двумя радиусами Сегмент Часть круга, ограниченная хордой Правильный многоугольник - Выпуклый многоугольник, у которого все стороны равны и все углы равны
- Около любого правильного многоугольника можно описать окружность
Определение 1.
 Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.Определение 2. Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1. Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3. Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2. Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
Формулы для длины окружности и её дуг
Площадь круга
Рассмотрим две окружности с общим центром (концентрические окружности) и радиусами радиусами 1 и R, в каждую из которых вписан правильный n – угольник (рис.
 1).
1).Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1.
- Рис.1
- Площадь правильного n – угольника, вписанного в окружность радиуса R, равна
Площадь правильного n – угольника, вписанного в окружность радиуса 1, равна
- Следовательно,
- Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1, стремится к π, то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R, стремится к числу πR2.
- Таким образом, площадь круга радиуса R, обозначаемая S, равна
- S = πR2.
Длина окружности
Рассмотрим правильный n – угольник B1B2…Bn , вписанный в окружность радиуса радиуса R, и опустим из центраO окружности перпендикуляры на все стороны многоугольника (рис. 2).
- Рис.2
- Поскольку площадь n – угольника B1B2…Bn равна
- то, обозначая длину окружности радиуса R буквой C, мы, в соответствии с определением 2, при увеличении n получаем равенство:
- откуда вытекает формула для длины окружности радиуса R:
- C = 2πR.

Следствие. Длина окружности радиуса 1 равна 2π.
Длина дуги
- Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
- Рис.
3
- В случае, когда величина α выражена в градусах, справедлива пропорция
- из которой вытекает равенство:
- В случае, когда величина α выражена в радианах, справедлива пропорция
- из которой вытекает равенство:
Площадь сектора
- Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
- Рис.4
- В случае, когда величина α выражена в градусах, справедлива пропорция
- из которой вытекает равенство:
- В случае, когда величина α выражена в радианах, справедлива пропорция
- из которой вытекает равенство:
Площадь сегмента
- Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.

- Рис.
5
- Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.
5), то в случае, когда величина α выражена в градусах, получаем
- Следовательно,
- В случае, когда величина α выражена в в радианах, получаем
Следовательно,
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Источник: https://www.resolventa.ru/demo/diaggia6.htm
Как посчитать длину круга зная диаметр. Как рассчитать длину окружности, если не указан диаметр и радиус круга
Окружность встречается в повседневной жизни не реже, чем прямоугольник. А у многих людей задача о том, как рассчитать длину окружности, вызывает затруднение. И все потому, что у нее нет углов. При их наличии все стало бы намного проще.
Что такое окружность и где она встречается?
Эта плоская фигура представляет собой некоторое количество точек, которые расположены на одинаковом удалении от еще одной, которая является центром.
 Это расстояние называется радиусом.
Это расстояние называется радиусом.В повседневной жизни нечасто приходится вычислять длину окружности, кроме людей, которые являются инженерами и конструкторами. Они создают проекты механизмов, в которых используются, например, шестеренки, иллюминаторы и колеса. Архитекторы создают дома, имеющие круглые или арочные окна.
В каждом из этих и других случаях требуется своя точность. Причем высчитать длину окружности совершенно точно оказывается невозможно. Связано это с бесконечностью основного числа, имеющегося в формуле. «Пи» до сих пор уточняется. И используется чаще всего округленное значение. Степень точности выбирается такой, чтобы дать максимально верный ответ.
Обозначения величин и формулы
Теперь легко ответить на вопрос о том, как рассчитать длину окружности по радиусу, для этого потребуется такая формула:
Поскольку радиус и диаметр связаны друг с другом, то есть и другая формула для расчетов.
 Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:
Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:l = π * d.
Как быть, если нужно вычислить периметр круга?
Просто вспомнить, что круг включает в себя все точки внутри окружности. А значит, его периметр совпадает с ее длиной. И после того, как рассчитать длину окружности, поставить знак равенства с периметром круга.
Кстати, и обозначения у них такие же. Это касается радиуса и диаметра, а периметром является латинская буква P.
Примеры заданий
Задача первая
Условие.
Узнать длину окружности, радиус которой равен 5 см.Решение.
Здесь несложно понять, как рассчитать длину окружности. Нужно только воспользоваться первой формулой. Поскольку радиус известен, то потребуется только подставить значения и сосчитать. 2 умноженное на радиус, равный 5 см, даст 10. Осталось еще умножить его на значение π. 3,14 * 10 = 31,4 (см).
3,14 * 10 = 31,4 (см).Ответ:
l = 31,4 см.Задача вторая
Условие.
Имеется колесо, длина окружности которого известна и равна 1256 мм. Необходимо вычислить его радиус.Решение.
В этом задании потребуется воспользоваться той же формулой. Но только известную длину нужно будет разделить на произведение 2 и π. Получается, что произведение даст результат: 6,28. После деления остается число: 200. Это искомая величина.Ответ:
r = 200 мм.Задача третья
Условие.
Вычислить диаметр, если известна длина окружности, которая равна 56,52 см.Решение.
Аналогично предыдущей задаче потребуется разделить известную длину на значение π, округленное до сотых. В результате такого действия получается число 18. Результат получен.Ответ:
d = 18 см.Задача четвертая
Условие.
Стрелки часов имеют длину 3 и 5 см. Нужно вычислить длины окружностей, которые описывают их концы.
Решение.
Поскольку стрелки совпадают с радиусами окружностей, то потребуется первая формула. Ею нужно воспользоваться два раза.Для первой длины произведение будет состоять из множителей: 2; 3,14 и 3. Итогом будет число 18,84 см.
Для второго ответа нужно перемножить 2, π и 5. Произведение даст число: 31,4 см.
Ответ:
l 1 = 18,84 см, l 2 = 31,4 см.Задача пятая
Условие.
Белка бегает в колесе диаметром 2 м. Какое расстояние она пробегает за один полный оборот колеса?Решение.
Это расстояние равно длине окружности. Поэтому нужно воспользоваться подходящей формулой. А именно перемножить значение π и 2 м. Подсчеты дают результат: 6,28 м.Ответ:
Белка пробегает 6,28 м.И в чем ее отличие от круга. Возьмите ручку или цвета и нарисуйте на листке бумаги обычный круг. Закрасьте всю середину полученной фигуры синим карандашом. Красный контур, обозначающий границы фигуры, — это окружность.
 А вот синее содержимое внутри нее — и есть круг.
А вот синее содержимое внутри нее — и есть круг.Размеры круга и окружности определяются диаметром. На красной линии, обозначающей окружность, отметьте две точки таким образом, чтобы они оказались зеркальным отражением друг друга. Соедините их линией. Отрезок обязательно пройдет через точку в центре окружности. Этот отрезок, соединяющий противоположные части окружности, и называется в геометрии диаметром.
Отрезок, который тянется не через центр окружности, но смыкается с ней противоположными концами, называется хордой. Следовательно, хорда, пролегающая через точку центра окружности, и является ее диаметром.
Обозначается диаметр латинской буквой D. Находить диаметр окружности можно по таким значениям, как площадь, длина и радиус круга.
Расстояние от центральной точки до точки, отложенной на окружности, называется радиусом и обозначается буквой R. Знание величины радиуса помогает вычислить диаметр окружности одним несложным действием:
К примеру, радиус — 7 см.
 Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.Иногда приходится определять диаметр окружности лишь по ее длине. Здесь необходимо применить специальную формулу, помогающую определить Формула L = 2 Пи * R, где 2 — это неизменная величина (константа), а Пи = 3,14. А так как известно, что R = D * 2, то формулу можно представить и другим способом
Данное выражение применимо и как формула диаметра окружности. Подставив известные в задаче величины, решаем уравнение с одним неизвестным. Допустим, длина равна 7 м. Следовательно:
- Ответ: диаметр равен 21,98 метрам.
- Если известно значение площади, то также можно определить диаметр окружности. Формула, которая применяется в данном случае, выглядит так:
- D = 2 * (S / Пи) * (1 / 2)
S — в данном случае Допустим, в задаче она равна 30 кв. м. Получаем:
- D = 2 * (30 / 3, 14) * (1 / 2) D = 9, 55414
- При обозначенной в задаче величине, равной объему (V) шара, применяется следующая формула нахождения диаметра: D = (6 V / Пи) * 1 / 3.

- Иногда приходится находить диаметр окружности, вписанной в треугольник. Для этого по формуле находим радиус представленной окружности:
- R = S / p (S — площадь заданного треугольника, а p — периметр, разделенный на 2).
- Полученный результат увеличиваем вдвое, учитывая, что D = 2 * R.
Нередко находить диаметр окружности приходится и в быту. К примеру, при определении что равносильно его диаметру. Для этого необходимо обмотать палец потенциального обладателя кольца ниткой. Отметить точки соприкосновения двух концов. Измерить линейкой длину от точки до точки.
Полученное значение умножаем на 3,14, следуя формуле определения диаметра при известной длине. Так что, утверждение о том, что познания в геометрии и алгебре в жизни не пригодятся, не всегда соответствует действительности.
А это является серьезным поводом для того, чтобы более ответственно относиться к школьным предметам.
Очень часто при решении школьных заданий по или физике возникает вопрос — как найти длину окружности, зная диаметр? На самом деле никаких сложностей в решении этой проблемы нет, нужно только чётко представлять себе, какие формулы
, понятия и определения требуются для этого.
Источник: https://kofejnja.ru/kak-poschitat-dlinu-kruga-znaya-diametr-kak-rasschitat-dlinu-okruzhnosti-esli-ne.html
Длина окружности
Длина окружности. Число Пи Площадь круга Площадь сферы. Объём шара
Возьмем циркуль. Установим ножку циркуля с иглой в точку «O», а ножку циркуля с карандашом будем вращать вокруг этой точки. Таким образом, мы получим замкнутую линию. Такую замкнутую линию называют — окружность.
Рассмотрим более подробно окружность. Разберёмся, что называют центром, радиусом и диаметром окружности.
- (·)O — называется центром окружности.
- Отрезок, который соединяет центр и любую точку окружности, называется радиусом окружности. Радиус окружности обозначается буквой «R». На рисунке выше — это отрезок «OA».
- Отрезок, который соединяет две точки окружности и проходит через её центр, называется диаметром окружности.Диаметр окружности обозначается буквой «D».
 На рисунке выше — это отрезок «BC».На рисунке также видно, что диаметр равен двум радиусам. Поэтому справедливо выражение «D = 2R».
На рисунке выше — это отрезок «BC».На рисунке также видно, что диаметр равен двум радиусам. Поэтому справедливо выражение «D = 2R».
Число π и длина окружности
Прежде чем разобраться, как считается длина окружности, необходимо выяснить, что такое число π (читается как «Пи»), которое так часто упоминают на уроках.
В далекие времена математики Древней Греции внимательно изучали окружность и пришли к выводу, что длина окружности и её диаметр взаимосвязаны.
Запомните!
Отношение длины окружности к её диаметру является одинаковым для всех окружностей и обозначается греческой буквой π («Пи»). π ≈ 3,14…
Число «Пи» относится к числам, точное значение которых записать невозможно ни с помощью обыкновенных дробей, ни с помощью десятичных дробей. Нам для наших вычислений достаточно использовать значение π, округленное до разряда сотых π ≈ 3,14…
Теперь, зная, что такое число π, мы можем записать формулу длины окружности.
Запомните!
Длина окружности — это произведение числа π и диаметра окружности.
 Длина окружности обозначается буквой «С» (читается как «Це»). C = πD C = 2πR , так как D = 2R
Длина окружности обозначается буквой «С» (читается как «Це»). C = πD C = 2πR , так как D = 2RКак найти длину окружности
Чтобы закрепить полученные знания, решим задачу на окружности.
Виленкин 6 класс. Номер 831
Условие задачи:
Найдите длину окружности, радиус которой равен 24 см. Число π округлите до сотых.
Воспользуемся формулой длины окружности:
C = 2πR ≈ 2 · 3,14 · 24 ≈ 150,72 см
- Разберем обратную задачу, когда мы знаем длину окружности, а нас просят найти её диаметр.
- Условие задачи:
Определите диаметр окружности, если её длина равна 56,52 дм. (π ≈ 3,14).
Выразим из формулы длины окружности диаметр.
C = πD D = С / π D = 56,52 / 3,14 = 18 дм
На рисунке ниже отметим на окружности две точки «A» и «B». Эти точки делят окружность на две части, каждую из которых называют дугой. Это синяя дуга «AB» и черная дуга «AB». Точки «A» и «B» называют концами дуг.

Соединим точки «A» и «B» отрезком. Полученный отрезок называют хордой.
Важно!
Точки «A» и «B» делят окружность на две дуги. Поэтому важно понимать, какую дугу вы имеете в виду, когда пишите дуга «AB».
Для того чтобы избежать путаницы, часто вводят дополнительную точку на нужной дуге и обращаются к ней по трем точкам.
Источник: http://math-prosto.ru/?page=pages%2Fcircle%2Fcircle_length_number_pi.php
Расчет радиуса формула. Как найти длину окружности: через диаметр и радиус
Класса учащиеся общеобразовательных школ в курсе изучают круг и окружность как геометрическую фигуру, и все, что с этой фигурой связано. Ребята знакомятся с такими понятиями, как радиус и диаметр, длина окружности или периметр , площадь круга.
Именно на этой теме они узнают про загадочное число Пи – это лудольфово число, как оно называлось раньше. Число Пи иррационально, так как его представление в виде десятичной дроби бесконечно. На практике используется его усеченный вариант из трех цифр: 3.
 14.
14.Эта константа выражает отношение длины любой окружности к ее диаметру. Шестиклассники решают задачи, выводя по одной данности и числа «Пи» остальные характеристики окружности и круга.
В тетрадях и на классной доске они в масштабе вычерчивают абстрактные сферы и производят мало что говорящие вычисления.
А на практике
На практике такая задача может возникнуть в ситуации, когда, например, возникает необходимость проложить трассу определенной протяженности для проведения каких-либо состязаний со стартом и финишем в одном месте.
Высчитав радиус, вы сможете на плане выбрать прохождение этой трассы, с циркулем в руке рассматривая варианты с учетом географических особенностей региона.
Перемещая ножку циркуля – равноудаленного центра от будущей трассы, можно уже на этом этапе предусмотреть, где на участках будут подъемы, где спуски, учитывая естественные перепады рельефа. Также сразу можно определиться и с участками, где лучше разместить трибуны для болельщиков.

Радиус из окружности
Итак, предположим, что вам для проведения соревнований по автокроссу необходима круговая трасса длиной 10 000 м. Вот нужная формула для определения радиуса (R) окружности при известной её длине (C): R=C/2п (п – число, равное 3.14).Подставив имеющиеся значения, вы легко получаете результат:
R = 10 000:3.14 = 3 184. 71 (м) или 3 км 184 м и 71 см.
От радиуса к площади
Зная радиус окружности, легко можно определить площадь, которая будет изъята из ландшафта. Формула площади круга (S): S=пR2При R = 3 184. 71 м она составит: S = 3.14 х 3 184. 71 х 3 184. 71 = 31 847 063 (кв. м) или почти 32 квадратных километров.
Подобные вычисления могут быть полезными при огораживании. Например, у вас имеется материал на ограду на столько-то . Взяв эту величину за периметр круга, вы легко определите его диаметр (радиус) и площадь, а, следовательно, зримо представите величину будущего огороженного участка.
Множество предметов в окружающем мире имеют круглую форму.
 Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.Существует несколько определений этой геометрической фигуры.
- Это замкнутая кривая, состоящая из точек, которые располагаются на одинаковом расстоянии от заданной точки.
- Это кривая, состоящая из точек А и В, являющихся концами отрезка, и всех точек, из которых А и В видны под прямым углом. При этом отрезок АВ – диаметр.
- Для того же отрезка АВ эта кривая включает все точки С, такие, что отношение АС/ВС неизменно и не равняется 1.
- Это кривая, состоящая из точек, для которых справедливо следующее: если сложить квадраты расстояний от одной точки до двух данных других точек А и В, получится постоянное число, большее 1/2 соединяющего А и В отрезка. Это определение выводится из теоремы Пифагора.
Обратите внимание!
Есть и другие определения. Круг – это область внутри окружности. Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.Определение окружности
Формулы
- Как вычислить длину окружности через радиус? Это делается по простой формуле:
- где L – искомая величина,
- π – число пи, примерно равное 3,1413926.
Обычно для нахождения нужной величины достаточно использовать π до второго знака, то есть 3,14, это обеспечит нужную точность.
На калькуляторах, в частности инженерных, может быть кнопка, которая автоматически вводит значение числа π.
Обозначения
Для нахождения через диаметр существует следующая формула:
Если L уже известно, можно легко узнать радиус или диаметр. Для этого L нужно поделить на 2π или на π соответственно.
Если уже дана круга, нужно понимать, как найти длину окружности по этим данным. Площадь круга равняется S = πR2. Отсюда находим радиус: R = √(S/π). Тогда
- L = 2πR = 2π√(S/π) = 2√(Sπ).

- Вычислить площадь через L также несложно: S = πR2 = π(L/(2π))2 = L2/(4π)
- Резюмируя, можно сказать, что существует три основных формулы:
- через радиус – L = 2πR;
- через диаметр – L = πD;
- через площадь круга – L = 2√(Sπ).
Число пи
Без числа π решить рассматриваемую задачу не получится. Число π впервые и было найдено как отношение длины окружности к ее диаметру. Это сделали еще древние вавилоняне, египтяне и индийцы. Нашли они его довольно точно – их результаты отличались от известного сейчас значения π не больше, чем на 1%. Постоянную приближали такими дробями как 25/8, 256/81, 339/108.
Далее значение этой постоянной считали не только с позиции геометрии, но и с точки зрения математического анализа через суммы рядов. Обозначение этой константы греческой буквой π впервые использовал Уильям Джонс в 1706 году, а популярно оно стало после работ Эйлера.
Сейчас известно, что эта постоянная представляет собой бесконечную непериодическую десятичную дробь, она иррациональна, то есть ее нельзя представить в виде отношения двух целых чисел.
 С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.Это интересно!
Для запоминания нескольких первых знаков числа π были придуманы различные мнемонические правила. Некоторые позволяют хранить в памяти большое число цифр, например, одно французское стихотворение поможет запомнить пи до 126 знака.Если вам необходима длина окружности, онлайн-калькулятор поможет в этом. Таких калькуляторов существует множество, в них нужно только ввести радиус или диаметр.
У некоторых из них есть обе эти опции, другие вычисляют результат только через R. Некоторые калькуляторы могут рассчитать искомую величину с разной точностью, нужно указать число знаков после запятой.
Также с помощью онлайн-калькуляторов можно посчитать площадь круга.
Такие калькуляторы легко найти любым поисковиком. Также существуют мобильные приложения, которые помогут решить задачу, как найти длину окружности.
Источник: https://hopaclub.ru/laryngitis/raschet-radiusa-formula-kak-naiti-dlinu-okruzhnosti-cherez-diametr-i-radius/
Длина окружности
Окружностью называется ряд равноудалённых точек от одной точки, которая, в свою очередь, является центром этой окружности.
 Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Окружность имеет также свой радиус, равный расстоянию этих точек от центра.Отношение длины, какой либо окружности к её диаметру, для всех окружностей одинаково. Это отношение есть число, являющееся математической константой, которое обозначается греческой буквой π.
Определение длины окружности
- Произвести расчёт окружности можно по следующей формуле:
- L = πD = 2πr
- r – радиус окружности
- D – диаметр окружности
- L – длина окружности
- π – 3.14
Задача:
Вычислить длину окружности, имеющей радиус 10 сантиметров.
Решение:
Формула для вычисления дины окружности имеет вид:
- L = πD = 2πr
- где L – длина окружности, π – 3,14, r – радиус окружности, D – диаметр окружности.
- Таким образом, длина окружности, имеющей радиус 10 сантиметров равна:
- L = 2 × 3,14 × 5 = 31,4 сантиметра
Окружность представляет собой геометрическую фигуру, являющуюся совокупностью всех точек на плоскости, удаленных от заданной точки, которая называется ее центром, на некоторое расстояние, не равное нулю и именуемое радиусом.

Определять ее длину с различной степенью точности ученые умели уже в глубокой древности: историки науки считают, что первая формула для вычисления длины окружности была составлена примерно в 1900 году до нашей эры в древнем Вавилоне.
С такими геометрическими фигурами, как окружности, мы сталкиваемся ежедневно и повсеместно. Именно ее форму имеет внешняя поверхность колес, которыми оснащаются различные транспортные средства.
Эта деталь, несмотря на свою внешнюю простоту и незатейливость, считаются одним из величайших изобретений человечества, причем интересно, что аборигены Австралии и американские индейцы вплоть до прихода европейцев совершенно не имели понятия о том, что это такое.
По всей вероятности, самые первые колеса представляли собой отрезки бревен, которые насаживались на ось. Постепенно конструкция колеса совершенствовалась, их конструкция становилась все более и более сложной, а для их изготовления требовалось использовать массу различных инструментов.

Сначала появились колеса, состоящие из деревянного обода и спиц, а затем, для того, чтобы уменьшить износ их внешней поверхности, ее стали обивать металлическими полосами.
Для того чтобы определить длины этих элементов, и требуется использовать формулу расчета длины окружности (хотя на практике, вероятнее всего, мастера это делали «на глаз» или просто опоясывая колесо полосой и отрезая требуемый ее участок).
Следует заметить, что колесо используется отнюдь не только в транспортных средствах. Например, его форму имеет гончарный круг, а также элементы шестеренок зубчатых передач, широко применяемых в технике.
Издавна колеса использовались в конструкциях водяных мельниц (самые древние из известных ученым сооружений такого рода строились в Месопотамии), а также прялок, применявшихся для изготовления нитей из шерсти животных и растительных волокон.
Окружности нередко можно встретить и в строительстве. Их форму имеют достаточно широко распространенные круглые окна, очень характерные для романского архитектурного стиля.

Изготовление этих конструкций – дело весьма непростое и требует высокого мастерства, а также наличия специального инструмента.
Одной из разновидностей круглых окон являются иллюминаторы, устанавливаемые в морских и воздушных судах.
Таким образом, решать задачу определения длины окружности часто приходится инженерам-конструкторам, разрабатывающим различные машины, механизмы и агрегаты, а также архитекторам и проектировщикам.
Поскольку число π, необходимое для этого, является бесконечным, то с абсолютной точностью определить этот параметр не представляется возможным, и поэтому при вычислениях учитывается та ее степень, которая в том или ином конкретном случае является необходимой и достаточной.
Источник: http://simple-math.ru/geometry/length-circle.php
Сегмент круга
Сегмент круга
- Круговой сегмент — часть круга ограниченная дугой и секущей (хордой).
- На рисунке:
L — длина дуги сегмента
c — хорда
R — радиус
a — угол сегмента
h — высота - Первый калькулятор рассчитывает параметры сегмента, если известен радиус и угол по следующим формулам:
Формулы вычисления параметров сегмента
Длина хорды:
Высота сегмента: Точность вычисленияЗнаков после запятой: 2
Однако, как справедливо заметил наш пользователь:«на практике часто случается, что как радиус дуги, так и угол неизвестны» (см.
 длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:Точность вычисления
Знаков после запятой: 2
Калькулятор вычисляет радиус круга по длине хорды и высоте сегмента по следующей формуле:
Следующий калькулятор вычисляет площадь сегмента по высоте и радиусу:
Точность вычисления
Знаков после запятой: 2
- Этот калькулятор вычисляет угол из высоты и радиуса по следующей формуле:
далее используется формула [1] для получения площади.
15 вычислений по сегменту круга в одной программе
Последний калькулятор включает в себя все оставшиеся вычисления параметров кругового сегмента:
- длина дуги
- угол
- хорда
- высота
- радиус
- площадь
Выберите два известных аргумента и калькулятор выдаст вам все оставшиеся.
Точность вычисления
Знаков после запятой: 2
Источник: https://planetcalc.ru/1421/
Длина окружности и площадь круга
- Длина любой окружности больше своего диаметра в одно и то же число раз, а именно, приблизительно в 3,14 раза.
 Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):
Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи): - Таким образом, длину окружности (C) можно вычислить, умножив константу π на диаметр (D), или умножив π на удвоенный радиус, так как диаметр равен двум радиусам. Следовательно, формула длины окружности будет выглядеть так:
- C = πD = 2πR
- где C – длина окружности, π – константа, D – диаметр окружности, R – радиус окружности.
- Так как окружность является границей круга, то длину окружности можно также назвать длиной круга или периметром круга.
Задача 1.
Найти длину окружности, если её диаметр равен 5 см.
Так как длина окружности равна π умноженное на диаметр, то длина окружности с диаметром 5 см будет равна:
C ≈ 3,14 · 5 = 15,7 (см)
Задача 2. Найти длину окружности, радиус которой равен 3,5 м.
- Сначала найдём диаметр окружности, умножив длину радиуса на 2:
- D = 3,5 · 2 = 7 (м)
- теперь найдём длину окружности, умножив π на диаметр:
- C ≈ 3,14 · 7 = 21,98 (м)
Задача 3.
 Найти радиус окружности, длина которой равна 7,85 м.
Найти радиус окружности, длина которой равна 7,85 м.Чтобы найти радиус окружности по её длине, надо длину окружности разделить на 2π
следовательно радиус будет равен:
R ≈ 7,85 = 7,85 = 1,25 (м) 2 · 3,14 6,28 - Площадь круга равна произведению числа π на квадрат радиуса. Формула нахождения площади круга:
- S = πr2
- где S – площадь круга, а r – радиус круга.
- Так как диаметр круга равен удвоенному радиусу, то радиус равен диаметру, разделённому на 2:
- следовательно, формула нахождения площади круга через диаметр будет выглядеть так:
S = π( D )2 = π D2 = π D2 2 22 4 Задачи на площадь круга
Задача 1. Найти площадь круга, если его радиус равен 2 см.

Так как площадь круга равна π умноженное на радиус в квадрате, то площадь круга с радиусом 2 см будет равна:
S ≈ 3,14 · 22 = 3,14 · 4 = 12,56 (см2)
Задача 2. Найти площадь круга, если его диаметр равен 7 см.
- Сначала найдём радиус круга, разделив его диаметр на 2:
- 7 : 2 = 3,5 (см)
- теперь вычислим площадь круга по формуле:
- S = πr2 ≈ 3,14 · 3,52 = 3,14 · 12,25 = 38,465 (см2)
- Данную задачу можно решить и другим способом. Вместо того чтобы сначала находить радиус, можно воспользоваться формулой нахождения площади круга через диаметр:
S = π D2 ≈ 3,14 72 = 3,14 49 = 153,86 = 38,465 (см2) 4 4 4 4 Задача 3. Найти радиус круга, если его площадь равна 12,56 м2.
- Чтобы найти радиус круга по его площади, надо площадь круга разделить π, а затем из полученного результата извлечь квадратный корень:
- r = √S : π
- следовательно радиус будет равен:
- r ≈ √12,56 : 3,14 = √4 = 2 (м)
Число π
Длину окружности предметов, окружающих нас, можно измерить с помощью сантиметровой ленты или верёвки (нитки), длину которой потом можно померить отдельно.

Но в некоторых случаях померить длину окружности трудно или практически невозможно, например, внутреннюю окружность бутылки или просто длину окружности начерченной на бумаге.
В таких случаях можно вычислить длину окружности, если известна длина её диаметра или радиуса.
Чтобы понять, как это можно сделать, возьмём несколько круглых предметов, у которых можно измерить и длину окружности и диаметр. Вычислим отношение длины к диаметру, в итоге получим следующий ряд чисел:
Ведро Таз Бочка Тарелка Стакан Окружность 91 см 157 см 220 см 78,5 см 23,9 см Диаметр 29 см 50 см 70 см 25 см 7,6 см Отношение (с точн. до 0,01) 3,14 3,14 3,14 3,14 3,14 Из этого можно сделать вывод, что отношение длины окружности к её диаметру это постоянная величина для каждой отдельной окружности и для всех окружностей в целом.
 Это отношение и обозначается буквой π.
Это отношение и обозначается буквой π.Используя эти знания, можно по радиусу или диаметру окружности находить её длину. Например, для вычисления длины окружности с радиусом 3 см нужно умножить радиус на 2 (так мы получим диаметр), а полученный диаметр умножить на π. В итоге, с помощью числа π мы узнали, что длина окружности с радиусом 3 см равна 18,84 см.
Источник: https://naobumium.info/planimetriya/dlina_okruzhnosti.php
Площадь кругов: формула, уравнение и диаметр
Круг — одна из самых распространенных форм. Если вы посмотрите на линии орбит планет в Солнечной системе, на простое, но эффективное функционирование колес или даже на молекулы на молекулярном уровне, круг продолжает появляться!
Окружность — это фигура, в которой все точки, составляющие границу, равноудалены от одной точки, расположенной в центре.
Элементы круга
Прежде чем мы обсудим площадь кругов, давайте рассмотрим уникальные характеристики, определяющие форму круга.
 На рисунке ниже изображен круг с центром O. Напомним из определения, что все точки, расположенные на границе окружности, равноудалены (равноудалены) от этой центральной точки O . Расстояние от центра круга до его границы называется радиусом , R .
На рисунке ниже изображен круг с центром O. Напомним из определения, что все точки, расположенные на границе окружности, равноудалены (равноудалены) от этой центральной точки O . Расстояние от центра круга до его границы называется радиусом , R .Диаметр , D , это расстояние от одной конечной точки окружности до другой, проходящей через центр окружности . Диаметр всегда в два раза больше длины радиуса, поэтому, если мы знаем одно из этих измерений, мы знаем и другое! А 9Хорда 0005 — это расстояние от одной конечной точки до другой на окружности, которая, в отличие от диаметра, должна проходить через центральную точку , а не .
Иллюстрация круга, StudySmarter Original
Площадь кругов: формула / уравнение
Теперь, когда мы рассмотрели элементы круга, давайте начнем с обсуждения площади круга. Во-первых, мы начнем с определения.

Площадь круга — это пространство, занимаемое кругом на поверхности или плоскости. Измерения площади записываются в квадратных единицах, например, фут 9.0043 2 и м 2 .
Чтобы вычислить площадь круга, мы можем использовать формулу:
Для этой формулы важно знать, что равно числу пи. Что такое пи? Это константа, представленная греческой буквой, и ее значение приблизительно равно 3,14159.
Пи равно математической константе, которая определяется как отношение длины окружности к диаметру круга.
Вам не нужно запоминать число пи, потому что в большинстве калькуляторов есть клавиша для быстрого ввода, показанная как . Давайте используем формулу площади в примере, чтобы увидеть, как мы можем применить этот расчет на практике.
Радиус круга 8 м. Вычислите его площадь.
Решение:
Сначала подставим значение радиуса в формулу площади круга.

Затем мы возводим значение радиуса в квадрат и умножаем его на число пи, чтобы найти площадь в квадратных единицах. Имейте в виду, что это не равно , а скорее равно .
Расчет площади круга диаметром
Мы видели формулу площади круга, в которой используется радиус . Однако мы также можем найти площадь круга, используя его диаметр . Для этого мы делим длину диаметра на 2, что дает нам значение радиуса для ввода в нашу формулу. (Напомним, что диаметр окружности в два раза больше длины ее радиуса.) Давайте рассмотрим пример, использующий этот метод.
Круг имеет диаметр 12 метров. Найдите площадь круга.
Решение:
Начнем с формулы площади круга:
Из формулы видно, что нам нужно значение радиуса. Чтобы найти радиус круга, мы делим диаметр на 2, например:
Теперь мы можем ввести значение радиуса 6 метров в формулу для определения площади:
Вычисление площади круги с окружностью
Помимо площади круга, другой распространенной и полезной мерой является его длина окружности.

Окружность круга — это периметр или охватывающая граница формы. Она измеряется в длине, что означает, что единицами являются метры, футы, дюймы и т. д.
Давайте посмотрим на некоторые формулы, связывающие длину окружности с радиусом и диаметром окружности:
Приведенные выше формулы показывают, что мы можем умножить на диаметр круга, чтобы вычислить его длину окружности. Поскольку диаметр в два раза больше длины радиуса, мы можем заменить его на , если нам нужно изменить уравнение окружности.
Вас могут попросить найти площадь круга, используя его длину окружности. Давайте поработаем на примере.
Длина окружности 10 м. Вычислите площадь круга.
Решение:
Сначала воспользуемся формулой длины окружности для определения радиуса круга:
Теперь, когда мы знаем радиус, мы можем использовать его для нахождения площади круга:
Итак, площадь круга с длиной окружности 10 м равна 7,95 м 2 .

Площадь полукругов и четвертей кругов с примерами
Мы также можем проанализировать форму круга с точки зрения половин или четвертей . В этом разделе мы обсудим площадь полукругов (кругов, разрезанных пополам) и четвертей кругов (кругов, разрезанных на четверти).
Площадь и длина окружности полукруга
Полукруг — это полукруг. Он образуется путем деления круга на две равные половины, разрезанные по его диаметру. Площадь полукруга можно записать как:
Где r радиус полукруга
Чтобы найти длину окружности полукруга , мы сначала разделим длину окружности пополам, а затем добавим дополнительную длину, равную диаметр d . Это связано с тем, что периметр или граница полукруга должны включать диаметр, чтобы замкнуть дугу. Формула длины окружности полукруга:
Вычислите площадь и длину окружности полукруга диаметром 8 см.
Решение:
Поскольку диаметр равен 8 см, радиус равен 4 см.
 Мы знаем это, потому что диаметр любого круга в два раза больше его радиуса. Используя формулу площади полукруга, получаем:
Мы знаем это, потому что диаметр любого круга в два раза больше его радиуса. Используя формулу площади полукруга, получаем:Для длины окружности вводим значение диаметра в формулу:
Площадь и длина окружности четверти круга
Окружность можно разделить на четыре равные четверти, что дает четыре четверти круга. Чтобы вычислить площадь четверти круга, уравнение выглядит следующим образом:
Чтобы получить длину окружности четверти окружности, мы начинаем с деления длины окружности на четыре, но это дает нам только длину дуги четверти окружности. Затем нам нужно дважды добавить длину радиуса, чтобы завершить границу четверти круга. Этот расчет можно выполнить с помощью следующего уравнения:
Вычислите площадь и длину окружности четверти круга с радиусом 5 см.
Решение:
Для площади получаем:
Окружность может быть рассчитана как:
Площадь кругов — основные выводы
- В круге все точки, составляющие границу фигуры, равноудалены от точки, расположенной в ее центре.

- Отрезок линии, протянувшийся от центра круга до точки на его границе, называется радиусом.
- Диаметр окружности — это расстояние от одной конечной точки окружности до другой, проходящее через центр окружности.
- Длина окружности – это длина дуги окружности.
- Площадь круга .
- Длина окружности .
THE_CIRCLE
Проект улучшения математического образования в школах (Times)
Возврат к индексу
Круг
Измерение и геометрия: модуль 17 -летний: 8
июня 2011
PDF Версия модуля
Assamed
.
- Неформальный опыт частей круга, в том числе радиуса, диаметра
и центр. - Знакомство с базовым языком геометрии, включая равнобедренные треугольники
и параллелограммы. - Знание площади и периметра квадратов, прямоугольников, треугольников и составных фигур.
- Арифметика дробей и десятичных знаков.
- Знакомство с простыми алгебраическими выражениями.

Мотивация
Круг — наиболее часто встречающаяся фигура, граница которой не является прямой линией. Монеты, тарелки и столы часто имеют форму круга, а беговые дорожки обычно имеют полукруглые концы, а вентиляторы движутся по кругу. Круглое колесо считается одним из самых важных изобретений человечества.
Когда мы строим, мы используем линейку для рисования линии и циркуль для рисования окружности. Таким образом, линии и окружности являются основой геометрии.
Когда колесо катится по песку за один оборот, какая длина получается? Эта длина является расстоянием вокруг окружности и называется окружностью окружности. Ясно, что чем больше радиус круга, тем больше длина окружности. Как именно связаны радиус и длина окружности?
Можем ли мы понять площадь, ограниченную кругом, так же, как мы определяем площадь прямоугольника? Опять же кажется очевидным, что чем больше радиус круга, тем больше площадь. Как именно связаны радиус круга и его площадь?
Экспериментальные данные (с использованием веревки) приводят к тому, что если радиус круга удваивается, то и длина окружности удваивается, и, в более общем смысле, длина окружности пропорциональна радиусу.
 Впервые это было исследовано греками, которые ввели понятие константы пропорциональности между длиной окружности и диаметром, которому мы теперь присваиваем символ π (пи).
Впервые это было исследовано греками, которые ввели понятие константы пропорциональности между длиной окружности и диаметром, которому мы теперь присваиваем символ π (пи).Мы используем термин «площадь круга» для обозначения площади области, содержащейся в круге. Строго говоря, круг вместе с его внутренней частью называется «диском», но мы обычно используем слово «круг» для обозначения как круга, так и диска.
Содержание
Окружность — это путь, прочерченный точкой, движущейся в плоскости, которая всегда находится на фиксированном расстоянии (радиус) от фиксированной точки (центра).
Части круга
Любой интервал (или отрезок), проведенный от центра данного круга до любой точки
на круге, называется радиусом (множественное число радиусов).Любой интервал, соединяющий две точки на окружности и проходящий через центр, называется
диаметром окружности.Поскольку каждый радиус имеет одинаковую длину и каждый диаметр имеет одинаковую длину, мы часто используем слова «радиус» и «диаметр» для обозначения либо рассматриваемого интервала, либо длины этого интервала.
 Таким образом, диаметр круга в два раза больше радиуса этого круга.
Таким образом, диаметр круга в два раза больше радиуса этого круга.Диаметр делит окружность на две конгруэнтные части. Каждая часть называется полукругом. Если мы проведем радиус, перпендикулярный диаметру полукруга, мы получим два конгруэнтных квадранта. Любые два радиуса делят окружность на две части. Каждая часть называется сектором (от латинского слова secare — резать).
Длина окружности
Длина окружности — это расстояние по окружности. Древние, вероятно, с помощью веревки, открыли, что удвоение диаметра круга удваивает длину окружности; утроение диаметра, утроение окружности и так далее. В общем случае длина окружности пропорциональна ее диаметру.
То есть соотношение един для всех кругов. Мы обозначаем это постоянное отношение греческой буквой π (произносится как «пирог»). Таким образом, в каждом круге
= число Преобразовав эту формулу, мы получим
C = πd,
, где C — длина окружности, а d — диаметр окружности.
 Поскольку диаметр в два раза больше радиуса, мы также можем написать
Поскольку диаметр в два раза больше радиуса, мы также можем написатьC = 2πr,
, где r — радиус окружности.
Число π не является ни целым, ни рациональным числом. Его приблизительное значение, с точностью до 7 знаков после запятой, равно 3,1415927, но десятичное расширение π продолжается вечно без видимой закономерности. Это число является одним из самых замечательных среди всех чисел в математике, и во многих местах оно снова появляется таинственным образом.
Обычно мы округляем до двух знаков после запятой как 3,14. Если требуется большая точность,
можно взять больше знаков после запятой.Хотя π не является рациональным числом (это нелегко доказать), оно близко к рациональному числу 3 = . Записано как десятичное число 3 = 3,4285, поэтому 3 отличается от π только третьим десятичным знаком. Это приближение часто используется в ситуациях, когда мы хотим избежать десятичных знаков.
При решении задач с числом π лучше оставить число через π до конца задачи, а затем, при необходимости, использовать приближение.

ПРИМЕР
Найдите длину окружности:
a диаметр которого 14 см b радиус 21 см
Дайте каждому ответу:
i через π ii как приблизительное значение, используя π ≈
iii как приблизительное значение, используя π ≈ 3,14.
Раствор
и и С = пд б и С = 2πr = 14π = 2 × π × 21 = 42π см II С = 14π II С = 42π ≈ 14 × ≈ 42 × = 44 см = 132 см III С = 14π III С = 42π ≈ 14 × 3,14 ≈ 42 × 3,14 = 43,96 см = 131,88 см Обратите внимание, что ответы в частях ii и iii являются приблизительными, поскольку мы использовали приближение для π.

нажмите для просмотра экранаУПРАЖНЕНИЕ 1
Фигура получается удалением двух полукругов из большого полукруга.
Каков периметр заштрихованной области?
нажмите для просмотра скринкастаУПРАЖНЕНИЕ 2
Длина окружности 50π см. Найдите радиус окружности.
Площадь круга
В модуле Введение в измерения мы определили площадь прямоугольника со сторонами, длина которых l и w, по формуле A = lw. Затем мы использовали эту формулу вместе с аргументами рассечения, чтобы найти площадь других фигур, ограниченных прямыми линиями,
Окружность имеет изогнутую границу, поэтому нельзя использовать аргументы, основанные на прямоугольниках и конечном числе разрезов. Без исчисления мы не можем дать строгое доказательство известной формулы площади круга A = πr2 при условии, что C = 2πr, но мы можем привести достаточно убедительные аргументы, используя интуитивные представления о пределах.

Действительно, даже неясно, как следует определять площадь круга — но мы можем привести достаточно убедительный аргумент, используя интуитивные представления о пределах.
Первый шаг — аппроксимировать площадь круга с помощью правильного многоугольника. Мы вписываем в окружность правильный многоугольник и разбиваем многоугольник на конгруэнтные равнобедренные треугольники, как показано ниже.
Мы можем определить площадь круга как предел суммы площадей треугольников по мере увеличения числа треугольников. Теперь эту идею можно использовать для нахождения формулы площади круга с радиусом r.
Разрежьте многоугольник на конгруэнтные равнобедренные треугольники и расположите их поочередно, как показано на рисунке ниже. Так как треугольники равнобедренные и конгруэнтные, то противолежащие стороны этого четырехугольника равны, значит, это параллелограмм.
По мере увеличения количества сторон многоугольника, а вместе с ним и количества треугольников, высота параллелограмма становится сколь угодно близкой к радиусу r окружности.
 Кроме того, основание каждого треугольника становится очень близким к изогнутой дуге окружности, поэтому длина параллелограмма очень близка к половине длины окружности C. Следовательно, предел площади параллелограмма равен
Кроме того, основание каждого треугольника становится очень близким к изогнутой дуге окружности, поэтому длина параллелограмма очень близка к половине длины окружности C. Следовательно, предел площади параллелограмма равенA = r × × C = r × × 2πr = πr2
Таким образом, мы можем считать, что площадь круга задается известной формулой
А = πr2.
ПРИМЕР
- и
- Найдите площадь круга, радиус которого равен 7 см, и дайте ответ в виде числа π.
- б
- Найдите площадь круга диаметром 7 см, используя приблизительное число π ≈ .
- с
- Найдите площадь круга, радиус которого равен 30 см, используя приближение
π ≈ 3,14.
Раствор
и А = πr2 б Поскольку диаметр равен 7 см, радиус равен см = 49π см2. 
А = πr2 = число ≈ × = 38 см2. 
с А = πr2 = 900π ≈ 900 × 3,14 = 2826 см2. 
щелкните для просмотра экранаУПРАЖНЕНИЕ 3
Греки избегали π, выражая площадь через длину окружности.
- и
- Выразите площадь круга радиусом r через его длину окружности C.
- б
- Длина окружности 12 см. Найдите его площадь.

нажмите для просмотра скринкастаУПРАЖНЕНИЕ 4
Альтернативный способ «обнаружения» площади круга заключается в следующем.
Представьте, что круг радиуса r состоит из большого количества концентрических круглых отрезков очень тонкой нити. Затем круги вырезаются по радиусу, куски нити выпрямляются и укладываются один поверх другого, как показано на диаграмме ниже, чтобы сформировать форму, которая приблизительно соответствует «треугольнику».
- и
- Найдите основание и высоту треугольника через r.
- б
- Выведите формулу площади круга.
Составные фигуры
Мы можем использовать сложение и вычитание площадей, чтобы найти площадь более сложных фигур.
ПРИМЕР
Найдите площадь заштрихованной области.
РЕШЕНИЕ
Площадь большого полукруга = × π × 32 = Площадь малого полукруга = × π × = см2 = — 2 × = см2
нажмите для просмотра экранаУПРАЖНЕНИЕ 5
Найдите белую область, заключенную между кружками на диаграмме ниже.
 Меньший круг имеет радиус 3 см, а больший радиус 5 см.
Меньший круг имеет радиус 3 см, а больший радиус 5 см.Такая область называется кольцом.
кликните для просмотра скринкастаУПРАЖНЕНИЕ 6
Фигура, состоящая из прямоугольника длиной 8 см и шириной 7 см и двух четвертей окружности радиусом 7 см, вырезана из куска картона.
- а
- Найдите площадь фигуры через число π.
- б
- Найдите приблизительную площадь фигуры, используя π ≈ 3,14.
нажмите для просмотра экранаУПРАЖНЕНИЕ 7
- a
- ABC — прямоугольный треугольник с прямым углом B. Показанная окружность — вписанная окружность треугольника. Найдите радиус r вписанной окружности.
- б
- Найдите радиус вписанной окружности прямоугольного треугольника
со сторонами 5, 12 и 13. - с
- Найдите радиус вписанной окружности прямоугольного треугольника
со сторонами a, b и c, где c — длина гипотенузы.
Ссылки Вперед
Ученики должны понять естественное обобщение круга до трех измерений, сферы.
К 240 г. до н.э. Архимед доказал, что объем сферы радиуса r равен πr3, а площадь ее поверхности равна 4πr2. Это было выдающимся достижением того времени. Сферы имеют большое значение. Земля имеет приблизительно сферическую форму, и вычисление расстояний по сфере — важная задача навигации, связанная с известным разделом математики.0232 как сферическая геометрия.
Обычно мы измеряем углы в градусах, например, 90° — это прямой угол, или 360° — это полный оборот. В основном это связано с историческими причинами — вавилоняне использовали систему счисления с основанием 60, а мы, например, до сих пор используем 60 минут в градусе. Радианная мера имеет решающее значение в более поздних работах по исчислению. Идея состоит в том, чтобы определить угол так, чтобы его размер был таким же, как размер дуги, стягивающей его в центре окружности единичного радиуса.
 Альтернативной системой является измерение углов в радианах.
Альтернативной системой является измерение углов в радианах.Пусть O — центр окружности радиусом 1.
Поскольку угол прямой равен 180° (в градусах) и опирается на дугу длины π в единичной окружности, 180° = π радианы. Отсюда другие углы могут быть представлены как кратные π. Например, угол 45° = радианы, а угол 30° = радианы.
История
Поиск длины окружности и площади круга уходит корнями в глубокую древность. Например, мы читаем в 3-й книге Царств 7:23: «И сделал он расплавленное море десятью локтями от края до края, кругом… и линия в тридцать локтей окружала его». Предполагая, что «море» круглое, это дает значение π, равное 3. Еще раньше вавилоняне дали (неверную) формулу A = C2 для площади круга в терминах длины окружности. Это также дает π = 3,
Египтяне использовали (неправильную) формулу A = , где d — диаметр круга. Это дает π = ≈ 3,164099 — неплохое приближение. Исламская математика в Средние века использовала приближение π ≈ т.
 к. = 3,1622….
к. = 3,1622….Греки, особенно Евклид, показали, что «окружности относятся друг к другу, как квадраты к диаметрам», что говорит нам о том, что площадь круга пропорциональна квадрату радиуса. Позднее Архимед (287-212 гг. до н. э.) доказал теорему: «Площадь любого круга равна площади прямоугольного треугольника, в котором один из катетов равен радиусу, а другой — длине окружности», что аналогично к нашему неформальному выводу формулы площади круга в разделе «Содержание» выше.
Во всех этих выражениях потребность в символе π была исключена за счет выражения площади через радиус и длину окружности. Буква π была выбрана в начале 18 века, потому что это первая буква греческого слова, обозначающего периметр (периметрон).
Архимед был также первым, кто сделал серьезную попытку оценить число π. Он вписал круги в правильные многоугольники. Используя многоугольник с 96 сторонами, он доказал, что 3 < π < 3. (Вы можете проверить, насколько это хорошее или плохое приближение.)
На протяжении веков число π связывали исключительно с кругами, сферами и конусами.

В 1593 году, используя многоугольники и некоторую геометрию, Франсуа Виет показал, что= · · ….
, который дает аналитическое «определение» π как предела произведения, но по существу не зависит от окружности.
В 1655 году появился удивительный продукт Уоллиса:
= . . . . . . . …
Хотя мы могли бы определить π, используя любую из этих формул, ни одна из них не особенно хороша для действительной аппроксимации π с точностью до многих знаков после запятой.
Используя формулу
= 4tan−1 − tan−1 ,
Мачин (1706) вычислил π вручную с точностью до 100 знаков после запятой. Излишне говорить, что это было значительно улучшено, и современные методы дают π с точностью до миллиардов знаков после запятой.
Число π встречается в математике во многих местах, где его появление априори не ожидалось.
 Одним из таких примеров является замечательная бесконечная сумма
Одним из таких примеров является замечательная бесконечная сумма+ + + + …. =
, открытый Эйлером около 1730 года.
Закон Кулона в физике утверждает, что величина электростатической силы F, действующей на заряд q1 из-за наличия второго заряда q2, определяется выражением
Ф =
где ε0 — константа, а r — расстояние между двумя зарядами.
Это одна из многих научных формул, в которых фигурирует число π.
Число π продолжает очаровывать и бросать вызов математикам. Мы знаем, что это иррациональное число, и подозреваем, что его цифры статистически случайны, но доказательств этого пока не найдено.
ССЫЛКИ
История математики: введение, 3-е издание, Victor J. Katz, Addison-Wesley, (2008)
History of Mathematics, D.
 E. Smith, Dover Publications New York, (1958)
E. Smith, Dover Publications New York, (1958)ОТВЕТЫ НА УПРАЖНЕНИЯ
25 смПлощадь треугольника = πr2.
УПРАЖНЕНИЕ 5
16π CM2
Упражнение 6
A (56 +) CM2
B 132,93 CM2
Упражнение 7
A R = 1 B R = 2 C
Проект улучшения математики в школах (Time) 2009- 2011 финансировался Министерством образования, занятости и трудовых отношений правительства Австралии.
Мнения, выраженные здесь, принадлежат автору и не обязательно отражают точку зрения Министерства образования, занятости и трудовых отношений правительства Австралии.
© Мельбурнский университет от имени Международного центра передового опыта в области образования по математике (ICE-EM), образовательного подразделения Австралийского института математических наук (AMSI), 2010 г. (если не указано иное). Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License.
https://creativecommons. org/licenses/by-nc-nd/3.0/
org/licenses/by-nc-nd/3.0/Круговые факты — площадь, окружность, диаметр, радиус
Эта запись была опубликована автором Anne Helmenstine (обновлено )
Круг представляет собой двумерную форму, образованную всеми точками, которые находятся на одинаковом расстоянии от центра.Исследуйте эту коллекцию фактов о кругах. Узнайте, как найти длину окружности, диаметр, радиус и площадь круга, а также получите определения круговых терминов, используемых в геометрии.
Круг Факты
- Окружность — это двумерная фигура, образованная всеми точками, которые находятся на одинаковом расстоянии от центральной точки.
- Технически только точки, равноудаленные от центра, образуют круг. Область, заключенная в круг, называется диском.
- Слово «круг» происходит от греческого слова κρίκος ( krikos ), означающего «обруч» или «кольцо».

- Круг — единственная односторонняя фигура, содержащая площадь. Прямая линия – это окружность, содержащая бесконечную площадь.
- Люди распознавали круги с древних времен. Естественные круги включают формы Солнца и Луны, человеческий глаз, поперечные сечения деревьев, некоторые цветы, некоторые ракушки и т. д.
- Расстояние по окружности является ее окружностью.
- Расстояние от центра до окружности является ее радиусом.
- Наибольшее расстояние между двумя точками на окружности — это диаметр, который представляет собой отрезок, проходящий через центр.
- Круг — это фигура с кратчайшим периметром, охватывающим площадь.
- Круг является наиболее симметричной формой, потому что каждая линия, проходящая через центр, представляет собой линию зеркальной симметрии. Он имеет симметрию вращения для каждого угла вокруг своего центра.
- Пи (π) — иррациональное число, представляющее собой отношение длины окружности к ее диаметру. Оно примерно равно 3,1415259.

- Архимед доказал, что площадь, заключенная в круг, равна площади треугольника с основанием, равным длине окружности круга, и высотой, равной радиусу круга.
- Полная дуга окружности составляет 360 градусов.
- Окружность представляет собой особый тип эллипса, в котором два фокуса находятся в одном и том же месте, а эксцентриситет равен 0,9.0202
- Написанный в 1700 г. до н. э. папирус Райнда описывает метод нахождения площади круга. В результате получается 256/81, что составляет около 3,16 (близко к числу пи).
- Внутри каждого треугольника можно нарисовать специальную окружность, называемую вписанной окружностью, где каждая из трех сторон треугольника касается окружности.
Как найти длину окружности
Окружность (C) — это расстояние по окружности. Есть несколько способов найти длину окружности. Вы можете рассчитать его либо по радиусу (r), либо по диаметру (d), либо измерить его.
- C = 2πr
- C = πd
- Длину окружности проще всего измерить с помощью веревки.
 Оберните нить вокруг круга, отметьте длину, а затем с помощью линейки или измерительного стержня измерьте длину нити.
Оберните нить вокруг круга, отметьте длину, а затем с помощью линейки или измерительного стержня измерьте длину нити.
Как найти диаметр окружности
Диаметр (d) — это длина отрезка с концами на окружности, проходящей через ее центр. Это самое длинное расстояние по кругу. Диаметр в два раза больше длины радиуса.
- d = 2r
- d = C/π
- Измерьте диаметр, найдя самый длинный отрезок, пересекающий окружность.
Как найти радиус круга
Радиус (r) — это расстояние от центра круга до его границы. Это половина длины диаметра.
- r = d/2
- r = C/2π
- Если вы нарисуете окружность с помощью циркуля, радиусом будет расстояние между двумя его точками. Измерение радиуса круга немного сложно, если вы не знаете его центр. Иногда проще измерить длину окружности или диаметр и вычислить радиус.
Как найти площадь круга
Площадь (A) круга — это область, ограниченная кругом, или площадь его диска.

- A = πr 2
- A = π(d/2) 2
- A = Cr/2 – Вы можете использовать доказательство Архимеда, чтобы найти площадь круга, используя его длину окружности и радиус. Установите основание треугольника равным длине окружности C и высоте равной радиусу r. Формула площади треугольника 1/2 bh становится A = Cr/2
Словарь терминов круга
Вот ключевые словарные термины, которые необходимо знать:
- Кольцо : Кольцо представляет собой кольцо, образованное между двумя концентрическими окружностями.
- Дуга : Дуга – это любой сегмент окружности, образованный соединенными точками.
- Центр ( Центр ): Центр — это точка, равноудаленная от всех точек окружности. Его также называют источником .
- Хорда : Хорда представляет собой отрезок с концами на окружности. Диаметр — самая длинная хорда.

- Окружность : Окружность — это расстояние по окружности.
- Закрыто : Регион, включающий его границы.
- Диаметр : Диаметр — это отрезок с концами на окружности и средней точкой в ее центре. Это наибольшее расстояние между любыми двумя точками на окружности.
- Диск : Диск — это область внутри круга.
- Линза : Линза — это область, разделяемая двумя перекрывающимися дисками.
- Открытый : Любой регион, за исключением его границ.
- Проход : Проход — это компланарная линия, не имеющая общих точек с окружностью.
- Радиус : Радиус — это отрезок, идущий от центра к окружности.
- Сектор : Сектор представляет собой область внутри круга, ограниченного двумя радиусами.
- Сегмент : Сегмент представляет собой область, ограниченную дугой и хордой.

- Секанс : Секанс — это хорда, выходящая за пределы круга. Другими словами, это копланарная прямая, пересекающая окружность в двух точках.
- Полукруг : Полуокружность – это дуга, диаметр которой является конечными точками, а центр – средней точкой. Внутренняя часть полукруга представляет собой полукруг.
- Касательная : Касательная — это компланарная линия, имеющая одну общую точку с окружностью.
Рабочие листы с кругами
Потренируйтесь находить длину окружности и площадь кругов с помощью этих математических листов.
Ссылки
- Гамелен, Теодор (1999). Введение в топологию г. Минеола, Нью-Йорк: Dover Publications. ISBN 0486406806 .
- Харкнесс, Джеймс (1898 г.). «Введение в теорию аналитических функций». Природа . 59 (1530): 30. doi:10.1038/059386a0
- Кац, Виктор Дж. (1998). История математики / Введение (2-е изд.
 ). Эддисон Уэсли Лонгман. ISBN 978-0-321-01618-8.
). Эддисон Уэсли Лонгман. ISBN 978-0-321-01618-8. - Огилви, К. Стэнли (1969). Экскурсии по геометрии . Дувр.
Решения Balbharati для математики 2 Геометрия 10-й стандарт SSC Maharashtra State Board глава 3 — Circle [Последнее издание]
Решения Бальбхарати для математики 2 Геометрия 10-й стандарт SSC Maharashtra State Board Глава 3 Круговая задача, набор 3 [Страницы 83 — 90]
Набор задач 3 | Вопрос 1.01 | Страница 83
Дано четыре альтернативных ответа на следующий вопрос. Выбрать правильный вариант.
Два круга радиусами 5,5 см и 3,3 см соответственно касаются друг друга. Каково расстояние между их центрами?4,4 см
8,8 см
2,2 см
8,8 или 2,2 см
ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 1.02 | Страница 82
На следующий вопрос даны четыре альтернативных ответа. Выбрать правильный вариант.
Две окружности пересекаются так, что каждая окружность проходит через центр другой.
 Если расстояние между их центрами равно 12, каков радиус каждого круга?
Если расстояние между их центрами равно 12, каков радиус каждого круга?6 см
12 см
24 см
затрудняюсь ответить
ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 1.03 | Страница 83
Дано четыре альтернативных ответа на следующий вопрос. Выбрать правильный вариант.
Окружность касается всех сторон параллелограмма. Таким образом, параллелограмм должен быть ______
прямоугольником
ромбом
квадратом
трапеция
ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 1.04 | Страница 83
Дано четыре альтернативных ответа на следующий вопрос. Выбрать правильный вариант.
Длина отрезка, проведенного из точки, находящейся на расстоянии 12,5 см от центра окружности, равна 12 см, найдите диаметр окружности.25 см
24 см
7 см
14 см
ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 1.
 05 | Страница 83
05 | Страница 83Дано четыре альтернативных ответа на следующий вопрос. Выбрать правильный вариант.
Если две окружности касаются снаружи, сколько общих касательных можно провести?One
Два
Три
Четыре
Просмотр Раствор
Проблема набор 3 | Вопрос 1.06 | Страница 83
Дано четыре альтернативных ответа на следующий вопрос. Выбрать правильный вариант.
∠ACB вписана в дугу ACB окружности с центром O. Если ∠ACB = 65°, найти m(дуга ACB).
65 °
130 °
295 °
230 °
Вид. Вопрос 1.07 | Страница 83
Дано четыре альтернативных ответа на следующий вопрос. Выбрать правильный вариант.
Хорды AB и CD окружности пересекаются внутри окружности в точке E. Если AE = 5,6, EB = 10, CE = 8, найти ED.7
8
11,2
Просмотр решения
Проблема набор 3 | Вопрос 1.
 08 | Страница 83
08 | Страница 83Дано четыре альтернативных ответа на следующий вопрос. Выберите правильный вариант
В циклическом ▢ABCD удвоенная мера ∠A в три раза больше ∠C. Найдите меру ∠C?
36 °
72 °
90 °
108 °
Посмотреть раствор
Проблемный набор 3 | Вопрос 1.09 | Страница 83
Дано четыре альтернативных ответа на следующий вопрос. Выбрать правильный вариант.
Точки A, B, C лежат на окружности так, что m(дуга AB) = m(дуга BC) = 120°. Ни одна точка, кроме точки B, не является общей для дуг. Какой тип ∆ABC?
ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 1.1 | Страница 83
Дано четыре альтернативных ответа на следующий вопрос. Выбрать правильный вариант.
Seg XZ — это диаметр окружности. Точка Y лежит внутри него. Сколько из следующих утверждений верны? (i) Невозможно, чтобы угол ∠XYZ был острым.
 (ii) ∠XYZ не может быть прямым углом. (iii) ∠XYZ — тупой угол. (iv) Невозможно сделать определенное утверждение для меры ∠XYZ.
(ii) ∠XYZ не может быть прямым углом. (iii) ∠XYZ — тупой угол. (iv) Невозможно сделать определенное утверждение для меры ∠XYZ.Только один
Только два
Только три
Все
ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | вопрос 2 | Страница 84
Прямая l касается окружности с центром O в точке P. Если радиус окружности равен 9 см, ответьте на следующий вопрос.
(1) Что такое d(O, P) = ? Почему ?
(2) Если d(O, Q) = 8 см, где находится точка Q?
(3) Если d(OQ) = 15 см, сколько положений точки Q являются прямыми на прямой l? На каком расстоянии каждый из них будет от точки P?ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 3 | Страница 84
На данном рисунке M — центр окружности, а отрезок KL — касательный отрезок.
Если MK = 12, KL = \[6\sqrt{3}\], то найти –
(1) Радиус окружности.
(2) Меры ∠K и ∠M.ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 4 | Страница 84
На данном рисунке O является центром окружности.
 Seg AB, seg AC являются касательными сегментами. Радиус окружности равен r и l(AB) = r. Докажите, что ▢ABOC — квадрат.
Seg AB, seg AC являются касательными сегментами. Радиус окружности равен r и l(AB) = r. Докажите, что ▢ABOC — квадрат.
Доказательство: Нарисуйте сегменты OB и OC.l(AB) = r ……[Дано] (I)
AB = AC ……[`квадрат`] (II)
Но OB = OC = r … …[`квадрат`] (III)
Из (i), (ii) и (iii)
AB = `квадрат` = OB = OC = r
∴ Четырехугольник ABOC является `квадратом`
Аналогично , ∠OBA = `квадрат` ……[Теорема о касании]
Если один из углов `квадрата` прямой, то это квадрат.
∴ Четырехугольник АВОС является квадратом.
ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 5 |
На данном рисунке ▢ABCD — параллелограмм. Он описывает окружность с центром T. Точки E, F, G, H являются точками касания. Если AE = 4,5, EB = 5,5, найдите AD.
ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 6 |
На данном рисунке окружность с центром M касается окружности с центром N в точке T.
 Радиус RM касается меньшего круга в точке S. Радиусы окружностей равны 9 см и 2,5 см. Найдите ответы на следующие вопросы, следовательно, найдите соотношение MS:SR.
Радиус RM касается меньшего круга в точке S. Радиусы окружностей равны 9 см и 2,5 см. Найдите ответы на следующие вопросы, следовательно, найдите соотношение MS:SR.
(1) Найдите длину отрезка MT
(2) Найдите длину отрезка MN
(3) Найдите меру ∠NSM.ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | вопрос 7 |
На соседней фигуре окружности с центрами X и Y касаются друг друга в точке Z. Секущая, проходящая через Z, пересекает окружности в точках A и B соответственно. Докажите, что радиус XA || радиус YВ. Заполните пропуски и завершите доказательство.
Конструкция: Нарисуйте сегменты XZ и YZ.
Доказательство :
По теореме о касании окружностей точки X, Z, Y являются «квадратными».
∴ ∠XZA ≅ `квадрат` …(противоположные углы)
Пусть ∠XZA = ∠BZY = a …(I)
Теперь отрезок XA ≅ отрезок XZ …[Радиусы 91 8 окружности] ∠XAZ = `квадрат` = a . ..[теорема о равнобедренном треугольнике](II)
..[теорема о равнобедренном треугольнике](II)
Аналогично,seg YB ≅ seg YZ …[Радиусы одной окружности]
∴∠BZY = `квадрат` = a . ..[теорема о равнобедренном треугольнике ] (III)
∴ из (I), (II), (III),
∠XAZ = «квадрат»
∴ радиус XA || радиус YZ …[`квадрат`]ПРОСМОТР РЕШЕНИЯ
Набор задач 3 | Вопрос 8 |
На данном рисунке окружности с центрами X и Y соприкасаются внутри в точке Z . Отрезок BZ является хордой большей окружности и пересекает меньшую окружность в точке A. Докажите, что отрезок AX || сегмент ПО.
ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 9 |
На рисунке линия l касается окружности с центром O в точке P. Q — середина радиуса OP. RS — хорда, проходящая через Q, такая, что хорды RS || линия л. Если RS = 12, найдите радиус окружности.
ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 10 |
На данном рисунке отрезок AB является диаметром окружности с центром C.
 Прямая PQ является касательной, которая касается окружности в точке T. Отрез AP ⊥ прямой PQ и отрезок BQ ⊥ прямой PQ. Докажите, что отрезок CP ≅ отрезок CQ.
Прямая PQ является касательной, которая касается окружности в точке T. Отрез AP ⊥ прямой PQ и отрезок BQ ⊥ прямой PQ. Докажите, что отрезок CP ≅ отрезок CQ.ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 11 |
Нарисуйте круги с центрами A, B и C радиусом 3 см каждый так, чтобы каждый круг касался двух других кругов.
ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 12 |
Докажите, что никакие три точки на окружности не могут лежать на одной прямой.
ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 13 |
На данном рисунке прямая PR касается окружности в точке Q. Ответьте на следующие вопросы с помощью рисунка.
(1) Чему равна сумма ∠ TAQ и ∠ TSQ?
(2) Найдите углы, равные ∠ AQP.
(3) Какие углы равны ∠ QTS?
(4) ∠TAS = 65°, найти меру ∠TQS и дуги TS.
(5) Если ∠AQP = 42° и ∠SQR = 58°, найдите меру ∠ATS.ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 14 |
На данном рисунке О — центр окружности, хорда PQ ≅ хорда RS Если ∠ POR = 70° и (дуга RS) = 80°, найти –
(1) м(дуга PR)
( 2) m(arc QS)
(3) m(arc QSR)ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 15 | Страница 87
На данном рисунке m(дуга WY) = 44°, m(дуга ZX) = 68°, тогда
(1) Найдите меру ∠ ZTX.
(2) Если WT = 4,8, TX = 8,0,
YT = 6,4, найти TZ.
(3) Если WX = 25, YT = 8,
YZ = 26, найти WT.ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 16 |
По данному рисунку
(1) m(дуга CE) = 54°, m(дуга BD) = 23°, найти меру ∠CAE.
(2) Если AB = 4,2, BC = 5,4, AE = 12,0, найдите AD
(3) Если AB = 3,6, AC = 9,0, AD = 5,4, найдите AEПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 17 | Страница 88
На данном рисунке хорда EF || аккорд ГГ. Докажите, что хорда EG ≅ хорда FH. Заполните пропуски и напишите доказательство.
ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 18 | Страница 88
На данном рисунке P – точка контакта.
(1) Если m(дуга PR) = 140°, ∠ POR = 36°, найти m(дуга PQ)
(2) Если OP = 7,2, OQ = 3,2, найти OR и QR
(3) Если OP = 7.2, OR = 16.2, найти QR.ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 19 | Страница 88
На данном рисунке окружности с центрами C и D соприкасаются внутри в точке E.
 D лежит на внутренней окружности. Хорда EB внешней окружности пересекает внутреннюю окружность в точке A. Докажите, что отрезок EA ≅ отрезок AB.
D лежит на внутренней окружности. Хорда EB внешней окружности пересекает внутреннюю окружность в точке A. Докажите, что отрезок EA ≅ отрезок AB.ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 20 |
На данном рисунке отрезок AB является диаметром окружности с центром O. Биссектриса ∠ ACB пересекает окружность в точке D. Докажите, что отрезок AD ≅ отрезок BD. Завершите следующее доказательство, заполнив пропуски.
ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 21 |
На данном рисунке отрезок MN — хорда окружности с центром O. MN = 25, L — точка на хорде MN такая, что ML = 9 и d(O,L) = 5. Найдите радиус круга.
ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 22 |
На данном рисунке две окружности пересекаются друг с другом в точках S и R. Их общая касательная PQ касается окружности в точках P, Q.
Докажите, что ∠ PRQ + ∠ PSQ = 180°ПОСМОТРЕТЬ РЕШЕНИЕ
Набор задач 3 | Вопрос 23 |
На данном рисунке две окружности пересекаются в точках M и N.


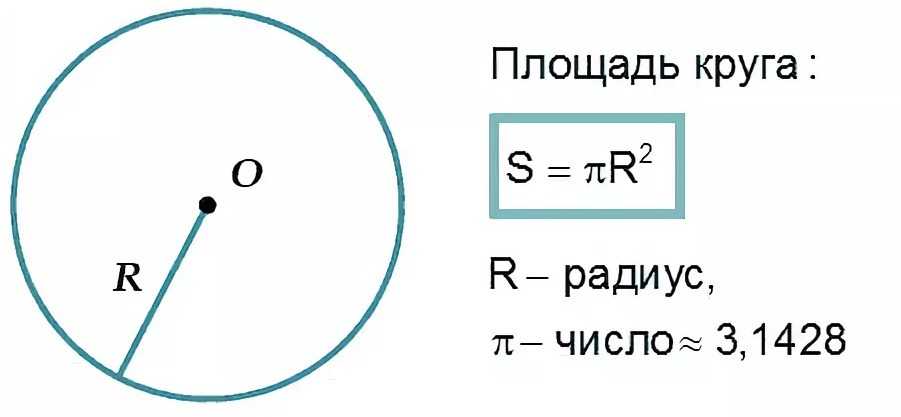 Её длину будем обозначать латинской буквой l.
Её длину будем обозначать латинской буквой l. 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.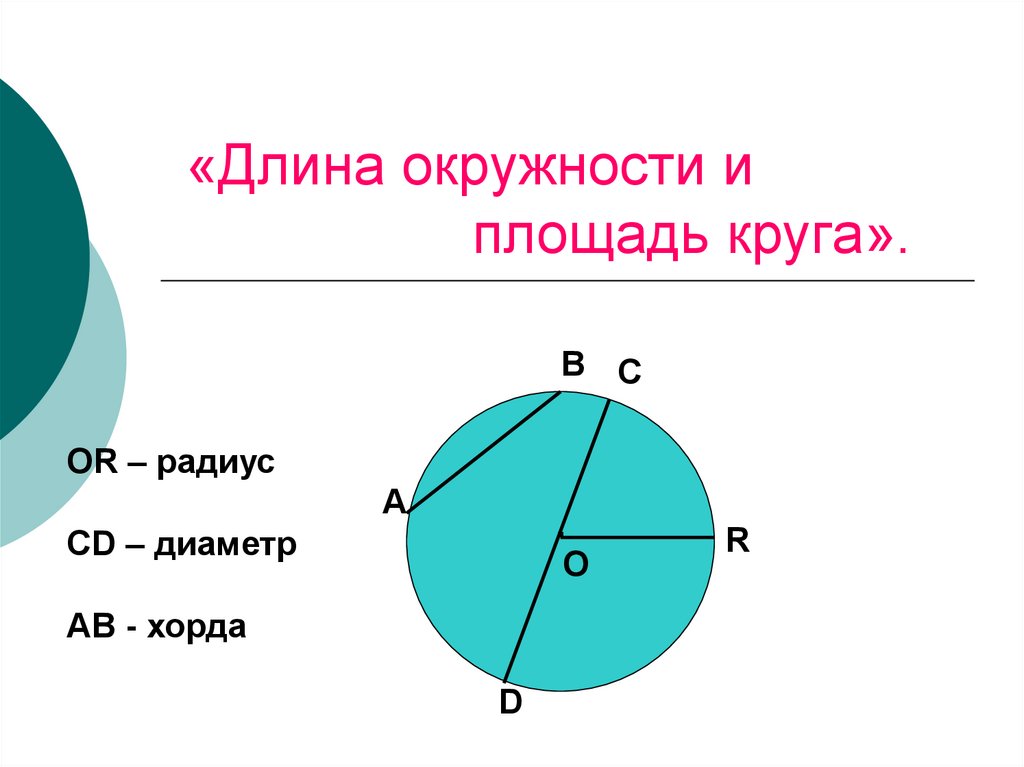
 Формула является достаточно простой и выглядит так: D = C/π = 2*R.
Формула является достаточно простой и выглядит так: D = C/π = 2*R.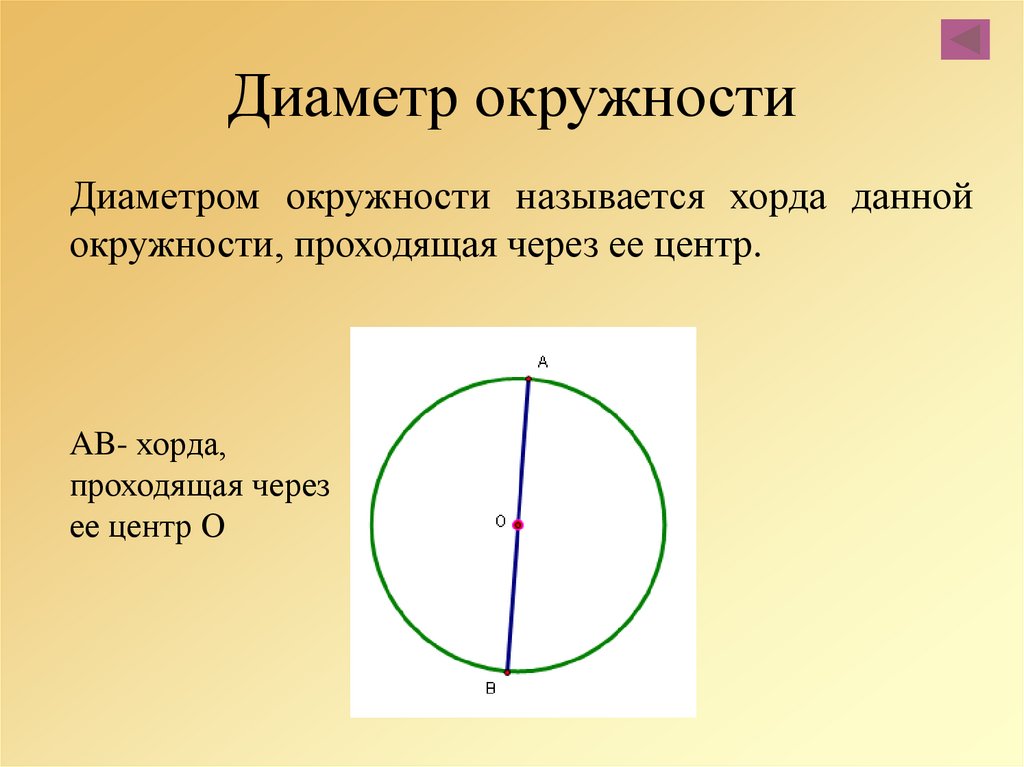


 Формула является достаточно простой и выглядит так: D = C/π = 2*R.
Формула является достаточно простой и выглядит так: D = C/π = 2*R. Он обозначается латинской буквой r.
Он обозначается латинской буквой r. 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м. Ведь нам известно, что диаметром является отрезок, который соединяет несколько точек на окружности, проходя при этом через ее центр. Из этого следует, что диаметр – это 2 радиуса. Тогда радиус мы находим по формуле: r=D/2, где r – это радиус окружности, а D, соответственно, ее диаметр. Например, диаметр по условию равен 32 см, тогда радиус мы вычисляем так: 32/2=16 см.
Ведь нам известно, что диаметром является отрезок, который соединяет несколько точек на окружности, проходя при этом через ее центр. Из этого следует, что диаметр – это 2 радиуса. Тогда радиус мы находим по формуле: r=D/2, где r – это радиус окружности, а D, соответственно, ее диаметр. Например, диаметр по условию равен 32 см, тогда радиус мы вычисляем так: 32/2=16 см.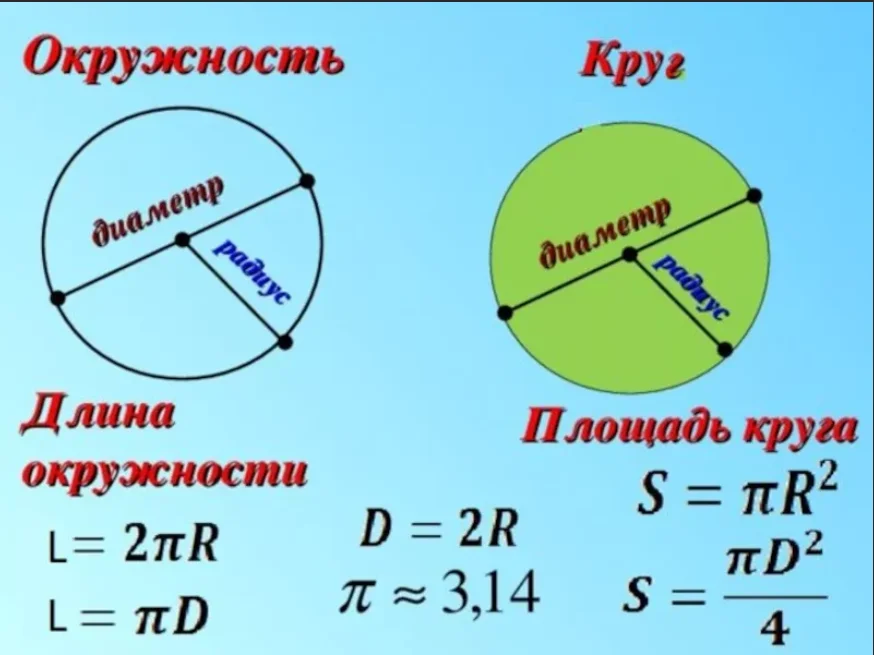 Отсюда находим формулу радиуса: r=√(S/π). Опять же рассмотрим все в цифровом исчислении. Пусть вам дана в условии задачи площадь, к примеру – 28,26 см2. Подставляем данные в выведенную нами формулу и получаем: √28,26/3,14=3 см.
Отсюда находим формулу радиуса: r=√(S/π). Опять же рассмотрим все в цифровом исчислении. Пусть вам дана в условии задачи площадь, к примеру – 28,26 см2. Подставляем данные в выведенную нами формулу и получаем: √28,26/3,14=3 см. Такая прямая называется касательной к окружности , а их общая точка называется точкой касания прямой и окружности .
Такая прямая называется касательной к окружности , а их общая точка называется точкой касания прямой и окружности . 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.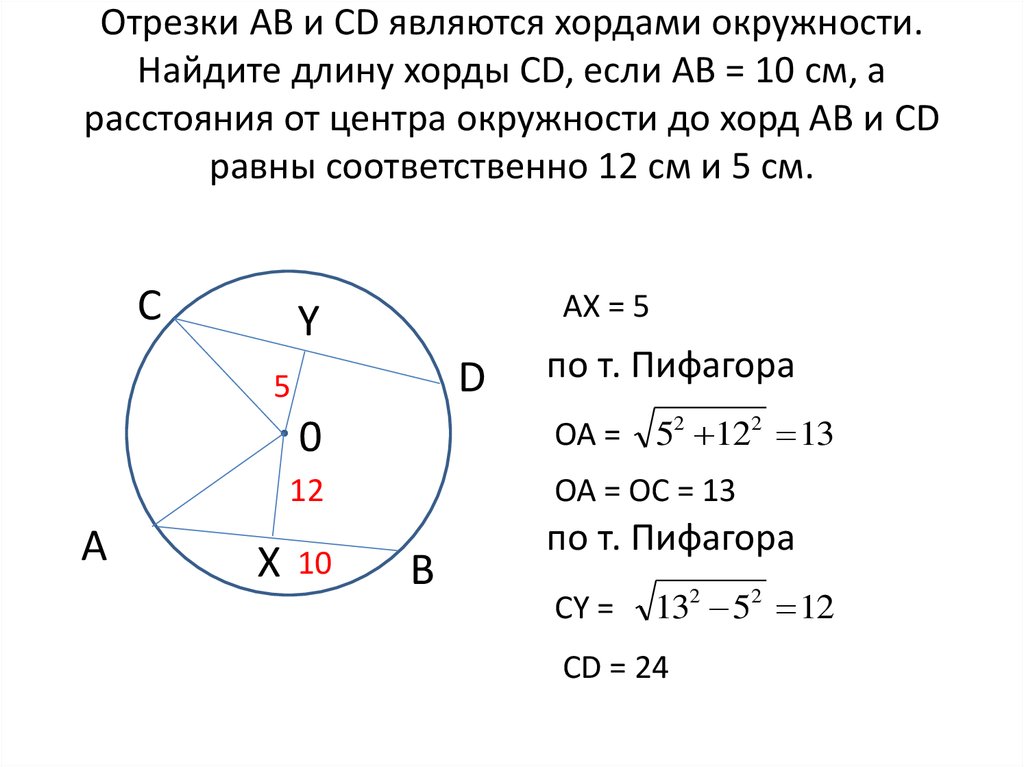 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м. При этом отрезок АВ – диаметр.
При этом отрезок АВ – диаметр.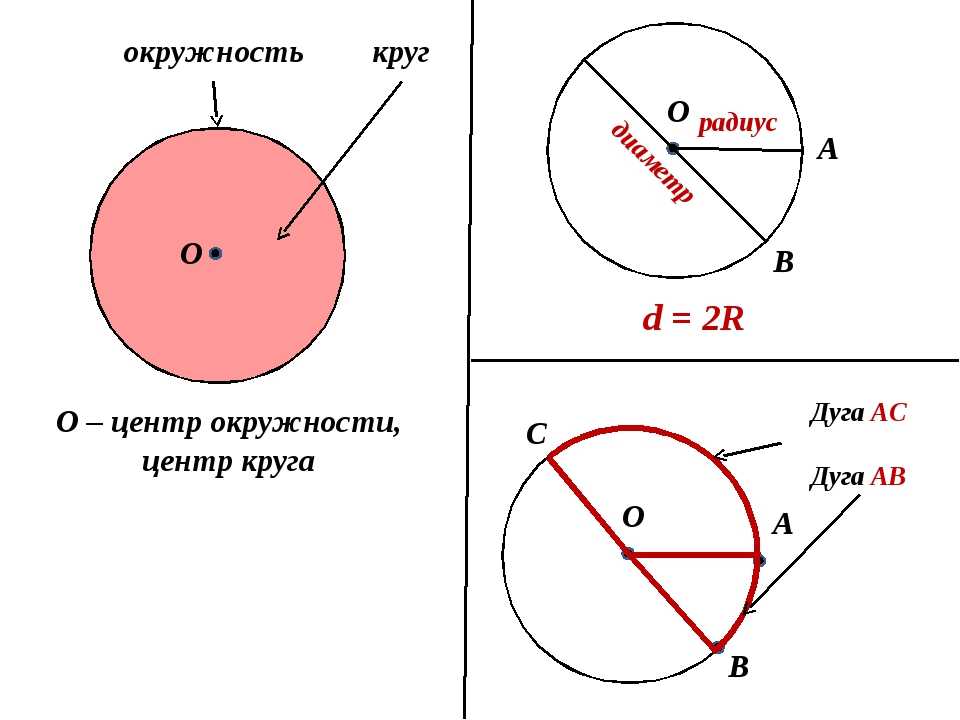 2/(4П) = 2209/12,56 = 175,87 кв. м.
2/(4П) = 2209/12,56 = 175,87 кв. м.

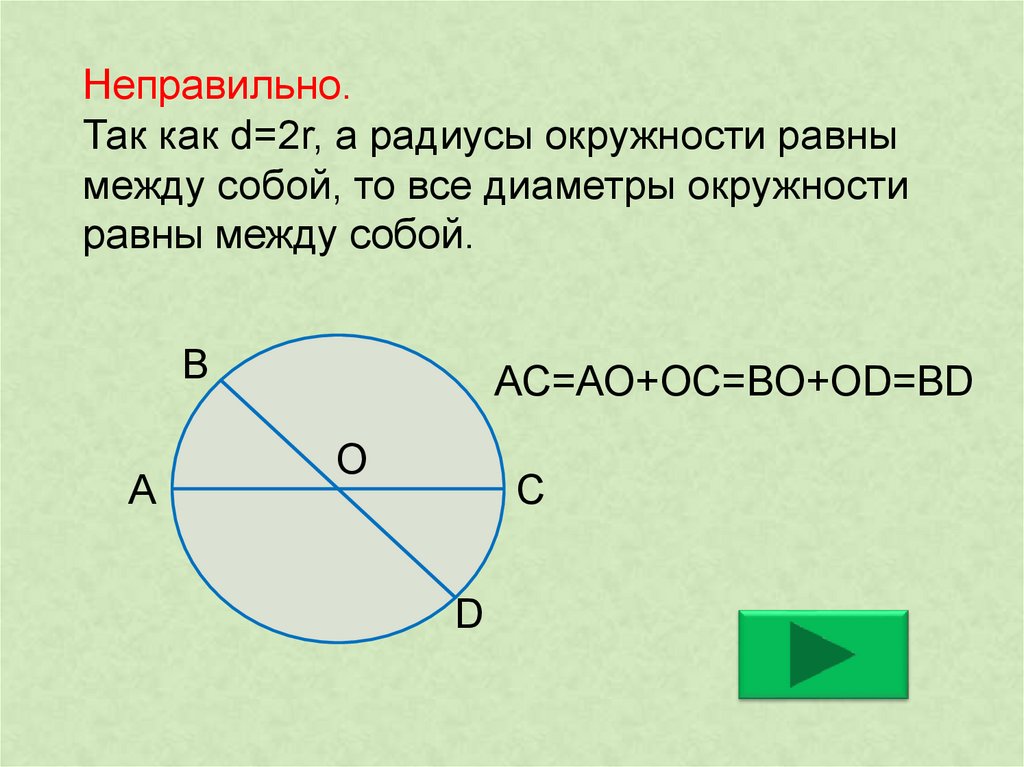
 {circ}
{circ}
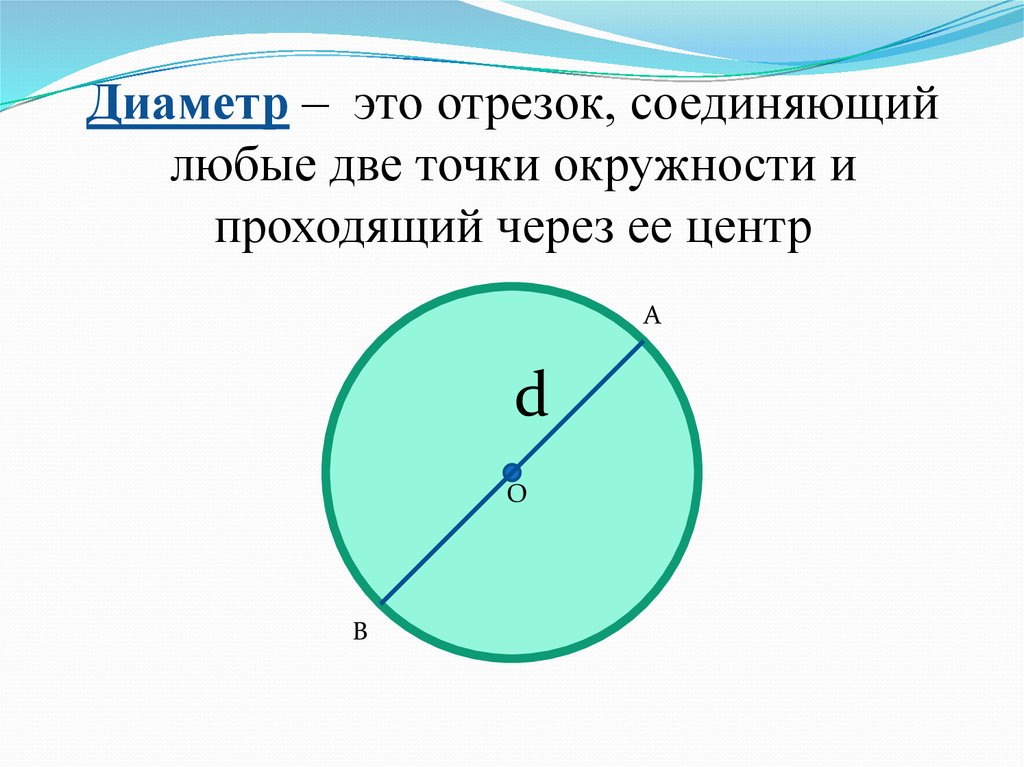 circ$
circ$ Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон. 1).
1).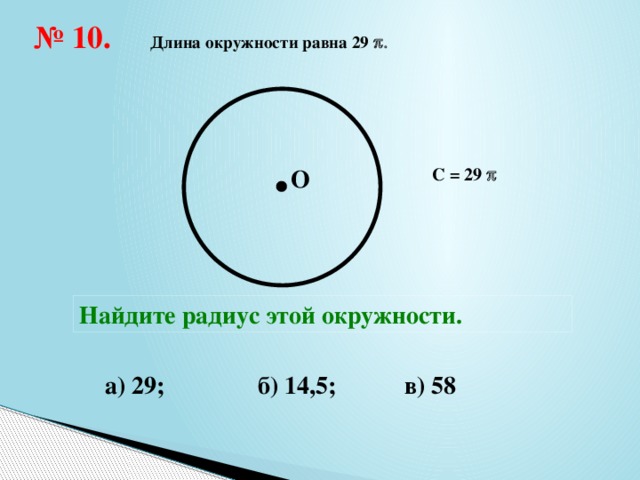
 Это расстояние называется радиусом.
Это расстояние называется радиусом. Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей:
Так как радиус в два раза меньше, то выражение немного видоизменится. И формула того, как рассчитать длину окружности, зная диаметр, будет следующей: 3,14 * 10 = 31,4 (см).
3,14 * 10 = 31,4 (см).
 А вот синее содержимое внутри нее — и есть круг.
А вот синее содержимое внутри нее — и есть круг.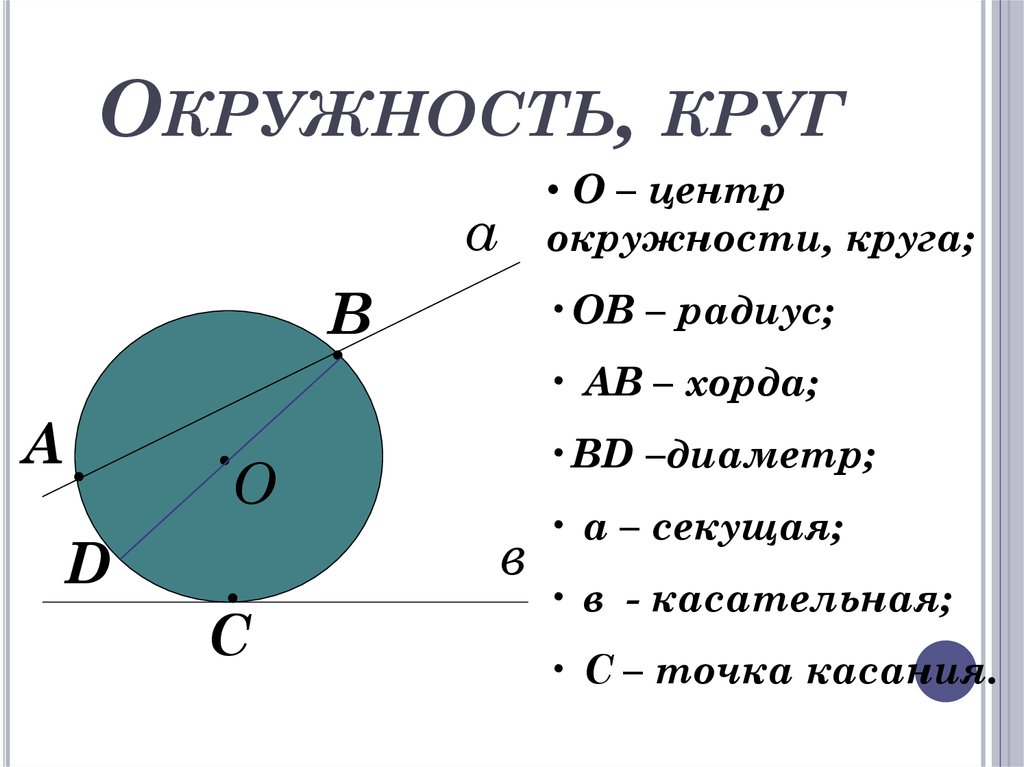 Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.
Умножаем 7 см на 2 и получаем величину, равную 14 см. Ответ: D заданной фигуры равен 14 см.

 На рисунке выше — это отрезок «BC».На рисунке также видно, что диаметр равен двум радиусам. Поэтому справедливо выражение «D = 2R».
На рисунке выше — это отрезок «BC».На рисунке также видно, что диаметр равен двум радиусам. Поэтому справедливо выражение «D = 2R». Длина окружности обозначается буквой «С» (читается как «Це»). C = πD C = 2πR , так как D = 2R
Длина окружности обозначается буквой «С» (читается как «Це»). C = πD C = 2πR , так как D = 2R
 14.
14.
 Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.
Это колеса, круглые оконные проемы, трубы, различная посуда и многое другое. Подсчитать, чему равна длина окружности, можно, зная ее диаметр или радиус.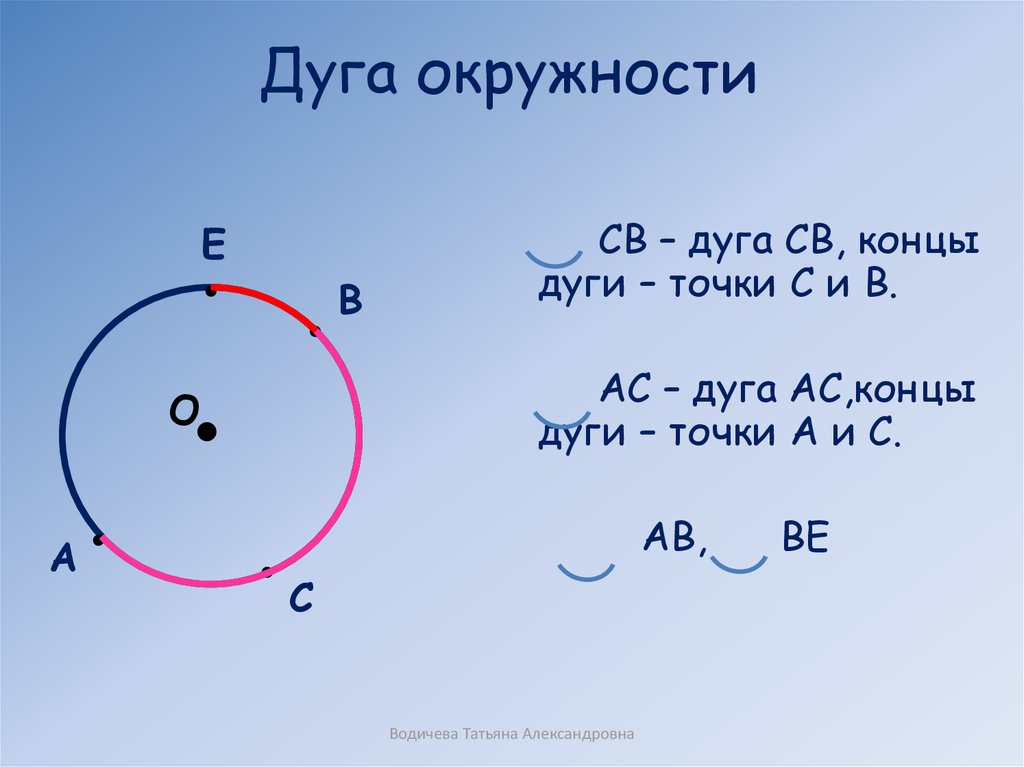 Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.
Периметр круга и есть ее длина. По разным определениям круг может включать или не включать саму кривую, являющуюся его границей.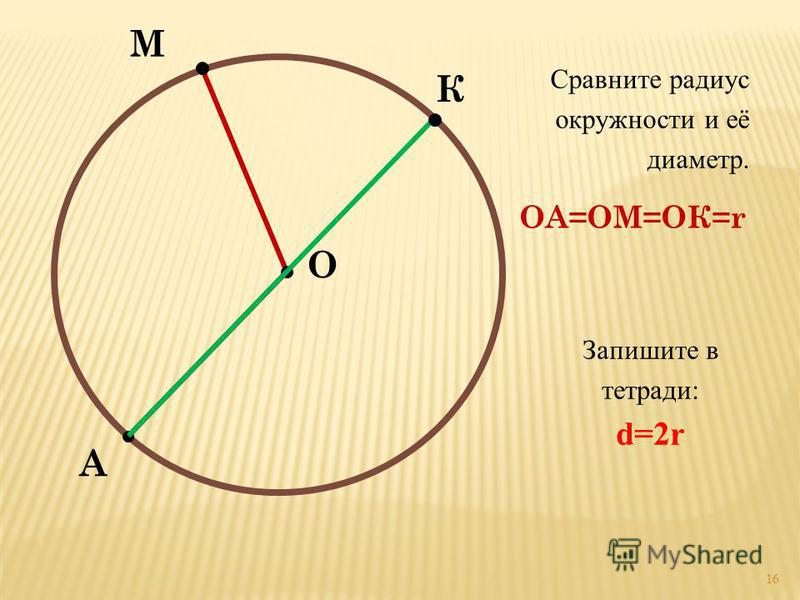
 С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы.
С помощью вычислений на суперкомпьютерах в 2011 году узнали 10-триллионный знак константы. Окружность имеет также свой радиус, равный расстоянию этих точек от центра.
Окружность имеет также свой радиус, равный расстоянию этих точек от центра.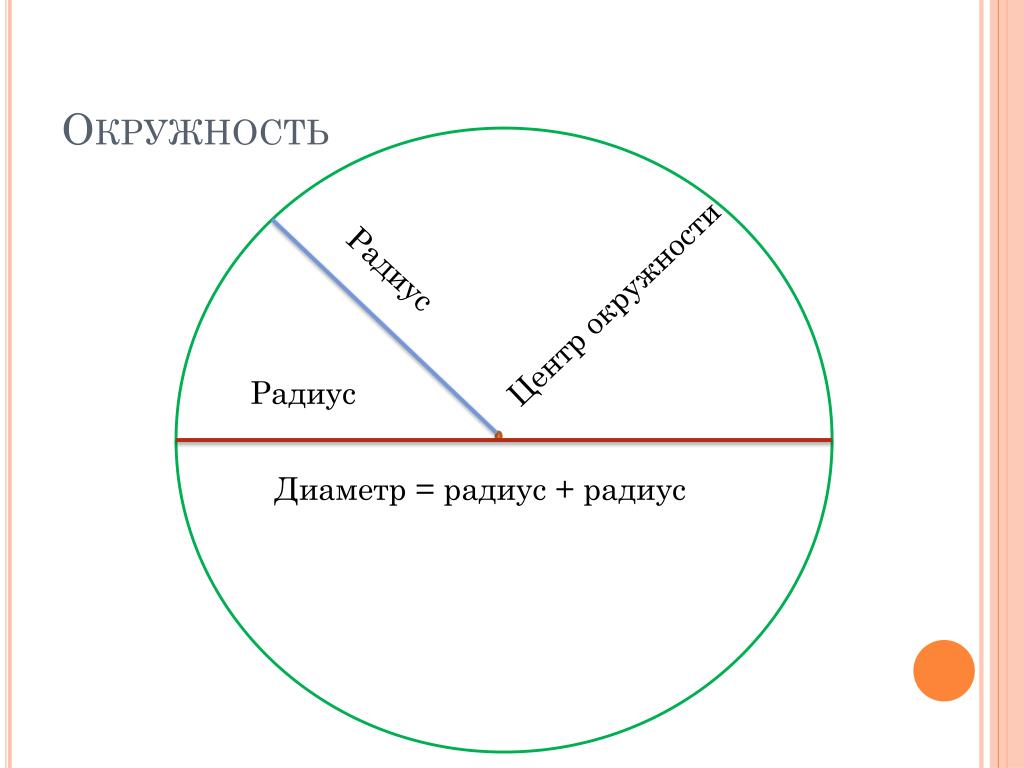
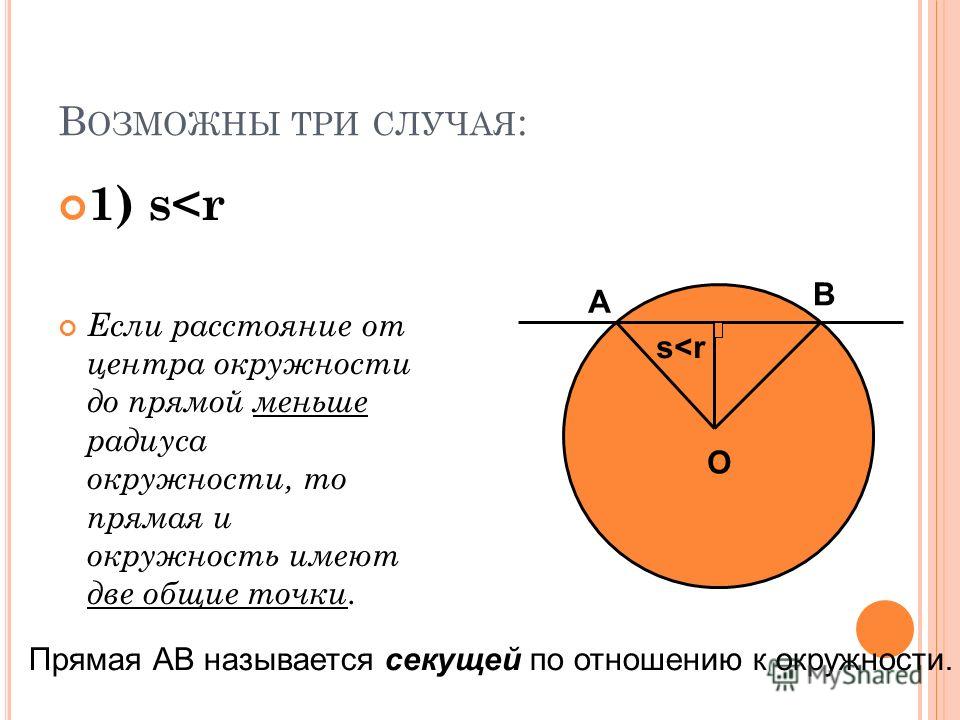
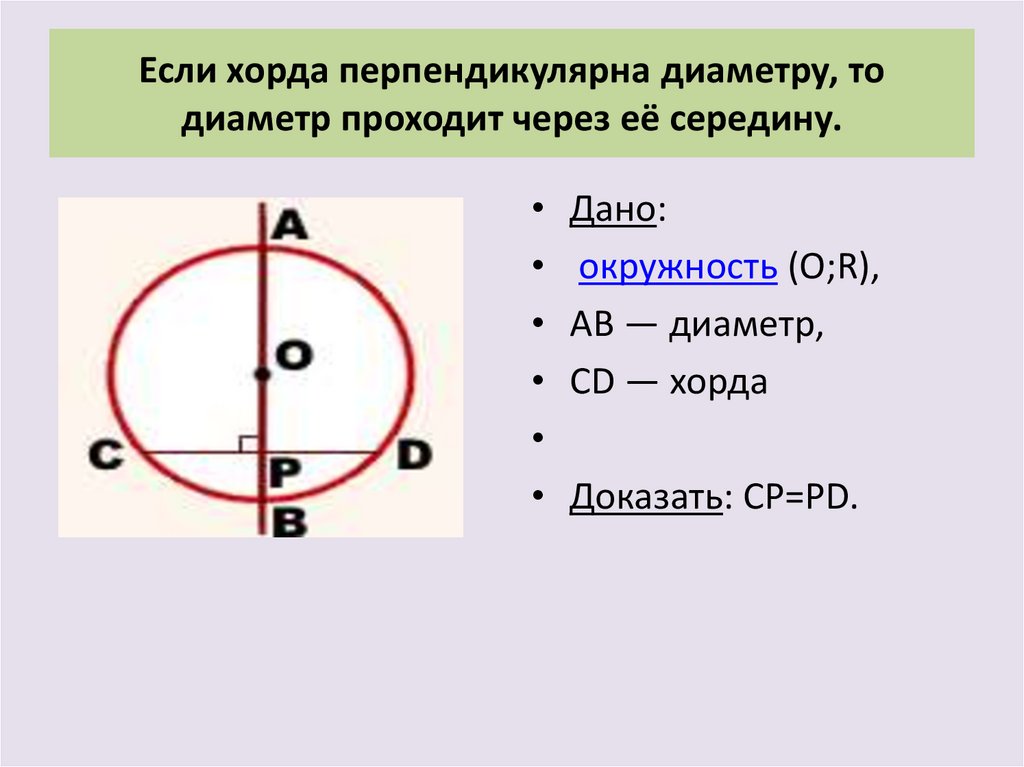
 длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор:
длина дуги ). Для этого случая для расчета площади сегмента и длины дуги можно использовать следующий калькулятор: Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи):
Для обозначения этой величины используется маленькая (строчная) греческая буква π (пи): Найти радиус окружности, длина которой равна 7,85 м.
Найти радиус окружности, длина которой равна 7,85 м.
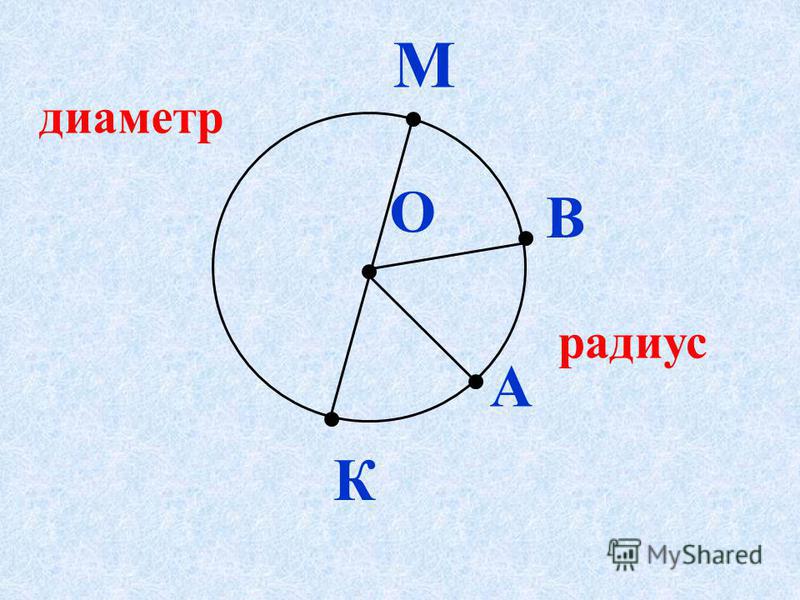
 Это отношение и обозначается буквой π.
Это отношение и обозначается буквой π.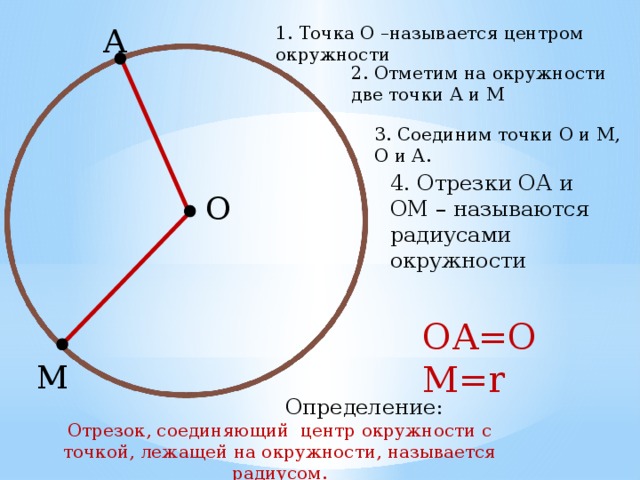 На рисунке ниже изображен круг с центром O. Напомним из определения, что все точки, расположенные на границе окружности, равноудалены (равноудалены) от этой центральной точки O . Расстояние от центра круга до его границы называется радиусом , R .
На рисунке ниже изображен круг с центром O. Напомним из определения, что все точки, расположенные на границе окружности, равноудалены (равноудалены) от этой центральной точки O . Расстояние от центра круга до его границы называется радиусом , R .



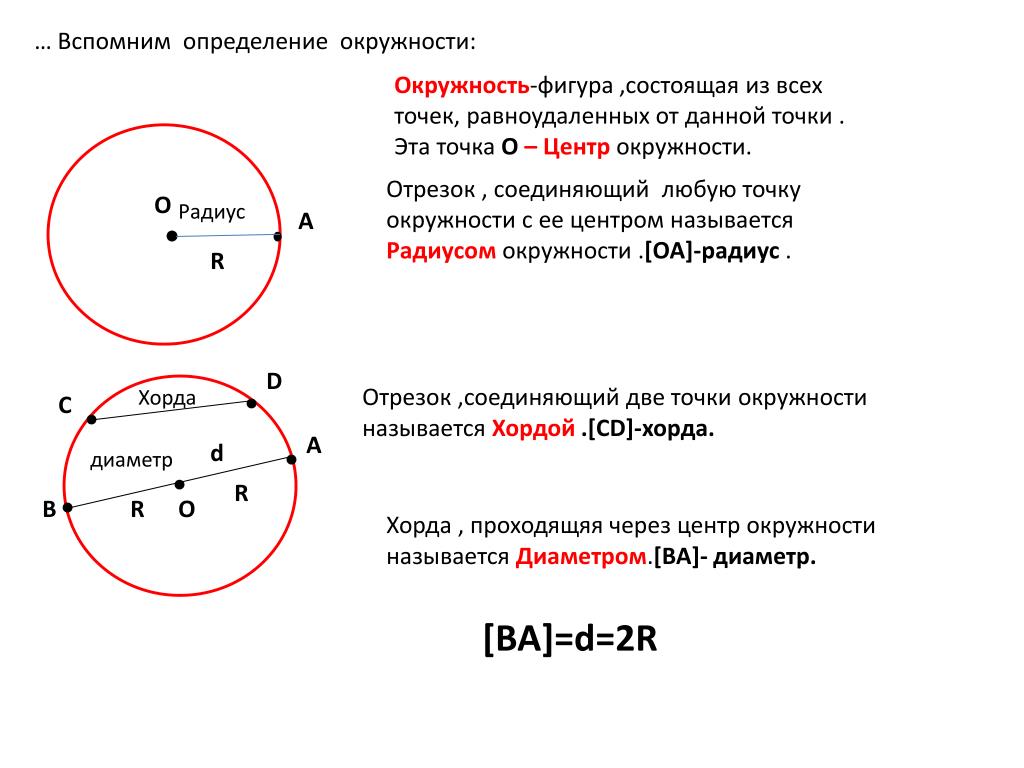 Мы знаем это, потому что диаметр любого круга в два раза больше его радиуса. Используя формулу площади полукруга, получаем:
Мы знаем это, потому что диаметр любого круга в два раза больше его радиуса. Используя формулу площади полукруга, получаем:

 Впервые это было исследовано греками, которые ввели понятие константы пропорциональности между длиной окружности и диаметром, которому мы теперь присваиваем символ π (пи).
Впервые это было исследовано греками, которые ввели понятие константы пропорциональности между длиной окружности и диаметром, которому мы теперь присваиваем символ π (пи). Таким образом, диаметр круга в два раза больше радиуса этого круга.
Таким образом, диаметр круга в два раза больше радиуса этого круга.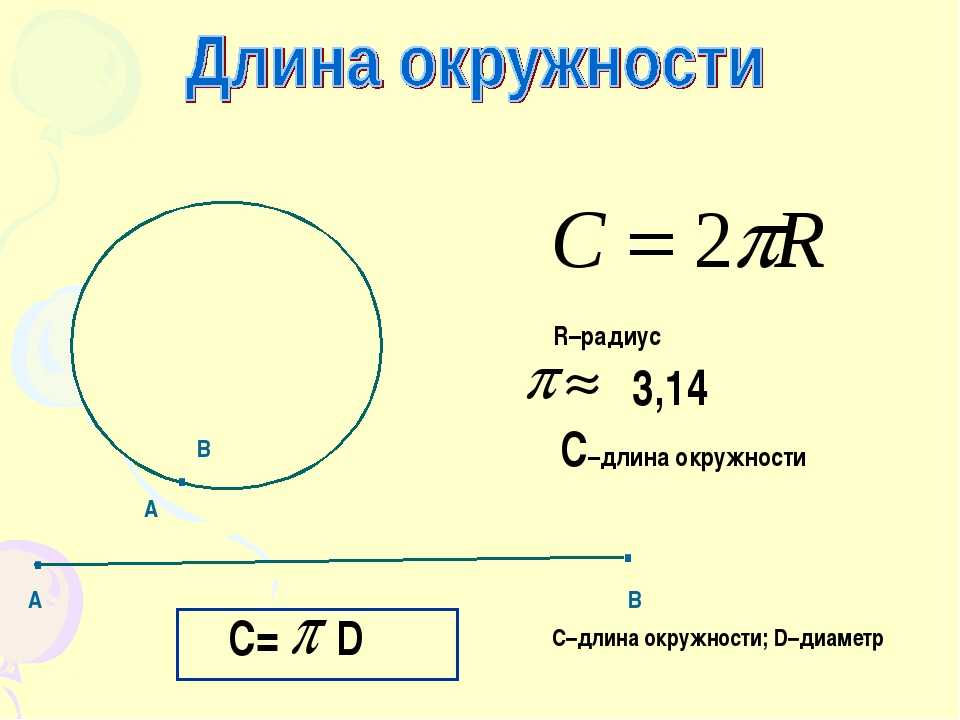 Поскольку диаметр в два раза больше радиуса, мы также можем написать
Поскольку диаметр в два раза больше радиуса, мы также можем написать
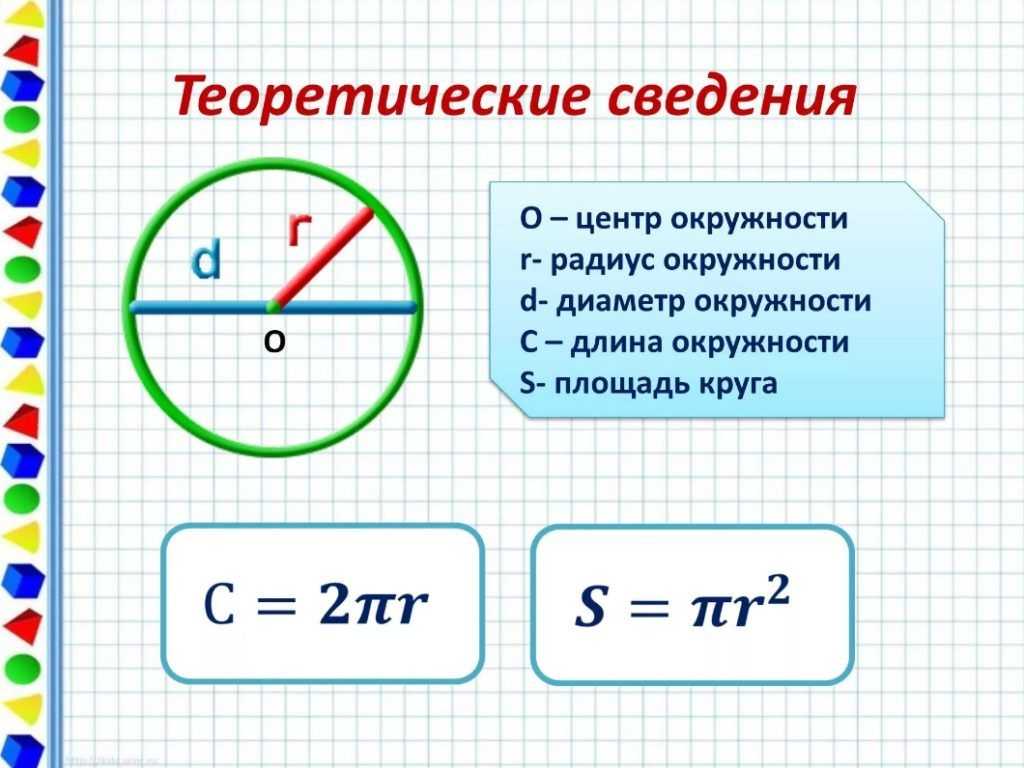
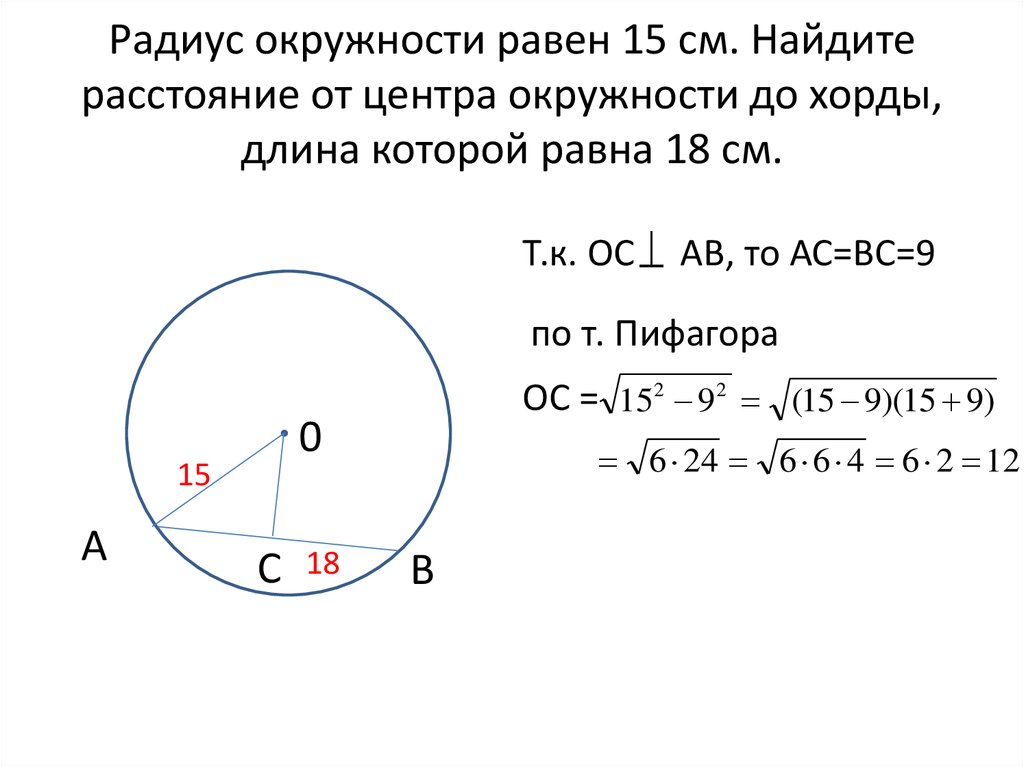
 Кроме того, основание каждого треугольника становится очень близким к изогнутой дуге окружности, поэтому длина параллелограмма очень близка к половине длины окружности C. Следовательно, предел площади параллелограмма равен
Кроме того, основание каждого треугольника становится очень близким к изогнутой дуге окружности, поэтому длина параллелограмма очень близка к половине длины окружности C. Следовательно, предел площади параллелограмма равен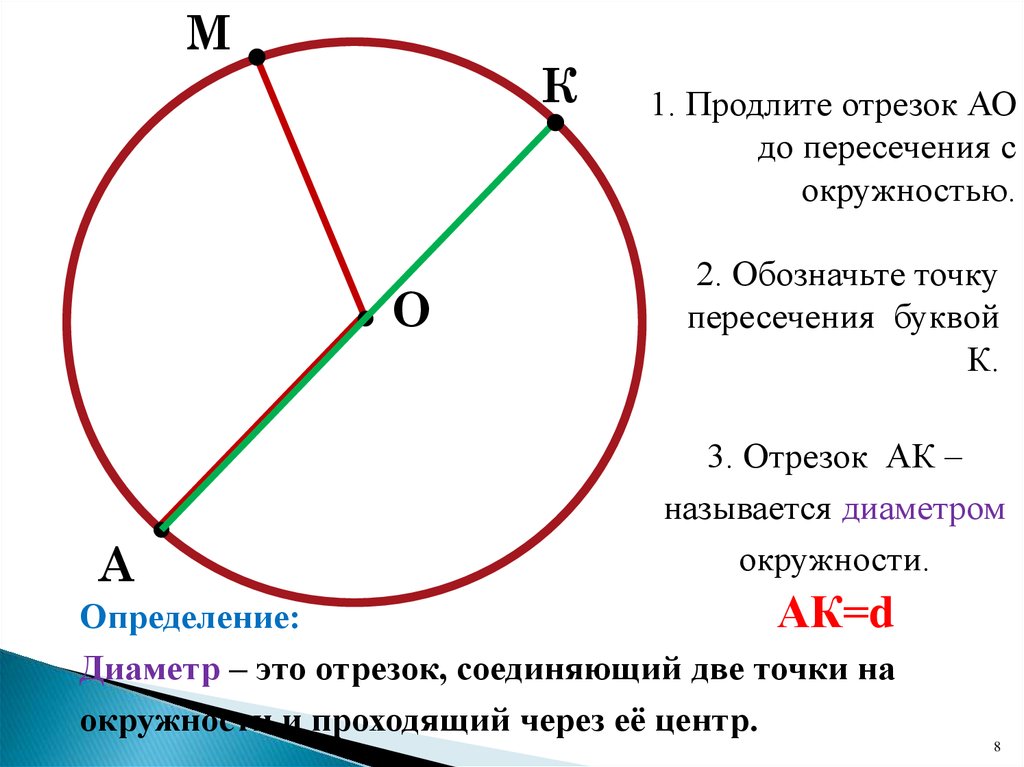
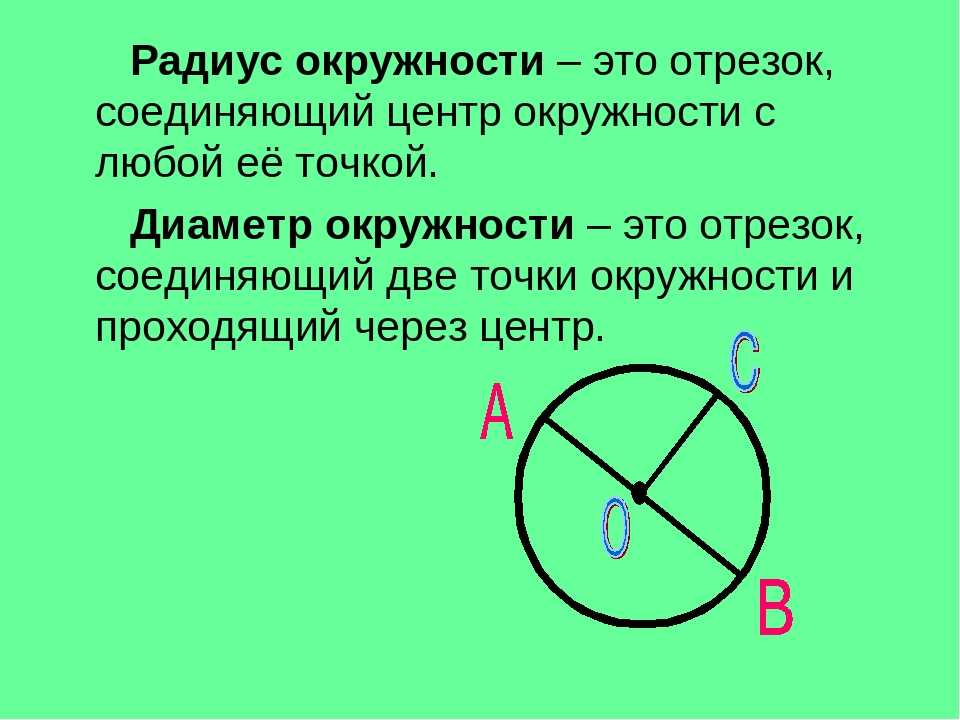


 Меньший круг имеет радиус 3 см, а больший радиус 5 см.
Меньший круг имеет радиус 3 см, а больший радиус 5 см.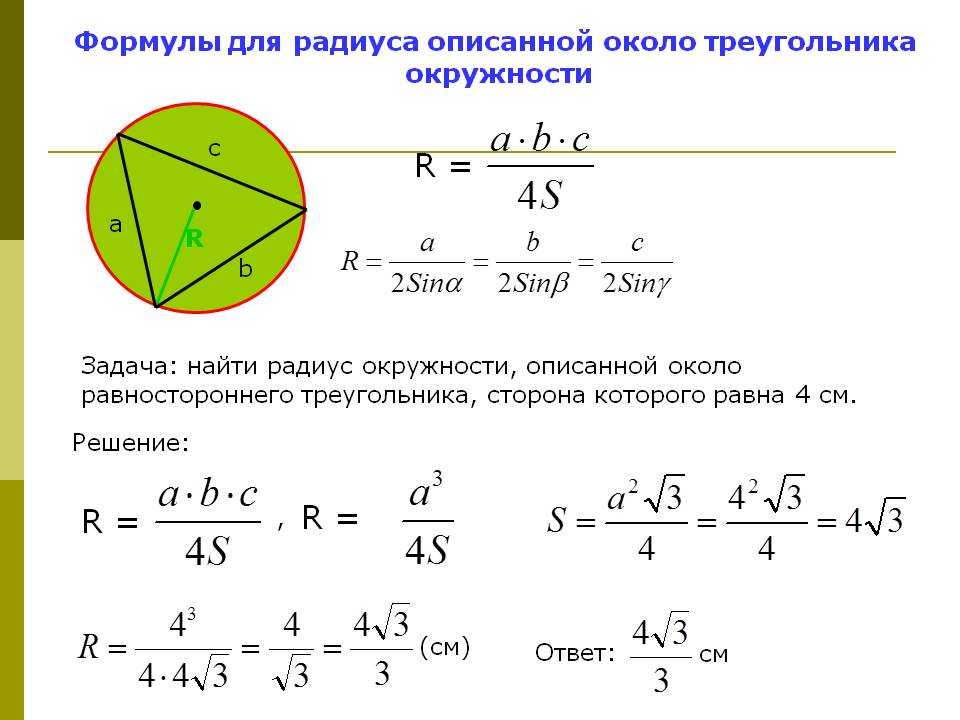
 Альтернативной системой является измерение углов в радианах.
Альтернативной системой является измерение углов в радианах.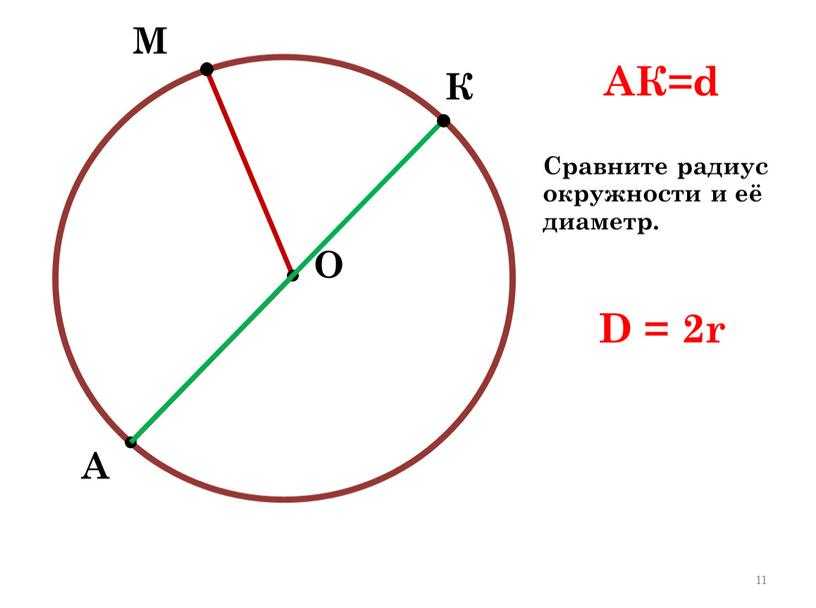 к. = 3,1622….
к. = 3,1622….
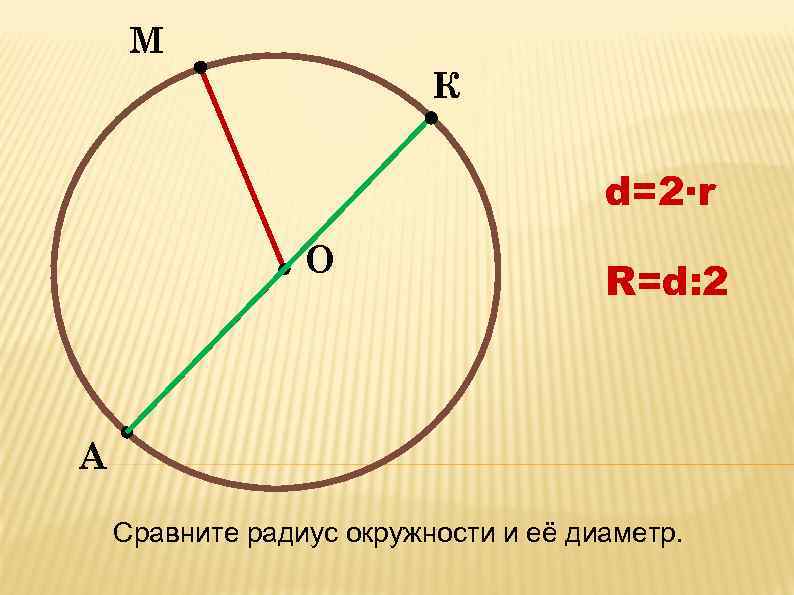 Одним из таких примеров является замечательная бесконечная сумма
Одним из таких примеров является замечательная бесконечная сумма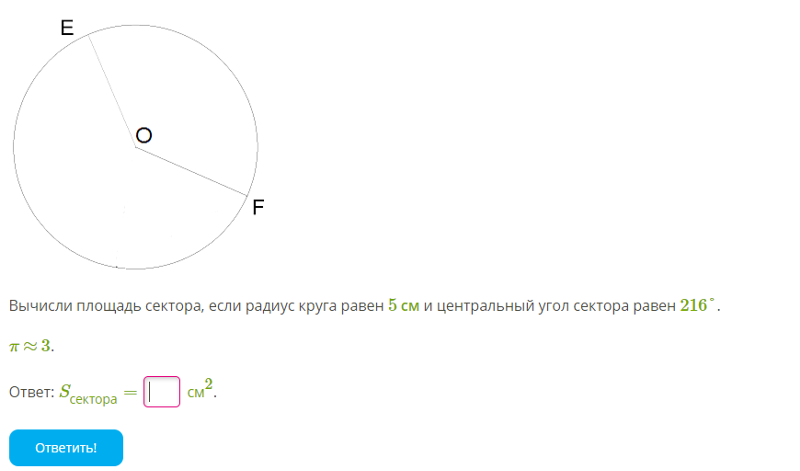 E. Smith, Dover Publications New York, (1958)
E. Smith, Dover Publications New York, (1958)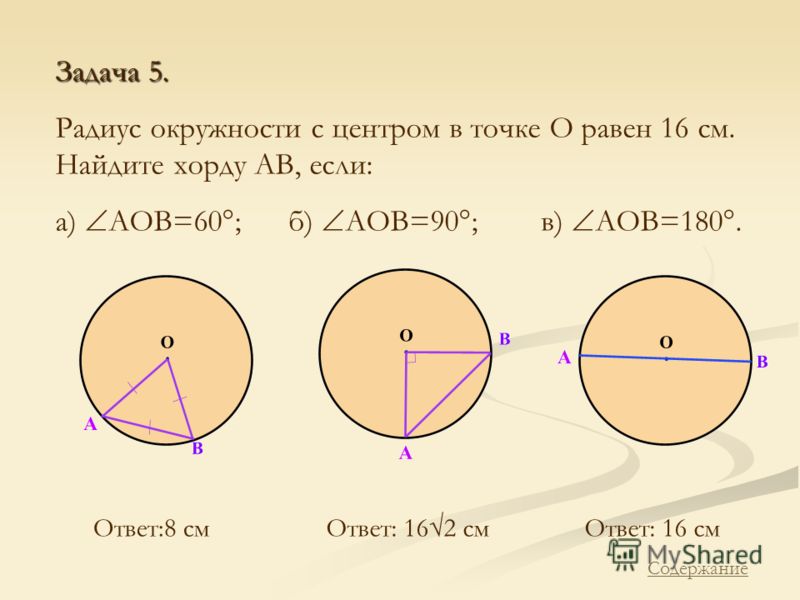 org/licenses/by-nc-nd/3.0/
org/licenses/by-nc-nd/3.0/

 Оберните нить вокруг круга, отметьте длину, а затем с помощью линейки или измерительного стержня измерьте длину нити.
Оберните нить вокруг круга, отметьте длину, а затем с помощью линейки или измерительного стержня измерьте длину нити.

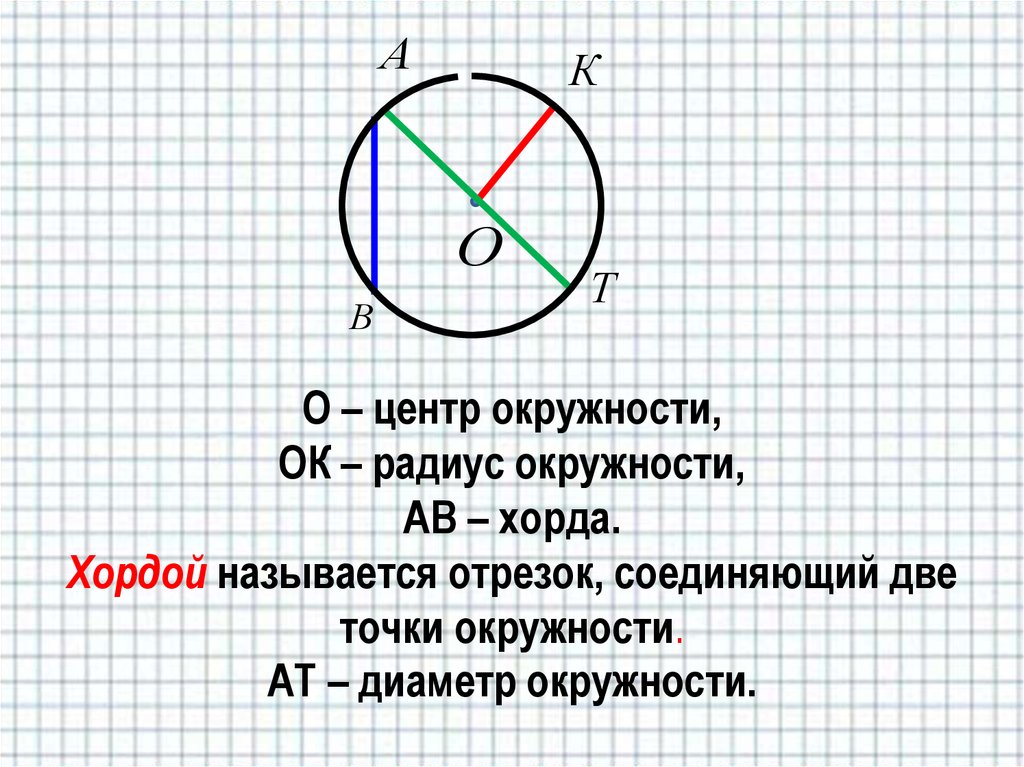
 ). Эддисон Уэсли Лонгман. ISBN 978-0-321-01618-8.
). Эддисон Уэсли Лонгман. ISBN 978-0-321-01618-8. Если расстояние между их центрами равно 12, каков радиус каждого круга?
Если расстояние между их центрами равно 12, каков радиус каждого круга?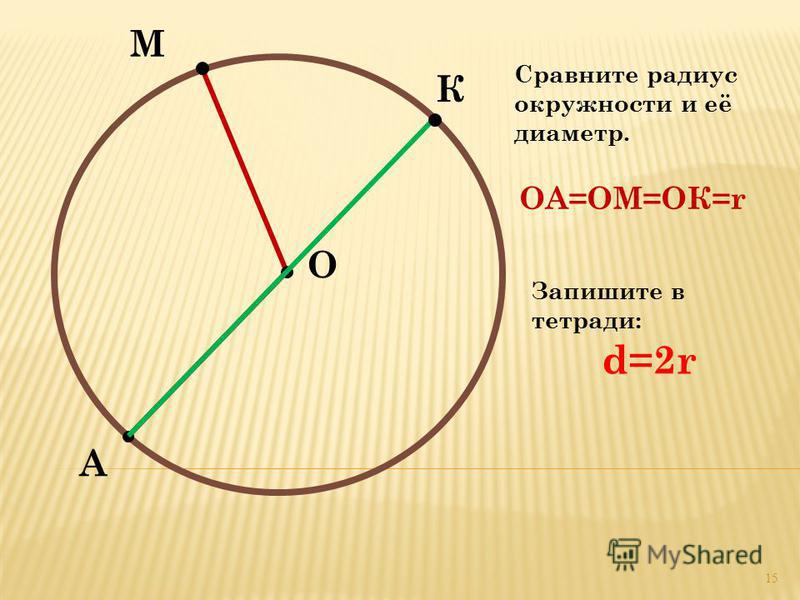 05 | Страница 83
05 | Страница 83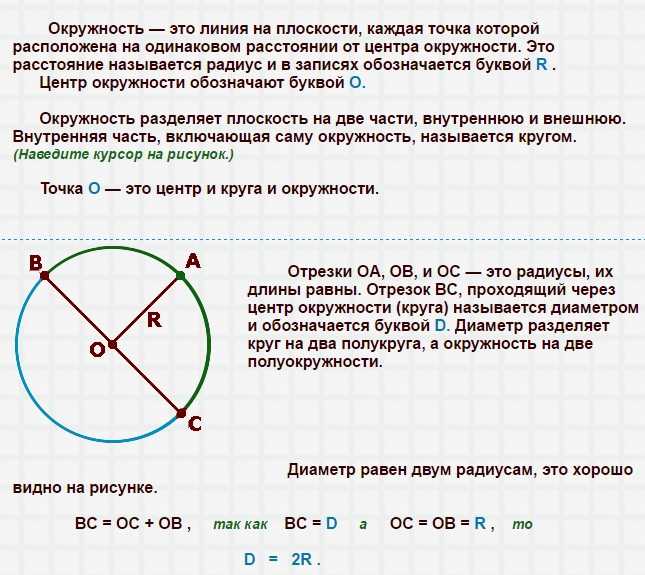 08 | Страница 83
08 | Страница 83 (ii) ∠XYZ не может быть прямым углом. (iii) ∠XYZ — тупой угол. (iv) Невозможно сделать определенное утверждение для меры ∠XYZ.
(ii) ∠XYZ не может быть прямым углом. (iii) ∠XYZ — тупой угол. (iv) Невозможно сделать определенное утверждение для меры ∠XYZ. Seg AB, seg AC являются касательными сегментами. Радиус окружности равен r и l(AB) = r. Докажите, что ▢ABOC — квадрат.
Seg AB, seg AC являются касательными сегментами. Радиус окружности равен r и l(AB) = r. Докажите, что ▢ABOC — квадрат. 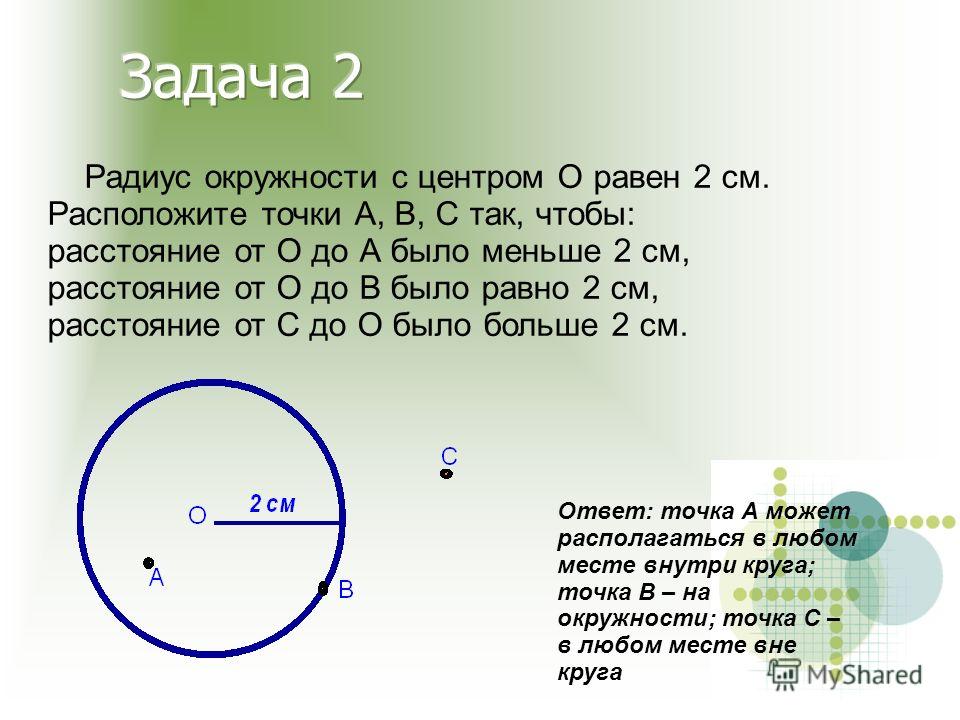 Радиус RM касается меньшего круга в точке S. Радиусы окружностей равны 9 см и 2,5 см. Найдите ответы на следующие вопросы, следовательно, найдите соотношение MS:SR.
Радиус RM касается меньшего круга в точке S. Радиусы окружностей равны 9 см и 2,5 см. Найдите ответы на следующие вопросы, следовательно, найдите соотношение MS:SR. 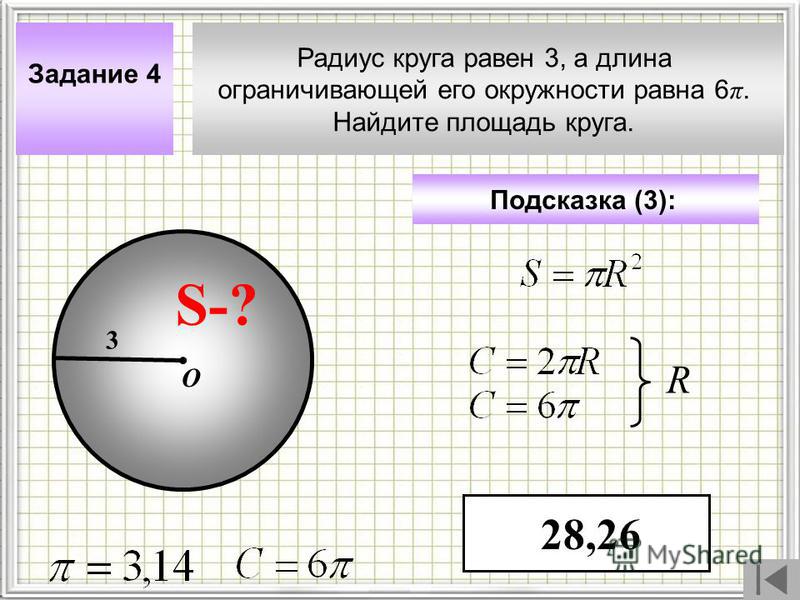 ..[теорема о равнобедренном треугольнике](II)
..[теорема о равнобедренном треугольнике](II)  Прямая PQ является касательной, которая касается окружности в точке T. Отрез AP ⊥ прямой PQ и отрезок BQ ⊥ прямой PQ. Докажите, что отрезок CP ≅ отрезок CQ.
Прямая PQ является касательной, которая касается окружности в точке T. Отрез AP ⊥ прямой PQ и отрезок BQ ⊥ прямой PQ. Докажите, что отрезок CP ≅ отрезок CQ.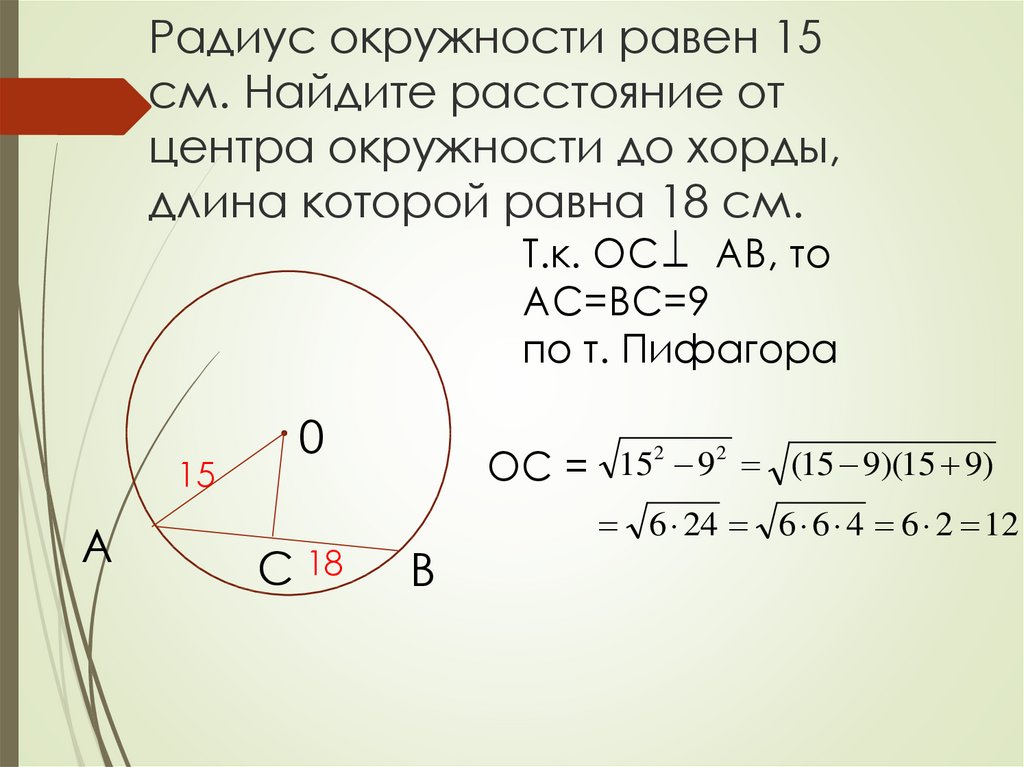
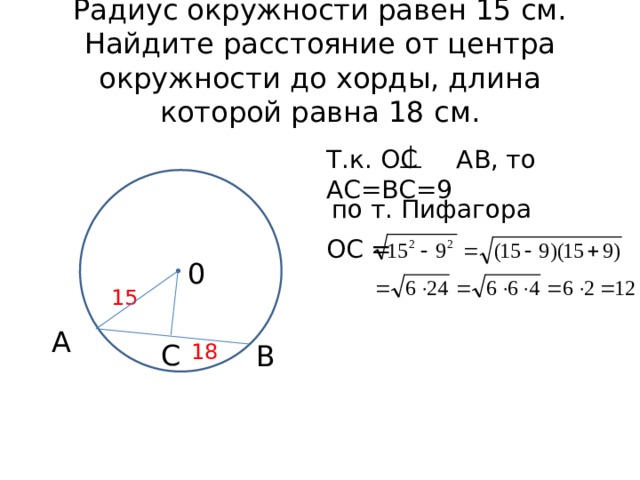 D лежит на внутренней окружности. Хорда EB внешней окружности пересекает внутреннюю окружность в точке A. Докажите, что отрезок EA ≅ отрезок AB.
D лежит на внутренней окружности. Хорда EB внешней окружности пересекает внутреннюю окружность в точке A. Докажите, что отрезок EA ≅ отрезок AB.