Транспонирование матрицы — Энциклопедия по экономике
Транспонировать матрицу размерностью 5 строк на 2 столбца или сокращенно — 5×2 (рис. 5.18). Элементы матрицы находятся в ячейках А1 В5. Первый элемент транспонированной матрицы начинается в ячейке D3. [c.366]Для оценки вектора неизвестных параметров р применим метод наименьших квадратов. Так как произведение транспонированной матрицы е» на саму матрицу е [c.83]
Знаком обозначается операция транспонирования матриц. [c.83]
Учитывая, что при транспонировании произведения матриц получается произведение транспонированных матриц, взятых в обратном порядке, т.е. (ХЬУ=Ь Х после раскрытия скобок получим [c.84]
Найдем транспонированный вектор остатков е . Так как при транспонировании матрица (Х Х) не меняется, т. е. [c.95]
Транспонирование матрицы — переход от матрицы А к матрице А (или АТ), в которой строки и столбцы поменялись местами с сохранением их порядка. [c.260]
Чоу 122, 123, 124 Точечная оценка 44 Транспонирование матрицы 260, 261
[c.
А — матрица кредитов предприятий (транспонированная матрица ). [c.84]
Отсюда видно, что при перемножении транспонированной матрицы на исходную (при условии, что столбцы исходной матрицы ортогональны) получаемая результирующая матрица является диагональной. Это свойство используется при планировании экспериментов уровни факторов выбираются так, чтобы векторы-столбцы исходной матрицы были ортогональны. [c.163]
Составляем исходную и транспонированную матрицы [c.167]
Вычисляем информационную матрицу, для чего транспонированную матрицу умножаем на исходную [c.188]
Рассмотрим транспонированную матрицу дТ. Из свойств определителя следует, что характеристическое уравнение матрицы дТ совпадает с характеристическим уравнением мат- [c.263]
Здесь det А — детерминант (определитель) этой матрицы [А..] — транспонированная матрица алгебраических дополнений. [c.233]
Для 7п х п матрицы А = (а ) транспонированной матрицей будем называть п х 7п матрицу Д, ij-й элемент которой равен a,ji.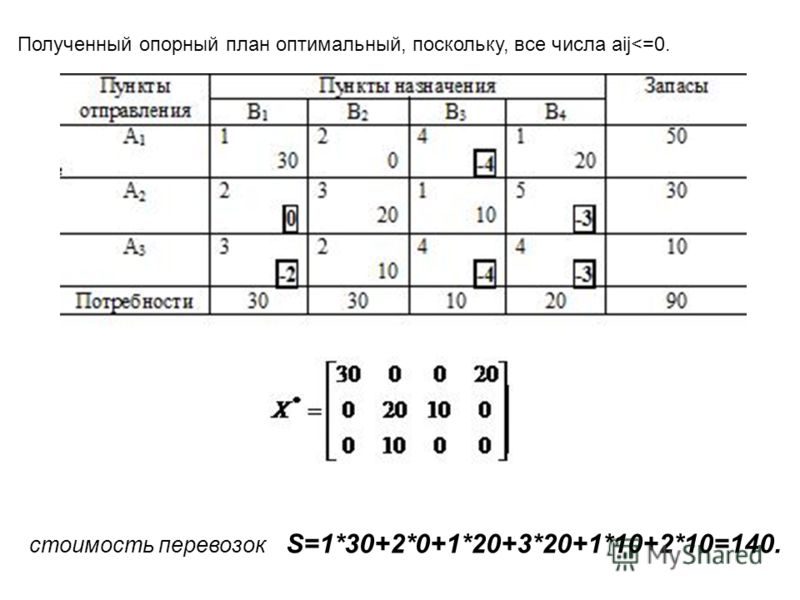
Транспонированной матрицей к Л, приведенной в (1), будет [c.32]
При вычислении якобиана функций, связанных с транспонированием матриц, часто приходится иметь дело с коммутационной матрицей К. Например, дифференциал функции [c.238]
Из (8) следует, что JJL = у. Прибавляя (7) к транспонированной матрице и используя (9), получим l l(Z — ггП) «1 = 0 и, как следствие, желаемый результат. П [c.396]
Если обозначить транспонированную матрицу X через А, то матрицы для записи нормальных уравнений могут быть представлены в виде [c.248]
Назовем эту таблицу для краткости таблицей выигрышей и обозначим ее буквой S, что понадобится нам при дальнейшем изложении. В математике таблицы чисел называются матрицами и над ними определены операции сложения, вычитания, умножения и транспонирования. Нам понадобятся только операции вычитания (сложения) и транспонирования матриц. [c.15]
Вектор-столбец кредитовых оборотов получаем умножением матрицы кредитовых оборотов, т. е. транспонированной матрицы, на оператор выделения итогового столбца [c.122]
е. транспонированной матрицы, на оператор выделения итогового столбца [c.122]
Для понимания главы 7 в целом достаточно того, что в ней сообщено об операции транспонирования матриц (таблиц), но, вместе с тем полезно иметь под рукой небольшой справочник, где бы содержались необходимые сведения о матрицах и основных операциях над ними. [c.363]
А а.. = а , т. е. он равен типичному элементу транспонированной матрицы A n m с переставленными (инвертированными индексами для всех i = 1, 2,. .., m и j = 1, 2,. .., п. В связи с этим, можно дать более строгое определение операции транспонирования матрицы. [c.376]
Дважды транспонированная матрица всегда равна исходной матрице, т. е. всегда (А ) = А . [c.376] Это свойство легко доказать, основываясь ла последнем определении транспонированной матрицы. [c.377]
Таким образом, четное число операций транспонирования матрицы не изменяет ее, нечетное число операций транспонирования исходной матрицы изменяет ее в общем случае.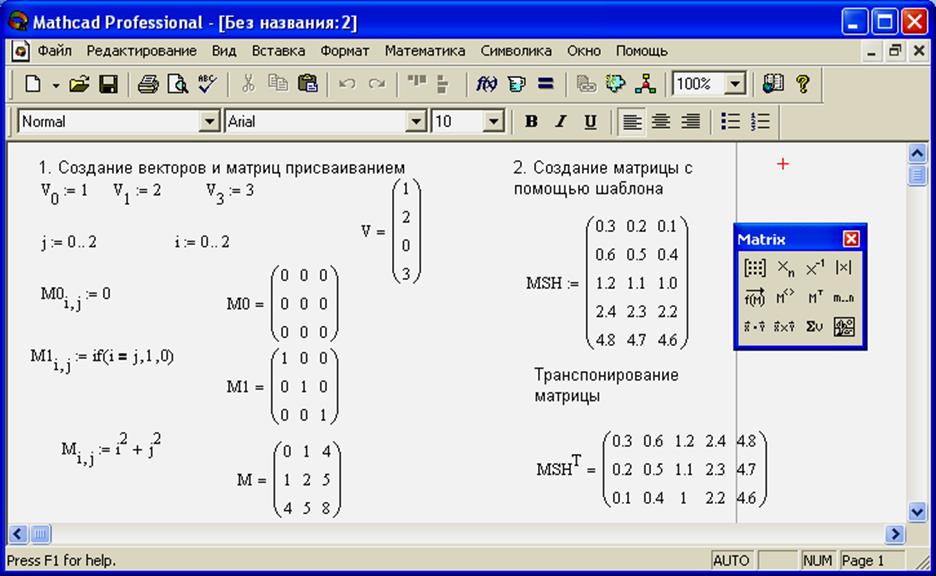 [c.377]
[c.377]
Задача теперь состоит только в том, чтобы найти такие проводки S(I, J), чтобы каждая их разность была бы равна соответствующему элементу транспонированной матрицы, т. е. нужно заполнить матрицу дебетовых оборотов S таким образом, чтобы AS = S — S и тогда будет получен нулевой баланс [c.384]
Из транспонированной матрицы сводных проводок S путем ее умножения на специальный вектор-столбец em +, выделяем вектор-столбец кредитовых оборотов [c.402]
Определение. Транспонированной матрицей называется матрица, у которой строки и столбцы поменялись местами, а именно для т х п матрицы А = (ojj) транспонированной является n x т матрица А = (а -), где о — = Ojj. Например, [c.490]
Предложение. Свойства операции транспонирования матриц (А + В) = А + В, (А) = А. [c.490]
См. также Блочная матрица, Блоч-но-диагональная матрица, Блочно-треу-голъная матрица, Вырожденная матрица, Диагональная матрица, Единичная матрица, Идемпотентная матрица, Квадратная матрица, Транспонированная матрица, Треугольная матрица, а также Алгебраическое дополнение, Главная диагональ матрицы, Обращение матрицы, Определитель матрицы, Плотность матрицы, Разлоокимость матрицы, Ранг матрицы. [c.188]
[c.188]
ТРАНСПОНИРОВАННАЯ МАТРИЦА [transposed matrix] — результат операции транспонирования, т.е. перемены местами столбцов и строк исходной матрицы. Если исходная матрица [а.], то транспонированная по отношению к ней записывается [а]. [c.366]
Определяется решение о з (t) системы г э = — Л г з, где А — транспонированная матрица. Таккака1=0, то система принимает вид (аз = 1) [c.87]
Последний пример -транепонирование симметричной матрицы в результате транспонирования ничего не изменилось и А = А. Во всех остальных случаях операция транспонирования матрицы изменяет ее и в общем случае А Ф А. Например, при транспонировании других, также особого вида матриц происходит их изменение [c.375]
Рассмотрим n-мерное векторное пространство Rn, снабженное стандартным евклидовым скалярным произведением (х, у) = х у = XtYt, где х — транспонированная матрица, т. е. в данном случае 1 х п вектор-строка. Пусть [c.36]
RESET-тест, 133 Точная идентификация, 236 Транспонирование матрицы, 490 Тренд, 285
[c. 575]
575]
Оператор транспонирования (клавиши trl + 1 ) Ат. Возвращает транспонированную матрицу размерности п х m (исходная матрица размерностью п х т). [c.178]
Как транспонировать матрицу в Python (с библиотеками и без них)
Перевод статьи «Transpose a Matrix».
Сегодня мы хотим разобрать, как транспонировать матрицу в Python. Однако сначала давайте рассмотрим, что представляет из себя матрица сама по себе и в чём заключается процесс транспонирования.
Итак, матрица состоит из строк и столбцов. Создать матрицу можно по-разному, но самый простой способ – использовать вложенные списки, как показано ниже:
matrix = [[1, 2, 4], [31, 17, 15]]
Внутренние списки представляют собой строки, а каждый элемент внутри списка называется столбцом. Итак, в приведенном выше примере у нас есть две строки и три столбца, т. е. мы имеем дело с матрицей 2 на 3. Стоит помнить, что индексация Python начинается с нуля.
е. мы имеем дело с матрицей 2 на 3. Стоит помнить, что индексация Python начинается с нуля.
Транспонирование матрицы означает, что мы меняем строки на столбцы или столбцы на строки. Теперь давайте обсудим различные методы транспонирования матрицы.
Метод 1. Транспонирование матрицы с помощью NumPy transpose()
Первый метод, который мы разберем, — это использование библиотеки NumPy. NumPy в основном работает с массивами в Python, а для транспонирования мы можем вызвать метод transpose().
Давайте разберем всё по порядку. Для начала нам нужно импортировать модуль NumPy как np.
Дальше, в ячейке номер [25] мы создаем массив NumPy с именем arr_matrix.
В ячейке номер [26] мы вызываем метод transpose() для нашей матрицы – объекта arr_matrix, который мы создали ранее.
В ячейке номер [27] мы выводим на экран исходную матрицу arr_matrix.
А в ячейке номер [28] – транспонированную матрицу arr_transpose. Можем заметить, что в результате мы получили именно то, что нам было нужно – транспонированную матрицу.
Можем заметить, что в результате мы получили именно то, что нам было нужно – транспонированную матрицу.
Метод 2. Использование метода numpy.transpose()
Мы также можем транспонировать матрицу в Python с помощью numpy.transpose(). При этом мы передаем матрицу в метод transpose() в качестве аргумента.
В ячейке номер [29] мы создаем матрицу, используя массив NumPy, с именем arr_matrix.
Далее мы передаем arr_matrix в метод transpose() и сохраняем результат в новую переменную arr_transpose.
В ячейке номер [31] мы печатаем исходную матрицу arr_matrix.
А дальше мы выводим на экран транспонированную матрицу arr_transpose. Получаем результат аналогичный тому, что получили в первом примере.
Метод 3. Транспонирование матрицы с использованием библиотеки SymPy
Применение библиотеки SymPy – это еще один подход к транспонированию матрицы. Эта библиотека использует символьную математику для решения алгебраических задач.
Сначала нам, конечно же, нужно импортировать библиотеку SymPy. Она не поставляется вместе с Python по умолчанию, поэтому вы должны установить её в своей системе, иначе код не будет работать.
В ячейке номер [34] мы создаем матрицу с помощью библиотеки sympy.
Дальше, в ячейке [35], мы вызываем transpose (T) при помощи точечного оператора и сохраняем результаты в новую переменную sympy_transpose.
В ячейке номер [36] мы печатаем исходную матрицу matrix. А в ячейке номер [37] – транспонированную матрицу sympy_transpose. Как видим, у нас получилась транспонированная матрица.
Метод 4. Транспонирование матрицы с использованием вложенного цикла
В Python матрицу можно транспонировать и без применения каких-либо библиотек. Для этого нам придется использовать вложенные циклы.
Мы создаем одну матрицу, а затем вторую (того же размера, что и первая) — для сохранения результатов после транспонирования. При этом важно отметить, что мы далеко не всегда знаем размерность исходной матрицы. Поэтому матрицу для результата мы создаем не напрямую, а используя размер исходной.
Поэтому матрицу для результата мы создаем не напрямую, а используя размер исходной.
В ячейке номер [38] мы создаем матрицу и выводим ее на экран.
В следующей ячейке мы применяем «питонический» способ узнать размерность транспонированной матрицы, используя исходную. А именно — используем генератор списков со вложенными циклами for.
В ячейке [40] мы запускаем два цикла for. Внешний цикл предназначен для строк, а вложенный – для столбцов.
В ячейке номер [41] мы выводим исходную матрицу Matrix. А в ячейке [42] — транспонированную матрицу trans_Matrix.
Метод 5. Использование генератора списка
Следующий метод, который мы разберем, — это использование генератора списка. Этот метод похож на предыдущий с использованием вложенных циклов, но он более «питонический». Можно сказать, что это более продвинутый способ транспонирования матрицы в одной строке кода без использования библиотек.
Сначала мы создаем матрицу m, используя вложенные списки.
Затем в ячейке номер [44] мы используем вложенные циклы, как и в предыдущем примере. Однако здесь мы делаем это в одну строчку, используя генератор списков. Более того, тут нет никакой необходимости менять индексы [j] [i] местами, как мы это делали в предыдущий раз.
В следующей ячейке мы выводим исходную матрицу m. После этого в ячейке номер [42] выводим транспонированную матрицу trans_m. Как видим, желаемый результат получен.
Метод 6. Транспонирование матрицы с помощью pymatrix
Pymatrix – ещё одна облегченная библиотека для матричных операций в Python. Мы можем выполнить транспонирование и с её помощью.
В ячейке номер [43] мы импортируем библиотеку pymatrix. Она не поставляется вместе с Python по умолчанию, поэтому, чтобы код работал корректно, нужно установить ее в своей системе перед использованием.
Затем при помощи библиотеки pymatrix мы создаем матрицу (в ячейке [44]).
В ячейке номер [45] вызываем метод trans() для нашей матрицы и сохраняем результаты в новую переменную pymatrix_transpose.
Потом мы выводим на экран исходную матрицу matrix. А в ячейке номер [47] выводим уже транспонированную матрицу pymatrix_transpose. Как видим, код отработал правильно.
Метод 7. Использование метода zip
Zip – еще один метод транспонирования матрицы.
В ячейке номер [63] мы создаем новую матрицу, используя вложенные списки.
В ячейке номер [64] мы передаем матрицу в zip с помощью оператора *. Мы вызываем каждую строку, а затем преобразуем эту строку в новый список, который становится транспонированной матрицей.
Заключение
Итак, сегодня мы рассмотрели, как транспонировать матрицу в Python. Мы разобрали различные методы, которые могут помочь нам в транспонировании матрицы (с использованием библиотек и без них).
Мы также познакомились с несколькими новыми библиотеками, такими как pymatrix и sympy.
Надеемся, теперь у вас не осталось вопросов о том, как транспонировать матрицу. Более того, вы можете выбрать наиболее подходящий способ для решения этой задачи.
Транспонирование матриц — Мегаобучалка
Транспонированием матрицы называется замена строк матрицы на ее столбцы с сохранением их порядка (или, что то же самое, замена столбцов матрицы на ее строки). Пусть дана исходная матрица А:
Тогда, согласно определению, транспонированная матрица А’ имеет вид
Сокращенная форма записи операции транспонирования матрицы:
Пример 3. Пусть даны матрицы А и В:
Тогда соответствующие транспонированные матрицы имеют вид
Нетрудно заметить две закономерности операции транспонирования матриц.
1. Дважды транспонированная матрица равна исходной матрице:
2. При транспонировании квадратных матриц элементы, находящиеся на главной диагонали, не меняют своих позиций, т.е. главная диагональ квадратной матрицы не меняется при транспонировании.
Умножение матриц
1. Умножение матриц — это специфическая операция, составляющая основу алгебры матриц. Строки и столбцы матриц можно рассматривать как векторы-строки и векторы-столбцы соответствующих размерностей: иными словами, любую матрицу можно интерпретировать как совокупность векторов-строк или векторов-столбцов.
Пусть даны матрица А размером т х п и матрица В размером п х k. Будем рассматривать матрицу А как совокупность т векторов-строк i размерности п каждый, а матрицу В — как совокупность k векторов-столбцов j, каждый из которых содержит по п координат:
Векторы-строки матрицы А и векторы-столбцы матрицы В показаны в записи этих матриц (13.3). Длина строки матрицы

Определение 3. Произведением матриц А и В называется матрица С, элементы которой cij равны скалярным произведениям векторов-строк i матрицы А на векторы-столбцы jматрицы В:
Произведение матриц А и В — матрица С — имеет размер т х k, поскольку длина п векторов-строк и векторов-столбцов исчезает при суммировании произведений координат этих векторов в их скалярных произведениях, как показано в формулах (13.4). Таким образом, для вычисления элементов первой строки матрицы С необходимо последовательно получить скалярные произведения первой строки матрицы А на все столбцы матрицы В; вторая строка матрицы С получается как скалярные произведения второй вектор-строки матрицы А на все векторы-столбцы матрицы В и так далее. Для удобства запоминания размера произведения матриц нужно перемножить отношения размеров матриц-сомножителей: , т. е. размер матрицы С равен произведению оставшихся в отношении чисел: т х k.
е. размер матрицы С равен произведению оставшихся в отношении чисел: т х k.
В операции умножения матриц есть характерная особенность: произведение матриц А и В имеет смысл, если число столбцов в А равно числу строк в В. Тогда если А и В — прямоугольные матрицы, то произведение В и А уже не будет иметь смысла, так как в скалярных произведениях, формирующих элементы соответствующей матрицы, должны участвовать векторы с одинаковым числом координат.
Если матрицы А и В квадратные размером n х n, то имеет смысл как произведение матриц АВ, так и произведение матриц BA, причем размер этих матриц такой же, как и у исходных сомножителей. При этом в общем случае перемножения матриц правило перестановочности не соблюдается, т.е. АВ ≠ ВА.
Рассмотрим примеры на умножение матриц.
Решение. Поскольку число столбцов матрицы А равно числу строк матрицы В, то произведение матриц АВ имеет смысл. По формулам (13.4) получаем в произведении матрицу размером 3 х 2:
По формулам (13.4) получаем в произведении матрицу размером 3 х 2:
Произведение ВА не имеет смысла, так как число столбцов матрицы В не совпадает с числом строк матрицы А.
Решение. Здесь мы найдем произведения данных матриц АВ и ВА:
Как видно из результата, матрица произведения зависит от порядка расположения матриц в произведении. В обоих случаях произведения матриц имеют тот же размер, что и у исходных сомножителей: 2 х 2.
Решение. В данном случае матрица В представляет собой вектор-столбец, т.е. матрицу, у которой три строки и один столбец. Вообще, векторы — это частные случаи матриц: вектор-строка длины п представляет собой матрицу с одной строкой и п столбцами, а вектор-столбец высоты n — матрицу с n строками и одним столбцом. Размеры данных матриц соответственно 2 х 3 и 3 х 1, так что произведение этих матриц определено. Имеем
Имеем
В произведении получена матрица размером 2 х 1 или вектор-столбец высоты 2.
Решение. Путем последовательного умножения матриц находим
2. Свойства произведения матриц. Пусть А, В и С — матрицы соответствующих размеров (чтобы произведения матриц были определены), а α — действительное число. Тогда следующие свойства произведения матриц имеют место:
1) (АВ)С = А(ВС),
2) (А + В)С = AC + ВС,
3) А(В + С) = АВ + АС,
4) α(АВ) = (αА)В = А(αВ).
В п. 1 этого раздела введено понятие единичной матрицы Е. Нетрудно убедиться, что в алгебре матриц она играет роль единицы, т.е. можно отметить еще два свойства, связанные с умножением на эту матрицу слева и справа в случае квадратных матриц:
5) АЕ = А,
6) ЕА = А.
Иными словами, произведение любой матрицы на единичную матрицу, если оно имеет смысл, не меняет исходную матрицу.
Обратная матрица
Ранг матрицы
Теорема о ранге матрицы. Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки (столбцы).
Ранг матрицы равен максимальному числу ее линейно независимых строк или столбцов, через которые линейно выражаются все остальные ее строки (столбцы).
Для прямоугольной матрицы максимальный ранг r = min (m, n). Для квадратной матрицы размером п х n ее максимальный ранг не может превышать п: r ≤ п.
Транспонирование и умножение матриц
Эти операции над матрицами не относятся к числу линейных.
ОПРЕДЕЛЕНИЕ. Транспонированной матрицей для матрицыразмераназывается матрица размера, полученная иззаменой всех ее строк столбцами с теми же порядковыми номерами.
То есть, если =, то,=1,2,…,,=1,2,…,.
ПРИМЕР.
=; ==
3х2 2х3 3х3 3х3
ОПРЕДЕЛЕНИЕ. Если
=,
то матрицаА называется симметрической.
Если
=,
то матрицаА называется симметрической.
Все диагональные матрицы симметрические, так как равны их элементы, симметричные относительно главной диагонали.
Очевидно, справедливы следующие свойства операции транспонирования:
ОПРЕДЕЛЕНИЕ. Пусть =– матрица размера,=– матрица размера. Произведение этих матриц– матрица=размера, элементы которой вычисляются по формуле:
, =1,2,…,,=1,2,…,,
то есть элемент -й строки и-го столбца матрицыравен сумме произведений соответствующих элементов-й строки матрицыи-го столбца матрицы.
ПРИМЕР.
= , =
2х3 3х1 2х3 3х1 2х1
Произведение – не существует.
3х1 2х3
CВОЙСТВА ОПЕРАЦИИ УМНОЖЕНИЯ МАТРИЦ
1.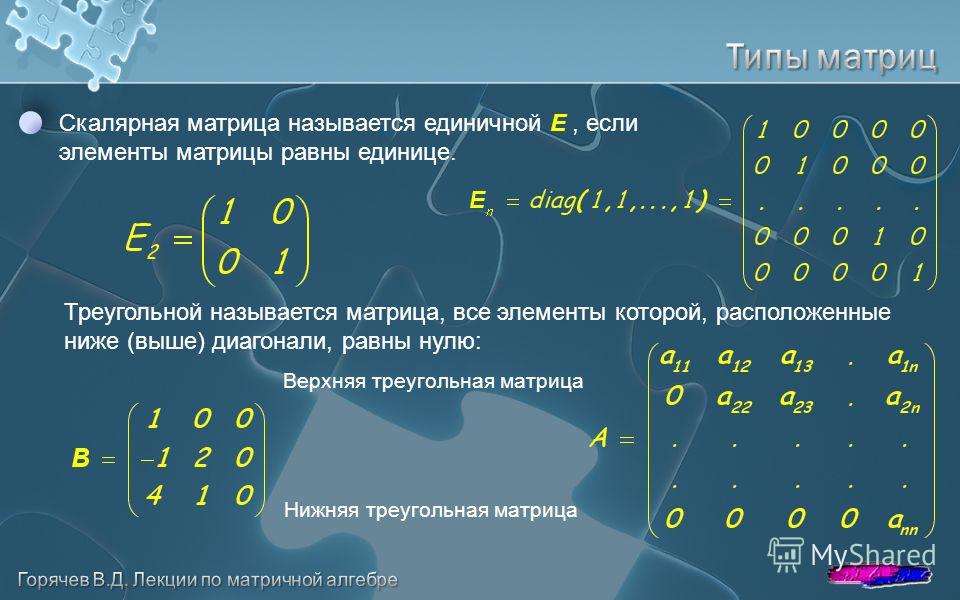 ,
даже если оба произведения определены.
,
даже если оба произведения определены.
ПРИМЕР. ,, хотя
ОПРЕДЕЛЕНИЕ. Матрицы иназываютсяперестановочными, если , в противном случаеиназываютсянеперестановочными.
Из определения следует, что перестановочными могут быть лишь квадратные матрицы одного размера.
ПРИМЕР.
матрицы иперестановочные.
, то есть ,
значит, и– перестановочные матрицы.
Вообще единичная матрица перестановочна с любой квадратной матрицей того же порядка, и для любой матрицы . Это свойство матрицыобъясняет, почему именно она называется единичной: при умножении чисел таким свойством обладает число 1.
Если соответствующие произведения определены, то:
2.
3. ,
4.
5.
ПРИМЕР.
,
2х2 2х1 2х1 1х2
1х2 2х2 1х2
ЗАМЕЧАНИЕ. Элементами матрицы могут быть не только числа, но и функции. Такая матрица называется функциональной.
ПРИМЕР.
Каждой квадратной матрице можно по определенным правилам поставить в соответствие некоторое число, которое называется ее определителем.
Рассмотрим квадратную матрицу второго порядка:
Её определителем называется число, которое записывается и вычисляется так:
(1.1)
Такой определитель называется определителем второго порядка и может
обозначаться
по-другому:
или.
Определителем третьего порядка называется число, соответствующее квадратной матрице , которое вычисляется по правилу:
(1.2)
Это правило вычисления определителя третьего порядка называется правилом треугольников и схематически его можно представить так:
ПРИМЕР. ;
Если справа от определителя приписать первый, а затем второй столбец, то правило треугольников можно модифицировать:
Сначала умножаются числа на главной диагонали и двух ей параллельных диагоналях, затем – числа на другой (побочной) диагонали и ей параллельных. Из суммы первых трех произведений вычитается сумма остальных.
Группируя слагаемые в (1.2) и используя (1.1), заметим, что
(1.3)
То есть при
вычислении определителя третьего
порядка используются определители
второго порядка, причем
– определитель матрицы, полученный извычеркиванием элемента(точнее, первой строки и первого столбца,
на пересечении которых стоит),– вычеркиванием элемента,– элемента.
ОПРЕДЕЛЕНИЕ. Дополнительным минором элементаквадратной матрицыназывается определитель матрицы, получаемой извычеркиванием-ой строки и-го столбца.
ПРИМЕР.
и так далее: матрица третьего порядка имеет 9 дополнительных миноров.
ОПРЕДЕЛЕНИЕ. Алгебраическим дополнением элемента квадратной матрицыназывается число.
ПРИМЕР.
Для матрицы :
Для матрицы :и так далее.
Итак, с учетом сформулированных определений (1.3) можно переписать в виде: .
Перейдем теперь к общему случаю.
ОПРЕДЕЛЕНИЕ. Определителем квадратной матрицы порядканазывается число, которое записывается и вычисляется следующим образом:
(1.4)
Равенство (1.4)
называется разложением
определителя по элементам первой строки.
В этой формуле алгебраические дополнения
вычисляются как определители
-го
порядка. Таким образом, при вычислении
определителя 4-го порядка по формуле
(1.4) надо, вообще говоря, вычислить 4
определителя 3-го порядка; при вычислении
определителя 5-го порядка – 5 определителей
4-го порядка и т.д. Однако если, к примеру,
в определителе 4-го порядка первая строка
содержит 3 нулевых элемента, то в формуле
(1.4) останется лишь одно ненулевое
слагаемое.
Таким образом, при вычислении
определителя 4-го порядка по формуле
(1.4) надо, вообще говоря, вычислить 4
определителя 3-го порядка; при вычислении
определителя 5-го порядка – 5 определителей
4-го порядка и т.д. Однако если, к примеру,
в определителе 4-го порядка первая строка
содержит 3 нулевых элемента, то в формуле
(1.4) останется лишь одно ненулевое
слагаемое.
ПРИМЕР.
Рассмотрим (без доказательства) свойства определителей:
Определитель можно разложить по элементам первого столбца:
(1.5)
ПРИМЕР.
ЗАМЕЧАНИЕ. Рассмотренные примеры позволяют сделать вывод: определитель треугольной матрицы равен произведению элементов главной диагонали.
При транспонировании матрицы величина ее определителя не меняется: .
Отсюда следует,
что строки и столбцы определителя
равноправны.
Если в определителе поменять местами две строки (два столбца), то определитель изменит свой знак, не изменившись по абсолютной величине.
Определитель, имеющий две равные строки (столбца), равен нулю.
Если все элементы некоторой строки (столбца) определителя умножить на число , то величина определителя умножится на это число.
Отсюда, в частности, следует, что общий множитель любой строки (столбца) можно выносить за знак определителя. Кроме того, определитель, имеющий нулевую строку или нулевой столбец, равен нулю.
Определитель, имеющий пропорциональные строки (столбцы), равен нулю.
Определитель можно разложить по элементам любой строки (любого столбца): (1.6)
или
(1.7)
Равенство
(1. 6) называется разложением
определителя по элементам
-й
строки.
6) называется разложением
определителя по элементам
-й
строки.
Равенство (1.7) называется разложением определителя по элементам -го столбца.
Сумма произведений всех элементов некоторой строки (столбца) на
алгебраические дополнения соответствующих элементов другой строки
(столбца) равна нулю, то есть при ипри.
Определитель не изменится от прибавления ко всем элементам некоторой строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.
Определитель произведения двух матриц одного порядка равен произведению определителей этих матриц: (– квадратные матрицы одного порядка).
ПРИМЕР.
,
так как элементы первой и второй строк
этого определителя соответственно
пропорциональны (свойство 6).
Особенно часто при вычислении определителей используется свойство 9, так как оно позволяет в любом определителе получать строку или столбец, где все элементы, кроме одного, равны нулю.
ПРИМЕР.
Транспонирование и умножение матриц на Python
В этом уроке мы напишем программы на Python для транспонирования и умножения матриц и вывода результатов.
Прежде чем писать программу транспонирования матрицы на Python, давайте сначала посмотрим на обзор транспонирования.
Транспонирование матрицы
Если вы заменяете строки матрицы столбцом той же матрицы, это называется транспонированием матрицы. Обозначается как X’. Например: Элемент в i-й строке и j-м столбце в X будет помещен в j-ю строку и i-й столбец в X’.
Пример: Предположим, мы взяли следующую матрицу A:
A = [[5, 4, 3]
[2, 4, 6]
[4, 7, 9]
[8, 1, 3]]
At будет транспонированием указанной выше матрицы, т. е. A [i] [j] = At [j] [i], и поэтому At должно быть:
е. A [i] [j] = At [j] [i], и поэтому At должно быть:
В = [5, 2, 4, 8] [4, 4, 7, 1] [3, 6, 9, 3]
Программа Python для транспонирования матрицы
Теперь мы напишем программу на Python для транспонирования входной заданной матрицы, где мы выполняем операцию, как мы выполнили в приведенном выше примере. Чтобы выполнить операцию транспонирования матрицы, мы будем использовать метод вложенного цикла for.
Давайте разберемся с использованием и реализацией этого метода на следующем примере.
Пример:
# Define a matrix A
A = [[5, 4, 3],
[2, 4, 6],
[4, 7, 9],
[8, 1, 3]]
# Define an empty matrix of reverse order
transResult = [[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0]]
# Use nested for loop on matrix A
for a in range(len(A)):
for b in range(len(A[0])):
transResult[b][a] = A[a][b] # store transpose result on empty matrix
# Printing result in the output
print("The transpose of matrix A is: ")
for res in transResult:
print(res)
Выход:
The transpose of matrix A is: [5, 2, 4, 8] [4, 4, 7, 1] [3, 6, 9, 3]
Умножение матриц
В этом разделе мы напишем программу на Python для умножения двух входных матриц и выведем результат на выходе. Эта программа укажет, как умножать две матрицы, имеющие определенные значения.
Эта программа укажет, как умножать две матрицы, имеющие определенные значения.
Прежде чем писать программу на Python, давайте сначала посмотрим на обзор умножения двух матриц.
Умножение матриц — это бинарная операция, в которой используется пара матриц для создания другой матрицы. Элементы в матрице умножаются в соответствии с элементарной арифметикой.
При умножении двух матриц элементы строки первой матрицы умножаются на элементы столбца второй матрицы.
Пример: предположим, что мы взяли следующие две матрицы A и B:
A = [[5, 4, 3]
[2, 4, 6]
[4, 7, 9]]
and, B = [[3, 2, 4]
[4, 3, 6]
[2, 7, 5]]
C будет объединением двух указанных выше матриц, т. е. C = A + B, и поэтому C должно быть:
C = [[37, 43, 59]
[34, 58, 62]
[58, 92, 103]]
Как мы видим, результирующая матрица C, также известная как произведение матриц, имеет то же количество строк, что и первая матрица (матрица A), и такое же количество столбцов, как и вторая матрица (матрица B). Мы также знаем этот тип умножения матриц как скалярное произведение матриц.
Мы также знаем этот тип умножения матриц как скалярное произведение матриц.
Умножение двух матриц
Теперь мы напишем программу Python для умножения двух матриц, где мы выполняем умножение, как мы это делали в приведенном выше примере. Мы можем использовать различные методы для написания такой программы на Python, но в этом руководстве будем использовать только следующие два метода:
- Использование метода вложенного цикла.
- Использование метода понимания вложенного списка.
В обоих методах мы напишем пример программы, чтобы понять их реализацию для умножения двух матриц.
Способ 1: Использование метода вложенного цикла
В этом методе мы собираемся использовать вложенный цикл for для двух матриц, выполнять над ними умножение и сохранять результат умножения в третьей матрице в качестве итогового значения.
Давайте разберемся с реализацией этого метода на следующем примере.
Пример:
# Define two matrix A and B in program
A = [[5, 4, 3],
[2, 4, 6],
[4, 7, 9]]
B = [[3, 2, 4],
[4, 3, 6],
[2, 7, 5]]
# Define an empty matrix to store multiplication result
multiResult = [[0, 0, 0],
[0, 0, 0],
[0, 0, 0]]
# Using nested for loop method on A & B matrix
for m in range(len(A)):
for n in range(len(B[0])):
for o in range(len(B)):
multiResult[m][n] += A[m][o] * B[o][n] # Storing multiplication result in empty matrix
# Printing multiplication result in the output
print("The multiplication result of matrix A and B is: ")
for res in multiResult:
print(res)
Выход:
The multiplication result of matrix A and B is: [37, 43, 59] [34, 58, 62] [58, 92, 103]
Способ 2: Использование метода понимания вложенного списка
В этом методе мы будем использовать понимание вложенного списка, чтобы получить результат умножения двух входных матриц. При использовании в программе метода понимания списка мы также будем использовать «zip в Python» для вложенного списка. Давайте разберемся с реализацией этого метода на следующем примере.
При использовании в программе метода понимания списка мы также будем использовать «zip в Python» для вложенного списка. Давайте разберемся с реализацией этого метода на следующем примере.
Пример:
# Define two matrix A & B in the program
A = [[5, 4, 3],
[2, 4, 6],
[4, 7, 9]]
B = [[3, 2, 4],
[4, 3, 6],
[2, 7, 5]]
# Using nested list method with zip in Python
multiResult = [[sum(a * b for a, b in zip(Arow, Bcol))
for Bcol in zip(*B)]
for Arow in A]
# Printing multiplication result in the output
print("The multiplication result of matrix A and B is: ")
for res in multiResult:
print(res)
Выход:
The multiplication result of matrix A and B is: [37, 43, 59] [34, 58, 62] [58, 92, 103]
119401cookie-checkТранспонирование и умножение матриц на Pythonyes
Перестановка матрицы на месте
Перестановка матрицы на месте, также называемый транспонирование матрицы на месте, это проблема перенос ан N×M матрица на месте в память компьютера, в идеале с О(1) (ограниченное) дополнительное хранилище или самое большее с дополнительным хранилищем, намного меньшим, чем НМ. Обычно предполагается, что матрица хранится в рядовой порядок или же порядок столбцов (т.е. смежные строки или столбцы, соответственно, расположенные последовательно).
Обычно предполагается, что матрица хранится в рядовой порядок или же порядок столбцов (т.е. смежные строки или столбцы, соответственно, расположенные последовательно).
Выполнение транспонирования на месте (транспонирование на месте) наиболее сложно, когда N ≠ M, т.е. для неквадратной (прямоугольной) матрицы, где она включает в себя сложную перестановка элементов данных, причем многие циклы длины больше 2. Напротив, для квадратной матрицы (N = M), все циклы имеют длину 1 или 2, и транспонирование может быть достигнуто с помощью простого цикла, чтобы поменять местами верхний треугольник матрицы с нижним треугольником. Дальнейшие сложности возникают, если кто-то хочет максимизировать место в памяти чтобы улучшить строка кеша использование или работать вне ядра (где матрица не помещается в основную память), поскольку транспонирование по своей сути включает непоследовательные обращения к памяти.
Проблема неквадратной транспозиции на месте изучается, по крайней мере, с конца 1950-х годов, и известно несколько алгоритмов, в том числе несколько, которые пытаются оптимизировать локальность для кеш-памяти, вне ядра или аналогичных контекстов, связанных с памятью.
Содержание
- 1 Фон
- 2 Пример
- 3 Свойства перестановки
- 4 Алгоритмы
- 4.1 Аксессуар транспонировать
- 4.2 Квадратные матрицы
- 4.3 Неквадратные матрицы: следование циклам
- 4.4 Улучшение локальности памяти за счет большего общего перемещения данных
- 5 Рекомендации
- 6 внешняя ссылка
- 6.1 Исходный код
Фон
На компьютер, часто можно избежать явного транспонирования матрицы в объем памяти просто обращаясь к тем же данным в другом порядке. Например, программные библиотеки за линейная алгебра, Такие как BLAS, обычно предоставляют опции, указывающие, что определенные матрицы должны интерпретироваться в транспонированном порядке, чтобы избежать перемещения данных.
Однако остается ряд обстоятельств, при которых необходимо или желательно физически переупорядочить матрицу в памяти в соответствии с ее транспонированным порядком. Например, с матрицей, хранящейся в рядовой порядок, строки матрицы являются смежными в памяти, а столбцы — несмежными. Если над столбцами необходимо выполнить повторяющиеся операции, например, в быстрое преобразование Фурье алгоритм (например, Frigo & Johnson, 2005), транспонирование матрицы в памяти (чтобы сделать столбцы смежными) может улучшить производительность за счет увеличения место в памяти. Поскольку эти ситуации обычно совпадают со случаем очень больших матриц (которые превышают размер кэша), становится желательным выполнение транспонирования на месте с минимальным дополнительным объемом памяти.
Если над столбцами необходимо выполнить повторяющиеся операции, например, в быстрое преобразование Фурье алгоритм (например, Frigo & Johnson, 2005), транспонирование матрицы в памяти (чтобы сделать столбцы смежными) может улучшить производительность за счет увеличения место в памяти. Поскольку эти ситуации обычно совпадают со случаем очень больших матриц (которые превышают размер кэша), становится желательным выполнение транспонирования на месте с минимальным дополнительным объемом памяти.
Кроме того, как чисто математическая проблема, транспонирование на месте связано с рядом интересных теория чисел головоломки, которые разрабатывались на протяжении нескольких десятилетий.
Пример
Например, рассмотрим матрицу 2 × 4:
- [1112131421222324].{ displaystyle { begin {bmatrix} 11 & 12 & 13 & 14 21 & 22 & 23 & 24 end {bmatrix}}.}
В строковом формате это будет сохранено в памяти компьютера как последовательность (11, 12, 13, 14, 21, 22, 23, 24), то есть две строки, сохраненные последовательно.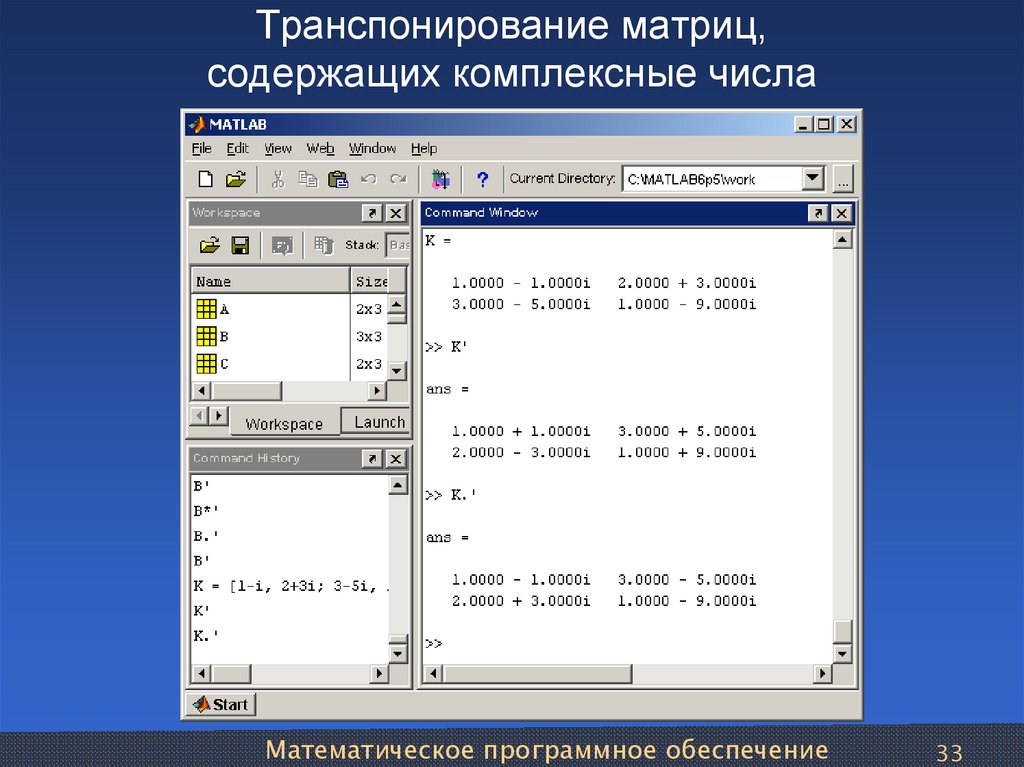 Если мы переставим это, мы получим матрицу 4 × 2:
Если мы переставим это, мы получим матрицу 4 × 2:
- [1121122213231424]{ displaystyle { begin {bmatrix} 11 и 21 12 и 22 13 и 23 14 и 24 end {bmatrix}}}
которая хранится в памяти компьютера в виде последовательности (11, 21, 12, 22, 13, 23, 14, 24).
Если пронумеровать ячейки памяти от 0 до 7 слева направо, то эта перестановка состоит из четырех циклов:
- (0), (1 2 4), (3 6 5), (7)
То есть значение в позиции 0 переходит в позицию 0 (цикл длины 1, движение данных отсутствует). Затем значение в позиции 1 (в исходном хранилище: 11, 12, 13, 14, 21, 22, 23, 24) переходит в позицию 2 (в транспонированной памяти 11, 21, 12, 22, 13, 23, 14, 24), а значение в позиции 2 (11, 12, 13, 14, 21, 22, 23, 24) переходит в позицию 4 (11, 21, 12, 22, 13, 23, 14, 24) и позиция 4 (11, 12, 13, 14, 21, 22, 23, 24) возвращается в позицию 1 (11, 21, 12, 22, 13, 23, 14, 24). Аналогично для значений позиции 7 и позиций (3 6 5).
Свойства перестановки
Далее мы предполагаем, что N×M матрица хранится в порядке старших строк с индексами, отсчитываемыми от нуля. Это означает, что (п,м) элемент, для п = 0,…,N−1 и м = 0,…,M−1, хранится по адресу а = Mn + м (плюс некоторое смещение в памяти, которое мы игнорируем). В транспонированном M×N матрица, соответствующая (м,п) элемент хранится по адресу а ‘ = Нм + п, снова в строчном порядке. Мы определяем перестановка транспозиции быть функцией а ‘ = п(а) такой, что:
- Nм+п=п(Mп+м){ Displaystyle Nm + N = P (Mn + m) ,} для всех (п,м)∈[0,N−1]×[0,M−1].{ Displaystyle (п, м) в [0, N-1] раз [0, M-1] ,.}
Это определяет перестановку чисел а=0,…,MN−1{ Displaystyle а = 0, ldots, MN-1}.
Оказывается, можно определить простые формулы для п и его обратное (Cate & Twigg, 1977). {d} -1, MN-1),}
{d} -1, MN-1),}
где μ — Функция Мёбиуса и сумма больше делители d из k.
Кроме того, цикл, содержащий а= 1 (т.е. второй элемент первой строки матрицы) всегда представляет собой цикл максимальной длины L, а длины k всех остальных циклов должны быть делителями L (Кейт и Твигг, 1977).
Для данного цикла C, каждый элемент Икс∈C{ displaystyle x in C} имеет тот же самый большой общий делитель d=gcd(Икс,MN−1){ Displaystyle d = gcd (х, MN-1)}.
Доказательство (Бреннер, 1973). |
|---|
Позволять s быть наименьшим элементом цикла, и d=gcd(s,MN−1){ Displaystyle d = gcd (s, MN-1)}. Из определения перестановки п выше, все остальные элементы Икс цикла получается многократным умножением s к N по модулю MN−1, поэтому любой другой элемент делится на d. Но с тех пор N и MN − 1 взаимно просты, Икс не может делиться ни на один множитель MN − 1 больше, чем d, и поэтому d=gcd(Икс,MN−1){ Displaystyle d = gcd (х, MN-1)}. |
Алгоритмы
Ниже кратко описаны опубликованные алгоритмы для выполнения транспонирования матрицы на месте. Исходный код реализацию некоторых из этих алгоритмов можно найти в приведенных ниже ссылках.
Аксессуар транспонировать
Поскольку физическое транспонирование матрицы требует больших вычислительных ресурсов, вместо перемещения значений в памяти вместо этого можно транспонировать путь доступа. Выполнить эту операцию для доступа к ЦП тривиально, поскольку пути доступа итераторы нужно просто обменять,[1] однако для аппаратного ускорения может потребоваться физическая перестройка.[2]
Квадратные матрицы
Для квадрата N×N матрица Ап,м = А(п,м), транспонирование на месте легко, потому что все циклы имеют длину 1 (диагонали Ап,п) или длиной 2 (верхний треугольник меняется местами с нижним). Псевдокод для этого (при условии, что множество индексы) это:
Псевдокод для этого (при условии, что множество индексы) это:
за от n = 0 до N - 2 за m = n + 1 на N - 1 поменять местами A (n, m) на A (m, n)
Этот тип реализации, хотя и прост, может демонстрировать низкую производительность из-за плохого использования строки кэша, особенно когда N это сила двух (из-за конфликтов строк кеша в Кэш процессора с ограниченной ассоциативностью). Причина этого в том, что, как м увеличивается во внутреннем цикле, адрес памяти соответствует А(п,м) или же А(м,п) перескакивает несмежно на N в памяти (в зависимости от того, имеет ли массив формат основных столбцов или строк соответственно). То есть алгоритм не использует местонахождение ссылки.
Одним из решений для улучшения использования кэша является «блокирование» алгоритма для работы сразу с несколькими числами в блоках, заданных размером строки кэша; К сожалению, это означает, что алгоритм зависит от размера строки кэша (он «учитывает кэш»), и на современном компьютере с несколькими уровнями кеширования он требует нескольких уровней машинно-зависимой блокировки. Вместо этого было предложено (Frigo и другие., 1999), что лучшую производительность можно получить рекурсивный Алгоритм: разделить матрицу на четыре подматрицы примерно равного размера, рекурсивно транспонируя две подматрицы по диагонали, а также переставляя и меняя местами две подматрицы над и под диагональю. (Когда N достаточно мала, простой алгоритм, описанный выше, используется в качестве базового случая, поскольку наивно повторяется вплоть до N= 1 будет иметь чрезмерные накладные расходы на вызов функции.) Это не обращающий внимания на тайник алгоритм в том смысле, что он может использовать строку кэша без явного параметра размера строки кэша.
Вместо этого было предложено (Frigo и другие., 1999), что лучшую производительность можно получить рекурсивный Алгоритм: разделить матрицу на четыре подматрицы примерно равного размера, рекурсивно транспонируя две подматрицы по диагонали, а также переставляя и меняя местами две подматрицы над и под диагональю. (Когда N достаточно мала, простой алгоритм, описанный выше, используется в качестве базового случая, поскольку наивно повторяется вплоть до N= 1 будет иметь чрезмерные накладные расходы на вызов функции.) Это не обращающий внимания на тайник алгоритм в том смысле, что он может использовать строку кэша без явного параметра размера строки кэша.
Неквадратные матрицы: следование циклам
Для неквадратных матриц алгоритмы более сложные. Многие из алгоритмов до 1980 г. можно было описать как алгоритмы «следования циклам». То есть они перебирают циклы, перемещая данные из одного места в другое в цикле. В форме псевдокода:
для каждого длина> 1 цикл C перестановки выберите начальный адрес s в C позволять D = данные в s позволять Икс = предшественник s в цикле пока Икс ≠ s переместить данные из Икс преемнику Икс позволять Икс = предшественник Икс переместить данные из D преемнику s
Различия между алгоритмами заключаются в основном в том, как они определяют местонахождение циклов, как они находят начальные адреса в каждом цикле и как они обеспечивают, чтобы каждый цикл перемещался ровно один раз. Обычно, как обсуждалось выше, циклы перемещаются попарно, поскольку s и MN−1−s находятся в циклах одинаковой длины (возможно, в одном цикле). Иногда небольшой массив царапин, обычно длиной M+N (например, Brenner, 1973; Cate & Twigg, 1977) используется для отслеживания подмножества посещенных местоположений в массиве с целью ускорения работы алгоритма.
Обычно, как обсуждалось выше, циклы перемещаются попарно, поскольку s и MN−1−s находятся в циклах одинаковой длины (возможно, в одном цикле). Иногда небольшой массив царапин, обычно длиной M+N (например, Brenner, 1973; Cate & Twigg, 1977) используется для отслеживания подмножества посещенных местоположений в массиве с целью ускорения работы алгоритма.
Чтобы определить, перемещен ли уже данный цикл, простейшей схемой было бы использование О(MN) вспомогательная память, одна кусочек на элемент, чтобы указать, был ли перемещен данный элемент. Использовать только О(M+N) или даже О(бревноMN) вспомогательная память, требуются более сложные алгоритмы, а известные алгоритмы имеют худший случай линейный вычислительная стоимость О(MN бревноMN) в лучшем случае, как впервые доказано Knuth (Фич и другие., 1995; Густавсон и Свирщ, 2007).
Такие алгоритмы предназначены для перемещения каждого элемента данных ровно один раз. Однако они также включают в себя значительный объем арифметики для вычисления циклов и требуют значительного непоследовательного доступа к памяти, поскольку соседние элементы циклов различаются мультипликативными коэффициентами N, как обсуждалось выше.
Однако они также включают в себя значительный объем арифметики для вычисления циклов и требуют значительного непоследовательного доступа к памяти, поскольку соседние элементы циклов различаются мультипликативными коэффициентами N, как обсуждалось выше.
Улучшение локальности памяти за счет большего общего перемещения данных
Было разработано несколько алгоритмов для достижения большей локальности памяти за счет большего перемещения данных, а также чуть более высоких требований к хранению. То есть они могут перемещать каждый элемент данных более одного раза, но они предполагают более последовательный доступ к памяти (большую пространственную локальность), что может повысить производительность современных процессоров, которые полагаются на кеши, а также на SIMD архитектуры, оптимизированные для обработки последовательных блоков данных. Самый старый контекст, в котором пространственная локальность транспозиции, по-видимому, изучалась, — это работа вне ядра (Alltop, 1975), когда матрица слишком велика, чтобы поместиться в основную память («основной «). {2}} блоки (что эффективно, поскольку перемещаемые блоки большие и последовательные, а длина циклов не превышает 2). Это дополнительно упрощается, если N кратно M (или наоборот), поскольку требуется только один из двух проходов вне места.
{2}} блоки (что эффективно, поскольку перемещаемые блоки большие и последовательные, а длина циклов не превышает 2). Это дополнительно упрощается, если N кратно M (или наоборот), поскольку требуется только один из двух проходов вне места.
Другой алгоритм для не-совмещать размеры, включающие множественные вспомогательные транспозиции, были описаны Catanzaro et al. (2014). Для случая, когда |N − M| мало, Доу (1995) описывает другой алгоритм, требующий |N − M| ⋅ мин (N,M) дополнительное хранилище, включая мин (N, M) ⋅ мин (N, M) квадратное транспонирование с предшествующим или последующим небольшим неуместным транспонированием. Frigo & Johnson (2005) описывают адаптацию этих алгоритмов для использования методов без учета кеша для процессоров общего назначения, использующих строки кеша для использования пространственной локальности.
Работа над транспонированием матрицы вне ядра, когда матрица не помещается в основную память и должна храниться в основном на жесткий диск, сосредоточился в основном на N = M квадратная матрица, за некоторыми исключениями (например, Alltop, 1975). Харрис, Марк (18 февраля 2013 г.). «Эффективное преобразование матрицы в CUDA C / C ++». Блог разработчиков NVIDIA.
Харрис, Марк (18 февраля 2013 г.). «Эффективное преобразование матрицы в CUDA C / C ++». Блог разработчиков NVIDIA.
- П. Ф. Виндли, «Транспонирование матриц в цифровом компьютере», Компьютерный журнал 2, п. 47-48 (1959).
- Г. Полл и Э. Сейден, «Проблема в абелевых группах, с приложением к транспонированию матрицы на электронном компьютере», Математика. Комп. 14, п. 189–192 (1960).
- Дж. Бутройд, «Алгоритм 302: транспонирование векторного сохраненного массива», Транзакции ACM на математическом ПО 10 (5), стр. 292–293 (1967). Дои:10.1145/363282.363304
- Сьюзан Лафлин и М. А. Бребнер, «Алгоритм 380: транспонирование прямоугольной матрицы на месте», Транзакции ACM на математическом ПО 13 (5), стр. 324-326 (1970). Дои:10.1145/362349.362368 Исходный код.
- Норман Бреннер, «Алгоритм 467: перестановка матрицы на место», Транзакции ACM на математическом ПО 16 (11), стр.
 692-694 (1973). Дои:10.1145/355611.362542 Исходный код.
692-694 (1973). Дои:10.1145/355611.362542 Исходный код. - W. O. Alltop, «Компьютерный алгоритм транспонирования неквадратных матриц», IEEE Trans. Comput. 24 (10), стр. 1038-1040 (1975).
- Эско Г. Кейт и Дэвид В. Твигг, «Алгоритм 513: анализ транспонирования на месте», Транзакции ACM на математическом ПО 3 (1), стр. 104-110 (1977). Дои:10.1145/355719.355729 Исходный код.
- Брайан Катандзаро, Александр Келлер и Майкл Гарланд, «Разложение для перестановки матрицы на месте», Труды 19-го симпозиума ACM SIGPLAN по Принципам и практике параллельного программирования (PPoPP ’14), стр. 193–206 (2014). Дои:10.1145/2555243.2555253
- Мюррей Доу, «Транспонирование матрицы на векторном компьютере», Параллельные вычисления 21 (12), с. 1997-2005 (1995).
- Дональд Э. Кнут, Искусство программирования Том 1: Основные алгоритмы, третье издание, раздел 1.3.3, упражнение 12 (Addison-Wesley: New York, 1997).
- М. Фриго, К. Э.
 Лейзерсон, Х. Прокоп и С. Рамачандран, «Алгоритмы без учета кеша», в Материалы 40-го симпозиума IEEE по основам компьютерных наук (FOCS 99), стр. 285-297 (1999). Дои:10.1109 / SFFCS.1999.814600
Лейзерсон, Х. Прокоп и С. Рамачандран, «Алгоритмы без учета кеша», в Материалы 40-го симпозиума IEEE по основам компьютерных наук (FOCS 99), стр. 285-297 (1999). Дои:10.1109 / SFFCS.1999.814600 - Дж. Сух и В. К. Прасанна, «Эффективный алгоритм транспонирования матрицы вне ядра», IEEE Trans. Компьютеры 51 (4), стр. 420-438 (2002). Дои:10.1109/12.995452
- С. Кришнамурти, Г. Баумгартнер, Д. Кочорва, К.-К. Лам и П. Садаяппан «.Эффективное параллельное транспонирование матрицы вне ядра,» Международный журнал высокопроизводительных вычислений и сетевых технологий 2 (2-4), с. 110-119 (2004).
- М. Фриго и С. Джонсон «Дизайн и реализация FFTW3,» Труды IEEE 93 (2), 216–231 (2005). Исходный код из FFTW библиотека, которая включает оптимизированные серийные и параллельно квадратные и неквадратные транспозиции, в дополнение к БПФ.
- Вера Э. Фич, Дж. Ян Манро и Патрисио В. Поблете, «Перестановка на месте», SIAM Журнал по вычислениям 24 (2), стр.
 266-278 (1995).
266-278 (1995). - Фред Г. Густавсон и Тадеуш Свирщ, «Транспонирование прямоугольных матриц на месте». Конспект лекций по информатике 4699, п. 560-569 (2007), из материалов семинара 2006 г. по современному состоянию [sic] в «Научных и параллельных вычислениях» (PARA 2006) (Умео, Швеция, июнь 2006 г.).
- Слоан, Н. Дж. А. (ред.). «Последовательность A093055 (Количество не одноэлементных циклов при транспонировании на месте прямоугольной матрицы j X k)». В Он-лайн энциклопедия целочисленных последовательностей. Фонд OEIS.
- Слоан, Н. Дж. А. (ред.). «Последовательность A093056 (Длина самого длинного цикла при транспонировании на месте прямоугольной матрицы j X k)». В Он-лайн энциклопедия целочисленных последовательностей. Фонд OEIS.
- Слоан, Н. Дж. А. (ред.). «Последовательность A093057 (количество элементов матрицы, оставшихся в фиксированной позиции при транспонировании на месте прямоугольной матрицы j X k)».
 В Он-лайн энциклопедия целочисленных последовательностей. Фонд OEIS.
В Он-лайн энциклопедия целочисленных последовательностей. Фонд OEIS.
внешняя ссылка
Исходный код
- OFFT — рекурсивное блочное транспонирование квадратных матриц на Фортране
- Джейсон Стратос Пападопулос, заблокировано транспонирование квадратных матриц на месте, в C, sci.math.num-analysis группа новостей (7 апреля 1998 г.).
- См. Ссылки «Исходный код» в разделе ссылок выше, чтобы узнать о дополнительном коде для выполнения транспонирования на месте как квадратных, так и неквадратных матриц.
- libmarshal Заблокировано местное транспонирование прямоугольных матриц для графических процессоров.
Транспонирование — Линейная алгебра
Транспонирование — Линейная алгебра—>
- Войти
- Биографии репетитора
- Подготовка к тесту
СРЕДНЯЯ ШКОЛА
- ACT Репетиторство
- SAT Репетиторство
- Репетиторство PSAT
- ASPIRE Репетиторство
- ШСАТ Репетиторство
- Репетиторство STAAR
ВЫСШАЯ ШКОЛА
- Репетиторство MCAT
- Репетиторство GRE
- Репетиторство по LSAT
- Репетиторство по GMAT
К-8
- Репетиторство AIMS
- Репетиторство по HSPT
- Репетиторство ISEE
- Репетиторство ISAT
- Репетиторство по SSAT
- Репетиторство STAAR
Поиск 50+ тестов
- Академическое обучение
репетиторство по математике
- алгебра
- Исчисление
- Элементарная математика
- Геометрия
- Предварительный расчет
- Статистика
- Тригонометрия
Репетиторство по естественным наукам
- Анатомия
- Биология
- Химия
- Физика
- Физиология
иностранные языки
- французский
- немецкий
- Латинский
- Китайский мандарин
- Испанский
начальное обучение
- Чтение
- Акустика
- Элементарная математика
прочее
- Бухгалтерия
- Информатика
- Экономика
- Английский
- Финансы
- История
- Письмо
- Лето
Поиск по 350+ темам
- О
- Обзор видео
- Процесс выбора наставника
- Онлайн-репетиторство
- Мобильное обучение
- Мгновенное обучение
- Как мы работаем
- Наша гарантия
- Влияние репетиторства
- Обзоры и отзывы
- Освещение в СМИ
- О преподавателях университета
Мы открыты в субботу и воскресенье!
Звоните прямо сейчас, чтобы записаться на обучение:
(888) 888-0446
Все ресурсы по линейной алгебре
4 Диагностические тесты 108 практических тестов Вопрос дня Карточки Learn by Concept
← Предыдущий 1 2 3 4 5 Следующий →
Справка по линейной алгебре » Операции и свойства » Транспонирование
Найдите транспонирование матрицы .
Возможные ответы:
Правильный ответ:
Объяснение:
Чтобы найти транспонирование, нам нужно превратить столбцы в строки.
Сообщить об ошибке
Транспонировать матрицу A где,
Возможные ответы:
Квадратную матрицу нельзя транспонировать Объяснение:
Транспонирование матрицы означает просто сделать столбцы исходной матрицы строками в транспонированной матрице. Пример: т. е. столбец 1 становится строкой 1, столбец 2 становится строкой 2 и т. д.0002
Невозможно с неквадратными матрицами Объяснение:
Транспонирование матрицы означает просто сделать столбцы исходной матрицы строками в транспонированной матрице. Пример: т. е. столбец 1 становится строкой 1, столбец 2 становится строкой 2 и т. д.
Пример: т. е. столбец 1 становится строкой 1, столбец 2 становится строкой 2 и т. д.
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Транспонирование матрицы означает просто сделать столбцы исходной матрицы строками в транспонированной матрице. Пример: т. е. столбец 1 становится строкой 1, столбец 2 становится строкой 2 и т. д.
Сообщить об ошибке Объяснение:
Транспонирование матрицы означает просто сделать столбцы исходной матрицы строками в транспонированной матрице. Пример: т. е. столбец 1 становится строкой 1, столбец 2 становится строкой 2 и т. д.
Отчет о ошибке
Возможные ответы:
Невозможно
Правильный ответ:
Объяснение:
Транспонирование матрицы означает просто сделать столбцы исходной матрицы строками в транспонированной матрице. Пример: т. е. столбец 1 становится строкой 1, столбец 2 становится строкой 2 и т. д.
Пример: т. е. столбец 1 становится строкой 1, столбец 2 становится строкой 2 и т. д.
Сообщить об ошибке
Возможные ответы:
Правильный ответ:
Объяснение:
Транспонирование матрицы означает просто сделать столбцы исходной матрицы строками в транспонированной матрице. Пример: т. е. столбец 1 становится строкой 1, столбец 2 становится строкой 2 и т. д.
Сообщить об ошибке
Что является транспонированием ?
Возможные ответы:
Правильный ответ:
Объяснение:
Поперечная — это матрица, в которой столбцы теперь являются соответствующими строками — первый столбец теперь является первой строкой, второй столбец теперь второй строкой и т. д.
д.
Сообщить об ошибке
Найти транспонирование матрицы A.
Возможные ответы:
Ни один из других ответов
20 Правильный ответ:0002
Объяснение:
Для матрицы A 3×2 транспонированная матрица A является матрицей 2×3, где столбцы образованы из соответствующих строк A.
Сообщить об ошибке
Найти транспонированную матрицу A.
Возможные ответы:
Ни один из других ответов
Объяснение:
Для матрицы A 2×4 транспонированием матрицы A является матрица 4×2, в которой столбцы формируются из соответствующих строк матрицы A. Уведомление
View Репетиторы по линейной алгебре
Кейси
Сертифицированный репетитор
Университет штата Аризона, бакалавр наук, математика. Университет штата Аризона, доктор философии, прикладная математика…
Университет штата Аризона, доктор философии, прикладная математика…
Посмотреть репетиторов по линейной алгебре
Уильям
Сертифицированный преподаватель
Салезианский колледж Дона Боско, бакалавр естественных наук. Universidad Rafael Landívar, бакалавр искусств, бизнес-реклама…
View Репетиторы линейной алгебры
Magdy
Сертифицированный репетитор
Каирский университет, Египет, бакалавр наук, электротехника. Университет штата Нью-Мексико, главный кампус, доктор фил…
Все ресурсы по линейной алгебре
4 диагностических теста 108 практических тестов Вопрос дня Карточки Учитесь по концепции
2.5: Транспонирование — Mathematics LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 19843
- Кен Каттлер
- Университет Бригама Янга via Lyryx 9{T}= \ \ \left[ \begin{array}{ccc} 1 & 3 & 2 \\ 4 & 1 & 6 \end{array} \right] \nonumber\]
Что случилось? Первый столбец стал первой строкой, а второй столбец стал второй строкой.
 Таким образом, матрица \(3\times 2\) стала матрицей \(2\times 3\). Число \(4\) было в первой строке и втором столбце, а оказалось во второй строке и первом столбце.
Таким образом, матрица \(3\times 2\) стала матрицей \(2\times 3\). Число \(4\) было в первой строке и втором столбце, а оказалось во второй строке и первом столбце.Определение транспонирования следующее.
Определение \(\PageIndex{1}\): транспонирование матрицы 9{T} = — A\), поэтому по определению \(\PageIndex{2}\) \(A\) кососимметрично.
Эта страница под названием 2.5: The Transpose распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Кен Каттлер
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу Содержание
- №
- Теги
- кососимметричная матрица
- источник@https://lyryx.
 com/first-course-linear-алгебра
com/first-course-linear-алгебра - транспонировать
Объяснение урока: Транспонирование матрицы
В этом объяснении мы узнаем, как найти транспонирование матрицы и определить симметричные и кососимметричные матрицы.
Давайте сначала вспомним определение матрицы.
Определение: Матрицы
Матрица размером 𝑚×𝑛 представляет собой прямоугольный массив записи с 𝑚 строки и столбцы 𝑛, определенные 𝐴=𝑎, где 𝑖∈{1,…,𝑚} и 𝑗∈{1,…,𝑛}. Каждый 𝑎 называется записью или элементом матрицы.
Теперь мы хотим исследовать транспонирование матрицы, которая операция, которая переворачивает матрицу по диагональным элементам. К лучшему Чтобы проиллюстрировать эту концепцию, рассмотрим следующую матрицу 3×2. 𝐴=30−2147.
В соответствии с нашим определением выше это можно записать как 𝐴=𝑎, где 𝑖∈{1,2,3} и 𝑗∈{1,2}.
 Когда
мы ссылаемся на диагональных записей, мы имеем в виду записи вида
𝑎, которые в данном случае являются записями
𝑎 и 𝑎. Мы выделяем эти
следующим образом:
Когда
мы ссылаемся на диагональных записей, мы имеем в виду записи вида
𝑎, которые в данном случае являются записями
𝑎 и 𝑎. Мы выделяем эти
следующим образом:Теперь, чтобы транспонировать матрицу, мы перевернуть матрицу на по диагонали, чтобы строки стали столбцами, а столбцы — строками. транспонированная матрица обозначается 𝐴, где 𝑇 Верхний индекс означает «транспонированный». Позволь нам покажите это ниже:
Обратите внимание, что только диагональные записи остаются на том же месте, а записи ниже диагонали поменялись местами с теми, что выше диагонали. В частности, строки и столбцы поменялись местами. Чтобы визуализировать это, пусть выделим первую строку исходной матрицы:
В транспонированной матрице это становится первым столбцом:
Точно так же вторая и третья строки становятся вторым и третьим столбцами, как показано ниже:
Итак, как мы видим, транспонирование матриц можно рассматривать как замену строки и столбцы друг с другом.

Поскольку строки и столбцы матрицы меняются местами, когда мы транспонируем матрица, количество строк и количество столбцов матрицы также поменялся местами. Для матрицы 𝐴, которая имеет порядок 2×3, мы можем видим, что 𝐴 имеет порядок 3×2. Мы можно обобщить следующим образом.
Определение: Порядок транспонирования матрицы
Если матрица 𝐴 имеет порядок 𝑚×𝑛, то транспонирование матрицы 𝐴 имеет порядок 𝑛×𝑚.
В нашем первом примере мы рассмотрим прямое использование этого определения для нахождения порядок матрицы.
Пример 1. Определение порядка транспонирования матрицы
Если 𝑋 — матрица порядка 4×1, то каков порядок матрица 𝑋?
Ответ
Матрица 𝑋 является транспонированной матрицей 𝑋. Напомним, что при транспонировании матрицы ее строки меняются местами со столбцами. В в частности, это означает, что количество строк и количество столбцов матрицы будут заменены.
 Другими словами, если матрица имеет порядок
𝑚×𝑛, транспонирование матрицы будет порядка
𝑛×𝑚.
Другими словами, если матрица имеет порядок
𝑚×𝑛, транспонирование матрицы будет порядка
𝑛×𝑚.В этом примере нам дано, что матрица 𝑋 имеет порядок 4×1, что означает 𝑚=4 и 𝑛=1. Следовательно, транспонирование 𝑋, которое это 𝑋, порядок 𝑛×𝑚=1×4.
Визуально мы можем видеть, что транспонирование оказывает следующее влияние на порядок матрицы: 𝑋=∗∗∗∗⟶𝑋=(∗∗∗∗).
Следовательно, порядок матрицы 𝑋 равен 1×4.
В предыдущем примере мы нашли порядок транспонирования матрицы. Позволять Теперь мы обсудим полное определение транспонирования матрицы и то, как идентифицировать его записи.
Определение: транспонирование матрицы
Рассмотрим матрицу 𝑚×𝑛 𝐴 определяется как 𝐴=𝑎. Транспонирование 𝐴, обозначаемый 𝐴, является матрица 𝑛×𝑚 определяется как 𝐴=𝑎.
В приведенном выше определении мы видим, что индексы строк и столбцов (𝑖 и 𝑗) меняются местами.
 Это имеет
тот же эффект замены строк и столбцов матрицы, как мы видели
выше. Например, мы можем видеть ниже эту запись 𝑎 в
матрица 𝐴 становится элементом 𝑎 в матрице 𝐴:
Это имеет
тот же эффект замены строк и столбцов матрицы, как мы видели
выше. Например, мы можем видеть ниже эту запись 𝑎 в
матрица 𝐴 становится элементом 𝑎 в матрице 𝐴:Другими словами, запись в строке 3 и столбце 1 становится записью в строке 1 и столбец 3. Любые диагональные записи, такие как 𝑎=3, не меняются.
Когда мы хотим найти транспонированную матрицу, первым делом нужно найти порядок новой матрицы. После этого мы должны найти записи, переворачивая матрица по диагонали. В следующем примере мы будем практиковаться, как сделать это.
Пример 2. Нахождение транспонирования матрицы
Учитывая, что 𝐴=−26−6184, найти 𝐴.
Ответ
Мы знаем, что 𝐴 является транспонированием матрицы 𝐴, поэтому нам нужно найти транспонирование данной матрицы в этот пример.
Напомним, что транспонирование матрицы 𝑚×𝑛 имеет вид заказ 𝑛×𝑚. Поскольку 𝐴 является Матрица 2 × 3, транспонированная 𝐴 будет матрицей 3×2, что приведет к следующему матрица с пустыми элементами: 𝐴=∗∗∗∗∗∗.

Теперь заполним элементами матрицы 𝐴. Отзывать что при транспонировании матрицы ее строки меняются местами со столбцами. В других слов, первая строка становится первым столбцом, вторая строка становится второй столбец и так далее. Итак, рассмотрим каждую строку 𝐴 и запишите каждый в виде соответствующих столбцов 𝐴.
Первая строка 𝐴 равна
В транспонированной матрице это становится первым столбцом:
Затем у нас есть вторая строка:
Это становится вторым столбцом:
Это приводит к транспонированной матрице 𝐴=−2168−64.
В предыдущем примере мы нашли транспонирование заданной матрицы, подставив каждая строка матрицы как соответствующий столбец транспонированной матрицы. Этот метод можно применять к матрицам любого порядка, как мы объясним ниже.
Практическое руководство. Транспонирование матрицы
Чтобы найти транспонирование матрицы 𝑚×𝑛, мы можем следуйте этой процедуре:
- Определите, что порядок матрицы транспонирования 𝑛×𝑚 и что, таким образом, он имеет 𝑛 строк и 𝑚 столбцы, как показано ниже:
- Рассмотрим каждую строку матрицы одну за другой и запишем ее в виде соответствующий столбец в транспонированной матрице:
- Завершите процесс транспонирования
𝐴:
𝐴=⎛⎜⎜⎝𝑎𝑎…𝑎𝑎𝑎…𝑎⋮⋮⋱⋮𝑎𝑎…𝑎⎞⎟⎟⎠.
 0008
0008
Следует отметить, что транспонирование матрицы имеет особое свойство, когда оно применяется два раза подряд. Мы проследим это свойство в следующем пример.
Пример 3. Применение дважды подряд транспонирования матрицы
Учитывая матрицу 𝐴=−84341−1, найти 𝐴.
Ответ
Мы знаем, что верхний индекс 𝑇 рядом с матрицей указывает транспонирование матрицы. Здесь мы видим, что есть два 𝑇 верхние индексы. Чтобы понять это обозначение, сначала отметим что 𝐴 является транспонированием данной матрицы 𝐴. Затем заметим, что 𝐴 равно транспонирование транспонирования данной матрицы 𝐴, означающее, что нам нужно применить транспонирование к матрице 𝐴 дважды подряд.
Следовательно, в этом примере нам нужно применить транспонирование к матрице 𝐴 два раза подряд. Мы можем начать с первого обнаружения матрица 𝐴, а затем применить транспонирование к результирующая матрица.

Напомним, что транспонирование матрицы 𝑚×𝑛 имеет вид заказ 𝑛×𝑚. Поскольку 𝐴 является Матрица 2×3, 𝐴 будет Матрица 3 × 2, ведущая к следующей матрице с пустые записи: 𝐴=∗∗∗∗∗∗.
Напомним, что мы можем найти транспонирование матрицы, поменяв местами строки и столбцы вокруг друг друга. Следовательно, первый ряд 𝐴 становится первым столбцом 𝐴:
Точно так же мы запишем вторую строку 𝐴 как вторую столбец 𝐴:
Таким образом, мы получили транспонирование 𝐴: 𝐴=−84413−1.
Мы повторяем процесс, снова выполняя транспонирование, чтобы найти 𝐴. Так как 𝐴 является Матрица 3×2, 𝐴 будет матрицей 2×3, что приведет к следующему матрица с пустыми элементами: 𝐴=∗∗∗∗∗∗.
Как и раньше, поменяем местами ряды 𝐴 со столбцами 𝐴. Начиная с первый ряд, у нас есть
Вторая строка дает нам
Для последней строки у нас есть
Как мы видим, эта матрица фактически идентична 𝐴.
 Это связано с тем, что замена строк и столбцов дважды приводит к тому, что они
такие же, как были раньше. В заключение имеем
𝐴=−84341−1.
Это связано с тем, что замена строк и столбцов дважды приводит к тому, что они
такие же, как были раньше. В заключение имеем
𝐴=−84341−1.В предыдущем примере мы видели, что применение транспонирования к заданной матрице два раза подряд приводили к одной и той же матрице. На самом деле это общее правило это относится к любой матрице.
Правило: двукратное применение транспонирования к матрице
Для матрицы 𝐴 двойное применение транспонирования приводит к та же матрица. Другими словами, 𝐴=𝐴.
Увидев, что последовательные применения транспонирования приводят к одному и тому же результату матрица, мы могли бы задаться вопросом, есть ли какие-либо другие свойства, которые матрица транспонировать есть. Например, существуют ли такие матрицы, что если применить транспонировать только один раз, мы все равно получим ту же матрицу? Как оказалось, есть определенный класс матриц, которые подчиняются такому свойству.

Определение: Симметричные и кососимметричные матрицы
Пусть 𝐴=𝑎 — матрица 𝑛×𝑛 (то есть квадратная матрица). Тогда 𝐴 является -симметричной -матрицей, если 𝐴=𝐴.
Альтернативно, 𝐴 является кососимметричной матрицей , если 𝐴=−𝐴.
Отметим, что в приведенном выше определении матрица должна быть квадратной матрицей. Это связано с тем, что если матрица не является квадратной, порядок матрицы изменится когда мы применяем транспонирование к матрице. Следовательно, симметричный и кососимметричный матрицы должны быть квадратными матрицами.
Также напомню, что когда мы используем транспонирование матрицы, мы меняем местами индексы каждой записи, поэтому 𝑎⟶𝑎. Следовательно, в чтобы матрица была равна своей транспонированной, мы требуем, чтобы 𝑎=𝑎. Аналогично для кососимметричных матриц требуется 𝑎=−𝑎. Заметим, что следствием этого является то, что диагональ элементы кососимметричной матрицы должны быть равны нулю, так как 𝑎=−𝑎 иначе не удовлетворился бы.
 Обобщим эти свойства ниже.
Обобщим эти свойства ниже.Свойство: индексы симметричных и кососимметричных матриц
Пусть 𝐴=𝑎 — квадратная матрица. 𝐴 является -симметричной -матрицей тогда и только тогда, когда 𝑎=𝑎𝑖,𝑗.для всех
Аналогично, 𝐴 является кососимметричной матрицей тогда и только тогда, когда 𝑎=−𝑎𝑖,𝑗.для всех
Имея в виду как определение, так и приведенное выше свойство, мы можем начать представьте, как выглядит симметричная или кососимметричная матрица. Рассмотрим следующую матрицу, где выделена диагональ:
Обратите внимание, что матрица останется неизменной, если мы будем отражать каждую запись в течение диагональ. В этом смысле матрица симметрична , где ось симметрии это диагональ. По индексам мы видим, что 𝑎=𝑎 для каждого 𝑖,𝑗; например, 𝑎=𝑎=7 и 𝑎=𝑎=0. Отметим, что по умолчанию диагональные элементы подчиняются этому свойству, поскольку они имеют вид 𝑎 (перестановка индексов строк и столбцов не дает никакого эффекта).

Аналогичным образом можно идентифицировать кососимметричные матрицы. Рассмотрим следующую матрицу:
В этом случае по обе стороны от диагонали элементы одинаковы, но с противоположные знаки. Например, 𝑏=−4, а 𝑏=4, и 𝑏=−6, а 𝑏=6. В частности, все диагональные элементы равны нулю, т. е. 𝑏=0 для 𝑖∈{1,2,3}. В в общем, мы можем видеть, что 𝑏=−𝑏; таким образом, 𝐵 равно кососимметричному . Мы видим, что диагональ записи, равные 0, являются необходимым следствием этого, поскольку 𝑏=−𝑏, что может быть верно только для 𝑏=0.
В качестве дополнительного примечания давайте рассмотрим случай, когда у нас есть квадрат-ноль matrix:
Транспонирование этой матрицы не даст никакого эффекта, так как все элементы подобные. Таким образом, 𝐶=𝐶 и 𝐶 симметрично. Однако отметим также, что 𝐶=−𝐶, что означает, что 𝐶 также кососимметрично. В самом деле, матрицы с квадратным нулем являются единственным типом матриц, которые одновременно являются симметричными и кососимметричными в в то же время.

Давайте теперь применим наши знания о симметричных матрицах в следующем пример.
Пример 4. Поиск неизвестных элементов, делающих данную матрицу симметричной
Найдите значение 𝑋, которое делает матрицу 𝐴=−15𝑥−3−43−8 симметрично.
Ответ
Напомним, что для того, чтобы матрица была симметричной, она должна быть квадратной и должен удовлетворить 𝐴=𝐴, где 𝐴 — транспонирование 𝐴. Как количество строк и количество столбцов 𝐴 оба равной 2, это действительно квадратная матрица, удовлетворяющая первому условию. Чтобы найти, какие значения 𝑥 удовлетворяют второму условие, мы можем применить транспонирование к 𝐴 и приравнять его к себе.
Для начала посчитаем 𝐴. С 𝐴 представляет собой матрицу 2 × 2, порядок транспонированной матрицы также будет 2×2. Чтобы найти записи 𝐴, мы можем переписать строки 𝐴 как столбцы 𝐴 следующим образом:
Таким образом, транспонирование 𝐴=−1−435𝑥−3−8.

Чтобы удовлетворить 𝐴=𝐴, приравняем эту матрицу к исходная матрица, данная нам, чтобы получить следующее матричное уравнение: −15𝑥−3−43−8=−1−435𝑥−3−8.
Чтобы проверить равенство двух матриц, мы должны проверить, что соответствующие записи равны. Ясно, что диагональные элементы такие же, как и транспонирование не меняет их. Выделим недиагональные записи который должен быть равен ниже:
Это дает нам два уравнения, которым мы должны удовлетворять: −43=5𝑥−3,5𝑥−3=−43.
Мы видим, что оба уравнения одинаковы. Поскольку это линейное уравнение, мы можем решить его, переставив его так, чтобы 𝑥 является предметом: −40=5𝑥−8=𝑥.
Следовательно, 𝑥=−8.
Обратите внимание, что в предыдущем примере также можно было бы найти 𝑥 с помощью следующего свойства симметричных матриц: 𝑎=𝑎𝑖,𝑗.для всех
Для матрицы 2×2 нам нужно только убедиться, что 𝑎=𝑎.
 Мы видим, что в данной матрице:
𝑎=5𝑥−3,𝑎=−43.
Мы видим, что в данной матрице:
𝑎=5𝑥−3,𝑎=−43.Таким образом, установка 𝑎=𝑎 приводит к тому же уравнению что мы нашли в примере.
Теперь рассмотрим пример, в котором мы рассматриваем кососимметричную матрицу.
Пример 5. Нахождение неизвестных элементов, делающих данную матрицу кососимметричной
Учитывая, что матрица 𝐵=0−2𝑥−63𝑧+1403𝑧−3𝑦+6𝑥−120 кососимметрично, найдите значение 𝑥+𝑦+𝑧.
Ответ
Напомним, что для того, чтобы матрица была кососимметричной, она должна быть квадратной и он должен удовлетворять условию 𝐵=−𝐵, где 𝐵 — транспонирование 𝐵. По количеству строк и количеству столбцов 𝐵 оба равны 3, это действительно квадратная матрица. По применяя транспонирование к 𝐵 и приравнивая его к себе, мы надеемся найти, какие значения 𝑥, 𝑦 и 𝑧 удовлетворяют второму условию.
Начнем с вычисления 𝐵. С 𝐵 имеет порядок 3×3, порядок 𝐵 также будет 3×3.
 Чтобы найти записи 𝐵,
мы можем переписать строки 𝐵 как столбцы
𝐵 следующим образом:
Чтобы найти записи 𝐵,
мы можем переписать строки 𝐵 как столбцы
𝐵 следующим образом:Таким образом, транспонирование 𝐵=0𝑧+14−3𝑦+6𝑥−2𝑥0−12−633𝑧0.
Теперь мы можем записать 𝐵=−𝐵, используя отрицание этого транспонированная матрица и исходная матрица: 0−2𝑥−63𝑧+1403𝑧−3𝑦+6𝑥−120=0−𝑧−143𝑦−6𝑥2𝑥01263−3𝑧0.
Чтобы это матричное уравнение удовлетворялось, соответствующие записи должны быть равны. Прежде всего отметим, что в обеих частях уравнения диагональные элементы равны нулю (что является необходимым условием для того, чтобы матрица была кососимметричный). Для недиагональных записей мы выделяем, где они должны быть равным:
Это приводит к шести уравнениям, хотя в тех случаях, когда мы использовали тот же цвет выделения, уравнения эквивалентны. Например, зеленые записи в позициях 𝑏 и 𝑏 дайте нам следующее эквивалентная пара уравнений: 𝑧+14=2𝑥⟺−2𝑥=−𝑧−14.

Таким образом, у нас есть три уникальных уравнения: 𝑧+14=2𝑥,−3𝑦+6𝑥=63,12=3𝑧.
Чтобы вычислить 𝑥+𝑦+𝑧, сначала решим эти одновременные уравнения чтобы найти 𝑥, 𝑦 и 𝑧 по отдельности. Из третье уравнение, мы имеем 12=3𝑧4=𝑧.
Итак, 𝑧=4. Мы можем заменить это в первый уравнение, 𝑧+14=2𝑥, чтобы получить 4+14=2𝑥18=2𝑥9=𝑥.
Таким образом, 𝑥=9. Наконец, мы можем заменить это на второе уравнение, −3𝑦+6𝑥=63, чтобы получить −3𝑦+6(9)=63−3𝑦+54=63−3𝑦=9𝑦=−3.
В сумме это дает нам 𝑥=9, 𝑦=−3 и 𝑧=4. Наконец, мы можем найти 𝑥+𝑦+𝑧, сложив их вместе, чтобы получить 𝑥+𝑦+𝑧=9−3+4=10.
В нашем последнем примере мы рассмотрим, как транспонирование взаимодействует с другими матричные операции.
Пример 6. Исследование свойств транспонированных матриц
Даны матрицы 𝑌=−422−7 и 𝑋=44−1−7, (𝑌−𝑋)=𝑌−𝑋?
Ответ
Мы знаем, что верхний индекс 𝑇 рядом с матрицей указывает транспонирование матрицы.
 Левая часть данного уравнения применима
транспонирование после вычитания матрицы, а правая часть
применяет транспонирование к каждой матрице перед вычитанием матрицы. Следовательно,
этот пример спрашивает, можем ли мы поменять порядок транспонирования
и вычитание.
Левая часть данного уравнения применима
транспонирование после вычитания матрицы, а правая часть
применяет транспонирование к каждой матрице перед вычитанием матрицы. Следовательно,
этот пример спрашивает, можем ли мы поменять порядок транспонирования
и вычитание.Теперь, чтобы проверить правильность этого уравнения, нам нужно вычислить каждый стороны от него и убедитесь, что матрицы равны.
Чтобы вычислить левую часть уравнения, сначала найдем разница 𝑌−𝑋. Напомним, что мы можем взять разность двух матриц того же порядка, взяв разность соответствующих записей в две матрицы. Это дает нам 𝑌−𝑋=−422−7−44−1−7=−8−230.
Затем мы можем применить транспонирование, чтобы найти матрицу (𝑌−𝑋). Напомним, что транспонирование 𝑚×𝑛 матрица представляет собой 𝑛×𝑚 матрица. Поскольку 𝑌−𝑋 — матрица 2 × 2, его транспонирование должно иметь тот же порядок.

Напомним также, что можно найти транспонирование матрицы, поменяв ее местами. строки со своими столбцами. Мы можем взять каждую строку матрицы 𝑌−𝑋 и поместите каждый в соответствующий столбец следующим образом:
Итак, имеем (𝑌−𝑋)=−83−20.
Теперь для правой части нужно вычислить 𝑌−𝑋. Начнем с поиска транспонирования 𝑌 и 𝑋 отдельно. Давайте сначала учтите 𝑌: 𝑌=−422−7.
Заметим, что 𝑌 является -симметричной -матрицей, так как значения по обе стороны от диагонали (𝑎 и 𝑎) равны. Таким образом, транспонирование 𝑌=−422−7.
Далее рассмотрим 𝑋: 𝑋=44−1−7.
Это не симметричная матрица, поэтому мы возьмем транспонирование путем замены его строки со своими столбцами:
Таким образом, мы имеем 𝑋=4−14−7.
Наконец, мы можем вычислить 𝑌−𝑋, используя матрицу вычитание следующим образом: 𝑌−𝑋=−422−7−4−14−7=−83−20.

Как мы видим, это совпадает с матрицей, которую мы рассчитали для (𝑌−𝑋). Таким образом, мы можем заключить, что (𝑌−𝑋)=𝑌−𝑋.
Отметим, что результат приведенного выше примера не случаен. Для общего матриц 𝐴 и 𝐵, оно выполняется, а также распространяется на матрицы при сложении. Мы называем это свойство дистрибутивностью .
Свойство: дистрибутивность преобразования матриц
Пусть 𝐴 и 𝐵 два 𝑚×𝑛 матрицы. Таким образом, у нас есть (𝐴+𝐵)=𝐴+𝐵,(𝐴−𝐵)=𝐴−𝐵.
В этом объяснении мы обсудили транспонирование матрицы и некоторые его интересные свойства. Подытожим основные моменты, которые мы узнали.
Ключевые точки
- Если матрица имеет порядок 𝑚×𝑛, то транспонирование матрицы имеет порядок 𝑛×𝑚.
- Если 𝐴=𝑎, то матрица транспонирования определяется как 𝐴=𝑎.
- Мы можем транспонировать элементы матрицы, записав ее строки как столбцы.

- Квадратная матрица 𝐴 равна симметричный если 𝐴=𝐴. Кроме того, квадратная матрица 𝐴=𝑎 симметричен тогда и только тогда, когда 𝑎=𝑎𝑖,𝑗.для всех
- Квадратная матрица 𝐴 является кососимметричной , если 𝐴=−𝐴. Точно так же квадратная матрица 𝐴=𝑎 кососимметричным тогда и только тогда, когда 𝑎=−𝑎𝑖,𝑗.для всех
- Пусть 𝐴 и 𝐵 два 𝑚×𝑛 матрицы. Таким образом, у нас есть (𝐴+𝐵)=𝐴+𝐵,(𝐴−𝐵)=𝐴−𝐵.
Mathwords: транспонирование матрицы
Mathwords: транспонирование матрицыиндекс: нажмите на букву индекс: предметные области Транспонирование матрицы
Матрица, образованная точением все строки данной матрицы в столбцы и наоборот.
 транспонировать матрицу A записывается как A T .
транспонировать матрицу A записывается как A T .См. также
Обратная матрица
эта страница обновлена 19 июля 17
Математические слова: термины и формулы от алгебры I до исчисления
написано, проиллюстрировано и создано веб-мастером Брюсом Симмонсом
Copyright © 2000 by Bruce Simmons
Все права защищеныТранспонирование матриц и симметричные матрицы | by adam dhalla
Все, что вам нужно знать о транспонировании матриц и симметричных матрицах
Матричное транспонирование и симметричные матрицы связаны — фактически, определение симметричной матрицы состоит в том, что транспонирование симметричной матрицы A возвращает ту же матрицу A
Это продолжение моей серии статей по линейной алгебре, связанной с курсом 18.
 06 MIT OCW Гилберта Стрэнга по вводной линейной алгебре. Давайте сразу перейдем к основам транспонирования.
06 MIT OCW Гилберта Стрэнга по вводной линейной алгебре. Давайте сразу перейдем к основам транспонирования.Транспонирование матрицы
Мы транспонируем двумерную матрицу, используя ее строки в качестве столбцов или, наоборот, используя ее столбцы в качестве строк. Это все, что нужно для выполнения простой операции.
Точнее, запись в позиции a ij становится записью в позиции аджи позиция. Конкретно, посмотрите, как e меняется от позиции (3, 1) к позиции (1, 3). Это все хорошо, но как насчет транспонирования суммы или произведения матриц?
Транспонирование суммы матриц
Транспонирование суммы (и, соответственно, разности) матриц довольно просто. Мы можем просто «распределить» транспонирование на оба числа.
Это, опять же, имеет вполне логичный смысл и не требует доказательств, чтобы считать его правдой. В левой части мы добавляем две матрицы, а затем транспонируем сумму. Справа их дополнительно транспонируем и добавляем.
 Одни и те же числа по-прежнему добавляются друг к другу, поэтому конечный результат тот же. Конкретный пример:
Одни и те же числа по-прежнему добавляются друг к другу, поэтому конечный результат тот же. Конкретный пример:Оба способа добавления эквивалентны. Нам часто приходится упрощать транспонирование в матричных уравнениях, так что имейте это в виду.
Транспонирование произведения матриц
Интуитивно понять это труднее, чем суммирование. Давайте посмотрим, что происходит, когда мы транспонируем продукт AB.
Если вы знакомы с обратным произведением, мы факторизуем его одинаково — мы транспонируем оба произведения, но обращаем порядок. Труднее взглянуть на это и понять, почему оно работает, поэтому давайте углубимся в детали умножения матриц, чтобы понять, почему это происходит.
Давайте рассмотрим ту же систему на конкретном примере.
Давайте посмотрим, откуда взялась первая строка нашей матрицы результатов. Возвращаясь назад с конца, мы видим, что эта строка на самом деле является столбцом до того, как она будет транспонирована. Этот столбец получается из первой и второй строк матрицы A, умноженной на первую колонку матрицы B.
 Можно сказать, что первая строка нашего результата есть произведение строк матрицы A на первую колонку матрицы B.
Можно сказать, что первая строка нашего результата есть произведение строк матрицы A на первую колонку матрицы B. Скажем мы переставили A и B перед их умножением. Как нам найти способ сохранить тот же расчет (строки A по первому столбцу B)? Давайте сделаем это и посмотрим, как.
Выделены одни и те же строки A (теперь столбцы A) и первый столбец B (теперь первая строка B). Их нужно перемножить, чтобы получить первую строку B. В каком порядке мы должны умножить их в для того, чтобы получить первую строку продукта? Ну было бы, конечно:
Сохраняем идентичное умножение, и таким образом получаем точно такое же произведение для первой строки. Таким образом, наше правило, изложенное ранее, корректируется.
Симметричные матрицы
Симметричные матрицы, как было сказано ранее, это матрицы, которые после транспонирования становятся идентичными. Официально:
Согласно нашему предыдущему определению того, что такое транспонирование, при транспонировании некоторый элемент в строке i и столбце j (aij) становится элементом в строке j и столбце i (aij).
Пары поменялись индексами. Например, 13 в первой строке — это индекс (1, 3). 13 в первом столбце (3, 1) Таким образом, в симметричной матрице aij должно = aji для всех aji. Глядя на пример симметричной матрицы, это очевидно.
Таким образом, в симметричной матрице aij должно = aji для всех aji. Глядя на пример симметричной матрицы, это очевидно.Хороший прием для обнаружения симметричных матриц состоит в том, что они выглядят зеркально отраженными по диагонали. На самом деле симметричные матрицы появляются довольно часто. Они хороши и аккуратны для целого ряда вычислений. Давайте рассмотрим еще несколько свойств симметричных матриц.
Инверсия симметричной матрицы также является симметричной
Поначалу это свойство может показаться немного неожиданным, но мы можем очень, очень быстро доказать это, слегка изменив формулу для симметричной матрицы.
Если A уже симметрична, значит, A = A(T), их обратные стороны также должны быть симметричными, потому что: в основном говоря, транспонирование обратного равно обратному. Это свойство часто пригодится.
Произведение матрицы и ее транспонирования симметрично
Произведение любой матрицы (квадратной или прямоугольной) и ее транспонирования всегда симметрично.
 В более понятных обозначениях это:
В более понятных обозначениях это:Это легко доказать, но трудно поверить, пока вы на самом деле не сделаете это , и тогда это становится совершенно очевидным. Давайте сначала рассмотрим конкретный случай, а затем докажем его с помощью матричных обозначений (легко).
Сделайте это умножение, чтобы действительно понять, почему мы получаем семь в углах. Проще говоря, для первых 7 мы умножаем (1, 2) на (3, 2), а для нижних 7 мы умножаем (3, 2) на (1, 2), что дает тот же продукт. Эту идею можно легко расширить до нескольких симметричных записей — мы просто умножаем некоторую строку в A, транспонируемую (a, b, c…. z) на столбец (z, y, z… a) в A, а затем позже, умножение некоторой строки в A, транспонированной (z, y, z…a) на некоторый столбец в A (a, b, c…. z), что дает два одинаковых ответа.
Давайте быстро докажем это с помощью изученного нами правила «перестановки произведений». Помните, тест на симметрию состоит в том, чтобы взять транспонирование и посмотреть, дает ли оно то же самое.

Здесь, если мы возьмем транспонирование нашего продукта, мы получим тот же продукт, что означает, что наше транспонирование A * A симметрично.
Мы упомянули это как небольшую оговорку, но мы получим симметричную, но другую матрицу, если мы поменяем порядок транспонирования и оригинала. Например, с неквадратной матрицей:
Мы видим, что наши продукты разные — черт возьми, они разных размеров! Но они оба симметричны. Наш результат с одним элементом слева по-прежнему симметричен, поскольку транспонирование скаляра 10 равно 10.
Гауссово исключение Что, если A в A = LDU симметричен?
Если вы не знакомы с методом исключения Гаусса, можете пропустить эту часть. Если вы знакомы с исключением, но не знаете факторизации A = LU или A = LDU, ознакомьтесь с моей последней статьей в мини-сериале «Исключение по Гауссу».
[3/3] Полное руководство по исключению Гаусса
Часть 3 из 3: Факторизация исключения Гаусса; А = ЛУ; способ, которым компьютеры выполняют исключение
medium.
 com
comЗдесь мы имеем дело с вероятностью того, что наша матрица коэффициентов A симметрична. Есть ли способ быстрее найти нижнюю и верхнюю треугольные матрицы A = U в A = LDU?
Что ж, если A симметрична или A(T) = A, то
Таким образом, найти нашу матрицу U еще проще, и нам не нужно беспокоиться о том, чтобы проделывать U так, чтобы мы может иметь матрицу D, содержащую точки опоры, и матрицу U, состоящую только из единиц по диагонали. В качестве примера, давайте вычислим матрицу A 2 x 2 и разложим ее на LDL(T).
Итак, начнем — это все, что нужно знать о транспонировании и симметричных матрицах в базовом начальном курсе линейной алгебры.
Спасибо за внимание!
Адам Дхалла учится в старшей школе из Ванкувера, Британская Колумбия. Он очарован внешним миром и в настоящее время изучает новые технологии для защиты окружающей среды. Чтобы не отставать,
Подпишитесь на его I nstagram и его LinkedIn .
 Чтобы получить больше подобного контента, подпишитесь на его информационный бюллетень здесь.
Чтобы получить больше подобного контента, подпишитесь на его информационный бюллетень здесь. Транспонирование матрицы — Математические инструменты онлайн
Скоро в продаже Эти математические инструменты уже в пути
Функции построения графиков
Рисовать графики математических функций.
Рисование формулы LaTeX
Создание изображения из выражения LaTeX.
Найти n-ю цифру
Вычислить n-ю цифру числа Эйлера.
Найти n-ю цифру золотого сечения
Вычислить n-ю цифру золотого сечения.
Найти n-ю цифру числа пи
Вычислить n-ю цифру числа пи.
Вычислить сумму e цифр
Найти сумму e цифр.
Вычислить сумму цифр золотого сечения
Найти сумму цифр золотого сечения.
Вычислить сумму пи цифр
Найти сумму пи цифр.
Генерировать цифры Чамперноуна
Генерировать цифры константы Чамперноуна.

Найти n-ю цифру Чамперноуна
Вычислить n-ю цифру константы Чамперноуна.
Декодирование последовательности «посмотри и скажи»
Выполните обратную операцию над последовательностью «посмотри и скажи».
Создание P-адических расширений
Вычисление p-адических расширений произвольных чисел.
Создать последовательность панцифровых чисел
Создать список панцифровых чисел.
Создать последовательность номеров Стэнли
Создать список номеров Стэнли.
Создать последовательность номеров звонков
Создать список номеров звонков.
Генерация последовательности номеров Кармайкла
Создание списка номеров Чармичел.
Создать последовательность каталонских номеров
Создать список каталонских номеров.
Создать последовательность треугольных чисел
Создать список треугольных чисел.
Создать последовательность составных чисел
Создать список составных чисел.

Генерация секущей числовой последовательности
Создать список секущих чисел.
Создать последовательность чисел Голомба
Создать список чисел Голомба-Сильвермана.
Создать последовательность чисел Эйлера Тотиент
Создать список фи-чисел Эйлера.
Создать последовательность номеров жонглеров
Создать список номеров жонглеров.
Создать последовательность счастливых номеров
Создать список счастливых номеров.
Создать последовательность номеров Моцкина
Создать список номеров Моцкина.
Создать последовательность номеров Padovan
Создать список номеров Padovan.
Создать последовательность псевдосовершенных чисел
Создать список полусовершенных чисел.
Создать последовательность номеров Ulam
Создать список номеров Ulam.
Создать последовательность странных чисел
Создать список странных чисел.
Создать последовательность суперсовершенных чисел
Создать список суперсовершенных чисел.

Продолжение последовательности цифр
Найти закономерность в числовой последовательности и расширить ее.
Разбить число
Найти все разбиения данного целого числа.
Создать последовательность номеров разделов
Создать список номеров функций разделов.
Создание арифметической прогрессии
Создание арифметической последовательности чисел.
Создание геометрической прогрессии
Создание геометрической последовательности чисел.
Создание полиномиальной прогрессии
Создать полиномиальную последовательность чисел.
Создать последовательность натуральных чисел
Создать список натуральных чисел.
Создание степеней двойки
Создание списка чисел степеней двойки.
Создание степеней десяти
Создание списка чисел в степени десятка.
Создание плотной матрицы
Создание матрицы с очень небольшим количеством нулевых элементов.
Создать разреженную матрицу
Создать матрицу с очень небольшим количеством ненулевых элементов.

Умножить матрицу на скаляр
Умножить все элементы матрицы на число.
Проверить, является ли матрица единственной.
Определить, является ли матрица вырожденной.
Найти матрицу кофакторов
Для заданной матрицы найти ее матрицу кофакторов.
Найдите вспомогательную матрицу
По заданной матрице найдите ее дополнение.
LU Factor a Matrix
Разложить матрицу на LU-факторы.
Найти собственные значения матрицы
Найти собственные значения матрицы.
Украсить матрицу
Украсить матрицу, аккуратно выровняв все ее столбцы.
Переформатировать матрицу
Преобразовать матрицу из одного формата в другой формат.
Рисование архимедовой спирали
Создание архимедовой спирали.
Рисование спирали Эйлера
Создание кривой спирали Корню (полиномиальной спирали).
Рисование спирали Фибоначчи
Создание кривой спирали Фибоначчи.
Нарисуйте спираль Теодора
Создание спирали квадратного корня.

Нарисуйте спираль Ферма
Создайте кривую в виде параболической спирали.
Рисование прямоугольников Фибоначчи
Создание рисунка прямоугольников Фибоначчи.
Нарисуйте головку семени Фибоначчи
Создайте головку цветка Фибоначчи.
Нарисовать фрактал Падована
Создать фрактал равнобуквенных треугольников Падована.
Нарисуйте аполлонову прокладку
Создайте фрактал аполлоновой прокладки.
Нарисовать фрактал Мандельброта
Создать фрактал Мандельброта.
Нарисовать фрактал Юлии
Создать фрактал Джулии.
Нарисовать фрактал Рози
Создать фрактал Рози.
Нарисовать кривую фрактала Бланманже
Создать фрактал Бланманже.
Рисование функции Вейерштрасса
Создание фрактала Вейерштрасса.
Нарисовать кривую Минковского в виде вопросительного знака
Создать фрактал Минковского в виде вопросительного знака.
Нарисуйте функцию Тома
Создайте функцию Тома (также известную как функция попкорна или капли дождя).

Нарисовать функцию Дирихле
Нарисовать функцию Дирихле.
Нарисуйте рог Гавриила
Нарисуйте геометрическую фигуру с бесконечной площадью поверхности и конечным объемом.
Преобразование слов в числа
Преобразование чисел из английского текста в реальные цифры.
Преобразование чисел в слова
Преобразование чисел в письменный текст на английском языке.
Преобразование десятичной записи в научную запись
Преобразование чисел, записанных в десятичной форме, в научную форму.
Преобразование научной записи в десятичную.
Преобразование чисел, записанных в научной форме, в десятичную форму.
Округление чисел вверх
Применение операции ceil к числам.
Округление чисел в меньшую сторону
Применить операцию пола к числам.
Анализ чисел
Подсчитайте, сколько раз встречается каждое число.
Преобразование числа в виде суммы
Создание суммы, которая в сумме составляет заданное число.


 Первый (а = 0) и последний (а = MN−1) элементы всегда остаются инвариантными при транспонировании.
Первый (а = 0) и последний (а = MN−1) элементы всегда остаются инвариантными при транспонировании. 692-694 (1973). Дои:10.1145/355611.362542 Исходный код.
692-694 (1973). Дои:10.1145/355611.362542 Исходный код. Лейзерсон, Х. Прокоп и С. Рамачандран, «Алгоритмы без учета кеша», в Материалы 40-го симпозиума IEEE по основам компьютерных наук (FOCS 99), стр. 285-297 (1999). Дои:10.1109 / SFFCS.1999.814600
Лейзерсон, Х. Прокоп и С. Рамачандран, «Алгоритмы без учета кеша», в Материалы 40-го симпозиума IEEE по основам компьютерных наук (FOCS 99), стр. 285-297 (1999). Дои:10.1109 / SFFCS.1999.814600 266-278 (1995).
266-278 (1995). В Он-лайн энциклопедия целочисленных последовательностей. Фонд OEIS.
В Он-лайн энциклопедия целочисленных последовательностей. Фонд OEIS. Таким образом, матрица \(3\times 2\) стала матрицей \(2\times 3\). Число \(4\) было в первой строке и втором столбце, а оказалось во второй строке и первом столбце.
Таким образом, матрица \(3\times 2\) стала матрицей \(2\times 3\). Число \(4\) было в первой строке и втором столбце, а оказалось во второй строке и первом столбце. com/first-course-linear-алгебра
com/first-course-linear-алгебра Когда
мы ссылаемся на диагональных записей, мы имеем в виду записи вида
𝑎, которые в данном случае являются записями
𝑎 и 𝑎. Мы выделяем эти
следующим образом:
Когда
мы ссылаемся на диагональных записей, мы имеем в виду записи вида
𝑎, которые в данном случае являются записями
𝑎 и 𝑎. Мы выделяем эти
следующим образом:
 Другими словами, если матрица имеет порядок
𝑚×𝑛, транспонирование матрицы будет порядка
𝑛×𝑚.
Другими словами, если матрица имеет порядок
𝑚×𝑛, транспонирование матрицы будет порядка
𝑛×𝑚. Это имеет
тот же эффект замены строк и столбцов матрицы, как мы видели
выше. Например, мы можем видеть ниже эту запись 𝑎 в
матрица 𝐴 становится элементом 𝑎 в матрице 𝐴:
Это имеет
тот же эффект замены строк и столбцов матрицы, как мы видели
выше. Например, мы можем видеть ниже эту запись 𝑎 в
матрица 𝐴 становится элементом 𝑎 в матрице 𝐴:
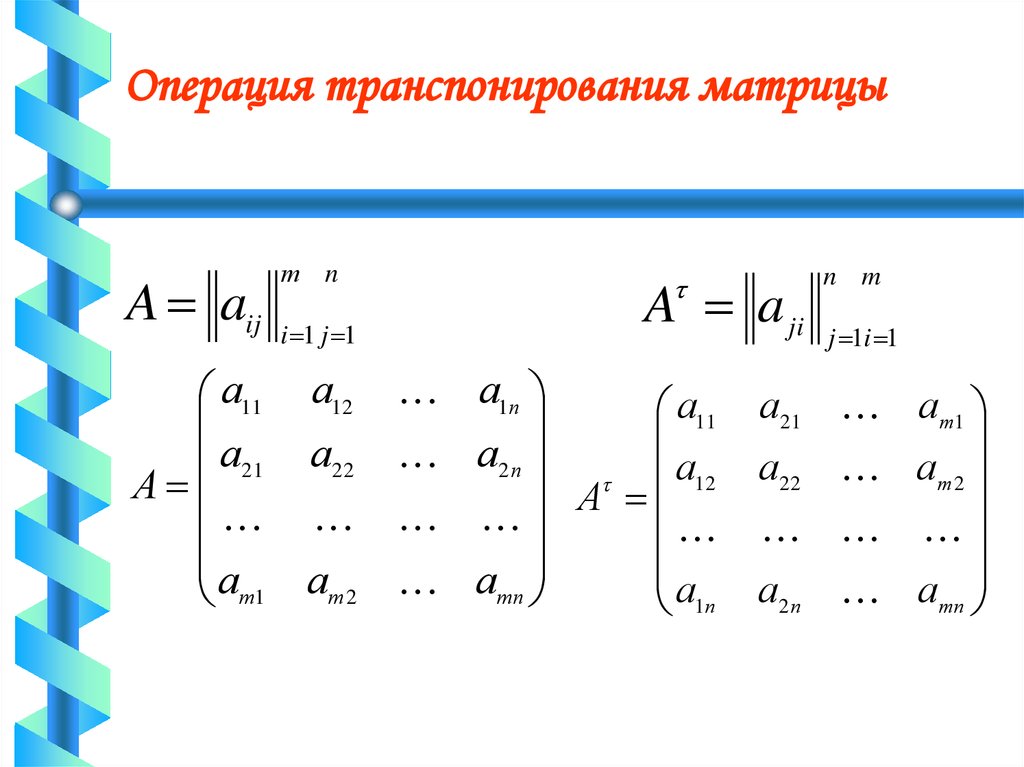 0008
0008
 Это связано с тем, что замена строк и столбцов дважды приводит к тому, что они
такие же, как были раньше. В заключение имеем
𝐴=−84341−1.
Это связано с тем, что замена строк и столбцов дважды приводит к тому, что они
такие же, как были раньше. В заключение имеем
𝐴=−84341−1.
 Обобщим эти свойства ниже.
Обобщим эти свойства ниже.


 Мы видим, что в данной матрице:
𝑎=5𝑥−3,𝑎=−43.
Мы видим, что в данной матрице:
𝑎=5𝑥−3,𝑎=−43. Чтобы найти записи 𝐵,
мы можем переписать строки 𝐵 как столбцы
𝐵 следующим образом:
Чтобы найти записи 𝐵,
мы можем переписать строки 𝐵 как столбцы
𝐵 следующим образом: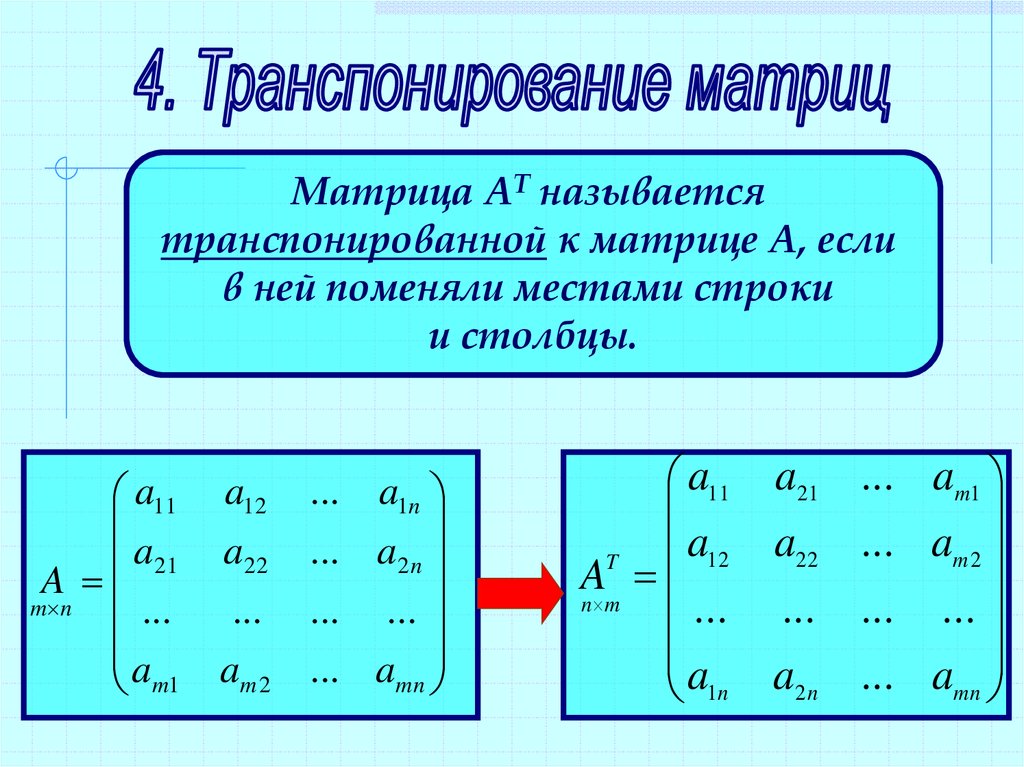
 Левая часть данного уравнения применима
транспонирование после вычитания матрицы, а правая часть
применяет транспонирование к каждой матрице перед вычитанием матрицы. Следовательно,
этот пример спрашивает, можем ли мы поменять порядок транспонирования
и вычитание.
Левая часть данного уравнения применима
транспонирование после вычитания матрицы, а правая часть
применяет транспонирование к каждой матрице перед вычитанием матрицы. Следовательно,
этот пример спрашивает, можем ли мы поменять порядок транспонирования
и вычитание.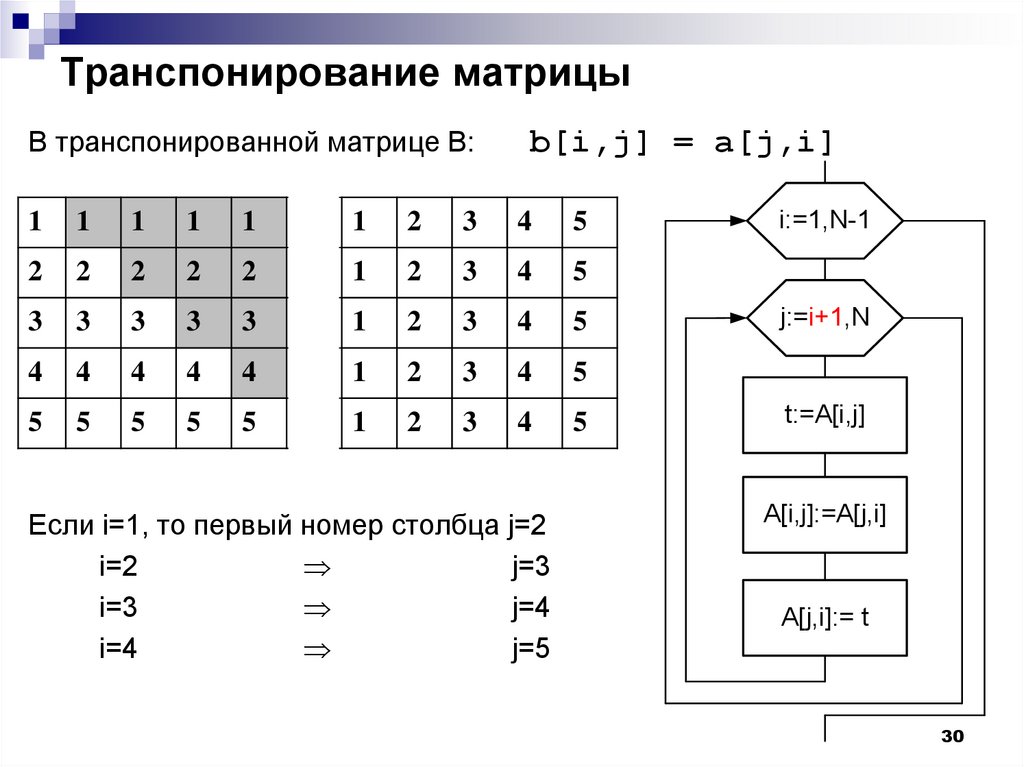
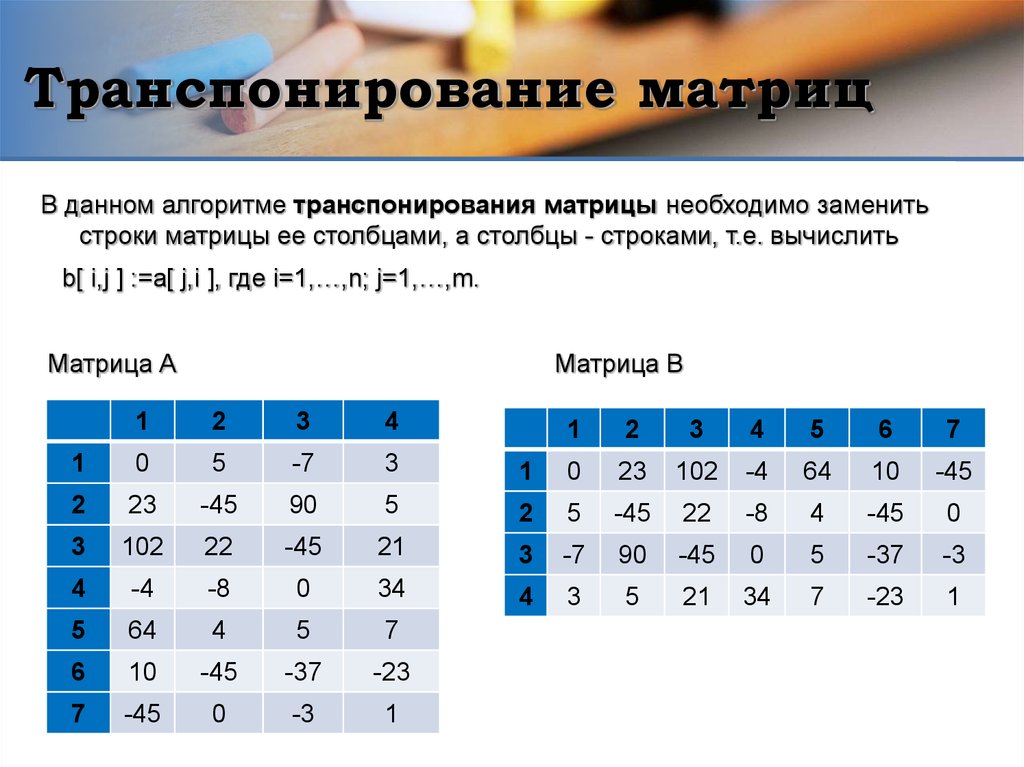

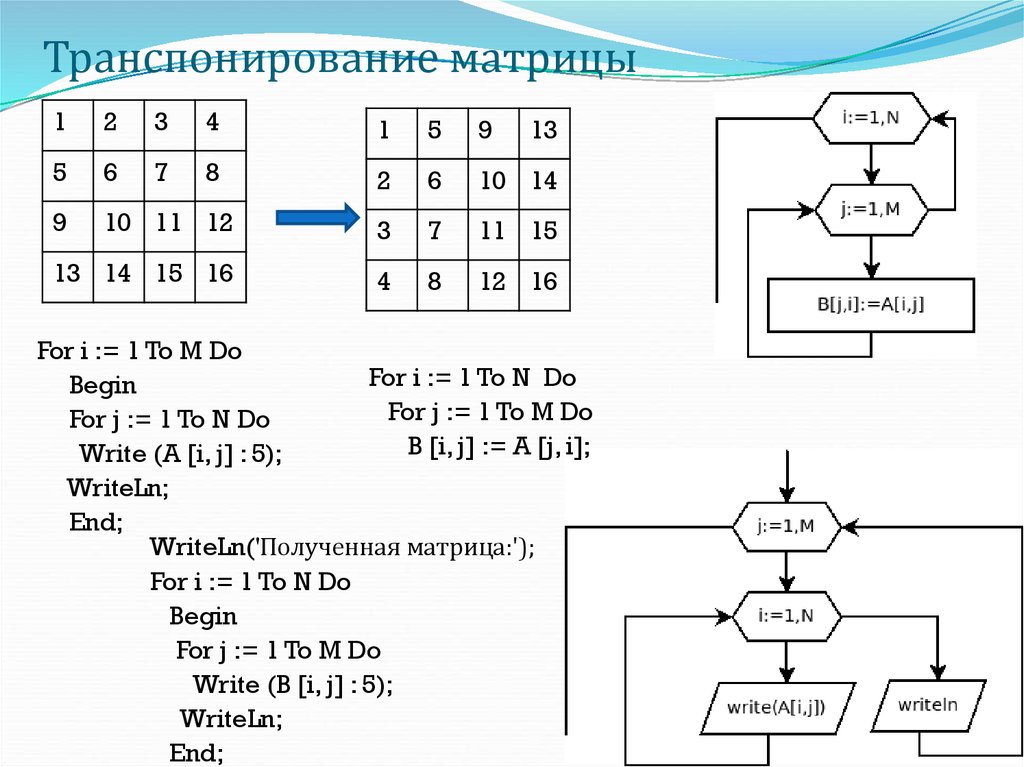 транспонировать матрицу A записывается как A T .
транспонировать матрицу A записывается как A T . 06 MIT OCW Гилберта Стрэнга по вводной линейной алгебре. Давайте сразу перейдем к основам транспонирования.
06 MIT OCW Гилберта Стрэнга по вводной линейной алгебре. Давайте сразу перейдем к основам транспонирования. Одни и те же числа по-прежнему добавляются друг к другу, поэтому конечный результат тот же. Конкретный пример:
Одни и те же числа по-прежнему добавляются друг к другу, поэтому конечный результат тот же. Конкретный пример: Можно сказать, что первая строка нашего результата есть произведение строк матрицы A на первую колонку матрицы B.
Можно сказать, что первая строка нашего результата есть произведение строк матрицы A на первую колонку матрицы B.  Таким образом, в симметричной матрице aij должно = aji для всех aji. Глядя на пример симметричной матрицы, это очевидно.
Таким образом, в симметричной матрице aij должно = aji для всех aji. Глядя на пример симметричной матрицы, это очевидно. В более понятных обозначениях это:
В более понятных обозначениях это: