Матрица размера m x n
Похожие презентации:
Матрицы, определители. Обратная матрица. Ранг матрицы. Системы линейных уравнений элементы векторной алгебры
Матрицы и определители
Матрицы и определители
Матрицы и определители
Матрицы и определители
Матрицы и определители. (Лекция 1)
Линейная алгебра. Матрицы
Матрицы и определители
Матрицы и операции над ними
Матрицы. Обозначение матриц
Математика — наиболее
совершенный способ водить
самого себя за нос.
А. ЭЙНШТЕЙН
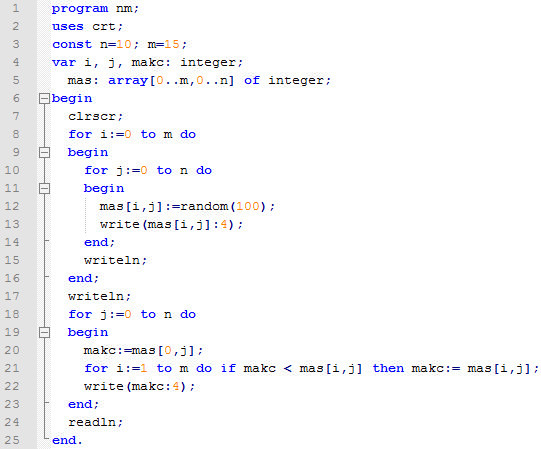
Матрицей размера m x n называется
прямоугольная таблица чисел,
содержащая m строк и n столбцов.
Числа, составляющие матрицу, называются
элементами матрицы.
Обозначение:
A
— матрица размерности m x n
a ij
— элемент матрицы i –ой строки и j -го
столбца
m n
Где
i=1,2…m
j=1,2…n
a11
a21
A ( aij )
m n
…
a
m1
a12
a22
..
am 2
… a1n
… a2 n
… …
… amn
Две матрицы называются равными, если
у них одинаковая размерность и
совпадают строки и столбцы.
Если число строк матрицы равно числу ее
столбцов, то такая матрица называется
квадратной.
0 2
1
A 2 4
5
0 3 1
— квадратная матрица размерности 3х3
Элементы матрицы aij , у которых номер
столбца совпадает с номером строки,
называются диагональными.
Если в квадратной матрице все
диагональные элементы равны 1, а
остальные элементы равны 0, то
она называется единичной.
1
0
E
…
0
0 … 0
1 … 0
… … …
0 … 1
Матрица любого размера называется
нулевой, если все ее элементы равны 0.
0
0
…
0
0 … 0
0 … 0
… … …
0 … 0
Матрица, состоящая из одной строки,
называется матрицей-строкой или
вектором-строкой.
A (a11 a12 … a1n )
Матрица, состоящая из одного столбца,
называется матрицей-столбцом или
вектором-столбцом.

b11
b21
B
b
n1
С
помощью матриц удобно
различного рода зависимости.
Например:
Распределение
экономики:
ресурсов
описывать
по
отраслям
Ресурсы
Промышленность
с/хозяйство
Эл.
энергия
Труд.
ресурсы
Водные
ресурсы
8
7.2
5
3
4.5
5.5
Эту зависимость можно представить в виде
матрицы:
8 7 .2
A 5
3
3 2
4 . 5 5 .5
Где элемент aij показывает сколько i – го
ресурса потребляет j – отрасль.
Например, a32 показывает, сколько воды
потребляет сельское хозяйство.
Чтобы умножить матрицу на число, надо
каждый элемент матрицы умножить на
это число.
Полученные
произведения
итоговую матрицу.
Пусть дана матрица
A (aij )
m n
Умножаем ее на число λ:
A B
Где каждый элемент матрицы В:
bij aij
Где:
i 1,2…m
j 1,2…n
Например:
Умножая матрицу
2 3 0
A
1 0 4
на число 2, получим:
2 2 3 2 0 2 4 6 0
A 2
1 2 0 2 4 2 2 0 8
Складываются матрицы одинаковой
размерности.
 Получается матрица той же
Получается матрица той жеразмерности, каждый элемент которой
равен сумме соответствующих
элементов исходных матриц.
Пусть даны матрицы
Складываем их:
A (aij )
B (bij )
A B C
Где каждый элемент матрицы С:
cij aij bij
Аналогично проводится вычитание матриц.
Найти сумму и разность матриц:
2 3 0
A
1 0 4
0 2 3
B
1 5 2
2 1 3
A B
2 5 6
2 5 3
A B
0 5 2
Умножение матриц возможно, если число
столбцов первой матрицы равно числу строк
второй.
Тогда каждый элемент полученной матрицы
равен сумме произведений элементов i – ой
строки
первой
матрицы
на
соответствующие элементы j-го столбца
второй.
Пусть даны матрицы
A (aij )
m k
B (bij )
k n
Умножаем их:
A B C
m k k n
m n
Где каждый элемент матрицы С:
cij ai1b1 j ai 2b2 j … aik bkj
i 1,2…m
j 1,2…n
Найти произведение матриц:
2 3 0
A
1 0 4
1 0
B 1 4
0 2
Число столбцов первой матрицы равно
числу строк второй, следовательно их
произведение существует:
2 1 3 1 0 0 2 0 3 4 0 2 5 12
A B
2 3 3 2
1 1 0 1 4 0 1 0 0 4 4 2 1 8
Теперь перемножим матрицы в обратном
порядке:
1 2 0 1 1 3 0 0 1 0 0 4 2 3 0
B A 1 2 4 1 1 3 4 0 1 0 4 4 6 3 16
3 2 2 3
0 2 2 1 0 3 4 0 0 0 2 4 2 0 8
Умножение
матриц
некоммутативно:
в
A B B A
общем
случае
Перечисленные операции над матрицами
обладают следующими свойствами:
А+В=В+А
2
(А+В)+С=А+(В+С)
3
λ(А+В)= λА+λВ
4
А(В+С)=АВ+АС
5
А(ВС)=(АВ)С
Матрица АТ называется
транспонированной к матрице А, если
в ней поменяли местами строки
и столбцы.

a11
a21
A
m n
…
a
m1
a12
a22
…
am 2
… a1n
… a2 n
… …
… amn
a11 a21
a12 a22
T
A
n m
… …
a1n a2 n
… am1
… am 2
… …
… amn
1
(АТ)Т=А
2
(А+В)Т=АТ+ВТ
3
(λА)Т= λАТ
4
(АВ)Т=ВТАТ
Транспонировать матрицу:
1 2 3
A 4 5 6
7 8 9
1 4 7
T
A 2 5 8
3 6 9
English Русский Правила
группа Matrix. — Клёвый код
Условие вида «дана матрица размера $$M \times N$$» означает, что вначале дается фактический размер двумерного массива-матрицы (количество строк $$M$$ и количество столбцов $$N$$), а затем приводятся элементы этого массива (количество элементов равно $$M*N$$). Если в задании явно не указывается, какие значения могут принимать размеры исходной матрицы, то предполагается, что и число строк, и число столбцов может меняться в пределах от $$2$$ до $$10$$. Порядковые номера начальной строки и начального столбца матрицы считаются равными $$1$$. Ввод и вывод элементов матрицы осуществляются по строкам. Квадратной матрицей порядка $$M$$ называется двумерный массив-матрица размера $$M \times M$$.
Ввод и вывод элементов матрицы осуществляются по строкам. Квадратной матрицей порядка $$M$$ называется двумерный массив-матрица размера $$M \times M$$.
Если в задании, связанном с созданием (преобразованием) матрицы, не описан результирующий набор данных, то предполагается, что этим набором является созданная (преобразованная) матрица, и необходимо вывести все ее элементы.
Формирование матрицы и вывод ее элементов
В заданиях на формирование матрицы предполагается, что размер результирующей матрицы не превосходит $$10 \times 10$$.
Matrix1. Даны целые положительные числа $$M$$ и $$N$$. Сформировать целочисленную матрицу размера $$M \times N$$, у которой все элементы $$I$$-й строки имеют значение $$10*I$$ $$(I = 1, …, M)$$.
Решение задачи, на языке: Паскаль
Matrix2. Даны целые положительные числа $$M$$ и $$N$$. Сформировать целочисленную матрицу размера $$M \times N$$, у которой все элементы J-го столбца имеют значение $$5*J$$ $$(J = 1, …, $$N$$)$$.
Решение задачи, на языке: Паскаль, C++
Matrix3. Даны целые положительные числа $$M$$, $$N$$ и набор из $$M$$ чисел. Сформировать матрицу размера $$M \times N$$, у которой в каждом столбце содержатся все числа из исходного набора (в том же порядке).
Решение задачи, на языке: Паскаль
Matrix4. Даны целые положительные числа $$M$$, $$N$$ и набор из $$N$$ чисел. Сформировать матрицу размера $$M \times N$$, у которой в каждой строке содержатся все числа из исходного набора (в том же порядке).
Решение задачи, на языке: Паскаль
Matrix5. Даны целые положительные числа $$M$$, $$N$$, число $$D$$ и набор из $$M$$ чисел.Сформировать матрицу размера $$M \times N$$, у которой первый столбец совпадает с исходным набором чисел, а элементы каждого следующего столбца равны сумме соответствующего элемента предыдущего столбца и числа $$D$$ (в результате каждая строка матрицы будет содержать элементы арифметической прогрессии).
Решение задачи, на языке: Паскаль
Matrix6. Даны целые положительные числа $$M$$, $$N$$, число $$Q$$ и набор из $$N$$ чисел. Сформировать матрицу размера $$M \times N$$, у которой первая строка совпадает с исходным набором чисел, а элементы каждой следующей строки равны соответствующему элементу предыдущей строки, умноженному на $$Q$$ (в результате каждый столбец матрицы будет содержать элементы геометрической прогрессии).
Решение задачи, на языке: Паскаль
Matrix7. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le M)$$. Вывести элементы $$K$$-й строки данной матрицы.
Решение задачи, на языке: Паскаль
Matrix8. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le $$N$$)$$. Вывести элементы $$K$$-го столбца данной матрицы.
Решение задачи, на языке: Паскаль
Matrix9. Дана матрица размера $$M \times N$$. Вывести ее элементы, расположенные в строках с четными номерами $$(2, 4, …)$$. Вывод элементов производить по строкам, условный оператор не использовать.
Вывод элементов производить по строкам, условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix10. Дана матрица размера $$M \times N$$. Вывести ее элементы, расположенные в столбцах с нечетными номерами $$(1, 3, …)$$. Вывод элементов производить по столбцам, условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix11. Дана матрица размера $$M \times N$$. Вывести ее элементы в следующем порядке: первая строка слева направо, вторая строка справа налево, третья строка слева направо, четвертая строка справа налево и т. д.
Решение задачи, на языке: Паскаль
Matrix12. Дана матрица размера $$M \times N$$. Вывести ее элементы в следующем порядке: первый столбец сверху вниз, второй столбец снизу вверх, третий столбец сверху вниз, четвертый столбец снизу вверх и т. д.
Решение задачи, на языке: Паскаль
Matrix13. Дана квадратная матрица $$A$$ порядка $$M$$. Начиная с элемента $$A_{1,1}$$, вывести ее элементы следующим образом («уголками»): все элементы первой строки; элементы последнего столбца, кроме первого (уже выведенного) элемента; оставшиеся элементы второй строки; оставшиеся элементы предпоследнего столбца и т. д.; последним выводится элемент $$A_{M,1}$$.
Начиная с элемента $$A_{1,1}$$, вывести ее элементы следующим образом («уголками»): все элементы первой строки; элементы последнего столбца, кроме первого (уже выведенного) элемента; оставшиеся элементы второй строки; оставшиеся элементы предпоследнего столбца и т. д.; последним выводится элемент $$A_{M,1}$$.
Решение задачи, на языке: Паскаль
Matrix14. Дана квадратная матрица $$A$$ порядка $$M$$. Начиная с элемента $$A_{1,1}$$, вывести ее элементы следующим образом («уголками»): все элементы первого столбца; элементы последней строки, кроме первого (уже выведенного) элемента; оставшиеся элементы второго столбца; оставшиеся элементы предпоследней строки и т. д.; последним выводится элемент $$A_{1,M}$$.
Решение задачи, на языке: Паскаль
Matrix15. Дана квадратная матрица $$A$$ порядка $$M$$ ($$M$$ — нечетное число). Начиная с элемента $$A_{1,1}$$ и перемещаясь по часовой стрелке, вывести все ее элементы по спирали: первая строка, последний столбец, последняя строка в обратном порядке, первый столбец в обратном порядке, оставшиеся элементы второй строки и т. д.; последним выводится центральный элемент матрицы.
д.; последним выводится центральный элемент матрицы.
Решение задачи, на языке: Паскаль
Matrix16. Дана квадратная матрица $$A$$ порядка $$M$$ ($$M$$ — нечетное число). Начиная с элемента $$A_{1,1}$$ и перемещаясь против часовой стрелки, вывести все ее элементы по спирали: первый столбец, последняя строка, последний столбец в обратном порядке, первая строка в обратном порядке, оставшиеся элементы второго столбца и т. д.; последним выводится центральный элемент матрицы.
Решение задачи, на языке: Паскаль
Анализ элементов матрицы
Matrix17. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le M)$$. Найти сумму и произведение элементов $$K$$-й строки данной матрицы.
Решение задачи, на языке: Паскаль
Matrix18. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le $$N$$)$$. Найти сумму и произведение элементов $$K$$-го столбца данной матрицы.
Решение задачи, на языке: Паскаль
Matrix19. Дана матрица размера $$M \times N$$. Для каждой строки матрицы найти сумму ее элементов.
Дана матрица размера $$M \times N$$. Для каждой строки матрицы найти сумму ее элементов.
Решение задачи, на языке: Паскаль
Matrix20. Дана матрица размера $$M \times N$$. Для каждого столбца матрицы найти произведение его элементов.
Решение задачи, на языке: Паскаль
Matrix21. Дана матрица размера $$M \times N$$. Для каждой строки матрицы с нечетным номером $$(1, 3, …)$$ найти среднее арифметическое ее элементов. Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix22. Дана матрица размера $$M \times N$$. Для каждого столбца матрицы с четным номером $$(2, 4, …)$$ найти сумму его элементов. Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix23. Дана матрица размера $$M \times N$$. В каждой строке матрицы найти минимальный элемент.
Решение задачи, на языке: Паскаль
Matrix24. Дана матрица размера $$M \times N$$. В каждом столбце матрицы найти максимальный элемент.
В каждом столбце матрицы найти максимальный элемент.
Решение задачи, на языке: Паскаль, C++
Matrix25. Дана матрица размера $$M \times N$$. Найти номер ее строки с наибольшей суммой элементов и вывести данный номер, а также значение наибольшей суммы.
Решение задачи, на языке: Паскаль
Matrix26. Дана матрица размера $$M \times N$$. Найти номер ее столбца с наименьшим произведением элементов и вывести данный номер, а также значение наименьшего произведения.
Решение задачи, на языке: Паскаль
Matrix27. Дана матрица размера $$M \times N$$. Найти максимальный среди минимальных элементов ее строк.
Решение задачи, на языке: Паскаль
Matrix28. Дана матрица размера $$M \times N$$. Найти минимальный среди максимальных элементов ее столбцов.
Решение задачи, на языке: Паскаль
Matrix29. Дана матрица размера $$M \times N$$. В каждой ее строке найти количество элементов, меньших среднего арифметического всех элементов этой строки.
Решение задачи, на языке: Паскаль
Matrix30. Дана матрица размера $$M \times N$$. В каждом ее столбце найти количество элементов, больших среднего арифметического всех элементов этого столбца.
Решение задачи, на языке: Паскаль
Matrix31. Дана матрица размера $$M \times N$$. Найти номера строки и столбца для элемента матрицы, наиболее близкого к среднему значению всех ее элементов.
Решение задачи, на языке: Паскаль
Matrix32. Дана целочисленная матрица размера $$M \times N$$. Найти номер первой из ее строк, содержащих равное количество положительных и отрицательных элементов (нулевые элементы матрицы не учитываются). Если таких строк нет, то вывести $$0$$.
Решение задачи, на языке: Паскаль
Matrix33. Дана целочисленная матрица размера $$M \times N$$. Найти номер последнего из ее столбцов, содержащих равное количество положительных и отрицательных элементов (нулевые элементы матрицы не учитываются). Если таких столбцов нет, то вывести $$0$$.
Если таких столбцов нет, то вывести $$0$$.
Решение задачи, на языке: Паскаль
Matrix34. Дана целочисленная матрица размера $$M \times N$$. Найти номер последней из ее строк, содержащих только четные числа. Если таких строк нет, то вывести $$0$$.
Решение задачи, на языке: Паскаль
Matrix35. Дана целочисленная матрица размера $$M \times N$$. Найти номер первого из ее столбцов, содержащих только нечетные числа. Если таких столбцов нет, то вывести $$0$$.
Решение задачи, на языке: Паскаль, C++
Matrix36. Дана целочисленная матрица размера $$M \times N$$, элементы которой могут принимать значения от $$0$$ до $$100$$. Различные строки матрицы назовем похожими, если совпадают множества чисел, встречающихся в этих строках. Найти количество строк, похожих на первую строку данной матрицы.
Решение задачи, на языке: Паскаль
Matrix37. Дана целочисленная матрица размера $$M \times N$$, элементы которой могут принимать значения от $$0$$ до $$100$$. Различные столбцы матрицы назовем похожими, если совпадают множества чисел, встречающихся в этих столбцах. Найти количество столбцов, похожих на последний столбец данной матрицы.
Различные столбцы матрицы назовем похожими, если совпадают множества чисел, встречающихся в этих столбцах. Найти количество столбцов, похожих на последний столбец данной матрицы.
Решение задачи, на языке: Паскаль
Matrix38. Дана целочисленная матрица размера $$M \times N$$. Найти количество ее строк, все элементы которых различны.
Решение задачи, на языке: Паскаль
Matrix39. Дана целочисленная матрица размера $$M \times N$$. Найти количество ее столбцов, все элементы которых различны.
Решение задачи, на языке: Паскаль
Matrix40. Дана целочисленная матрица размера $$M \times N$$. Найти номер последней из ее строк, содержащих максимальное количество одинаковых элементов.
Решение задачи, на языке: Паскаль
Matrix41. Дана целочисленная матрица размера $$M \times N$$. Найти номер первого из ее столбцов, содержащих максимальное количество одинаковых элементов.
Решение задачи, на языке: Паскаль
Matrix42. Дана матрица размера $$M \times N$$. Найти количество ее строк, элементы которых упорядочены по возрастанию.
Дана матрица размера $$M \times N$$. Найти количество ее строк, элементы которых упорядочены по возрастанию.
Решение задачи, на языке: Паскаль
Matrix43. Дана матрица размера $$M \times N$$. Найти количество ее столбцов, элементы которых упорядочены по убыванию.
Решение задачи, на языке: Паскаль, C++
Matrix44. Дана матрица размера $$M \times N$$. Найти минимальный среди элементов тех строк, которые упорядочены либо по возрастанию, либо по убыванию. Если упорядоченные строки в матрице отсутствуют, то вывести $$0$$.
Решение задачи, на языке: Паскаль
Matrix45. Дана матрица размера $$M \times N$$. Найти максимальный среди элементов тех столбцов, которые упорядочены либо по возрастанию, либо по убыванию. Если упорядоченные столбцы в матрице отсутствуют, то вывести $$0$$.
Решение задачи, на языке: Паскаль
Matrix46. Дана целочисленная матрица размера $$M \times N$$. Найти элемент, являющийся максимальным в своей строке и минимальным в своем столбце. Если такой элемент отсутствует, то вывести $$0$$.
Если такой элемент отсутствует, то вывести $$0$$.
Решение задачи, на языке: Паскаль
Преобразование матрицы
При выполнении заданий из данного пункта (за исключением заданий Matrix74 и Matrix75) не следует использовать вспомогательные двумерные массивы-матрицы.
Matrix47. Дана матрица размера $$M \times N$$ и целые числа $$K_1$$ и $$K_2$$ $$(1 \le K_1 < K_2 \le M)$$. Поменять местами строки матрицы с номерами $$K_1$$ и $$K_2$$ .
Решение задачи, на языке: Паскаль
Matrix48. Дана матрица размера $$M \times N$$ и целые числа $$K_1$$ и $$K_2$$ $$(1 \le K_1 < K_2 \le N)$$. Поменять местами столбцы матрицы с номерами $$K_1$$ и $$K_2$$ .
Решение задачи, на языке: Паскаль
Matrix49. Дана матрица размера $$M \times N$$. Преобразовать матрицу, поменяв местами минимальный и максимальный элемент в каждой строке.
Решение задачи, на языке: Паскаль
Matrix50. Дана матрица размера $$M \times N$$. Преобразовать матрицу, поменяв местами минимальный и максимальный элемент в каждом столбце.
Преобразовать матрицу, поменяв местами минимальный и максимальный элемент в каждом столбце.
Решение задачи, на языке: Паскаль
Matrix51. Дана матрица размера $$M \times N$$. Поменять местами строки, содержащие минимальный и максимальный элементы матрицы.
Решение задачи, на языке: Паскаль
Matrix52. Дана матрица размера $$M \times N$$. Поменять местами столбцы, содержащие минимальный и максимальный элементы матрицы.
Решение задачи, на языке: Паскаль
Matrix53. Дана матрица размера $$M \times N$$. Поменять местами столбец с номером $$1$$ и последний из столбцов, содержащих только положительные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль
Matrix54. Дана матрица размера $$M \times N$$. Поменять местами столбец с номером $$N$$ и первый из столбцов, содержащих только отрицательные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль
Matrix55. Дана матрица размера $$M \times N$$ ($$M$$ — четное число). Поменять местами верхнюю и нижнюю половины матрицы.
Решение задачи, на языке: Паскаль, C++
Matrix56. Дана матрица размера $$M \times N$$ ($$N$$ — четное число). Поменять местами левую и правую половины матрицы.
Решение задачи, на языке: Паскаль
Matrix57. Дана матрица размера $$M \times N$$ ($$M$$ и $$N$$ — четные числа). Поменять местами левую верхнюю и правую нижнюю четверти матрицы.
Решение задачи, на языке: Паскаль
Matrix58. Дана матрица размера $$M \times N$$ ($$M$$ и $$N$$ — четные числа). Поменять местами левую нижнюю и правую верхнюю четверти матрицы.
Решение задачи, на языке: Паскаль
Matrix59. Дана матрица размера $$M \times N$$. Зеркально отразить ее элементы относительно горизонтальной оси симметрии матрицы (при этом поменяются местами строки с номерами $$1$$ и $$M$$, $$2$$ и $$M-1$$ и т. д.).
д.).
Решение задачи, на языке: Паскаль
Matrix60. Дана матрица размера $$M \times N$$. Зеркально отразить ее элементы относительно вертикальной оси симметрии матрицы (при этом поменяются местами столбцы с номерами $$1$$ и $$N$$, $$2$$ и $$N-1$$ и т. д.).
Решение задачи, на языке: Паскаль
Matrix61. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le M)$$. Удалить строку матрицы с номером $$K$$.
Решение задачи, на языке: Паскаль
Matrix62. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le $$N$$)$$. Удалить столбец матрицы с номером $$K$$.
Решение задачи, на языке: Паскаль, C++
Matrix63. Дана матрица размера $$M \times N$$. Удалить строку, содержащую минимальный элемент матрицы.
Решение задачи, на языке: Паскаль
Matrix64. Дана матрица размера $$M \times N$$. Удалить столбец, содержащий максимальный элемент матрицы.
Решение задачи, на языке: Паскаль
Matrix65. Дана матрица размера $$M \times N$$. Удалить ее первый столбец, содержащий только положительные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Дана матрица размера $$M \times N$$. Удалить ее первый столбец, содержащий только положительные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль
Matrix66. Дана матрица размера $$M \times N$$. Удалить ее последний столбец, содержащий только отрицательные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль
Matrix67. Дана матрица размера $$M \times N$$, содержащая как положительные, так и отрицательные элементы. Удалить все ее столбцы, содержащие только положительные элементы. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль
Matrix68. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le M)$$. Перед строкой матрицы с номером $$K$$ вставить строку из нулей.
Решение задачи, на языке: Паскаль
Matrix69. Дана матрица размера $$M \times N$$ и целое число $$K$$ $$(1 \le K \le $$N$$)$$. После столбца матрицы с номером $$K$$ вставить столбец из единиц.
После столбца матрицы с номером $$K$$ вставить столбец из единиц.
Решение задачи, на языке: Паскаль
Matrix70. Дана матрица размера $$M \times N$$. Продублировать строку матрицы, содержащую ее максимальный элемент.
Решение задачи, на языке: Паскаль
Matrix71. Дана матрица размера $$M \times N$$. Продублировать столбец матрицы, содержащий ее минимальный элемент.
Решение задачи, на языке: Паскаль
Matrix72. Дана матрица размера $$M \times N$$. Перед первым столбцом, содержащим только положительные элементы, вставить столбец из единиц. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль
Matrix73. Дана матрица размера $$M \times N$$. После последнего столбца, содержащего только отрицательные элементы, вставить столбец из нулей. Если требуемых столбцов нет, то вывести матрицу без изменений.
Решение задачи, на языке: Паскаль
Matrix74. Дана матрица размера $$M \times N$$. Элемент матрицы называется ее локальным минимумом, если он меньше всех окружающих его элементов. Заменить все локальные минимумы данной матрицы на нули. При решении допускается использовать вспомогательную матрицу.
Дана матрица размера $$M \times N$$. Элемент матрицы называется ее локальным минимумом, если он меньше всех окружающих его элементов. Заменить все локальные минимумы данной матрицы на нули. При решении допускается использовать вспомогательную матрицу.
Решение задачи, на языке: Паскаль
Matrix75. Дана матрица размера $$M \times N$$. Элемент матрицы называется ее локальным максимумом, если он больше всех окружающих его элементов. Поменять знак всех локальных максимумов данной матрицы на противоположный. При решении допускается использовать вспомогательную матрицу.
Решение задачи, на языке: Паскаль, C++
Matrix76. Дана матрица размера $$M \times N$$. Упорядочить ее строки так, чтобы их первые элементы образовывали возрастающую последовательность.
Решение задачи, на языке: Паскаль, С++
Matrix77. Дана матрица размера $$M \times N$$. Упорядочить ее столбцы так, чтобы их последние элементы образовывали убывающую последовательность.
Решение задачи, на языке: Паскаль
Matrix78. Дана матрица размера $$M \times N$$. Упорядочить ее строки так, чтобы их минимальные элементы образовывали убывающую последовательность.
Решение задачи, на языке: Паскаль
Matrix79. Дана матрица размера $$M \times N$$. Упорядочить ее столбцы так, чтобы их максимальные элементы образовывали возрастающую последовательность.
Решение задачи, на языке: Паскаль
Диагонали квадратной матрицы
Matrix80. Дана квадратная матрица $$A$$ порядка $$M$$. Найти сумму элементов ее главной диагонали, то есть диагонали, содержащей следующие элементы:
$$A_{1,1}, A_{2,2}, A_{3,3}, …, A_{M,M}$$.
Решение задачи, на языке: Паскаль
Matrix81. Дана квадратная матрица $$A$$ порядка $$M$$. Найти среднее арифметическое элементов ее побочной диагонали, то есть диагонали, содержащей следующие элементы:
$$A_{1,M}, A_{2,M-1}, A_{3,M-2}, …, A_{M,1}$$.
Решение задачи, на языке: Паскаль
Matrix82. Дана квадратная матрица $$A$$ порядка $$M$$. Найти сумму элементов каждой ее диагонали, параллельной главной (начиная с одноэлементной диагонали $$A_{1,M}$$).
Дана квадратная матрица $$A$$ порядка $$M$$. Найти сумму элементов каждой ее диагонали, параллельной главной (начиная с одноэлементной диагонали $$A_{1,M}$$).
Решение задачи, на языке: Паскаль
Matrix83. Дана квадратная матрица $$A$$ порядка $$M$$. Найти сумму элементов каждой ее диагонали, параллельной побочной (начиная с одноэлементной диагонали $$A_{1,1}$$).
Решение задачи, на языке: Паскаль, C++
Matrix84. Дана квадратная матрица $$A$$ порядка $$M$$. Найти среднее арифметическое элементов каждой ее диагонали, параллельной главной (начиная с одноэлементной диагонали $$A_{1,M}$$).
Решение задачи, на языке: Паскаль
Matrix85. Дана квадратная матрица $$A$$ порядка $$M$$. Найти среднее арифметическое элементов каждой ее диагонали, параллельной побочной (начиная с одноэлементной диагонали $$A_{1,1}$$).
Решение задачи, на языке: Паскаль
Matrix86. Дана квадратная матрица $$A$$ порядка $$M$$. Найти минимальный элемент для каждой ее диагонали, параллельной главной (начиная с одноэлементной диагонали $$A_{1,M}$$).
Найти минимальный элемент для каждой ее диагонали, параллельной главной (начиная с одноэлементной диагонали $$A_{1,M}$$).
Решение задачи, на языке: Паскаль
Matrix87. Дана квадратная матрица $$A$$ порядка $$M$$. Найти максимальный элемент для каждой ее диагонали, параллельной побочной (начиная с одноэлементной диагонали $$A_{1,1}$$).
Решение задачи, на языке: Паскаль
Matrix88. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие ниже главной диагонали. Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix89. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие выше побочной диагонали. Условный оператор не использовать.
Решение задачи, на языке: Паскаль, C++
Matrix90. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие на побочной диагонали и ниже нее. Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix91. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие на главной диагонали и выше нее. Условный оператор не использовать.
Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие на главной диагонали и выше нее. Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix92. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие одновременно выше главной диагонали и выше побочной диагонали. Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix93. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие одновременно выше главной диагонали и ниже побочной диагонали. Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix94. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие одновременно ниже главной диагонали (включая эту диагональ) и выше побочной диагонали (также включая эту диагональ). Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix95. Дана квадратная матрица порядка $$M$$. Обнулить элементы матрицы, лежащие одновременно ниже главной диагонали (включая эту диагональ) и ниже побочной диагонали (также включая эту диагональ). Условный оператор не использовать.
Обнулить элементы матрицы, лежащие одновременно ниже главной диагонали (включая эту диагональ) и ниже побочной диагонали (также включая эту диагональ). Условный оператор не использовать.
Решение задачи, на языке: Паскаль
Matrix96. Дана квадратная матрица $$A$$ порядка $$M$$. Зеркально отразить ее элементы относительно главной диагонали (при этом элементы главной диагонали останутся на прежнем месте, элемент $$A_{1,2}$$ поменяется местами с $$A_{2,1}$$, элемент $$A_{1,3}$$ — с $$A_{3,1}$$ и т. д.). Вспомогательную матрицу не использовать.
Решение задачи, на языке: Паскаль
Matrix97. Дана квадратная матрица $$A$$ порядка $$M$$. Зеркально отразить ее элементы относительно побочной диагонали. (при этом элементы побочной диагонали останутся на прежнем месте, элемент $$A_{1,1}$$ поменяется местами с $$A_{M,M}$$, элемент $$A_{1,2}$$ — с $$A_{M-1,M}$$ и т. д.). Вспомогательную матрицу не использовать.
Решение задачи, на языке: Паскаль
Matrix98. \circ$$ в отрицательном направлении, то есть по часовой стрелке (при этом элемент $$A_{1,1}$$ перейдет в $$A_{1,M}$$, элемент $$A_{1,M}$$ — в $$A_{M,M}$$ и т. д.). Вспомогательную матрицу не использовать.
\circ$$ в отрицательном направлении, то есть по часовой стрелке (при этом элемент $$A_{1,1}$$ перейдет в $$A_{1,M}$$, элемент $$A_{1,M}$$ — в $$A_{M,M}$$ и т. д.). Вспомогательную матрицу не использовать.
Решение задачи, на языке: Паскаль
Если вы хотите выложить решение для задач, но нет решения на нужном языке, или вообще к задаче нет решений. Можете разместить его в виде комментария к данной статье.
Другие задачи по программированию, для проверки своих знаний.
Матрица размера m x n презентация, доклад
Математика — наиболее совершенный способ водить самого себя за нос.
А. ЭЙНШТЕЙН
1. МАТРИЦЫ
И
ОПРЕДЕЛИТЕЛИ
1.1. МАТРИЦЫ И ДЕЙСТВИЯ
НАД НИМИ
Матрицей размера m x n называется
прямоугольная таблица чисел,
содержащая m строк и n столбцов.
Числа, составляющие матрицу, называются элементами матрицы.
Обозначение:
Где
i=1,2…m
j=1,2…n
— матрица размерности m x n
— элемент матрицы i –ой строки и j -го столбца
матрица размерности m x n
Две матрицы называются равными, если
у них одинаковая размерность и
Если число строк матрицы равно числу ее
столбцов, то такая матрица называется
квадратной.
Пример:
— квадратная матрица размерности 3х3
Элементы матрицы aij , у которых номер
столбца совпадает с номером строки,
называются диагональными.
Если в квадратной матрице все
диагональные элементы равны 1, а
остальные элементы равны 0, то
она называется единичной.
единичная матрица
Матрица любого размера называется
нулевой, если все ее элементы равны 0.
нулевая матрица
Матрица, состоящая из одной строки,
называется матрицей-строкой или
вектором-строкой.
матрица-строка
Матрица, состоящая из одного столбца,
называется матрицей-столбцом или
вектором-столбцом.
матрица-столбец
Распределение ресурсов по отраслям экономики:
С помощью матриц удобно описывать различного рода зависимости.
Например:
Эту зависимость можно представить в виде матрицы:
Где элемент aij показывает сколько i – го ресурса потребляет j – отрасль.
Например, a32 показывает, сколько воды потребляет сельское хозяйство.
ДЕЙСТВИЯ НАД МАТРИЦАМИ
1. Умножение матрицы на число
Чтобы умножить матрицу на число, надо
каждый элемент матрицы умножить на
это число.
Полученные произведения образуют итоговую матрицу.
Пусть дана матрица
Умножаем ее на число λ:
Где каждый элемент матрицы В:
Где:
Например:
Умножая матрицу
на число 2, получим:
2. Сложение матриц
Складываются матрицы одинаковой
размерности. Получается матрица той же
размерности, каждый элемент которой
равен сумме соответствующих
элементов исходных матриц.
Пусть даны матрицы
Складываем их:
Где каждый элемент матрицы С:
Аналогично проводится вычитание матриц.
Пример.
Найти сумму и разность матриц:
Решение:
3. Умножение матриц
Умножение матриц возможно, если число столбцов первой матрицы равно числу строк второй.
Тогда каждый элемент полученной матрицы равен сумме произведений элементов i – ой строки первой матрицы на соответствующие элементы j-го столбца второй.
Пусть даны матрицы
Умножаем их:
Где каждый элемент матрицы С:
Пример.
Найти произведение матриц:
Число столбцов первой матрицы равно числу строк второй, следовательно их произведение существует:
Решение:
Теперь перемножим матрицы в обратном порядке:
Умножение матриц в общем случае некоммутативно:
Перечисленные операции над матрицами обладают следующими свойствами:
А+В=В+А
(А+В)+С=А+(В+С)
1
2
λ(А+В)= λА+λВ
А(В+С)=АВ+АС
А(ВС)=(АВ)С
3
4
5
4. Транспонирование матриц
Транспонирование матриц
Матрица АТ называется
транспонированной к матрице А, если
в ней поменяли местами строки
и столбцы.
(АТ)Т=А
(А+В)Т=АТ+ВТ
свойства операции
траспонирования:
1
2
(λА)Т= λАТ
(АВ)Т=ВТАТ
3
4
Пример.
Транспонировать матрицу:
Решение:
Скачать презентацию
Задания по теме Двумерные массивы
1. Дана квадратная матрица. Произвести циклический сдвиг элементов каждого столбца матрицы на один элемент влево.
2. Дана квадратная матрица. Произвести циклический сдвиг элементов каждого столбца матрицы на один элемент вправо.
3. Дана квадратная матрица.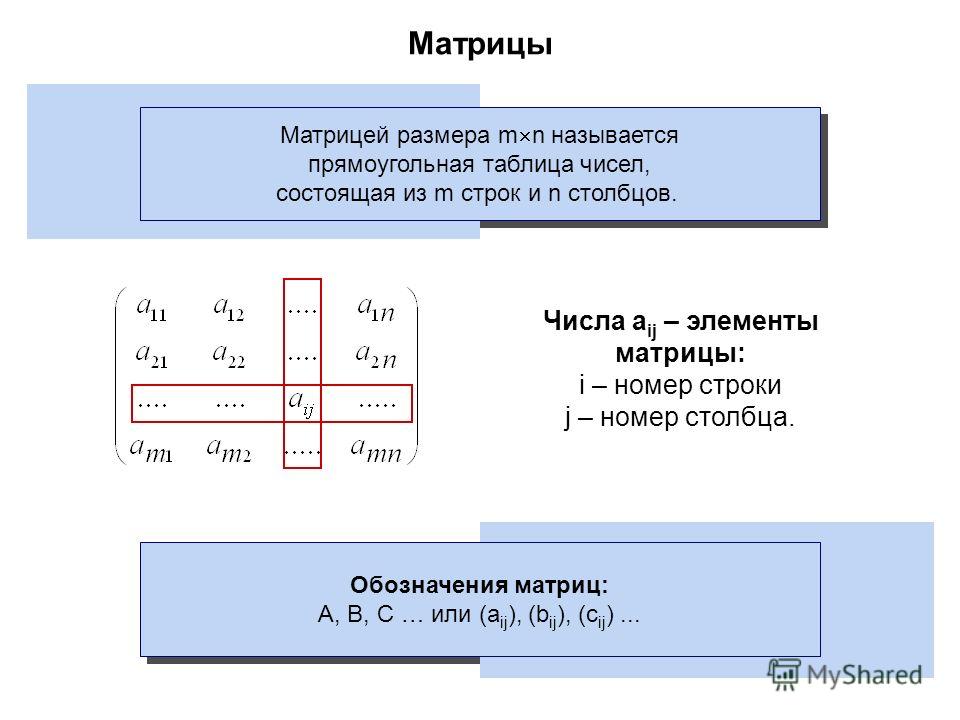 Произвести циклический сдвиг элементов каждой строки матрицы на К элементов влево.
Произвести циклический сдвиг элементов каждой строки матрицы на К элементов влево.
4. Дана прямоугольная матрица размерности MxN. Сформировать новую матрицу размерности MxN-2, в которой для каждой строки исходной матрицы из последовательности элементов A[I,1], A[I,2], …, A[I, N-1], A[I, N] создать новую последовательность A[I,1]*A[I,3], A[I,2]*A[I,4], …A[I, N-2]*A[I, N] без использования дополнительного массива.
5. Дана прямоугольная матрица размерности MxN. Сформировать одномерный массив, в который занести только первые (сверху вниз ) отрицательные элементы каждого столбца матрицы. Если таких элементов нет, то вывести соответствующее сообщение.
6. Дана прямоугольная матрица размерности MxN. Сформировать одномерный массив, в который занести только последние отрицательные элементы каждой строки матрицы. Если таких элементов нет, то вывести соответствующее сообщение.
7. Дана прямоугольная матрица размерности MxN, все элементы, которой различны. Сформировать одномерный массив, в который занести наибольшие элементы каждого столбца матрицы.
Сформировать одномерный массив, в который занести наибольшие элементы каждого столбца матрицы.
8. Дана прямоугольная матрица размерности MxN, все элементы, которой различны. Сформировать одномерный массив, в который занести наименьшие элементы каждой строки матрицы
9. Дана прямоугольная матрица размерности MxN. Сформировать одномерный массив, в который занести первые (сверху вниз ) максимальные элементы каждого столбца матрицы
10. Дана прямоугольная матрица размерности MxN. Сформировать одномерный массив, в который занести последние (сверху вниз ) минимальные элементы каждого столбца матрицы
11. Дана прямоугольная матрица размерности MxN. Сформировать одномерный массив, в который занести последние минимальные элементы каждой строки матрицы.
12. Дана прямоугольная матрица размерности MxN. Сформировать два одномерных массива: в первый занести количество положительных элементов в каждом столбце; во второй – количество отрицательных элементов в каждом столбце матрицы.
13. Дана прямоугольная матрица размерности MxN. Сформировать вектор В, где: B[I]=1, если элементы I строки составляют строго возрастающую последовательность; B[I]=0 если элементы I строки не составляют строго возрастающую последовательность.
14. Дана прямоугольная матрица размерности MxN. Сформировать вектор В, где: B[I]=1, если элементы I столбца составляют строго убывающую последовательность; B[I]=0 если элементы I столбца не составляют строго убывающую последовательность.
15. Дана прямоугольная матрица размерности Nx2N. Сформировать новую матрицу той же размерности, в которой для каждой строки исходной матрицы из последовательности A[I,1],A[I,2],….A[I,2N-1],A[I,2N] сформировать новую последовательность A[I,1], A[I,2N], A[I,2], A[I,2N-1], …, A[I, N], A[I, N+1].
16. Дана прямоугольная матрица размерности 2NxN. Сформировать новую матрицу той же размерности, в которой для каждого столбца исходной матрицы из последовательности A[1,I],A[2,I],…,A[2N-1,I],A[2N, I] сформировать новую последовательность A[2N, I],A[N, I],A[2N-1,I],A[N-1,I],…,A[N+1,I],A[1,I].
17. Дана прямоугольная матрица размерности MxN. Сформировать вектор В, где: B[I] – это количество элементов в I –том столбце, равных заданному значению.
18. Дана прямоугольная матрица размерности MxN и заданное значение. Составить и вывести новый одномерный массив, в который занести произведение I*J элементов исходной матрицы, равных заданному значению (I, J – номера строки и столбца).
19. Дана прямоугольная матрица размерности MxN и заданное значение. Составить и вывести новый одномерный массив со значениями элементов исходной матрицы, не равных заданному значению.
20. Дана прямоугольная матрица размерности MxN. Сформировать вектор В, где: B[I] – это процент нулевых элементов в I –том столбце матрицы.
21. Дана прямоугольная матрица размерности MxN. Сформировать вектор В, где: B[I]=1, если сумма положительных элементов в I – том столбце больше модуля сумы отрицательных элементов в этом столбце и B[I]=0 — если нет.
22. Дана прямоугольная матрица размерности MxN. Сформировать одномерный массив, в который занести номера тех строк, в которых есть одинаковые элементы. Если таких строк нет, то вывести соответствующее сообщение
Дана прямоугольная матрица размерности MxN. Сформировать одномерный массив, в который занести номера тех строк, в которых есть одинаковые элементы. Если таких строк нет, то вывести соответствующее сообщение
23. Дана прямоугольная матрица размерности MxN и заданное значение. Создать одномерный массив, в который занести элементы данной матрицы, меньшие заданного значения.
24. Дана прямоугольная матрица размерности MxN «A». Вводится дополнительный массив «B» разрешенных значений. Создать новый массив “C”, где C[I] – количество элементов I-той строки исходной матрицы»A», имеющих неразрешенные значения
25. Дана прямоугольная матрица размерности MxN «A». Вводится дополнительный массив «B» разрешенных значений. Создать новый массив “C”, где C[I] – количество элементов I-того столбца исходной матрицы»A», имеющих неразрешенные значения
26. Дана прямоугольная матрица размерности MxN «A».Переписать элементы каждого столбца матрицы «A»в обратном порядке на том же месте (перевернуть каждый столбец матрицы «A» без использования дополнительного массива).
27. Дана квадратная матрица. Произвести транспонирование (переворот) матрицы относительно ее главной диагонали. Сформировать новый одномерный массив, в который занести элементы четных строк полученной матрицы в последовательности сверху вниз и слева направо.
28. Дана квадратная матрица. Произвести переворот матрицы относительно ее побочной диагонали. Поменять местами элементы главной и побочной диагонали в каждой строке полученной матрицы.
29. Дана прямоугольная целочисленная матрица. Произвести инвертирование (переворот) элементов нечетных столбцов без использования дополнительного массива и затем сформировать новый одномерный массив, в который занести элементы матрицы, кратные 2 .
30. Дана прямоугольная матрица. Сформировать новый одномерный массив, в который занести элементы, кратные семи и расположенные на соседних двух диагоналях, параллельных главной. Если таких элементов нет, то вывести соответствующее сообщение.
Поиск в 2-D Matrix
Сложность: Medium
Спрос в: Amazon, Microsoft
Понимание задачи
Задача Описание
. Вам дают матрицу
Вам дают матрицу ARP из M X N Size. Напишите программу для поиска значения k в arr . Этот arr имеет следующие свойства:
- Целые числа в каждой строке сортируются слева направо.
- Первое значение каждой строки больше, чем последнее значение предыдущей строки.
Если значение найдено, вернуть 1, иначе вернуть 0. Пример 1
Ввод:
обр[][] = [
[23, 25, 35, 37],
[40, 41, 42, 43],
[50, 60, 74, 80]
]
к = 41
Выход: 1
Объяснение: В массиве arr присутствует значение 41. Итак, возвращается 1. Пример 2
Ввод:
обр[][] = [
[23, 25, 35, 37],
[40, 41, 42, 43],
[50, 60, 74, 80]
]
к = 100
Выход: 0
Объяснение: Значение 100 отсутствует в массиве обр. Итак, возвращается 0. Решения
Мы обсудим различные решения проблемы
- Линейный обход : Обход всей матрицы, сравнивая каждый элемент с целью
- Удалить столбец строки в каждом сравнении : Начиная с верхнего правого матрицы, двигайтесь к левому нижнему углу в поисках целевого элемента.

- Двоичный поиск : Рассматривая матрицу как единый массив, выполните двоичный поиск цели.
Вы можете решить эту задачу здесь.
1. Линейный поиск
Простая идея состоит в том, чтобы обойти массив и сравнить целевой элемент со всеми элементами в матрице один за другим.
Шаг решения
- Запустить вложенный цикл, внешний цикл для строки и внутренний цикл для столбца
- Проверить каждый элемент с целью и, если элемент найден, вернуть True
- Если элемент не найден, то вернуть Ложь.
Псевдокод
bool searchMatrix(int[][] matrix, int target) {
если (матрица.пусто())
вернуть ложь
int n = матрица.размер()
int м = матрица [0]. размер ()
for(int i = 0 to i < m) {
for (int j = 0 до j < n)
//если элемент найден
если (мат[i][j] == цель) {
вернуть истину
}
}
вернуть ложь
} Анализ сложности
Временная сложность: O(m*n)
Пространственная сложность: O(1)
Критические идеи для размышления
- Использовали ли мы отсортированные строки, характерные для входной матрицы, для поиска целевого элемента?
- Можете ли вы придумать лучший подход с точки зрения временной сложности?
2.
 Удалить столбец строки в каждом сравнении
Удалить столбец строки в каждом сравнении Начать с верхнего правого угла: row = 0, col = m-1
- если
matrix[row][col]равно target, вернуть true . - если
матрица[строка][столбец]меньше целевого,строка = строка + 1;указывает, что эта строка не может содержать цель, потому что эта строка в этой строке является самой большой, считая от «строки». - , если
matrix[row][col]больше целевого,col = col — 1; указать, что этот столбец не может содержать цель, потому что этот в этом столбце является наименьшим, считая от «столбца».
Псевдокод
bool searchMatrix(int[][] matrix, int target) {
если (матрица.пусто())
вернуть ложь
int n = матрица.размер()
int м = матрица [0]. размер ()
целая строка = 0, столбец = m-1
в то время как (строка < n и столбец> = 0) {
если (матрица [строка] [столбец] == цель)
вернуть истину
иначе если (матрица [строка] [столбец] < цель)
ряд = ряд + 1
еще
столбец = столбец - 1
}
вернуть ложь
} Анализ сложности
Временная сложность: O(m + n)
Пространственная сложность: O(1)
Критические идеи для размышления
- ] < цель ?
- Как мы сокращаем наше проблемное пространство при каждом сравнении?
- Попробуйте этот алгоритм на пробном прогоне нескольких примеров.

3. Бинарный поиск
Постановка задачи гласит, что значения последнего столбца -й -й строки больше, чем первый столбец (i+1)-й -й строки. Кроме того, каждая строка сортируется.
Это означает, что если расположить элементы каждой строки линейно, то мы получим отсортированный массив. Итак, теперь мы можем выполнить бинарный поиск по нему.
Как матрица будет вести себя как массив без фактического создания вспомогательного массива?
Этого можно добиться по следующей формуле →
A n * m матрица, преобразованная в массив: matrix[x][y] → a[x * m + y]
Массив можно преобразовать в матрицу n * m : a[x] → matrix[x / m][x % m]
Шаги решения
- Обработайте матрицу как массив, используя приведенную выше формулу
- Выполнить двоичный поиск целевого элемента по матрице
Псевдокод
bool searchMatrix(int[][] matrix, int target) {
int n = матрица. размер()
int м = матрица [0]. размер ()
int l = 0, r = m * n - 1
в то время как (л != г) {
середина = (л + г - 1) / 2
if (matrix[mid / m][mid % m] < target)
л = середина + 1
еще
г = середина
}
если (матрица [r / m] [r % m] == цель)
вернуть истину
еще
вернуть ложь
}
размер()
int м = матрица [0]. размер ()
int l = 0, r = m * n - 1
в то время как (л != г) {
середина = (л + г - 1) / 2
if (matrix[mid / m][mid % m] < target)
л = середина + 1
еще
г = середина
}
если (матрица [r / m] [r % m] == цель)
вернуть истину
еще
вернуть ложь
} Анализ сложности
Временная сложность: O(log(m*n)) = O(log(m) + log(n))
Пространственная сложность: O(1)
Критические идеи для размышления
- Почему мы инициализировали
rс помощьюm*n -1? - Каким будет среднее положение l и r в матрице?
- Как мы преобразовали индекс массива в индекс матрицы и индекс матрицы в индекс массива?
Сравнение решений
Предлагаемые проблемы для решения
- Поиск в матрице, отсортированной по строкам и столбцам
- Проверить, может ли сетка стать отсортированной по строкам и по столбцам после замены соседних элементов
- Вывести все элементы в отсортированном порядке из таблицы Матрица, отсортированная по строкам и столбцам
- Отсортируйте матрицу по строкам и столбцам
Если у вас есть другие подходы или вы обнаружите ошибку/ошибку в приведенных выше решениях, пожалуйста, прокомментируйте ниже.
Приятного программирования!
Наслаждайтесь алгоритмами!
Операции с матрицами
Что касается линейной алгебры, то двумя наиболее важными операциями с векторами являются сложение векторов [сложение двух (или более) векторов] и скалярное умножение (умножение вектора на скаляр). Аналогичные операции определены для матриц.
Добавление матрицы . Если А и В матрицы одинакового размера , то их можно сложить. (Это похоже на ограничение на сложение векторов, а именно, только векторы из одного и того же пространства R n можно добавить; например, вы не можете добавить 2-вектор к 3-вектору.) Если A = [ a ij ] и B = [ b ij ] оба равны m m n матриц, то их сумма C = A + B также является матрицей m x n , а ее элементы задаются формулой
Таким образом, чтобы найти записи A + B , просто добавьте соответствующие записи A и B .
Пример 1 : Рассмотрим следующие матрицы:
Какие два можно добавить? Какова их сумма?
Поскольку можно добавлять только матрицы одинакового размера, определяется только сумма F + H ( G нельзя добавлять ни к F , ни к H ). Сумма F и H это
Поскольку сложение действительных чисел коммутативно, отсюда следует, что сложение матриц (когда оно определено) также коммутативно; то есть для любых матриц A и B одинакового размера A + B всегда будет равно B + A .
Пример 2 : Если любую матрицу A добавить к нулевой матрице того же размера, то результат явно равен A :
Это матричный аналог утверждения a + 0 = 0 + a = a , которое выражает тот факт, что число 0 является аддитивной единицей в множестве действительных чисел.
Пример 3 : Найдите матрицу B такую, что A + B = C , где
Если
, то матричное уравнение A + B = C становится
Поскольку две матрицы равны тогда и только тогда, когда они имеют одинаковый размер и их соответствующие элементы равны, это последнее уравнение подразумевает
Следовательно,
Этот пример мотивирует определение матрицы вычитания : если A и B являются матрицами одинакового размера, то элементы A − B находятся путем простого вычитания элементов B из соответствующие записи А . Поскольку уравнение A + B = C эквивалентно B = C − A , использование матричного вычитания выше даст тот же результат:
Скалярное умножение . Матрицу можно умножить на скаляр следующим образом. Если A = [ a ij ] — матрица, а k — скаляр, то
Матрицу можно умножить на скаляр следующим образом. Если A = [ a ij ] — матрица, а k — скаляр, то
То есть матрица кА получается путем умножения каждой записи A на k .
Пример 4 : Если
, то скаляр, кратный 2 A , получается путем умножения каждой записи A на 2:
Пример 5 : Если A и B являются матрицами одинакового размера, то A − B = A + (− B ), где − B скаляр −1) В . Если
, затем
Это определение вычитания матриц согласуется с определением, показанным в примере 8.
Пример 6 : Если
, затем
Умножение матриц . Безусловно, наиболее важной операцией с матрицами является умножение матриц , процесс умножения одной матрицы на другую. Первый шаг в определении умножения матриц — вспомнить определение скалярного произведения двух векторов. Пусть r и c — два n ‐вектора. Записав r в виде матрицы строк 1 x n и c в виде матрицы столбцов n x 1, скалярное произведение r и c равно
Первый шаг в определении умножения матриц — вспомнить определение скалярного произведения двух векторов. Пусть r и c — два n ‐вектора. Записав r в виде матрицы строк 1 x n и c в виде матрицы столбцов n x 1, скалярное произведение r и c равно
Обратите внимание, что для определения скалярного произведения r и c оба должны содержать одинаковое количество записей. Кроме того, здесь важен порядок, в котором эти матрицы записаны в этом произведении: сначала идет вектор-строка, затем — вектор-столбец.
Теперь последний шаг: как перемножаются две общие матрицы? Во-первых, чтобы сформировать продукт AB, количество столбцов A должно совпадать с количеством строк B ; если это условие не выполняется, то продукт AB не определен. Этот критерий следует из установленного выше ограничения на умножение матрицы-строки r на матрицу-столбец c , а именно, что количество элементов в r должно совпадать с количеством элементов в с . Если A равен m x n и B равен n x p , то произведение AB определено, а размер матрицы произведения 2 5 2 9 9 x 9 5 2 2 AB 902 стр . Следующая диаграмма помогает определить, определен ли матричный продукт, и если да, то размерность продукта:
Если A равен m x n и B равен n x p , то произведение AB определено, а размер матрицы произведения 2 5 2 9 9 x 9 5 2 2 AB 902 стр . Следующая диаграмма помогает определить, определен ли матричный продукт, и если да, то размерность продукта:
Думая о матрице m x n A , составленной из векторов-строк r 1 , r 2 ,…, r m from R n and the n x p matrix B as composed of the column vectors c 1 , c 2 ,…, c p from R n ,
и
правило вычисления элементов матричного произведения AB is r i · c j = ( AB ) 902, 8 2ij 2ij Пример 7 : Даны две матрицы определить, какой матричный продукт, AB или BA , определен, и оценить его. Поскольку A имеет размер 2 x 3, а B имеет размер 3 x 4, произведение AB в указанном порядке определено, а размер матрицы произведения равен AB будет 2 x 4. Продукт BA определяется , а не , поскольку первый фактор ( B ) имеет 4 столбца, а второй фактор ( A ) имеет только 2 строки. Количество столбцов первой матрицы должно совпадать с количеством строк второй матрицы, чтобы можно было определить их произведение. Скалярное произведение строки 1 в A и столбца 1 в B дает запись (1, 1) в AB . С 90 005 запись (1, 1) в AB равна 1: Скалярное произведение строки 1 в A и столбца 2 в B дает запись (1, 2) в AB , и скалярное произведение строки 1 в A и столбца 3 в B дает запись (1, 3) в AB : Первая строка произведения завершается путем скалярного произведения строки 1 в A и столбца 4 в B , что дает запись (1, 4) в AB : Теперь для второй строки AB : скалярное произведение строки 2 в A и столбца 1 в B дает (2, 1) запись в AB , и скалярное произведение строки 2 в A и столбца 2 в B дает запись (2, 2) в AB : Наконец, взяв скалярное произведение строки 2 в A со столбцами 3 и 4 в B дает (соответственно) (2, 3) и (2, 4) записи в AB : Следовательно, Пример 8 : Если и вычислить запись (3, 5) произведения CD . Во-первых, обратите внимание, что поскольку C имеет размер 4 x 5, а D имеет размер 5 x 6, произведение CD действительно определено, и его размер равен 4 x 6. Однако нет необходимости вычислять все двадцать четыре записи из CD , если требуется только одна конкретная запись. Запись (3, 5) числа CD представляет собой скалярное произведение строки 3 числа C и столбца 5 числа D : Пример 9 : Если убедиться, что но В частности, обратите внимание, что хотя оба продукта AB и BA определены, AB не равно BA ; на самом деле, они даже не одного размера! Предыдущий пример иллюстрирует, пожалуй, самое важное различие между умножением скаляров и умножением матриц. Для действительных чисел a и b всегда выполняется уравнение ab = ba , т. Поскольку C имеет размер 3 x 2, а D имеет размер 2 x 2, продукт CD определен, его размер равен 3 x 2, а Произведение DC , однако, не определено, поскольку количество столбцов D (которое равно 2) не равно количеству строк C (которое равно 3). Следовательно, CD ≠ DC , поскольку DC даже не существует. Из-за чувствительности к порядку записи коэффициентов обычно не говорят просто: «Умножьте матрицы на и B на ». Пример 10 : Если и x — это вектор (−2, 3), покажите, как A можно умножить справа на x и вычислить произведение. Поскольку A равно 2 x 2, чтобы умножить A справа на матрицу, эта матрица должна иметь 2 строки. Следовательно, если x записывается как 2 x 1 столбец матрицы , то можно вычислить произведение A x , и результатом будет другая матрица столбцов 2 x 1: Пример 11 : Рассмотрим матрицы Если A умножить справа на B , получится , но если A умножить слева на B , получится Обратите внимание, что оба продукта определены и имеют одинаковый размер, но они не равны. Пример 12 : Если A и B являются квадратными матрицами такими, что AB = BA , то говорят, что A и B коммутируют с . Покажите, что любые две квадратные диагональные матрицы порядка 2 коммутируют. Пусть — две произвольные диагональные матрицы 2 x 2. Затем и Since a 11 b 11 = b 11 a 11 and a 22 b 22 = b 22 a 22 , AB действительно равно BA , как и требовалось. Хотя умножение матриц обычно не коммутативно, оно иногда коммутативно; например, если , затем Несмотря на подобные примеры, следует отметить, что в общем случае умножение матриц не является коммутативным . Есть еще одно различие между умножением скаляров и умножением матриц. Если a и b — действительные числа, то уравнение ab = 0 подразумевает, что a = 0 или b = 0. То есть, произведение действительных чисел может равняться 0 только в том случае, если по крайней мере один из множителей сам равен 0. Однако аналогичное утверждение для матриц неверно. Например, если , затем Обратите внимание, что хотя ни G , ни H не являются нулевой матрицей, произведение GH является таковым. Еще одно различие между умножением скаляров и умножением матриц заключается в отсутствии общего закона сокращения для умножения матриц. Если 90 251 a, b 90 252 и 90 251 c 90 252 — действительные числа, причем 90 251 a 90 252 ≠ 0, то при сокращении множителя 90 251 a 90 252 уравнение ab = ac подразумевает b = c . Для матричного умножения такого закона не существует; то есть утверждение AB = AC означает, что не подразумевает B = C , даже если A не равно нулю. потом оба и Таким образом, хотя AB = AC и A не является нулевой матрицей, B не равно C . Пример 13 : Хотя умножение матриц не всегда коммутативно, оно равно всегда ассоциативно . То есть, если A, B и C являются любыми тремя матрицами, для которых определено произведение (AB)C , то произведение A(BC) также определено, и То есть, пока порядок факторов неизменен, то как они сгруппированы не имеет значения. Проверить закон ассоциативности для матриц Первый с продукт (AB)C - это Сейчас, с продукт A(BC) Следовательно, (AB)C = A(BC) , как и ожидалось. Обратите внимание, что ассоциативный закон подразумевает, что произведение A, B и C (в таком порядке) может быть записано просто как ABC ; круглые скобки не нужны для устранения какой-либо неоднозначности, потому что двусмысленности нет. Пример 14 : Для матриц проверьте уравнение ( AB ) T = B T A T . Первый, подразумевает Сейчас, с B T A T действительно равно ( AB ) T . На самом деле уравнение справедливо для любых двух матриц, для которых определено произведение AB . Это говорит о том, что если произведение AB определено, то транспонирование произведения равно произведению транспонирования в обратном порядке . Матрицы идентичности . Нулевая матрица 0 m x n играет роль аддитивной единицы в наборе m x n матриц точно так же, как число 0 играет роль в множестве действительных чисел (вспомните пример 7). То есть если A представляет собой матрицу m x n и 0 = 0 m x n , затем Это матричный аналог утверждения, что для любого действительного числа a , Имея на руках аддитивную идентичность, вы можете спросить: «А как насчет мультипликативной идентичности ?» В наборе действительных чисел мультипликативным тождеством является число 1, так как Есть ли матрица, играющая эту роль ? Рассмотрим матрицы и убедитесь, что и Таким образом, AI = IA = A . — это мультипликативная идентичность в наборе матриц 2 x 2. Аналогично, матрица — это мультипликативная идентичность в наборе матриц 3 x 3 и так далее. (Обратите внимание, что I 3 — это матрица [δ ij ] 3 x 3 .) В общем случае матрица I n — матрица n x 2 диагональных элементов с диагональю 1—2 n 90 называется единичной матрицей порядка n и служит мультипликативной идентичностью в наборе всех n x n матриц. Существует ли мультипликативная идентичность в наборе всех m x n матриц, если m ≠ n ? Для любой матрицы A в M M x N ( R ), матрица I M - Left Identity ( I MS , , , 

 е. умножение действительных чисел коммутативно; порядок, в котором записаны факторы, не имеет значения. Однако утверждение о том, что умножение матриц коммутативно, совершенно неверно. Для матриц А и B , приведенный в Примере 9, оба продукта AB и BA были определены, но они определенно не были идентичными. На самом деле матрица АВ была 2 х 2, а матрица ВА была 3 х 3. Вот еще одна иллюстрация некоммутативности матричного умножения: Рассмотрим матрицы
е. умножение действительных чисел коммутативно; порядок, в котором записаны факторы, не имеет значения. Однако утверждение о том, что умножение матриц коммутативно, совершенно неверно. Для матриц А и B , приведенный в Примере 9, оба продукта AB и BA были определены, но они определенно не были идентичными. На самом деле матрица АВ была 2 х 2, а матрица ВА была 3 х 3. Вот еще одна иллюстрация некоммутативности матричного умножения: Рассмотрим матрицы Обычно важно указать, какая матрица стоит первой, а какая второй в продукте. По этой причине утверждение «Умножить A справа на B » означает получение произведения AB , а «Умножить A слева на B » означает получение произведения BA .
Обычно важно указать, какая матрица стоит первой, а какая второй в продукте. По этой причине утверждение «Умножить A справа на B » означает получение произведения AB , а «Умножить A слева на B » означает получение произведения BA .

 Например, если
Например, если 
 Фактически, можно легко показать, что для этой матрицы I оба произведения AI и IA будут равны A для любой матрицы 2 x 2 A . Следовательно,
Фактически, можно легко показать, что для этой матрицы I оба произведения AI и IA будут равны A для любой матрицы 2 x 2 A . Следовательно, - это правильный идентификатор ( AI n = A ). Таким образом, в отличие от набора 90 251 n x n 90 252 матриц, набор неквадратных 90 251 m x n 90 252 матриц не обладает кв. 90 251 двусторонней 90 252 идентичностью, потому что I м ≠ I n если м ≠ n .
- это правильный идентификатор ( AI n = A ). Таким образом, в отличие от набора 90 251 n x n 90 252 матриц, набор неквадратных 90 251 m x n 90 252 матриц не обладает кв. 90 251 двусторонней 90 252 идентичностью, потому что I м ≠ I n если м ≠ n .
Пример 15 : Если A является квадратной матрицей, то A 2 обозначает произведение AA, A 3 обозначает произведение AAA и так далее. Если А это матрица
показывают, что A 3 = − A .
Расчет
показывает, что А 2 = − I . Умножение обеих частей этого уравнения на 90 251 A 90 252 дает 90 251 A 90 252 90 259 3 90 262 = − 90 251 A 90 252 , что и требовалось. [Техническое примечание: можно показать, что в определенном смысле набор матриц вида
, где a и b — действительные числа, структурно идентичен набору комплексных чисел , a + bi . Поскольку матрица A в этом примере имеет такой вид (с a = 0 и b = 1), A соответствует комплексному числу 0 + 1 i = i и аналогу полученного выше матричного уравнения A 2 = − I i 2 = −1, уравнение, определяющее мнимую единицу, i .]
Поскольку матрица A в этом примере имеет такой вид (с a = 0 и b = 1), A соответствует комплексному числу 0 + 1 i = i и аналогу полученного выше матричного уравнения A 2 = − I i 2 = −1, уравнение, определяющее мнимую единицу, i .]
Пример 16 : Найти недиагональную матрицу, коммутирующую с
Проблема просит недиагональную матрицу B такой, что AB = BA . Как и A , матрица B должна быть 2 x 2. Один из способов получения такой матрицы B состоит в том, чтобы сформировать A 2 , поскольку если B = A 2 , 90 ассоциативность подразумевает 90 ассоциативность.
(Это уравнение доказывает, что A 2 будет коммутировать с A для любой квадратной матрицы A ; кроме того, оно подсказывает, как можно доказать, что каждые интегральная степень квадратной матрицы A будет коммутировать с A . )
)
В данном случае
, который не является диагональным. Эта матрица B действительно коммутирует с A , что подтверждается вычислениями
и
Пример 17 : Если
докажи что
для каждого положительного целого числа n .
Несколько предварительных вычислений показывают, что данная формула верна:
Однако, чтобы установить, что формула верна для всех натуральных чисел n , необходимо привести общее доказательство. Это будет сделано здесь с использованием принципа математической индукции , который звучит следующим образом. Пусть P(n) обозначает предложение относительно натурального числа n . Если можно показать, что
и
, то оператор P(n) действителен для всех положительных целых чисел n . В данном случае оператор P(n) является утверждением
В данном случае оператор P(n) является утверждением
Поскольку A 1 = A , утверждение P (1) безусловно верно, поскольку
Теперь, если предположить, что P(n) верно, то есть предположить, что
теперь необходимо установить справедливость утверждения P ( n + 1), то есть
Но это утверждение действительно верно, потому что
По принципу математической индукции доказательство завершено.
Обратная матрица . Пусть a — заданное действительное число. Поскольку 1 является мультипликативной единицей в наборе действительных чисел, если существует число b такое, что
, затем b называется обратной или мультипликативное обратное от к и обозначается через -1 (или 1/ через ). Аналог этого утверждения для квадратных матриц выглядит следующим образом. Пусть A будет заданной n x n матрицей. Поскольку I = I n является мультипликативным тождеством в наборе n x n матриц, если существует матрица B такая, что
Аналог этого утверждения для квадратных матриц выглядит следующим образом. Пусть A будет заданной n x n матрицей. Поскольку I = I n является мультипликативным тождеством в наборе n x n матриц, если существует матрица B такая, что
затем B называется (мультипликативным) , обратным числа A , и обозначается как A −1 (читается « A , обратный»).
Пример 18 : Если
, затем
с
и
Еще одно различие между умножением скаляров и умножением матриц обеспечивается существованием инверсий. Хотя каждое ненулевое действительное число имеет обратное, существуют ненулевые матрицы, не имеющие обратной .
Пример 19 : Показать, что ненулевая матрица
не имеет обратного.
Если бы у этой матрицы была обратная, то
для некоторых значений a, b, c и d . Однако, поскольку вторая строка A является нулевой строкой, вы можете видеть, что вторая строка произведения также должна быть нулевой строкой:
(Когда звездочка * появляется в качестве записи в матрице, это означает, что фактическое значение этой записи не имеет отношения к настоящему обсуждению.) Поскольку запись (2, 2) произведения не может равняться 1, произведение не может равняться единичной матрице. Поэтому построить матрицу, обратную для 9, невозможно.0251 А .
Если матрица имеет обратную, говорят, что она обратима . Матрица в примере 23 обратима, а матрица в примере 24 — нет. Позже вы изучите различные критерии для определения того, является ли данная квадратная матрица обратимой.
Пример 20 : Пример 18 показал, что
Учитывая, что
проверьте уравнение ( AB ) −1 = B −1 А -1 .
Сначала вычислите AB :
Затем вычислите B −1 A −1 :
Теперь, поскольку произведение AB и B −1 A −1 равно I ,
B -1 A -1 действительно является инверсией AB . На самом деле уравнение
верно для любых обратимых квадратных матриц того же размера. Это говорит о том, что если A и B — обратимые матрицы одного размера, то их произведение AB также обратимо, и обратное произведение равно произведению обратных в обратном порядке . (Сравните это уравнение с уравнением, включающим транспонирование в примере 14 выше.) Этот результат можно доказать в общем случае, применив ассоциативный закон для матричного умножения. С
и
следует, что ( AB ) -1 = B -1 A -1 , как и требуется.
Пример 21 : обратная матрица
это
Покажите, что обратное число B T равно ( B −1 ) T .
Форма B T и ( B −1 ) T и умножить:
Этот расчет показывает, что ( B −1 ) T является обратным к B T . [Строго говоря, это показывает только то, что ( B −1 ) T есть правая обратная к B T , то есть когда оно умножает B T справа, продукт является личностью. Верно и то, что ( B -1 ) T B T = I , что означает ( B - 1 ) T - 1 ) T - 1 ) B - 1 ) B - 1 ) B - 1 ). Однако нет необходимости явно проверять оба уравнения: если квадратная матрица имеет обратную, нет различия между левой и правой обратной матрицей.] Таким образом,
Однако нет необходимости явно проверять оба уравнения: если квадратная матрица имеет обратную, нет различия между левой и правой обратной матрицей.] Таким образом,
уравнение, которое на самом деле верно для любой обратимой квадратной матрицы В . Это уравнение говорит о том, что если матрица обратима, то обратима и ее транспонирование, а инверсия транспонирования — это транспонирование инверсии.
Пример 22 : Используйте распределительное свойство для умножения матриц, A ( B ± C ) = AB ± AC , чтобы ответить на этот вопрос: если матрица 2 x 2 удовлетворяет D 902 уравнение D 2 − D − 6 I = 0 , какое выражение для D −1 ?
По приведенному выше распределительному свойству D 2 − D = D 2 − DI = D(D − I) . Поэтому из уравнения D 2 − D − 6 I = 0 следует D(D − I) = 6 I . Умножение обеих частей этого уравнения на 1/6 дает
Поэтому из уравнения D 2 − D − 6 I = 0 следует D(D − I) = 6 I . Умножение обеих частей этого уравнения на 1/6 дает
, что подразумевает
В качестве иллюстрации этого результата матрица
удовлетворяет уравнению D 2 − D − 6 I = 0 , как вы можете убедиться. С 90 005
и
матрица 1/6 ( DI ) действительно равна D -1 , как утверждается.
Пример 23 : Уравнение ( a + b ) 2 = a 2 + 2 ab + b 2 является тождеством, если a и b — действительные числа. Покажите, однако, что ( A + B ) 2 = A 2 + 2 AB + B 2 IS AN AN AN AN AN AN AN AN AN AN AN AN AN AN B 2 AB AB AB AB . являются матрицами 2 x 2. [Примечание: распределительные законы для умножения матриц таковы: A ( B ± C ) = AB ± AC , приведенный в примере 22, и в Законе о сопутствующих, ( A ± B ) C ± B ) C 5 ± B ) C ± B 1 C a ± b .]
являются матрицами 2 x 2. [Примечание: распределительные законы для умножения матриц таковы: A ( B ± C ) = AB ± AC , приведенный в примере 22, и в Законе о сопутствующих, ( A ± B ) C ± B ) C 5 ± B ) C ± B 1 C a ± b .]
Дистрибутивные законы для матричного умножения подразумевают
Поскольку умножение матриц не является коммутативным, BA обычно не будет равно AB , поэтому сумма BA + AB не может быть записана как 2 АБ . В общем случае ( А + В ) 2 ≠ А 2 + 2 АВ + В 2 . [Любые матрицы A и B , которые не коммутируют (например, матрицы в примере 16 выше), дадут конкретный контрпример к утверждению ( A + B ) 2 = A 2 2 2 2 2 2 2 2 + 2 AB + B 2 , что также установило бы, что это не личность. ]
]
Пример 24 : Предположим, что B обратим. Если A коммутирует с B , покажите, что A также будет коммутировать с B −1 .
Доказательство . Сказать « A коммутирует с B » означает AB = BA . Умножьте это уравнение на B −1 слева и справа и используйте ассоциативность:
Пример 25 : Число 0 имеет только один квадратный корень: 0. Покажите, однако, что нулевая матрица (2 на 2) имеет бесконечно много квадратных корней, найдя все матрицы 2 x 2 A такие, что A 2 = 0 .
Точно так же, как число a называется квадратным корнем из b , если a 2 = b , матрица A называется квадратным корнем из B , если А 2 = В . Пусть
— произвольная матрица 2 x 2. Возведение его в квадрат и установка результата равным 0 дает
Возведение его в квадрат и установка результата равным 0 дает
Элементы (1, 2) в последнем уравнении подразумевают b ( a + d ) = 0, что верно, если (случай 1) b = 0 или (случай 2) d = − и .
Случай 1. Если b = 0, диагональные записи подразумевают a = 0 и d = 0, а записи (2, 1) подразумевают, что c произвольно. Таким образом, для любого значения c каждая матрица формы
— это квадратный корень из 0 2x2 .
Случай 2. Если d = − a , то обе недиагональные записи будут равны 0, а диагональные записи будут равны a 2 + bc . Таким образом, пока b и c выбраны так, что bc = − a 2 , A 2 будет равно 0 .
Аналогичная цепочка рассуждений, начинающаяся с (2, 1) записей, приводит либо к a = c = d = 0 (и b произвольно), либо к тому же выводу, что и раньше: пока b и c выбраны так, что bc = − a 2 , матрица A 2 будет равна 0 .
Все эти случаи можно резюмировать следующим образом. Любая матрица следующей формы будет обладать тем свойством, что ее квадрат равен нулевой матрице 2 на 2:
Поскольку существует бесконечно много значений a, b и c , таких что bc = − a 2 , нулевая матрица 0 2x2 имеет бесконечно много квадратных корней. Например, выбрав a = 4, b = 2 и c = −8 дает ненулевую матрицу
, квадрат которого равен
python - Как определить двумерный массив?
Задавать вопрос
Спросил
Изменено 3 месяца назад
Просмотрено 2,8 м умножить на
Я хочу определить двумерный массив без инициализированной длины следующим образом:
Матрица = [][]
Но выдает ошибку:
IndexError: индекс списка вне допустимого диапазона
- питон
- список
- многомерный массив
3
Технически вы пытаетесь индексировать неинициализированный массив. Вы должны сначала инициализировать внешний список списками перед добавлением элементов; Python называет это
«понимание списка».
Вы должны сначала инициализировать внешний список списками перед добавлением элементов; Python называет это
«понимание списка».
# Создает список, содержащий 5 списков, каждый из 8 элементов, все установлены на 0 ш, ч = 8, 5 Матрица = [[0 для x в диапазоне (w)] для y в диапазоне (h)]
#Теперь вы можете добавлять элементы в список:
Matrix[0][0] = 1 Matrix[6][0] = 3 # ошибка! диапазон... Matrix[0][6] = 3 # действительно
Обратите внимание, что матрица является старшим адресом "y", другими словами, "индекс y" предшествует "индексу x".
print Matrix[0][0] # печатает 1 х, у = 0, 6 print Matrix[x][y] # печатает 3; будьте осторожны с индексацией!
Хотя вы можете называть их как хотите, я смотрю на это таким образом, чтобы избежать некоторой путаницы, которая может возникнуть при индексации, если вы используете «x» как для внутреннего, так и для внешнего списков и хотите неквадратную матрицу.
14
Если вам действительно нужна матрица, вам лучше использовать numpy . Матричные операции в
Матричные операции в numpy чаще всего используют тип массива с двумя измерениями. Есть много способов создать новый массив; одной из наиболее полезных является функция нулей , которая принимает параметр формы и возвращает массив заданной формы со значениями, инициализированными до нуля:
>>> import numpy
>>> numpy.zeros ((5, 5))
массив([[ 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]])
Вот несколько других способов создания двумерных массивов и матриц (с удаленным выводом для компактности):
numpy.arange(25).reshape((5, 5)) # создать одномерный диапазон и изменить форму numpy.array(range(25)).reshape((5, 5)) # передать диапазон Python и изменить форму numpy.array([5] * 25).reshape((5, 5)) # передать список Python и изменить форму numpy.empty((5, 5)) # размещаем, но не инициализируем numpy.ones((5, 5)) # инициализируем единицами
число также предоставляет тип матрицы , но он больше не рекомендуется для любого использования и может быть удален из numpy в будущем.
6
Вот более короткая запись для инициализации списка списков:
матрица = [[0]*5 для i в диапазоне (5)]
К сожалению, сокращение этого до чего-то вроде 5*[5*[0]] на самом деле не работает, потому что вы получаете 5 копий одного и того же списка, поэтому, когда вы изменяете одну из них, они все меняются, например:
>>> матрица = 5*[5*[0]] >>> матрица [[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [ 0, 0, 0, 0, 0]] >>> матрица[4][4] = 2 >>> матрица [[0, 0, 0, 0, 2], [0, 0, 0, 0, 2], [0, 0, 0, 0, 2], [0, 0, 0, 0, 2], [ 0, 0, 0, 0, 2]]
11
Если вы хотите создать пустую матрицу, правильный синтаксис:
matrix = [[]]
И если вы хотите создать матрицу размера 5, заполненную 0,
матрица = [[0 для i в xrange(5)] для i в xrange(5)]
3
Если все, что вам нужно, это двумерный контейнер для хранения некоторых элементов, вместо этого вы можете удобно использовать словарь:
Matrix = {}
Тогда вы можете сделать:
Matrix[1,2] = 15 печатать Матрица[1,2]
Это работает, потому что 1,2 — это кортеж, и вы используете его как ключ для индексации словаря. Результат подобен тупой разреженной матрице.
Результат подобен тупой разреженной матрице.
Как указали osa и Josap Valls, вы также можете использовать Matrix = collections.defaultdict(lambda:0) , чтобы отсутствующие элементы имели значение по умолчанию 0 .
Ватсал также указывает, что этот метод, вероятно, не очень эффективен для больших матриц и его следует использовать только в некритичных к производительности частях кода.
8
В Python вы будете создавать список списков. Вам не нужно объявлять размеры заранее, но вы можете. Например:
матрица = [] матрица.дополнение([]) матрица.дополнение([]) матрица [0].append(2) матрица[1].append(3)
Теперь matrix[0][0] == 2 и matrix[1][0] == 3. Вы также можете использовать синтаксис понимания списка. В этом примере он используется дважды для построения «двумерного списка»:
из itertools import count, takewhile матрица = [[i для i в takewhile (лямбда j: j < (k + 1) * 10, count (k * 10))] для k в диапазоне (10)]
1
строк = int(input())
столбцы = интервал (ввод ())
матрица = []
для я в диапазоне (строки):
строка = []
для j в диапазоне (столбцы):
строка. добавлять(0)
matrix.append(строка)
печать (матрица)
добавлять(0)
matrix.append(строка)
печать (матрица)
Почему такой длинный код, который тоже в Python спросите вы?
Давным-давно, когда мне не нравился Python, я увидел однострочные ответы для написания 2D-матрицы и сказал себе, что больше не буду использовать 2-D матрицу в Python. (Эти отдельные строки были довольно пугающими, и они не дали мне никакой информации о том, что делает Python. Также обратите внимание, что я не знаю об этих сокращениях.)
В любом случае, вот код для новичка, который исходит из C, CPP и фон Java
Примечание для любителей и экспертов Python: пожалуйста, не голосуйте против только потому, что я написал подробный код.
0
Принятый ответ хороший и правильный, но мне потребовалось некоторое время, чтобы понять, что я также могу использовать его для создания совершенно пустого массива.
л = [[] для _ в диапазоне (3)]
приводит к
[[], [], []]
0
Вы должны составить список из списков, и лучше всего использовать вложенные включения:
>>> matrix = [[0 для i в диапазоне (5)] для j в диапазоне (5)] >>> pprint.pprint(матрица) [[0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0], [0, 0, 0, 0, 0]]
В вашем примере [5][5] вы создаете список с целым числом «5» внутри и пытаетесь получить доступ к его 5-му элементу, и это, естественно, вызывает IndexError, потому что 5-го элемента нет:
>>> л = [5] >>> л[5] Traceback (последний последний вызов): Файл "", строка 1, в IndexError: индекс списка вне допустимого диапазона
1
Использование:
матрица = [[0]*5 для i в диапазоне (5)]
*5 для первого измерения работает, потому что на этом уровне данные неизменяемы.
1
Так я обычно создаю 2D-массивы в Python.
столбец = 3 ряд = 4 массив = [[0] * столбец для _ в диапазоне (строка)]
Я нахожу этот синтаксис легко запоминающимся по сравнению с использованием двух циклов for при анализе списка.
Переписать для удобства чтения:
# 2D массив/матрица # 5 рядов, 5 столбцов количество_строк = 5 cols_count = 5 # Создайте # создание выглядит наоборот # создать массив столбцов "cols_count" для каждой из строк "rows_count" # все элементы инициализируются 0 two_d_array = [[0 для j в диапазоне (cols_count)] для i в диапазоне (rows_count)] # индекс от 0 до 4 # для строк и столбцов # начиная с 5 строк, 5 столбцов # использовать two_d_array[0][0] = 1 print two_d_array[0][0] # печатает 1 # 1-я строка, 1-й столбец (верхний левый элемент матрицы) two_d_array[1][0] = 2 print two_d_array[1][0] # печатает 2 # 2-я строка, 1-й столбец two_d_array[1][4] = 3 print two_d_array[1][4] # печатает 3 # 2-я строка, последний столбец two_d_array[4][4] = 4 print two_d_array[4][4] # печатает 4 # последняя строка, последний столбец (справа, нижний элемент матрицы)
0
Объявить матрицу нулей (единиц):
numpy.zeros((x, y))
напр.
>>> numpy.zeros ((3, 5))
массив([[ 0., 0., 0., 0., 0.],
[0., 0., 0., 0., 0.],
[ 0., 0., 0., 0., 0.]])
или numpy.ones ((х, у)) например
>>> np.ones((3, 5)) массив([[ 1., 1., 1., 1., 1.], [1., 1., 1., 1., 1.], [ 1., 1., 1., 1., 1.]])
Возможно даже трехмерное изображение. (http://www.astro.ufl.edu/~warner/prog/python.html см. --> Многомерные массивы)
Я работаю над своим первым скриптом Python, и меня немного смутил пример с квадратной матрицей, поэтому я надеюсь, что приведенный ниже пример поможет вам сэкономить время:
# Создает матрицу 2 x 5 Матрица = [[0 для y в xrange(5)] для x в xrange(2)]
, так что
Matrix[1][4] = 2 # Действительно Matrix[4][1] = 3 # IndexError: индекс списка вне допустимого диапазона
Вы можете создать пустой двумерный список, вложив две или более квадратных скобок или третью скобку ( [] , разделенные запятой) с квадратной скобкой, как показано ниже:
Матрица = [[], []]
Теперь предположим, что вы хотите добавить 1 к Matrix[0][0] , затем введите:
Matrix[0].append(1)
Теперь введите Matrix и нажмите Enter. Вывод будет:
[[1], []]
Если вы ввели следующий оператор вместо
Matrix[1].append(1)
, тогда Матрица будет
[[], [1]]
Используя NumPy, вы можете инициализировать пустую матрицу следующим образом:
импортировать numpy как np мм = np.matrix([])
А позже добавьте данные следующим образом:
мм = np.append(мм, [[1,2]], ось=1)
1
Я читаю файлы, разделенные запятыми, следующим образом:
data=[]
для l в файле:
л = разделить (',')
data.append(l)
Список "данные" представляет собой список списков с индексом data[row][col]
0
Вот для чего создан словарь
! матрица = {}
Можно определить ключи и значения двумя способами:
матрица[0,0] = значение
или
матрица = {(0,0) : значение}
Результат:
[значение, значение, значение, значение, значение], [значение, значение, значение, значение, значение], ...
Использование:
импортная копия
def ndlist(*args, init=0):
дп = инициализация
для x в обратном (аргументы):
dp = [copy.deepcopy(dp) для _ в диапазоне(x)]
вернуть дп
l = ndlist(1,2,3,4) # 4-х мерный список, инициализированный нулями
л[0][1][2][3] = 1
Я думаю, что NumPy — это то, что нужно. Вышеприведенное является общим, если вы не хотите использовать NumPy.
1
Если вы хотите иметь возможность думать об этом как о двумерном массиве, а не думать в терминах списка списков (на мой взгляд, гораздо более естественно), вы можете сделать следующее:
import numpy Nx=3; Ню=4 my2Dlist= numpy.zeros((Nx,Ny)).tolist()
Результатом является список (не массив NumPy), и вы можете перезаписывать отдельные позиции числами, строками и т. д.
1
l=[[0]*(L) для _ в диапазоне(W)]
Будет быстрее, чем:
l = [[0 для x в диапазоне (L)] для y в диапазоне (W)]
1
с помощью списка:
matrix_in_python = [['Рой',80,75,85,90,95],['Джон',75,80,75,85,100],['Дэйв',80,80, 80,90,95]]
с помощью dict: вы также можете сохранить эту информацию в хеш-таблице для быстрого поиска, например
matrix = { '1':[0,0] , '2':[0,1],'3':[0,2],' 4' : [1,0],'5':[1,1],'6':[1,2],'7':[2,0],'8':[2,1],' 9':[2,2]};
matrix['1'] даст вам результат за время O(1)
*nb : вам нужно справиться с коллизией в хеш-таблице
Если у вас нет информации о размере перед запуском, создайте два одномерных списка.
список 1: для хранения строк список 2: Фактическая двумерная матрица
Сохранить всю строку в 1-м списке. После этого добавьте список 1 в список 2:
из случайного импорта randint
координаты=[]
темп=[]
points=int(raw_input("Введите количество координат >"))
для i в диапазоне (0, баллы):
случайный x = случайный (0,1000)
случайный = случайный (0,1000)
темп=[]
temp.append(randomx)
temp.append(случайный)
координаты.append(temp)
распечатать координаты
Вывод:
Введите количество координат >4 [[522, 96], [378, 276], [349, 741], [238, 439]]
# Создает список, содержащий 5 списков, инициализированных до 0 Матрица = [[0]*5]*5
Будьте осторожны с этим коротким выражением, см. полное объяснение в ответе @FJ
6
Вот фрагмент кода для создания матрицы в Python:
# получить входные строки и столбцы
строки = интервал (ввод ("строки:"))
cols = int(input("Cols : "))
# инициализируем список
l=[[0]*столбцы для i в диапазоне (строки)]
# заполняем его случайными значениями
для я в диапазоне (0, строки):
для j в диапазоне (0, столбцы):
л [я] [j] = я + j
# распечатать список
для я в диапазоне (0, строки):
Распечатать()
для j в диапазоне (0, столбцы):
распечатать (л [я] [j], конец = " ")
Пожалуйста, подскажите, если я что-то пропустил.
Обычно переходным модулем является NumPy:
импортировать numpy как np # Генерируем случайную матрицу чисел с плавающей запятой np.random.rand (столбцы, строки) # Генерируем случайную матрицу целых чисел np.random.randint (1, 10, размер = (столбцы, строки))
Попробуйте так:
строк = int(input('Введите строки\n'))
мой_список = []
для я в диапазоне (строки):
my_list.append(список(карта(int, input().split())))
Если вам нужна матрица с предопределенными номерами, вы можете использовать следующий код:
матрица определения (строки, столбцы, начало = 0):
return [[c + start + r * cols для c в диапазоне (столбцы)] для r в диапазоне (строки)]
утверждать матрицу (2, 3, 1) == [[1, 2, 3], [4, 5, 6]]
Пользовательская функция для ввода матрицы и печати
def inmatrix(m,n):
#Запустить функцию и передать строку и столбец в качестве параметра
a=[] #создать пустую матрицу
для i в диапазоне (м): # Row input
b=[]#пустой список
для j в диапазоне (n): # ввод столбца
elm=int(input("Введите число в Pocket ["+str(i)+"]["+str(j)+"] ")) #Показать номер строки и столбца
b. append(elm) # добавить значение в список b
a.append(b)# Добавить список в матрицу
вернуть матрицу #return
def Matrix(a): #функция для матрицы печати
для i в диапазоне (len (a)): #row
для j в диапазоне (len (a [0])): # столбец
print(a[i][j],end=" ") #вывести значение с пробелом
print()#печатать строку После печати строки
m=int(input("Введите номер строки")) #input row
n=int(input("Введите номер столбца"))
a=inmatrix(m,n) #вызвать входную матричную функцию
print("Матрица это...")
Matrix(a) #print матричная функция
append(elm) # добавить значение в список b
a.append(b)# Добавить список в матрицу
вернуть матрицу #return
def Matrix(a): #функция для матрицы печати
для i в диапазоне (len (a)): #row
для j в диапазоне (len (a [0])): # столбец
print(a[i][j],end=" ") #вывести значение с пробелом
print()#печатать строку После печати строки
m=int(input("Введите номер строки")) #input row
n=int(input("Введите номер столбца"))
a=inmatrix(m,n) #вызвать входную матричную функцию
print("Матрица это...")
Matrix(a) #print матричная функция
Если вы хотите создать двумерную матрицу, размерность которой определяется двумя переменными, и инициализировать ее значением по умолчанию для всех ее элементов. Вы можете использовать этот простой синтаксис
n_rows=3 n_cols=4 aux_matrix= [[1]*n_cols]*n_rows
Найти строку с максимальным числом единиц
Сложность: Средняя, Запрашиваемые: Amazon, Microsoft, Paytm
Ключевой вывод: Это отличная матричная задача, которую можно решить с помощью линейной временной сложности. Мы используем свойство отсортированного порядка и вложенные циклы, чтобы улучшить решение по сравнению с подходом бинарного поиска.
Мы используем свойство отсортированного порядка и вложенные циклы, чтобы улучшить решение по сравнению с подходом бинарного поиска.
Давайте разберемся в задаче
Дан логический двумерный массив размера m x n, где каждая строка отсортирована. Найдите строку с максимальным количеством единиц.
Примеры
Ввод: X[][] 0 1 1 1 1 1 1 1 <- строка с максимальным количеством единиц 0 0 1 1 0 0 0 0 Выход: 1 (индексация на основе 0) Ввод: Х[][] 0 0 1 1 0 0 0 1 0 1 1 1 <- строка с максимальным количеством единиц 0 0 0 1 Вывод: 2Обсуждаемые подходы к решению
- Решение грубой силы с использованием построчного обхода
- Использование построчного двоичного поиска
- Эффективное решение с использованием двух вложенных циклов
Решение грубой силы с использованием линейного поиска по строкам
Идея решения Прямой метод заключается в выполнении линейного поиска по строкам, подсчете количества единиц в каждой строке и отслеживании индекса строки с помощью максимум 1 счет.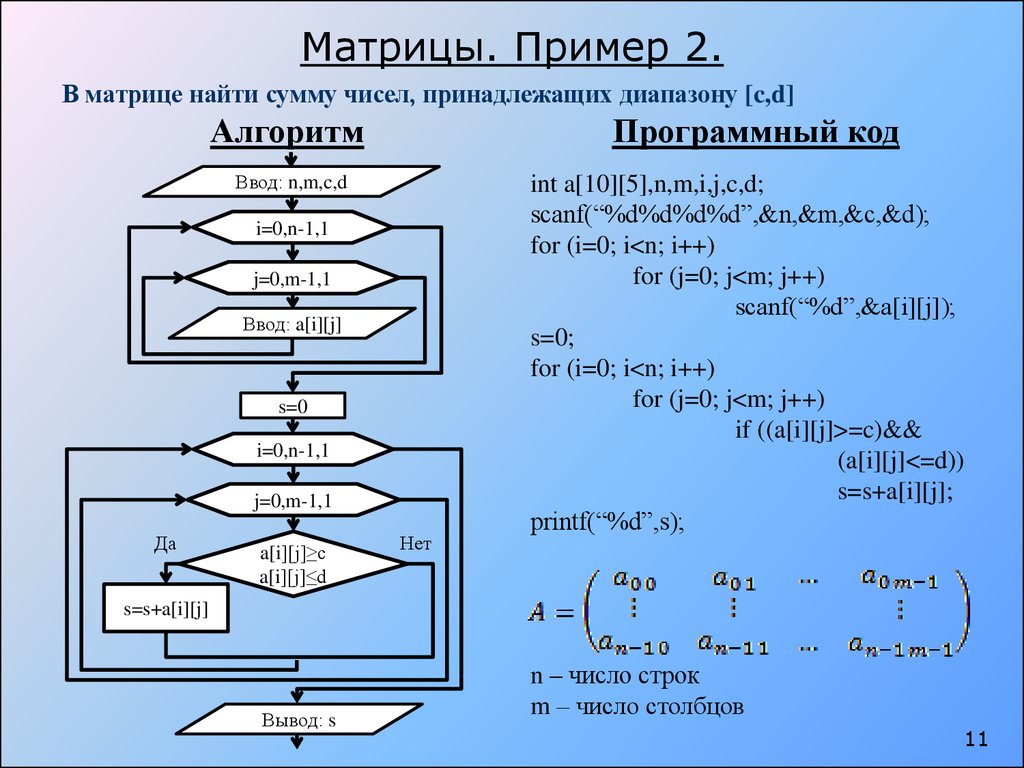 Чтобы реализовать это, мы используем два вложенных цикла и три переменные:
Чтобы реализовать это, мы используем два вложенных цикла и три переменные:
- rowOneCount для отслеживания количества единиц в каждой строке.
- maxOneCount для отслеживания максимального количества единиц.
- maxRowIndex для отслеживания индекса строки с максимальным количеством единиц.
int row_with_max_ones(int X[][], int row, int col)
{
интервал maxOneCount = 0
интервал maxRowIndex = -1
для (целое я = 0; я <строка; я = я + 1)
{
int rowOneCount = 0
для (int j = 0; j < col; j = j + 1)
{
если (X[i][j] == 1)
рядОдинСчетчик = рядОдинСчетчик + 1
}
если (rowOneCount > maxOneCount)
{
maxOneCount = количество строк
maxRowIndex = я
}
}
вернуть maxRowIndex
} Анализ временной и пространственной сложности Мы обходим каждый элемент матрицы, используя вложенные циклы и выполняя операцию O(1) на каждой итерации. Таким образом, сложность времени = n*m*O(1) = O(нм). Мы используем постоянные дополнительные переменные, поэтому пространственная сложность = O(1).
Таким образом, сложность времени = n*m*O(1) = O(нм). Мы используем постоянные дополнительные переменные, поэтому пространственная сложность = O(1).
Использование идеи бинарного поиска
Идея решенияМы уже знаем, что каждая строка отсортирована. Можем ли мы использовать эту информацию для улучшения временной сложности? Давай подумаем!
- Для каждой строки вместо использования линейного поиска мы можем применить бинарный поиск, чтобы найти первое вхождение 1, где бинарный поиск вернет индекс первого вхождения.
- Теперь мы можем легко вычислить количество единиц в строке, равное общему количеству столбцов минус индекс первой единицы.
- Во время этого процесса мы также обновляем счетчик максимального количества единиц и индекс строки с максимальным количеством единиц.
Мы объявляем четыре переменные для отслеживания количества единиц в строке (rowOneCount), общего максимального количества единиц (maxOneCount), индекса первого вхождения 1 (firstOneIndex) и индекса строки с максимальным количеством единиц ( максиндекс строки). Для доступа к каждой строке мы запускаем цикл от i = 0 до строки - 1:
Для доступа к каждой строке мы запускаем цикл от i = 0 до строки - 1:
int row_with_max_ones(int X[][], int row, int col)
{
интервал maxOneCount = 0
интервал maxRowIndex = -1
для (целое я = 0; я <строка; я = я + 1)
{
int firstOneIndex = searchFirstOne (X [i], 0, столбец-1)
int rowOneCount = столбец - firstOneIndex
если (firstOneIndex != -1 && rowOneCount > maxOneCount)
{
maxOneCount = количество строк
maxRowIndex = я
}
}
вернуть maxRowIndex
} Поиск первого вхождения 1: searchFirstOne(X[], l, r) Как упоминалось выше, мы можем применить бинарный поиск, чтобы найти первое вхождение единицы. Для этого мы используем рекурсивный бинарный поиск, в котором базовый случай возникает, когда l > r. Итак, если (l <= r), мы выполняем следующие шаги:
- Вычисляем средний индекс, т.е. mid = l + (r - l)/2
Если значение в середине равно 1, а предыдущее значение в середине - 1 равно 0, это означает, что первая 1 присутствует в индексе середины.
 Есть еще один угловой случай, когда первый присутствует в первой позиции: если mid = 0 и X[mid] == 1. В обоих случаях мы возвращаем mid-index как первое вхождение.
Есть еще один угловой случай, когда первый присутствует в первой позиции: если mid = 0 и X[mid] == 1. В обоих случаях мы возвращаем mid-index как первое вхождение.если ((X[mid - 1] == 0 || mid == 0) && X[mid] == 1) вернуться в середине
- Если (X[mid] == 0), все значения левой половины будут равны нулю, а первая 1 может присутствовать где-то в правой половине. Таким образом, мы ищем вхождение первой единицы в правой половине, рекурсивно используя ту же функцию с mid + 1 и r в качестве левого и правого концов.
В противном случае, если оба приведенных выше условия ложны, то средний индекс равен 1, а не первому вхождению. Другими словами, первый будет присутствовать где-то в левой половине. Таким образом, нам нужно найти вхождение первого 1 в левой половине, используя ту же функцию рекурсивно с l и mid - 1 в качестве левого и правого конца.
иначе если (X[mid] == 0) вернуть searchFirstOne(X, середина + 1, r) еще return searchFirstOne(X, l, mid - 1)
- Когда рекурсия достигает базового случая, это означает, что мы не нашли ни одной единицы в массиве.
 Возвращаем -1.
Возвращаем -1.
int searchFirstOne(int X[], int l, int r)
{
если (л <= г)
{
инт середина = l + (r - l)/2
если ((X[mid - 1] == 0 || mid == 0) && X[mid] == 1)
вернуться в середине
иначе если (X[mid] == 0)
вернуть searchFirstOne(X, середина + 1, r)
еще
вернуть searchFirstOne(X, l, середина - 1)
}
возврат -1
} Анализ временной и пространственной сложности Временная сложность = количество строк * временная сложность бинарного поиска для нахождения первого 1 в каждой строке = n * O(logm) = O(nlogm), где n — количество строк , а m — количество столбцов.
Мы используем рекурсивный бинарный поиск, поэтому сложность пространства зависит от размера стека вызовов, который равен высоте дерева рекурсии. Пространственная сложность = O(logn) (Подумайте!)
Эффективный подход с использованием двух вложенных циклов
Идея решения Можем ли мы еще больше улучшить временную сложность? Считать! Вот два наблюдения из данной входной матрицы: 1) Каждая строка отсортирована, поэтому все единицы в любой строке будут выстроены в линию до правого конца. 2) Для первого 1 в любой строке, если в том же столбце в следующей строке есть 1, то количество единиц в строке <= количество единиц в следующей строке. Та же идея применима ко всем последовательным строкам i и i + 1.
2) Для первого 1 в любой строке, если в том же столбце в следующей строке есть 1, то количество единиц в строке <= количество единиц в следующей строке. Та же идея применима ко всем последовательным строкам i и i + 1.
Вот захватывающая идея решения:
- Начните с верхнего правого угла матрицы и продолжайте двигаться влево, пока не найдем 0. В процессе мы обновляем значение максимального индекса строки.
- Теперь продолжайте двигаться вниз по этому столбцу, пока не встретите 1 в какой-то строке i. В этом случае во всех промежуточных строках от 1 до (i-1) количество единиц меньше, чем в первой строке.
- Опять же, в строке i продолжаем двигаться влево, пока не найдем 0 и не обновим значение максимального индекса строки.
- Мы будем продолжать описанный выше процесс, пока не дойдем до последней строки.
- Мы инициализируем переменную maxRowIndex для отслеживания индекса строки с максимальным значением 1 и currCol для отслеживания текущего столбца.

Теперь запускаем цикл от i=0 до строки - 1:
- Если (currCol >= 0 && X[i][currCol] == 1), мы продолжаем двигаться влево от верхнего правого угла, пока не найдем 0. Мы также продолжаем обновлять значение maxRowIndex.
в то время как (currCol >= 0 && X[i][currCol] == 1) { курркол = курркол - 1 maxRowIndex = я }- Когда приведенное выше условие ложно, мы продолжаем движение вниз в каждом столбце, увеличивая значение i, пока не встретим 1 в какой-либо строке.
- Описанный выше процесс будет продолжаться до i = row.
- К концу цикла мы возвращаем значение, хранящееся в maxRowIndex.
int row_with_max_ones(int X[][], int row, int col)
{
интервал maxRowIndex = -1
int currCol = столбец - 1
для (целое я = 0; я <строка; я = я + 1)
{
в то время как (currCol >= 0 && X[i][currCol] == 1)
{
курркол = курркол - 1
maxRowIndex = я
}
}
вернуть maxRowIndex
} Анализ временной и пространственной сложности В коде есть два вложенных цикла, временная сложность выглядит O(mn), но это неправильный анализ. Если внимательно присмотреться, мы обходим каждую строку и столбец по одному разу, т. е. внешний цикл проходит по каждой строке, а внутренний цикл — по каждому столбцу (подумайте!).
Если внимательно присмотреться, мы обходим каждую строку и столбец по одному разу, т. е. внешний цикл проходит по каждой строке, а внутренний цикл — по каждому столбцу (подумайте!).
Давайте подумаем с другой точки зрения: когда мы обходим любую строку слева направо, то все столбцы на этом пути будут пройдены один раз. Точно так же, когда мы перемещаемся по любому столбцу сверху вниз, все строки на этом пути будут пройдены один раз. (Подумай!)
- Всего итераций цикла = общее количество строк + общее количество столбцов = m + n.
- На каждой итерации цикла мы выполняем операцию O(1).
- Временная сложность = общее число итераций цикла * O(1) = (m + n) * O(1) = O(m + n)
Мы используем постоянное количество переменных, поэтому пространственная сложность = O(1)
Критические идеи!- Каков наихудший и наилучший сценарий эффективного подхода?
- Почему мы начинаем с верхнего правого угла? Можем ли мы решить проблему с другой отправной точки?
- Можем ли мы реализовать второе решение с помощью итеративного бинарного поиска?
- Почему мы перемещаемся по одной и той же строке, если текущая ячейка имеет значение 1?
- Использование построчного обхода: Время = O(нм), Пространство = O(1)
- Использование двоичного поиска: Время = O(nlogm), Пробел = O(logn)
- Использование вложенных циклов: Time = O(m + n), Space = O(1)
- Поиск 2D-матрицы
- Повернуть матрицу на 90 градусов против часовой стрелки
- Транспонировать матрицу
- Установка нулей матрицы
- 01 Матрица
- Изменение матрицы
- Матрица Теплица
Наслаждайтесь обучением, Наслаждайтесь программированием, Наслаждайтесь алгоритмами!
Ранг матрицы
Этот урок знакомит с концепцией матрицы ранга и
объясняет, как ранг
матрица
раскрывается его
эшелонированная форма.
Ранг матрицы
Матрицу r x c можно рассматривать как набор из r строк векторы, каждый имеет c элементов; или вы можете думать об этом как о наборе c векторы-столбцы, каждый из которых имеет r элементов.
Ранг матрицы определяется как (a) максимальное количество линейно независимые столбца векторов в матрице или (b) максимальное количество линейно независимых строк векторов в матрице. Оба определения эквивалентны.
Для матрицы r x c
- Если r меньше c , то максимальный ранг матрицы стоит р .
- Если r больше c , то максимальный ранг матрицы это c .
Ранг матрицы был бы равен нулю только в том случае, если бы в матрице не было элементов. Если бы в матрице был хотя бы один элемент, ее минимальный ранг был бы равен единице.
Как найти ранг матрицы
В этом разделе мы опишем метод нахождения ранга любой матрицы. Этот метод предполагает знакомство с
ступенчатые матрицы
а также
ступенчатые преобразования.
Этот метод предполагает знакомство с
ступенчатые матрицы
а также
ступенчатые преобразования.
Максимальное количество линейно независимых векторов в матрице равно к количеству ненулевых строк в его ступенчатая матрица строк. Поэтому, чтобы найти ранг матрицы, мы просто преобразовать матрицу в ступенчатую форму строки и подсчитать количество ненулевые строки.
Рассмотрим матрицу А и его рядный эшелон матрица, A ref . Раньше мы показывали как найти форму эшелона строк для матрицы A .
| ⇒ |
| ||||||||||||||||||||||
| A | A ref |
Потому что форма эшелона ряда A ref имеет две ненулевые строки, мы знаем, что матрица A имеет два независимых вектора-строки; а также мы знаем, что ранг матрицы A равен 2,
Вы можете убедиться, что это правильно. Ряд 1 и Ряд 2
матрицы A линейно
независимый. Тем не менее, строка 3 является
линейная комбинация
рядов 1 и 2. В частности, ряд 3 = 3*(строка 1) + 2*(строка 2).
Следовательно, матрица A имеет только два независимых вектора-строки.
Ряд 1 и Ряд 2
матрицы A линейно
независимый. Тем не менее, строка 3 является
линейная комбинация
рядов 1 и 2. В частности, ряд 3 = 3*(строка 1) + 2*(строка 2).
Следовательно, матрица A имеет только два независимых вектора-строки.
Реклама
Полноранговые матрицы
Когда все векторы в матрице линейно независимый, говорят, что матрица полный ранг . Рассмотрим матрицы A и B ниже.
| A = |
| B = |
|
Обратите внимание, что строка 2 матрицы A является скалярным числом, кратным
ряд 1; то есть строка 2 вдвое больше строки 1. Следовательно, строки 1 и 2 равны
линейно зависимы. Matrix A имеет только один линейно независимый
строка, поэтому ее ранг равен 1. Следовательно, матрица A не имеет полного ранга.
Следовательно, строки 1 и 2 равны
линейно зависимы. Matrix A имеет только один линейно независимый
строка, поэтому ее ранг равен 1. Следовательно, матрица A не имеет полного ранга.
Теперь посмотрим на матрицу B . Все его строки линейно независимы, поэтому ранг матрицы B равен 3. Матрица B имеет полный ранг.
Проверьте свое понимание
Задача 1
Рассмотрим матрицу X , показанную ниже.
| X = |
|
Каков его ранг?
(А) 0
(B) 1
(C) 2
(D) 3
(E) 4
Решение
Правильный ответ (C). Поскольку в матрице больше нуля элементов,
его ранг должен быть больше нуля. И поскольку у него меньше строк, чем
столбцов, его максимальный ранг равен максимальному количеству
линейно независимые строки.
И поскольку ни одна строка не зависит линейно от другой строки,
матрица имеет 2 линейно независимых строки; поэтому ее ранг равен 2.
Поскольку в матрице больше нуля элементов,
его ранг должен быть больше нуля. И поскольку у него меньше строк, чем
столбцов, его максимальный ранг равен максимальному количеству
линейно независимые строки.
И поскольку ни одна строка не зависит линейно от другой строки,
матрица имеет 2 линейно независимых строки; поэтому ее ранг равен 2.
Задача 2
Рассмотрим матрицу Y , показанный ниже.
| Y = |
|
Каков его ранг?
(А) 0
(Б) 1
(В) 2
(Г) 3
(Д) 4
Решение
Правильный ответ (С). Поскольку в матрице больше нуля элементов,
его ранг должен быть больше нуля. И поскольку у него меньше столбцов, чем
строк, его максимальный ранг равен максимальному числу линейно независимых
столбцы.
И поскольку у него меньше столбцов, чем
строк, его максимальный ранг равен максимальному числу линейно независимых
столбцы.
Столбцы 1 и 2 независимы, потому что ни один из них не может быть получен как скалярно кратно другому. Однако столбец 3 линейно зависит от столбцов 1 и 2, потому что столбец 3 равен столбцу 1 плюс столбец 2. Это оставляет матрицу с максимум двумя линейными независимые столбцы; то есть., столбец 1 и столбец 2. Таким образом, ранг матрицы равен 2,9.0005
Последний урок Следующий урок
Порядок матрицы - формула, определение, типы, примеры
Порядок матрицы представляет количество строк и столбцов в матрице. Матрица — это массив элементов, расположенных в строках и столбцах, и порядок матрицы помогает получить количество строк и столбцов в матрице. Кроме того, порядок матрицы помогает узнать тип матрицы и общее количество элементов в матрице.
Порядок матрицы является важным аспектом, который помогает решить, может ли конкретная арифметическая операция выполняться над двумя матрицами. Здесь, основываясь на порядке матрицы, мы можем узнать о различных типах матриц и различных арифметических операциях, которые можно выполнять над матрицами.
Здесь, основываясь на порядке матрицы, мы можем узнать о различных типах матриц и различных арифметических операциях, которые можно выполнять над матрицами.
| 1. | Что такое порядок матрицы? |
| 2. | Тип матриц на основе порядка матрицы |
| 3. | Порядок матрицы для различных операций над матрицей |
| 4. | Примеры порядка матрицы |
| 5. | практических вопросов |
| 6. | Часто задаваемые вопросы о порядке матрицы |
Что такое порядок матрицы?
Порядок матрицы дает размерность матрицы и количество строк и столбцов, присутствующих в матрице. Порядок матрицы обычно представляется как A m × n , где m — количество строк, а n — количество столбцов в данной матрице. Кроме того, ответ на умножение порядка матрицы (m × n) дает количество элементов в матрице.
В приведенной выше матрице мы видим m строк и n столбцов. Первое число в порядке матрицы всегда представляет количество строк, а второе число в порядке матрицы всегда представляет количество столбцов в матрице.
Тип матриц на основе порядка матрицы
Порядок матрицы дает размеры матрицы и определяет различные типы матриц. Давайте проверим порядок некоторых из различных типов матриц.
- Порядок матрицы строк: Матрица строк состоит из одной строки и множества столбцов. Следовательно, порядок матрицы-строки имеет вид 1 × n. \[A_{1 × n} = \begin{bmatrix}a_1&a_2&a_3&\cdots&a_n\end{bmatrix}\]
- Порядок матрицы столбцов: Матрица столбцов состоит из одного столбца и множества строк. Следовательно, порядок матрицы-столбца равен n × 1. \[A_{n × 1} = \begin{bmatrix}a_1\\a_2\\a_3\\ \vdots\\a_n\end{bmatrix}\]
- Порядок квадратной матрицы: Квадратная матрица, как следует из названия, имеет одинаковое количество строк и столбцов.
 Следовательно, порядок квадратной матрицы имеет вид n × n. Здесь у нас есть равное количество 3 строк и 3 столбцов в приведенной ниже матрице. \[A_{3×3} = \begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}\]
Следовательно, порядок квадратной матрицы имеет вид n × n. Здесь у нас есть равное количество 3 строк и 3 столбцов в приведенной ниже матрице. \[A_{3×3} = \begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}\] - Порядок прямоугольной матрицы: Прямоугольная матрица имеет неравное количество строк и столбцов, поэтому порядок прямоугольной матрицы имеет вид m × n. Здесь, в приведенной ниже матрице, у нас есть 2 строки и 3 столбца. \[A_{2×3} = \begin{bmatrix}a&b&c\\ \\ d&e&f\end{bmatrix}\] 9T_{3×2} = \begin{bmatrix}a&d\\b&e\\c&f\end{bmatrix}\]
Порядок матрицы для различных операций над матрицей
Порядок матрицы относится к типу матрицы. Кроме того, многие арифметические операции с матрицами основаны на порядке упомянутой матрицы. Давайте проверим, как выполняются следующие операции над матрицами в зависимости от порядка .matrix.
Сложение и вычитание матриц: Для сложения или вычитания двух матриц порядок обеих матриц должен быть одинаковым. Количество строк в обеих матрицах должно быть одинаковым, и количество столбцов в обеих матрицах также должно быть равным. Давайте разберемся в этом на простом примере.
Количество строк в обеих матрицах должно быть одинаковым, и количество столбцов в обеих матрицах также должно быть равным. Давайте разберемся в этом на простом примере.
\( \left[\begin{массив}{ccc}
2 & {-1} & 3 \\\
0 & 5 & 2 \end{массив}\right]_{\!2 \!× \!3} + \left[\begin{массив}{ccc}
\!0 &\! 2&\!7\\\
\!1 & \!-2 & \!9
\end{массив}\right]_{\!2 \!× \!3}\)
\(= \left[\begin{массив}{ccc}
2+0 и {-1} \!+\!2 и 3 \!+\!7\\ \\
0\!+\!1 и 5\!+\!(-2) и 2\!+\!9
\!\end{массив}\right] \)
\(= \left[\begin{массив}{ccc}
\!2 & \!1 & \!10 \\ \\
\!1 & \!3 & \!11
\end{array}\right]_{\!2 \!× \!3} \)
Здесь соответствующие элементы обеих матриц складываются, чтобы получить элементы результирующей матрицы, а значит, количество элементов и порядок обеих матриц должен быть одинаковым. Порядок обеих матриц в приведенном выше сложении матриц равен 2 × 3.
Умножение матриц: Умножение матриц включает особое условие порядка матрицы. Количество столбцов в первой матрице для умножения должно быть равно количеству строк во второй матрице. Далее порядок полученной матрицы равен количеству строк первой матрицы и количеству столбцов второй матрицы.
Количество столбцов в первой матрице для умножения должно быть равно количеству строк во второй матрице. Далее порядок полученной матрицы равен количеству строк первой матрицы и количеству столбцов второй матрицы.
\(AB=\left[ \begin{matrix} \!1 & \!2 & \!3 \\ \\ \!3 & \!1 & \!0 \\\end{matrix} \right] _{\!2 \!× \!3} \times \left[ \begin{matrix} \!1 & \!4 \\ \!3 & \!-1 \\ 2 & -3 \\\end{ матрица} \right]_{\!3 \!× \!2}\)
\(=\begin{bmatrix}\!1\!×\!1 \!+ \!2\!×\!3 \!+ \!3\!×\!2 &\!1 \!×\!4 \!+\!2\!×\!(-1) \!+\!3\!×\!(- 3)\\\!3\!×\!1 \!+ \!1\!×\!3 \!+ \!0\!×\!2 &\!3 \!×\!4 \!+ \!1\!×\!(-1) \!+\!0\!×\!(-3)\end{bmatrix}\)
\(=\left[ \begin{matrix} \!13 & \!-7\\ \\ \!6 & \!11 \\ \end{matrix} \right]_{\!2 × \!2}\)
В приведенном выше примере количество столбцов в первой матрице и количество строк во второй матрице равно 3. А порядок результирующей матрицы 2 × 2, так как она имеет 2 строки (что равно количество строк в первой матрице) и 2 столбца (что равно количеству столбцов во второй матрице).
☛ Связанные темы:
Следующие связанные темы помогут лучше понять концепцию порядка матрицы.
- Матричный калькулятор
- Транспонирование матрицы
- Сопряженная матрица
- Обратная матрица
Важные примечания по порядку матрицы:
Следующие пункты обобщают некоторые ключевые моменты, полученные в отношении порядка матрицы.
- В порядке матрицы m × n первое число m всегда представляет количество строк, а второе число n всегда представляет количество столбцов.
- Для сложения и вычитания двух матриц порядок матриц должен быть одинаковым.
- Для умножения двух матриц количество столбцов в первой матрице должно быть равно количеству строк в первой матрице.
- При умножении двух матриц порядок результирующей матрицы таков, что количество строк равно первой матрице, а количество столбцов равно второй матрице.
Часто задаваемые вопросы по порядку матрицы
Как найти порядок матрицы?
Порядок матрицы можно легко вычислить, проверив расположение элементов матрицы. Матрица — это набор элементов, расположенных в виде строк и столбцов. Порядок матрицы записывается как m × n, где m — количество строк в матрице, а n — количество столбцов в матрице.
Матрица — это набор элементов, расположенных в виде строк и столбцов. Порядок матрицы записывается как m × n, где m — количество строк в матрице, а n — количество столбцов в матрице.
Как узнать количество элементов по порядку матрицы?
Порядок матрицы записывается как m × n, и это произведение дает количество элементов в матрице. В качестве примера рассмотрим матрицу порядка 2 × 3, и это произведение 2 × 3 = 6 есть количество элементов в матрице.
Каково условие порядка матрицы для сложения и вычитания?
Чтобы сложить/вычесть две или более матриц, они должны быть одного порядка. Например, матрица порядка 2 x 3 не может быть добавлена к матрице порядка 3 x 2.
Каково условие порядка матрицы для умножения матриц?
Важным условием умножения на основе порядка матрицы является то, что количество столбцов в первой матрице равно количеству строк во второй матрице. Также результирующая матрица умножения матриц имеет количество строк, равное количеству строк в первой матрице, и количество столбцов, равное количеству столбцов во второй матрице.



 размер()
int м = матрица [0]. размер ()
int l = 0, r = m * n - 1
в то время как (л != г) {
середина = (л + г - 1) / 2
if (matrix[mid / m][mid % m] < target)
л = середина + 1
еще
г = середина
}
если (матрица [r / m] [r % m] == цель)
вернуть истину
еще
вернуть ложь
}
размер()
int м = матрица [0]. размер ()
int l = 0, r = m * n - 1
в то время как (л != г) {
середина = (л + г - 1) / 2
if (matrix[mid / m][mid % m] < target)
л = середина + 1
еще
г = середина
}
если (матрица [r / m] [r % m] == цель)
вернуть истину
еще
вернуть ложь
}  добавлять(0)
matrix.append(строка)
печать (матрица)
добавлять(0)
matrix.append(строка)
печать (матрица)
 pprint(матрица)
[[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]]
pprint(матрица)
[[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0],
[0, 0, 0, 0, 0]]
 zeros((x, y))
zeros((x, y))
 append(1)
append(1)
 ..
..
 append(elm) # добавить значение в список b
a.append(b)# Добавить список в матрицу
вернуть матрицу #return
def Matrix(a): #функция для матрицы печати
для i в диапазоне (len (a)): #row
для j в диапазоне (len (a [0])): # столбец
print(a[i][j],end=" ") #вывести значение с пробелом
print()#печатать строку После печати строки
m=int(input("Введите номер строки")) #input row
n=int(input("Введите номер столбца"))
a=inmatrix(m,n) #вызвать входную матричную функцию
print("Матрица это...")
Matrix(a) #print матричная функция
append(elm) # добавить значение в список b
a.append(b)# Добавить список в матрицу
вернуть матрицу #return
def Matrix(a): #функция для матрицы печати
для i в диапазоне (len (a)): #row
для j в диапазоне (len (a [0])): # столбец
print(a[i][j],end=" ") #вывести значение с пробелом
print()#печатать строку После печати строки
m=int(input("Введите номер строки")) #input row
n=int(input("Введите номер столбца"))
a=inmatrix(m,n) #вызвать входную матричную функцию
print("Матрица это...")
Matrix(a) #print матричная функция
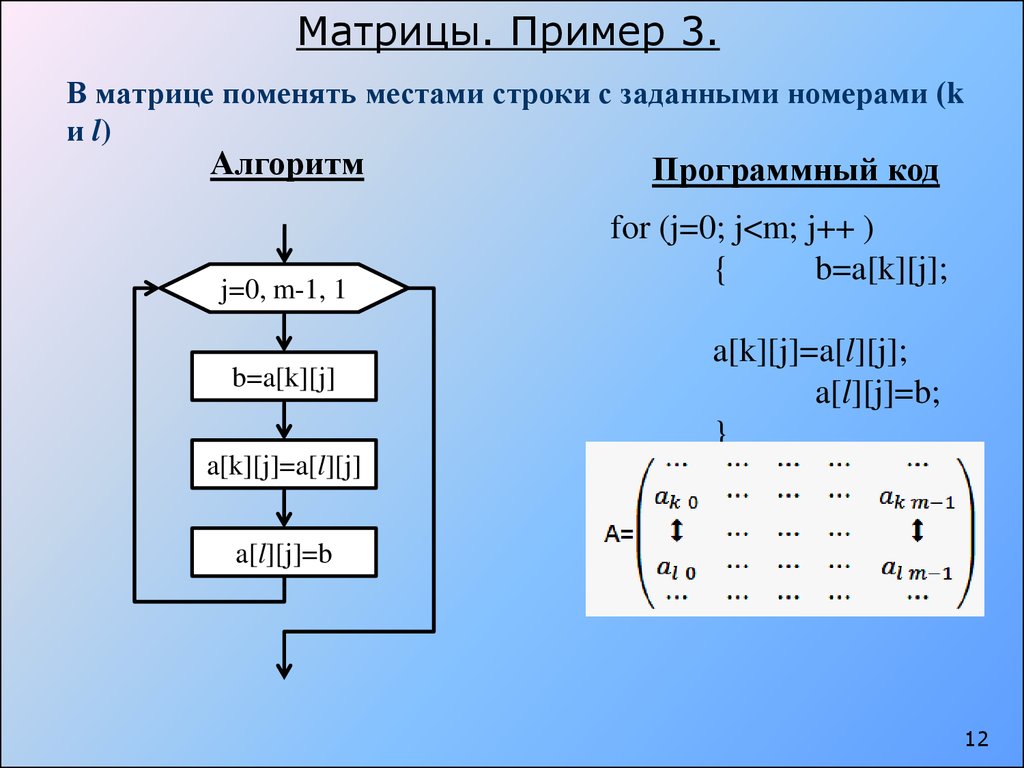 Есть еще один угловой случай, когда первый присутствует в первой позиции: если mid = 0 и X[mid] == 1. В обоих случаях мы возвращаем mid-index как первое вхождение.
Есть еще один угловой случай, когда первый присутствует в первой позиции: если mid = 0 и X[mid] == 1. В обоих случаях мы возвращаем mid-index как первое вхождение. Возвращаем -1.
Возвращаем -1.
 Следовательно, порядок квадратной матрицы имеет вид n × n. Здесь у нас есть равное количество 3 строк и 3 столбцов в приведенной ниже матрице. \[A_{3×3} = \begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}\]
Следовательно, порядок квадратной матрицы имеет вид n × n. Здесь у нас есть равное количество 3 строк и 3 столбцов в приведенной ниже матрице. \[A_{3×3} = \begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}\]