Деление полиномов
Введение
Общий вид одночлена
f(x)=axn, где:
—a — коэффициент, который может принадлежать любому из множеств N, Z, Q, R, C
—x — переменная
—n показатель степени, который принадлежит множеству N
Два одночлена подобны, если они имеют одну и ту же переменную и одинаковый показатель степени.
Примеры: 3x2 и -5x2; ½x4 и 2√3x4
Сумма одночленов, не подобных друг другу, называется многочленом (или полиномом). В этом случае одночлены являются слагаемыми полинома. Полином, содержащий два слагаемых, называется биномом (или двучленом).
Пример: p(x)=3x2-5; h(x)=5x-1
Полином, содержащий три слагаемых, называется трехчленом.
Общий вид многочлена с одной переменной
p(x)=anxn+an-1xn-1+…+a1x1
где:
- an,an-1,an-2,.
 ..,a1,a0 — коэффициенты полинома. Они могут быть натуральными, целыми, рациональными, действительными или комплексными числами.
..,a1,a0 — коэффициенты полинома. Они могут быть натуральными, целыми, рациональными, действительными или комплексными числами. - an — коэффициент при слагаемом с наибольшим показателем степени (ведущий коэффициент)
- a0 — коэффициент при слагаемом с наименьшим показателем степени (свободный член, или константа)
- n — степень полинома
Пример 1
p(x)=5x3-2x2+7x-1
- полином третьей степени с коэффициентами 5, -2, 7 и -1
- 5 — ведущий коэффициент
- -1 — свободный член
- x — переменная
Пример 2
h(x)=-2√3x4+½x-4
- полином четвертой степени с коэффициентами -2√3,½ и -4
- -2√3 — ведущий коэффициент
- -4 — свободный член
- x — переменная
p(x) и q(x) — два полинома:
p(x)=anxn+an-1xn-1+.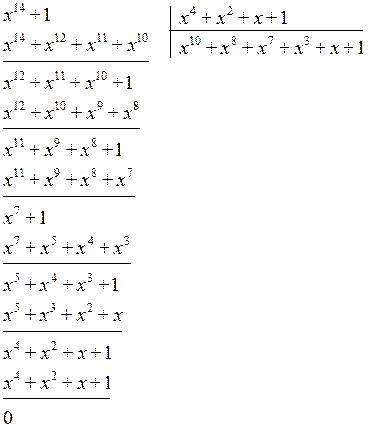 ..+a1x1 +a0
..+a1x1 +a0
q(x)=apxp+ap-1xp-1+…+a1x1 +a0
Чтобы найти частное и остаток от деления p(x) на q(x), нужно использовать следующий алгоритм:
- Степень p(x) должна быть больше либо равной степени q(x).
- Мы должны записать оба полинома в порядке понижения степени. Если в p(x) нет члена с какой-либо степенью, его надо дописать с коэффициентом 0.
- Ведущий член p(x) делится на ведущий член q(x), и результат записывается под разделительной линией (в знаменателе).
- Складываем почленно слагаемые с одинаковыми степенями.
- К результату приписываем оставшиеся члены p(x).
- Делим ведущий член полученного полинома на первый член полинома q(x) и повторяем шаги 3-6.
 2-x+1$
2-x+1$3) x5-3x4+2x3+7x2-3x+5
x2-x+1
x3
4) x5-3x4+2x3+7x2-3x+5
-x5+x4-x3
x2-x+1
x3
5) x5-3x4+2x3+7x2-3x+5
-x5+x4-x3
/ -2x4-x3
x2-x+1
x3
6) x5-3x4+2x3+7x2-3x+5
-x5+x4-x3
/ -2x4-x3+7x2-3x+5
x2-x+1
x3
7) x5-3x4+2x3+7x2-3x+5
-x5+x4-x3
/ -2x4+x3+7x2-3x+5
2x4-2x3+2x2
/ -x3+9x2-3x+5
x2-x+1
x3-2x2
8) x5-3x4+2x3+7x2-3x+5
-x5+x4-x3
/ -2x4-x3+7x2-3x+5
2x4-2x3+2x2
/ -x3+9x2-3x+5
x3 — x2+x
/ 8x
-8x2+8x-8
/ 6x-3 СТОП
x2-x+1
x3-2x2-x+8 —> C(x) Частное
Ответ: p(x) = x5 — 3x4 + 2x3 + 7x2— 3x + 5 = (x2 — x + 1)(x3 — 2x2 — x + 8) + 6x — 3Пример 2
p(x)=x4+3x2+2x-8
q(x)=x2-3xx4+0x3+3x2+2x-8
-x4+3x3
/ 3x3+3x2+2x-8
-3x3+9x2
/ 12x2+2x-8
-12x2+36x
/ 38x-8 r(x) СТОП
x2-3x
x2+3x+12 —> C(x) Частное
Ответ: x4 + 3x2 + 2x — 8 = (x2 — 3x)(x2 + 3x + 12) + 38x — 8Деление на полином первой степениЭто деление можно выполнить с использованием вышеупомянутого алгоритма или даже более быстрым образом, если воспользоваться методом Горнера.

Если f(x)=anxn+an-1xn-1 +…+a1x+a0, полином можно переписать в виде f(x)=a0+x(a1+x(a2+…+x(an-1+anx)…))
q(x) — полином первой степени ⇒ q(x)=mx+n
Тогда полином в частном будет иметь степень n-1.По методу Горнера, $x_0=-\frac{n}{m}$.
bn-1=an
bn-2=x0.bn-1+an-1
bn-3=x0.bn-2+an-2
…
b1=x0.b2+a2
b0=x0.b1+a1
r=x0.b0+a0
где bn-1xn-1+bn-2xn-2+…+b1x+b0 — частное. Остатком будет полином нулевой степени, поскольку степень полинома в остатке должна быть меньше, чем степень делителя.
Деление с остатком ⇒ p(x)=q(x).c(x)+r ⇒ p(x)=(mx+n).c(x)+r если $x_0=-\frac{n}{m}$
Отметим, что p(x0)=0.c(x0)+r ⇒ p(x0)=rПример 3
p(x)=5x4-2x3+4x2-6x-7
q(x)=x-3
p(x)=-7+x(-6+x(4+x(-2+5x)))
x0=3b3=5
b2=3.5-2=13
b1=3.13+4=43 ⇒ c(x)=5x3+13x2+43x+123; r=362
b0=3.43-6=123
r=3.123-7=362
5x4-2x3+4x2-6x-7=(x-3)(5x3+13x2+43x+123)+362Пример 4
p(x)=-2x5+3x4+x2-4x+1
q(x)=x+2
p(x)=-2x5+3x4+0x3+x2-4x+1
q(x)=x+2
x0=-2
p(x)=1+x(-4+x(1+x(0+x(3-2x))))b4=-2 b1=(-2).
 2-5x+9$.
2-5x+9$.Вернуться к списку тем
Задать вопрос на форуме
Записаться на занятия
Онлайн-занятия по высшей математике
Деление многочленов
Продолжаем изучать многочлены. В данном уроке мы научимся их делить.
Деление многочлена на одночлен
Чтобы разделить многочлен на одночлен, нужно разделить на этот одночлен каждый член многочлена, затем сложить полученные частные.
Например, разделим многочлен 15x2y3 + 10xy2 + 5xy3 на одночлен xy. Запишем это деление в виде дроби:
Теперь делим каждый член многочлена 15x2y3 + 10xy2 + 5xy3 на одночлен xy. Получающиеся частные будем складывать:
Получили привычное для нас деление одночленов. Выполним это деление:
Таким образом, при делении многочлена 15x2y3 + 10xy2 + 5xy3 на одночлен xy получается многочлен 15xy2 + 10y + 5y2.

При делении одного числа на другое, частное должно быть таким, чтобы при его перемножении с делителем, получалось делимое. Это правило сохраняется и при делении многочлена на одночлен.
В нашем примере произведение полученного многочлена 15xy2 + 10y + 5y2 и делителя xy должно быть равно многочлену 15x2y3 + 10xy2 + 5xy3, то есть исходному делимому. Проверим так ли это:
(15xy2 + 10y + 5y2)xy = 15x2y3 + 10xy2 + 5xy3
Деление многочлена на одночлен очень похоже на сложение дробей с одинаковыми знаменателями. Мы помним, что для сложения дробей с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменений.
Например, чтобы сложить дроби , и нужно записать следующее выражение:
Если мы вычислим выражение , то получим дробь , значение которой равно 1,5.

При этом выражение мы можем вернуть в исходное состояние , и вычислить по отдельности каждую дробь, затем сложить полученные частные. Результат по прежнему будет равен 1,5
Тоже самое происходит при делении многочлена на одночлен. Одночлен берёт на себя роль общего знаменателя для всех членов многочлена. Например, при делении многочлена ax + bx + cx на многочлен x, образуется три дроби с общим знаменателем x
Вычисление каждой дроби даст в результате многочлен a + b + c
Пример 2. Разделить многочлен 8m3n + 24m2n2 на одночлен 8m2n
Пример 3. Разделить многочлен 4c2d − 12c4d3 на одночлен −4c2d
Деление одночлена на многочлен
Не существует тождественного преобразования, позволяющего разделить одночлен на многочлен.

Допустим, мы захотели разделить одночлен 2xy на многочлен 5x + 3y + 5.
Результатом этого деления должен быть многочлен, перемножение которого с многочленом 5x + 3y + 5 даёт одночлен 2xy. Но не существует многочлена, перемножение которого с многочленом 5x + 3y + 5 давало бы в результате одночлен 2xy, поскольку перемножение многочленов даёт в результате многочлен, а не одночлен.
Но в учебниках можно встретить задания на нахождение значения выражения при заданных значениях переменных. В исходных выражениях таких заданий бывает выполнено деление одночлена на многочлен. В этом случае никаких преобразований выполнять не нужно. Достаточно подставить значения переменных в исходное выражение и вычислить получившееся числовое выражение.
Например, найдём значение выражения при x = 2.
Выражение представляет собой деление одночлена на многочлен. В данном случае мы не сможем выполнить какие-либо преобразования.
 Единственное, что мы сможем сделать — это подставить число 2 в исходное выражение вместо переменной x и найти значение выражения:
Единственное, что мы сможем сделать — это подставить число 2 в исходное выражение вместо переменной x и найти значение выражения:Деление многочлена на многочлен
Если первый многочлен умножить на второй многочлен, получается третий многочлен. Например, если умножить многочлен x + 5 на многочлен x + 3, получается многочлен x2 + 8x + 15
(x + 5)(x + 3) = x2 + 5x + 3x + 15 = x2 + 8x + 15
(x + 5)(x + 3) = x2 + 8x + 15
Если произведение разделить на множитель, то получится множимое. Это правило распространяется не только для чисел, но и для многочленов.
Тогда согласно этому правилу, деление полученного нами многочлена x2 + 8x + 15 на многочлен x + 3 должно давать в результате многочлен x + 5.
Деление многочлена на многочлен выполняется уголком.
 Отличие будет в том, что при делении многочленов не нужно определять первое неполное делимое, как в случае деления обычных чисел.
Отличие будет в том, что при делении многочленов не нужно определять первое неполное делимое, как в случае деления обычных чисел.Выполним уголком деление многочлена x2 + 8x + 15 на многочлен x + 3. Так мы поэтапно увидим, как получается многочлен x + 5.
В данном случае результат нам известен заранее. Это будет многочлен x + 5. Но чаще всего результат бывает неизвестным. Поэтому решение будем комментировать так, будто результат нам неизвестен.
Результатом деления должен быть новый многочлен. Члены этого многочлена будут появляться один за другим в процессе деления.
Сейчас наша задача найти первый член нового многочлена. Как это сделать?
Когда мы изначально перемножали многочлены x + 5 и x + 3, мы сначала умножили первый член первого многочлена на первый член второго многочлена. Тем самым мы получили первый член третьего многочлена:
Если мы обратно разделим первый член третьего многочлена на первый член второго многочлена, то получим первый член первого многочлена.
 А это то, что нам нужно. Ведь мы должны прийти к многочлену x + 5.
А это то, что нам нужно. Ведь мы должны прийти к многочлену x + 5.Этот же принцип нахождения первого члена будет выполняться и при решении других задач на деление многочленов.
Итак, чтобы найти первый член нового многочлена, нужно первый член делимого разделить на первый член делителя.
Если первый член делимого (в нашем случае это x2) разделить на первый член делителя (это x), получится x. То есть первым членом нового многочлена является x. Записываем его под правым углом:
Теперь, как и при делении обычных чисел, умножаем x на делитель x + 3. На этом этапе нужно суметь умножить одночлен на многочлен. При умножении x на x + 3, получается x2 + 3x. Записываем этот многочлен под делимым x2+ 8x+ 15 так, чтобы подобные члены располагались друг под другом:
Теперь из делимого x2 + 8x + 15 вычитаем x2 + 3x.
 Подобные члены вычитаем из подобных им членов. Если из x2 вычесть x2, получится 0. Ноль не записываем. Далее если из 8x вычесть 3x, получится 5x. Записываем 5x так, чтобы этот член оказался под членами 3x и 8x
Подобные члены вычитаем из подобных им членов. Если из x2 вычесть x2, получится 0. Ноль не записываем. Далее если из 8x вычесть 3x, получится 5x. Записываем 5x так, чтобы этот член оказался под членами 3x и 8xТеперь, как и при делении обычных чисел, сносим следующий член делимого. Следующий член это 15. Сносить его нужно вместе со своим знаком:
Теперь делим многочлен 5x + 15 на x + 3. Для этого нужно найти второй член нового многочлена. Чтобы его найти, нужно первый член делимого (сейчас это член 5x) разделить на первый член делителя (это член x). Если 5x разделить на x, получится 5. То есть вторым членом нового многочлена является 5. Записываем его под правым углом, вместе со своим знаком (член 5 в данном случае положителен)
Теперь умножаем 5 на делитель x + 3. При умножении 5 на x + 3, получается 5x + 15.
 Записываем этот многочлен под делимым 5x + 15
Записываем этот многочлен под делимым 5x + 15Теперь из делимого 5x + 15 вычитаем 5x + 15. Если из 5x + 15 вычесть 5x + 15 получится 0.
На этом деление завершено.
После выполнения деления можно выполнить проверку, умножив частное на делитель. В нашем случае, если частное x + 5 умножить на делитель x + 3, должен получаться многочлен x2 + 8x + 15
(x + 5)(x + 3) = x2 + 5x + 3x + 15 = x2 + 8x + 15
Пример 2. Разделить многочлен x2 − 8x + 7 на многочлен x − 7
Записываем уголком данное деление:
Находим первый член частного. Разделим первый член делимого на первый член делителя, получим x. Записываем x под правым углом:
Умножаем x на x − 7, получаем x2 − 7x.
 Записываем этот многочлен под делимым x2 − 8x + 7 так, чтобы подобные члены располагались друг под другом:
Записываем этот многочлен под делимым x2 − 8x + 7 так, чтобы подобные члены располагались друг под другом:Вычитаем из x2 − 8x + 7 многочлен x2 − 7x. При вычитании x2 из x2 получается 0. Ноль не записываем. А при вычитании −7x из −8x получается −x, поскольку −8x − (−7x) = −8x + 7x = −x. Записываем −x под членами −7x и −8x. Далее сносим следующий член 7
Следует быть внимательным при вычитании отрицательных членов. Часто на этом этапе допускаются ошибки. Если на первых порах вычитание в столбик даётся тяжело, то можно использовать обычное вычитание многочленов в строку, которое мы изучили ранее. Для этого нужно отдельно выписать делимое и вычесть из него многочлен, который под ним располагается. Преимущество этого метода заключается в том, что следующие члены делимого сносить не нужно — они автоматически перейдут в новое делимое.
 Давайте воспользуемся этим методом:
Давайте воспользуемся этим методом:Вернёмся к нашей задаче. Разделим многочлен −x + 7 на x − 7. Для этого нужно найти второй член частного. Чтобы его найти, нужно первый член делимого (сейчас это член −x) разделить на первый член делителя (это член x). Если −x разделить на x, получится −1. Записываем −1 под правым углом вместе со своим знаком:
Умножаем −1 на x − 7, получаем −x + 7. Записываем этот многочлен под делимым −x + 7
Теперь из −x + 7 вычитаем −x + 7. Если из −x + 7 вычесть −x + 7 получится 0
Деление завершено. Таким образом, частное от деления многочлена x2 − 8x + 7 на многочлен x − 7 равно x − 1
Выполним проверку. Умножим частное x − 1 на делитель x − 7. У нас должен получиться многочлен x2 − 8x + 7
(x − 1)(x − 7) = x2 − x − 7x + 7 = x2 − 8x + 7
Пример 3.
 Разделить многочлен x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3
Разделить многочлен x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3Найдём первый член частного. Разделим первый член делимого на первый член делителя, получим x4
Умножаем x4 на делитель x2 + x3 и полученный результат записываем под делимым. Если x4 умножить на x2 + x3 получится x6 + x7. Члены этого многочлена записываем под делимым так, чтобы подобные члены располагались друг под другом:
Теперь из делимого вычитаем многочлен x6 + x7. Вычитание x6 из x6 даст в результате 0. Вычитание x7 из x7 тоже даст в результате 0. Оставшиеся члены 2x4 и 2x5 снесём:
Получилось новое делимое 2x4 + 2x5.
 Это же делимое можно было получить, выписав отдельно многочлен x6 + 2x4 + x7 + 2x5 и вычтя из него многочлен x6 + x7
Это же делимое можно было получить, выписав отдельно многочлен x6 + 2x4 + x7 + 2x5 и вычтя из него многочлен x6 + x7Разделим многочлен 2x4 + 2x5 на делитель x2 + x3. Как и раньше сначала делим первый член делимого на первый член делителя, получим 2x2. Записываем этот член в частном:
Умножаем 2x2 на делитель x2 + x3 и полученный результат записываем под делимым. Если 2x2 умножить на x2 + x3 получится 2x4 + 2x5. Записываем члены этого многочлена под делимым так, чтобы подобные члены располагались друг под другом. Затем выполним вычитание:
Вычитание многочлена 2x4 + 2x5 из многочлена 2x4 + 2x5 дало в результате 0, поэтому деление успешно завершилось.

В промежуточных вычислениях члены нового делимого располагались друг от друга, образуя большие расстояния. Это было по причине того, что при умножении частного на делитель, результаты были записаны так, чтобы подобные члены располагались друг под другом.
Эти расстояния между членами нового делимого образуются тогда, когда члены исходных многочленов расположены беспорядочно. Поэтому перед делением желательно упорядочить члены исходных многочленов в порядке убывания степеней. Тогда решение примет более аккуратный и понятный вид.
Решим предыдущий пример, упорядочив члены исходных многочленов в порядке убывания степеней. Если члены многочлена x6 + 2x4 + x7 + 2x5 упорядочить в порядке убывания степеней, то получим многочлен x7 + x6 + 2x5 + 2x4. А если члены многочлена x2 + x3 упорядочить в порядке убывания степеней, то получим многочлен x3 + x2
Тогда деление уголком многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 примет следующий вид:
Деление завершено.
 Таким образом, частное от деления многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 равно x4 + 2x2
Таким образом, частное от деления многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 равно x4 + 2x2Выполним проверку. Умножим частное x4 + 2x2 на делитель x2 + x3. У нас должен получиться многочлен x6 + 2x4 + x7 + 2x5
(x4 + 2x2)(x2 + x3) = x4 (x2 + x3) + 2x2(x2 + x3) = x6 + 2x4 + x7 + 2x5
При перемножении многочленов члены исходных многочленов тоже желательно упорядочивать в порядке убывания степеней.
 Тогда члены полученного многочлена тоже будут упорядочены в порядке убывания степеней.
Тогда члены полученного многочлена тоже будут упорядочены в порядке убывания степеней.Перепишем умножение (x4 + 2x2)(x2 + x3) упорядочив члены многочленов в порядке убывания степеней.
(x4 + 2x2)(x3 + x2) = x4(x3 + x2) + 2x2(x3 + x2) = x7 + x6 + 2x5 + 2x4
Пример 4. Разделить многочлен 17x2 − 6x4 + 5x3 − 23x + 7 на многочлен 7 − 3x2 − 2x
Упорядочим члены исходных многочленов в порядке убывания степеней и выполним уголком данное деление:
Значит,
Пример 5.
 Разделить многочлен 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2
Разделить многочлен 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2Найдем первый член частного. Разделим первый член делимого на первый член делителя, получим 4a2. Записываем 4a2 в частном:
Умножим 4a2 на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым:
Вычтем из делимого полученный многочлен 4a4 − 12a3b − 36a2b2
Теперь делим −2a3b + 12a2b2 − 54b4 на делитель a2 − 3ab − 9b2. Разделим первый член делимого на первый член делителя, получим −2ab.
 Записываем −2ab в частном:
Записываем −2ab в частном:Умножим −2ab на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым −2a3b + 12a2b2 − 54b4
Вычтем из многочлена −2a3b + 12a2b2 − 54b4 многочлен −2a3b + 12a2b2 − 18ab3. При вычитании подобных членов обнаруживаем, что члены −54b4 и 18ab3 не являются подобными, а значит их вычитание не даст никакого преобразования. В этом случае выполняем вычитание там где это можно, а именно вычтем −2a3b из −2a3b и 6a2b2 из 12a2b2, а вычитание 18ab3 из −54b4 запишем в виде разности −54b4 − (+18ab3) или −54b4 − 18ab3
Этот же результат можно получить, если выполнить вычитание многочленов в строку с помощью скобок:
Вернёмся к нашей задаче.
 Разделим 6a2b2 − 54b4 − 18ab3 на делитель a2 − 3ab − 9b2. Делим первый член делимого на первый член делителя, получим 6b2. Записываем 6b2 в частном:
Разделим 6a2b2 − 54b4 − 18ab3 на делитель a2 − 3ab − 9b2. Делим первый член делимого на первый член делителя, получим 6b2. Записываем 6b2 в частном:Умножим 6b2 на делитель a2 − 3ab − 9b2 и полученный результат запишем под делимым 6a2b2 − 54b4 − 18ab3. Сразу вычтем этот полученный результат из делимого 6a2b2 − 54b4 − 18ab3
Деление завершено. Таким образом, частное от деления многочлена 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2 равно 4a2 − 2ab + 6b2.

Выполним проверку. Умножим частное 4a2 − 2ab + 6b2 на делитель a2 − 3ab − 9b2. У нас должен получиться многочлен 4a4 − 14a3b − 24a2b2 − 54b4
Как и при делении обычных чисел, при делении многочлена на многочлен может образоваться остаток от деления.
Для начала вспомним деление обычных чисел с остатком. Например, разделим уголком 15 на 2. С остатком это деление будет выполнено так:
То есть при делении 15 на 2 получается 7 целых и 1 в остатке. Ответ записывается следующим образом:
Рациональное число читается как семь целых плюс одна вторая. Знак «плюс» по традиции не записывают. Но если при делении многочлена на многочлен образуется остаток, то этот плюс записывать нужно.
Например, если при делении многочлена a на многочлен b получится частное c, да еще останется остаток q, то ответ будет записан так:
Например, разделим многочлен 2x3 − x2 − 5x + 4 на многочлен x − 3
Найдем первый член частного.
 Разделим первый член делимого на первый член делителя, получим 2x2. Записываем 2x2 в частном:
Разделим первый член делимого на первый член делителя, получим 2x2. Записываем 2x2 в частном:Умножим 2x2 на делитель x − 3 и полученный результат запишем под делимым:
Вычтем из делимого полученный многочлен 2x3 − 6x2
Теперь делим 5x2 − 5x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 5x. Записываем 5x в частном:
Умножим 5x на делитель x − 3 и полученный результат запишем под делимым 5x2 − 5x + 4
Вычтем из многочлена 5x2 − 5x + 4 многочлен 5x2 − 15x
Теперь делим 10x + 4 на делитель x − 3. Разделим первый член делимого на первый член делителя, получим 10. Записываем 10 в частном:
Умножим 10 на делитель x − 3 и полученный результат запишем под делимым 10x + 4.
 Сразу вычтем этот полученный результат из делимого 10x + 4
Сразу вычтем этот полученный результат из делимого 10x + 4Число 34, полученное в результате вычитания многочлена 10x − 30 из многочлена 10x + 4, является остатком. Мы не сможем найти следующий член частного, который при умножении с делителем x − 3 дал бы нам в результате 34.
Поэтому при делении многочлена 2x3 − 2x2 − 5x + 4 на многочлен x − 3 получается 2x2 + 5x + 10 и 34 в остатке. Ответ записывается таким же образом, как и при делении обычных чисел. Сначала записывается целая часть (она располагается под правым углом) плюс остаток, разделенный на делитель:
Когда деление многочленов невозможно
Деление многочлена на многочлен невозможно в случае, если степень делимого окажется меньше степени делителя.
Например, нельзя разделить многочлен x3 + x на многочлен x4 + x2, поскольку делимое является многочленом третьей степени, а делитель — многочленом четвёртой степени.

Вопреки этому запрету можно попробовать разделить многочлен x3 + x на многочлен x4 + x2, и даже получить частное x−1, которое при перемножении с делителем будет давать делимое:
Но при делении многочлена на многочлен должен получаться именно многочлен, а частное x−1 многочленом не является. Ведь многочлен состоит из одночленов, а одночлен в свою очередь это произведение чисел, переменных и степеней. Выражение x−1 это дробь , которая не является произведением.
Пусть имеется прямоугольник со сторонами 4 и 2
Площадь этого прямоугольника будет равна 4 × 2 = 8 кв.ед.
Увеличим длину и ширину этого прямоугольника на x
Достроим отсутствующие стороны:
Теперь прямоугольник имеет длину x + 4 и ширину x + 2. Площадь этого прямоугольника будет равна произведению (x + 4)(x + 2) и выражаться многочленом x2 + 6x + 8
(x + 4)(x + 2) = x2 + 4x + 2x + 8 = x2 + 6x + 8
При этом мы можем выполнить обратную операцию, а именно разделить площадь x2 + 6x + 8 на ширину x + 2 и получить длину x + 4.

Степень многочлена x2 + 6x + 8 равна сумме степеней многочленов-сомножителей x + 4 и x + 2, а значит ни одна из степеней многочленов-сомножителей не может превосходить степень многочлена-произведения. Следовательно, чтобы обратное деление было возможным, степень делителя должна быть меньше степени делимого.
Задания для самостоятельного решения
Задание 1. Выполните деление:
Решение:
Показать решение
Задание 2. Выполните деление:
Решение:
Показать решение
Задание 3. Выполните деление:
Решение:
Показать решение
Задание 4. Выполните деление:
Решение:
Показать решение
Задание 5. Выполните деление:
Решение:
Показать решение
Задание 6. Выполните деление:
Решение:
Показать решение
Задание 7. Выполните деление:
Решение:
Показать решение
Задание 8. Выполните деление:
Решение:
Показать решение
Задание 9.
 Выполните деление:
Выполните деление:Решение:
Показать решение
Задание 10. Выполните деление:
Решение:
Показать решение
Задание 11. Выполните деление:
Решение:
Показать решение
Задание 12. Выполните деление:
Решение:
Показать решение
Задание 13. Выполните деление:
Решение:
Показать решение
Задание 14. Выполните деление:
Решение:
Показать решение
Задание 15. Выполните деление:
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых урокахВозникло желание поддержать проект?
Опубликовано Автор
Используй кнопку нижеДеление многочлена на многочлен «уголком»
В этой статье рассмотрим один из способов разложения на множители многочленов высших степеней.
 2=(a-b)(a+b)\).
2=(a-b)(a+b)\).
\((x-1)(x-2)(x-\sqrt{2})(x+\sqrt{2})≥0\)
Вот сейчас все готово для применения метода интервалов.
Запишем ответ.
Ответ: \((-∞;-\sqrt{2}]∪[1;\sqrt{2}]∪[2;∞)\).
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Справочник по математике Алгебра Деление многочленов.
Корни многочленовНапомним, что разделить натуральное число a на натуральное число b – это значит представить число a в виде:
a = bc + r ,
где частное c и остаток r – целые неотрицательные числа, причем остаток r удовлетворяет неравенству:
Если друг на друга делить многочлены, то возникает похожая ситуация.

Действительно, при выполнении над многочленами операций сложения, вычитания и умножения результатом всегда будет многочлен. В частности, при перемножении двух многочленов, отличных от нуля, степень произведения будет равна сумме степеней сомножителей.
Однако в результате деления многочленов многочлен получается далеко не всегда.
Говорят, что один многочлен нацело (без остатка) делится на другой многочлен, если результатом деления является многочлен.
Если же один многочлен не делится нацело на другой многочлен, то всегда можно выполнить деление многочленов с остатком, в результате которого и частное, и остаток будут многочленами.
Определение. Разделить многочлен a(x) на многочлен b(x) с остатком – это значит представить многочлен a(x) в виде
a(x) = b(x) c(x) + r(x) ,
где многочлен c(x) – частное, а многочлен r(x) – остаток, причем, степень остатка удовлетворяет неравенству:
Очень важно отметить, что формула
a(x) = b(x) c(x) + r(x)
является тождеством, т.
 е. равенством, справедливым при всех значениях переменной x .
е. равенством, справедливым при всех значениях переменной x .При делении (с остатком или без остатка) многочлена на многочлен меньшей степени в частном получается многочлен, степень которого равна разности степеней делимого и делителя.
Один из способов деления многочленов с остатком – это деление многочленов «уголком», что представляет собой полную аналогию с тем, как это происходит при делении целых чисел.
К описанию этого способа деления многочленов мы сейчас и переходим.
Пример. Заранее расположив многочлены по убывающим степеням переменной, разделим многочлен
2x4 – x3 + 5x2 – 8x + 1
на многочлен
x2 – x + 1 .
Решение. Опишем алгоритм деления многочленов «уголком» по шагам:
- Делим первый член делимого 2x4 на первый член делителя x2.
 Получаем первый член частного 2x2 .
Получаем первый член частного 2x2 . - Умножаем первый член частного 2x2 на делитель x2 – x + 1, а результат умножения
- Вычитаем из делимого написанный под ним многочлен. Получаем первый остаток
- Делим первый член остатка x3 на первый член делителя x2 .
 Получаем второй член частного x .
Получаем второй член частного x . - Умножаем второй член частного x на делитель x2 – x + 1 , а результат умножения
- Вычитаем из первого остатка написанный под ним многочлен. Получаем второй остаток
- Делим первый член второго остатка 4x2 на первый член делителя x2 .
 Получаем третий член частного 4.
Получаем третий член частного 4. - Умножаем третий член частного 4 на делитель x2 – x + 1 , а результат умножения
- Вычитаем из второго остатка написанный под ним многочлен. Получаем третий остаток
– 5x – 3 .
Степень этого остатка равна 1, что меньше, чем степень делителя. Следовательно, процесс деления закончен.
- Таким образом,
2x4 – 2x3 + 2x2
пишем под делимым 2x4 – x3 + 5x2 – 8x + 1 .
x3 + 3x2– 8x .
Если бы этот остаток был равен нулю, или был многочленом, степень которого меньше, чем степень делителя ( в данном случае меньше 2), то процесс деления был бы закончен. Однако это не так, и деление продолжается.
x3 – x2 + x
пишем под первым остатком x3 + 3x2– 8x .
4x2 – 9x + 1 .
Если бы этот остаток был бы равен нулю, или был многочленом, степень которого меньше, чем степень делителя, то процесс деления был бы закончен. Однако это не так, и деление продолжается.
4x2 – 4x + 4
пишем под вторым остатком.
2x4 – x3 + 5x2 – 8x + 1 =
= (x2 – x + 1) (2x2 + x +
+ 4) – 5x – 3 ,где
Запись изложенного процесса деления многочленов «уголком» имеет следующий вид:
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.

Умножение и деление полиномов MatLab
RADIOMASTER
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
Кнопка вызова помощи со шрифтом брайля Система вызова персонала invakor.ru Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11
- Главная / org/Breadcrumb»>База знаний
/ - Делим первый член делимого 2x4 на первый член делителя x2.
- CAD / CAM /
- MatLab
- Длинное деление многочленов
- Синтетическое деление многочлена
- Алгоритм деления многочленов
- Деление двух многочленов
- Деление многочлена на линейный множитель
Пример 1: Алекс застрял на задаче, работая над делением многочленов. Можете ли вы помочь ему получить частное: (x 4 — 10x 3 + 27x 2 — 46х + 28) ÷ (х — 7).
Решение:
Следовательно, частное равно x 3 — 3x 2 + 6x — 4.
Пример 2: Стейси нужна помощь в нахождении остатка при делении многочленов. Вы можете помочь ей решить эту проблему?
(4x 3 + 5x 2 + 5x + 8) ÷ (4x + 1)
Решение: Используя метод деления многочленов в длину, получаем,
Следовательно, остаток равен 7.

- Метод синтетического деления
- Метод длинного деления
- Деление одного монома на другой моном.
- Деление многочлена на одночлен.
- Деление многочлена на двучлен.
- Деление многочлена на другой многочлен.

- Шаг 1. Расположите члены в порядке убывания их индексов (если требуется). Запишите пропущенные члены с нулевыми коэффициентами.
- Шаг 2. Для первого члена частного разделить первый член делимого на первый член делителя.
- Шаг 3. Умножьте этот член частного на делитель, чтобы получить произведение.
- Шаг 4. Вычтите это произведение из делимого и уменьшите следующий член (если есть). Разница и сокращенный срок образуют новый дивиденд.
- Шаг 5. Выполняйте этот процесс, пока не получите остаток, который может быть равен нулю или иметь меньший индекс, чем делитель.
- Шаг 1. Разделите первый член делимого (6x 2 ) на первый член делителя (x) и подставьте его в качестве первого члена в частном (6x).
- Шаг 2.
 Умножьте делитель на этот ответ, поместите произведение (6x 2 — 18x) под делимым.
Умножьте делитель на этот ответ, поместите произведение (6x 2 — 18x) под делимым. - Шаг 3. Вычтите, чтобы создать новый полином (14x — 24).
- Шаг 4. Повторите тот же процесс с новым полиномом, полученным после вычитания.
- Шаг 1: Разделите первое слагаемое делимого (6x 3 ) на первое слагаемое делителя (x 2 ) и поставьте его как первое слагаемое в частном (6x).
- Шаг 2 : Умножьте делитель на этот ответ, поместите произведение (6x 3 + 24x 2 + 18x) ниже дивиденда.
- Шаг 3: Вычтите, чтобы создать новый полином (-12x 2 — 16x + 25).
- Шаг 4: Повторите тот же процесс с новым полиномом, полученным после вычитания.
- p(x) — дивиденд.
- q(x) — частное.
- g(x) — делитель.
- r(x) — остаток.
- r(x) = 0 или степень r(x) < степени g(x)
- Синтетическое деление многочлена
- Алгоритм деления многочленов
- Деление двух многочленов
- Деление многочлена на линейный множитель
- Расположите термины в порядке убывания их индексов (если требуется). Запишите пропущенные члены с нулевыми коэффициентами.
- Для первого члена частного разделите первый член делимого на первый член делителя.
- Умножьте этот член частного на делитель, чтобы получить произведение.
- Вычтите это произведение из делимого и уменьшите следующий член (если есть). Разница и сокращенный срок образуют новый дивиденд.
- Выполняйте этот процесс, пока не получите остаток, который может быть равен нулю или иметь меньший индекс, чем делитель.
- Используйте деление в большую сторону для деления многочленов.
- Используйте синтетическое деление для деления многочленов.
- Задайте задачу деления.
- Определите первый член частного, разделив старший член делимого на старший член делителя.
- Умножьте ответ на делитель и запишите его под аналогичными членами делимого.
- Вычтите нижний бином из членов над ним.
- Уменьшите следующий член дивиденда. 9{2}+4x+5[/latex] на [latex]x+2[/latex] с использованием алгоритма длинного деления.
Окончательный вид процесса выглядел так:
В таблице много повторов. Если мы не будем записывать переменные, а вместо этого выстроим их коэффициенты в столбцы под знаком деления, а также исключим частичные произведения, мы уже получим более простую версию всей задачи.

Синтетическое деление несет в себе это упрощение еще на несколько шагов. Сверните таблицу, переместив каждую из строк вверх, чтобы заполнить все свободные места. Кроме того, вместо деления на 2, как при делении целых чисел, а затем умножения и вычитания среднего произведения, мы меняем знак «делителя» на -2, умножаем и складываем. Процесс начинается с уменьшения старшего коэффициента. 92} -7x+18[/latex], а остаток равен –31. Процесс будет более понятен в следующих примерах.
A Общее примечание: Синтетическое деление
Синтетическое деление — это сокращение, которое можно использовать, когда делитель является биномом в форме x — k . В синтетическом делении в процессе деления используются только коэффициенты.
Как сделать: Имея два полинома, разделите их синтетическим делением
- Запишите k для делителя.
- Запишите коэффициенты делимого.
- Уменьшить старший коэффициент.

- Умножить старший коэффициент на k . Напишите произведение в следующем столбце.
- Добавьте условия второго столбца.
- Умножить результат на k . Напишите произведение в следующем столбце.
- Повторите шаги 5 и 6 для остальных столбцов.
- Используйте нижние числа, чтобы написать частное. Число в последнем столбце является остатком и имеет степень 0, следующее число справа имеет степень 1, следующее число справа имеет степень 2 и так далее. 9{2}-23x+6[/латекс]. Ширина прямоугольника равна x + 6. Найдите выражение для длины прямоугольника.
Показать решение
Ключевые уравнения
Алгоритм деления [латекс]f\влево(х\вправо)=d\влево(х\вправо)q\влево(х\вправо)+r\влево(х\вправо)[/латекс], где [латекс]q\влево( х\справа)\ne 0[/латекс] Ключевые понятия
- Длинное деление полинома можно использовать для деления полинома на любой полином равной или меньшей степени.

- Алгоритм деления говорит нам, что полиномиальное делимое может быть записано как произведение делителя и частного, прибавленного к остатку.
- Синтетическое деление — это сокращение, которое можно использовать для деления многочлена на двучлен вида x – k .
- Полиномиальное деление можно использовать для решения прикладных задач, включая площадь и объем.
Глоссарий
- Алгоритм деления
- с учетом полиномиального делимого [латекс]f\влево(х\вправо)[/латекс] и ненулевого полиномиального делителя [латекс]d\влево(х\вправо)[/латекс], где степень [латекс]d \left(x\right)[/latex] меньше или равно степени [latex]f\left(x\right)[/latex], существуют уникальные многочлены [latex]q\left(x\right )[/latex] и [latex]r\left(x\right)[/latex] такие, что [latex]f\left(x\right)=d\left(x\right)q\left(x\right )+r\left(x\right)[/latex], где [latex]q\left(x\right)[/latex] – частное, а [latex]r\left(x\right)[/latex] – остаток.
 Остаток либо равен нулю, либо имеет степень строго меньше, чем [latex]d\left(x\right)[/latex].
Остаток либо равен нулю, либо имеет степень строго меньше, чем [latex]d\left(x\right)[/latex].
- синтетический отдел
- сокращенный метод, который можно использовать для деления многочлена на двучлен вида x – k
- Служба национальных парков. «Статистика здания Мемориала Линкольна». http://www.nps.gov/linc/historyculture/lincoln-memorial-building-statistics.htm. По состоянию на 03.04.2014 ↵
Использование полиномиального деления — SAT Mathematics
Все ресурсы SAT Mathematics
137 Практические тесты Вопрос дня Карточки Learn by Concept
SAT Mathematics Help » Полиномы и квадраты » Использование полиномиального деления
На какое выражение можно умножить, чтобы получить произведение ?
Возможные ответы:
Правильный ответ:
Объяснение:
Разделите на , установив деление в большую сторону.

Разделить первый член дивиденда, , на первый член делителя, ; результат
Введите это как первый член частного. Умножьте это на делитель:
Вычтите это из делимого. Это показано на рисунке ниже.
Повторите процесс с новой разницей:
Повторение:
3
3 Правильный ответ — и частное.
Сообщить об ошибке
Разделить многочлен на .
Возможные ответы:
Правильный ответ:
Объяснение:
Наш первый шаг — перечислить коэффициенты многочленов в порядке убывания и записать первый коэффициент.
Мы умножаем то, что находится под чертой, на и помещаем произведение в верхнюю часть строки. Находим сумму этого числа со следующим коэффициентом и помещаем сумму под чертой. Мы продолжаем повторять эти шаги, пока не достигнем последних коэффициентов.

Чтобы написать ответ, мы используем числа под чертой в качестве наших новых коэффициентов. Последнее число — это наш остаток.
с остатком
Это можно переписать как:
Имейте в виду: высшая степень нашего нового многочлена всегда будет на единицу меньше степени исходного многочлена.
Сообщить об ошибке
Разделить многочлен на .
Возможные ответы:
Правильный ответ:
Объяснение:
Наш первый шаг — перечислить коэффициенты многочленов в порядке убывания и записать первый коэффициент.
Помните , чтобы поставить если не указан коэффициент.
Мы умножаем то, что находится под чертой, на и помещаем произведение в верхнюю часть строки. Находим сумму этого числа со следующим коэффициентом и помещаем сумму под чертой.
 Мы продолжаем повторять эти шаги, пока не достигнем последних коэффициентов.
Мы продолжаем повторять эти шаги, пока не достигнем последних коэффициентов.Чтобы написать ответ, мы используем числа под чертой в качестве наших новых коэффициентов. Последнее число — это наш остаток.
с остатком
Это можно переписать как:
Имейте в виду: высшая степень нашего нового многочлена всегда будет на единицу меньше, чем степень исходного многочлена.Сообщить об ошибке
Использовать синтетическое деление для деления на .
Возможные ответы:
Остаток
Остаток
Правильный ответ:
Пояснение:
Чтобы разделить синтетически, мы начнем с рисования прямоугольника. Внутри, через пробел, пишем коэффициенты членов нашего многочлена при делении. Снаружи пишем корень, который удовлетворял бы нашему двучлену , а именно .
 Оставив место для другой строки чисел, мы затем рисуем линию под нашей строкой коэффициентов.
Оставив место для другой строки чисел, мы затем рисуем линию под нашей строкой коэффициентов.Затем мы начинаем деление, просто перенося наш первый коэффициент (1) вниз под чертой.
Затем мы умножаем эту 1 на наш делитель (3) и записываем полученное произведение (3) под нашим следующим коэффициентом.
Затем мы складываем два числа в этом столбце и записываем сумму (5) под чертой.
Затем мы просто продолжаем процесс, умножая это 5 на наш делитель 3 и записывая это произведение в следующий столбец, добавляя его к следующему коэффициенту и продолжая, пока не закончим столбцы.
Затем нам нужно перевести нижний ряд чисел в коэффициенты нашего нового частного. Поскольку первый столбец изначально соответствовал нашему кубическому члену, теперь он будет соответствовать квадратичному члену, означающему, что нашу 1 можно перевести как . Точно так же наш второй столбец переходит от квадратичного к линейному, в результате чего наша 5 становится . Наконец, наш третий столбец становится постоянным членом, то есть 8 просто остается постоянным 8.
 Наконец, наш прежний постоянный столбец становится столбцом для нашего остатка. Однако, поскольку у нас есть 0, у нас нет остатка, и мы можем его игнорировать.
Наконец, наш прежний постоянный столбец становится столбцом для нашего остатка. Однако, поскольку у нас есть 0, у нас нет остатка, и мы можем его игнорировать.Сборное все это вместе дает нам окончательный ответ
Отчет о ошибке
Разделение с использованием синтетического дивизии:
Возможные ответы:
Правильный ответ:
. Объяснение:
Сначала поставьте синтетическую задачу деления, выстроив коэффициенты. Есть несколько разных стратегий — для этого мы поместим -7 в верхний угол и добавим столбцы.
_________________________
Первый шаг — сбить первую 1. Затем умножить то, что ниже строки, на -7 в рамке, записать это ниже следующего коэффициента, а затем добавить столбцы:
_________________________
Мы можем интерпретировать этот ответ как означающий
Сообщить об ошибке
Каков результат, когда делится на ?
Возможные ответы:
Правильный ответ:
Объяснение:
Наш первый шаг — перечислить коэффициенты многочленов в порядке убывания и записать первый коэффициент.

Мы умножаем то, что находится под чертой, на и помещаем произведение в верхнюю часть строки. Находим сумму этого числа со следующим коэффициентом и помещаем сумму под чертой. Мы продолжаем повторять эти шаги, пока не достигнем последнего коэффициента.
Чтобы написать ответ, мы используем числа под чертой в качестве наших новых коэффициентов. Последнее число — это наш остаток.
с напоминанием
Это можно переписать как:
Сообщить об ошибке
Какое из следующих утверждений эквивалентно приведенному выше выражению для ?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы правильно ответить на этот вопрос, вам нужно знать основной метод полиномиального деления. Это работает так же, как деление в длину, которому вы научились в начальной школе, но вместо деления чисел, состоящих из нескольких цифр, вы делите многочлены с несколькими членами.

Подлый трюк в этом вопросе заключается в том, что выражение представлено с остаточным членом первым и главным частным членом во вторую! Это противоположно стандартной форме такого выражения. Но это все же технически математически правильно, поскольку изменение порядка членов в выражении сложения не меняет его значения. SAT любит сбивать студентов с толку такими хитрыми, но математически обоснованными уловками. Всегда следите за ними!
Итак, первое, что вы должны сделать, это преобразовать выражение в вопросе в его наиболее естественную стандартную форму: . Теперь вы можете видеть, что это выражение является результатом операции полиномиального деления с 4 в качестве главного частного и 2 в остатке.
Теперь, когда вы видите, что 4 является главным частным, вы можете понять, что это результат деления на , поэтому они должны быть первым членом числителя и первым членом знаменателя (который мы называем делителем). Поэтому мы можем исключить неправильные варианты ответа и , и сосредоточиться на оставшихся вариантах ответа с в числителе.
 На самом деле это самая сложная часть решения этого вопроса. Многих студентов смущает порядок членов, и они ошибочно принимают 2 за главное частное, а 4 за остаток. Эта ошибка может привести, в частности, к неправильному выбору ответа.
На самом деле это самая сложная часть решения этого вопроса. Многих студентов смущает порядок членов, и они ошибочно принимают 2 за главное частное, а 4 за остаток. Эта ошибка может привести, в частности, к неправильному выбору ответа.Важно понимать, что остаточный член всегда представляет собой дробный член с первоначальным делителем, который все еще присутствует в качестве знаменателя этого дробного члена. То, что мы часто называем «остатком», например 2 в данном случае, на самом деле является числителем этого остатка.
Мы также можем исключить неправильный вариант ответа , потому что эта операция деления даст значение 4 без остатка. Это оставляет только правильных вариантов ответа , . Делитель входит в числитель четыре раза, поэтому главный член в частном равен 4. Мы умножаем на 4, чтобы получить , мы вычитаем , чтобы получить 2. Это наш остаток, который дает нам остаточный член. Таким образом, мы правильно получили оба члена исходного выражения в вопросе, .

Сообщить об ошибке
Какое из следующих выражений эквивалентно ?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы правильно ответить на этот вопрос, вам необходимо знать основной метод полиномиального деления. Это работает так же, как деление в длину, которому вы научились в начальной школе, но вместо деления чисел, состоящих из нескольких цифр, вы делите многочлены с несколькими членами.
Первый шаг процесса полиномиального деления в этом вопросе довольно прост: первым членом будет x, потому что это результат деления первого члена числителя на первый член знаменателя (делителя).
Первая сложная часть возникает, когда вы умножаете на , чтобы получить , что вы должны написать под и вычесть. Будьте очень осторожны при выполнении шагов вычитания при решении операций полиномиального деления! В базовом делении чисел на длинное число все цифры положительны, поэтому шаги вычитания такие же, как и при обычном вычитании.
 Но при полиномиальном делении члены могут быть как положительными, так и отрицательными, и сложнее правильно выполнить вычитание с отрицательными членами. Поэтому рекомендуется выполнять такие шаги вычитания на меняем все знаки второго многочлена и затем добавляем . В данном случае это означает, что вместо того, чтобы пытаться выполнить шаг вычитания , вы должны изменить все знаки второго многочлена на и затем добавить: . Тогда вы получите правильный результат. Учащиеся, которые допустили ошибку на этом шаге и получили положительный результат в результате вычитания, скорее всего, получат один из неправильных вариантов ответа или .
Но при полиномиальном делении члены могут быть как положительными, так и отрицательными, и сложнее правильно выполнить вычитание с отрицательными членами. Поэтому рекомендуется выполнять такие шаги вычитания на меняем все знаки второго многочлена и затем добавляем . В данном случае это означает, что вместо того, чтобы пытаться выполнить шаг вычитания , вы должны изменить все знаки второго многочлена на и затем добавить: . Тогда вы получите правильный результат. Учащиеся, которые допустили ошибку на этом шаге и получили положительный результат в результате вычитания, скорее всего, получат один из неправильных вариантов ответа или .Следующим шагом будет уменьшение последнего члена числителя -2, чтобы получилось . Теперь вы видите, что делитель входит в этот многочлен -1 раз, поэтому следующий член частного равен -1. Все частное теперь .
Теперь вам нужно умножить на -1, чтобы получить значение, которое вы должны написать внизу и вычесть.
 Опять же, как рекомендовалось выше, теперь лучше всего изменить все знаки второго многочлена на и затем добавить: . Тогда вы получите правильный результат -4. Учащиеся, допустившие ошибку на этом шаге, могут получить 0 в результате вычитания и выбрать неправильный вариант ответа .
Опять же, как рекомендовалось выше, теперь лучше всего изменить все знаки второго многочлена на и затем добавить: . Тогда вы получите правильный результат -4. Учащиеся, допустившие ошибку на этом шаге, могут получить 0 в результате вычитания и выбрать неправильный вариант ответа .Теперь, когда у вас есть частное и остаток -4, вы можете видеть, что правильный вариант ответа .
Сообщить об ошибке
Что из следующего эквивалентно ?
Возможные ответы:
Правильный ответ:
Пояснение:
Чтобы правильно ответить на этот вопрос, вам необходимо знать основной метод полиномиального деления. Это работает так же, как и деление в длинную, которое вы изучали в начальной школе, но вместо чисел, состоящих из нескольких цифр, вы делите многочлены с несколькими членами.

Первый шаг процесса полиномиального деления в этом вопросе довольно прост: первый член будет потому что это результат деления первого члена числителя на первый член знаменателя (делителя) .
Затем вы умножаете на , чтобы получить , что вы должны написать внизу и вычесть. Результат вычитания .
Теперь вы должны четко понимать следующий шаг: вы можете сделать еще один шаг полиномиального деления и получить еще один член в частном. Делитель выглядит «больше», но важно то, что первые члены одинаковы, поэтому результат деления положительный 1. Теперь у вас есть целое частное. Учащиеся, которые не понимают, что они могут получить этот второй член частного, могут выбрать неправильный вариант ответа .
Затем вам нужно умножить на 1, чтобы получить , что вы должны написать ниже и вычесть. Это важный ключевой шаг: вы действительно выполняете вычитание, поэтому правильный результат равен -3.
 Учащиеся, допустившие ошибку на этом шаге, могут получить в результате положительную оценку 3 и выбрать неправильный вариант ответа .
Учащиеся, допустившие ошибку на этом шаге, могут получить в результате положительную оценку 3 и выбрать неправильный вариант ответа .Теперь, когда у вас есть частное и остаток -3, вы можете видеть, что правильный вариант ответа .
Сообщить об ошибке
Для полиномиальной функции значение равно . Какое из следующих утверждений должно быть верным?
Возможные ответы:
является коэффициентом .
Остаток при делении на равен .
является коэффициентом .
является коэффициентом .
Правильный ответ:
Остаток при делении на равен .
Объяснение:
Этот вопрос действительно проверяет ваше понимание концепции множителя многочлена. Множителем полинома называется делитель, на который полином равен 9.0093 делится на без остатка. Эта концепция работает так же, как и с обычными числами: множитель числа — это делитель, на который число делится точно без остатка.
 Например, 5 — это коэффициент 30, потому что именно так, без остатка. Но 5 не является множителем 32, потому что с остатком 2.
Например, 5 — это коэффициент 30, потому что именно так, без остатка. Но 5 не является множителем 32, потому что с остатком 2.Вот важная концепция для понимания о множителях многочленов: если, например, является множителем , то значение должно быть равно 0. На самом деле это та же самая связь, которую вы обнаруживаете, когда решаете квадратное уравнение, разлагая его на множители: если один из множителей равен , то вы знаете, что является решением уравнения. Что ж, поскольку вы всегда делаете другую часть квадратного уравнения равной 0, чтобы решить его, то на самом деле вы обнаружили вот что. Другой способ описать это состоит в том, что -1 – это пересечение по оси x графика функции .
Вот ключевой момент о том, как эта концепция связана с этим вопросом: если у вас нет информации ни о каких значениях полиномиальной функции равных 0, то у вас нет информации ни о каких факторах полиномиальной функции ! Единственная информация, которую дает нам этот вопрос, заключается в том, что .
 Поскольку у нас нет возможности определить какие-либо значения , равные 0, у нас нет способа определить, каковы какие-либо из факторов . Уже по одному этому факту мы уже знаем, что все три варианта ответа, в которых упоминается множитель , должны быть неверными!! В процессе исключения правильный вариант ответа должен быть «Остаток при делении на есть «.
Поскольку у нас нет возможности определить какие-либо значения , равные 0, у нас нет способа определить, каковы какие-либо из факторов . Уже по одному этому факту мы уже знаем, что все три варианта ответа, в которых упоминается множитель , должны быть неверными!! В процессе исключения правильный вариант ответа должен быть «Остаток при делении на есть «.Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы по математике SAT
137 Практические тесты Вопрос дня Карточки Learn by Concept
Объяснение урока: деление полинома на длинное с остатком
В этом объяснении мы узнаем, как найти частное и остаток при делении многочленов, в том числе и случай, когда дивизор неприводим.
Как и в случае с целыми числами, деление многочлена 𝑝(𝑥) (делимого) на делитель 𝑑(𝑥) дает частное 𝑞(𝑥) и остаток 𝑟(𝑥).
Напомним, что многочлен — это конечная сумма одночленов, у которой есть неотрицательные показатели.
 Следовательно,
выражения вида 2𝑥+2, 𝑥𝑦−10𝑥𝑦+𝑥 и
8 являются примерами многочленов, тогда как такие выражения, как √𝑥,
3𝑥 и 3𝑥 не являются полиномиальными выражениями. В этом объяснении мы сосредоточимся на делении полиномов одной переменной.
Следовательно,
выражения вида 2𝑥+2, 𝑥𝑦−10𝑥𝑦+𝑥 и
8 являются примерами многочленов, тогда как такие выражения, как √𝑥,
3𝑥 и 3𝑥 не являются полиномиальными выражениями. В этом объяснении мы сосредоточимся на делении полиномов одной переменной.Обычно при рассмотрении деления многочленов мы пишем 𝑝(𝑥)𝑑(𝑥), а не 𝑝(𝑥)÷𝑑(𝑥). Мы можем думать о длинном делении как нахождение полиномов 𝑞 и 𝑟 таких, что 𝑝(𝑥)𝑑(𝑥)=𝑞(𝑥)+𝑟(𝑥)𝑑(𝑥) и мы говорим, что деление дает частное 𝑞(𝑥) и остаток 𝑟(𝑥).
Мы можем записать это эквивалентно как уравнение умножения следующим образом:
Однако не все уравнения в этой форме являются уравнениями деления. Например, рассмотрим уравнение 2𝑥+7𝑥−4=(𝑥−3)×(𝑥−1)+𝑥+11𝑥−7.
Это можно записать как 2𝑥+7𝑥−4𝑥−3=(𝑥−1)+𝑥+11𝑥−7𝑥−3 но это не квалифицируется как деление на 𝑥−3, потому что, как и в случае целочисленное деление, остаток всегда должен иметь меньшую степень, чем делитель.
Правильное уравнение деления в этом случае было бы 2𝑥+7𝑥−4𝑥−3=(2𝑥+13)+35𝑥−3.

Остаток равен 35, что имеет степень 0, что меньше степени из 𝑥−3, что равно 1.
Когда мы используем алгоритм деления, чтобы получить 𝑟 степени меньше, чем 𝑑, частное 𝑞 и остаток 𝑟 равны однозначно определяется. Теперь мы обрисуем в общих чертах алгоритм деления, который мы можем использовать, чтобы найти 𝑞 и 𝑑.
Длинное деление многочленов во многом похоже на длинное деление целых чисел: на каждом шаге мы сравнить старший коэффициент делителя с текущим остатком, который начинается с сам дивиденд. Целью каждого шага является удаление этого ведущего члена. Давайте посмотрим на примере, как это сделать.
Мы будем использовать пример деления 2𝑥+7𝑥−4 на 𝑥−3 для демонстрации метода.
На первом шаге член высшей степени дивиденда делим на член высшая степень делителя. Следовательно, делим 2𝑥 на 𝑥 чтобы получить 2𝑥.
Результат этого деления пишем над чертой.
Теперь мы умножаем этот член на делитель и записываем результат под делимым, так что что условия равной степени совпадают.

Вычтем полученное выражение из делимого.
Это должно привести к исключению термина с наивысшей степенью. Затем мы можем сбить условия из дивиденда, чтобы получить выражение для нашего первого остатка. Если это из равной или большей степени, чем делитель, как здесь, мы повторяем этот процесс снова.
Следовательно, мы делим члены высшей степени. То есть делим 13𝑥 на 𝑥 чтобы получить 13.
Мы пишем это над строкой рядом с нашим последним термином.
Теперь умножим этот член на делитель и запишем результат под делимым так, чтобы условия равной степени совпадают.
Теперь мы вычтем полученное выражение из первого остатка.
Это должно привести к исключению термина с наивысшей степенью. В этот момент мы остаются с членом меньшей степени, чем делитель, поэтому мы останавливаемся. частное 𝑞(𝑥) — это выражение над чертой, а остаток это выражение внизу.
Обычно мы записываем это кратко следующим образом: члены многочленов меняются.
 Однако техника та же.
Однако техника та же.Пример 1: Полиномиальное длинное деление с делителем первой степени
Используйте полиномиальное деление для упрощения 2𝑥+5𝑥+7𝑥+4𝑥+1.
Ответ
В этом примере мы ожидаем нулевой остаток:
Таким образом, упрощение 2𝑥+5𝑥+7𝑥+4𝑥+1=2𝑥+3𝑥+4.
Следствием нулевого остатка является то, что мы получаем факторизацию. В особом случае линейного делителя получаем следующее.
Факторная теорема
Многочлен 𝑝(𝑥) делится на (𝑥−𝑎) (с нулевым остатком) тогда и только тогда, когда 𝑝(𝑎)=0.
Другими словами, когда 𝑎 является нулем многочлена.
Итак 𝑝(𝑥)=(𝑥−𝑎)𝑞(𝑥) именно тогда, когда 𝑝(𝑎)=0.
Пример 2. Теорема о факторах и деление в длинное число
С помощью факторизации найти все решения уравнения учитывая, что (𝑥+4) является множителем 𝑥−𝑥−14𝑥+24.
Ответ
Поскольку (𝑥+4) является множителем этого многочлена, мы можем использовать множитель теорема, чтобы заключить, что −4 является нулем многочлена.
 Мы можем использовать
полиномиальное деление, чтобы найти другие множители.
Мы можем использовать
полиномиальное деление, чтобы найти другие множители.Итак 𝑥−𝑥−14𝑥+24=(𝑥+4)𝑥−5𝑥+6 и мы можем факторизовать этот квадрат, например, путем проверки: 𝑥−5𝑥+6=(𝑥−2)(𝑥−3) и поэтому 𝑥−𝑥−14𝑥+24=(𝑥+4)(𝑥−2)(𝑥−3).
Множитель (𝑥−2) соответствует нулю 𝑥=2, множитель (𝑥−3) дает ноль 𝑥=3. Итак, нули 𝑥=2, 𝑥=3, 𝑥=−4.
Используя тот же метод, мы можем выполнить полиномиальное деление в длину, когда делитель степени больше единицы. В следующем примере мы продемонстрируем это.
Пример 3. Полиномиальное длинное деление с делителями высших степеней
Используйте полиномиальное деление, чтобы найти частное и остаток 𝑟(𝑥) для 𝑝(𝑥)𝑑(𝑥), где 𝑝(𝑥)=𝑥+𝑥+𝑥+𝑥+𝑥+1 и 𝑑(𝑥)=𝑥+𝑥+1.
Ответ
Применяя алгоритм длинного деления, получаем следующее деление:
Следовательно, частное 𝑞(𝑥)=𝑥+𝑥−𝑥−𝑥 и остаток 𝑟(𝑥)=3𝑥+2𝑥+1.
Конечно, не всегда следует ожидать, что результирующие полиномы 𝑞(𝑥) и 𝑟(𝑥) иметь целые коэффициенты, даже когда 𝑝(𝑥) и 𝑑(𝑥) делают.
 Следующий
пример демонстрирует это.
Следующий
пример демонстрирует это.Пример 4: Полиномиальное длинное деление
Экспресс-деление 𝑝(𝑥)𝑑(𝑥)=2𝑥−𝑥+52𝑥−5𝑥+8 в виде 𝑞(𝑥)+𝑟(𝑥)𝑑(𝑥).
Ответ
Используя алгоритм деления в длину, мы получаем следующее деление в длину:
Следовательно, 2𝑥−𝑥+52𝑥−5𝑥+8=𝑥+52+𝑥−152𝑥−5𝑥+8.
Факторная теорема является частным случаем теоремы об остатках.
Теорема об остатках
Когда многочлен 𝑝(𝑥) делится на (𝑥−𝑎), остаток есть константа 𝑝(𝑎).
Пример 5: Теорема об остатке
Найдите остаток от деления 4𝑥+4𝑥+3 на 2𝑥−3.
Ответ
Хотя это можно сделать делением в большую сторону, мы также можем использовать теорему об остатках. Мы должны быть осторожны с приложением, потому что (2𝑥−3) не (𝑥−𝑎) для любого 𝑎. Однако предположим, что 𝑝(𝑥)=4𝑥+4𝑥+3=(2𝑥−3)𝑞(𝑥)+𝑟 с остатком константа 𝑟 и частное 𝑞(𝑥). С 2𝑥−3=2𝑥−32, мы можем переписать приведенное выше как 4𝑥+4𝑥+3=2𝑥−32𝑞(𝑥)+𝑟.

Это говорит о том, что остаток при делении 4𝑥+4𝑥+3 на 2𝑥−3 совпадает с остатком от деления на 𝑥−32. Поскольку это имеет правильную форму, применяется теорема об остатках и 𝑟=𝑃32=432+432+3=44(9)+42(3)+3=9+6+3=18.
Пример 6. Использование полиномиального длинного деления
Найдите значение 𝑘, которое делает выражение 30𝑥+57𝑥−48𝑥−20𝑥+𝑘 делится на 5𝑥−8.
Ответ
Мы можем сделать это полиномиальным делением. Мы должны ожидать остаток степени 1 или меньше, что будет включать константу 𝑘 и установку ее на ноль определит необходимое 𝑘.
Первый шаг — убедиться, что делимое записано правильно по убыванию силы 𝑥: 𝑝(𝑥)=30𝑥−20𝑥−48𝑥+57𝑥+𝑘.
Используя алгоритм:
находим, что остаток имеет степень 0 и равен 𝑘+40.
Поскольку 5𝑥−8 является множителем только в том случае, если деление дает нулевой остаток, условие на 𝑘 состоит в том, что 𝑘+40=0; другими словами 𝑘=−40.

- Длинное деление полинома можно использовать для деления полинома на любой полином равной или меньшей степени.
Урок 16. Численные методы
Элементарные средства решения СЛУ
Функции для решения систем линейных уравнений с ограничениями
Решение СЛУ с разреженными матрицами
Точное решение, метод наименьших квадратов и сопряженных градиентов
Двунаправленный метод сопряженных градиентов
Устойчивый двунаправленный метод
Метод сопряженных градиентов
Квадратичный метод сопряженных градиентов
Метод минимизации обобщенной невязки
Квазиминимизация невязки — функция qmr
Вычисление нулей функции одной переменной
Минимизация функции одной переменной
Минимизация функции нескольких переменных
Аппроксимация производных
Аппроксимация Лапласиана
Аппроксимация производных конечными разностями
Вычисление градиента функции
Численное интегрирование
Метод трапеций
Численное интегрирование методом квадратур
Работа с полиномами
Умножение и деление полиномов
Вычисление полиномов
Вычисление производной полинома
Решение полиномиальных матричных уравнений
Разложение на простые дроби
Решение обыкновенных дифференциальных уравнений
Решатели ОДУ
Использование решателей систем ОДУ
Описание системы ОДУ
Дескрипторная поддержка параметров решателя
Пакет Partial Differential Equations Toolbox
Что нового мы узнали?
Ниже приведены
функции, осуществляющие умножение и деление полиномов, или, что то же самое,
свертку двух входных векторов, в которых находятся коэффициенты полиномов, и
операцию, обратную свертке.
w = conv(u.v) — возвращает свертку векторов и и v. Алгебраически свертка — то же самое, что и произведение полиномов, чьи коэффициенты — элементы векторов и и v. Если длина вектора и равна т, а длина вектора v — п, то вектор w имеет длину т+п-1, а его k-й элемент вычисляется по следующей формуле
Пример:
» f=[2.3.5.6];d=[7,8,3]:r=conv(f,d)
r =
14 37 65 91 63 18
[q,r]
= deconv(v.u) —возвращает результат деления полинома v на полином и. Вектор
q представляет собой частное от деления, а г — остаток от деления, так что
выполняется соотношение v=conv(u,q)+r.
Пример:
» t=[14,37.65.91,63,18]:r=[7.8.3];[w.e]=deconv(t.r)
w =
2.0000 3.0000 5.0000 6.0000
е =
1.0е-013
0 0 0.1421 -0.1421-0.2132-0.1066
Нравится
Твитнуть
Теги MatLab САПР
Сюжеты MatLab
Знакомство с матричной лабораторией MATLAB MatLab
7970 0
Визуализация и графические средства MatLab
9461 0
Техническая документация по системе MatLab
6024 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте Использование материалов Контакты
Новости Статьи База знаний
Радиомастер
© 2005–2022 radiomaster.ru
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster. ru обязательна. 0.2067 s
ru обязательна. 0.2067 s
Деление многочленов — определение, синтетическое деление, длинное деление, примеры
Деление многочленов — это арифметическая операция, при которой мы делим многочлен на другой многочлен, как правило, с меньшей степенью по сравнению с делимым. Деление двух многочленов может привести к полиному, а может и не получиться. Давайте узнаем о делении многочленов в этой статье подробно.
| 1. | Что такое деление многочленов? |
| 2. | Деление многочленов на одночлены |
| 3. | Деление многочленов на двучлены |
| 4. | Деление полиномов с помощью синтетического деления |
| 5. | Часто задаваемые вопросы о полиномах деления |
Что такое деление многочленов?
Полиномы — это алгебраические выражения, состоящие из переменных и коэффициентов. Записывается в следующем формате: 5х 2 + 6x — 17. Этот многочлен имеет три члена, которые расположены в соответствии с их степенями. Сначала ставится термин с высшей степенью, затем с низшей. Разделение многочленов — это алгоритм решения рационального числа, представляющего собой многочлен, разделенный на одночлен или другой многочлен. Делитель и делимое располагаются точно так же, как и при обычном делении. Например, если нам нужно разделить 5х 2 + 7х + 25 на 6х — 25, то запишем это так: 92+7 x+25)}{(6 x -25)}\]
Записывается в следующем формате: 5х 2 + 6x — 17. Этот многочлен имеет три члена, которые расположены в соответствии с их степенями. Сначала ставится термин с высшей степенью, затем с низшей. Разделение многочленов — это алгоритм решения рационального числа, представляющего собой многочлен, разделенный на одночлен или другой многочлен. Делитель и делимое располагаются точно так же, как и при обычном делении. Например, если нам нужно разделить 5х 2 + 7х + 25 на 6х — 25, то запишем это так: 92+7 x+25)}{(6 x -25)}\]
Многочлен, написанный над чертой, является числителем ( 5x 2 + 7x + 25), а многочлен, написанный под чертой, равен знаменатель (6x — 25). Это можно понять из следующего рисунка, который показывает, что числитель становится делимым, а знаменатель становится делителем.
Деление многочленов на одночлены
При делении многочленов на одночлены деление может производиться двумя способами. Один из них заключается в простом разделении знаков оператора «+» и «-». То есть мы отрываем многочлен от знака оператора и решаем каждую часть отдельно. Другой метод заключается в простой факторизации и дальнейшем упрощении. Давайте посмотрим на оба метода подробно.
То есть мы отрываем многочлен от знака оператора и решаем каждую часть отдельно. Другой метод заключается в простой факторизации и дальнейшем упрощении. Давайте посмотрим на оба метода подробно.
Метод разделения членов
Разделить члены многочлена, разделенные оператором ( ‘+’ или ‘-‘ ), между ними и упростить каждый член. Например, (4x 2 — 6x) ÷ (2x) можно решить, как показано здесь. Сначала мы берем общие термины из числителей и знаменателей обоих терминов, мы получаем [(4x 2 ) / (2x)] — [(6x) / (2x)]. Вычеркивая общий член 2x из числителя и знаменателя, получаем 2x — 3.
Метод факторизации
Когда вы делите многочлены, вам может потребоваться разложить многочлен на множители, чтобы найти общий множитель между числителем и знаменателем. Например: Разделите следующий многочлен: (2x 2 + 4x) ÷ 2x. И числитель, и знаменатель имеют общий делитель 2х. Таким образом, выражение можно записать как 2x(x + 2)/2x. Сократив общий член 2x, мы получим в качестве ответа x+2.
Деление многочленов на двучлены
Для деления многочленов на двучлены или многочлены любого другого типа наиболее распространенным и общим методом является метод деления в длину. Если между числителем и знаменателем нет общих множителей или если вы не можете найти множители, вы можете использовать процесс длинного деления, чтобы упростить выражение.
Деление многочленов с помощью длинного деления
Рассмотрим алгоритм деления многочленов на двучлены на примере: Разделить: (4x 2 — 5x — 21) ÷ (x — 3). Здесь (4x 2 — 5x — 21) — делимое, а (x — 3) — делитель, являющийся двучленом. Обратите внимание на разделение, показанное ниже, а затем на шаги.
Шаг 1. Разделите первый член делимого (4x 2 ) на первый член делителя (x) и подставьте его в качестве первого члена в частном (4x).
Шаг 2. Умножьте делитель на этот ответ, поместите произведение (4x 2 — 12x) под делимым.
Шаг 3. Вычтите, чтобы создать новый многочлен (7x — 21).
Шаг 4. Повторите тот же процесс с новым многочленом, полученным после вычитания.
Итак, когда мы делим многочлен (4x 2 — 5x — 21) на двучлен (x — 3), частное равно 4x+7, а остаток равен 0.
Деление многочленов с помощью синтетического деления
Синтетическое деление — это метод деления многочлена на линейный двучлен с учетом только значений коэффициентов. В этом методе мы сначала записываем полиномы в стандартной форме от члена высшей степени к члену низшей степени. При записи в убывающей степени используйте 0 в качестве коэффициентов пропущенных терминов. Например, x 3 +3 нужно записать как x 3 + 0x 2 + 0x + 3. Для деления многочленов методом синтетического деления выполните следующие действия:
Разделим x 2 + 3 на x — 4.
Шаг 1: Запишите делитель в виде x — k и запишите k в левой части деления. Здесь делитель равен x-4, поэтому значение k равно 4.
Здесь делитель равен x-4, поэтому значение k равно 4.
Шаг 2: Установите деление, записав коэффициенты делимого справа и k слева. [Примечание: используйте 0 для отсутствующих членов дивиденда]
Шаг 3: Теперь уменьшите коэффициент члена наивысшей степени дивиденда, как он есть. Здесь старший коэффициент равен 1 (коэффициент x 2 ).
Шаг 4: Умножьте k на этот старший коэффициент и запишите произведение под вторым коэффициентом слева от делимого. Итак, мы получаем, 4×1=4, что мы запишем ниже 0.
Шаг 5: Складываем числа, написанные во втором столбце. Здесь, сложив, мы получаем 0+4=4.
Шаг 6: Повторите тот же процесс умножения k на число, полученное в шаге 5, и запишите произведение в следующем столбце справа.
Шаг 7: Наконец, запишем окончательный ответ, который будет на одну степень меньше делимого. Итак, здесь в нашем делимом член высшей степени равен x 2 , следовательно, в частном член высшей степени будет x. Следовательно, полученный ответ равен х+4+(19/х-4).
Следовательно, полученный ответ равен х+4+(19/х-4).
Темы, связанные с делением многочленов
Прочтите эти статьи, чтобы узнать больше о концепции деления многочленов и связанных с ней темах.
Примеры деления многочленов
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему математика стоит за нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
Практические вопросы по делению многочленов
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о полиномах деления
Что такое деление многочленов?
Деление многочленов — это одна из арифметических операций, выполняемая над двумя заданными многочленами. При этом делимое обычно имеет более высокую степень, а делитель является полиномом более низкой степени.
Почему деление многочленов важно?
Деление многочленов важно, потому что оно предоставляет алгоритм для решения рационального числа, представляющего многочлен, разделенный на одночлен или другой многочлен.
Как проще всего делить многочлены?
Самый простой способ разделить многочлены — это использовать метод деления в длину. Однако в случае деления многочленов на моном его можно решить непосредственно путем расщепления членов или факторизации.
Однако в случае деления многочленов на моном его можно решить непосредственно путем расщепления членов или факторизации.
Какие существуют два метода деления многочленов?
Ниже приведены два метода деления многочленов:
Для чего в реальной жизни используется полиномиальное деление?
Мы используем полиномиальное деление для различных аспектов нашей повседневной жизни. Нам это нужно для кодирования, проектирования, проектирования, архитектуры и многих других областей реальной жизни.
Какой метод деления многочленов на моном лучше всего?
В случае деления многочленов на моном его можно решить напрямую, расщепив члены или разложив на множители. Мы можем разделить каждый член делимого на заданный моном и найти результат.
Многочлен длинного деления — определение, метод, деление длинного члена с мономами, двучлены
Деление многочлена длинной — это процесс деления одного полинома на другой. Деление может быть выполнено между различными типами многочленов, т. е. между двумя мономами, многочленом и мономом или между двумя многочленами. Многочлен представляет собой n алгебраических выражений с переменными, членами и коэффициентами со степенью выражений. Давайте изучим деление многочленов, узнав о методах деления с использованием деления в длину, деления в длину с многочленами, деления в длину с отсутствующими членами, алгоритма и решив несколько примеров, чтобы лучше понять процесс.
Деление может быть выполнено между различными типами многочленов, т. е. между двумя мономами, многочленом и мономом или между двумя многочленами. Многочлен представляет собой n алгебраических выражений с переменными, членами и коэффициентами со степенью выражений. Давайте изучим деление многочленов, узнав о методах деления с использованием деления в длину, деления в длину с многочленами, деления в длину с отсутствующими членами, алгоритма и решив несколько примеров, чтобы лучше понять процесс.
| 1. | Что такое длинное деление многочленов? |
| 2. | шагов для длинного деления многочленов |
| 3. | Длинное деление многочлена на отсутствующие члены |
| 4. | Длинное деление многочленов на мономы |
| 5. | Длинное деление многочленов на другие мономы |
| 6. | Длинное деление многочленов на биномы |
7. | Длинное деление многочленов на другие многочлены |
| 8. | Алгоритм длинного деления полиномов |
| 9. | Часто задаваемые вопросы о длинном делении многочленов |
Что такое длинное деление многочленов?
Многочлен с длинным делением — это алгоритм деления многочлена на другой многочлен той же или меньшей степени. Длинное деление многочленов также состоит из делителя, частного, делимого и остатка, как и в методе длинного деления чисел. Обратите внимание на числитель и знаменатель в длинном делении многочленов, как показано на рисунке.
Длинное деление многочленов также состоит из делителя, частного, делимого и остатка.
В алгебре алгебраические выражения можно разделить тремя способами:
шагов для длинного деления многочленов
Следующие шаги деления многочленов в длину:
Длинное деление многочлена на отсутствующие члены
При делении многочленов в длину в выражении может быть пропущен член, например, 6x 4 + 3x — 9x 2 + 6, x 3 отсутствует. В этом случае мы либо оставляем пробел при делении, либо записываем коэффициент равным нулю. Давайте разберемся, как выполнить длинное деление многочленов на том же примере. Нам нужно разделить многочлен a(x) = 6x 4 + 3x — 9x 2 + 6 квадратичным полиномом b(x) = x 2 — 2
В этом случае мы либо оставляем пробел при делении, либо записываем коэффициент равным нулю. Давайте разберемся, как выполнить длинное деление многочленов на том же примере. Нам нужно разделить многочлен a(x) = 6x 4 + 3x — 9x 2 + 6 квадратичным полиномом b(x) = x 2 — 2
Расположите полином в порядке убывания степени переменной.
a(x) = 6x 4 — 9x 2 + 3x + 6
b(x) = x 2 — 2
Разделите a(x) на b(x) так же, как делим числа.
Добавьте отсутствующие индексы с нулем (0) в качестве коэффициента.
Разделить 6x 4 на x 2 , чтобы получить первый член частного. Получаем 6х 2 .
Умножьте делитель на 6x 2 .
Разделите 3x 2 на x 2 , чтобы получить следующий член частного.
Поскольку степень следующего делимого меньше делителя, мы получаем искомый остаток. Пожалуйста, помните, что поскольку остаток, который мы получили, является ненулевым членом, мы можем сказать, что x 2 — 2 не является множителем 6x 9.0043 4 — 9x 2 + 3x + 6. Следовательно, частное равно 6x 2 + 3, а остаток равен 3x.
Пожалуйста, помните, что поскольку остаток, который мы получили, является ненулевым членом, мы можем сказать, что x 2 — 2 не является множителем 6x 9.0043 4 — 9x 2 + 3x + 6. Следовательно, частное равно 6x 2 + 3, а остаток равен 3x.
Длинное деление многочленов на мономы
При делении многочленов на одночлены запишите общий множитель между числителем и знаменателем многочлена и разделите каждый член отдельно. Получив результат, сложите все термины вместе, чтобы сформировать выражение. Например: разделите следующий многочлен: (2x 2 + 4x + 8xy) ÷ 2x. И числитель, и знаменатель имеют общий делитель 2х. Таким образом, выражение можно записать как 2x(x + 2 + 4y) / 2x. Сократив общий член 2x, мы получим в качестве ответа x + 4y + 2.
Длинное деление многочленов на другой одночлен
Длинное деление многочленов на другой одночлен выполняется аналогично тому, как это делается для многочленов одночленами. Перечисляются множители одночлена как числителя, так и знаменателя, и происходит длинное деление. Например, разделить 62x 3 в 2 раза. Множители 62x 3 = 2 × 31 × x × x × x и 2x = 2 × x. Общими коэффициентами для обоих являются 2x. Следовательно, 62x 3 /2x = 31x 2 .
Перечисляются множители одночлена как числителя, так и знаменателя, и происходит длинное деление. Например, разделить 62x 3 в 2 раза. Множители 62x 3 = 2 × 31 × x × x × x и 2x = 2 × x. Общими коэффициентами для обоих являются 2x. Следовательно, 62x 3 /2x = 31x 2 .
Длинное деление многочленов на биномы
Длинное деление многочленов на двучлены производится, когда нет общих множителей между числителем и знаменателем или если вы не можете найти множители. Разберем алгоритм деления многочленов на двучлены на примере: Разделить: (6x 2 — 4х — 24) ÷ (х — 3). Здесь (6x 2 — 4x — 24) — делимое, а (x — 3) — делитель, являющийся двучленом. Обратите внимание на разделение, показанное ниже, а затем на шаги.
Итак, когда мы делим многочлен (6x 2 — 4x — 24) на двучлен (x — 3), частное равно 6x + 14, а остаток равен 18.
Длинное деление многочленов на другой многочлен
Длинное деление многочлена на другой многочлен производится, когда выражение записано в стандартной форме, т. е. члены делимого и делителя расположены в порядке убывания их степеней. Метод деления в длинную сторону для многочленов считается обобщенной версией простого метода деления в длинную с числами. Давайте посмотрим на пример, чтобы понять это лучше. Процесс деления очень похож на остальные методы. Разделите многочлен 6x 3 + 12х 2 + 2х + 25 на х 2 + 4х + 3. Здесь 6х 3 + 12х 2 + 2х + 25 — делимое, а х 3 + 4х + 2 . является делителем, который также является полиномом.
Здесь 6х 3 + 12х 2 + 2х + 25 — делимое, а х 3 + 4х + 2 . является делителем, который также является полиномом.
Итак, когда мы делим многочлен 6x 3 + 12x 2 + 2x + 25 на двучлен x 2 + 4x + 3, частное равно 6x — 12, а остаток равен 32x + 61,
Алгоритм длинного деления полиномов
Алгоритм деления многочленов гласит, что если p(x) и g(x) — два многочлена, где g(x) ≠ 0, то мы можем записать деление многочленов как: p(x) = q(x) × г(х) + г(х).
Где
Если мы сравним это с обычным делением чисел, мы можем легко понять это как: Делимое = (Делитель X Частное) + Остаток. Возьмем предыдущий пример:
p(x) = 6x 3 + 12x 2 + 2x + 25
g(x) = x 2 + 4x + 3
q(x) = 6 — 12
r(x) = 32x + 61
Применить алгоритм деления, q(x) × g(x) + r(x)
(6x — 12) × (x 2 + 4x + 3 ) + (32x + 61)
6x 3 + 24x 2 + 18x — 12x 2 — 48x — 36 + 32x + 61
6x 3 + 12x 2 — 2x + 25
= P (x).
Следовательно, алгоритм деления проверен.
Связанные темы
Ознакомьтесь с этими статьями, чтобы узнать больше о концепции деления многочленов и связанных с ней темах.
Часто задаваемые вопросы о длинном делении многочленов
Что означает длинное деление многочленов?
Длинное деление многочленов — это метод, применяемый в алгебре для деления многочлена на другой многочлен более низкой или той же степени.
Как делить многочлены на длинное деление?
Следующие шаги деления многочленов в длину:
Какое значение имеет длинное деление многочленов?
Длинное деление многочленов — это способ проверить, имеет ли один многочлен другой в качестве множителя. Это также помогает разбить дивиденд на простую последовательность с помощью простых шагов.
Каковы преимущества длинного деления многочленов?
Преимущество длинного деления многочленов заключается в том, что это простой и широко используемый метод деления двух многочленов, занимающий меньше места и требующий меньших вычислений.
Каковы недостатки длинного деления многочленов?
Единственный недостаток длинного деления многочленов состоит в том, что в случае нелинейного делителя вычисления усложняются.
Каковы основные области применения синтетического деления многочленов?
Основное применение синтетического деления многочленов заключается в том, что оно применяется, когда делитель линейный и коэффициент при переменной в нем равен единице.
Длинное полиномиальное деление | Пурпурная математика
SimplificationExamples
Purplemath
Если вы делите многочлен на что-то более сложное, чем простой моном (то есть на что-то более сложное, чем одночленный многочлен), вам нужно использовать другой метод. для упрощения. Этот метод называется «долгое полиномиальное деление», и он работает точно так же, как длинное (числовое) деление, которым вы занимались в начальной школе, за исключением того, что теперь вы делите переменные.
Вспомните время, когда вы выполняли деление в длинное со старыми простыми числами. Вам будет дано одно число (называемое делителем), которое вы должны разделить на другое число (называемое делимым). Вы установили символ длинного деления, вставили два числа в нужные места, а затем начали строить догадки о том, что должно стоять над символом.
Вам будет дано одно число (называемое делителем), которое вы должны разделить на другое число (называемое делимым). Вы установили символ длинного деления, вставили два числа в нужные места, а затем начали строить догадки о том, что должно стоять над символом.
Содержание продолжается ниже
MathHelp.com
И вы не сразу угадали весь ответ; вместо этого вы начали работать с «передней» частью (то есть с большей разрядной частью) числа, которое вы делили. Например, если бы вы делили 1137 на 82, вы бы посмотрели на «8» и «10» и предположили, что, вероятно, «1» должна стоять сверху над «11», потому что 8 вписывается один раз в 11.
Длинное деление многочленов работает примерно так же:
Во-первых, я настрою деление, поместив делимое (вещь, на которую делится) внутрь, а делитель (вещь, которая делит) снаружи и слева:
На данный момент я проигнорирую все мимо ведущих терминов. Как и в случае с числовым делением, я буду смотреть только на начальные x делителя и начальные x 2 делимого.
Если я разделю интерлиньяж x 2 внутри на интерлиньяж x впереди, что бы я получил? Я бы взял x. Итак, я помещу x поверх символа деления, прямо над x 2 внутри:
Теперь я возьму это x сверху и умножу его на делитель. , x + 1. Во-первых, я умножу x (сверху) на x (сбоку) и перенесу полученное x 2 снизу, поместив его прямо под х 2 из делимого:
Затем я умножу x (сверху) на 1 (сбоку) и перенесу 1 x снизу, поместив его прямо под −9 x в делимом:
Затем я нарисую горизонтальную полосу «равно» под тем, что я только что поместил под делимым, чтобы я мог выполнить вычитание.
Чтобы вычесть многочлены, я сначала меняю все знаки во второй строке…
…а потом прибавляю. Первый срок ( x 2 ) сократится (по замыслу), а −9 x — 1 x станет −10 x :
. термин «вычесть десять») из дивиденда:
термин «вычесть десять») из дивиденда:
В этот момент я начинаю игнорировать дивиденд и вместо этого работаю над итоговой строкой моего длинного деления.
Я смотрю на x из делителя и нового ведущего члена, -10 x , в нижней строке деления. Если я разделю −10 x на x , я бы получил -10, поэтому я помещу это сверху, прямо над -9 x :
Теперь я умножу -10 (сверху) на начальные x (на «стороне») и перенесите -10 x вниз, прямо под -10 x предыдущей строки :
… и я умножу -10 (сверху) на 1 (сбоку) и перенесите -10 вниз, прямо под -10 предыдущей строки:
Я нарисую еще одну горизонтальную полосу «равно» и меняю знаки на все слагаемые в нижнем ряду:
Потом прибавляю:
По замыслу, 10 х отменили. По воле случая, 10-е тоже отменили. Тогда мой ответ сверху символа деления будет таким:
x − 10
. «вышло ровно». Когда вы выполняете обычное деление чисел и деление «выходит четным», это означает, что число, на которое вы делите, является множителем числа, которое вы делите.
Когда вы выполняете обычное деление чисел и деление «выходит четным», это означает, что число, на которое вы делите, является множителем числа, которое вы делите.
Например, если вы разделите 50 на 10, ответом будет аккуратная «5» с нулевым остатком, потому что 10 — это коэффициент 50.
В случае вышеупомянутого деления полинома нулевой остаток говорит Нам следует, что x + 1 является коэффициентом x 2 – 9 x – 10, что вы можете подтвердить, разложив исходное квадратичное делимое на множители: Каждый раз, когда вы получаете нулевой остаток, делитель является фактором делимого.
Кстати, обратите внимание на то, как я понял, что поставить поверх символа деления в приведенном выше упражнении: я разделил старший член того, на что я делил, на старший член того, что я делил по. Независимо от того, будет ли конкретное деление иметь ненулевой остаток, этот метод всегда будет давать правильное значение для того, что вам нужно сверху. Таким образом, полиномиальное длинное деление проще, чем численное длинное деление, где вам приходилось угадывать и проверять, чтобы выяснить, что было наверху.
Таким образом, полиномиальное длинное деление проще, чем численное длинное деление, где вам приходилось угадывать и проверять, чтобы выяснить, что было наверху.
Давайте сделаем еще один пример с делением, которое получается «четным», чтобы мы могли проверить наш результат, выполнив факторизацию и отмену.
Это дробное сокращение можно выполнить одним из двух способов: я могу разложить квадратное число на множители, а затем исключить общий множитель, например:
«показать мою работу» для длинного полиномиального деления на тесте)? Как и ранее, я начну деление в длинную очередь, работая с ведущими членами делителя и делимого.
Старший член делимого равен x 2 , а старший член делителя равен x . Разделив x 2 на x , мы получим x , вот что я положил сверху, непосредственно над x 2 в делимом: на делитель x + 7, и полученное x 2 + 7 поместите под делимым:
Затем я рисую горизонтальную полосу «равно», меняю знаки, прибавляю и опускаю +14 вниз, получая 2 x + 14 под чертой «равно»:
Деление ведущего 2 x на x в начале делителя дает мне 2, так что это то, что я поместил поверх символа деления, прямо над 9 x в делимом:
Затем я умножил это 2 сверху на x + 7, и ставлю результат, 2 x + 14, снизу:
Затем меняю знаки и прибавляю, получая нулевой остаток:
Ответом на деление является частное, являющееся многочленом над символом деления:
x + 2
URL: https://www. purplemath.com/modules/polydiv2. htm
purplemath.com/modules/polydiv2. htm
Стр. 1 Стр. 3
Деление многочленов | Колледж Алгебра
Результаты обучения
Внешний вид Мемориала Линкольна в Вашингтоне, округ Колумбия, представляет собой большое прямоугольное тело длиной 61,5 м (м), шириной 40 м и высотой 30 м. 93} \справа)[/латекс]. Предположим, мы знаем объем, длину и ширину. Мы могли бы разделить, чтобы найти высоту.
[латекс]\begin{array}{l}h=\frac{V}{l\cdot w}\hfill \\ \text{}h=\frac{73,800}{61.5\cdot 40}\hfill \ \ \text{}h=30\hfill \end{array}[/latex]
Как мы можем подтвердить из приведенных выше размеров, высота составляет 30 м. Мы можем использовать аналогичные методы, чтобы найти любое из недостающих измерений. Мы также можем использовать тот же метод, если какие-либо или все измерения содержат переменные выражения. {2}+54х[/латекс] . Длина тела равна 3 х ; ширина определяется как [латекс]х — 2[/латекс]. Чтобы найти высоту тела, мы можем использовать полиномиальное деление, которому посвящен этот раздел.
{2}+54х[/латекс] . Длина тела равна 3 х ; ширина определяется как [латекс]х — 2[/латекс]. Чтобы найти высоту тела, мы можем использовать полиномиальное деление, которому посвящен этот раздел.
Мемориал Линкольна, Вашингтон, округ Колумбия (кредит: Рон Когсуэлл, Flickr)
Полиномиальное длинное деление
Мы знакомы с алгоритмом длинного деления для обычной арифметики. Начнем с деления на цифры делимого, имеющие наибольшую разрядную стоимость. Мы делим, умножаем, вычитаем, включаем цифру в следующую разрядную позицию и повторяем. Например, давайте разделим 178 на 3 в длинное деление.
Решение можно рассматривать как сумму частей. Это должно выглядеть знакомо, так как это тот же метод, который используется для проверки деления в элементарной арифметике.
[латекс]\begin{массив}{l}\left(\text{делитель}\cdot \text{частное}\right)\text{ + остаток}\text{ = делимое}\hfill \\ \left( 3\cdot 59\right)+1 = 177+1 = 178\hfill \end{array}[/latex]
Мы называем это алгоритмом деления и обсудим его более формально после рассмотрения примера. 9{2}-7x+18\right)-31[/latex]
9{2}-7x+18\right)-31[/latex]
Мы можем идентифицировать делимое , делитель , частное и остаток .
Запись результата таким образом иллюстрирует алгоритм деления.
Общее примечание: Алгоритм деления
Алгоритм деления утверждает, что при заданном полиномиальном делимом [латекс]f\left(x\right)[/latex] и ненулевом полиномиальном делителе [латекс]d\left (x\right)[/latex], где степень [латекса]d\left(x\right)[/latex] меньше или равна степени [латекса]f\left(x\right)[/ латекс], существуют уникальные многочлены [латекс]q\left(x\right)[/latex] и [latex]r\left(x\right)[/latex] такие, что
[латекс]f\влево(х\вправо)=d\влево(х\вправо)q\влево(х\вправо)+r\влево(х\вправо)[/латекс]
[латекс]q\ left(x\right)[/latex] – частное, а [latex]r\left(x\right)[/latex] – остаток. Остаток либо равен нулю, либо имеет степень строго меньше, чем [latex]d\left(x\right)[/latex].
Если [латекс]r\влево(х\вправо)=0[/латекс], то [латекс]d\влево(х\вправо)[/латекс] равномерно делится на [латекс]f\влево(х\вправо) )[/латекс]. Это означает, что оба [латекс]d\left(x\right)[/latex] и [латекс]q\left(x\right)[/latex] являются множителями [латекс]f\left(x\right)[ /латекс].

 2-x+1$
2-x+1$

 2-5x+9$.
2-5x+9$.
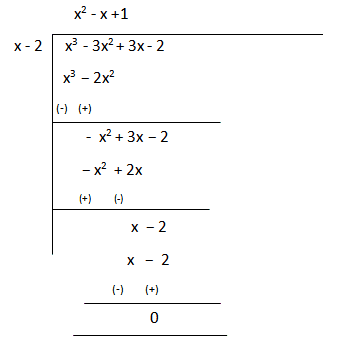

 Единственное, что мы сможем сделать — это подставить число 2 в исходное выражение вместо переменной x и найти значение выражения:
Единственное, что мы сможем сделать — это подставить число 2 в исходное выражение вместо переменной x и найти значение выражения: Отличие будет в том, что при делении многочленов не нужно определять первое неполное делимое, как в случае деления обычных чисел.
Отличие будет в том, что при делении многочленов не нужно определять первое неполное делимое, как в случае деления обычных чисел. А это то, что нам нужно. Ведь мы должны прийти к многочлену x + 5.
А это то, что нам нужно. Ведь мы должны прийти к многочлену x + 5. Подобные члены вычитаем из подобных им членов. Если из x2 вычесть x2, получится 0. Ноль не записываем. Далее если из 8x вычесть 3x, получится 5x. Записываем 5x так, чтобы этот член оказался под членами 3x и 8x
Подобные члены вычитаем из подобных им членов. Если из x2 вычесть x2, получится 0. Ноль не записываем. Далее если из 8x вычесть 3x, получится 5x. Записываем 5x так, чтобы этот член оказался под членами 3x и 8x Записываем этот многочлен под делимым 5x + 15
Записываем этот многочлен под делимым 5x + 15 Записываем этот многочлен под делимым x2 − 8x + 7 так, чтобы подобные члены располагались друг под другом:
Записываем этот многочлен под делимым x2 − 8x + 7 так, чтобы подобные члены располагались друг под другом: Давайте воспользуемся этим методом:
Давайте воспользуемся этим методом: Разделить многочлен x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3
Разделить многочлен x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 Это же делимое можно было получить, выписав отдельно многочлен x6 + 2x4 + x7 + 2x5 и вычтя из него многочлен x6 + x7
Это же делимое можно было получить, выписав отдельно многочлен x6 + 2x4 + x7 + 2x5 и вычтя из него многочлен x6 + x7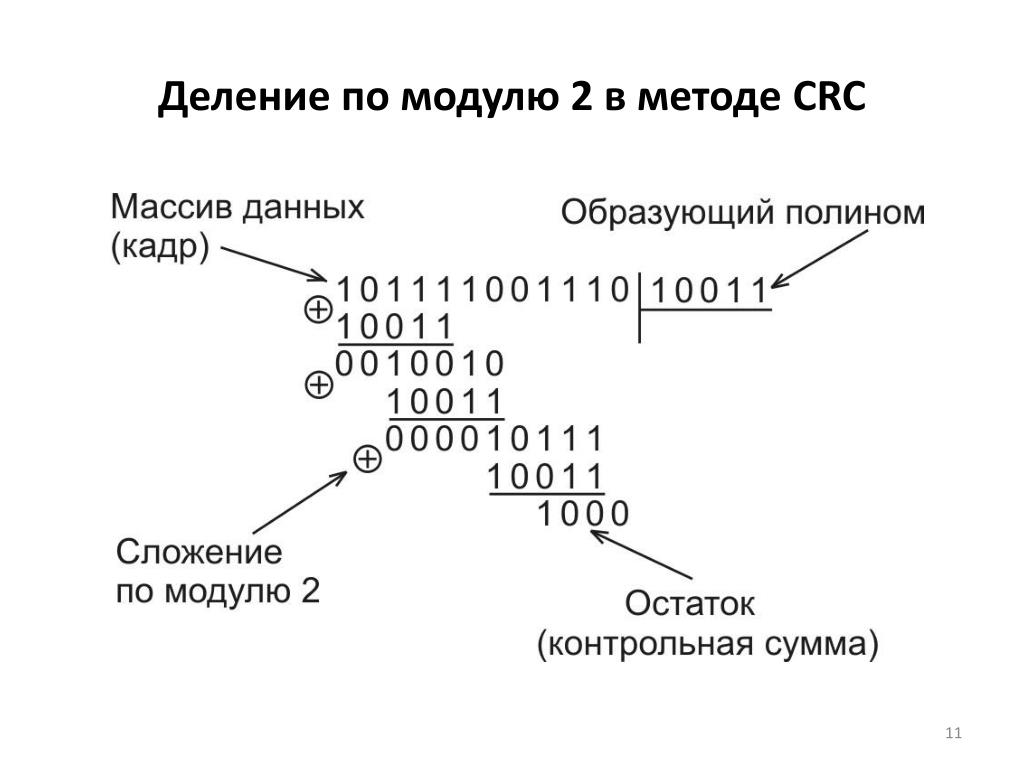
 Таким образом, частное от деления многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 равно x4 + 2x2
Таким образом, частное от деления многочлена x6 + 2x4 + x7 + 2x5 на многочлен x2 + x3 равно x4 + 2x2 Тогда члены полученного многочлена тоже будут упорядочены в порядке убывания степеней.
Тогда члены полученного многочлена тоже будут упорядочены в порядке убывания степеней. Разделить многочлен 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2
Разделить многочлен 4a4 − 14a3b − 24a2b2 − 54b4 на многочлен a2 − 3ab − 9b2 Записываем −2ab в частном:
Записываем −2ab в частном: Разделим 6a2b2 − 54b4 − 18ab3 на делитель a2 − 3ab − 9b2. Делим первый член делимого на первый член делителя, получим 6b2. Записываем 6b2 в частном:
Разделим 6a2b2 − 54b4 − 18ab3 на делитель a2 − 3ab − 9b2. Делим первый член делимого на первый член делителя, получим 6b2. Записываем 6b2 в частном:
 Разделим первый член делимого на первый член делителя, получим 2x2. Записываем 2x2 в частном:
Разделим первый член делимого на первый член делителя, получим 2x2. Записываем 2x2 в частном: Сразу вычтем этот полученный результат из делимого 10x + 4
Сразу вычтем этот полученный результат из делимого 10x + 4

 Выполните деление:
Выполните деление: 2=(a-b)(a+b)\).
2=(a-b)(a+b)\).

 е. равенством, справедливым при всех значениях переменной x .
е. равенством, справедливым при всех значениях переменной x . Получаем первый член частного 2x2 .
Получаем первый член частного 2x2 . Получаем второй член частного x .
Получаем второй член частного x . Получаем третий член частного 4.
Получаем третий член частного 4.