Умножение и деление положительных отрицательных чисел правило. Умножение и деление чисел с разными знаками
Главная > ВПР > Умножение и деление положительных отрицательных чисел правило. Умножение и деление чисел с разными знаками
На этом уроке мы повторим правила сложения положительных и отрицательных чисел. Также научимся умножать числа с разными знаками и узнаем правила знаков для умножения. Рассмотрим примеры умножения положительных и отрицательных чисел.
Свойство умножения на ноль остается верным и в случае отрицательных чисел. Ноль умножить на любое число — будет ноль.
Список литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. — М.: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. — Гимназия. 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. — М.: Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5-6 класс.
 — М.: ЗШ МИФИ, 2011.
— М.: ЗШ МИФИ, 2011. - Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5-6. Пособие для учащихся 6-х классов заочной школы МИФИ. — М.: ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5-6 классов средней школы. — М.: Просвещение, Библиотека учителя математики, 1989.
Домашнее задание
- Интернет-портал Mnemonica.ru ().
- Интернет-портал Youtube.com ().
- Интернет-портал School-assistant.ru ().
- Интернет-портал Bymath.net ().
В данной статье дадим определение деления отрицательного числа на отрицательное, сформулируем и обоснуем правило, приведем примеры деления отрицательных чисел и разберем ход их решения.
Деление отрицательных чисел. Правило
Напомним, в чем суть операции деления. Данное действие представляет собой нахождение неизвестного множителя по известному произведению и известному другому множителю. Число с называется частным от деления чисел a и b , если верно произведение c · b = a .
Правило деления отрицательных чисел
Частное ои деления одного отрицательного числа на другое отрицательное число равно частному от деления модулей этих чисел.
Пусть a и b — отрицательные числа. Тогда
a ÷ b = a ÷ b .
Данное правило сводит деление двух отрицательных чисел к делению положительных чисел. Оно справедливо не только для целых чисел, но также для рациональных и действительных чисел. Результат деления отрицательного числа на отрицательное есть всегда положительное число.
Приведем еще одну формулировку данного правила, подходящую для рациональных и действительных чисел. Она дается с помощью взаимно-обратных чисел и гласит: для деления отрицательного числа a на число undefined умножить на число b — 1 , обратное числу b .
a ÷ b = a · b — 1 .
Это же правило, сводящее деление к умножению, можно применять также и для деления чисел с разными знаками.
Равенство a ÷ b = a · b — 1 можно доказать, используя свойство умножения действительных чисел и определение взаимно обратных чисел.
a · b — 1 · b = a · b — 1 · b = a · 1 = a .
В силу определения операции деления, данное равенство доказывает, что есть частное от деления числа на число b.
Перейдем к рассмотрению примеров.
Начнем с простых случаяв, переходя к более сложным.
Пример 1. Как делить отрицательные числа
Разделим — 18 на — 3 .
Модули делителя и делимого соответственно равны 3 и 18 . Запишем:
18 ÷ — 3 = — 18 ÷ — 3 = 18 ÷ 3 = 6 .
Пример 2. Как делить отрицательные числа
Разделим — 5 на — 2 .
Аналогично, записываем по правилу:
5 ÷ — 2 = — 5 ÷ — 2 = 5 ÷ 2 = 5 2 = 2 1 2 .
Такой же результат получится, если использовать вторую формурировку правила с обратным числом.
5 ÷ — 2 = — 5 · — 1 2 = 5 · 1 2 = 5 2 = 2 1 2 .
Деля дробные рациональные числа удобнее всего представлять их в виде обыкновенных дробей. Однако, можно делить и конечные десятичные дроби.
Пример 3. Как делить отрицательные числа
Разделим — 0 , 004 на — 0 , 25 .
Сначала записываем модули этих чисел: 0 , 004 и 0 , 25 .
Теперь можно выбрать один из двух способов:
- Разделить десятичные дроби столбиком.
- Перейти к обыкновенным дробям и выполнить деление.
Разберем оба способа.
1. Выполняя деление десятичных дробей столбиком, перенесем запятую на две цифры вправо.
Ответ: — 0 , 004 ÷ 0 , 25 = 0 , 016
2. Теперь приведем решение с переводом десятичных дробей в обыкновенные.
0 , 004 = 4 1000 ; 0 , 25 = 25 100 0 , 004 ÷ 0 , 25 = 4 1000 ÷ 25 100 = 4 1000 · 100 25 = 4 250 = 0 , 016
Полученные результаты совпадают.
В заключение отметим, что если делимое и делитель являются иррациональными числами и задаются в виже корней, степеней, логарифмов и т.д., результат деления записывается в виде числового выражения, приблизительное значение которого вычисляется в случае необходимости.
Пример 4. Как делить отрицательные числа
Вычислим частное от деления чисел — 0 , 5 и — 5 .
0 , 5 ÷ — 5 = — 0 , 5 ÷ — 5 = 0 , 5 ÷ 5 = 1 2 · 1 5 = 1 2 5 = 5 10 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Задача 1. Точка движется по прямой слева направо со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка по прошествии 5 секунд?
Нетрудно сообразить, что точка будет находиться на 20 дм. вправо от A. Запишем решение этой задачи относительными числами. Для этого условимся в следующих знакоположениях:
1) скорость вправо будем обозначать знаком +, а влево знаком –, 2) расстояние движущейся точки от A вправо будем обозначать знаком + и влево знаком –, 3) промежуток времени после настоящего момента знаком + и до настоящего момента знаком –. В нашей задаче даны, след., такие числа: скорость = + 4 дм. в секунду, время = + 5 секунд и получилось, как сообразили арифметически, число + 20 дм., выражающее расстояние движущейся точки от A через 5 секунд. По смыслу задачи мы видим, что она относится к умножению. Поэтому решение задачи удобно записать:
(+ 4) ∙ (+ 5) = + 20.
Задача 2. Точка движется по прямой слева направо со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A. Где находилась эта точка 5 секунд назад?
Ответ ясен: точка находилась влево от A на расстоянии 20 дм.
Решение удобно, согласно условиям относительно знаков, и, имея в виду, что смысл задачи не изменился, записать так:
(+ 4) ∙ (– 5) = – 20.
Задача 3. Точка движется по прямой справа налево со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка спустя 5 секунд?
Ответ ясен: на 20 дм. слева от A. Поэтому, согласно тем же условиям относительно знаков, мы можем записать решение этой задачи так:
(– 4) ∙ (+ 5) = – 20.
Задача 4. Точка движется по прямой справа налево со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A. Где находилась движущаяся точка 5 секунд тому назад?
Ответ ясен: на расстоянии 20 дм. справа от A. Поэтому решение этой задачи следует записать так:
Поэтому решение этой задачи следует записать так:
(– 4) ∙ (– 5) = + 20.
Рассмотренные задачи указывают, как следует распространить действие умножения на относительные числа. Мы имеем в задачах 4 случая умножения чисел со всевозможными комбинациями знаков:
1) (+ 4) ∙ (+ 5) = + 20;
2) (+ 4) ∙ (– 5) = – 20;
3) (– 4) ∙ (+ 5) = – 20;
4) (– 4) ∙ (– 5) = + 20.
Во всех четырех случаях абсолютные величины данных чисел следует перемножить, у произведения приходится ставить знак + тогда, когда у множителей одинаковые знаки (1-й и 4-й случаи) и знак –, когда у множителей разные знаки (случаи 2-й и 3-й).
Отсюда же видим, что от перестановки множимого и множителя произведение не изменяется.
Упражнения.
Выполним один пример на вычисление, где входят и сложение и вычитание и умножение.
Чтобы не спутать порядка действий, обратим внимание на формулу
Здесь написана сумма произведений двух пар чисел: надо, следовательно, сперва число a умножить на число b, потом число c умножить на число d и затем полученные произведения сложить.
надо сперва число b умножить на c и затем полученное произведение вычесть из a.
Если бы требовалось произведение чисел a и b сложить с c и полученную сумму умножить на d, то следовало бы написать: (ab + c)d (сравнить с формулой ab + cd).
Если бы надо было разность чисел a и b умножить на c, то написали бы (a – b)c (сравнить с формулой a – bc).
Поэтому установим вообще, что если порядок действий не обозначен скобками, то надо сначала выполнить умножение, а потом уже сложение или вычитание.
Приступаем к вычислению нашего выражения: выполним сначала сложения, написанные внутри всех маленьких скобок, получим:
Теперь надо выполнить умножение внутри квадратных скобок и затем из вычтем полученное произведение:
Теперь выполним действия внутри витых скобок: сначала умножение и потом вычитание:
Теперь останется выполнить умножение и вычитание:
16. Произведение нескольких множителей. Пусть требуется найти
(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5).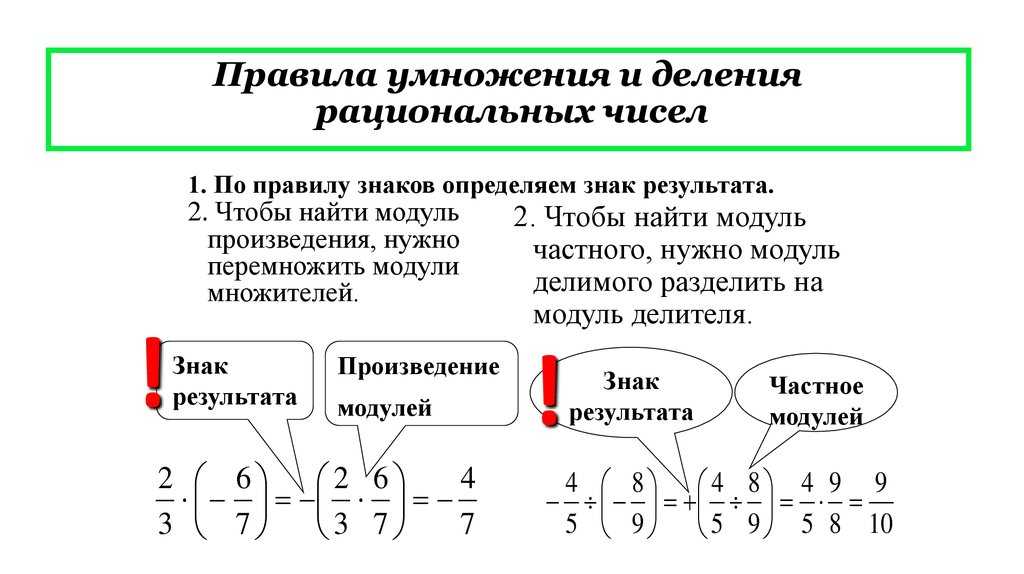
Здесь надо первое число умножить на второе, полученное произведение на 3-е и т. д. Не трудно на основании предыдущего установить, что абсолютные величины всех чисел надо между собою перемножить.
Если бы все множители были положительны, то на основании предыдущего найдем, что и у произведения надо написать знак +. Если бы какой-либо один множитель был отрицателен
напр., (+2) ∙ (+3) ∙ (+4) ∙ (–1) ∙ (+5) ∙ (+6),
то произведение всех предшествующих ему множителей дало бы знак + (в нашем примере (+2) ∙ (+3) ∙ (+4) = +24, от умножения полученного произведения на отрицательное число (в нашем примере +24 умножить на –1) получили бы у нового произведения знак –; умножив его на следующий положительный множитель (в нашем примере –24 на +5), получим опять отрицательное число; так как все остальные множители предполагаются положительными, то знак у произведения более изменяться не может.
Если бы было два отрицательных множителя, то, рассуждая, как выше, нашли бы, что сначала, пока не дошил до первого отрицательного множителя, произведение было бы положительно, от умножения его на первый отрицательный множитель новое произведение получилось бы отрицательным и таковы бы оно и оставалось до тех пор, пока не дойдем до второго отрицательного множителя; тогда от умножения отрицательного числа на отрицательно новое произведение получилось бы положительным, которое таким останется и в дальнейшем, если остальные множители положительны.
Если бы был еще третий отрицательный множитель, то полученное положительно произведение от умножения его на этот третий отрицательный множитель сделалось бы отрицательным; оно таковым бы и осталось, если остальные множители были все положительны. Но если есть еще четвертый отрицательный множитель, то от умножения на него произведение сделается положительным. Рассуждая так же, найдем, что вообще:
Чтобы узнать знак произведения нескольких множителей, надо посмотреть, сколько среди этих множителей отрицательных: если их вовсе нет, или если их четное число, то произведение положительно: если же отрицательных множителей нечетное число, то произведение отрицательно.
Итак, теперь мы легко узнаем, что
(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5) = +4200.
(+3) ∙ (–2) ∙ (+7) ∙ (+3) ∙ (–5) ∙ (–1) = –630.
Теперь нетрудно видеть, что знак произведения, а также и его абсолютная величина, не зависят от порядка множителей.
Удобно, когда имеем дело с дробными числами, находить произведение сразу:
Удобно это потому, то не приходится делать бесполезных умножений, так как предварительно полученное дробное выражение сокращается, сколько возможно.
§ 1 Умножение положительных и отрицательных чисел
В этом уроке познакомимся с правилами умножения и деления положительных и отрицательных чисел.
Известно, что любое произведение можно представить в виде суммы одинаковых слагаемых.
Cлагаемое -1 нужно сложить 6 раз:
(-1)+(-1)+(-1) +(-1) +(-1) + (-1) =-6
Значит произведение -1 и 6 равно -6.
Числа 6 и -6 -противоположные числа.
Таким образом, можно сделать вывод:
При умножении -1 на натуральное число получится противоположное ему число.
Для отрицательных чисел, так же как для положительных, выполняется переместительный закон умножения:
Если натуральное число умножить на -1, то также получится противоположное число
При умножении любого неотрицательного числа на 1 получится это же число.
Например:
Для отрицательных чисел данное утверждение тоже верно: -5 ∙1 = -5; -2 ∙ 1 = -2.
При умножении любого числа на 1 получится это же число.
Мы уже убедились, что при умножении минус 1 на натуральное число получится противоположное ему число. При умножении отрицательного числа данное утверждение тоже справедливо.
При умножении отрицательного числа данное утверждение тоже справедливо.
Например: (-1) ∙ (-4) = 4.
Также -1 ∙ 0 = 0, число 0 противоположно само себе.
При умножении любого числа на минус 1 получится противоположное ему число.
Перейдем к другим случаям умножения. Найдем произведение чисел -3 и 7.
Отрицательный множитель -3 можно заменить произведением -1 и 3. Тогда можно применить сочетательный закон умножения:
1 ∙ 21 = -21, т.е. произведение минус 3 и 7 равно минус 21.
При умножении двух чисел с разными знаками получается отрицательное число, модуль которого равен произведению модулей множителей.
А чему равно произведение чисел с одинаковыми знаками?
Мы знаем, что при умножении двух положительных чисел получится положительное число. Найдем произведение двух отрицательных чисел.
Заменим один из множителей произведением с множителем минус 1.
Применим выведенное нами правило, при умножении двух чисел с разными знаками получается отрицательное число, модуль которого равен произведению модулей множителей,
получится -80.
Сформулируем правило:
При умножении двух чисел с одинаковыми знаками получается положительное число, модуль которого равен произведению модулей множителей.
§ 2 Деление положительных и отрицательных чисел
Перейдем к делению.
Подбором найдем корни следующих уравнений:
y ∙ (-2) = 10. 5 ∙ 2 = 10, значит х = 5; 5 ∙ (-2) = -10, значит а = 5; -5 ∙ (-2) = 10, значит y = -5.
Запишем решения уравнений. В каждом уравнении неизвестен множитель. Неизвестный множитель находим, разделив произведение на известный множитель, значения неизвестных множителей мы уже подобрали.
Проанализируем.
При делении чисел с одинаковыми знаками (а это первое и второе уравнения) получается положительное число, модуль которого равен частному модулей делимого и делителя.
При делении чисел с разными знаками (это третье уравнение) получается отрицательное число, модуль которого равен частному модулей делимого и делителя. Т.е. при делении положительных и отрицательных чисел знак частного определяется по тем же правилам, что знак произведения. А модуль частного равен частному модулей делимого и делителя.
А модуль частного равен частному модулей делимого и делителя.
Таким образом, мы сформулировали правила умножения и деления положительных и отрицательных чисел.
Список использованной литературы:
- Математика. 6 класс: поурочные планы к учебнику И.И. Зубаревой, А.Г. Мордковича//автор-составитель Л.А. Топилина. – Мнемозина, 2009.
- Математика. 6 класс: учебник для учащихся общеобразовательных учреждений. И.И. Зубарева, А.Г. Мордкович. — М.: Мнемозина, 2013.
- Математика. 6 класс: учебник для учащихся общеобразовательных учреждений./Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – М.: Мнемозина, 2013.
- Справочник по математике — http://lyudmilanik.com.ua
- Справочник для учащихся в средней школе http://shkolo.ru
В данной статье сформулируем правило умножения отрицательных чисел и дадим ему объяснение. Будет подробно рассмотрен процесс умножения отрицательных чисел. На примерах показаны все возможные случаи.
Умножение отрицательных чисел
Определение 1
Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел – a , — b данное равенство считается верным.
Данное правило записывается так: для любых отрицательных чисел – a , — b данное равенство считается верным.
(- а) · (- b) = a · b .
Выше приведено правило умножения двух отрицательных чисел. Исходя из него, докажем выражение: (- а) · (- b) = a · b . Статья умножение чисел с разными знаками рассказывает о том, что равенств а · (- b) = — a · b справедливое, как и (- а) · b = — a · b . Это следует из свойства противоположных чисел, благодаря которому равенства запишутся следующим образом:
(- a) · (- b) = (- a · (- b)) = — (- (a · b)) = a · b .
Тут явно видно доказательство правила умножения отрицательных чисел. Исходя из примеров явно, что произведение двух отрицательных чисел – положительное число. При перемножении модулей чисел результат всегда положительное число.
Данное правило применимо для умножения действительных чисел, рациональных чисел, целых чисел.
Теперь рассмотрим подробно примеры умножения двух отрицательных чисел. При вычислении необходимо пользоваться правилом, написанным выше.
Пример 1
Произвести умножение чисел — 3 и — 5 .
Решение.
По модулю умножаемые данные два числа равны положительным числам 3 и 5 . Их произведение дает в результате 15 . Отсюда следует, что произведение заданных чисел равно 15
Запишем кратко само умножение отрицательных чисел:
(- 3) · (- 5) = 3 · 5 = 15
Ответ: (- 3) · (- 5) = 15 .
При умножении отрицательных рациональных чисел, применив разобранное правило, можно мобилизоваться к умножению дробей, умножению смешанных чисел, умножению десятичных дробей.
Пример 2
Вычислить произведение (- 0 , 125) · (- 6) .
Решение.
Используя правило умножения отрицательных чисел, получим, что (− 0 , 125) · (− 6) = 0 , 125 · 6 . Для получения результата необходимо выполнить умножение десятичной дроби на натуральное число столбиков. Это выглядит так:
Получили, что выражение примет вид (− 0 , 125) · (− 6) = 0 , 125 · 6 = 0 , 75 .
Ответ: (− 0 , 125) · (− 6) = 0 , 75 .
В случае, когда множители – иррациональные числа, тогда их произведение может быть записано в виде числового выражения. Значение вычисляется только по необходимости.
Пример 3
Необходимо произвести умножение отрицательного — 2 на неотрицательное log 5 1 3 .
Решение
Находим модули заданных чисел:
2 = 2 и log 5 1 3 = — log 5 3 = log 5 3 .
Следуя из правил умножения отрицательных чисел, получим результат — 2 · log 5 1 3 = — 2 · log 5 3 = 2 · log 5 3 . Это выражение и является ответом.
Ответ: — 2 · log 5 1 3 = — 2 · log 5 3 = 2 · log 5 3 .
Для продолжения изучения темы необходимо повторить раздел умножение действительных чисел.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Умножение положительных и отрицательных чисел
Задача 1. Точка движется по прямой слева направо со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка по прошествии 5 секунд?
Нетрудно сообразить, что точка будет находиться на 20 дм. вправо от A. Запишем решение этой задачи относительными числами. Для этого условимся в следующих знакоположениях:
вправо от A. Запишем решение этой задачи относительными числами. Для этого условимся в следующих знакоположениях:
1) скорость вправо будем обозначать знаком +, а влево знаком –, 2) расстояние движущейся точки от A вправо будем обозначать знаком + и влево знаком –, 3) промежуток времени после настоящего момента знаком + и до настоящего момента знаком –. В нашей задаче даны, след., такие числа: скорость = + 4 дм. в секунду, время = + 5 секунд и получилось, как сообразили арифметически, число + 20 дм., выражающее расстояние движущейся точки от A через 5 секунд. По смыслу задачи мы видим, что она относится к умножению. Поэтому решение задачи удобно записать:
(+ 4) ∙ (+ 5) = + 20.
Задача 2. Точка движется по прямой слева направо со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A. Где находилась эта точка 5 секунд назад?
Ответ ясен: точка находилась влево от A на расстоянии 20 дм.
Решение удобно, согласно условиям относительно знаков, и, имея в виду, что смысл задачи не изменился, записать так:
(+ 4) ∙ (– 5) = – 20.
Задача 3. Точка движется по прямой справа налево со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка спустя 5 секунд?
Ответ ясен: на 20 дм. слева от A. Поэтому, согласно тем же условиям относительно знаков, мы можем записать решение этой задачи так:
(– 4) ∙ (+ 5) = – 20.
Задача 4. Точка движется по прямой справа налево со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A. Где находилась движущаяся точка 5 секунд тому назад?
Ответ ясен: на расстоянии 20 дм. справа от A. Поэтому решение этой задачи следует записать так:
(– 4) ∙ (– 5) = + 20.
Рассмотренные задачи указывают, как следует распространить действие умножения на относительные числа. Мы имеем в задачах 4 случая умножения чисел со всевозможными комбинациями знаков:
1) (+ 4) ∙ (+ 5) = + 20;
2) (+ 4) ∙ (– 5) = – 20;
3) (– 4) ∙ (+ 5) = – 20;
4) (– 4) ∙ (– 5) = + 20.
Во всех четырех случаях абсолютные величины данных чисел следует перемножить, у произведения приходится ставить знак + тогда, когда у множителей одинаковые знаки (1-й и 4-й случаи) и знак –, когда у множителей разные знаки (случаи 2-й и 3-й).
Отсюда же видим, что от перестановки множимого и множителя произведение не изменяется.
Упражнения.
Выполним один пример на вычисление, где входят и сложение и вычитание и умножение.
Чтобы не спутать порядка действий, обратим внимание на формулу
ab + cd.
Здесь написана сумма произведений двух пар чисел: надо, следовательно, сперва число a умножить на число b, потом число c умножить на число d и затем полученные произведения сложить. Также в формуле
a – bc
надо сперва число b умножить на c и затем полученное произведение вычесть из a.
Если бы требовалось произведение чисел a и b сложить с c и полученную сумму умножить на d, то следовало бы написать: (ab + c)d (сравнить с формулой ab + cd).
Если бы надо было разность чисел a и b умножить на c, то написали бы (a – b)c (сравнить с формулой a – bc).
Поэтому установим вообще, что если порядок действий не обозначен скобками, то надо сначала выполнить умножение, а потом уже сложение или вычитание.
Приступаем к вычислению нашего выражения: выполним сначала сложения, написанные внутри всех маленьких скобок, получим:
Теперь надо выполнить умножение внутри квадратных скобок и затем из вычтем полученное произведение:
Теперь выполним действия внутри витых скобок: сначала умножение и потом вычитание:
Теперь останется выполнить умножение и вычитание:
16. Произведение нескольких множителей. Пусть требуется найти
(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5).
Здесь надо первое число умножить на второе, полученное произведение на 3-е и т. д. Не трудно на основании предыдущего установить, что абсолютные величины всех чисел надо между собою перемножить.
Если бы все множители были положительны, то на основании предыдущего найдем, что и у произведения надо написать знак +. Если бы какой-либо один множитель был отрицателен
напр., (+2) ∙ (+3) ∙ (+4) ∙ (–1) ∙ (+5) ∙ (+6),
то произведение всех предшествующих ему множителей дало бы знак + (в нашем примере (+2) ∙ (+3) ∙ (+4) = +24, от умножения полученного произведения на отрицательное число (в нашем примере +24 умножить на –1) получили бы у нового произведения знак –; умножив его на следующий положительный множитель (в нашем примере –24 на +5), получим опять отрицательное число; так как все остальные множители предполагаются положительными, то знак у произведения более изменяться не может.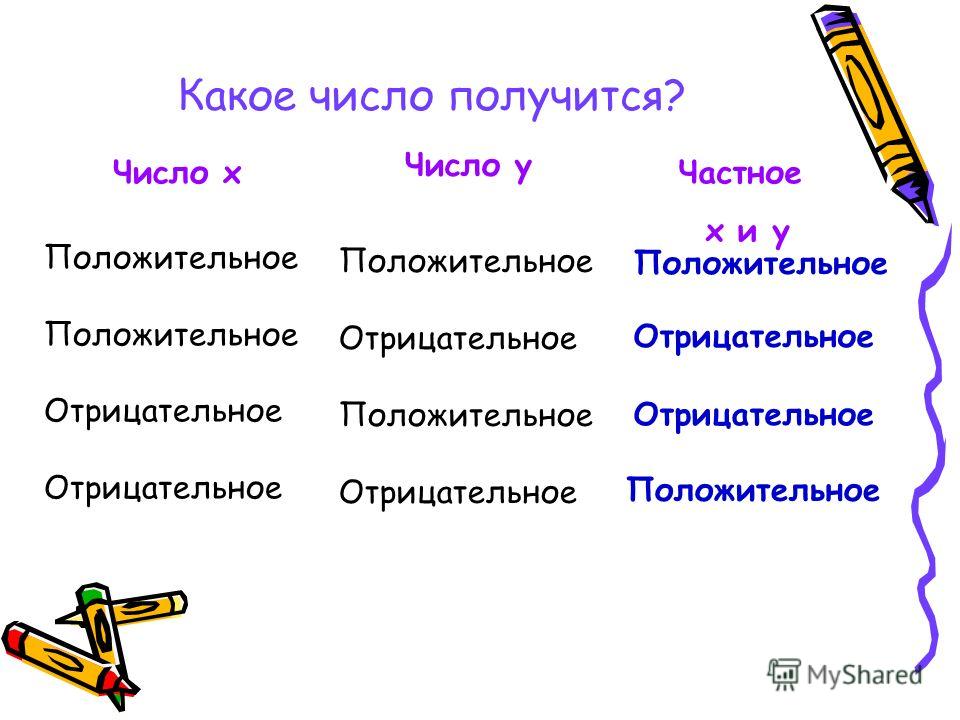
Если бы было два отрицательных множителя, то, рассуждая, как выше, нашли бы, что сначала, пока не дошил до первого отрицательного множителя, произведение было бы положительно, от умножения его на первый отрицательный множитель новое произведение получилось бы отрицательным и таковы бы оно и оставалось до тех пор, пока не дойдем до второго отрицательного множителя; тогда от умножения отрицательного числа на отрицательно новое произведение получилось бы положительным, которое таким останется и в дальнейшем, если остальные множители положительны.
Если бы был еще третий отрицательный множитель, то полученное положительно произведение от умножения его на этот третий отрицательный множитель сделалось бы отрицательным; оно таковым бы и осталось, если остальные множители были все положительны. Но если есть еще четвертый отрицательный множитель, то от умножения на него произведение сделается положительным. Рассуждая так же, найдем, что вообще:
Чтобы узнать знак произведения нескольких множителей, надо посмотреть, сколько среди этих множителей отрицательных: если их вовсе нет, или если их четное число, то произведение положительно: если же отрицательных множителей нечетное число, то произведение отрицательно.
Итак, теперь мы легко узнаем, что
(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5) = +4200.
Также
(+3) ∙ (–2) ∙ (+7) ∙ (+3) ∙ (–5) ∙ (–1) = –630.
Теперь нетрудно видеть, что знак произведения, а также и его абсолютная величина, не зависят от порядка множителей.
Удобно, когда имеем дело с дробными числами, находить произведение сразу:
Удобно это потому, то не приходится делать бесполезных умножений, так как предварительно полученное дробное выражение сокращается, сколько возможно.
Пример на вычисление:
В тесноте, да не в обиде . Путешествие по Карликании и Аль-Джебре
(Таня — Нулику)
Бедный, бедный Нулик! Ну и каша у тебя в голове! Сначала изобрёл какие-то отрицательные пирожные; потом — положительных и отрицательных Нуликов!
Запомни раз и навсегда: нуль — единственное число, которое не бывает ни положительным, ни отрицательным. Это что-то вроде пограничника, который стоит на рубеже между положительными и отрицательными числами.
Конечно, в твоей школе тоже есть положительные и отрицательные Нулики. Но это ведь совсем другое дело. Просто одни из них хорошие, а другие — плохие.
Второй твой вопрос — о Великанах — очень интересный. Но ответил на него не автомат, а мама-Двойка. Она говорит, что ты любознательный ребёнок.
Оба конца монорельсовой дороги и вправду ведут в Бесконечность. А в Бесконечности, понятно, живут числа — Великаны. Бесконечность тоже бывает положительная и отрицательная. Только там свои, особые законы. Положительные и отрицательные Великаны прекрасно уживаются. Но как это им удаётся, мы не узнали. Это как раз один из тех вопросов, на которые мама-Двойка отвечает: «Всякому овощу своё время».
А теперь танцуй! Мы научились умножать и делить отрицательные числа.
Ты ведь знаешь, что умножение можно рассматривать как сложение.
Умножить два на три — всё равно что сложить три двойки:
То же самое происходит, когда отрицательное число умножают на положительное. Разве умножить минус два на плюс три — это не то же самое, что сложить три отрицательные двойки? А так как при сложении отрицательных чисел вагончики двигаются влево от Нулевой станции, то и произведение будет отрицательное — минус шесть:
Разве умножить минус два на плюс три — это не то же самое, что сложить три отрицательные двойки? А так как при сложении отрицательных чисел вагончики двигаются влево от Нулевой станции, то и произведение будет отрицательное — минус шесть:
— Ну, а если умножить минус три на плюс два? — спросил Сева. — Тогда что? — Какая же разница? — сказала мама-Двойка. — Как было минус шесть, так и останется минус шесть. Вот смотрите:
— Ясно! — кивнул Сева. — Пусть себе множители меняются знаками сколько хотят, произведение всё равно остаётся то же. Оно всегда будет отрицательным, если мы перемножаем два числа с разными знаками. — Сева важно посмотрел на всех. Он был страшно собой доволен. — Все поняли? Тогда поехали дальше. Выясним теперь, что получится, если оба множителя отрицательные?
— Ну что ж, выясняйте, — сказала мама-Двойка, — мы с удовольствием вас послушаем.
— Вы меня не поняли, — смутился Сева. — Это я вас собирался послушать.
— Ах вот оно что! Тогда другое дело.
Всем нам стало неловко за Севу. Мы подумали, что мама-Двойка обиделась, но она посмотрела на нас смеющимися глазами и продолжала:
— Вы хотели знать, что происходит при перемножении двух отрицательных чисел? Нетрудно догадаться. Чтобы умножить любое число на положительное, надо отложить его на монорельсе в ту же сторону от Нулевой станции, с какой оно находится. Это мы только что видели.
Когда же мы умножаем любое число на отрицательное, всё происходит наоборот. Вы ведь знаете, какие упрямцы эти отрицательные числа! Поэтому умножаемое откладывается не с той стороны, где оно находится, а по другую сторону от нуля:
Теперь нетрудно понять, что получится при умножении отрицательного числа на отрицательное; в этом случае умножаемое надо откладывать вправо от нуля:
— Вот те раз! — Брови у Севы стали прямо как два вопросительных знака. — Отрицательное число, умноженное на отрицательное, становится положительным?! Чудеса!
— Такие чудеса случаются у нас в Аль-Джебре на каждом шагу, — ответила мама-Двойка.
— Ну, если так, расскажите нам поскорее про деление. Там, наверное, будут какие-нибудь новые чудеса?
— Ничуть не бывало. Деление — действие, обратное умножению. Стало быть, и правила знаков не меняются:
Мы почувствовали себя ужасно образованными. А пуще всех — Сева.
— Теперь нам всё нипочём! — заявил он. — Мы знаем эту дорогу как свои пять пальцев!
— Ошибаетесь, — сказала мама-Двойка, — вы познакомились только с целыми числами.
— А разве здесь есть и другие?
— А как же!
— Вы, наверное, подразумеваете дробные числа, — предположил Олег.
— Не только. Дробные числа — это те, что расположены между целыми числами. — Мама-Двойка указала на палочки ограды, которые мы недавно пересчитывали. — Здесь расстояние между двумя целыми числами разделено на десять равных частей. Каждая из них составляет одну десятую единицы. Но ведь этих делений может быть и гораздо больше. Мысленно мы можем разделить это расстояние на любое число частей.
Мысленно мы можем разделить это расстояние на любое число частей.
— Значит, вагончик может останавливаться не только у целого числа, но и у любой дроби, то есть между станциями?
— Ну конечно! В любом месте, по первому требованию!
Мы тут же вызвали вагончик и заставили его остановиться сперва против числа 2,5 а потом против 3,44… Этого нам показалось мало. Мы назвали число минус пять и четыре миллионных: ?5,000 004, и красный вагончик, миновав Нулевую станцию, превратился в синий и остановился на волосок дальше станции минус 5.
— Выходит, — неуверенно сказал Сева, — вся эта бесконечная дорога сплошь заполнена числами?
— Именно сплошь! — ответила мама-Двойка. — Можно сказать, непрерывно. У нас очень большая плотность населения. На всём пути не сыскать ни одной точечки, не заселённой каким-нибудь числом. Есть среди этих чисел и такие, величину которых мы никогда не можем вычислить точно.
— Что ж это за число, которое нельзя вычислить?
— Ну хотя бы корень квадратный из двух:
Попробуйте найти число, которое при возведении в квадрат давало бы два.
Сева наморщил лоб, подумал немного, потом махнул рукой и засмеялся:
— И много таких чисел?
— Бесконечное множество. Их называют иррациональными в отличие от рациональных. Латинское слово «рацио» значит «разум». Следовательно, рациональные числа — это разумные числа, то есть числа, постижимые разумом.
Сева прямо задохнулся от смеха:
— Ой, умираю! Рациональные — значит разумные. А иррациональные — безумные, что ли?
— Ну зачем же так! — обиделась мама-Двойка. — Просто они не поддаются точному вычислению. Поэтому их долгое время не признавали числами. Но с тех пор как у нас появилась воздушная монорельсовая дорога (или числовая прямая — так её называют по-другому), иррациональные числа после долгих скитаний получили, наконец, точный адрес. Вычислить их по-прежнему можно только приближённо. Зато легко указать место на монорельсовой дороге, где они живут. Вместе с числами рациональными они образуют дружную семью действительных чисел, — закончила мама-Двойка и снова заставила нас удивиться.
— А разве бывают и недействительные?
— Конечно. Есть числа мнимые, есть комплексные.
Сева не дал ей договорить.
— Вспомнил! — заорал он. — И Мнимая Единица на что-нибудь да годится!
— Да, да, — подтвердила я, — так ответил автомат маленькой буковке с зонтиком: i.
— Оно и понятно, — сказала мама-Двойка, — латинской буквой i (по-русски — И) в Аль-Джебре обозначается Мнимая Единица.
— Но почему мнимая? Она что, воображаемая?
— Настолько воображаемая, что ей, как и другим мнимым числам, не нашлось местечка на всей бесконечной монорельсовой дороге.
— Так вот почему она была такая грустная! — смекнул Сева.
— А где же тогда живут мнимые числа? — спросил Олег.
— Всякому овощу своё время.
Пришлось спрятать любопытство в карман. Мы распрощались с мамой-Двойкой и пошли… Куда бы ты думал? Конечно, в Парк Науки и Отдыха.
Как мы там отдыхали, узнаешь из следующего письма.
Таня.
Умножение и деление отрицательных чисел — РОСТОВСКИЙ ЦЕНТР ПОМОЩИ ДЕТЯМ № 7
Содержание
Умножение и деление отрицательных чисел
Мы уже умеем складывать и вычитать отрицательные числа.
Теперь давайте разберемся с умножением и делением.
Предположим, нам нужно умножить +3 на -4. Как это сделать?
Давайте рассмотрим такой случай. Три человека залезли в долги, и у каждого по 4 доллара долга. Чему равен общий долг? Для того чтобы его найти, надо сложить все три долга: 4 доллара + 4 доллара + 4 доллара = 12 долларов. Мы с вами решили, что сложение трех чисел 4 обозначается как 3×4. Поскольку в данном случае мы говорим о долге, перед 4 стоит знак «-». Мы знаем, что общий долг равен 12 долларам, так что теперь наша задача имеет вид 3х(-4)=-12.
Мы получим тот же результат, если по условию задачи каждый из четырех человек имеет долг по 3 доллара. Другими словами, (+4)х(-3)=-12. А поскольку порядок сомножителей значения не имеет, получаем (-4)х(+3)=-12 и (+4)х(-3)=-12.
Давайте обобщим результаты. При перемножении одного положительного и одного отрицательного числа результат всегда будет отрицательным числом
. Численная величина ответа будет той же самой, как и в случае положительных чисел. Произведение (+4)х(+3)=+12. Присутствие знака «-» влияет только на знак, но не влияет на численную величину.
А как перемножить два отрицательных числа?
К сожалению, на эту тему очень трудно придумать подходящий пример из жизни. Легко себе представить долг в сумме 3 или 4 доллара, но совершенно невозможно вообразить -4 или -3 человека, которые залезли в долги.
Пожалуй, мы пойдем другим путем. В умножении при изменении знака одного из множителей меняется знак произведения. Если мы меняем знаки у обоих множителей, мы должны дважды сменить знак произведения, сначала с положительного на отрицательный, а затем наоборот, с отрицательного на положительный, то есть у произведения будет первоначальный знак.
Если мы меняем знаки у обоих множителей, мы должны дважды сменить знак произведения, сначала с положительного на отрицательный, а затем наоборот, с отрицательного на положительный, то есть у произведения будет первоначальный знак.
Следовательно, вполне логично, хотя немного странно, что (-3)х(-4)=+12.
Положение знака при умножении изменяется таким образом:
- положительное число х положительное число = положительное число;
- отрицательное число х положительное число = отрицательное число;
- положительное число х отрицательное число = отрицательное число;
- отрицательное число х отрицательное число = положительное число.
Иначе говоря, перемножая два числа с одинаковыми знаками, мы получаем положительное число. Перемножая два числа с разными знаками, мы получаем отрицательное число.
Такое же правило справедливо и для действия противоположного умножению – для деления.
(+12):(+3)=+4;
(+12):(-3)=-4;
(-12):(+3)=-4;
(-12):(-3)=+4.
Вы легко можете в этом убедиться, проведя обратные операции умножения. Если в каждом из примеров, приведенных выше, вы умножите частное на делитель, то получите делимое, и убедитесь, что оно имеет тот же самый знак, например (-3)х(-4)=(+12).
Поскольку скоро зима, то пора уже подумать о том, в что переобуть своего железного коня, что бы не скользить по льду и чувствовать себя уверено на зимних дорогах. Можно, например, взять шины йокогама на сайте: mvo.ru или какие-то другие, главное, что бы качественный, больше информации и цены вы можете узнать на сайте Mvo.ru.
Материалы по теме:
Поделиться с друзьями:
Загрузка…
Умножение и деление положительных и отрицательных чисел
Положительные и отрицательные числа изучаются в самом начале курса математики, в шестом классе. Хотя дальнейшее обучение требует постоянно работать с этими числами, неудивительно, что по прошествии времени некоторые мелочи забываются — и люди начинают совершать грубые ошибки.
Хотя дальнейшее обучение требует постоянно работать с этими числами, неудивительно, что по прошествии времени некоторые мелочи забываются — и люди начинают совершать грубые ошибки.
Умножение и деление — одни из самых частых действий с числами, имеющими разные знаки.
Разберемся и вспомним, как нужно перемножать и делить такие числа между собой, ставя в ответе правильный знак.
Умножение чисел с разными знаками
Это правило — одно из самых простых в арифметике.
- Если перед нами есть некое положительное число «а», и его требуется умножить на отрицательное число «z», то мы просто перемножаем числа — а потом ставим перед результатом знак «минус».
- Можно сказать и так — чтобы умножить друг на друга числа с разными знаками, нужно перемножить между собой модули множителей, а потом вернуть знак «минус» в ответ.
Для утверждения справедлива следующая цифровая запись: -а*z = — (|а|*|z|). Также напомним, что для нуля действуют особые правила — если на него умножается какое-либо число, положительное или отрицательное, ответ в любом случае будет равен нулю.
Возьмем пару простых примеров.
- Если выражение выглядит, как – 5*6, то решать его нужно следующим образом: -5*6 = — (|5|*|6|) = — 30.
- Если выражение следующего типа — — 7*0, то в ответе сразу пишется 0.
Деление чисел с разными знаками
Для таких случаев тоже действует очень простое правило. Оно похоже на предыдущее — если задача требует разделить «–а» на «b», или «a» на «–b», то для начала мы берем модули чисел, их абсолютные значения, и совершаем процесс деления безо всякой перестановки делимого и делителя.
Таким образом находится частное — а затем к нему добавляется знак «минус». Неважно, выступает ли в роли делимого отрицательное число, или наоборот, мы делим число со знаком «плюс» на отрицательное — ответ всегда будет со знаком «минус». Иначе говоря, числовым методом мы записываем это так: -a : b = — (|a| : |b|).
Например, — 10: 2 = — (10:2) = — 5, или 21: (-3) = — (21:3) = — 7. В конечном итоге деление совсем не сложное и сводится к привычным нам действиям над модулями чисел.
В конечном итоге деление совсем не сложное и сводится к привычным нам действиям над модулями чисел.
И точно так же, как в предыдущем случае, на особенном положении находится нуль. Его присутствие в выражении автоматически дает нуль в ответе. И неважно, это 0:а или а:0 — и попытка деления нуля, и деление на нуль дают одинаковый результат.
Похожие статьи
7. Умножение и деление положительных и отрицательных чисел.
п. 35. УМНОЖЕНИЕ
ПОЛУЧЕНИЕ НОВОГО ЗНАНИЯ.
ОТРАБОТКА УМЕНИЙ И НАВЫКОВ.
Данный модуль представляет собой задание с пошаговым контролем и состоит из пяти шагов. Задание предназначено для отработки умения и навыков учащихся умножать положительные и отрицательные числа. Загрузить модуль.
КОНТРОЛЬ УМЕНИЙ И НАВЫКОВ.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ.
Данный модуль представляет собой задание повышенной сложности, состоящее из трех уровней. Задание направлено на проверку знаний свойств нуля при умножении. Загрузить модуль.
Задание направлено на проверку знаний свойств нуля при умножении. Загрузить модуль.
п. 36. ДЕЛЕНИЕ
ПОЛУЧЕНИЕ НОВОГО ЗНАНИЯ.
Правила и примеры.
ОТРАБОТКА УМЕНИЙ И НАВЫКОВ.
КОНТРОЛЬ УМЕНИЙ И НАВЫКОВ.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ.
п. 37. РАЦИОНАЛЬНЫЕ ЧИСЛА
ПОЛУЧЕНИЕ НОВОГО ЗНАНИЯ.
ОТРАБОТКА УМЕНИЙ И НАВЫКОВ.
Данный модуль состоит из 5 заданий. Задания предназначены для отработки умений и навыков учащихся умножать и делить отрицательные числа; числа с разными знаками; применять эти умения при решении уравнений. Загрузить модуль.
КОНТРОЛЬ УМЕНИЙ И НАВЫКОВ.
Данный модуль состоит из 5 заданий. Задания предназначены для проверки умений и навыков учащихся умножать и делить отрицательные числа; числа с разными знаками; применять эти умения при решении уравнений. Загрузить модуль.
Загрузить модуль.
п. 38. СВОЙСТВА ДЕЙСТВИЙ С РАЦИОНАЛЬНЫМИ ЧИСЛАМИ
ПОЛУЧЕНИЕ НОВОГО ЗНАНИЯ.
ОТРАБОТКА УМЕНИЙ И НАВЫКОВ.
КОНТРОЛЬ УМЕНИЙ И НАВЫКОВ.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ.
Данный модуль представляет собой задания повышенной сложности, состоящее из трех уровней. Задание направлено на формирование рациональных вычислительных приемов: умение применять переместительное и сочетательное свойства сложения и умножения для нахождения значения числового выражения. Загрузить модуль.
ОБОБЩЕНИЕ ПО ТЕМЕ
Игра «Плюс и минус». Можно выбрать действия с положительными и отрицательными числами, а также скорость игры. И проверить себя как вы умеете определять знак результата.
Деление отрицательных чисел и чисел с разными знаками
Министерство образования и науки РД
МКОУ «Джибахнинская СОШ»
Открытый урок по математике для
6 класса
«Деление отрицательных чисел и чисел с разными знаками»
Подготовила:
Магомедова П. М,
М,
учитель математики
МКОУ «Джибахнинская СОШ»
2018
Конспект урока математики в 6 классе по теме
«Деление отрицательных чисел и чисел с разными знаками»
Цели урока:
Сформулировать правило деления отрицательных чисел и чисел с разными знаками.
Проверить справедливость свойств единицы и нуля при делении положительных и отрицательных чисел.
Закрепление правил по данной теме;
Формирование умений и навыков работы с операциями умножения и деления чисел с разными знаками.
Развитие познавательного интереса;
Развитие логического мышления, памяти, внимания.
Задачи урока:
Образовательные:
Закрепление правил по данной теме;
Формирование умений и навыков работы с операциями умножения и деления чисел с разными знаками.
Развивающие:
Развитие познавательного интереса;
Развитие логического мышления, памяти, внимания.
Воспитательные:
Воспитание активности;
Привитие учащимся навыков самостоятельной работы;
Воспитание любви к природе, привитие интереса к народным приметам.
Тип урока: Урок открытия новых знаний, обретения новых умений и навыков.
Оборудование: Интерактивная доска, компьютер, карточки с заданиями.
План урока
Организационный момент
Актуализация знаний
Открытия новых знаний, обретения новых умений и навыков
Выполнение теста
Решение упражнений
Рефлексия. Самостоятельная работа и проверка по эталону
Итог урока
Домашнее задание.
Ход урока
1. Организационный момент.
– Здравствуйте, ребята! Проверяю визуально готовность ребят к уроку и настраиваю на получении хорошей оценки (слайд 1). Я хочу вас спросить, с чем у вас ассоциируется слово «Действие»? (слайд 2). Слушаем рассуждения детей.
2.Актуализация знаний
В математике мы знаем четыре действия с числами. Действия: сложение и вычитание. Давайте решим данные примеры вспомним правила их выполнения. (слайд 3)
Действия: сложение и вычитание. Давайте решим данные примеры вспомним правила их выполнения. (слайд 3)
Реши сам:
21 + ( — 8 ) =13;
-10 + ( — 16 ) =-26;
7 – ( -15 ) = 22;
— 32 – ( — 22 ) = -10;
-16 + 5 = -11;
Идет фронтальная работа с классом с проговариванием правил сложения и вычитания чисел с разными знаками.
Следующие действия: умножение и деление (слайд 4)
Реши сам: (слайд 5)
11 ∙ ( — 8 ) = -88;
-10 ∙ ( — 1,6 ) = 16;
-7 ∙ 0,5 = -3,5 ;
— 33 ∙ (- ) = 11;
-15 ∙ = -5;
Также идет фронтальная работа с классом с проговариванием правил умножения чисел с разными знаками. Обращаю внимание класса на последние два примера. Вопрос классу: — Каким действием можно было заменить умножение, чтобы ответ остался прежним? (Делением). Строим предположения и делаем выводы о правилах деления чисел с разными знаками. Наводящими вопросами подвожу к теме сегодняшнего урока.
3.Открытия новых знаний, обретения новых умений и навыков
Итак, тема урока: Деление (слад 6)
Вместе с классом формулируем цели данного урока(слайд 7)
Формулируем правило деления чисел с разными знаками и записываем в тетрадь (слайд 8)
Вспоминаем, записываем свойства единицы и нуля (слайд 9).
Закрепляем полученные знания при выполнении следующей работы (слайд 10)
Выполните деление:
4,8:(-8 ) = -0,6
-24:(-0,2) = 120
0:(-49) = 0
-4,9: 7 = -0,7
-15:(-1) = 15
Учащиеся меняются тетрадями, выполняют проверку и ставят оценку.
— Мы с вами плодотворно поработали, давайте отвлечемся на физминутку (слайд 11)
– Далее продолжим работать над умножением и делением положительных и отрицательных чисел. Задача каждого из вас – разобраться в том, как он освоил эту тему, и если потребуется – доработать то, что еще не совсем получается. Кроме того вы узнаете много интересного о первом месяце весны – марте.
-Когда-то в старину на Руси отсчет лет вели с 1 марта, с начала сельскохозяйственной весны, с первой весенней капели. Март был “зачинателем” года. Название месяца “март” идет от римлян. Они назвали этот месяц в честь одного из своих богов, узнать, что это за бог, вам поможет тест.
4. Выполнение теста «Составьте слово» (слайд 12).
-25:(-25)= 5. -50:(-25)=
-45: 9= 6. 32:(-2)=
-1,5×2= 7. -0,25×(-1)=
-204:2=
И | У | А | Р | С | М | Т |
2 | -16 | — 5 | -3 | 0,25 | 1 | -102 |
Ответ: Мартиус
-У римлян один месяц года в честь бога войны Марса был назван мартиусом. На Руси это название упростили, взяв лишь первые четыре буквы (слайд 13).
В народе говорят: “ Март неверен, то плачет, то смеется”. С мартом связано много народных примет. Некоторые дни его имеют свои названия. Давайте сейчас все вместе мы составим народный месяцеслов на март.
5. Решение упражнений.
Учащиеся у доски решают примеры, ответы которых являются числами месяца. На доске появляется пример, а затем день месяца с названием и народной приметой.
-2,5:5×(-26) (слайд 14)
13 марта – Василий-капельник: с крыш каплет. Птицы гнезда завивают, а перелетные летят из теплых мест.
-29,12:(-2,08) (слайд 15)
14 марта – Евдокия (Авдотья-плющиха) – снег плющит настом. Вторая встреча весны (первая на Стретение). Какова Евдокия – таково и лето. Евдокия красна – и весна красна; на Евдокию снег – к урожаю.
(-6-36:4)×(-1)(слайд 16)
15 марта – Федот. На Федота ветер и метель – долго травы не будет.
7,15×(-4):(-1,3) (слайд 17)
22 марта – Сороки – день равен ночи. Зима кончается, весна начинается, прилетают жаворонки. По старинному обычаю из теста пекут жаворонков и куликов.
Зима кончается, весна начинается, прилетают жаворонки. По старинному обычаю из теста пекут жаворонков и куликов.
6. Рефлексия. Самостоятельная работа и проверка по эталону
Проверь себя: (слайд 18-19)
4,9: (-0,7) = -7
2. -2·(-3,4) = 6,8
3. -5,2:26 = -0,2
4. -2· = —
5. —: (-4) =
Критерии оценки:
нет ошибок —- оценка 5
1 ошибка —— оценка 4
2 ошибки —— оценка 3
По окончанию самостоятельной работы, с помощью готовых ответов на экране, учащиеся осуществили самопроверку и выставили оценку.
7.Итог урока.
– Ребята, понравился ли вам сегодняшний урок?
– Что нового вы сегодня узнали?
– Мы достигли поставленных целей урока? (слайд 20)
– Я предлагаю вам подготовить самим месяцеслов на апрель. Вы должны найти приметы апреля и составить примеры с ответами, соответствующими дню месяца.
8. Домашнее задание:
стр. 218 №1174, 1179(1) (слайд 21)
Умножение и деление целых чисел.
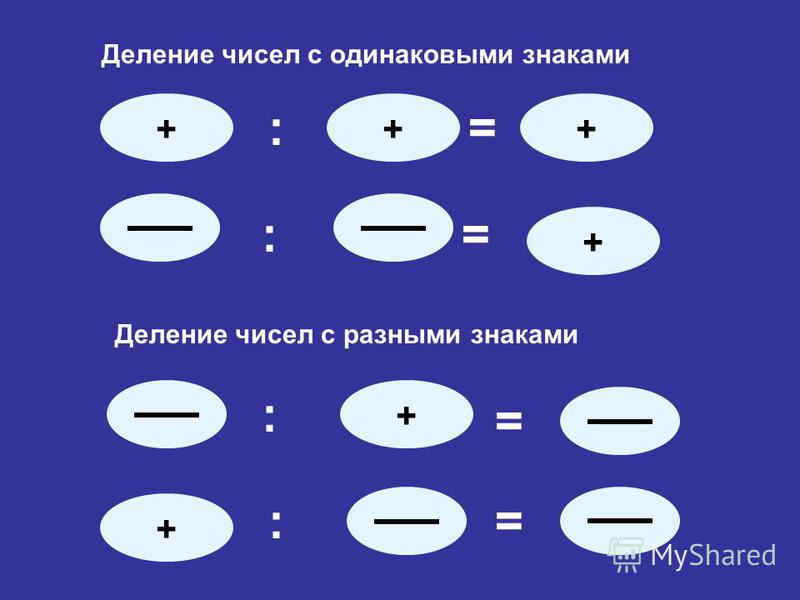 Возведение в степень
Возведение в степеньУмножение
При умножении двух целых чисел умножаются их абсолютные величины. Перед произведением ставится знак плюс, если знаки сомножителей одинаковы, и минус, если они разные
Примеры:
3 · 5 = 15,
3 · (-5) = -15,
-3 · 5 = -15,
-3 · (-5) = 15.
Ниже представлена схема (правило знаков при умножении):
| + | · | + | = | + |
| + | · | — | = | — |
| — | · | + | = | — |
| — | · | — | = | + |
Из данных примеров следует, что в результате умножения двух чисел с разными знаками получится отрицательное число, а результате умножения двух чисел с одинаковыми знаками – положительное.
При умножении любого числа на -1 получится число противоположное данному.
Примеры:
-15 · (-1) = 15,
25 · (-1) = -25.
Деление
При делении одного целого числа на другое делят абсолютную величину первого на абсолютную величину второго. Перед частным ставится знак плюс, если знаки делимого и делителя одинаковы, и минус, если они разные.
Примеры:
15 : 5 = 3,
15 : (-5) = -3,
-15 : 5 = -3,
-15 : (-5) = 3.
При делении используется то же правило, что и для умножения. Ниже представлена схема (правило знаков при делении):
| + | : | + | = | + |
| + | : | — | = | — |
| — | : | + | = | — |
| — | : | — | = | + |
Из данных примеров следует, что
частное двух чисел с разными знаками – отрицательное число, а частное двух чисел с одинаковыми знаками – положительное число.
При делении любого числа на -1 получится число противоположное данному.
Примеры:
-15 : (-1) = 15,
25 : (-1) = -25.
Возведение в степень
При возведении в степень целого числа в результате может получится как положительное число, так и отрицательное.
Степень положительного числа всегда будет положительным числом.
Примеры:
52 = 5 · 5 = 25,
43 = 4 · 4 · 4 = 64.
Степень отрицательного числа может быть как положительным, так и отрицательным числом.
Примеры:
Нечётный показатель степени:
| (-3)3 = | (-3) · (-3) | · (-3) = |
| + |
= 9 · (-3) = -27,
то есть (-3)3 < 0.
Чётный показатель степени:
| (-4)4 = | (-4) · (-4) | · | (-4) · (-4) | = |
| + | + |
= 16 · 16 = 256,
то есть (-4)4 > 0.
следовательно, степень отрицательного числа положительна, если показатель степени чётный, и отрицательна, если показатель степени нечётный.
Умножение и деление рациональных чисел
В данном уроке рассматривается умножение и деление рациональных чисел.
Умножение рациональных чисел
Правила умножения целых чисел справедливы и для рациональных чисел. Иными словами, чтобы умножать рациональные числа, нужно уметь умножать целые числа.
Необходимо также знать основные законы умножения такие как переместительный закон умножения, сочетательный закон умножения, распределительный закон умножения и закон умножения на ноль.
Пример 1. Найти значение выражения
Это умножение рациональных чисел с разными знаками.Чтобы перемножить рациональные числа с разными знаками, нужно перемножить их модули и перед полученным ответом поставить минус.
Чтобы хорошо увидеть, что мы имеем дело с числами, у которых разные знаки, заключим каждое рациональное число в скобки вместе со своими знаками
Модуль числа равен , а модуль числа равен . Перемножив полученные модули, как положительные дроби, мы получили ответ , но перед ответом поставили минус, как от нас требовало правило. Чтобы обеспечить перед ответом этот минус, умножение модулей выполнялось в скобках, перед которыми и поставлен минус.
Перемножив полученные модули, как положительные дроби, мы получили ответ , но перед ответом поставили минус, как от нас требовало правило. Чтобы обеспечить перед ответом этот минус, умножение модулей выполнялось в скобках, перед которыми и поставлен минус.
Таким образом, значение выражения равно
Короткое решение выглядит следующим образом:
Пример 2. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус:
Решение для данного примера можно записать покороче:
Пример 3. Найти значение выражения
Это умножение отрицательных рациональных чисел. Чтобы перемножить отрицательные рациональные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
Решение для данного примера можно записать покороче:
Пример 4. Найти значение выражения
Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс
Перемножим модули этих чисел и перед полученным ответом поставим плюс
Решение для данного примера можно записать покороче:
Пример 5. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Короткое решение будет выглядеть значительно проще:
Пример 6. Найти значение выражения
Переведём смешанное число в неправильную дробь. Остальное перепишем, как есть
Получили умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение
Решение для данного примера можно записать покороче
Пример 7. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Сначала в ответе получилась неправильная дробь , но мы выделили в ней цéлую часть. Обратите внимание, что целая часть была выделена от модуля дроби . Получившееся смешанное число было заключено в скобки, перед которыми поставлен минус. Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.
Обратите внимание, что целая часть была выделена от модуля дроби . Получившееся смешанное число было заключено в скобки, перед которыми поставлен минус. Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.
Решение для данного примера можно записать покороче:
Пример 8. Найти значение выражения
Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.
Сначала перемножим и и полученное число перемножим с оставшимся числом 5. Запись с модулями пропустим, чтобы не загромождать выражение.
Первое действие:
Второе действие:
Ответ: значение выражения равно −2.
Пример 9. Найти значение выражения:
Переведём смешанные числа в неправильные дроби:
Получили умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение
Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение
Пример 10. Найти значение выражения
Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.
Не будем изобретать велосипед, а вычислим данное выражение слева направо в порядке следования сомножителей. Запись с модулями пропустим, чтобы не загромождать выражение
Первое действие:
Второе действие:
Третье действие:
Четвёртое действие:
Ответ: значение выражения равно
Пример 11. Найти значение выражения
Вспоминаем закон умножения на ноль. Этот закон гласит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 12. Найти значение выражения
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 13. Найти значение выражения
Можно воспользоваться порядком действий и сначала вычислить выражение в скобках и полученный ответ перемножить с дробью .
Ещё можно воспользоваться распределительным законом умножения — умножить каждое слагаемое суммы на дробь и полученные результаты сложить. Этим способом и воспользуемся.
Согласно порядку действий, если в выражении присутствует сложение и умножение, то в первую очередь нужно выполнять умножение. Поэтому в получившемся новом выражении возьмём в скобки те дроби, которые должны быть перемножены. Так мы хорошо увидим, какие действия выполнить раньше, а какие позже:
Далее вычисляем выражение по действиям. Сначала вычислим выражения в скобках, и полученные результаты сложим
Сначала вычислим выражения в скобках, и полученные результаты сложим
Первое действие:
Второе действие:
Третье действие:
Ответ: значение выражения равно
Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:
Видно, что данный пример можно было решить даже в уме. Поэтому следует развивать в себе навык анализа выражения до начала его решения. Вполне вероятно, что его можно решить в уме и сэкономить много времени и нервов. А на контрольных и экзаменах, как известно время очень дорого стоит.
Пример 14. Найти значение выражения −4,2 × 3,2
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь перемножить десятичные дроби.
Пример 15. Найти значение выражения −0,15 × 4
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь перемножить десятичную дробь и целое число.
Пример 16. Найти значение выражения −4,2 × (−7,5)
Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс
Деление рациональных чисел
Деление рациональных чисел свóдится к умножению этих же чисел. Для этого первую дробь умножают на дробь, обратную второй. Затем применяются правила умножения рациональных чисел.
Пример 1. Выполнить деление:
Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь . На неё и умножим первую дробь:
Получили умножение рациональных чисел с разными знаками. А как вычислять такие выражения мы уже знаем. Для этого нужно перемножить модули данных рациональных чисел и перед полученным ответом поставить минус.
А как вычислять такие выражения мы уже знаем. Для этого нужно перемножить модули данных рациональных чисел и перед полученным ответом поставить минус.
Дорешаем данный пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение
Таким образом, значение выражения равно
Подробное решение выглядит следующим образом:
Короткое решение можно записать так:
Пример 2. Выполнить деление
Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь . На неё и умножим первую дробь:
Короткое решение можно записать так:
Пример 3. Выполнить деление
Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь
Получили умножение отрицательных рациональных чисел. Выполним данное умножение. Запись с модулями можно пропустить, чтобы не загромождать выражение:
Пример 4. Выполнить деление
В данном случае нужно первое число −3 умножить на дробь, обратную дроби .
Обратная для дроби это дробь . Затем следует применить правило умножения рациональных чисел с разными знаками:
Пример 6. Выполнить деление
Умнóжим первую дробь на число, обратное числу 4.
Обратное числу 4 это дробь . На неё и умножим первую дробь
Пример 5. Выполнить деление
Умнóжим первую дробь на число, обратное числу −3
Обратное числу −3 это дробь
Пример 6. Найти значение выражение −14,4 : 1,8
Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно модуль делимого разделить на модуль делителя и перед полученным ответом поставить минус
Обратите внимание, как модуль делимого был разделён на модуль делителя. В данном случае потребовалось суметь разделить десятичную дробь на другую десятичную дробь.
Если нет желания работать с десятичными дробями (а это бывает часто), то эти десятичные дроби можно перевести в смешанные числа, затем перевести эти смешанные числа в неправильные дроби, а затем заняться непосредственно делением.
Вычислим предыдущее выражение −14,4 : 1,8 этим способом. Переведём десятичные дроби в смешанные числа:
Теперь переведём полученные смешанные числа в неправильные дроби:
Теперь можно заняться непосредственно делением, а именно разделить дробь на дробь . Для этого нужно первую дробь умножить на дробь, обратную второй:
Пример 7. Найти значение выражения
Переведём десятичную дробь −2,06 в неправильную дробь, и умножим эту дробь на дробь, обратную второй:0
Пример 8. Найти значение выражения −7,2 : (−0,6)
Это деление отрицательных рациональных чисел. Чтобы выполнить данное деление, нужно первую дробь умножить на дробь обратную второй.
Перенесём в обеих дробях запятую на одну цифру вправо, получим деление −72:(−6)
Многоэтажные дроби
Часто можно встретить выражение, в котором деление дробей записано с помощью дробной черты. Например, выражение может быть записано следующим образом:
В чём же разница между выражениями и ? На самом деле разницы никакой. Эти два выражения несут одно и то же значение и между ними можно поставить знак равенства:
Эти два выражения несут одно и то же значение и между ними можно поставить знак равенства:
В первом случае знак деления представляет собой двоеточие и выражение записано в одну строку. Во втором случае деление дробей записано с помощью дробной черты. В результате получается дробь, которую в народе договорились называть многоэтажной.
При встрече с такими многоэтажными выражениями, нужно применять те же правила деления обыкновенных дробей. Первую дробь необходимо умножать на дробь, обратную второй.
Использовать в решении подобные дроби крайне неудобно, поэтому можно записать их в понятном виде, используя в качестве знака деления не дробную черту, а двоеточие.
Например, запишем многоэтажную дробь в понятном виде. Для этого сначала нужно разобраться, где первая дробь и где вторая, потому что сделать это правильно удаётся не всегда. В многоэтажных дробях имеется несколько дробных черт, которые могут запутать. Главная дробная черта, которая отделяет первую дробь от второй, обычно бывает длиннее остальных.
После определения главной дробной черты можно без труда понять, где первая дробь и где вторая:
И далее можно воспользоваться методом деления дробей — умножить первую дробь на дробь, обратную второй.
Пример 2. Запишем в понятном виде многоэтажную дробь
Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление целого числа −3 на обыкновенную дробь
А если бы мы по ошибке приняли вторую дробную черту за главную (ту, что короче), то получилось бы, что мы делим дробь на целое число 5В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является число −3, а делителем — дробь .
Пример 3. Запишем в понятном виде многоэтажную дробь
Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление дроби на целое число 2
А если бы мы по ошибке приняли первую дробную черту за главную (ту, что короче), то получилось бы, что мы делим целое число −5 на дробь В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является дробь , а делителем — целое число 2.
Несмотря на то, что многоэтажные дроби неудобны в работе, сталкиваться мы с ними будем очень часто, особенно при изучении высшей математики.
Естественно, на перевод многоэтажной дроби в понятный вид уходит дополнительное время и место. Поэтому можно воспользоваться более быстрым методом. Данный метод удобен и на выходе позволяет получить готовое выражение, в котором первая дробь уже умножена на дробь, обратную второй.
Реализуется этот метод следующим образом:
Если дробь четырехэтажная, например как , то цифру находящуюся на первом этаже поднимают на самый верхний этаж. А цифру, находящуюся на втором этаже поднимают на третий этаж. Полученные цифры нужно соединить значками умножения ( × )
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратную второй. Удобство да и только!
Чтобы не допускать ошибок при использовании данного метода, можно руководствоваться следующим правилом:
С первого на четвёртый. Со второго на третий.
Со второго на третий.
В правиле речь идет об этажах. Цифру с первого этажа нужно поднимать на четвертый этаж. А цифру со второго этажа нужно поднимать на третий этаж.
Попробуем вычислить многоэтажную дробь пользуясь вышеприведённым правилом.
Итак, цифру находящуюся на первом этаже поднимаем на четвёртый этаж, а цифру находящуюся на втором этаже поднимаем на третий этаж
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратной второй. Далее можно воспользоваться имеющимися знаниями:
Попробуем вычислить многоэтажную дробь пользуясь новой схемой.
Здесь имеется только первый, второй и четвёртый этажи. Третий этаж отсутствует. Но мы не отходим от основной схемы: цифру с первого этажа поднимаем на четвёртый этаж. А поскольку третий этаж отсутствует, то цифру находящуюся на втором этаже оставляем, как есть
В результате, минуя промежуточную запись мы получили новое выражение , в котором первое число −3 уже умножено на дробь, обратную второй. Далее можно воспользоваться имеющимися знаниями:
Далее можно воспользоваться имеющимися знаниями:
Попробуем вычислить многоэтажную дробь , пользуясь новой схемой.
Здесь имеется только второй, третий и четвёртый этажи. Первый этаж отсутствует. Поскольку первый этаж отсутствует, подниматься на четвёртый этаж нечему, но зато мы можем поднять цифру со второго этажа на третий:
В результате, минуя промежуточную запись мы получили новое выражение , в котором первая дробь уже умножена на число, обратное делителю. Далее можно воспользоваться имеющимися знаниями:
Использование переменных
Если выражение сложное и вам кажется, что оно запутает вас в процессе решения задачи, то часть выражения можно занести в переменную и далее работать с этой переменной.
Математики часто так и делают. Сложную задачу разбивают на более лёгкие подзадачи и решают их. Затем собирают решённые подзадачи в одно единое целое. Это творческий процесс и этому учатся годами, упорно тренируясь.
Использование переменных оправдано, при работе с многоэтажными дробями. Например:
Например:
Найти значение выражения
Итак, имеется дробное выражение в числителе и в знаменателе котором дробные выражения. Другими словами, перед нами снова многоэтажная дробь, которую мы так не любим.
Выражение, находящееся в числителе можно занести в переменную с любым названием, например:
Но в математике в подобном случае переменным принято давать название из больших латинских букв. Давайте не будем нарушать эту традицию, и обозначим первое выражение через большую латинскую букву A
А выражение, находящееся в знаменателе можно обозначить через большую латинскую букву B
Теперь наше изначальное выражение принимает вид . То есть мы сделали замену числового выражения на буквенное, предварительно занеся числитель и знаменатель в переменные A и B.
Теперь мы можем отдельно вычислить значения переменной A и значение переменной B. Готовые значения мы вставим в выражение .
Найдём значение переменной A
Найдём значение переменной B
Теперь подставим в главное выражения вместо переменных A и B их значения:
Мы получили многоэтажную дробь в которой можно воспользоваться схемой «с первого на четвёртый, со второго на третий», то есть цифру находящуюся на первом этаже поднять на четвёртый этаж, а цифру находящуюся на втором этаже поднять на третий этаж. Дальнейшее вычисление не составит особого труда:
Дальнейшее вычисление не составит особого труда:
Таким образом, значение выражения равно −1.
Конечно, мы рассмотрели простейший пример, но нашей целью было узнать, как можно использовать переменные для облегчения себе задачи, чтобы свести к минимуму допущение ошибок.
Отметим также, что решение для данного примера можно записать не применяя переменные. Выглядеть оно будет как
Это решение более быстрое и короткое и в данном случае его целесообразнее так и записать, но если выражение окажется сложным, состоящим из нескольких параметров, скобок, корней и степеней, то желательно вычислять его в несколько этапов, занося часть его выражений в переменные.
Задания для самостоятельного решения
Задание 1. Выполните умножение:
Решение:
Задание 2. Выполните умножение:
Решение:
Задание 3. Выполните умножение:
Решение:
Задание 4. Выполните умножение:
Решение:
Задание 5. Выполните умножение:
Решение:
Задание 6. Выполните умножение:
Выполните умножение:
Решение:
Задание 7. Выполните умножение:
Решение:
Задание 8. Выполните умножение:
Решение:
Задание 9. Выполните деление:
Решение:
Задание 10. Выполните деление:
Решение:
Задание 11. Выполните деление:
Решение:
Задание 12. Выполните деление:
Решение:
Задание 13. Выполните деление:
Решение:
Задание 14. Выполните деление:
Решение:
Задание 15. Выполните деление:
Решение:
Задание 16. Выполните деление:
Решение:
Задание 17. Выполните деление:
Решение:
Задание 18. Вычислите выражение:
Решение:
Задание 19. Вычислите выражение:
Решение:
Задание 20. Вычислите выражение:
Решение:
Задание 21. Вычислите выражение:
Решение:
Задание 22. Вычислите выражение:
Решение:
Задание 23. Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:
Решение:
Задание 24. Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:
Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:
Решение:
Задание 25. Запишите следующую многоэтажную дробь с помощью двоеточия и вычислите:
Решение:
Задание 26. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Решение:
Задание 27. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Решение:
Задание 28. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Решение:
Задание 29. Используя метод «С первого на четвёртый, со второго на третий», запишите следующую дробь в виде умножения и вычислите:
Решение:
Задание 30. Найдите значение выражения:
Решение:
Задание 31. Найдите значение выражения:
Решение:
Задание 32. Найдите значение выражения:
Решение:
Задание 33. Найдите значение выражения:
Найдите значение выражения:
Решение:
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Умножение дробей с разными знаками. Умножение и деление отрицательных чисел
В данном уроке рассматривается умножение и деление рациональных чисел.
Содержание урока
Умножение рациональных чисел
Правила умножения целых чисел справедливы и для рациональных чисел. Иными словами, чтобы умножать рациональные числа, нужно уметь
Также, необходимо знать основные законы умножения, такие как: переместительный закон умножения, сочетательный закон умножения, распределительный закон умножения и умножение на ноль.
Пример 1. Найти значение выражения
Это умножение рациональных чисел с разными знаками.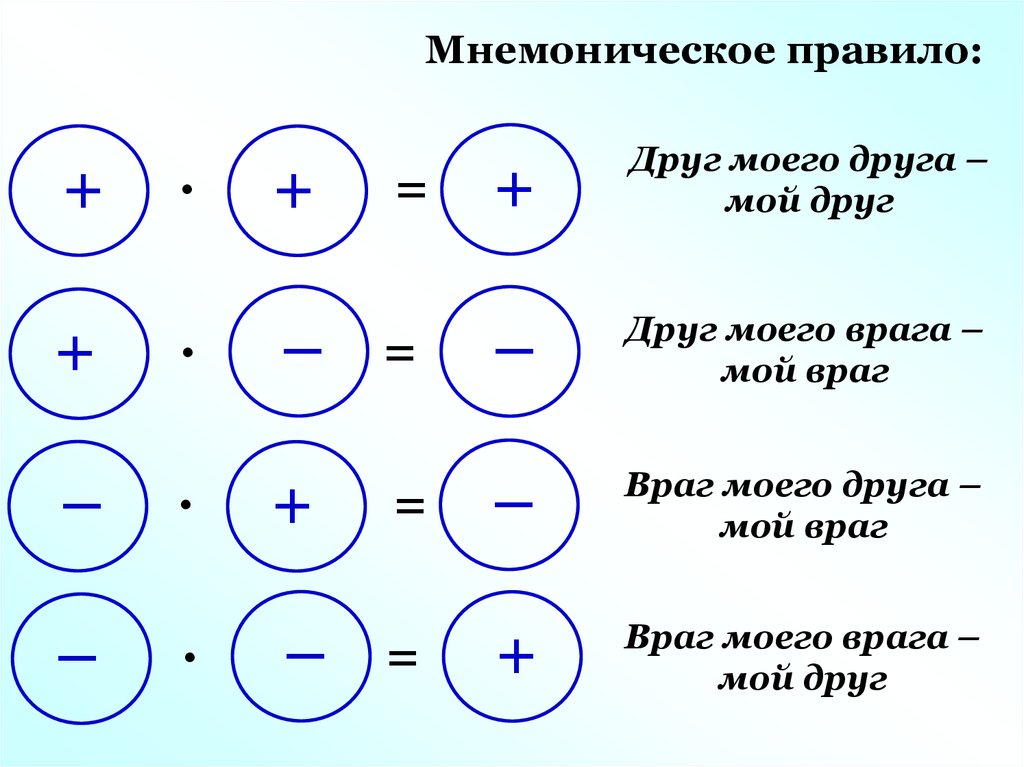 Чтобы перемножить рациональные числа с разными знаками, нужно перемножить их модули и перед полученным ответом поставить минус.
Чтобы перемножить рациональные числа с разными знаками, нужно перемножить их модули и перед полученным ответом поставить минус.
Чтобы хорошо увидеть, что мы имеем дело с числами, у которых разные знаки, заключим каждое рациональное число в скобки вместе со своими знаками
Модуль числа равен , а модуль числа равен . Перемножив полученные модули, как положительные дроби, мы получили ответ , но перед ответом поставили минус, как от нас требовало правило. Чтобы обеспечить перед ответом этот минус, умножение модулей выполнялось в скобках, перед которыми и поставлен минус.
Короткое решение выглядит следующим образом:
Пример 2. Найти значение выражения
Пример 3. Найти значение выражения
Это умножение отрицательных рациональных чисел. Чтобы перемножить отрицательные рациональные числа, нужно перемножить их модули и перед полученным ответом поставить плюс
Решение для данного примера можно записать покороче:
Пример 4. Найти значение выражения
Решение для данного примера можно записать покороче:
Пример 5. Найти значение выражения
Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Короткое решение будет выглядеть значительно проще:
Пример 6. Найти значение выражения
Переведём смешанное число в неправильную дробь. Остальное перепишем, как есть
Получили умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение
Решение для данного примера можно записать покороче
Пример 7. Найти значение выражения
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Сначала в ответе получилась неправильная дробь , но мы выделили в ней целую часть. Обратите внимание, что целая часть была выделена от модуля дроби . Получившееся смешанное число было заключено в скобки, перед которыми поставлен минус. Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.
Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.
Решение для данного примера можно записать покороче:
Пример 8. Найти значение выражения
Сначала перемножим и и полученное число перемножим с оставшимся числом 5. Запись с модулями пропустим, чтобы не загромождать выражение.
Ответ: значение выражения равно −2.
Пример 9. Найти значение выражения:
Переведём смешанные числа в неправильные дроби:
Получили умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение
Пример 10. Найти значение выражения
Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.
Не будем изобретать велосипед, а вычислим данное выражение слева направо в порядке следования сомножителей. Запись с модулями пропустим, чтобы не загромождать выражение
Третье действие:
Четвёртое действие:
Ответ: значение выражения равно
Пример 11. Найти значение выражения
Вспоминаем закон умножения на ноль. Этот закон гласит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 12. Найти значение выражения
Произведение равно нулю, если хотя бы один из сомножителей равен нулю.
В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения равно нулю:
Пример 13. Найти значение выражения
Можно воспользоваться порядком действий и сначала вычислить выражение в скобках и полученный ответ перемножить с дробью .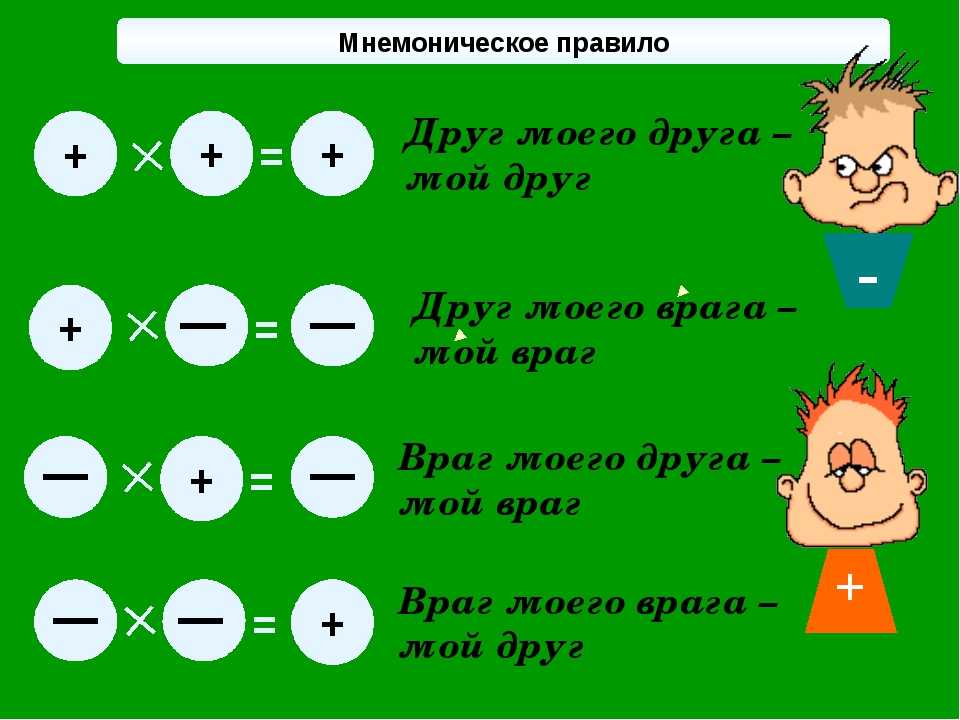
Ещё можно воспользоваться распределительным законом умножения — умножить каждое слагаемое суммы на дробь и полученные результаты сложить. Этим способом и воспользуемся.
Согласно порядку действий, если в выражении присутствует сложение и умножение, то в первую очередь нужно выполнять умножение. Поэтому в получившемся новом выражении возьмём в скобки те параметры, которые должны быть перемножены. Так мы хорошо увидим, какие действия выполнить раньше, а какие позже:
Третье действие:
Ответ: значение выражения равно
Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:
Видно, что данный пример можно было решить даже в уме. Поэтому следует развивать в себе навык анализа выражения до начала его решения. Вполне вероятно, что его можно решить в уме и сэкономить много времени и нервов. А на контрольных и экзаменах, как известно время очень дорого стоит.
Пример 14. Найти значение выражения −4,2 × 3,2
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось .
Пример 15. Найти значение выражения −0,15 × 4
Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус
Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь .
Пример 16. Найти значение выражения −4,2 × (−7,5)
Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс
Деление рациональных чисел
Правила деления целых чисел справедливы и для рациональных чисел. Иными словами, чтобы уметь делить рациональные числа, нужно уметь
В остальном же применяются те же методы деления обыкновенных и десятичных дробей. Чтобы разделить обыкновенную дробь на другую дробь, нужно первую дробь умножить на дробь, обратную второй.
Чтобы разделить обыкновенную дробь на другую дробь, нужно первую дробь умножить на дробь, обратную второй.
А чтобы разделить десятичную дробь на другую десятичную дробь, нужно в делимом и в делителе перенести запятую вправо на столько цифр, сколько их после запятой в делителе, затем выполнить деление, как на обычное число.
Пример 1. Найти значение выражения:
Это деление рациональных чисел с разными знаками. Чтобы вычислить такое выражение, нужно первую дробь умножить на дробь, обратную второй.
Итак, умножим первую дробь на дробь обратную второй.
Получили умножение рациональных чисел с разными знаками. А как вычислять такие выражения мы уже знаем. Для этого нужно перемножить модули этих рациональных чисел и перед полученным ответом поставить минус.
Дорешаем данный пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение
Таким образом, значение выражения равно
Подробное решение выглядит следующим образом:
Короткое решение будет выглядеть так:
Пример 2. Найти значение выражения
Найти значение выражения
Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно первую дробь умножить на дробь, обратную второй.
Обратная для второй дроби это дробь . На неё и умножим первую дробь:
Короткое решение будет выглядеть следующим образом:
Пример 3. Найти значение выражения
Это деление отрицательных рациональных чисел. Чтобы вычислить данное выражение, опять же нужно первую дробь умножить на дробь обратную второй.
Обратная для второй дроби это дробь . На неё и умножим первую дробь:
Получили умножение отрицательных рациональных чисел. Как вычисляется подобное выражение мы уже знаем. Нужно перемножить модули рациональных чисел и перед полученным ответом поставить плюс.
Дорешаем этот пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение:
Пример 4. Найти значение выражения
Чтобы вычислить данное выражение, нужно первое число −3 умножить на дробь, обратную дроби .
Обратная для дроби это дробь . На неё и умножим первое число −3
Пример 6. Найти значение выражения
Чтобы вычислить данное выражение, нужно первую дробь умножить на число, обратное числу 4.
Обратное для числа 4 это дробь . На неё и умножим первую дробь
Пример 5. Найти значение выражения
Чтобы вычислить данное выражение, нужно первую дробь умножить на число, обратное числу −3
Обратное для числа −3 это дробь . На неё и умножим первую дробь:
Пример 6. Найти значение выражение −14,4: 1,8
Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно модуль делимого разделить на модуль делителя и перед полученным ответом поставить минус
Обратите внимание, как модуль делимого был разделён на модуль делителя. В данном случае, чтобы сделать это правильно, потребовалось суметь .
Если нет желания возиться с десятичными дробями (а это бывает часто), то эти , затем перевести эти смешанные числа в неправильные дроби, а затем заняться непосредственно делением.
Вычислим предыдущее выражение −14,4: 1,8 этим способом. Переведём десятичные дроби в смешанные числа:
Теперь переведём полученные смешанные числа в неправильные дроби:
Теперь можно заняться непосредственно делением, а именно разделить дробь на дробь . Для этого нужно первую дробь умножить на дробь, обратную второй:
Пример 7. Найти значение выражения
Переведём десятичную дробь −2,06 в неправильную дробь, и умножим эту дробь на дробь, обратную второй:
Многоэтажные дроби
Часто можно встретить выражение, в котором деление дробей записано с помощью дробной черты. Например, выражение может быть записано следующим образом:
В чём же разница между выражениями и ? На самом деле разницы никакой. Эти два выражения несут одно и то же значение и между ними можно поставить знак равенства:
В первом случае знак деления представляет собой двоеточие и выражение записано в одну строку. Во втором случае деление дробей записано с помощью дробной черты. В результате получается дробь, которую в народе договорились называть многоэтажной .
В результате получается дробь, которую в народе договорились называть многоэтажной .
При встрече с такими многоэтажными выражениями, нужно применять те же правила деления обыкновенных дробей. Первую дробь необходимо умножать на дробь, обратную второй.
Использовать в решении подобные дроби крайне неудобно, поэтому можно записать их в понятном виде, используя в качестве знака деления не дробную черту, а двоеточие.
Например, запишем многоэтажную дробь в понятном виде. Для этого сначала нужно разобраться, где первая дробь и где вторая, потому что сделать это правильно удаётся не всегда. В многоэтажных дробях имеется несколько дробных черт, которые могут запутать. Главная дробная черта, которая отделяет первую дробь от второй, обычно бывает длиннее остальных.
После определения главной дробной черты можно без труда понять, где первая дробь и где вторая:
Пример 2.
Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление целого числа −3 на обыкновенную дробь
А если бы мы по ошибке приняли вторую дробную черту за главную (ту, что короче), то получилось бы, что мы делим дробь на целое число 5В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является число −3, а делителем — дробь .
Пример 3. Запишем в понятном виде многоэтажную дробь
Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление дроби на целое число 2
А если бы мы по ошибке приняли первую дробную черту за главную (ту, что короче), то получилось бы, что мы делим целое число −5 на дробь В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является дробь , а делителем — целое число 2.
Несмотря на то, что многоэтажные дроби неудобны в работе, сталкиваться мы с ними будем очень часто, особенно при изучении высшей математики.
Естественно, на перевод многоэтажной дроби в понятный вид уходит дополнительное время и место. Поэтому можно воспользоваться более быстрым методом. Данный метод удобен и на выходе позволяет получить готовое выражение, в котором первая дробь уже умножена на дробь, обратную второй.
Реализуется этот метод следующим образом:
Если дробь четырехэтажная, например как , то цифру находящуюся на первом этаже поднимают на самый верхний этаж. А цифру, находящуюся на втором этаже поднимают на третий этаж. Полученные цифры нужно соединить значками умножения (×)
А цифру, находящуюся на втором этаже поднимают на третий этаж. Полученные цифры нужно соединить значками умножения (×)
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратную второй. Удобство да и только!
Чтобы не допускать ошибок при использовании данного метода, можно руководствоваться следующим правилом:
С первого на четвёртый. Со второго на третий.
В правиле речь идет об этажах. Цифру с первого этажа нужно поднимать на четвертый этаж. А цифру со второго этажа нужно поднимать на третий этаж.
Попробуем вычислить многоэтажную дробь пользуясь вышеприведённым правилом.
Итак, цифру находящуюся на первом этаже поднимаем на четвёртый этаж, а цифру находящуюся на втором этаже поднимаем на третий этаж
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратной второй. Далее можно воспользоваться имеющимися знаниями:
Попробуем вычислить многоэтажную дробь пользуясь новой схемой.
Здесь имеется только первый, второй и четвёртый этажи. Третий этаж отсутствует. Но мы не отходим от основной схемы: цифру с первого этажа поднимаем на четвёртый этаж. А поскольку третий этаж отсутствует, то цифру находящуюся на втором этаже оставляем, как есть
В результате, минуя промежуточную запись мы получили новое выражение , в котором первое число −3 уже умножено на дробь, обратную второй. Далее можно воспользоваться имеющимися знаниями:
Попробуем вычислить многоэтажную дробь , пользуясь новой схемой.
Здесь имеется только второй, третий и четвёртый этажи. Первый этаж отсутствует. Поскольку первый этаж отсутствует, подниматься на четвёртый этаж нечему, но зато мы можем поднять цифру со второго этажа на третий:
В результате, минуя промежуточную запись мы получили новое выражение , в котором первая дробь уже умножена на число, обратное делителю. Далее можно воспользоваться имеющимися знаниями:
Использование переменных
Если выражение сложное и вам кажется, что оно запутает вас в процессе решения задачи, то часть выражения можно занести в переменную и далее работать с этой переменной.
Математики часто так и делают. Сложную задачу разбивают на более лёгкие подзадачи и решают их. Затем собирают решённые подзадачи в одно единое целое. Это творческий процесс и этому учатся годами, упорно тренируясь.
Использование переменных оправдано, при работе с многоэтажными дробями. Например:
Найти значение выражения
Итак, имеется дробное выражение в числителе и в знаменателе котором дробные выражения. Другими словами, перед нами снова многоэтажная дробь, которую мы так не любим.
Выражение, находящееся в числителе можно занести в переменную с любым названием, например:
Но в математике в подобном случае переменным принято давать название из больших латинских букв. Давайте не будем нарушать эту традицию, и обозначим первое выражение через большую латинскую букву A
А выражение, находящееся в знаменателе можно обозначить через большую латинскую букву B
Теперь наше изначальное выражение принимает вид . То есть, мы сделали замену числового выражения на буквенное, предварительно занеся числитель и знаменатель в переменные A и B.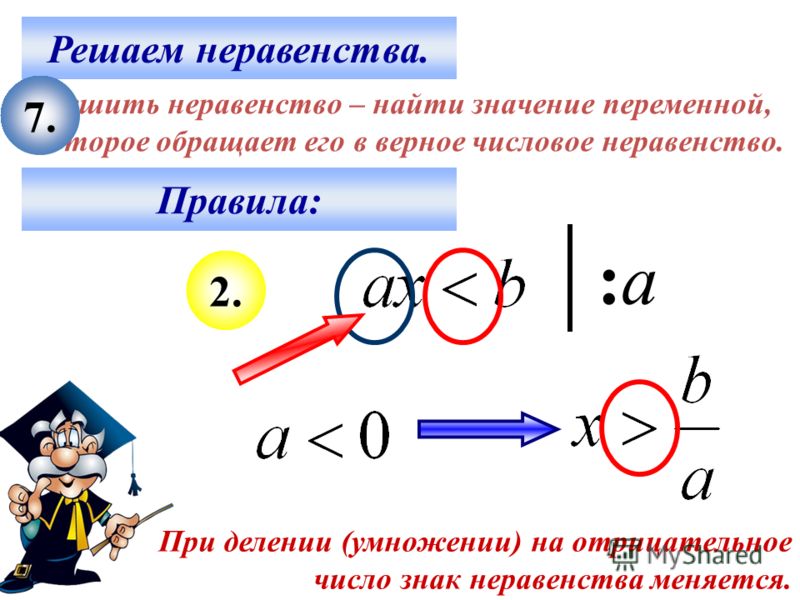
Теперь мы можем отдельно вычислить значения переменной A и значение переменной B. Готовые значения мы вставим в выражение .
Найдём значение переменной A
Найдём значение переменной B
Теперь подставим в главное выражения вместо переменных A и B их значения:
Мы получили многоэтажную дробь в которой можно воспользоваться схемой «с первого на четвёртый, со второго на третий», то есть цифру находящуюся на первом этаже поднять на четвёртый этаж, а цифру находящуюся на втором этаже поднять на третий этаж. Дальнейшее вычисление не составит особого труда:
Таким образом, значение выражения равно −1.
Конечно, мы рассмотрели простейший пример, но нашей целью было узнать, как можно использовать переменные для облегчения себе задачи, чтобы свести к минимуму допущение ошибок.
Отметим также, что решение для данного примера можно записать не применяя переменные. Выглядеть оно будет как
Это решение более быстрое и короткое и в данном случае его целесообразнее так и записать, но если выражение окажется сложным, состоящим из нескольких параметров, скобок, корней и степеней, то желательно вычислять его в несколько этапов, занося часть его выражений в переменные.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
В этой статье мы разберемся с умножением чисел с разными знаками . Здесь мы сначала сформулируем правило умножения положительного и отрицательного числа, обоснуем его, а после этого рассмотрим применение данного правила при решении примеров.
Навигация по странице.
Правило умножения чисел с разными знаками
Умножение положительного числа на отрицательное, а также отрицательного на положительное, проводится по следующему правилу умножения чисел с разными знаками : чтобы умножить числа с разными знаками, надо умножить , и перед полученным произведением поставить знак минус.
Запишем данное правило в буквенном виде. Для любого положительного действительного числа a
и действительного отрицательного числа −b
справедливо равенство a·(−b)=−(|a|·|b|) , а также для отрицательного числа −a
и положительного числа b
справедливо равенство (−a)·b=−(|a|·|b|) .
Правило умножения чисел с разными знаками полностью согласуется со свойствами действий с действительными числами . Действительно, на их основе несложно показать, что для действительных и положительных чисел a и b справедлива цепочка равенств вида a·(−b)+a·b=a·((−b)+b)=a·0=0 , которая доказывает, что a·(−b) и a·b – противоположные числа, откуда следует равенство a·(−b)=−(a·b) . А из него следует справедливость рассматриваемого правила умножения.
Следует отметить, что озвученное правило умножения чисел с разными знаками справедливо как для действительных чисел, так и для рациональных чисел и для целых чисел . Это следует из того, что действия с рациональными и целыми числами обладают теми же свойствами, которые использовались при доказательстве выше.
Понятно, что умножение чисел с разными знаками по полученному правилу сводится к умножению положительных чисел.
Осталось лишь рассмотреть примеры применения разобранного правила умножения при умножении чисел с разными знаками.
Примеры умножения чисел с разными знаками
Разберем решения нескольких примеров умножения чисел с разными знаками . Начнем с простого случая, чтобы сосредоточиться на шагах правила, а не на вычислительных сложностях.
Пример.
Выполните умножение отрицательного числа −4 на положительное число 5 .
Решение.
По правилу умножения чисел с разными знаками нам сначала нужно перемножить модули исходных множителей. Модуль −4 равен 4 , а модуль 5 равен 5 , а умножение натуральных чисел 4 и 5 дает 20 . Наконец, осталось поставить знак минус перед полученным числом, имеем −20 . На этом умножение завершено.
Кратко решение можно записать так: (−4)·5=−(4·5)=−20 .
Ответ:
(−4)·5=−20 .
При умножении дробных чисел с разными знаками нужно уметь выполнять умножение обыкновенных дробей , умножение десятичных дробей и их комбинаций с натуральными и смешанными числами.
Пример.
Проведите умножение чисел с разными знаками 0,(2)
и .
Решение.
Выполнив перевод периодической десятичной дроби в обыкновенную дробь , а также выполнив переход от смешанного числа к неправильной дроби , от исходного произведения мы придем к произведению обыкновенных дробей с разными знаками вида . Это произведение по правилу умножения чисел с разными знаками равно . Осталось лишь перемножить обыкновенные дроби в скобках, имеем .
Умножение и деление на целые числа (предалгебра, изучение и понимание целых чисел) — Mathplanet
Вы также должны обращать внимание на знаки при умножении и делении. Следует помнить два простых правила:
Когда вы умножаете отрицательное число на положительное, произведение всегда отрицательное.
Когда вы умножаете два отрицательных числа или два положительных числа, произведение всегда будет положительным.
Это похоже на правило сложения и вычитания: два знака минус становятся плюсом, а плюс и минус становятся минусом.Однако при умножении и делении вы вычисляете результат, как если бы не было знаков минус, а затем смотрите на знаки, чтобы определить, положительный или отрицательный результат. Два примера быстрого умножения:
Два примера быстрого умножения:
$$ 3 \ cdot (-4) = — 12 $$
3 умножить на 4 равно 12. Поскольку существует одно положительное и одно отрицательное число, произведение отрицательное 12.
$$ (- 3) \ cdot (-4) = 12 $$
Теперь у нас есть два отрицательных числа, поэтому результат положительный.
Переходя к делению, вы можете вспомнить, что вы можете подтвердить полученный ответ, умножив частное на знаменатель.Если вы ответили правильно, то произведение этих двух чисел должно совпадать с числителем. Например,
$$ \ frac {12} {3} = 4 $$
Чтобы проверить, является ли 4 правильным ответом, мы умножаем 3 (знаменатель) на 4 (частное):
$$ 3 \ cdot 4 = 12 $$
Что произойдет, если разделить два отрицательных числа? Например,
$$ \ frac {(- 12)} {(- 3)} = \:? $$
Чтобы знаменатель (-3) стал числителем (-12), вам нужно умножить его на 4, поэтому частное равно 4.
Итак, частное отрицательного и положительного чисел отрицательно, и, соответственно, частное положительного и отрицательного чисел также отрицательно. Можно сделать вывод, что:
Можно сделать вывод, что:
Когда вы делите отрицательное число на положительное, то частное отрицательное.
Когда вы делите положительное число на отрицательное, частное также становится отрицательным.
Когда вы делите два отрицательных числа, получается положительное частное.
Те же правила верны и для умножения.
Видеоурок
Вычислить следующие выражения
$$ (- 4) \ cdot (-12), \: \: \: \: \ frac {-12} {3} $$
Умножение и деление положительных и отрицательных чисел
Правила умножения и деления чисел очень похожи. Ключ состоит в том, чтобы определить, совпадают ли знаки у данных двух чисел или разные, потому что это определит окончательный знак ответа.
Правила умножения и деления чисел со знаком
Примеры того, как найти произведение или частное числа со знаком
Пример 1 : Найдите произведение (3) (6) и частное 12 ÷ 6 .
- Найдите произведение (3) (6):
Поскольку числа 3 и 6 имеют одинаковые знаки (оба положительные), их произведение положительно.
(3) (6) = 18
- Найдите частное от 12 ÷ 6:
Поскольку числа 12 и 6 имеют одинаковые знаки (оба положительные), их частное положительное.
12 ÷ 6 = 2
Пример 2 : Найдите произведение (–5) (- 3) и частное — 21 ÷ (–7) .
- Найдите произведение (–5) (- 3):
Числа −5 и −3 имеют отрицательные знаки. Наличие такого же знака означает, что их продукт также должен быть положительным.
(–5) (- 3) = 15
- Найдите частное от — 21 ÷ (–7) :
У чисел −5 и −3 есть отрицательные знаки. Частное двух чисел с одинаковым знаком положительно.
— 21 ÷ (–7) = 3
Пример 3 : Умножьте числа (9) (- 3) и разделите числа 18 ÷ (–9) .
Число 9 имеет положительный знак, а число −3 имеет отрицательный знак. Умножение этих двух чисел на разные знаки должно дать отрицательный ответ.
(9) (- 3) = –27
Число 9 положительно, а −3 отрицательно. Разделение двух чисел с разными знаками должно дать отрицательный ответ.
18 ÷ (–9) = –2
Пример 4 : Упростите числовое выражение.
Мы можем упростить числитель, умножив два числа.Сделайте то же самое со знаменателем.
Числа в числителе имеют разные знаки, поэтому мы ожидаем, что их произведение будет отрицательным. Между тем в знаменателе есть два числа с одинаковым знаком (оба отрицательные), поэтому их произведение должно быть положительным.
Завершим это делением числителя на знаменатель. Не забывайте также о правилах деления. Числитель отрицательный, а знаменатель положительный, наличие разных знаков должно давать отрицательный ответ.
Пример 5 : Умножьте числа (–1) (- 2) (- 3) (- 4) .
До сих пор мы умножали числа по два за раз. На этот раз мы можем найти произведение трех или более чисел.
Мы можем решить это, умножая два числа за раз, потому что мы знаем, как это сделать.
Но есть быстрый способ определить знак, не умножая их по два за раз.
Обратите внимание, что у нас есть четное количество отрицательных знаков , то есть четыре отрицательных числа.Если вы столкнулись с чем-то вроде этого, воспользуйтесь правилом:
Четное число отрицательных знаков означает, что мы ожидаем положительного ответа.
(–1) (- 2) (- 3) (- 4) = +24
Пример 6 : умножить числа (–1) (–1) (–1 ) (–1) (–1) (–1) (–1) (–1) (–1) .
Эта проблема не предназначена для того, чтобы вас обмануть. Вместо этого думайте об этом как о еще одной возможности научиться решать такой вопрос.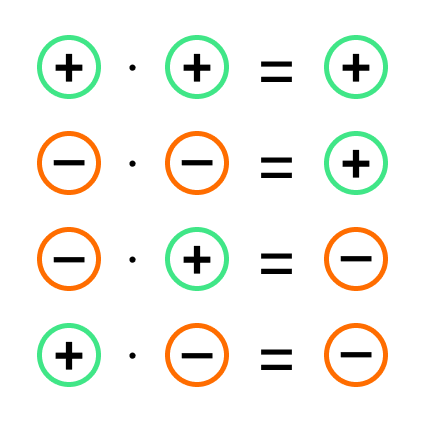 Ваш учитель может использовать что-то подобное в вашей викторине, чтобы проверить, хорошо ли вы знаете тему.
Ваш учитель может использовать что-то подобное в вашей викторине, чтобы проверить, хорошо ли вы знаете тему.
Не обращая внимания на знаки, все числа — единицы. Следовательно, мы предполагаем, что ответ может быть +1 или -1 .
Подсчитав количество отрицательных знаков, мы получим девять (9), что является нечетным!
Запомните правило:
Нечетное количество отрицательных знаков означает, что наш окончательный ответ должен быть отрицательным.
(–1) (–1) (–1) (–1) (–1) (–1) (–1) (–1) (–1) = –1
Пример 7 : Разделите числа (–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) .
Правило нечетного и четного числа отрицательных чисел также работает при делении чисел.
Поскольку у нас есть семь (7) отрицательных знаков, нечетное число, ответ должен быть отрицательным.
(–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) ÷ (–1) = –1
Умножение и деление чисел со знаком — Предварительно -Алгебра
После того, как вы закончите этот урок, просмотрите все наши уроки предварительной алгебры и практические задачи.
В этом видео мы научимся умножать и делить положительные и отрицательные числа.
Когда два знака совпадают +
Когда два знака разные —
Умножение и деление
Пример 1
Правило умножения целых чисел:
Если два знака совпадают, ответ положительный.
Если два знака различны, ответ отрицательный.
Поскольку оба числа положительны, ответ будет положительным.
Следовательно,
Пример 2
Правило деления целых чисел:
Если два знака совпадают, ответ положительный.
Если два знака различны, ответ отрицательный.
Поскольку у двух чисел разные знаки, ответ отрицательный.
Следовательно,
Стенограмма видеоурока
Давайте посмотрим на умножение и деление чисел со знаком.
Это означает умножение и деление положительных и отрицательных чисел.
Правило очень простое. То же самое правило для умножения и деления.
Если два знака совпадают, ответ положительный.
Если два знака различны, ответ отрицательный.
Приведем несколько быстрых примеров.
Для этого оба числа положительные, поэтому ответ положительный.
Даже если оба числа отрицательные, поскольку оба знака совпадают, ответ все равно будет положительным.
Эти два числа имеют разные знаки, поэтому ответ отрицательный.
Опять разные знаки поэтому ответ отрицательный.
Порядок здесь не имеет значения.
То же самое и с делением.
Знаки другие, значит отрицательный.
Давай
Знаки те же, значит, положительный.
Что делать, если у нас более двух чисел?
Например:
Давайте решим по два за раз.
Знаки другие, значит отрицательный. Затем переходите к умножению другого числа.
В этом случае оба числа имеют одинаковый знак, поэтому ответ положительный.
Напомню, что у нас одни и те же правила умножения и деления.
Если два знака совпадают, ответ положительный.
Если два знака различны, ответ отрицательный.
Умножение и деление целых чисел — методы и примеры
В математике арифметические операции с целыми числами включают вычитание, сложение, деление и умножение всех типов действительных чисел. В частности, целые числа — это числа, которые включают положительные, отрицательные и нулевые числа. Умножение и деление целых чисел регулируются аналогичными правилами.
Как умножать целые числа?
Умножение определяется как повторное сложение целых чисел. Умножение целых чисел включает три случая:
- Умножение двух положительных целых чисел
- Умножение двух отрицательных целых чисел
- Умножение положительного и отрицательного целого числа.

Умножение двух целых чисел со знаком равенства всегда дает положительный результат. Это означает, что произведение двух положительных или двух отрицательных целых чисел положительно.С другой стороны, целые числа продукта со знаком отличия всегда будут отрицательными.
Многие студенты сталкиваются с проблемой запоминания приведенных выше правил умножения целых чисел. В этой статье есть сценарий, который поможет вам избежать путаницы. В этом сценарии положительный знак (+) используется для обозначения « ХОРОШО », а отрицательный знак символизирует фразу « BAD ». «Давайте взглянем на эту мнемонику.
- Если хорошие (+) вещи случаются с хорошими (+) людьми, то это хорошо (+)
- Если хорошие (+) вещи случаются с плохими (-) людьми, то это плохо (-)
- Если плохие (-) вещи случаются с хорошими (+) людьми, тогда это плохо (-)
- Если плохие (-) вещи случаются с плохими (-) людьми, то это хорошо (+)
Чтобы умножить целые числа, просто умножьте числовые числа без знака и поставьте знак на продукте, вспомнив приведенные выше правила.
Пример 1
- 7 x 5 = 35
- 7 × (-6) = -42
- (-9) × 5 = -45
- (-4) × (-5) = 20
Если количество отрицательных множимых в предложении умножения нечетное, произведение будет отрицательным числом.
Пример 2
(-2) × (−4) × (−3) = −24; здесь количество множимых = 3 (нечетное число)
Когда количество отрицательных множимых в предложении умножения четное, произведение будет положительным.
Пример 3
(-4) × (-3) = 12; Здесь число множимых равно 2 (четным)
Как разделить целые числа?
Если умножение — это суммирование целых чисел, то деление — это распределение целых чисел. Мы можем просто сказать, что деление — это обратное умножение. Правила деления целых чисел аналогичны правилам умножения. Единственная разница в делении состоит в том, что частное может не быть целым числом.
Давайте также посмотрим на правила деления:
- Частное положительного целого числа всегда положительно.
 Если и делимое, и делитель являются положительными целыми числами, значение частного будет положительным. Например, (+ 9) ÷ (+ 3) = + 3
Если и делимое, и делитель являются положительными целыми числами, значение частного будет положительным. Например, (+ 9) ÷ (+ 3) = + 3 - Частное двух отрицательных чисел всегда положительно. Это означает, что если дивиденд и делитель отрицательны, то частное всегда положительно. Например;
(- 9) ÷ (- 3) = + 3
Следовательно, при делении двух целых чисел с одинаковыми знаками мы делим числа без знака и ставим положительный знак результату. - Деление положительного и отрицательного целого числа дает отрицательный ответ. Например; (+ 16) ÷ (- 4) = — 4
Таким образом, чтобы разделить целые числа с разными знаками, числовые значения делятся без знаков, а результат ставится знаком минус.
Практические вопросы
- Вы насчитали всего 120 рук в своем классе. Сколько было учтено студентов?
- В тесте по математике 20 вопросов. За каждый правильный ответ дается три балла, за неправильный — 1 балл.
 Студент неправильно ответил на 5 вопросов. Сколько баллов потерял студент?
Студент неправильно ответил на 5 вопросов. Сколько баллов потерял студент? - Дайвер спускается со скоростью 40 футов в минуту от уровня моря. Найдите положение дайвера по отношению к уровню моря через 5 минут спуска?
- Мужчина должен банку 8000 долларов. Если каждый из его 4 друзей готов погасить ссуду, внося равную сумму. Определите, сколько денег вложил каждый из его друзей.
- 26 человек разделили между собой 5 876 долларов поровну. Сколько получил каждый?
Предыдущий урок | Главная страница | Следующий урок
Правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.[Решено]
Вопрос: Перечислите правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.

Четыре основные арифметические операции, связанные с целыми числами:
- Сложение целых чисел
- Вычитание целого числа
- Умножение целых чисел
- Деление целых чисел
Ответ: Есть некоторые правила сложения, вычитания, умножения и деления положительных и отрицательных чисел.
Прежде чем мы начнем изучать эти методы операций с целыми числами, нам нужно запомнить несколько вещей. Если перед числом нет знака, это означает, что число положительное.
Пояснение:
Ниже приведены правила сложения, вычитания, умножения и деления положительных и отрицательных чисел
Правило сложения целых чисел:
Случай 1: Знаки одинаковые
Если знаки такие же, добавить и сохранить тот же знак.
- (+) + (+) = сложите числа и получите положительный ответ
Пример: 2 + 5 = 7
- (-) + (-) = сложите числа, и ответ будет отрицательным
Пример: (-5) + (-4) = -9
Случай 2: Знаки разные
Если знаки разные, вычтите числа и используйте знак большего числа
- (+) + (-) = вычесть числа и принять знак большего числа
Пример: 7 + (-3) = 4
- (-) + (+) = вычесть числа и принять знак большего числа
Пример: (-9) + 6 = -3
Правило вычитания целых чисел:
Чтобы вычесть число из другого числа, следует изменить знак числа (которое должно быть вычтено), а затем это число с измененным знаком следует прибавить к первому числу.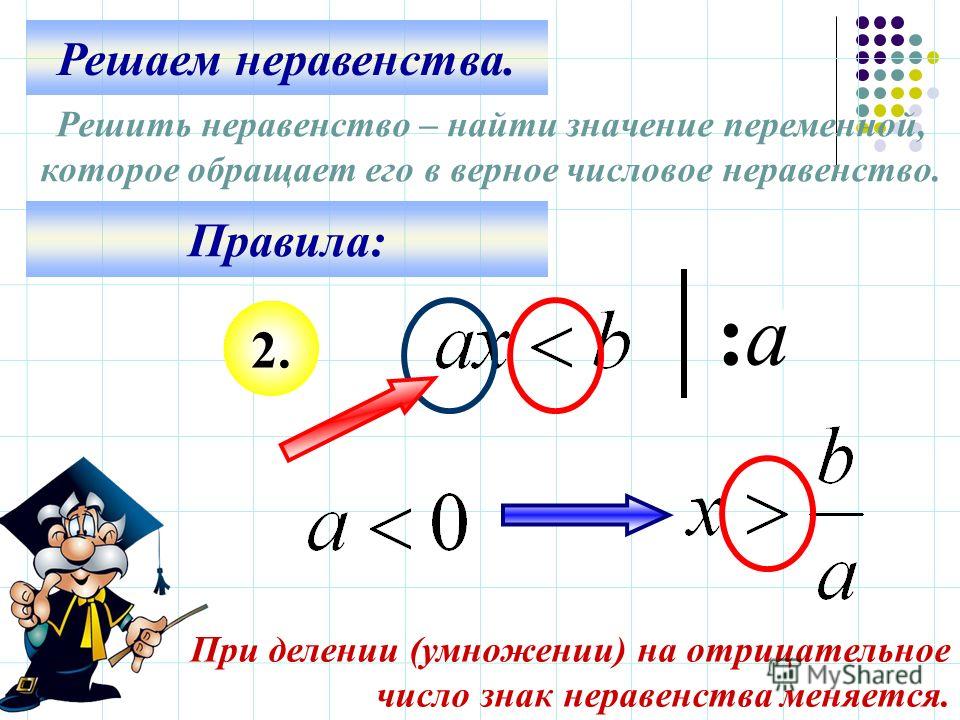
- (+) — (+) = Измените знак числа, которое нужно вычесть, и сложите их. Результат принимает знак большего числа
Пример: (+6) — (+2)
= (+6) + (-2) = 6-2 = 4
- (-) — (-) = Измените знак числа, которое нужно вычесть, и сложите их. Результат принимает знак большего числа
Пример: (-9) — (-6)
= (-9) + (+6) = -9 + 6 = -3
- (+) — (-) = Измените знак числа, которое нужно вычесть, и сложите их.Результат всегда положительный
Пример: (+5) — (-3)
= (+5) + (+ 3) = 5 + 3 = 8
- (-) — (+) = Измените знак числа, которое нужно вычесть, и сложите их. Результат всегда отрицательный
Пример: (-7) — (+2)
= (-7) + (-2) = -7-2 = -9
Правило умножения и деления целых чисел:
Случай 1: Знаки одинаковые
Если знаки одинаковые, умножьте или разделите, и ответ всегда будет положительным.
Пример: 5 × 4 = 20
Пример: 16 ÷ 4 = 4
Пример: (-7) × (-9) = 63
Пример: (-20) ÷ (-2) = 10
Случай 2: Знаки разные
Если знаки разные, умножить или разделить, ответ всегда отрицательный.
Пример: 6 × (-10) = -60
Пример: 30 ÷ (-15) = -2
Пример: -3 × 11 = 33
Пример: -25 ÷ 5 = -5
Таким образом, мы научились складывать, вычитать, умножать и делить положительные и отрицательные числа.
вещественных чисел | Начальная алгебра
Результаты обучения
- Сложить и вычесть действительные числа
- Сложить вещественные числа с одинаковыми и разными знаками
- Вычесть действительные числа с одинаковыми и разными знаками
- Упростите комбинации, которые требуют как сложения, так и вычитания действительных чисел.
- Умножение и деление действительных чисел
- Умножение двух или более действительных чисел.
- Разделить действительные числа
- Упростите выражения умножением и делением
- Упростите выражения с помощью действительных чисел
- Распознавать и комбинировать похожие термины в выражении
- Используйте порядок операций для упрощения выражений
- Упростите составные выражения с помощью действительных чисел
- Упростите выражения с помощью дробных черт, скобок и круглых скобок
- Используйте свойство распределения для упрощения выражений с помощью символов группировки
- Упростить выражения, содержащие абсолютные значения
Перед тем, как мы начнем, следует запомнить некоторые важные термины:
- целые числа: подсчет чисел, таких как 1, 2, 3 и т.
 Д., включая негативы и ноль
Д., включая негативы и ноль - вещественное число: дроби, отрицательные числа, десятичные дроби, целые числа и ноль — все это действительные числа
- абсолютное значение: расстояние от нуля до числа; это всегда положительно. [латекс] | -7 | = 7 [/ латекс]
- знак: это относится к положительному или отрицательному числу, мы используем [latex] + [/ latex] для положительного (справа от нуля в числовой строке) и [latex] — [/ latex] для отрицательного. (слева от нуля в числовой строке)
- разница: результат вычитания
- сумма: результат сложения
Умение комфортно работать с отрицательными числами необходимо для успеха в алгебре.По этой причине мы сделаем краткий обзор сложения, вычитания, умножения и деления целых чисел. Целые числа — это все положительные целые числа, ноль и их противоположности (отрицательные). Поскольку это обзор целых чисел, описания и примеры не будут такими подробными, как на обычном уроке.
Сложение и вычитание действительных чисел
При сложении целых чисел необходимо рассмотреть два случая. Первый случай — совпадают ли знаки (положительные или отрицательные). Если знаки совпадают, мы сложим числа и сохраним знак.
Если знаки не совпадают (одно положительное и одно отрицательное число), мы вычтем числа (как если бы все они были положительными), а затем используем знак из большего числа. Это означает, что если большее число положительно, ответ будет положительным. Если большее число отрицательно, ответ отрицательный.
Чтобы сложить два числа с одинаковым знаком (положительное или отрицательное)
- Добавьте их абсолютных значений (без знака [latex] + [/ latex] или [latex] — [/ latex])
- Поставьте сумму тем же знаком.
Чтобы сложить два числа с разными знаками (одно положительное и одно отрицательное)
- Найдите разность из их абсолютных значений. (Обратите внимание, что когда вы обнаруживаете разницу абсолютных значений, вы всегда вычитаете меньшее абсолютное значение из большего.
 )
) - Укажите для суммы тот же знак, что и у числа с большим абсолютным значением.
Пример
Найдите [латекс] 23–73 [/ латекс].
Показать решение Вы не можете использовать свой обычный метод вычитания, потому что 73 больше 23.Перепишите вычитание как добавление противоположного.
[латекс] 23+ \ влево (-73 \ вправо) [/ латекс]
Слагаемые имеют разные знаки, поэтому найдите разницу их абсолютных значений.
[латекс] \ begin {array} {c} \ left | 23 \ right | = 23 \, \, \, \ text {and} \, \, \, \ left | −73 \ right | = 73 \\ 73-23 = 50 \ end {array} [/ latex]
Поскольку [латекс] \ left | −73 \ right |> \ left | 23 \ right | [/ latex], окончательный ответ отрицательный.
Ответ
[латекс] 23–73 = −50 [/ латекс]
Другой способ подумать о вычитании — это подумать о расстоянии между двумя числами на числовой прямой.В приведенном ниже примере [latex] 382 [/ latex] соответствует правому из 0 на [latex] 382 [/ latex] единиц, а [latex] -93 [/ latex] находится к левому из 0 на 93 ед. Расстояние между ними — это сумма расстояний до 0: [латекс] 382 + 93 [/ латекс].
Расстояние между ними — это сумма расстояний до 0: [латекс] 382 + 93 [/ латекс].
Пример
Найдите [латекс] 382– \ left (−93 \ right) [/ latex].
Показать решение Вы убираете отрицательный знак, поэтому думайте об этом как об удалении отрицательного знака. Это становится дополнительной проблемой. [латекс] -93 [/ латекс] становится [латекс] +93 [/ латекс]
[латекс] 382 + 93 = 475 [/ латекс]
Ответ
[латекс] 382 — (- 93) = 475 [/ латекс]
В следующем видео объясняется, как вычесть два целых числа со знаком.
Пример
Найдите [латекс] — \ frac {3} {7} — \ frac {6} {7} + \ frac {2} {7} [/ latex]
Показать решение Сложите первые два и дайте результату знак минус:
Так как знаки у первых двух одинаковые, найти сумму абсолютных значений дробей
Поскольку оба числа отрицательны, сумма отрицательна. Если вы должны деньги, то занимайте больше, и сумма вашей задолженности становится больше.
Если вы должны деньги, то занимайте больше, и сумма вашей задолженности становится больше.
[латекс] \ левый | — \ frac {3} {7} \ right | = \ frac {3} {7} [/ latex] и [latex] \ left | — \ frac {6} {7} \ right | = \ frac {6} {7} [/ латекс]
[латекс] \ begin {array} {c} \ frac {3} {7} + \ frac {6} {7} = \ frac {9} {7} \\\\ — \ frac {3} {7 } — \ frac {6} {7} = — \ frac {9} {7} \ end {array} [/ latex]
Теперь добавьте третье число.Знаки разные, поэтому найдите разницы их абсолютных значений.
[латекс] \ левый | — \ frac {9} {7} \ right | = \ frac {9} {7} [/ latex] и [latex] \ left | \ frac {2} {7} \ right | = \ frac {2} {7} [/ латекс]
[латекс] \ frac {9} {7} — \ frac {2} {7} = \ frac {7} {7} [/ latex]
Поскольку [latex] \ left | \ frac {-9} {7} \ right |> \ left | \ frac {2} {7} \ right | [/ latex], знак окончательной суммы такой же, как знак [латекс] — \ frac {9} {7} [/ латекс].
[латекс] — \ frac {9} {7} + \ frac {2} {7} = — \ frac {7} {7} [/ латекс]
Ответ
[латекс] — \ frac {3} {7} + \ left (- \ frac {6} {7} \ right) + \ frac {2} {7} = — \ frac {7} {7} [/ латекс]
В следующем видео вы увидите пример того, как сложить три дроби с общим знаменателем и разными знаками.
Пример
Оценить [латекс] 27,832 + (- 3,06) [/ латекс]. Когда вы добавляете десятичные дроби, не забудьте выровнять десятичные дроби так, чтобы вы добавляли десятые доли к десятым, сотые к сотым и т. Д.
Показать решение Поскольку слагаемые имеют разные знаки, вычтите их абсолютные значения.
[латекс] \ begin {array} {r} \ underline {\ begin {array} {r} 27.832 \\ — \ text {} 3.06 \, \, \, \ end {array}} \\ 24.772 \ end { array} [/ latex]
[латекс] \ влево | -3,06 \ вправо | = 3.06 [/ латекс]
Сумма имеет тот же знак, что и 27,832, абсолютное значение которого больше.
Ответ
[латекс] 27,832+ \ влево (-3,06 \ вправо) = 24,772 [/ латекс]
В следующем видео представлены примеры сложения и вычитания десятичных знаков с разными знаками.
youtube.com/embed/3FHZQ5iKcpI?feature=oembed» frameborder=»0″ gesture=»media» allow=»encrypted-media» allowfullscreen=»»>Умножение и деление действительных чисел
Умножение и деление — это обратные операции , так же как сложение и вычитание. Вы можете вспомнить, что когда вы делите дроби, вы умножаете их на обратную.Обратные операции «отменяют» друг друга.
Умножение действительных чисел
Умножение действительных чисел ничем не отличается от умножения целых чисел и положительных дробей. Однако вы не знаете, как отрицательный знак влияет на товар.
С целыми числами вы можете думать об умножении как о повторяющемся сложении. Используя числовую линию, вы можете совершить несколько прыжков заданного размера. Например, на следующем рисунке продукт [latex] 3 \ cdot4 [/ latex] показан в виде 3 прыжков по 4 единицы каждый.
Итак, чтобы умножить [latex] 3 (−4) [/ latex], вы можете повернуться лицом влево (в отрицательную сторону) и сделать три «прыжка» вперед (в отрицательном направлении).
Произведение положительного числа и отрицательного числа (или отрицательного и положительного) дает отрицательное значение.
Произведение положительного и отрицательного числа
Чтобы умножить положительное число и отрицательное число , умножьте их абсолютные значения. Произведение минус .
Пример
Найдите [латекс] −3,8 (0,6) [/ латекс].
Показать решение Умножьте абсолютные значения, как обычно. Установите десятичную точку, считая разряды. 3.8 имеет 1 место после десятичной точки, а 0.6 имеет 1 место после десятичной точки, поэтому продукт имеет [латекс] 1 + 1 [/ latex] или 2 разряда после десятичной точки.
[латекс] \ begin {array} {r} 3.8 \\\ underline {\ times \, \, \, 0.6} \\ 2.28 \ end {array} [/ latex]
Произведение отрицательного и положительного отрицательного.
Ответ
[латекс] -3,8 (0,6) = — 2,28 [/ латекс]
Следующее видео содержит примеры умножения десятичных чисел с разными знаками.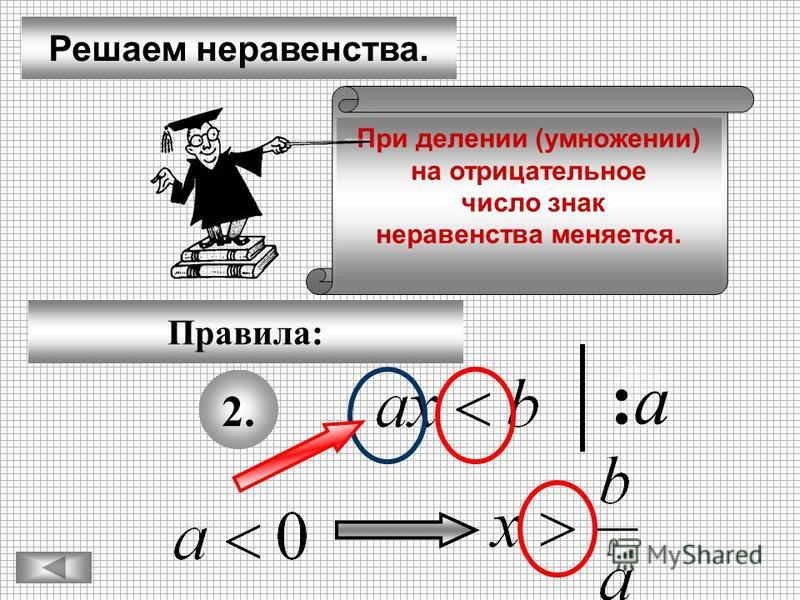
Произведение двух чисел с одинаковым знаком (как положительных, так и отрицательных)
Чтобы умножить два положительных числа , умножьте их абсолютные значения. Продукт положительный .
Чтобы умножить два отрицательных числа на , умножьте их абсолютные значения.Продукт положительный .
Пример
Найдите [латекс] ~ \ left (- \ frac {3} {4} \ right) \ left (- \ frac {2} {5} \ right) [/ latex]
Показать решение Умножьте абсолютные значения чисел. Сначала умножьте числители, чтобы получить числитель произведения. Затем умножьте знаменатели, чтобы получить знаменатель произведения. При необходимости перепишите в минимальных терминах.
[латекс] \ left (\ frac {3} {4} \ right) \ left (\ frac {2} {5} \ right) = \ frac {6} {20} = \ frac {3} {10} [/ латекс]
Произведение двух отрицательных чисел положительно.
Ответ
[латекс] \ left (- \ frac {3} {4} \ right) \ left (- \ frac {2} {5} \ right) = \ frac {3} {10} [/ latex]
В следующем видео показаны примеры умножения двух дробей со знаком, включая упрощение ответа.
Суммируем:
- положительный [латекс] \ cdot [/ latex] положительный : Продукт положительный .
- отрицательный [латекс] \ cdot [/ latex] отрицательный : Продукт положительный .
- отрицательный [латекс] \ cdot [/ latex] положительный : Продукт отрицательный .
- положительный [латекс] \ cdot [/ latex] отрицательный : Продукт отрицательный .

Как видите, произведение двух отрицательных чисел является положительным числом. Итак, если вы умножаете более двух чисел, вы можете подсчитать количество отрицательных множителей.
Умножение более двух отрицательных чисел
Если есть четное число (0, 2, 4,…) отрицательных множителей для умножения, произведение будет положительным .
Если имеется нечетное число (1, 3, 5,…) отрицательных факторов, произведение отрицательное .
Пример
Найдите [латекс] 3 (−6) (2) (- 3) (- 1) [/ latex].
Показать решение Умножьте абсолютные значения чисел.
[латекс] \ begin {array} {l} 3 (6) (2) (3) (1) \\ 18 (2) (3) (1) \\ 36 (3) (1) \\ 108 ( 1) \\ 108 \ end {array} [/ latex]
Подсчитайте количество отрицательных факторов. Есть три [латекса] \ left (−6, −3, −1 \ right) [/ latex].
[латекс] 3 (−6) (2) (- 3) (- 1) [/ латекс]
Поскольку существует нечетное количество отрицательных факторов, произведение отрицательное.
Ответ
[латекс] 3 (−6) (2) (- 3) (- 1) = — 108 [/ латекс]
Следующее видео содержит примеры умножения более двух целых чисел со знаком.
Разделить действительные числа
Вы можете помнить, что когда вы делили дроби, вы умножали на обратную величину . Reciprocal — это другое название мультипликативного обратного (точно так же, как напротив — другое название для аддитивного обратного).
Самый простой способ найти обратное умножение — просто «перевернуть» числитель и знаменатель, как вы это делали, чтобы найти обратное.Вот несколько примеров:
- Обратное значение [latex] \ frac {4} {9} [/ latex] равно [latex] \ frac {9} {4} [/ latex], потому что [latex] \ frac {4} {9} \ left (\ frac {9} {4} \ right) = \ frac {36} {36} = 1 [/ латекс].
- Обратное значение 3 равно [latex] \ frac {1} {3} [/ latex], потому что [latex] \ frac {3} {1} \ left (\ frac {1} {3} \ right) = \ frac {3} {3} = 1 [/ латекс].

- Обратное значение [latex] — \ frac {5} {6} [/ latex] равно [latex] \ frac {-6} {5} [/ latex], потому что [latex] — \ frac {5} {6} \ left (- \ frac {6} {5} \ right) = \ frac {30} {30} = 1 [/ latex].
- Обратное значение 1 равно 1, так как [латекс] 1 (1) = 1 [/ латекс].
Когда вы делите на положительные дроби, вы научились умножать на обратную. Вы также делаете это, чтобы разделить вещественных числа на .
Подумайте о том, чтобы разделить мешок из 26 шариков на два мешка меньшего размера с одинаковым количеством шариков в каждом. Вы также можете сказать, что каждая сумка меньшего размера содержит и половину шариков.
[латекс] 26 \ div 2 = 26 \ left (\ frac {1} {2} \ right) = 13 [/ latex]
Обратите внимание, что 2 и [latex] \ frac {1} {2} [/ latex] являются обратными величинами.
Попробуйте еще раз, разделив мешок из 36 шариков на мешочки поменьше.
| Количество мешков | Деление на количество мешков | Умножение на обратное |
|---|---|---|
| 3 | [латекс] \ frac {36} {3} = 12 [/ латекс] | [латекс] 36 \ left (\ frac {1} {3} \ right) = \ frac {36} {3} = \ frac {12 (3)} {3} = 12 [/ latex] |
| 4 | [латекс] \ frac {36} {4} = 9 [/ латекс] | [латекс] 36 \ left (\ frac {1} {4} \ right) = \ frac {36} {4} = \ frac {9 \ left (4 \ right)} {4} = 9 [/ латекс] |
| 6 | [латекс] \ frac {36} {6} = 6 [/ латекс] | [латекс] 36 \ left (\ frac {1} {6} \ right) = \ frac {36} {6} = \ frac {6 \ left (6 \ right)} {6} = 6 [/ латекс] |
Деление на число аналогично умножению на обратную величину. (То есть вы используете обратную величину от делителя , второго числа в задаче деления.)
(То есть вы используете обратную величину от делителя , второго числа в задаче деления.)
Пример
Найдите [латекс] 28 \ div \ frac {4} {3} [/ latex]
Показать решение Перепишите деление как умножение на обратную. Аналог [latex] \ frac {4} {3} [/ latex] — это [latex] \ frac {3} {4} [/ latex].
[латекс] 28 \ div \ frac {4} {3} = 28 \ left (\ frac {3} {4} \ right) [/ latex]
Умножить.
[латекс] \ frac {28} {1} \ left (\ frac {3} {4} \ right) = \ frac {28 \ left (3 \ right)} {4} = \ frac {4 \ left ( 7 \ right) \ left (3 \ right)} {4} = 7 \ left (3 \ right) = 21 [/ латекс]
Ответ
[латекс] 28 \ div \ frac {4} {3} = 21 [/ латекс]
Теперь давайте посмотрим, что это значит, когда одно или несколько чисел отрицательны.Число и его обратная величина имеют один и тот же знак. Поскольку деление переписывается как умножение с использованием обратной величины делителя, а взятие обратной величины не меняет никаких знаков, деление следует тем же правилам, что и умножение.
Правила подкласса
При делении перепишите задачу как умножение, используя обратную величину делителя в качестве второго множителя.
Когда одно число — положительное , а другое — отрицательное , частное будет отрицательным .
Когда оба числа являются отрицательными , частное равно положительным .
Когда оба числа являются положительными , частное составляет положительных .
Пример
Найдите [латекс] 24 \ div \ left (- \ frac {5} {6} \ right) [/ latex].
Показать решение Перепишите деление как умножение на обратную.
[латекс] 24 \ div \ left (- \ frac {5} {6} \ right) = 24 \ left (- \ frac {6} {5} \ right) [/ latex]
Умножить.Поскольку одно число положительное, а другое отрицательное, произведение отрицательное.
[латекс] \ frac {24} {1} \ left (- \ frac {6} {5} \ right) = — \ frac {144} {5} [/ latex]
Ответ
[латекс] 24 \ div \ left (- \ frac {5} {6} \ right) = — \ frac {144} {5} [/ latex]
Пример
Найдите [латекс] 4 \, \ left (- \ frac {2} {3} \ right) \, \ div \ left (-6 \ right) [/ latex]
Показать решение
Перепишите деление как умножение на обратную.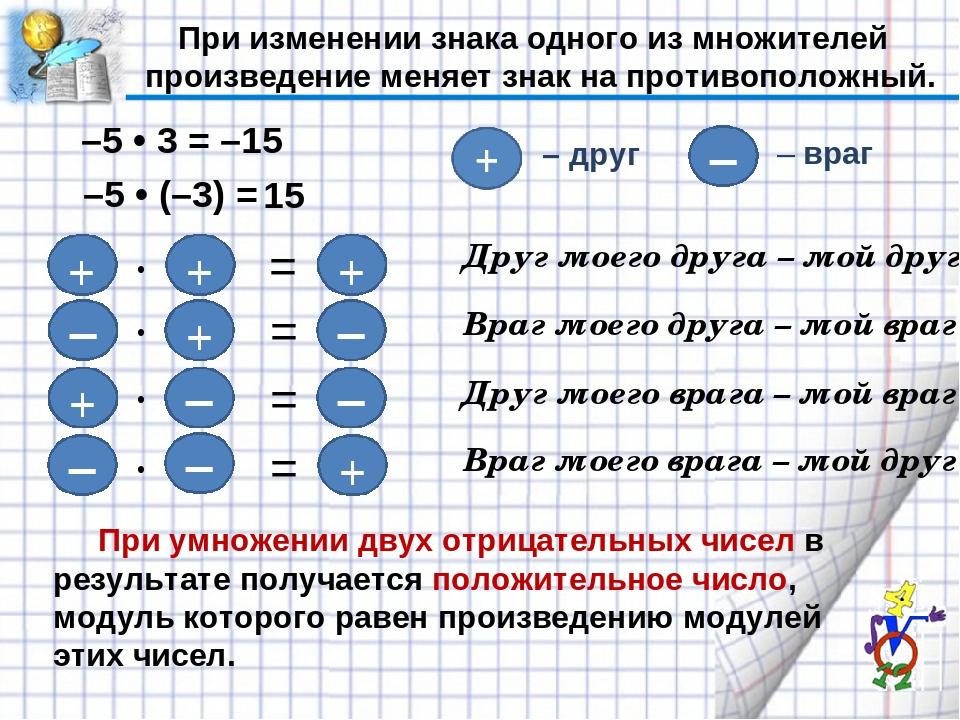
[латекс] \ frac {4} {1} \ left (- \ frac {2} {3} \ right) \ left (- \ frac {1} {6} \ right) [/ latex]
Умножить.Число отрицательных чисел четное, значит, произведение положительное.
[латекс] \ frac {4 \ left (2 \ right) \ left (1 \ right)} {3 \ left (6 \ right)} = \ frac {8} {18} [/ latex]
Запишите дробь наименьшим числом.
Ответ
[латекс] 4 \ left (- \ frac {2} {3} \ right) \ div \ left (-6 \ right) = \ frac {4} {9} [/ latex]
В следующем видео рассказывается, как делить дроби со знаком.
Помните, что черта дроби также указывает на деление, поэтому отрицательный знак перед дробью идет вместе с числителем, знаменателем или целой дробью: [latex] — \ frac {3} {4} = \ frac {-3 } {4} = \ frac {3} {- 4} [/ latex].
В каждом случае общая дробь отрицательная, потому что при делении есть только одно отрицательное число.
В следующем видео рассказывается, как делить дроби со знаком.
Упростите выражения с помощью действительных чисел
Прежде чем мы начнем, немного важной терминологии:
- операции / операторы: В математике мы называем такие вещи, как операции умножения, деления, сложения и вычитания. Это глаголы математического мира, выполняющие работу с числами и переменными. 2b [/ латекс] или [латекс] -3 [/ латекс] и [латекс] 8 [/ латекс]. Если у нас есть одинаковые термины, нам разрешено складывать (или вычитать) числа перед переменными, а затем оставлять переменные такими же. Когда мы комбинируем одинаковые термины, нам нужно интерпретировать знаки вычитания как часть следующего термина. Это означает, что если мы видим знак вычитания, мы рассматриваем следующий термин как отрицательный. Знак всегда соответствует сроку.

Это показано в следующих примерах:
Пример
Объедините похожие термины: [латекс] 5x-2y-8x + 7y [/ latex]
Показать решениеПодобные термины в этом выражении:
[латекс] 5x [/ латекс] и [латекс] -8x [/ латекс]
[латекс] -2y [/ латекс] и [латекс] -7y [/ латекс]
Обратите внимание, как мы держали табличку перед каждым термином.
Объедините похожие термины:
[латекс] 5x-8x = -3x [/ латекс]
[латекс] -2y-7y = -9y [/ латекс]
Обратите внимание, как знаки становятся операциями, когда вы объединяете одинаковые термины.
Упрощенное выражение:
[латекс] 5x-2y-8x + 7y = -3x-9y [/ латекс]
В следующем видео вам будет показано, как комбинировать одинаковые термины, используя идею распределительного свойства. Обратите внимание, что это другой метод, чем показан в письменных примерах на этой странице, но он дает тот же результат.2 \\ — 3x + 3x = 0 \, \, \, \, \, \, \, \, \, \, \, \\ 9-1 = 8 \, \, \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]
В следующем видео вам будет показан еще один пример объединения похожих терминов.
 Обратите внимание, почему вы не можете объединить все три термина в примере.
Обратите внимание, почему вы не можете объединить все три термина в примере.Порядок действий
Вы можете вспомнить или не вспомнить порядок операций для применения нескольких математических операций к одному выражению. Так же, как для нас принято ездить по правой стороне дороги, порядок операций — это набор соглашений, используемых для обеспечения порядка, когда вам необходимо использовать несколько математических операций для одного выражения.На приведенном ниже рисунке показан порядок выполнения математических операций.
Порядок работы
Пример
Упростить [латекс] 7–5 + 3 \ cdot8 [/ latex].
Показать решение Согласно порядку операций умножение предшествует сложению и вычитанию.Умножить [латекс] 3 \ cdot8 [/ latex].
[латекс] \ begin {array} {c} 7–5 + 3 \ cdot8 \\ 7–5 + 24 \ end {array} [/ latex]
Теперь сложите и вычтите слева направо.
 [латекс] 7–5 [/ латекс] на первом месте.
[латекс] 7–5 [/ латекс] на первом месте.[латекс] 2 + 24 [/ латекс].
Наконец, доп.
[латекс] 2 + 24 = 26 [/ латекс]
Ответ
[латекс] 7–5 + 3 \ cdot8 = 26 [/ латекс]
В следующем примере вам будет показано, как упростить выражение, которое содержит как умножение, так и вычитание, используя порядок операций.
Когда вы применяете порядок операций к выражениям, содержащим дроби, десятичные дроби и отрицательные числа, вам также необходимо вспомнить, как выполнять эти вычисления.
Пример
Упростите [латекс] 3 \ cdot \ frac {1} {3} -8 \ div \ frac {1} {4} [/ latex].
Показать решение Согласно порядку операций умножение и деление предшествуют сложению и вычитанию. Иногда полезно добавить круглые скобки, чтобы вы знали, что идет первым, поэтому давайте заключим в скобки умножение и деление, поскольку оно будет стоять перед вычитанием.
[латекс] 3 \ cdot \ frac {1} {3} -8 \ div \ frac {1} {4} [/ латекс]
Сначала умножьте [латекс] 3 \ cdot \ frac {1} {3} [/ latex].
[латекс] \ begin {array} {c} \ left (3 \ cdot \ frac {1} {3} \ right) — \ left (8 \ div \ frac {1} {4} \ right) \\\ текст {} \\ = \ left (1 \ right) — \ left (8 \ div \ frac {1} {4} \ right) \ end {array} [/ latex]
Теперь разделите [латекс] на 8 \ div \ frac {1} {4} [/ latex].
[латекс] \ begin {array} {c} 8 \ div \ frac {1} {4} = \ frac {8} {1} \ cdot \ frac {4} {1} = 32 \\\ text {} \\ 1-32 \ end {array} [/ latex]
Вычесть.
[латекс] 1–32 = −31 [/ латекс]
Ответ
[латекс] 3 \ cdot \ frac {1} {3} -8 \ div \ frac {1} {4} = — 31 [/ латекс]
В следующем видео показано, как использовать порядок операций для упрощения выражения, содержащего умножение, деление и вычитание, с помощью членов, содержащих дроби.{3}} = 72 [/ латекс]
В следующем видео выражение с показателями степени упрощено с использованием порядка операций.

Группировка символов
Группирующие символы, такие как круглые скобки (), квадратные скобки [], фигурные скобки [латекс] \ displaystyle \ left \ {{} \ right \} [/ latex] и дробные черты, могут использоваться для дальнейшего управления порядком четырех арифметических операций. . Правила порядка операций требуют, чтобы сначала были выполнены вычисления внутри символов группировки, даже если вы добавляете или вычитаете внутри символов группировки и у вас есть умножение вне символов группировки.После вычисления внутри символов группировки разделите или умножьте слева направо, а затем вычтите или сложите слева направо. Если в составе символов группировки есть символы группировки, выполняйте вычисления изнутри наружу. То есть сначала начните упрощать внутри самых внутренних символов группировки.
Помните, что скобки также могут использоваться для обозначения умножения.
 В следующем примере показаны оба использования круглых скобок — как способ представления группы, так и способ выражения умножения.{3}} \ cdot 32 = \ frac {3} {4} [/ латекс]
В следующем примере показаны оба использования круглых скобок — как способ представления группы, так и способ выражения умножения.{3}} \ cdot 32 = \ frac {3} {4} [/ латекс]Упростите составные выражения действительными числами
В этом разделе мы будем использовать навыки из последнего раздела, чтобы упростить математические выражения, которые содержат много символов группировки и множество операций. Мы используем термин составной для описания выражений, которые имеют много операций и много группирующих символов. При применении порядка операций с этими выражениями требуется больше внимания. Кроме того, вы увидите, как обрабатывать абсолютные значения при упрощении выражений.{2}} + 2} [/ латекс]
Показать решение В этой задаче есть скобки, круглые скобки, дроби, показатели, умножение, вычитание и сложение.Сначала обрабатываются символы группировки. Скобки вокруг [latex] -6 [/ latex] не являются символом группировки; они просто дают понять, что отрицательный знак принадлежит цифре 6.
 Начните с самого внутреннего набора круглых скобок, которые являются символом группировки. В этом примере самые внутренние скобки будут в числителе дроби, [latex] (2 \ cdot (−6)) [/ latex].{2} +2} = \ frac {14} {11} [/ latex]
Начните с самого внутреннего набора круглых скобок, которые являются символом группировки. В этом примере самые внутренние скобки будут в числителе дроби, [latex] (2 \ cdot (−6)) [/ latex].{2} +2} = \ frac {14} {11} [/ latex]Следующее видео содержит пример, аналогичный написанному выше. Обратите внимание, как числитель и знаменатель дроби упрощаются по отдельности.
Распределительная собственность
Круглые скобки используются для группировки или объединения выражений и терминов в математике. Вы можете увидеть, как они используются, когда вы работаете с формулами, и когда вы переводите реальную ситуацию в математическую задачу, чтобы найти количественное решение.
Распределительная собственность Combo Meal
Например, вы собираетесь пообщаться с друзьями и звоните им, чтобы спросить, не хотят ли они чего-нибудь из вашего любимого проезда.
 Три человека хотят одно и то же комбинированное блюдо из 2 тако и одного напитка. Вы можете использовать свойство distributive, чтобы узнать, сколько всего тако и сколько всего напитков вы должны им принести.
Три человека хотят одно и то же комбинированное блюдо из 2 тако и одного напитка. Вы можете использовать свойство distributive, чтобы узнать, сколько всего тако и сколько всего напитков вы должны им принести.[латекс] \ begin {array} {c} \, \, \, 3 \ left (2 \ text {tacos} + 1 \ text {drink} \ right) \\ = 3 \ cdot {2} \ text { тако} +3 \ текст {напитки} \\\, \, = 6 \ текст {тако} +3 \ текст {напитки} \ конец {массив} [/ латекс]
Свойство распределенности позволяет нам явно описать сумму, которая является результатом группы групп.В случае комбинированных блюд у нас есть три группы (два тако плюс один напиток). Следующее определение описывает, как использовать свойство распределения в общих чертах.
Распределительное свойство умножения
Для всех действительных чисел a, b, и c , [латекс] a (b + c) = ab + ac [/ latex].
Это означает, что когда число в скобках умножает выражение, вы можете распределить умножение на каждый член выражения индивидуально.
Чтобы упростить [латекс] 3 \ left (3 + y \ right) -y + 9 [/ latex], может быть полезно увидеть выражение, переведенное в слова:
умножьте три на (сумму трех и y), затем вычтите y, затем прибавьте 9
Чтобы умножить три на сумму трех и y, вы используете свойство распределения —
[латекс] \ begin {array} {c} \, \, \, \, \, \, \, \, \, 3 \ left (3 + y \ right) -y + 9 \\\, \, \, \, \, \, \, \, \, = \ underbrace {3 \ cdot {3}} + \ underbrace {3 \ cdot {y}} — y + 9 \\ = 9 + 3y-y + 9 \ end {array} [/ latex]
Теперь вы можете вычесть y из 3y и прибавить 9 к 9.
[латекс] \ begin {array} {c} 9 + 3y-y + 9 \\ = 18 + 2y \ end {array} [/ latex]
В следующем примере показано, как использовать свойство распределения, когда один из задействованных терминов отрицательный.
Пример
Упростить [латекс] a + 2 \ left (5-a \ right) +3 \ left (a + 4 \ right) [/ latex]
Показать решениеЭто выражение содержит два набора круглых скобок с заблокированными в них переменными.
 Мы будем использовать свойство distributive, чтобы убрать круглые скобки.
Мы будем использовать свойство distributive, чтобы убрать круглые скобки.[латекс] \ begin {array} {c} a + 2 \ left (5-a \ right) +3 \ left (a + 4 \ right) \\ = a + 2 \ cdot {5} -2 \ cdot {a} +3 \ cdot {a} +3 \ cdot {4} \ end {array} [/ latex]
Обратите внимание, как мы поместили отрицательный знак, который был на b, перед 2, когда мы применили свойство распределения.Когда вы умножаете отрицательный результат на положительный, результат будет отрицательным, поэтому [latex] 2 \ cdot {-a} = — 2a [/ latex]. При использовании распределительного свойства важно быть осторожным с отрицательными знаками.
[латекс] \ begin {array} {c} a + 2 \ cdot {5} -2 \ cdot {a} +3 \ cdot {a} +3 \ cdot {4} \\ = a + 10-2a + 3a + 12 \\ = 2a + 22 \ end {array} [/ latex]
Мы объединили все возможные условия, чтобы получить окончательный результат.
Ответ
[латекс] a + 2 \ left (5-a \ right) +3 \ left (a + 4 \ right) = 2a + 22 [/ латекс]
Абсолютное значение
Выражения абсолютного значения — это последний метод группировки, который вы можете увидеть.
 Напомним, что абсолютное значение количества всегда положительно или равно 0.
Напомним, что абсолютное значение количества всегда положительно или равно 0.Когда вы видите выражение абсолютного значения, включенное в большее выражение, относитесь к абсолютному значению как к символу группировки и сначала оцените выражение внутри знака абсолютного значения. Затем возьмите абсолютное значение этого выражения. Пример ниже показывает, как это делается.
Пример
Упростите [латекс] \ frac {3+ \ left | 2-6 \ right |} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} [/ latex].
Показать решение В этой задаче есть абсолютные значения, десятичные дроби, умножение, вычитание и сложение.Сначала обрабатываются символы группировки, включая абсолютное значение. Упростите числитель, а затем знаменатель.
Оценить [латекс] \ left | 2–6 \ right | [/ latex].
[латекс] \ begin {array} {c} \ frac {3+ \ left | 2-6 \ right |} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} \\\\\ frac {3+ \ left | -4 \ right |} {2 \ left | 3 \ cdot1.
 5 \ right | — \ left (-3 \ right)} \ end {array} [/ latex]
5 \ right | — \ left (-3 \ right)} \ end {array} [/ latex]Возьмите абсолютное значение [латекс] \ left | −4 \ right | [/ latex].
[латекс] \ begin {массив} {c} \ frac {3+ \ left | -4 \ right |} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} \\\\\ frac {3 + 4} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} \ end {array} [/ latex]
Сложите числа в числителе.
[латекс] \ begin {array} {c} \ frac {3 + 4} {2 \ left | 3 \ cdot1.5 \ right | — \ left (-3 \ right)} \\\\\ frac {7 } {2 \ left | 3 \ cdot 1.5 \ right | — (- 3)} \ end {array} [/ latex]
Теперь, когда числитель упростился, обратимся к знаменателю.
Сначала вычислите выражение абсолютного значения. [латекс] 3 \ cdot 1,5 = 4,5 [/ латекс], что дает
[латекс] \ begin {array} {c} \ frac {7} {2 \ left | {3 \ cdot {1.5}} \ right | — (- 3)} \\\\\ frac {7} {2 \ left | {4.5} \ right | — (- 3)} \ end {array} [/ latex]
Выражение «[латекс] 2 \ left | 4.5 \ right | [/ latex]» читается как «двойное абсолютное значение 4,5».
 Умножить 2 раза на 4,5.
Умножить 2 раза на 4,5.[латекс] \ begin {array} {c} \ frac {7} {2 \ left | 4.5 \ right | — \ left (-3 \ right)} \\\\\ frac {7} {9- \ left (-3 \ справа)} \ end {array} [/ latex]
Вычесть.
[латекс] \ begin {array} {c} \ frac {7} {9- \ left (-3 \ right)} \\\\\ frac {7} {12} \ end {array} [/ latex]
Ответ
[латекс] \ frac {3+ \ left | 2-6 \ right |} {2 \ left | 3 \ cdot1.5 \ right | -3 \ left (-3 \ right)} = \ frac {7} {12} [/ латекс]
В следующем видео порядок операций используется для упрощения выражения в форме дроби, которое содержит элементы абсолютного значения. Обратите внимание, как абсолютные значения обрабатываются как круглые и квадратные скобки при использовании порядка операций.
Правила деления отрицательных чисел
Учащиеся изучают правила сложения и вычитания чисел в очень раннем возрасте.
 Когда учащиеся усваивают эти понятия и переходят в более высокие оценки, они начинают изучать предмет умножения и деления отрицательных чисел.При работе с отрицательными числами необходимо выучить и соблюдать несколько правил.
Когда учащиеся усваивают эти понятия и переходят в более высокие оценки, они начинают изучать предмет умножения и деления отрицательных чисел.При работе с отрицательными числами необходимо выучить и соблюдать несколько правил.Два положительных результата
При делении одно число, делимое, делится на другое число.
Умножение положительных и отрицательных чисел — «Семья и Школа»
Содержание
Умножение и деление положительных и отрицательных чисел
Умножение отрицательных чисел
Правило умножения отрицательных чисел:
Замечание 1
Для умножения двух отрицательных чисел нужно выполнить умножение их модулей.
Согласно правилу можно записать:
$(−a) \cdot (−b)=a \cdot b$,
где $a$ и $b$ – положительные действительные числа.
Из правила умножения следует, что результатом произведения двух отрицательных чисел является положительное число.
Правило умножения справедливо для целых, рациональных и действительных чисел.
Пример 1
Выполнить умножение двух отрицательных чисел $−8$ и $−11$.
Решение.
Найдем модули данных чисел:
$|-8|=8$;
$|-11|=11$.
Произведение модулей равно $8 \cdot 11=88$.
Краткая запись решения:
$(−8) \cdot (−11)= 8 \cdot 11=88$.
Ответ: $(−8) \cdot (−11)=88$.
Помощь со студенческой работой на тему
Умножение и деление положительных и отрицательных чисел
Замечание 2
Для умножения отрицательных рациональных чисел необходимо числа преобразовать к виду смешанных чисел, обыкновенных или десятичных дробей.
Умножение чисел с противоположными знаками
Правило умножения чисел с разными знаками:
Замечание 3
Для умножения чисел с противоположными знаками необходимо выполнить умножение чисел и перед полученным значением поставить знак $«–»$.
Согласно данному правилу можно записать:
$a \cdot (−b)=−(|a| \cdot |b|)$,
$(−a) \cdot b=−(|a| \cdot |b|)$,
где $a$ и $b$ – положительные действительные числа.
Данное правило умножения чисел с противоположными знаками применяется для целых, рациональных и действительных чисел.
Согласно рассмотренному правилу умножение чисел с противоположными знаками сводится к выполнению умножения положительных чисел.
Пример 2
Выполнить умножение положительного числа $7$ и отрицательного числа $–12$.
Решение.
Согласно правилу умножения чисел с противоположными знаками сначала выполним умножение модулей данных чисел:
$|7|=7$;
$|-12|=12$;
$7 \cdot 12=84$.
Поставим знак $«–»$ перед полученным значением и получим $−84$.
Краткая запись решения:
$7 \cdot (–12)=−(7 \cdot 12)=−84$.
Ответ: $7 \cdot (–12)=−84$.
Замечание 4
Для умножения дробных чисел с противоположными знаками необходимо преобразовать данные числа к удобному виду: обыкновенных или десятичных дробей.
Деление отрицательных чисел
Правило деления отрицательных чисел:
Замечание 5
Для деления одного отрицательного числа на другое необходимо выполнить деление модулей данных чисел. {−1}$.
{−1}$.
Данное правило применимо для выполнения деления чисел с противоположными знаками.
Пример 3
Разделить отрицательные числа $−24$ и $−6$.
Решение.
Согласно правилу деления отрицательных чисел найдем модули данных чисел и выполним их деление. Получим:
$|-24|=24$;
$|-6|=6$;
$24:6=4$.
Краткая запись решения:
$(–24):(–6)=|–24|:|–6|=24:6=4$.
Ответ: $(–24):(–6)=4$.
Замечание 7
Для выполнения деления дробных рациональных чисел для удобства нужно преобразовать их к виду обыкновенных дробей, но можно делить и десятичные дроби.
Деление чисел с противоположными знаками
Правило деления чисел с противоположными знаками:
Замечание 8
Для деления положительного числа на отрицательное или отрицательного числа на положительное необходимо выполнить деление модулей данных чисел и перед полученным значением поставить знак $«–»$.
Согласно данному правилу можно записать:
$a:(–b)=−|a|:|–b|$,
$(–a):b=−|–a|:|b|$.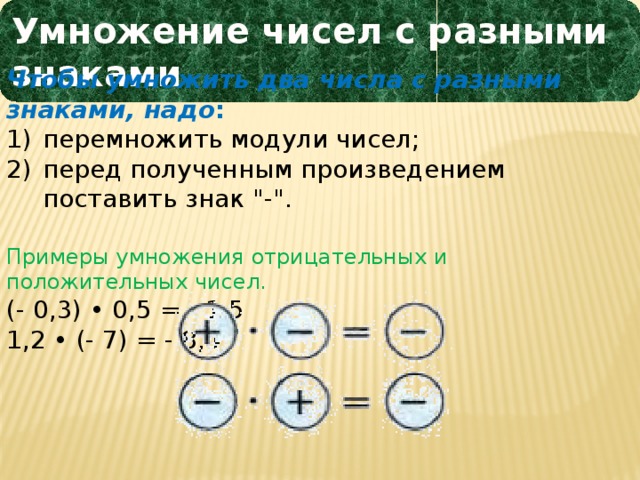 {−1}$.
{−1}$.
Данное правило применимо для деления отрицательных чисел.
Пример 4
Разделить положительное число $28$ на отрицательное число $–7$.
Решение.
Согласно правилу деления чисел с противоположными знаками найдем модули данных чисел и выполним их деление:
$|28|=28$;
$|-7|=7$;
$28:7=4$.
Поставим знак $«–»$ перед полученным значением и получим $–4$.
Краткая запись решения:
$28:(–7)=-|28|:|-7|=-(28:7)=-4$.
Ответ: $28:(–7) = –4$.
Замечание 10
Для деления дробных рациональных чисел с противоположными знаками числа удобнее представлять в виде обыкновенных дробей.
Умножение и деление отрицательных чисел
Мы уже умеем складывать и вычитать отрицательные числа.
Теперь давайте разберемся с умножением и делением.
Предположим, нам нужно умножить +3 на -4. Как это сделать?
Давайте рассмотрим такой случай. Три человека залезли в долги, и у каждого по 4 доллара долга. Чему равен общий долг? Для того чтобы его найти, надо сложить все три долга: 4 доллара + 4 доллара + 4 доллара = 12 долларов. Мы с вами решили, что сложение трех чисел 4 обозначается как 3×4. Поскольку в данном случае мы говорим о долге, перед 4 стоит знак «-». Мы знаем, что общий долг равен 12 долларам, так что теперь наша задача имеет вид 3х(-4)=-12.
Чему равен общий долг? Для того чтобы его найти, надо сложить все три долга: 4 доллара + 4 доллара + 4 доллара = 12 долларов. Мы с вами решили, что сложение трех чисел 4 обозначается как 3×4. Поскольку в данном случае мы говорим о долге, перед 4 стоит знак «-». Мы знаем, что общий долг равен 12 долларам, так что теперь наша задача имеет вид 3х(-4)=-12.
Мы получим тот же результат, если по условию задачи каждый из четырех человек имеет долг по 3 доллара. Другими словами, (+4)х(-3)=-12. А поскольку порядок сомножителей значения не имеет, получаем (-4)х(+3)=-12 и (+4)х(-3)=-12.
Давайте обобщим результаты. При перемножении одного положительного и одного отрицательного числа результат всегда будет отрицательным числом. Численная величина ответа будет той же самой, как и в случае положительных чисел. Произведение (+4)х(+3)=+12. Присутствие знака «-» влияет только на знак, но не влияет на численную величину.
А как перемножить два отрицательных числа?
К сожалению, на эту тему очень трудно придумать подходящий пример из жизни. Легко себе представить долг в сумме 3 или 4 доллара, но совершенно невозможно вообразить -4 или -3 человека, которые залезли в долги.
Легко себе представить долг в сумме 3 или 4 доллара, но совершенно невозможно вообразить -4 или -3 человека, которые залезли в долги.
Пожалуй, мы пойдем другим путем. В умножении при изменении знака одного из множителей меняется знак произведения. Если мы меняем знаки у обоих множителей, мы должны дважды сменить знак произведения, сначала с положительного на отрицательный, а затем наоборот, с отрицательного на положительный, то есть у произведения будет первоначальный знак.
Следовательно, вполне логично, хотя немного странно, что (-3)х(-4)=+12.
Положение знака при умножении изменяется таким образом:
- положительное число х положительное число = положительное число;
- отрицательное число х положительное число = отрицательное число;
- положительное число х отрицательное число = отрицательное число;
- отрицательное число х отрицательное число = положительное число.
Иначе говоря, перемножая два числа с одинаковыми знаками, мы получаем положительное число. Перемножая два числа с разными знаками, мы получаем отрицательное число.
Перемножая два числа с разными знаками, мы получаем отрицательное число.
Такое же правило справедливо и для действия противоположного умножению – для деления.
(+12):(+3)=+4;
(+12):(-3)=-4;
(-12):(+3)=-4;
(-12):(-3)=+4.
Вы легко можете в этом убедиться, проведя обратные операции умножения. Если в каждом из примеров, приведенных выше, вы умножите частное на делитель, то получите делимое, и убедитесь, что оно имеет тот же самый знак, например (-3)х(-4)=(+12).
Поскольку скоро зима, то пора уже подумать о том, в что переобуть своего железного коня, что бы не скользить по льду и чувствовать себя уверено на зимних дорогах. Можно, например, взять шины йокогама на сайте: mvo.ru или какие-то другие, главное, что бы качественный, больше информации и цены вы можете узнать на сайте Mvo.ru.
Материалы по теме:
Поделиться с друзьями:
Загрузка…
Отрицательные дроби.
 Действия с отрицательными дробями
Действия с отрицательными дробямиОтрицательные дроби — это дроби, числитель или знаменатель которых является отрицательным числом.
Отрицательные дроби могут быть записаны по-разному. Например, рассмотрим два частных:
-2 : 7 и 2 : (-7),
каждое из них равно отрицательному числу
Каждое из данных частных можно записать в виде дроби, в которой дробная черта заменит знак деления:
| -2 : 7 | = | -2 | и | 2 : (-7) | = | 2 | . |
| 7 | -7 |
Следовательно, при записи отрицательных дробей знак минус
можно ставить перед дробью, перед числителем или перед знаменателем:
Сложение и вычитание
Чтобы сложить две отрицательные дроби, надо сначала привести их к общему знаменателю, а затем сложить числители по правилам сложения рациональных чисел.
Пример.
Приведём дроби к общему знаменателю:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | . |
| 5 | 4 | 20 | 20 |
Теперь сложим числители дробей по правилам сложения рациональных чисел:
| -8 | + | -5 | = | -8 + (-5) | = | -13 | = | — | 13 | . |
| 20 | 20 | 20 | 20 | 20 |
Таким образом:
| — | 2 | + (- | 1 | ) = | -8 | + | -5 | = |
| 5 | 4 | 20 | 20 |
| = | -8 + (-5) | = | -13 | = | — | 13 | . |
| 20 | 20 | 20 |
Для вычисления разности двух отрицательных дробей можно вычитание заменить сложением, взяв уменьшаемое со свои знаком, а вычитаемое с противоположным.
Пример.
| — | 5 | — (- | 11 | ) = | — | 5 | + (+ | 11 | ) = |
| 12 | 12 | 12 | 12 |
| = | — | 5 | + | 11 | = | -5 + 11 | = | 6 | . |
| 12 | 12 | 12 | 12 |
Сложение и вычитание отрицательных дробей производится по правилам сложения обыкновенных дробей, то есть сначала идёт приведение к общему знаменателю, если это нужно, а затем производятся вычисления.
Умножение и деление
Чтобы найти произведение двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем перемножить дроби по правилу умножения дробей.
Пример.
| — | 2 | · (- | 4 | ) = | -2 | · | -4 | = | -2 · (-4) | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
Так как при умножении двух отрицательных чисел результат будет положительным, то данный пример можно решить сразу, отбросив оба минуса:
| — | 2 | · (- | 4 | ) = | 2 | · | 4 | = | 2 · 4 | = | 8 | . |
| 3 | 5 | 3 | 5 | 3 · 5 | 15 |
При умножении отрицательной дроби на положительную результат будет отрицательным.
Пример.
| — | 2 | · | 4 | = | — | 2 · 4 | = | — | 8 | . |
| 3 | 5 | 3 · 5 | 15 |
К отрицательным дробям можно применять любые законы умножения. Поэтому предыдущий пример можно переписать так:
| 4 | · (- | 2 | ) = | — | 4 · 2 | = | — | 8 | . |
| 5 | 3 | 5 · 3 | 15 |
То есть при умножении положительной дроби на отрицательную результат будет отрицательным.
Чтобы найти частное двух отрицательных дробей, надо знаки минус перенести или в числители, или в знаменатели, а затем произвести вычисления.
Пример.
| — | 2 | : (- | 4 | ) = | -2 | : | -4 | = |
| 3 | 5 | 3 | 5 |
| = | -2 · 5 | = | -10 | = | 10 | . |
| 3 · (-4) | -12 | 12 |
Знак результата умножения или деления отрицательных дробей можно узнать по правилам знаков целых чисел.
Умножение положительных и отрицательных чисел
Задача 1. Точка движется по прямой слева направо со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка по прошествии 5 секунд?
Нетрудно сообразить, что точка будет находиться на 20 дм. вправо от A. Запишем решение этой задачи относительными числами. Для этого условимся в следующих знакоположениях:
1) скорость вправо будем обозначать знаком +, а влево знаком –, 2) расстояние движущейся точки от A вправо будем обозначать знаком + и влево знаком –, 3) промежуток времени после настоящего момента знаком + и до настоящего момента знаком –. В нашей задаче даны, след., такие числа: скорость = + 4 дм. в секунду, время = + 5 секунд и получилось, как сообразили арифметически, число + 20 дм. , выражающее расстояние движущейся точки от A через 5 секунд. По смыслу задачи мы видим, что она относится к умножению. Поэтому решение задачи удобно записать:
, выражающее расстояние движущейся точки от A через 5 секунд. По смыслу задачи мы видим, что она относится к умножению. Поэтому решение задачи удобно записать:
(+ 4) ∙ (+ 5) = + 20.
Задача 2. Точка движется по прямой слева направо со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A. Где находилась эта точка 5 секунд назад?
Ответ ясен: точка находилась влево от A на расстоянии 20 дм.
Решение удобно, согласно условиям относительно знаков, и, имея в виду, что смысл задачи не изменился, записать так:
(+ 4) ∙ (– 5) = – 20.
Задача 3. Точка движется по прямой справа налево со скоростью 4 дм. в секунду и в настоящий момент проходит через точку A. Где будет находиться движущаяся точка спустя 5 секунд?
Ответ ясен: на 20 дм. слева от A. Поэтому, согласно тем же условиям относительно знаков, мы можем записать решение этой задачи так:
(– 4) ∙ (+ 5) = – 20.
Задача 4. Точка движется по прямой справа налево со скоростью по 4 дм. в секунду и в настоящий момент проходит через точку A. Где находилась движущаяся точка 5 секунд тому назад?
в секунду и в настоящий момент проходит через точку A. Где находилась движущаяся точка 5 секунд тому назад?
Ответ ясен: на расстоянии 20 дм. справа от A. Поэтому решение этой задачи следует записать так:
(– 4) ∙ (– 5) = + 20.
Рассмотренные задачи указывают, как следует распространить действие умножения на относительные числа. Мы имеем в задачах 4 случая умножения чисел со всевозможными комбинациями знаков:
1) (+ 4) ∙ (+ 5) = + 20;
2) (+ 4) ∙ (– 5) = – 20;
3) (– 4) ∙ (+ 5) = – 20;
4) (– 4) ∙ (– 5) = + 20.
Во всех четырех случаях абсолютные величины данных чисел следует перемножить, у произведения приходится ставить знак + тогда, когда у множителей одинаковые знаки (1-й и 4-й случаи) и знак –, когда у множителей разные знаки (случаи 2-й и 3-й).
Отсюда же видим, что от перестановки множимого и множителя произведение не изменяется.
Упражнения.
Выполним один пример на вычисление, где входят и сложение и вычитание и умножение.
Чтобы не спутать порядка действий, обратим внимание на формулу
ab + cd.
Здесь написана сумма произведений двух пар чисел: надо, следовательно, сперва число a умножить на число b, потом число c умножить на число d и затем полученные произведения сложить. Также в формуле
a – bc
надо сперва число b умножить на c и затем полученное произведение вычесть из a.
Если бы требовалось произведение чисел a и b сложить с c и полученную сумму умножить на d, то следовало бы написать: (ab + c)d (сравнить с формулой ab + cd).
Если бы надо было разность чисел a и b умножить на c, то написали бы (a – b)c (сравнить с формулой a – bc).
Поэтому установим вообще, что если порядок действий не обозначен скобками, то надо сначала выполнить умножение, а потом уже сложение или вычитание.
Приступаем к вычислению нашего выражения: выполним сначала сложения, написанные внутри всех маленьких скобок, получим:
Теперь надо выполнить умножение внутри квадратных скобок и затем из вычтем полученное произведение:
Теперь выполним действия внутри витых скобок: сначала умножение и потом вычитание:
Теперь останется выполнить умножение и вычитание:
16. Произведение нескольких множителей. Пусть требуется найти
Произведение нескольких множителей. Пусть требуется найти
(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5).
Здесь надо первое число умножить на второе, полученное произведение на 3-е и т. д. Не трудно на основании предыдущего установить, что абсолютные величины всех чисел надо между собою перемножить.
Если бы все множители были положительны, то на основании предыдущего найдем, что и у произведения надо написать знак +. Если бы какой-либо один множитель был отрицателен
напр., (+2) ∙ (+3) ∙ (+4) ∙ (–1) ∙ (+5) ∙ (+6),
то произведение всех предшествующих ему множителей дало бы знак + (в нашем примере (+2) ∙ (+3) ∙ (+4) = +24, от умножения полученного произведения на отрицательное число (в нашем примере +24 умножить на –1) получили бы у нового произведения знак –; умножив его на следующий положительный множитель (в нашем примере –24 на +5), получим опять отрицательное число; так как все остальные множители предполагаются положительными, то знак у произведения более изменяться не может.
Если бы было два отрицательных множителя, то, рассуждая, как выше, нашли бы, что сначала, пока не дошил до первого отрицательного множителя, произведение было бы положительно, от умножения его на первый отрицательный множитель новое произведение получилось бы отрицательным и таковы бы оно и оставалось до тех пор, пока не дойдем до второго отрицательного множителя; тогда от умножения отрицательного числа на отрицательно новое произведение получилось бы положительным, которое таким останется и в дальнейшем, если остальные множители положительны.
Если бы был еще третий отрицательный множитель, то полученное положительно произведение от умножения его на этот третий отрицательный множитель сделалось бы отрицательным; оно таковым бы и осталось, если остальные множители были все положительны. Но если есть еще четвертый отрицательный множитель, то от умножения на него произведение сделается положительным. Рассуждая так же, найдем, что вообще:
Чтобы узнать знак произведения нескольких множителей, надо посмотреть, сколько среди этих множителей отрицательных: если их вовсе нет, или если их четное число, то произведение положительно: если же отрицательных множителей нечетное число, то произведение отрицательно.
Итак, теперь мы легко узнаем, что
(–5) ∙ (+4) ∙ (–2) ∙ (–3) ∙ (+7) ∙ (–1) ∙ (+5) = +4200.
Также
(+3) ∙ (–2) ∙ (+7) ∙ (+3) ∙ (–5) ∙ (–1) = –630.
Теперь нетрудно видеть, что знак произведения, а также и его абсолютная величина, не зависят от порядка множителей.
Удобно, когда имеем дело с дробными числами, находить произведение сразу:
Удобно это потому, то не приходится делать бесполезных умножений, так как предварительно полученное дробное выражение сокращается, сколько возможно.
Пример на вычисление:
правило, примеры, умножение отрицательных чисел на положительные
В данной статье сформулируем правило умножения отрицательных чисел и дадим ему объяснение. Будет подробно рассмотрен процесс умножения отрицательных чисел. На примерах показаны все возможные случаи.
Умножение отрицательных чисел
Определение 1
Правило умножения отрицательных чисел заключается в том, что для того, чтобы умножить два отрицательных числа, необходимо перемножить их модули. Данное правило записывается так: для любых отрицательных чисел –a, -b данное равенство считается верным.
Данное правило записывается так: для любых отрицательных чисел –a, -b данное равенство считается верным.
(-а)·(-b)=a·b.
Выше приведено правило умножения двух отрицательных чисел. Исходя из него, докажем выражение: (-а)·(-b)=a·b. Статья умножение чисел с разными знаками рассказывает о том, что равенств а·(-b)=-a·b справедливое, как и (-а)·b=-a·b. Это следует из свойства противоположных чисел, благодаря которому равенства запишутся следующим образом:
(-a)·(-b)=(-a·(-b))=-(-(a·b))= a·b.
Тут явно видно доказательство правила умножения отрицательных чисел. Исходя из примеров явно, что произведение двух отрицательных чисел – положительное число. При перемножении модулей чисел результат всегда положительное число.
Данное правило применимо для умножения действительных чисел, рациональных чисел, целых чисел.
Примеры умножения отрицательных чисел
Теперь рассмотрим подробно примеры умножения двух отрицательных чисел. При вычислении необходимо пользоваться правилом, написанным выше.
Пример 1
Произвести умножение чисел -3 и -5.
Решение.
По модулю умножаемые данные два числа равны положительным числам 3 и 5. Их произведение дает в результате 15. Отсюда следует, что произведение заданных чисел равно 15
Запишем кратко само умножение отрицательных чисел:
(-3)·(-5)=3·5=15
Ответ: (-3)·(-5)=15.
При умножении отрицательных рациональных чисел, применив разобранное правило, можно мобилизоваться к умножению дробей, умножению смешанных чисел, умножению десятичных дробей.
Нужна помощь преподавателя?
Опиши задание — и наши эксперты тебе помогут!
Описать задание
Пример 2
Вычислить произведение (-0,125)·(-6).
Решение.
Используя правило умножения отрицательных чисел, получим, что (−0,125)·(−6)=0,125·6. Для получения результата необходимо выполнить умножение десятичной дроби на натуральное число столбиков. Это выглядит так:
Получили, что выражение примет вид (−0,125)·(−6)=0,125·6=0,75.
Ответ: (−0,125)·(−6)=0,75.
В случае, когда множители – иррациональные числа, тогда их произведение может быть записано в виде числового выражения. Значение вычисляется только по необходимости.
Пример 3
Необходимо произвести умножение отрицательного -2 на неотрицательное log5 13.
Решение
Находим модули заданных чисел:
-2=2 и log513=-log5 3=log5 3.
Следуя из правил умножения отрицательных чисел, получим результат -2·log5 13=-2·log5 3=2·log5 3. Это выражение и является ответом.
Ответ: -2·log5 13=-2·log5 3=2·log5 3.
Для продолжения изучения темы необходимо повторить раздел умножение действительных чисел.
Автор:
Ирина Мальцевская
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Сложение и вычитание отрицательных и положительных чисел. Решение примеров.
Существуют разные типы чисел — четные числа, нечетные числа, простые числа, составные числа. Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.
Также на основе знака числа могут быть двух видов — положительные числа и отрицательные числа. Эти числа могут быть представлены на числовой линией. Среднее число в этой строке равно нулю. С левой стороны от нуля находятся отрицательные числа, а с правой стороны — положительные.
Ноль — это нейтральный элемент относительно сложения целых чисел. В основном в этой статье мы будем изучать операции сложения и вычитания с отрицательными числами. Существуют определенные правила для знаков при сложении и вычитании:
- Для того чтобы сложить два отрицательных числа, надо сложить два числа и поставить знак минус.
\((-2)+(-3)=-5\)
- Если первое число положительное, а второе отрицательное, смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа:
\((-8)+4=4-8=-4\)
\(9+(-4)=9-4=5\)
Для каждого числа кроме \(0\) существует противоположный элемент, при сумме с ним образуется ноль:
\(-9+9=0\) \(7,1+(-7,1)=0\)
- При вычитания двух чисел, в которых оба отрицательные, следует знать правило: минус на минус дает плюс.
 То есть, если стоят рядом два минуса, в сумме получается плюс.
То есть, если стоят рядом два минуса, в сумме получается плюс.
\((-7)-(-6)=(-7)+6=(-1)\)
- Если первое число положительное, а второе отрицательное, вычитаем по тому же принципу, что и складываем: смотрим, какое число по модулю больше, отнимаем от большего меньшее число и ставим знак большего числа.
\(7-9=-2\) так как \(9>7\)
- Также не стоит забывать минус на минус дает плюс:
\(7-(-9)=7+9=16\)
Задача 1. Вычислите:
- \(4+(-5)\)
- \(-36+15\)
- \((-17)+(-45)\)
- \(-9+(-1)\)
Решение:
- \(4+(-5)=4-5=-1\)
- \(-36+15=-21\)
- \((-17)+(-45)\) \(=-17-45=-62\)
- \(-9+(-1)=-9-1=-10\)
Задача 2. Вычислите:
- \(3-(-6)\)
- \(-16-35\)
- \(-27-(-5)\)
- \(-94-(-61)\)
Решение:
- \(3-(-6)=3+6=9\)
- \(-16-35=-51\)
- \(-27-(-5)=-27+5=-22\)
- \(-94-(-61)=-94+61=-33\)
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Наши преподаватели
Оставить заявку
Репетитор по математике
Омский государственный педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 7-11 классов. Реализую дифференцированный подход к обучению, осуществляю подготовку учеников к ОГЭ и ЕГЭ. Почему я люблю математику? Меня завораживают строки формул и выражений, кажется, что это шифр, к которому нужно подобрать ключ. Поэтому математика — это ключ к тайнам Вселенной.
Оставить заявку
Репетитор по математике
Гомельский государственный университет им. Ф. Скорины
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-9 классов. Математикой я был увлечен со школы, часто участвовал в олимпиадах. За время своей работы понял, что в изучении предмета большую роль играет эмоциональное отношение ученика к предмету. В школе часто создается впечатление, что математика — это сложно. На занятиях я стараюсь помочь ученикам преодолеть этот психологический барьер (если он есть) и начать решать легко и весело. При обучении использую примеры не только из книг, но и из жизни, помогая формировать образное мышление, которое позволяет просто запоминать формулы и табличные данные.
Математикой я был увлечен со школы, часто участвовал в олимпиадах. За время своей работы понял, что в изучении предмета большую роль играет эмоциональное отношение ученика к предмету. В школе часто создается впечатление, что математика — это сложно. На занятиях я стараюсь помочь ученикам преодолеть этот психологический барьер (если он есть) и начать решать легко и весело. При обучении использую примеры не только из книг, но и из жизни, помогая формировать образное мышление, которое позволяет просто запоминать формулы и табличные данные.
Оставить заявку
Репетитор по математике
БГПУ им.М.Танка
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-6 классов. Люблю математику за её красоту и элегантность. «Математика — это музыка в цифрах.» При обучении всегда провожу параллели с примерами из жизни.
Математика 10 класс
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Курсы ОГЭ
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Математика по Skype
- — Индивидуальные занятия
- — В любое удобное для вас время
- — Бесплатное вводное занятие
Похожие статьи
Как правильно умножать отрицательные числа?
Основные определения
Вспомним, как отличить положительное число от отрицательного, что такое умножение и какие у него свойства.
Начнем с того, что проведем прямую и отметим на ней начало отсчета — точку нуль (0). А теперь укажем направление движения по прямой вправо от начала координат. В этом нам поможет красивая стрелка:
Два главных определения:
Положительные числа — это точки координатной прямой, которые лежат правее начала отсчета (нуля). Иногда рядом с ними ставят знак плюс — «+», но чаще всего положительные числа никак не обозначают. То есть «+1» и «1» — это одно и тоже число.
Запоминаем!
Положительные числа — это те, что больше нуля, а отрицательные — меньшие.
Отрицательные числа — это точки координатной прямой, которые лежат левее начала отсчета (нуля). Их всегда обозначают знаком минус — «-».
Нуль (0) — ни положительное, ни отрицательное число. Вот это ему повезло!
Числовую ось можно расположить как горизонтально (стрелка вверх), так и вертикально (стрелка вправо).
Если стрелка направлена вверх, то в верхней части от начала отсчета всегда расположены положительные числа, а в нижней — отрицательные. Смотрите:
Смотрите:
Прямая, на которой отмечена начальная точка, положительное направление и единичный отрезок, называется координатной или числовой осью.
Умножение — арифметическое действие в котором участвуют два аргумента. Один множимый, второй множитель. Результат их умножения называется произведением.
Свойства умножения
|
Вычислять можно в уме, при помощи таблицы умножения или в столбик. Продвинутые школьники могут использовать онлайн-калькулятор.
Правило умножения отрицательных чисел: чтобы умножить два отрицательных числа, нужно перемножить их модули. Это значит, что для любых отрицательных чисел -a, -b верно равенство:
А вот как умножить два числа с разными знаками:
- перемножить модули этих чисел
- перед полученным числом поставить знак минус
А теперь упростим правила. Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:
Сформулируем их в легкой форме с минимумом слов, чтобы проще запомнить:
- «—» — при умножении минус на минус ответ будет положительным
или минус на минус дает плюс - «-+» — при умножении минуса на плюс ответ будет отрицательным
или минус на плюс дает минус - «+-» — при умножении плюса на минус ответ будет отрицательным
или плюс на минус дает минус - «++» — при умножении плюса на плюс ответ будет положительным
или плюс на плюс дает плюс.
Примеры умножения отрицательных чисел
Пример 1. Вычислить: (-2)∗(-2) и (-3)∗(-7)
Как решаем:
Вспомним правило: отрицательное число умножить на отрицательное — получается ответ со знаком плюс. Считаем:
- (-2)∗(-2) = 4
- (-3)∗(-7) = 21
Ответ: 4; 21.
Пример 2. Вычислить: (-11)∗11 и (-20)∗2
Как решаем:
Вспомним правило: отрицательное число умножить на положительное — получается ответ со знаком минус. Считаем:
Считаем:
- -11 * 11 = -121
- (-20) * 2 = -40
Ответ: -121; -40.
Пример 3. Вычислить произведение: 5∗(-5) и 12∗(-8)
Как решаем:
Вспомним правило: умножение положительного на отрицательное число дает отрицательный результат. Считаем:
- 5 ∗ (-5)= -25
- 12 ∗ (-8)= -96
Ответ: -25; -96.
Пример 4. Вычислить произведение: (-0,125 ) * (-6)
Как решаем:
- Используем правило умножения отрицательных чисел:
(-0,125 ) * (-6) = 0,125 * 6. - Выполним умножение десятичной дроби на натуральное число столбиком:
Ответ: 0,75.
Умножение отрицательных дробей — Видео и стенограмма урока
Умножение отрицательных дробей
Вот четыре шага для умножения отрицательных дробей. Давайте воспользуемся следующей задачей, чтобы проиллюстрировать шаги.
Помните, что числители — это числа над чертой в дробной части, а знаменатели — это числа под чертой в долях.
Помните, что целое число можно превратить в дробь, просто поместив целое число над 1.Например, целое число 7 становится 7/1.
Попрактикуемся
Давайте вместе попробуем. Давайте найдем произведение -2/7 * 3/4
Шаг 1) Когда мы умножим числители (2 * 3), ответ будет 6.
Шаг 2) Когда мы умножим знаменатели (7 * 4), ответ равно 28.
Шаг 3) Новая дробь — 6/28. Оба числа делятся на 2 и могут быть упрощены до 3/14.
Шаг 4) У дробей разные знаки, так как одна положительная, а другая отрицательная, поэтому ответ отрицательный.
Произведение -2/7 * 3/4 = -3/14.
Попробуем еще парочку. Не стесняйтесь брать лист бумаги и карандаш и самостоятельно решать следующие задачи, прежде чем искать решение.
Решить: -3/4 * 2/3
Шаг 1) Умножить числители: 3 * 2 = 6
Шаг 2) Умножить знаменатели: 4 * 3 = 12
Шаг 3) Упростить 6/12 ( оба делятся на 6) до 1/2
Шаг 4) Знаки разные, поэтому ответ отрицательный.
Ответ -1/2.
Решить: -1/2 * 3/4
Шаг 1) Умножить числители: 1 * 3 = 3
Шаг 2) Умножить знаменатели: 2 * 4 = 8
Шаг 3) 3/8 уже в простейшей форме
Шаг 4) Знаки разные, поэтому ответ отрицательный.
Итак, -1/2 * 3/4 = -3/8.
Краткое содержание урока
При умножении дробей помните, что если дроби имеют одинаковый знак, ответ будет положительным, а если дроби имеют разные знаки, ответ будет отрицательным.Также помните, что умножение отрицательных дробей состоит из четырех простых шагов, и это, безусловно, положительный момент!
Умножение и деление на целые числа (предалгебра, изучение и понимание целых чисел) — Mathplanet
Вы также должны обращать внимание на знаки при умножении и делении. Следует помнить два простых правила:
Когда вы умножаете отрицательное число на положительное, произведение всегда отрицательное.
Когда вы умножаете два отрицательных числа или два положительных числа, произведение всегда будет положительным.
Это похоже на правило сложения и вычитания: два знака минус становятся плюсом, а плюс и минус становятся минусом. Однако при умножении и делении вы вычисляете результат, как если бы не было знаков минус, а затем смотрите на знаки, чтобы определить, положительный или отрицательный результат. Два примера быстрого умножения:
$$ 3 \ cdot (-4) = — 12 $$
3 умножить на 4 равно 12. Поскольку существует одно положительное и одно отрицательное число, произведение равно отрицательному 12.
$$ (- 3) \ cdot (-4) = 12 $$
Теперь у нас есть два отрицательных числа, поэтому результат положительный.
Переходя к делению, вы можете вспомнить, что вы можете подтвердить полученный ответ, умножив частное на знаменатель. Если вы ответили правильно, то произведение этих двух чисел должно совпадать с числителем. Например,
$$ \ frac {12} {3} = 4 $$
Чтобы проверить, является ли 4 правильным ответом, мы умножаем 3 (знаменатель) на 4 (частное):
$$ 3 \ cdot 4 = 12 $$
Что произойдет, если разделить два отрицательных числа? Например,
$$ \ frac {(- 12)} {(- 3)} = \:? $$
Чтобы знаменатель (-3) стал числителем (-12), вам нужно умножить его на 4, поэтому частное равно 4.
Итак, частное отрицательного и положительного чисел отрицательно, и, соответственно, частное положительного и отрицательного чисел также отрицательно. Можно сделать вывод, что:
Если вы разделите отрицательное число на положительное, то частное будет отрицательным.
Когда вы делите положительное число на отрицательное, частное также становится отрицательным.
Когда вы делите два отрицательных числа, получается положительное частное.
Те же правила верны и для умножения.
Видеоурок
Вычислить следующие выражения
$$ (- 4) \ cdot (-12), \: \: \: \: \ frac {-12} {3} $$
Умножение и деление отрицательных чисел
Purplemath
Если перейти от сложения и вычитания, как вы производите умножение и деление с отрицательными числами? Собственно, сложную часть мы уже рассмотрели: вы уже знаете правила «знака»:
плюс раз плюс плюс
(добавление большого количества горячих кубиков повышает температуру)
минус раз плюс минус
(удаление большого количества горячих кубиков снижает температуру)
плюс умножить на минус — это минус
(добавление большого количества холодных кубиков снижает температуру)
минус умножить на минус равно плюс
(удаление большого количества холодных кубиков повышает температуру)
MathHelp.
 com
comПравила знаков действуют одинаково для деления; просто замените «раз» на «деленное на». Вот пример правил в разделе:
(Помните, что дроби — это просто еще одна форма деления! «Дроби — это деление»!)
Некоторым людям нравится думать об отрицательных числах в терминах долгов.Так, например, если вы должны 10 долларов шести людям, ваш общий долг составит 6 × 10 долларов = 60 долларов. В этом контексте имеет смысл получить отрицательный ответ. Но в каком контексте может иметь смысл деление отрицательного на отрицательное (и получение положительного)?
Подумайте о том, чтобы перекусить в кафе. Когда вы идете платить, у ребенка возникают проблемы с использованием вашей дебетовой карты. Он проводит по ней шесть раз, прежде чем, наконец, вернуть карту вам. Вернувшись домой, вы проверяете свой банковский счет в Интернете. По сумме можно сказать, что да, он действительно взимал с вас или более одного раза.Некоторая часть этого общего дебета (отрицательная на вашем счете) неверна.
Прежде чем звонить в банк для исправления ситуации, вы хотите подтвердить количество превышенных комиссий. Как в этом разобраться? Вы можете разделить всю сумму (скажем, 76,02 доллара США) на сумму, указанную в квитанции (скажем, 12,67 доллара США), которая является суммой одного платежа. Каждое списание является минусом на вашем счету, поэтому математика составляет:
.
(- 76,02 доллара) ÷ (- 12 долларов.67) = 6
Итак, всего действительно было шесть зарядов. Количество зарядов, 6, при подсчете количества событий, должно быть положительным. В этом реальном контексте деление минуса на минус и получение плюса имеет смысл. И теперь вы знаете, что нужно указать службе поддержки клиентов отменить ровно пять начислений.
Вы можете заметить, что люди отменяют знак минус.Они пользуются тем, что «минус, умноженный на минус, есть плюс». Например, предположим, что у вас есть (–2) (- 3) (- 4). Любые два отрицательных результата при умножении становятся одним положительным. Так что выберите любые два из перемноженных (или разделенных) отрицаний и «отмените» их знаки:
Так что выберите любые два из перемноженных (или разделенных) отрицаний и «отмените» их знаки:
Начну с того, что уберу одну пару знаков «минус».Потом размножу как обычно.
(–2) (- 3) (- 4)
= (–2) (- 3) (–4)
= (+6) (–4)
= –24
Если вам дано длинное умножение с отрицательными числами, просто уберите знаки «минус» в парах:
Первое, что я сделаю, это подсчитаю знаки «минус». Один два три четыре пять шесть семь. Итак, есть три пары, которые я могу отменить, оставив одну. В результате мой окончательный ответ должен быть отрицательным. Если я получу положительный результат, я буду знать, что сделал что-то не так.
(–1) (- 2) (- 1) (- 3) (- 4) (- 2) (- 1)
= (–1) (- 2) (–1) (- 3) (- 4) (- 2) (- 1)
= (+1) (+ 2) (–1) (- 3) (- 4) (- 2) (- 1)
= (1) (2) (–1) (- 3) (–4) (- 2) (- 1)
= (1) (2) (+1) (+ 3) (–4) (- 2) (- 1)
= (1) (2) (1) (3) (–4) (- 2) (–1)
= (1) (2) (1) (3) (+4) (+ 2) (–1)
= (1) (2) (1) (3) (4) (2) (- 1)
= (2) (3) (4) (2) (- 1)
= 48 (–1)
= –48
Я получил отрицательный ответ, поэтому знаю, что мой знак правильный.
Вот еще один пример, показывающий тот же процесс отмены в контексте разделения:
Отрицательные скобки
Основная трудность, с которой люди сталкиваются с негативом, заключается в том, чтобы иметь дело со скобками; в частности, в переносе отрицания через круглые скобки. Обычная ситуация примерно такая:
Если бы у вас было «3 ( x + 4)», вы бы знали, что нужно «распределить» 3 «над» круглыми скобками:
3 ( x + 4) = 3 ( x ) + 3 (4) = 3 x + 12
Те же правила применяются, когда вы имеете дело с негативом.Если у вас проблемы с отслеживанием, используйте маленькие стрелки:
← проведите по экрану , чтобы просмотреть изображение полностью →
Мне нужно взять 3 в скобки:
3 ( x — 5) = 3 ( x ) + 3 (–5) = 3 x — 15
Здесь я возьму «минус» в скобках; Я буду распределять –2 на x и минус 3.
–2 ( x — 3) = –2 ( x ) — 2 (–3) = –2 x + 2 (+3) = –2 x + 6
Обратите внимание, как я внимательно следил за знаками в круглых скобках. «Минус» был сохранен рядом с цифрой 3 за счет использования еще одного набора круглых скобок. Не стесняйтесь использовать символы группировки, чтобы обозначить предполагаемый смысл как для оценщика, так и для вас самих.
«Минус» был сохранен рядом с цифрой 3 за счет использования еще одного набора круглых скобок. Не стесняйтесь использовать символы группировки, чтобы обозначить предполагаемый смысл как для оценщика, так и для вас самих.
Другая проблема, связанная с предыдущей, связана с вычитанием скобок. Вы можете отслеживать знак вычитания, преобразовав вычитание в умножение на минус:
Я начну с написания маленькой цифры «1» перед круглыми скобками. Затем я нарисую стрелки от этой единицы к терминам в круглых скобках, чтобы напомнить себе о том, что мне нужно сделать.
← проведите по экрану , чтобы просмотреть изображение полностью →
Не бойтесь написать эту маленькую цифру «1» и нарисовать эти маленькие стрелки.Вы должны делать все, что вам нужно, чтобы ваша работа была прямой и постоянно получала правильный ответ.
Упростить 6 — (3
x — 4 [1 — x ]).
Я буду работать изнутри, упрощая сначала символы внутренней группировки в соответствии с Порядком операций. Итак, первое, что я сделаю, это возьму –4 через скобки.Тогда я упрощу; Я продолжу, поставив 1 перед круглыми скобками и, чтобы помочь мне отслеживать тот -1, который я буду распространять, я нарисую маленькие стрелки.
Итак, первое, что я сделаю, это возьму –4 через скобки.Тогда я упрощу; Я продолжу, поставив 1 перед круглыми скобками и, чтобы помочь мне отслеживать тот -1, который я буду распространять, я нарисую маленькие стрелки.
← проведите по экрану , чтобы просмотреть изображение полностью →
Филиал
Это хитрый. Они заставляют меня вычесть дробь. Мне нужно объединить дроби, что означает объединение числителей. Чтобы не упустить из виду, что именно означает этот «минус» (а именно, что я вычитаю весь числитель второй дроби, а не только x ), я конвертирую минус с плюсом –1:
← проведите по экрану , чтобы просмотреть изображение полностью →
Обратите внимание, что я преобразовал вычитание дроби в добавление отрицательного числа, умноженного на единицу дроби.Очень легко «потерять» минус, когда вы добавляете такие беспорядочные полиномиальные дроби. Самая распространенная ошибка — ставить минус на x и забывать отнести его к –2. Будьте особенно осторожны с дробями!
Будьте особенно осторожны с дробями!
Для дополнительной практики со скобками попробуйте здесь.
URL: https://www.purplemath.com/modules/negative3.htm
Рационалов (числа со знаком, включая дроби)
Рационалы (числа со знаком, включая дроби)
Напомним, что целые числа — это положительные и отрицательные целые числа и ноль.Когда дроби и завершающие или повторяющиеся десятичные дроби между целыми числами включены, полная группа чисел упоминается как рациональное число. Это числа со знаком, включая дроби. Более техническое определение рационального числа — это любое число, которое может быть записано в виде дроби, где числитель является целым числом или целым числом, а знаменатель — натуральным числом. Обратите внимание, что дроби могут быть помещены в числовую линию, как показано на рисунке 1
.
Числовая строка, показывающая целые числа и дроби.
Дроби могут быть как отрицательными, так и положительными. Отрицательные дроби обычно записываются следующим образом:
Хотя все они равны.
Правила для знаков при сложении целых чисел применимы и к дробям. Помните: Чтобы сложить дроби, вы должны сначала получить общий знаменатель.
Добавьте следующее.
Правила для знаков при сложении целых чисел также применимы к смешанным числам.
Добавьте следующее.
Правила для знаков при вычитании целых чисел применимы и к дробям. Запомните: Чтобы вычесть дроби, вы должны сначала получить общий знаменатель.
Вычтите следующее.
Правила для знаков при вычитании целых чисел также применимы к смешанным числам. Помните: Чтобы вычесть смешанные числа, вы должны сначала получить общий знаменатель. Если заимствование из столбца необходимо, остерегайтесь простых ошибок.
Вычтите следующее.
Проблемы, подобные предыдущим, обычно легче всего решить, сложив число с большим абсолютным значением наверху, вычтя и сохранив знак числа с большим абсолютным значением.
Правила для знаков при умножении целых чисел применимы и к дробям. Помните: Чтобы умножить дроби, умножьте числители, а затем знаменатели. По возможности всегда упрощайте до минимальных условий.
Умножьте следующее.
Можно отменить при умножении положительной и отрицательной дробей. Просто отмените, как вы это делаете при умножении положительных дробей, но обратите особое внимание на соответствующие знаки.Следуйте правилам знаков при умножении целых чисел, чтобы получить правильный знак. Помните: Отсутствие знака означает, что понимается положительный знак.
Умножьте следующее.
Следуйте правилам знаков при умножении целых чисел, чтобы получить правильный знак. Запомните: Перед умножением смешанных чисел вы должны сначала преобразовать их в неправильные дроби.
Умножьте следующее.
Следуйте правилам знаков при делении целых чисел, чтобы получить правильный знак. Помните: При делении дробей сначала инвертируйте делитель, а затем умножайте.
Помните: При делении дробей сначала инвертируйте делитель, а затем умножайте.
Разделите следующее.
Следуйте правилам знаков при делении целых чисел, чтобы получить правильный знак. Запомните: Перед тем, как делить смешанные числа, вы должны сначала изменить их на неправильные дроби. Затем вы должны инвертировать делитель и умножить.
Разделите следующее.
Упрощение выражения с помощью дроби
Результаты обучения
- Определите отрицательные дроби, которые эквивалентны, учитывая, что их отрицательный знак находится в другом месте
- Упростите выражения, содержащие дробные черты, используя порядок операций
Где идет знак минус в дроби? Обычно перед дробью ставится знак минус, но иногда можно увидеть дробь с отрицательным числителем или знаменателем.Помните, что дроби представляют собой деление. Дробь [латекс] — \ frac {1} {3} [/ latex] может быть результатом деления [latex] \ frac {-1} {3} [/ latex], отрицательного на положительный или деления [latex] \ frac {1} {- 3} [/ latex], положительное за отрицательным. Когда числитель и знаменатель имеют разные знаки, частное отрицательное.
Когда числитель и знаменатель имеют разные знаки, частное отрицательное.
Если и числитель, и знаменатель отрицательны, тогда сама дробь положительна, потому что мы делим отрицательное значение на отрицательное.
[латекс] \ frac {-1} {- 3} = \ frac {1} {3} \ frac {\ text {negative}} {\ text {negative}} = \ text {positive} [/ latex]
Знак минус в дробной части
Для любых положительных чисел [латекс] a \ text {и} b [/ latex],
[латекс] \ frac {-a} {b} = \ frac {a} {- b} = — \ frac {a} {b} [/ latex]
Пример
Какая из следующих фракций эквивалентна [latex] \ frac {7} {- 8}? [/ Latex]
[латекс] \ frac {-7} {- 8}, \ frac {-7} {8}, \ frac {7} {8}, — \ frac {7} {8} [/ latex]
Решение:
Частное положительного и отрицательного отрицательно, поэтому [latex] \ frac {7} {- 8} [/ latex] отрицательно.Из перечисленных фракций [latex] \ frac {-7} {8} \ text {и} — \ frac {7} {8} [/ latex] также отрицательны.
Упрощение выражения с помощью дроби
Полоски дроби действуют как символы группировки. Выражения над и под дробной чертой следует рассматривать так, как если бы они были заключены в круглые скобки. Например, [латекс] \ frac {4 + 8} {5 — 3} [/ latex] означает [латекс] \ left (4 + 8 \ right) \ div \ left (5 — 3 \ right) [/ latex] . Порядок операций говорит нам сначала упростить числитель и знаменатель — как если бы были круглые скобки — перед тем, как делить.
Мы добавим дробные черты к нашему набору символов группировки из раздела «Использование языка алгебры», чтобы получить здесь более полный набор.
Группировка символов
Упростите выражение с помощью дробной линейки
- Упростим числитель.
- Упростим знаменатель.
- Упростите дробь.
Пример
Упростить: [латекс] \ frac {4 + 8} {5 — 3} [/ латекс]
Показать решение
Решение:
| [латекс] \ frac {4 + 8} {5 — 3} [/ латекс] | |
Упростите выражение в числителе. | [латекс] \ frac {12} {5 — 3} [/ латекс] |
| Упростим выражение в знаменателе. {2} +2} [/ latex] | |
| Используйте порядок операций.{2}} {64 — 16} [/ латекс] | |
| Упростим числитель и знаменатель. | [латекс] \ frac {16} {48} [/ латекс] |
| Упростим дробь. | [латекс] \ frac {1} {3} [/ латекс] |
Пример
Упростить: [латекс] \ frac {4 \ left (-3 \ right) +6 \ left (-2 \ right)} {- 3 \ left (2 \ right) -2} [/ latex]
Показать решение
Решение:
| [латекс] \ frac {4 \ left (-3 \ right) +6 \ left (-2 \ right)} {- 3 \ left (2 \ right) -2} [/ латекс] | |
| Умножить. | [латекс] \ frac {-12+ \ left (-12 \ right)} {- 6 — 2} [/ латекс] |
| Упростить. | [латекс] \ frac {-24} {- 8} [/ латекс] |
| Разделить. | [латекс] 3 [/ латекс] |
Посмотрите это видео, чтобы увидеть еще один пример того, как упростить выражение с помощью дробной линейки, содержащей несколько различных операций.
Умножение положительных и отрицательных чисел: 3 простых правила
При умножении положительных и отрицательных чисел существует меньше правил, чем при сложении и вычитании положительных и отрицательных чисел.Следует запомнить всего три правила:
Правило 1. Положительное число, умноженное на положительное, равно положительному числу.
Это умножение, которое вы делали все время: положительные числа, умноженные на положительные числа, равны положительным числам.
Например, 5 x 3 = 15. 5 — положительное число, 3 — положительное число, а умножение дает положительное число: 15.
Ответ: 5 x 3 = 15.
Правило 2: Отрицательное число, умноженное на положительное, равняется отрицательному числу.
Когда вы умножаете отрицательное число на положительное, ваш ответ — отрицательное число. Не имеет значения, в каком порядке вы умножаете положительные и отрицательные числа, ответ всегда будет отрицательным.
Например: -2 x 4, что по сути то же самое, что -2 + (-2) + (-2) + (-2)
Ответ: -2 х 4 = -8.
И, как мы уже сказали, если около 4 x -2 наоборот, ответ все тот же: -8.
Ответ: 4 х -2 = -8.
Правило 3. Отрицательное число, умноженное на отрицательное число, равняется положительному числу.
Два отрицательных числа дают положительное число, поэтому отрицательное число, умноженное на отрицательное число, дает положительное число. Если вы посмотрите на него на числовой прямой, идя назад и повернувшись лицом в отрицательном направлении, вы двинетесь в положительном направлении.
Например. -2 x -4 отрицательны, поэтому мы знаем, что ответ будет положительным.
Ответ: -2 x -4 = 8.
Вот общее правило, которое следует помнить при умножении положительных и отрицательных чисел:
Два одинаковых знака дают положительный знак:
Два непохожих знака образуют знак минус:
Если вы все еще не понимаете, почему отрицательное число, умноженное на отрицательное, дает положительное число, Диана Браун с факультета математики Университета Джорджии объясняет это разными способами в этой статье.
Скотт из About.com также собрал удобное видео о том, как создать шпаргалку для умножения отрицательных и положительных чисел (прокрутите страницу вниз, и вы найдете видео).
Как складывать, вычитать, умножать и делить положительные и отрицательные числа
Давайте посмотрим на следующую числовую строку и заметим, что каждая точка (точка) на числовой прямой соответствует одному числу:
В числовой строке выше мы видим три типа чисел или целых чисел: отрицательные числа, ноль и положительные числа.Отрицательные числа находятся слева от нуля, поэтому они меньше нуля. Положительные числа справа от нуля, поэтому они больше нуля. Ноль, разделительная точка, не является ни положительным, ни отрицательным.
Для числовой строки выше «1» соответствует или относится к красной точке, «2» относится к зеленой точке, «3» относится к синей точке и так далее. Когда мы перемещаемся вправо по числовой строке, мы увеличиваем числа. Мы определили это как дополнение. Когда мы движемся влево, мы уменьшаемся.И мы определили это как вычитание. Обычно так работает числовая линия.
Когда мы движемся влево, мы уменьшаемся.И мы определили это как вычитание. Обычно так работает числовая линия.
Когда мы складываем два положительных числа или умножаем два положительных числа, мы получаем положительное число. Однако мы можем вычесть положительное число из положительного, и внезапно мы не получим положительное число!
Например, если мы вычтем 7 из 4, мы начнем с 4 в числовой строке и переместимся влево на 7 позиций. Это подводит нас к -3. Поскольку -3 находится слева от 0, оно меньше нуля.
Глядя на обратную операцию, мы можем сказать, что если 4-7 = -3, то -3 + 7 = 4. И это правильно. Если мы начнем с -3 и переместим на 7 делений вправо, мы получим 4.
Положительные числа — это не только целые числа справа от нуля, но и все типы чисел, такие как дроби, десятичные дроби и радикалы. Отрицательные числа также включают различные формы и различные типы чисел, которые появляются слева от нуля.
У нас не всегда есть числовая линия, с которой можно работать, поэтому нам нужно выучить несколько правил работы с отрицательными числами.Во-первых, нам нужно определить абсолютное значение. Абсолютное значение числа — это количество единиц, отсчитываемых от нуля. Он всегда выражается положительно, но без знака «плюс».
Абсолютное значение 3 равно 3. Абсолютное значение -3 также равно 3. И 3, и -3 — три единицы от нуля. Абсолютное значение обозначается путем написания числа между двумя вертикальными полосами.
| 3 | = 3 и | -3 | = 3
| Добавление отрицательных чисел |
Если перед числом вы не видите отрицательный или положительный знак, это положительный знак.
При сложении чисел одного знака (положительного или отрицательного) сложите их абсолютные значения и дайте результату тот же знак.
6 + 5 = 11 (6 и 5 положительны; 6 + 5 равно 11, что положительно)
-7 + -8 = -15
(-7 и -8 оба отрицательны; сложите | 7 | + | 8 |, что равно 7 + 8, чтобы получить 15; ответ -15)
Если все числа в добавляемой группе отрицательные: -2 + -3 + -4 = -9, снова сложите абсолютные значения 2 + 3 + 4, чтобы получить 9 и поставить отрицательный знак.
| Сложение положительных и отрицательных чисел |
При сложении чисел с противоположным знаком возьмите их абсолютные значения, вычтите меньшее из большего и присвойте результату знак числа с большим абсолютным значением.
7 + -3 = | 7 | — | 3 | = 4
-8 + 6 = | 8 | что равно 8 и | 6 | что составляет 6. Вычтите меньшее из большего:
8-6, что дает результат 2 и дает ему знак большего числа, равного 8.
Ответ — -2.
| Вычитание положительных и отрицательных чисел |
При вычитании положительного числа из отрицательного используйте то же правило, что и для сложения двух отрицательных чисел: сложите абсолютные значения и присвойте разнице отрицательный знак.
-5 — 4 = | 5 | + | 4 | = | 9 | = -9 (это как -5 + -4 = -9)
-2 — 12 = | 2 | + | 12 | = | 14 | = -14
При вычитании отрицательного числа из положительного, двойной отрицательный результат вычитания отрицательного становится положительным, поэтому используйте то же правило, что и для сложения двух положительных чисел: сложите абсолютные значения и присвойте разнице положительный знак.
5 — -4 = | 5 | + | 4 | = 5 + 4 = 9
Если бы вы использовали числовую строку, вы бы пошли влево для вычитания, а затем перевернули (вправо) для отрицательного числа, так что окончательный ответ будет справа от исходного числа.
16 — -10 = | 16 | + | 10 | = 16 + 10 = 26
Аддитивное обратное число — это число с противоположным знаком, так что при сложении двух результат равен нулю.
а + (-а) = 0
Как видите, это положительные и отрицательные числа одного и того же абсолютного значения.
10 + -10 = 0
-24 + 24 = 0
| Умножение положительных и отрицательных чисел |
При умножении положительного числа и отрицательного числа (или отрицательного числа на положительное число) умножьте абсолютные значения и дайте ответ отрицательный знак.
8 х -5 = | 8 | х | 5 | = 8 x 5 = 40, но дайте ему отрицательный знак, сделав -40
-13 x 3 = -39
9 х -3 = -27
Чтобы умножить несколько чисел, посчитайте количество отрицательных знаков в числах, которые нужно умножить. Если это четное число, произведение будет положительным, а если нечетное, произведение будет отрицательным.
Если это четное число, произведение будет положительным, а если нечетное, произведение будет отрицательным.
6 х -2 х -3 х 5 = | 6 | х | 2 | х | 3 | х | 5 |
6 x 2 = 12, 12 x 3 = 36 и 36 x 5 = 180
Имеется два отрицательных знака (четное число), поэтому ответ положительный.
Если бы было -6 x -2 x -3 x 5, ответ был бы -180
| Умножение двух отрицательных чисел |
При умножении двух отрицательных чисел два отрицательных числа компенсируют друг друга, поэтому умножьте абсолютные значения и дайте ответ положительный знак.
-21 х -3 = | 21 | х | 3 | = 63 (остается положительным)
-7 x -8 = | 7 | х | 8 | = 56
| Деление отрицательного числа на отрицательное |
Чтобы разделить два числа с одинаковым знаком (два положительных или два отрицательных), используйте абсолютные значения, и результат будет положительным.
16 ¸ 4 = | 16 | ¸ | 4 | = 4
-20 ¸ -10 = | 20 | ¸ | 10 | = 2
Деление положительного числа на отрицательное или отрицательного числа на положительное
Чтобы разделить пару чисел с разными знаками (отрицательное на положительное или положительное на отрицательное), используйте абсолютные значения двух чисел и присвойте результату отрицательный знак.
-12 ¸ 3 = | 12 | ¸ | 3 | = 4, но это -4
18 ¸ -3 = | 18 | ¸ | 3 | = 6, но это -6
| Использование отрицательных чисел |
Отрицательные числа используются для обозначения низких температур. Цифры ниже 0 ° C отрицательны и ниже точки замерзания. (Помните, что значения ниже 32 ° F ниже точки замерзания, но температура часто опускается ниже 0 ° F.)
Отрицательные числа используются для отображения измерений ниже уровня моря. Уровень моря равен 0.
Уровень моря равен 0.
Отрицательные числа используются с деньгами, чтобы показать задолженность или денежную задолженность. Если человек или домохозяйство тратят больше денег, чем зарабатывают, мы говорим, что они «отрицательные на определенную сумму», или называем это «красным», потому что бухгалтеры используют красные чернила для отображения отрицательных чисел.
| Больше и меньше и наборы чисел |
Набор чисел — это группа чисел, которая соответствует заданному описанию.Например, набор целых чисел меньше 0 будет выражен как n Все целые числа больше 0 будут выражены как n> 0. Набор чисел, удовлетворяющий этим условиям, будет набором всех положительных целых чисел. Каждое из этих целых чисел будет называться членом или элементом этого набора.
Какие целые числа от 3 до 8? Это будет 4, 5, 6 и 7. Другой способ выразить это — набор чисел больше 3, но меньше 8, которые можно представить в виде математического предложения, которое выглядит так:
Другой способ выразить это — набор чисел больше 3, но меньше 8, которые можно представить в виде математического предложения, которое выглядит так:
3
Прочтите это: n такое, что n больше 3 и меньше 8
Поскольку 3
И n
п = 4, 5, 6, 7
Мы могли бы сказать 3 n
Часто эти ответы «больше» и «меньше» необходимо выражать с помощью числовой строки, потому что было бы невозможно перечислить все числа для ответа.
Конспект урока по математике «Умножение положительных и отрицательных чисел» 6 класс
Амикеевская средняя общеобразовательная школа
Тема урока:
Умножение положительных и отрицательных чисел.
Учительница математики:
Мурзина Силуза Назиповна
Цели урока:
Организовать совместную деятельность, нацеленную на предметный результат: вывести правила умножения отрицательных чисел и чисел с разными знаками;
Создать условия для развития умений сравнивать, выявлять закономерности, обобщать, учить думать, высказывать свое мнение;
развивать математическую речь, логическое мышление, внимание, память,
воспитывать трудолюбие, взаимопомощь, умение работать в группах.

Ход урока:
1. Организационный момент.
-Здравствуйте, ребята!
2. Мотивация урока.
“Жил на свете богач, самый богатый на земле, но все ему казалось, что он еще недостаточно богат.
И вот однажды пришел к этому самому богатому богачу самый бедный бедняк на свете и сказал:
– О, господин! Сияние твоих сокровищ слепит глаза. И все-таки у меня есть способ умножить твое богатство. А заодно и свое.
Богач прямо затрясся от жадности:
– Чего ты стоишь? Умножай скорее!
– А ты не будешь на меня в обиде? – опасливо спросил бедняк.
– Да ты что! Ведь ты хочешь умножить мое богатство!
– Конечно, умножить, – подтвердил бедняк.
– Так умножай, и дело с концом! – закричал богач, теряя терпение.
– Быть по-твоему, – ответил тот. – Раз, два, три! Готово!
Богач бросился к своим сундукам да как закричит:
– Что ты наделал, негодный?! Ты меня разорил! Где мое золото? Где алмазы? Где жемчуга?
– Были у тебя, теперь они у меня, – сказал бедняк. – Ведь ты же сам просил меня умножить! Я и умножил.″
– Ведь ты же сам просил меня умножить! Я и умножил.″
Создание проблемной ситуации.
Как вы думаете, почему так получилось?
Какое действие с числами нужно знать, что бы ответить на этот вопрос? (умножение)
А вы знаете, как выполняется умножение чисел? (натуральных и дробных положительных, да)
Тогда какая задача нашего сегодняшнего урока, что бы вы хотели узнать? (как умножить положительные и отрицательные числа)
А какие числа еще можно перемножать? (отрицательные)
Итак, тема нашего урока: «Умножение положительных и отрицательных чисел».
3.Актуализация
Прежде чем, приступить к изучению темы вспомните пожалуйста понятие модуля числа.( На доске с помощью координатной прямой надо показать модуль числа)
А теперь вспомним правило сложения отрицательных чисел.(Слайд 3)
Вычислите:
-3,7 — 4,8;
-5,2 — 4,7;
— 5,6 — 3,8;
-1,1 + 1,1;
-5+5;
-6+6.
4. Изучение нового материала.
Выполните умножение (задание, создающее ситуацию успеха).
2 * 3 = 6 (1)
Докажите.
Доказательство: 2+2+2=3+3
Выполните умножение (задание, создающее ситуацию сбоя): (Слайд 5)
(- 2) * 3 =
(- 3) * 2 =
Дети предполагают, что в результате может быть число либо 6, либо -6 и “изобретают” нужное правило с помощью практических задач (о доходах и расходах, изменение температуры), замечая, что второй множитель – натуральное число, поэтому можно воспользоваться “старым” определением, известным еще из начальной школы:
(-2)*3 есть сумма трех слагаемых, каждое из которых равно (-2). Поэтому
(-2)*3=(-2)+(-2)+(-2)=-6, т.е.
(-2)*3 =-6 (2)
(-3)*2=-6 (3)
— При перестановке множителей произведение (3) не меняется, поэтому сохранится и правило: (-3)*2=-3+(-3)=-6.

Сформулируйте правило. (Слайд 6)
Чтобы перемножить два числа с разными знаками, надо перемножить модули этих чисел и поставить перед полученным знаком знак минус.
Или: Произведение двух чисел разных знаков отрицательно.
Или: “Плюс на минус дает минус”.
(Слайд 7)
(- 2) * (-3) =
Дети предполагают, что ответ может быть либо 6, либо -6.
Применить предыдущее доказательство не могут, так как нельзя взять число -2 (-3) сомножителем -3 (-2) раза!
Тогда работая в группах, одни начинают сравнивать знаки у множителей в произведениях ((2), (3)) и (4) и делают вывод, что при изменении знака одного из множителей знак произведения тоже меняется, а его модуль остается тем же.
(Слайд 8)
Другие говорят о том, что если произведение (- 2) * 3 равно -6, то произведение (-2)*(-3)
не может тоже равняться -6, значит будет в результате 6.
 Поэтому
Поэтому(-2) * (-3) = 6 (4)
Это предположения, а как можно вывести правило с более точных математических соображений?
В качестве доказательства используют распределительный закон умножения: при сложении двух чисел -2*3 и -2*(-3) в результате получается ноль, то есть данные числа противоположные, значит произведение двух чисел оказывается положительным!
(-2)*(-3) + (-2)*3 = (-2)*(-3+3) = -2*0=0.
Чтобы перемножить два отрицательных числа, надо перемножить их модули.
Или: Произведение двух чисел одного знака положительно.
Или: “Минус на минус дает плюс”.
Вот как объяснил это правило в XVIII веке великий русский ученый Леонард Эйлер.
(Ясно, что (-2)*3 = -6. Поэтому произведение (-2)*(-3) не может быть равно -6. Однако оно должно быть как-то связано с числом 6. Остается одна возможность: (-2)*(-3)=6).

4. Первичное закрепление нового материала.
Устная работа. Внимание на экран (слайд 12)
8 * (-0,7) = — 5,6;
— 0,5 * 40 = — 20;
— 0,1 * (- 0,3) = 0,03;
— 0,125 * (-6,4) = 0,8;
-1 * 3,2 = — 3,2.
-5,3*(-6)=31,8
5.Работа в парах
– Откройте учебники, прочитайте правила, проговаривайте друг другу , сравните их с теми, которые мы вывели сами
– Давайте вернемся к сказке, которую вы услышали в начале урока. Можете ли вы сейчас ответить на вопрос, почему богач лишился своего богатства, на какое число бедняк умножил богатство богача?
— Выполнение упражнения по учебнику. Продолжаем работу в парах, каждый из вас решает по одному примеру и объясняет свое решение другу
№1121
1. а),в)
2. г),д)
3. и),к)
4. л),о)
5. п),р)
6. с),т)
7. б),е)
8.ж),з)
Решая примеры, замечают, что лучше вначале найти знак, а потом уже найти модуль произведения и пытаются составить схему (алгоритм) умножения рациональных чисел:
Выводы:
Произведение двух чисел одного знака положительно, а произведение двух чисел с разными знаками отрицательно;
Задание парам:
– Выясните в каждом примере число отрицательных множителей?
– Какой вывод можно сделать относительно знака произведения?
Раздаются карточки с примерами
(-7) · (-5) · 2 =
(-4) · (-10) · 8 =
(-2) · (-3) · (-4) =
(-1,2) · (-2) · (-12)=
(-1) · (-2) · (-5) · (-4,2) · 2 =
4· (-1,6) ·(-10) ·(-0,5) ·(-3) =
(-1) · (-2) · (-5) · (-4,2) · 2 · (-0,5) =
4· (-1,6) ·(-10) ·(-0,5) ·(-3) ·(-1) ·(-2)=
Вывод:
1. Если число отрицательных множителей нечетное, то произведение — число отрицательное.
Если число отрицательных множителей нечетное, то произведение — число отрицательное.
2. Если число отрицательных множителей чётное, то произведение — число положительное.
6. Физкультминутка.
Учитель произносит слова и показывает движения, учащиеся повторяют.
— Быстро встали, улыбнулись.
— Выше-выше потянулись.
— Ну-ка, плечи распрямите,
— Вправо, влево повернитесь,
— Рук коленями коснитесь.
— Сели, встали. Сели, встали
— И на месте побежали.
7. Итоги урока. Рефлексия
– А теперь давайте попытаемся понять, что же каждому из нас дал сегодняшний урок. Интересно ли вам сегодня было? Чему научились? Что вызвало затруднение?
Выполнение теста в двух вариантах (5 заданий)
1 вариант
Выполните умножение:
1).2,1* 5=
2). (-4,5)*2=
3). (-3)*(-1,5)=
4). (-2)*(-6)*(-1)*2=
5). 6*(-1)*(-2)*(-1,2)*(-2,1)=
2 вариант
Выполните умножение:
1). 2,3* 3=
2,3* 3=
2). (-5)*2,4=
3). (-4)*(-2,5)=
4). (-3)*(-5)*(-4)*0=
5). 8*(-1)*(-3)*(-1,2)*(-2,1)=
Домашнее задание: п. 35, правила ; решить № 1143(а-ж), 1144(а,б,г)
Умножение и деление с отрицательными числами Видео
1%
Обработка, подождите…
Обработано успешно!
ЧТО ТАКОЕ УМНОЖЕНИЕ И ДЕЛЕНИЕ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ?
Вы уже умеете умножать и делить положительные числа. Когда одно или несколько чисел отрицательны, вы можете найти произведение или частное таким же образом. Единственное отличие состоит в том, что вам нужно определить знак результата.
Чтобы лучше понять умножение и деление с отрицательными числами…
ЧТО ТАКОЕ УМНОЖЕНИЕ И ДЕЛЕНИЕ ОТРИЦАТЕЛЬНЫХ ЧИСЕЛ?.
Вы уже знаете, как умножать и делить положительные числа. Когда одно или несколько чисел отрицательны, вы можете найти произведение или частное таким же образом. Единственное отличие состоит в том, что вам нужно определить знак результата. Чтобы лучше понять умножение и деление с отрицательными числами…
Чтобы лучше понять умножение и деление с отрицательными числами…
ДАВАЙТЕ РАЗЪЯСНИМ!
Умножить положительное число на отрицательное.
В метеосводке говорится, что температура будет снижаться на 3 градуса каждый день в течение 4 дней. Представьте ежедневное снижение на 3 градуса как целое число −3. Поскольку температура изменяется на -3 градуса в течение 4 дней, общее изменение температуры (понижение) можно представить как (-3) + (-3) + (-3) + (-3) или 4 × (-3). Вы можете использовать числовую строку, чтобы помочь вам найти продукт. Начните с 0. Переместитесь на 3 места влево всего 4 раза. Вы приземляетесь на -12. Это означает, что 4 × (-3) = -12. Когда вы умножаете и ровно один множитель отрицательный, результат будет отрицательным. Это потому, что вы постоянно добавляете отрицательное число, поэтому ответ должен быть отрицательным! Попробуйте сами: Сколько будет (−10) × 8?
Умножить положительное число на отрицательное. В метеосводке говорится, что в течение 4 дней температура будет снижаться на 3 градуса каждый день. Представьте ежедневное снижение на 3 градуса как целое число −3. Поскольку температура изменяется на -3 градуса в течение 4 дней, общее изменение температуры (понижение) можно представить как (-3) + (-3) + (-3) + (-3) или 4 × (-3). Вы можете использовать числовую строку, чтобы помочь вам найти продукт. Начните с 0. Переместитесь на 3 места влево всего 4 раза. Вы приземляетесь на -12. Это означает, что 4 × (-3) = -12. Когда вы умножаете и ровно один множитель отрицательный, результат будет отрицательным. Это потому, что вы постоянно добавляете отрицательное число, поэтому ответ должен быть отрицательным! Попробуйте сами: чему равно (−10) × 8?
Представьте ежедневное снижение на 3 градуса как целое число −3. Поскольку температура изменяется на -3 градуса в течение 4 дней, общее изменение температуры (понижение) можно представить как (-3) + (-3) + (-3) + (-3) или 4 × (-3). Вы можете использовать числовую строку, чтобы помочь вам найти продукт. Начните с 0. Переместитесь на 3 места влево всего 4 раза. Вы приземляетесь на -12. Это означает, что 4 × (-3) = -12. Когда вы умножаете и ровно один множитель отрицательный, результат будет отрицательным. Это потому, что вы постоянно добавляете отрицательное число, поэтому ответ должен быть отрицательным! Попробуйте сами: чему равно (−10) × 8?
Умножить отрицательное число на отрицательное число.
Умение умножать два отрицательных числа поможет вам разобраться в фондовом рынке. Люди, которые анализируют фондовый рынок, должны «убирать убытки». Это означает, что они умножают отрицательное число на отрицательное число. Вы знаете, что (-4) × 5 = -20. На числовой прямой это значение находится на 20 позиций левее 0. Когда мы делаем что-то отрицательным, это то же самое, что изменять его направление на числовой прямой. Когда вы вводите еще одно отрицательное выражение в выражение, умножая (-4) × (-5), измените направление на числовой прямой. Итак, произведение равно 20, что положительно. При умножении двух отрицательных чисел произведение положительное. Попробуйте сами: Произведение (-55) × (-5) положительное или отрицательное?
Когда мы делаем что-то отрицательным, это то же самое, что изменять его направление на числовой прямой. Когда вы вводите еще одно отрицательное выражение в выражение, умножая (-4) × (-5), измените направление на числовой прямой. Итак, произведение равно 20, что положительно. При умножении двух отрицательных чисел произведение положительное. Попробуйте сами: Произведение (-55) × (-5) положительное или отрицательное?
Умножить отрицательное число на отрицательное число. Изучение того, как умножать два отрицательных числа, может помочь вам понять фондовый рынок. Люди, которые анализируют фондовый рынок, должны «убирать убытки». Это означает, что они умножают отрицательное число на отрицательное число. Вы знаете, что (-4) × 5 = -20. На числовой прямой это значение находится на 20 позиций левее 0. Когда мы делаем что-то отрицательным, это то же самое, что изменять его направление на числовой прямой. Когда вы вводите еще одно отрицательное выражение в выражение, умножая (-4) × (-5), измените направление на числовой прямой. Итак, произведение равно 20, что положительно. При умножении двух отрицательных чисел произведение положительное. Попробуйте сами: произведение (-55) × (-5) положительное или отрицательное?
Итак, произведение равно 20, что положительно. При умножении двух отрицательных чисел произведение положительное. Попробуйте сами: произведение (-55) × (-5) положительное или отрицательное?
Разделить отрицательное число на положительное.
Вы и двое ваших друзей занимаете 240 долларов, чтобы основать компанию по производству кресел для скейтборда. Общая сумма долга составляет 240 долларов, что можно представить как -240 долларов. Сколько каждый из вас должен? -240 ÷ 3 = ? Это то же самое, что? × 3 = -240. Чтобы произведение было отрицательным, отсутствующий множитель должен быть отрицательным. -240 ÷ 3 = -80. Каждый человек должен 80 долларов, представленных -80 долларов. Отрицательное число, деленное на положительное число, всегда является отрицательным числом. Что делать, если делимое число отрицательное? 240 ÷(-3) = ? такой же как ? × (−3) = 240. Чтобы произведение было положительным, отсутствующий множитель должен быть отрицательным. Итак, 240 ÷ (-3) = −80. Попробуйте сами: Что такое (-66) ÷6?
Разделить отрицательное число на положительное. Вы и двое ваших друзей занимаете 240 долларов, чтобы основать компанию по производству кресел для скейтборда. Общая сумма долга составляет 240 долларов, что можно представить как -240 долларов. Сколько каждый из вас должен? -240 ÷ 3 = ? Это то же самое, что? × 3 = -240. Чтобы произведение было отрицательным, отсутствующий множитель должен быть отрицательным. -240 ÷ 3 = -80. Каждый человек должен 80 долларов, представленных -80 долларов. Отрицательное число, деленное на положительное число, всегда является отрицательным числом. Что делать, если делимое число отрицательное? 240 ÷(-3) = ? такой же как ? × (−3) = 240. Чтобы произведение было положительным, отсутствующий множитель должен быть отрицательным. Итак, 240 ÷ (-3) = −80. Попробуйте сами: что такое (-66) ÷6?
Вы и двое ваших друзей занимаете 240 долларов, чтобы основать компанию по производству кресел для скейтборда. Общая сумма долга составляет 240 долларов, что можно представить как -240 долларов. Сколько каждый из вас должен? -240 ÷ 3 = ? Это то же самое, что? × 3 = -240. Чтобы произведение было отрицательным, отсутствующий множитель должен быть отрицательным. -240 ÷ 3 = -80. Каждый человек должен 80 долларов, представленных -80 долларов. Отрицательное число, деленное на положительное число, всегда является отрицательным числом. Что делать, если делимое число отрицательное? 240 ÷(-3) = ? такой же как ? × (−3) = 240. Чтобы произведение было положительным, отсутствующий множитель должен быть отрицательным. Итак, 240 ÷ (-3) = −80. Попробуйте сами: что такое (-66) ÷6?
Разделить отрицательное число на отрицательное число.
Если вы хотите посадить дрон на 500 метров ниже уровня моря, вы можете представить это расстояние как −500. Если вы спускаетесь со скоростью 50 метров в минуту, вы можете представить это число как -50. Чтобы узнать, сколько времени потребуется, чтобы опуститься на 500 метров ниже уровня моря, разделите -500 на -50. −500 -50= ? Это то же самое, что? × (−5) = −500. Чтобы произведение было отрицательным, недостающий множитель должен быть положительным! −500 -50= 10. Требуется 10 минут, чтобы опуститься на 500 метров ниже уровня моря со скоростью 50 метров в минуту. Попробуйте сами: Сколько будет (−100) ÷ (−5)?
Чтобы узнать, сколько времени потребуется, чтобы опуститься на 500 метров ниже уровня моря, разделите -500 на -50. −500 -50= ? Это то же самое, что? × (−5) = −500. Чтобы произведение было отрицательным, недостающий множитель должен быть положительным! −500 -50= 10. Требуется 10 минут, чтобы опуститься на 500 метров ниже уровня моря со скоростью 50 метров в минуту. Попробуйте сами: Сколько будет (−100) ÷ (−5)?
Разделить отрицательное число на отрицательное число. Если вы хотите посадить дрон на 500 метров ниже уровня моря, вы можете представить это расстояние как -500. Если вы спускаетесь со скоростью 50 метров в минуту, вы можете представить это число как -50. Чтобы узнать, сколько времени потребуется, чтобы опуститься на 500 метров ниже уровня моря, разделите -500 на -50. −500 -50= ? Это то же самое, что? × (−5) = −500. Чтобы произведение было отрицательным, недостающий множитель должен быть положительным! −500 -50= 10. Требуется 10 минут, чтобы опуститься на 500 метров ниже уровня моря со скоростью 50 метров в минуту. Попробуйте сами: чему равно (−100) ÷ (−5)?
Попробуйте сами: чему равно (−100) ÷ (−5)?
УМНОЖЕНИЕ И ДЕЛЕНИЕ С ОТРИЦАТЕЛЬНЫМИ ЧИСЛАМИ СЛОВАРЬ
Целое число
Набор целых чисел и отрицательных целых чисел.
Целое число
Набор счетных чисел и нуля.
Абсолютное значение
Расстояние числа от 0 на числовой прямой.
Коэффициент
Число, умножаемое в задаче на умножение.
Продукт
Результат умножения.
Дивиденд
Число, которое делится в задаче на деление.
Делитель
Число на деление в задаче на деление.
Частное
Результат деления.
Положительное число
Число справа от нуля на числовой прямой.
Отрицательное число
Число слева от нуля на числовой прямой.
Противоположности
Число, находящееся на таком же расстоянии от нуля, но по другую сторону от нуля на числовой прямой.
УМНОЖЕНИЕ И ДЕЛЕНИЕ НА ОТРИЦАТЕЛЬНЫЕ ЧИСЛА ВОПРОСЫ ДЛЯ ОБСУЖДЕНИЯ
Произведение двух целых чисел отрицательно.
 Что должно быть правдой в цифрах?
Что должно быть правдой в цифрах?Одно число должно быть положительным, а другое — отрицательным.
Два целых числа делятся, и их частное положительно. Что должно быть правдой в цифрах?
Числа (делимое и делитель) имеют одинаковый знак.
Как связаны правила умножения и деления целых чисел?
Знак произведения и частного подчиняются тем же правилам в отношении знака двух умножаемых или делимых чисел. Если числа имеют одинаковый знак, произведение или частное положительно. Если они имеют разные знаки, произведение или частное отрицательно.
Произведение (−5) × (−2) × (−3) положительное или отрицательное? Объяснять.
Произведение отрицательное, так как число отрицательных факторов нечетное. Каждая пара отрицательных факторов приводит к положительному произведению, которое затем умножается на отрицательное число.
Приведите пример задачи на деление двух целых чисел, частное которых меньше нуля.
Ответы будут разными. 50 ÷(-10)=-5
50 ÷(-10)=-5
Вернуться к уроку
Как складывать, вычитать и умножать отрицательные числа? – Angola Transparency
Как складывать и вычитать несколько отрицательных и положительных чисел?
Каково правило добавления минусов?
Правила:
| Правило | Пример | |
|---|---|---|
| +(+) | Два одинаковых знака становятся положительным знаком | 3+(+2) = 3 + 2 = 5 |
| −(−) | 6−(−3) = 6 + 3 = 9 | |
| +(-) | Два разных знака становятся отрицательным знаком | 7+(−2) = 7 − 2 = 5 |
| −(+) | 8−(+2) = 8−2 = 6 |
Добавляете ли вы, когда вычитаете отрицательное число?
Вычитание отрицательного значения = добавление положительного .
Каково правило вычитания с отрицанием?
Правило 1: Вычитание отрицательного числа из отрицательного числа (-) Знак минус, за которым следует знак минус, превращает два знака в знак плюс.
2 декабря 2021 г.
Как вычесть отрицательное число из отрицательного числа?
Правило 3: вычитание отрицательного числа из отрицательного числа — знак минус, за которым следует знак минус, превращает два знака в знак плюс . Таким образом, вместо вычитания минуса вы добавляете плюс.
Как умножать положительные и отрицательные числа?
Следует помнить два простых правила: При умножении отрицательного числа на положительное произведение всегда отрицательное . Когда вы умножаете два отрицательных числа или два положительных числа, произведение всегда положительно.
Два минуса дают плюс?
Когда у вас есть два отрицательных знака, один переворачивается, и они складываются вместе, чтобы получить положительный .
Как складывать и вычитать отрицательные числа без числовой строки?
Цитата из видео: Вы должны на самом деле вычитать числа, а при вычитании чисел всегда вычитать для нас большее число, а затем брать меньшее число. Так что из большего вычтите меньшее.
Можно ли складывать отрицательные числа?
Когда вы добавляете отрицательное число к отрицательному числу, это становится вычитанием, когда вы начинаете с отрицательной точки на строке чисел и двигаетесь влево . Например, -3 + (-2). Это читается как «минус три плюс минус 2».
Почему вы добавляете два отрицательных числа?
Сложить два отрицательных числа вместе? Просто сложите абсолютное значение каждого числа вместе , поставьте перед ним знак минус, и вы получите ответ!
Каковы правила сложения и вычитания целых чисел?
Чтобы сложить целые числа с одинаковым знаком, сохраните тот же знак и добавьте абсолютное значение каждого числа. Чтобы сложить целые числа с разными знаками, сохраните знак числа с наибольшим абсолютным значением и вычтите наименьшее абсолютное значение из наибольшего. Вычтите целое число, добавив его противоположное значение.
Вычтите целое число, добавив его противоположное значение.
Как вы работаете с отрицательными числами?
Цитата из видео: Задачи — это превратить их в задачи на сложение, выполнив нечто, называемое отрицательным плюсом. Итак, у меня есть 7 минус 10, и я хочу, чтобы вы сделали это вычитание. Знак.
Что произойдет, если из отрицательного вычесть отрицательное?
Цитата из видео: А при вычитании. Хорошо, это означает, что вы отнимаете правильно, поэтому, когда вы вычитаете, это означает, что вы на самом деле собираетесь идти назад. Хорошо, но когда вы работаете с отрицательными числами, вы видите отрицательные
Как найти разницу между двумя отрицательными числами?
Зная отрицательные значения, которые вы сравниваете, вы можете вычислить разницу. Сделайте это, вычитая одно отрицательное значение из другого . Например, вы должны вычесть -7 из -5, чтобы получить -2.
Что произойдет, если из положительного вычесть отрицательное?
Цитата из видео: В форме задачи минус минус восемь мы берем положительное число и вычитаем отрицательное, чтобы решить эту задачу. Мы берем два отрицательных знака, превращаем их в положительные 9.0215
Мы берем два отрицательных знака, превращаем их в положительные 9.0215
Что дают 3 минуса?
Когда мы умножаем:
| Пример | ||
|---|---|---|
| × | два плюса дают плюс: | 3 × 2 = 6 |
| × | два минуса дают плюс: | (−3) × (−2) = 6 |
| × | отрицательное и положительное дают отрицательное: | (−3) × 2 = −6 |
| × | плюс и минус дают минус: | 3 × (−2) = −6 |
Почему негативы сокращаются?
Когда вы умножаете два отрицательных числа, первое из них меняет знак с положительного на отрицательное, а второе — обратно. Другими словами, отрицательные числа компенсируют друг друга: , когда вы умножаете отрицательное число на отрицательное число, вы получаете положительное число .
Что получится, если умножить отрицательное число на отрицательное?
Отрицательные числа – как складывать, вычитать, умножать и делить
Как складывать отрицательные и положительные числа?
Чтобы получить сумму отрицательного и положительного числа, используйте знак большего числа и вычтите . Например: (–7) + 4 = –3. 6 + (–9) = –3.
Например: (–7) + 4 = –3. 6 + (–9) = –3.
26 января 2020 г.
Как складывать и вычитать отрицательные и положительные числа без числовой строки?
Цитата из видео: Вы должны на самом деле вычитать числа, а при вычитании чисел всегда вычитать для нас большее число, а затем брать меньшее число. Так что из большего вычтите меньшее.
Каковы правила сложения, вычитания, умножения и деления положительных и отрицательных чисел?
Для умножения и деления: если знаки совпадают, результат положительный. Если знаки разные, результат отрицательный. Дополнение: обратите внимание, что величина числа со знаком совпадает с его абсолютным значением. При добавлении положительного числа и положительного числа: Добавьте величины.
Как складывать и вычитать положительные и отрицательные дроби?
Цитата из видео: Можно добавить обратное. Итак, давайте добавим обратное хорошо противоположное. Из положительных 2 12 получается отрицательное 2 12, теперь мы можем сложить наши числители. Отрицательное 9 плюс отрицательное 2 равно отрицательному 11.
Отрицательное 9 плюс отрицательное 2 равно отрицательному 11.
Каковы правила сложения и вычитания отрицательных дробей?
Вычитание отрицательной дроби из другой равносильно добавлению положительного дополнения к этой дроби . Сделайте знаменатели (нижние части дроби) одинаковыми, если они уже не равны. Вы можете складывать только половинки к половинкам, четверти к четвертям, десятые к десятым и так далее.
13 марта 2018 г.
Как сложить отрицательную дробь и положительную дробь?
Цитата из видео: И когда вы добавляете отрицательное к положительному, вы должны вычесть два абсолютных значения друг из друга, и вы используете знак большего абсолютного значения. Ценность.
Умножение и деление целых чисел
Умножение и деление
Начнем с обзора того, что означает умножение и деление чисел со знаком. Результат умножения действительных чисел называется произведением результата умножения. а результат деления называется частным Результат после деления.. Напомним, что умножение эквивалентно сложению:
а результат деления называется частным Результат после деления.. Напомним, что умножение эквивалентно сложению:
Ясно, что произведение двух положительных чисел положительно. Точно так же произведение положительного числа и отрицательного числа можно записать так:
Мы видим, что произведение положительного числа на отрицательное число отрицательно. Затем изучите результаты умножения двух отрицательных чисел. Рассмотрите продукты на следующем рисунке и попытайтесь определить закономерность:
Это показывает, что произведение двух отрицательных чисел положительно. Подводя итог,
Правила деления те же, потому что деление всегда можно переписать как умножение:
Правила умножения и деления не следует путать с тем фактом, что сумма двух отрицательных чисел является отрицательной.
Пример 1: Упрощение:
a. (−3)+(−5)
б. (−3)(−5)
Решение: Здесь мы складываем и умножаем два одинаковых отрицательных числа.
а. Результат сложения двух отрицательных чисел отрицательный.
б. Результат умножения двух отрицательных чисел положительный.
Ответы: а. −8; б. 15
Для любых действительных чисел a , b и c мы имеем следующие свойства умножения:
4 5⋅0
б. 10⋅1
Решение:
а. Умножение на ноль дает ноль.
б. Умножение любого действительного числа на единицу дает одно и то же действительное число.
Ответы: а. 0; б. 10
Пример 3: Упрощение:
a. (3⋅7)⋅2
б. 3⋅(7⋅2)
Решение:
а.
б.
Значение каждого выражения равно 42. Изменение группировки чисел не меняет результат.
Ответы: а. 42; б. 42
Здесь мы подчеркиваем, что умножение является коммутативным: порядок, в котором мы умножаем, не имеет значения и дает тот же результат.
С другой стороны, деление некоммутативно.
Используйте эти свойства для выполнения последовательных операций, включая умножение и деление. При этом важно выполнять эти операции в порядке слева направо.
Пример 4: Упрощение: 3(−2)(−5)(−1).
Решение: Умножьте два числа за один раз следующим образом:
Ответ: −30
Поскольку умножение является коммутативным, порядок умножения не влияет на окончательный ответ. Когда последовательные операции включают умножение и деление, порядок имеет значение; следовательно, мы должны работать операции от слева направо для получения правильного результата.
Пример 5: Упрощение: 10÷(−2)(−5).
Решение: Сначала выполните деление; в противном случае результат будет неверным.
Ответ: 25
Обратите внимание, что порядок умножения и деления влияет на окончательный результат. Поэтому важно выполнять операции умножения и деления так, как они появляются слева направо.
Поэтому важно выполнять операции умножения и деления так, как они появляются слева направо.
Пример 6: Упрощение: −6(3)÷(−2)(−3).
Решение: Выполняйте операции по одной слева направо.
Попробуйте! Упростить: −5÷5⋅2(−3).
Ответ: 6
Решение для видео
(щелкните, чтобы посмотреть видео)В текстовых приложениях для умножения используется символ звездочки. Символ (*), обозначающий умножение в текстовых приложениях. (*) и символ, используемый для деления, — косая черта (/).
Набор четных целых чисел Целые числа, которые делятся на два или кратны двум. это множество всех целых чисел, которые без остатка делятся на 2. Мы также можем получить множество четных целых чисел, умножив каждое целое число на 2.
Множество нечетных целых чисел, которые не делятся на 2. это множество всех целых чисел, которые не делятся на 2 без остатка.
Простое число Целые числа больше 1, которые делятся только на 1 и на себя. целое число больше 1, которое делится только на 1 и на себя. Наименьшее простое число равно 2, а остальные обязательно нечетные.
целое число больше 1, которое делится только на 1 и на себя. Наименьшее простое число равно 2, а остальные обязательно нечетные.
Любое целое число больше 1, не являющееся простым, называется составным числом. Целые числа больше 1, которые не являются простыми. и может быть записано как произведение простых чисел. Когда составное число, такое как 30, записывается как произведение 30=2⋅15, мы говорим, что 2⋅15 — это факторизация. Любая комбинация факторов, умноженных вместе, дает произведение. из 30 и что 2 и 15 являются множителями. Любые числа или выражения, образующие произведение.. Обратите внимание, что множители делят число поровну. Мы можем продолжать записывать составные множители как произведения, пока не останется только произведение простых чисел.
Факторизация простых чисел Уникальная факторизация натурального числа, записанного в виде произведения простых чисел. 30 равно 2⋅3⋅5.
Пример 7: Определите простую факторизацию числа 70.
Решение: Начните с записи 70 в виде произведения с 2 в качестве множителя. Затем представьте любой составной множитель в виде произведения простых чисел.
Так как простая факторизация уникальна, не имеет значения, как мы сначала разложим число, потому что конечный результат один и тот же.
Ответ: простая факторизация числа 70 равна 2⋅5⋅7.
Ниже приведены некоторые тесты (называемые тестами на делимость), полезные для нахождения простых делителей составных чисел:
- Если целое число четное, то 2 является делителем.
- Если сумма цифр делится на 3 без остатка, то 3 является множителем.
- Если последняя цифра 5 или 0, то 5 является множителем.
Часто возникает необходимость перевести английские предложения, содержащие термины умножения и деления, в математические выражения. Ниже перечислены некоторые ключевые слова, которые переводятся для данной операции.
Пример 8: Вычислите частное 20 и −10.
Решение: Ключевое слово «частное» подразумевает, что мы должны делить.
Ответ: Частное 20 и -10 равно -2.
Пример 9: Чему равно произведение первых трех положительных четных чисел?
Решение: Первые три положительных четных числа равны {2, 4, 6}, а ключевое слово «произведение» подразумевает, что мы должны умножать.
Ответ: Произведение первых трех положительных четных чисел равно 48.
Пример 10: Джо может проехать 342 мили на 18 галлонах бензина. Сколько это миль на галлоне бензина?
Решение: Ключевое слово «за» указывает на то, что мы должны разделить количество пройденных миль на количество израсходованных галлонов:
Ответ: Джо получает 19 миль за галлон своего автомобиля.
В повседневной жизни мы часто хотим использовать одно значение, которое типизирует набор значений. Один из способов сделать это — использовать так называемое среднее арифметическое — числовое значение, типизирующее набор чисел. Он рассчитывается путем сложения чисел в наборе и деления на количество элементов в наборе. или среднее. Используется по отношению к среднему арифметическому. Чтобы вычислить среднее значение, разделите сумму значений в наборе на количество значений в этом наборе.
Один из способов сделать это — использовать так называемое среднее арифметическое — числовое значение, типизирующее набор чисел. Он рассчитывается путем сложения чисел в наборе и деления на количество элементов в наборе. или среднее. Используется по отношению к среднему арифметическому. Чтобы вычислить среднее значение, разделите сумму значений в наборе на количество значений в этом наборе.
Пример 11: Студент получает 75, 86 и 94 балла за первые три экзамена. Каков средний балл студента?
Решение: Сложите баллы и разделите сумму на 3.
Ответ: Среднее значение теста студента равно 85.
Ноль и деление
Вспомните связь между умножением и делением: числитель частного. 12 делится поровну на делитель Знаменатель частного. 6, чтобы получить частное, 2. В целом верно, что если мы умножим делитель на частное, мы получим делимое. Теперь рассмотрим случай, когда делимое равно нулю, а делитель отличен от нуля:
Это показывает, что ноль, разделенный на любое ненулевое действительное число, должен быть равен нулю. Теперь рассмотрим ненулевое число, деленное на ноль:
Теперь рассмотрим ненулевое число, деленное на ноль:
Свойство нулевого коэффициента умножения утверждает, что любое действительное число, умноженное на 0, равно 0. Мы заключаем, что не существует действительного числа, такого что 0⋅?=12, и, таким образом, частное остается undefinedЧастное, такое как 50, которое не имеет смысла и не имеет интерпретации. Попробуйте 12÷0 на калькуляторе. Что это говорит? Для наших целей мы будем писать просто «undefined».
Итак, для любого действительного числа a≠0, тогда
Нам осталось рассмотреть случай, когда и делимое, и делитель равны нулю.
Здесь работает любое реальное число. Например, 0⋅5=0 и 0⋅3=0. Следовательно, частное является неопределенным или неопределенным. Частное, такое как 00, является неопределенной или неоднозначной величиной.
В этом курсе мы утверждаем, что 0÷0 не определено.
Ключевые выводы
- Положительное число, умноженное на отрицательное, дает отрицательное значение.
 Отрицательное число, умноженное на отрицательное число, является положительным.
Отрицательное число, умноженное на отрицательное число, является положительным. - Умножение коммутативно, а деление — нет.
- При упрощении выполняйте операции умножения и деления в порядке слева направо.
- Четные целые числа — это числа, которые делятся на 2 без остатка или кратны 2, а все остальные целые числа нечетны.
- Простое число — это целое число больше 1, которое делится только на 1 и на себя.
- Составные числа — это целые числа больше 1, которые не являются простыми. Составные числа можно однозначно записать как произведение простых чисел.
- Разложение составного числа на простые множители можно найти, продолжая делить его на множители до тех пор, пока не останется только произведение простых чисел.
- Чтобы вычислить среднее значение набора чисел, разделите сумму значений в наборе на количество значений в наборе.

- Ноль, разделенный на любое ненулевое число, равен нулю. Любое число, деленное на ноль, не определено.
Тематические упражнения
Часть A: Умножение и деление
Умножить и разделить.
1. 5(−7)
2. −3(−8)
3. 2(−4)(−9)
4. −3⋅2⋅5
5. −12( 3)(0)
6. 0(−12)(−5)
7. (−1)(−1)(−1)(−1)
8. (−1)(−1) (−1)
9. −100÷25
10. 25÷5(−5)
11. −15(−2)÷10(−3)
12. −5⋅10÷2( −5)
13. (−3)(25)÷(−5)
14. 6*(−3)/(−9)
15. 20/(−5)*2
16. −50/2*5
17. Найдите произведение 11 и −3.
18. Определите произведение −7 и −22.
19. Найдите произведение 5 и −12.
20. Найдите частное отрицательных двадцати пяти и пяти.
21. Определить частное чисел -36 и 3.
22. Определить частное 26 и -13.
23. Вычислите произведение 3 и −8, деленное на −2.
24. Вычислите произведение −1 и −3, деленное на 3.
25. Найдите произведение первых трех положительных четных целых чисел.
26. Найдите произведение первых трех положительных нечетных чисел.
Определите простую факторизацию следующих целых чисел.
27. 105
28. 78
29. 138
30. 154
31. 165
32. 330
Рассчитайте среднее количество чисел в каждом из следующих наборов.
33. {50, 60, 70}
34. {9, 12, 30}
35. {3, 9, 12, 30, 36}
36. {72, 84, 69, 71}
37. Первые четыре положительных четных числа.
38. Первые четыре положительных нечетных числа.
Пройденное расстояние D равно средней скорости r , умноженной на пройденное время t при этой скорости: D=rt. Определить пройденный путь, зная скорость и время.
39. 60 миль в час в течение 3 часов
40. 55 миль в час в течение 3 часов
41. 15 миль в час в течение 5 часов
42. 75 футов в секунду в течение 5 секунд
75 футов в секунду в течение 5 секунд
43. 60 километров в час за 10 часов
44. 60 метров в секунду за 30 секунд
45. Студенческий клуб провел сбор средств в квадроцикле по продаже хот-догов. Студенты продали 122 порции хот-дога по 3 доллара за штуку. Их стоимость включала 50 долларов за хот-доги и булочки, 25 долларов за индивидуально упакованные упаковки чипсов и 35 долларов за газированные напитки. Какова была их прибыль?
46. Мужчина весом 230 фунтов теряет 4 фунта каждую неделю в течение 8 недель. Сколько он весит в конце 8 недель?
47. Мэри обнаружила, что может проехать 264 мили на 12 галлонах бензина. Сколько миль на галлон расходует ее машина?
48. Заправив машину бензином, Билл заметил, что показания его одометра составляют 45 346 миль. После использования своей машины в течение недели он заправил свой бак 14 галлонами бензина и отметил, что его одометр показал 45 724 мили. Сколько миль на галлон проехала машина Билла за эту неделю?
Часть B: Ноль и деление со смешанной практикой
Выполните операции.
49. 0÷9
50. 15÷0
51. 4(−7)÷0
52. 7(0)÷(−15)
53. −5(0)÷9 (0)
54. 5⋅2(−3)(−5)
55. −8−5+(−13)
56. −4(−8)÷16(−2)
57 50÷(−5)÷(−10)
58. 49÷7÷(−1)
59. 3⋅4÷12
60. 0−(−8)−12
61. − 8⋅4(−3)÷2
62. 0/(−3*8*5)
63. (−4*3)/(2*(−3))
64. −16/( −2*2)*3
65. −44/11*2
66. −5*3/(−15)
67. 4*3*2/6
68. −6*7/( −2)
69. В течение 5 последовательных зимних дней дневные минимумы были −7°, −3°, 0°, − 5° и −10°. Рассчитайте среднюю низкую температуру.
70. В очень холодный день температура регистрировалась каждые 4 часа со следующими результатами: -16°, -10°, 2°, 6°, -5°, -13°. Определить среднюю температуру.
71. Ученик получает 9, 8, 10, 7 и 6 баллов за первые 5 тестов по химии. Каков ее средний балл по тесту?
72. Веб-сайт отслеживал посещения своей главной страницы во время праздника Благодарения. Количество просмотров за каждый день с четверга по воскресенье составило 12 250; 4400; 7750; и 10 200 соответственно. Каково было среднее количество посещений в день в период праздников?
Каково было среднее количество посещений в день в период праздников?
Часть C: Темы на доске обсуждений
73. Продемонстрируйте ассоциативность умножения любых трех действительных чисел.
74. Покажите, что деление некоммутативно.
75. Обсудите важность выполнения операций умножения и деления слева направо. Придумайте пример, где порядок имеет значение, и поделитесь решением.
76. Обсудите деление на 0. На примерах объясните, почему результат иногда равен 0 и почему иногда он не определен.
77. Изучите и обсудите основную теорему арифметики.
78. Найдите и обсудите другие тесты на делимость. Приведите пример для каждого теста.
79. Среднее арифметическое является одним из способов типизации набора значений. Изучите другие методы, используемые для типизации набора значений.
Ответы
1: −35
3: 72
5: 0
7: 1
9: −4
11: -9
13: 15
15: −8
17 17 : −33
19: −60
21: −12
23: 12
25: 48
27: 3Z5ac7
29: 2=3t23
31: 3 ОТДЫХА5111
33: 60
35: 18
37: 5
39: 180 миль
41: 75 миль
43: 600 километров
45: 256,00 $
47: 22 мили на галлон
49: 00003
47: 22 мили на галлон
9000 2 49: 0000347: 22 мили на галлон
9000 49: 0,0047: 22 мили на галлон
9000 49: 256,0047: 22 мили на галлон
9000 2 49: 0,0047: 22 мили на галлон
9000 2 45. 00
0051: Не определено
53: 0
55: −26
57: 1
59: 1
61: 48
63: 2
65: −8
67: 4
69: −5°
71: 8 баллов
Странные свойства Зеро — Как работает Зеро
То, что ноль может быть как неотрицательным, так и неположительным целым числом, но при этом не быть ни отрицательным, ни положительным, является лишь одним из уникальных свойств числа. На самом деле существует группа этих странных характеристик, называемых свойствами нуля .
Свойство сложения нуля говорит о том, что если вы прибавите или вычтете ноль из любого другого числа, результатом всегда будет другое число. 5+0=5 и 9,000,017-0=9,000,017, например. Он отражает концепцию нуля как ничего не представляющего, поэтому ничего не прибавляя к чему-то, оставляет это что-то неизменным — ноль — это единственное число, которое не изменяет другие числа при сложении или вычитании.
Реклама
аддитивное обратное свойство нуля отражает его позицию точки опоры между отрицательными и положительными целыми числами. Любые два числа, сумма которых равна нулю, являются аддитивными инверсиями друг друга. Например, если вы прибавите -5 к 5, вы получите ноль. Таким образом, -5 и 5 являются аддитивными инверсиями друг друга.
Любые два числа, сумма которых равна нулю, являются аддитивными инверсиями друг друга. Например, если вы прибавите -5 к 5, вы получите ноль. Таким образом, -5 и 5 являются аддитивными инверсиями друг друга.
Свойство умножения гласит то, что знает каждый третьеклассник: умножение любого числа на ноль дает в сумме ноль. Это очевидно, когда-то укоренившееся, но, возможно, причина упускается из виду. Умножение, в одном эффекте, является ярлыком для сложения. 3×2 — это то же самое, что 2+2+2, поэтому идея о том, что число может быть добавлено ноль раз или что ноль может быть добавлен к самому себе любое количество раз, математически бессмысленна [источник: Carasco].
Понятие деления на ноль еще более бессмысленно, настолько, что для него нет свойства; концепции просто не существует, поскольку она не может быть осуществлена. Даже математики часто пытаются объяснить, почему деление на ноль не работает. Причина в основном связана со свойством умножения. При делении числа на другое число, например 6/2, результат (в данном случае 3) можно осмысленно подставить в формулу, где ответ, умноженный на делитель, равен делимому. Другими словами, 6/2=3 и 3×2=6. Это не работает с нулем, когда мы заменяем им 2 в качестве делителя; 3×0=0, а не 6 [источник: Utah Math]. Концепция деления на ноль чревата настолько нелогичными последствиями, что ее мифическая разрушительная сила стала шуткой в Интернете.
Другими словами, 6/2=3 и 3×2=6. Это не работает с нулем, когда мы заменяем им 2 в качестве делителя; 3×0=0, а не 6 [источник: Utah Math]. Концепция деления на ноль чревата настолько нелогичными последствиями, что ее мифическая разрушительная сила стала шуткой в Интернете.
Существует также свойство нулевого показателя; из-за существования отрицательных показателей, числа в отрицательной степени, числа в нулевой степени всегда равны единице. Хотя это работает математически, это также создает логические проблемы. В основном, ноль в нулевой степени по-прежнему равен единице, хотя ноль, добавленный или вычитаемый или умноженный сам на себя, должен равняться нулю [источник: Stapel].
Вот сила нуля.
Связанные статьи
Источники
- Аршам, Хоссейн. «Ноль в четырех измерениях». Университет Балтимора. По состоянию на 18 апреля 2011 г. http://home.ubalt.edu/ntsbarsh/zero/zero.htm
- Ask Dr. Math. «Деление на ноль.» Математический форум в Университете Дрекселя.
 По состоянию на 5 апреля 2011 г. http://mathforum.org/dr.math/faq/faq.divideby0.html
По состоянию на 5 апреля 2011 г. http://mathforum.org/dr.math/faq/faq.divideby0.html - Караско, Шут. «Свойства нуля». Basic-Mathematics.com. По состоянию на 18 апреля 2011 г. http://www.basic-mathematics.com/properties-of-zero.html
- Forex Realm. «Биография и факты Фибоначчи». По состоянию на 15 апреля 2010 г. http://www.forexrealm.com/technical-analysis/fibonacci/fibonacci-biography-history-facts.html
- Грей, Джереми. «Рецензия на книгу: Ноль: биография опасной идеи». Уведомления АМС. October 200. http://www.ams.org/notices/200009/rev-gray.pdf
- Knott, Dr. Ron. «Кем был Фибоначчи?» Университет Суррея. 11 марта 1998 г. http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fibBio.html
- Мэтсон, Джон. «Происхождение нуля». Научный американец. 21 августа 2009 г. http://www.scientificamerican.com/article.cfm?id=history-of-zero
- О’Коннор, Дж.Дж. и Робертсон, Э. Ф. «История нуля». Университет Сент-Эндрюс. Ноябрь 2000 г. http://www-history.
 mcs.st-and.ac.uk/HistTopics/Zero.html
mcs.st-and.ac.uk/HistTopics/Zero.html - Пепперберг, Ирэн и Гордон, Джесси Д. «Понимание чисел серым попугаем (Psittacus erithacus), включая нулевое понятие». Журнал сравнительной психологии. 2005. http://www.alexfoundation.org/papers/JCPAlexComp.pdf
- Saudi Aramco World. «Ноль, ключ к числам». Ноябрь 1961 г. http://www.saudiaramcoworld.com/issue/196109/zero.key.to.numbers.htm
- Сейф, Чарльз. «Ноль: биография опасной идеи». Пингвин. 2000. http://books.google.com/books?id=obJ70nxVYFUC 9.0540
- Сингх, Саймон. «5 цифр — ноль». Би-би-си. 11 марта 2002 г. http://www.bbc.co.uk/radio4/science/5numbers1.shtml
- Стапель, Элизабет. «Отрицательные показатели». Пурпурная математика. По состоянию на 18 апреля 2011 г. http://www.purplemath.com/modules/exponent2.htm
- Stockton, J.K. «Дата альманаха I». 10 марта 2010 г. http://www.merlyn.demon.co.uk/miscdate.htm#AstDat
- Терези, Дик. «Нуль.» Атлантический океан. Июль 1997 г. http://www.theatlantic.



 Если и делимое, и делитель являются положительными целыми числами, значение частного будет положительным. Например, (+ 9) ÷ (+ 3) = + 3
Если и делимое, и делитель являются положительными целыми числами, значение частного будет положительным. Например, (+ 9) ÷ (+ 3) = + 3 Студент неправильно ответил на 5 вопросов. Сколько баллов потерял студент?
Студент неправильно ответил на 5 вопросов. Сколько баллов потерял студент? Д., включая негативы и ноль
Д., включая негативы и ноль )
)


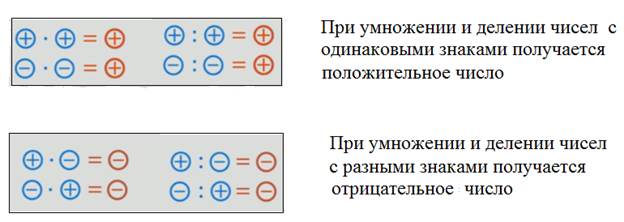 Обратите внимание, почему вы не можете объединить все три термина в примере.
Обратите внимание, почему вы не можете объединить все три термина в примере. [латекс] 7–5 [/ латекс] на первом месте.
[латекс] 7–5 [/ латекс] на первом месте.

 В следующем примере показаны оба использования круглых скобок — как способ представления группы, так и способ выражения умножения.{3}} \ cdot 32 = \ frac {3} {4} [/ латекс]
В следующем примере показаны оба использования круглых скобок — как способ представления группы, так и способ выражения умножения.{3}} \ cdot 32 = \ frac {3} {4} [/ латекс] Начните с самого внутреннего набора круглых скобок, которые являются символом группировки. В этом примере самые внутренние скобки будут в числителе дроби, [latex] (2 \ cdot (−6)) [/ latex].{2} +2} = \ frac {14} {11} [/ latex]
Начните с самого внутреннего набора круглых скобок, которые являются символом группировки. В этом примере самые внутренние скобки будут в числителе дроби, [latex] (2 \ cdot (−6)) [/ latex].{2} +2} = \ frac {14} {11} [/ latex] Три человека хотят одно и то же комбинированное блюдо из 2 тако и одного напитка. Вы можете использовать свойство distributive, чтобы узнать, сколько всего тако и сколько всего напитков вы должны им принести.
Три человека хотят одно и то же комбинированное блюдо из 2 тако и одного напитка. Вы можете использовать свойство distributive, чтобы узнать, сколько всего тако и сколько всего напитков вы должны им принести.
 Мы будем использовать свойство distributive, чтобы убрать круглые скобки.
Мы будем использовать свойство distributive, чтобы убрать круглые скобки. Напомним, что абсолютное значение количества всегда положительно или равно 0.
Напомним, что абсолютное значение количества всегда положительно или равно 0. 5 \ right | — \ left (-3 \ right)} \ end {array} [/ latex]
5 \ right | — \ left (-3 \ right)} \ end {array} [/ latex] Умножить 2 раза на 4,5.
Умножить 2 раза на 4,5. Когда учащиеся усваивают эти понятия и переходят в более высокие оценки, они начинают изучать предмет умножения и деления отрицательных чисел.При работе с отрицательными числами необходимо выучить и соблюдать несколько правил.
Когда учащиеся усваивают эти понятия и переходят в более высокие оценки, они начинают изучать предмет умножения и деления отрицательных чисел.При работе с отрицательными числами необходимо выучить и соблюдать несколько правил.