Найти собственные числа матрицы и собственные векторы матрицы онлайн: Собственные числа и собственные векторы

Содержание

как найти собственное значение матрицы

Вы искали как найти собственное значение матрицы? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и как найти собственные векторы и собственные значения матрицы, не исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению в вуз. И какой бы пример, какой бы запрос по математике вы не ввели — у нас уже есть решение. Например, «как найти собственное значение матрицы».

Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который может решить задачи, такие, как как найти собственное значение матрицы,как найти собственные векторы и собственные значения матрицы,как найти собственные значения и собственные векторы матрицы,как найти собственный вектор матрицы,калькулятор собственных значений и собственных векторов матрицы,найдите собственные векторы и собственные значения матрицы,найдите собственные значения и собственные векторы матрицы,найдите собственные значения и собственные векторы матрицы онлайн,найти онлайн собственные значения матрицы,найти собственное значение матрицы онлайн,найти собственное число матрицы,найти собственные векторы и собственные значения,найти собственные векторы и собственные значения матрицы,найти собственные векторы и собственные значения матрицы онлайн,найти собственные векторы и собственные значения матрицы онлайн калькулятор,найти собственные векторы и собственные числа,найти собственные векторы и собственные числа матрицы,найти собственные векторы и собственные числа матрицы онлайн,найти собственные векторы матрицы онлайн,найти собственные значения и собственные векторы,найти собственные значения и собственные векторы линейного преобразования,найти собственные значения и собственные векторы матрицы,найти собственные значения и собственные векторы матрицы калькулятор онлайн,найти собственные значения и собственные векторы матрицы онлайн,найти собственные значения и собственные векторы матрицы онлайн калькулятор,найти собственные значения матрицы,найти собственные значения матрицы онлайн,найти собственные числа и собственные векторы,найти собственные числа и собственные векторы матрицы,найти собственные числа и собственные векторы матрицы онлайн,нахождение собственных векторов,нахождение собственных векторов и собственных чисел,нахождение собственных чисел и собственных векторов,нахождение собственных чисел и собственных векторов матриц онлайн,онлайн калькулятор найти собственные значения и собственные векторы матрицы,онлайн собственное значение матрицы,онлайн собственные векторы и собственные значения матрицы,онлайн собственные числа,онлайн собственные числа и собственные векторы матрицы,определить собственные значения и собственные векторы матрицы 3 порядка,собственное значение,собственное значение и собственный вектор,собственное значение и собственный вектор матрицы,собственное значение матрицы,собственное значение матрицы как найти,собственное значение матрицы онлайн,собственное число,собственное число матрицы,собственное число матрицы онлайн,собственные вектора матрицы,собственные векторы,собственные векторы и собственные значения,собственные векторы и собственные значения матрицы,собственные векторы и собственные значения матрицы онлайн,собственные векторы и собственные числа,собственные векторы и собственные числа матрицы,собственные векторы матрицы,собственные векторы матрицы онлайн,собственные векторы онлайн,собственные значения,собственные значения и собственные векторы,собственные значения и собственные векторы матрицы,собственные значения и собственные векторы матрицы калькулятор онлайн,собственные значения и собственные векторы матрицы онлайн,собственные значения и собственные векторы матрицы онлайн калькулятор,собственные значения матрицы,собственные значения матрицы найти,собственные значения матрицы онлайн,собственные значения онлайн,собственные и собственные векторы матрицы,собственные числа,собственные числа и собственные векторы,собственные числа и собственные векторы матрицы,собственные числа и собственные векторы матрицы онлайн,собственные числа матрицы,собственные числа матрицы найти,собственные числа найти,собственный вектор,собственный вектор и собственное значение,собственный вектор и собственное значение матрицы,собственный вектор матрицы,собственный вектор матрицы как найти,собственный вектор матрицы онлайн.

На этой странице вы найдёте калькулятор, который поможет решить любой вопрос, в том числе и как найти собственное значение матрицы. Просто введите задачу в окошко и нажмите «решить» здесь (например, как найти собственные значения и собственные векторы матрицы).

Где можно решить любую задачу по математике, а так же как найти собственное значение матрицы Онлайн?

Решить задачу как найти собственное значение матрицы вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице калькулятора.

4.3.6 Собственные числа и собственные векторы линейного оператора

Наиболее просто устроены матрицы диагонального вида . Возникает вопрос, нельзя ли найти базис, в котором матрица линейного оператора имела бы диагональный вид. Такой базис существует.

Пусть дано линейное пространство и действующий в нем линейный оператор ; в этом случае оператор переводит в себя, то есть .

Определение. Ненулевой вектор называется собственным вектором оператора , если оператор переводит в коллинеарный ему вектор, то есть . Число называется собственным значением или собственным числом оператора , соответствующим собственному вектору .

Отметим некоторые свойства собственных чисел и собственных векторов.

1. Любая линейная комбинация собственных векторов оператора , отвечающих одному и тому же собственному числу , является собственным вектором с тем же собственным числом.

2. Собственные векторы оператора с попарно различными собственными числами линейно независимы.

3. Если собственные числа , то собственному числу соответствует не более линейно независимых собственных векторов.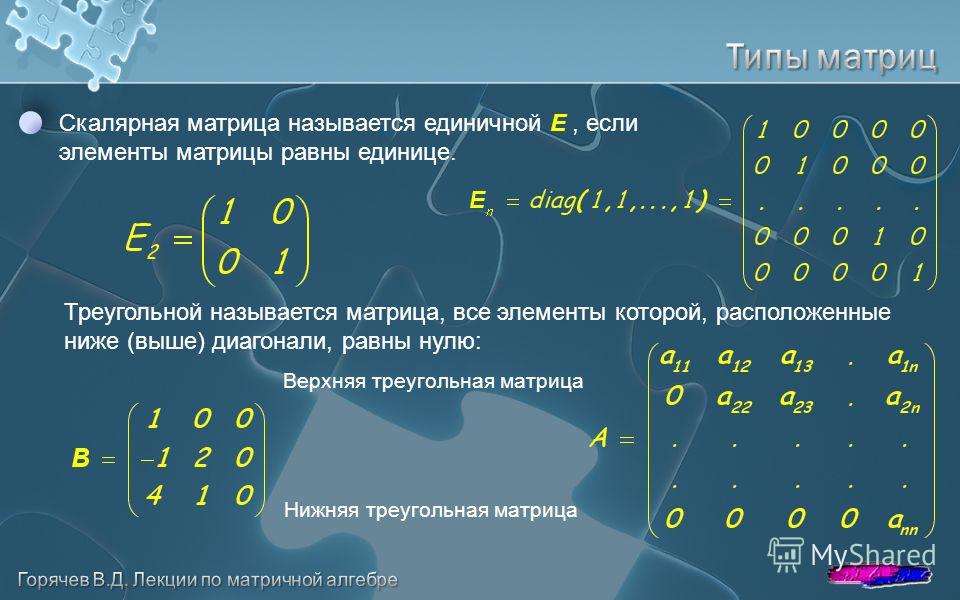

Итак, если имеется линейно независимых собственных векторов , соответствующих различным собственным числам , то они линейно независимы, следовательно, их можно принять за базис пространства . Найдем вид матрицы линейного оператора в базисе из его собственных векторов, для чего подействуем оператором на базисные векторы: тогда .

Таким образом, матрица линейного оператора в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора .

Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора в базисе имеет диагональный вид тогда и только тогда, когда все векторы базиса – собственные векторы оператора .

Правило отыскания собственных чисел и собственных векторов.

Пусть дан вектор , где – координаты вектора относительно базиса и – собственный вектор линейного оператора , соответствующий собственному числу , то есть .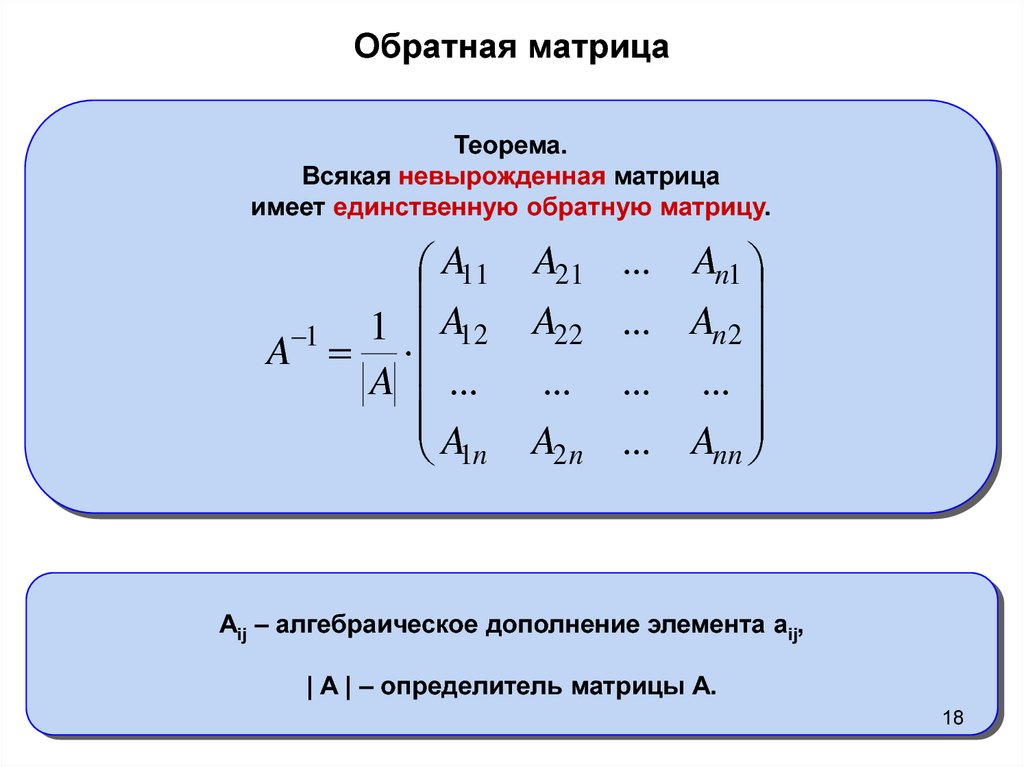

Это соотношение можно записать в матричной форме

. (*)

Уравнение (*) можно рассматривать как уравнение для отыскания , причем , то есть нас интересуют нетривиальные решения, поскольку собственный вектор не может быть нулевым. Известно, что нетривиальные решения однородной системы линейных уравнений существуют тогда и только тогда, когда . Таким образом, для того, чтобы было собственным числом оператора необходимо и достаточно, чтобы .

Если уравнение (*) расписать подробно в координатной форме, то получим систему линейных однородных уравнений:

(1)

Где – матрица линейного оператора.

Система (1) имеет ненулевое решение, если ее определитель равен нулю

Получили уравнение для нахождения собственных чисел.

Это уравнение называется характеристическим уравнением, а его левая часть – характеристическим многочленом матрицы (оператора) . Если характеристический многочлен не имеет вещественных корней, то матрица не имеет собственных векторов и ее нельзя привести к диагональному виду.

Пусть – вещественные корни характеристического уравнения, причем среди них могут быть и кратные. Подставляя по очереди эти значения в систему (1), находим собственные векторы.

Пример 12. Линейный оператор действует в по закону , где – координаты вектора в базисе , , . Найти собственные числа и собственные векторы этого оператора.

Решение. Строим матрицу этого оператора:

Составляем систему для определения координат собственных векторов:

Составляем характеристическое уравнение и решаем его:

Подставляя в систему, имеем:

или

Так как , то зависимых переменных два, а свободное одно.

Пусть – свободное неизвестное, тогда Решаем эту систему любым способом и находим общее решение этой системы: Фундаментальная система решений состоит из одного решения, так как .

Множество собственных векторов, отвечающих собственному числу , имеет вид: , где – любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив : .

Рассуждая аналогично, находим собственный вектор, отвечающий собственному числу : .

В пространстве базис состоит из трех линейно независимых векторов, мы же получили только два линейно независимых собственных вектора, из которых базис в составить нельзя. Следовательно, матрицу линейного оператора привести к диагональному виду не можем.

Пример 13. Дана матрица .

1. Доказать, что вектор является собственным вектором матрицы . Найти собственное число, соответствующее этому собственному вектору.

2. Найти базис, в котором матрица имеет диагональный вид.

Решение.

1. Если , то – собственный вектор

Вектор – собственный вектор. Собственное число .

Диагональный вид матрица имеет в базисе, состоящем из собственных векторов. Один из них известен. Найдем остальные.

Собственные векторы ищем из системы:

Характеристическое уравнение: ;

; ;

Найдем собственный вектор, отвечающий собственному числу :

Ранг матрицы этой системы равен двум и равен числу неизвестных, поэтому эта система имеет только нулевое решение . здесь может быть любым, отличным от нуля, например, . Таким образом, вектор является собственным вектором, отвечающим . Проверим:

Если , то получаем систему

Ранг матрицы равен двум. Последнее уравнение вычеркиваем.

Пусть – свободное неизвестное. Тогда , , .

Полагая , имеем – собственный вектор, отвечающий собственному числу . Проверка:

Так как собственные числа действительные и различны, то векторы, им отвечающие, линейно независимы, поэтому их можно принять за базис в . Таким образом, в базисе , , матрица имеет вид:

Не всякую матрицу линейного оператора можно привести к диагональному виду, поскольку для некоторых линейных операторов линейно независимых собственных векторов может быть меньше . Однако, если матрица симметрическая, то корню характеристического уравнения кратности соответствует ровно линейно независимых векторов.

Определение. Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой .

Замечания. 1. Все собственные числа симметрической матрицы вещественны.

2. Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.

В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

< Предыдущая		Следующая >

Лекция 7 Собственные числа и векторы

Лекция 7 21.03.2007

Собственные числа и собственные вектора матриц.

Определение :

Рассмотрим квадратную матрицу А m-го порядка и m-го мерный вектор-столбец X , т.е.

При исследовании структуры матриц большую роль играют такие векторы , при которых

, где  — число.

Если  и ненулевой вектор X удовлетворяют этому уравнению , то  называется собственным числом или собственным значением матрицы А , а Х – собственным вектором матрицы А , отвечающим  .

Замечание: Собственный вектор не может быть нулевым.

Вопрос : Сколько собственных чисел и какие их характеристики ?

Перепишем уравнение в виде:

Матрица

называется характеристической.

Тогда матричное уравнение может быть записано так

Одна из координат собственного вектора должна быть отлична от нуля.

Для того , чтобы система линейных однородных уравнений имела ненулевое ( нетривиальное) решение , необходимо и достаточно , чтобы определитель этой системы был равен нулю, т.е.

Таким образом , число _k будет собственным , если соответствующая характеристическая матрица будет вырожденной.

Уравнение det(E-A)=0 называется характеристическим уравнением матрицы А.

Это по сути есть алгебраическое уравнение относительно  степени m .

Понятно , что здесь имеется m корней.

Определение: Множество всех корней характеристического уравнения называется спектром матрицы А.

Среди корней могут оказаться и совпадающие между собой.

Каждому собственному значению спектра ставится в соответствие собственный вектор, определенный с точностью до скалярного множителя.

Пример:

Найти собственные числа и собственные вектора матрицы

имеем

Характеристический полином имеет вид:

или

Собственные числа ₁=-2 , ₂=1, ₃=4

Согласно определению , собственные вектора будут такие:

₁=-2

₂=1

₃=4

Надо заметить , что не всегда так просто решить характеристическое уравнение .

Задача нахождения собственных чисел и собственных векторов в общем случае сложнее чем решение СЛАУ методом итераций. Общего алгоритма решения характеристического полинома нет.

Однако! Если матрица А треугольная ( может быть верхней треугольной , нижней треугольной или диагональной) , то собственные числа в точности совпадают с диагональными элементами.

Пример 1.

Найти собственные числа и собственные вектора матрицы

имеем

Характеристический полином имеет вид:

Собственные числа ₁=-1 , ₂=1, ₃=4

Согласно определению , собственные вектора будут такие:

₁=-1

₂=1

₃=4

Более простой пример

Найти собственные числа и собственные вектора матрицы

имеем

Характеристический полином имеет вид:

Собственные числа ₁=4, ₂=2, ₃=3

Согласно определению , собственные вектора будут такие:

₃=4

₁=2

₂=3

Можно записать проще

Тогда

Два теста для вычисления собственных чисел:

1. Сумма m собственных чисел матрицы А равняется следу матрицы, т.е.

₁+₂+…+_m=a₁₁+a₂₂+…+a_mm

2. Произведение m собственных чисел матрицы А равно определителю матрицы А

₁₂…_m=detA

Локализация собственных значений

Иногда удается получить грубые оценки расположения собственных чисел.

Рассмотрим величину — сумма внедиагональных элементов i-той строки матрицы А. Это некие радиусы кругов S_i на комплексной плоскости с центрами в точках соответствующих диагональных элементов a_ii и называются они кругами Гершгорина .

Теорема Гершгорина:

Все собственные числа матрицы А лежат в объединении кругов Гершгорина S₁,S₂…….S_n.если какой либо круг изолирован , то он содержит ровно одно собственное значение матрицы А.

Уравнение (А-λЕ)х=0 в скалярной форме

— максимальная по модулю координата вектора x.

Пример :

Найти все собственные числа матрицы и изобразить на плоскости круги Гершгорина.

Радиусы кругов

Составим характеристическое уравнение

Произведем замену переменной: , тогда имеем:

Число действительных корней зависит от знака дискриминанта D=q²+p³

D= -198,38 – три действительных различных корня .

Матрицы и системы ОДУ.

В механике для определения частот свободных колебаний применяется метод решения систем линейных ДУ с постоянными коэффициентами при помощи теории матриц. Также получаемые в результате использования данного метода данные позволяют делать выводы об устойчивости системы .

Рассмотрим систему ОДУ

Запишем в виде матрицы А и вектора неизвестных Y

Решение Y ищем в форме

Подставляем предложенное решение в уравнение , имеем

Это основное уравнение относительно собственного числа  и собственного вектора X : , тогда характеристическое уравнение для матрицы А , или

Полученный характеристический полином может быть преобразован:

Определяем собственные вектора ( аналогично рассмотренным примерам)

Получаем вектора ( по порядку, соответственно собственным числам), кратные

Тогда имеем три чисто экспоненциальных решения:

Полученные векторы являются решением линейного и однородного уравнения, следовательно возможна суперпозиция решений , т. е. при произвольных скалярах с₁,с₂,с₃ линейная комбинация тоже будет решением

Теперь вопрос , могут ли коэффициенты с₁,с₂,с₃ быть выбраны таким образом , чтобы удовлетворить заданным начальным условиям , например:

При t=0 u=-4,v=4,w=8 , что эквивалентно записи в векторной форме

Или векторное уравнение

Здесь введено обозначение s-матрица , в столбцах которой расположены собственные вектора, а С- вектор-столбец с произвольными постоянными

Решая , получаем значения произвольных постоянных

Тогда решение исходного уравнения с учетом начальных условий

Или отдельно

Собственные числа и проблема устойчивости .

Для различных динамических конструкций устойчивость понимается по-разному.

Наиболее важной характеристикой любой динамической системы являются собственные числа.

Рассмотрим линейную динамическую систему с постоянными коэффициентами

, где

Мы хотим исследовать решение при t.

Как уже известно, любое частное решение ДУ есть некоторая комбинация m экспоненциальных решений ДУ.

Устойчивость определяется множителем exp(t).

Если они стремятся к нулю , то и все решение будет стремиться к нулю ,

Если ограничены- ограничено,

Если хотя бы один из множителей растет- то решение тоже будет расти.

Устойчивость определяется только вещественными частями :

Мнимые части  дают чистые колебания.

Устойчивость по Ляпунову.

Рассмотрим систему ДУ, описывающую динамику системы

Вспомним понятие эвклидовой нормы

Каждое частное решение называем движением.

Начальное значение Y₀(t) – невозмущенное. Дадим начальному значению вектора Y₀ небольшое по модулю приращение и назовем получаемое движение возмущенным.

Определение:

Движение Y₀(t) системы называется устойчивым по Ляпунову , если для каждого >0 найдется >0 такое , что при условии для любого возмущенного движения при всех t>t₀ имеет место неравенство

Если выполняется движение называется асимптотически устойчивым.

Теорема.

Для того, чтобы положение равновесия Y0 было асимптотически устойчивым ,необходимо и достаточно , чтобы все собственные числа матрицы А имели отрицательные вещественные части.

Пример.

Для рассмотренной системы ДУ имеем асимптотическую устойчивость по Ляпунову , поскольку все собственные числа отрицательны.

Теорема Ляпунова

А- постоянная матрица , все собственные числа имеют отрицательные вещественные части и при tt₀ и достаточно малом Y

, где  и М — положительные постоянные. Тогда положение равновесия Y0 системы уравнений асимптотически устойчиво.

Пример

Матрица А имеет вид

стр. из

Собственный вектор матрицы — Энциклопедия по экономике

Найти собственные значения и собственные векторы матрицы [c.272]
Используя иерархический синтез для взвешивания собственных векторов матриц весами критериев, вычисляется сумма по всем соответствующим взвешенным компонентам собственных векторов матриц целей уровня иерархии, лежащего ниже. [c.98]

Отсюда следует, что либо 1 = 0, либо z — неотрицательный собственный вектор матрицы А. Если z О, то г > 0, что противоречит равенству [c.265]

Пусть вектор X = (xl,…,xn,xn+l) = (x,xn+]) является собственным вектором матрицы А, т. е. АХ =ЛХ. В силу определения матрицы А это равносильно тому, что [c.267]

В [7.7] рассмотрено несколько способов согласования матриц А-(оу 0″,У=1Д…/ ), различающихся по сложности и точности. Показано, что самым точным является нахождение главного собственного вектора матрицы, который после нормализации становится вектором коэффициентов. Численная оценка согласованности матриц этим методом рассмотрена в разделе 7. 5. [c.232]

Пусть i/ ,…, Up — нормированные собственные векторы матрицы R, расположенные в порядке убывания соответствующих им собственных чисел A,t А,2 . .. А,р. Тогда /-я главная компонента [14, п. 10.5.2] определяется как линейная ком- [c.255]

Собственные векторы Ut (i = 1,р) матрицы S являются и собственными векторами матрицы S + kl с собственными числами ii — hi + k. Следовательно, матрица (S + kl)-1 = [c.269]

Нетрудно проверить, что определенный этими соотношениями вектор с, действительно является собственным вектором матрицы а1 , а угол в, вычисленный из уравнения (3.26), есть угол поворота в плоскости, перпендикулярной вектору с/. (Для доказательства удобно перейти в систему координат, в которой вектор с,- имеет единственную отличную от нуля компоненту.) [c.41]

ЛА.5. Пусть А — п х п матрица А = (1 — а)1 + агг, где г — [1. .. 1] — п х 1 вектор. Найдите собственные числа и собственные векторы матрицы А. [c.507]

Произведение матриц . . . .. 22 1 2 5 Собственные значения и собственные векторы матрицы 25 1 2 6 Ранг матрицы . 26 12 7 Понятие о ратной матрицы . . 26 [c.3]

Собственное значение матрицы 26 Собственный вектор матрицы 26 Среднее квадратическое отклонение 203 [c.463]

Ненулевой вектор х = (х, х2,. .., х )Т называется собственным вектором квадратной матрицы А порядка пхп, если Ах = Ах, где Я — некоторое число, называемое собственным значением матрицы. При этом говорят, что х есть собственный вектор матрицы А, принадлежащий ее собственному значению Л. [c.11]

Столбцы матрицы G являются собственными векторами матрицы К и находятся из уравнений [c.84]

Найдем теперь собственные значения и собственные векторы матрицы А. Ее характеристическое уравнение [c.115]

Мы видим, что at — собственный вектор матрицы X X, соответствующий характеристическому корню Яг. Из (11.2) и (11.4) следует, что [c.323]

В случае А > О все неотрицательные собственные векторы матрицы А положительны и принадлежат только ее максимальному по модулю сйбственному значению ХА. Кроме того, в этом случае любые два положительных собственных вектора х и У отличаются лишь числовым множителем у = ССх. [c.262]

Замечание. Если х — собственный вектор матрицы Л, у — собственный вектор матрицы Б, то вектор х у будет, очевидно, собственным вектором для А (8) В. Однако в общем случае неверно, что каждый собственный вектор матрицы А В есть кронекеровское произведение собственных векторов матриц А и В. Пусть, например, [c.55]

Проблема отыскания собственных значений и собственных векторов матриц составляет основу специального раздела алгебры далее мы еще вернемся к этому вопросу. Здесь лишь отметим один важный резу ч ьтат алгебры матриц- для симметрических матриц (1 2.3) все и соб ственных значений являются деиствнге [ьными числами. [c.26]

Максимальное значение А— это наибольшее собственное значение а — собственный вектор матрицы. Элементы Ь — это д искрим и нантные коэффициенты или веса, соответствующие первой дискриминантной функции. В целом можно определить меньше, чем 1) или k функций, каждую с ей собственным значением, функции оценивают Другими словами, первая функция вносит большой вклад в межгрупповую [c. 714]

В соответствии с теоремой Фробениуса-Перрона максимальное по модулю собственное значение АА неотрицательной квадратной матрицы А > О неотрицательно, а среди собственных векторов, принадлежащих ЛА, имеется неотрицательный вектор. В случае А > О все неотрицательные собственные векторы матрицы А положительны и принадлежат только ее максимальному по модулю собственному значению ЛА. Кроме того, в этом случае любые два положительных собственных вектора у и х отличаются лишь числовым множителем, т.е. у= ах. Максимальное по модулю собственное значение ЛА неотрицательной матрицы А называется числом Фробениуса матрицы А, а соответствующий ему неотрицательный собственный вектор — вектором Фробениуса для матрицы А. [c.11]

Токажите, что матрица А идемпотентная и определите ее ранг. Найдите собствен-[ые значения н соответствующие им собственные векторы матрицы А, а затем юстройте ортогональную матрицу, которая приводит А к диагональному виду. [c.121]

В выражении (8. 26) D1/2 есть диагональная матрица, диагональные элементы которой служат арифметическими значениями квадратны корней из собственных значений матрицы Ми, а столбцы матриць Р — собственные векторы матрицы Ми. Так как Ми имеет порядок n — k, этот подход требует вычисления п — k собственных значений и векторов, их подстановки в (8.26) для получения матрицы Сь с помощью которой из (8.27) можно найти С , и, наконец, определить е-из (8.25). [c.255]

О Пример. Найти со-Омстгзвенные значения и собственные векторы матрицы [c.67]

Квадратная матрица А порядка п тогда и только тогда приводится к диагональному виду, когда у матрицы А имеется п линейно независимы х собственных векторов. Матрица Т, столбцами которой служат координаты этих собственных векторов, приводит матрицу А к диагональному виду. Этот критерий, в частности выполняется, когда у матрицы порядка п и мсеет ся п различных собственных значений. [c.68]

Вычисление собственных значений матрицы

Назначение сервиса . Калькулятор предназначен для нахождения в онлайн режиме собственных чисел и собственных векторов матрицы. (см. пример решения)

Решение онлайн
Видеоинструкция
Оформление Word

Решение онлайн
Видеоинструкция
Оформление Word

Читайте также:

II. Из жития в бозе преставившегося иеросхимонаха старца Зосимы, составлено с собственных слов его Алексеем Федоровичем Карамазовым. Сведения биографические 1 страница
II. Из жития в бозе преставившегося иеросхимонаха старца Зосимы, составлено с собственных слов его Алексеем Федоровичем Карамазовым. Сведения биографические 2 страница
VIII. Долина создания душ: понимание матрицы
XVI. Просветленность — это судьба: двойная жизнь волшебников матрицы
XVIII. Стать богом: жизнь за пределами матрицы
Анализ собственных ролей
Базовый вопрос первой матрицы – ЧТО ТЫ МНЕ МОЖЕШЬ ДАТЬ.
Видение собственных грехов.
ВУРФНЫЕ ОТНОШЕНИЯ РУССКОЙ МАТРИЦЫ
Вычисление абсолютной и относительной
Вычисление высот пунктов съемочной основы.
Вычисление индуктивности

Планшетного компьютера, камеры) и принести запись

Для участия в Конкурсе необходимо снять любой ролик

Объявляется конкурс: SCARY MOVIE

Приносите свои рисунки, куклы и прочие поделки в Администрацию Центра до 3 ноября.

Конкурс: crafts for Halloween.

Для групп уровней Junior, Beginner, Elementary объявляется

Внимание. Конкурс!

С 28 октября по 3 ноября

Для групп уровней Pre-Intermediate, Intermediate,

Upper-Intermediate, Advanced, подготовка к FCE

на тему Halloween (с помощью мобильного телефона,

в Администрацию Центра или выслать по адресу Svetlana. [email protected] до 5 ноября.

Победители будут отмечены призами. Все участники получат баллы в зачет бонусной системы.

Целый ряд инженерных задач сводится к рассмотрению систем уравнений, имеющих единственное решение лишь в том случае, если известно значение некоторого входящего в них параметра. Этот особый параметр называется характеристическим, или собственным, значением системы.

Алгоритмы решения задач на собственные значения делятся на две группы. Итерационные методы очень удобны и хорошо приспособлены для определения наименьшего и наибольшего собственных значений. Методы преобразований подобия несколько сложней, зато позволяют определить все собственные значения и собственные векторы.

Рассмотрим матрицу n-го порядка:

Вектор x=(x₁,x₂,…,x_n) называется собственным вектором матрицы А, соответствующим собственному значению l, если он удовлетворяет системе уравнений: Аx=lx.

Поскольку при умножении собственного вектора на скаляр он остается собственным вектором той же матрицы, то его можно нормировать. В частности, каждую координату собственного вектора можно разделить на максимальную из них или на длину вектора, в последнем случае получится единичный собственный вектор.

Характеристической матрицей С данной матрицы А называется матрица вида

где λ– собственное значение, Е- единичная матрица.

Тогда систему уравнений можно записать так: (A-lE)x=0 или Cx=0.

Если перейти к координатной форме записи вектора x, то систему можно записать в виде

Эта система имеет ненулевое решение лишь тогда, когда ее определитель равен 0: det(A-λE)=0. Причем решение не единственно. Так как обычно одно уравнение является следствием остальных.

Определитель матрицы С является многочленном n-ой степени относительно λ: det C=c_{λ n + c₁ λ n -1 + ….+ c_n_-1 λ 1 + c_n λ 0 — характеристический многочлен.}

Корни этого многочлена являются собственными значениями матрицы А.

Вычислить собственные числа и собственный вектор матрицы .

Составим характеристический многочлен: .

Найдем корни этого многочлена: λ₁=2, λ₂=5.

Для нахождения собственных векторов x₁, x₂ составим соответствующие системы уравнений вида Ax=λx:

При λ₁=2 получим или в виде системы уравнений: . Преобразовав, получим: .

Уравнения линейно зависимы, даже совпадают. Поэтому оставляем одно из них.

Тогда собственный вектор, соответствующий λ₁=2, имеет вид x₁=(1,-1).

Аналогично находим второй собственный вектор, соответствующий значению λ₂=5 – x₂=(1,2)

В общем случае, особенно для матриц высокого порядка, задача нахождения их собственных значений и векторов, называемая полной проблемой собственных значений, значительно более сложная.

Часто в практических вычислениях бывают нужны не все собственные значения, а лишь некоторые из них. В этих случаях нецелесообразно решать полную проблему собственных значений.

Для решения частичной проблемы собственных значений обычно используют итерационные методы. Итерационный процесс строится на применении методов итерации к решению системы уравнений AХ = λ Х.

Дата добавления: 2015-07-02 ; Просмотров: 619 ; Нарушение авторских прав? ;

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

Без рубрики
Дримкаст аксессуары
Дримкаст игры
Дримкаст прохождения
Дримкаст эмуляторы
История
Компьютеры
Помощь
Приставки

Adblock
detector

Собственные значения и собственные векторы матрицы презентация, доклад

Слайд 1Текст слайда:

Лекция №10

Лектор: доц. Лаптева Надежда Александровна

Тема: Собственные значения и собственные векторы матрицы

Слайд 2Текст слайда:

Пусть — матрица, — вектор,
— число.

Рассмотрим уравнение

называется собственным значением, — собственным вектором.

Такое преобразование изменяет длину вектора в раз.

Слайд 3Текст слайда:

Например, если то т.е. длина вектора увеличивается в 2 раза.

Если же то длина вектора
уменьшается в 2 раза.

Слайд 4Текст слайда:

Рассмотрим

Запишем матричное уравнение в координатной форме.

Слайд 5Текст слайда:

Преобразуем

Слайд 6Текст слайда:

Получилась система линейных однородных уравнений. Такая система всегда имеет нулевое решение. Нас интересует случай, когда система имеет ненулевое решение.

Теорема. Система линейных уравнений имеет ненулевое решение, если её определитель равен нулю.

Слайд 7Текст слайда:

Пример.

Система имеет бесконечное множество решений. Все решения являются точками прямой

Слайд 8Текст слайда:

Вернемся к нашей системе. Составим определитель системы

или

Получилось квадратное уравнение. Такое уравнение называется характеристическим. Корни уравнения – это собственные значения матрицы

Слайд 9Текст слайда:

Примеры.

1. Найти собственные значения матрицы

Запишем матрицу

Слайд 10Текст слайда:

Находим корни характеристического уравнения

или

Мы нашли собственные значения.

Ответ:

Слайд 11Текст слайда:

Нахождение собственных векторов

1. Найдем собственный вектор, соответствующий собственному значению

Рассмотрим уравнение и вместо подставим

Слайд 12Текст слайда:

Тогда получим или

Слайд 13Текст слайда:

Отсюда

Положим тогда

Получилось

Слайд 14Текст слайда:

Можно считать, что мы нашли собственный вектор. Но обычно этот вектор нормируют, т.е. приводят его к вектору единичной длины. Для этого найдем длину вектора

и каждую координату разделим на

Слайд 15Текст слайда:

Получим

— собственный вектор, соответствующий собственному значению

Слайд 16Текст слайда:

Аналогично найдем т.е. собственный вектор, соответствующий

Слайд 17Текст слайда:

Пусть тогда

Нормируем, т.е. разделим на

Получим

Слайд 18Текст слайда:

Ответ:

соответствует

Слайд 19Текст слайда:

Функция. Предел функции в точке. Односторонние пределы. Пределы на бесконечности. Непрерывность функции. Точки разрыва функции и их классификация.

Слайд 20Текст слайда:

1. Предел в точке.

Рассмотрим пример. Построить график функции

Слайд 21Текст слайда:

Слайд 22Текст слайда:

В этом случае пишут:

По-другому:

при

Слайд 23Текст слайда:

Способы вычисления предела

1. Предел дроби при деление на старшую степень.

Пример.

Слайд 24Текст слайда:

2. Разложение на множители, когда

Пример.

Слайд 25Текст слайда:

Односторонние пределы

Пример 1.

Слайд 26Текст слайда:

Пример 2.

Слайд 27Текст слайда:

Опр. Функция называется непрерывной в точке если

Все элементарные функции непрерывны на своей области определения.

Пример. — непрерывные функции.

Слайд 28Текст слайда:

Опр. Если в точке функция не является непрерывной, то — точка разрыва.

Рассматриваются точки разрыва 1-го и 2-ого рода.

Слайд 29Текст слайда:

Пример.

— точка разрыва 1-го рода (конечный разрыв).

Слайд 30Текст слайда:

Пример.

— точка разрыва 2-ого рода (бесконечный разрыв).

Скачать презентацию

Калькулятор собственных значений — Как найти собственные значения матрицы

Онлайн-калькулятор собственных значений может определить собственные значения данной квадратной матрицы с помощью характеристического уравнения. Этот искатель собственных значений позволяет вам заменить любую матрицу из 2 x 2, 3 x 3, 4 x 4 и 5 x 5. В этом контексте вы можете узнать, как найти собственные значения матрицы и многое другое.

Что такое собственные значения матрицы?

В математике собственные значения — это скалярные значения, которые связаны с линейными уравнениями (также называемыми матричными уравнениями). Его еще называют скрытым корнем. Собственные значения — это специальный набор скаляров, приписываемых линейным уравнениям. Он в основном используется для матричных уравнений. «Eigen» — это немецкое слово, означающее «характерный» или «собственный». Короче говоря, собственное значение — это скаляр, используемый для преобразования собственного вектора.

Вычисление следа и определителя:

Для матрицы 2×2 след и определитель матрицы полезны для получения двух очень специальных чисел для нахождения собственных векторов и собственных значений. К счастью, калькулятор собственных значений найдет их автоматически. Если вы хотите проверить, дан ли правильный ответ или просто хотите посчитать его вручную, то сделайте следующее:

След: След матрицы определяется как сумма элементов на главной диагонали (сверху слева вниз справа). Он также равен сумме собственных значений (с учетом кратности). В случае матрицы 2×2

Tr X = x_1 + b_2

Определитель: Определитель матрицы полезен в нескольких дополнительных операциях, таких как нахождение обратной матрицы. Для матрицы 2×2

|X| = x_1 y_2 – x_2 y_1

Как найти собственные значения?

Уравнение, выражающее основную связь между собственными значениями и его собственным вектором, имеет вид Xv = λv, где λ — скаляр, X — матрица с m строками и m столбцами, а v — вектор столбцов. И в этом отношении истинное значение λ является собственным значением. Оно должно удовлетворять уравнению, чтобы что-то имело истинную ценность.

Приведенное выше уравнение Xv = λv можно преобразовать в X – I = 0, где «I» – единичная матрица. Вы можете начать выполнять операции вычитания и умножения матриц, результатом будет многочлен. Многочлен устанавливается равным нулю. Тогда корни этих членов являются собственными значениями. Собственные значения могут быть действительными или комплексными. Комплексное собственное значение имеет действительную составляющую и мнимое собственное значение. Если мы хотим найти соответствующие собственные векторы с помощью калькулятора собственных значений, который использует исходное уравнение Xv = λv, тогда мы вычисляем для каждого возможного значения v. Значение, которое мы находим для v, является собственным вектором.

Однако онлайн-калькулятор якобиана поможет вам найти матрицу якобиана и определитель набора функций.

Пример:

Вычислить собственные значения для матрицы {{6,1}, {8, 3}}.

Решение:

Нахождение собственных значений для матрицы 2 x 2:

Сначала вычислитель собственных значений вычитает λ из диагональных элементов данной матрицы

$$ \begin{vmatrix} 6.0 – λ \\ 1.0 && 8.0 \ \ 3.0 – λ \end{vmatrix} $$ 92 — 9,0 λ + 10. 0 = 0

Корни (значения собственных значений)

λ_1 = 7,7015

λ_2 = 1,2984

(λ_1, λ_2) = (7. 7016, 1. 2984)

Как можно найти eigenvalues. матрицы 3×3?

Чтобы найти собственные значения матрицы 3×3, X, вам необходимо:
Сначала вычтите λ из главной диагонали X, чтобы получить X – λI.
Теперь запишите определитель квадратной матрицы, который равен X – λI.
Затем решите уравнение, представляющее собой det(X – λI) = 0, для λ. Решения уравнения на собственные значения являются собственными значениями X.

Как работает калькулятор собственных значений?

Онлайн-калькулятор собственных значений вычисляет собственные значения матрицы, вычисляя характеристическое уравнение, выполнив следующие шаги:

Ввод:

Сначала выберите размер матрицы из раскрывающегося списка.
Теперь подставьте значения во все поля. Вы можете сгенерировать случайные значения для матрицы, нажав кнопку «Создать матрицу». И удалите все значения, очистив все поля.
Нажмите кнопку расчета для следующей процедуры.

Вывод:

Калькулятор собственных значений матрицы отображает значения и решает уравнение.
Он также принимает определитель полученной матрицы и предоставляет значения корней.

Часто задаваемые вопросы:

Зачем нам оценивать собственные значения?

Собственные векторы упрощают понимание линейных преобразований. Это «оси», где линейное преобразование работает только путем «растяжения/сжатия» и/или «переворачивания»; собственные значения указывают фактор, при котором происходит это сжатие.

Могут ли собственные значения быть равны нулю?

Собственные значения могут быть нулевыми. Мы не рассматриваем нулевые векторы как собственные векторы: поскольку X 0 = 0 = λ0 для каждого скаляра λ, соответствующее собственное значение не определено.

Где мы используем собственные значения?

Мы можем использовать собственные значения для:

Анализ собственных значений используется при разработке автостереоскопических систем для воспроизведения вибраций автомобиля, вызванных музыкой.
Электротехника: применение собственных значений можно использовать для разделения трехфазных систем путем преобразования симметричных компонентов.

Итог:

Используйте этот калькулятор собственных значений, который определяет собственные значения данной матрицы и вычисляет корни характеристического уравнения. Характеристическое уравнение получается приравниванием полинома нулю.

Ссылка:

Из источника Википедии: характеристическое значение, характеристический многочлен, собственные значения матриц, алгебраическая кратность, собственные пространства, геометрическая кратность и собственный базис для матриц.

Из источника Medium: использование собственных значений, строительные блоки собственных значений, сложение матриц, умножение скаляра на матрицу, умножение матриц.

Из источника Libre Text: определение собственного значения, характеристический полином, характеристическое уравнение, поиск собственных значений, нулевое собственное значение, специальные типы матриц.

Калькулятор собственных значений — с шагами

Калькуляторы
::
Матрицы
::
Калькулятор собственных значений

Этот калькулятор вычисляет собственные значения квадратной матрицы, используя характеристический многочлен.

Матрица ввода

работающий…

Полиномиальные калькуляторы

Факторные полиномы
Полиномиальные корни
Синтетический отдел
Полиномиальные операции
Графические полиномы
Расширить и упростить
Генерировать из корней

Рациональные выражения

Упрощение
Умножение/деление
Сложение/вычитание

Подкоренные выражения

Рационализировать знаменатель
Упрощение

Решение уравнений

Квадратные уравнения (с шагами)
Полиномиальные уравнения
Решение уравнений — с шагами

Квадратное уравнение

Решение (с шагами)
Квадратичный плоттер
Факторинг трехчленов

Геометрия

Равносторонний треугольник
Прямоугольный треугольник
Косой треугольник
Калькулятор площади
Калькулятор прямоугольника
Калькулятор круга
Калькулятор шестиугольника
Калькулятор ромба

Комплексные номера

Модуль, обратный, полярная форма
Подразделение
Упростить выражение

Системы уравнений

Система 2×2
Система 3х3
Система 4×4

Матрицы

Векторы (2D и 3D)
Сложить, вычесть, умножить
Калькулятор определителя
Матрица обратная
Характеристический полином
собственные значения
Собственные векторы
Разложение матрицы

Расчетные калькуляторы

Калькулятор лимита
Калькулятор производных
Интегральный калькулятор

Последовательности и серии

Арифметические последовательности
Геометрические последовательности
Найти n ^th Срок

Аналитическая геометрия

Расстояние и середина
Калькулятор треугольника
Графические линии
Пересечение линий
Двухточечная форма
Расстояние от линии до точки
Параллельно/Перпендикулярно
Уравнение окружности
Круг из 3 точек
Пересечение круговой линии

Тригонометрия

Градусов в Радиан
Триггер Уравнения

Номера

Длинная дивизия
Вычислить выражения
Калькулятор дробей
Наибольший общий делитель НОД
Наименее распространенный кратный LCM
Простые множители
Научная нотация
Калькулятор процентов
Dec / Bin / Hex

Калькулятор вероятности
Распределения вероятностей
Описательная статистика
Стандартное отклонение
Z — Калькулятор очков
Нормальное распределение
Калькулятор Т-теста
Корреляция и регрессия

Финансовые калькуляторы

Простые проценты
Сложные проценты
Калькулятор амортизации
Калькулятор ренты

Прочие калькуляторы

Наборы
Проблемы с работой

примеров

пример 1:ex 1:

Найти собственные значения $ A = \left[ \begin{массив}{cc} 3 и -3 \\ -2 и -4 \end{массив} \right]$.

пример 2:ex 2:

Вычислить собственные значения $ A = \left[ \begin{массив}{cc} 5 и 2 и 0 \\ 2 и 5 и 0 \\ -2 и 6/5 и 3/2 \end{массив} \right]$.

пример 3:ex 3:

Найти собственные значения матрицы $ A = \left[ \begin{массив}{cc} -1 и 2 и 4 и 1 \\ 5 и 3 и 1 и 1 \\ 3 и 7 и 9& 3 \\ 2 и -1 и 2 и 4 \end{массив} \right]$.

Как ввести матрицу?

1: Матрица ввода, начиная с верхнего левого угла.

Пример: Для ввода матрицы:

$ \left[ \begin{массив}{cc} -7 и 1/4\ -1,3 и -2/5 \end{массив} \right] $

тип

2: Нули вводить не нужно.

Пример: Для ввода матрицы:

$ \left[ \begin{массив}{ccc} 0 и 1 и 0 \\ -1 & 0 & 0 \\ 0 и 0 и 2/3 \end{массив} \right] $

тип

3: Вы можете скопировать и вставить матрицу из Excel в 3 шага.

Шаг 1: Скопируйте матрицу из Excel	Шаг 2: Выберите верхнюю правую ячейку	Шаг 3: Нажмите Ctrl+V

4: Вам не нужно использовать полосы прокрутки, так как калькулятор автоматически удалит пустые строки и столбцы.

5: Для удаления матрицы

Выделить всю матрицу	и нажмите удалить

Найдите в нашей базе данных более 200 калькуляторов

228 103 286 решенных задач

Дифференциальные уравнения — действительные собственные значения

Онлайн-заметки Пола
Главная / Дифференциальные уравнения / Системы ЦЭ / Реальные собственные значения

Показать мобильное уведомление Показать все примечания Скрыть все примечания

Мобильное уведомление

Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.

Раздел 5-7: Вещественные собственные значения

9{\ лямбда т}} \]

где $\lambda$ и $\vec \eta $являются собственными значениями и собственными векторами матрицы $A$. Мы будем работать с системами $2 \times 2$, так что это означает, что мы будем искать два решения: ${\vec x_1}\left( t \right)$ и ${\vec x_2}\left( t \right)$, где определитель матрицы,

\[X = \left( {{{\vec x}_1}\,\,\,{{\vec x}_2}} \right)\]

не равно нулю.

Начнем с рассмотрения случая, когда наши два собственных значения, ${\lambda _{\,1}}$ и ${\lambda _{\,2}}$, действительны и различны. . Другими словами, это будут реальные простые собственные значения. Напомним также, что собственные векторы простых собственных значений линейно независимы. Это означает, что решения, которые мы получим из них, также будут линейно независимыми. Если решения линейно независимы, матрица $X$ должна быть невырожденной, и, следовательно, эти два решения будут фундаментальным набором решений. Общее решение в этом случае будет 9{\ влево ( 2 \ вправо)}} \]

Обратите внимание, что каждый из наших примеров фактически будет разбит на два примера. В первом примере будет решаться система, а во втором — набросок фазового портрета системы. Фазовые портреты не всегда преподаются в курсе дифференциальных уравнений, поэтому мы исключим их из процесса решения, чтобы, если вы не рассмотрели их в своем классе, вы могли игнорировать пример фазового портрета для системы.

Пример 1. Решите следующую IVP. \[\vec x’ = \left({\begin{array}{*{20}{c}}1&2\\3&2\end{массив}} \right)\vec x,\hspace{0,25in}\vec x\left( 0 \right) = \left( {\begin{array}{*{20}{c}}0\\{ — 4}\end{array}} \right)\] 92} — 3 \ лямбда — 4 \\ & = \ влево ( {\ лямбда + 1} \ вправо) \ влево ( {\ лямбда — 4} \ вправо) \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} {\ lambda _1} = — 1, \, \, {\ lambda _2} = 4 \ end {align *} \]

Теперь давайте найдем собственные векторы для каждого из них.

${\lambda _{\,1}} = — 1$ :
Нам нужно решить,

\[\left( {\begin{array}{*{20}{c}}2&2\\3&3\end{array}} \right)\left( {\begin{array}{*{20}{c} }{{\eta _1}}\\{{\eta _2}}\end{массив}} \right) = \left( {\begin{array}{*{20}{c}}0\\0\ конец {массив}} \right)\hspace{0.25in} \Rightarrow \hspace{0.25in}2{\eta _1} + 2{\eta _2} = 0\hspace{0.25in} \Rightarrow \hspace{0.25in {\эта _1} = — {\эта _2}\] 9{\left( 1 \right)}} = \left( {\begin{array}{*{20}{c}}{ — 1}\\1\end{array}} \right),\,\, \,\,\,\,\,{\эта _2} = 1\]

${\lambda _{\,2}} = 4$ :
Нам нужно решить,

\[\left( {\begin{array}{*{20}{c}}{ — 3}&2\\3&{ — 2}\end{array}} \right)\left( {\begin{array} {*{20}{c}}{{\eta _1}}\\{{\eta _2}}\end{массив}} \right) = \left( {\begin{array}{*{20}{ c}}0\\0\end{массив}} \right)\hspace{0.25in} \Rightarrow \hspace{0. 25in} — 3{\eta _1} + 2{\eta _2} = 0\hspace{0.25 in} \Rightarrow \hspace{0,25in}{\eta _1} = \frac{2}{3}{\eta _2}\] 9{4t}}\left( {\begin{array}{*{20}{c}}2\\3\end{array}} \right)\]

Теперь нам нужно найти константы. Для этого нам просто нужно применить начальные условия.

\[\left( {\begin{array}{*{20}{c}}0\\{ — 4}\end{array}} \right) = \vec x\left( 0 \right) = {c_1 }\left( {\begin{array}{*{20}{c}}{ — 1}\\1\end{array}} \right) + {c_2}\left( {\begin{array}{* {20}{c}}2\\3\конец{массив}} \справа)\]

Все, что нам нужно сделать сейчас, это перемножить константы, и тогда мы получим два уравнения (по одному на каждую строку), которые мы можем решить для констант. Это дает,

\[\оставил. {\begin{массив}{*{20}{c}}{-{c_1} + 2{c_2} = 0}\\{{c_1} + 3{c_2} = — 4}\end{массив}} \ вправо\}\hspace{0,25 дюйма} \Rightarrow \hspace{0,25 дюйма}{c_1} = — \frac{8}{5},\,\,\,{c_2} = — \frac{4}{5} \]

Тогда решение

\[\vec x\left( t \right) = — \ frac{8}{5}{{\bf{e}}^{ — t}}\left({\begin{array}}{*{20} {c}}{ — 1}\\1\end{массив}} \right) — \frac{4}{5}{{\bf{e}}^{4t}}\left( {\begin{array }{*{20}{c}}2\\3\end{массив}} \right)\]

Теперь давайте посмотрим на фазовый портрет системы. {\ left ( 2 \ right)}} & = \ left ( {\ begin {array} {* {20} {c}} 2 \\ 3 \ end {array}} \ right) \ end {align *}\] 9{\ влево ( 2 \ вправо)}} \). Кроме того, поскольку экспонента будет увеличиваться по мере увеличения $t$, то в этом случае траектория теперь будет удаляться от начала координат по мере увеличения $t$. Обозначим это стрелками на линиях на графике выше.

Обратите внимание, что мы могли бы получить эту информацию, не обращаясь к решению. Все, что нам действительно нужно сделать, это посмотреть на собственные значения. Отрицательные собственные значения будут соответствовать решениям, которые будут двигаться к началу координат по мере увеличения $t$ в направлении, параллельном его собственному вектору. Точно так же положительные собственные значения удаляются от начала координат по мере увеличения $t$ в направлении, параллельном его собственному вектору. 9{\left( 2 \right)}}\) и далее по этому вектору вверх. Набросав некоторые из них, вы получите следующий фазовый портрет. Вот набросок этого с траекториями, соответствующими собственным векторам, отмеченным синим цветом.

В этом случае равновесное решение $\left( {0,0} \right)$ называется седловой точкой и является неустойчивым. В этом случае неустойчивость означает, что решения удаляются от нее при увеличении $t$.

Итак, мы решили систему в матричной форме, но помните, что мы начали без систем в матричной форме. Теперь давайте кратко рассмотрим пример системы, изначально не имеющей матричной формы.

Пример 3 Найдите решение следующей системы. \[\begin{align*}{{x’}_1} & = {x_1} + 2{x_2}\hspace{0.25in}{x_1}\left( 0 \right) = 0\\ {{x’} _2} & = 3{x_1} + 2{x_2}\hspace{0.25in}{x_2}\left( 0 \right) = — 4\end{align*}\]

Показать решение

Сначала нам нужно преобразовать это в матричную форму. Это достаточно легко. Вот матричная форма системы.

\[\vec x’ = \left({\begin{array}{*{20}{c}}1&2\\3&2\end{массив}} \right)\vec x,\hspace{0,25in}\vec x\left( 0 \right) = \left( {\begin{array}{*{20}{c}}0\\{ — 4}\end{array}} \right)\] 9{4t}}\end{выравнивание*}\]

Давайте рассмотрим еще один пример.

Пример 4. Решите следующую IVP. \[\vec x’ = \left( {\begin{array}{*{20}{c}}{ — 5}&1\\4&{ — 2}\end{array}} \right)\vec x, \ hspace {0,25 дюйма} \ vec x \ left ( 0 \ right) = \ left ( {\ begin {array} {* {20} {c}} 1 \\ 2 \ end {array}} \ right) \]

Показать решение

Итак, первое, что нам нужно сделать, это найти собственные значения матрицы. 92} + 7 \ лямбда + 6 \\ & = \ влево ( {\ лямбда + 1} \ вправо) \ влево ( {\ лямбда + 6} \ вправо) \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} {\ lambda _1} = — 1, \, \, {\ lambda _2} = — 6 \ end {align *} \]

Теперь давайте найдем собственные векторы для каждого из них.

${\lambda _{\,1}} = — 1$ :
Нам нужно решить,

\[\left( {\begin{array}{*{20}{c}}{ — 4}&1\\4&{ — 1}\end{array}} \right)\left( {\begin{array} {*{20}{c}}{{\eta _1}}\\{{\eta _2}}\end{массив}} \right) = \left( {\begin{array}{*{20}{ c}}0\\0\end{массив}} \right)\hspace{0.25in} \Rightarrow \hspace{0.25in} — 4{\eta _1} + {\eta _2} = 0\hspace{0.25in } \ Rightarrow \ hspace {0,25 дюйма} {\ eta _2} = 4 {\ eta _1} \] 9{\left( 1 \right)}} = \left( {\begin{array}{*{20}{c}}1\\4\end{array}} \right),\,\,\,\ ,\,\,\,{\эта _1} = 1\]

${\lambda _{\,2}} = — 6$ :
Нам нужно решить,

\[\left( {\begin{array}{*{20}{c}}1&1\\4&4\end{array}} \right)\left( {\begin{array}{*{20}{c} }{{\eta _1}}\\{{\eta _2}}\end{массив}} \right) = \left( {\begin{array}{*{20}{c}}0\\0\ конец {массив}} \right)\hspace{0. 25in} \Rightarrow \hspace{0.25in}{\eta _1} + {\eta _2} = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}{ \эта _1} = — {\эта _2}\] 9{ — 6t}}\left( {\begin{array}{*{20}{c}}{ — 1}\\1\end{array}} \right)\]

Теперь нам нужно найти константы. Для этого нам просто нужно применить начальные условия.

\[\left( {\begin{array}{*{20}{c}}1\\2\end{array}} \right) = \vec x\left( 0 \right) = {c_1}\left ( {\ begin {array} {* {20} {c}} 1 \\ 4 \ end {array}} \ right) + {c_2} \ left ( {\ begin {array} {* {20} {c} }{ — 1}\\1\конец{массив}} \справа)\] 9{ — 6t}}\left( {\begin{array}{*{20}{c}}{ — 1}\\1\end{array}} \right)\]

Теперь найдем фазовый портрет для этой системы.

Пример 5 Нарисуйте фазовый портрет для следующей системы. \[\vec x’ = \left( {\begin{array}{*{20}{c}}{- 5}&1\\4&{- 2}\end{array}} \right)\vec x\ ]

Показать решение

Из последнего примера мы знаем, что собственные значения и собственные векторы для этой системы равны 9{\left( 2 \right)}} & = \left( {\begin{array}{*{20}{c}}{ — 1}\\1\end{array}} \right)\end{align *}\]

Этот немного отличается от первого. Тем не менее, он начинается так же. Сначала нарисуем траектории, соответствующие собственным векторам. Обратите также внимание, что оба собственных значения отрицательны, и поэтому их траектории будут двигаться к началу координат по мере увеличения $t$. Когда мы будем набрасывать траектории, мы добавим стрелки, чтобы обозначить направление, которое они принимают по мере увеличения $t$. Вот схема этих траекторий.

Вот здесь и проявляется небольшое отличие от первого фазового портрета. Все траектории будут двигаться к началу координат по мере увеличения $t$, так как оба собственных значения отрицательны. Вопрос, который нам нужно решить, заключается в том, как они это делают. На самом деле это проще, чем может показаться на первый взгляд.

Второе собственное значение больше первого. Для больших и положительных $t$ это означает, что решение для этого собственного значения будет меньше, чем решение для первого собственного значения. Следовательно, по мере увеличения \ (t \) траектория будет двигаться к началу координат и делать это параллельно \ ({\ vec \ eta ^ {\ left (1 \ right)}} \). {\left(2 \right)}}\).

Добавление некоторых траекторий дает следующий набросок.

В этих случаях мы называем равновесное решение $\left( {0,0} \right)$ узлом и оно асимптотически устойчиво. Равновесные решения асимптотически устойчивы, если все траектории сближаются с ним при увеличении $t$.

Обратите внимание, что узлы также могут быть нестабильными. В последнем примере, если бы оба собственных значения были положительны, все траектории ушли бы от начала координат, и в этом случае равновесное решение было бы неустойчивым.

Прежде чем перейти к следующему разделу, нам нужно сделать еще один пример. Когда мы впервые начали говорить о системах, было упомянуто, что мы можем преобразовать дифференциальное уравнение более высокого порядка в систему. Нам нужно сделать такой пример, чтобы мы могли увидеть, как решать дифференциальные уравнения более высокого порядка, используя системы.

Пример 6 Преобразуйте следующее дифференциальное уравнение в систему, решите систему и используйте это решение, чтобы получить решение исходного дифференциального уравнения. \[2y» + 5y’ — 3y = 0,\hspace{0.25in}y\left( 0 \right) = — 4\,\,\,\,y’\left( 0 \right) = 9\]

Показать решение

Итак, сначала нам нужно преобразовать это в систему. Вот замена переменных,

\[\begin{align*}{x_1} & = y & \hspace{0,25in}{{x’}_1} & = y’ = {x_2}\\ {x_2} & = y’ & \hspace{0,25 in}{{x’}_2} & = y» = \frac{3}{2}y — \frac{5}{2}y’ = \frac{3}{2}{x_1} — \frac {5}{2}{x_2}\end{выравнивание*}\]

Система тогда,

\[\vec x’ = \left( {\begin{array}{*{20}{c}}0&1\\{\frac{3}{2}}&{ — \frac{5}{2}} \end{array}} \right)\vec x\hspace{0.25in}\vec x\left( 0 \right) = \left( {\begin{array}{*{20}{c}}{ — 4 }\\9\конец{массив}} \справа)\]

где,

\[\vec x\left( t \right) = \left( {\begin{array}{*{20}{c}}{{x_1}\left( t \right)}\\{{x_2}\ влево ( т \ вправо)} \ конец {массив}} \ вправо) = \ влево ( {\ begin {массив} {* {20} {c}} {г \ влево ( т \ вправо)} \\ {у ‘ \left( t \right)}\end{массив}} \right)\] 92} + \frac{5}{2}\lambda — \frac{3}{2}\\ & = \frac{1}{2}\left( {\lambda + 3} \right)\left( { 2\lambda — 1} \right)\hspace{0,25 дюйма}{\lambda _1} = — 3,\,\,\,{\lambda _2} = \frac{1}{2}\end{align*} \]

Теперь найдем собственные векторы.

${\lambda _{\,1}} = — 3$ :
Нам нужно решить,

\[\ влево ( {\ begin {массив} {* {20} {c}} 3 & 1 \\ {\ frac {3} {2}} & {\ frac {1} {2}} \ end {массив}} \right)\left( {\begin{array}{*{20}{c}}{{\eta _1}}\\{{\eta _2}}\end{array}} \right) = \left( {\ begin {array} {* {20} {c}} 0 \\ 0 \ end {array}} \ right) \ hspace {0,25 дюйма} \ Rightarrow \ hspace {0,25 дюйма} 3 {\ eta _1} + { \eta _2} = 0\hspace{0,25 дюйма} \Rightarrow \hspace{0,25in}{\eta _2} = — 3{\eta _1}\] 9{\left( 1 \right)}} = \left( {\begin{array}{*{20}{c}}1\\{ — 3}\end{array}} \right),\,\, \,\,\,\,\,{\эта _1} = 1\]

${\lambda _{\,2}} = \frac{1}{2}$:
Нам нужно решить,

\[\left( {\begin{array}{*{20}{c}}{-\frac{1}{2}}&1\\{\frac{3}{2}}&{- 3}\ end{массив}} \right)\left( {\begin{array}{*{20}{c}}{{\eta _1}}\\{{\eta _2}}\end{массив}} \right ) = \left( {\begin{array}{*{20}{c}}0\\0\end{array}} \right)\hspace{0,25in} \Rightarrow \hspace{0,25in} — \frac {1}{2}{\eta _1} + {\eta _2} = 0\hspace{0,25 дюйма} \Rightarrow \hspace{0,25in}{\eta _2} = \frac{1}{2}{\eta _1}\] 9{\ frac {t} {2}}} \ left ( {\ begin {array} {* {20} {c}} 2 \\ 1 \ end {array}} \ right) \]

Применить начальное условие.

\[\left( {\begin{array}{*{20}{c}}{ — 4}\\9\end{array}} \right) = \vec x\left( 0 \right) = {c_1 }\left( {\begin{array}{*{20}{c}}1\\{ — 3}\end{array}} \right) + {c_2}\left( {\begin{array}{* {20}{c}}2\\1\конец{массив}} \справа)\]

Это дает систему уравнений, которую мы можем решить для констант. 9{\ frac {t} {2}}} \ left ( {\ begin {array} {* {20} {c}} 2 \\ 1 \ end {array}} \ right) \]

Вспоминая об этом,

\[\vec x\left( t \right) = \left( {\begin{array}{*{20}{c}}{y\left( t \right)}\\{y’\left( t \справа)}\конец{массив}} \справа)\]

мы видим, что решение исходного дифференциального уравнения — это просто верхняя строка решения матричной системы. Тогда решение исходного дифференциального уравнения 9{\ гидроразрыва {т} {2}}} \]

Обратите внимание, что в качестве проверки в этом случае нижняя строка должна быть производной от верхней строки.

Калькулятор собственных значений матрицы с шагами, методом и решением

Введение в калькулятор собственных значений

Калькулятор матриц собственных значений 4×4 представляет собой онлайн-инструмент, используемый для вычисления собственного значения матрицы для формирования ее собственного вектора. Он использует метод линейного преобразования в матрицах для нахождения собственных значений.

В матричной алгебре важно найти собственные значения, потому что они используются для решения многих дифференциальных уравнений и других задач. Чтобы упростить поиск собственных значений, мы представляем онлайн-инструмент, который может легко вычислять собственные значения.

Зачем использовать собственные значения матричного калькулятора?

Концепция собственного значения важна, потому что вы не можете найти собственный вектор для матрицы, не найдя собственные значения. Это означает, что собственные векторы зависят от собственных значений. Использование онлайн-инструмента может сделать его более эффективным.

При вычислении собственных значений вы можете запутаться между собственными векторами и собственными значениями, поскольку оба они связаны с одним собственным уравнением. Вам нужно использовать калькулятор собственных значений для матриц 2×2, 3×3 и 4×4.

Как использовать калькулятор собственных значений матрицы с шагами

Решатель собственных значений упростил поиск собственных значений матрицы с помощью нескольких простых шагов. Вы можете выполнить следующие шаги, чтобы использовать этот инструмент. Вот эти шаги:

Первым шагом этого инструмента является ввод количества строк и столбцов матрицы. Например, если вы хотите вычислить собственное значение для матрицы 2 на 2, введите 2 в соответствующие поля.
Теперь нужно ввести значения матрицы по количеству строк и столбцов.
Нажмите кнопку «Рассчитать».

Вы получите результат через несколько секунд после простого нажатия на кнопку расчета собственных значений матричного калькулятора.

Как вычисляется собственное значение?

Собственное значение можно рассчитать с помощью линейного преобразования и собственного уравнения с помощью этого калькулятора собственных значений.

Предположим, вам нужно найти собственный вектор для матрицы A, который определяется как:

$$ А \;=\; \begin{bmatrix} 1 и 4 \\ -4 и -7 \\ \end{bmatrix} $$

Линейное преобразование определяется как:

$$ Ср \;=\; λv $$

Переписав приведенное выше уравнение, чтобы сформировать собственное уравнение:

$$ (A \;-\; λI)v \;=\; 0 $$

Где — собственное значение, I — единичная матрица, а v — собственный вектор, который необходимо найти. 92 \;=\; 0 $$

Следовательно,

$$ λ \;=\; -3, \;-3 $$

Калькулятор собственных значений для матрицы 3 на 3 использует приведенную выше формулу для вычисления собственного значения.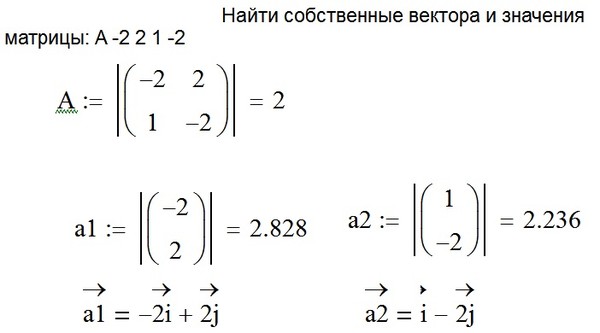 Хотя этот инструмент позволяет вычислять собственное значение в цифровом виде, важно понимать его концепцию. Таким образом, он решает проблему поэтапно, так что вы можете изучить метод, а также его концептуальное понимание.

Преимущества использования калькулятора метода собственных значений

В матричной алгебре и науке о данных собственные значения и собственные векторы упрощают линейную операцию. Это также помогает объяснить дисперсию данных. Вы можете использовать инструмент поиска собственных значений, чтобы быстро и легко решать проблемы, связанные с собственными значениями. Собственное значение матричного калькулятора способствует изучению и пониманию различных задач и расчетов.

Калькулятор собственных значений позволяет использовать его по-разному. Некоторые из этих полезных применений:

Собственные значения матричного калькулятора решают задачи легко и просто, объясняя каждый шаг.
Позволяет использовать без ограничений; вам не нужно регистрироваться, чтобы использовать его, или платить какую-либо плату за расчет собственных значений матриц 4×4, 3×3 и 2×2.
Это надежно, потому что результаты, полученные этим инструментом, точны.
Вы можете сэкономить время, используя этот инструмент, чтобы понять, как находить собственные значения на калькуляторе.
Калькулятор собственных значений матрицы позволяет выбрать случайную матрицу, чтобы можно было попрактиковаться с различными значениями.

Алан Уокер

Последнее обновление 02 июня 2022 г.

Изучает математические науки и технологии. Технический гик и автор контента. Помешанный на Википедии, который хочет знать все. Любит путешествия, природу, чтение. Математика и технологии сделали свое дело, и теперь пришло время извлечь выгоду из этого.

Алгебраическая и геометрическая кратность собственных значений

Марко Табога, доктор философии

Алгебраическая кратность собственного значения — это количество раз, которое оно встречается как корень характеристического многочлена (т. е. многочлена, корни которого собственные значения матрицы).

Геометрическая кратность собственного значения есть размерность линейной пространство связанных с ним собственных векторов (т. е. его собственное пространство).

В этой лекции мы даем строгие определения двух концепций алгебраическая и геометрическая кратность, и мы доказываем некоторые полезные факты о их.

Ищете калькулятор геометрической кратности или пошаговое руководство о том, как рассчитать геометрическую кратность? Перейдите по этой ссылке.

Table of contents

Algebraic multiplicity
Geometric multiplicity
Relationship between algebraic and geometric multiplicity
Defective eigenvalues
Solved exercises
1. Упражнение 1
2. Упражнение 2

Алгебраическая кратность

Начнем с определения.

Определение Позволять быть матрица. Обозначим через в возможно повторяется собственные значения , которые решают характеристику уравнениеМы сказать, что собственное значение имеет алгебраическую кратность тогда и только тогда, когда их не больше и не меньше решения характеристического уравнения, равные .

Давайте посмотрим на некоторые примеры.

Пример Рассмотрим матрица характеристический полином это корни многочлена, то есть решения Таким образом, имеет два различных собственных значения. Их алгебраические кратности равны потому что они не повторяются.

Пример Определите матрица Его характеристический полином это корни многочлена, то есть решения Таким образом, имеет одно повторяющееся собственное значение, алгебраическая кратность которого равна

Геометрическая кратность

Напомним, что каждое собственное значение связано с линейное пространство собственных векторов, называется собственным пространством.

Определение Позволять быть матрица. Позволять быть одним из собственных значений и обозначим его ассоциированное собственное пространство через . Размер называется геометрической кратностью собственного значения .

Давайте теперь сделаем несколько примеров.

Определение Рассмотрим матрица характеристический полином это корни многочлена являются собственные векторы, связанные с являются векторами что решить уравнениеили последнее уравнение подразумевает чтоПоэтому, собственное пространство это линейное пространство, которое содержит все векторы принадлежащий формагде может быть любым скаляром. Таким образом, собственное пространство генерируется не замужем векторСледовательно, он имеет измерение . Как следствие, геометрическая кратность является .

Пример Рассмотрим матрица характеристический полином остров его корни Таким образом, существует повторяющееся собственное значение () с алгебраической кратностью, равной 2. Его ассоциированные собственные векторы решать в уравнениеили уравнение выполняется для и любое значение . Как следствие, собственное пространство это линейное пространство, которое содержит все векторы принадлежащий формагде может быть любым скаляром. Поскольку собственное пространство генерируется одним векторэто имеет измерение . Как следствие, геометрическая кратность равно 1, что меньше его алгебраической кратности, равной 2.

Пример Определите матрица характеристический полином остров его корни Таким образом, существует повторяющееся собственное значение () с алгебраической кратностью, равной 2. Его ассоциированные собственные векторы решать в уравнениеили уравнение выполняется для любого значения а также . Как следствие, собственное пространство это линейное пространство, которое содержит все векторы принадлежащий формагде а также являются скалярами, которые могут быть выбраны произвольно. Таким образом, собственное пространство создается двумя линейно независимый векторыСледовательно, он имеет измерение . Как следствие, геометрическая кратность равно 2, что равно его алгебраической кратности.

Вывод из предыдущих примеров состоит в том, что алгебраическая и геометрическая кратность собственного значения не обязательно совпадают.

Связь между алгебраической и геометрической кратностью

Следующее предложение устанавливает важное свойство кратностей.

Предложение Позволять быть матрица. Позволять быть одним из собственных значений . Тогда геометрическая кратность меньше или равно его алгебраической кратности.

Доказательство

Предположим, что геометрическая кратность равно , так что есть линейно независимые собственные векторы связаны с . Произвольно выбрать векторы , все имеющие измерение и такой, что столбцы векторов линейно независимы. Определите матрица За Любые , обозначать через вектор, который решает, какой гарантированно существует, потому что является полноранговым (его столбцы линейно независимы). Определите матрица и обозначать через его верхний блокировать и по ниже блок:обозначить по в единичная матрица. Для любого скаляра , у нас есть что так как является полноправным и, как следствие, его определитель ненулевое, мы можем написатьгде в ногу мы использовали результат о определитель блочные матрицы. Собственные значения решить характеристическое уравнение или же, эквивалентно, уравнениеЭто уравнение имеет корень это повторяется по крайней мере раз. Следовательно, алгебраическая кратность не меньше его геометрической кратности . Может быть больше, если также является корнем

Дефектные собственные значения

Когда геометрическая кратность повторяющегося собственного значения строго меньше его алгебраической кратности, то это собственное значение называется дефектный .

Собственное значение, которое не повторяется, имеет связанный с ним собственный вектор, равный отличное от нуля. Следовательно, размерность его собственного пространства равна 1, его геометрическая кратность равна 1 и равна его алгебраической множественность. Таким образом, неповторяющееся собственное значение также является недефектным.

Решенные упражнения

Ниже вы можете найти несколько упражнений с поясненными решениями.

Упражнение 1

Найдите, является ли матрица имеет любые дефектные собственные значения.

Решение

Характеристический многочлен остров его корни Таким образом, нет повторяющихся собственных значений и, как следствие, дефектных собственные значения.

Упражнение 2

Определить

Определить имеет дефектные собственные значения.

Решение

Характеристический полином это здесь в ногу мы использовали Лаплас расширение по третьему ряду. Корни многочлена Таким образом, существует повторяющееся собственное значение () с алгебраической кратностью, равной 2. Его ассоциированные собственные векторы решать в уравнениеили уравнение выполняется для любого значения а также . Как следствие, собственное пространство это линейное пространство, которое содержит все векторы принадлежащий формагде скаляр может быть выбран произвольно. Следовательно, собственное пространство генерируется одним векторТаким образом, он имеет измерение , геометрическая кратность равен 1, его алгебраическая кратность равна 2, и он дефектен.

Как цитировать

Пожалуйста, указывайте как:

Taboga, Marco (2021). «Алгебраическая и геометрическая кратность собственных значений», Лекции по матричной алгебре. https://www.statlect.com/matrix-алгебра/алгебраическая-и-геометрическая-кратность-собственных значений.

Нахождение собственных значений и собственных векторов матриц 2×2

Нахождение собственных значений и собственных векторов матриц 2×2 — Math Insight

Нахождение собственных значений и собственных векторов матриц 2×2

Математика 2241, весна 2022 г.
Имя:
Идентификационный номер:

Срок сдачи: 9 февраля 2022 г., 23:59.
Номер стола/группы:
Члены группы:

Всего баллов: 1

Иногда, когда мы умножаем матрицу $A$ на вектор, мы получаем тот же результат, что и умножение вектора на скаляр $\lambda$: $$A\vc{x}=\лямбда \vc{x}$$ Вектор $\vc{x}$, удовлетворяющий этому уравнению при некотором значении $\lambda$, называется собственным вектором вектора $A$, а значение $\lambda$ называется соответствующим собственное значение . Независимо от того, что такое $A$, всегда есть один вектор $\vc{x}$, для которого это уравнение верно, независимо от того, что такое $\lambda$. Что это за вектор? (1,0) (0,1) (1,1) (0,0)
Поскольку этот вектор всегда является решением, мы не считаем его собственным вектором.
Собственные значения и собственные векторы многое говорят нам о влиянии матрицы. Давайте разберемся, как их найти.
1. Мы ограничим наше внимание матрицами $2\times 2$. Мы ищем решения уравнения $$A\vc{x}=\лямбда \vc{x}.$$ Мы знаем, как решить $B\vc{y}=\vc{z}$, если знаем $\vc{z}$, поэтому первым шагом является преобразование уравнения в этот формат. Начните с вычитания $\lambda \vc{x}$ с обеих сторон и введите новое уравнение ниже.
  (В Интернете введите $\lambda$ как лямбда или с символом λ. Для первого варианта, чтобы написать $\lambda x$, вам нужен пробел или звездочка, как в лямбда х или лямбда*х. Просто введите вектор $\vc{x}$ как x; не беспокойтесь о том, чтобы сделать его полужирным $\vc{x}$ или добавить стрелку, например $\vec{x}$. )
  Далее мы хотим разложить $\vc{x}$ так, чтобы оно умножалось только на единицу. Однако мы должны быть осторожны с этим. Что означает $A-\lambda$, если $A$ — матрица, а $\lambda$ — скаляр? Вычтите λ из каждого элемента A. Вычтите λ из диагональных элементов A. Ничего: вычитание константы из матрицы — неопределенная операция.
  . Чтобы это имело смысл, нам нужно преобразовать $\lambda \vc{x}$ в матрицу, умноженную на $\vc{x}$. Матрица $$I=\begin{bmatrix} 1 и 0 \\ 0 и 1\end{bmatrix}$$ называется единичной матрицей. Единичная матрица $I$ действует как $1$, в чем можно убедиться, умножив $I$ на $\vc{x}$:
  $\displaystyle \begin{bmatrix} 1 & 0 \\ 0 & 1\end {bmatrix} \begin{bmatrix} x \\ y\end{bmatrix} = $
  
  Везде, где у нас есть вектор $\vc{x}$, мы можем заменить его на $I\vc{x}$. С этим изменением мы имеем $$A\vc{x}-\lambda I \vc{x} = \vc{0}$$ Что значит умножить матрицу на скаляр? Умножьте каждый элемент матрицы на скаляр. Ничего: умножение матрицы на скаляр — неопределенная операция. Умножьте диагональные элементы матрицы на скаляр.
  Это означает, что
  $\displaystyle \lambda \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix} = $
  
  Теперь мы можем разложить $\vc{x}$, чтобы получить $(A-\lambda I)\vc{x}=\vc{0}$. Предположим, что $\displaystyle A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$. затем
  $\displaystyle A-\lambda I = $
2. Мы ищем решения $(A-\lambda I)\vc{x}=\vc{0}$. В начале этого вопроса мы заметили, что один конкретный вектор всегда был решением этого уравнения для любого выбора $A$ и $\lambda$. Что это был за вектор?
  Мы хотим, чтобы другой вектор был решением. Напомним, что определитель матрицы может сказать нам, сколько решений имеет система. Система имеет ровно одно решение, если $\det (A-\lambda I) \neq$
  , и либо не имеет решений, либо бесконечно много решений, если $\det (A-\lambda I) =$
  . Поскольку мы знаем, что система имеет хотя бы одно решение, последнее условие гарантирует наличие другого решения.
  Это условие $\det (A-\lambda I) = ＿$ для собственных значений является настолько важным уравнением в линейной алгебре, что мы даем ему имя,
  0550 характеристическое уравнение .
  Первым делом нужно найти значения $\lambda$, которые решают характеристическое уравнение. Давайте поработаем на примере: $$A=\begin{bmatrix} -1 и 1 \\ 4 и -1 \end{bmatrix}$$ затем
  $\displaystyle A-\lambda I = $
  Поскольку у нас есть матрица $2 \times 2$, характеристическое уравнение $\det (A-\lambda I )= 0$ будет квадратным уравнением относительно $\lambda$. Запишите квадратное здесь:
  
  $=0$
  Мы можем найти корни характеристического уравнения, либо факторизуя, либо используя квадратичную формулу. Запишите корни в порядке возрастания:
  ,
  Эти корни являются собственными значениями $A$.
3. Чтобы найти собственные векторы, нам нужно найти решения $(A-\lambda I)\vc{x}=\vc{0}$ для каждого значения $\lambda$. Начнем с меньшего из двух собственных значений: $\lambda=＿$. Запишите, чему равно $A-\lambda I$ для этого собственного значения (онлайн сделает это за вас). $$- ＿ + AI=\left[\begin{matrix}- ＿ — 1 & 1\\4 & — ＿ — 1\end{matrix}\right]$$ Мы будем называть эту матрицу $B$. Обратите внимание, что вторая строка в два раза больше первой. Для матриц $2 \times 2$ строки всегда будут скалярно кратны друг другу, если вы правильно нашли собственное значение. Мы можем найти все решения уравнения $B\vc{x}=\vc{0}$, просто взглянув на первую строку. Пусть $\vc{x}=\begin{bmatrix}x \\ y \end{bmatrix}$. У нас должно быть $2x+y=0$. Любой выбор $x$ позволит нам найти значение $y$, которое будет работать. Например, мы можем подставить $x=1$ и найти, что $y=$
  . Таким образом, один собственный вектор равен
  $\displaystyle \vc{x}= $
  
  Мы могли бы выбрать другое значение для $x$, отличное от $x=1$. Например, если бы мы выбрали $x=2$, мы просто получили бы удвоенное значение $y$ или $y=$
  , что дало бы нам собственный вектор $\begin{bmatrix} 2\\＿\end{ bматрица}$. Этот собственный вектор в два раза длиннее исходного собственного вектора $\begin{bmatrix} ＿ \\ ＿ \end{bmatrix}$, но считается тем же вектором. Фактически любой скаляр, кратный $\begin{bmatrix} ＿ \\ ＿ \end{bmatrix}$ (кроме умножения на ноль), считается собственным вектором для $\lambda=＿$ . (Этот факт соответствует тому факту, что мы могли инвертировать или масштабировать вектор при графическом определении собственных векторов.)
4. Далее мы найдем собственный вектор для большего из двух собственных значений: $\lambda=＿$. Запишите, чему равно $A-\lambda I$ для этого собственного значения (онлайн сделает это за вас). $$- ＿ + AI=\left[\begin{matrix}- ＿ — 1 & 1\\4 & — ＿ — 1\end{matrix}\right]$$ Мы будем называть эту матрицу $C$. Обратите внимание, что вторая строка снова кратна первой строке. Мы можем найти все решения уравнения $C\vc{x}=\vc{0}$, просто взглянув на первую строку. Пусть $\vc{x}=\begin{bmatrix}x \\ y \end{bmatrix}$. У нас должно быть $-2x+y=0$. Любой выбор $x$ позволит нам найти значение $y$, которое будет работать. Например, мы можем подставить $x=1$ и найти, что $y=$
  . Таким образом, один собственный вектор равен
  $\displaystyle \vc{x}= $
  
  Все остальные собственные векторы для $\lambda=＿$ являются скалярными кратными $\begin{bmatrix} ＿ \\ ＿ \end{bmatrix}$.
5. Постройте собственные векторы, которые вы нашли в этом апплете. (Любой скаляр, кратный найденным вами собственным векторам, подойдет.)
  Обратная связь от апплета
  собственных векторов:
Найдите собственные значения и собственные векторы матрицы $$A=\begin{bmatrix} 6 & -4 \\ 3 & -1 \end{bmatrix}$$
1. Шаг 1. Найдите собственные значения.
  $\displaystyle A-\lambda I = $
  
  Что такое характеристическое уравнение?
  
  =0 Найдите собственные значения и запишите их (порядок не имеет значения): $\lambda_1=$
  , $\lambda_2=$
2. Шаг 2: Найдите собственный вектор, соответствующий первому введенному вами собственному значению, $\lambda_1=＿$
  $\displaystyle A-\lambda_1 I = $
  
  Запишите уравнение, соответствующее первой строке $(A-\lambda_1 I)\vc{x}=\vc{0}$, где $\vc{x}=\begin{bmatrix} x \\ y \end {bmatrix}$ и $\vc{0}=\begin{bmatrix} 0 \\ 0 \end{bmatrix}$.
  Выберите значение для $x$:
  . Каково соответствующее значение $y$?
  Запишите найденный собственный вектор:
3. Шаг 3: Найдите собственный вектор, соответствующий второму введенному вами собственному значению, $\lambda_2=＿$
  $\displaystyle A-\lambda_2 I = $
  
  Запишите уравнение, соответствующее первой строке $(A-\lambda_2 I)\vc{x}=\vc{0}$, где $\vc{x}=\begin{bmatrix} x \\ y \end {bmatrix}$ и $\vc{0}=\begin{bmatrix} 0 \\ 0 \end{bmatrix}$.
  Выберите значение для $x$:
  . Каково соответствующее значение $y$?
  Запишите найденный собственный вектор:
Найдите собственные значения и собственные векторы матрицы $$B=\begin{bmatrix} -3 и 2 \\ 4 и 4 \end{bmatrix}$$
$\displaystyle B-\lambda I = $

Что такое характеристическое уравнение $\det (B-\lambda I )=0$?

Найдите собственные значения и запишите их (порядок значения не имеет): $\lambda_1=$
, $\lambda_2=$
Найдите собственный вектор, соответствующий первому введенному вами собственному значению, $\lambda_1=＿$
$\displaystyle B-\lambda_1 I = $

Запишите уравнение, соответствующее первой строке $(B-\lambda_1 I)\vc{x}=\vc{0}$, где $\vc{x}=\begin{bmatrix} x \\ y \end {bmatrix}$ и $\vc{0}=\begin{bmatrix} 0 \\ 0 \end{bmatrix}$.
Выберите значение для $x$:
. Каково соответствующее значение $y$?
Запишите найденный собственный вектор:
Найдите собственный вектор, соответствующий второму введенному вами собственному значению, $\lambda_2=＿$
$\displaystyle B-\lambda_2 I = $

Запишите уравнение, соответствующее первой строке $(B-\lambda_2 I)\vc{x}=\vc{0}$, где $\vc{x}=\begin{bmatrix} x \\ y \end {bmatrix}$ и $\vc{0}=\begin{bmatrix} 0 \\ 0 \end{bmatrix}$.
Выберите значение для $x$:
. Каково соответствующее значение $y$?
Запишите найденный собственный вектор:
Найдите собственные значения и собственные векторы $A=\left[\begin{matrix}1 & 2\\3 & 4\end{matrix}\right]$.
1. Шаг 1. Вычислить собственные значения.
  Запишите характеристическое уравнение для собственных значений, т.е. $\det(A — \lambda I)=0$?
  Решите это уравнение для собственных значений. $\lambda_1 = $
  , $\lambda_2 = $
  (Порядок не имеет значения. Если вы округлите свои ответы, они должны быть правильными как минимум до 5 значащих цифр.)
2. Шаг 2. Вычислите собственный вектор, соответствующий первому введенному вами собственному значению, $\lambda_1=＿$.
  Для $\lambda_1=＿$,
  $\displaystyle A-\lambda_1 I = $
  
  При округлении укажите в ответе не менее 5 значащих цифр.
  Запишите уравнение, соответствующее первой строке $(A-\lambda_1I)\vc{x}=\vc{0}$, где $\vc{x} = (x,y)$ и $\vc{ 0}=(0,0)$.
  
  Выберите значение для $x$:
  . Каково соответствующее значение $y$?
  Запишите найденный собственный вектор:
3. Шаг 3. Вычислите собственный вектор, соответствующий второму введенному вами собственному значению, $\lambda_2=＿$.
  Для $\lambda_2=＿$,
  $\displaystyle A-\lambda_2 I = $
  
  При округлении укажите в ответе не менее 5 значащих цифр.
  Запишите уравнение, соответствующее первой строке $(A-\lambda_2I)\vc{x}=\vc{0}$, где $\vc{x} = (x,y)$ и $\vc{ 0}=(0,0)$.
  
  Выберите значение для $x$:
  . Каково соответствующее значение $y$?
  Запишите найденный собственный вектор:
Необязательная бонусная задача
Найдем собственные значения матрицы $$A = \left[\begin{matrix}1 & -1\\1 & 1\end{matrix}\right].$$ Матрица выглядит достаточно невинно.
1. Сначала рассчитаем характеристическое уравнение как квадратное по $\lambda$:
2. Вы могли бы попробовать разложить уравнение на множители, но вы далеко не уйдете. Лучше использовать квадратную формулу.
  Собственные значения (в любом порядке) равны
  $\lambda_1=$
  $\lambda_2=$
3. Прекрасно, у нас есть комплексные числа для собственных значений. Что это должно означать?
  Мы уже видели эту матрицу в наборе графических задач на умножение матриц. Там, когда мы исследовали действие этой матрицы с помощью следующего апплета, мы не смогли найти ни одного направления, в котором матрица растягивала или переворачивала векторы, и мы пришли к выводу, что у нее нет собственных векторов или собственных значений. Наш вывод был не совсем правильным. Мы должны были заключить, что в матрице нет действительных собственных значений или собственных векторов. Оказывается, у него есть комплексные собственные значения. (У него тоже есть сложные собственные векторы, но мы не будем об этом.)
  Когда вы умножаете векторы на эту матрицу, что матрица $A$ делает с векторами? Он масштабирует векторы, чтобы они были как меньше, так и больше, и поворачивает их в разных направлениях. Он масштабирует векторы, чтобы они были как меньше, так и больше, и поворачивает их в одном направлении. Он масштабирует все векторы, чтобы они были больше, и вращает их в разных направлениях. Он масштабирует все векторы, чтобы они были меньше, и вращает их в разных направлениях. Он масштабирует все векторы, чтобы они были больше, и поворачивает их в одном направлении. Он масштабирует все векторы, чтобы они были меньше, и поворачивает их в одном направлении.
  Оказывается, это согласованное направление вращения связано с тем, что собственные значения являются комплексными.
  No related posts.

как найти собственное значение матрицы

Где можно решить любую задачу по математике, а так же как найти собственное значение матрицы Онлайн?

4.3.6 Собственные числа и собственные векторы линейного оператора

Лекция 7 Собственные числа и векторы

Собственный вектор матрицы — Энциклопедия по экономике

Вычисление собственных значений матрицы

Собственные значения и собственные векторы матрицы презентация, доклад

Калькулятор собственных значений — Как найти собственные значения матрицы

Как можно найти eigenvalues. матрицы 3×3?

Калькулятор собственных значений — с шагами

Полиномиальные калькуляторы

Рациональные выражения

Подкоренные выражения

Решение уравнений

Квадратное уравнение

Геометрия

Комплексные номера

Системы уравнений

Матрицы

Расчетные калькуляторы

Последовательности и серии

Аналитическая геометрия

Тригонометрия

Номера

Финансовые калькуляторы

Прочие калькуляторы

Как ввести матрицу?

1: Матрица ввода, начиная с верхнего левого угла.

2: Нули вводить не нужно.

3: Вы можете скопировать и вставить матрицу из Excel в 3 шага.

4: Вам не нужно использовать полосы прокрутки, так как калькулятор автоматически удалит пустые строки и столбцы.

5: Для удаления матрицы

Дифференциальные уравнения — действительные собственные значения

Раздел 5-7: Вещественные собственные значения

Калькулятор собственных значений матрицы с шагами, методом и решением

Введение в калькулятор собственных значений

Зачем использовать собственные значения матричного калькулятора?

Как использовать калькулятор собственных значений матрицы с шагами

Как вычисляется собственное значение?

Преимущества использования калькулятора метода собственных значений

Алан Уокер

Алгебраическая и геометрическая кратность собственных значений

Алгебраическая кратность

Геометрическая кратность

Связь между алгебраической и геометрической кратностью

Дефектные собственные значения

Решенные упражнения

Упражнение 1

Упражнение 2

Как цитировать

Нахождение собственных значений и собственных векторов матриц 2×2

Нахождение собственных значений и собственных векторов матриц 2×2

Добавить комментарий Отменить ответ