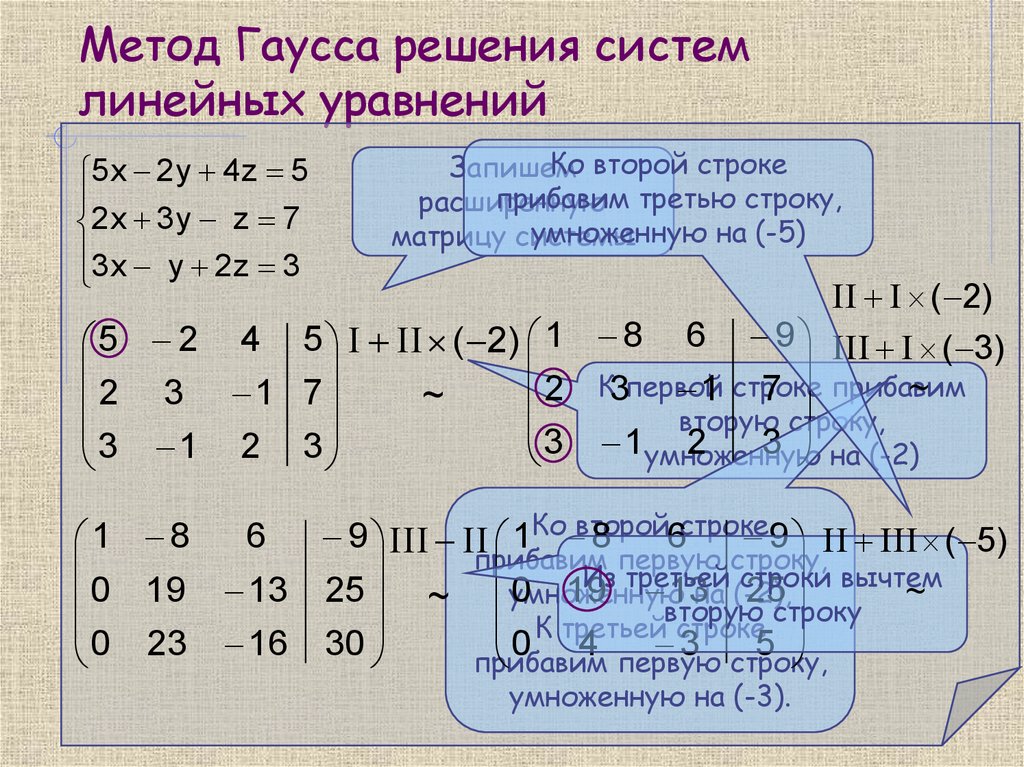
Дана система линейных уравнений. Решить её тремя способами.
Пример 1:
Дана система линейных уравнений. Решить её тремя способами:
1) по формулам Крамера;
2) матричным методом;
3) методом Гаусса.
Решение от преподавателя:
а) формулы Крамера:
2)Матричный метод.
Для решения уравнения вида: , необходимо найти обратную матрицу А, чтобы привести уравнение к виду: .
Находим сначала определитель матрицы А:
, значит, обратная матрица существует, и мы ее можем найти.
Находим алгебраические дополнения:
Тогда обратная матрица:
в)Метод Гаусса.
В соответствии с методом Гаусса, путем алгебраических преобразований приводим матрицу к треугольному виду. Исходная матрица:
3 | -1 | 2 | 7 |
1 | 2 | -1 | 2 |
2 | 1 | 1 | 7 |
Вторую строку умножаем на 3 и отнимаем от нее первую строку. Третью строку умножаем на 3 и отнимаем от нее первую умноженную на 2:
Третью строку умножаем на 3 и отнимаем от нее первую умноженную на 2:
3 | -1 | 2 | 7 |
0 | 7 | -5 | -1 |
0 | 5 | -1 | 7 |
Третью строку умножаем на 7 и отнимаем от нее вторую умноженную на 5:
3 | -1 | 2 | 7 |
0 | 7 | -5 | -1 |
0 | 0 | 18 | 54 |
Последняя матрица соответствует системе:
Ответ:x=1, y=2, z=3.
1.3. Решение систем линейных уравнений
Рассмотрим три способа решения систем линейных уравнений: по формулам Крамера, матричным способом, методом Гаусса.
Пусть дана система линейных уравнений
(1.5)
. При решении системы (1.5)по формулам Крамера, неизвестные находятся из соотношений:
,, …,, (1.6)
где определитель системы,,, …,определители неизвестных, которые получаются иззаменой его первого, второго и т.д. столбца соответственно столбцом свободных членов.
. Решение системы линейных уравнений (1.5)матричным способом.
Если ввести матричные обозначения
,,,
то систему можно записать матричным уравнением
. (1.7)
Решение системы матричным методом определяется соотношением
.
То есть, чтобы решить систему (1.5), необходимо найти матрицу , обратную до матрицы системы, и умножить ее на матрицу свободных членов (см. раздел 1.2).
Формулу (1.8) называют матричной записью решения системы(1.5) илирешением матричного уравнения(1.7).
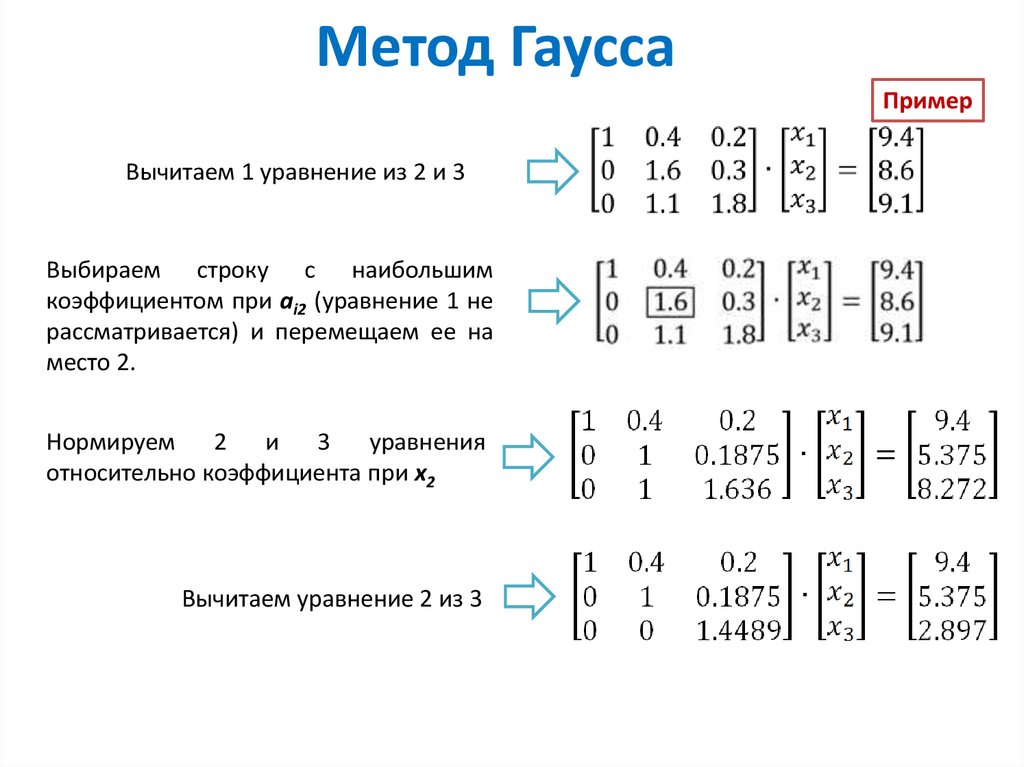
. Решение систем линейных уравненийметодом Гаусса.
Одним из наиболее простых методов решения систем линейных уравнений есть метод непосредственного исключения неизвестных или метод Гаусса. Этот метод предложен К. Гауссом и базируется на элементарных преобразованиях системы уравнений, или проще, расши-ренной матрицы.
Расширенной матрицей системы линейных уравнений (1.5) называют матрицу коэффициентов системы с добавленным еще одним столбцом свободных членов, который отделяется черточкой, т.е.
. (1.9)
Под элементарными преобразованиями расширенной матрицы подразумевается следующее:
перестановка любых двух строк матрицы;
2) умножение какой-либо строки матрицы на любое, отличное от нуля число;
3) прибавление к любой строке матрицы
соответствующих членов другой строки,
умноженных на одно и то же число.
Идея метода Гауссасостоит в том, чтобы с помощью элементарных преобразований привести расширенную матрицу к равносильной матрице треугольного (или трапециевидного) вида.
Затем, по полученной расширенной матрице восстанавливается равносильная система линейных уравнений, из которой последовательно находятся все неизвестные.
1. Решить систему алгебраических уравнений
а) по формулам Крамера,б) матричным способом,в) методом Гаусса.
а) Решим задачу по формулам Крамера, которые имеют вид
,,,
где – определитель системы уравнений;,,– определители неизвестных, полученные иззаменой его первого, второго и третьего столбца соответственно, столбцом свободных членов.
Запишем определители ,,,и раскроем их:
Теперь найдем неизвестные ,,по формулам (1.6)
;;.
Ответ:;;.
б) Решим систему уравнений матричным способом.
Обозначим через матрицу исходной системы уравнений, черезвектор-столбец неизвестных и черезвектор-столбец свободных членов:
, ,
Если система линейных уравнений в матричном виде записывается , то матрица неизвестных находится из уравнения.
Для нахождения матрицы неизвестных найдем обратную матрицу (см. раздел 1.2) и умножим ее на матрицу-столбец свободных членов.Так как матрица невырожденная, (как было определено ранее, (), то для нее существует обратная матрица.
Обратную матрицу найдем в следующей последовательности:
1) Запишем транспонированную матрицу , т.е. матрицу, в которой строки матрицызаменены ее столбцами с тем же номером
.
Обратную матрицу можно получить по формуле:
,
где
– определитель матрицы,– алгебраические дополнения (миноры),
равные определителям, которые получаются
с помощью вычеркивания-й
строки и-го
столбца транспонированной матрицы,
взятые со знаком.
Найдем алгебраические дополнения транспонированной матрицы :
;;;
;;;
;;.
а решение системы уравнений равно
.
Найдем значения , , .
= ;
= ;
=.
Подставляя вместо , , числовые значения, получим:
.
Ответ:;;.
в) Решим систему уравнений методом Гаусса.
Запишем расширенную матрицу системы
и сделаем элементарные преобразования.
Сделаем коэффициент равным единице и обнулим коэффициенты,и.
Для этого:
а) поменяем местами первую и вторую строки, а затем вычтем из первой строки вторую. Результат запишем на место первой строки
~
~
б) вычтем из второй строки первую,
умноженную на 2.