Даны координаты вершин пирамиды а1а2а3а4 найти угол между ребрами: Даны координаты вершин пирамиды. — примеры, решения

Даны координаты вершин пирамиды. — примеры, решения

Пример 1:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти:

1) координаты и модули векторов А₁ А₂и А₁ А₄;  

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) площадь грани А₁ А₂ А₃;         

4) объем пирамиды;

5) уравнение прямой А₁ А₂;

6) уравнение плоскости А₁ А₂ А₃;

7) уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3.

Сделать чертеж.

А₁ (0; 4; -4), А₂ (5; 1; -1), А₃ (-1; -1; 3), А₄ (0; -3; 7).

Решение от преподавателя:

 

Пример 2:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

8) уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

1. А₁ (7; 7; 3), А₂ (6; 5; 8), А₃ (3; 5; 8), А₄ (8; 4; 1).

Решение от преподавателя:

 

Пример 3:

Решение от преподавателя:

 Уравнение плоскости.  
Если точки A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂), A₃(x₃; y₃; z₃) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением: 

x-x1 y-y1 z-z1 x2-x1 y2-y1 z2-z1 x3-x1 y3-y1 z3-z1

= 0

Уравнение плоскости A₁A₂A₃ 

x-3 y-2 z+2 -2 1 3 3 0 2

= 0

(x-3)(1*2-0*3) — (y-2)((-2)*2-3*3) + (z+2)((-2)*0-3*1) = 2x + 13y — 3z-38 = 0 

Угол между прямой A₁A₄ и плоскостью A₁A₂A₃.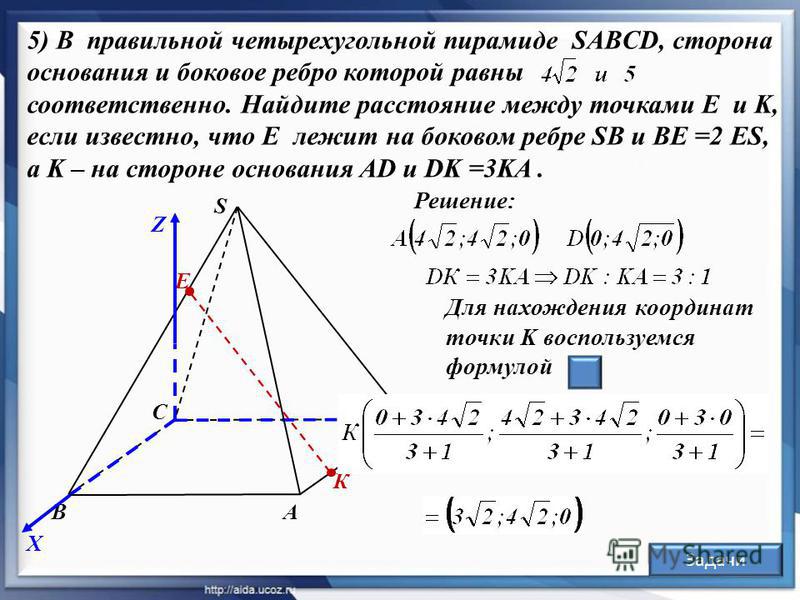  
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 

Уравнение плоскости A₁A₂A₃: 2x + 13y — 3z-38 = 0 
Уравнение прямой A₁A₄: 

γ = arcsin(0.267) = 15.486^o 

Уравнение высоты пирамиды через вершину A₄(0,2,2) 
Прямая, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями: 
Уравнение плоскости A₁A₂A₃: 2x + 13y — 3z-38 = 0 

Уравнение плоскости через вершину A₄(0,2,2) 
Плоскость, проходящая через точку M₀(x₀;y₀;z₀) и параллельная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением: 
A(x-x₀) + B(y-y₀) + C(z-z₀) = 0 
Уравнение плоскости A₁A₂A₃: 2x + 13y — 3z-38 = 0 
2(x-0)+13(y-2)-3(z-2) = 0 
или 
2x+13y-3z-20 = 0

Пример 4:

Решение от преподавателя:

Даны координаты пирамиды: A₁(0,1,1), A₂(3,4,4), A₃(-3,9,3), A₄(0,5,4) 

 

1. Уравнение плоскости.  
   Если точки A₁(x₁; y₁; z₁), A₂(x₂; y₂; z₂), A₃(x₃; y₃; z₃) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением: 

 

x-x1 y-y1 z-z1 x2-x1 y2-y1 z2-z1 x3-x1 y3-y1 z3-z1

= 0

Уравнение плоскости A₁A₂A₃ 

x-0 y-1 z-1 3 3 3 -3 8 2

= 0

(x-0)(3*2-8*3) — (y-1)(3*2-(-3)*3) + (z-1)(3*8-(-3)*3) = -18x — 15y + 33z-18 = 0 
Упростим выражение: -6x — 5y + 11z-6 = 0 

2) Угол между прямой A₁A₄ и плоскостью A₁A₂A₃.  
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 

Уравнение плоскости A₁A₂A₃: -6x — 5y + 11z-6 = 0 
Уравнение прямой A₁A₄: 

γ = arcsin(0.193) = 11.128^o 

3) Уравнение высоты пирамиды через вершину A₄(0,5,4) 
Прямая, проходящая через точку M₀(x₀;y₀;z₀) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями: 
Уравнение плоскости A₁A₂A₃: -6x — 5y + 11z-6 = 0 

4) Уравнение плоскости через вершину A₄(0,5,4) 
Плоскость, проходящая через точку M₀(x₀;y₀;z₀) и параллельная плоскости

Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением: 
A(x-x₀) + B(y-y₀) + C(z-z₀) = 0 
Уравнение плоскости A₁A₂A₃: -6x — 5y + 11z-6 = 0 
-6(x-0)-5(y-5)+11(z-4) = 0 
или 
-6x-5y+11z-19 = 0 

5)  Координаты вектора  A₁A₄(0;4;3) 

Уравнение прямой, проходящей через точку А₁(0,1,1) параллельно вектору А₁А₂(0,4,3) имеет вид:

Пример 5:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

8) уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

А₁ (4; 4; 10), А₂ (4; 10; 2), А₃ (2; 8; 4), А₄ (9; 6; 9).

Решение от преподавателя:

Пример 6:

Решение от преподавателя:

1) Даны координаты  вершин пирамиды: A₁(0,1,1), A₂(3,4,4), A₃(-3,9,3), A₄(0,5,4) 
Координаты векторов.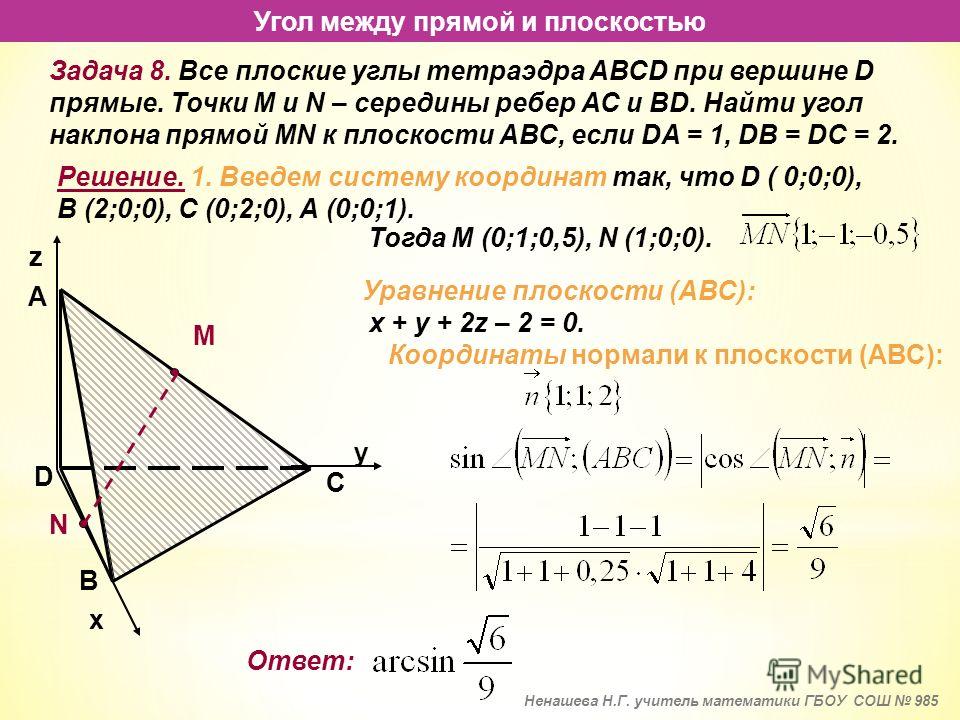  
Координаты векторов:       A₁A₂(3;3;3)        A₁A₄(0;4;3) 

Модули векторов (длина ребер пирамиды) 
Длина вектора a(X;Y;Z) выражается через его координаты формулой: 

Угол между ребрами.

 Угол между векторами a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂) можно найти по формуле: 
   ,    где a₁a₂ = X₁X₂ + Y₁Y₂ + Z₁Z₂ 
Найдем угол между ребрами A₁A₂(3;3;3) и A₁A₃(0;4;3): 

А₁ = arccos(0,808)

2) Площадь грани 

Найдем площадь грани с учётом геометрического смысла векторного произведения: 
S =
Найдем векторное произведение

i j k 3 3 3 -3 8 2

=

=i(3*2-8*3) — j(3*2-(-3)*3) + k(3*8-(-3)*3) = -18i — 15j + 33k 

3) Объем пирамиды.  
Объем пирамиды, построенный на векторах a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂), a₃(X₃;Y₃;Z₃) равен: 

X1 Y1 Z1 X2 Y2 Z2 X3 Y3 Z3

Координатывекторов:A₁A₂(3;3;3)    A₁A₃(-3;8;2) A₁A₄(0;4;3) :      

3 3 3 -3 8 2 0 4 3

где определитель матрицы равен: 
∆ = 3*(8*3-4*2)-(-3)*(3*3-4*3)+0*(3*2-8*3) = 39 

Пример 7:

Решение от преподавателя:

1. Угол между ребрами.  
   Угол между векторами a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂) можно найти по формуле: 
   
   где a₁a₂ = X₁X₂ + Y₁Y₂ + Z₁Z₂ 
   Найдем угол между ребрами A₁A₂(-2;1;3) и A₁A₃(3;0;2): 
   
   γ = arccos(0) = 90.003⁰ 
2. Площадь грани 
   Площадь грани можно найти по формуле: 
   
   где 
   
   Найдем площадь грани A₁A₂A₃ 
   Найдем угол между ребрами A₁A₂(-2;1;3) и A₁A₃(3;0;2): 
   
   
   Площадь грани A₁A₂A₃ 
3. Объем пирамиды, построенный на векторах a₁(X₁;Y₁;Z₁), a₂(X₂;Y₂;Z₂), a₃(X₃;Y₃;Z₃) равен: 

X1 Y1 Z1 X2 Y2 Z2 X3 Y3 Z3

 

-2 1 3 3 0 2 -3 0 4

где определитель матрицы равен: 
∆ = (-2)*(0*4-0*2)-3*(1*4-0*3)+(-3)*(1*2-0*3) = -18 

Пример 8:

Даны координаты вершин пирамиды А₁А₂А₃А₄ . Найти:

1) длину ребра А₁А₂;

2) угол между рёбрами А₁А₂  и А₁А₄ ;

3) угол между ребром А₁А₄ и гранью А₁А₂А₃;

4) площадь грани А₁А₂А₃;

5) объём пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

8) уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃;

Сделать чертёж.

А₁(3; 5; 4),        А₂(8; 7; 4),            А₃(5; 10; 4),          А₄(4; 7; 8).

Решение от преподавателя:

1) Длина ребра A₁A₂;

2) угол между ребрами А₁А₂ и А₁А₄;

3) угол между ребрами А₁А₄ и гранью А₁А₂А₃;

Найдем уравнение стороны А₁А₄:

Вектор нормали:  к плоскости А₁А₂А₃.

4) площадь грани А₁А₂А₃;

5) объем пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости А₁А₂А₃;

Итак: z=4 – уравнение плоскости А₁А₂А₃.

8) уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃.

A₄O – высота:

Уравнение A₄O:

Т.к. , то

В результате получаем уравнение высоты:

 

 

 

Пример 9:

Даны координаты вершин пирамиды А₁А₂А₃А₄.

Найти: 1) длину ребра А₁ А₂;

2) угол между ребрами А₁ А₂и А₁ А₄;          

3) угол между ребром А₁ А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;         

5) объем пирамиды;

6) уравнение прямой А₁ А₂;

7) уравнение плоскости А₁ А₂ А₃;

8) уравнение высоты, опущенной из вершины  А₄ на грань А₁ А₂ А_3. Сделать чертеж.

А₁ (4; 4; 10), А₂ (4; 10; 2), А₃ (2; 8; 4), А₄ (9; 6; 9).

Решение от преподавателя:

Работа вам нужна срочно. Не волнуйтесь, уложимся!

Заполните, пожалуйста, данные для автора:

• 22423 авторов готовы помочь тебе.
• 2402 онлайн

Контрольная работа по мат. анализу 06

Элементы векторной алгебры и аналитической геометрии

Контрольная работа 1

1.  Даны координаты вершин пирамиды. Найти: 1) длину рёбер А1А2 и А1А3; 2) Угол между рёбрами А1А2 и А1А3; 3) Площадь грани А1А2А3; 4) Объём пирамиды; 5) Уравнение прямой А1А2; 6) Уравнение плоскости А1А2А3; 7) Угол между ребром А1А4 и гранью А1А2А3; 8) Уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Координаты вершин: А1(5;1;0), А2 (0;1;2), А3(3;0;1), А4(2;2;2).

Решение

Координаты векторов:

Координаты векторов находим по формуле: X = xj — xi; Y = yj — yi; Z = zj — zi

Здесь X, Y,Z координаты вектора; xi, yi, zi — координаты точки Аi; xj, yj, zj — координаты точки Аj; Для вектора A1A2 : X = x2 — x1; Y = y2 — y1; Z = z2 — z1

X = 0-5; Y = 1-1; Z = 2-0

A1A2(-5;0;2)

A1A3(-2;-1;1)

1)  Длина рёбер А1А2 и А1А3;

Длина вектора a(X;Y;Z) выражается через его координаты формулой:

2)  Угол между рёбрами А1А2 и А1А3;

Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле:

, где a1a2 = X1X2 + Y1Y2 + Z1Z2

Найдем угол между ребрами A1A2 и A1A3

, γ = arccos(0. 91) = 24.50

3)  Площадь грани А1А2А3;

Найдем площадь грани с учётом геометрического смысла векторного произведения:

Векторное произведение:

i(0•1-(-1)•2)-j((-5)•1-(-2)•2)+k((-5)•(-1)-(-2)•0)=2i+j+5k

4)  Объём пирамиды;

Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:

Находим Определитель матрицы

∆ = (-5) • ((-1) • 2-1 • 1)-(-2) • (0 • 2-1 • 2)+(-3) • (0 • 1-(-1) • 2) = 5

5)  Уравнение прямой А1А2;

Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями:

Уравнение прямой A1A2

6)  Уравнение плоскости А1А2А3;

Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:

Уравнение плоскости A1A2A3

(x-5)(0 • 1-(-1) • 2) — (y-1)((-5) • 1-(-2) • 2) + (z-0)((-5) • (-1)-(-2) • 0) = 2x+y+5z-11=0

2x + y + 5z-11 = 0

7)  Угол между ребром А1А4 и гранью А1А2А3;

Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле

,

8) Уравнение высоты, опущенной из вершины А4 на грань А1А2А3.

Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:

,

2.  Линия задана уравнением В полярной системе координат

1.  построить линию по точкам, начиная от До И придавая значения через промежуток ;

2.  найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс с полярной осью;

3.  по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

Решение

1) Построим линию по точкам, начиная от До и придавая Значения через промежуток

	0
R	1	4,26	-2,41	-1,18	-1	-1,18	-2,41	4,26	1	0,57	0,41	0,35
R	0,33	0,35	0,41	0,57	1

2) Построим уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью.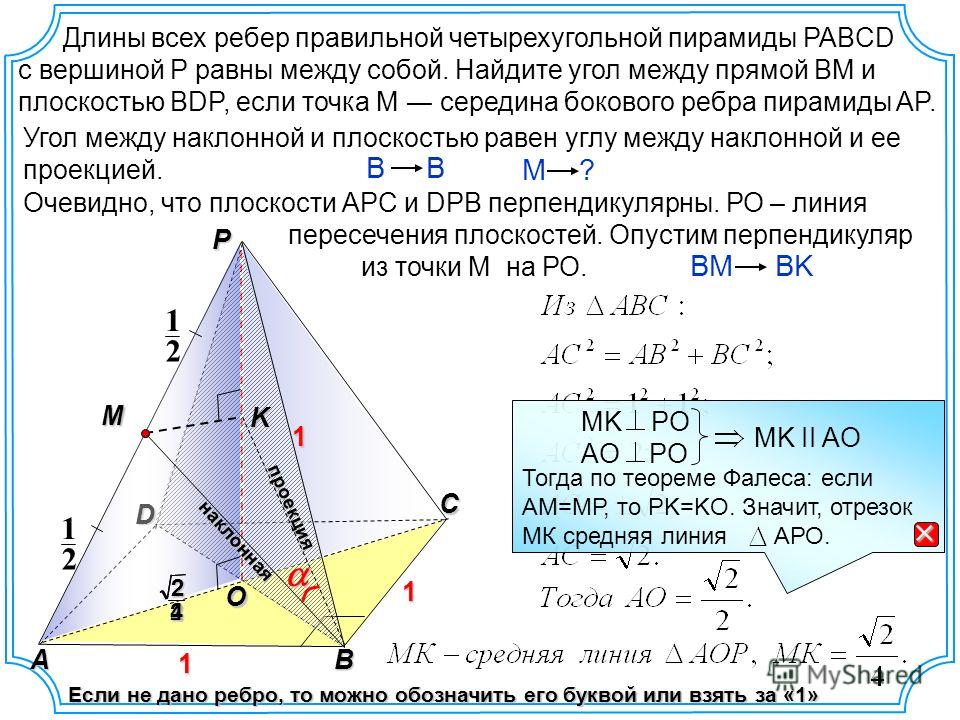

3) Найдём уравнение данной линии в декартовой системе координат:

Используем формулы перехода от полярной системы координат к декартовой:

Тогда

По уравнению в декартовой прямоугольной системе координат определяем, что это линия — гипербола.

Элементы линейной алгебры

Контрольная работа 2

I.  Даны две матрицы А и В. Найти (2АТ-3В)*(А+2ВТ)

,

Решение

, ,

, ,

II.  Определить собственные значения и собственные векторы матрицы третьего порядка.

Решение

Исходная матрица имеет вид:

Составляем систему для определения координат собственных векторов:

(5 — λ)x1-2×2 + 2×3 = 0

0x1 + (5 — λ)x2 + 0x3 = 0

0x1 + 2×2 + (3 — λ)x3 = 0

Составляем характеристическое уравнение и решаем его.

Для этого находим определитель матрицы и приравниваем полученное выражение к нулю.

(5 — λ) • ((5 — λ) • (3 — λ)-2 • 0)-0 • (-2 • (3 — λ)-2 • 2)+0 • (-2 • 0-(5 — λ) • 2) = 0

После преобразований, получаем: — λ3 + 13λ2 — 55λ + 75 = 0

Один из корней уравнения равен λ1 = 3

Тогда характеристическое уравнение можно записать как

(λ -3)( — λ2 + 10λ — 25)=0.

— λ2 +10 λ — 25 = 0

D = 102 — 4 • (-1) • (-25) = 0

Получили собственные числа: λ1 = 3,

Найдём собственный вектор для λ1.

Составляем систему для определения координат собственных векторов:

Подставляя λ = 3 в систему, имеем:

Пусть x1 — свободное неизвестное, тогда выразим через него все остальные x1.

Множество собственных векторов, отвечающих собственному числу λ1= 3 , имеет вид: , где x1 — любое число, отличное от нуля. Выберем из этого множества один вектор, например, положив x1 = 1: .

Рассуждая аналогично, находим собственный вектор, отвечающий собственным числам:

. Следовательно, — любое,

Множество собственных векторов, отвечающих собственным числам , имеет вид: . При x1 = 1 и x3 = 0: , при x1 = 0 и x3 = 1: .

Ответ: Собственные числа: λ1=3, , собственные векторы: , , .

III.  Дано комплексное число z. Требуется: 1) записать число z в алгебраической и тригонометрической формах; 2) Найти все корни уравнения w3+z=0

Решение

1) — алгебраическая форма

Тригонометрическая форма:

— тригонометрическая форма

2) Найдем корни уравнения w3 =0,

Применим формулу извлечения корней из комплексного числа:

, к=0,1,…,n-1

,

Так как a=, то

Дифференциальное исчисление

Контрольная работа 3

I.   Найти пределы функций, не пользуясь правилом Лопиталя.

1. 

2. 

3. 

4. 

Решение

1. 

2.   

3. 

Использовали эквивалентности бесконечно малых величин при :

4. 

II.  Задана функция . Найти точки разрыва функции, если они существуют. Сделать чертёж

Решение

Построим график заданной функции:

Функция определена на всём множестве чисел и неэлементарная.

Каждая из составляющих функций непрерывна на своём промежутке; заданная функция может иметь точки разрыва только в точках смены аналитических выражений, то есть в точках и .

Исследуем поведение функции в этих точках: найдём значение функции в этих точках и пределы справа и слева,

, . Так как , Следовательно, в этой точке функция имеет разрыв 1-го рода – скачок

, . Так как , то в этой точке функция имеет разрыв 1-го рода – скачок.

III.  Найти производные первого порядка данных функций.

1)  ;

2)  ;

3)  ;

4)  ;

5) 

Решение

1)   

2)   

3)   

4)  ;

Прологарифмируем данную функцию:

Найдём производную от правой и левой части по х, считая у сложной функцией, зависящей от х.

Тогда

5) 

Дифференцируем обе части равенства по х:

Разрешаем равенство относительно :

Окончательно:

IV.  Найти и для заданных функций:

1)  ;

2) 

Решение

1)  ;

2) 

Приложение дифференциального исчисления

Контрольная работа 4

Интегральное исчисление

Контрольная работа 5

I.  Вычислить определённые интегралы. В п. 1) и 2) результаты проверить дифференцированием.

1) 

2) 

3) 

4) 

Решение

1) 

Проверка:

— верно

2)   

Проверка:

— верно

3) 

Разложим подынтегральное выражение на простые дроби:

Тогда

4)   

 

II.  Вычислить несобственный интеграл или доказать его расходимость.

Решение

III.  Вычислить (с точностью до двух знаков после запятой) длину дуги данной линии

Решение

По формуле .

В нашем случае

Найдём

Тогда

Имеем

Ответ:

< Предыдущая		Следующая >

Задача на нахождение угла между векторами

Задача на нахождение угла между векторами

• Решение

  Чтобы найти угол при вершине, мы представим два соседних ребра в виде векторов и вычислим угол между этими векторами.

  Напомним, что

  • Определение угла между двумя векторами

  Угол между двумя векторами — это угол, образуемый дугой, которая непосредственно их соединяет, при условии, что векторы имеют одно и то же основание.

  В результате представляем два ребра в виде векторов, основанием которых является вершина пирамиды:

  Рассмотрим ребра, идущие из вершины $(0,0,1)$ либо в $(1,1,0)$ или $(1,-1,0)$.

  Напомним, что

  • Вычитание дает вектор между двумя точками

  Вектор, идущий из $\mathbf{a}$ в $\mathbf{b}$, равен $\bfb — \bfa$.

  Следовательно, эти два ребра представлены векторами $(1,1,0) -(0,0,1) = (1,1,-1)$ и $(1,-1,0) — (0 ,0,1) = (1,-1,-1).$

  Мы свели задачу к нахождению угла между векторами $(1,1,-1)$ и $(1,-1,-1)$.

  Вспомним взаимосвязь между скалярным произведением и углами:

  • Формула угла скалярного произведения

  Если $\theta$ угол между векторами $\bfx$ и $\bfy$, то $\bfx\cdot\bfy = \left| \bfx\право| \влево| \bfy \правильно| \cos\тета. $

  Чтобы использовать эту формулу, пусть $\bfx = (1,1,-1)$ и $\bfy = (1,-1,-1).$

  • Прямое вычисление скалярного произведения

  Мы можем вычислить, что \begin{align}\bfx \cdot \bfy &= (1,1,-1)\cdot(1,-1,-1) \\ &= 1 -1 +1\\&= 1
  \end{выравнивание}

  • Определение длины вектора

  Мы вычисляем, что $\left| \bfx\право| = \ влево | \bfy \правильно| = \sqrt{3}$.

  9\circ$.

Похожие темы

• Многомерное исчисление

  (147 задач)

  • Векторы

    (55 задач)

    • Длина вектора

      (32 задачи)

      • Длина вектора $\mathbf{x} = \langle x_1, x_2, x_3 \rangle$ равна $
        |\mathbf{x}| = \sqrt{x_1^2 + x_2^2 + x_3^2}$.

        No related posts.