Даны такие арифметическая прогрессия: Арифметическая прогрессия — урок. Алгебра, 9 класс.

Дана арифметическая прогрессия (an). Известно, что a1=8,5 и d=1,1. В… — Учеба и наука

Ответы

21. 02.16

21. 02.16 Ответ понравился автору вопроса

Михаил Александров Читать ответы

Андрей Андреевич Читать ответы

Eleonora Gabrielyan Читать ответы

Посмотреть всех экспертов из раздела Учеба и наука > Математика

Похожие вопросы

Данный пример использовался на экзамене upsc в декабре 2013 и лишь один человек смог решить его . .. 1,3,5,7,9,11,13,15 нужно взять 3 числа и только сложением получить 30.

Мастер даёт сеанс одновременной игры в шахматы на нескольких досках. К концу первых двух часов он выиграл 10 процентов всех партий, а 8 партий

у мамы есть бублик и длинная булка.мама решила что сделает 7 разрезов.одним разрезом она режет бублик или булку в одном месте.какое самое большое число гостей ей удастся угостить

Решено

Маша может пробежать некоторую дистанцию за 35 минут, а Коля ту же дистанцию — за 28 минут. Они начали бег с двух концов этой дистанции навстречу

треугольник авс вписан в окружность ДА касательная угол с = 59 , угол в = 93. найти угол АДС

Пользуйтесь нашим приложением

Арифметическая прогрессия а n. Арифметическая и геометрическая прогрессии

Многие слышали об арифметической прогрессии, но не все хорошо представляют, что это такое.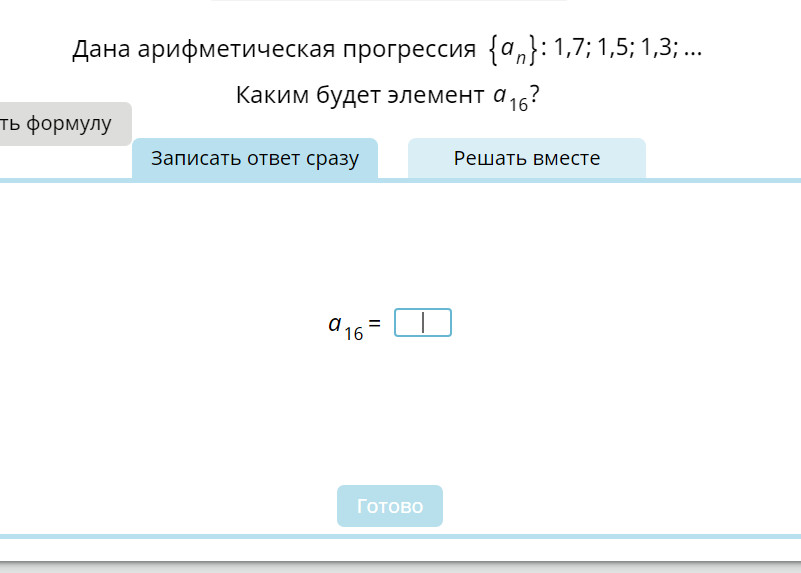 В данной статье дадим соответствующее определение, а также рассмотрим вопрос, как найти разность прогрессии арифметической, и приведем ряд примеров.

Математическое определение

Итак, если речь идет о прогрессии арифметической или алгебраической (эти понятия определяют одно и то же), то это означает, что имеется некоторый числовой ряд, удовлетворяющий следующему закону: каждые два соседних числа в ряду отличаются на одно и то же значение. Математически это записывается так:

Здесь n означает номер элемента a n в последовательности, а число d — это разность прогрессии (ее название следует из представленной формулы).

О чем говорит знание разности d? О том, как «далеко» друг от друга отстоят соседние числа. Однако знание d является необходимым, но не достаточным условием для определения (восстановления) всей прогрессии. Необходимо знать еще одно число, которым может быть совершенно любой элемент рассматриваемого ряда, например, a 4 , a10, но, как правило, используют первое число, то есть a 1 .

Формулы для определения элементов прогрессии

В общем, информации выше уже достаточно, чтобы переходить к решению конкретных задач. Тем не менее до того, как будет дана прогрессия арифметическая, и найти разность ее будет необходимо, приведем пару полезных формул, облегчив тем самым последующий процесс решения задач.

Несложно показать, что любой элемент последовательности с номером n может быть найден следующим образом:

a n = a 1 + (n — 1) * d

Действительно, проверить эту формулу может каждый простым перебором: если подставить n = 1, то получится первый элемент, если подставить n = 2, тогда выражение выдает сумму первого числа и разности, и так далее.

Условия многих задач составляются таким образом, что по известной паре чисел, номера которых в последовательности также даны, необходимо восстановить весь числовой ряд (найти разность и первый элемент). Сейчас мы решим эту задачу в общем виде.

Итак, пусть даны два элемента с номерами n и m. Пользуясь полученной выше формулой, можно составить систему из двух уравнений:

a n = a 1 + (n — 1) * d;

a m = a 1 + (m — 1) * d

Для нахождения неизвестных величин воспользуемся известным простым приемом решения такой системы: вычтем попарно левую и правую части, равенство при этом останется справедливым. Имеем:

a n = a 1 + (n — 1) * d;

a n — a m = (n — 1) * d — (m — 1) * d = d * (n — m)

Таким образом, мы исключили одну неизвестную (a 1). Теперь можно записать окончательное выражение для определения d:

d = (a n — a m) / (n — m), где n > m

Мы получили очень простую формулу: чтобы вычислить разность d в соответствии с условиями задачи, необходимо лишь взять отношение разностей самих элементов и их порядковых номеров. Следует обратить на один важный момент внимание: разности берутся между «старшим» и «младшим» членами, то есть n > m («старший» — имеется в виду стоящий дальше от начала последовательности, его абсолютное значение может быть как больше, так и меньше более «младшего» элемента).

Выражение для разности d прогрессии следует подставить в любое из уравнений в начале решения задачи, чтобы получить значение первого члена.

В наш век развития компьютерных технологий многие школьники стараются найти решения для своих заданий в Интернете, поэтому часто возникают вопросы такого типа: найти разность арифметической прогрессии онлайн. По подобному запросу поисковик выдаст ряд web-страниц, перейдя на которые, нужно будет ввести известные из условия данные (это могут быть как два члена прогрессии, так и сумма некоторого их числа) и моментально получить ответ. Тем не менее такой подход к решению задачи является непродуктивным в плане развития школьника и понимания сути поставленной перед ним задачи.

Решение без использования формул

Решим первую задачу, при этом не будем использовать никакие из приведенных формул. Пусть даны элементы ряда: а6 = 3, а9 = 18. Найти разность прогрессии арифметической.

Известные элементы стоят близко друг к другу в ряду. Сколько раз нужно добавить разность d к наименьшему, чтобы получить наибольшее из них? Три раза (первый раз добавив d, мы получим 7-й элемент, второй раз — восьмой, наконец, третий раз — девятый). Какое число нужно добавить к трем три раза, чтобы получить 18? Это число пять. Действительно:

Таким образом, неизвестная разность d = 5.

Конечно же, решение можно было выполнить с применением соответствующей формулы, но этого не было сделано намеренно. Подробное объяснение решения задачи должно стать понятным и ярким примером, что такое арифметическая прогрессия.

Задача, подобная предыдущей

Теперь решим похожую задачу, но изменим входные данные. Итак, следует найти если а3 = 2, а9 = 19.

Конечно, можно прибегнуть снова к методу решения «в лоб». Но поскольку даны элементы ряда, которые стоят относительно далеко друг от друга, такой метод станет не совсем удобным. А вот использование полученной формулы быстро приведет нас к ответу:

d = (а 9 — а 3) / (9 — 3) = (19 — 2) / (6) = 17 / 6 ≈ 2,83

Здесь мы округлили конечное число. Насколько это округление привело к ошибке, можно судить, проверив полученный результат:

a 9 = a 3 + 2,83 + 2,83 + 2,83 + 2,83 + 2,83 + 2,83 = 18,98

Этот результат отличается всего на 0,1 % от значения, данного в условии. Поэтому использованное округление до сотых можно считать успешным выбором.

Задачи на применение формулы для an члена

Рассмотрим классический пример задачи на определение неизвестной d: найти разность прогрессии арифметической, если а1 = 12, а5 = 40.

Когда даны два числа неизвестной алгебраической последовательности, причем одним из них является элемент a 1 , тогда не нужно долго думать, а следует сразу же применить формулу для a n члена. В данном случае имеем:

a 5 = a 1 + d * (5 — 1) => d = (a 5 — a 1) / 4 = (40 — 12) / 4 = 7

Мы получили точное число при делении, поэтому нет смысла проверять точность рассчитанного результата, как это было сделано в предыдущем пункте.

Решим еще одну аналогичную задачу: следует найти разность арифметической прогрессии, если а1 = 16, а8 = 37.

Используем аналогичный предыдущему подход и получаем:

a 8 = a 1 + d * (8 — 1) => d = (a 8 — a 1) / 7 = (37 — 16) / 7 = 3

Что еще следует знать о прогрессии арифметической

Помимо задач на нахождение неизвестной разности или отдельных элементов, часто необходимо решать проблемы суммы первых членов последовательности. Рассмотрение этих задач выходит за рамки темы статьи, тем не менее для полноты информации приведем общую формулу для суммы n чисел ряда:

∑ n i = 1 (a i) = n * (a 1 + a n) / 2

Инструкция

Арифметическая прогрессия — это последовательность вида a1, a1+d, a1+2d…, a1+(n-1)d. Число d шагом прогрессии .Очевидно, что общая произвольного n-го члена арифметической прогрессии имеет вид: An = A1+(n-1)d. Тогда зная один из членов прогрессии , член прогрессии и шаг прогрессии , можно , то есть номер члена прогресси. Очевидно, он будет определяться по формуле n = (An-A1+d)/d.

Пусть теперь известен m-ый член прогрессии и -то другой член прогрессии — n-ый, но n , как и в предыдущем случае, но известно, что n и m не совпадают.Шаг прогрессии может быть вычислен по формуле: d = (An-Am)/(n-m). Тогда n = (An-Am+md)/d.

Если известна сумма нескольких элементов арифметической прогрессии , а также ее первый и последний , то количество этих элементов тоже можно определить.Сумма арифметической прогрессии будет равна: S = ((A1+An)/2)n. Тогда n = 2S/(A1+An) — чденов прогрессии . Используя тот факт, что An = A1+(n-1)d, эту формулу можно переписать в виде: n = 2S/(2A1+(n-1)d). Из этой можно выразить n, решая квадратное уравнение.

Арифметической последовательностью называют такой упорядоченный набор чисел, каждый член которого, кроме первого, отличается от предыдущего на одну и ту же величину. Эта постоянная величина называется разностью прогрессии или ее шагом и может быть рассчитана по известным членам арифметической прогрессии.

Инструкция

Если из условий задачи известны значения первого и второго или любой другой пары соседних членов , для вычисления разности (d) просто отнимите от последующего члена предыдущий. Получившаяся величина может быть как положительным, так и отрицательным числом — это зависит от того, является ли прогрессия возрастающей . В общей форме решение для произвольно взятой пары (aᵢ и aᵢ₊₁) соседних членов прогрессии запишите так: d = aᵢ₊₁ — aᵢ.

Для пары членов такой прогрессии, один из которых является первым (a₁), а другой — любым другим произвольно выбранным, тоже можно составить формулу нахождения разности (d). Однако в этом случае обязательно должен быть известен порядковый номер (i) произвольного выбранного члена последовательности. Для вычисления разности сложите оба числа, а полученный результат разделите на уменьшенный на единицу порядковый номер произвольного члена. В общем виде эту формулу запишите так: d = (a₁+ aᵢ)/(i-1).

Если кроме произвольного члена арифметической прогрессии с порядковым номером i известен другой ее член с порядковым номером u, измените формулу из предыдущего шага соответствующим образом. В этом случае разностью (d) прогрессии будет сумма этих двух членов, поделенная на разность их порядковых номеров: d = (aᵢ+aᵥ)/(i-v).

Формула вычисления разности (d) несколько усложнится, если в условиях задачи дано значение первого ее члена (a₁) и сумма (Sᵢ) заданного числа (i) первых членов арифметической последовательности. Для получения искомого значения разделите сумму на количество составивших ее членов, отнимите значение первого числа в последовательности, а результат удвойте. Получившуюся величину разделите на уменьшенное на единицу число членов, составивших сумму. В общем виде формулу вычисления дискриминанта запишите так: d = 2*(Sᵢ/i-a₁)/(i-1).

И. В. Яковлев | Материалы по математике | MathUs.ru

Арифметическая прогрессия

Арифметическая прогрессия это специального вида последовательность. Поэтому прежде чем давать определение арифметической (а затем и геометрической) прогрессии, нам нужно вкратце обсудить важное понятие числовой последовательности.

Последовательность

Вообразите устройство, на экране которого высвечиваются одно за другим некоторые числа. Скажем, 2; 7; 13; 1; 6; 0; 3; : : : Такой набор чисел как раз и является примером последовательности.

Определение. Числовая последовательность это множество чисел, в котором каждому числу можно присвоить уникальный номер (то есть поставить в соответствие единственное натуральное число)1 . Число с номером n называется n-м членом последовательности.

Так, в приведённом выше примере первый номер имеет число 2 это первый член последовательности, который можно обозначить a1 ; номер пять имеет число 6 это пятый член последовательности, который можно обозначить a5 . Вообще, n-й член последовательности обозначается an (или bn , cn и т. д.).

Очень удобна ситуация, когда n-й член последовательности можно задать некоторой формулой. Например, формула an = 2n 3 задаёт последовательность: 1; 1; 3; 5; 7; : : : Формула an = (1)n задаёт последовательность: 1; 1; 1; 1; : : :

Не всякое множество чисел является последовательностью. Так, отрезок не последовательность; в нём содержится ¾слишком много¿ чисел, чтобы их можно было перенумеровать. Множество R всех действительных чисел также не является последовательностью. Эти факты доказываются в курсе математического анализа.

Арифметическая прогрессия: основные определения

Вот теперь мы готовы дать определение арифметической прогрессии.

Определение. Арифметическая прогрессия это последовательность, каждый член которой (начиная со второго) равен сумме предыдущего члена и некоторого фиксированного числа (называемого разностью арифметической прогрессии).

Например, последовательность 2; 5; 8; 11; : : : является арифметической прогрессией с первым членом 2 и разностью 3. Последовательность 7; 2; 3; 8; : : : является арифметической прогрессией с первым членом 7 и разностью 5. Последовательность 3; 3; 3; : : : является арифметической прогрессией с разностью, равной нулю.

Эквивалентное определение: последовательность an называется арифметической прогрессией, если разность an+1 an есть величина постоянная (не зависящая от n).

Арифметическая прогрессия называется возрастающей, если её разность положительна, и убывающей, если её разность отрицательна.

1 А вот более лаконичное определение: последовательность есть функция, определённая на множестве натуральных чисел. Например, последовательность действительных чисел есть функция f: N ! R.

По умолчанию последовательности считаются бесконечными, то есть содержащими бесконечное множество чисел. Но никто не мешает рассматривать и конечные последовательности; собственно, любой конечный набор чисел можно назвать конечной последовательностью. Например, конечная последовательность 1; 2; 3; 4; 5 состоит из пяти чисел.

Формула n-го члена арифметической прогрессии

Легко понять, что арифметическая прогрессия полностью определяется двумя числами: первым членом и разностью. Поэтому возникает вопрос: как, зная первый член и разность, найти произвольный член арифметической прогрессии?

Получить искомую формулу n-го члена арифметической прогрессии нетрудно. Пусть an

арифметическая прогрессия с разностью d. Имеем:
an+1 = an + d (n = 1; 2; : : :):
В частности, пишем:
a2 = a1 + d;
a3 = a2 + d = (a1 + d) + d = a1 + 2d;
a4 = a3 + d = (a1 + 2d) + d = a1 + 3d;
и теперь становится ясно, что формула для an имеет вид:
an = a1 + (n 1)d:

Задача 1. В арифметической прогрессии 2; 5; 8; 11; : : : найти формулу n-го члена и вычислить сотый член.

Решение. Согласно формуле (1 ) имеем:

an = 2 + 3(n 1) = 3n 1:

a100 = 3 100 1 = 299:

Свойство и признак арифметической прогрессии

Свойство арифметической прогрессии. В арифметической прогрессии an для любого

Иначе говоря, каждый член арифметической прогрессии (начиная со второго) является средним арифметическим соседних членов.

	Доказательство. Имеем:
	a n 1+ a n+1		(an d) + (an + d)

что и требовалось.

Более общим образом, для арифметической прогрессии an справедливо равенство

a n = a n k+ a n+k

при любом n > 2 и любом натуральном k

Оказывается, формула (2 ) служит не только необходимым, но и достаточным условием того, что последовательность является арифметической прогрессией.

Признак арифметической прогрессии. Если для всех n > 2 выполнено равенство (2 ), то последовательность an является арифметической прогрессией.

Доказательство. Перепишем формулу (2 ) следующим образом:

a na n 1= a n+1a n:

Отсюда видно, что разность an+1 an не зависит от n, а это как раз и означает, что последовательность an есть арифметическая прогрессия.

Свойство и признак арифметической прогрессии можно сформулировать в виде одного утверждения; мы для удобства сделаем это для трёх чисел (именно такая ситуация часто встречается в задачах).

Характеризация арифметической прогрессии. Три числа a, b, c образуют арифметическую прогрессию тогда и только тогда, когда 2b = a + c.

Задача 2. (МГУ, экономич. ф-т, 2007) Три числа 8x, 3 x2 и 4 в указанном порядке образуют убывающую арифметическую прогрессию. Найдите x и укажите разность этой прогрессии.

Решение. По свойству арифметической прогрессии имеем:

2(3 x2 ) = 8x 4 , 2×2 + 8x 10 = 0 , x2 + 4x 5 = 0 , x = 1; x = 5:

Если x = 1, то получается убывающая прогрессия 8, 2, 4 с разностью 6. Если x = 5, то получается возрастающая прогрессия 40, 22, 4; этот случай не годится.

Ответ: x = 1, разность равна 6.

Сумма первых n членов арифметической прогрессии

Легенда гласит, что однажды учитель велел детям найти сумму чисел от 1 до 100 и сел спокойно читать газету. Однако не прошло и нескольких минут, как один мальчик сказал, что решил задачу. Это был 9-летний Карл Фридрих Гаусс, впоследствии один из величайших математиков в истории.

Идея маленького Гаусса была такова. Пусть

S = 1 + 2 + 3 + : : : + 98 + 99 + 100:

Запишем данную сумму в обратном порядке:

S = 100 + 99 + 98 + : : : + 3 + 2 + 1;

и сложим две этих формулы:

2S = (1 + 100) + (2 + 99) + (3 + 98) + : : : + (98 + 3) + (99 + 2) + (100 + 1):

Каждое слагаемое в скобках равно 101, а всего таких слагаемых 100. Поэтому

2S = 101 100 = 10100;

Мы используем эту идею для вывода формулы суммы

S = a1 + a2 + : : : + an + a n n: (3)

Полезная модификация формулы (3 ) получается, если в неё подставить формулу n-го члена an = a1 + (n 1)d:

		2a1 + (n 1)d

Задача 3. Найти сумму всех положительных трёхзначных чисел, делящихся на 13.

Решение. Трёхзначные числа, кратные 13, образуют арифметическую прогрессию с первым членом 104 и разностью 13; n-й член этой прогрессии имеет вид:

an = 104 + 13(n 1) = 91 + 13n:

Давайте выясним, сколько членов содержит наша прогрессия. Для этого решим неравенство:

an 6 999; 91 + 13n 6 999;

n 6 908 13 = 6911 13 ; n 6 69:

Итак, в нашей прогрессии 69 членов. По формуле (4 ) находим искомую сумму:

S = 2 104 + 68 13 69 = 37674: 2

Понятие числовой последовательности подразумевает соответствие каждому натуральному числу некоторого действительного значения. Такой ряд чисел может быть как произвольным, так и обладать определенными свойствами – прогрессия. В последнем случае каждый последующий элемент (член) последовательности можно вычислить с помощью предыдущего.

Арифметическая прогрессия – последовательность числовых значений, в которой ее соседние члены разнятся между собой на одинаковое число (подобным свойством обладают все элементы ряда, начиная со 2-ого). Данное число – разница между предыдущим и последующим членом – постоянно и называется разностью прогрессии.

Разность прогрессии: определение

Рассмотрим последовательность, состоящую из j значений A = a(1), a(2), a(3), a(4) … a(j), j принадлежит множеству натуральных чисел N. Арифметическая прогрессия, согласно своего определения, – последовательность, в которой a(3) – a(2) = a(4) – a(3) = a(5) – a(4) = … = a(j) – a(j-1) = d. Величина d – искомая разность данной прогрессии.

d = a(j) – a(j-1).

Выделяют:

• Возрастающую прогрессию, в таком случае d > 0. Пример: 4, 8, 12, 16, 20, …
• Убывающую прогрессию, тогда d

Разность прогрессии и ее произвольные элементы

Если известны 2 произвольных члена прогрессии (i-ый, k-ый), то установить разность для данной последовательности можно на базе соотношения:

a(i) = a(k) + (i – k)*d, значит d = (a(i) – a(k))/(i-k).

Разность прогрессии и ее первый член

Данное выражение поможет определить неизвестную величину лишь в случаях, когда известен номер элемента последовательности.

Разность прогрессии и ее сумма

Сумма прогрессии – это сумма ее членов. Для вычисления суммарного значения ее первых j элементов воспользуйтесь соответствующей формулой:

S(j) =((a(1) + a(j))/2)*j, но т.к. a(j) = a(1) + d(j – 1), то S(j) = ((a(1) + a(1) + d(j – 1))/2)*j=((2a(1) + d(– 1))/2)*j.

Или арифметическая — это вид упорядоченной числовой последовательности, свойства которой изучают в школьном курсе алгебры. В данной статье подробно рассмотрен вопрос, как найти сумму арифметической прогрессии.

Что это за прогрессия?

Прежде чем переходить к рассмотрению вопроса (как найти сумму арифметической прогрессии), стоит понять, о чем пойдет речь.

Любая последовательность действительных чисел, которая получается путем добавления (вычитания) некоторого значения из каждого предыдущего числа, называется алгебраической (арифметической) прогрессией. Это определение в переводе на язык математики принимает форму:

Здесь i — порядковый номер элемента ряда a i . Таким образом, зная всего одно начальное число, можно с легкостью восстановить весь ряд. Параметр d в формуле называется разностью прогрессии.

Можно легко показать, что для рассматриваемого ряда чисел выполняется следующее равенство:

a n = a 1 + d * (n — 1).

То есть для нахождения значения n-го по порядку элемента следует n-1 раз добавить разность d к первому элементу a 1 .

Чему равна сумма арифметической прогрессии: формула

Прежде чем приводить формулу для указанной суммы, стоит рассмотреть простой частный случай. Дана прогрессия натуральных чисел от 1 до 10, необходимо найти их сумму. Поскольку членов в прогрессии немного (10), то можно решить задачу в лоб, то есть просуммировать все элементы по порядку.

S 10 = 1+2+3+4+5+6+7+8+9+10 = 55.

Стоит учесть одну интересную вещь: поскольку каждый член отличается от последующего на одно и то же значение d = 1, то попарное суммирование первого с десятым, второго с девятым и так далее даст одинаковый результат. Действительно:

11 = 1+10 = 2+9 = 3+8 = 4+7 = 5+6.

Как видно, этих сумм всего 5, то есть ровно в два раза меньше, чем число элементов ряда. Тогда умножая число сумм (5) на результат каждой суммы (11), вы придете к полученному в первом примере результату.

Если обобщить эти рассуждения, то можно записать следующее выражение:

S n = n * (a 1 + a n) / 2.

Это выражение показывает, что совсем не обязательно суммировать подряд все элементы, достаточно знать значение первого a 1 и последнего a n , а также общего числа слагаемых n.

Считается, что впервые до этого равенства додумался Гаусс, когда искал решение на заданную его школьным учителем задачу: просуммировать 100 первых целых чисел.

Сумма элементов от m до n: формула

Формула, приведенная в предыдущем пункте, дает ответ на вопрос, как найти сумму арифметической прогрессии (первых элементов), но часто в задачах необходимо просуммировать ряд чисел, стоящих в середине прогрессии. Как это сделать?

Ответить на этот вопрос проще всего, рассматривая следующий пример: пусть необходимо найти сумму членов от m-го до n-го. Для решения задачи следует представить заданный отрезок от m до n прогрессии в виде нового числового ряда. В таком представлении m-й член a m будет первым, а a n станет под номер n-(m-1). В этом случае, применяя стандартную формулу для суммы, получится следующее выражение:

S m n = (n — m + 1) * (a m + a n) / 2.

Пример использования формул

Зная, как найти сумму арифметической прогрессии, стоит рассмотреть простой пример использования приведенных формул.

Ниже дана числовая последовательность, следует найти сумму ее членов, начиная с 5-го и заканчивая 12-м:

Приведенные числа свидетельствуют, что разность d равна 3. Используя выражение для n-го элемента, можно найти значения 5-го и 12-го членов прогрессии. Получается:

a 5 = a 1 + d * 4 = -4 + 3 * 4 = 8;

a 12 = a 1 + d * 11 = -4 + 3 * 11 = 29.

Зная значения чисел, стоящих на концах рассматриваемой алгебраической прогрессии, а также зная, какие номера в ряду они занимают, можно воспользоваться формулой для суммы, полученной в предыдущем пункте. Получится:

S 5 12 = (12 — 5 + 1) * (8 + 29) / 2 = 148.

Стоит отметить, что это значение можно было получить иначе: сначала найти сумму первых 12 элементов по стандартной формуле, затем вычислить сумму первых 4 элементов по той же формуле, после этого вычесть из первой суммы вторую.

Объяснение урока: Нахождение арифметической последовательности

В этом объяснении мы узнаем, как находить арифметические последовательности, зная информацию об их терминах и отношениях между ними.

Напомним, что арифметическая последовательность или арифметическая прогрессия — это такая последовательность чисел, что разница между любыми двумя последовательные члены в последовательности постоянны. Мы называем эту постоянную разницу «общей разницей».

Если последовательность имеет конечное число членов, то мы называем ее конечной арифметической последовательностью; в противном случае мы называем это просто арифметическая последовательность.

Например, если первый член нашей арифметической последовательности равен 100, а общая разность между любыми двумя членами последовательность равна −5, то мы можем найти следующий член последовательности.

Обозначая второй член последовательности как 𝑇, разность между вторым и первым членами должно быть −5. Поэтому, 𝑇−100=−5𝑇=−5+100𝑇=95.

Мы можем продолжить это, чтобы найти бесконечное число членов последовательности.

Это эквивалентно утверждению, что мы находим следующий член последовательности, добавляя общую разность к предыдущий срок.

Мы можем использовать этот же процесс для любой арифметической последовательности. Если мы обозначим 𝑛-й член в арифметическом последовательность как 𝑇 и общая разность как 𝑑, так что первый член в последовательности равно 𝑇, то мы можем найти формулу для 𝑛-го члена этой арифметической прогрессии.

Поскольку разница между любыми двумя последовательными терминами должна быть общей разностью 𝑑, то разница между первым и вторым членами последовательности должна быть 𝑑: 𝑇−𝑇=𝑑.

Перестановка дает нам 𝑇=𝑇+𝑑.

То же самое будет, если мы возьмем разницу между вторым и третьим членами: 𝑇−𝑇=𝑑𝑇=𝑑+𝑇.

Тогда мы можем подставить в наше выражение для 𝑇: 𝑇=𝑑+𝑇+𝑑𝑇=𝑇+2𝑑.

Другими словами, чтобы построить третий член нашей арифметической последовательности, мы берем первый член и добавляем общий разница в два раза. Этот процесс будет продолжаться для любого количества терминов, таких как 𝑛, что дает нам следующее выражение для 𝑛-го члена нашей арифметической прогрессии: 𝑇=𝑇+(𝑛−1)𝑑.

Мы можем обобщить это следующим образом.

Определение: арифметические последовательности

Арифметическая последовательность или прогрессия — это последовательность чисел, в которой разница между любыми двумя последовательными членами постоянна.

𝑛-й член арифметической прогрессии с общей разностью 𝑑 и первым членом 𝑇 дан кем-то 𝑇=𝑇+(𝑛−1)𝑑.

Мы можем использовать эту формулу для определения информации об арифметических последовательностях, используя члены последовательности. Давайте рассмотрим несколько примеров нахождения арифметической последовательности с учетом информации о ее членах.

Пример 1. Нахождение арифметической последовательности по двум непоследовательным слагаемым а предпоследний член равен -115.

Ответ

Мы хотим найти выражение для конечной арифметической последовательности, используя информацию о ее членах. Мы помним, что арифметическая последовательность — это последовательность чисел, в которой разница между любыми двумя последовательными членами постоянна, называется общей разностью.

Чтобы найти выражение для этой конечной арифметической последовательности, нам нужно найти первый член, последний член, и общая разница последовательности. Начнем с того, что вспомним формулу для 𝑛-й срок в арифметическая прогрессия с первым членом 𝑇 и обыкновенной разностью 𝑑: 𝑇=𝑇+(𝑛−1)𝑑.

Вопрос говорит нам 𝑇=−82 и 𝑇=−203, и мы можем заменить 𝑛=12 в эту формулу: 𝑇=𝑇+(12−1)𝑑=𝑇+11𝑑.

Тогда мы можем использовать значения 𝑇 и 𝑇: −203=−82+11𝑑.

Теперь мы можем переставить 𝑑: −203+82=11𝑑−121=11𝑑𝑑=−11.

Теперь мы знаем первый член этой конечной арифметической последовательности, 𝑇=−82, и общий разница, 𝑑=−11. Нам еще нужно определить последний член этой арифметической прогрессии. Чтобы определить последний член в этой последовательности, мы будем использовать тот факт, что предпоследний член равен −115.

Чтобы найти последний член, вспомним, что подразумевается под предпоследним членом. Если мы позволим 𝑇 быть последним членом, то арифметическая последовательность задается выражением 𝑇,𝑇,…,𝑇,𝑇,𝑇. 

𝑇 будет предпоследним сроком, так как он предпоследний.

𝑇 будет предпоследним сроком; мы можем продолжить это, чтобы увидеть 𝑇 будет предпоследний срок. Поэтому, 𝑇=𝑇+(𝑙−11−1)𝑑=𝑇+(𝑙−12)𝑑.

−115=−82+(𝑙−12)(−11)−115+82=(𝑙−12)(−11)−33=(𝑙−12)(−11)3=𝑙−12𝑙=15.

Таким образом, последовательность имеет 15 членов и мы можем найти последний член: 𝑇=-82+(15-1)(-11)=-82-154=-236.

Следовательно, первый член нашей последовательности равен −82, последний член равен −236, а общий разница равна -11, что дает нам последовательность (-82,-93,-104,…,-236).

Пример 2. Нахождение арифметической последовательности по суммам ее членов

Найдите арифметическую последовательность, в которой сумма первого и третьего членов равна −142 а сумма третьего и четвертого членов равна -151.

Ответ

Мы хотим найти выражение для конечной арифметической последовательности, используя информацию о ее членах. Напомним, что арифметическая прогрессия — это последовательность чисел, разность между любыми двумя последовательные члены постоянны и называются общей разностью.

𝑛-й член арифметической прогрессии с первым членом 𝑇 и общей разностью 𝑑 дается 𝑇=𝑇+(𝑛−1)𝑑.

В вопросе сказано, что 𝑇+𝑇=−142 и 𝑇+𝑇=−151. Мы можем использовать нашу формулу для записи 𝑇 и 𝑇 через 𝑇 и 𝑑: 𝑇=𝑇+2𝑑𝑇=𝑇+3𝑑.

Подставляя наше выражение для 𝑇 в первую сумму, получаем 𝑇+𝑇=−142𝑇+(𝑇+2𝑑)=−1422𝑇+2𝑑=−142𝑇+𝑑=−71.

Мы можем сделать то же самое с нашим выражением для 𝑇: 𝑇+𝑇=-151(𝑇+2𝑑)+(𝑇+3𝑑)=-1512𝑇+5𝑑=-151.

У нас есть два линейных уравнения с двумя переменными; мы можем решить эту систему, исключив переменную. Преобразование первого уравнения дает нам 𝑇+𝑑=−71𝑇=−71−𝑑.

Затем мы подставляем это во второе уравнение: 2𝑇+5𝑑=−1512(−71−𝑑)+5𝑑=−151−142−2𝑑+5𝑑=−1513𝑑=−9𝑑=−3. 

Затем мы можем использовать это, чтобы найти значение 𝑇: 𝑇+𝑑=−71𝑇+(−3)=−71𝑇=−68.

Следовательно, первый член в нашей последовательности равен −68, а общая разность равна −3, что дает нам последовательность (−68,−71,−74,…).

Давайте теперь рассмотрим пример, в котором нам дана сумма и произведение различных членов в арифметической последовательности.

Пример 3. Нахождение арифметической последовательности по сумме и произведению ее членов

Найдите арифметическую последовательность, в которой 𝑇+𝑇=−28 и 𝑇×𝑇=140.

Ответ

В арифметической прогрессии разница между любыми двумя последовательными членами постоянна; это называется общей разностью.

Напомним, что 𝑛-й член арифметической прогрессии с первым членом 𝑇 и общей разностью 𝑑 дается 𝑇=𝑇+(𝑛−1)𝑑.

Мы можем использовать это, чтобы найти выражения для четырех терминов, данных нам в вопросе: 𝑇=𝑇+(2−1)𝑑=𝑇+𝑑,𝑇=𝑇+(3−1)𝑑=𝑇+2𝑑,𝑇=𝑇+(4−1)𝑑=𝑇+3𝑑,𝑇=𝑇+( 5−1)𝑑=𝑇+4𝑑. 

Затем мы можем подставить эти выражения в два данных нам уравнения.

Первый, 𝑇+𝑇=−28(𝑇+𝑑)+(𝑇+3𝑑)=−282𝑇+4𝑑=−28𝑇+2𝑑=−14.

Секунда, 𝑇 × 𝑇 = 140 (𝑇+2𝑑) × (𝑇+4𝑑) = 140𝑇+4𝑇𝑑+2𝑇𝑑+8𝑑 = 140𝑇+6𝑇𝑑+8𝑑 = 140.

Следовательно, имеем два уравнения с двумя переменными; мы можем решить их, исключив переменную. Начнем с преобразования уравнения, чтобы найти 𝑇 через 𝑑: 𝑇+2𝑑=−14𝑇=−14−2𝑑.

Затем мы можем подставить это в наше другое уравнение: 𝑇+6𝑇𝑑+8𝑑=140(−14−2𝑑)+6(−14−2𝑑)𝑑+8𝑑=140196+56𝑑+4𝑑−84𝑑−12𝑑+8𝑑=140−28𝑑=−56𝑑=2. 

Затем мы можем подставить 𝑑=2, чтобы найти значение 𝑇: 𝑇+2𝑑=−14𝑇+2(2)=−14𝑇=−18.

Следовательно, первый член в нашей последовательности равен −18, а общая разность равна 2, что дает нам последовательность (−18,−16,−14,…).

В следующем примере нам говорят, что два члена арифметической последовательности являются аддитивными инверсиями. друг друга. Нам нужно использовать эту информацию и значение другого термина в последовательности найти всю последовательность.

Пример 4. Нахождение арифметической последовательности при заданных соотношениях между ее элементами

Найдите арифметическую последовательность, для которой 𝑇=279 и 𝑇 является аддитивным обратным к 𝑇.

Ответ

В арифметической прогрессии разница между любыми двумя последовательными членами постоянна; это называется общей разностью. Мы можем определить любую арифметическую прогрессию по ее первому члену и общей разности.

Напомним, что 𝑛-й член арифметической прогрессии с первым членом 𝑇 и общей разностью 𝑑 дается 𝑇=𝑇+(𝑛−1)𝑑.

Подставив 𝑛=43 в эту формулу, мы можем использовать это, чтобы найти выражение для 𝑇: 𝑇=𝑇+(43−1)𝑑=𝑇+42𝑑.

В вопросе сказано 𝑇=279, поэтому 279=𝑇+42𝑑.

Далее мы хотим использовать тот факт, что 𝑇 является аддитивной инверсией 𝑇. Напомним, что два числа являются аддитивными инверсиями друг друга, если при их сложении получается ноль. Поэтому, 𝑇+𝑇=0.

Мы можем найти выражения для этих членов, подставив 𝑛=11 и 𝑛=13 в нашу формулу: 𝑇=𝑇+10𝑑,𝑇=𝑇+12𝑑.

Поскольку это аддитивные инверсии, сложение этих выражений вместе должно дать нам ноль: 𝑇+𝑇=0𝑇+10𝑑+𝑇+12𝑑=02𝑇+22𝑑=0𝑇+11𝑑=0.

Помните, мы уже показывали 279=𝑇+42𝑑.

Это означает, что у нас есть два уравнения с двумя неизвестными; мы можем решить их, вычитая одно уравнение из другого: 𝑇+11𝑑=0−(𝑇+42𝑑=279)−31𝑑=−279

Затем мы можем найти 𝑑: −31𝑑=−279𝑑=9.

Мы можем использовать это, чтобы найти 𝑇: 𝑇+11𝑑=0𝑇+11(9)=0𝑇=−99.

Следовательно, первый член нашей последовательности равен −99, а общая разность равна 9, что дает нам последовательность (-99,-90,-81,…).

В нашем следующем примере нас просят найти арифметическую последовательность, учитывая информацию о терминах в словах, а не в математической записи.

Пример 5. Нахождение арифметической прогрессии при определенном условии

Найдите арифметическую прогрессию, двадцатый член которой равен 28, при условии, что сумма ее третьего и шестого членов больше ее девятого члена на 8.

Ответ

Мы хотим найти арифметическую прогрессию. Для этого начнем с того, что вспомним, что в арифметической прогрессии разница между любыми двумя последовательными терминами одинакова; это называется общей разностью. Мы также знаем что в арифметической прогрессии с первым членом 𝑇 и общей разностью 𝑑 𝑛-й член можно найти по следующей формуле: 𝑇=𝑇+(𝑛−1)𝑑.

В вопросе сказано, что двадцатый член равен 28, и мы можем найти это, подставив 𝑛=20: 28=𝑇+(20−1)𝑑=𝑇+19𝑑.

Мы также можем найти выражения для третьего, шестого и девятого слагаемых: 𝑇=𝑇+2𝑑,𝑇=𝑇+5𝑑𝑇=𝑇+8𝑑.

В вопросе нам говорят 𝑇+𝑇=𝑇+8, поэтому мы можем подставить эти выражения в это уравнение, что даст нам 𝑇+𝑇=𝑇+8(𝑇+2𝑑)+(𝑇+5𝑑)=(𝑇+8𝑑)+82𝑇+7𝑑=𝑇+8𝑑+8𝑇−𝑑=8. 

Помните, мы уже показывали 28=𝑇+19𝑑.

Это означает, что у нас есть пара одновременных уравнений с двумя неизвестными. Мы можем решить их, удалив переменную: 𝑇+19𝑑=28−(𝑇−𝑑=8)20𝑑=20

Следовательно, 𝑑=1. Подставив это в одно из наших одновременных уравнений, мы получим 𝑇−1=8𝑇=9.

Следовательно, первый член этой арифметической последовательности равен 9, а общая разность равна 1. Это последовательность (9,10,11,…).

В нашем следующем примере мы увидим, как использовать информацию о знаках членов нашей последовательности, чтобы найти арифметическую последовательность.

Пример 6. Нахождение арифметической последовательности по заданным отношениям между произведениями ее членов

Найдите арифметическую прогрессию, если и все члены положительны.

Ответ

Мы хотим выразить арифметическую последовательность, используя информацию о ее членах. Напомним, что арифметическая прогрессия — это последовательность чисел, разность между любыми двумя последовательными терминами постоянна и называется общей разностью.

Мы также знаем, что 𝑛-й член арифметической прогрессии с первым членом 𝑇 а общая разность 𝑑 определяется выражением 𝑇=𝑇+(𝑛−1)𝑑.

Мы можем использовать это, чтобы найти выражения для всех терминов, используемых в уравнениях, данных нам в вопросе: 𝑇=𝑇+11𝑑,𝑇=𝑇+5𝑑,𝑇=𝑇+30𝑑,𝑇=𝑇+6𝑑,𝑇=𝑇+25𝑑. 9000 каждое из уравнений.

Первый, 𝑇𝑇=1708𝑇(𝑇+11𝑑)=1708𝑇+11𝑇𝑑=1708.

Секунда, 𝑇𝑇−𝑇𝑇=336(𝑇+5𝑑)(𝑇+30𝑑)−(𝑇+6𝑑)(𝑇+25𝑑)=336.

и упрощение дает использование скобок 𝑇+30𝑇𝑑+5𝑇𝑑+150𝑑−𝑇−25𝑇𝑑−6𝑇𝑑−150𝑑=3364𝑇𝑑=336𝑇𝑑=84.0003

Мы можем подставить это значение для 𝑇𝑑 в наше первое уравнение: 𝑇+11𝑇𝑑=1708𝑇+11(84)=1708𝑇=784.

Теперь, поскольку нам сказали, что все члены последовательности положительны, мы можем найти 𝑇, взяв положительный квадратный корень: 𝑇=√784=28.

Затем мы можем подставить это в уравнение 𝑇𝑑=84, чтобы найти значение 𝑑: (28)𝑑=84𝑑=3.

Следовательно, первый член этой арифметической последовательности равен 28, а общая разность равна 3. Это последовательность (28,31,34,…).

В нашем следующем примере мы найдем арифметическую последовательность с заданной информацией о ее членах в виде рекуррентного соотношения.

Пример 7. Поиск арифметической последовательности по терму и рекуррентному отношению

Найдите арифметическую последовательность по данным 𝑇=13 и 𝑇=18𝑇.

Ответ

Мы хотим найти арифметическую прогрессию. Для этого начнем с того, что вспомним, что в арифметической прогрессии разница между любыми двумя последовательными терминами одинакова и называется общей разностью. Мы также знаем, что, в арифметической прогрессии с первым членом 𝑇 и общей разностью 𝑑 𝑛-й член можно найти по следующей формуле: 𝑇=𝑇+(𝑛−1)𝑑.

Мы можем использовать это, чтобы найти выражения для 𝑇 и 𝑇 через 𝑑, 𝑇 и 𝑛: 𝑇=𝑇+(18𝑛−1)𝑑=𝑇+18𝑑𝑛−𝑑. 

В нашем случае 𝑇=13; это дает нам 𝑇=13+18𝑑𝑛−𝑑.

Далее, 𝑇=𝑇+(𝑛−1)𝑑=13+(𝑛−1)𝑑=13+𝑑𝑛−𝑑.

Теперь мы можем подставить эти выражения в уравнение, данное нам в вопросе: 𝑇 = 18𝑇13+18𝑑𝑛–𝑑 = 18 (13+𝑑𝑛 — 𝑑) 13+18𝑑𝑛 — 𝑑 = 234+18𝑑𝑛 — 18𝑑0 = 221–17𝑑17𝑑 = 221𝑑 = 13.

Следовательно, первый термин в нашей последовательности равно 13, а общая разность равна 13, что дает нам последовательность (13,26,39,…).

В нашем последнем примере мы найдем арифметическую прогрессию путем решения одновременных уравнений.

Пример 8. Нахождение арифметической последовательности при определенном условии

Определите арифметическую последовательность, в которой 𝑇+𝑇=500 и 𝑇+𝑇+𝑇=138.

Ответ

Напомним, что в арифметической прогрессии разница между любыми двумя последовательными членами постоянна. Мы можем определить любую арифметическую прогрессию от его первого члена и общей разности, где 𝑛-й член в арифметической прогрессии с первым членом 𝑇 а общая разность 𝑑 определяется выражением 𝑇=𝑇+(𝑛−1)𝑑. 

Используя эту формулу, мы можем построить выражения для каждого члена уравнений, данных нам в вопросе: 𝑇=𝑇+49𝑑,𝑇=𝑇+27𝑑,𝑇=𝑇+2𝑑,𝑇=𝑇+10𝑑,𝑇=𝑇+34𝑑. эти выражения в уравнения, данные нам в вопросе.

Первый, 𝑇+𝑇=500(𝑇+49𝑑)+(𝑇+27𝑑)=5002𝑇+76𝑑=500𝑇+38𝑑=250.

Секунда, 𝑇+𝑇+𝑇=138(𝑇+2𝑑)+(𝑇+10𝑑)+(𝑇+34𝑑)=1383𝑇+46𝑑=138.

Это дает нам два уравнения с двумя неизвестными , мы можем решить их, исключив одну переменную. Мы можем изменить первое уравнение: 𝑇+38𝑑=250𝑇=250−38𝑑.

Затем мы подставляем это выражение вместо 𝑇 во второе уравнение: 3𝑇+46𝑑=1383(250−38𝑑)+46𝑑=138750−114𝑑+46𝑑=138612−68𝑑=0𝑑=9.

Наконец, мы подставляем это значение для 𝑑 в одно из наших уравнений, чтобы найти первый член в нашем последовательность: 𝑇+38𝑑=250𝑇+38(9)=250𝑇+342=250𝑇=−92.

Следовательно, первый член этой арифметической последовательности равен −92, а общая разность равна 9. Это последовательность (-92,-83,-74,…).

Давайте закончим, повторив некоторые основные моменты.

Ключевые моменты

• Арифметическая последовательность или прогрессия — это последовательность, в которой разница между любыми двумя последовательными членами постоянна; эта постоянная называется общей разностью.
• 𝑛-й член арифметической прогрессии с первым членом 𝑇 и общей разностью 𝑑 можно найти по формуле 𝑇=𝑇+(𝑛−1)𝑑.
• Мы можем использовать эту формулу, чтобы построить выражение для любого члена нашей арифметической последовательности через начальный член и общая разница. Если мы можем составить два уравнения с этими переменными, то мы можем решить их как одновременные уравнения.

Арифметическая прогрессия — Уроки Византа

Прогрессия — это еще один термин для последовательности
. Таким образом, арифметические прогрессии (также известные как арифметические последовательности) 90 267 представляют собой специальные последовательности, определяемые тем свойством, что разница между любыми двумя 90 267 последовательными членами последовательности является постоянной. В то время как правило для регулярных последовательностей 90 267 состоит в том, что разница между последовательными терминами должна иметь какую-то связь, 90 267 она может быть или не быть постоянной. Отношения могут даже не иметь «различия»
, но может иметь «мультипликативный» характер. Это не так для арифметических последовательностей,
связь должна носить только разностный характер. Эта общая разница
обозначается буквой d .

В качестве примера взгляните на последовательность ниже;

чтобы приведенная ниже последовательность была арифметической прогрессией, разница между последовательными
членами должна быть некоторой константой d такой, что:

since that relationship must hold true, we can move further and say that

the same applies to a ₄

the same also применяется к последнему члену a _n , где a _n-1
является вторым последним членом

Итак, теперь давайте заменим члены в последовательности их соответствующими0267 членов, которые мы получили

Из приведенной выше новой последовательности мы должны заметить, что для получения следующего члена вы всегда
добавляете первый член к произведению общей разности и на единицу меньше, чем
позиции следующего срок.

т. е. если следующий член обозначается буквой n, то

Вышеупомянутое соотношение всегда должно выполняться как отношение между последовательными
членами в арифметической прогрессии. Вы можете проверить, что это правда, подставив
для значений последовательности, с которой мы работали.

Это то, что делает арифметические прогрессии такими особыми последовательностями, все, что вам
нужно знать, это первый член и общую разность d и тогда вы сможете
найти любой член в последовательности без необходимости находить его предшествующий срок.

Например, зная, что общая разность в арифметической прогрессии равна 5
, а первый член равен 3, найдите 10-й и 25-й члены последовательности.

solution:

The common relationship between all terms in an arithmetic progression is given
by

Arithmetic Series

Since there exist Arithmetic Sequences, Arithmetic Series also exist and are
сумм членов в арифметических последовательностях.

Мы уже видели, что ряд задается в виде

, где S _n — обозначение суммы ряда.

Мы также установили, что приведенные выше члены также могут быть записаны в терминах первого члена
и общей разности

, но вышеприведенное также может быть записано в терминах последнего члена следующим образом

Если мы если бы сложить две суммы, мы получили бы следующее0267 получается красивое простое выражение

Итак, теперь у нас есть выражение для суммы только через первый и последний члены
как

но мы можем еще больше упростить это выражение, так как мы уже установили способ выражения
любой член с точки зрения первого члена и общей разности d

, так что теперь у нас есть два варианта формулы для нахождения суммы арифметической прогрессии.

Вспоминая из раздела о сериях, обозначение для суммирования:

Примеры арифметической прогрессии

Пример 1

Найдите сумму приведенной ниже арифметической прогрессии, учитывая, что общее количество
членов равно 15 общая разница textbf{d} в том, что нам нужно
найти это сначала

Шаг 2

Далее, чтобы найти сумму, все, что нам нужно сделать, это подставить в формулу, так как мы уже
имеет первые и последние условия

Шаг 3

Шаг 4

Пример 2

, что следующее, что следующее, что следующее, что следующее, как следующее.