Примеры с обыкновенными дробями: Примеры и задачи с дробями

Дроби обыкновенные — intmag24.ru

80,00 ₽

Примеры с обыкновенными дробями на сложение, вычитание, умножение и деление (можно выбрать действия).  В примерах дроби с разными знаменателями. С ответами. Для печати А4.

Артикул: i-5497 Категория: Для учебы Метки: Дроби, 5-8 класс

• Описание
• Детали
• Отзывы (0)

Описание

Программа формирует карточки с примерами, в которых представлены обыкновенные дроби и математические операции с ними.

Программа имеет внутренние настройки, с помощью которых можно выбрать вид математических операций:

• сложение и вычитание дробей с разными знаменателями
• все действия (сложение, вычитание, умножение и деление) дробей с разными знаменателями.

Решении данного задания позволит ребенку закрепить навыки счета, в том числе:

• приведение дробей к общему знаменателю,
• преобразование неправильных дробей в смешанные дроби,
• преобразование смешанных дробей в неправильные дроби,
• сложение и вычитание двух обыкновенных дробей,
• умножение и деление двух обыкновенных дробей.

В конце карточки формируются ответы на примеры, которые после печати карточки можно отрезать. Нумерация карточек и ответов позволяет быстро находить ответы к каждой карточке, даже если их напечатано много.

Программа написана в Excel с помощью макросов. Задания формируются на листе формата А4 случайным образом, количество генераций не ограничено. Для ознакомления с программой можно бесплатно скачать примеры, которые получаются при использовании программы. Для

получения новой карточки примеров достаточно скачать, нажать на кнопку генерации и распечатать.

Основные виды дробей, их свойства, а также все операции, которые можно выполнять с дробями: сокращение, приведение, сравнение, сложение, вычитание, умножение и деление описаны в статье «Математические дроби – просто о сложном».

Другие программы, которые помогут закрепить навыки счета с дробями:

• Сложение и вычитание простых дробей с одинаковыми знаменателями
• Сложение и вычитание простых дробей с разными знаменателями
• Десятичные дроби (разные виды операций)
• Дроби смешанные
• Математический диктант 5 класс

На сайте представлен каталог программ, в котором все программы распределены по группам. С помощью каталога Вы можете выбрать те программы, которые подходят именно Вам.

 

Вам также будет интересно…

• Простые проценты

  Оценка 5. 00 из 5

  80,00 ₽В корзину

• Порядок действий в пределах 1000 (все действия)

  90,00 ₽В корзину

• Дроби десятичные

  80,00 ₽В корзину

• Сложение и вычитание в столбик

  Оценка 5.00 из 5

  70,00 ₽В корзину

• Дроби смешанные

  100,00 ₽В корзину

• Головоломка «Спички»

  Оценка 5.00 из 5

  Распродажа! 150,00 ₽ 90,00 ₽ В корзину

• Задачи на движение (разные виды)

  100,00 ₽В корзину

• Математический диктант 5 класс

  140,00 ₽В корзину

• Раскрыть скобки в примерах

  Оценка 5.00 из 5

  120,00 ₽В корзину

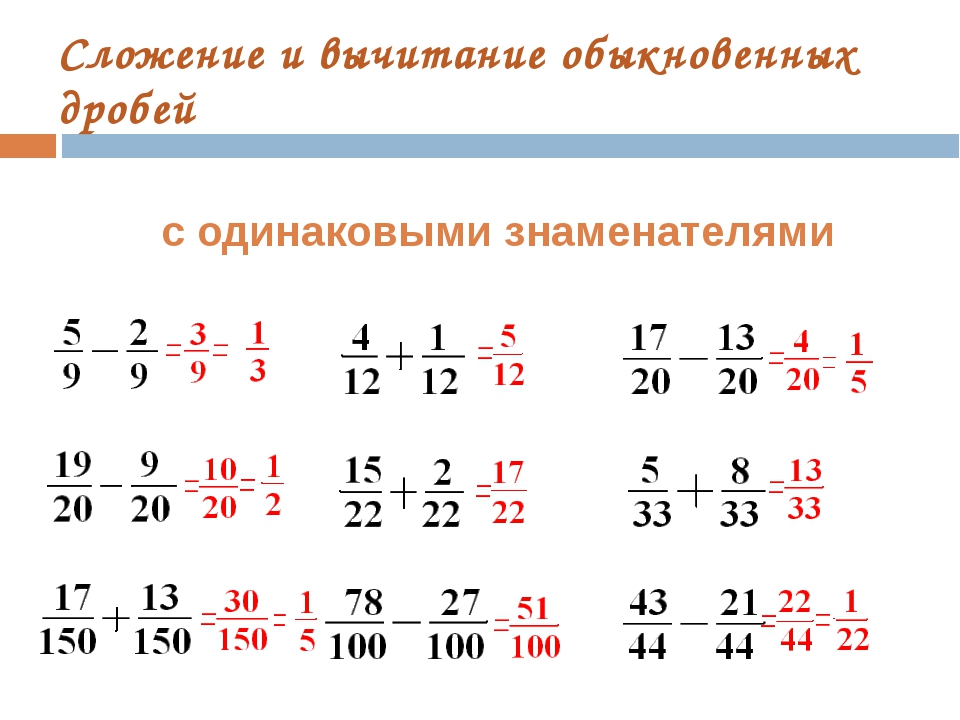
Примеры на вычитание дробей с одинаковыми знаменателями.

Сложение и вычитание дробей

Действия с дробями. В этой статье разберём примеры, всё подробно с пояснениями. Рассматривать будем обыкновенные дроби. В дальнейшем разберём и десятичные. Рекомендую посмотреть весь и изучать последовательно.

1. Сумма дробей, разность дробей.

Правило: при сложении дробей с равными знаменателями, в результате получаем дробь – знаменатель которой остаётся тот же, а числитель её будет равен сумме числителей дробей.

Правило: при вычислении разности дробей с одинаковыми знаменателями получаем дробь – знаменатель остаётся тот же, а из числителя первой дроби вычитается числитель второй.

Формальная запись суммы и разности дробей с равными знаменателями:

Примеры (1):

Понятно, что когда даны обыкновенные дроби, то всё просто, а если смешанные? Ничего сложного…

Вариант 1 – можно перевести их в обыкновенные и далее вычислять.

Вариант 2 – можно отдельно «работать» с целой и дробной частью.

Примеры (2):

Ещё:

А если будет дана разность двух смешанных дробей и числитель первой дроби будет меньше числителя второй? Тоже можно действовать двумя способами.

Примеры (3):

*Перевели в обыкновенные дроби, вычислили разность, перевели полученную неправильную дробь в смешанную.

*Разбили на целые и дробные части, получили тройку, далее представили 3 как сумму 2 и 1, при чём единицу представили как 11/11, далее нашли разность 11/11 и 7/11 и вычислили результат. Смысл изложенных преобразований заключается в том, чтобы взять (выделить) единицу и представить её в виде дроби с нужным нам знаменателем, далее от этой дроби мы уже можем вычесть другую.

Ещё пример:

Вывод: имеется универсальный подход – для того, чтобы вычислить сумму (разность) смешанных дробей с равными знаменателями их всегда можно перевести в неправильные, далее выполнить необходимое действие. После этого если в результате получаем неправильную дробь переводим её в смешанную.

Выше мы рассмотрели примеры с дробями, у которых равные знаменатели. А если знаменатели будут отличаться? В этом случае дроби приводятся к одному знаменателю и выполняется указанное действие. Для изменения (преобразования) дроби используется основное свойство дроби.

Рассмотрим простые примеры:

В данных примерах мы сразу видим каким образом можно преобразовать одну из дробей, чтобы получить равные знаменатели.

Если обозначить способы приведения дробей к одному знаменателю, то этот назовём СПОСОБ ПЕРВЫЙ .

То есть, сразу при «оценке» дроби нужно прикинуть сработает ли такой подход – проверяем делится ли больший знаменатель на меньший. И если делится, то выполняем преобразование — домножаем числитель и знаменатель так чтобы у обеих дробей знаменатели стали равными.

Теперь посмотрите на эти примеры:

К ним указанный подход не применим. Существуют ещё способы приведения дробей к общему знаменателю, рассмотрим их.

Способ ВТОРОЙ .

Умножаем числитель и знаменатель первой дроби на знаменатель второй, а числитель и знаменатель второй дроби на знаменатель первой:

*Фактически мы приводим дроби к виду, когда знаменатели становятся равными. Далее используем правило сложения робей с равными знаменателями.

Пример:

*Данный способ можно назвать универсальным, и он работает всегда. Единственный минус в том, что после вычислений может получится дробь которую необходимо будет ещё сократить.

Рассмотрим пример:

Видно что числитель и знаменатель делится на 5:

Способ ТРЕТИЙ.

Необходимо найти наименьшее общее кратное (НОК) знаменателей. Это и будет общий знаменатель. Что это за число такое? Это наименьшее натуральное число, которое делится на каждое из чисел.

Посмотрите, вот два числа: 3 и 4, есть множество чисел, которые делятся на них – это 12, 24, 36, … Наименьшее из них 12. Или 6 и 15, на них делятся 30, 60, 90 …. Наименьшее 30. Вопрос – а как определить это самое наименьшее общее кратное?

Имеется чёткий алгоритм, но часто это можно сделать и сразу без вычислений. Например, по указанным выше примерам (3 и 4, 6 и 15) никакого алгоритма не надо, мы взяли большие числа (4 и 15) увеличили их в два раза и увидели, что они делятся на второе число, но пары чисел могут быть и другими, например 51 и 119.

Алгоритм. Для того, чтобы определить наименьшее общее кратное нескольких чисел, необходимо:

— разложить каждое из чисел на ПРОСТЫЕ множители

— выписать разложение БОЛЬШЕГО из них

— умножить его на НЕДОСТАЮЩИЕ множители других чисел

Рассмотрим примеры:

50 и 60 => 50 = 2∙5∙5 60 = 2∙2∙3∙5

в разложении большего числа не хватает одной пятёрки

=> НОК(50,60) = 2∙2∙3∙5∙5 = 300

48 и 72 => 48 = 2∙2∙2∙2∙3 72 = 2∙2∙2∙3∙3

в разложении большего числа не хватает двойки и тройки

=> НОК(48,72) = 2∙2∙2∙2∙3∙3 = 144

* Наименьшее общее кратное двух простых чисел равно их произведению

Вопрос! А чем полезно нахождение наименьшего общего кратного, ведь можно пользоваться вторым способом и полученную дробь просто сократить? Да, можно, но это не всегда удобно.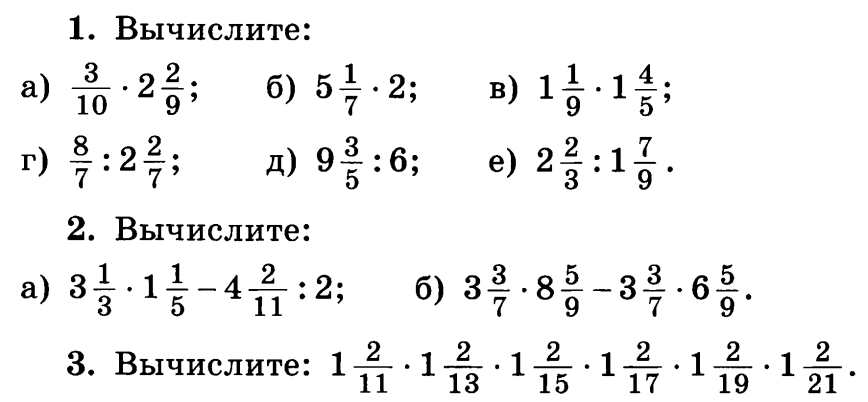

Посмотрите, какой получится знаменатель для чисел 48 и 72, если их просто перемножить 48∙72 = 3456. Согласитесь, что приятнее работать с меньшими числами.

Рассмотрим примеры:

*51 = 3∙17 119 = 7∙17

в разложении большего числа не хватает тройки

=> НОК(51,119) = 3∙7∙17

А теперь применим первый способ:

*Посмотрите какая разница в вычислениях, в первом случае их минимум, а во втором нужно потрудиться отдельно на листочке, да ещё и дробь которую получили сократить необходимо. Нахождение НОК упрощает работу значительно.

Ещё примеры:

*Во втором примере и так видно, что наименьшее число, которое делится на 40 и 60 равно 120.

ИТОГ! ОБЩИЙ АЛГОРИТМ ВЫЧИСЛЕНИЙ!

— приводим дроби к обыкновенным, если есть целая часть.

— приводим дроби к общему знаменателю (сначала смотрим делится ли один знаменатель на другой, если делится то умножаем числитель и знаменатель этой другой дроби; если не делится действуем посредством других указанных выше способов).

— получив дроби с равными знаменателями, выполняем действия (сложение, вычитание).

— если необходимо, то результат сокращаем.

— если необходимо, то выделяем целую часть.

2. Произведение дробей.

Правило простое. При умножении дробей умножаются их числители и знаменатели:

Примеры:

Задача. На базу привезли 13 тонн овощей. Картофель составляет ¾ от всех завезённых овощей. Сколько килограмм картофеля завезли на базу?

С произведением закончим.

*Ранее обещал вам привести формальное объяснение основного свойства дроби через произведение, пожалуйста:

3. Деление дробей.

Деление дробей сводится к их умножению. Здесь важно запомнить, что дробь являющаяся делителем (та, на которую делят) переворачивается и действие меняется на умножение:

Данное действие может быть записано в виде так называемой четырёхэтажной дроби, ведь само деление «:» тоже можно записать как дробь:

Примеры:

На этом всё! Успеха вам!

С уважением, Александр Крутицких.

Действия с дробями.

Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)

Итак, что из себя представляют дроби, виды дробей, преобразования — мы вспомнили. Займёмся главным вопросом.

Что можно делать с дробями? Да всё то, что и с обычными числами. Складывать, вычитать, умножать, делить.

Все эти действия с десятичными дробями ничем не отличаются от действий с целыми числами. Собственно, этим они и хороши, десятичные. Единственно, запятую правильно поставить надо.

Смешанные числа , как я уже говорил, малопригодны для большинства действий. Их всё равно надо переводить в обыкновенные дроби.

А вот действия с обыкновенными дробями похитрее будут. И гораздо важнее! Напомню: все действия с дробными выражениями с буковками, синусами, неизвестными и прочая и прочая ничем не отличаются от действий с обыкновенными дробями ! Действия с обыкновенными дробями — это основа для всей алгебры. Именно по этой причине мы очень подробно разберём здесь всю эту арифметику.

Сложение и вычитание дробей.

Сложить (отнять) дроби с одинаковыми знаменателями каждый сможет (очень надеюсь!). Ну уж совсем забывчивым напомню: при сложении (вычитании) знаменатель не меняется. Числители складываются (вычитаются) и дают числитель результата. Типа:

Короче, в общем виде:

А если знаменатели разные? Тогда, используя основное свойство дроби (вот оно и опять пригодилось!), делаем знаменатели одинаковыми! Например:

Здесь нам из дроби 2/5 пришлось сделать дробь 4/10. Исключительно с целью сделать знаменатели одинаковыми. Замечу, на всякий случай, что 2/5 и 4/10 это одна и та же дробь ! Только 2/5 нам неудобно, а 4/10 очень даже ничего.

Кстати, в этом суть решений любых заданий по математике. Когда мы из неудобного выражения делаем то же самое, но уже удобное для решения .

Ещё пример:

Ситуация аналогичная. Здесь мы из 16 делаем 48. Простым умножением на 3. Это всё понятно. Но вот нам попалось что-нибудь типа:

Как быть?! Из семёрки девятку трудно сделать! Но мы умные, мы правила знаем! Преобразуем каждую дробь так, чтобы знаменатели стали одинаковыми. Это называется «приведём к общему знаменателю»:

Во как! Откуда же я узнал про 63? Очень просто! 63 это число, которое нацело делится на 7 и 9 одновременно. Такое число всегда можно получить перемножением знаменателей. Если мы какое-то число умножили на 7, к примеру, то результат уж точно на 7 делиться будет!

Если надо сложить (вычесть) несколько дробей, нет нужды делать это попарно, по шагам. Просто надо найти знаменатель, общий для всех дробей, и привести каждую дробь к этому самому знаменателю. Например:

И какой же общий знаменатель будет? Можно, конечно, перемножить 2, 4, 8, и 16. Получим 1024. Кошмар. Проще прикинуть, что число 16 отлично делится и на 2, и на 4, и на 8. Следовательно, из этих чисел легко получить 16. Это число и будет общим знаменателем. 1/2 превратим в 8/16, 3/4 в 12/16, ну и так далее.

Кстати, если за общий знаменатель взять 1024, тоже всё получится, в конце всё посокращается. Только до этого конца не все доберутся, из-за вычислений…

Дорешайте уж пример самостоятельно. Не логарифм какой… Должно получиться 29/16.

Итак, со сложением (вычитанием) дробей ясно, надеюсь? Конечно, проще работать в сокращённом варианте, с дополнительными множителями. Но это удовольствие доступно тем, кто честно трудился в младших классах… И ничего не забыл.

А сейчас мы поделаем те же самые действия, но не с дробями, а с дробными выражениями . Здесь обнаружатся новые грабли, да…

Итак, нам надо сложить два дробных выражения:

Надо сделать знаменатели одинаковыми. Причём только с помощью умножения ! Уж так основное свойство дроби велит. Поэтому я не могу в первой дроби в знаменателе к иксу прибавить единицу. (а вот бы хорошо было!). А вот если перемножить знаменатели, глядишь, всё и срастётся! Так и записываем, черту дроби, сверху пустое место оставим, потом допишем, а снизу пишем произведение знаменателей, чтобы не забыть:

И, конечно, ничего в правой части не перемножаем, скобки не открываем! А теперь, глядя на общий знаменатель правой части, соображаем: чтобы в первой дроби получился знаменатель х(х+1), надо числитель и знаменатель этой дроби умножить на (х+1). А во второй дроби — на х. Получится вот что:

Обратите внимание! Здесь появились скобки! Это и есть те грабли, на которые многие наступают. Не скобки, конечно, а их отсутствие. Скобки появляются потому, что мы умножаем весь числитель и весь знаменатель! А не их отдельные кусочки…

В числителе правой части записываем сумму числителей, всё как в числовых дробях, затем раскрываем скобки в числителе правой части, т.е. перемножаем всё и приводим подобные. Раскрывать скобки в знаменателях, перемножать что-то не нужно! Вообще, в знаменателях (любых) всегда приятнее произведение! Получим:

Вот и получили ответ. Процесс кажется долгим и трудным, но это от практики зависит. Порешаете примеры, привыкните, всё станет просто. Те, кто освоил дроби в положенное время, все эти операции одной левой делают, на автомате!

И ещё одно замечание. Многие лихо расправляются с дробями, но зависают на примерах с целыми числами. Типа: 2 + 1/2 + 3/4= ? Куда пристегнуть двойку? Никуда не надо пристёгивать, надо из двойки дробь сделать. Это не просто, а очень просто! 2=2/1. Вот так. Любое целое число можно записать в виде дроби. В числителе — само число, в знаменателе — единица. 7 это 7/1, 3 это 3/1 и так далее. С буквами — то же самое. (а+в) = (а+в)/1, х=х/1 и т.д. А дальше работаем с этим дробями по всем правилам.

Ну, по сложению — вычитанию дробей знания освежили. Преобразования дробей из одного вида в другой — повторили. Можно и провериться. Порешаем немного?)

Вычислить:

Ответы (в беспорядке):

71/20; 3/5; 17/12; -5/4; 11/6

Умножение/деление дробей — в следующем уроке. Там же и задания на все действия с дробями.

Если Вам нравится этот сайт…

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

можно познакомиться с функциями и производными.

Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.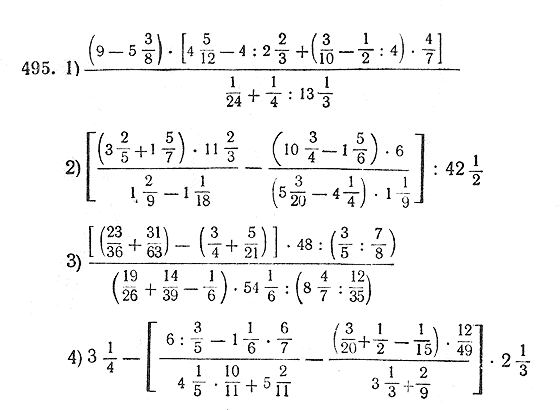

Вычитание дробей с одинаковыми знаменателями, примеры:

,

,

Вычитание правильной дроби из единицы.

Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.

Пример вычитания правильной дроби из единицы:

Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.

Вычитание правильной дроби из целого числа.

Правила вычитания дробей — правильной из целого числа (натурального числа) :

• Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
• Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
• Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.

Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.

Пример вычитания дробей:

В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.

Вычитание дробей с разными знаменателями.

Или, если сказать другими словами, вычитание разных дробей .

Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.

Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.

Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!

Порядок действий при вычитании дробей с разными знаменателями.

• найти НОК для всех знаменателей;
• поставить для всех дробей дополнительные множители;
• умножить все числители на дополнительный множитель;
• полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
• произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.

Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.

Вычитание дробей, примеры:

Вычитание смешанных дробей.

При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.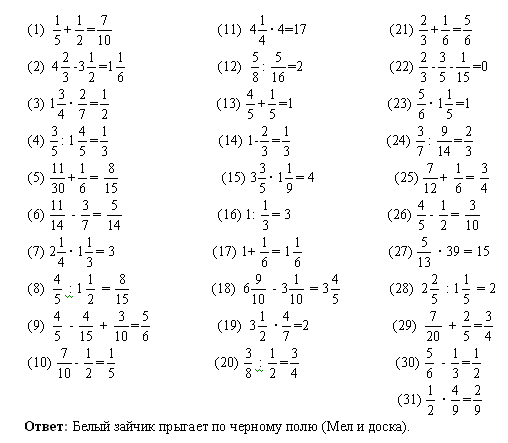

Первый вариант вычитания смешанных дробей.

Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).

Например:

Второй вариант вычитания смешанных дробей.

Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.

Например:

Третий вариант вычитания смешанных дробей.

Дробная часть уменьшаемого меньше дробной части вычитаемого.

Пример:

Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.

Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.

В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:

Найдите числитель и знаменатель. Дробь включает два числа: число, которое расположено над чертой, называется числителем, а число, которое находится под чертой – знаменателем. Знаменатель обозначает общее количество частей, на которые разбито некоторое целое, а числитель – это рассматриваемое количество таких частей.

• Например, в дроби ½ числителем является 1, а знаменателем 2.

Определите знаменатель. Если две и более дроби имеют общий знаменатель, у таких дробей под чертой находится одно и то же число, то есть в этом случае некоторое целое разбито на одинаковое количество частей. Складывать дроби с общим знаменателем очень просто, так как знаменатель суммарной дроби будет таким же, как у складываемых дробей. Например:

• У дробей 3/5 и 2/5 общий знаменатель 5.
• У дробей 3/8, 5/8, 17/8 общий знаменатель 8.

Определите числители. Чтобы сложить дроби с общим знаменателем, сложите их числители, а результат запишите над знаменателем складываемых дробей.

• У дробей 3/5 и 2/5 числители 3 и 2.
• У дробей 3/8, 5/8, 17/8 числители 3, 5, 17.

Сложите числители. В задаче 3/5 + 2/5 сложите числители 3 + 2 = 5. В задаче 3/8 + 5/8 + 17/8 сложите числители 3 + 5 + 17 = 25.

Запишите суммарную дробь. Помните, что при сложении дробей с общим знаменателем он остается без изменений – складываются только числители.

• 3/5 + 2/5 = 5/5
• 3/8 + 5/8 + 17/8 = 25/8

Если нужно, преобразуйте дробь. Иногда дробь можно записать в виде целого числа, а не обыкновенной или десятичной дроби. Например, дробь 5/5 легко преобразуется в 1, так как любая дробь, у которой числитель равен знаменателю, есть 1. Представьте пирог, разрезанный на три части. Если вы съедите все три части, то вы съедите целый (один) пирог.

• Любую обыкновенную дробь можно преобразовать в десятичную; для этого разделите числитель на знаменатель. Например, дробь 5/8 можно записать так: 5 ÷ 8 = 0,625.

Если возможно, упростите дробь. Упрощенная дробь – эта дробь, числитель и знаменатель которой не имеют общих делителей.

• Например, рассмотрим дробь 3/6. Здесь и у числителя, и у знаменателя есть общий делитель, равный 3, то есть числитель и знаменатель нацело делятся на 3. Поэтому дробь 3/6 можно записать так: 3 ÷ 3/6 ÷ 3 = ½.

Если нужно, преобразуйте неправильную дробь в смешанную дробь (смешанное число). У неправильной дроби числитель больше знаменателя, например, 25/8 (у правильной дроби числитель меньше знаменателя). Неправильную дробь можно преобразовать в смешанную дробь, которая состоит из целой части (то есть целого числа) и дробной части (то есть правильной дроби). Чтобы преобразовать неправильную дробь, например, 25/8, в смешанное число, выполните следующие действия:

• Разделите числитель неправильной дроби на ее знаменатель; запишите неполное частное (целый ответ). В нашем примере: 25 ÷ 8 = 3 плюс некоторый остаток. В данном случае целый ответ – это целая часть смешанного числа.
• Найдите остаток. В нашем примере: 8 х 3 = 24; полученный результат вычтите из исходного числителя: 25 — 24 = 1, то есть остаток равен 1. В данном случае остаток – это числитель дробной части смешанного числа.
• Запишите смешанную дробь. Знаменатель не меняется (то есть равен знаменателю неправильной дроби), поэтому 25/8 = 3 1/8.

Обратите внимание! Перед тем как написать окончательный ответ, посмотрите, может можно сократить дробь , которую вы получили.

Вычитание дробей с одинаковыми знаменателями, примеры:

,

,

Вычитание правильной дроби из единицы.

Если необходимо вычесть из единицы дробь, которая является правильной , единицу переводят к виду неправильной дроби , у нее знаменатель равен знаменателю вычитаемой дроби.

Пример вычитания правильной дроби из единицы:

Знаменатель вычитаемой дроби = 7 , т.е., единицу представляем в виде неправильной дроби 7/7 и вычитаем по правилу вычитания дробей с одинаковыми знаменателями.

Вычитание правильной дроби из целого числа.

Правила вычитания дробей — правильной из целого числа (натурального числа) :

• Переводим заданные дроби, которые содержат целую часть, в неправильные. Получаем нормальные слагаемые (не важно если они с разными знаменателями), которые считаем по правилам, приведенным выше;
• Далее вычисляем разность дробей, которые мы получили. В результате мы почти найдем ответ;
• Выполняем обратное преобразование, то есть избавляемся от неправильной дроби — выделяем в дроби целую часть.

Вычтем из целого числа правильную дробь: представляем натуральное число в виде смешанного числа. Т.е. занимаем единицу в натуральном числе и переводим её к виду неправильной дроби, знаменатель при этом такой же, как у вычитаемой дроби.

Пример вычитания дробей:

В примере единицу мы заменили неправильной дробью 7/7 и вместо 3 записали смешанное число и от дробной части отняли дробь.

Вычитание дробей с разными знаменателями.

Или, если сказать другими словами, вычитание разных дробей .

Правило вычитания дробей с разными знаменателями. Для того, чтобы произвести вычитание дробей с разными знаменателями, необходимо, для начала, привести эти дроби к наименьшему общему знаменателю (НОЗ) , и только послеиэтого произвести вычитание как с дробями с одинаковыми знаменателями.

Общий знаменатель нескольких дробей — это НОК (наименьшее общее кратное) натуральных чисел, которые являются знаменателями данных дробей.

Внимание! Если в конечной дроби у числителя и знаменателя есть общие множители , то дробь необходимо сократить. Неправильную дробь лучше представить в виде смешанной дроби. Оставить результат вычитания, не сократив дробь, где есть возможность, — это незаконченное решение примера!

Порядок действий при вычитании дробей с разными знаменателями.

• найти НОК для всех знаменателей;
• поставить для всех дробей дополнительные множители;
• умножить все числители на дополнительный множитель;
• полученные произведения записываем в числитель, подписывая под всеми дробями общий знаменатель;
• произвести вычитание числителей дробей, подписывая под разностью общий знаменатель.

Таким же образом проводится сложение и вычитание дробей при наличии в числителе букв.

Вычитание дробей, примеры:

Вычитание смешанных дробей.

При вычитании смешанных дробей (чисел) отдельно из целой части вычитают целую часть, а из дробной части вычитают дробную часть.

Первый вариант вычитания смешанных дробей.

Если у дробных частей одинаковые знаменатели и числитель дробной части уменьшаемого (из него вычитаем) ≥ числителю дробной части вычитаемого (его вычитаем).

Например:

Второй вариант вычитания смешанных дробей.

Когда у дробных частей разные знаменатели. Для начала приводим к общему знаменателю дробные части, а после этого выполняем вычитание целой части из целой, а дробной из дробной.

Например:

Третий вариант вычитания смешанных дробей.

Дробная часть уменьшаемого меньше дробной части вычитаемого.

Пример:

Т.к. у дробных частей разные знаменатели, значит, как и при втором варианте, сначала приводим обыкновенные дроби к общему знаменателю.

Числитель дробной части уменьшаемого меньше числителя дробной части вычитаемого. 3 Значит, занимаем единицу из целой части и приводим эту единицу к виду неправильной дроби с одинаковым знаменателем и числителем = 18.

В числителе от правой части пишем сумму числителей, дальше раскрываем скобки в числителе от правой части, то есть умножаем все и приводим подобные. В знаменателе скобки не раскрываем. В знаменателях принято оставлять произведение. Получаем:

Общий знаменатель — определение, как найти общий знаменатель, примеры, часто задаваемые вопросы

Общий знаменатель полезен для выполнения многочисленных математических операций над числами. Важным понятием в математике является сложение и вычитание дробей. Дроби включают числитель (число вверху) и знаменатель (число внизу). Дроби, имеющие одинаковые знаменатели, такие знаменатели называются общими знаменателями. Рассмотрим следующие примеры: 1/2 + 1/2 = 1 и 3/4 + 1/4 = 1. В обоих случаях знаменатели у дробей общие, поэтому вычислить ответ несложно.

Однако, если бы вам дали задачу с другими знаменателями, как бы вы ее решили. Расчет 2/5 + 3/4 выполнить сложно из-за разных знаменателей. Поскольку знаменатели у дробей неодинаковые, приходится решать их другим методом. Давайте рассмотрим эту тему, чтобы узнать больше об общих знаменателях.

1.	Что такое общий знаменатель?
2.	Как найти общий знаменатель?
3.	Примеры общего знаменателя
4.	Методы общего знаменателя
5.	Часто задаваемые вопросы об общем знаменателе

Что такое общий знаменатель?

Две или более дроби, имеющие одинаковый знаменатель, называются общим знаменателем. Общий знаменатель помогает легко выполнять числовые вычисления. Число, указанное в нижней части дроби, называется 9.0045 знаменатель . Знаменатель показывает, на сколько равных частей делится предмет.

На приведенном выше рисунке первая пицца состоит из 4 ломтиков. Таким образом, оно представляется как 1, то есть целое. Когда мы убираем один кусочек, у нас остается 3 из 4 кусочков. Таким образом, доля оставшихся ломтиков равна 3/4. Это также означает, что 1/4 часть была удалена. Если сложить эти два, то получится: 1/4 + 3/4 = 4/4 = 1. Далее, в зависимости от размера пиццы, вы можете разделить ее на сколько угодно частей.

Как найти общий знаменатель?

Хотя пример с пиццей показывает, насколько просто найти общий знаменатель, такая ситуация может возникнуть не всегда. Могут быть случаи, когда вас попросят сложить дроби с разными знаменателями, например 3/7 + 12/13. В таких случаях нам нужно найти общий знаменатель, а затем решить дроби. Давайте рассмотрим более простой пример 1/3 + 1/6. Ниже приведены два общих знаменателя методов найти ответ:

• Путем нахождения наименьшего общего кратного
• Перекрестным умножением

При нахождении общего знаменателя методом НОК вы найдете наименьшее общее кратное данных чисел. В этом уравнении наименьшее общее кратное равно 6. Следовательно, уравнение принимает вид 1/3 + 1/6 = (1 x 2 + 1)/6 = (2 + 1)/6 = 3/6 = 1/2. Если вы перекрестите умножение, вы найдете решение как: 1/3 + 1/6 = 2/6 + 1/6 = (2 + 1)/6 = 3/6 = 1/2

Примеры общего знаменателя

Примеры общих знаменателей в нашей повседневной жизни включают кусочки пиццы, деньги, приготовление пищи и выпечку и так далее. Например, пицца может быть нарезана на четыре части, а возможные части пиццы могут составлять 1/4. 2/4, 3/4 соответственно. Кроме того, мы можем найти общие знаменатели в случаях, когда мы разделяем равные количества количества. В такой ситуации общие знаменатели будут равны 1/2 и 1/2 или 1/4 и 1/4 соответственно.

Практически многие примеры из повседневной жизни, в которых количества были разделены, могут быть выражены в виде общего знаменателя. Еще один хороший пример общего знаменателя можно найти в кулинарии и выпечке — вам нужны дроби и знаменатели, чтобы измерить ингредиенты для приготовления торта.

Метод общего знаменателя

Методы общего знаменателя, как объяснялось выше, включают вычисление наименьшего общего кратного или перекрестное умножение. Общие знаменатели – это произведения знаменателей данных дробей. Однако нужно помнить, что помимо этого общими знаменателями являются также факторы, которые являются общими для дробей, и факторы, делающие каждую дробь различной. Общий знаменатель включает в себя все факторы из каждой дроби.

Связанные темы

Ниже перечислены несколько тем, связанных с общим знаменателем, посмотрите.

• Наименьшее общее кратное
• HCF — наивысший общий делитель
• Наибольший общий делитель
• Делитель

Часто задаваемые вопросы об общем знаменателе

Что такое общий знаменатель?

Общий знаменатель — это тот, в котором знаменатель, т. е. число под дробью, везде одинаков, что упрощает процесс вычислений. Если у двух дробей нет общего знаменателя, то вам нужно вычислить общий знаменатель, чтобы получить ответ.

Как найти общий знаменатель?

Для суммы, подобной 3/4 + 1/4 = 1, общий знаменатель равен 4. Однако, если вам дано вычисление, такое как 3/4 + 1/2, вам нужно будет найти общий знаменатель для оба 3/4 + 1/2. Вы можете сделать это, либо найдя наименьшее общее кратное, либо перекрестно умножив приведенное выше уравнение.

Какой общий знаменатель у чисел 3 и 4?

В отличие от предыдущего примера, в данном случае ни 3, ни 4 не являются делителями друг друга. В этом случае вы можете вычислить значение общего знаменателя, перемножив оба числа, чтобы получить 12.

Какое другое название общего знаменателя?

Другим возможным названием общего знаменателя является общий делитель. Далее, исходя из знаменателей, общим знаменателем может быть lcm двух знаменателей. Кроме того, если один знаменатель является множителем другого знаменателя, то мы можем взять большее число в качестве наименьшего общего знаменателя.

Как найти наименьший общий знаменатель?

Наименьший общий знаменатель зависит от вида знаменателя. Для знаменателей с взаимно простыми числами наименьший общий знаменатель равен произведению двух знаменателей. Кроме того, наименьший общий знаменатель равен lcm двух заданных знаменателей. Рассмотрим два значения знаменателя: 4, 6. Наименьшим общим знаменателем является lcm числа 4, 6, то есть число 12.

Что такое наибольший общий знаменатель?

Наибольший общий знаменатель двух или более дробей, не равных нулю, — это наибольшее положительное целое число, на которое делится каждый из данных знаменателей.

Может ли общий знаменатель быть равен нулю или 1?

Для дроби с общим знаменателем, равным нулю, она становится неопределенной. А для дробей с целыми числами в числителях и 1 в знаменателе общий знаменатель равен 1. В случае, когда целые числа рассматриваются как дроби, общий знаменатель равен 1.

Общий знаменатель – определение, примеры и диаграммы

Определение

Когда знаменатели двух или более дробей совпадают, они являются общими знаменателями. Например, в дробях ${\dfrac{2}{9}}$, ${\dfrac{5}{9}}$ и ${\dfrac{8}{9}}$ 9 равно общий знаменатель.

Общий знаменатель

Почему важен общий знаменатель

Мы можем складывать, вычитать или сравнивать две или более дроби, только если знаменатели совпадают. Дроби с общими знаменателями называются как дроби . Напротив, дроби с разными знаменателями называются , в отличие от дробей .

Например, мы можем легко сложить две дроби, ${\dfrac{4}{11}}$ и ${\dfrac{3}{11}}$, поскольку их знаменатели совпадают.

Сложение Вычитание Сравнение дробей с общим знаменателем

${\dfrac{14}{19}+\dfrac{3}{19}}$

Решение:

Как мы знаем,
знаменатель здесь обычное, т.е. 19.
${\следовательно \dfrac{14}{19}+\dfrac{3}{19}=\dfrac{17}{19} }$

Вычесть ${\dfrac{8}{21} }$ from ${\dfrac{11}{21}}$

Решение:

Как мы знаем,
знаменатель здесь общий, т.е. 21.
${\dfrac{11}{21}-\ dfrac{8}{21}}$
${\следовательно \dfrac{11}{21}-\dfrac{8}{21}=\dfrac{3}{21}}$
${=\dfrac{1 {7} }$

Сравните и закажите ${\dfrac{17}{26}}$, ${\dfrac{15}{26}}$ и ${\dfrac{21}{ 26}}$ в порядке возрастания.

Решение:

Здесь общий знаменатель равен 26. Итак, расположим дробь по числителям в порядке возрастания.
${\dfrac{15}{26}

Как найти общий знаменатель для разнородных дробей

Мы можем складывать и вычитать неодинаковые дроби дроби легче преобразовать в подобные дроби. Это делается путем умножения числителя и знаменателя дроби на знаменатель другой дроби.

Например, в дробях ${\dfrac{2}{3}}$ и ${\dfrac{4}{9}}$ мы умножаем 9 на 2 и 3, а 3 на 4 и 9 как показано ниже.

Умножьте верх и низ каждой дроби на знаменатель другой.

Как найти общий знаменатель

Давайте изучим это на нескольких примерах.

Например, чтобы сложить ${\dfrac{4}{5}}$ и ${\dfrac{7}{10}}$, мы найдем LCD (наименьший общий знаменатель).

${\dfrac{4}{5}+\dfrac{7}{10} }$

Теперь LCM 5 и 10 равно 10,

${\следовательно \dfrac{4\times 2+7\times 1}{10}}$
${=\dfrac{8+7}{10}}$
${=\dfrac{15}{ 10}=\dfrac{3}{2}}$
${=1\dfrac{1}{2}}$

Вычитая две разные дроби: ${\dfrac{9}{13}}$, и ${\dfrac{7}{26}}$.

НОК 13 и 26 равно 26. умножить на 1} {26}}$

${=\dfrac{18-7}{26}}$

${=\dfrac{11}{26}}$

Вычесть: ${ \dfrac{8}{15}-\dfrac{3}{20}}$

Решение:

Как мы знаем,
НОК 15 и 20 равно 60.