Операции над множествами, их приоритеты
Введем операции над множествами и установим некоторую аналогию с операциями над другими математическими объектами, например, высказываниями.
Операции над множествами и их свойства во многом аналогичны алгебре высказываний в математической логике. Это отражает единство математической науки и, благодаря использованию методов математического моделирования, позволяет находить ее связь с различными областями знаний.
ОБЪЕДИНЕНИЕМ множествAиBназывается множество , содержащее те и только те элементы, которые принадлежат хотя бы одному из множествAилиB, без повторений.
Схематично эта операция изображена на рис. 7.1. с помощью кругов Эйлера. (По приоритету уступает операциям дополнения и пересечения, определённых ниже)
Рис.
7.1. Объединение множеств
.
Важно, что каждый элемент из множествAиB включаются в их объединение , без повторений, толькоодин раз, даже при их наличии одновременно и в A, и вB.
Эта операция удовлетворяет коммутативному и ассоциативному законам:
Проиллюстрируйте геометрически эти законы.
Очевидны соотношения:
Множество EназываетсяУНИВЕРСАЛЬНЫМ для некоторой системы множеств, если каждое из них принадлежит этому множеству, то есть является его подмножеством. Его ещё, часто, обозначаютU.
Можно считать поэтому, что
Важно заметить, что универсальное
множество Еможет быть «индивидуальным» для каждой
отдельной задачи, то есть определяться
её условием. Например, при решении
линейной задачи nx = m, гдеn N– множество
натуральных чисел иm Z –
множество целых чисел, тоx = m/n Q – множество рациональных чисел. Следовательно все элементы из этой
задачи принадлежат универсальному
множествуЕ ≡ Q,
так как в этих задачахN ZQ E, в них других
чисел нет.
Следовательно все элементы из этой
задачи принадлежат универсальному
множествуЕ ≡ Q,
так как в этих задачахN ZQ E, в них других
чисел нет.
ПЕРЕСЕЧЕНИЕМмножествAиBназывается множество , содержащее те и только те элементы, которые принадлежат иA,и Bодновременно. Они входят в без повторений.
Дайте геометрическую иллюстрацию этим законам.
Для этой операции также справедливы коммутативный и ассоциативный законы:
;
Множества A и B называются НЕПЕРЕСЕКАЮЩИМИСЯ, если
Операции объединения и пересечения множеств подчиняются законам дистрибутивности (распределительным законам):
;
.
Рис. 7.2. Пересечение множеств .
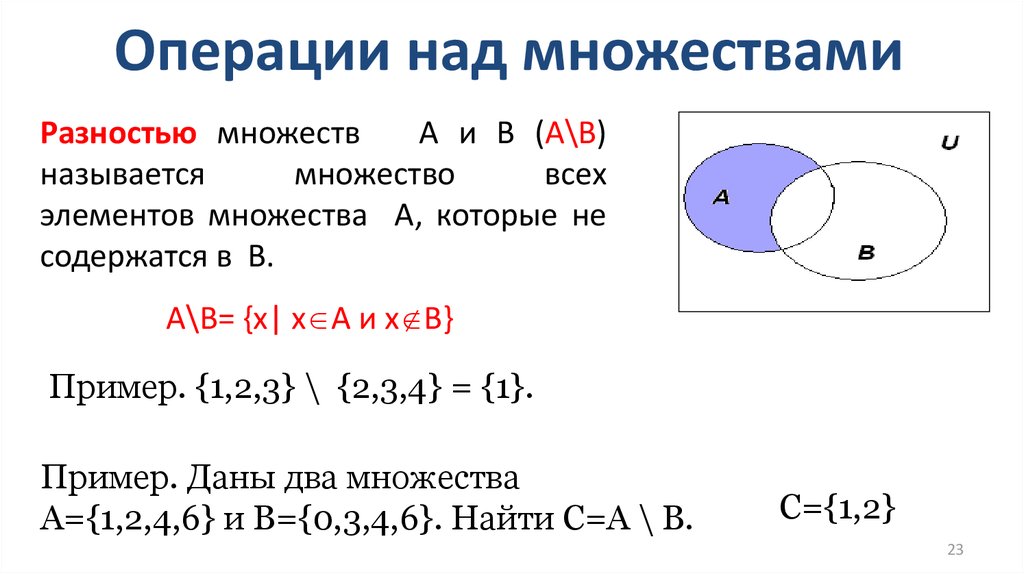
РАЗНОСТЬЮ двух множествAиBназывается множествоA\B, состоящее из тех и только тех элементов, которые принадлежатA, но не принадлежатB. (Эта операция имеет самый низкий приоритет).Рис. 7.3. Разность множеств .
Результаты применения этой операции изображены на рис. 7.3.
ДОПОЛНЕНИЕМмножестваAдо универсального множестваE называется разностьE\Aи обозначается (рис. 7.4). (Эта операция имеет наивысший
приоритет – выполняется первой).
Рисунок 7.4 является простейшей диаграммой
Вена, включающей и универсальное
множествоЕ,
и его подмножестваA и :Е = A U .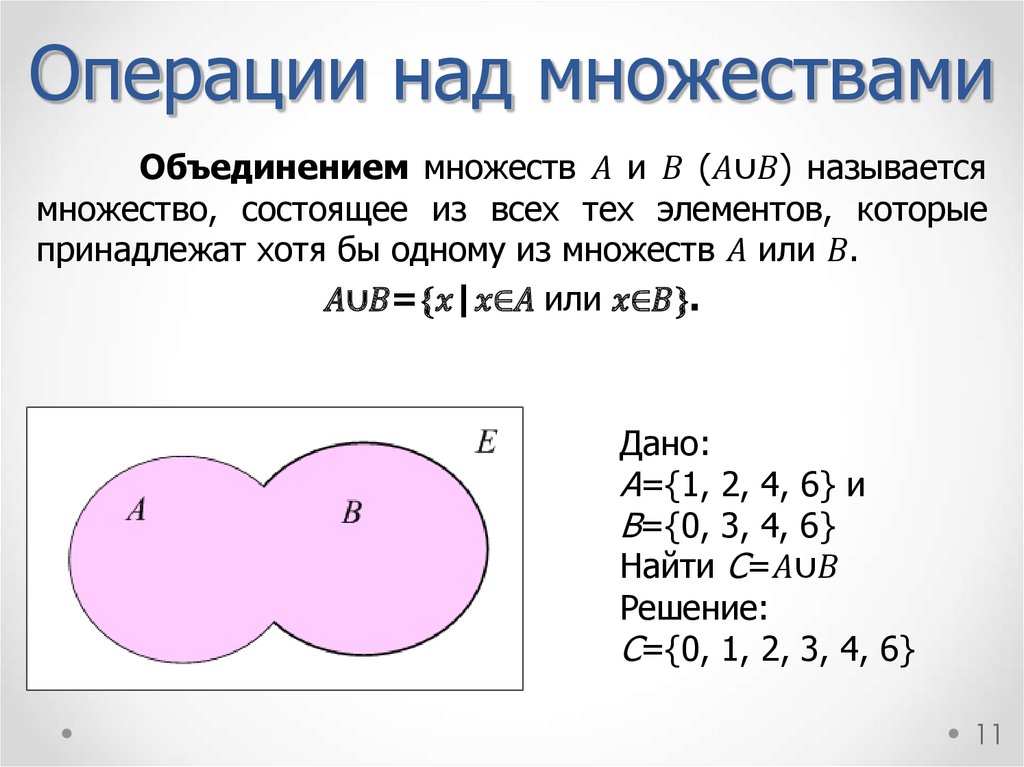
Рис. 7.4. Дополнение множества Адо универсального множестваЕ :.
Символ «:» читают, как «такое, что …», «для … верно, что …».
Дайте им геометрическую трактовку.
Cправедливы соотношения:
Какие аналогии можно установить между операциями над множествами и, например, логическими операциями?
1. .
2. .
3. .
Интерпретируйте логи-ческими высказываниями эти соотношения.
4. .
5. .
Предложите аналоги на языке множеств для известных Вам логических тавтологий.
6. .7. .
Приоритеты: Существует, как и в алгебре, строгий
порядок выполнения действий с множествами. Первым выполняется действие в скобках. Когда
скобки отсутствуют, первой выполняется операция “дополнение”, второй – “пересечение”, третьей – “объединение” и четвёртой – операция “исключение”, слева направо.
Первым выполняется действие в скобках. Когда
скобки отсутствуют, первой выполняется операция “дополнение”, второй – “пересечение”, третьей – “объединение” и четвёртой – операция “исключение”, слева направо.
Числом часто обозначают количество элементов множества A, если оно конечно. Его называют мощностью множества A .
Для конечных множеств AиBсправедлива формула:
( 7. 1 )
Действительно, если множества AиBне пересекаются, то
,
его мощность
,
и поэтому верно
.
Если множества 7.5), справедливо равенство
(7.1).
7.5), справедливо равенство
(7.1).
Конкретный пример с обозначением элементов дан на рис. 7.5.
Рис. 7.5. Общие элементы в объединении конечных пересекающихся множеств.
Если множества конечны, то сравнение числа их элементов может быть уподоблено сравнению натуральных чисел. Труднее сравнить множества бесконечные. Чего больше: натуральных чисел, рациональных или действительных чисел, точек отрезка или точек квадрата, построенного на нем? Очевидно, что часть меньше целого. Но будет ли это “очевидное” сохраняться, когда мы имеем дело с бесконечными множествами? Изучение феноменов «бесконечного» породило принципиально новые оценки самих множеств.
Сам
Г. Кантор определил понятие мощности
множества весьма расплывчато: “Мощностью
данного множества Аназывается идея, которая остается у
нас, когда мы мыслями об этом множестве
отвлекаемся как от всех свойств его
элементов, так и от их порядка”.
Г. Кантор
Соответствия между множествами
Математика не всегда интересуется природой элементов множеств, больший интерес представляет сравнение множеств. Поэтому должна быть введена универсальная характеристика, которая могла бы их описать. Этой характеристикой стала мощность множества.
МОЩНОСТЬконечного множества – это число его элементов.
Определение кажется тривиальным. Однако такой критерий для оценки бесконечных множеств будет, вряд ли, приемлем, так как простой пересчет элементов множества для их последующего сравнения невозможен.
“Я далек от мысли, что я могу сказать последнее слово в столь трудном, сложном и всеобъемлющем вопросе, как проблема бесконечности”.
Г. Кантор
Г. Кантор нашел выход из создавшегося
положения. Он предложил установить
связь между любыми множествами, включая
и конечные множества, через взаимно
однозначное соответствие. Это явилось
принципиально новым взглядом на теорию
множеств. Пусть, например, дан репертуар
оперных спектаклей театра, составленный
на неделю. Представим его в виде
таблицы9.
Это явилось
принципиально новым взглядом на теорию
множеств. Пусть, например, дан репертуар
оперных спектаклей театра, составленный
на неделю. Представим его в виде
таблицы9.
Таблица 9. Соответствие между элементами конечных множеств.
Тогда между множеством и множеством B={“Князь Игорь”, “Иоланта”, …, “Черевички”} может быть установлено соответствие, по которому каждому элементу множества А указывается один определенный элемент множества В и обратно: каждому элементу множества В ставится в соответствие также один определенный элемент множества A. Этот способ позволяет без пересчета указать, что множества A и B содержат одинаковое количество элементов. Именно эта идея и положена в основу сравнения бесконечныхмножеств.
Будем говорить, что между множествами AиBустановлено
Если между множествами AиBудается установить взаимно однозначное соответствие, то говорят, что ониЭКВИВАЛЕНТНЫ, или имеютОДИНАКОВУЮ МОЩНОСТЬ.
Для таких множеств принята запись :
Читают: «Множество Aэквивалентно множествуB».
Мощность конечных множеств есть численная характеристика, совпадающая с числом элементов множества. А «мощность» бесконечных множеств есть характеристика сравнительная, вытекающая из возможности установить взаимно однозначное соответствие между парами различных множеств.
Рассмотрим примеры.
1. Пусть A = N–множество натуральных чисел, аB–множество их квадратов.
Установим следующее взаимно однозначное
соответствие между этими множествами
(см. таблицу 10). Мы видим, что это возможно.
таблицу 10). Мы видим, что это возможно.
Таблица 10. Взаимно однозначное соответствие между
04. Основные операции над множествами
|
Рис. 2.2. |
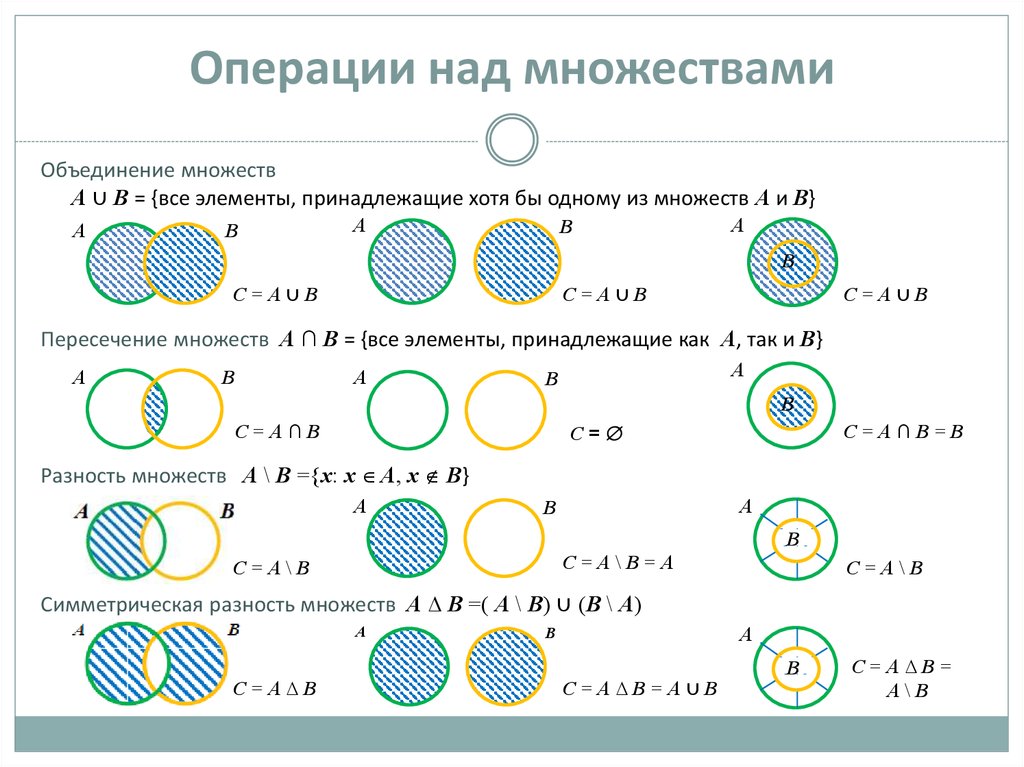
Суммой или Объединением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из заданных множеств. Эта операция над множествами обозначается знаком . |
|
Рис. 2.3. |
Произведением или пересечением двух или произвольного (даже бесконечного) числа заданных множеств называется множество, состоящее из всех элементов, принадлежащих каждому из заданных множеств. |
Два множества называются Непересекающимися (или расчлененными) если . Практический интерес представляют разбиения множества на взаимно непересекающиеся подмножества (эту задачу иногда называются Классификацией). Разбиением множества называется такая расчлененная система непустых подмножеств множества , что каждый элемент множества является элементом некоторого единственного множества этой системы. Возможность разбиения множества на непересекающиеся подмножества зависит от признака, по которому производится разбиение.
|
Рис. 2.4. |
Разностью множеств и или Дополнением до называется множество, состоящее только из тех элементов , которые не входят в . |
|
Рис. 2.5. |
Часто все рассматриваемые множества считают подмножествами одного основного множества . В таком случае разность (дополнение до ) обозначают, как , а операцию называют взятием дополнения. |
|
Рис. 2.6. |
Симметрической разностью множеств и называется множество : . Обозначается симметрическая разность: или . |
Для подмножеств данного множества выполняются следующие законы:
· Закон коммутативности (переместительный закон):
; ;
· Закон ассоциативности (сочетательный закон) для любой тройки множеств , и :
;
;
· Закон дистрибутивности (распределительный закон) для любой тройки множеств , и :
;
;
· ; ;
· ;;
· ; ;
· ;
· ;
· ; ;
· ; ;
· ; ;
· ; .
Если операции объединения множеств поставить в соответствие операцию сложения чисел, операции пересечения множеств – операцию умножения, универсальному множеству – единицу, а пустому множеству – ноль, то возникает аналогия между множествами и числами. Операции объединения и пересечения множеств, как и действия над действительными числами, подчиняются законам коммутативности, ассоциативности и дистрибутивности. Можно также провести аналогию между свойствами логических операций, где логической эквивалентности соответствует операция равенства, а операциям конъюнкции и дизъюнкции – операции объединения и пересечения.
Свойства фигурируют попарно таким образом, что каждое получается из соседнего заменой на , на и наоборот. Такие выражения называются Двойственными друг другу.
Принцип двойственности. Для любого тождества множеств двойственное ему выражение также является тождеством.
Очевидно, что операция Разность не обладает свойствами коммутативности и ассоциативности, в то же время операция Симметрическая разность и коммутативна, и ассоциативна.
Большое значение в современной математике имеет множественная операция Декартово произведение. Если заданы два множества и , то из их элементов можно составить упорядоченные пары, взяв сначала какой-либо элемент первого множества, а затем – элемент второго множества. Декартовым произведением двух исходных множеств и называется множество , составленное из упорядоченных пар (). Декартово произведение множеств и обозначается .
Очевидно, что и ‑ различные множества, т. е. операция декартова произведения не коммутативна, но, в то же время, она обладает свойством ассоциативности.
| < Предыдущая | Следующая > |
|---|
действие в nLab
Пропустить навигационные ссылки | Домашняя страница | Все страницы | Последние версии | Обсудить эту страницу |
Действияэта запись о понятии действия в алгебре (одного алгебраического объекта на другой объект).
О понятии функционала действия в физике см. там.
Контекст
Алгебра
высшая алгебра
универсальная алгебра
Алгебраические теории
алгебраическая теория / 2-алгебраическая теория / (∞,1)-алгебраическая теория
монада / (∞,1)-монада
операда / (∞,1)-операда
Алгебры и модули
алгебра над монадой
∞-алгебра над (∞,1)-монадой
алгебра над алгебраической теорией
∞-алгебра над (∞,1)-алгебраической теорией
алгебра над операдой
∞-алгебра над (∞,1)-операдой
- действие
, действие ∞
представление, ∞-представление
- модуль
, ∞-модуль
ассоциированный пучок, ассоциированный ∞-пучок
Высшие алгебры
моноидальная (∞,1)-категория
симметричная моноидальная (∞,1)-категория
моноид в (∞,1)-категории
коммутативный моноид в (∞,1)-категории
симметричная моноидальная (∞,1)-категория спектров
разбить произведение спектров
симметричное моноидальное произведение спектров
кольцевой спектр, модульный спектр, алгебраический спектр
A-∞ алгебра
- Кольцо A-∞, пространство A-∞
C-∞ алгебра
кольцо E-∞, алгебра E-∞
∞-модуль, (∞,1)-расслоение модулей
теория мультипликативных когомологий
L-∞ алгебра
- теория деформации
Презентации категории моделей
модельная структура на симплициальных Т-алгебрах / гомотопических Т-алгебрах
структура модели на операдах
Структура моделина алгебрах над операдой
Геометрия на формальных дуальных алгебрах
Двойственность Исбелла
производная геометрия
Теоремы
Гипотеза Делиня
гипотеза раскрытия петли
моноидальный корреспонденция Долд-Кан
Изменить эту боковую панель
Теория представлений
Теория представлений
геометрическая теория представлений
Ингредиенты
- линейная алгебра, алгебра, высшая алгебра
Определения
представление, 2-представление, ∞-представление
группа, ∞-группа
групповая алгебра, алгебраическая группа, алгебра Ли
векторное пространство, n-векторное пространство
аффинное пространство, симплектическое векторное пространство
действие, ∞-действие
- модуль
, эквивариантный объект
бимодуль, эквивалент Морита
индуцированное представление, взаимность Фробениуса
гильбертово пространство, банахово пространство, преобразование Фурье, функциональный анализ
- Орбита
, коприсоединенная орбита, форма Киллинга
унитарное представительство
геометрическое квантование, когерентное состояние
цоколь, колчан
модульная алгебра, комодульная алгебра, действие Хопфа, измерение
Геометрическая теория представлений
D-модуль, извращенная связка,
Группа Гротендика, лямбда-кольцо, симметрическая функция, формальная группа
главное расслоение, торсор, векторное расслоение, алгеброид Атьи Ли
геометрическая теория функций, группоидификация
Категория Эйленберга-Мура, алгебра над операдой, категория, скрещенный модуль
теоремы реконструкции
Теоремы
Теорема Бореля-Вейля-Ботта
Be?linson-Bernstein локализация?
Теория Каждана-Люстига
Теорема разложения BBDG
Изменить эту боковую панель
Теория моноидов
Теория моноидов по алгебре:
моноид, бесконечность-моноид
моноидный объект, моноидный объект в категории (бесконечность, 1)
- полукольцо, установка, кольцо, ассоциативная алгебра с единицей
Пн, CПн
гомоморфизм моноидов
субмоноид, частный моноид?
делитель, кратный?, частное?
обратный элемент, единица, неприводимый элемент
идеально в моноиде
главный идеал в моноиде
коммутативный моноид
- тензорное произведение коммутативных моноидов
сокращаемый моноид
НОД моноид
уникальный моноид факторизации
моноид Безу
главный идеальный моноид
группа, абелева группа
абсорбирующий моноид
делитель нуля
цельный моноид
свободный моноид, свободный коммутативный моноид
графический моноид
моноидная затворная группа
- Модуль
поверх моноида
локализация моноида
завершение группы
моноид эндоморфизма
суперкоммутативный моноид
Изменить эту боковую панель
- Идея
- Определения
- Действия группы
- Действия моноида
- Действия категории
- Действия группового объекта
- Действия объекта моноида
- Действия набора
- Примеры
- Связанные понятия
- Каталожные номера
- Групповые действия
Идея
Существуют различные варианты понятия чего-то действующего на что-то другое. Все они тесно связаны.
Все они тесно связаны.
Простейшая концепция действия предполагает, что один набор XX действует на другой набор YY, и такое действие задается функцией от произведения XX на YY на YY
act:X×Y→Y. действие\двоеточие X \times Y \to Y \,.
Для фиксированного x∈Xx \in X это дает эндофункцию act(x,−):Y→Yact(x,-) \colon Y \to Y и, следовательно, некоторое «преобразование» или «действие» на YY. Таким образом, все XX действует на YY. 9Y, чтобы иметь структуру кольца/алгебры, YY должен быть своего рода абелевой группой или векторным пространством с действием линейными функциями; тогда действие вызывается также модулем или представлением .
В терминах некарриванного действия X×Y→YX\times Y\to Y условие «сохранения», грубо говоря, говорит о том, что последовательное действие с двумя элементами в XX равносильно сначала их умножению, а затем действию с результатом:
действие(x2,действие(x1,y))=действие(x2⋅x1,y).
действие (x_2, действие (x_1, y)) = действие (x_2 \ cdot x_1, y)
\,.
Точнее, это условие для левого действия ; правильное действие определяется двойственно в терминах отображения Y×X→YY\times X\to Y. Если XX не имеет алгебраической структуры или если его релевантная структура коммутативна, то между ними нет существенной разницы; но в целом они могут быть совершенно разными.
Это свойство действия также часто можно отождествить со свойством функтора: оно характеризует функтор от развертывания цикла BX\mathbf{B}X моноида XX до категории (такой как Set), объектом которой является YY. Различие между левыми и правыми действиями отражается в дисперсии; действие слева дает ковариантный функтор, тогда как действие справа выражается через контравариантность.
Таким образом, практически каждый вид функтора, n-функтор и обогащенный функтор можно рассматривать как определяющий обобщенный вид действия. Этот взгляд на действия особенно распространен в теории обогащенных категорий, где, например, коэнды можно рассматривать как производящие тензорные произведения действий в этом общем функторном смысле.
При построении Гротендика (или одном из его вариантов) эта перспектива превращается в перспективу, где действием XX является некоторое расслоение Y/XY/X над BX\mathbf{B}X, слоем которого является YY:
Y⟶Y/X↓BX. \множество{ Y &\longrightarrow& Y/X \\ && \Кнопка «Стрелка вниз \\ && \mathbf{B}X } \,.
Здесь тотальное пространство Y/XY/X этого расслоения обычно является «слабым» фактором (например, гомотопическим фактором) действия, откуда и обозначение. Если рассматривать BX\mathbf{B}X как классификационное пространство для XX-универсального основного расслоения, то это расслоение Y/X→BXY/X \to \mathbf{B}X является YY-расслоением, которое ассоциировано через действие к этому универсальному пакету. Подробнее об этом взгляде на действия см. в разделе 9.0006 ∞-действие .
Определения
Действия группы
Действие группы GG на объект SS в категории 𝒞\mathcal{C} является представлением GG на SS, то есть гомоморфизмом групп ρ:G→Aut (S)\rho \colon G \to Aut(S), где Aut(S)Aut(S) — группа автоморфизмов SS в 𝒞\mathcal{C}.
Групповые действия, особенно непрерывные действия на топологических пространствах, также известны как групп преобразований (начиная с Klein 1872, Sec. 1, см. также Koszul 65 Bredon 72, tom Dieck 79, Том Дик 87). В качестве альтернативы, если группа GG, которая действует, понята, можно назвать (Бредон 72, гл. II) пространство XX, снабженное действием GG, топологическим G-пространством (или G-множеством , G-многообразием ). и др., в зависимости от обстоятельств).
Как указано выше, более абстрактное, но эквивалентное определение рассматривает группу GG как категорию (группоид), обозначаемую BG\mathbf{B} G, с единственным объектом *\ast. Тогда действие GG в категории CC эквивалентно функтору вида
ρ:БГ→𝒞 \rho \colon \mathbf{B} G \to \mathcal{C}
Здесь объект SS предыдущего определения есть ρ(*)\rho(\ast) этого единственного объекта.
Конкретно, если 𝒞\mathcal{C} является категорией, подобной Set, то действие эквивалентно функции
G×S⟶S(g,s)↦ρ(g)(s) \множество{ G \times S &\longrightarrow& S \\ (g,s) &\mapsto& \rho(g)(s) }
, удовлетворяющее свойству действия
(1)∀g1,g2,sρ(g1⋅g2)(s)=ρ(g1)(ρ(g2)(s))
\занижено{
г_1, г_2, с
}{\для всех}
\;\;\;
\rho(g_1 \cdot g_2)(s)
знак равно
\ро(g_1)
\большой(
\ро(г_2)(ы)
\большой)
9{\mathbf{B} М}. Когда CC является SetSet, это называется MSet.
Когда CC является SetSet, это называется MSet.
Рассмотрение этого в расширенной теории категорий дает внутреннее понятие объектов действия .
Действия категории
Можно также 1 определить действие категории DD на категорию CC как функтор от DD до CC, но обычно его называют просто функтором.
Другая точка зрения на ту же ситуацию: (малая) категория — это монада в категории интервалов в Set. Действие категории является алгеброй для этой монады. См. действие категории в наборе.
С другой стороны, действие моноидальной категории (а не в моноидальной категории, как указано выше) называется актегорией. Это понятие можно, конечно, расширить до действий в моноидальной бикатегории, где в случае CatCat как моноидальной бикатегории оно специализируется на понятии актегории.
Действия группового объекта
Предположим, у нас есть категория CC с бинарными произведениями и конечным объектом **. Существует альтернативный способ просмотра групповых действий в Set, так что мы можем говорить о действии группового объекта GG в CC на объект XX из CC. 9A, в Set гомоморфизм групп
9A, в Set гомоморфизм групп
α:G→Aut(X)\alpha: G\to Aut(X)
соответствует функции
act:G×X→Xact: G\times X\to X
, который будет иметь различные свойства, кодирующие, что α\alpha был гомоморфизмом групп:
act(g1g2,x)=act(g1,act(g2,x))act(g_1g_2,x) = act(g_1, act(g_2,x))
act(1,x)=xact(1,x) = x
и их можно закодировать схематически.
Благодаря этому мы можем определить действие группового объекта GG в CC на объект XX из CC как морфизм
act:G×X→Xact: G\times X\to X
удовлетворяющие условиям, что некоторые диаграммы (предоставленные читателю), кодирующие эти два правила, коммутируют.
Преимущество этого состоит в том, что не требуется, чтобы категория CC имела внутренние групповые объекты автоморфизмов для всех рассматриваемых объектов.
Например, только локально компактные топологические пространства имеют группы топологических автоморфизмов с хорошим поведением, и поэтому действия топологических пространств на топологических пространствах должны быть либо ограничены действиями на локально компактных пространствах, либо определены как выше.
В качестве другого примера, в категории проконечных групп, рассматриваемых как топологические группы, не все объекты имеют группы автоморфизмов, для которых естественная топология проконечна. Таким образом, проконечные групповые действия на (основном топологическом пространстве) проконечной группы должны быть либо заданы в этой форме, либо ограничены действиями на проконечных группах, для которых группа автоморфизмов естественно проконечна.
Действия моноидного объекта
Предположим, у нас есть категория CC с бинарными произведениями и конечным объектом **. Существует альтернативный способ просмотра действий моноида в Set, так что мы можем говорить о действии объекта моноида MM в CC на объект XX из CC. 9A, в Set моноидному гомоморфизму
α:M→End(X)\alpha: M\to End(X)
соответствует функция
act:M×X→Xact: M\times X\to X
, который будет иметь различные свойства, кодирующие, что α\alpha был гомоморфизмом моноидов:
act(m1m2,x)=act(m1,act(m2,x))act(m_1m_2,x) = act(m_1, act(m_2,x))
act(1,x)=xact(1,x) = x
и их можно закодировать схематически.
Из-за этого мы можем определить действие моноидного объекта MM в CC на объект XX из CC как морфизм
act:M×X→Xact:M\times X\to X
удовлетворяющие условиям, что некоторые диаграммы (предоставленные читателю), кодирующие эти два правила, коммутируют.
Преимущество этого состоит в том, что не требуется, чтобы категория CC имела внутренние моноидные объекты эндоморфизма для всех рассматриваемых объектов.
Действия множества
Действие множества на множество было определено выше; он состоит из функции act:X×Y→Yact: X\times Y\to Y. Это может быть эквивалентно представлено колчаном с YY в качестве вершины, с его ребрами, помеченными элементами XX, и такой, что каждая вершина имеет с каждой меткой выходит ровно одна стрелка. (Это своего рода «конструкция Гротендика».) Это также то же самое, что и простой (непрерывный) детерминированный автомат, где YY — множество состояний, а XX — множество входов.
То, что действие является типом колчана, помеченного ребром, можно увидеть, явно задав функции проекции произведения, p1p_1 и p2p_2, X×YX\×Y. \quad}{\leftarrow}X\times Y\underoverset{\quad act \quad}{p_2}{\rightrightarrows}Y
\quad}{\leftarrow}X\times Y\underoverset{\quad act \quad}{p_2}{\rightrightarrows}Y
Форма этой диаграммы соответствует форме ребра, помеченного колчаном:
Labels←labelEdges⇉ targetsourceVerticesLabels\overset{\quad label \quad}{\leftarrow}Ребра\underoverset{\quad target \quad}{source}{\rightrightarrows}Вершины 9{*}_1, у)
Действие множества XX само по себе также называется бинарной операцией , а множество XX называется магмой .
Примеры
Представление — это «линейное действие».
В симплектической геометрии рассматриваются гамильтоновы действия.
В топологии: топологическое G-пространство
действие круга
групповое действие на н-сфере
(…)
объект действия
действие , ∞-действие,
сопряженное действие, сопряженное действие
диагональное действие
переходное действие, свободное действие, обычное действие
правильное действие, правильное прерывистое действие
сотрудничество
представление, ∞-представление
- модуль
, ∞-модуль
монада действия
ассоциированный пучок, ассоциированный ∞-пучок
частное, частное стек, частное тип
теория представлений, теория инвариантов
эквивариантная гомотопическая теория
- Структура модели Бореля
биактион
Ссылки
Групповые действия
О групповых действиях, в основном в топологических пространствах, следовательно, в виде топологических G-пространств:
Историческое происхождение:
Felix Klein, Vergleichende Betrachtungen über neuere geometrische Forschungen (1872) Mathematische Annalen, том 43, страницы 63–100 1893 (doi: 10.
 1007/BF01446615)
1007/BF01446615)Английский перевод MW Haskell:
Сравнительный обзор последних исследований по геометрии , Bull. Нью-Йоркская математика. соц. 2, (1892-1893), 215-249. (euclid: 1183407629, версия LaTeX, перепечатанная Nitin C. Rughoonauth: arXiv: 0807.3161)
Счета учебников:
Глен Бредон, Введение в компактные группы преобразования , Academic Press 1972 (ISBN 9780080873596
, pdf)
Tammo tom Dieck, Группы преобразований и теория представлений , Lecture Notes in Mathematics 766, Springer 1979 (doi:10.1007/BFb0085965)
Tammo tom Dieck, Transformation Groups , de Gruyter 1987 (doi:10.1515/9783110858372)
Конспект лекций:
Жан-Луи Кошул, Лекции о группах преобразований , Институт Тата, 1965 (pdf, pdf)
Патрик Моранди, Групповые действия (pdf)
Одним из примеров такого относительно редкого использования является Уильям Лоувер: Качественные различия между некоторыми топосами обобщенных графов , Contemporary Mathematics 92 (1989), в которых этот смысл действия обычно используется.
 ↩
↩
Последняя редакция: 25 мая 2022 г., 02:16:28. См. историю этой страницы для получения списка всех вкладов в нее.
Точные групповые действия группы на наборе
Точные групповые действия группы на наборе
Fold Содержание Верные групповые действия группы на наборе Пример 1 Пример 2 Пример 3 |
| Определение: Пусть $(G, \cdot)$ — группа, а $A$ — множество. Пусть $(g, a) \to ga$ — (левое) групповое действие группы $G$ на множестве $A$. Это групповое действие называется Верным , если соответствующий ассоциированный гомоморфизм представления перестановок $\varphi : G \to S_A$ определяется для всех $g \in G$ как $\varphi(g) = \sigma_g$ (где $\ sigma_g : A \to A$ определяется для всех $a \in A$ равенством $\sigma_g(a) = ga$) является инъективным. |
Другими словами, левое (или правое) групповое действие является точным, если $\varphi : G \to S_A$ является групповым мономорфизмом.
Теперь мы рассмотрим несколько примеров групповых действий, которые являются верными/неверными.
Пример 1
На странице Тривиальное групповое действие группы на множестве мы определили тривиальное групповое действие группы $(G, \cdot)$ на множество $A$ для всех $g \in G$ и для всех $a \in A$ через $(g, a) \to a$. Мы отметили, что соответствующий ассоциированный гомоморфизм представления перестановок $\varphi : G \to S_A$ на самом деле является гомоморфизмом $G$ на тривиальную подгруппу $\{ \mathrm{id}_A \}$ группы $S_A$.
Если $(G, \cdot)$ тривиальная группа, то тривиальное групповое действие $G$ на множестве $A$ является точным.
Если $(G, \cdot)$ не является тривиальной группой, то тривиальное групповое действие $G$ на множестве $A$ НЕ является точным.
Пример 2
На странице Левое и правое регулярное групповое действие группы на самой себе мы определили левое регулярное групповое действие группы $(G, \cdot)$ на множество $A = G$ для всех $ g \in G$ и для всех $a \in A$ $(g, a) = g \cdot a$.
Для каждого $g \in G$ пусть $\sigma_g : A \to A$ определяется для всех $a \in A$ равенством $\sigma_g(a) = g \cdot a$. Пусть $\varphi : G \to S_A = S_G$ — соответствующий ассоциированный гомоморфизм представления подстановки. Мы утверждаем, что регулярное слева представление группы $G$ на множестве $G$ является точным, т. е. $\varphi$ является групповым мономорфизмом.
Пусть $g_1, g_2 \in G$ и $\varphi(g_1) = \varphi(g_2)$. Тогда $\sigma_{g_1} = \sigma_{g_2}$. То есть для всех $a \in A = G$ имеем:
(1)
\begin{align} \quad \sigma_{g_1}(a) &= \sigma_{g_2}(a) \\ \quad g_1 \cdot a &= g_2 \cdot a \end{align}
закон отмены для групп, мы имеем, что $g_1 = g_2$. Так что $\varphi$ действительно инъективен, значит, регулярное слева групповое действие является точным. Аналогичный аргумент показывает, что правильное регулярное групповое действие также является точным.
Пример 3
На странице A Group Action of the Symmetric Group SX на странице Set X мы определили групповое действие симметрической группы $S_X$ на множестве $X$ для всех $\sigma \in S_X$ и для все $x \in X$ на $(\sigma, x) \to \sigma(x)$.

 Эта операция над множествами обозначается знаком . Если , то множества и называются непересекающимися.
Эта операция над множествами обозначается знаком . Если , то множества и называются непересекающимися. Эта операция над множествами обозначается знаком .
Эта операция над множествами обозначается знаком . О понятии функционала действия в физике см. там.
О понятии функционала действия в физике см. там.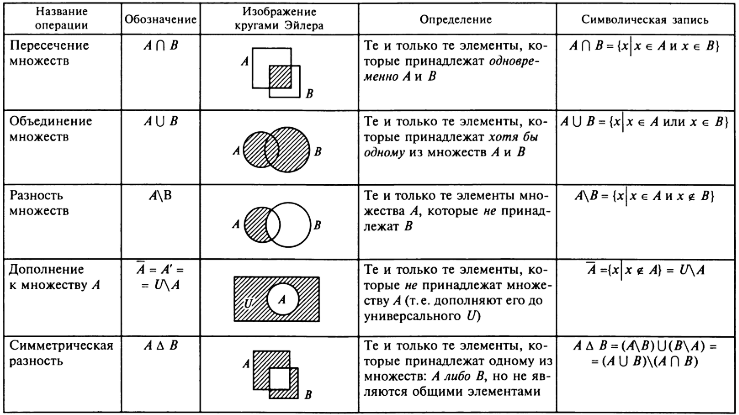 1007/BF01446615)
1007/BF01446615) ↩
↩