Система 3 уравнений с 4 неизвестными – Как решить систему с тремя неизвестными 🚩 вся правда о мужчинах книга 🚩 Математика

Как решить систему с тремя неизвестными 🚩 вся правда о мужчинах книга 🚩 Математика

14 июня 2011

Автор КакПросто!

Линейная система с тремя неизвестными имеет несколько способов решения. Найти решение системы можно с помощью правила Кремера через определители, методом Гаусса или используя простой способ подстановки. Метод подстановки является основным для решения систем линейных уравнений небольшого порядка. Он заключается в поочередном выражении из каждого уравнения системы одной неизвестной переменной, подстановки ее в следующее уравнение и упрощение получаемых выражений.

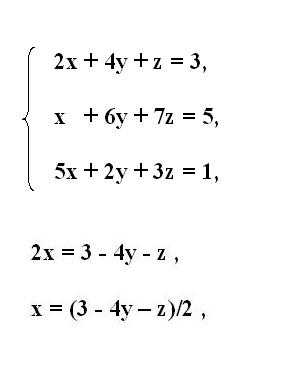
Статьи по теме:

Инструкция

Запишите исходную систему уравнений третьего порядка. Из первого уравнения системы выразите первую неизвестную переменную х. Для этого перенесите члены, содержащие другие переменные за знак равенства. Перенесенным членам поменяйте знак на противоположный. Если при множителе с выражаемой переменной присутствует коэффициент отличный от единицы, поделите на его значение все уравнение. Таким образом, вы получите переменную х, выраженную через остальные члены уравнения.

Подставьте во второе уравнение вместо х то выражение, которое вы получили из первого уравнения. Упростите полученную запись, произведя сложение или вычитание подобных членов. Аналогично предыдущему шагу выразите из второго уравнения следующую неизвестную переменную у. Также перенесите все другие члены за знак равенства и поделите все уравнение на коэффициент при у.

В последнее третье уравнение подставьте вместо двух неизвестных переменных х и у выраженные значения из первого и второго уравнений системы. Причем в выражении х также замените переменную у. Упростите полученное уравнение. В нем в качестве неизвестной величины останется лишь третья переменная z. Выразите ее из уравнения, как описано выше, и высчитайте ее значение.

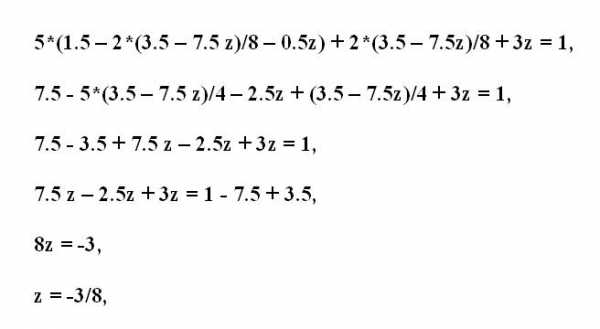
В выражение у из второго уравнения подставьте известное значение переменной z. Подсчитайте значение переменной у. Далее в выражение переменной х подставьте значения переменных у и z. Вычислите х. Запишите полученные значения х, у и z – это и есть решение системы с тремя неизвестными.

Система из трех уравнений с тремя неизвестными может и не иметь решений, несмотря на достаточное количество уравнений. Можно пытаться решить ее с помощью метода подстановки или с помощью метода Крамера. Метод Крамера помимо решения системы позволяет оценить, является ли система разрешимой, до того, как отыскать значения неизвестных.

Инструкция

Метод подстановки заключается в последовательном выражении одной неизвестной через две других и подстановке полученного результата в уравнения системы. Пусть дана система из трех уравнений в общем виде:

a1x + b1y + c1z = d1

a2x + b2y + c2z = d2

a3x + b3y + c3z = d3

Выразите из первого уравнения x: x = (d1 — b1y — c1z)/a1 — и подставьте во второе и третье уравнения, затем из второго уравнения выразите y и подставьте в третье. Вы получите линейное выражение для z через коэффициенты уравнений системы. Теперь идите «обратно»: подставьте z во второе уравнение и найдите y, а затем z и y подставьте в первое и найдите x. Процесс в общем виде отображен на рисунке до нахождения z. Дальше запись в общем виде будет слишком громоздкой, на практике, подставив числа, вы довольно легко найдете все три неизвестные.

Метод Крамера заключается в составлении матрицы системы и вычислении определителя этой матрицы, а также еще трех вспомогательных матриц. Матрица системы составляется из коэффициентов при неизвестных членах уравнений. Столбец, содержащий числа, стоящие в правых частях уравнений, называется столбцом правых частей. В матрице системы он не используется, но используется при решении системы. Пусть, как и раньше, дана система из трех уравнений в общем виде:

a1x + b1y + c1z = d1

a2x + b2y + c2z = d2

a3x + b3y + c3z = d3

Тогда матрицей этой системы уравнений будет следующая матрица:

| a1 b1 c1 |

| a2 b2 c2 |

| a3 b3 c3 |

Прежде всего найдите определитель матрицы системы. Формула нахождения определителя: |A| = a1b2c3 + a3b1c2 + a2b3c1 — a3b2c1 — a2b1c3 — a1b3с2. Если он не равен нулю, то система разрешима и имеет единственное решение. Теперь нужно найти определители еще трех матриц, которые получаются из матрицы системы путем подставления столбца правых частей вместо первого столбца (эту матрицу обозначим Ax), вместо второго (Ay) и третьего (Az). Вычислите их определители. Тогда x = |Ax|/|A|, y = |Ay|/|A|, z = |Az|/|A|.

Источники:

• Системы трёх линейных уравнений с тремя неизвестными

Уравнением называют аналитическую запись задачи о разыскании значений аргументов, при которых значения двух данных функций равны. Система – это совокупность уравнений, для которых требуется найти значения неизвестных, удовлетворяющих одновременно всем этим уравнениям. Так как успешное решение задачи невозможно без правильно составленной системы уравнений, необходимо знать основные принципы составления подобных систем.

Инструкция

Во-первых, определите неизвестные величины, которые требуется найти в данной задаче. Обозначьте их через переменные. Наиболее распространенные переменные, используемые при решении систем уравнений, это x, y и z. В отдельных задачах удобнее применять общепринятые обозначения, например, V для обозначения объема, или a для обозначения ускорения. Пример. Пусть гипотенуза прямоугольного треугольника равна 5 м. Необходимо определить катеты, если известно, что после того, как один из них увеличить в 3 раза, а другой в 4, то сумма их длин составит 29 м. Для данной задачи необходимо обозначить длины катетов через переменные x и y.

Далее внимательно читайте условие задачи и связывайте неизвестные величины уравнениями. Иногда взаимосвязь между переменными будет очевидна. Например, в приведенном выше примере, катеты связывает следующее соотношение.Если «один из них увеличить в 3 раза» (3 * x), «а другой в 4» (4 * y), «то сумма их длин составит 29 м»: 3 * x + 4 * y = 29.

Другое уравнение для данной задачи менее очевидно. Оно кроется в условии задаче о том, что дан прямоугольный треугольник. Значит, можно применить теорему Пифагора. Т.е. x^2 + y^2 = 25. Итого получается два уравнения:
3 * x + 4 * y = 29 и x^2 + y^2 = 25.Для того чтобы система имела однозначное решение, количество уравнений должно быть равно количеству неизвестных. В приведенном примере имеется две переменных и два уравнения. Значит, система имеет одно конкретное решение: x = 3 м, y = 4 м.

При решении физических задач «неочевидные» уравнения могут заключаться в формулах, связывающих физические величины. Например, пусть в условии задачи необходимо найти скорости пешеходов Va и Vb. Известно, что пешеход A проходит расстояние S на 3 часа медленнее, чем пешеход B. Тогда можно составить уравнение, воспользовавшись формулой S = V * t, где S – это расстояние, V – скорость, t – время: S / Va = S / Vb + 3. Здесь S / Va — это время, за которое пройдет заданное расстояние пешеход A. S / Vb — время, за которое пройдет заданное расстояние пешеход B. По условию это время на 3 часа меньше.

Видео по теме

Обратите внимание

Все уравнения в системе должны поставлять дополнительную независимую от других уравнений информацию. Иначе система будет недоопределена и однозначного решения найти будет не возможно.

Полезный совет

После решения системы уравнений подставьте найденные значения в исходную систему и проверьте, что они удовлетворяют всем уравнениям.

Само по себе уравнение с тремя неизвестными имеет множество решений, поэтому чаще всего оно дополняется еще двумя уравнениями или условиями. В зависимости от того, каковы исходные данные, во многом будет зависеть ход решения.

Вам понадобится

• — система из трех уравнений с тремя неизвестными.

Инструкция

Если два из трех уравнений системы имеют лишь две неизвестные из трех, попытайтесь выразить одни переменные через другие и подставить их в уравнение с тремя неизвестными. Ваша цель при этом – превратить его в обычное уравнение с одной неизвестной. Если это удалось, дальнейшее решение довольно просто – подставьте найденное значение в другие уравнения и найдите все остальные неизвестные. Некоторые системы уравнений можно решить вычитанием из одного уравнения другого. Посмотрите, нет ли возможности умножить одно из выражений на число или переменную так, чтобы при вычитании сократились сразу две неизвестные. Если такая возможность есть, воспользуйтесь ею, скорее всего, последующее решение не составит труда. Не забывайте, что при умножении на число необходимо умножать как левую часть, так и правую. Точно также, при вычитании уравнений необходимо помнить о том, что правая часть должна также вычитаться.

Если предыдущие способы не помогли, воспользуйтесь общим способом решений любых уравнений с тремя неизвестными. Для этого перепишите уравнения в виде а11х1+a12х2+а13х3=b1, а21х1+а22х2+а23х3=b2, а31х1+а32х2+а33х3=b3. Теперь составьте матрицу коэффициентов при х (А), матрицу неизвестных (Х) и матрицу свободных членов (В). Обратите внимание, умножая матрицу коэффициентов на матрицу неизвестных, вы получите матрицу, равную матрице свободных членов, то есть А*Х=В.

Найдите матрицу А в степени (-1) предварительно отыскав определитель матрицы, обратите внимание, он не должен быть равен нулю. После этого умножьте полученную матрицу на матрицу В, в результате вы получите искомую матрицу Х, с указанием всех значений.

Найти решение системы из трех уравнений можно также с помощью метода Крамера. Для этого найдите определитель третьего порядка ∆, соответствующий матрице системы. Затем последовательно найдите еще три определителя ∆1, ∆2 и ∆3, подставляя вместо значений соответствующих столбцов значения свободных членов. Теперь найдите х: х1=∆1/∆, х2=∆2/∆, х3=∆3/∆.

Источники:

• решений уравнений с тремя неизвестными

www.kakprosto.ru

4.4 Система m уравнений с n неизвестными

Случай, когда число уравнений mбольше числа переменныхn, путем последовательного исключения неизвестных из уравнений приводится к случаюm=nилиmn. Первый случай рассмотрен ранее.

Во втором случае, когда число уравнений меньше числа неизвестных mnи уравнения независимы, выделяютсяm основных переменныхи (n—m)неосновных переменных. Основными являются переменные удовлетворяющие условию: определитель, составленный из коэффициентов при этих переменных, не равен нулю. Основными могут быть различные группы переменных. Общее количество таких групп Nравно числу сочетаний изnэлементов поm:

.

Если система имеет хотя бы одну группу основных переменных, то эта система является

неопределенной, то есть имеет множество решений.

Если система не имеет ни одной группы основных переменных, то система является несовместной, то есть не имеет ни одного решения.

В том случае, когда система имеет множество решений, среди них выделяют базисное решение.

Базисным решениемназывают такое решение, в котором неосновные переменные равны нулю. У системы имеется не более чембазисных решений.

Решения системы делятся на допустимыеинедопустимые.

Допустимыминазывают такие решения, у которых значения всех переменных неотрицательны.

Если хотя бы одно значение переменной отрицательно, то решение называют недопустимым.

Пример 4.5

Найти базисные решения системы уравнений

Найдем число базисных решений

.

Итак, среди множества решений системы есть не более трех базисных. Выделим две основные переменные среди трех. Предположим, что это х₁их₂. Проверим определитель из коэффициентов при них

.

Так как этот определитель не равен нулю, то переменные х₁,х₂являются основными.

Теперь положим, что х₃=0. Тогда получим систему в виде

Решим ее по формулам Крамера:

, .

Итак, первое базисное решение имеет вид

х₁=1,х₂=0,х₃=0 .

Проверим теперь на принадлежность к основным переменные х₁

их₃.

.

Получим, что х₁их₃— вторая группа основных переменных. Положимх₂=0 и решим систему

, .

Второе базисное решение имеет вид

х₁=1,х₂=0,х₃=0.

Теперь проверим на принадлежность к основным переменные х₂их₃.

то есть переменные х₂их₃неосновные. Итак, всего у данной системы оказалось два базисных решения. Оба эти решения допустимые.

Условие совместности системы mлинейных уравненийcnпеременными дается с помощью понятия ранг матрицы.

Ранг матрицы– это число равное наибольшему порядку минора отличного от нуля.

Для матрицы А

минором k-ого порядкаслужит определитель, составленный из элементов любыхkстрок иkстолбцов.

Например,

Пример 2

Найти ранг матрицы

Вычислим определитель матрицы

Для этого первую строку умножим на (-4) и сложим со второй строкой, затем первую строку умножим на (-7) и сложим с третей строкой, в результате получим определитель

Т.к. строки полученного определителя пропорциональны, то .

Отсюда видно, что минор 3-его порядка равен 0, а минор 2-ого порядка не равен 0.

Следовательно ранг матрицы r=2.

Расширенная матрицасистемы имеет вид

Теорема Кронекера — Капелли

Для того, чтобы линейная система была совместной необходимо и достаточно, чтобы ранг расширенной матрицы был равен рангу основной матрицы .

Если _,то система несовместна.

Для совместной системы линейных уравнений возможны три случая:

1)Если , то система ЛУ имеет (m-r) линейно зависимых уравнений, их можно исключить из системы;

2) Если , то система ЛУ имеет единственное решение;

3) Если , то система ЛУ имеет множество решений

studfiles.net

ГЛАВА 4. РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

 

Система линейных уравнений

 

Системой m линейных уравнений с n неизвестными называется система m алгебраических уравнений первой степени вида

(4.1.1)

где — неизвестные, подлежащие определению;

— числа, называемые коэффициентами при неизвестных;

— числа, называемые свободными членами.

Решением системы уравнений (4.1.1) называется совокупность n чисел таких, что если в каждое уравнение системы вместо неизвестных подставить эти числа ( вместо , вместо вместо ), то все уравнения обратятся в тождества.

Если система линейных уравнений (4.1.1) имеет хотя бы одно решение, то она называется совместной. В противном случае система называется несовместной.

Совместная система, имеющая единственное решение, называется определенной, а система, имеющая более одного решения – неопределенной.

Две системы линейных уравнений называются эквивалентными, если любое решение каждой из них является одновременно решением и другой системы.

Две произвольные несовместные системы считаются эквивалентными.

Системе линейных уравнений (4.1.1) поставим в соответствие матрицу и расширенную матрицу

,

полученную присоединением к матрице А столбца свободных членов.

 

Методы решения системы n линейных уравнений с n неизвестными

 

Рассмотрим систему n линейных уравнений с n неизвестными

(4.2.1)

 

Определитель |A| матрицы А называется определителем системы (4.2.1).

Теорема Крамера. Если определитель |A| системы (4.2.1) отличен от нуля, то система совместна и имеет единственное решение.

Доказательство. Пусть система (4.2.1) совместна и — одно из ее решений. Тогда получим n тождеств:

 

(4.2.2)

 

Умножим обе части первого из равенств (4.2.2) на алгебраическое дополнение , обе части второго равенства умножим на алгебраическое дополнение и т.д. и обе части n-ого равенства – на . Складывая левые и правые части полученных выражений, придем к следующему равенству:

 

(4.2.3)

 

Коэффициент при равен определителю |A| системы (4.2.1), коэффициент при равен нулю, а правая часть равенства (4.2.3) является определителем, полученным из определителя |A| путем замены j-го столбца столбцом свободных членов.

Обозначим данный определитель через

Тогда равенство (4.2.3) примет вид: , откуда

(4.2.4)

 

Из формулы (4.2.4) следует, что если система (4.2.1) совместна, то она обладает единственным решением.

Формулы (4.2.4) называются формулами Крамера.

Непосредственной подстановкой значений , во все уравнения системы убедимся в том, что они образуют ее решение:

.

При , при , .

Таким образом, получим

.

 

Теорема доказана.

Пример. Решить систему линейных уравнений методом Крамера:

 

Решение. Вычислим определитель :

,

,

,

откуда

 

Решение системы линейных уравнений с определителем |A|, отличным от нуля, можно найти с помощью обратной матрицы. Для этого запишем систему (4.2.1) в виде матричного уравнения

 

где .

 

Решение матричного уравнения (4.2.5) имеет вид

(4.2.6)

 

Пример. Решить систему линейных уравнений с помощью обратной матрицы

Решение. Вычислим для матрицы

ее обратную матрицу

.

 

Определим неизвестную матрицу-столбец Х:

,

откуда

 

Формулы Крамера (4.2.4) могут быть получены из выражения (4.2.6). Действительно, запишем матричное равенство в развернутом виде:

.

Из полученного выражения непосредственно следуют формулы Крамера:

.

 

Теорема Кронекера-Капелли

 

Теорема. Система линейных уравнений (4.1.1) совместна тогда и только тогда, когда .

Доказательство.

Необходимость. Пусть система (4.1.1) совместна и пусть числа — одно из ее решений. Подставляя эти числа вместо неизвестных в систему (4.1.1), получим m тождеств, которые показывают, что последний столбец матрицы является линейной комбинацией всех остальных столбцов, взятых соответственно с коэффициентами . Всякий другой столбец матрицы входит и в матрицу

А. Поэтому максимальное число линейно независимых столбцов матриц А и совпадает. Следовательно, .

Достаточность. Пусть дано, что . Отсюда следует, что максимальное число линейно независимых столбцов матриц А и совпадает и равно r. Для определенности предположим, что первые r столбцов матриц А и линейно независимы, а остальные (n-r) столбцов является их линейными комбинациями. Выражая последний столбец матрицы А как линейную комбинацию первых r столбцов, получим:

откуда следует, что числа являются решением системы (4.1.1), т.е. система (4.1.1) совместна. Теорема доказана.

На основании теоремы Кронекера-Капелли имеем:

1. Если , то система (4.1.1) несовместна;

2. Если , то система (4.1.1) совместна.

Пусть для определенности базисный минор порядка r расположен в верхнем левом углу матрицы А. Тогда первые r строк матрицы А линейно независимы, а остальные ее строки являются линейной комбинацией первых r строк. Но это означает, что первые r уравнений системы (4.1.1) линейно независимы, а остальные (m-r) ее уравнений являются их линейными комбинациями. Поэтому достаточно решить систему r уравнений; решения такой системы будут, очевидно, удовлетворять и остальным (m-r) уравнениям.

 

При этом возможны два случая:

1. . Тогда систему, состоящую из первых r уравнений системы (4.1.1)

можно решить, например, по правилу Крамера. В этом случае система имеет единственное решение, т.е. система совместна и определена;

 

2. . Рассмотрим первые r уравнений системы (4.1.1). Оставив в левых частях первые r неизвестных, перенесем остальные в правые части. Получим систему:

 

Очевидно, что полученная система и, следовательно, система (4.1.1) являются совместными и неопределенными.

Таким образом, если , то система (4.1.1) совместна (определенная или неопределенная), если , то система (4.1.1) несовместна.

Если в системе n линейных уравнений с n неизвестными определитель системы равен нулю, то . Тогда если , то система является совместной и неопределенной. Если , то система несовместна.

Теорема Кронекера-Капелли устанавливает необходимое и достаточное условие совместности системы (4.1.1), но не дает способа нахождения решения этой системы. Рассмотрим метод Жордана-Гаусса – метод решения системы m линейных уравнений с n неизвестными.

 

Метод Жордана-Гаусса

 

Метод Жордана-Гаусса основан на элементарных преобразованиях (п.3.2) строк расширенной матрицы

системы (4.1.1).

В результате каждого из элементарных преобразований расширенная матрица изменяется, однако системы линейных уравнений, соответствующие полученным матрицам, эквивалентны исходной системе линейных уравнений.

Пусть дана система m линейных уравнений с n неизвестными. Применяя элементарные преобразования, построим эквивалентную систему специального вида. Для этого выберем в качестве первого уравнений одно из тех уравнений системы, где коэффициент при х₁ отличен от нуля. Не нарушая общности, предположим, что . Тогда первым уравнением системы будет уравнение

.

Умножим первое уравнение на . Затем умножим это же уравнение на , и прибавим его почленно к уравнениям системы с номерами i=2,3,…,m. После этого преобразования в уравнениях с номерами i>1 будет исключено неизвестное х₁. Первый шаг метода Жордана-Гаусса закончен.

 

.

Может случиться, что на первом шаге вместе с неизвестными х₁ будут исключены неизвестными , но найдется хотя бы одно уравнение, в котором сохранится неизвестное . Одно из таких уравнений примем в качестве второго уравнения системы. В этом случае расширенная матрица , соответствующая полученной системе, имеет вид:

.

 

Используем второе уравнение для исключения неизвестного из всех уравнений, кроме второго. После второго шага метода Жордана-Гаусса получим расширенную матрицу

 

.

 

Продолжая процесс, после r шагов получим матрицу , содержащую r единичных столбцов на месте первых n столбцов матрицы А (r – ранг матрицы А системы).

При этом возможны три случая:

1. Если , то матрица преобразуется в матрицу

 

Система имеет единственное решение: .

2. Если и r<n, то

 

Система имеет бесконечное множество решений. Общее решение имеет вид:

 

Неизвестные называются базисными. – свободными неизвестными.

Свободным неизвестным можно придавать какие угодно значения, получая при этом соответствующие значения неизвестных . В результате имеем бесконечное множество частных значений.

Среди частных решений системы выделим базисные решения, которые получают при равенстве нулю всех свободных неизвестных. Очевидно, что одним из базисных решений является следующее:

.

В общем случае число базисных решений не превышает .

2. Если , то

где хотя бы один из элементов отличен от нуля. В этом случае система (4.1.1) несовместна.

Таким образом, метод Жордана-Гаусса состоит из r итераций (r шагов). На каждой S-ой итерации выбирается направляющий элемент соответственно направляющие строка и столбец. С помощью элементарных преобразований столбец преобразуется в единичный с единицей в строке .

Рассмотрим алгоритм произвольной итерации метода Жордана-Гаусса. Положим .

Шаг 1. Сформировать множество .

Шаг 2. Если , то процесс элементарных преобразований закончить. В противном случае перейти к шагу 3.

Шаг 3. Если для , то процесс элементарных преобразований закончить. В противном случае найти направляющий элемент и перейти к шагу 4.

Шаг 4. Разделить направляющую строку на .

Шаг 5. К i-ой строке, , прибавим строку , умноженную на .

Покажем, что столбец преобразуется в единичный с единицей в строке . Пусть . Элементы матрицы выражаются через элементы матрицы следующим образом:

 

	(4.4.1)
	(4.4.2)
	(4.4.3)
	(4.4.4)

Полагая j=k, из (4.4.1) и (4.4.3) имеем

.

Пример. Решить систему линейных уравнений методом Жордана-Гаусса.

а)

 

Решение. Составим из данной системы расширенную матрицу

Полагаем .

Итерация 1.

Шаг 1. .

Шаг 2. , переходим к шагу 3.

Шаг 3. Находим .

Шаг 4. Делим третью строку на .

Шаг 5. К первой, второй и четвертой строкам прибавляем третью строку, соответственно умноженную на –2, -2, -3. В результате матрица преобразуется в матрицу

 

.

 

Итерация 2.

Шаг 1. .

Шаг 2. , переходим к шагу 3.

Шаг 3. Находим .

Шаг 4. Делим первую строку на .

Шаг 5. Ко второй, третьей и четвертой строкам прибавляем первую строку, соответственно умноженную на –4, -3, 1. Получим матрицу

.

 

Итерация 3.

Шаг 1. .

Шаг 2. , переходим к шагу 3.

Шаг 3. Находим .

Шаг 4. Делим четвертую строку на .

Шаг 5. К первой, второй, третьей строкам прибавляем четвертую строку, соответственно умноженную на 0, -5, -2. Получим матрицу

.

Итерация 4.

Шаг 1. .

Шаг 2. , переходим к шагу 3.

Шаг 3. Находим .

Шаг 4. Делим четвертую строку на .

Шаг 5. К первой, третьей и четвертой строкам прибавляем вторую строку, соответственно умноженную на -1, 2, 0. Получим матрицу

.

Итерация 5.

Шаг 1. .

Шаг 2. , поэтому процесс элементарных преобразований закончен. На основании вида матрицы получаем единственное решение исходной системы: .

б)

 

Решение. Составим расширенную матрицу

.

В результате итерации 1, полагая , получим матрицу

После итерации 2, полагая , получим матрицу

 

Итерация 3.

Шаг 1. .

Шаг 2. .

Шаг 3. Так как , то процесс элементарных преобразований закончен.

Матрица определяет общее решение системы:

— базисные, — свободные переменные.

Получим одно из базисных решений:

.

 

в)

 

Решение. Матрицы , , имеют вид:

 

Очевидно, что процесс элементарных преобразований следует закончить, так как . Из первой (или третьей) строки матрицы следует, что исходная система линейных уравнений несовместна. Действительно, первой строке соответствует уравнение , которое не может быть удовлетворено ни при каких значениях неизвестных .

Используя метод Жордана-Гаусса, рассмотрим еще один метод вычисления обратной матрицы .

Рассмотрим матричное уравнение

 

,

(4.4.5)

где , Е – единичная матрица.

Очевидно, что матричное уравнение (4.4.5) имеет единственное решение .

 

Решение матричного уравнения (4.4.5) сводится к решению n систем n линейных уравнений с n неизвестными вида

(4.4.6)

 

Системе линейных уравнений (4.4.6) соответствует расширенная матрица . Применяя к матрице алгоритм метода Жордана-Гаусса, получим матрицу . Покажем, что . Расширенной матрице соответствует матричное уравнение , которое имеет единственное решение Х=В. Матрица получена из матрицы методом Жордана-Гаусса. Поэтому системы линейных уравнений, соответствующие матрицам и , равносильны, т.е. имеют одно и то же решение. Отсюда следует, что , следовательно, .

Таким образом, чтобы для невырожденной матрицы А вычислить обратную матрицу , необходимо составить матрицу . Методом Жордана-Гаусса в матрице преобразовать матрицу А к виду единичной матрицы Е, тогда на месте единичной матрицы Е получим обратную матрицу .

Пример. Вычислить обратную матрицу для матрицы

.

Решение. Составим матрицу

.

На итерации 1, полагая , получим

.

На итерации 2, полагая , получим

.

На итерации 3, полагая , получим

,

откуда .

---

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

zdamsam.ru

Случаи систем уравнений с тремя неизвестными

67. Особенные случаи систем уравнений с тремя неизвестными. Возьмем следующую систему уравнений:

3x + 4y + 5z = 17
2x + 3y + 4z = 15
5x + 7y + 9z = 32

Наблюдательный человек здесь может подметить, что третье уравнение вовсе не является новым, а является следствием двух первых: каждый член 3-го уравнения получается от сложения соответствующих членов 1-го и 2-го уравнения (5x = 3x + 2x, 7y = 4y + 3y; 9z = 5z + 4z; 32 = 17 + 15), и само собою понятно, что если
3x + 4y + 5z должно равняться 17,
2x + 3y + 4z должно равняться 15,
то (3x + 4y + 5z) + (2x + 3y + 4z) должно равняться 32.

Поэтому мы здесь имеем, в сущности, только 2 уравнения с 3 неизвестными, и они имеют бесконечно много решений.

Можно составлять такие системы и более сложным путем. Возьмем два уравнения:

x – 2y + 3z = 7
2x + y – z = 5

Умножим каждое из них на какое-либо число и сложим (или вычтем) по частям полученные уравнения. Умножим обе части 1-го уравнения, например, на 3 и обе части второго на (–2) и полученные уравнения сложим. Тогда получим уравнения:

–x – 8y + 11z = 11.

Это уравнение является следствием двух первых и поэтому все три уравнения, взятые вместе, должны иметь бесконечно много решений.

Попробуем решать эти уравнения: 1) из 1-го и 3-го сложением по частям исключим x; 2) из 2-го и 3-го, умножив предварительно третье на 2, также исключим x:

Если теперь разделить обе части 1-го из полученных уравнений на 2 и обе части 2-го на 3, то получим одно и то же уравнение, а именно:

–5y + 7z = 9.

Это обстоятельство и является признаком того, что наша система имеет бесконечно много решений.

Если мы изберем такой план: 1) из 1-го и, напр., 3-го уравнений определим x и y через z; 2) подставим полученные выражения в 3-е уравнение, то должны получить само собою очевидное равенство, вроде 0 = 0 или 7 = 7 или 15 = 15 или –11 = –11 и т. п.

В самом деле:

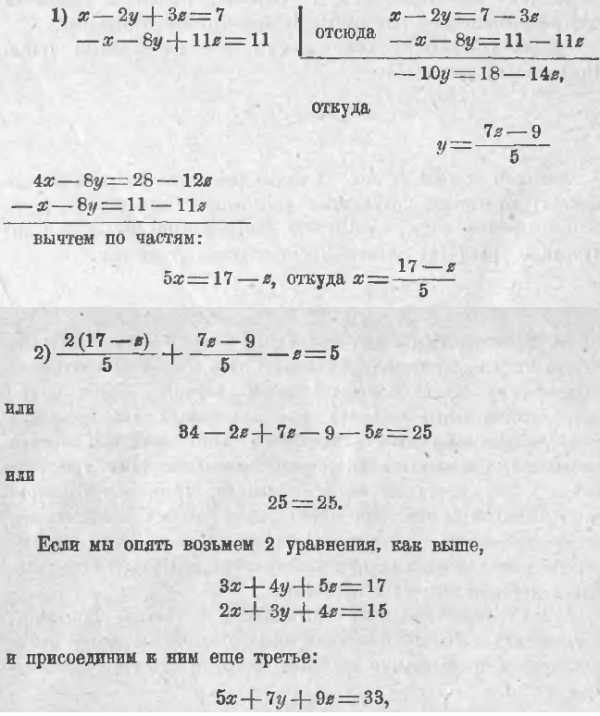
то после предыдущего становится ясным, что эти 3 уравнения совместно решить нельзя. В самом деле, ведь левая часть 3-го уравнения получается от сложения левых частей 1-го и 2-го уравнений, а в таком случае эта сумма должна равняться 17 + 15 или 32, но не может равняться 33.

Также точно можно, взяв 2 уравнения произвольно, составить третье, несовместимое с ними, умножением каждого из взятых двух уравнений на какое-нибудь число и сложением (или вычитанием) полученных уравнений, причем известный член должно как-либо изменить. Например, если первое из взятых уравнений умножим на 2 (получим: 6x + 8y + 10z = 34), второе на 3 (получим: 6x + 9y + 12z = 45), сложим полученные уравнения по частям, но вторую часть как-либо изменим (напр., вместо получающейся суммы 79 возьмем 100), то полученное уравнение

12x + 17y + 22z = 100

не совместимо с первыми двумя.

Если кто-либо стал бы решать систему несовместимых уравнений, то пришел к результату явно нелепому, например:

0 = 5 или 7 = 11 или –5 = +5 и т. п.

maths-public.ru

Системы линейных уравнений. Решение и исследование системы трех линейных уравнений с тремя неизвестными.

Пусть дана система трех линейных уравнений с тремя неизвестными — x, y, z :

,

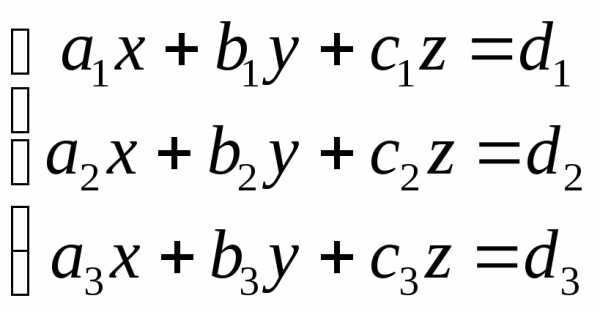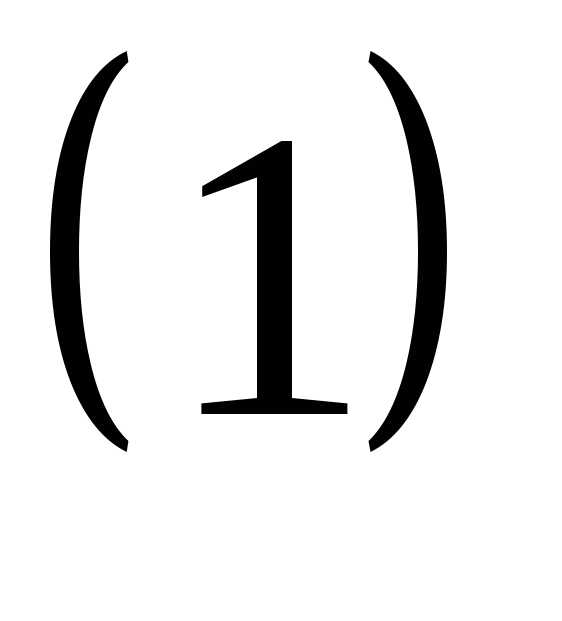
ее главный определитель, составленный из коэффициентов при неизвестных, имеет вид

.

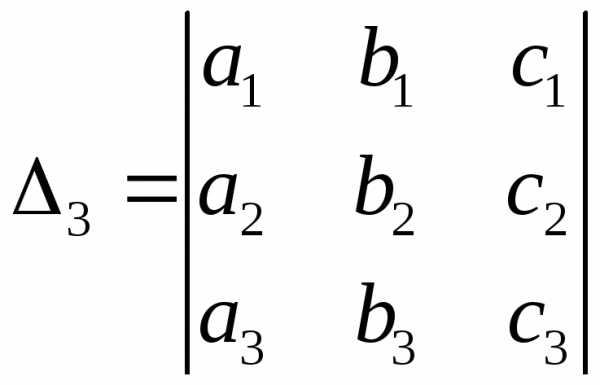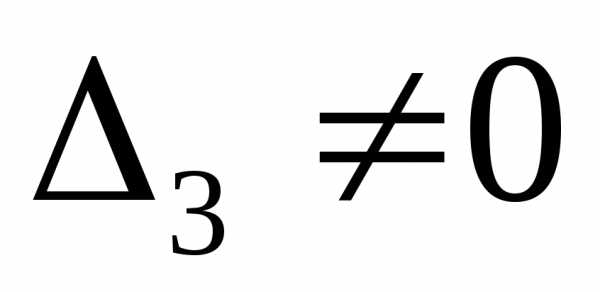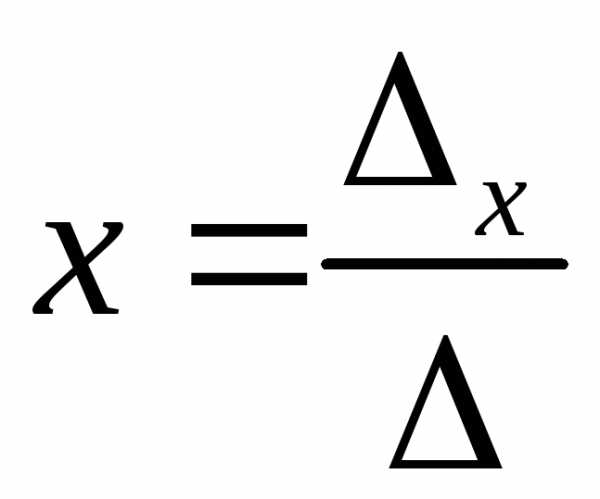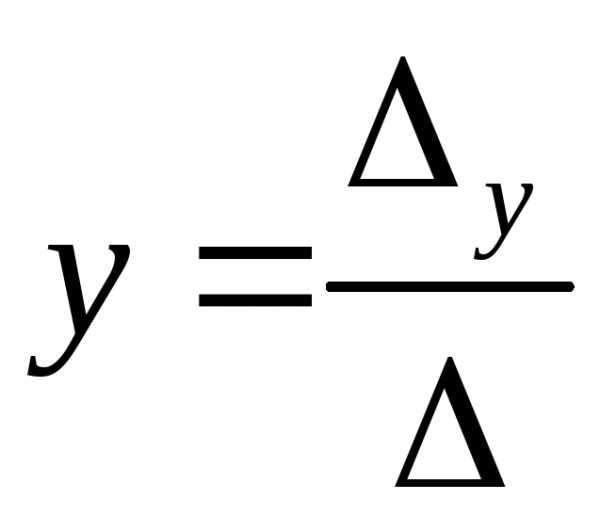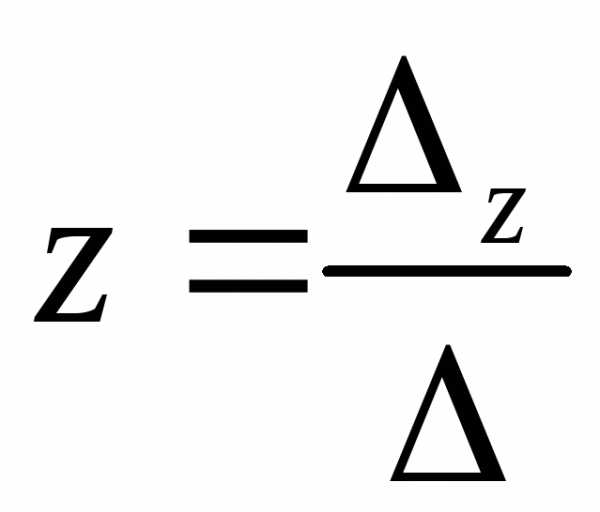Если , то,,, где

, ,.

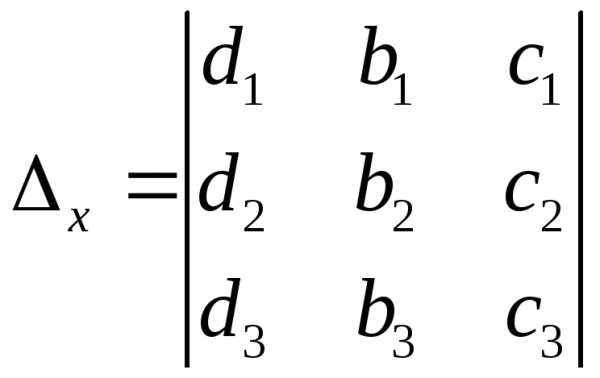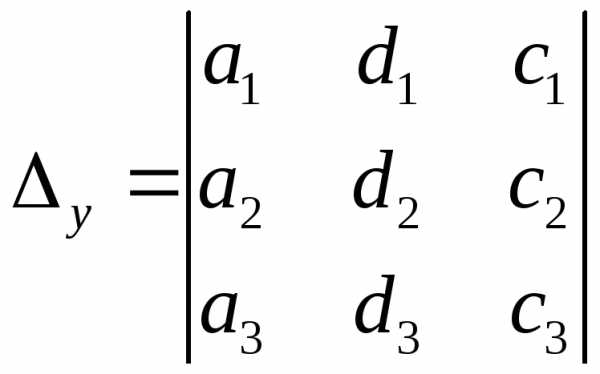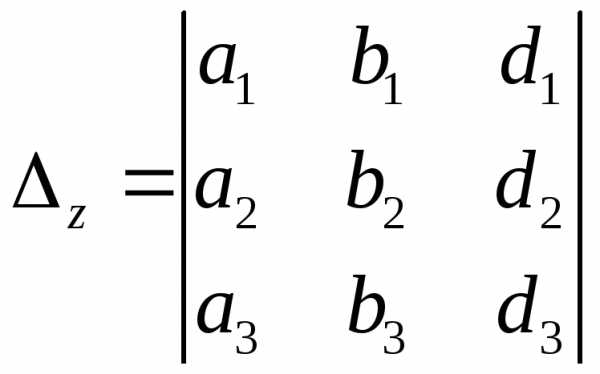Пусть тепер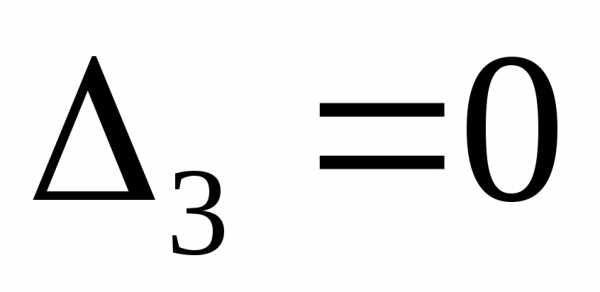ь , но есть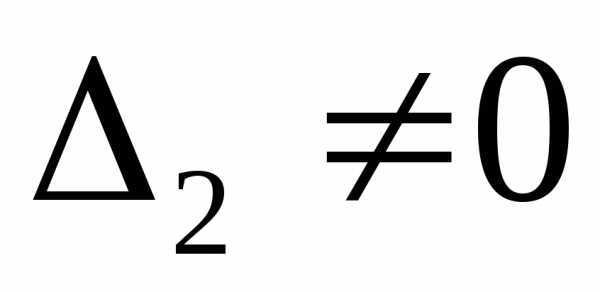. Тогда можно утверждать, что, например,

.

Если же и , то в системе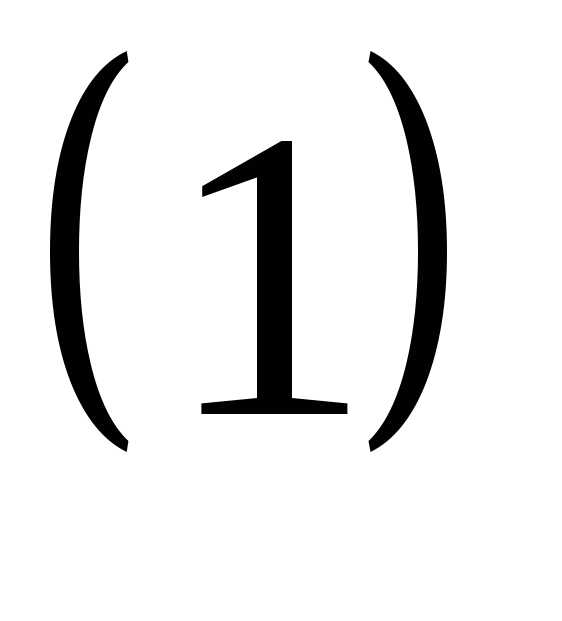есть лишь два независимых уравнения, а третье является их следствием. В силу этого система сводится к двум уравнениям с тремя неизвестными. Такая система неопределенна и имеет бесчисленное множество решений: одному можно придавать любое значение, а остальные неизвестные определяются из двух независимых – все решения лежат на прямой, т.е. на пересечении двух плоскостей. В этом случае.

Если же , то система несовместна и не имеет решений. В этом случае среди определителей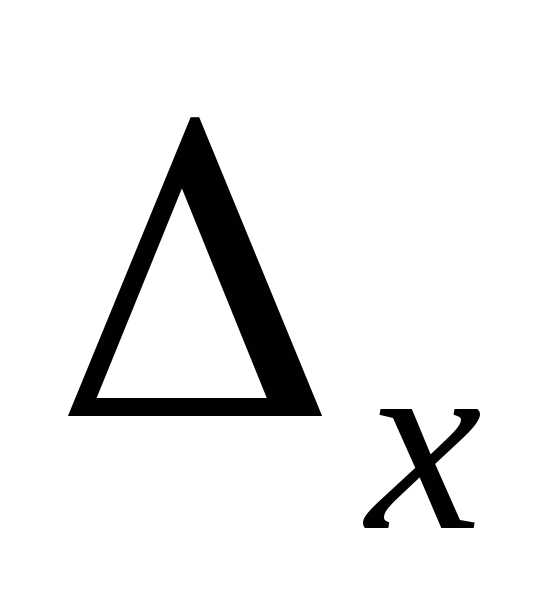,,есть хотя бы один, не равный нулю.

Случай, когда , т.е. равны нулю и все его миноры второго порядка, но есть элементы, не равные нулю, приводит к выражениям

и

.

Если же и 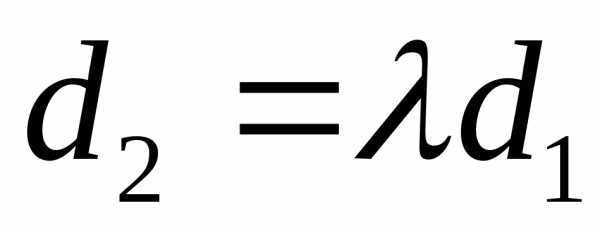,,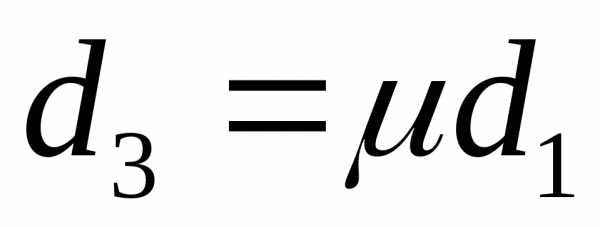 то в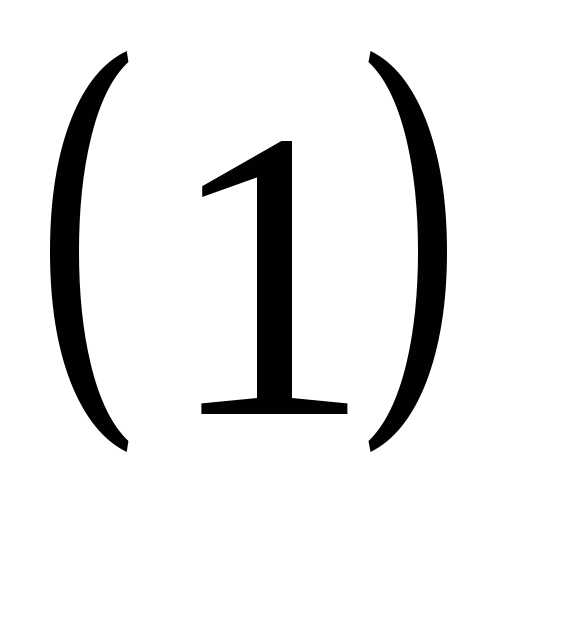есть лишь одно независимое уравнение. Система неопределенна, имеет бесчисленное множество решений (точки плоскости). В этом случае, и определители всех миноров второго порядка также равны нулю.

Если же 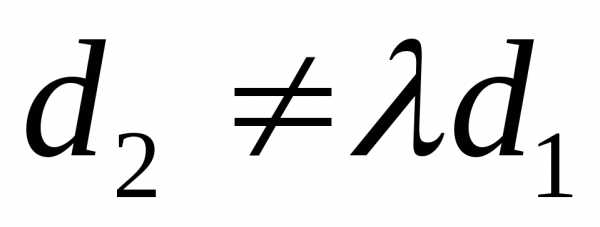, или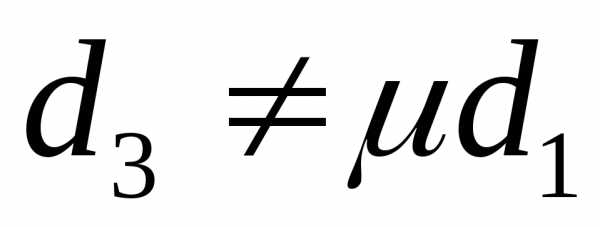, то система противоречива и не имеет решений – параллельные плоскости.

Однородная система трех линейных уравнений с тремя неизвестными.

Однородной называют систему, в которой ,.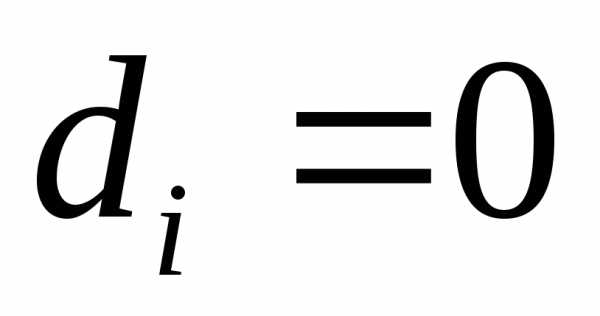

.

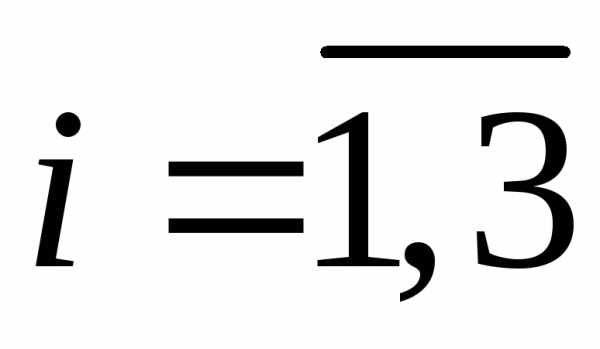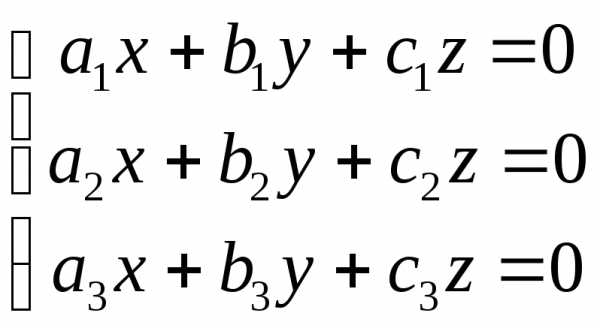Система — неоднородна.

Если вне равен нулю, то система имеет единственное решение.

Если же 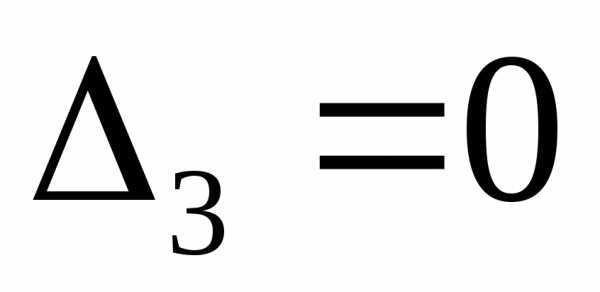, то среди его строк есть линейная зависимость и в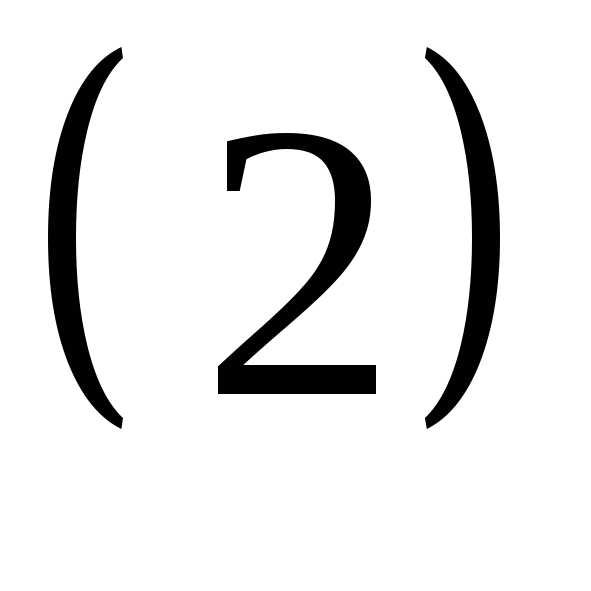остается два или одно независимое уравнение.

Решение произвольных систем линейных уравнений

Пусть задана система 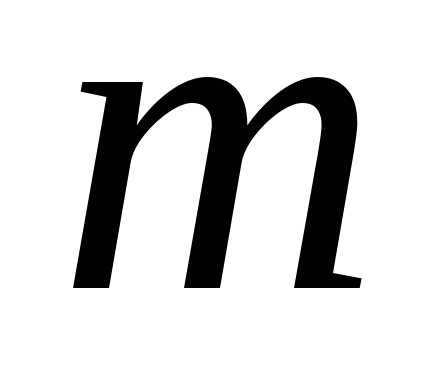линейных уравнений с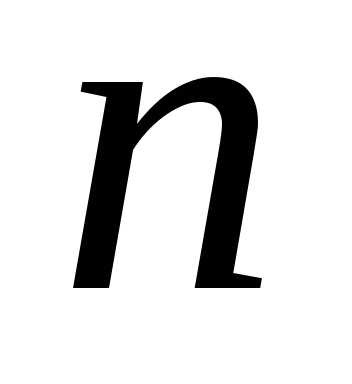неизвестными,:

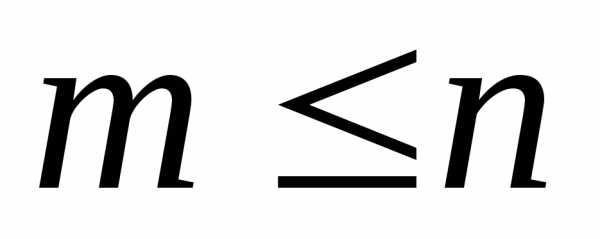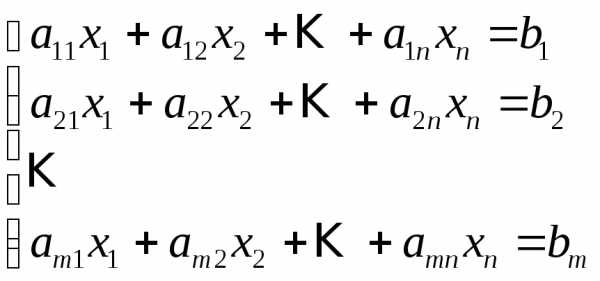, (1)

или в матричной форме

, (2)

где

, ,.

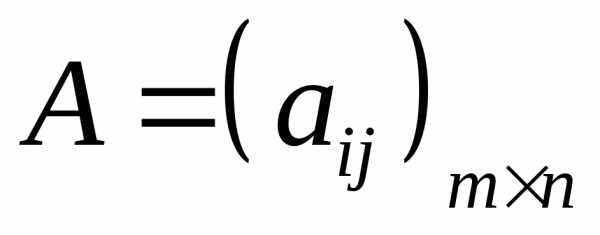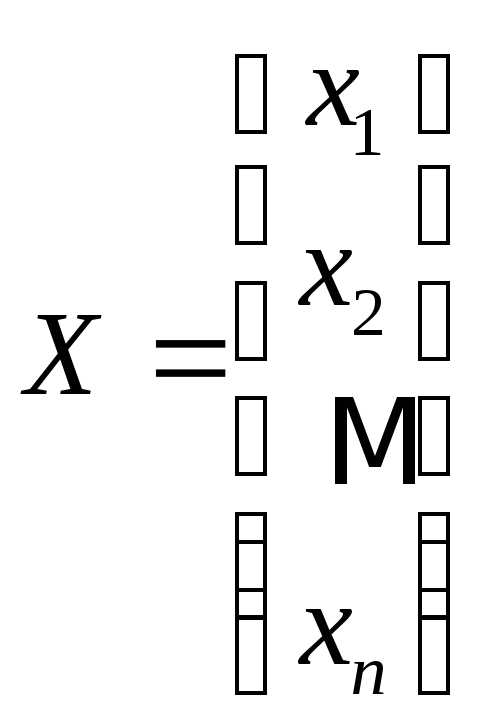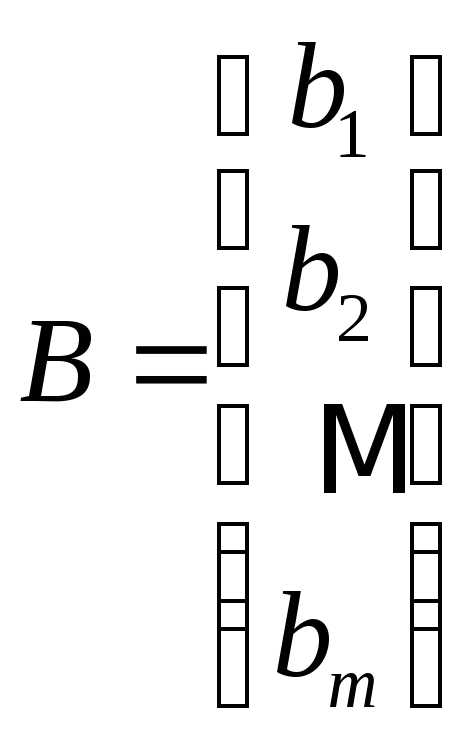Решением системы (1) или (2) называется любой 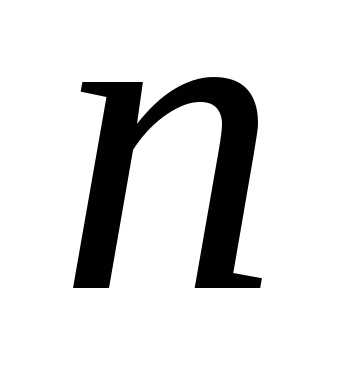-компонентный вектор-столбец или матрица-столбец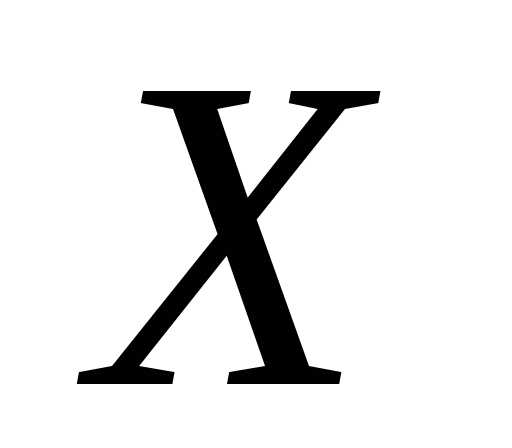, обращающий в верное равенство системы (1) или (2).

Система называется совместной, если у нее существует хотя бы одно решение. В противном случае, система несовместна. Две системы называют эквивалентными, если множества их решений совпадают.

Теорема Кронекера–Капелли. Чтобы система вида (1) была совместна, необходимо и достаточно, чтобы

,

где 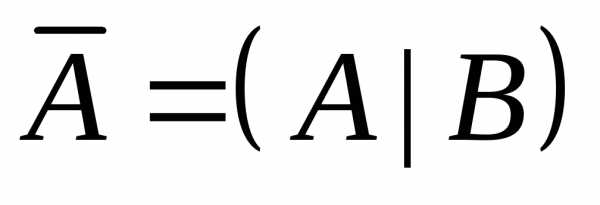— расширенная матрица системы.

Пусть теперь в системе (2) , т.е. она совместна. Можно считать, не ограничивая общности, что не равный нулю минор порядка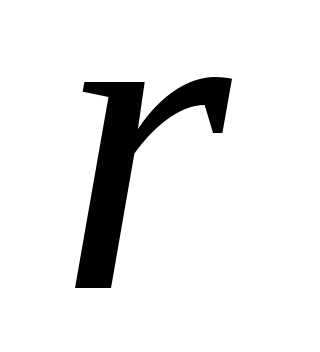располагается в первых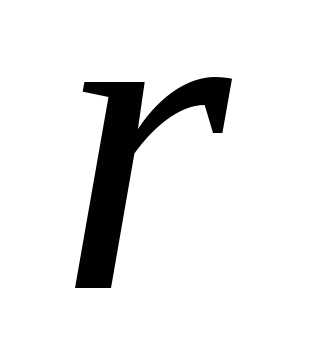строках и столбцах матрицы.

Запишем «укороченную» систему для (1), отбросив последние 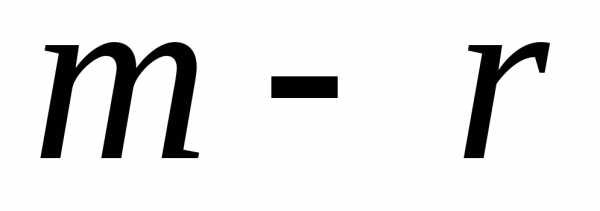уравнений, в виде:

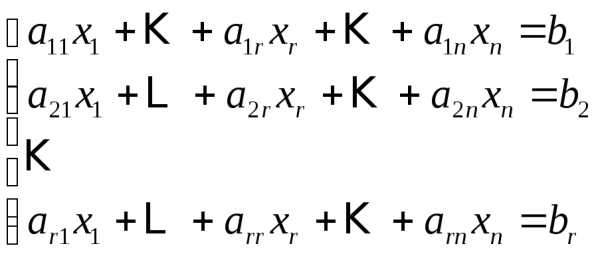(3)

Эта система эквивалентна исходной, т.к. отброшенные уравнения являются линейной комбинацией оставшихся уравнений.

Неизвестные называют базисными, а- свободными. Перенесем теперь свободные переменные в правую часть (3). В результате получим систему относительно базисных неизвестных:

.

Эта система для любого набора значений свободных неизвестных имеет единственное решение:

,

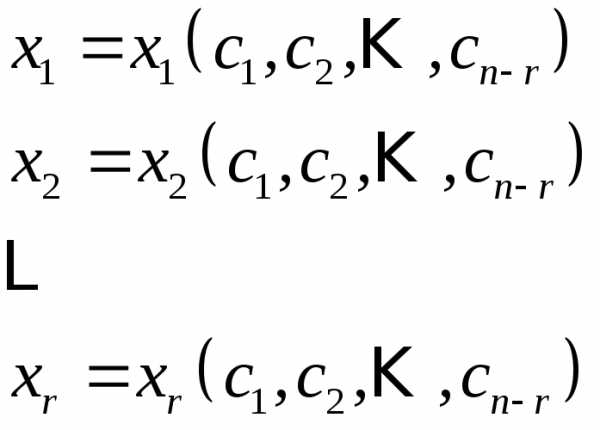где 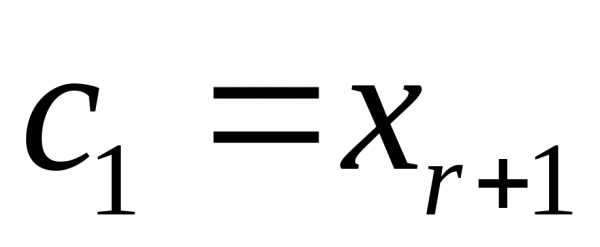,,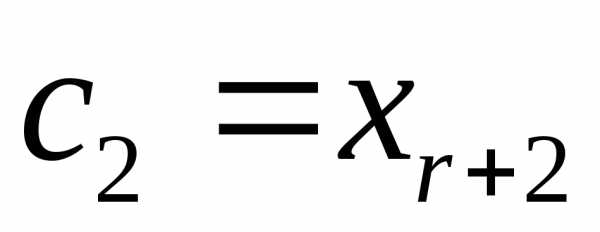,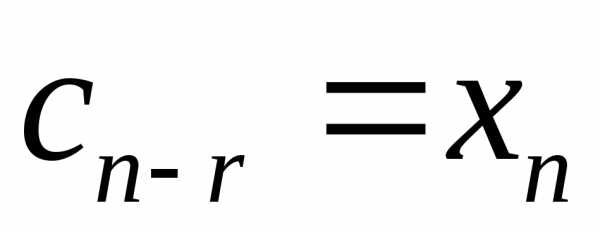— набор свободных неизвестных.

Соответствующее решение укороченной, а следовательно и исходной системы имеет вид:

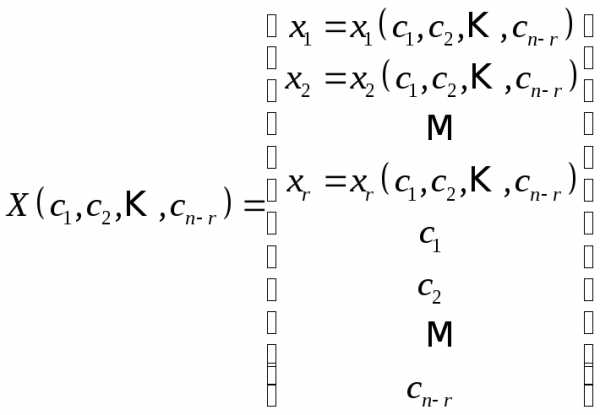. (4)

Формула (4) выражает произвольное решение системы (1) в виде функций от 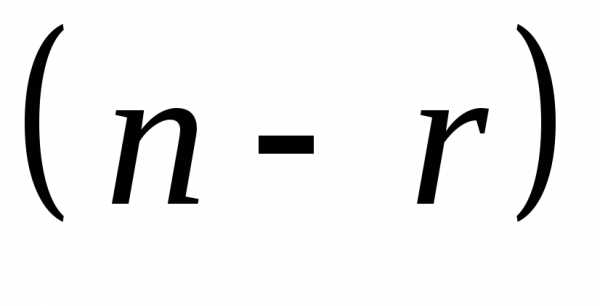свободных неизвестных и называетсяобщим решением системы. Каждому конкретному набору соответствуетчастное решение.

studfiles.net

Системы 3-х линейных уравнений с тремя неизвестными

⇐ ПредыдущаяСтр 3 из 7Следующая ⇒

Рассмотрим систему трех линейных уравнений с тремя неизвестными

(2.4)

 

а₁₁, a₁₂, …, a₃₃ – коэффициенты при неизвестных,

b₁, b₂, b₃ – свободные члены.

 

Решить систему (2.4) – значит найти такую упорядоченную тройку чисел x₁=c₁, x₂=c₂, x₃=c₃, при подстановке которых в уравнения системы последние обращаются в тождества.

 

Система уравнений, имеющая решения (единственное или бесчисленное множество), называется совместной, система уравнений, не имеющая решений, – несовместной.

 

Приведем три способа решений системы (2.4).

 

Правило Крамера

Составим определитель системы из коэффициентов при неизвестных

 

(2.5)

 

Если , то система (2.4) имеет единственное решение, которое находится по формулам Крамера:

 

(2.6)

 

где , , получены из определителя заменой соответственно первого, второго, третьего столбца столбцом из свободных членов системы (2.4).

 

(2.7)

 

 

Пример 7. Решить систему

 

Вычисляем определитель системы (2.5) и определители , , (2.6).

 

следовательно, система имеет единственное решение.

 

 

По формулам Крамера (2.6) находим:

 

 

Можно сделать проверку, подставив значения неизвестных в уравнения системы.

Итак, x₁=x₂=x₃=1 – решение системы.

 

 

Метод Гаусса

 

Рассмотрим систему (2.4):

 

Метод Гаусса, иначе метод последовательного исключения неизвестных, состоит в следующем. Пусть Исключим из 2-го и 3-го уравнений системы x₁. Получим систему:

 

 

Далее исключим x₂ из 3-го уравнения:

 

 

Получим систему треугольного вида. Из 3-го уравнения найдем x₃, подставляя его во 2-ое уравнение, найдем x₂, затем из 1-го уравнения найдем x₁, подставляя в него x₂ и x₃.

 

Пример 8. Решить систему

Переставим 3-е и 1-ое уравнения, чтобы в 1-ом уравнении коэффициент при x₁ был равен 1.

 

Исключим x₁ из 2-го и 3-его уравнений. Для этого умножим 1-ое уравнение на (-4) и сложим его со 2-м уравнением; затем умножим 1-ое уравнение на (-6) и сложим с 3-м уравнением. Получим систему:

 

 

Исключим x₂ из 3-его уравнения. Для этого умножим 2-ое уравнение на (-13/10) и сложим с 3-м уравнением. Получим систему:

 

 

Из последнего уравнения находим x₃= -1, подставляем во 2-ое уравнение:

 

-10x₂ — 13(-1) = -7, -10x₂ = — 20, x₂ = 2.

 

Подставляя x₂ и x₃ в 1-ое уравнение, получим

 

Итак, решение системы: x₁ = 1, x₂ = 2, x₃ = -1.

Решение системы с помощью обратной матрицы

 

Дана система: (2.8)

 

Составим матрицу А из коэффициентов при неизвестных, матрицу-столбец Х – из неизвестных, матрицу-столбец В – из свободных членов.

 

,

 

Систему (2.8) можно записать в матричной форме так:

 

Матрица-решение Х находится по формуле:

 

(2.9)

 

А^-1 – обратная матрица для матрицы А, она составляется из алгебраических дополнений элементов матрицы А по формуле (2.3):

 

 

– детерминант или определитель матрицы А, .

 

Пример 9. Решить систему:

 

Введем матрицы: ,

 

Обратная матрица вычислена в примере 6. По формуле (2.9) находим решение системы

 

 

 

Итак, x₁=1, x₂=1, x₃=1.

Элементы векторной алгебры

Вектор – направленный отрезок; обозначается или . А – начало вектора, В – конец.

Длинаили модуль вектора обозначается .

Рис. 21.

В координатном пространстве 0xyz вектор может быть представлен в виде

 

(3.1)

 

Эта формула дает разложение вектора по базису векторов , , ; , , — прямоугольные декартовые координаты вектора (иначе проекции вектора на оси координат).

Формулу (3.1) можно записать так:

 

– вектор имеет координаты , , .

 

Длина (модуль) вектора находится по формуле:

 

. (3.2)

 

Если вектор задан задан координатами начала A(x₁,y₁,z₁)и конца B(x₂,y₂,z₂), то координаты находятся по формулам:

 

(3.3)

Если известны разложения векторов и по осям координат , то при сложении (вычитании) векторов их одноименные координаты складываются (вычитаются), при умножении вектора на число координаты вектора умножаются на это число, т.е.

 

(3.4)

Скалярным произведением векторов и , обозначается , называется число, равное произведению длин этих векторов на косинус угла между ними

. (3.5)

Если , , то

 

. (3.6)

 

Если векторы и коллинеарны (параллельны), то

 

. (3.7)

Если векторы и ортогональны (перпендикулярны), то

 

или (3.8)

 

Пример 10. Даны точки А₁(1,0,-1), A₂(2,-1,1), A₃(0,1,-2). Средствами векторной алгебры, учитывая, что найти:

1) координаты векторов и .

Используем формулу (3.3):

или ;

или .

2) Координаты вектора

Используя формулы (3.4) и (3.5), получим

или

3) длину вектора

По формуле (3.2):

 

4) Скалярное произведение

По формуле (3.6):

5) Проверить, коллинеарны или ортогональны векторы и

Проверяем условия (3.7) и (3.8).

векторы и неколлинеарны.

векторы неортогональны.

 

Примеры для самостоятельного решения

 

1. Вычислить определители.

 

1.1. а) б)

 

1.2. По правилу треугольников:

а) б)

 

1.3. Разложив по элементам 1-ой строки:

 

1.4. Разложив по элементам строки (столбца), где больше нулей:

 

 

 

1. Решить системы и сделать проверку.

 

2.1. По формулам Крамера.

 

а) б)

 

2.2. По методу Гаусса.

 

а) б)

 

2.3. С помощью обратной матрицы

 

а) б)

 

 

2. Даны точки А(-3, 4, 1), В(2,3,4). Найти разложение вектора по базису векторов , , и длину вектора . Отв.:

 

3. Даны точки А(0,-2,3), В(2,1,4), С(3,4,5). Найти:

а) координаты (проекции) векторов и

б) координаты вектора

с) длину вектора

 

4. Даны векторы Найти скалярное произведение векторов .

 

5. Доказать, что векторы и коллинеарны.

 

6. Доказать, что векторы ортогональны.

Рекомендуемые страницы:

lektsia.com

Системы линейных уравнений. Решение и исследование системы трех линейных уравнений с тремя неизвестными.

Пусть дана система трех линейных уравнений с тремя неизвестными — x, y, z :

,

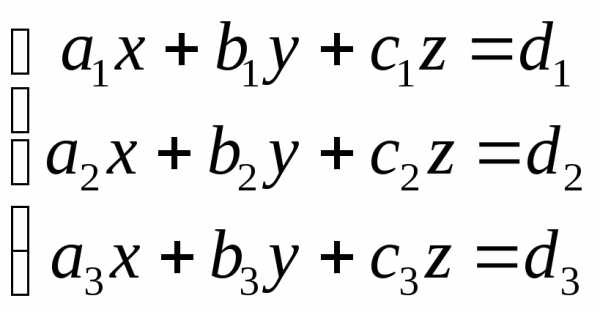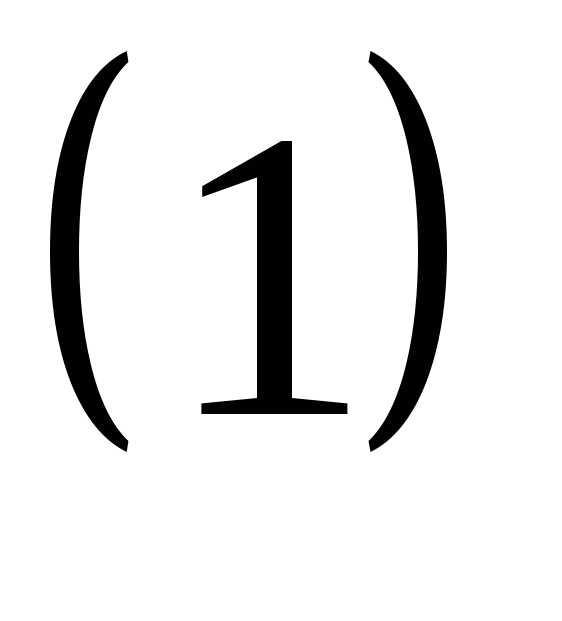
ее главный определитель, составленный из коэффициентов при неизвестных, имеет вид

.

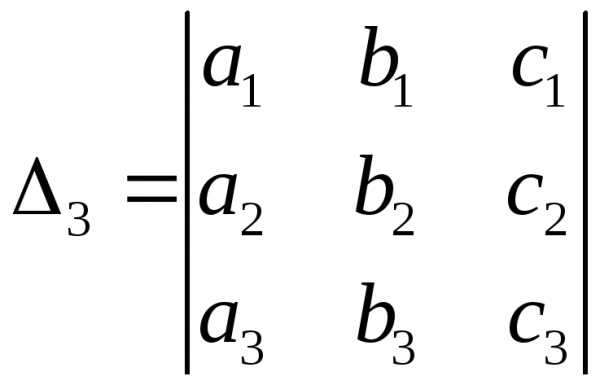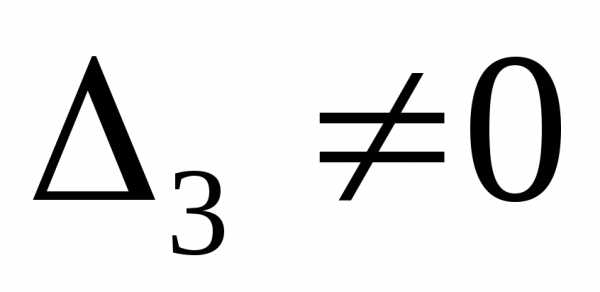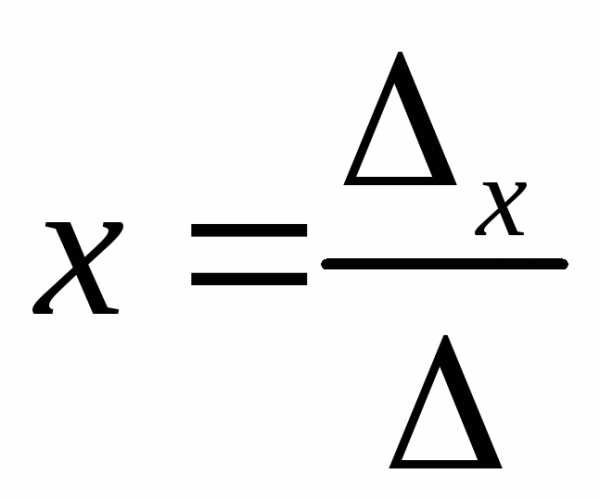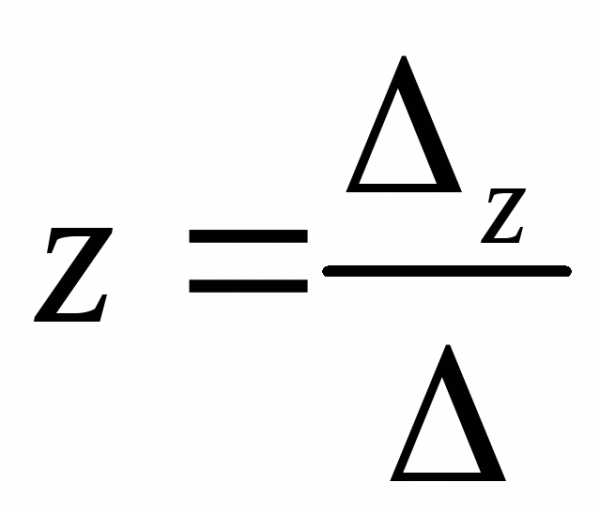Если , то,,, где

, ,.

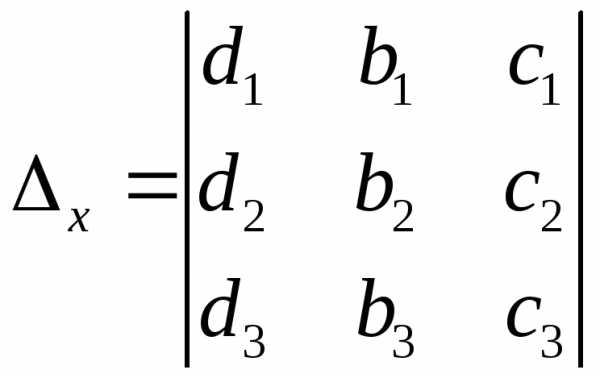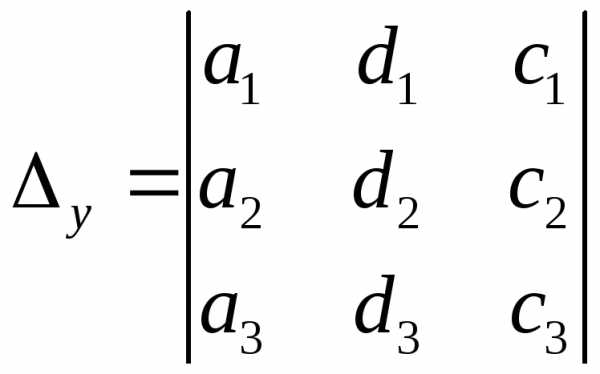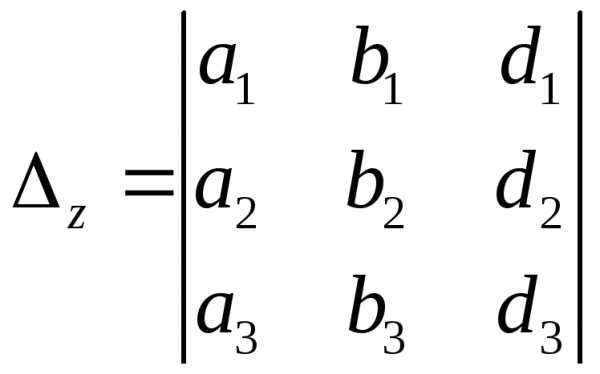Пусть тепер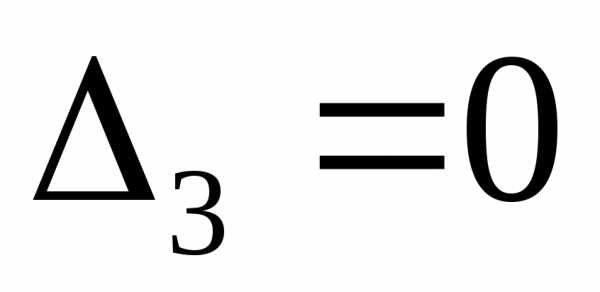ь , но есть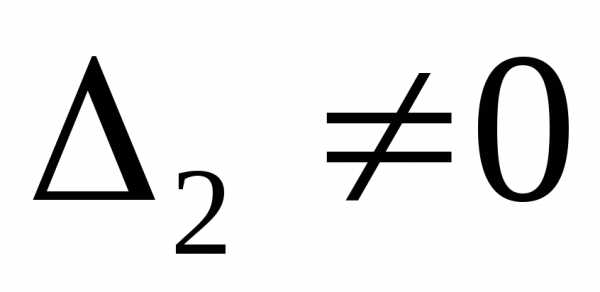. Тогда можно утверждать, что, например,

.

Если же и , то в системе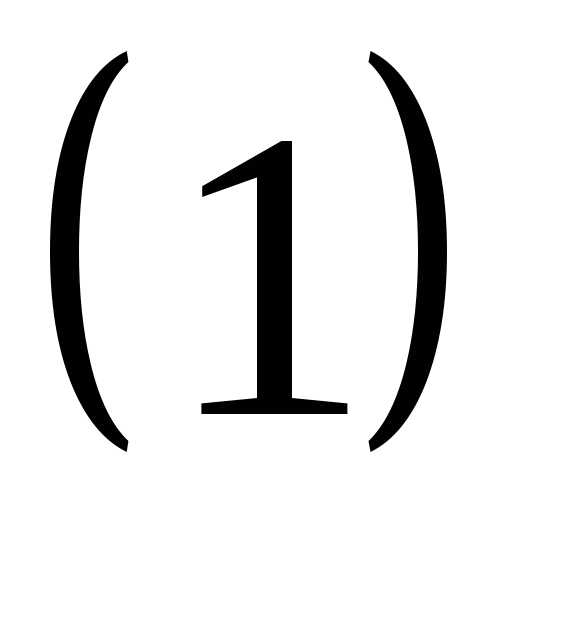есть лишь два независимых уравнения, а третье является их следствием. В силу этого система сводится к двум уравнениям с тремя неизвестными. Такая система неопределенна и имеет бесчисленное множество решений: одному можно придавать любое значение, а остальные неизвестные определяются из двух независимых – все решения лежат на прямой, т.е. на пересечении двух плоскостей. В этом случае.

Если же , то система несовместна и не имеет решений. В этом случае среди определителей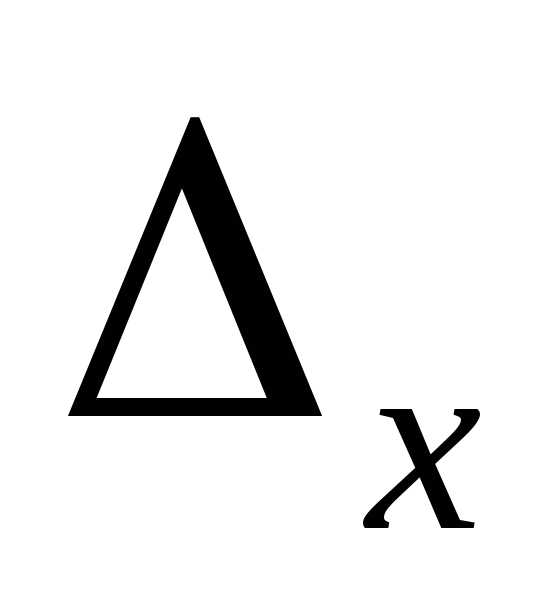,,есть хотя бы один, не равный нулю.

Случай, когда , т.е. равны нулю и все его миноры второго порядка, но есть элементы, не равные нулю, приводит к выражениям

и

.

Если же и 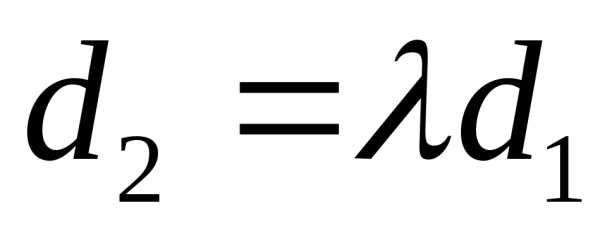,,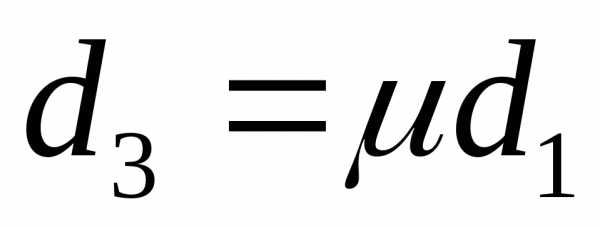 то в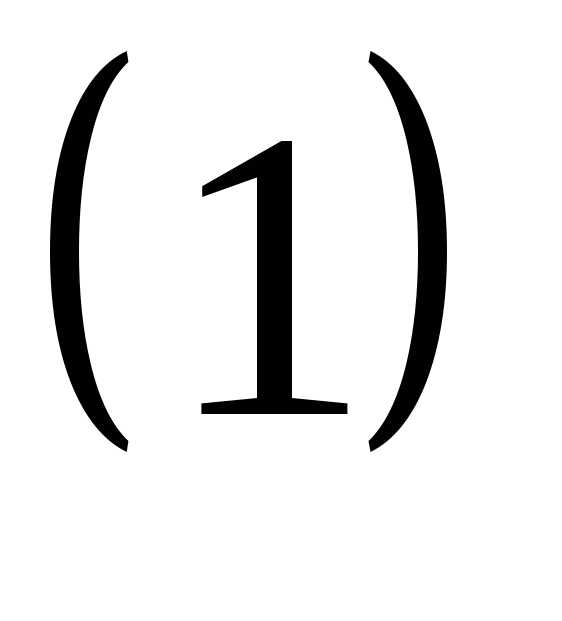есть лишь одно независимое уравнение. Система неопределенна, имеет бесчисленное множество решений (точки плоскости). В этом случае, и определители всех миноров второго порядка также равны нулю.

Если же 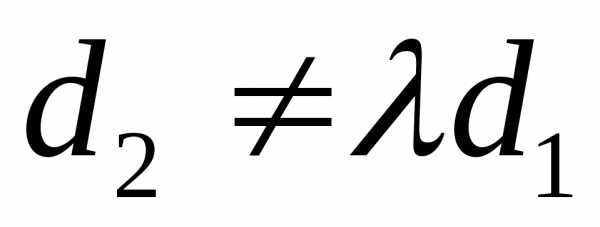, или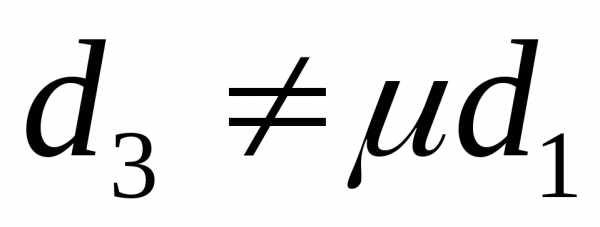, то система противоречива и не имеет решений – параллельные плоскости.

Однородная система трех линейных уравнений с тремя неизвестными.

Однородной называют систему, в которой ,.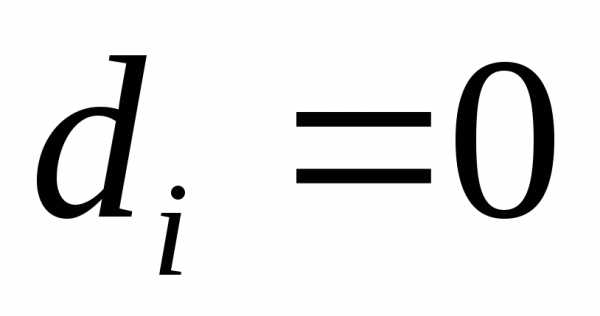

.

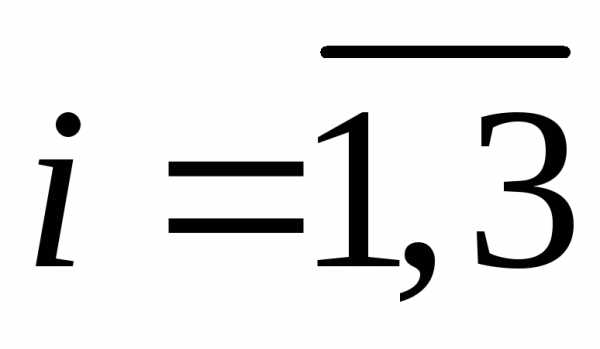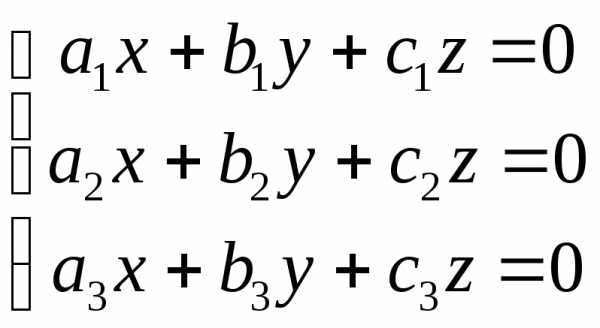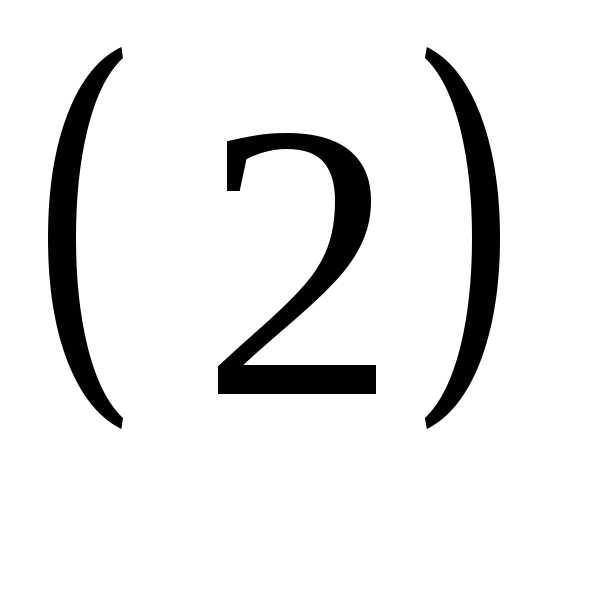
Система 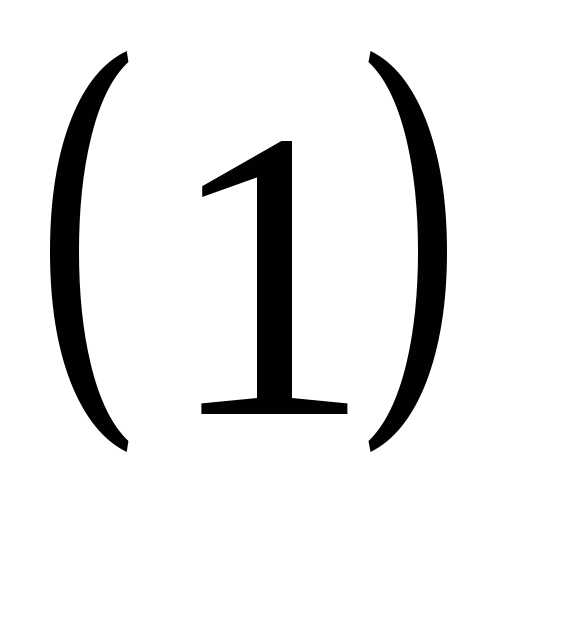— неоднородна.

Если в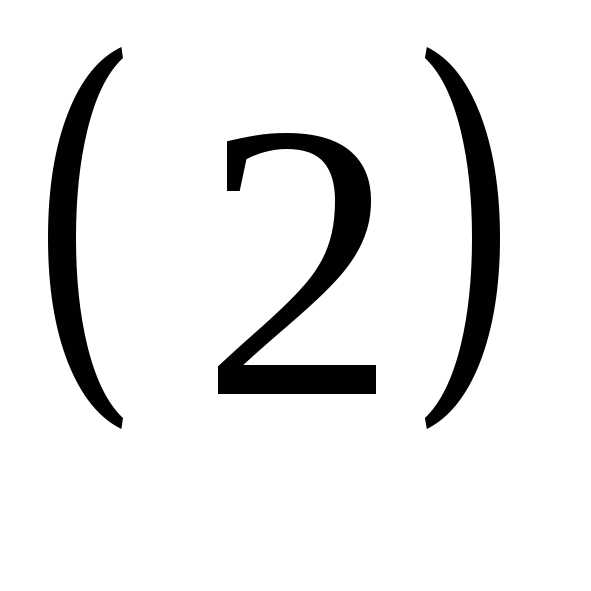не равен нулю, то система имеет единственное решение.

Если же 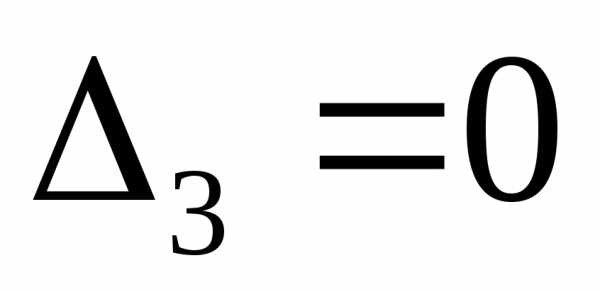, то среди его строк есть линейная зависимость и в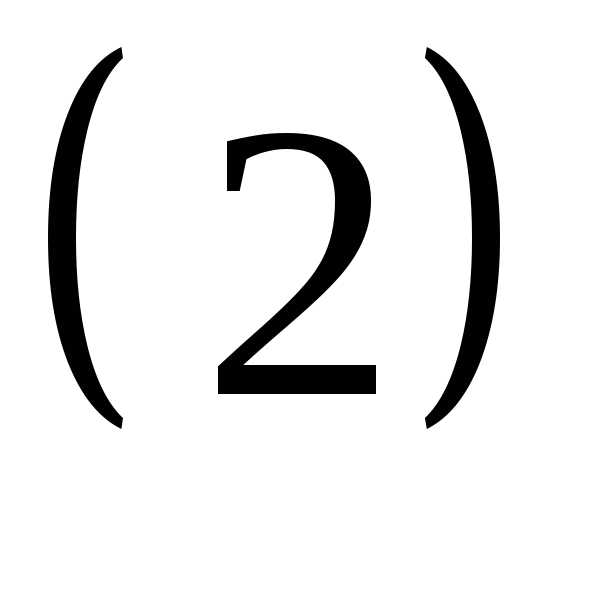остается два или одно независимое уравнение.

Решение произвольных систем линейных уравнений

Пусть задана система 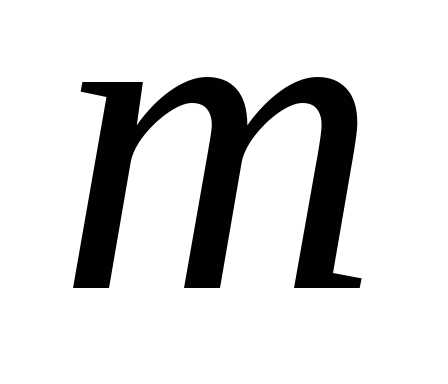линейных уравнений с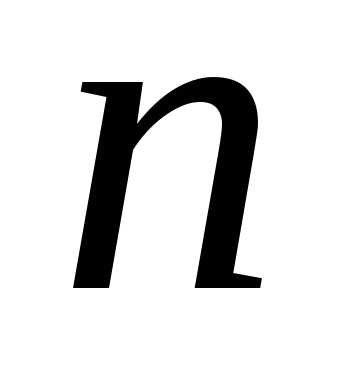неизвестными,:

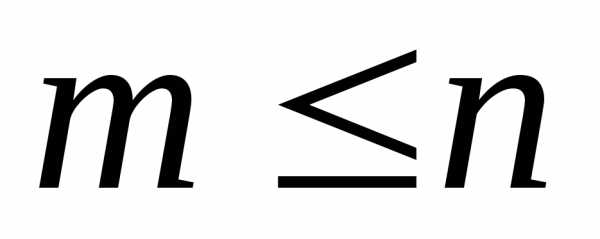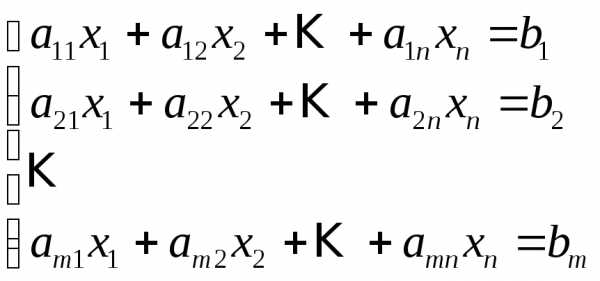, (1)

или в матричной форме

, (2)

где

, ,.

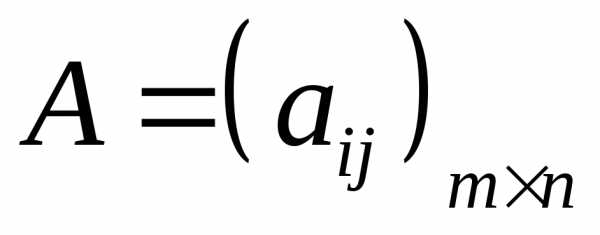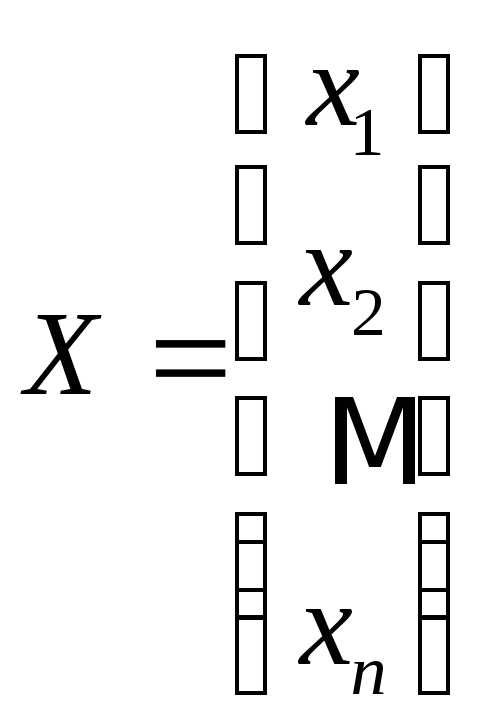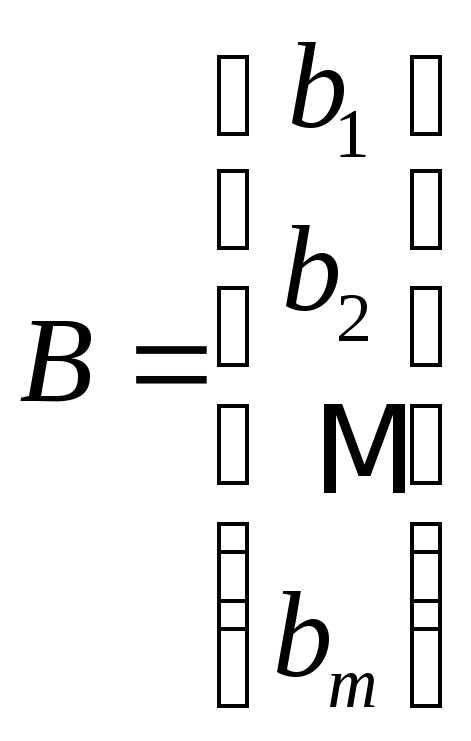Решением системы (1) или (2) называется любой 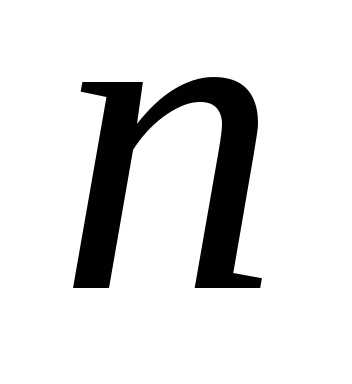-компонентный вектор-столбец или матрица-столбец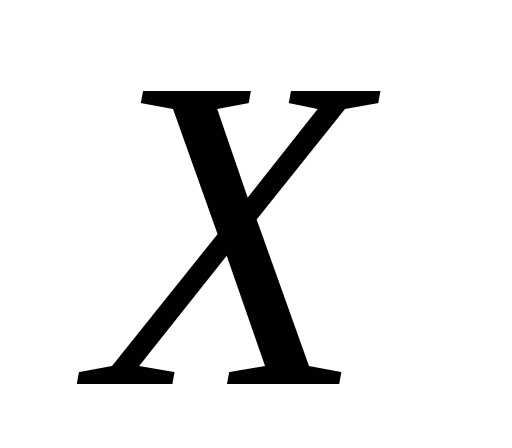, обращающий в верное равенство системы (1) или (2).

Система называется совместной, если у нее существует хотя бы одно решение. В противном случае, система несовместна. Две системы называют эквивалентными, если множества их решений совпадают.

Теорема Кронекера–Капелли. Чтобы система вида (1) была совместна, необходимо и достаточно, чтобы

,

где 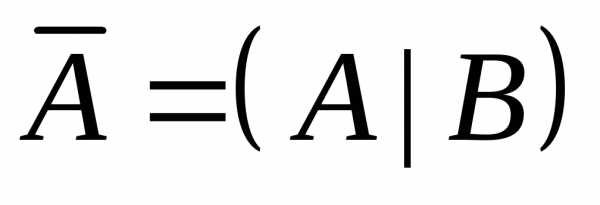— расширенная матрица системы.

Пусть теперь в системе (2) , т.е. она совместна. Можно считать, не ограничивая общности, что не равный нулю минор порядка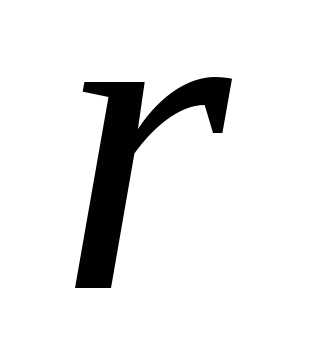располагается в первых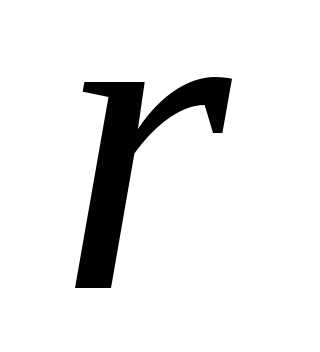строках и столбцах матрицы.

Запишем «укороченную» систему для (1), отбросив последние 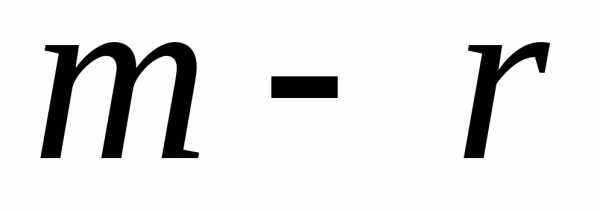уравнений, в виде:

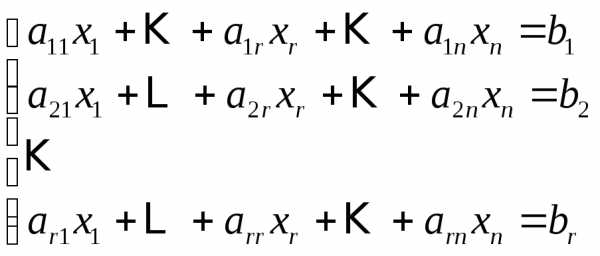(3)

Эта система эквивалентна исходной, т.к. отброшенные уравнения являются линейной комбинацией оставшихся уравнений.

Неизвестные называют базисными, а- свободными. Перенесем теперь свободные переменные в правую часть (3). В результате получим систему относительно базисных неизвестных:

.

Эта система для любого набора значений свободных неизвестных имеет единственное решение:

,

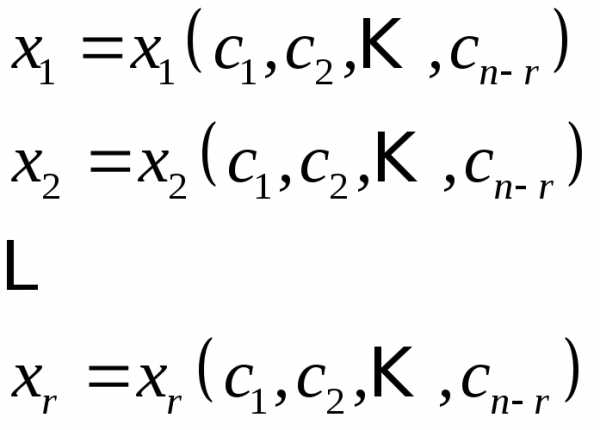где ,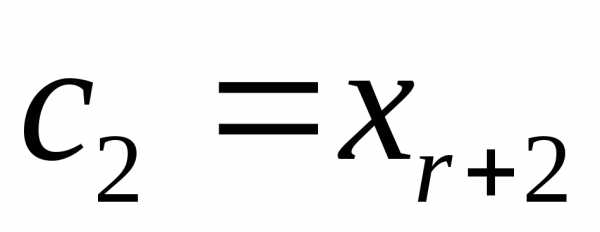,,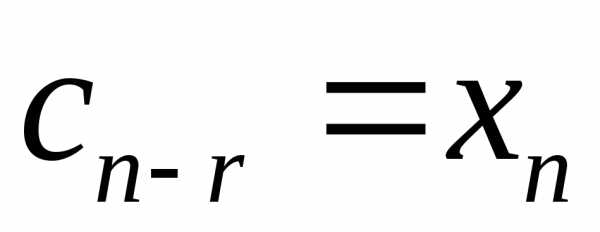— набор свободных неизвестных.

Соответствующее решение укороченной, а следовательно и исходной системы имеет вид:

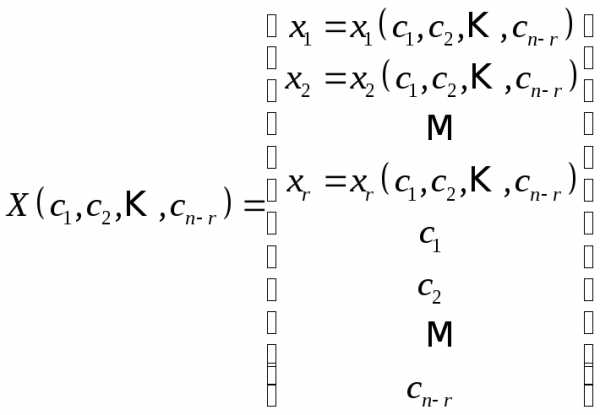. (4)

Формула (4) выражает произвольное решение системы (1) в виде функций от 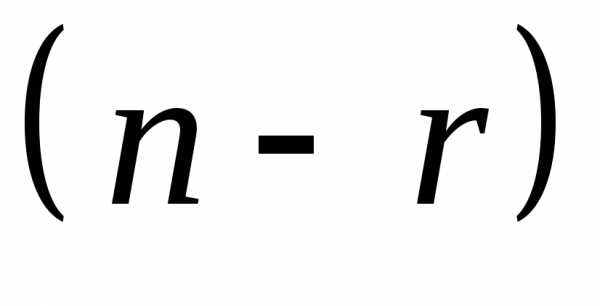свободных неизвестных и называетсяобщим решением системы. Каждому конкретному набору соответствуетчастное решение.

studfiles.net

No related posts.