Тема 2. Операции над множествами
Содержание
Пересечение множеств.
Объединение множеств.
Законы пересечения и объединения множеств.
Вычитание множеств. Дополнение одного множества до другого.
Понятие разбиения множества на классы.
Декартово произведение множеств.
Основная литература 7, 10, 11, 16, 23, 33, 34;
Дополнительная литература 82, 87, 92
1. Пересечение множеств
Из элементов двух и более множеств можно образовать новые множества. Считают, что эти новые множества являются результатомопераций над множествами.
Пример
Пусть
даны два множества: А = 2,
4, 6, 8
и В = 5,
6, 7, 8, 9.
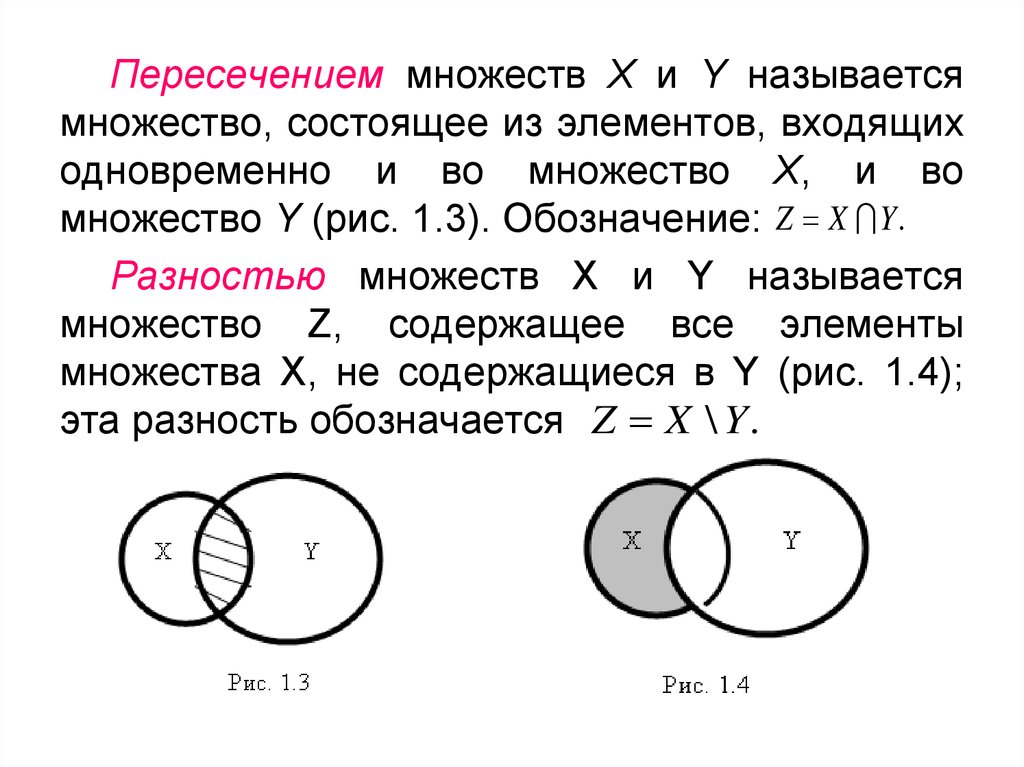
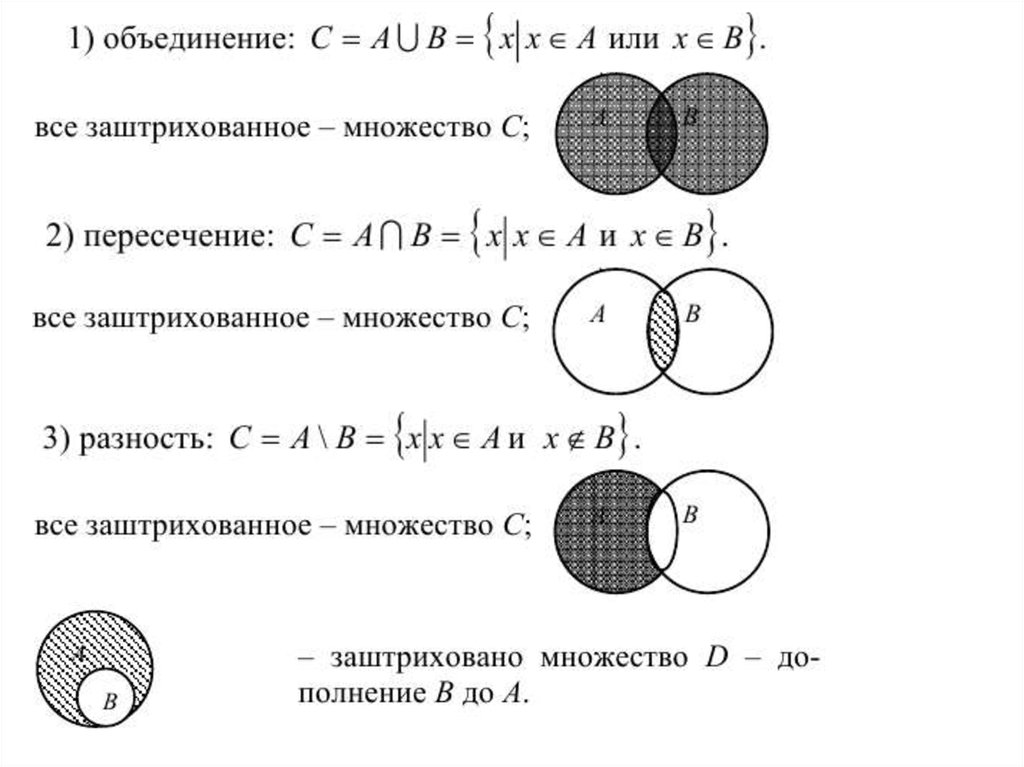
Определение. Пересечением множеств А и В называется множество, содержащее только такие элементы, которые принадлежат множеству А и множеству В.
Пересечение множеств А и В обозначают А В. Тогда определение можно представить в символической записи:
х х и х .
Если изображать множества А и В при помощи кругов Эйлера, то пересечение данных множеств изобразится заштрихованной частью.
В том случае, когда множества А и В не имеют общих элементов, говорят, что их пересечение пусто и пишут: А В = .
Замечание
. Операция, при помощи которой находят
пересечение множеств, называется также
пересечением
Операция, при помощи которой находят
пересечение множеств, называется также
пересечениемЕсли элементы множеств А и В перечислены, то, чтобы найти АВ, достаточно перечислить элементы, которые принадлежат А и В, т.е. их общие элементы.
Пример
Найдем пересечение множества А – четных натуральных чисел и множества В – двузначных натуральных чисел.
Характеристическое свойство элементов множества А – «быть четным натуральным числом», характеристическое свойство элементов множества В – «быть двузначным натуральным числом». Тогда, согласно определению, элементы пересечения данных множеств должны обладать свойством «быть четным и двузначным натуральным числом». Таким образом, множество А В состоит из четных двузначных чисел (союз «и» в данном случае можно опустить). Полученное множество не пусто. Например, 24 АВ, поскольку число 24 четное и двузначное.
Пример
Найти
пересечение множества А – четных
натуральных чисел и множества В –
натуральных чисел, кратных 4. Данные
множества А и В бесконечные, и множество
В – подмножество множества А. Поэтому
элементами, принадлежащими множеству
А и множеству В, будут элементы множества
В. Следовательно, А
В = В.
Данные
множества А и В бесконечные, и множество
В – подмножество множества А. Поэтому
элементами, принадлежащими множеству
А и множеству В, будут элементы множества
В. Следовательно, А
В = В.
2. Объединение множеств
Для того, чтобы объяснить школьнику, что 2 + 3 = 5, учитель берет 2 красных кружка и 3 синих. Просит перечислить эти кружки, затем предлагает к красным кружкам придвинуть синие (т.е. объединить эти две совокупности, два множества) и пересчитать все кружки совокупности. Устанавливается, что их 5, т.е. 2 +3 = 5. Таким образом, сложение чисел опирается на операцию объединения
двух множеств.В рассмотренном примере объединялись множества, не имеющие общих элементов. В математике приходится выполнять объединение и пересекающихся множеств.
Определение. Объединением множеств А и В называется множество, содержащее такие элементы, которые принадлежат множеству А или множеству В.
Объединение
множеств А и В обозначают
. В символической записи: х
х
или х
.
В символической записи: х
х
или х
.
Если изобразить пересекающиеся множества при помощи кругов Эйлера, то их объединение изобразится заштрихованной областью (рис. 1). Если множества А и В не пересекаются, то их объединение изображают так (рис. 2).
Рис 1. Рис. 2.
Операция, при помощи которой находят объединение множеств, называют также объединением.
Если все элементы множеств А и В перечислены, то, чтобы найти , достаточно перечислить элементы, принадлежащие А или В, т.е. хотя одному из множеств.
Пример
Так, если А = 2, 4, 6, 8, В = 5, 6, 7, 8, 9, то А В = 2, 4, 5, 6, 7, 8, 9.
Пример
Найти
объединение множества А четных чисел
и множества В двузначных чисел.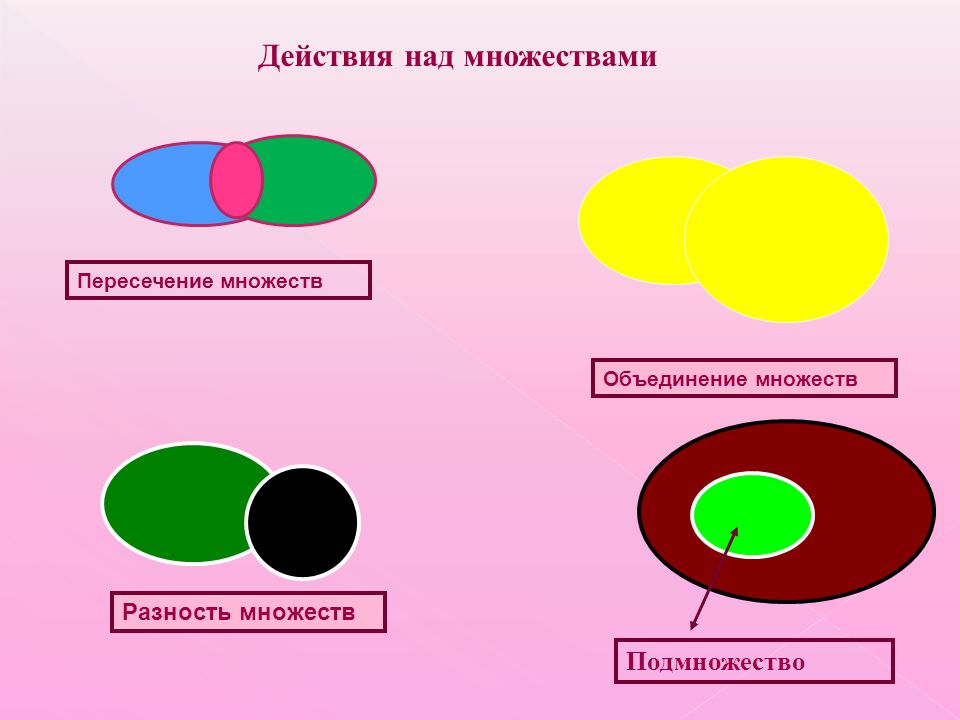 Так как
свойство элементов множества А – «быть
четным числом», а свойство элементов В
– «быть двузначным числом», то в
объединение данных множеств войдут
числа, характеристическое свойство
которых — «быть четным или двузначным
числом».
Так как
свойство элементов множества А – «быть
четным числом», а свойство элементов В
– «быть двузначным числом», то в
объединение данных множеств войдут
числа, характеристическое свойство
которых — «быть четным или двузначным
числом».
Например, в А В есть числа: 8, поскольку оно четное; 17, поскольку оно двузначное; 36, поскольку оно четное и двузначное.
Пример
Найти объединение множеств А – четных натуральных чисел и множества В – натуральных чисел, кратных 4.
Ранее было установлено, что В А. Поэтому элементами, принадлежащими множеству А , будут элементы множества А.
Следовательно, в данном случае = А.
Множества, операции над множествами — Дискретная математика (Математика)
1. Множества.
1.1. Множества, операции над множествами.
1.1.1. Основные определения.
Наиболее простая структура данных, используемых в математике, имеет место в случае, когда между отдельными данными присутствуют какие- либо взаимосвязи.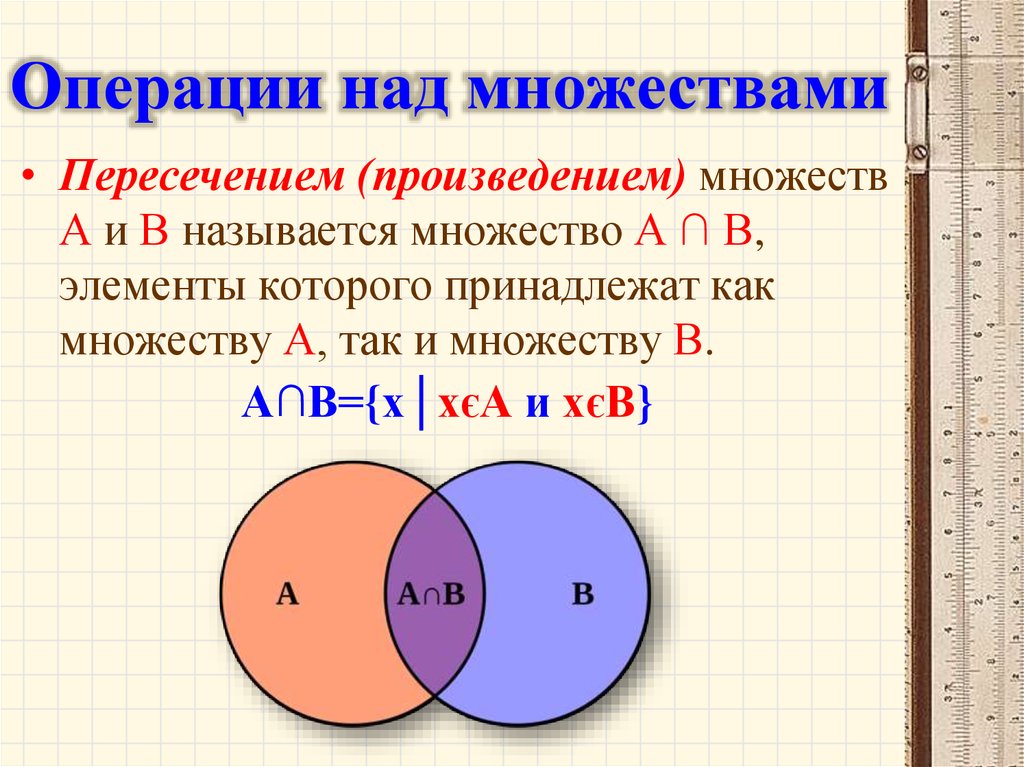 Совокупность таких данных представляет собой множество.
Совокупность таких данных представляет собой множество.
Понятие множество принадлежит к числу фундаментальных неопределяемых понятий математики.
Множество можно представить себе как совокупность объектов, обладающих общим свойством. Объекты, из которых составлено множество, называются его элементами.
Для того чтобы некоторую совокупность элементов можно было назвать множеством, необходимо, чтобы выполнялись условия:
q должно существовать правило, позволяющее определить, принадлежит ли некоторый элемент множеству;
q должно существовать правило, позволяющее отличать элементы друг от друга (множество не может содержать двух одинаковых элементов).
Множества обычно обозначают большими латинскими буквами (например, A, S, D), а их элементы — строчными (например, a, s, d).
Если элемент х принадлежит множеству А, то это обозначается: хА; в противном случае говорят, что элемент не принадлежит множеству, это обозначается: хА.
Примеры множеств.
1. Множество N — множество натуральных чисел. 1N. -1N.
Множество N — множество натуральных чисел. 1N. -1N.
2. Множество L — множество букв русского алфавита. фL. vL.
Множество не содержащие элементов называется пустым. Это множество обозначается .
Множества можно задавать следующими способами.
1. Перечисление элементов: P={точка, прямая, плоскость, тело}, S={0,1,2}.
2. Задание характеристического свойства: L={n|nN и n<7}.
1.1.2. Сравнение множеств.
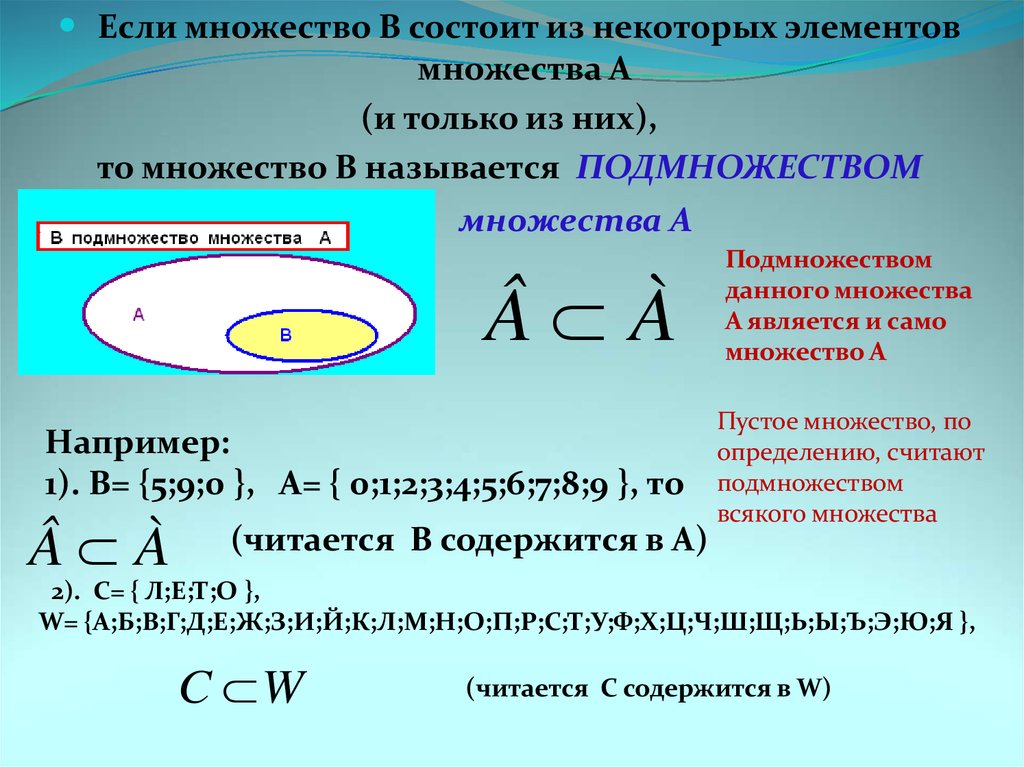
Множество А содержится во множестве В (множество В включает множество А, множество А является подмножеством В), если каждый элемент множества А является элементом множества В. Обозначение: АВ.
АВ хА хВ.
Два множества называются равными, если они являются подмножествами друг друга. Обозначение: А=В.
А=В АВ и ВА.
Если непустое множество А является подмножеством В и множества А и В не являются равными, то А является собственным подмножеством В.
Пример: М={4, 6, 8, 10}, К={6, 8}; КМ, МК, МК, К – собственное подмножество М.
Для множеств существует понятие мощность. Для конечных множеств мощность совпадает с количеством элементов.
Пример: ||=0, |{}|=1, |{1, 2, 3, 4}|=4.
1.1.3. Операции над множествами.
Объединение двух множеств А и В – это новое множество, элементами которого являются элементы, принадлежащие множеству А или множеству В. Обозначение: АВ.
АВ={x| хА или хВ}.
Пересечение двух множеств А и В – это новое множество, элементами которого являются элементы, принадлежащие множеству А и множеству В. Обозначение: АВ.
АВ={x| хА и хВ}.
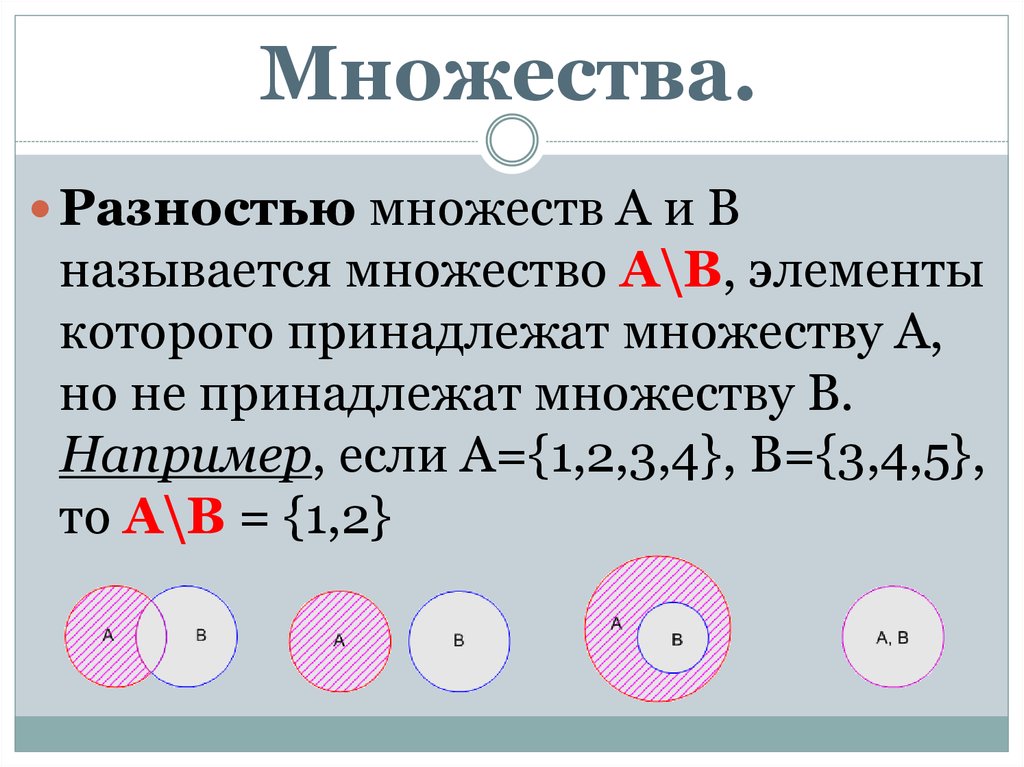
Разность двух множеств А и В – это новое множество, элементами которого являются элементы, принадлежащие множеству А и не принадлежащие множеству В. Обозначение: А В.
А В={x| хА и хВ}.
Обычно элементы множеств выбираются из некоторого достаточно широкого множества U, которое называется универсум. В связи с этим понятием можно ввести операцию дополнение.
Дополнением множества А называется множества, которое состоит из элементов универсума, не принадлежащих множеству А. Обозначение: .
Обозначение: .
=U A или ={x| хА и хU}.
Пример: U={1, 2, 3, 4, 5, 6, 7}, A={1, 2, 3, 4, 5}, В={2, 4, 6}.
АВ = {1, 2, 3, 4, 5, 6} АВ = {2, 4} А В = {1, 3, 5}
В А = {6} = {6, 7} = {1, 3, 5, 7}
Для наглядного изображения соотношений между множествами и изображения результатов операций над множествами используют диаграммы Эйлера.
Пример:
Свойства операций над множествами.
1. Идемпотентность пересечения, объединения.
АА = А АА = А
2. Коммутативность пересечения, объединения.
АВ = ВА АВ = ВА
3. Ассоциативность пересечения, объединения.
(АВ) С = А (В С) (АВ) С = А (В С)
4. Законы поглощения.
(АВ) А = А (АВ) A = А
5. Свойства пустого множества.
А = А = А
6. Свойства универсума.
А U = A АU = U
7. Инволютивность.
Инволютивность.
= А
Лекция «7. Экстремальные события на производстве» также может быть Вам полезна.
8. Законы де Моргана.
9. Свойства дополнения.
А = А = U
10. Выражения для разности.
А В = А
14.1: Группы, действующие на множества
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 81141
- Томас В. Джадсон
- Государственный университет Стивена Ф. Остина via Abstract Algebra: Theory and Applications
Пусть \(X\) — множество и \(G\) — группа. Действие (слева) оператора \(G\) на \(X\) представляет собой отображение \(G \times X \rightarrow X\), заданное формулой \((g,x) \mapsto gx\text{ ,}\), где
- \(ex = x\) для всех \(x \in X\text{;}\)
- \((g_1 g_2)x = g_1(g_2 x)\) для всех \(x \in X\) и всех \(g_1, g_2 \in G\text{.
 }\)
}\)
При этих рассуждениях \(X\) называется \(G\)-множеством . Обратите внимание, что мы не требуем, чтобы \(X\) каким-либо образом был связан с \(G\). Верно, что каждая группа \(G\) действует на каждое множество \(X\) тривиальным действием \((g,x) \mapsto x\text{;}\), однако групповые действия более интересны, если множество \(X\) каким-то образом связано с группой \(G\text{.}\) 92\) и \(I\) — единичная матрица, то \(Iv = v\text{.}\) Если \(A\) и \(B\) \(2 \times 2\) обратимые матрицы , то \((AB)v = A(Bv)\), так как умножение матриц ассоциативно.
Пример \(14.2\)
Пусть \(G = D_4\) — группа симметрии квадрата. Если \(X = \{ 1, 2, 3, 4 \}\) множество вершин квадрата, то мы можем считать, что \(D_4\) состоит из следующих перестановок:
\[ \{ ( 1), (1 \, 3), (2 \, 4), (1 \, 4 \, 3 \, 2), (1 \, 2 \, 3 \, 4), (1 \, 2)( 3 \, 4), (1 \, 4)(2 \, 3), (1 \, 3)(2 \, 4) \}\text{.} \nonumber \]
Решение
Элементы \(D_4\) действуют на \(X\) как функции.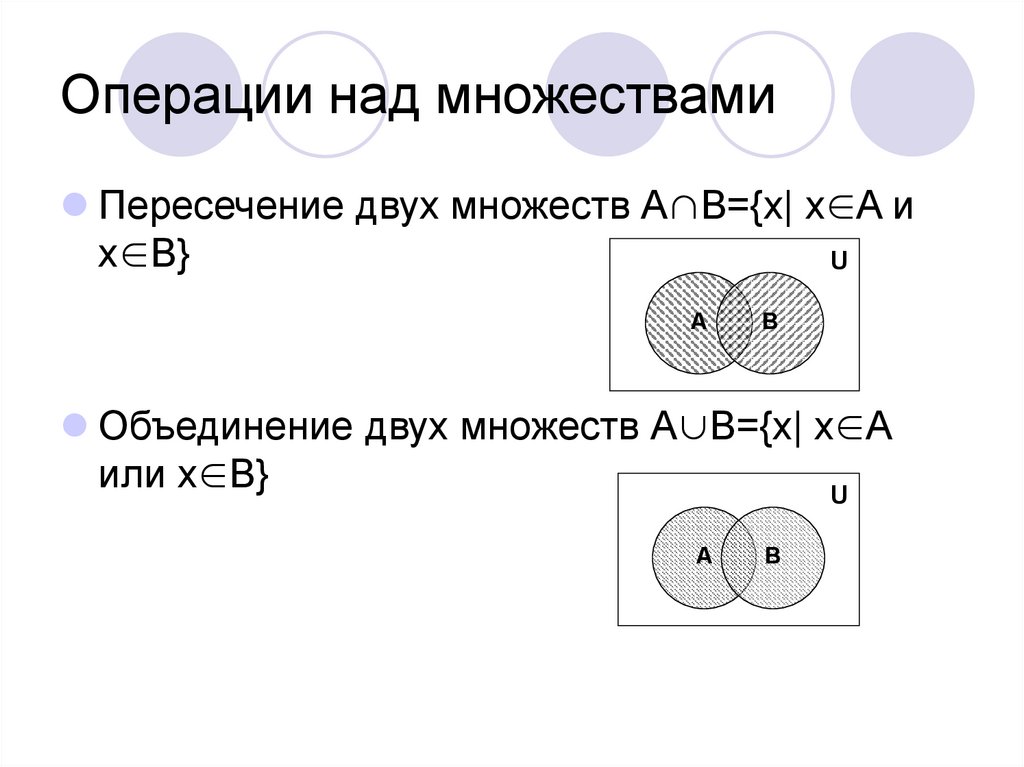 Перестановка \((1 \, 3)(2 \, 4)\) действует на вершину \(1\), отправляя ее в вершину \(3\text{,}\) на вершине \(2\), отправляя его в вершину \(4\text{,}\) и так далее. Легко видеть, что аксиомы группового действия выполняются.
Перестановка \((1 \, 3)(2 \, 4)\) действует на вершину \(1\), отправляя ее в вершину \(3\text{,}\) на вершине \(2\), отправляя его в вершину \(4\text{,}\) и так далее. Легко видеть, что аксиомы группового действия выполняются.
В общем случае, если \(X\) — любое множество, а \(G\) — подгруппа \(S_X\text{,}\), то группа всех перестановок, действующих на \(X\text{,}\), тогда \(X\) является \(G\)-множеством относительно группового действия
\[ (\sigma, x) \mapsto \sigma(x) \nonumber \]
для \(\sigma \in G\) и \(x \in X\text{.}\)
Пример \(14.3\)
Если положить \(X = G\text{,}\), то каждая группа \(G\) действует сама на себя по левому регулярному представлению; то есть \((g,x) \mapsto \lambda_g(x) = gx\text{,}\) где \(\lambda_g\) — умножение слева:
\begin{gather*} e \cdot x = \lambda_e x = ex = x\\ (gh) \cdot x = \lambda_{gh}x = \lambda_g \lambda_h x = \lambda_g(hx) = g \cdot ( h \cdot x)\text{.} \ конец {собрать *}
Решение
Если \(H\) является подгруппой \(G\text{,}\), то \(G\) является \(H\)-множеством относительно левого умножения на элементы \( Н\текст{.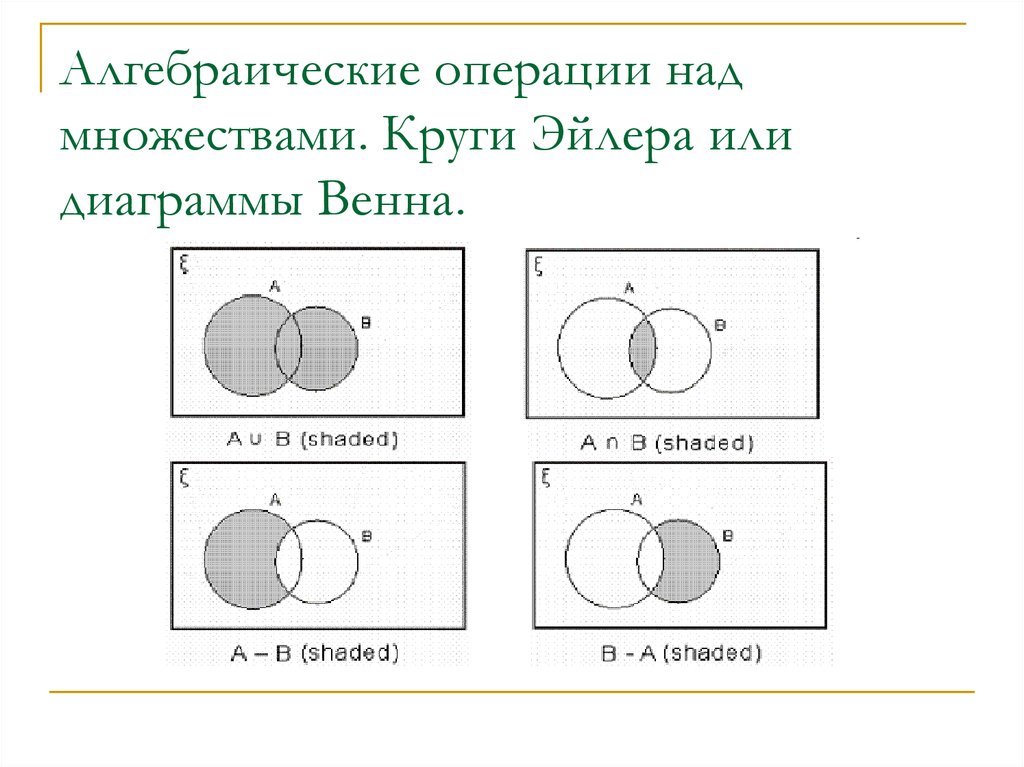
Пример \(14.4\)
Пусть \(G\) — группа и предположим, что \(X=G\text{.}\) Если \(H\) — подгруппа \(G\text{, }\) тогда \(G\) является \(H\)-множеством относительно сопряжения ; то есть мы можем определить действие \(H\) на \(G\text{,}\)
\[ H \times G \rightarrow G\text{,} \nonumber \] 9{-1}\\ & = (h_1, (h_2, g))\text{,} \end{align*}
видим, что второе условие также выполняется.
Пример \(14.5\)
Пусть \(H\) — подгруппа \(G\) и \({\mathcal L}_H\) множество левых смежных классов \(H\text{.}\ ) Множество \({\mathcal L}_H\) является \(G\)-множеством под действием
\[ (g, xH) \mapsto gxH\text{.} \nonumber \]
Решение
Опять же, легко видеть, что первая аксиома верна. Поскольку \((g g’)xH = g( g’x H)\text{,}\), вторая аксиома также верна.
Если \(G\) действует на множестве \(X\) и \(x, y \in X\text{,}\), то \(x\) называется \(G\) — эквивалентно  }\) Мы пишем \(x \sim_G y\) или \(x \ sim y\), если два элемента \(G\)-эквивалентны.
}\) Мы пишем \(x \sim_G y\) или \(x \ sim y\), если два элемента \(G\)-эквивалентны.
Предложение \(14.6\)
Пусть \(X\) есть \(G\) -множество. Тогда \(G\) -эквивалентность является отношением эквивалентности на \(X\text{.}\)
- 9{-1}y=x\text{;}\) следовательно, \(y \sim x\text{.}\) Чтобы показать, что отношение транзитивно, предположим, что \(x \sim y\) и \( y \sim z\text{.}\) Тогда должны существовать групповые элементы \(g\) и \(h\) такие, что \(gx = y\) и \(hy= z\text{.}\) Итак, \(z = hy = (hg)x\text{,}\) и \(x\) эквивалентно \(z\text{.}\)
Если \(X\) является \(G\)-множеством, то каждое разбиение \(X\), связанное с \(G\)-эквивалентностью, называется орбитой множества \(X\) при \(G\text{.}\) Обозначим орбиту, содержащую элемент \(x\) из \(X\), через \({\mathcal O}_x\text{.}\)
Пример \(14.7\)
Пусть \(G\) — группа перестановок, определенная формулой
\[ G =\{(1), (1 \, 2 \, 3), (1 \, 3 \, 2), (4 \, 5), (1 \, 2 \, 3)(4 \, 5), (1 \, 3 \, 2)(4 \, 5) \} \номер\]
и \(X = \{ 1, 2, 3, 4, 5\}\text{.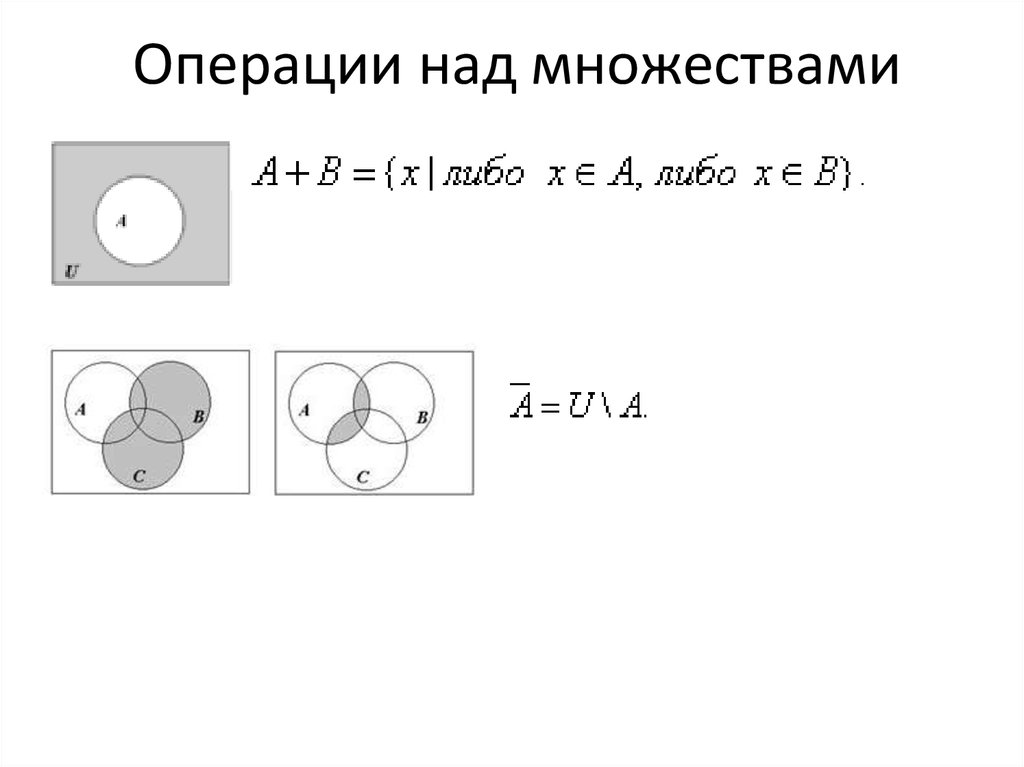 }\)
}\)
Решение
Тогда \(X\) является \(G\)-множеством. Орбиты равны \({\mathcal O}_1 = {\mathcal O}_2 = {\mathcal O}_3 =\{1, 2, 3\}\) и \({\mathcal O}_4 = {\mathcal О}_5 = \{4, 5\}\текст{.}\)
Теперь предположим, что \(G\) — группа, действующая на множестве \(X\), и пусть \(g\) — элемент множества \(G\text{.}\).0032 набор фиксированных точек из \(g\) в \(X\text{,}\), обозначенный \(X_g\text{,}\), является набором всех \(x \in X\) таких что \(gx = x\text{.}\) Мы также можем изучать групповые элементы \(g\), которые фиксируют данное \(x \in X\text{.}\) Это множество больше, чем подмножество \(G\text{,}\) это подгруппа. Эта подгруппа называется стабилизирующей подгруппой или изотропной подгруппой группы \(x\text{.}\). Мы будем обозначать стабилизирующую подгруппу группы \(x\) через \(G_x\text{.} \)
Замечание \(14.8\)
Закон об идеальном газе легко запомнить и применять при решении задач, если вы получаете правильные значения a
Пример \(14. 9\)
9\)
Пусть \(X = \{1, 2, 3, 4, 5, 6\}\) и пусть \(G\) является группой перестановок, заданной перестановками
\ [ \{ (1), (1 \, 2)(3 \, 4 \, 5 \, 6), (3 \, 5)(4 \, 6), (1 \, 2)( 3 \, 6 \, 5 \, 4) \}\text{.} \nonumber \]
Решение
Тогда множества неподвижных точек \(X\) под действием \(G\) равны
\begin{gather*} X_{(1)} = X,\\ X_{(3 \, 5)(4 \, 6)} = \{1,2\},\\ X_{(1 \ , 2)(3 \, 4 \, 5 \, 6)} = X_{(1 \, 2)(3 \, 6 \, 5 \, 4)} = \emptyset\text{,} \end{gather *}
и подгруппы стабилизатора
\begin{gather*} G_1 = G_2 = \{(1), (3 \, 5)(4 \, 6) \},\\ G_3 = G_4 = G_5 = G_6 = \{(1)\}\text{.} \end{gather*}
Легко видеть, что \(G_x\) является подгруппой \(G\) для каждого \(x \in X\ текст{.}\)
Предложение \(14.10\)
Пусть \(G\) — группа, действующая на множестве \(X\) и \(x \in X\text{.}\) Стабилизатор группы \(x\text{,} \) \(G_x\text{,}\) является подгруппой \(G\text{.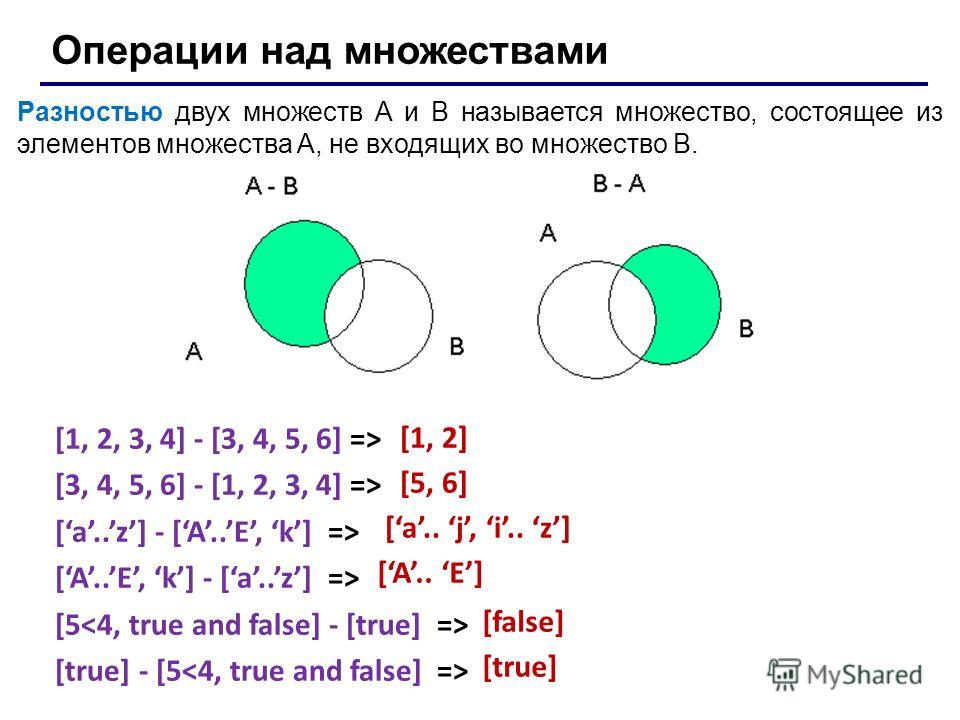 {-1}\) находится в \(G_x\text{.}\)
{-1}\) находится в \(G_x\text{.}\)
Мы будем обозначать количество элементов в множестве неподвижных точек элемента \(g \in G\) через \(|X_g|\) и обозначать количество элементов в орбите \(x \in X\) на \(|{\mathcal O}_x|\text{.}\) Следующая теорема демонстрирует связь между орбитами элемента \(x \in X\) и левыми смежными классами \(G_x\) в \( Г\текст{.}\)
Теорема \(14.11\)
Пусть \(G\) — конечная группа и \(X\) — конечное \(G\) -комплект. Если \(x \in X\text{,}\) , то \(|{\mathcal O}_x| = [G:G_x]\text{.}\)
- Доказательство
Мы знаем, что \(|G|/|G_x|\) есть число левых смежных классов \(G_x\) в \(G\) по теореме Лагранжа (теорема \(6.10\)). Мы определим биективное отображение \(\phi\) между орбитой \({\mathcal O}_x\) из \(X\) и набором левых смежных классов \({\mathcal L}_{G_x}\) из \(G_x\) в \(G\text{.}\) Пусть \(y \in {\mathcal O}_x\text{.
 }\) Тогда существует \(g\) в \(G\ ) такой, что \(g x = y\text{.}\) Определим \(\phi\) как \(\phi( y ) = g G_x\text{.}\) Чтобы показать, что \(\phi\) является взаимно однозначно, предположим, что \(\phi(y_1) = \phi(y_2)\text{.}\) Тогда
}\) Тогда существует \(g\) в \(G\ ) такой, что \(g x = y\text{.}\) Определим \(\phi\) как \(\phi( y ) = g G_x\text{.}\) Чтобы показать, что \(\phi\) является взаимно однозначно, предположим, что \(\phi(y_1) = \phi(y_2)\text{.}\) Тогда\[ \phi(y_1) = g_1 G_x = g_2 G_x = \phi(y_2)\text{,} \nonumber \]
где \(g_1 x = y_1\) и \(g_2 x = y_2\text{.}\) Поскольку \(g_1 G_x = g_2 G_x\text{,}\) существует \(g \in G_x\) такой, что \(g_2 = g_1 g\text{,}\)
\[ y_2 = g_2 x = g_1 g x = g_1 x = y_1; \номер\]
, следовательно, карта \(\phi\) взаимно однозначна. Наконец, мы должны показать, что отображение \(\phi\) на. Пусть \(g G_x\) — левый смежный класс. Если \(g x = y\text{,}\), то \(\phi(y) = g G_x\text{.}\)
Эта страница под названием 14.1: Группы, действующие на множества, распространяется в соответствии с лицензией GNU Free Documentation License 1.3 и была создана, изменена и/или курирована Томасом В.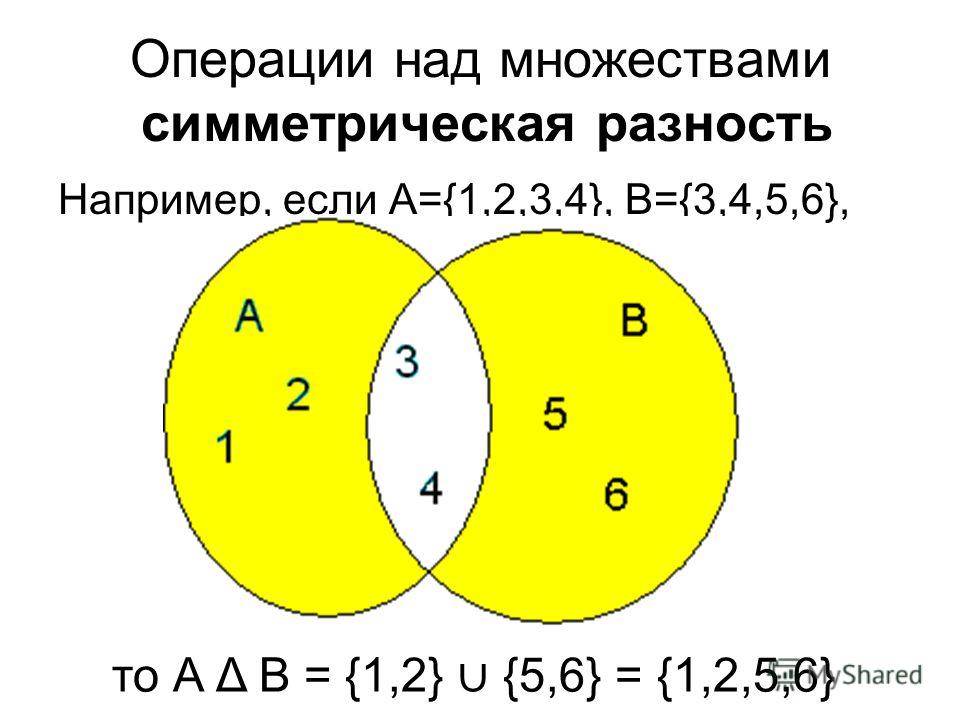 Джадсоном (Абстрактная алгебра: теория и приложения) через исходное содержимое, которое было отредактировано. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
Джадсоном (Абстрактная алгебра: теория и приложения) через исходное содержимое, которое было отредактировано. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Томас В. Джадсон
- Лицензия
- ГНУ ФДЛ
- Версия лицензии
- 1,3
- Показать страницу TOC
- нет
- Теги
- источник@http://abstract.
 ups.edu/aata
ups.edu/aata
- источник@http://abstract.
Набор действий — Таблица
Используйте набор действий, чтобы ваша аудитория могла напрямую взаимодействовать с визуализацией или приборной панелью для управления аспектами своего анализа. Когда кто-то выбирает метки в представлении, действия набора могут изменить значения в наборе. Примеры использования установленных действий см. в разделе Примеры установленных действий.
Посмотрите видео : чтобы увидеть связанные концепции, продемонстрированные в Tableau, посмотрите Set Actions(ссылка открывается в новом окне), 7-минутное бесплатное обучающее видео. Используйте свою учетную запись tableau.com(ссылка открывается в новом окне) для входа.
Действия набора берут существующий набор и обновляют значения, содержащиеся в этом наборе, на основе действий пользователя в а именно. Вы можете определить установленное действие, чтобы оно включало:
- исходный лист или листы, к которым оно применяется.

- поведение пользователя, которое запускает действие (наведение, выбор или меню).
- целевой набор (используемый источник данных и набор).
- что происходит, когда выделение очищается.
Чтобы изменить или повлиять на визуализацию, набор, указанный в действии, должен каким-то образом использоваться в визуализации. Это можно сделать разными способами, например, используя набор в вычисляемом поле, которое затем используется для построения визуальной визуализации, или поместив набор в представление или в свойство карточки Marks.
Вы можете создавать наборы действий в Tableau Desktop, Tableau Cloud и Tableau Server.
Общие этапы настройки действий
Создайте один или несколько наборов. Создаваемые наборы будут связаны с выбранным в данный момент источником данных.
 Подробнее о создании наборов см. в разделе Создание наборов.
Подробнее о создании наборов см. в разделе Создание наборов.Создайте действие набора, использующее один из созданных вами наборов. Вы можете создать несколько наборов действий для разных целей.
В зависимости от поведения, которое вы хотите предоставить пользователям для анализа, вы можете создать вычисляемое поле, использующее этот набор. Дополнительные сведения о создании вычисляемых полей см. в разделе Создание вычисляемого поля.
Создайте визуализацию, использующую набор, на который ссылается действие набора. Например, если вы создаете вычисляемое поле, использующее набор, создайте представление с использованием этого вычисляемого поля. Или перетащите набор в поле «Цвет» на карточке «Метки».

Протестируйте установленное действие и при необходимости измените его настройки, чтобы получить желаемое поведение аудитории.
Приступая к работе : Обзор того, что вам нужно знать для создания действий набора, см. в разделе На ваших метках, настройтесь, вперед: все, что вам нужно знать, чтобы начать работу с действиями набора (ссылка открывается в новом окне) на Блог Data Viz Linds (ссылка открывается в новом окне).
Создать набор действий
На рабочем листе выберите Рабочий лист > Действия. На панели инструментов выберите Панель инструментов > Действия.
В диалоговом окне «Действия» нажмите «Добавить действие» и затем выберите «Изменить заданные значения».

В диалоговом окне «Добавить/изменить действие набора» укажите осмысленное имя для действия.
Выберите исходный лист или источник данных. Текущий лист выбран по умолчанию. Если вы выбираете источник данных или информационную панель, вы можете выбрать отдельные листов внутри него.
Выберите, как пользователи будут выполнять действие.
Hover — запускается, когда пользователь наводит курсор мыши на метку в представлении.
Select — запускается, когда пользователь щелкает метку в представлении.
 Этот вариант хорошо работает для заданных действий.
Этот вариант хорошо работает для заданных действий.Меню — запускается, когда пользователь щелкает правой кнопкой мыши (удерживая нажатой клавишу Control на Mac) выбранную метку в представлении, а затем выбирает параметр в контекстном меню.
Укажите целевой набор. Сначала выберите источник данных, а затем выберите набор.
Наборы, доступные в списках Target Set определяются выбранным источником данных и наборами, созданными в рабочей книге, которые связаны с этим источником данных.
В этом примере целевой набор использует Global Superstore 2016 в качестве источника данных и High Shipping Orders в качестве набора.

Укажите, что происходит, когда действие выполняется в представлении:
Назначить значения для набора — Заменяет все значения в наборе выбранными значениями.
Добавить значения в набор — Добавляет в набор индивидуально выбранные значения.
Удалить значения из набора — Удаляет индивидуально выбранные значения из набора.
Укажите, что происходит при снятии выделения в представлении:
Сохранить установленные значения — Текущие значения в наборе остаются в наборе.
Добавить все значения в набор — Добавляет все возможные значения в набор.
Удалить все значения из набора — Удаляет ранее выбранные значения из набора.

Нажмите OK, чтобы сохранить изменения и вернуться к представлению.
Проверьте установленное действие, взаимодействуя с визуализацией. Настройте некоторые параметры действия, чтобы настроить поведение выбора по мере необходимости.
Примечание: Выбор Добавить значения для набора или Удалить значения из набора в диалоговом окне «Действие набора» изменяет значения, выбранные на вкладке «Общие» определения набора — так же, как это делает Назначить значения для набора .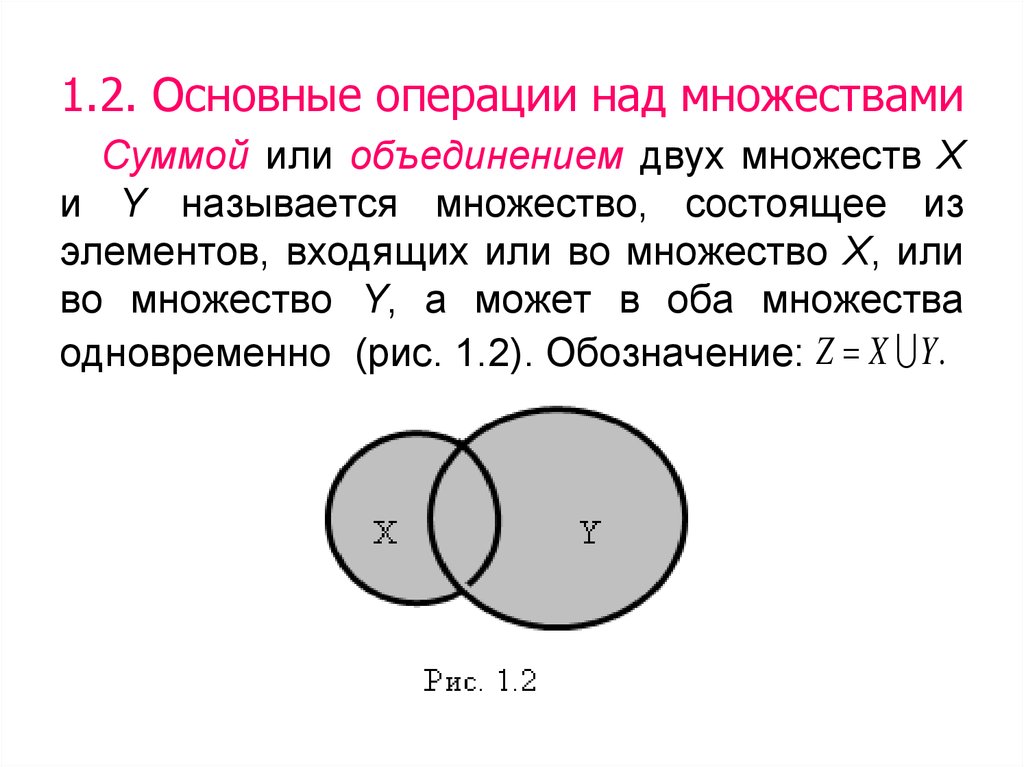 Это отличается от функций «Добавить в » и « Удалить из », доступных только в авторском режиме через контекстное меню набора во всплывающей подсказке. Последний объединяет или удаляет значения в наборе и из набора после того, как заданное условие было применено.
Это отличается от функций «Добавить в » и « Удалить из », доступных только в авторском режиме через контекстное меню набора во всплывающей подсказке. Последний объединяет или удаляет значения в наборе и из набора после того, как заданное условие было применено.
Примеры действий с наборами
В следующих примерах показаны лишь некоторые способы использования действий с наборами. Чтобы продолжить, вам необходимо ознакомиться с созданием и использованием наборов и вычисляемых полей. Дополнительные сведения см. в разделах Создание наборов и Создание вычисляемого поля.
Узнать больше : Дополнительные подробные примеры того, как вы можете использовать набор действий, продемонстрированных в Tableau, см.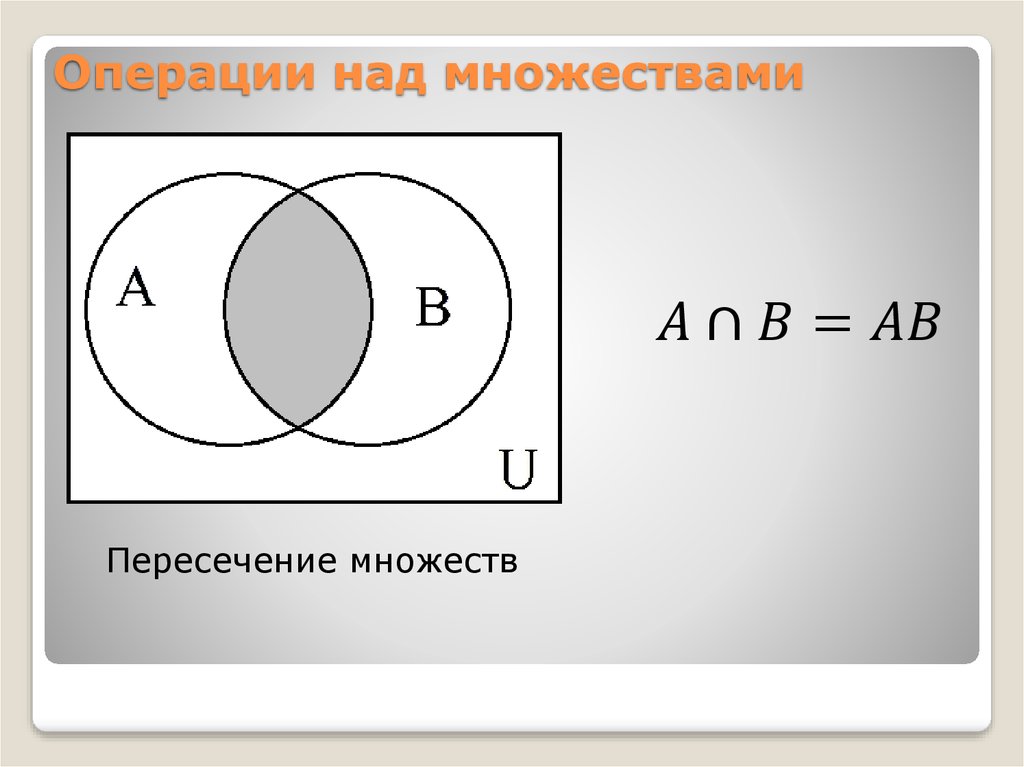 :
:
- 8 способов представить аудитории новые мощные сравнения с заданными действиями(ссылка открывается в новом окне) в блоге Tableau(ссылка открывается в новом окне)
- 8 аналитических концепций, которые можно выразить с помощью набора действий Tableau(ссылка открывается в новом окне) (блог Tableau)
- Разработка приложений расширенной аналитики с помощью набора действий Tableau(ссылка открывается в новом окне) (блог Tableau)
- Темы по набору действий в блоге Data Viz Linds (ссылка открывается в новом окне)
- Установите примеры действий на веб-сайте Art of the Vizable(ссылка открывается в новом окне) от TabLabs.
Смотреть видео :
- Готово, установлено, действие!(Ссылка открывается в новом окне) (1 час)
- Наборы Обращение (1 час)
- Вне установленных действий | Интерактивная статистика(Ссылка открывается в новом окне) (1 час)
Пропорциональное закрашивание
Классический вариант использования заданных действий — это пропорциональное закрашивание, описанное в разделе Как сделать пропорциональное выделение с заданными действиями(ссылка открывается в новом окне) в блоге Tableau(ссылка открывается в новом окне) и Tableau Set Действия(ссылка открывается в новом окне) из блога The Information Lab(ссылка открывается в новом окне) (вместе с другими примерами).
Детали примера пропорциональной чистки
В этом примере используется источник данных Sample — Superstore . Это действие набора изменяет цвет существующих меток в представлении в зависимости от доли метки, которая находится в наборе или вне его.
Подключиться к образцу — данные Superstore в Tableau Desktop.
903:50На другом пустом листе перетащите показатель Продажи в Столбцы и перетащите Подкатегория 9.0341 измерение для строк.

Создайте набор для измерения Segment с именем Segment Set .
На листе, который показывает Продажи по подкатегориям, перетащите Набор сегментов на Цвет в карточке Метки.
Поменять местами цвета, используемые для отображения меток IN или OUT в наборе.
Создайте новую панель мониторинга.
 Перетащите оба листа на панель инструментов.
Перетащите оба листа на панель инструментов.В меню «Информационная панель» выберите «Действия». Нажмите «Добавить действие», а затем выберите «Изменить заданные значения».
Настройте действие, используя те же настройки, что и на изображении ниже.
Нажмите OK, чтобы сохранить изменения и вернуться к представлению.
Проверьте установленное действие, щелкнув метки для каждого сегмента.
На новом листе перетащите меру Продажи в Столбцы, а измерение Сегмент — в Строки.
Асимметричная детализация
Действия над наборами также можно использовать в нескольких наборах для более сложных взаимодействий. Если набор данных имеет иерархическую информацию, такую как категория, подкатегория и производитель, обычно при детализации иерархии раскрываются все значения на заданном уровне. Однако вы можете использовать заданные действия для асимметричной детализации, открывая только следующий уровень иерархии для выбранного значения.
Если набор данных имеет иерархическую информацию, такую как категория, подкатегория и производитель, обычно при детализации иерархии раскрываются все значения на заданном уровне. Однако вы можете использовать заданные действия для асимметричной детализации, открывая только следующий уровень иерархии для выбранного значения.
Подробности примера асимметричной детализации
В этом примере используется источник данных Sample — Superstore .
Заданные действия используются здесь в сочетании с двумя вычисляемыми полями для создания асимметричной детализации.
Создайте набор для поля Категория с именем Набор категорий .
Выберите любую категорию, чтобы стать членом этого набора. Членство является временным и будет перезаписано установленным действием.
Создайте вычисляемое поле с именем Асимметричная подкатегория .

Щелкните правой кнопкой мыши поле Sub-Category на панели данных и выберите «Создать вычисляемое поле».
Введите следующий расчет:
IF [Набор категорий] THEN [Подкатегория] ELSE [Категория] КОНЕЦЕсли категория метки или меток в представлении находится в наборе категорий, расчет вернет подкатегории для этой категории. В противном случае он снова вернет категорию.
Набор еще не используется в представлении и не имеет связанных с ним действий, поэтому на данный момент он статичен.
Создайте представление, перетащив поля Категория и Асимметричная подкатегория в строки (в указанном порядке).
 Затем перетащите Sales в Text на карточке Marks.
Затем перетащите Sales в Text на карточке Marks.Создать заданное действие.
В меню Рабочий лист выберите Действия. Нажмите «Добавить действие», а затем выберите «Изменить заданные значения».
Назовите действие Асимметричное сверление в подкатегории .
Выберите следующие параметры:
- Исходные листы: убедитесь, что выбран только текущий лист.
- Выполнить действие: выберите «Выбрать». Это заставит действие применяться, когда пользователь выбирает метку или метки в представлении.

- Целевой набор: выберите текущий источник данных из первого раскрывающегося списка и набор категорий из второго раскрывающегося списка.
- Отмена выбора: выберите Удалить все значения из набора.
Нажмите OK, чтобы сохранить изменения.
Проверить заданное действие.
Когда вы щелкаете заголовок или метку в представлении, оно разворачивается на следующий уровень. Щелкнув строку категории, вы развернете ее подкатегории.
Масштабирование цвета
Значения цвета в визуализации часто могут быть искажены выбросами. Когда одна страна имеет значительно более высокое значение, чем другие страны, нюанс различий между этими неэкстремальными значениями может быть потерян.
Действие набора может обновлять значения в наборе стран на основе выбора, а именно. Этот набор затем используется в вычисляемом поле, которое вычисляет значение соответствующей меры только для стран в этом наборе, и это вычисляемое поле помещается в цвет. Теперь, когда на карте выбраны страны, цветовая палитра основывается только на этих странах, показывая большие визуальные различия между этими значениями.
Подробности примера масштабирования цвета
В этом примере используется источник данных Global Superstore.
Создайте набор в поле Country с именем Country set . Выберите любую страну, которая будет участником набора. Членство является временным и будет перезаписано установленным действием.
Создайте вычисляемое поле с именем Стоимость доставки по стране .

Щелкните правой кнопкой мыши панель данных и выберите «Создать вычисляемое поле».
Введите следующий расчет:
ЕСЛИ [Набор страны] ТО ([Стоимость доставки]) КОНЕЦЕсли страна маркировки в представлении находится в наборе Country, расчет возвращает стоимость доставки. В противном случае он ничего не делает.
Вычисляемое поле связывает набор с представлением.
Дважды щелкните значок Country 9.0341 измерение для автоматического создания карты.
Перетащите Стоимость доставки по стране , чтобы раскрасить карту Метки.
 Карта должна автоматически обновиться до заполненной карты.
Карта должна автоматически обновиться до заполненной карты.Создайте действие набора: Масштабирование цвета страны .
В меню Рабочий лист выберите Действия. Нажмите «Добавить действие», а затем выберите «Изменить заданные значения».
Назовите действие Масштабирование цвета страны .
Выберите следующие параметры:
- Исходные листы: выберите только текущий лист.
- Выполнить действие: выберите «Выбрать». Это заставит действие применяться, когда пользователь выбирает метку или метки в представлении.

- Целевой набор: выберите текущий источник данных из первого раскрывающегося списка и набор категорий из второго раскрывающегося списка.
- Отмена выбора: выберите Добавить все значения для установки.
Нажмите OK, чтобы сохранить изменения.
Проверить заданное действие.
Когда вы выбираете метку или группу меток в представлении, цветовая палитра реагирует, представляя значения для этих меток, а не всего набора данных.
Относительные даты
Этот пример панели мониторинга содержит несколько расчетов относительных дат. В зависимости от целевой даты панель мониторинга отображает разницу с предыдущим днем, процентное изменение по сравнению с тем же месяцем в предыдущем году, продажи с начала года для текущего года и продажи с начала года для предыдущего года.
В зависимости от целевой даты панель мониторинга отображает разницу с предыдущим днем, процентное изменение по сравнению с тем же месяцем в предыдущем году, продажи с начала года для текущего года и продажи с начала года для предыдущего года.
Установленное действие на этой информационной панели обновляет целевую дату и соответствующие вычисления даты в ответ на нажатие пользователем метки на временной шкале.
Подробности примера относительной даты
В этом примере используется источник данных Global Superstore.
Действие set в этом примере применяется к листу временной шкалы на информационной панели и использует этот лист для управления поведением информационной панели. Когда пользователь выбирает метку на временной шкале, установленное действие обновляет набор «Выбранная дата» с одним значением даты.
В этом примере:
Набор выбранной даты создается на основе поля «Дата заказа».

Действие «Обновить набор целевых дат» обновляет набор «Выбранная дата», поэтому значение даты для метки, выбранной в представлении, является единственным значением в наборе.
Вычисляемое поле Целевая дата фиксирует значение даты из набора Выбранная дата, и на это вычисляемое поле ссылаются другие вычисления относительных дат, а именно.
Каждый лист на информационной панели использует вычисляемые поля для обновления отображаемых значений.
Примечание . Поскольку этот пример более сложный, в приведенном ниже описании дается сводка основных шагов и необходимых настроек, а не конкретные детали.

 }\)
}\) }\) Тогда существует \(g\) в \(G\ ) такой, что \(g x = y\text{.}\) Определим \(\phi\) как \(\phi( y ) = g G_x\text{.}\) Чтобы показать, что \(\phi\) является взаимно однозначно, предположим, что \(\phi(y_1) = \phi(y_2)\text{.}\) Тогда
}\) Тогда существует \(g\) в \(G\ ) такой, что \(g x = y\text{.}\) Определим \(\phi\) как \(\phi( y ) = g G_x\text{.}\) Чтобы показать, что \(\phi\) является взаимно однозначно, предположим, что \(\phi(y_1) = \phi(y_2)\text{.}\) Тогда ups.edu/aata
ups.edu/aata
 Подробнее о создании наборов см. в разделе Создание наборов.
Подробнее о создании наборов см. в разделе Создание наборов.
 Этот вариант хорошо работает для заданных действий.
Этот вариант хорошо работает для заданных действий.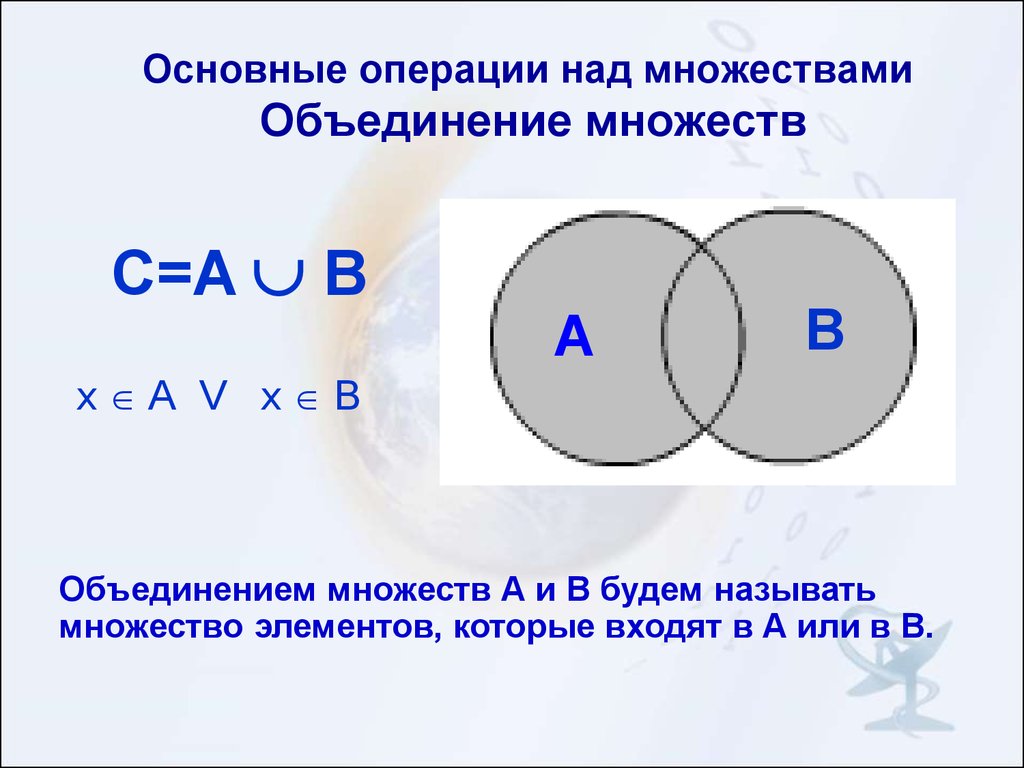


 Перетащите оба листа на панель инструментов.
Перетащите оба листа на панель инструментов.
 Затем перетащите Sales в Text на карточке Marks.
Затем перетащите Sales в Text на карточке Marks.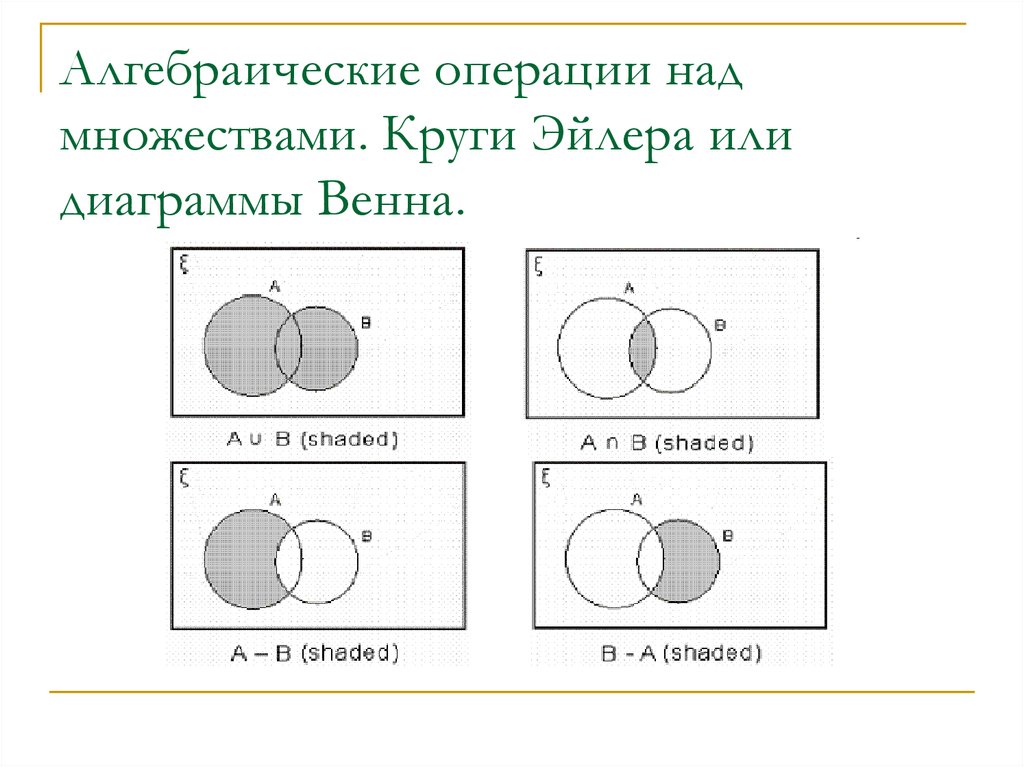

 Карта должна автоматически обновиться до заполненной карты.
Карта должна автоматически обновиться до заполненной карты.
