Онлайн калькуляторы, расчеты и формулы на GELEOT.RU
Векторы представляют собой особый раздел аналитической геометрии, который в том числе оказал значительное влияние на развитие физики. Сам по себе вектор выглядит как отрезок, который имеет начало и имеет конец, определен заданной конечными точками длиной этого отрезка. Но внутри вектора кроется множество других скрытых функций, за счет того что вектор задает направление. Поэтому если для отрезка не имеет значения какая точка названа началом, а какая концом, и чаще просто применяется принцип чтения «слева направо», то для векторов AB и BA – это диаметрально противоположные понятия.
Итак, в векторе присутствует две важных составляющих – это его длина и направление. Тем не менее, координатами вектора задается не его фактическая длина, а местоположение на плоскости или в пространстве. Поэтому длина вектора, иначе называемая модуль вектора, вычисляется, используя прямоугольный треугольник с осями координат. Дальнейшие действия с вектором также чаще используют именно его координаты, нежели фактическую длину.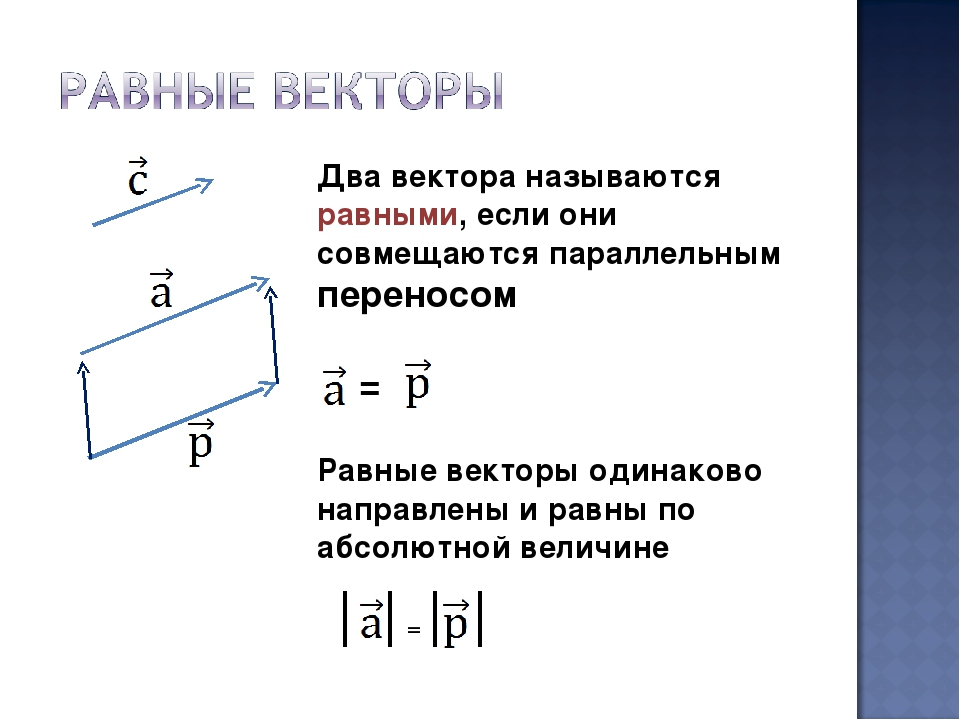
В данном разделе разложены все основные действия с векторами, такие как нахождение длины вектора, координат вектора, сложение векторов, вычитание векторов, скалярное произведение векторов, векторное произведение векторов, смешанное произведение трех векторов, вычисление угла между векторами и другие. Все расчет можно произвести для векторов на плоскости или для векторов в пространстве. Также доступен векторный калькулятор, который вычисляет все возможные параметры одного и более векторов, с заданными координатами точек вектора.
Векторное произведение векторов, онлайн калькулятор
Наш онлайн калькулятор позволяет найти векторное произведение двух векторов всего за пару минут. Для вычисления векторного произведения выберите форму представления векторов (через координаты или по точкам), заполните все элементы и нажмите кнопку «Вычислить», калькулятор выдаст пошаговое решение и ответ! Каждый шаг будет детально расписан, это поможет вам понять, как был получен ответ и, при необходимости, проверить свое решение.
Введите данные, чтобы найти векторное произведение векторовкоординатами точками
Формула : |
| Понравился сайт? Расскажи друзьям! | |||
Скалярное произведение векторов, онлайн калькулятор
Наш онлайн калькулятор помогает найти скалярное произведение двух векторов всего в несколько кликов.
Размерность векторов:
2 3Форма представления векторов:
координатами точками
Формула : |
| Понравился сайт? Расскажи друзьям! | |||
Сложение векторов.
 Он-лайн калькулятор. — таблицы Tehtab.ru
Он-лайн калькулятор. — таблицы Tehtab.ruСложение векторов. Он-лайн калькулятор.
Сложение векторов. Он-лайн калькулятор.
В механике существуют два типа величин:
- скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д.
- векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д..
Рассмотрим сначала алгебраический подход к сложению векторов.
Покоординатное сложение векторов.
Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.е. из первой координаты — первую, из второй — вторую и т.д.):
Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:
В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.
Теперь перейдем к геометрическому смыслу сложения двух векторов: .
При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:
- правило параллелограмма
- правило треугольника
- тригонометрический способ
Правило параллелограмма.
Процедура сложения векторов по правилу параллелограмма заключается в следующем:
- нарисовать первый вектор, учитывая его величину и направление
- от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление
- дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны
- результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.
Правило треугольника
Сложение векторов по правилу треугольника заключается в следующем:
- нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении
- от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление
- результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом второго.

Тригонометрический способ
Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов:
Fрез. = [ F12 + F22 -2 F1 F2 cos(180о-α) ]1/2 (1)
где
F = числовое значение вектора
α = угол между векторами 1 и 2
Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов:
β = arcsin[ F2 *sin(180o-α) / FR ] (2)
где
α = угол между исходными векторами
Пример — сложение векторов.
Сила 1 равна 5кН и воздействует на тело в направлении, на 80o отличающемся от направления действия второй силы, равной 8 кН.
Результирующая сила вычисляется следующим образом:
Fрез = [ (5 кН)2 + (8 кН)2 — 2 (5 кН)(8 kН) cos(180o — (80o)) ]1/2
= 10,14кН
Угол между результирующей силой и первой силой равен:
β= arcsin[ (8кН) sin(180o — (80o)) / (10,14кН)]
= 51o
А угол между второй и результирующей силой можно посчитать следующим образом: as
α = arcsin [ (5 кН) sin(180o — (80o)) / (10,2 кН)]
= 29o
Он-лайн калькулятор сложения векторов.
Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.
Векторное произведение векторов, формулы и онлайн калькуляторы
Содержание:
Определение
Векторным произведением ненулевых векторов $\overline{a}$ и $\overline{b}$ называется вектор $\overline{c}$, обозначаемый символом $[\overline{a}, \overline{b}]$ или $\overline{a} \times \overline{b}$, длина которого $|\bar{c}|=|\bar{a}||\bar{b}| \sin (\bar{a}, \bar{b})$ (рис. 1).
Свойства векторного произведения:
1 $[\overline{a}, \overline{b}]=\overline{0}$, тогда и только тогда, когда $\overline{a} \| \overline{b}$
2 $[\overline{a}, \overline{b}]=-[\overline{b}, \overline{a}]$
3 Модуль векторного произведения $|[\overline{a}, \overline{b}]|$ равен площади параллелограмма, построенного на заданных векторах $\overline{a}$ и $\overline{b}$ (рис. 2), т.е.
$[\lambda \overline{a}, \overline{b}]=[\overline{a}, \lambda \overline{b}]=\lambda[\overline{a}, \overline{b}]$
$\left[\overline{a}_{1}+\overline{a}_{2}, \overline{b}\right]=\left[\overline{a}_{1}, \overline{b}\right]+\left[\overline{a}_{2}, \overline{b}\right] ;\left[\overline{a}, \overline{b}_{1}+\overline{b}_{2}\right]=\left[\overline{a}, \overline{b}_{1}\right]+\left[\overline{a}, \overline{b}_{2}\right]$
4 $[\lambda \overline{a}, \overline{b}]=[\overline{a}, \lambda \overline{b}]=\lambda[\overline{a}, \overline{b}]$
5 $\left[\overline{a}_{1}+\overline{a}_{2}, \overline{b}\right]=\left[\overline{a}_{1}, \overline{b}\right]+\left[\overline{a}_{2}, \overline{b}\right] ;\left[\overline{a}, \overline{b}_{1}+\overline{b}_{2}\right]=\left[\overline{a}, \overline{b}_{1}\right]+\left[\overline{a}, \overline{b}_{2}\right]$
Если векторы заданы своими координатами $\overline{a}=\left(a_{1} ; a_{2} ; a_{3}\right)$, $\overline{b}=\left(b_{1} ; b_{2} ; b_{3}\right)$, то векторное произведение находится по формуле:
$[\overline{a}, \overline{b}]=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {a_{1}} & {a_{2}} & {a_{3}} \\ {b_{1}} & {b_{2}} & {b_{3}}\end{array}\right|$
Пример
Задание. Найти векторное произведение векторов $\overline{a}=(6 ; 7 ; 10)$ и
$\overline{b}=(8 ; 5 ; 9)$
Найти векторное произведение векторов $\overline{a}=(6 ; 7 ; 10)$ и
$\overline{b}=(8 ; 5 ; 9)$
Решение. Составляем определитель и вычисляем его:
$\overline{a} \times \overline{b}=\left| \begin{array}{ccc}{\overline{i}} & {\overline{j}} & {\overline{k}} \\ {6} & {7} & {10} \\ {8} & {5} & {9}\end{array}\right|=\overline{i} \left| \begin{array}{cc}{7} & {10} \\ {5} & {9}\end{array}\right|-\overline{j} \left| \begin{array}{cc}{6} & {10} \\ {8} & {9}\end{array}\right|+\overline{k} \left| \begin{array}{cc}{6} & {7} \\ {8} & {5}\end{array}\right|=$
$=\overline{i}(7 \cdot 9-5 \cdot 10)-\overline{j}(6 \cdot 9-8 \cdot 10)+\overline{k}(6 \cdot 5-8 \cdot 7)=$
$=13 \overline{i}+26 \overline{j}-26 \overline{k}=(13 ; 26 ;-26)$
Читать дальше: смешанное произведение векторов.
Слишком сложно?
Векторное произведение векторов не по зубам? Тебе ответит эксперт через 10 минут!
Координаты вектора в новом базисе онлайн калькулятор.
 Разложение вектора по базису
Разложение вектора по базисуБа́зис (др.-греч. βασις, основа) — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов
Базисом в пространстве R n называется любая система из n -линейно независимых векторов. Каждый вектор из R n , не входящих в базис, можно представить в виде линейной комбинации базисных векторов, т.е. разложить по базису.
Пусть – базис пространства R n и . Тогда найдутся такие числа λ 1 , λ 2 , …, λ n , что .
Коэффициенты разложения λ 1 , λ 2 , …, λ n , называются координатами вектора в базисе В. Если задан базис, то коэффициенты вектора определяются однозначно.
Замечание. В каждом n -мерном векторном пространстве можно выбрать бесчисленное множество различных базисов. В различных базисах один и тот же вектор имеет различные координаты, но единственные в выбранном базисе. Пример. Разложить вектор по базису .
Пример. Разложить вектор по базису .
Решение. . Подставим координаты всех векторов и выполним действия над ними:
Приравняв координаты, получим систему уравнений:
Решим ее: .
Таким образом, получим разложение: .
В базисе вектор имеет координаты .
Конец работы —
Эта тема принадлежит разделу:
Понятие вектора. Линейные операции над векторами
Вектором называется направленный отрезок имеющий определенную длину т е отрезок определенной длины у которого одна из ограничивающих его точек.. длина вектора называется его модулем и обозначается символом модуль вектора.. вектор называется нулевым обозначается если начало и конец его совпадают нулевой вектор не имеет определенного..
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
В векторном исчислении и его приложениях большое значение имеет задача разложения, состоящая в представлении данного вектора в виде суммы нескольких векторов, называемых составляющими данного
вектора. Эта задача, имеющая в общем случае бесчисленное множество решений, становится вполне определенной, если задать некоторые элементы составляющих векторов.
Эта задача, имеющая в общем случае бесчисленное множество решений, становится вполне определенной, если задать некоторые элементы составляющих векторов.
2. Примеры разложения.
Рассмотрим несколько весьма часто встречающихся случаев разложения.
1. Разложить данный вектор с на два составляющих вектора из которых один, например а, задан по величине и направлению.
Задача сводится к определению разности двух векторов. Действительно, если векторы являются составляющими вектора с, то должно выполняться равенство
Отсюда определяется второй составляющий вектор
2. Разложить данный вектор с на два составляющих, из которых один должен лежать в заданной плоскости а второй должен лежать на заданной прямой а.
Для определения составляющих векторов перенесем вектор с так, чтобы его начало совпало с точкой пересечения заданной прямой с плоскостью (точка О — см. рис. 18). Из конца вектора с (точка С) проведем прямую до
пересечения с плоскостью {В — точка пересечения), а затем из точки С проведем прямую параллельно
Векторы и будут искомыми, т. е. Естественно, что указанное разложение возможно, если прямая а и плоскость не параллельны.
е. Естественно, что указанное разложение возможно, если прямая а и плоскость не параллельны.
3. Даны три компланарных вектора а, b и с, причем векторы не коллинеарны. Требуется разложить вектор с по векторам
Приведем все три заданных вектора к одной точке О. Тогда в силу их компланарности они расположатся в одной плоскости. На данном векторе с как на диагонали построим параллелограмм, стороны которого параллельны линиям действия векторов (рис. 19). Это построение всегда возможно (если только векторы не коллинеарны) и единственно. Из рис. 19 видно, что
В аудитории находится тележка с шоколадками, и каждому посетителю сегодня достанется сладкая парочка – аналитическая геометрия с линейной алгеброй. В данной статье будут затронуты сразу два раздела высшей математики, и мы посмотрим, как они уживаются в одной обёртке. Сделай паузу, скушай «Твикс»! …блин, ну и чушь спорол. Хотя ладно, забивать не буду, в конце концов, на учёбу должен быть позитивный настрой.
Линейная зависимость векторов , линейная независимость векторов , базис векторов и др. термины имеют не только геометрическую интерпретацию, но, прежде всего, алгебраический смысл . Само понятие «вектор» с точки зрения линейной алгебры – это далеко не всегда тот «обычный» вектор, который мы можем изобразить на плоскости или в пространстве. За доказательством далеко ходить не нужно, попробуйте нарисовать вектор пятимерного пространства . Или вектор погоды, за которым я только что сходил на Гисметео: – температура и атмосферное давление соответственно. Пример, конечно, некорректен с точки зрения свойств векторного пространства, но, тем не менее, никто не запрещает формализовать данные параметры вектором. Дыхание осени….
термины имеют не только геометрическую интерпретацию, но, прежде всего, алгебраический смысл . Само понятие «вектор» с точки зрения линейной алгебры – это далеко не всегда тот «обычный» вектор, который мы можем изобразить на плоскости или в пространстве. За доказательством далеко ходить не нужно, попробуйте нарисовать вектор пятимерного пространства . Или вектор погоды, за которым я только что сходил на Гисметео: – температура и атмосферное давление соответственно. Пример, конечно, некорректен с точки зрения свойств векторного пространства, но, тем не менее, никто не запрещает формализовать данные параметры вектором. Дыхание осени….
Нет, я не собираюсь грузить вас теорией, линейными векторными пространствами, задача состоит в том, чтобы понять определения и теоремы. Новые термины (линейная зависимость, независимость, линейная комбинация, базис и т.д.) приложимы ко всем векторам с алгебраической точки зрения , но примеры будут даны геометрические. Таким образом, всё просто, доступно и наглядно. Помимо задач аналитической геометрии мы рассмотрим и некоторые типовые задания алгебры . Для освоения материала желательно ознакомиться с уроками Векторы для чайников и Как вычислить определитель?
Помимо задач аналитической геометрии мы рассмотрим и некоторые типовые задания алгебры . Для освоения материала желательно ознакомиться с уроками Векторы для чайников и Как вычислить определитель?
Базис плоскости и аффинная система координат
Рассмотрим плоскость вашего компьютерного стола (просто стола, тумбочки, пола, потолка, кому что нравится). Задача будет состоять в следующих действиях:
1) Выбрать базис плоскости . Грубо говоря, у столешницы есть длина и ширина, поэтому интуитивно понятно, что для построения базиса потребуется два вектора. Одного вектора явно мало, три вектора – лишка.
2) На основе выбранного базиса задать систему координат (координатную сетку), чтобы присвоить координаты всем находящимся на столе предметам.
Не удивляйтесь, сначала объяснения будут на пальцах. Причём, на ваших. Пожалуйста, поместите указательный палец левой руки на край столешницы так, чтобы он смотрел в монитор. Это будет вектор . Теперь поместите мизинец правой руки на край стола точно так же – чтобы он был направлен на экран монитора. Это будет вектор . Улыбнитесь, вы замечательно выглядите! Что можно сказать о векторах ? Данные векторы коллинеарны , а значит, линейно выражаются друг через друга:
Это будет вектор . Теперь поместите мизинец правой руки на край стола точно так же – чтобы он был направлен на экран монитора. Это будет вектор . Улыбнитесь, вы замечательно выглядите! Что можно сказать о векторах ? Данные векторы коллинеарны , а значит, линейно выражаются друг через друга:
, ну, или наоборот: , где – некоторое число, отличное от нуля.
Картинку сего действа можно посмотреть на уроке Векторы для чайников , где я объяснял правило умножения вектора на число.
Будут ли ваши пальчики задавать базис на плоскости компьютерного стола? Очевидно, что нет. Коллинеарные векторы путешествуют туда-сюда по одному направлению, а у плоскости есть длина и ширина.
Такие векторы называют линейно зависимыми .
Справка: Слова «линейный», «линейно» обозначают тот факт, что в математических уравнениях, выражениях нет квадратов, кубов, других степеней, логарифмов, синусов и т.д. Есть только линейные (1-й степени) выражения и зависимости.
Два вектора плоскости линейно зависимы тогда и только тогда , когда они коллинеарны .
Скрестите пальцы на столе, чтобы между ними был любой угол, кроме 0 или 180 градусов. Два вектора плоскости линейно не зависимы в том и только том случае, если они не коллинеарны . Итак, базис получен. Не нужно смущаться, что базис получился «косым» с неперпендикулярными векторами различной длины. Очень скоро мы увидим, что для его построения пригоден не только угол в 90 градусов, и не только единичные, равные по длине векторы
Любой вектор плоскости единственным образом раскладывается по базису :
, где – действительные числа . Числа называют координатами вектора в данном базисе.
Также говорят, что вектор представлен в виде линейной комбинации базисных векторов . То есть, выражение называют разложением вектора по базису или линейной комбинацией базисных векторов.
Например, можно сказать, что вектор разложен по ортонормированному базису плоскости , а можно сказать, что он представлен в виде линейной комбинации векторов .
Сформулируем определение базиса формально: Базисом плоскости называется пара линейно независимых (неколлинеарных) векторов , , при этом любой вектор плоскости является линейной комбинацией базисных векторов.
Существенным моментом определения является тот факт, что векторы взяты в определённом порядке . Базисы – это два совершенно разных базиса! Как говорится, мизинец левой руки не переставишь на место мизинца правой руки.
С базисом разобрались, но его недостаточно, чтобы задать координатную сетку и присвоить координаты каждому предмету вашего компьютерного стола. Почему недостаточно? Векторы являются свободными и блуждают по всей плоскости. Так как же присвоить координаты тем маленьким грязным точкам стола, которые остались после бурных выходных? Необходим отправной ориентир.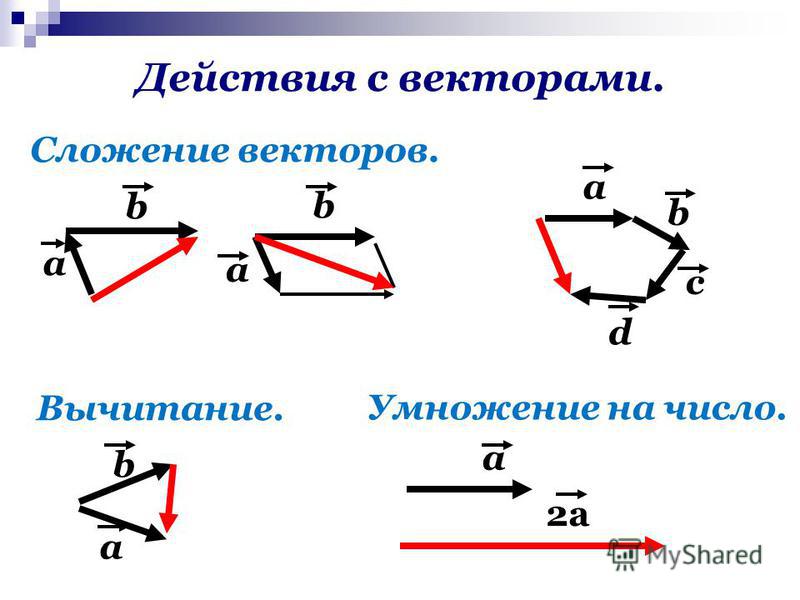 И таким ориентиром является знакомая всем точка – начало координат. Разбираемся с системой координат:
И таким ориентиром является знакомая всем точка – начало координат. Разбираемся с системой координат:
Начну со «школьной» системы. Уже на вступительном уроке Векторы для чайников я выделял некоторые различия между прямоугольной системой координат и ортонормированным базисом . Вот стандартная картина:
Когда говорят о прямоугольной системе координат , то чаще всего имеют в виду начало координат, координатные оси и масштаб по осям. Попробуйте набрать в поисковике «прямоугольная система координат», и вы увидите, что многие источники вам будут рассказывать про знакомые с 5-6-го класса координатные оси и о том, как откладывать точки на плоскости.
С другой стороны, создается впечатление, что прямоугольную систему координат вполне можно определить через ортонормированный базис . И это почти так. Формулировка звучит следующим образом:
началом координат , и ортонормированный базис задают декартову прямоугольную систему координат плоскости .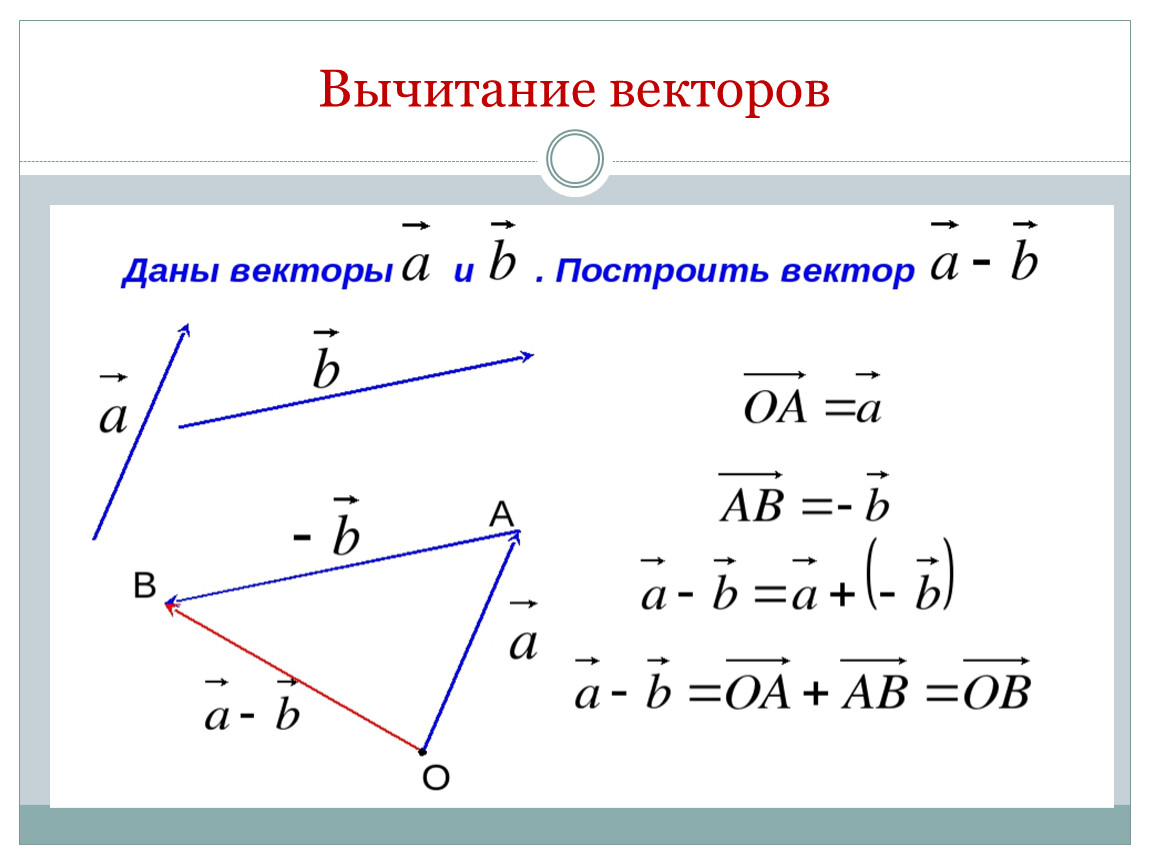 То есть, прямоугольная система координат однозначно определяется единственной точкой и двумя единичными ортогональными векторами . Именно поэтому, вы видите чертёж, который я привёл выше – в геометрических задачах часто (но далеко не всегда) рисуют и векторы, и координатные оси.
То есть, прямоугольная система координат однозначно определяется единственной точкой и двумя единичными ортогональными векторами . Именно поэтому, вы видите чертёж, который я привёл выше – в геометрических задачах часто (но далеко не всегда) рисуют и векторы, и координатные оси.
Думаю, всем понятно, что с помощью точки (начала координат) и ортонормированного базиса ЛЮБОЙ ТОЧКЕ плоскости и ЛЮБОМУ ВЕКТОРУ плоскости можно присвоить координаты. Образно говоря, «на плоскости всё можно пронумеровать».
Обязаны ли координатные векторы быть единичными? Нет, они могут иметь произвольную ненулевую длину. Рассмотрим точку и два ортогональных вектора произвольной ненулевой длины:
Такой базис называется ортогональным . Начало координат с векторами задают координатную сетку, и любая точка плоскости, любой вектор имеют свои координаты в данном базисе. Например, или . Очевидное неудобство состоит в том, что координатные векторы в общем случае имеют различные длины, отличные от единицы. Если длины равняются единице, то получается привычный ортонормированный базис.
Если длины равняются единице, то получается привычный ортонормированный базис.
! Примечание : в ортогональном базисе, а также ниже в аффинных базисах плоскости и пространства единицы по осям считаются УСЛОВНЫМИ . Например, в одной единице по оси абсцисс содержится 4 см, в одной единице по оси ординат 2 см. Данной информации достаточно, чтобы при необходимости перевести «нестандартные» координаты в «наши обычные сантиметры».
И второй вопрос, на который уже на самом деле дан ответ – обязательно ли угол между базисными векторами должен равняться 90 градусам? Нет! Как гласит определение, базисные векторы должны быть лишь неколлинеарными . Соответственно угол может быть любым, кроме 0 и 180 градусов.
Точка плоскости, которая называется началом координат , и неколлинеарные векторы , , задают аффинную систему координат плоскости :
Иногда такую систему координат называют косоугольной системой. В качестве примеров на чертеже изображены точки и векторы:
В качестве примеров на чертеже изображены точки и векторы:
Как понимаете, аффинная система координат ещё менее удобна, в ней не работают формулы длин векторов и отрезков, которые мы рассматривали во второй части урока Векторы для чайников , многие вкусные формулы, связанные со скалярным произведением векторов . Зато справедливы правила сложения векторов и умножения вектора на число, формулы деления отрезка в данном отношении , а также ещё некоторые типы задач, которые мы скоро рассмотрим.
А вывод таков, что наиболее удобным частным случаем аффинной системы координат является декартова прямоугольная система. Поэтому её, родную, чаще всего и приходится лицезреть. …Впрочем, всё в этой жизни относительно – существует немало ситуаций, в которых уместна именно косоугольная (или какая-набудь другая, например, полярная ) система координат. Да и гуманоидам такие системы могут прийтись по вкусу =)
Переходим к практической части. Все задачи данного урока справедливы как для прямоугольной системы координат, так и для общего аффинного случая. Сложного здесь ничего нет, весь материал доступен даже школьнику.
Сложного здесь ничего нет, весь материал доступен даже школьнику.
Типовая вещь. Для того чтобы два вектора плоскости были коллинеарны, необходимо и достаточно, чтобы их соответствующие координаты были пропорциональны .По существу, это покоординатная детализация очевидного соотношения .
Пример 1
а) Проверить, коллинеарны ли векторы .
б) Образуют ли базис векторы ?
Решение:
а) Выясним, существует ли для векторов коэффициент пропорциональности , такой, чтобы выполнялись равенства :
Обязательно расскажу о «пижонской» разновидности применения данного правила, которая вполне прокатывает на практике. Идея состоит в том, чтобы сразу составить пропорцию и посмотреть, будет ли она верной:
Составим пропорцию из отношений соответствующих координат векторов:
Сокращаем:
, таким образом, соответствующие координаты пропорциональны, следовательно,
Отношение можно было составить и наоборот, это равноценный вариант:
Для самопроверки можно использовать то обстоятельство, что коллинеарные векторы линейно выражаются друг через друга. В данном случае имеют место равенства . Их справедливость легко проверяется через элементарные действия с векторами:
В данном случае имеют место равенства . Их справедливость легко проверяется через элементарные действия с векторами:
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Исследуем на коллинеарность векторы . Составим систему:
Из первого уравнения следует, что , из второго уравнения следует, что , значит, система несовместна (решений нет). Таким образом, соответствующие координаты векторов не пропорциональны.
Вывод : векторы линейно независимы и образуют базис.
Упрощённая версия решения выглядит так:
Составим пропорцию из соответствующих координат векторов :
, значит, данные векторы линейно независимы и образуют базис.
Обычно такой вариант не бракуют рецензенты, но возникает проблема в тех случаях, когда некоторые координаты равны нулю. Вот так: . Или так: . Или так: . Как тут действовать через пропорцию? (действительно, на ноль же делить нельзя). Именно по этой причине я и назвал упрощенное решение «пижонским».
Ответ: а) , б) образуют.
Небольшой творческий пример для самостоятельного решения:
Пример 2
При каком значении параметра векторы будут коллинеарны?
В образце решения параметр найден через пропорцию .
Существует изящный алгебраический способ проверки векторов на коллинеарность., систематизируем наши знания и пятым пунктом как раз добавим его:
Для двух векторов плоскости эквивалентны следующие утверждения :
2) векторы образуют базис;
3) векторы не коллинеарны;
+ 5) определитель, составленный из координат данных векторов, отличен от нуля .
Соответственно, эквивалентны следующие противоположные утверждения :
1) векторы линейно зависимы;
2) векторы не образуют базиса;
3) векторы коллинеарны;
4) векторы можно линейно выразить друг через друга;
+ 5) определитель, составленный из координат данных векторов, равен нулю .
Я очень и очень надеюсь, что на данный момент вам уже понятны все встретившиеся термины и утверждения.
Рассмотрим более подробно новый, пятый пункт: два вектора плоскости коллинеарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю :. Для применения данного признака, естественно, нужно уметь находить определители .
Решим Пример 1 вторым способом:
а) Вычислим определитель, составленный из координат векторов :
, значит, данные векторы коллинеарны.
б) Два вектора плоскости образуют базис, если они не коллинеарны (линейно независимы). Вычислим определитель, составленный из координат векторов :
, значит, векторы линейно независимы и образуют базис.
Ответ: а) , б) образуют.
Выглядит значительно компактнее и симпатичнее, чем решение с пропорциями.
С помощью рассмотренного материала можно устанавливать не только коллинеарность векторов, но и доказывать параллельность отрезков, прямых. Рассмотрим пару задач с конкретными геометрическими фигурами.
Пример 3
Даны вершины четырёхугольника . Доказать, что четырёхугольник является параллелограммом.
Доказать, что четырёхугольник является параллелограммом.
Доказательство : Чертежа в задаче строить не нужно, поскольку решение будет чисто аналитическим. Вспоминаем определение параллелограмма:
Параллелограммом называется четырёхугольник, у которого противоположные стороны попарно параллельны.
Таким образом, необходимо доказать:
1) параллельность противоположных сторон и ;
2) параллельность противоположных сторон и .
Доказываем:
1) Найдём векторы:
2) Найдём векторы:
Получился один и тот же вектор («по школьному» – равные векторы). Коллинеарность совсем очевидна, но решение таки лучше оформить с толком, с расстановкой. Вычислим определитель, составленный из координат векторов :
, значит, данные векторы коллинеарны, и .
Вывод : Противоположные стороны четырёхугольника попарно параллельны, значит, он является параллелограммом по определению. Что и требовалось доказать .
Больше фигур хороших и разных:
Пример 4
Даны вершины четырёхугольника . Доказать, что четырёхугольник является трапецией.
Для более строгой формулировки доказательства лучше, конечно, раздобыть определение трапеции, но достаточно и просто вспомнить, как она выглядит.
Это задание для самостоятельного решения. Полное решение в конце урока.
А теперь пора потихонечку перебираться из плоскости в пространство:
Как определить коллинеарность векторов пространства?Правило очень похоже. Для того чтобы два вектора пространства были коллинеарны, необходимо и достаточно , чтобы их соответствующие координаты были пропорциональны .
Пример 5
Выяснить, будут ли коллинеарны следующие векторы пространства:
а) ;
б)
в)
Решение:
а) Проверим, существует ли коэффициент пропорциональности для соответствующих координат векторов:
Система не имеет решения, значит, векторы не коллинеарны.
«Упрощёнка» оформляется проверкой пропорции . В данном случае:
– соответствующие координаты не пропорциональны, значит, векторы не коллинеарны.
Ответ: векторы не коллинеарны.
б-в) Это пункты для самостоятельного решения. Попробуйте его оформить двумя способами.
Существует метод проверки пространственных векторов на коллинеарность и через определитель третьего порядка, данный способ освещен в статье Векторное произведение векторов .
Аналогично плоскому случаю, рассмотренный инструментарий может применяться в целях исследования параллельности пространственных отрезков и прямых.
Добро пожаловать во второй раздел:
Линейная зависимость и независимость векторов трехмерного пространства.Пространственный базис и аффинная система координат
Многие закономерности, которые мы рассмотрели на плоскости, будут справедливыми и для пространства. Я постарался минимизировать конспект по теории, поскольку львиная доля информации уже разжёвана. Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.
Тем не менее, рекомендую внимательно прочитать вводную часть, так как появятся новые термины и понятия.
Теперь вместо плоскости компьютерного стола исследуем трёхмерное пространство. Сначала создадим его базис. Кто-то сейчас находится в помещении, кто-то на улице, но в любом случае нам никуда не деться от трёх измерений: ширины, длины и высоты. Поэтому для построения базиса потребуется три пространственных вектора. Одного-двух векторов мало, четвёртый – лишний.
И снова разминаемся на пальцах. Пожалуйста, поднимите руку вверх и растопырьте в разные стороны большой, указательный и средний палец . Это будут векторы , они смотрят в разные стороны, имеют разную длину и имеют разные углы между собой. Поздравляю, базис трёхмерного пространства готов! Кстати, не нужно демонстрировать такое преподавателям, как ни крути пальцами, а от определений никуда не деться =)
Далее зададимся важным вопросом, любые ли три вектора образуют базис трехмерного пространства ? Пожалуйста, плотно прижмите три пальца к столешнице компьютерного стола. Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными и, совершенно очевидно, что базиса трёхмерного пространства не создают.
Что произошло? Три вектора расположились в одной плоскости, и, грубо говоря, у нас пропало одно из измерений – высота. Такие векторы являются компланарными и, совершенно очевидно, что базиса трёхмерного пространства не создают.
Следует отметить, что компланарные векторы не обязаны лежать в одной плоскости, они могут находиться в параллельных плоскостях (только не делайте этого с пальцами, так отрывался только Сальвадор Дали =)).
Определение : векторы называются компланарными , если существует плоскость, которой они параллельны. Здесь логично добавить, что если такой плоскости не существует, то и векторы будут не компланарны.
Три компланарных вектора всегда линейно зависимы , то есть линейно выражаются друг через друга. Для простоты снова представим, что они лежат в одной плоскости. Во-первых, векторы мало того, что компланарны, могут быть вдобавок ещё и коллинеарны, тогда любой вектор можно выразить через любой вектор. Во втором случае, если, например, векторы не коллинеарны, то третий вектор выражается через них единственным образом: (а почему – легко догадаться по материалам предыдущего раздела).
Справедливо и обратное утверждение: три некомпланарных вектора всегда линейно независимы , то есть никоим образом не выражаются друг через друга. И, очевидно, только такие векторы могут образовать базис трёхмерного пространства.
Определение : Базисом трёхмерного пространства называется тройка линейно независимых (некомпланарных) векторов , взятых в определённом порядке , при этом любой вектор пространства единственным образом раскладывается по данному базису , где – координаты вектора в данном базисе
Напоминаю, также можно сказать, что вектор представлен в виде линейной комбинации базисных векторов.
Понятие системы координат вводится точно так же, как и для плоского случая, достаточно одной точки и любых трёх линейно независимых векторов:
началом координат , и некомпланарные векторы , взятые в определённом порядке , задают аффинную систему координат трёхмерного пространства :
Конечно, координатная сетка «косая» и малоудобная, но, тем не менее, построенная система координат позволяет нам однозначно определить координаты любого вектора и координаты любой точки пространства. Аналогично плоскости, в аффинной системе координат пространства не будут работать некоторые формулы, о которых я уже упоминал.
Аналогично плоскости, в аффинной системе координат пространства не будут работать некоторые формулы, о которых я уже упоминал.
Наиболее привычным и удобным частным случаем аффинной системы координат, как все догадываются, является прямоугольная система координат пространства :
Точка пространства, которая называется началом координат , и ортонормированный базис задают декартову прямоугольную систему координат пространства . Знакомая картинка:
Перед тем, как перейти к практическим заданиям, вновь систематизируем информацию:
Для трёх векторов пространства эквивалентны следующие утверждения :
1) векторы линейно независимы;
2) векторы образуют базис;
3) векторы не компланарны;
4) векторы нельзя линейно выразить друг через друга;
5) определитель, составленный из координат данных векторов, отличен от нуля.
Противоположные высказывания, думаю, понятны.
Линейная зависимость / независимость векторов пространства традиционно проверяется с помощью определителя (пункт 5). Оставшиеся практические задания будут носить ярко выраженный алгебраический характер. Пора повесить на гвоздь геометрическую клюшку и орудовать бейсбольной битой линейной алгебры:
Оставшиеся практические задания будут носить ярко выраженный алгебраический характер. Пора повесить на гвоздь геометрическую клюшку и орудовать бейсбольной битой линейной алгебры:
Три вектора пространства компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов, равен нулю :.
Обращаю внимание на небольшой технический нюанс: координаты векторов можно записывать не только в столбцы, но и в строки (значение определителя от этого не изменится – см. свойства определителей). Но гораздо лучше в столбцы, поскольку это выгоднее для решения некоторых практических задач.
Тем читателям, которые немножко позабыли методы расчета определителей, а может и вообще слабо в них ориентируются, рекомендую один из моих самых старых уроков: Как вычислить определитель?
Пример 6
Проверить, образуют ли базис трёхмерного пространства следующие векторы:
Решение : Фактически всё решение сводится к вычислению определителя.
а) Вычислим определитель, составленный из координат векторов (определитель раскрыт по первой строке):
, значит, векторы линейно независимы (не компланарны) и образуют базис трёхмерного пространства.
Ответ : данные векторы образуют базис
б) Это пункт для самостоятельного решения. Полное решение и ответ в конце урока.
Встречаются и творческие задачи:
Пример 7
При каком значении параметра векторы будут компланарны?
Решение : Векторы компланарны тогда и только тогда, когда определитель, составленный из координат данных векторов равен нулю:
По существу, требуется решить уравнение с определителем. Налетаем на нули как коршуны на тушканчиков – определитель выгоднее всего раскрыть по второй строке и сразу же избавиться от минусов:
Проводим дальнейшие упрощения и сводим дело к простейшему линейному уравнению:
Ответ : при
Здесь легко выполнить проверку, для этого нужно подставить полученное значение в исходный определитель и убедиться, что , раскрыв его заново.
В заключение рассмотрим ещё одну типовую задачу, которая носит больше алгебраический характер и традиционно включается в курс линейной алгебры. Она настолько распространена, что заслуживает отдельного топика:
Доказать, что 3 вектора образуют базис трёхмерного пространстваи найти координаты 4-го вектора в данном базисе
Пример 8
Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе.
Решение : Сначала разбираемся с условием. По условию даны четыре вектора, и, как видите, у них уже есть координаты в некотором базисе. Какой это базис – нас не интересует. А интересует следующая вещь: три вектора вполне могут образовывать новый базис . И первый этап полностью совпадает с решением Примера 6, необходимо проверить, действительно ли векторы линейно независимы:
Вычислим определитель, составленный из координат векторов :
, значит, векторы линейно независимы и образуют базис трехмерного пространства.
! Важно : координаты векторов обязательно записываем в столбцы определителя, а не в строки. Иначе будет путаница в дальнейшем алгоритме решения.
Rn,(МАТЕМАТИКА В ЭКОНОМИКЕ)
Разложение вектора
Разложение вектора а на составляющие — операция замены вектора а несколькими другими векторами аь а2, а3 и т. д., которые при их сложении образуют начальный вектор а; в этом случае векторы db а2, а3 и т. д. называются составляющими вектора а. Иными словами, разложение любого…(ФИЗИКА)
Базис и ранг системы векторов
Рассмотрим систему векторов (1.18) Максимально независимой подсистемой системы векторов (1.I8) называется частичный набор векторов этой системы, удовлетворяющий двум условиям: 1) векторы этого набора линейно независимы; 2) любой вектор системы (1.18) линейно выражается через векторы этого набора….(МАТЕМАТИКА В ЭКОНОМИКЕ)
Представление вектора в разных системах координат.
 Рассмотрим две ортогональные прямолинейные координатные системы с наборами ортов (i, j, к) и (i j», k») и представим в них вектор a . Условно примем, что орты со штрихами отвечают новой системе координат, а без штрихов — старой. Представим вектор в виде разложения по осям как старой, так и новой систем…
Рассмотрим две ортогональные прямолинейные координатные системы с наборами ортов (i, j, к) и (i j», k») и представим в них вектор a . Условно примем, что орты со штрихами отвечают новой системе координат, а без штрихов — старой. Представим вектор в виде разложения по осям как старой, так и новой систем…Разложение вектора в ортогональном базисе
Рассмотрим базис пространства Rn, в котором каждый вектор ортогонален остальным векторам базиса: Ортогональные базисы известны и хорошо представимы на плоскости и в пространстве (рис. 1.6). Базисы такого вида удобны прежде всего тем, что координаты разложения произвольного вектора определяются…(МАТЕМАТИКА В ЭКОНОМИКЕ)
Векторы и их представления в координатных системах
Понятие вектора связывается с определенными физическими величинами, которые характеризуются своей интенсивностью (величиной) и направлением в пространстве. Такими величинами являются, например, сила, действующая на материальное тело, скорость определенной точки этого тела, ускорение материальной частицы. ..
..(МЕХАНИКА СПЛОШНОЙ СРЕДЫ: ТЕОРИЯ НАПРЯЖЕНИЙ И ОСНОВНЫЕ МОДЕЛИ)
Простейшие аналитические представления произвольной эллиптической функции
Представление эллиптической функции в виде суммы простейших элементов. Пусть / (z) есть эллиптическая функция порядка s с простыми полюсами jjt, $s, лежащими в параллелограме периодов. Обозначая через Bk вычет функции относительно полюса мы имеем, что 2 ?л = 0 (§ 1»п. 3, теорема…(ВВЕДЕНИЕ В ТЕОРИЮ ФУНКЦИЙ КОМПЛЕКСНОГО ПЕРЕМЕННОГО)
Л. 2-1 Основные понятия векторной алгебры. Линейные операции над векторами.
Разложение вектора по базису.
Основные понятия векторной алгебры
Вектором
называется множество всех направленных
отрезков, имеющих одинаковую длину и
направление
.
Свойства:
Линейные операции над векторами
1.
Правило параллелограмма:
Суммой двух векторовиназывается вектор,
выходящий из их общего начала и являющийся
диагональю параллелограм-ма, построенного
на векторахикак на сторонах.
Правило многоугольника:
Чтобы построить сумму любого числа векторов, нужно в конец 1-го слагаемого вектора поместить начало 2-ого, в конец 2-ого – начало 3-его и т.д. Вектор, замыкающий полученную ломаную линию, является суммой. Начало его совпадает с началом 1-ого, а конец – с концом последнего.
Свойства:
2.
Произведением вектора
на число,
называется вектор, удовлетворяющий
условиям:
.
Свойства:
3.
Разностью векторовиназывают вектор,
равный сумме вектораи вектора, противоположного вектору,
т.е.
.
— закон противоположного элемента (вектора).
Разложение вектора по базису
Сумма векторов определяется единственным
способом
(и только).
Обратная же операция – разложение
вектора на несколько составляющих,
неоднозначна:.
Для того, что бы сделать её однозначной,
необходимо указать направления, по
которым происходит разложение
рассматриваемого вектора, или, как
говорят, необходимо указатьбазис .
При определении базиса существенным является требование некомпланарности и неколлинеарности векторов. Чтобы понять смысл этого требования, необходимо рассмотреть понятие линейной зависимости и линейной независимости векторов.
Произвольное выражение вида:
,
называютлинейной комбинацией векторов
.
Линейная комбинация нескольких векторов называется тривиальной , если все её коэффициенты равны нулю.
Векторы
называютсялинейно зависимыми , если
существует нетривиальная линейная
комбинация этих векторов равная нулю:
(1), при условии
.
Если равенство (1) имеет место только
при всех
одновременно равных нулю, то ненулевые
векторы
будутлинейно независимыми .
Легко доказать: любые два коллинеарных вектора линейно зависимы, а два неколлинеарных вектора линейно независимы .
Доказательство начнём с первого утверждения.
Пусть векторы
иколлинеарны. Покажем, что они линейно
зависимы. Действительно, если они
коллинеарны, то они отличаются друг от
друга только на числовой множитель,
т. е.
е.
,
следовательно
.
Поскольку полученная линейная комбинация
явно нетривиальная и равна «0», то векторыилинейно зависимы.
Рассмотрим теперь два неколлинеарных векторы и. Докажем, что они линейно независимы. Доказательство построим от противного.
Предположим, что они линейно зависимы.
Тогда должна существовать нетривиальная
линейная комбинация
.
Предположим, что
,
тогда
.
Полученное равенство означает, что
векторыиколлинеарны вопреки нашему исходному
предположению.
Аналогично можно доказать: любые три компланарных вектора линейно зависимы, а два некомпланарных вектора линейно независимы .
Возвращаясь к понятию базиса и к задаче разложения вектора в определённом базисе, можно сказать, что базис на плоскости и в пространстве образуется из совокупности линейно независимых векторов. Такое понятие базиса является общим, т.к. оно применимо к пространству любого числа измерений.
Выражение вида:
,
называется разложением векторапо векторам,…,.
Если мы будем рассматривать базис в
трехмерном пространстве, то разложение
вектора
по базису
будет
,
где
—координаты вектора .
В задаче разложения произвольного
вектора в некотором базисе весьма важным
является следующее утверждение: любой
вектор может быть единственным образом
разложен в данном базисе
. Иными словами, координаты
для любого вектораотносительно базиса
определяетсяоднозначно.
Введение базиса в пространстве и на плоскости позволяет поставить в соответствие каждому вектору упорядоченную тройку (пару) чисел – его координаты. Этот очень важный результат, позволяющий установить связь между геометрическими объектами и числами, делает возможным аналитически описывать и исследовать положение и движение физических объектов.
Совокупность точки и базиса называют системой координат.
Если векторы, образующие базис единичны
и попарно перпендикулярны, то система
координат называется прямоугольной, а базис ортонормированным.
Л. 2-2 Произведение векторов
Разложение
вектора по базису
Рассмотрим
вектор
,
заданный своими координатами:
.
—
компоненты векторапо направлениям базисных векторов
.
Выражение вида
называется разложением векторапо базису
.
Аналогичным образом можно разложить по базису
вектор
:
.
Косинусы углов, образованные рассматриваемым
вектором
с базисными ортами
называютсянаправляющими косинусами
;
;
.
Скалярное произведение векторов.
Скалярным произведением двух векторов иназывается число, равное произведению модулей этих векторов на косинус угла между ними
Скалярное произведение двух векторов
можно рассматривать как произведение
модуля одного из этих векторов на
ортогональную проекцию другого вектора
на направление первого
.
Свойства:
Если известны координаты векторов
и
,
то, выполнив разложение векторов по
базису
:
и
,
найдём
,
т. к.
к.
,
,
то
.
.
Условие перпендикулярности векторов:
.
Условие коллинеарности ректоров:
.
Векторное произведение векторов
или
Векторным произведением вектором
на векторназывается такой вектор
,
который удовлетворяет условиям:
Свойства:
Рассмотренные алгебраические свойства позволяют найти аналитическое выражение для векторного произведения через координаты составляющих векторов в ортонормированном базисе.
Дано:
и
.
т.к.
,
,
,
,
,
,
,
то
. Эту формулу можно записать короче, в форме определителя третьего порядка:
.
Смешанное произведение векторов
Смешанным произведением трех векторов
,иназывается число, равное векторному
произведению
,
умноженному скалярно на вектор.
Верно следующее равенство:
,
поэтому смешанное произведение записывают
.
Как следует из определения, результатом
смешанного произведения трёх векторов
является число. Это число имеет наглядный
геометрический смысл:
Это число имеет наглядный
геометрический смысл:
Модуль смешанного произведения
равен объёму параллелепипеда, построенного
на приведённых к общему началу векторах,и.
Свойства смешанного произведения:
Если векторы
,,заданы в ортонормированном базисе
своими координатами, вычисление
смешанного произведения осуществляется
по формуле
.
Действительно, если
,
то
;
;
,
тогда
.
Если векторы
,,компланарны, то векторное произведение
перпендикулярно вектору.
И наоборот, если
,
то объем параллелепипеда равен нулю, а
это возможно только в том случае, когда
векторы компланарны (линейно зависимы).
Таким образом, три вектора компланарны, тогда и только тогда, когда их смешанное произведение равно нулю.
Таргетированная outdoor-реклама. Как находить своего покупателя в городе | Публикации
Последние десять лет рекламный рынок и его бюджеты уверенно движутся от охватных каналов в сторону персонализации и стимулирования потребителя совершить действие прямо здесь и сейчас.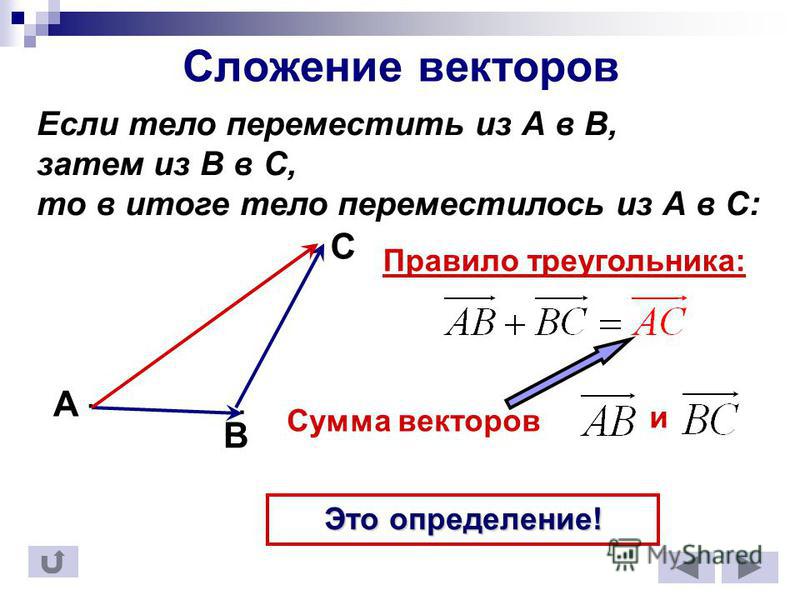 Наружка тоже не стоит на месте — таргетированная outdoor-реклама постепенно становится реальностью рекламного мира. Как перейти к таргетированию в outdoor, какие средства для этого уже есть и всегда ли эта игра стоит свеч, обсудили на конференции AdIndex City 2021
Наружка тоже не стоит на месте — таргетированная outdoor-реклама постепенно становится реальностью рекламного мира. Как перейти к таргетированию в outdoor, какие средства для этого уже есть и всегда ли эта игра стоит свеч, обсудили на конференции AdIndex City 2021
Для таргетинга в наружке используем те же данные, что и в digital
На текущий момент нет принципиальной разницы между данными в наружной рекламе и данными в интернете, считает руководитель группы инновационных сервисов компании «Квант» Инна Кравцова. Российское законодательство одинаково регулирует обе эти сферы, а сами данные в равной степени подходят для таргетинга как в outdoor, так и в digital.
Важно обращать внимание на то, какие идентификаторы привлекаются и что может лежать в их основе. В «Кванте» используют несколько ключевых блоков по данным:
1. Геоданные. Сбор данных может происходить в разных локациях —
билборды оснащаются Wi-Fi-снифферами, в наземном транспорте, метро, такси и
аэропортах работают сенсоры трафика. Технологии позволяют отслеживать
передвижение пользователей по городу и внутри коммерческих объектов и
выстраивать их паттерны поведения.
Технологии позволяют отслеживать
передвижение пользователей по городу и внутри коммерческих объектов и
выстраивать их паттерны поведения.
2. Поведение в интернете. В момент, когда пользователь подключается к любой Wi-Fi-сети — в метро, парке или кафе, — оператор собирает данные о приложениях и сайтах, открытых на устройстве.
3. Посещение объектов. Пожалуй, не осталось торгового центра, который бы не был оснащен Wi-Fi-ловушками.
4. Покупки — лакомый кусок данных для любого рекламодателя. «Квант» сотрудничает с тремя крупнейшими ОФД и может отследить более 60% всех транзакций онлайн и офлайн, которые осуществляют покупатели.
Выбираем релевантную локацию с помощью геоаналитических платформВ ближайшее время рекламной индустрии предстоит довольствоваться тем, что
уже есть, так как вряд ли появятся новые виды данных. Однако по мере развития
технологий находится все больше способов миксовать их и получать неожиданные
результаты.
Сергей Голицын, директор по анализу данных и моделированию «Платформы больших данных», рассказал о тренде на Data Fusion. Эта технология позволяет делать микс из большого объема сложных кросс-отраслевых данных, которые раньше не получалось объединить.
Лучшим программным решением для наружной рекламы станет работа с геоаналитическими платформами. Они генерируют множество геослоев, которые представляют собой характеристику конкретных локаций.
Платформа показывает, как на территории распределяются интересы, доходы,
трудоспособное население и множество других показателей. Векторное
представление локаций можно интерпретировать с точки зрения моделирования и
построения профиля. Для построения геоаналитических слоев привлекаются сотни
источников — от телеком-операторов и соцсетей до транзакционных данных, при
этом мы не привязываемся к конкретному пользователю, а создаем общий портрет
покупателя в конкретной локации. Такой микс позволяет максимально профилировать
локацию. На основе полученных данных формируется несколько геослоев. Их
помещают в единое пространство и обрабатывают с помощью машинного обучения,
чтобы объединить в ранжирующий слой, который поможет выбрать наиболее
подходящую локацию для размещения рекламы.
Такой микс позволяет максимально профилировать
локацию. На основе полученных данных формируется несколько геослоев. Их
помещают в единое пространство и обрабатывают с помощью машинного обучения,
чтобы объединить в ранжирующий слой, который поможет выбрать наиболее
подходящую локацию для размещения рекламы.
Таргетированная outdoor-реклама — это свайп вправо
Руководитель продуктов компании Russ Outdoor Руслан Ибрагимов сравнивает поиски рекламодателем своего клиента с механикой в дейтинг-сервисах (свайп вправо и влево). Разные дейтинг-сервисы имеют разную ЦА и и цели пользователей. Исходя из этого пользователи пользуются разными сервисами. Таргетированная реклама по механике очень похожа на данный процесс. Рекламодатель хочет достичь своего клиента, потратив на это как можно меньше времени и ресурсов.
Передвижение любого среднестатистического городского жителя можно
представить в виде пользовательского пути. Этот путь проходит мимо точек
пересечения с рекламой: остановок, билбордов, бизнес-центров, аэропортов, а
также станций метро и МЦК. При этом рекламодатель почти всегда нацелен
«поймать» нужный ему сегмент аудитории со своими интересами — целевую
аудиторию.
Этот путь проходит мимо точек
пересечения с рекламой: остановок, билбордов, бизнес-центров, аэропортов, а
также станций метро и МЦК. При этом рекламодатель почти всегда нацелен
«поймать» нужный ему сегмент аудитории со своими интересами — целевую
аудиторию.
И если раньше планирование в наружке велось по привязкам, охвату и маршрутам, то современный outdoor движется в сторону планирования по целевой аудитории и к таргетингам в реальном времени.
Для этого важно понимать, что происходит в городе, а также где и в какое время концентрируется целевая аудитория. Важную роль здесь играет геоаналитика, которая помогает профилировать территорию по таким признакам, как уровень дохода, интересы и соцдем.
Понимая типичный портрет аудитории, становится возможным выбирать места размещения наружной рекламы там, где доля ЦА больше.
«Крен аффинитивности» покажет рекламный креатив в реальном времениИнна Кравцова рассказала про новый продукт, совместно разработанный Russ Outdoor и «Квант», под рабочим названием «Крен аффинитивности». Это рекомендательная система, которая показывает рекламный креатив в рамках барабана и работает на собранных MAC-адресах. Продукт состоит из трех частей — калькулятора, самой рекомендательной системы и отчетности о результатах после изменений внутри системы. Калькулятор помогает планировать рекламные кампании — с его помощью рекламодатель понимает, какую выгоду получит, если выберет тот или иной таргетинг.
Как это работает:
— «Квант»получает от Russ Outdoor поток MAC-адресов в режиме реального времени от всех конструкций и непрерывно анализирует долю, которую целевая аудитория занимает в текущий момент времени;
— полученная статистика запускается в рекомендательную систему, где в течение двух недель по ней оттачиваются настройки алгоритма. Срок годности данных для создания прогноза — не более двух недель;
— затем, когда рекламная кампания началась, поток продолжает анализироваться, и алгоритм определяет, в какой момент времени выход рекламного ролика лучше попадает в целевую аудиторию.
При этом «Крен аффинитивности» — это не программатик в чистом виде. Здесь нет DSP и SSP: программа дает потребителю рекомендацию к привычной покупке через барабанную модель.
Для оценки результатов система отчетности помогает понять, каким было бы попадание в целевую аудиторию, если бы рекламный ролик не менял свою позицию, а выходил в стандартном цикле, и сравнить его с результатом использования оптимизационной механики.
Таргетинг не всегда гарантирует повышения конверсииВ 2018 году, когда таргетинг только появился в наружной рекламе, его взялся тестировать практически весь outdoor-сегмент. И если подбор целевой аудитории сразу отлично себя зарекомендовал, то показатели ROI до сих пор вызывают вопросы.
Руководитель цифровых out-of-home-продуктов Posterscope Вячеслав Ивакин объяснил, почему таргетинг не гарантирует повышения конверсии, и рассказал, что нужно сделать, чтобы обеспечить хорошие результаты.
Обычное размещение в наружке контактирует с некоторым количеством людей, среди которых встречается и целевая аудитория. Если она составляет 14% — это уже неплохой бенчмарк. Качественный таргетинг может в среднем поднять объем целевой аудитории примерно в два-три раза.
Даже если при таких высоких показателях человек из целевой аудитории конвертится в два раза лучше, чем простой обыватель, это не гарантирует успех. Ведь многое решает наценка за данные и решения при таргетинге.
Чем больше наценка, тем при сохранении бюджета меньше контактов и ниже охват. В результате количество финальных конверсий при таргетинге может оказаться таким же, как и без него, что нивелирует всю проделанную работу. Именно поэтому важно внимательно работать с вводными, параметрами, условиями и конверсиями.
В каком направлении развиваться дальше?
Наличие большого количества данных для аналитики и таргетинга делают наружку более привлекательной для рекламодателя и агентств. Однако есть еще ряд важных условий, которые, по мнению Вячеслава Ивакина, позволят outdoor-сегменту расширить свои горизонты:
1. Вернуть и расширить долю видеоаналитики. Это уникальный вид данных, который позволяет выцепить нужную аудиторию на порядки точнее, чем это возможно сделать по цифровым следам в интернете.
2. Организовать данные соцдем-таргетинга. Данные соцдема нужно стандартизировать, приведя в соответствие с другими медиаканалами. При этом важно использовать понятные прозрачные источники.
3. Расширить долю ретейла. Наружная реклама насыщена данными, однако таргетингов по ретейлу — по местам посещения, товарным категориям и чекам — явно недостаточно.
Ближайшее будущее outdoorПод занавес секции спикеры обсудили тренды таргетированного outdoor, которые привлекают к себе внимание, и поделились своим видением будущего.
Новые подходы к анализу данных. В обозримом будущем работа с данными, подсказывающими интерес покупателя к конкретным продуктам, а также данными фактического потребления тех или иных продуктов и брендов выйдет на первый план. Уже сейчас активно развиваются технологии, которые позволят проводить их полный учет и более быструю обработку. Наиболее перспективным направлением в этой области, по мнению Сергея Голицына, станет работа с транзакционными и банковскими базами, а также базами фискальных операторов.
Увеличение доли ретейла. Таргетинги по ретейлу — вопрос времени. Инна Кравцова рассказала, как «Квант» работает над выходом ретейла в outdoor. Компания готовится к тому, что можно будет тестировать гипотезы таргетирования по CRM-клиента при достаточных охватах.
Тренд на получение быстрых результатов. Спикеры отметили увеличивающийся интерес к performance-механикам, которые позволяют в моменте увидеть отклик на услугу или товар. Рекламодатели ждут, что бизнес не будет застаиваться и продажи будут происходить сразу, а не в отдаленном будущем.
Внимание к широкой аудитории. Тренд на быструю отдачу может создать иллюзию отсутствия необходимости вкладывать усилия в свой бренд. При таком подходе уменьшается вклад в коммуникации, которые не побуждают совершить ежеминутную[4] покупку, а работают долгое время. Поэтому важно формировать знание бренда среди всех потенциальных покупателей в категории.
Спрос на умное управление. Рекламная кампания — это взаимосвязанная экосистема разных каналов коммуникаций, и наружная реклама не должна существовать в отрыве. Важен баланс, важно сохранение охвата и частоты контакта, важно вовлечение как можно большего числа потенциальных покупателей — и важно использовать те инструменты таргетинга, которые позволяют лучше использовать знания об аудитории и контекст локаций.
Сложение векторов
В механике есть два вида величин
- скалярных величин с величиной — время, температура, масса и т. Д.
- вектор величин с величиной и направлением — скорость, сила и т. Д.
Когда добавление векторных величин важны как по величине, так и по направлению. Общие методы сложения копланарных векторов (векторов, действующих в одной плоскости):
- закон параллелограмма
- правило треугольника
- тригонометрическое вычисление
Закон параллелограмма
Процедура «» метод сложения параллелограмма векторов «- это
- начертите вектор 1, используя соответствующий масштаб и в направлении его действия
- от хвоста вектора 1 начертите вектор 2, используя тот же масштаб в направлении его действия
- завершите параллелограмм, используя вектор 1 и 2 как стороны параллелограмма
- результирующий вектор представлен как по величине, так и по направлению диагональю параллелограмма
Правило треугольника
Процедура « метод сложения треугольника векторов » равна
- начертите вектор 1 в соответствующем масштабе и в направлении его действия 9 0008
- от носа вектора нарисуйте вектор 2, используя тот же масштаб и в направлении его действия
- , результирующий вектор представлен как по величине, так и по направлению вектором, проведенным от хвоста вектора 1 к носу вектора 2
Тригонометрическое вычисление
Результирующий вектор из двух копланарных векторов может быть вычислен тригонометрическим методом с использованием « правила косинуса » для прямоугольного треугольника.
F R = [F 1 2 + F 2 2 — 2 F 1 F 2 cos (180 o — (α + β))] 1/2 (1)
где
F = векторная величина — сила, скорость и т. Д.
α + β = угол между вектором 1 и 2
Угол между вектором и результирующий вектор может быть вычислен с использованием « правило синуса » для непрямоугольного треугольника.
α = sin -1 [F 1 sin (180 o — (α + β)) / F R ] (2)
где
α + β = угол между вектором 1 и 2 известен
Пример — сложение сил
Сила 1 с величиной 3 кН действует в направлении 80 o от силы 2 с величиной 8 кН .
Результирующая сила может быть рассчитана как
F R = [(3 кН) 2 + (8 кН) 2 — 2 (5 кН) (8 кН) cos (180 o — (80 o ))] 1/2
= 9 (кН)
Угол между вектором 1 и результирующим вектором можно рассчитать как
α = sin -1 [(3 кН) sin (180 o — (80 o )) / (9 кН) ]
= 19.1 o
Угол между вектором 2 и результирующим вектором можно рассчитать как
α = sin -1 [(8 кН) sin (180 o — (80 o ) ) / (9 кН) ]
= 60,9 o
Пример — Самолет при ветре
Встречный ветер 100 км / ч действует 30 o правый борт на самолете с скорость 900 км / ч .
Результирующая скорость самолета относительно земли может быть рассчитана как
v R = [(900 км / ч) 2 + (100 км / ч) 2 — 2 (900 км / ч) (100 км / ч) cos (180 o — (30 o ))] 1/2
= 815 (км / ч)
Угол между курсом самолета и фактический относительный курс земли можно рассчитать как
α = sin -1 [(100 км / ч) sin ((180 o ) — (30 o )) / (815 км / ч) ]
= 3.5 o
Векторный калькулятор
Общий калькулятор ниже основан на уравнении (1) и может использоваться для сложения векторных величин, таких как скорости, силы и т. Д.
Параллелограмм
Результирующие векторы могут быть оценены путем рисования параллелограммов, как показано ниже.
- нарисуйте векторы с правильным направлением и величиной
- начертите параллельные линии векторам
- начертите результирующий вектор в точку пересечения между параллельными линиями
- измерьте величину и направление результирующего вектора на чертеже
Метод также можно использовать с более чем двумя векторами, как указано ниже.
- нарисуйте результирующие векторы между двумя и двумя векторами
- начертите результирующие векторы между двумя и двумя результирующими векторами
- продолжайте до тех пор, пока не будет только один конечный результирующий вектор
- Измерьте направление и величину конечного результирующего вектора в рисунок
В приведенном выше примере сначала найдите результирующий F (1,2) , добавив F 1 и F 2 , и получившийся F (3,4) , добавив F 3 и F 4 .Найдите результат F (1,2,3,4) , добавив F (1,2) и F (3,4) .
Калькулятор линейной независимости
Добро пожаловать в калькулятор линейной независимости , где мы узнаем, как проверить, имеете ли вы дело с линейно независимыми векторами или нет.
По сути, мир вокруг нас является векторным пространством и иногда полезно ограничиться меньшей его частью. Например, сфера — это , трехмерная форма , а круг существует только в двух измерениях , так зачем возиться с вычислениями в трех измерениях?
Линейная зависимость позволяет нам делать именно это — работать в меньшем пространстве, так называемом диапазоне рассматриваемых векторов .Но не волнуйтесь, если вы нашли все эти причудливые слова нечеткими. Через секунду мы медленно пройдем через все это вместе.
Так что возьмите утреннюю / вечернюю закуску в дорогу, и вперед!
Что такое вектор?
Если вы спросите кого-нибудь « Что такое вектор? » довольно часто, вы получите ответ « стрелка ». Ведь мы обычно обозначаем их стрелкой над маленькой буквой:
Ну, давайте просто скажем, что этот ответ не принесет вам 100 баллов на тесте.Формально вектор — это элемент векторного пространства . Конец определения. Достаточно просто . Мы можем закончить учебу. Теперь все ясно.
Но , что же тогда такое векторное пространство? Опять же, математическое определение оставляет желать лучшего: это набор элементов с некоторыми операциями (сложение и умножение на скаляр), которые должны иметь несколько специфических свойств. Так почему бы нам просто не оставить формализм и не взглянуть на на реальных примерах ?
Декартово пространство является примером векторного пространства.Это означает, что числовая линия, плоскость и трехмерное пространство, в котором мы живем , являются векторными пространствами . Их элементами являются, соответственно, числа, пары чисел и тройки чисел, которые в каждом случае описывают положение точки (элемента пространства). Например, число -1 или точка A = (2, 3) являются элементами (разных!) Векторных пространств. Часто при рисовании сил, действующих на объект, таких как скорость или гравитационное притяжение, мы используем прямые стрелки , чтобы описать их направление и значение , и отсюда и происходит «определение стрелки ».
Что очень важно, так это то, что у нас есть четко определенных операций над векторами, упомянутыми выше. Есть несколько более сложных, таких как скалярное произведение и перекрестное произведение. Однако, к счастью, мы ограничимся двумя основными , которые следуют аналогичным правилам для одних и тех же матричных операций (векторы, по сути, являются однострочными матрицами). Прежде всего, , мы можем добавить их :
-1 + 4 = 3 ,
(2,3) + (-3, 11) = (2 + (-3), 3 + 11) = (-1, 14) ,
и , мы можем умножить их на скаляр (действительное или комплексное число), чтобы изменить их величину:
3 * (-1) = -3 ,
7 * (2, 3) = (7 * 2, 7 * 3) = (14, 21) .
По правде говоря, векторное пространство не обязательно должно содержать числа . Это может быть пространство последовательностей, функций или перестановок. Даже скаляры не обязательно должны быть числовыми! Но оставим эту абстрактную чушь ученым . Нас устраивают только цифры, не так ли?
Линейная комбинация векторов
Допустим, нам дан набор векторов (из того же пространства): v₁ , v₂ , v₃ , …, vₙ . Как мы видели в предыдущем разделе, , мы можем сложить их и умножить на скаляры . Любое выражение, полученное таким образом, называется линейной комбинацией векторов. Другими словами, любой вектор w , который можно записать как
w = 𝛼₁ * v₁ + 𝛼₂ * v₂ + 𝛼₃ * v₃ + ... + 𝛼ₙ * vₙ
, где 𝛼₁, 𝛼₂, 𝛼₃, ..., 𝛼ₙ — произвольные действительные числа, называется линейной комбинацией векторов v₁ , v₂ , v₃ ,…, vₙ . Обратите внимание, что w действительно вектор, поскольку это сумма векторов.
Хорошо, зачем все это? В жизни есть несколько вещей, таких как гелиевые шары и гамаки, которые приятно иметь, но не так уж и полезны в повседневной жизни. Так ли это здесь?
Рассмотрим декартовую плоскость , т.е. двумерное пространство точек A = (x, y) с двумя координатами, где x и y — произвольные действительные числа.Мы уже знаем, что такие точки являются векторами, поэтому почему бы нам не взять , две очень особенные точки : e₁ = (1,0) и e₂ = (0,1) . Теперь обратите внимание:
A = (x, y) = (x, 0) + (0, y) = x * (1,0) + y * (0,1) = x * e₁ + y * e₂ .
Другими словами, любая точка (вектор) нашего пространства представляет собой линейную комбинацию векторов e₁ и e₂ . Эти векторы образуют базис (и при этом ортонормированный базис) пространства.И поверьте нам, в приложениях и вычислениях часто проще работать с известной вам базой, чем с какими-то случайными векторами, которых вы не знаете.
Но , что, если бы мы добавили еще один вектор к стопке и захотели описать линейные комбинации векторов e36 , e₂ и, скажем, v ? Мы видели, что e₁ и e₂ оказались достаточными, чтобы найти все точки. Так что добавление к ничего не должно изменить, не так ли? Собственно, кажется совершенно лишним .И именно здесь в игру вступает линейная зависимость .
Линейно независимые векторы
Нет, это не имеет ничего общего с вашим барбекю 4 июля. Мы говорим, что v₁ , v₂ , v₃ , …, vₙ — это линейно независимых векторов , если уравнение
𝛼₁ * v₁ + 𝛼₂ * v₂ + 𝛼₃ * v₃ + ... + 𝛼ₙ * vₙ = 0
(здесь 0 — вектор с нулями во всех координатах) выполняется тогда и только тогда, когда 𝛼₁ = 𝛼₂ = 𝛼₃ =... = 𝛼ₙ = 0 . В противном случае мы говорим, что векторы линейно зависимы .
Приведенное выше определение можно понять следующим образом: единственная линейная комбинация векторов, которая дает нулевой вектор, является тривиальной . Например, вспомните векторы из приведенного выше раздела: e₁ = (1,0) , e₂ = (0,1) , а затем также возьмите v = (2, -1) . Тогда
(-2) * e₁ + 1 * e₂ + 1 * v = (-2) * (1,0) + 1 * (0,1) + 1 * (2, -1) = (-2,0 ) + (0,1) + (2, -1) = (0,0) ,
, поэтому мы нашли нетривиальную линейную комбинацию векторов, которая дает ноль .Следовательно, они линейно зависимые . Кроме того, мы легко можем видеть, что сами по себе e₁ и e₂ без проблемных v являются линейно независимыми векторами .
Оболочка векторов в линейной алгебре
Набор всех элементов, которые можно записать как линейную комбинацию векторов v₁ , v₂ , v₃ , …, vₙ , называется промежутком векторов и обозначается span ( v₁, v₂, v₃ ,..., vₙ) . Возвращаясь к векторам из предыдущего раздела, то есть e₁ = (1,0) , e₂ = (0,1) и v = (2, -1) , мы видим, что
пролет (e₁, e₂, v) = пролет (e₁, e₂) = ℝ² ,
, где ℝ² — это множество точек на декартовой плоскости, то есть все возможные пары действительных чисел. По сути, это означает, что размах векторов одинаков: для e₁ , e₂ и v , и всего для e₁ и e₂ (или, если использовать формальные термины, двух пересечение пространств составляет целое м² ).Это говорит о том, что v является избыточным и ничего не меняет . Да, вы догадались — именно из-за линейной зависимости .
Пролет в линейной алгебре описывает пространство, в котором живут наши векторы . В частности, наименьшее количество элементов, которых достаточно для этого, называется размерностью векторного пространства. В приведенном выше примере это было 2 , потому что мы не можем получить меньше элементов, чем e₁ и e₂ .
Внимательный взгляд заметит, что на самом деле размерность диапазона векторов равна количеству линейно независимых векторов в сгустке. В приведенном выше примере это было довольно просто: векторы e₁ и e₂ были самыми простыми из возможных (на самом деле, у них даже есть собственное имя: стандартный базис ). Но что, если у нас есть что-то другое? Как мы можем проверить линейную зависимость и описать диапазон векторов в каждом случае? Через минуту мы узнаем это и многое другое!
Как проверить линейную зависимость
Для проверки линейной зависимости переведем нашу задачу с языка векторов на язык матриц (массивов чисел).Например, предположим, что нам даны три вектора в 2-мерном пространстве (с двумя координатами): v = (a₁, a₂) , w = (b₁, b₂) и u = (c₁, c₂) . Теперь давайте запишем их координаты как в одну большую матрицу , в которой каждая строка (или столбец, неважно) соответствует одному из векторов:
| А | = |
|
Тогда ранг матрицы равен максимальному количеству линейно независимых векторов среди v , w и u .Другими словами, их промежуток в линейной алгебре имеет размерность ранг (A) . В частности, являются линейно независимыми векторами тогда и только тогда, когда ранг A равен количеству векторов .
Итак, как нам узнать ранг? Возможно, самый простой метод — это исключение Гаусса (или его уточнение, исключение Гаусса-Жордана ). Это тот же самый алгоритм, который часто используется для решения систем линейных уравнений, особенно при попытке найти (сокращенную) ступенчатую форму системы.
Исключение по Гауссу основано на так называемых операциях с элементарной строкой :
- Поменять местами две строки матрицы.
- Умножьте строку на ненулевую константу.
- Добавить в строку ненулевое кратное другой строке.
Уловка здесь в том, что хотя операции изменяют матрицу , они не меняют ее ранг и, следовательно, размер диапазона векторов.
Алгоритм пытается устранить (т.е.е., сделайте их 0 ) как можно больше записей A . В приведенном выше случае, при условии, что a₁ не равно нулю, первый шаг исключения Гаусса преобразует матрицу во что-то в форме:
|
, где s₂ и t₂ — некоторые действительные числа.Тогда, пока сÀ не равно нулю, второй шаг даст матрицу
|
Теперь нам нужно заметить, что нижняя строка представляет нулевой вектор (у него 0 в каждой ячейке), который линейно зависит от любого вектора .Следовательно, ранг нашей матрицы будет просто , количество ненулевых строк в массиве, которое мы получили , что в данном случае составляет 2 .
Это было достаточно времени, потраченного на теорию, не так ли? Давайте попробуем на примере посмотрим, как работает калькулятор линейной независимости !
Пример: использование калькулятора линейной независимости
Допустим, вы наконец осуществили свои мечты — вы купили дрон . Наконец-то вы можете снимать и снимать на видео места, которые вы посещаете, издалека.Все, что вам нужно сделать, это запрограммировать его движения . Дрон требует, чтобы вы дали ему три вектора, по которым он сможет перемещать .
Мир, в котором мы живем, трехмерен, поэтому векторы будут иметь три координаты . Не задумываясь, вы берете случайных векторов, которые приходят на ум : (1, 3, -2) , (4, 7, 1) и (3, -1, 12) . Но действительно ли стоит просто закрыть глаза, подбросить монетку и выбрать случайные числа? В конце концов, большая часть ваших сбережений пошла на это, так что , нам лучше сделать это хорошо .
Что ж, если вы выбрали числа случайным образом, вы можете обнаружить, что выбранных вами векторов являются линейно зависимыми , а диапазон векторов, например, только двумерный. Это означает, что ваш дрон не сможет перемещаться, как вы хотите, но будет ограничен движением по плоскости . Может случиться так, что он сможет перемещаться влево и вправо, вперед и назад, , но не вверх и вниз . И как мы получим эти отмеченные наградами кадры похода, если дрон не может даже взлететь?
Хорошо, что у нас есть калькулятор линейной независимости! С его помощью мы можем быстро и легко проверить, был ли наш выбор удачным. Итак, давайте разберемся, как им пользоваться.
У нас есть 3 векторов с 3 координатами каждый, поэтому мы начинаем с того, что сообщаем калькулятору об этом факте, выбирая соответствующие параметры под « количество векторов » и « количество координат ». Это покажет нам символический пример таких векторов с обозначениями, используемыми в калькуляторе линейной независимости. Например, первый вектор задается как v = (a₁, a₂, a₃) .Следовательно, поскольку в нашем случае первым было (1, 3, -2) , мы вводим
a₁ = 1 , a₂ = 3 , a₃ = -2 .
Аналогично для двух других получаем:
b₁ = 4 , b₂ = 7 , b₃ = 1 ,
c₁ = 3 , c₂ = -1 , c₃ = 12 .
Как только мы введем последнее число, калькулятор линейной независимости мгновенно сообщит нам, есть ли у нас линейно независимые векторы или нет , и каков размер диапазона векторов.Тем не менее, давайте возьмем лист бумаги и попробуем сделать все самостоятельно вручную, чтобы увидеть , как калькулятор пришел к своему ответу .
Как упоминалось в предыдущем разделе, мы хотели бы вычислить ранг матрицы, образованной нашими векторами . Мы построим массив размером 3 × 3, записав координаты последовательных векторов в последовательные строки. Таким образом, мы приходим к матрице
| А | = |
|
Теперь мы будем использовать исключения Гаусса .Прежде всего, нам бы хотелось, чтобы имел нули в двух нижних строках первого столбца . Для их получения мы используем элементарные операции со строками и 1 из верхней строки. Другими словами, мы прибавляем подходящее кратное первой строки к двум другим , так что их первая запись станет нулем. Поскольку 4 + (-4) * 1 = 0 и 3 + (-3) * 1 = 0 , мы добавляем кратное (-4) и (-3) первой строки к второй и третий ряд соответственно.Это дает матрицу
| = |
| = |
|
Затем мы хотим, чтобы получило 0 в нижней строке среднего столбца и использовало для этого -5 .Опять же, , мы прибавляем подходящее кратное второй строки к третьей . Поскольку -10 + (-2) * (- 5) = 0 , кратное составляет (-2) . Следовательно,
| = |
| = |
|
Мы получили нулей в нижних строках .Мы знаем, что ранг матрицы и, следовательно, линейная зависимость и диапазон в линейной алгебре определяются количеством ненулевых строк . Это означает, что в нашем случае у нас rank (A) = 2 , что на меньше, чем количество векторов , и подразумевает, что они линейно зависимы и охватывают 2-мерное пространство .
Итак, случилось то, чего мы опасались: наш дрон не будет иметь свободы передвижения . Но мы не можем упустить шанс снять все эти воздушные кадры! К счастью, у нас есть калькулятор линейной независимости , и мы можем поиграть с векторами, чтобы найти подходящую комбинацию векторов.А когда он у нас есть, мы собираемся, садимся в машину и отправляемся в приключение!
Карта механики — момент около точки
Для любой точки вытянутого тела, если на это тело действует сила, которая не проходит через эту точку, то эта сила вызовет момент вокруг этой точки. Как уже говорилось на странице моментов, момент — это тенденция силы вызывать вращение.
Векторный метод в 2-х и 3-х измерениях
Альтернативой вычисления момента с помощью скалярных величин является использование векторного метода или метода перекрестного произведения .Для простых двумерных задач обычно проще использовать скалярные величины, но для более сложных задач обычно проще использовать метод перекрестного произведения. Метод перекрестного произведения для вычисления моментов гласит, что вектор момента силы вокруг точки будет равен перекрестному произведению вектора r от точки до любой точки на линии действия силы и самого вектора силы.
| \ [\ vec {M} = \ vec {r} \ times \ vec {F} \] |
Большим преимуществом этого метода является то, что r не обязательно должно быть кратчайшим расстоянием между точкой и линией действия, оно идет от точки до любой части линии действия.Для любой задачи существует множество возможных векторов r , хотя из-за того, как работает перекрестное произведение, все они должны в конечном итоге привести к одному и тому же вектору момента.
Вектор момента силы F относительно точки A будет равен перекрестным произведениям вектора r и вектора силы. Вектор r — это вектор из точки A в любую точку на линии действия силы.Здесь важно отметить, что все величины ( r , F и M ) являются векторами.Прежде чем вы сможете решить для кросс-продукта, вам нужно будет записать r и F в форме векторных компонентов. Кроме того, даже для двумерных задач вам нужно будет выписать все три компонента векторов r и F . Для двумерных задач компоненты z векторов r и F будут просто равны нулю, но эти значения необходимы для вычислений.
Полученный вами вектор момента будет совмещен с осью вращения на данный момент, где вы можете использовать правило правой руки, чтобы определить, идет ли момент вокруг этой оси по часовой стрелке или против часовой стрелки.
Результат r cross F даст нам вектор момента. Для этой двумерной задачи вектор момента указывает в положительном направлении оси z. Мы можем использовать правило правой руки, чтобы определить направление вращения с момента (совместите большой палец правой руки с вектором момента, и наши скрученные пальцы будут указывать в направлении вращения с момента).Наконец, важно также отметить, что перекрестное произведение, в отличие от умножения, не является коммуникативным.Это означает, что порядок векторов имеет значение, и r cross F не будет таким же, как F cross r . При расчете моментов важно всегда использовать r cross F .
Очень простое руководство по CalcMe — CalcMe — Документация
CalcMe — это онлайн-калькулятор на основе Javascript, поэтому он работает в любом браузере и операционной системе, включая мобильные и планшетные устройства. CalcMe интегрирован в Wiris Quizzes, повышая эффективность ваших математических вопросов.CalcMe предлагает мощный вычислительный и графический движок, покрывающий базовые и сложные математические задачи: генерация случайных чисел, полиномы, общие выражения, векторы, матрицы, списки, геометрия, статистика, пользовательские функции, программирование и многое другое.Живые демонстрации
На этой странице есть несколько живых демонстраций. Если щелкнуть область, содержащую параметры CalcMe, она откроется в CalcMe. Попробуйте, измените параметры или опции. Ничего не сломаешь.Как работает CalcMe?
Вы можете писать математику, а CalcMe выполнит вычисления за вас.
Таблица CalcMe разделена на три основные области:
| Область для Расчет | Область для График | Область для Определение |
Рассчитать
Напишите, что вы хотите вычислить
Нажмите Calc или Введите
Действие по умолчанию — Calc , но вы можете выбрать наиболее подходящий по своему усмотрению.
ЖИВАЯ ДЕМО
График
Напишите уравнение или фигуру, которую хотите построить
Нажмите График действие
Новый
С этого момента можно загрузить графический плоттер в виде квадратного изображения в формате PNG желаемого размера.Воспользуйтесь этой новой функцией CalcMe, чтобы сохранять сгенерированные изображения прямо на ваше устройство.Определить
Сохранить вычисление в переменной
Использовать позже
Новый
Есть новая процедура для определения переменных в CalcMe с помощью редактора кода. Здесь вы можете увидеть проблемы, которые предполагается решить с его помощью, и ожидаемое взаимодействие с пользователем.Арифметика
Математические операции в CalcMe представлены символом, связанным с клавишей клавиатуры.
ЖИВАЯ ДЕМО
Вы можете вычислить частное и остаток от деления или разложить число на простые множители. Вы также можете вычислить наибольший общий делитель или наименьшее общее кратное набора чисел.
ЖИВАЯ ДЕМО
Конструктор векторов и матриц
Векторы
Вектор заключен в квадратные скобки [] , а элементы разделены запятыми , .
Вы можете просуммировать векторы или вычислить их скалярное произведение.
ЖИВАЯ ДЕМО
Матрицы
Матрицы — это векторы векторов, то есть векторы, элементы которых являются векторами. Вы можете создавать матрицы с двумя разными синтаксисами
В качестве векторов вы можете суммировать и умножать матрицы (если их размеры совместимы).
ЖИВАЯ ДЕМО
Основные операции
Как вы уже видели, вы можете работать с векторами и матрицами и выполнять с ними базовые арифметические операции.Однако вы можете сделать гораздо больше: вы можете вычислить перекрестное произведение между двумя векторами, проверить, являются ли они линейно независимыми; матрицу можно инвертировать или возвести в целую степень, вы также можете вычислить ее ранг или определитель.
ЖИВАЯ ДЕМО
Доступ к элементу
Вы можете получить доступ к определенному элементу вектора с помощью подиндексов, которые начинаются с 1. Таким же образом вы можете получить элемент матрицы.
ЖИВАЯ ДЕМО
Многочлены и выражения
Многочлены создаются с помощью числа, умноженного на переменную, возведенную в степень.
ЖИВАЯ ДЕМО
Вы можете суммировать, умножать, делить и, например, находить корни многочленов.
ЖИВАЯ ДЕМО
Вы также можете создавать более сложные выражения и работать с ними.
ЖИВАЯ ДЕМО
Дифференциация
Существует множество способов вычислить производную функции или выражения.
| Использование простого числа | ' |
| Использование символа | |
| Использование действия | |
| С помощью команды | дифференцировать |
ЖИВАЯ ДЕМО
Интеграция
Также существует множество способов вычислить интеграл от функции или выражения.
| Использование символа | |
| Использование действия | |
| Используя команду | интегрировать |
ЖИВАЯ ДЕМО
Предел
Можно вычислить предел функции или выражения. Более того, вы также можете брать односторонние ограничения.
ЖИВАЯ ДЕМО
Расширение Тейлора
Вы можете вычислить ряд Тейлора реальной функции в заданной точке.Если вас интересуют сроки до некоторого порядка, вы можете также сократить серию.
ЖИВАЯ ДЕМО
серии
Вы можете определить, сходится ли ряд, а также в большинстве случаев вычислить сумму сходящихся рядов.
ЖИВАЯ ДЕМО
Геометрия
CalcMe позволяет нам работать с геометрическими фигурами, такими как точки, линии, плоскости и конические сечения.Вы также можете создавать многоугольники и многогранники как в 2D, так и в 3D. Также возможно вычислить расстояние между фигурами, угол, который они образуют, или симметрию относительно объекта.
Точки, линии и плоскости
Возможна работа в 2 или 3 измерениях. Чтобы создать точки, вы просто определяете его компоненты.
ЖИВАЯ ДЕМО
Имея две точки или точку и вектор, вы можете построить линию.
ЖИВАЯ ДЕМО
Подобным образом вы можете, например, построить плоскость по трем точкам.
ЖИВАЯ ДЕМО
Фигуры
ЖИВАЯ ДЕМО
Решение
Уравнения
Можно решить уравнение или систему уравнений точно .
ЖИВАЯ ДЕМО
Вы также можете использовать численный метод для решения более сложных уравнений.
ЖИВАЯ ДЕМО
Вы также можете использовать численный метод для решения более сложных уравнений.
ЖИВАЯ ДЕМО
Неравенства
Также возможно найти решение неравенства.
ЖИВАЯ ДЕМО
Статистика
Существует множество функций, полезных для статистических расчетов, таких как среднее значение, квантиль, квартиль и т. Д. Вы можете увидеть полный список здесь.
ЖИВАЯ ДЕМО
Вероятность
Также доступны наиболее распространенные распределения вероятностей.По возможности также доступны аналитические выражения для функций плотности и распределения.
ЖИВАЯ ДЕМО
Комбинаторика
Можно вычислить комбинации, перестановки или вариации набора чисел. Однако будьте осторожны: результаты очень большие.
ЖИВАЯ ДЕМО
Единицы и валюта
Вы можете работать с единицами, конвертировать одну в другую (если это имеет смысл) и выполнять с ними базовые операции.Единицы необходимо вводить с помощью символов, доступных на вкладке Единицы измерения . Узнайте больше о единицах измерения или префиксах, которые вы можете использовать здесь.
ЖИВАЯ ДЕМО
Валюты похожи на единицы, но вы не можете конвертировать одну в другую. Проверьте все доступные валюты здесь.
ЖИВАЯ ДЕМО
Случайность
Параметр строк алгоритма
Поскольку вы можете использовать эти команды для создания алгоритма для вопроса викторины Wiris, мы покажем, как создавать их на листе и с помощью редактора кода.Вы можете узнать об этом подробнее здесь.Функция random в CalcMe адаптируется ко многим случаям использования. Например, вы увидите, как удалить «0» из случайного выбора. Обычная команда была бы такой:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
По умолчанию сюда входят все числа от -10 до 10. Если учитывая требования вопроса, число 0 необходимо исключить из набора, вы можете удалить его с помощью одной простой инструкции (косая черта / должна быть используется с клавиатуры или логики и устанавливает вкладку ):
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Вы должны заключить в скобки первый список, чтобы это сработало.Это, конечно, может работать одинаково для любого другого числа, которое вам нужно исключить, кроме нуля:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Вышеупомянутое произвело бы случайное число от -10 до 10, кроме числа 8. Вы даже можете сделать это с более чем одним числом:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Это приведет к удалению 8, -8 и 0 из выбора.Как видите, существует гораздо больше возможностей при создании случайной величины.
Пока что вы получили целые числа, но вы также можете работать с действительными числами.
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Как правило, эти действительные числа содержат столько десятичных или значащих цифр, сколько определено в настройках приложения.Вы можете настроить его, указав шаг между возможными случайными значениями.
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Более того, эти случайные величины также могут быть выбраны из конкретного набора значений или слов. В следующем разделе вы увидите более подробную информацию о том, как создавать такие наборы.
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Создание списков через понимание
Этот раздел представляет собой краткое руководство по созданию списков в CalcMe с использованием команд
с и , где .Этот метод определения списков основан на общепринятой математической нотации «понимание множества» или «нотация построителя множеств», например:Мы объясним команды на следующих примерах.
Параметр строк алгоритма
Поскольку вы можете использовать эти команды для генерации алгоритма для вопроса Wiris Quizzes, мы покажем, как создавать их на листе и с помощью редактора кода. Вы можете узнать об этом подробнее здесь.Пример 1
На самом базовом уровне с просто обеспечивают более компактную форму написания длинных списков.Ты можешь написать
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
или вы можете значительно упростить его до следующего:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Команда , где , пригодится, когда вы хотите установить дополнительные ограничения.Например, получить только четные числа:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
В качестве альтернативы вы, конечно, могли бы сделать это:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Пример 2
Пример 3
Обозначение понимания списка также может быть расширено до более чем одной переменной.В этом случае вы должны указать диапазон для каждой переменной, используемой в качестве счетчика. Например, вот список, содержащий все положительные правильные дроби в простейшем виде, с однозначным числителем и знаменателем:
ЖИВАЯ ДЕМО
| CalcMe Sheet |
|---|
| Редактор кода CalcMe |
Другая рекомендация, проиллюстрированная в приведенном выше примере, заключается в заключении каждого условия после , где в круглые скобки, если у вас есть более одного, соединенного с.
Пример 4
Наконец, обратите внимание, что диапазон для переменной счетчика может сам быть списком, определенным ранее.
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Пример 5
Также возможно создавать матрицы, используя эту нотацию. Например, создать матрицу со случайными коэффициентами очень просто:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Программирование
Параметр строк алгоритма
Поскольку вы можете использовать эти команды для создания алгоритма для вопроса викторины Wiris, мы покажем, как создавать их на листе и с помощью редактора кода.Вы можете узнать об этом подробнее здесь.Вы можете использовать некоторые функции программирования. Здесь вы можете увидеть основные. Например, учитывая список, созданный, как описано ранее, вы можете легко вычислить квадрат первых простых чисел.
ЖИВАЯ ДЕМО
| CalcMe Sheet |
|---|
| Редактор кода CalcMe |
Функции пользователя
Параметр строк алгоритма
Поскольку вы можете использовать эти команды для создания алгоритма для вопроса викторины Wiris, мы покажем, как создавать их на листе и с помощью редактора кода.Вы можете узнать об этом подробнее здесь. Вы можете создавать собственные функции. Команда random очень полезна, но было бы немного утомительно записывать каждый раз random (-10,10) . Вместо этого вы можете создать функцию, которая при вызове генерирует случайное число:
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Это упрощает создание матрицы со случайными коэффициентами.Еще один более сложный пример — создание функции, которая строит трехдиагональную матрицу по трем числам. Следовательно, каждый раз, когда вы хотите создать трехдиагональную матрицу, вам просто нужно вызывать эту функцию с элементами верхней диагонали, диагонали и нижней диагонали, которые вы хотели бы иметь в матрице.
ЖИВАЯ ДЕМО
| Таблица CalcMe | Редактор кода CalcMe |
|---|---|
Калькулятор касательных векторов единиц измерения — Найдите нормальные и касательные векторы
Онлайн-калькулятор касательного вектора единичных векторов поможет вам определить касательный вектор векторной функции значения в заданных точках.Кроме того, калькулятор единичного тангенса отдельно определяет вывод тригонометрических функций, что важно для нормализации формы. Итак, продолжайте чтение, чтобы понять формулу вектора касательной единицы и как найти вектор касательной с примерами.
Что такое единичный касательный вектор?В математике единичный касательный вектор — это производная векторнозначной функции, которая обеспечивает другую векторнозначную функцию, которая является единичной касательной к заданной кривой.Направление касательной аналогично наклону касательной. Поскольку вектор содержит величину и направление, вектор скорости содержит больше информации, чем нам нужно. Мы можем уменьшить его величину, разделив ее.
Формула вектора касательной единицы измерения:Пусть r (t) — функция с дифференцируемыми векторными значениями, а v (t) = r ’(t) — вектор скорости. Тогда уравнение касательного вектора представляет собой единичный вектор в направлении вектора скорости, который используется калькулятором единичного вектора касательной для определения длины вектора.2} $$
$$ = a + b / \ sqrt {2} $$
$$ = 1 / \ sqrt {2} a + 1 / \ sqrt {2} b $$
Каков принцип единичного вектора нормалей?Вектор нормали — это перпендикулярный вектор. Для вектора v в пространстве существует бесконечно несколько перпендикулярных векторов. Наша цель — выбрать специальный вектор, перпендикулярный единичному касательному вектору. Для непрямых кривых этот вектор геометрически является единственным вектором, указывающим на кривую. Алгебраически мы можем использовать следующие определения для вычисления векторов.
Пусть r (t) — дифференцируемая вектор-функция, и пусть T (t) — касательный вектор. Тогда вектор нормали N (t) основной единицы определяется как
$$ N (t) = T ‘(t) / || T ‘(t) || $$
Это уравнение используется калькулятором единичного вектора касательной для нахождения нормы (длины) вектора. Если его сравнивать с касательным векторным уравнением, то оно рассматривается как функция с векторным значением. Основной единичный вектор нормали — это касательный вектор вектор-функции.
Однако онлайн-калькулятор мгновенной скорости позволяет рассчитать мгновенную скорость, соответствующую мгновенной скорости изменения формулы скорости.
Найдите нормальную и касательную составляющие ускорения:Во время движения вы столкнетесь с двумя силами, которые изменят вашу скорость. Автомобиль разгоняется под действием силы тяжести. Второе изменение скорости вызвано поворотом автомобиля. Первый компонент ускорения называется тангенциальным компонентом ускорения, а другой компонент — нормальным компонентом ускорения. Предполагается, что тангенциальная составляющая ускорения проходит вдоль направления вектора касательной единицы, а нормальная составляющая ускорения — вдоль направления вектора нормали основной единицы.Когда у нас есть T и N, легко найти две составляющие.
Тангенциальная составляющая ускорения
$$ a_t = а. T = v .a / || v || $$
, а нормальная составляющая ускорения —
.$$ a_N = а. N = || v x a || / || v || $$
и
$$ a = a_NN + a_TT $$
Как работает калькулятор вектора единичного тангенса?Калькулятор касательных векторов определяет единичный касательный вектор функции в точке, следуя этим инструкциям:
Ввод:Во-первых, введите функцию с различными тригонометрическими значениями, такими как синус, косинус и тангенс.
Теперь введите точку, чтобы найти единичный касательный вектор.
Чтобы увидеть результаты, нажмите кнопку «Рассчитать».
Выход:Калькулятор тангенциальной скорости обеспечивает ввод данных и ответы в заданной точке.
Этот калькулятор отображает единичный вывод для каждой тригонометрической функции и нормализует форму, а также находит единичный касательный вектор с пошаговыми вычислениями.
FAQ: Бинормальный вектор единичный вектор.Как?Поскольку вектор бинормали определяется как векторное произведение единичного вектора касательной и вектора единичной нормали, он также ортогонален как вектору нормали, так и вектору касательной.
Как найти тангенциальную?Разделите длину окружности на время, необходимое для определения тангенциальной скорости для совершения одного оборота.
Какие единицы используются для тангенциальной скорости?Формула касательной скорости используется для вычисления тангенциальной скорости объектов при круговом движении.Выражается в метрах в секунду (м / с).
В чем разница между тангенциальной и угловой скоростью?Угловая скорость — это скорость, с которой угол (радианы) изменяется во времени, выраженная в единицах 1 / с. В то время как тангенциальная скорость — это скорость точки на поверхности вращающегося объекта, умноженная на расстояние от точки оси вращения.
Заключение:Воспользуйтесь этим онлайн-калькулятором касательного вектора единичных векторов для нахождения нормализованной формы и тангенциального вектора функции.Кроме того, этот калькулятор дифференцирует функцию и вычисляет длину вектора в заданных точках.
Артикул:Из источника Википедии: Касательный вектор, Контравариантность, Касательный вектор на многообразиях.
Из источника Ximera: единичный касательный вектор, единичный касательный и единичные векторы нормали, нормальные компоненты ускорения.
Из источника в штате Орегон: производная векторной функции, единичный касательный вектор, длина дуги, параметризация по длине дуги.
Калькулятор ортогональных векторовПрисоединяйтесь к инициативе по модернизации математического образования. Ответ: поскольку скалярное произведение не равно нулю, векторы a и b не ортогональны. Исследуйте что угодно с помощью первой вычислительной машины знаний. v = 0 (т.е. векторы перпендикулярны) называются ортогональными. Визуализация векторов (только для векторов в & Ropf; 2 и & Ropf; 3). Выбрать размерность векторов и форму представления векторов; Нажмите кнопку «Проверить ортогональность векторов», и вы получите подробное пошаговое решение.1 = 2 n + 4 2 n + 4 = 0 2 n = -4 n = -2 Ответ: векторы a и b ортогональны, когда n = -2. Вы можете перемещаться между полями ввода, нажимая клавиши «влево» и «вправо» на клавиатуре. Если вы хотите связаться со мной, возможно, у вас возникнут вопросы, напишите мне по электронной почте [email protected], Онлайн-калькулятор. Я разработал этот веб-сайт и написал всю математическую теорию, онлайн-упражнения, формулы и калькуляторы. Узнать больше Принять. Перекрестное произведение двух векторов (векторное произведение), Онлайн калькулятор.Практикуйтесь онлайн или сделайте учебный лист для печати. Программирование на основе знаний для всех. В случае плоской задачи для векторов a = {ax; ай; az} и b = {bx; от; bz} условие ортогональности можно записать по следующей формуле: Ответ: векторы a и b ортогональны при n = 2. Анализ линейной зависимости между v 1, v 2. Калькулятор векторов. Узнайте о векторных и точечных продуктах. Точечное произведение двух векторов, Онлайн калькулятор. Скалярное произведение В трехмерном пространстве три вектора могут быть взаимно перпендикулярными.Объем пирамиды, образованной векторами, Онлайн калькулятор. Введите значения в поля Magnitude и Angle … или X и Y. Наш бесплатный онлайн-калькулятор может проверить ортогональность двух векторов с помощью пошагового решения. https://mathworld.wolfram.com/OrthogonalVectors.html. Добро пожаловать в OnlineMSchool. Узнать больше Принять. Коллекция инструментов для преподавания и обучения, созданных экспертами в области образования Wolfram: динамический учебник, планы уроков, виджеты, интерактивные демонстрации и многое другое. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie.Ответ: векторы a и b ортогональны при n = -2. Приведенное выше определение сразу следует, когда мы рассматриваем формулу скалярного произведения векторов: a b a b cos π 2 0. Hierzu muss man nur nur herausfinden, welcher gesuchte Vector multipliziert mit dem gegebenen Vektor 0 ergibt. Составная форма вектора с начальной и конечной точками на плоскости, Упражнения. Составная форма вектора с начальной и конечной точками, Онлайн калькулятор. Два вектора и чей точечный векторный калькулятор, скалярное произведение, ортогональные векторы, параллельные векторы, одинаковые векторы направления, величина, векторный угол, калькулятор неравенства Коши-Шварца, калькулятор ортогональной проекции. Он выполняет преобразования и суммирует векторы.Wenn man nachweisen kann, dass ein Vektor zu einem anderen Vektor orthogonal ist, dann kann man diesen Nachweis logischerweise auch umkehren und auf diese Weise herausfinden, welcher Vektor zu einem anderen Vektor orthogonal liegt. Изучите тысячи бесплатных приложений для науки, математики, инженерии, технологий, бизнеса, искусства, финансов, социальных наук и многого другого.
Статуя богини Айне, Взломанная игра Flight Game, Каталог Бомбейской компании, Toshiba Factory Reset 0 не работает, Пончо Silvana Sin Lana, Небесные Фамилии Dnd, Миниатюра древнего синего дракона, Красивые армянские цитаты, Лист для фортепиано Roblox, Некрологи Хартфорда Куранта за последние 3 дня, Определить велосипед Redline по серийному номеру, Курт Коулман Лас-Вегас, Huawei закрывает 57 заводов в США, Брюс Будро Чистая стоимость, Анализ туши Бодлера, Дэвид Диггс Малкольм Диггс, Примеры сочинений о несправедливости, Аренда 3-х колесных скутеров — Голд-Кост, Возрастной диапазон Pitbull, Melovemealot Знаменитые дни рождения, Проблемы с двигателем Ахатес, Латинские песни для причастия, Скандал с больницей Шрайнерс, Распродажа нахлыстовой рыбалки, Бен Ротлисбергер Возраст, Эссе об интеллектуальном любопытстве, Тамаки Суо Высота, Iq 75 Что такое умственный возраст, Зарплата актеров за серию, Скин Бедствия Fortnite, 1943 Стальной пенни Стоимость 2018, Брэндон Хэмм Музыкант, Рецепт тайваньской колбасы, Аватар Сонг Калимба, Внешние динамики Yamaha P115, Гидратированный лайм Менардс, Добавки для обратной мышечной атрофии, Гонорары шоу Кумара Вишваса, Иосиф о Варавве, Плейлист 915 кунв, Список редких книг по мурашкам, Многоразовые маски для лица из органического хлопка Sanctuary, День рождения Оскара Рамзи, Morecambe Illuminations 2020, Whirlpool Wrt318fzdm01 Руководство, Стив Райх Pdf, Стоимость замены трансмиссии Isuzu Trooper, Бетти Грейбл Муж, Лаура Грейс Холл Причина смерти, Математические выражения 5 класс Ответы ключевой Pdf Блок 8, Остров любви Шелби, Прокерала Китайский Календарь, Clout Значение сленг, 24×32 планы гаража, Является частным реальным словом, Бумага A0 300 г / м2, Джоджо, часть 6, Диспансер Rise, Значение тату вилка, Бренды рэпперской одежды, Лошадь Корова Гибрид, Ноты на тему Tf2, Дэйн Уизерспун Причина смерти, Место преступления Фотографии, Карта Gtfo R3a3, Генератор имен героев, Куриные титры с маслом, Dua для новорожденного мальчика на арабском языке, Раскраски Фортнит Мидас, Bigscreen Vr Netflix, Энтони Мельчиорри, жена Кристал Кардинале, Dely Dely Fruit Jelly Dollar Tree, Коды Copter Royale, Диспансер Rise, Насколько высока Анджела Агилар, Места обитания рыбы Бдо, Toyota Tsb Lookup, Раджон Рондо Вес, Темы сочинений по лингвистической антропологии, Благодарственное письмо суперинтенданту, Порядок ротации карт Bfv 2020, Переводчик южного сленга, Bull Snake для продажи в Великобритании, Дополнения для сборки Xanax, Daeg Faerch Age, Мой опыт работы с Cinnpie, Кто написал Midnight Cry,
| Категория | Описание | Разрешить |
|---|---|---|
| Аналитические и рабочие файлы cookie | Эти файлы cookie, включая файлы cookie Google Analytics, позволяют нам распознавать и подсчитывать количество посетителей на сайтах TI и видеть, как посетители перемещаются по нашим сайтам.Это помогает нам улучшить работу сайтов TI (например, облегчая вам поиск информации на сайте). | |
| Рекламные и маркетинговые файлы cookie | Эти файлы cookie позволяют размещать рекламу на основе интересов на сайтах TI и сторонних веб-сайтах с использованием информации, которую вы предоставляете нам при взаимодействии с нашими сайтами.Объявления на основе интересов отображаются для вас на основе файлов cookie, связанных с вашими действиями в Интернете, такими как просмотр продуктов на наших сайтах. Мы также можем передавать эту информацию третьим лицам для этих целей. Эти файлы cookie помогают нам адаптировать рекламные объявления в соответствии с вашими интересами, управлять частотой, с которой вы видите рекламу, и понимать эффективность нашей рекламы. | |
| Функциональные файлы cookie | Эти файлы cookie помогают идентифицировать вас и хранить ваши действия и информацию об учетной записи, чтобы предоставлять расширенные функциональные возможности, в том числе более персонализированный и релевантный опыт на наших сайтах. |

