Деление дробей (8 класс) доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экономика
Презентация на тему Презентация по алгебре на тему: Деление дробей (8 класс), предмет презентации: Алгебра.
Этот материал в формате pptx (PowerPoint) содержит 23 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Добро пожаловать
на урок математики!
8 класс
Эпиграф к уроку:
«Деятельность – единственный путь к знанию».
Бернард Шоу – известный ирландский
драматург,романист и сценарист.
А сейчас, ребята, поудобнее садитесь,
Не шумите, не вертитесь
И внимательно решайте,
А спрошу вас- отвечайте
Вам условие понятно? ??________
Это слышать мне приятно.
Приглашаю вас в страну
Очень нужную страну,
Где каждый должен быть в строю.
Задания выполняйте не спеша,
Задания выполняйте, где нужно, сообща.
ПЛАН ДЕЙСТВИЙ НА УРОК
1. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ.
2. ОПРЕДЕЛЕНИЕ ТЕМЫ И ПОСТАНОВКА ЦЕЛИ УРОКА.
3. ПОВТОРЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА — РАБОТА В ГРУППАХ.
4.ВЫРАБОТКА АЛГОРИТМА ДЕЙСТВИЙ ПРИ РЕШЕНИИ, ПЕРВИЧНОЕ ЗАКРЕПЛЕНИЕ ПОЛУЧЕННОГО МАТЕРИАЛА.
5. ПОДВЕДЕНИЕ ИТОГА УРОКОВ И ОЦЕНИВАНИЕ.
Тема урока:
«Деление дробей»
Повторить правила сокращения, умножения и деления рациональных дробей.
Закрепить знания и умения по делению рациональных дробей;
ЦЕЛЬ УРОКА:
1. Какое из рациональных выражений не является дробным?
1 группа
2 группа
3 группа
х + 5
1)
3)
2)
4)
1)
2)
3)
4)
1)
2)
3)
4)
3.
Укажите допустимые значения переменной в выражении:
1 группа
2 группа
3 группа
Все числа,
кроме 1
Все числа,
Все числа,
кроме 0
Все числа,
кроме 0 и 2
Все числа,
кроме -2 и 0
Все числа,
кроме -2
Все числа,
кроме 0 и 9
Все числа,
кроме -3 и 3
Все числа,
кроме 0 и 3
Все числа,
кроме -3, 0 и 3
1)
3)
2)
4)
1)
2)
3)
4)
1)
2)
3)
4)
Все числа,
кроме 0
Все числа
3. Найдите значение дробного выражения
2) -3,5
3)
4) 4,5
Вычисляем устно
Ответить на вопросы:
2.
3. Как выполнить деление дробей?
Из истории…
1. Что значит сократить дробь?
Расшифруйте пентаграмму
Выполните действия.
Найдите соответствующую вашему ответу букву в таблице.
Математический папирус Ахмеса -древнеегипетское учебное руководство по
арифметике и геометрии периода
Среднего царства.
Написано в1650 до н. э. писцом по имени
Ахмес,свиток папируса длиной 5,25 м.
и шириной 33см.Язык:среднеегипетский.
Папирус Ахмеса был обнаружен в 1858г
В 1870 папирус был расшифрован.
Ныне большая часть рукописи находится в Британском музее в Лондоне, а вторая часть — в Нью-Йорке.
АХМЕС
«Деление 7 хлебов между 8 людьми».
Деление дробей
Чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь обратную второй.
Над алгебраическими дробями можно осуществлять преобразования аналогичные тем, которые указали
для обыкновенной дроби.
НАПОМИНАНИЕ
Прежде, чем выполнять умножение и деление
алгебраических дробей, полезно их числители
и знаменатели разложить на множители – это
облегчит сокращение той алгебраической дроби, которая получится в результате умножения или деления.
Внимание!
Выполните деление
дробей
Самостоятельная работа
Проверьте
Домашнее задание:
Подведение итогов урока.
Как разделить дробь на дробь?
Каков алгоритм этого действия?
Спасибо за урок.
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Умножение, деление и сокращение алгебраических дробей
Тема: Умножение и деление алгебраических дробей
Образование есть то, что остается, когда все выученное уже забыто
Лауэ
Цели:
Образовательные:
закрепить ЗУН по теме
провести первичный текущий контроль знаний
работать над пробелами
Развивающие:
способствовать развитию коммуникативной компетенции, т.
е. умению эффективно сотрудничать с другими людьми.
способствовать развитию кооперативной компетенции, т.е. умению работать в парах.
способствовать развитию проблемной компетенции, т.е. умению понимать неизбежности возникновения трудностей в ходе любой деятельности.
Воспитательные:
прививать умение адекватно оценивать работу, проделанную товарищем;
при работе в парах воспитывать качества взаимопомощи, поддержки.
Методические:
создание условий для проявления индивидуальности, познавательной активности учащихся;
показать методику проведения урока с проектированием результатов учебной деятельности и способам их исследования на основе компетентностного подхода.
Оборудование: доска, цветной мел. Таблица «Умножение и деление алгебраических дробей»; карточки для индивидуальной работы, карточки-«памятки». Задание в свободную минуту.
Ход урока
Организационный момент
План урока записан на доске:
Устная разминка.
Индивидуальная работа.
Решение заданий.
Парная работа.
Итог урока.
Домашнее задание.
Учитель: В старину на Руси считалось, что если человек был сведущ в математике, то это означало высшую степень учености. А умение правильно видеть и слышать первый шаг к мудрости. Хочется, чтобы сегодня все ученики вашего класса показали насколько они мудры и насколько сведущие люди в алгебре 7 класса.
Итак, тема урока «Умножение и деление алгебраических дробей» На прошлом уроке вы начали изучать данную тему, и мы обсуждали, зачем ее изучаем. Давайте вспомним, где она нам пригодится уже через несколько уроков.
Учащиеся: Для совместных действий с алгебраическими дробями, для решения уравнений, а значит и задач.
Учитель: Еще в старину на Руси говорили, что умноженье — мученье, а с делением — беда. Тот, кто умел быстро и безошибочно умножать и делить считался большим математиком.
Какие вы цели поставите перед собой?
Учащиеся: Продолжить изучать тему, научиться быстро и безошибочно умножать и делить.
Учитель: Чтобы достичь поставленных целей мы (открывает план, записанный на доске, проговаривает его)
1. Устная разминка: (в это время 3 — 4 человека решают тренажер по сокращению дробей в парах) разложите на множители, заполнив пропуски
1= (у-1) (…), 5а+5b=… (a+b), ху-х=х (…), 14-2х=…
сократите дробь
Дроби, дроби, дроби бей сокращай их не жалей.
найдите ошибку, допущенную при умножении и делении алгебраических дробей
Учитель: Где допущена ошибка? Почему ошибка допущена? Какого правила, ученик не знал? Какое знал? Как надо правильно сделать?
2. Работа в тетради, № из учебника 488 (1) Анализ, решение, проверка.
Учитель: А сейчас вам представится возможность показать свои знания при выполнении теста, а чтобы воодушевить вас на работу прочитаю стишок «Чтоб записал учитель «5» в твой дневник числитель на числитель сумей умножить вмиг, а чтоб преподаватель доволен был тобой, ты первый знаменатель умножишь на второй»
Самопроверка, взаимопроверка.
По критериям (вывешены на доске) В-1 (321), В-2 (132) по правильным кодам оценивание в парах. Первоначальный результат. Оценки.
Работа над ошибками в парах «ученик-учитель»
Если в парах нет ошибок делают задание в свободную минуту.
Упростите выражение и найдите его значение при
5. Итог урока
В заключение урока, мне хотелось бы узнать у вас, какие виды работы вызвали у вас затруднения? Как вы думаете, почему? Что узнали нового? Кто из вас доволен своей работой на уроке? Как вы считаете, цели, поставленные в начале урока достигнуты?
Учитель: Закончить урок я хотела бы словами французского инженера-физика Лауэ: «Образование есть то, что остается, когда все выученное уже забыто»
Надеюсь, что этот материал вы не забудете, чтобы этого не случилось надо выполнить д/з №486,487,488 четные.
На данном уроке будут рассмотрены правила умножения и деления алгебраических дробей, а также примеры на применение данных правил. Умножение и вычитание алгебраических дробей не отличается от умножения и деления обыкновенных дробей.
Вместе с тем, наличие переменных приводит к несколько более сложным способам упрощения полученных выражений. Несмотря на то, что умножение и деление дробей выполняется проще, чем их сложение и вычитание, к изучению данной темы необходимо подойти крайне ответственно, поскольку в ней существует много «подводных камней», на которые обычно не обращают внимания. В рамках урока мы не только изучим правила умножения и деления дробей, но и разберём нюансы, которые могут возникнуть при их применении.
Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями
Урок: Умножение и деление алгебраических дробей
1. Правила умножения и деления обыкновенных и алгебраических дробейПравила умножения и деления алгебраических дробей абсолютно аналогичны правилам умножения и деления обыкновенных дробей. Напомним их:
То есть, для того, чтобы умножить дроби, необходимо умножить их числители (это будет числитель произведения), и умножить их знаменатели (это будет знаменатель произведения).
Деление на дробь — это умножение на перевёрнутую дробь, то есть, для того, чтобы разделить две дроби, необходимо первую из них (делимое) умножить на перевёрнутую вторую (делитель).
2. Частные случаи применения правил умножения и деления дробейНесмотря на простоту данных правил, многие при решении примеров по данной теме допускают ошибки в ряде частных случаев. Рассмотрим подробнее эти частные случаи:
Во всех этих правилах мы пользовались следующим фактом: .
3. Примеры умножения и деления обыкновенных дробейРешим несколько примеров на умножение и деление обыкновенных дробей, чтобы вспомнить, как пользоваться указанными правилами.
Пример 1
Примечание: при сокращении дробей мы пользовались разложением числа на простые множители. Напомним, что простыми числами называются такие натуральные числа, которые делятся только на и на само себя. Остальные числа называются составными . Число не относится ни к простым, ни к составным.
Примеры простых чисел: .
Пример 2
Рассмотрим теперь один из частных случаев с обыкновенными дробями.
Пример 3
Как видим, умножение и деление обыкновенных дробей, в случае правильного применения правил, не является сложным.
4. Примеры умножения и деления алгебраических дробей (простые случаи)Рассмотрим умножение и деление алгебраических дробей.
Пример 4
Пример 5
Отметим, что сокращать дроби после умножения можно и даже нужно по тем же правилам, которые мы до этого рассматривали на уроках, посвящённых сокращению алгебраических дробей. Рассмотрим несколько простых примеров на частные случаи.
Пример 6
Пример 7
Рассмотрим теперь несколько более сложных примеров на умножение и деление дробей.
Пример 8
Пример 9
Пример 10
Пример 11
Пример 12
Пример 13
5.
Примеры умножения и деления алгебраических дробей (сложные случаи) До этого мы рассматривали дроби, в которых и числитель, и знаменатель являлись одночленами. Однако в ряде случаев необходимо перемножить или поделить дроби, числители и знаменатели которых являются многочленами. В этом случае правила остаются такими же, а для сокращения необходимо использовать формулы сокращённого умножения и вынесение за скобки.
Пример 14
Пример 15
Пример 16
Пример 17
Пример 18
На данном уроке мы рассмотрели правила умножения и деления алгебраических дробей , а также применение этих правил для конкретных примеров.
Список литературы
1. Башмаков М. И. Алгебра 8 класс. — М.: Просвещение, 2004.
2. Дорофеев Г. В., Суворова С. Б., Бунимович Е. А. и др. Алгебра 8. — 5-е изд. — М.: Просвещение, 2010.
3. Никольский С. М., Потапов М. А., Решетников Н. Н., Шевкин А. В. Алгебра 8 класс. Учебник для общеобразовательных учреждений.
— М.: Просвещение, 2006.
1. Портал для всей семьи.
2. Фестиваль педагогических идей «Открытый урок» .
3. Вся элементарная математика.
Домашнее задание
1. №№73-77, 80. Дорофеев Г. В., Суворова С. Б., Бунимович Е. А. и др. Алгебра 8. — 5-е изд. — М.: Просвещение, 2010.
2. Выполнить умножение: а), б)
3. Выполнить деление: а) , б)
На данном уроке будут рассмотрены правила умножения и деления алгебраических дробей, а также примеры на применение данных правил. Умножение и деление алгебраических дробей не отличается от умножения и деления обыкновенных дробей. Вместе с тем, наличие переменных приводит к несколько более сложным способам упрощения полученных выражений. Несмотря на то, что умножение и деление дробей выполняется проще, чем их сложение и вычитание, к изучению данной темы необходимо подойти крайне ответственно, поскольку в ней существует много «подводных камней», на которые обычно не обращают внимания. В рамках урока мы не только изучим правила умножения и деления дробей, но и разберём нюансы, которые могут возникнуть при их применении.
Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями
Урок: Умножение и деление алгебраических дробей
Правила умножения и деления алгебраических абсолютно аналогичны правилам умножения и деления обыкновенных дробей. Напомним их:
То есть, для того, чтобы умножить дроби, необходимо умножить их числители (это будет числитель произведения), и умножить их знаменатели (это будет знаменатель произведения).
Деление на дробь — это умножение на перевёрнутую дробь, то есть, для того, чтобы разделить две дроби, необходимо первую из них (делимое) умножить на перевёрнутую вторую (делитель).
Несмотря на простоту данных правил, многие при решении примеров по данной теме допускают ошибки в ряде частных случаев. Рассмотрим подробнее эти частные случаи:
Во всех этих правилах мы пользовались следующим фактом: .
Решим несколько примеров на умножение и деление обыкновенных дробей, чтобы вспомнить, как пользоваться указанными правилами.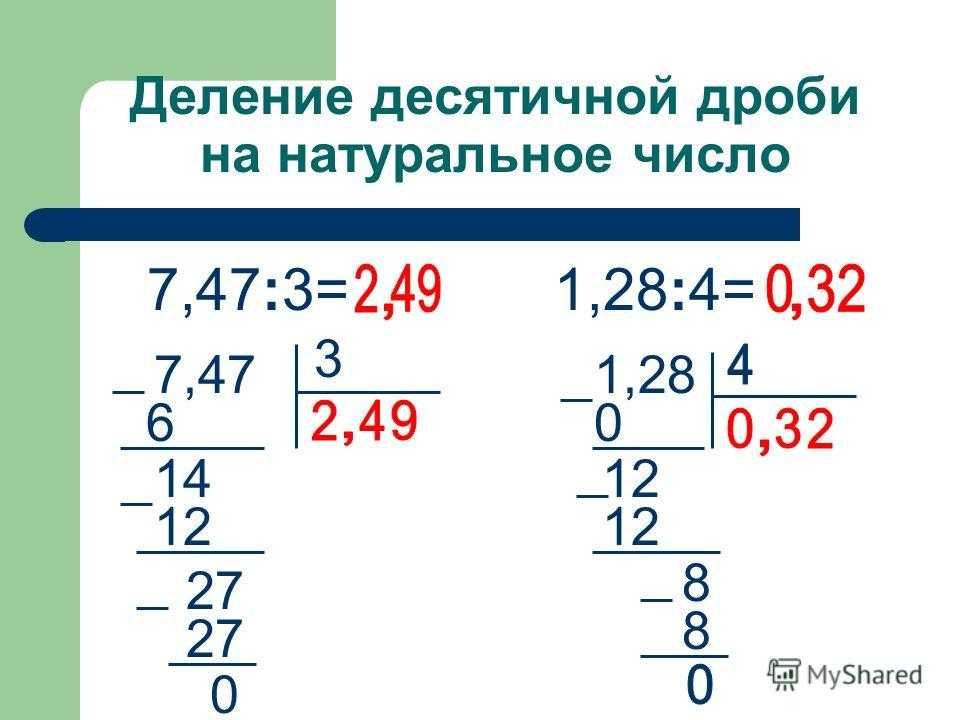
Пример 1
Примечание: при сокращении дробей мы пользовались разложением числа на простые множители. Напомним, что простыми числами называются такие натуральные числа, которые делятся только на и на само себя. Остальные числа называются составными . Число не относится ни к простым, ни к составным. Примеры простых чисел: .
Пример 2
Рассмотрим теперь один из частных случаев с обыкновенными дробями.
Пример 3
Как видим, умножение и деление обыкновенных дробей, в случае правильного применения правил, не является сложным.
Рассмотрим умножение и деление алгебраических дробей.
Пример 4
Пример 5
Отметим, что сокращать дроби после умножения можно и даже нужно по тем же правилам, которые мы до этого рассматривали на уроках, посвящённых сокращению алгебраических дробей. Рассмотрим несколько простых примеров на частные случаи.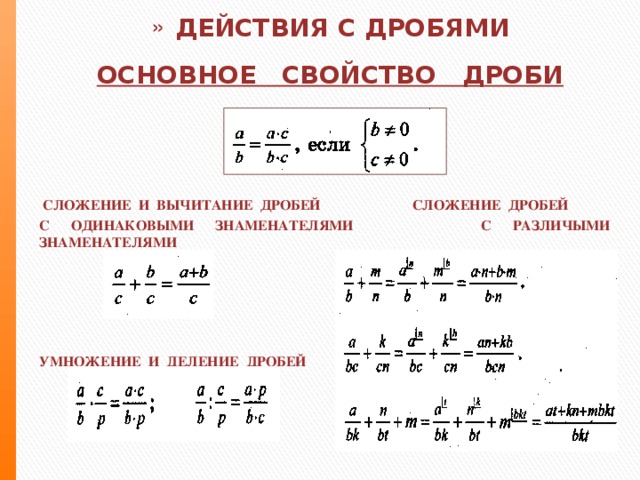
Пример 6
Пример 7
Рассмотрим теперь несколько более сложных примеров на умножение и деление дробей.
Пример 8
Пример 9
Пример 10
Пример 11
Пример 12
Пример 13
До этого мы рассматривали дроби, в которых и числитель, и знаменатель являлись одночленами. Однако в ряде случаев необходимо перемножить или поделить дроби, числители и знаменатели которых являются многочленами. В этом случае правила остаются такими же, а для сокращения необходимо использовать формулы сокращённого умножения и вынесение за скобки.
Пример 14
Пример 15
Пример 16
Пример 17
Пример 18
В этой статье мы продолжаем изучение основных действий, которые можно выполнять с алгебраическими дробями. Здесь мы рассмотрим умножение и деление: сначала выведем нужные правила, а затем проиллюстрируем их решениями задач.
Как правильно делить и умножать алгебраические дроби
Чтобы выполнить умножение алгебраических дробей или разделить одну дробь на другую, нам нужно использовать те же правила, что и для обыкновенных дробей. Вспомним их формулировки.
Когда нам надо умножить одну обыкновенную дробь на другую, мы выполняем отдельно умножение числителей и отдельно знаменателей, после чего записываем итоговую дробь, расставив по местам соответствующие произведения. Пример такого вычисления:
2 3 · 4 7 = 2 · 4 3 · 7 = 8 21
А когда нам надо разделить обыкновенные дроби, мы делаем это с помощью умножения на дробь, обратную делителю, например:
2 3: 7 11 = 2 3 · 11 7 = 22 7 = 1 1 21
Умножение и деление алгебраических дробей выполняется в соответствии с теми же принципами. Сформулируем правило:
Определение 1
Чтобы перемножить две и более алгебраические дроби, нужно перемножить отдельно числители и знаменатели. Результатом будет дробь, в числителе которой будет стоять произведение числителей, а в знаменателе – произведение знаменателей.
В буквенном виде правило можно записать как a b · c d = a · c b · d . Здесь a , b , c и d будут представлять из себя определенные многочлены, причем b и d не могут быть нулевыми.
Определение 2
Для того чтобы разделить одну алгебраическую дробь на другую, нужно выполнить умножение первой дроби на дробь, обратную второй.
Это правило можно также записать как a b: c d = a b · d c = a · d b · c . Буквы a , b , c и d здесь означают многочлены, из которых a , b , c и d не могут быть нулевыми.
Отдельно остановимся на том, что такое обратная алгебраическая дробь. Она представляет из себя такую дробь, которая при умножении на исходную дает в итоге единицу. То есть такие дроби будут аналогичны взаимно обратным числам. Иначе можно сказать, что обратная алгебраическая дробь состоит из таких же значений, что и исходная, однако числитель и знаменатель у нее меняются местами. Так, по отношению к дроби a · b + 1 a 3 дробь a 3 a · b + 1 будет обратной.
Решение задач на умножение и деление алгебраических дробей
В этом пункте мы посмотрим, как правильно применять озвученные выше правила на практике. Начнем с простого и наглядного примера.
Пример 1
Условие: умножьте дробь 1 x + y на 3 · x · y x 2 + 5 , а потом разделите одну дробь на другую.
Решение
Сначала выполним умножение. Согласно правилу, нужно отдельно перемножить числители и знаменатели:
1 x + y · 3 · x · y x 2 + 5 = 1 · 3 · x · y (x + y) · (x 2 + 5)
Мы получили новый многочлен, который нужно привести к стандартному виду. Заканчиваем вычисления:
1 · 3 · x · y (x + y) · (x 2 + 5) = 3 · x · y x 3 + 5 · x + x 2 · y + 5 · y
Теперь посмотрим, как правильно разделить одну дробь на другую. По правилу нам надо заменить это действие умножением на обратную дробь x 2 + 5 3 · x · y:
1 x + y: 3 · x · y x 2 + 5 = 1 x + y · x 2 + 5 3 · x · y
Приведем полученную дробь к стандартному виду:
1 x + y · x 2 + 5 3 · x · y = 1 · x 2 + 5 (x + y) · 3 · x · y = x 2 + 5 3 · x 2 · y + 3 · x · y 2
Ответ: 1 x + y · 3 · x · y x 2 + 5 = 3 · x · y x 3 + 5 · x + x 2 · y + 5 · y ; 1 x + y: 3 · x · y x 2 + 5 = x 2 + 5 3 · x 2 · y + 3 · x · y 2 .
Довольно часто в процессе деления и умножения обыкновенных дробей получаются результаты, которые можно сократить, например, 2 9 · 3 8 = 6 72 = 1 12 . Когда мы выполняем эти действия с алгебраическими дробями, мы также можем получить сократимые результаты. Для этого полезно предварительно разложить числитель и знаменатель исходного многочлена на отдельные множители. Если нужно, перечитайте статью о том, как правильно это делать. Разберем пример задачи, в которой нужно будет выполнить сокращение дробей.
Пример 2
Условие: перемножьте дроби x 2 + 2 · x + 1 18 · x 3 и 6 · x x 2 — 1 .
Решение
Перед тем, как вычислять произведение, разложим на отдельные множители числитель первой исходной дроби и знаменатель второй. Для этого нам потребуются формулы сокращенного умножения. Вычисляем:
x 2 + 2 · x + 1 18 · x 3 · 6 · x x 2 — 1 = x + 1 2 18 · x 3 · 6 · x (x — 1) · (x + 1) = x + 1 2 · 6 · x 18 · x 3 · x — 1 · x + 1
У нас получилась дробь, которую можно сократить:
x + 1 2 · 6 · x 18 · x 3 · x — 1 · x + 1 = x + 1 3 · x 2 · (x — 1)
О том, как это делается, мы писали в статье, посвященной сокращению алгебраических дробей.
Перемножив одночлен и многочлен в знаменателе, мы получим нужный нам результат:
x + 1 3 · x 2 · (x — 1) = x + 1 3 · x 3 — 3 · x 2
Вот запись всего решения без пояснений:
x 2 + 2 · x + 1 18 · x 3 · 6 · x x 2 — 1 = x + 1 2 18 · x 3 · 6 · x (x — 1) · (x + 1) = x + 1 2 · 6 · x 18 · x 3 · x — 1 · x + 1 = = x + 1 3 · x 2 · (x — 1) = x + 1 3 · x 3 — 3 · x 2
Ответ: x 2 + 2 · x + 1 18 · x 3 · 6 · x x 2 — 1 = x + 1 3 · x 3 — 3 · x 2 .
В некоторых случаях исходные дроби перед умножением или делением удобно преобразовать, чтобы дальнейшие вычисления стали быстрее и проще.
Пример 3
Условие: разделите 2 1 7 · x — 1 на 12 · x 7 — x .
Решение: начнем с упрощения алгебраической дроби 2 1 7 · x — 1 , чтобы избавиться от дробного коэффициента. Для этого умножим обе части дроби на семь (это действие возможно благодаря основному свойству алгебраической дроби). В итоге у нас получится следующее:
2 1 7 · x — 1 = 7 · 2 7 · 1 7 · x — 1 = 14 x — 7
Видим, что знаменатель дроби 12 · x 7 — x , на которую нам нужно разделить первую дробь, и знаменатель получившейся дроби являются противоположными друг другу выражениями.
Изменив знаки числителя и знаменателя 12 · x 7 — x , получим 12 · x 7 — x = — 12 · x x — 7 .
После всех преобразований можем наконец перейти непосредственно к делению алгебраических дробей:
2 1 7 · x — 1: 12 · x 7 — x = 14 x — 7: — 12 · x x — 7 = 14 x — 7 · x — 7 — 12 · x = 14 · x — 7 x — 7 · — 12 · x = = 14 — 12 · x = 2 · 7 — 2 · 2 · 3 · x = 7 — 6 · x = — 7 6 · x
Ответ: 2 1 7 · x — 1: 12 · x 7 — x = — 7 6 · x .
Как умножить или разделить алгебраическую дробь на многочлен
Чтобы выполнить такое действие, мы можем воспользоваться теми же правилами, что мы приводили выше. Предварительно нужно представить многочлен в виде алгебраической дроби с единицей в знаменателе. Это действие аналогично преобразованию натурального числа в обыкновенную дробь. Например, можно заменить многочлен x 2 + x − 4 на x 2 + x − 4 1 . Полученные выражения будут тождественно равны.
Пример 4
Условие: разделите алгебраическую дробь на многочлен x + 4 5 · x · y: x 2 — 16 .
Решение
x + 4 5 · x · y: x 2 — 16 = x + 4 5 · x · y: x 2 — 16 1 = x + 4 5 · x · y · 1 x 2 — 16 = = x + 4 5 · x · y · 1 (x — 4) · x + 4 = (x + 4) · 1 5 · x · y · (x — 4) · (x + 4) = 1 5 · x · y · x — 4 = = 1 5 · x 2 · y — 20 · x · y
Ответ: x + 4 5 · x · y: x 2 — 16 = 1 5 · x 2 · y — 20 · x · y .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Чтобы выполнить умножение алгебраических (рациональных) дробей, надо:
1) В числитель записать произведение числителей, в знаменатель — произведение знаменателей этих дробей.
При этом многочлены нужно .
2) Если можно, сократить дробь.
Замечание.
При умножении сумму и разность необходимо заключить в скобки.
Примеры умножения алгебраических дробей.
При умножении алгебраических дробей отдельно умножаем числители, отдельно — знаменатели этих дробей:
Сокращаем 36 и 45 на 9, 22 и 55 на 11, a² и на a a, b и b на b, c⁵ и c² на c²:
Чтобы умножить алгебраические дроби, нужно числитель умножить на числитель, а знаменатель — на знаменатель.
Так как в числителях и знаменателях данных дробей стоят многочлены, их нужно .
В числителе первой дроби выносим за скобки общий множитель 3. Числитель второй дроби раскладываем на множители как разность квадратов. В знаменателе первой дроби — квадрат разности. В знаменателе второй дроби выносим за скобки общий множитель 5:
Дробь можно сократить на (x+3) и (2x-1):
Умножаем числитель на числитель, знаменатель — на знаменатель. Знаменатель второй дроби раскладываем на множители по формуле разности квадратов:
(a-b) и (b-a) отличаются только знаком. Вынесем «минус» за скобки, например, в числителе. После этого сократим дробь на (a-b) и на a:
При умножении алгебраических дробей числитель умножаем на числитель, знаменатель — на знаменатель. Входящие в них многочлены пытаемся разложить на множители.
В первой дроби в числителе — полный квадрат суммы, в знаменателе — сумма кубов. Во второй дроби в числителе — (часть формулы суммы кубов), в знаменателе есть общий множитель 3, который выносим за скобки:
Сокращаем дробь на (x+3)² и (x²-3x+9):
В алгебре действия с алгебраическими (рациональными) дробями могут встречаться как в виде отдельного задания, так и в ходе решении других примеров, например, решения уравнений и неравенств.
Вот почему важно вовремя научиться умножать, делить, складывать и вычитать такие дроби.
Рубрика: |
Умножение и деление алгебраических дробей. Умножение алгебраических дробей Алгебраические дроби умножение и деление дробей примеры
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания. Все материалы проверены антивирусной программой.
Обучающие пособия и тренажеры в интернет-магазине «Интеграл» для 8 класса
Электронная рабочая тетрадь по алгебре для 8 класса
Мультимедийное учебное пособие для 8 класса «Алгебра за 10 минут»
Предварительное разложение алгебраической дроби на множители
Перед началом работы с дробями, а именно на умножении и делении, желательно произвести разложение числителя и знаменателя на множители. Это облегчит разложение на множители дроби, которая получится в результате математического действия.
2)}{(b-3)}$.
Разделы: Математика
Цель: Научиться выполнять действия умножения и деления алгебраических дробей.
Форма урока: урок изучения нового материала.
Метод обучения: проблемный, с самостоятельным поиском решения.
Оборудование: Компьютер, проектор, раздаточный материал по уроку, таблица.
Ход урока
Урок проводится с использованием компьютерной презентации. (Приложение 1)
Ι. Организация урока.
1. Подготовка технической части.
2. Карточки для работы в парах и самостоятельной работы.
ΙΙ. Актуализация опорных знаний с целью подготовки к изучению новой темы.
Устно:
(Ответы выводятся с помощью компьютера.)
1. Разложить на множители:
2. Сократить дробь:
3. Умножить дроби:
Как называются эти числа? (Взаимообратные числа)
Найти число, обратное числу
Какие два числа называются взаимообратными? (Два числа называются взаимообратными, если их произведение равно 1.
)
Найти дробь обратную:
Разделить дроби:
Проговариваем правила умножения и деления обыкновенных дробей. Плакат с правилами размещен на доске.
ΙΙΙ. Новая тема
Обращаясь к плакату, учитель говорит: a , b , c , d — в данном случае числа. А если это будут алгебраические выражения, как называются такие дроби? (Алгебраические дроби)
Правила их умножения и деления остаются теми же самыми.
Выполнить действия:
Первый и второй пример самостоятельно, с последующей записью решения учащимися на доске. Решение третьего примера учитель показывает на доске.
ΙV. Закрепление
1)Работа по задачнику: № 5.2 (б, в), № 5.11 (а, б). Стр.32
2) Работа в парах по карточкам:
(Решения и ответы отражены через проектор.)
V. Итог урока
Самостоятельная работа.
Выполнить умножение или деление:
Ι Вариант | ΙΙ Вариант | |
Ученики сдают тетради с работами.
VI. Домашнее задание
№ 5.8; № 5.10; № 5.13(а, б).
Видеоурок «Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень» — вспомогательное средство для ведения урока математики по данной теме. С помощью видеоурока учителю легче сформировать у учеников умение выполнять умножение и деление алгебраических дробей. Наглядное пособие содержит подробное понятное описание примеров, в которых выполняются операции умножения и деления. Материал может быть продемонстрирован во время объяснения учителя или стать отдельной частью урока.
Чтобы сформировать умение решать задания на умножение и деление алгебраических дробей, по ходу описания решения даются важные комментарии, моменты, требующие запоминания и глубокого понимания выделяются с помощью цвета, жирного шрифта, указателей. С помощью видеоурока учитель может повысить эффективность урока. Данное наглядное пособие поможет быстро и эффективно достичь учебных целей.
Видеоурок начинается с представления темы.
После этого указывается, что операции умножения и деления с алгебраическими дробями производятся аналогично операциям с обыкновенными дробями. На экране демонстрируются правила умножения, деления и возведения в степень дробей. С помощью буквенных параметров демонстрируется умножение дробей. Отмечается, что при умножении дробей числители, а также знаменатели перемножаются. Так получается результирующая дробь a/b·c/d=ac/bd. Демонстрируется деление дробей на примере выражения a/b:c/d. Указывается, что для выполнения операции деления необходимо в числитель записать произведение числителя делимого и знаменателя делителя. Знаменателем частного становится произведение знаменателя делимого и числителя делителя. Таким образом, операция деления превращается в операцию умножения дроби делимого и дроби, обратной делителю. Возведение в степень дроби приравнивается дроби, в которой числитель и знаменатель возводятся в назначенную степень.
Далее рассматривается решение примеров. В примере 1 необходимо выполнить действия (5х-5у)/(х-у)·(х 2 -у 2)/10х.
Чтобы решить данный пример, числитель второй дроби, входящей в произведение, раскладывается на множители. Используя формулы сокращенного умножения, делается преобразование х 2 -у 2 =(х+у)(х-у). Затем числители дробей и знаменатели перемножаются. После проведения операций видно, что в числителе и знаменателе есть множители, которые можно сократить, используя основное свойство дроби. В результате преобразований получается дробь (х+у) 2 /2х. Здесь же рассматривается выполнение действий 7а 3 b 5 /(3a-3b)·(6b 2 -12ab+6a 2)/49a 4 b 5 . Все числители и знаменатели рассматриваются на предмет возможности разложения на множители, выделения общих множителей. Затем перемножаются числители и знаменатели. После умножения производятся сокращения. Результатом преобразования становится дробь 2(a-b)/7а.
Рассматривается пример, в котором необходимо выполнить действия (х 3 -1)/8у:(х 2 +х+1)/16у 2 . Чтобы решить выражение, предлагается преобразовать числитель первой дроби, используя формулу сокращенного умножения х 3 -1=(х-1)(х 2 +х+1).
Согласно правилу деления дробей, первая дробь умножается на дробь, обратную второй. После перемножения числителей и знаменателей получается дробь, которая содержит в числителе и знаменателе одинаковые множители. Они сокращаются. В результате получается дробь (х-1)2у. Здесь же описывается решение примера (a 4 -b 4)/(ab+2b-3a-6):(b-a)(a+2). Аналогично предыдущему примеру, для преобразования числителя применяется формула сокращенного умножения. Также преобразуется знаменатель дроби. Затем первая дробь перемножается с дробью, обратной второй дроби. После умножения выполняются преобразования, сокращения числителя и знаменателя на общие множители. В результате получается дробь -(a+b)(a 2 +b 2)/(b-3). Обращается внимание учеников, как меняются знаки числителя и знаменателя при умножении.
В третьем примере необходимо выполнить действия с дробями ((х+2)/(3х 2 -6х)) 3:((х 2 +4х+4)/(х 2 -4х+4)) 2 . В решении данного примера применяется правило возведения дроби в степень. И первая, и вторая дробь возведены в степень.
Они преобразуются возведением в степень числители и знаменателя дроби. Кроме того, для преобразования знаменателей дробей применяется формула сокращенного умножения, выделение общего множителя. Чтобы поделить первую дробь на вторую, необходимо умножить первую дробь на обратную дробь ко второй. В числителе и знаменателе образуются выражения, которые можно сократить. После преобразования получается дробь (х-2)/27х 3 (х+2).
Видеоурок «Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень» применяется для повышения эффективности традиционного урока математики. Материал может быть полезен учителю, осуществляющему обучение дистанционно. Детальное понятное описание решения примеров поможет ученикам, самостоятельно осваивающим предмет или требующим дополнительных занятий.
В этой статье мы продолжаем изучение основных действий, которые можно выполнять с алгебраическими дробями. Здесь мы рассмотрим умножение и деление: сначала выведем нужные правила, а затем проиллюстрируем их решениями задач.
Как правильно делить и умножать алгебраические дроби
Чтобы выполнить умножение алгебраических дробей или разделить одну дробь на другую, нам нужно использовать те же правила, что и для обыкновенных дробей. Вспомним их формулировки.
Когда нам надо умножить одну обыкновенную дробь на другую, мы выполняем отдельно умножение числителей и отдельно знаменателей, после чего записываем итоговую дробь, расставив по местам соответствующие произведения. Пример такого вычисления:
2 3 · 4 7 = 2 · 4 3 · 7 = 8 21
А когда нам надо разделить обыкновенные дроби, мы делаем это с помощью умножения на дробь, обратную делителю, например:
2 3: 7 11 = 2 3 · 11 7 = 22 7 = 1 1 21
Умножение и деление алгебраических дробей выполняется в соответствии с теми же принципами. Сформулируем правило:
Определение 1
Чтобы перемножить две и более алгебраические дроби, нужно перемножить отдельно числители и знаменатели. Результатом будет дробь, в числителе которой будет стоять произведение числителей, а в знаменателе – произведение знаменателей.
В буквенном виде правило можно записать как a b · c d = a · c b · d . Здесь a , b , c и d будут представлять из себя определенные многочлены, причем b и d не могут быть нулевыми.
Определение 2
Для того чтобы разделить одну алгебраическую дробь на другую, нужно выполнить умножение первой дроби на дробь, обратную второй.
Это правило можно также записать как a b: c d = a b · d c = a · d b · c . Буквы a , b , c и d здесь означают многочлены, из которых a , b , c и d не могут быть нулевыми.
Отдельно остановимся на том, что такое обратная алгебраическая дробь. Она представляет из себя такую дробь, которая при умножении на исходную дает в итоге единицу. То есть такие дроби будут аналогичны взаимно обратным числам. Иначе можно сказать, что обратная алгебраическая дробь состоит из таких же значений, что и исходная, однако числитель и знаменатель у нее меняются местами. Так, по отношению к дроби a · b + 1 a 3 дробь a 3 a · b + 1 будет обратной.
Решение задач на умножение и деление алгебраических дробей
В этом пункте мы посмотрим, как правильно применять озвученные выше правила на практике. Начнем с простого и наглядного примера.
Пример 1
Условие: умножьте дробь 1 x + y на 3 · x · y x 2 + 5 , а потом разделите одну дробь на другую.
Решение
Сначала выполним умножение. Согласно правилу, нужно отдельно перемножить числители и знаменатели:
1 x + y · 3 · x · y x 2 + 5 = 1 · 3 · x · y (x + y) · (x 2 + 5)
Мы получили новый многочлен, который нужно привести к стандартному виду. Заканчиваем вычисления:
1 · 3 · x · y (x + y) · (x 2 + 5) = 3 · x · y x 3 + 5 · x + x 2 · y + 5 · y
Теперь посмотрим, как правильно разделить одну дробь на другую. По правилу нам надо заменить это действие умножением на обратную дробь x 2 + 5 3 · x · y:
1 x + y: 3 · x · y x 2 + 5 = 1 x + y · x 2 + 5 3 · x · y
Приведем полученную дробь к стандартному виду:
1 x + y · x 2 + 5 3 · x · y = 1 · x 2 + 5 (x + y) · 3 · x · y = x 2 + 5 3 · x 2 · y + 3 · x · y 2
Ответ: 1 x + y · 3 · x · y x 2 + 5 = 3 · x · y x 3 + 5 · x + x 2 · y + 5 · y ; 1 x + y: 3 · x · y x 2 + 5 = x 2 + 5 3 · x 2 · y + 3 · x · y 2 .
Довольно часто в процессе деления и умножения обыкновенных дробей получаются результаты, которые можно сократить, например, 2 9 · 3 8 = 6 72 = 1 12 . Когда мы выполняем эти действия с алгебраическими дробями, мы также можем получить сократимые результаты. Для этого полезно предварительно разложить числитель и знаменатель исходного многочлена на отдельные множители. Если нужно, перечитайте статью о том, как правильно это делать. Разберем пример задачи, в которой нужно будет выполнить сокращение дробей.
Пример 2
Условие: перемножьте дроби x 2 + 2 · x + 1 18 · x 3 и 6 · x x 2 — 1 .
Решение
Перед тем, как вычислять произведение, разложим на отдельные множители числитель первой исходной дроби и знаменатель второй. Для этого нам потребуются формулы сокращенного умножения. Вычисляем:
x 2 + 2 · x + 1 18 · x 3 · 6 · x x 2 — 1 = x + 1 2 18 · x 3 · 6 · x (x — 1) · (x + 1) = x + 1 2 · 6 · x 18 · x 3 · x — 1 · x + 1
У нас получилась дробь, которую можно сократить:
x + 1 2 · 6 · x 18 · x 3 · x — 1 · x + 1 = x + 1 3 · x 2 · (x — 1)
О том, как это делается, мы писали в статье, посвященной сокращению алгебраических дробей.
Перемножив одночлен и многочлен в знаменателе, мы получим нужный нам результат:
x + 1 3 · x 2 · (x — 1) = x + 1 3 · x 3 — 3 · x 2
Вот запись всего решения без пояснений:
x 2 + 2 · x + 1 18 · x 3 · 6 · x x 2 — 1 = x + 1 2 18 · x 3 · 6 · x (x — 1) · (x + 1) = x + 1 2 · 6 · x 18 · x 3 · x — 1 · x + 1 = = x + 1 3 · x 2 · (x — 1) = x + 1 3 · x 3 — 3 · x 2
Ответ: x 2 + 2 · x + 1 18 · x 3 · 6 · x x 2 — 1 = x + 1 3 · x 3 — 3 · x 2 .
В некоторых случаях исходные дроби перед умножением или делением удобно преобразовать, чтобы дальнейшие вычисления стали быстрее и проще.
Пример 3
Условие: разделите 2 1 7 · x — 1 на 12 · x 7 — x .
Решение: начнем с упрощения алгебраической дроби 2 1 7 · x — 1 , чтобы избавиться от дробного коэффициента. Для этого умножим обе части дроби на семь (это действие возможно благодаря основному свойству алгебраической дроби). В итоге у нас получится следующее:
2 1 7 · x — 1 = 7 · 2 7 · 1 7 · x — 1 = 14 x — 7
Видим, что знаменатель дроби 12 · x 7 — x , на которую нам нужно разделить первую дробь, и знаменатель получившейся дроби являются противоположными друг другу выражениями.
Изменив знаки числителя и знаменателя 12 · x 7 — x , получим 12 · x 7 — x = — 12 · x x — 7 .
После всех преобразований можем наконец перейти непосредственно к делению алгебраических дробей:
2 1 7 · x — 1: 12 · x 7 — x = 14 x — 7: — 12 · x x — 7 = 14 x — 7 · x — 7 — 12 · x = 14 · x — 7 x — 7 · — 12 · x = = 14 — 12 · x = 2 · 7 — 2 · 2 · 3 · x = 7 — 6 · x = — 7 6 · x
Ответ: 2 1 7 · x — 1: 12 · x 7 — x = — 7 6 · x .
Как умножить или разделить алгебраическую дробь на многочлен
Чтобы выполнить такое действие, мы можем воспользоваться теми же правилами, что мы приводили выше. Предварительно нужно представить многочлен в виде алгебраической дроби с единицей в знаменателе. Это действие аналогично преобразованию натурального числа в обыкновенную дробь. Например, можно заменить многочлен x 2 + x − 4 на x 2 + x − 4 1 . Полученные выражения будут тождественно равны.
Пример 4
Условие: разделите алгебраическую дробь на многочлен x + 4 5 · x · y: x 2 — 16 .
Решение
x + 4 5 · x · y: x 2 — 16 = x + 4 5 · x · y: x 2 — 16 1 = x + 4 5 · x · y · 1 x 2 — 16 = = x + 4 5 · x · y · 1 (x — 4) · x + 4 = (x + 4) · 1 5 · x · y · (x — 4) · (x + 4) = 1 5 · x · y · x — 4 = = 1 5 · x 2 · y — 20 · x · y
Ответ: x + 4 5 · x · y: x 2 — 16 = 1 5 · x 2 · y — 20 · x · y .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
На данном уроке будут рассмотрены правила умножения и деления алгебраических дробей, а также примеры на применение данных правил. Умножение и деление алгебраических дробей не отличается от умножения и деления обыкновенных дробей. Вместе с тем, наличие переменных приводит к несколько более сложным способам упрощения полученных выражений. Несмотря на то, что умножение и деление дробей выполняется проще, чем их сложение и вычитание, к изучению данной темы необходимо подойти крайне ответственно, поскольку в ней существует много «подводных камней», на которые обычно не обращают внимания.
В рамках урока мы не только изучим правила умножения и деления дробей, но и разберём нюансы, которые могут возникнуть при их применении.
Тема: Алгебраические дроби. Арифметические операции над алгебраическими дробями
Урок: Умножение и деление алгебраических дробей
Правила умножения и деления алгебраических абсолютно аналогичны правилам умножения и деления обыкновенных дробей. Напомним их:
То есть, для того, чтобы умножить дроби, необходимо умножить их числители (это будет числитель произведения), и умножить их знаменатели (это будет знаменатель произведения).
Деление на дробь — это умножение на перевёрнутую дробь, то есть, для того, чтобы разделить две дроби, необходимо первую из них (делимое) умножить на перевёрнутую вторую (делитель).
Несмотря на простоту данных правил, многие при решении примеров по данной теме допускают ошибки в ряде частных случаев. Рассмотрим подробнее эти частные случаи:
Во всех этих правилах мы пользовались следующим фактом: .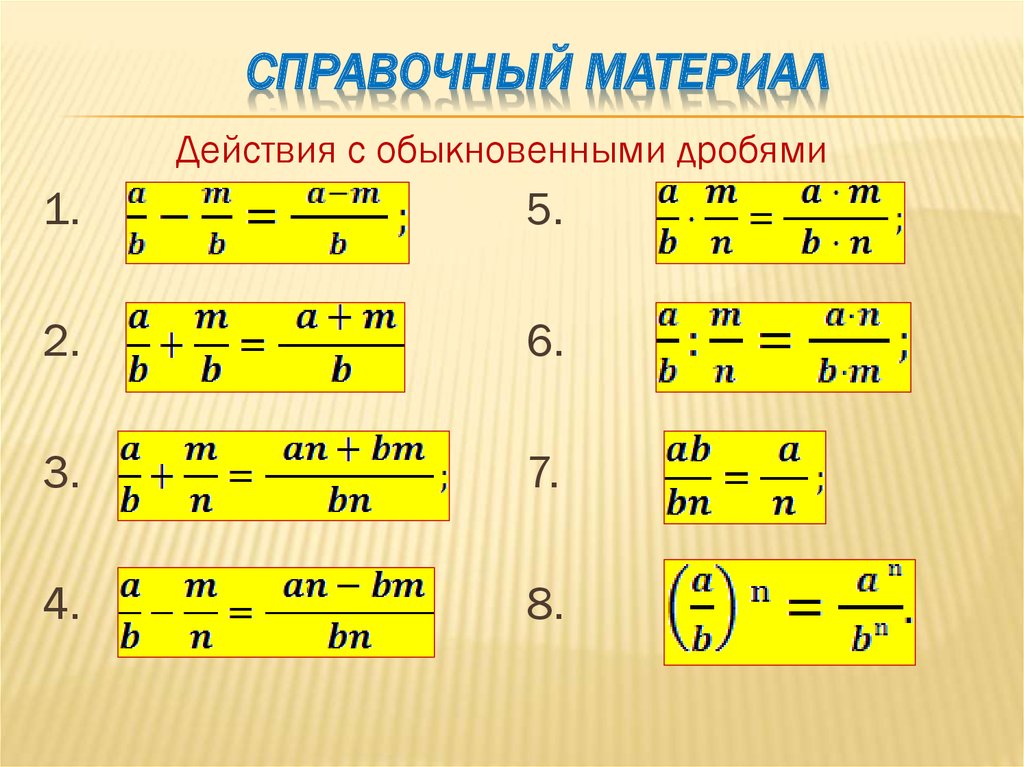
Решим несколько примеров на умножение и деление обыкновенных дробей, чтобы вспомнить, как пользоваться указанными правилами.
Пример 1
Примечание: при сокращении дробей мы пользовались разложением числа на простые множители. Напомним, что простыми числами называются такие натуральные числа, которые делятся только на и на само себя. Остальные числа называются составными . Число не относится ни к простым, ни к составным. Примеры простых чисел: .
Пример 2
Рассмотрим теперь один из частных случаев с обыкновенными дробями.
Пример 3
Как видим, умножение и деление обыкновенных дробей, в случае правильного применения правил, не является сложным.
Рассмотрим умножение и деление алгебраических дробей.
Пример 4
Пример 5
Отметим, что сокращать дроби после умножения можно и даже нужно по тем же правилам, которые мы до этого рассматривали на уроках, посвящённых сокращению алгебраических дробей.
Рассмотрим несколько простых примеров на частные случаи.
Пример 6
Пример 7
Рассмотрим теперь несколько более сложных примеров на умножение и деление дробей.
Пример 8
Пример 9
Пример 10
Пример 11
Пример 12
Пример 13
До этого мы рассматривали дроби, в которых и числитель, и знаменатель являлись одночленами. Однако в ряде случаев необходимо перемножить или поделить дроби, числители и знаменатели которых являются многочленами. В этом случае правила остаются такими же, а для сокращения необходимо использовать формулы сокращённого умножения и вынесение за скобки.
Пример 14
Пример 15
Пример 16
Пример 17
Пример 18
Деление дробей | Математические вкусности
Форма поиска
Поиск
Деление показывает, сколько раз одна величина содержится в другой величине. Например, на иллюстрации ниже видно, что целое число 2 содержит 6 третей.
Поскольку 2 содержит 6 третей, мы можем сказать, что 2 разделить на одну треть равно 6.
| , значит, | 2 | ÷ | = | 6 | ||||
| и | 2 | х | 3 | = | 6 | |||
Как видите, деление первой дроби на вторую ненулевую дробь равносильно умножению первой дроби на обратную вторую дробь. Это приводит нас к следующей процедуре.
Процедура: Чтобы разделить первую дробь на вторую, ненулевую дробь, умножьте первую тягу на величину, обратную второй дроби.
Этот метод деления дробей также называется инвертировать и умножать , так как мы инвертируем делитель, а затем умножаем. По сути, мы меняем задачу деления на задачу умножения после инвертирования делителя. Это позволяет нам умножить первую дробь на обратную вторую дробь.
Пример 1: Разделить.
Анализ:
Решение:
Пример 2: Разделить.
Анализ:
Решение:
В примере 2 необходимо было разделить общие множители.
Пример 3: Разделить.
Анализ:
Решение:
В примере 3 нужно было упростить результат.
Пример 4: Divide
Анализ:
Решение:
Пример 5: Кэнди — 3/4 дюймового дюйма.
Если его разделить на части длиной 1/8 дюйма, то сколько частей получится?
Анализ: Чтобы решить эту задачу, мы разделим 3/4 на 1/8.
Решение:
Ответ: Будет 6 конфет.
Итог: Чтобы разделить первую дробь на вторую, ненулевую дробь, умножьте первую дробь на обратную величину второй дроби. При необходимости упростите результат.
Упражнения
Указания: Разделите дроби в каждом упражнении ниже. При необходимости обязательно упростите результат. Щелкните один раз в ПОЛЕ ОТВЕТА и введите свой ответ; затем нажмите ВВОД. После того, как вы нажмете ENTER, в ОКНЕ РЕЗУЛЬТАТОВ появится сообщение, указывающее, является ли ваш ответ правильным или неправильным. Чтобы начать сначала, нажмите ОЧИСТИТЬ.
Примечание: Чтобы записать дробь три четверти, введите 3/4 в форму. Чтобы написать смешанное число четыре и две трети, введите 4, пробел, а затем 2/3 в форму.
| 1. | |
| ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: | |
| 2. | |
| ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: | |
| 3. | |
| ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: | |
4. | |
| ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: | |
| 5. | Джастин отдал 2/3 своей пиццы 4 друзьям, которые разделили пиццу поровну. Какую часть первоначальной пиццы получил каждый друг? |
| ОКНО ОТВЕТОВ: ОКНО РЕЗУЛЬТАТОВ: | |
| Уроки умножения и деления дробей и смешанных чисел | |
1. | Умножение дробей |
| 2. | Умножение дробей путем исключения общих множителей |
| 3. | Умножение смешанных чисел |
| 4. | Обратные связи |
| 5. | Деление дробей |
| 6. | Разделение смешанных чисел |
| 6. | Решение задач Word |
| 7. | Практические упражнения |
| 8. | Упражнения с вызовом |
| 9. | Решения |
Подпишитесь на нашу БЕСПЛАТНУЮ рассылку!
Подпишитесь на нашу БЕСПЛАТНУЮ рассылку новостей!
Адрес электронной почты *
В этом уроке мы делим дроби, используя ярлык (умножить на обратную величину делителя или «перевернуть и умножить»). В видео ниже концептуально объясняются обратные числа и «правило» деления дробей.
1. Решить. Превратите смешанные числа в дроби перед делением. Проверить каждое деление умножением.
2. Напишите предложение с делением на каждую проблему и решить ее.
3. Решите эти проблемы рассуждая логически. Напишите предложение на деление для каждой задачи.
4. На рисунке показано, сколько
пирог остался. Которая делится между определенным количеством людей.
5. Плитку шоколада весом 1/4 кг делят поровну на троих.
6. Сколько кусков длиной 3/8 фута вы можете отрезать
7. Пять братьев и сестер унаследовали участок земли площадью
2 4/10
акров 8. Среди многих других ингредиентов рецепт требует 2/3 стакана пшеничной муки. В ее кладовой Сары было много
из всех а. 1/3 стакана пшеничной муки? б. 1 стакан пшеничной муки?
9. Аэропорт занимает прямоугольную площадь площадью 2 1/8
миль
10. Взлетно-посадочная полоса аэропорта имеет длину две мили и занимает
Площадь 1/16 квадрата
11.
12.
13. Сколько порций по 2/3 чашки можно приготовить из 5 чашек мороженого?
14.
15. Стороны прямоугольника соотношение 2:3, а его периметр равен 1 1/4 дюйма. а. Какова длина его сторон? б. Нарисуйте прямоугольник.
16. Огород Марии 6 лет 1/2 фута на 6 1/2 фута. а. Найдите его площадь в квадратных метрах. б. Найдите его площадь в квадратных дюймах. c. Мэри разделила свой сад на четыре части, чтобы посадить четыре разных Этот урок взят из книги Марии Миллер Math Mammoth Fractions 2 и размещен на сайте www.HomeschoolMath. Mammoth Fractions 2 Самообучающийся учебник, обучающий дробям с помощью визуальных моделей, продолжение Math Mammoth Fractions 1. В книге рассказывается об упрощении дробей, умножении и делении дробей и смешанных чисел, преобразовании дробей в десятичные дроби. , и коэффициенты. Скачать ($5,75) . Также доступен в виде печатной копии. => Узнайте больше и посмотрите бесплатные образцы! Смотрите другие актуальные книги Mammoth Mammoth Меню уроков математики | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Урок также включает в себя множество текстовых задач. Предыдущий урок знакомит с обратными числами и исследует их концептуально.
1
Сколько раз 
Каждый получает по
Разделите между пятью людьми:
Сколько порций рецепта она может приготовить, если она
имеет …
Решите уравнения.
Решите эти простые задачи на деление !
Сэм посадил помидоры в своем саду, это
прямоугольная площадь
площадью 2 1/2 кв. 
net с разрешения автора. Авторское право © Мария Миллер. 8 Удивительные упражнения для деления дробей
К тому времени, когда учащиеся приступят к делению дробей, они уже достаточно много взаимодействуют с дробями, и многие учащиеся испытывают страх или неприязнь к дробям. Я чувствую, что деление дробей — это тема, которая может помочь учащимся научиться обращаться с дробями, потому что это не слишком сложно.
Все, что нужно сделать учащимся, это перевернуть вторые дроби, а затем умножить их. Мне нравится преподавать эту тему, потому что даже упорные ученики могут быстро добиться успеха.
Итак, если вы ищете новые способы обучения и практики деления дробей, попробуйте эти 8 простых упражнений!
Как и в большинстве тем, после того, как учащиеся поймут концепцию, им потребуется много практики. Студенты будут гораздо более вовлечены, если вы будете использовать некоторые игры и задания вместо традиционных рабочих листов.
Этот список занятий поможет вашим ученикам работать и развлекаться. Эти действия включают действия с цифровыми фракциями, бумажные ресурсы и действия, доступные как в бумажном, так и в цифровом формате. Вы можете использовать один из них или даже объединить их вместе, чтобы выбрать занятие на доске.
Dividing Fractions Digital Escape Room
Dividing Fractions Maze (цифровой и бумажный)
Dividing Knockout Game
Dividing Fractions Paper Chains
Dividing Fractions Games Карточки с заданиями (цифровые и бумажные) Fish 4 900 0 Онлайн
90 Kit Kat ЗадачаТест на деление дробей
Если вы еще не пробовали квест-рум со своими учениками, знайте, что ученики их любят.
Самый частый ответ, который я получаю от учителей, прост: их ученики любят квест-комнаты. В этой квест-комнате ученики учатся делить дроби и разгадывать загадки.
Для завершения учащиеся решают ряд математических задач. Затем, после каждого набора вопросов, студенты должны использовать свои ответы, чтобы взломать код. Это занятие выполняется полностью онлайн через Google Slides и может использоваться на многих обучающих платформах. Студенты гораздо более мотивированы делить дроби с дополнительным удовольствием от разгадывания загадки.
Мы большие поклонники использования математических лабиринтов, чтобы дать учащимся необходимую практику. У нас есть множество тем по лабиринтам для 6-го класса, и этот набор из 3 делящихся дробей — идеальный способ попрактиковаться для ваших учеников.
Учащиеся продвигаются по лабиринту, правильно разделяя дроби. Использование лабиринтов разрушит некоторые стены для студентов и побудит их попробовать во время практики. Наличие дополнительной задачи по поиску пути мотивирует учащихся продолжать работу
Одной из лучших особенностей этого набора из трех лабиринтов является то, что их можно распечатать или использовать в Интернете.
Вы можете поделиться ими со своими учениками в виде интерактивных слайдов Google или раздать копии ученикам. Каким бы ни был ваш класс, лабиринты станут отличным дополнением.
Задачи на деление дробей в этих лабиринтах просты и не требуют от учеников использования больших чисел. Они отлично подходят для начала занятий, и вы можете использовать их снова в конце года, чтобы повторить деление дробей.
Хотите попробовать бесплатный математический лабиринт сегодня? Зарегистрируйтесь в клубе «Лабиринт месяца» и получайте бесплатный лабиринт по математическим понятиям средней школы, который каждый месяц будет приходить прямо на ваш почтовый ящик. У каждого лабиринта есть 2 версии: версия для печати и цифровая версия, встроенная в Google Slides (идеально подходит для любого вида вашего класса!) Кроме того, вы получите сложение и вычитание целых чисел maz e сразу.
ДА! Запишите меня в клуб «Лабиринт месяца»!
Игры на выбывание — это обзорная игра для всего класса, в которой участвует весь класс.
Чтобы играть, вы просто показываете эту игру с делением дробей на проекторе и играете с классом. Вы также можете играть в эту игру удаленно во время видеоконференции, если вы преподаете удаленно. Поделившись своим экраном, учащиеся могут видеть игровое поле и играть вместе с ним.
Затем учащиеся выбирают вопрос, выбирая значок на игровом поле. Затем вы щелкаете, чтобы показать вопрос всему классу, и учащиеся работают над поиском ответа. Они отслеживают свои баллы за правильные вопросы. Некоторые вопросы имеют специальные бонусы, от которых учащиеся действительно получают удовольствие.
Эта игра дает вам возможность неформально оценить, как учащиеся справляются с делением дробей. Вы можете увидеть, забывают ли они перевернуть вторую дробь или не упрощают, попросив их показать вам свою работу на персональной доске. Если вам нужен увлекательный способ повторить деление дробей со всем классом, попробуйте эту игру на выбывание.
Бумажные цепи хорошо работают в качестве партнерской деятельности.
Для завершения учащиеся ставят ряд задач на деление дробей и ответы, чтобы в основном решить головоломку. Как учитель, вы ходите по комнате, даете ученикам указания и сообщаете им, нужно ли им что-то исправить. Если все в порядке, учащиеся могут склеить свою бумажную цепочку.
Я использую бумажную цепочку деления дробей в качестве упражнения, которое мы делаем сразу после изучения шагов. Работа с партнером и веселые занятия на этом этапе обучения, по-видимому, мотивируют их. Они также с удовольствием развешивают свой конечный продукт по комнате для демонстрации. Однажды мои интервенционные студенты объединили свои бумажные цепочки из разных тем в гигантскую бумажную цепочку в коридоре. Это превратилось в забавное и визуальное напоминание обо всей работе, которую они проделали.
Карточки с заданиями очень универсальны, и этот набор карточек с разделяющими дробями можно использовать для занятий с партнерами или для обзора всего класса. Есть смесь словесных вопросов, основных задач и задач со словами, которые заставят учащихся делить дроби.
Мне нравится использовать карточки с заданиями, чтобы играть в такие игры, как целевая игра, со всем классом. Этот набор карточек с заданиями включает бумажную версию и цифровую версию, так что вы можете использовать их в самых разных обстоятельствах.
Если вы ищете глупую тренировочную онлайн-игру, то эта игра вам подойдет. Это быстрая практика, и студенты могут «ловить рыбу» во время практики. Студенты любят такие игры, которые добавляют немного видеоигры в их практику. В этой игре используются только основные задачи, и я бы использовал ее со своим классом интервенций, чтобы немного мотивировать их практиковать деление дробей.
Если вы хотите углубиться в эту тему, попробуйте эту математическую задачу из трех задач. В нем есть много разных способов использования шоколадных батончиков Kit Kat для изучения дробей, и самый последний из них предназначен для деления дробей. Математические задачи в трех действиях уходят глубже и заставляют детей использовать то, что они знают, чтобы угадать, что произойдет, а затем делать выводы после того, как ответ будет раскрыт.
Кроме того, это выглядит как забавный способ добавить конфеты на урок математики.
В этой веселой игре ученики тренируются во время игры. По сути, такие игры-викторины, как эта, выглядят как игра, но они очень похожи на викторину. Это идеальный способ увидеть, что студенты знают в веселой обстановке. Quizizz также позволяет настроить игровой процесс в соответствии с вашим классом. Вы можете играть в живую игру (аналогично Kahoot), играть в живую игру в командах или предлагать учащимся выполнять их по собственному расписанию, используя настройку «домашнее задание». (Я также отключаю таймер, чтобы скорость не учитывалась при оценке учащихся).
В этой игре учащиеся будут практиковаться в делении дробей и работе со смешанными числами. Вы всегда можете сократить викторину Quizizz, сделав собственную копию и удалив некоторые вопросы. Например, когда я использую его в конце урока для быстрой проверки, я обычно отвечаю только на 5 вопросов.
Вовлеките учащихся в деление дробей
Лучший способ для учащихся закрепить эту тему в своей голове — это много раз повторять ее.