Статьи. Теоретический материал. ‘Математика’
Список доступных материалов. Математика
Показательные и логарифмические функции
Сложность: 10 класс
Читать далее
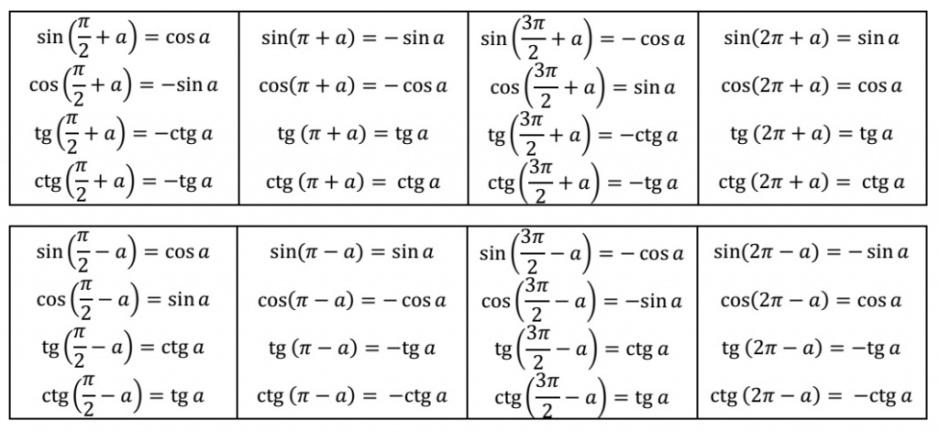
Формулы приведения
Сложность: 10 класс
Рассказываются основные понятия, связанные с формулами приведения
Читать далее
Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Сложность: 10 класс
Здесь рассмотрены основные свойства тригонометрических функций и их графики. Теория описана кратко, но в тоже время содержательно. Текст взят из учебника Е.П. Нелина, В.А. Лазарева "Алгебра и начала математического анализа 10 класс".
Читать далее
Простейшие тригонометрические уравнения
Сложность: 10 класс
Описаны решения простейших тригонометрических уравнений
Читать далее
Применение тригонометрических функций
Сложность: 10 класс
В статье рассматриваются темы: История тригонометрических функций Геометрическое приложение Радианная мера угла Связь с окружающим миром ТФ угла и числового аргумента Список использованной литературы:
Читать далее
Тригонометрические уравнения и неравенства
Сложность: 10 класс
В теоретическом материале представлены основные разделы темы «Тригонометрические уравнения и неравенства». Данный теоретический материал может помочь учащимся 9-11 классов в изучении курса математики, а также студентам первого курса.
Данный теоретический материал может помочь учащимся 9-11 классов в изучении курса математики, а также студентам первого курса.
Читать далее
Тригонометрические функции
Сложность: 10 класс
Изложена история тригонометрических функций. Геометрические приложение тригонометрических функций,связь с окружающим миром.
Читать далее
Производная. Геометрический и механический смысл производной
Сложность: 10 класс
Раскрытие понятия производной .Геометрический смысл производной. Уравнение касательной. Механический смысл производной.
Читать далее
Обобщенный метод интервалов при решении алгебраических неравенств (Автор Колчанов А.В.)
Сложность: 10 класс
Рассмотрен один из самых распространенных способов решения неравенств, левая часть которых представляет собой дробь, числитель и знаменатель которой, представляют произведение некоторых функций, а правая – равна нулю является метод интервалов.
Читать далее
Радианная мера углов
Сложность: 10 класс
Параграф из учебника Е. П. Нелин, В. А. Лазарев АЛГЕБРА и начала математического анализа 10 класс Учебник для общеобразовательных учреждений Базовый и профильный уровни Москва «Илекса» 2011
Читать далее
§ 9. Делимость целых чисел. Сравнения по модулю m. Решение уравнений в целых числах.
Сложность: 10 класс
АЛГЕБРА и начала математического анализа
Читать далее
Свойства тригонометрических функций
Сложность: 10 класс
Алгебра и начала математического анализа 10 класс. Е. П. Нелин, В. А. Лазарев
Читать далее
10. Многочлены от одной переменной и действия над ними.
Сложность: 10 класс
10.1. ОПРЕДЕЛЕНИЕ МНОГОЧЛЕНОВ ОТ ОДНОЙ ПЕРЕМЕННОЙ И ИХ ТОЖДЕСТВЕННОЕ РАВЕНСТВО
10.2. ДЕЛЕНИЕ МНОГОЧЛЕНА НА МНОГОЧЛЕН С ОСТАТКОМ
10. 3. ТЕОРЕМА БЕЗУ. КОРНИ МНОГОЧЛЕНА. ФОРМУЛЫ ВИЕТА
10.4. СХЕМА ГОРНЕРА
10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ.
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ К РАЗДЕЛУ 1
3. ТЕОРЕМА БЕЗУ. КОРНИ МНОГОЧЛЕНА. ФОРМУЛЫ ВИЕТА
10.4. СХЕМА ГОРНЕРА
10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ.
ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ К РАЗДЕЛУ 1
Читать далее
§ 14. Свойства функций синуса, косинуса, тангенса и котангенса и их графики
Сложность: 10 класс
14.1. СВОЙСТВА ФУНКЦИИ y = sin x И ЕЕ ГРАФИК 14.2 СВОЙСТВА ФУНКЦИИ y = cos x И ЕЕ ГРАФИК
Читать далее
10.4. СХЕМА ГОРНЕРА
Сложность: 10 класс
10.4. СХЕМА ГОРНЕРА
Читать далее
10.5. Нахождение рациональных корней многочлена с целыми коэффициентами.
Сложность: 10 класс
Нахождение рациональных корней многочлена с целыми коэффициентами.
Читать далее
Дополнительные упражнения к разделу 1
Сложность: 10 класс
Задачи
Читать далее
Многочлены от одной переменной и действия над ними.
 Определение многочленов от одной переменной и их тождественное равенство
Определение многочленов от одной переменной и их тождественное равенствоСложность: 10 класс
Многочлены одной переменной и действия над ними. Определение многочленов от одной переменной и их тождественное равенство
Читать далее
Действия над многочленами. Деление многочлена на многочлен с остатком
Сложность: 10 класс
Действия над многочленами. Деление многочлена на многочлен с остатком
Читать далее
§ 22. Примеры решения более сложных тригонометрических уравнений и их систем.
Сложность: 10 класс
Е.П.Нелин, В.А.Лазарев Алгебра и начало математического анализа 10 класс Учебник для общеобразовательных учреждений. Базовый и профильный уровни. § 22. Примеры решения более сложных тригонометрических уравнений и их систем (Оформление и автор интерактивных технологий Цукахина В.)
Читать далее
§ 1. Множества и операции над ними
Сложность: 10 класс
Е. П. Нелин, В.А. Лазарев
АЛГЕБРА
и начала математического анализа
10 класс
Учебник для общеобразовательных учреждений.
Базовый и профильный уровни
§ 1. Множества и операции над ними
(Оформление и автор интерактивных технологий Баранник Л.С.)
П. Нелин, В.А. Лазарев
АЛГЕБРА
и начала математического анализа
10 класс
Учебник для общеобразовательных учреждений.
Базовый и профильный уровни
§ 1. Множества и операции над ними
(Оформление и автор интерактивных технологий Баранник Л.С.)
Читать далее
Параграф 2.1. Понятие числовой функции. Простейшие свойства числовых функций.
Сложность: 10 класс
Е.П. Нелин, В.А. Лазарев Алгебра и начала математического анализа 10 класс Учебник для общеобразовательных учреждений. Базовый и профильный уровни Параграф 2. Повторение и расширение сведений о функции. (оформление и автор интерактивных технологий Косярский А.А,)
Читать далее
Параграф 2.2. Свойства и графики основных функций.
Сложность: 10 класс
В данном параграфе даны графики основных функций
Читать далее
3.Уравнения-следствия и равносильные преобразования уравнений
Сложность: 10 класс
3. Уравнения-следствия и равносильные преобразования уравнений
Уравнения-следствия и равносильные преобразования уравнений
Читать далее
Уравнения и неравенства, содержащие знак модуля
Сложность: 10 класс
Уравнения и неравенства, содержащие знак модуля
Читать далее
§ 3. УРАВНЕНИЯ
Сложность: 10 класс
§ 3. УРАВНЕНИЯ
Читать далее
§ 19. РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Сложность: 10 класс
Е.П. Нелин, В.А. Лазарев Алгебра и начала математического анализа 10 класс Учебник для общеобразовательных учреждений. Базовый и профильный уровни § 19. Решение простейших тригонометрических уравнений (Оформление и автор интерактивных технологий Михеева-Петрова В.)
ФОРМУЛЫ СЛОЖЕНИЯ И ИХ СЛЕДСТВИЯ
Сложность: 10 класс
16.1. формулы сложения. 16.2. формулы двойного аргумента. 16.3. формулы приведения
Читать далее
§ 21.
 РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
РЕШЕНИЕ СИСТЕМ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙСложность: 10 класс
Е.П. Нелин, В.А. Лазарев АЛГЕБРА и начала математического анализа 10 класс Учебник для общеобразовательных учреждений. Базовый и профильный уровни
Читать далее
7 параграф
Сложность: 10 класс
про уровнения
Читать далее
§4. Неравенства: равносильные преобразования неравенств и общий метод интервалов
Сложность: 10 класс
§4. Неравенства: равносильные преобразования неравенств и общий метод интервалов
Читать далее
Решение тригонометрических уравнений, отличающихся от простейших
Сложность: 10 класс
§ 20 Решение тригонометрических уравнений, отличающихся от простейших
20.1. Замена переменных при решении тригонометрических уравнений
20.2. Решение тригонометрических уравнений приведением к одной функции (с одинаковым аргументом)
20. 3. Решение однородных тригонометрических уравнений и приведение тригонометрического уравнения к однородному
20.4. Решение тригонометрических уравнений вида f (x) = 0 с помощью разложения на множители
20.5. Отбор корней тригонометрических уравнений
3. Решение однородных тригонометрических уравнений и приведение тригонометрического уравнения к однородному
20.4. Решение тригонометрических уравнений вида f (x) = 0 с помощью разложения на множители
20.5. Отбор корней тригонометрических уравнений
Читать далее
Параграф 2.3. Построение графиков функций с помощью геометрических преобразований известных графиков функций.
Сложность: 10 класс
Е.П. Нелин, В.А. Лазарев Алгебра и начала математического анализа 10 класс Учебник для общеобразовательных учреждений. Базовый и профильный уровни. Параграф 2. Повторение и расширение сведений о функции. (Оформление и автор интерактивных технологий Кондратьева В.А.)
Читать далее
12 параграф. Тригонометрические функции угла и числового аргумента
Сложность: 10 класс
Е. П. Нелин, В. А. Лазарев АЛГЕБРА и начала математического анализа 10 класс Учебник для общеобразовательных учреждений Базовый и профильный уровни Параграф 12
Читать далее
Параграф 6
Сложность: 10 класс
Учебник
Читать далее
§ 22.
 Примеры решения более сложных тригонометрических уравнений и их систем
Примеры решения более сложных тригонометрических уравнений и их системСложность: 10 класс
Вы начинаете изучать новый предмет «Алгебра и начала математического анализа», который объединяет материал нескольких отраслей математической науки. Как и в курсе алгебры, значительное внимание будет уделено преобразованию выражений, решению уравнений, неравенств и их систем и изучению свойств функций. Наряду с решением знакомых задач, связанных с многочленами, рациональными дробями, степенями и корнями, в 10 классе будут рассмотрены новые виды функций: тригонометрические, показательные и логарифмические и соответствующие уравнения и неравенства.
Читать далее
Тригонометрические уравнения и неравенства
Сложность: 10 класс
Понятие обратной функции.
Читать далее
Формулы сложения и их следствия
Сложность: 10 класс
Е. П. Нелин, В. А. Лазарев
АЛГЕБРА
и начала математического анализа
10 класс
Учебник для общеобразовательных учреждений. Базовый и профильный уровни
§ 16. Формулы сложения и их следствия
Базовый и профильный уровни
§ 16. Формулы сложения и их следствия
Читать далее
10. Многочлены от одной переменной и действия над ними.
Сложность: 10 класс
10.1. ОПРЕДЕЛЕНИЕ МНОГОЧЛЕНОВ ОТ ОДНОЙ ПЕРЕМЕННОЙ И ИХ ТОЖДЕСТВЕННОЕ РАВЕНСТВО 10.2. ДЕЛЕНИЕ МНОГОЧЛЕНА НА МНОГОЧЛЕН С ОСТАТКОМ 10.3. ТЕОРЕМА БЕЗУ. КОРНИ МНОГОЧЛЕНА. ФОРМУЛЫ ВИЕТА 10.4. СХЕМА ГОРНЕРА 10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ. ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ К РАЗДЕЛУ 1Читать далее
10. Многочлены от одной переменной и действия над ними
Сложность: 10 класс
10.1. ОПРЕДЕЛЕНИЕ МНОГОЧЛЕНОВ ОТ ОДНОЙ ПЕРЕМЕННОЙ И ИХ ТОЖДЕСТВЕННОЕ РАВЕНСТВО 10.2. ДЕЛЕНИЕ МНОГОЧЛЕНА НА МНОГОЧЛЕН С ОСТАТКОМ 10.3. ТЕОРЕМА БЕЗУ. КОРНИ МНОГОЧЛЕНА. ФОРМУЛЫ ВИЕТА 10.4. СХЕМА ГОРНЕРА 10.5. НАХОЖДЕНИЕ РАЦИОНАЛЬНЫХ КОРНЕЙ МНОГОЧЛЕНА С ЦЕЛЫМИ КОЭФФИЦИЕНТАМИ. ДОПОЛНИТЕЛЬНЫЕ УПРАЖНЕНИЯ К РАЗДЕЛУ 1
Читать далее
§ 18.
 Обратные тригонометрические функции
Обратные тригонометрические функцииСложность: 10 класс
В данном параграфе представлена вся информация по теме "Обратные тригонометрические функции;, а так же примеры решения задач и упражнения для самостоятельного решения.
Читать далее
§ 15. Соотношения между тригонометрическими функциями одного аргумента
Сложность: 10 класс
§ 15. Соотношения между тригонометрическими функциями одного аргумента
Читать далее
§8 Метод математической индукции
Сложность: 10 класс
Математическая индукция — метод математического доказательства, который используется, чтобы доказать истинность некоторого утверждения для всех натуральных чисел.
Читать далее
Функция у = secх – называется функцией секанса, а функция у = cosecх – функцией косеканса. | |
Основные свойства: | |
у = secх | у = соsecх |
1. Область определения: , 2. Область значений: 3. 4. Функция периодическая: Т=. Наименьший положительный период . | 1. Область определения: , 2. Область значений: 3. Функция у = cosecх – нечетная т.к. . 4. Функция периодическая: Т=, . Наименьший положительный период . |
График функции у = secх | График функции у = cosecх |
5 формул для базы и профиля ⋆ MAXIMUM Блог
Чуть больше 30% выпускников справляется с тригонометрией на ЕГЭ по математике.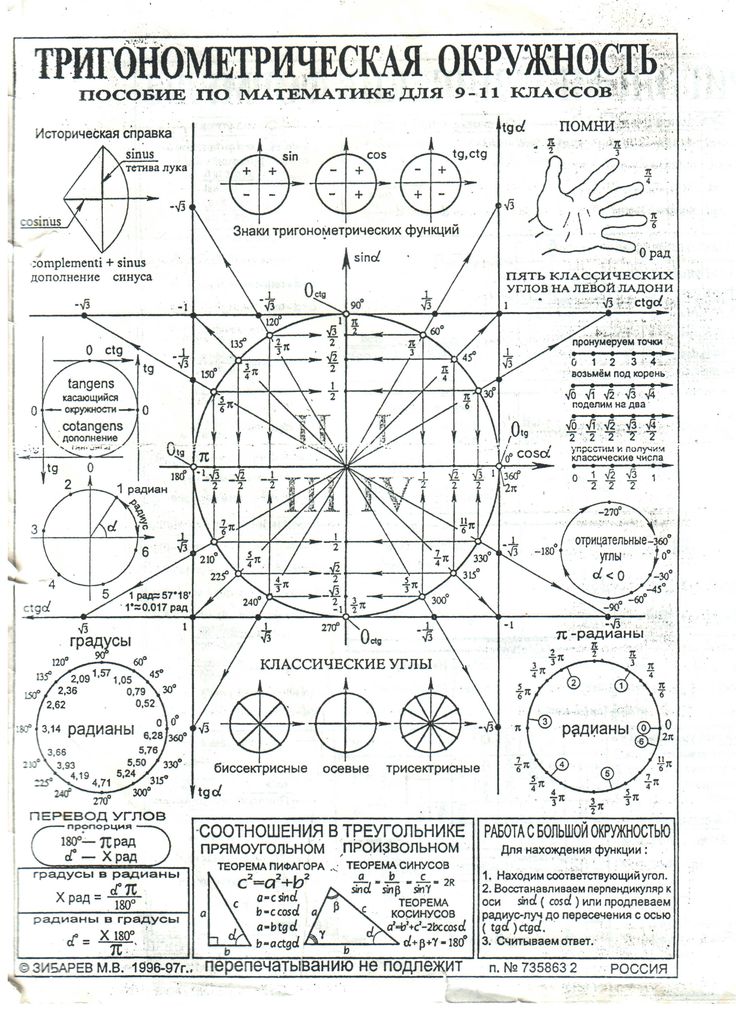 И неудивительно: для решения заданий из базы и профиля надо знать очень много формул, которые сложно освоить за 1-2 года. На самом деле, это миф! Чтобы решить задания по тригонометрии, нужно знать всего 5 формул — и просто уметь ими пользоваться.
И неудивительно: для решения заданий из базы и профиля надо знать очень много формул, которые сложно освоить за 1-2 года. На самом деле, это миф! Чтобы решить задания по тригонометрии, нужно знать всего 5 формул — и просто уметь ими пользоваться.
Тригонометрия на ЕГЭ: основные проблемы темы
Чаще всего тригонометрию начинают изучать в 10 классе — но в некоторых школах оставляют до 11. В первом случае у учеников есть 2 года, чтобы освоить новую тему. А во втором, к сожалению, всего год. И это проблема. Дело в том, что в тригонометрии очень много формул, которые нужно знать, чтобы успешно решать задания. Если за 2 года их можно успеть выучить, то за год это будет сделать проблематично.
Ситуация осложняется ещё двумя факторами. Во-первых, в самой математике много формул, признаков, теорем и т.д. Во-вторых, кроме математики есть и другие экзамены, для которых нужно выучить большой объём информации.
Именно поэтому я всегда советую своим ученикам не учить формулы для тригонометрии на ЕГЭ, а выводить! Но об этом мы поговорим чуть позже, а сейчас давайте обсудим, почему тригонометрия так важна и где в ЕГЭ ее можно встретить.
Задания по тригонометрии в базе и профиле на ЕГЭ
Так как ЕГЭ по математике делится на базовый и профильный, а тригонометрия встречается в обоих, то давайте рассмотрим оба уровня экзамена.
Тригонометрия в базе
Что касается Базового уровня, то в нём всего 3 задания, в которых можно столкнуться с тригонометрией:
В № 7 в виде простейшего выражения
Как правило, для успешного решения таких заданий достаточно воспользоваться формулами из справочного материала.
Пример задания № 7 по тригонометрии, демоверсия ЕГЭВ № 8 в виде формулы прикладной задачи
Стоит отметить, что в базовом ЕГЭ в прикладных задачах тригонометрия попадается редко, но нужно быть готовыми.
Пример задания № 8 по тригонометрии, демоверсия ЕГЭВ № 15 как тригонометрия в геометрии
В справочном материале есть вся необходимая информация для успешного решения данного задания, а именно определение всех тригофункций в прямоугольном треугольнике.
Тригонометрия в профиле
Базовый уровень мы рассмотрели, теперь перейдём к профильному. Здесь уже больше вариантов, в которых можно встретиться с тригонометрией. Давайте посмотрим на Части 1 и 2.
В № 3 как тригонометрия в геометрии (Часть 1)
То же самое задание, как в базовом ЕГЭ, вот только в справочном материале уже нет необходимой информации.
Пример задания № 3 по тригонометрии, демоверсия ЕГЭВ № 4 в виде выражения (Часть 1)
То же самое задание, как в базовом ЕГЭ.
Пример задания № 4 по тригонометрии, демоверсия ЕГЭВ № 7 в виде формулы прикладной задачи (Часть 1)
То же самое задание, как в базовом ЕГЭ. Для успешного решения подойдут базовые навыки работы с тригонометрией.
Пример задания № 7 по тригонометрии, демоверсия ЕГЭВ № 11 как часть функции (Часть 1)
Функцию нужно проанализировать для поиска наибольшего/наименьшего значения или точек максимума/минимума.
Пример задания № 11 по тригонометрии, демоверсия ЕГЭЕсли с Частью 1 профиля всё более-менее очевидно, то во второй части бывают сюрпризы, о которых ученики даже не подозревают. Да-да, тригонометрия на ЕГЭ умеет прятаться и в Части 2. Давайте посмотрим на эти задания.
Да-да, тригонометрия на ЕГЭ умеет прятаться и в Части 2. Давайте посмотрим на эти задания.
В № 12 (Часть 2)
Тут сюрпризов нет. Это уравнение второй части, в котором ученики как раз ожидают увидеть тригонометрию, хотя она там бывает не всегда!
Пример задания № 12 по тригонометрии, демоверсия ЕГЭВ № 13 — стереометрия (Часть 2)
Да, тригонометрия может встретиться здесь в виде теоремы синусов или теоремы косинусов, а ещё в виде формул в методе координат (для любителей решать этим методом).
В № 16 — планиметрия (Часть 2)
Здесь всё аналогично стереометрии: есть геометрические формулы, в которых прячется тригонометрия. Ведь, как я и сказала выше, в геометрии она тоже бывает!
5 формул тригонометрии: теория для ЕГЭ
А теперь предлагаю перейти к самому интересному — а именно к формулам. К сожалению, их действительно много. А ещё они похожи, и если их просто учить (или бездумно зубрить), то велик риск перепутать «+» с «–» или забыть какую-нибудь единичку.
Именно поэтому я рекомендую не учить формулы, а выводить. Это очень удобно тем более, что в профильном ЕГЭ по математике весь справочный материал состоит из 5-ти формул тригонометрии, из которых очень легко выводятся все остальные.
Но прежде чем я расскажу вам, как выводятся тригонометрические формулы, пообещайте, что обязательно отработаете все правила выведения! Для этого нужно будет регулярно выводить формулы по указанным ниже схемам.
Вот формулы, которые будут у вас в справочном материале:
Тригонометрия: теория для ЕГЭ — 5 основных формулФормула № 1 и как она пригодится в поиске котангенса и тангенса
Первая формула — основное тригонометрическое тождество (ОТТ):
Тригонометрия: теория для ЕГЭ — формула № 1Обычно ученики знают ее очень хорошо. Она связывает синус и косинус и помогает найти одну функцию через другую.
С этой формулой косвенно связана другая (ее нет в справочном материале), которая тоже легко дается школьникам:
Тригонометрия: теория для ЕГЭЭту формулу очень легко запомнить, если знать, как можно расписать тангенс и котангенс через синус и косинус:
Тригонометрия: теория для ЕГЭЭти 2 формулы связывают по отдельности синус с косинусом и тангенс с котангенсом. Но иногда требуется, чтобы были связаны все 4 функции, и здесь на помощь приходят следствия из ОТТ (как раз та самая формула № 1).
Но иногда требуется, чтобы были связаны все 4 функции, и здесь на помощь приходят следствия из ОТТ (как раз та самая формула № 1).
Чтобы вывести следствия нужно всего лишь разделить ОТТ на sin2 и cos2:
Тригонометрия: теория для ЕГЭ — что выводится из формулы № 1Теперь можно легко найти:
- котангенс, зная синус,
- или тангенс, зная косинус.
Формула № 2 и что из нее можно вывести
С тождествами разобрались, давайте перейдём к формулам двойного угла. Что касается синуса двойного угла (вторая формула в справочном материале):
Тригонометрия: теория для ЕГЭ — формула № 2Здесь всё просто, берёте и применяете формулу, если видите, что она нужна для задания.
Формула № 3 и что из нее можно вывести
А вот с косинусом двойного угла (третья формула в справочном материале) всё интереснее. Безусловно, косинус двойного угла:
Тригонометрия: теория для ЕГЭ — формула № 3в чистом виде встречается, и тогда вы делаете всё тоже самое, что с синусом. Но на самом деле есть ещё 2 формулы, которые очень просто вывести, используя ОТТ (формулу № 1). Для начала нужно выразить квадрат синуса и квадрат косинуса из ОТТ (Шаг 1):
Но на самом деле есть ещё 2 формулы, которые очень просто вывести, используя ОТТ (формулу № 1). Для начала нужно выразить квадрат синуса и квадрат косинуса из ОТТ (Шаг 1):
А потом нужно подставить эти значения в формулу (6, или третья формула справочного материала) (Шаг 2):
Тригонометрия: теория для ЕГЭ — как еще найти косинус двойного угла (Шаг 2)Вот мы вывели ещё 2 формулы! А сейчас я покажу вам как практически ничего не делая получить ещё 2. Мы будем выводить формулы понижения степени из формул двойного угла. Смотрите, нужно всего лишь выразить одно из другого:
Тригонометрия: теория для ЕГЭ — что выводится из формулы № 3Формулы № 4 и 5 и что из них можно вывести
Давайте посмотрим на справочный материал, у нас там ещё целых 2 формулы, из которых мы получим конечно же ещё 2! Сейчас вообще ничего удивительного не будет. Вот формулы, которые уже даны:
Тригонометрия: теория для ЕГЭ — формулы № 4 и 5Как вы заметили, они для суммы углов, а чтобы получить формулы для разности углов, нам нужно всего лишь поменять знаки в формуле на противоположные (разумеется, я говорю про «+» и «–»):
Тригонометрия: теория для ЕГЭ — что выводится из формул № 4 и 5Вот так при помощи нехитрых преобразований из 5-ти формул справочного материала мы получили целых 14!
Все скриншоты взяты из открытого банка заданий ФИПИ или из демоверсий ЕГЭ по математике 2022.
Что еще пригодится вам для тригонометрии на ЕГЭ
Скажу по секрету, что это далеко не все формулы тригонометрии, которые существуют. Есть и другие:
- некоторые можно вывести из вышеуказанных,
- некоторые можно обобщить и вместо огромного количества формул использовать короткое правило.
Но мне кажется, что пока этого и так много!
Советую сначала хорошо отработать формулы, которые я перечислила в этой статье, и только потом браться за другие. Так вы не загрузите свою память и будете быстрее решать сложные задания по тригонометрии из ЕГЭ. Это, кстати, касается любой темы на экзамене по математике: а в ЕГЭ их очень много. Поэтому чтобы получить высокий балл, надо правильно и системно отработать их все.
Именно так я и строю подготовку к ЕГЭ по математике вместе со своими учениками: строгая система подготовки — ключ к успеху на экзамене. Сначала мы разбираем простые темы и задания и учимся решать их самыми удобными способами — почти на автомате. А после я добавляю более хитрые и сложные задания. В итоге ребята и имеют хорошую базу знаний по математике, и умеют решать самые разные типы задач. Так что если вы хотите по-настоящему знать математику, а не зазубривать формулы, приходите на мои уроки!
А после я добавляю более хитрые и сложные задания. В итоге ребята и имеют хорошую базу знаний по математике, и умеют решать самые разные типы задач. Так что если вы хотите по-настоящему знать математику, а не зазубривать формулы, приходите на мои уроки!
А чтобы отрабатывать выведение было не так скучно, держите моего котика, который любезно согласился позировать в позе котангенса:
Тригонометрия ЕГЭ: КОТангенсТригонометрические тождества — Класс 10
Тригонометрия — это раздел математики, который занимается изучением измерения сторон и углов треугольника. Концепция тригонометрии полностью основана на прямоугольных треугольниках. Существует шесть тригонометрических отношений, а именно синус, косинус, тангенс, котангенс, секанс и косеканс исходного угла. Все эти тригонометрические отношения выражаются как отношения гипотенузы, основания и перпендикулярной стороны прямоугольного треугольника.
Тригонометрические тождества. Класс 10 устанавливает взаимосвязь между этими различными тригонометрическими соотношениями. Эти тригонометрические тождества являются основными формулами, верными для всех значений опорного угла.
Эти тригонометрические тождества являются основными формулами, верными для всех значений опорного угла.
Существует шесть тригонометрических отношений, а именно синус, косинус, тангенс-котангенс, секанс и косеканс. Определение каждого тригонометрического отношения для опорного угла «θ» упоминается в терминах сторон прямоугольного треугольника. Они:
Основные тригонометрические соотношения
Свойство | Математическая ценность | |
SING θ | 7||
SING θ 9000 | 9007||
SING θ 9000 | 9007||
SING θ 9000 | 9007||
9000 2 | 7||
.0003 | ||
COS θ | База/Гипотеновая. cosec θ | Гипотенуза/перпендикуляр |
cot θ | Основание/перпендикуляр | 3{2}a\]



 Сколько корней имеет уравнение cosx = 0,5
Сколько корней имеет уравнение cosx = 0,5 2 arccosx + 3arcsinx =
2 arccosx + 3arcsinx =  2 sinx + 3 sin5x + cos5x = 0
2 sinx + 3 sin5x + cos5x = 0
 Функция у = secх — четная, т.к. .
Функция у = secх — четная, т.к. .
 Решите уравнение .
Решите уравнение .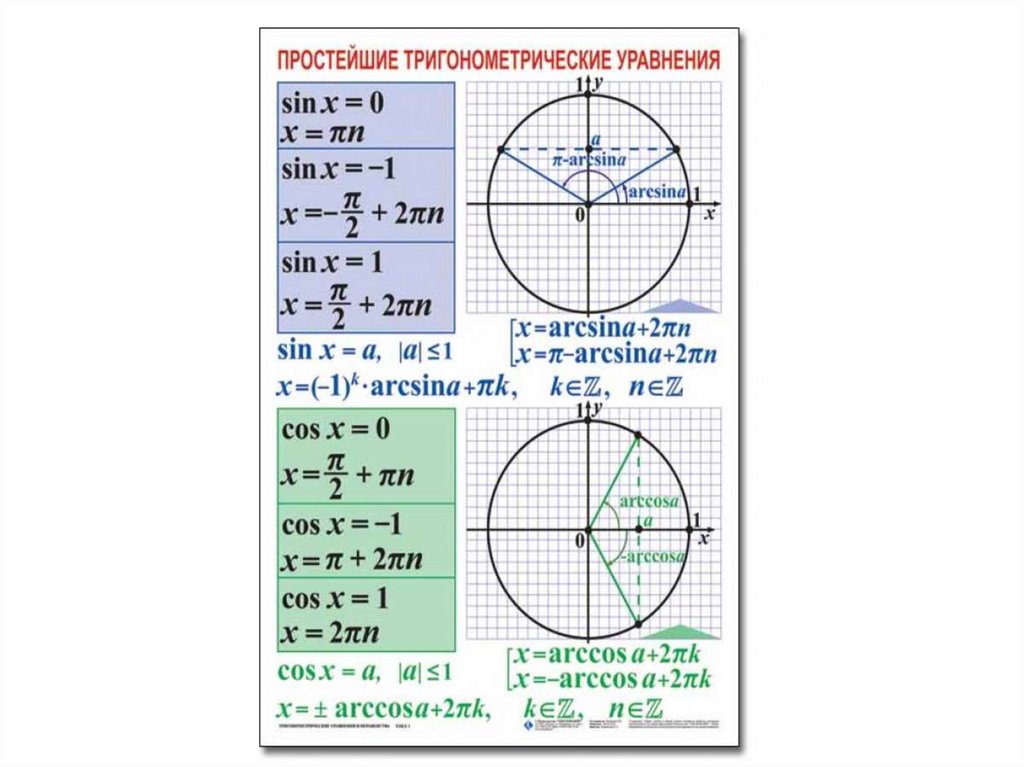 Два; В. Один; С. Три;
Два; В. Один; С. Три; Найдите его наименьший положительный корень.
Найдите его наименьший положительный корень.

 Эти формулы составляют основу математических исследований продвинутого уровня, которые определяют успех учащихся. Изучение математических формул 10 класса также упрощает решение сложных задач с легкостью и точностью. Математические формулы — это методы вычисления величин и точной оценки значений, которые также используются в практических ситуациях.
Эти формулы составляют основу математических исследований продвинутого уровня, которые определяют успех учащихся. Изучение математических формул 10 класса также упрощает решение сложных задач с легкостью и точностью. Математические формулы — это методы вычисления величин и точной оценки значений, которые также используются в практических ситуациях.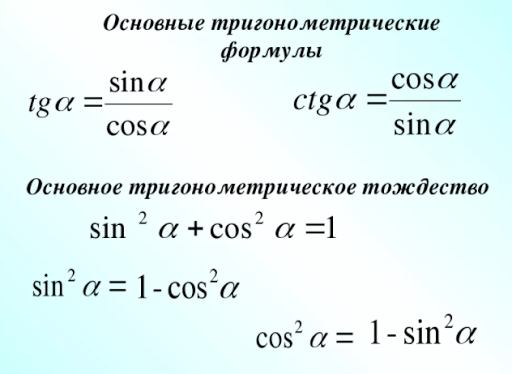 Например, полиномиальные уравнения являются одними из наиболее распространенных алгебраических уравнений, в которых используются приравнивающие полиномы. Изучение формул алгебры 10 класса поможет преобразовать различные текстовые задачи в их математические формы. Зная эти формулы, учащиеся могут легко научиться распознавать тип уравнения и применять правила для их решения. Эти алгебраические формулы имеют различные входные и выходные данные с различными интерпретациями. Вот все важные формулы алгебры класса 10:
Например, полиномиальные уравнения являются одними из наиболее распространенных алгебраических уравнений, в которых используются приравнивающие полиномы. Изучение формул алгебры 10 класса поможет преобразовать различные текстовые задачи в их математические формы. Зная эти формулы, учащиеся могут легко научиться распознавать тип уравнения и применять правила для их решения. Эти алгебраические формулы имеют различные входные и выходные данные с различными интерпретациями. Вот все важные формулы алгебры класса 10: Эти шаблоны обычно известны как последовательности. Две такие последовательности представляют собой арифметическую и геометрическую последовательности. Различные числа, встречающиеся в последовательности, называются ее членами. Члены последовательности обозначены 1 а 2 , а 3 , …………… а n . Арифметическая прогрессия — это последовательность чисел, разность между последовательными членами которых равна.
Эти шаблоны обычно известны как последовательности. Две такие последовательности представляют собой арифметическую и геометрическую последовательности. Различные числа, встречающиеся в последовательности, называются ее членами. Члены последовательности обозначены 1 а 2 , а 3 , …………… а n . Арифметическая прогрессия — это последовательность чисел, разность между последовательными членами которых равна.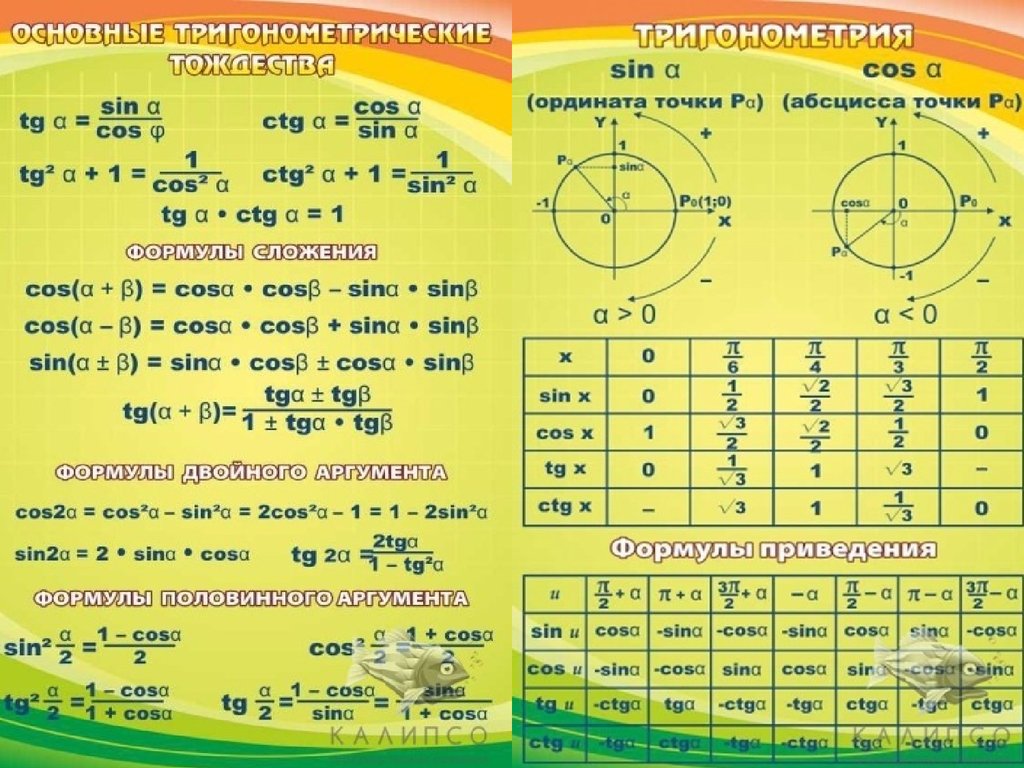
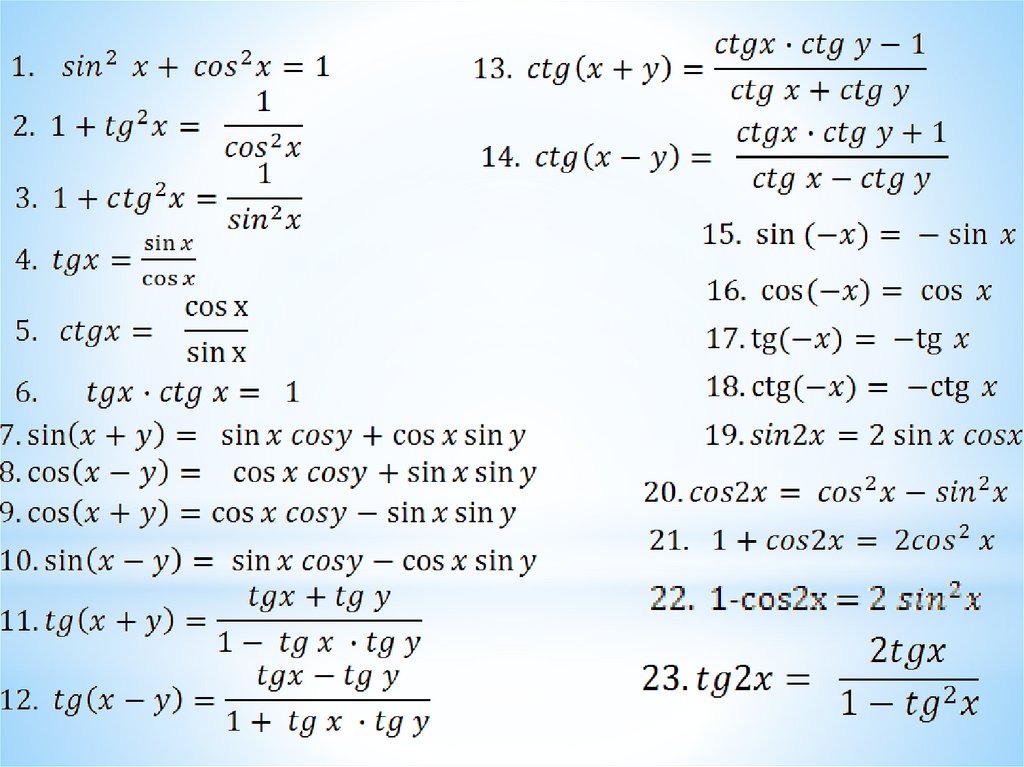 Эти расчеты необходимы в повседневной жизни, независимо от того, нужно ли выяснить, сколько жидкости необходимо для заполнения контейнера, или нужно рассчитать площадь поверхности любого объекта. Математические формулы класса 10 относительно того же можно найти, как показано ниже:
Эти расчеты необходимы в повседневной жизни, независимо от того, нужно ли выяснить, сколько жидкости необходимо для заполнения контейнера, или нужно рассчитать площадь поверхности любого объекта. Математические формулы класса 10 относительно того же можно найти, как показано ниже: Они имеют большое значение в нашей жизни. Математические формулы класса 10 применяются в различных расчетах для определения нескольких значений. Ниже приведены некоторые из распространенных применений математических формул класса 10.
Они имеют большое значение в нашей жизни. Математические формулы класса 10 применяются в различных расчетах для определения нескольких значений. Ниже приведены некоторые из распространенных применений математических формул класса 10. д.
д.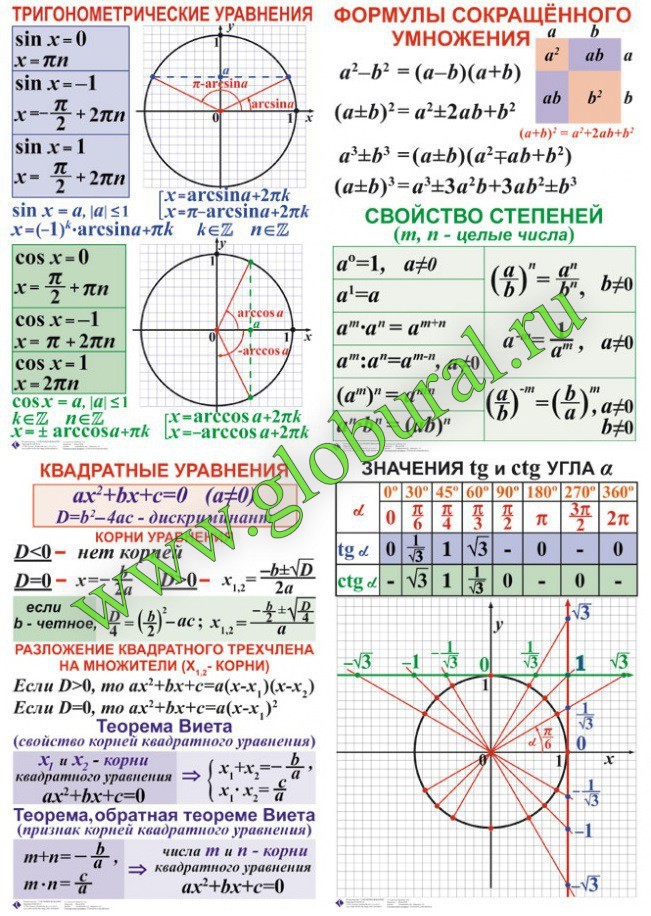
 Математика?
Математика? Запоминание основных формул действительных чисел 10 класса поможет учащимся понять различные понятия, связанные с натуральными числами, целыми числами и действительными числами и т. д. Формулы многочленов помогают находить корни уравнений. В геометрии важно, чтобы учащиеся запомнили основные формулы, относящиеся к площади и объему различных трехмерных форм и объектов, таких как сферы, конусы, призмы и т. д.
Запоминание основных формул действительных чисел 10 класса поможет учащимся понять различные понятия, связанные с натуральными числами, целыми числами и действительными числами и т. д. Формулы многочленов помогают находить корни уравнений. В геометрии важно, чтобы учащиеся запомнили основные формулы, относящиеся к площади и объему различных трехмерных форм и объектов, таких как сферы, конусы, призмы и т. д.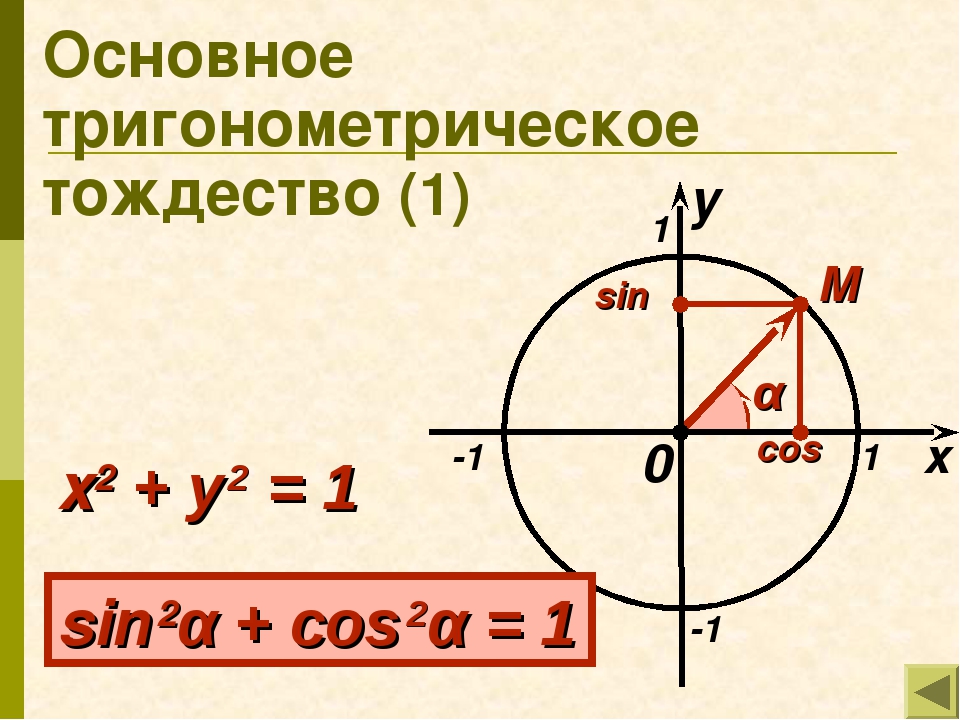 и объем, статистика, вероятность.
и объем, статистика, вероятность.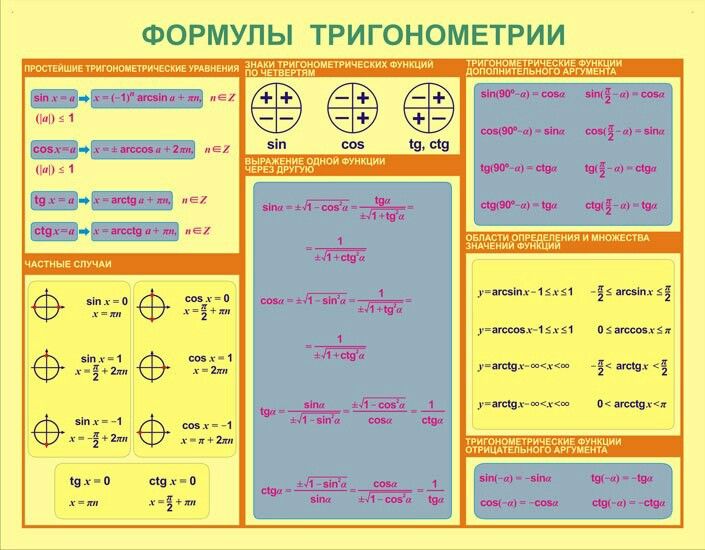 .
. Таким образом, проблема становится 9 в степени 1/2. В знаменателе 2, поэтому извлекаем квадратный корень из 9.что равно 3. Числитель равен 1, поэтому мы возводим 3 в 1-ю степень, и ответ равен 3.
Таким образом, проблема становится 9 в степени 1/2. В знаменателе 2, поэтому извлекаем квадратный корень из 9.что равно 3. Числитель равен 1, поэтому мы возводим 3 в 1-ю степень, и ответ равен 3. использовал. Таким образом, ответ представляет собой квадратный корень из x, записанный как √x.
использовал. Таким образом, ответ представляет собой квадратный корень из x, записанный как √x.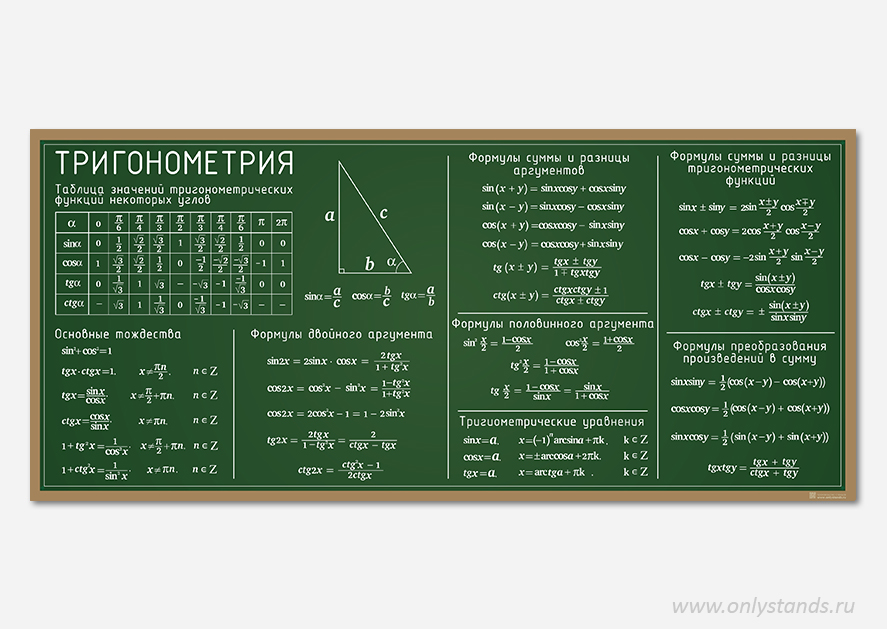
 APR.B.2
APR.B.2
 Чтобы получить график g(x), сдвинув график f(x), вы должны сдвинуть f(x) вниз на 7 единиц, чтобы измениться с +2 на -5.
Чтобы получить график g(x), сдвинув график f(x), вы должны сдвинуть f(x) вниз на 7 единиц, чтобы измениться с +2 на -5. Длина смежной стороны — это значение x в точке на единичной окружности. Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение отношения косинуса любого угла в единичной окружности — это значение x точки на единичной окружности, соответствующей этому углу. Тригонометрическое отношение тангенса равно длине противолежащей стороны, деленной на длину прилежащей стороны. Длина противоположной стороны — это значение y в точке единичной окружности, а длина соседней стороны — это значение x в точке единичной окружности. Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение отношения тангенсов любого угла в единичной окружности — это отношение yx от точки на единичной окружности, соответствующей этому углу. В этом вопросе тангенс(5π/4)=1. Это отношение берется из точки (−2/√2, −2/√2), которая соответствует углу величиной 5π/4 радиана. Таким образом, используя приведенную выше информацию, значение cos(5π4) совпадает со значением x в точке (−2/√2, −2/√2).
Длина смежной стороны — это значение x в точке на единичной окружности. Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение отношения косинуса любого угла в единичной окружности — это значение x точки на единичной окружности, соответствующей этому углу. Тригонометрическое отношение тангенса равно длине противолежащей стороны, деленной на длину прилежащей стороны. Длина противоположной стороны — это значение y в точке единичной окружности, а длина соседней стороны — это значение x в точке единичной окружности. Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение отношения тангенсов любого угла в единичной окружности — это отношение yx от точки на единичной окружности, соответствующей этому углу. В этом вопросе тангенс(5π/4)=1. Это отношение берется из точки (−2/√2, −2/√2), которая соответствует углу величиной 5π/4 радиана. Таким образом, используя приведенную выше информацию, значение cos(5π4) совпадает со значением x в точке (−2/√2, −2/√2).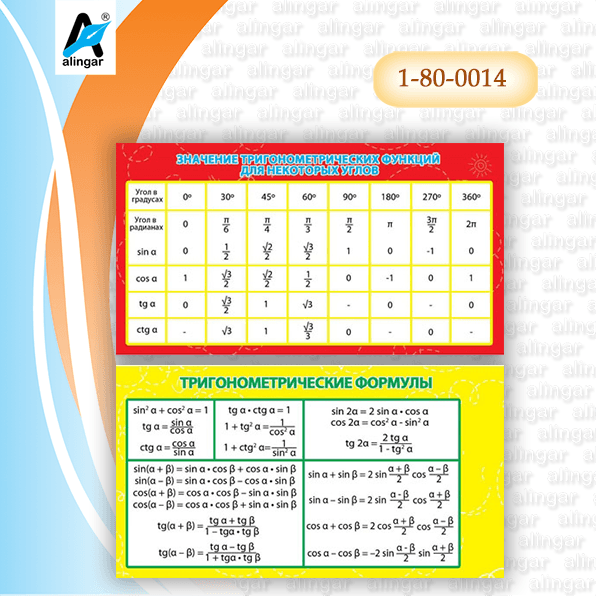 Следовательно, значение cos(5π/4) =-2/√2.
Следовательно, значение cos(5π/4) =-2/√2. Поскольку они находятся в соответствующих местах с поперечной (AX), правильный ответ — A
Поскольку они находятся в соответствующих местах с поперечной (AX), правильный ответ — A В качестве преобразования это расширение записывается как (x, y) → 1/4 (x, y). Соединяя перевод и расширение вместе, правило (x, y) → 1/4 (x, y + 10).
В качестве преобразования это расширение записывается как (x, y) → 1/4 (x, y). Соединяя перевод и расширение вместе, правило (x, y) → 1/4 (x, y + 10). Найдите значение на числовой прямой, прибавив 6 к позиции точки E. −7 +6=-1. Значение на числовой прямой, которая делит отрезок EF в отношении 3:1, равно -1.
Найдите значение на числовой прямой, прибавив 6 к позиции точки E. −7 +6=-1. Значение на числовой прямой, которая делит отрезок EF в отношении 3:1, равно -1. Окружность пресс-папье 9π см. Если коробка соответствует сфере точно так, что стороны сферы касаются коробки, каков объем наименьшей коробки, которую компания может использовать для доставки?
Окружность пресс-папье 9π см. Если коробка соответствует сфере точно так, что стороны сферы касаются коробки, каков объем наименьшей коробки, которую компания может использовать для доставки?