Продукт | RICOH THETA Z1
Концепция
360° качества.
Флагманская модель серии THETA с высочайшим качеством изображения.
Возможности
Простота использования и великолепная работа.
Естественные панорамные снимки с разрешением примерно 23 мегапикселей(6720 × 3360,7K) и исключительноточная сшивка.
Прекрасное шумоподавление даже при съемке ночью или в плохо освещенном помещении благодаря 1,0-дюймовомуКМОП-датчику изображений с задней подсветкой.
Новый объектив избавляет от посторонних изображений, бликов и «бахромы». Механизм диафрагмы улучшает воспринимаемое разрешение и снижает количество «выбитых» светлых точек.
Поддержка различных сценариев съемки благодаря множеству режимов.
Невероятно реалистичные сферические видео при съемке с разрешением 4K (3840 × 1920, 29,97 кадров/с).
Первая модель в серии, которая позволяет делать снимки в формате RAW (DNG). (Одновременно их можносохранять в формате JPEG.
)
Прямая потоковая передача панорамного видео с разрешением 4K. Транслируйте великолепные реалистичныевидеозаписи на весь мир.
Четырехканальный микрофон. Во время съемки видео четыре встроенных независимых микрофона записывают звукпо четырем разным направлениями.
Конструкция
Чтобы все могли наслаждаться панорамной съемкой.
Корпус камеры изготовлен из прочного и приятного на ощупь магниевого сплава.
Несмотря на большой размер датчика изображений, внутренняя конструкция оптимизирована таким образом, что камера имеет очень компактный размер и при этом обеспечивает высокую скорость и качество изображений.
Кроме того, камера оборудована экраном, на котором отображается различная информация: уровень заряда аккумулятора, количество оставшихся кадров, режим съемки и пр.
Творчество
Создавайте собственные изображения, используя функции редактирования.
Панорамные снимки с камеры можно редактировать в Adobe Photoshop Lightroom Classic CC.
Импортируйте дваизображения с помощью специального плагина RICOH THETA Stitcher.
Запись видео с разрешением 4K и пространственного звука для более реалистичного виртуального мира.
Специальные приложения THETA+ и THETA+ Video для окончательной обработки отснятых материалов.
Обмен
Делитесь своими работами с людьми по всему миру с помощью специальных приложений.
Загрузка снимков на theta360.com, специальный сайт для обмена панорамными изображениями. Показывайте своиснимки миру, где бы вы ни находились.
Удобные специальные приложения для компьютера и смартфона. Исследуйте мир с RICOH THETA.
Facebook и LINE — загрузка панорамных фотографий без предварительной подготовки. Легко делитесь панорамными снимками с друзьями.
Публикуйте фотографии и видео, обработанные в THETA+, в Instagram и Twitter.
Используйте ссылки на различные облачные службы и решения, использующие панорамные снимки, например на сервисы виртуальных туров.
Дополнительные возможности
Ваша камера THETA может больше.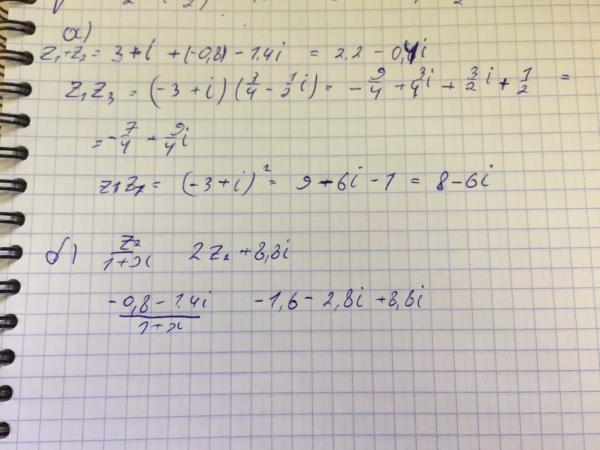
В качестве базовой системы для новой ОС используется Android™. Плагины для дополнительных возможностей камеры THETA.
Компании и пользователи со всего мира могут разрабатывать собственные плагины в дополнение к плагинам Ricoh.
Для продаваемых в Японии «RICOH THETA Z1 51GB» действуют следующие ограничения.
• Использование некоторых плагинов, которые работают в клиентском режиме
• Разработка плагинов
Технические данные
RICOH THETA Z1 51GB / RICOH THETA Z1
- Дата выпуска
RICOH THETA Z1 51GB：-
RICOH THETA Z1：5/2019 - Внешние/внутренние габариты 48 мм (Ш) × 132,5 мм (В) × 29,7 мм（24mm *9）(Г)
- Масса Около 182 г
- Разрешение фотографий 6720×3360
- Разрешение видео/частота кадров/скорость передачи в битах
4K 3840 × 1920/29,97 кадров/с/56 Мбит/с
2K 1920 × 960/29,97 кадров/с/16 Мбит/с - Разрешение потоковой передачи/частота кадров (USB)
4K, h364: 3840 ×1920/29,97 кадров/с/120 Мбит/с
2K, h364: 1920 ×960/29,97 кадров/с/42 Мбит/с - Микрофон 4-канальный
- Внутренняя память/сколько фотографий можно записать, время*2】
RICOH THETA Z1 51GB：
Внутренняя память объемом около 51 ГБ
Фотографии: RAW+ около 900, JPEG около 6350
видео (время одной записи): макс.
5 минут/25 минут *3 *4
Видео (общее время записи): (4K, H.264) около 110 минут
(2K, H.264) около 360 минутRICOH THETA Z1：
Внутренняя память объемом около 19 ГБ
Фотографии: RAW+ около 350, JPEG около 2400
видео (время одной записи): макс. 5 минут/25 минут *3 *4
Видео (общее время записи): (4K, H.264) около 40 минут
(2K, H.264) около 130 минут - Совместимые аксессуары Штатив/подставка (имеется отверстие для штатива)
- В комплекте Мягкий футляр и кабель USB
- Расстояние до объекта Около 40 см — ∞ (от переднего края объектива)
- Режим съемки
Фотографии/видео: автоматический, приоритет диафрагмы, приоритет выдержки,приоритет чувствительности ISO, ручной *3
Потоковая передача: автоматический - Метод контроля экспозиции Программный режим, приоритет диафрагмы, приоритет выдержки, приоритет чувствительности ISO, ручная экспозиция
- Компенсация экспозиции Фотографии/видео: вручную (от -2,0 до +2,0 EV с шагом 1/3 EV) *3
- Чувствительность ISO (стандартная выходная чувствительность)
Фотографии/видео: (автоматический режим) ISO 80–6400
(верхний предел регулируется) ISO 200–6400
(ручной режим) ISO 80–6400 *3
Потоковая передача: ISO 80–6400 - Режим баланса белого
Фотографии/видео: авто, на улице, в тени, облачность, лампы накаливания 1, лампы накаливания 2,
флуоресцентные лампы дневного света, флуоресцентные лампы естественного белого цвета, флуоресцентные лампы
белого цвета, флуоресцентные лампы под электрическое освещение, настройка цветовой температуры (от 2500 до10 000 K) *3
Потоковая передача: автоматический - Выдержка
Фотографии: (автоматический режим) 1/25 000–1/8 секунды,
(режим приоритета выдержки) 1/25 000–15 секунды *1
(ручной режим) 1/25 000–60 секунд *1
Видео: (автоматический режим) 1/25 000–1/30 секунды
(режим приоритета выдержки, ручной режим) 1/25 000–1/30 секунды *3
Потоковая передача: (автоматический режим) 1/25 000–1/30 секунды - Функции съемки
Фотографии: шумоподавление, компенсация динамического диапазона, расширенный динамический диапазон, Ручной HDR ,интервальная съемка, интервальная составная съемка, брекетинг, съемка с автоспуском(2–10 секунд), Мои настройки
Видео: съемка с автоспуском (2–10 секунд), Мои настройки - Источник питания
Литийионный аккумулятор (встроенный)
- Срок службы аккумулятора без подзарядки
Фотографии: около 300 *8
Видео: около 60 минут *8 - [Формат файла]
Фотографии: RAW (DNG) *2, JPEG (Exif версии 2. 3)
Видео: MP4 (видео: MPEG-4 AVC/H.264, аудио: AAC-LC (моно) + линейная импульсно-кодовая модуляция(4-канальный пространственный звук)
Потоковая передача: видео: H.264, аудио: линейная импульсно-кодовая модуляция (4 канала) - Внешний интерфейс USB Type-C: USB 3.0
- Удаленный спуск затвора Совместимый с CA-3
- Конфигурация объектива 14 элементов в 10 группах
- Светосила объектива F2.1, 3.5, 5.6
- Размер датчика изображений 1-дюймовый (x2)
- Эффективные пиксели Около 20 мегапикселей (x2)
- Пиксели на выходе Около 23 мегапикселей
- Соответствие стандартам беспроводной связи
IEEE802.11 a/b/g/n/ac (2,4 ГГц и 5 ГГц) *5
IEEE802. 11 b/g/n (только 2,4 ГГц)
Bluetooth 4.2 - Поддержка беспроводных каналов
2,4 ГГц: каналы с 1 по 11 или с 1 по 13 *6
5 ГГц: W52 (каналы с 36 по 48, поддерживается полоса пропускания канала 20, 40 и 80 МГц) *5 - Протокол беспроводной связи (WLAN) HTTP (совместим с Open Spherical Camera API версии 2)
- Протокол беспроводной связи (Bluetooth) GATT (Generic Attribute Profile)
- Диапазон температур для эксплуатации От 0 до 40 °C
- Диапазон влажности для эксплуатации Не более 90 %
- Диапазон температур для хранения От -20 до 60 °C
5 минут/25 минут *3 *4 
3) 
11 b/g/n (только 2,4 ГГц) *1 Количество изображений и время записи ориентировочное, только для информации. Фактические цифры зависят от условий съемки.
*2 Только для одновременной записи фотографий в форматах RAW и JPEG.
*3 Для переключения режимов и выполнения ручных настроек необходим смартфон.
*4 При повышении внутренней температуры запись останавливается автоматически.
*5 RICOH THETA Z1 ДРУГИЕ СТРАНЫ (L85612/КОД EDP: 910776 /КОД RIM: S0910776/КОД JAN: 4961311935442/КОД UPC:026649107771) не поддерживает 5 ГГц.
*7 Для зарядки подключите камеру к компьютеру с помощью кабеля USB из комплекта поставки.
*8 Возможное количество изображений рассчитано по методу компании RICOH. Фактическое количество зависит от условий использования.
*9 Без учета объектива.
■Характеристики и конструкция могут меняться без предварительного уведомления.
■Характеристики являются актуальными на февраль 2019 года.
Главная страница
Направляющий вектор прямой, координаты направляющего вектора прямой, сколько направляющих векторов существует к любой прямой
С понятием прямой линии тесно связано понятие ее направляющего вектора.
Часто в задачах бывает удобнее рассматривать его вместо самой прямой. В рамках данного материала мы разберем, что же такое направляющий вектор прямой в пространстве и на плоскости, и расскажем, для чего можно его использовать.
В первом пункте мы сформулируем определение и покажем основные понятия на иллюстрациях, дополнив их конкретными примерами направляющего вектора. Далее мы посмотрим, как прямая и направляющие векторы взаимодействуют в прямоугольной системе координат и как можно вычислить координаты этого вектора, если мы знаем уравнение прямой. Все правила, как всегда, будут проиллюстрированы примерами решений задач.
Что такое направляющий вектор прямой
Для того чтобы понять эту тему, нам нужно хорошо представлять, что такое вообще прямая и как она может размещаться в пространстве и на плоскости. Кроме того, важно вспомнить ранее изученное понятие вектора. Об этом мы уже писали в отдельном материале. Если нужно, найдите и перечитайте эти статьи.
Сформулируем, что такое направляющий вектор.
Направляющим вектором прямой является любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.
Получается, что у каждой прямой есть бесконечное множество направляющих векторов. При этом все они будут являться коллинеарными в силу озвученного определения, ведь они лежат на одной прямой или параллельной ей другой прямой. Выходит, что если a→ является направляющий вектором прямой a, то другой направляющий вектор мы можем обозначить как t·a→ при любом значении t, соответствующем действительному числу.
Также из определения выше можно сделать вывод, что направляющие векторы двух параллельных прямых будут совпадать: если прямые a и a1 являются параллельными, то вектор a→ будет направляющим и для a, и для a1.
Третий вывод, следующий из определения: если у нас есть направляющий вектор прямой a, то он будет перпендикулярным по отношению к любому нормальному вектору той же прямой.
Приведем пример направляющего вектора: в прямоугольной системе координат для осей Ox, Oy и Oz направляющими будут координатные векторы i→, j→ и k→.
Как вычислить координаты направляющего вектора по уравнениям прямой
Допустим, что у нас есть некая прямая с направляющими векторами, лежащая в прямоугольной системе координат. Сначала мы разберем случай с плоской декартовой системой Oxy, а потом с системой Oxyz, расположенной в трехмерном пространстве.
1. Прямую линию в Oxy можно описать с помощью уравнения прямой на плоскости. В этом случае координаты направляющих векторов будут соответствовать направляющим векторам исходной прямой. А если нам известно уравнение прямой, как вычислить координаты ее направляющего вектора? Это легко сделать, если мы имеем дело с каноническим или параметрическим уравнением.
Допустим, у нас есть канонический случай уравнения, которое имеет вид x-x1ax=y-y1ay. С его помощью на плоскости задана прямая с направляющим вектором a→=(ax, ay).
Чтобы вычислить координаты направляющего вектора, нам нужно взять числа из знаменателя канонического уравнения прямой.
Приведем пример задачи.
В прямоугольной системе координат задана прямая, которую можно описать уравнением x-14=y+12-3. Вычислите координаты одного из направляющих векторов прямой.
Решение
Из уравнения мы можем сразу взять координаты направляющего вектора. Берем числа в знаменателях и записываем: 4, -3. Это и будет нужный нам ответ.
Ответ: 4, -3.
Если же прямая описана уравнением параметрического типа, то нам нужно смотреть на коэффициенты при параметре. Они будут соответствовать координатам нужного нам направляющего вектора.
Пример 2У нас есть прямая, которую можно описать с помощью системы параметрических уравнений x=-1y=7-5·λ, при этом λ∈R. Найдите координаты направляющих векторов.
Решение
Для начала перепишем данные параметрические уравнения в виде x=-1+0·λy=7-5·λ. Посмотрим на коэффициенты. Они сообщат нам нужные координаты направляющего вектора – a→=(0, 5). Учитывая, что все направляющие векторы одной прямой будут коллинеарны, мы можем задать их в виде t·a→ или 0, -5·t, где t может быть любым действительным числом.
О том, как проводить действия с векторами в координатах, мы писали в отдельной статье.
Ответ: 0, -5·t, t∈R, t≠0
Теперь разберем случай, как найти координаты вектора, если прямая задана общим уравнением вида Ax+By+C=0. Если A=0, то исходное уравнение можно переписать как By+C=0. Оно определяет прямую, которая будет параллельна оси абсцисс. Значит, в качестве ее направляющего вектора мы можем взять координатный вектор i→=1, 0.
А если B=0, то уравнение прямой мы можем записать как Ax+C=0. Описываемая им прямая будет параллельна оси ординат, поэтому ее координатный вектор j→=0, 1 также будет направляющим. Рассмотрим конкретную задачу.
Пример 3У нас есть прямая, заданная при помощи общего уравнения x-2=0. Найдите координаты любого направляющего вектора.
Решение
В прямоугольной системе координат исходное уравнение будет соответствовать прямой, параллельной оси ординат. Значит, мы можем взять координатный вектор j→=(0, 1).
Он будет для нее направляющим.
Ответ: (0, 1)
А как быть в случае, если ни один коэффициент в Ax+By+C=0 не будет равен 0? Тогда мы можем использовать несколько разных способов.
1. Мы можем переписать основное уравнение так, чтобы оно превратилось в каноническое. Тогда координаты вектора можно будет взять из его значений.
2. Можно вычислить отдельно начальную и конечную точку направляющего вектора. Для этого надо будет взять координаты двух любых несовпадающих точек исходной прямой.
3. Третий способ заключается в вычислении координат любого вектора, который будет перпендикулярен нормальному вектору этой прямой n→=A, B.
Самым простым является первый подход. Проиллюстрируем его на примере задачи.
Пример 4Есть прямая на плоскости, заданная уравнением 3x+2y-10=0. Запишите координаты любого направляющего вектора.
Решение
Перепишем исходное уравнение в каноническом виде. Сначала перенесем все слагаемые из левой части, кроме 3x, в правую с противоположным знаком.
У нас получится:
3x+2y-10=0⇔3x=-2y+10
Получившееся равенство преобразовываем и получаем:
3x=-2y+10⇔3x=-2(y-5)⇔x-2=y-53
Отсюда мы уже можем вывести координаты нужного нам направляющего вектора: -2, 3
Ответ: -2, 3
К общему виду легко свести и такие типы уравнений, как уравнение прямой в отрезках xa+yb=1 и уравнение прямой с угловым коэффициентом y=k·x+b, так что если они встретились вам в задаче на нахождение координат направляющего вектора, то можно также использовать этот подход.
Далее мы разберем, как найти эти координаты, если прямая у нас задана не в плоскости, а в пространстве.
Определение 2Вектор a→=(ax, ay, az) является направляющим для прямой, выраженной с помощью:
1) канонического уравнения прямой в пространстве x-x1ax=y-y1ay=z-z1az
2) параметрического уравнения прямой в пространстве x-x1ax=y-y1ay=z-z1az
Таким образом, для вычисления координат направляющего вектора нужно взять числа из знаменателей или коэффициентов при параметре в соответствующем уравнении.
Рассмотрим конкретную задачу.
Пример 5Прямая в пространстве задана уравнением вида x-14=y+120=z-3. Укажите, какие координаты будет иметь направляющий вектор данной прямой.
Решение
В каноническом уравнении необходимые числа видны сразу в знаменателях. Получается, что ответом будет вектор с координатами 4, 0, -3. Координаты всех направляющих векторов данной прямой можно записать в виде 4·t, 0, -3·t при условии, что t является действительным числом.
Ответ: 4·t, 0, -3·t, t∈R, t≠0
Пример 6Вычислите координаты любого направляющего вектора для прямой, которая задана в пространстве с помощью параметрического уравнения x=2y=1+2·λz=-4-λ.
Решение
Перепишем данные уравнения в виде x=2+0·λy=1+2·λz=-4-1·λ.
Из этой записи можно вычленить координаты нужного нам вектора – ими будут коэффициенты перед параметром.
Ответ: 0, 2, -1
Разберем еще один случай. Как вычислить нужные координаты, если прямая задана уравнением двух пересекающихся плоскостей вида A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0?
Есть два способа.
Можно записать это уравнение в параметрическом виде, где будут видны нужные координаты. Но можно использовать и другой способ. Объясним его.
Вспомним, что такой нормальный вектор плоскости. Он по определению будет лежать на прямой, перпендикулярной исходной плоскости. Значит, любой направляющий вектор прямой, которая в ней находится, будет перпендикулярен ее любому нормальному вектору.
Направляющий вектор прямой, образованной пересечением двух плоскостей A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0, будет перпендикулярен нормальным векторам n1→=(A1, B1, C1) и n2→=(A2, B2, C2). То есть в качестве направляющего вектора мы может взять произведение векторов n1→=(A1, B1, C1) и n2→=(A2, B2, C2).
n1→×n2→=i→j→k→A1B1C1A2B2C2 — это и есть направляющий вектор прямой, по которой пересекаются исходные плоскости.
Решим задачу, в которой применяется этот подход.
Пример 7Запишите координаты направляющего вектора прямой, выраженной с помощью уравнения x+2y+3z-1=02x+4y-4z+5=0.
Решение
Возьмем произведение двух нормальных векторов плоскостей x+2y+3z-1=0 и 2x+4y-4z+5=0.
У них следующие координаты: 1, 2, 3 и 2, 4, -4.
У нас получится:
n1→×n2→=i→j→k→12324-4=i→·2·(-4)+j→·3·2+k→·1·4—k→·2·2-i→·3·4-j→·1·(-4)=-20·i→+10·j→+0·k→
Выходит, что вектор n1→×n2→=-20·i→+10·j→+0·k→⇔n1→×n2→=-20, 10, 0 – это и есть нужный нам направляющий вектор прямой.
Ответ: -20, 10, 0
В конце статьи отметим, что умение вычислять направляющий вектор пригодится для решения многих задач, таких, как сопоставление двух прямых, доказательство их параллельности и перпендикулярности, вычисление угла между пересекающимися или скрещивающимися прямыми и др.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Шаг за шагом Решение:
Шаг 1:
1.1 Оценка: (Z -1) 4 = Z 4 -4Z 3 +6Z 2 -4Z + 1
Шаг 2:
Вытягивание, как Условия:
2.1. Вытягивая, как факторы:
Z 4 — 4Z 3 + 6Z 2 — 4Z =
Z • (Z 3 — — 4z 2 + 6z — 4)
Проверка идеального куба:
2.2 Z 3 — 4Z 2 + 6Z — 4 не является идеальным кубом
, пытаясь избавиться от вытяжения:
2,3 Факторинг: Z 3 — 4Z 2 + 6Z — 4
4 — 4Z 2 + 6Z — 4 9005
44 Вдумчиво разбейте имеющееся выражение на группы, в каждой группе по два члена:
Группа 1: 6z — 4
Группа 2: -4z 2 + z 3
Вытащить из каждой группы отдельно:
Группа 1 : (3z — 2) • (2)
Группа 2: (z — 4) • (z 2 )
Плохие новости !! Разложение на множители путем вытягивания не удается:
Группы не имеют общего множителя и не могут быть сложены для образования умножения.
Калькулятор корней полиномов :
2.4 Найти корни (нули) из : F(z) = z 3 — 4z 2 + 6z — 4
Калькулятор корней полиномов представляет собой набор методов, предназначенных для z поиска значений который F(z)=0
Rational Roots Test является одним из вышеупомянутых инструментов. Он найдет только рациональные корни, то есть числа z , которые можно выразить как частное двух целых чисел 9.0005
Теорема о рациональном корне утверждает, что если многочлен равен нулю для рационального числа P/Q , то P является множителем замыкающей константы, а Q – множителем старшего коэффициента
В этом случае старший коэффициент равен 1, а Константа трейлинга: -4.
Коэффициент(ы):
ведущего коэффициента: 1
константы замыкания: 1 ,2 ,4
Проверим….0105
00
The Factor Theorem states that if P/Q является корнем многочлена, то этот многочлен можно разделить на q*x-p.
Обратите внимание, что q и p происходят из P/Q, сведенного к наименьшим членам
В нашем случае это означает, что
z 3 — 4Z 2 + 6Z — 4
можно разделить с z — 2
Длинное отделение полинома:
2,5 Полиномиальное длинное разделение
Разделитие: Z 3 — 4Z 2 + 6Z — 4
( «Dividend»)
By : z — 2 («Divisor»)
| dividend | z 3 | — | 4z 2 | + | 6z | — | 4 | ||
| — divisor | * z 2 | z 3 | — | 2z 2 | |||||
| remainder | — | 2z 2 | + | 6z | — | 4 | |||
| — divisor | * -2z 1 | — | 2z 2 | + | 4z | ||||
| remainder | 2z | — | 4 | ||||||
| — divisor | * 2z 0 | 2z | — | 4 | |||||
| remainder | 0 |
Quotient : z 2 -2z+2 Remainder: 0
Trying to factor by разбивая средний член
2.
6 Разложение на множители z 2 -2z+2
Первый член z 2 его коэффициент равен 1 .
Средний член равен -2z, его коэффициент равен -2.
Последний член, «константа», равен +2
Шаг 1: умножьте коэффициент первого члена на константу 1 • 2 = 2
Шаг 2: найдите два множителя 2, сумма которых равна коэффициенту среднего члена, который равен -2 .
| -2 | + | -1 | = | -3 | ||
| -1 | + | -2 | = | -3 | ||
| 1 | + | 2 | = | 3 | ||
| 2 | + | 1 | = | 3 |
Наблюдение : Невозможно найти два таких фактора !!
Заключение: Трехчлен нельзя разложить на множители
Уравнение в конце шага 2 :
z • (z 2 - 2z + 2) • (z - 2) = 0
Шаг 3 :
Теория – корни произведения:
3.
1 Произведение нескольких членов равно нулю.
Если произведение двух или более слагаемых равно нулю, то хотя бы одно из слагаемых должно быть равно нулю.
Теперь мы будем решать каждый термин = 0 отдельно
Другими словами, мы собираемся решить столько уравнений, сколько членов в произведении
Любое решение термина = 0 также решает произведение = 0.
Решение уравнения с одной переменной:
3,2 Решение: z = 0
Решение -z = 0
Парабола, обнаружение вершины:
3,3 Найдите вершину y = z 2 -2Z+2
Параболы имеют самую высокую или наиболее низкую точку. называется Вершина. Наша парабола раскрывается и, соответственно, имеет низшую точку (абсолютный минимум). Мы знаем это еще до того, как начертили «у», потому что коэффициент первого члена, 1 , положителен (больше нуля).
Каждая парабола имеет вертикальную линию симметрии, проходящую через ее вершину. Из-за этой симметрии линия симметрии, например, будет проходить через середину двух точек пересечения x (корней или решений) параболы.
То есть, если парабола действительно имеет два действительных решения.
Параболы могут моделировать многие реальные жизненные ситуации, такие как высота над землей объекта, брошенного вверх через некоторый период времени. Вершина параболы может предоставить нам такую информацию, как максимальная высота, на которую может подняться объект, брошенный вверх. По этой причине мы хотим иметь возможность найти координаты вершины.
Для любой параболы, Az 2 +Bz+C, z -координата вершины определяется как -B/(2A) . В нашем случае координата z равна 1,0000
Подключение к формуле Parabola 1.0000 для z Мы можем рассчитать y-координату:
Y = 1,0 * 1,00 * 1,00-2,0 * 1,00 + 2,0
или Y = 1.000
Parabola, график вертекс и x-intercepts:
Корневой график для : y = z 2 -2z+2
Ось симметрии (штриховая) {z}={ 1,00}
Вершина в {z,y} = { 1,00, 1,00}
Функция не имеет действительных корней
Решите квадратное уравнение, заполнив квадрат
3.
4 Решение z 2 -2z+2 = 0, заполнив квадрат .
Вычтите 2 из обеих частей уравнения:
z 2 -2z = -2
Теперь немного хитрости: возьмите коэффициент z, равный 2, разделите на два, получите 1, и, наконец, возведите его в квадрат, получив 1
Добавьте 1 к обеим частям уравнения:
В правой части имеем:
-2 + 1 или (-2/1)+(1/1)
Общий знаменатель двух дробей равен 1 Добавление (-2/1)+(1/1) дает -1/1
Таким образом, прибавив к обеим сторонам, мы окончательно получим :
z 2 -2z+1 = -1
Добавление 1 дополнит левую часть до полного квадрата:
z 2 -2z+1 =
(z -1) • (z-1) =
(z-1) 2
Вещи, равные одной и той же вещи, равны и друг другу. Так как
z 2 -2z+1 = -1 и
z 2 -2z+1 = (z-1) 2
, то по закону транзитивности
(z-1) 2 = -1
Мы будем называть это уравнение уравнением #3.
4.1
Принцип квадратного корня гласит, что когда две вещи равны, их квадратные корни равны.
Обратите внимание, что квадратный корень из
(z-1) 2 равен
(z-1) 2/2 =
(z-1) 1 =
90 0 z-4, применяя Принцип квадратного корня в уравнении #3.4.1 мы получаем:
z-1 = √ -1
Добавьте 1 к обеим частям, чтобы получить:
z = 1 + √ -1
В математике i называется мнимой единицей. Это удовлетворяет i 2 =-1. И i , и -i являются квадратными корнями из -1
Поскольку квадратный корень имеет два значения, одно положительное, а другое отрицательное,
z 2 — 2z + 2 = 0
имеет два решения:
z = 1 + √ 1 • i
или
z = 1 — √ 1 • i
Решить квадратное уравнение, используя квадратную формулу
3.5 Решение z 2 -2z+2 = , используя квадратную формулу.
Согласно квадратичной формуле, z , решение для Az 2 +BZ +C = 0, где A, B и C цифры, часто называемые коэффициентами, определяются:
-B ± √ B 2 -4AC
z = ———— ——
2A
В нашем случае A = 1
B = -2
C = 2
Соответственно, B 2 -4AC =
4 -8 =
-4
Применение формулы квадрата:
2 ± √ -4
z = —————
2
В множестве действительных чисел отрицательные корни не имеют квадратных корней.
Был изобретен новый набор чисел, называемый комплексным, чтобы отрицательные числа имели квадратный корень. Эти цифры написаны (a+b*i)
И I, и -i-квадратные корни минус 1
Соответственно, √ -4 =
√ 4 • (-1) =
√ 4 • √ -1 =
± √ 4 • i
Можно ли упростить √ 4 ?
Да! Первичная факторизация 4 это
2•2
Чтобы иметь возможность удалить что-то из-под корня, должно быть 2 экземпляра этого (потому что мы берем квадрат, то есть второй корень).
√ 4 = √ 2 • 2 =
± 2 • √ 1 =
± 2
, так что теперь мы смотрим на:
z = (2 ± 2i)/2
0041
z = (2+√-4)/2=1+i= 1,0000+1,0000i или:
z = (2-√-4)/2=1-i= 1,0000-1,0000i
Решение единого переменного уравнения:
3,6 Решение: Z-2 = 0
Добавить 2 к обеим сторонам уравнения:
z = 2
. z =(2-√-4)/2=1-i= 1,0000-1,0000i
| 1 | Найдите том | сфера (5) | | |
| 2 | Найдите площадь | круг (5) | | |
| 3 | Найдите площадь поверхности | сфера (5) | | |
| 4 | Найдите площадь | круг (7) | | |
| 5 | Найдите площадь | круг (2) | | |
| 6 | Найдите площадь | круг (4) | | |
| 7 | Найти площадь | круг (6) | | |
| 8 | Найдите том | сфера (4) | | |
| 9 | Найдите площадь | круг (3) | | |
| 10 | Оценить | 9(1/2)|||
| 11 | Найти простую факторизацию | 741 | ||
| 12 | Найдите том | сфера (3) | | |
| 13 | Оценить | 3 квадратный корень из 8*3 квадратный корень из 10 | ||
| 14 | Найдите площадь | круг (10) | | |
| 15 | Найдите площадь | круг (8) | | |
| 16 | Найдите площадь поверхности | сфера (6) | | |
| 17 | Найти простую факторизацию | 1162 | ||
| 18 | Найдите площадь | круг (1) | | |
| 19 | Найдите окружность | круг (5) | | |
| 20 | Найдите том | сфера (2) | | |
| 21 | Найдите том | сфера (6) | | |
| 22 | Найдите площадь поверхности | сфера (4) | | |
| 23 | Найдите том | сфера (7) | | |
| 24 | Оценить | квадратный корень из -121 | ||
| 25 | Найти простую факторизацию | 513 | ||
| 26 | Оценить | квадратный корень из 3/16* квадратный корень из 3/9 | ||
| 27 | Найдите том | коробка (2)(2)(2) | | |
| 28 | Найдите окружность | круг (6) | | |
| 29 | Найдите окружность | круг (3) | | |
| 30 | Найдите площадь поверхности | сфера (2) | | |
| 31 | Оценить | 2 1/2÷22000000 | ||
| 32 | Найди том | коробка (5)(5)(5) | | |
| 33 | Найдите том | коробка (10)(10)(10) | | |
| 34 | Найдите окружность | круг (4) | | |
| 35 | Преобразование в проценты | 1,7 | ||
| 36 | Оценить | (5/6)÷(4/1) | ||
| 37 | Оценить | 3/5+3/5 | ||
| 38 | Оценить | ф(-2) | 92 | |
| 40 | Найдите площадь | круг (12) | | |
| 41 | Найдите том | коробка (3)(3)(3) | | |
| 42 | Найдите том | коробка (4)(4)(4) | 92-4*-1+2||
| 45 | Найти простую факторизацию | 228 | ||
| 46 | Оценить | 0+0 | ||
| 47 | Найдите площадь | круг (9) | | |
| 48 | Найдите окружность | круг (8) | | |
| 49 | Найдите окружность | круг (7) | | |
| 50 | Найдите том | сфера (10) | | |
| 51 | Найдите площадь поверхности | сфера (10) | | |
| 52 | Найдите площадь поверхности | сфера (7) | | |
| 53 | Определить, является простым или составным | 5 | ||
| 60 | Преобразование в упрощенную дробь | 2 1/4 | ||
| 61 | Найдите площадь поверхности | сфера (12) | | |
| 62 | Найдите том | сфера (1) | | |
| 63 | Найдите окружность | круг (2) | | |
| 64 | Найдите том | коробка (12)(12)(12) | | |
| 65 | Добавить | 2+2= | ||
| 66 | Найдите площадь поверхности | коробка (3)(3)(3) | | |
| 67 | Оценить | корень пятой степени из 6* корень шестой из 7 | ||
| 68 | Оценить | 7/40+17/50 | ||
| 69 | Найти простую факторизацию | 1617 | ||
| 70 | Оценить | 27-(квадратный корень из 89)/32 | ||
| 71 | Оценить | 9÷4 | ||
| 72 | Оценка 92 | |||
| 74 | Оценить | 1-(1-15/16) | ||
| 75 | Преобразование в упрощенную дробь | 8 | ||
| 76 | Оценка | 656-521 | 9-2 | |
| 79 | Оценить | 4-(6)/-5 | ||
| 80 | Оценить | 3-3*6+2 | ||
| 81 | Найдите площадь поверхности | коробка (5)(5)(5) | | |
| 82 | Найдите площадь поверхности | сфера (8) | | |
| 83 | Найдите площадь | круг (14) | | |
| 84 | Преобразование в десятичное число | 5 ноября | ||
| 85 9-2 | ||||
| 88 | Оценить | 1/2*3*9 | ||
| 89 | Оценить | 4/4-17/-4 | ||
| 90 | Оценить | 11. 02+17.19 | ||
| 91 | Оценить | 3/5+3/10 | ||
| 92 | Оценить | 4/5*3/8 | ||
| 93 | Оценить | 6/(2(2+1)) | ||
| 94 | Упростить | квадратный корень из 144 | ||
| 95 | Преобразование в упрощенную дробь | 725% | ||
| 96 | Преобразование в упрощенную дробь | 6 1/4 | ||
| 97 | Оценить | 7/10-2/5 | ||
| 98 | Оценить | 6÷3 | ||
| 99 | Оценить | 5+4 | ||
| 100 | Оценить | квадратный корень из 12- квадратный корень из 192 |
ANSI/ASQ Z1.
4 и Z1.9 Стандарты плана выборочного контроля для контроля качестваУзнайте о качестве
- О Z1.4 и Z1.9
- Ресурсы
- Похожие темы
Стандарты 101
Ресурсы Z1.4 и Z1.9
Наши стандарты
Z1.4 и Z1.9 Связанные темы
- Дом /
- Качественные ресурсы /
- З14 З19
Что такое стандарт Z1.
4?ANSI/ASQ Z1.4-2003 (R2018): процедуры и таблицы выборочного контроля для проверки по атрибутам — это система приемочного контроля, которая должна использоваться с правилами переключения в непрерывном потоке партий для заданного предела приемочного качества (AQL). В нем предусмотрены усиленные, нормальные и сокращенные планы для проверки атрибутов на процент несоответствий или несоответствий на 100 единиц.
- Версия для печати в мягкой обложке
- Электронный стандарт (PDF)
- Лицензия сайта для внутренней сети вашей организации
Пример содержания в ANSI/ASQ Z1.4
Что такое стандарт Z1.9?
ANSI/ASQ Z1.9-2003 (R2018): Процедуры и таблицы выборочного контроля по переменным для процента несоответствия — это система приемочного отбора, которая должна использоваться в непрерывном потоке партий для заданного предела приемочного качества (AQL). Он предоставляет сжатые, нормальные и сокращенные планы для использования при измерениях с нормальным распределением.
Вариация может измеряться стандартным отклонением выборки, диапазоном выборки или известным стандартным отклонением. Он применим только тогда, когда обеспечена нормальность измерений.
- Версия для печати в мягкой обложке
- Электронный стандарт (PDF)
- Лицензия сайта для внутренней сети вашей организации
Пример содержания в ANSI/ASQ Z1.9
История Z1.4 и Z1.9
Прочтите обзор выборки, в котором описываются происхождение и цели статистических стандартов ANSI/ASQ Z1.4 , который устанавливает планы и процедуры выборочного контроля для проверки по признакам, и ANSI / ASQ Z1.9, который устанавливает планы и процедуры выборочного контроля для проверки по переменным.
Узнайте больше о Z1.4 и Z1.9
Посетите блог Ask the Standard Experts , чтобы получить ответы на вопросы о стандартах Z1.4 и Z1.9.
Просмотрите ранее отвеченные вопросы по Z1.4 и Z1.9 или задайте свой вопрос.
Обучение стандартам Z1.4 и Z1.9
- Инструменты и методы улучшения: диаграммы, элементы управления, диаграммы, методы улучшения, выборка и решение проблем
- Подготовка к сертификации сертифицированного инженера по качеству
Сертификация инженера по качеству
- Инженер по качеству (CQE)
- Дополнительная информация о сертификации
Книги по стандартам контроля качества
- Планы отбора проб с нулевым приемочным номером, пятое издание
- Глоссарий и таблицы для статистического контроля качества, четвертое издание
Статьи о приемочном отборе
Сравнение стандартов приемочного отбора, Часть I ( Quality Engineering ) В этой первой части серии статей, состоящей из двух частей, обсуждаются и сравниваются общие стандарты выборки атрибутов.
Сравнение стандартов выборочного контроля, часть II ( Инжиниринг качества ) Во второй части этой серии обсуждение перейдет к разработке стандартов выборочного контроля по переменным, которые находят свою связь с военным стандартом и будут служить для обсуждения и сравнить эти производные стандарты таким же образом, как стандарты атрибутов рассматривались в Части 1.