Как найти частное двух комплексных чисел: формула, примеры
Sign in
Password recovery
Восстановите свой пароль
Ваш адрес электронной почты
MicroExcel.ru Математика Алгебра Деление комплексных чисел
В данной публикации мы рассмотрим формулы, с помощью которых можно найти частное двух комплексных чисел, представленных в алгебраической или тригонометрической форме. Также приведены примеры для лучшего понимания теоретического материала.
- Деление в алгебраической форме
- Деление в геометрической форме
Деление в алгебраической форме
Результатом деления (т.е. частное) двух комплексных чисел x = a1 + b1i и y = a2 + b2i также является комплексное число z:
Порядок действий следующий:
- Делимое и делитель умножаем на число, комплексно сопряженное делителю.
Примечание: Для (a + bi) комплексно сопряженным будет число (a – bi), т.е. действительная часть остается той же, а у мнимой знак меняется на противоположный. - В результате выполнения умножения в знаменателе получается обычное действительное число.
(a2 + b2i)(a2 – b2i) = a2 ⋅ a2 – a2 ⋅ b2i + b2i ⋅ a2 – b2i ⋅ b2i = a22 – b22 ⋅ i2 = a22 + b22. - Теперь выполним аналогичное действие в числителе:
(a1 + b1i)(a2 – b2i) = a1 ⋅ a2 – a1 ⋅ b2i + b1i ⋅ a2 – b1i ⋅ b2i = a1a2 – b 1b2i2 – a1b2i + b1a2i = (a1a2 + b1b2) + (a2b1 – a1b2) ⋅ i. - Делим полученный числитель на знаменатель:
Пример 1:
Разделим комплексное число (3 – i) на (-5 + 2i).
Решение:
Руководствуемся планом действий, описанным выше, и получаем:
Деление в геометрической форме
Если комплексные числа заданы в тригонометрической форме, например, x = |x| ⋅ (cos φ1 + i ⋅ sin φ1) и y = |y| ⋅ (cos φ2 + i ⋅ sin φ2), то разделить их можно по формуле ниже:
Пример 2
Найдем частное комплексных чисел: x = 4 ⋅ (cos 60° + i ⋅ sin 60°)
Решение:
|x| : |y| = 4 : 2 = 2
φ1 – φ2 = 60° – 25° = 35°
x : y = 2 ⋅ (cos 35° + i ⋅ sin 35°)
ЧАЩЕ ВСЕГО ЗАПРАШИВАЮТ
Таблица знаков зодиака
Нахождение площади трапеции: формула и примеры
Нахождение длины окружности: формула и задачи
Римские цифры: таблицы
Таблица синусов
Тригонометрическая функция: Тангенс угла (tg)
Нахождение площади ромба: формула и примеры
Нахождение объема цилиндра: формула и задачи
Тригонометрическая функция: Синус угла (sin)
Геометрическая фигура: треугольник
Нахождение объема шара: формула и задачи
Тригонометрическая функция: Косинус угла (cos)
Нахождение объема конуса: формула и задачи
Таблица сложения чисел
Нахождение площади квадрата: формула и примеры
Что такое тетраэдр: определение, виды, формулы площади и объема
Нахождение объема пирамиды: формула и задачи
Признаки подобия треугольников
Нахождение периметра прямоугольника: формула и задачи
Формула Герона для треугольника
Что такое средняя линия треугольника
Нахождение площади треугольника: формула и примеры
Нахождение площади поверхности конуса: формула и задачи
Что такое прямоугольник: определение, свойства, признаки, формулы
Разность кубов: формула и примеры
Степени натуральных чисел
Нахождение площади правильного шестиугольника: формула и примеры
Тригонометрические значения углов: sin, cos, tg, ctg
Нахождение периметра квадрата: формула и задачи
Теорема Фалеса: формулировка и пример решения задачи
Сумма кубов: формула и примеры
Нахождение объема куба: формула и задачи
Куб разности: формула и примеры
Нахождение площади шарового сегмента
Что такое окружность: определение, свойства, формулы
как делать в алгебраической, показательной и тригонометрической форме
Содержание:
- Деление комплексных чисел — основные правила
- В каких формах это можно делать
- Формула деления в алгебраической форме
- Формула деления в тригонометрической форме
- Формула деления в показательной форме
- Примеры решения задач
- Деление комплексных чисел — основные правила
- В каких формах это можно делать
- Формула деления в алгебраической форме
- Формула деления в тригонометрической форме
- Формула деления в показательной форме
- Примеры решения задач
Деление комплексных чисел — основные правила
Определение 1
Частным двух комплексных чисел \(z_{1}=a_{1}+b_{1} i\) и \(z_{2}=a_{2}+b_{2} \)i называют число z, заданное соотношением: \(z=\frac{z_{1}}{z_{2}}=\frac{a_{1} a_{2}+b_{1} b_{2}}{a_{2}^{2}+b_{2}^{2}}+\frac{a_{2} b_{1}-a_{1} b_{2}}{a_{2}^{2}+b_{2}^{2}} i\)
Общий алгоритм для деления комплексных чисел на практике:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления).
Если нет возможности написать самому, закажите тут.
- умножение делимого и делителя на число, комплексно сопряженное делителю, что преобразует делитель в действительное число;
- в числителе умножают пару комплексных чисел;
- полученную дробь почленно делят.
В каких формах это можно делать
Комплексные числа делят разными методами, подтвержденными доказательствами. Существуют алгебраическая, тригонометрическая и показательная формы для подобных операций. В каждом перечисленном случае необходимо использовать определенную формулу.
Формула деления в алгебраической форме
Когда требуется выполнить деление комплексных чисел в алгебраической форме, в первую очередь числитель и знаменатель умножают на число, сопряженное к знаменателю. Таким образом, удается исключить комплексность в знаменателе:
\(\frac{z_1}{z_2} = \frac{a_1 + b_1 i}{a_2 + b_2 i} = \frac{(a_1+b_1 i)(a_2-b_2i)}{(a_2+b_2i)(a_2-b_2i)} = \frac{a_1 \cdot a_2 + b_1 \cdot b_2}{a_2 ^2 + b_2 ^2} + i\frac{a_2 \cdot b_1 — a_1 \cdot b_2}{a_2 ^2 + b_2 ^2}\)
Формула деления в тригонометрической форме
Деление в тригонометрической форме подразумевает деление модулей комплексных чисел.
{(\varphi_1 — \varphi_2)i}\)
Примеры решения задач
Задача 1
Задача
Необходимо найти частное пары комплексных чисел:
\(z_1 = 3+i\) и \(z_2 = 2-3i\)
Решение:
Заметим, что комплексные числа заданы в алгебраической форме. В связи с этим целесообразно использовать в действиях соответствующую формулу.
\(\frac{z_1}{z_2} = \frac{3+i}{2-3i} =\)
Сопряженное комплексное число к знаменателю:
\(\overline{z_2} = 2+3i\)
Нужно домножить и разделить на сопряженное комплексное число к знаменателю дроби. Таким образом, получится исключить комплексность в знаменателе:
\(= \frac{(3+i)(2+3i)}{(2-3i)(2+3i)} = \frac{6 + 9i + 2i — 3}{4 + 6i — 6i + 9} =\)
Далее следует привести подобные слагаемые и записать вывод с ответом:
\(= \frac{3 + 11i}{13} = \frac{3}{13} + \frac{11}{13}i\)
Ответ: \(\frac{z_1}{z_2} = \frac{3}{13} + \frac{11}{13}i\)
Задача 2
Задача
Требуется выполнить деление комплексных чисел:
\(z_1 = 2(\cos \frac{\pi}{3} + i\sin \frac{\pi}{6})\)
\(z_2 = 4(\cos \frac{\pi}{6} + i\sin \frac{\pi}{6})\)
Решение:
Комплексные числа в условии задачи записаны в тригонометрической форме.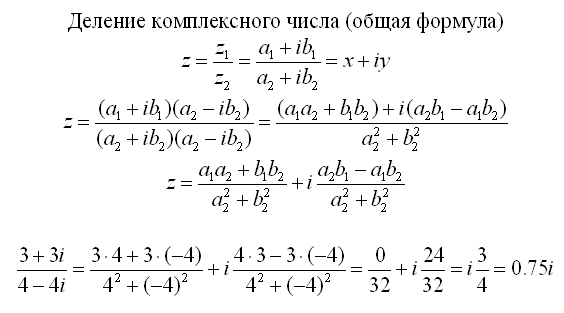
{2}}=\)
\(=\frac{-3-i}{1-(-1)}=\frac{-3-i}{2}=-\frac{3}{2}-\frac{i}{2}\)
Ответ:\( \frac{-2+i}{1-i}=-\frac{3}{2}-\frac{i}{2}\)
Задача 5
Задача
Необходимо найти частное:
\(\frac{z_{1}}{z_{2}}\)
При условии, что:
\(z_{1}=2 \cdot\left(\cos \frac{3 \pi}{4}+i \sin \frac{3 \pi}{4}\right)\)
\(z_{2}=\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}\)
Решение:
Искомое частное:
\(\frac{z_{1}}{z_{2}}=\frac{2 \cdot\left(\cos \frac{3 \pi}{4}+i \sin \frac{3 \pi}{4}\right)}{\cos \frac{\pi}{4}+i \sin \frac{\pi}{4}}=\)
\(=\frac{2}{1} \cdot\left[\cos \left(\frac{3 \pi}{4}-\frac{\pi}{4}\right)+i \sin \left(\frac{3 \pi}{4}-\frac{\pi}{4}\right)\right]=\)
\(=2 \cdot\left[\cos \frac{\pi}{2}+i \sin \frac{\pi}{2}\right]=2 \cdot(0+i)=2 i\)
Ответ: \(\frac{z_{1}}{z_{2}}=2 \cdot\left(\cos \frac{\pi}{2}+i \sin \frac{\pi}{2}\right)=2 i\)
Задача 6
Задача
Необходимо разделить два комплексных числа:
\(z_{1}=-1+3i\)
\(z_{2}=1+2i\)
Решение:
С помощью соответствующей формулы можно записать уравнение:
\(z_{1} \div z_{2} = \frac{-1+3i}{1+2i} = \frac{(-1+3i)(1-2i)}{(1+2i)(1-2i)} = \frac{-1 \cdot 1 + 3 \cdot 2}{1^{2}+2^{2}} + i \frac{3 \cdot 1 + (-1) \cdot (-2)}{1^{2}+2^{2}} =\)
\(= \frac{5}{5} + i \frac{5}{5}=1+i\)
Ответ: \( z_{1} \div z_{2} = 1+i\)
Задача 7
Задача
Необходимо вычислить частное комплексных чисел:
\(z_{1}=\sqrt{2} \left( \cos \frac{\pi}{2} + i \sin \frac{\pi}{2} \right)\)
\(z_{2}=\sqrt{2} \left( \cos \frac{\pi}{4} + i \sin \frac{\pi}{4} \right)\)
Решение:
Используя соответствующую формулу, запишем:
\(z_{1} \div z_{2} = \frac{r_{1}}{r_{2}} (\cos ( \varphi _{1} — \varphi _{2}) + i \sin ( \varphi _{1} — \varphi _{2})) = \frac{\sqrt{2}}{\sqrt{2}} \left( \cos \left( \frac{\pi}{2}-\frac{\pi}{4} \right) + i \sin \left( \frac{\pi}{2}-\frac{\pi}{4} \right) \right) =\)
\(= 1 \cdot \left( \cos \frac{\pi}{4} + i \sin \frac{\pi}{4} \right) = \cos \frac{\pi}{4} + i \sin \frac{\pi}{4}\)
Ответ:\( z_{1} \div z_{2} = \cos \frac{\pi}{4} + i \sin \frac{\pi}{4}\)
Задача 8
Задача
Требуется разделить два комплексных числа:
\(z_{1} = \sqrt{2} e^{-\frac{\pi}{2}i}\)
\(z_{2} = 2 e^{-\frac{\pi}{4}i}\)
Решение:
Используя соответствующую формулу деления комплексных чисел, можно решить уравнение:
\(z_{1} \div z_{2} = \frac{r_{1}}{r_{2}} \cdot e^{i ( \varphi _{1} — \varphi _{2})} = \frac{\sqrt{2}}{2} \cdot e^{i \left( -\frac{\pi}{2} +\frac{\pi}{4} \right) } = \frac{\sqrt{2}}{2} \cdot e^{-\frac{\pi}{4}i}\)
Ответ: \(z_{1} \div z_{2} = \frac{\sqrt{2}}{2} \cdot e^{-\frac{\pi}{4}i}\)
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
Объяснение урока: Деление комплексных чисел
В этом объяснении мы научимся выполнять деление комплексных чисел.
Когда учащийся впервые сталкивается с комплексными числами, такие выражения, как 3−6𝑖1−5𝑖 может показаться немного загадочным или, по крайней мере, может показаться трудно понять, как можно вычислить результат. Этот объяснитель свяжет это идея к более знакомым областям математики и поможет вам понять, как вычислять выражения так. Прежде чем мы займемся делением комплексных чисел вообще, рассмотрим два более простых случая деления на действительное число и деление на чисто мнимое число.
Пример 1: Деление комплексного числа на вещественное число
Учитывая 𝑧=5+3𝑖, выразить 𝑧2 в виде 𝑎+𝑏𝑖.
Ответ
Подставляя значение 𝑧, получаем 𝑧2=5+3𝑖2.
Мы можем распределить 12 по комплексному числу, чтобы получить 𝑧2=52+32𝑖.
Во многих отношениях деление комплексного числа на действительное число является довольно тривиальным упражнением. Однако деление комплексного числа на мнимое не так тривиально, как следующее пример продемонстрирует.
Пример 2. Деление комплексного числа на мнимое число
Упростить 2+4𝑖𝑖.
Ответ
Чтобы упростить эту дробь, нам нужно как-то преобразовать знаменатель в действительное число. Этого можно добиться, используя тот факт, что 𝑖=−1. Следовательно, если мы умножаем и числитель и знаменатель на 𝑖, получим вещественное числа в знаменателе, что позволит нам упростить дробь. Следовательно, 2+4𝑖𝑖=2+4𝑖𝑖×𝑖𝑖=(2+4𝑖)𝑖𝑖.
Распределяя по скобкам в числителе, имеем 2+4𝑖𝑖=2𝑖+4𝑖𝑖.
Используя 𝑖=−1, получаем 2+4𝑖𝑖=−4+2𝑖−1=4−2𝑖.
Метод, который мы использовали выше, можно обобщить, чтобы помочь нам понять, как разделить любые два
комплексные числа.
Первое, что нам нужно сделать, это определить комплексное число, которое, когда
умножение на знаменатель дает действительное число. Тогда мы можем умножить оба числителя
и знаменатель на это число и упростить. Вопрос в том, что задано комплексное число
𝑧, какое число при умножении на 𝑧 дает действительное
число? Это тот момент, когда мы должны вспомнить свойства комплексного сопряжения, в
в частности, что для комплексного числа 𝑧=𝑎+𝑏𝑖, 𝑧𝑧=𝑎+𝑏, является действительным числом. Следовательно, умножая
числитель и знаменатель комплексным сопряжением знаменателя, мы можем
исключить мнимую часть из знаменателя, а затем упростить результат. Эта техника
не должно быть новым для большинства людей. Узнавая о радикалах, мы сталкиваемся с похожей проблемой.
пытаясь упростить выражения вида 𝑎+𝑏√𝑐𝑑+𝑒√𝑓.
В этом случае мы умножаем числитель и знаменатель на сопряженное число
знаменатель. Этот прием часто называют рационализацией знаменателя.
С комплексом
чисел, во многом мы используем ту же технику в особом случае, когда
𝑓 — отрицательное число.
Теперь давайте рассмотрим пример, где нам нужно упростить деление двух комплексные числа, подобно тому, как мы рационализируем знаменатель с помощью радикалы.
Пример 3: Деление комплексных чисел
Упростить 3−6𝑖1−5𝑖.
Ответ
Начнем с определения комплексного числа, которое при умножении на знаменатель дает в реальном числе. Обычно мы используем комплексное сопряжение знаменателя: 1+5𝑖. Теперь умножаем и числитель, и знаменатель на это числа следующим образом: 3−6𝑖1−5𝑖=3−6𝑖1−5𝑖×1+5𝑖1+5𝑖=(3−6𝑖)(1+5𝑖)(1−5𝑖)(1+5𝑖).
Раскрывая скобки в числителе и знаменателе, имеем 3−6𝑖1−5𝑖=3+15𝑖−6𝑖−30𝑖1+5𝑖−5𝑖−25𝑖.
Используя 𝑖=−1 и собирая подобные термины, мы получаем 3−6𝑖1−5𝑖=33+9𝑖26.
Наконец, мы выражаем это в форме 𝑎+𝑏𝑖 следующим образом:
3−6𝑖1−5𝑖=3326+926𝑖.
Практическое руководство. Деление комплексных чисел
Чтобы разделить комплексные числа, мы используем следующую технику (иногда называемую «реализуя» знаменатель):
- Умножить числитель и знаменатель на комплексно-сопряженное число знаменатель.
- Раскройте скобки в числителе и знаменателе.
- Соберите одинаковые термины (действительные и мнимые), помня, что 𝑖=−1.
- Ответ представите в виде 𝑎+𝑏𝑖, сократив любые дроби.
Используя эту технику, мы можем получить общую форму для деления сложных числа, как продемонстрирует следующий пример.
Пример 4: Общая форма сложного деления
- Разверните и упростите (𝑝+𝑞𝑖)(𝑝−𝑞𝑖).
- Развернуть (𝑎+𝑏𝑖)(𝑝−𝑞𝑖).
- Следовательно, найдите дробь, эквивалентную 𝑎+𝑏𝑖𝑝+𝑞𝑖 и чей знаменатель действителен.
Ответ
Часть 1
Раскрывая скобки с помощью FOIL или любого другого метода, мы имеем
(𝑝+𝑞𝑖)(𝑝−𝑞𝑖)=𝑝−𝑝𝑞𝑖+𝑝𝑞𝑖−𝑞𝑖.
Используя 𝑖=−1 и упрощая, имеем (𝑝+𝑞 𝑖)(𝑝−𝑞𝑖)=𝑝+𝑞.
Часть 2
Аналогично, раскрывая скобки, получаем 𝑏𝑞𝑖.
Сбор похожих терминов и использование 𝑖=−1 , имеем (𝑎+𝑏𝑖)(𝑝−𝑞𝑖)=(𝑎𝑝+𝑏𝑞)+(𝑏𝑝−𝑎𝑞)𝑖.
Часть 3
Чтобы выразить эту дробь действительным знаменателем, мы умножаем числитель и знаменателя на комплексное сопряжение знаменателя следующим образом:
Подставляя наши ответы из части 1 и части 2, мы имеем
Несмотря на то, что мы вывели общую формулу для сложных разделение, желательно знакомиться с техникой, а не просто запоминать формулу.
Пример 5: Свойства комплексного деления
Если 𝑎+𝑏𝑖=−3−5𝑖−3+5𝑖, верно ли, что 𝑎+𝑏=1?
Ответ
Чтобы выразить −3−5𝑖−3+5𝑖 в виде 𝑎+𝑏𝑖, умножаем числитель и знаменатель на комплексное сопряжение знаменателя следующим образом: −3−5𝑖−3+5𝑖=(−3−5𝑖)(−3−5𝑖)(−3+5𝑖)(−3−5𝑖).
Расширение скобки, мы имеем −3–5𝑖 — 3+5𝑖 = 9+15𝑖+15𝑖+25𝑖9+15𝑖 — 15𝑖 — 25𝑖.
Используя 𝑖 = −1 и собирая, как термины, у нас есть -3 −5𝑖−3+5𝑖=−16+30𝑖34.
Упрощая, имеем −3−5𝑖−3+5𝑖=−817+1517𝑖.
Следовательно, 𝑎=−817 и 𝑏=1517. Сейчас мы можем рассмотреть сумму их квадратов:
Следовательно, верно, что 𝑎+𝑏=1.
Тот факт, что 𝑎+𝑏=1 в предыдущем вопросе, не случаен. В на самом деле, это пример общего правила: если 𝑎+𝑏𝑖=𝑧𝑧 для некоторого комплексного числа 𝑧, то 𝑎+𝑏=1. Это можно доказать, работая с алгеброй. Однако это не очень поучительно. Наоборот, такие результаты лучше всего понять, когда мы узнать о модуле и аргументе.
Пример 6. Решение сложных уравнений деления
Решите уравнение 𝑧(2+𝑖)=3−𝑖 относительно 𝑧.
Ответ
Мы начинаем с деления обеих частей уравнения на 2+𝑖, что приводит к следующее уравнение: 𝑧=3−𝑖2+𝑖.
Теперь упростим дробь, выполнив сложное деление. Следовательно, умножая оба
числителя и знаменателя комплексно-сопряженным знаменателю, получаем
𝑧=(3−𝑖)(2−𝑖)(2+𝑖)(2−𝑖).
Раскрыв скобки, мы имеем 𝑧=6−3𝑖−2𝑖+𝑖4+2𝑖−2𝑖−𝑖.
Используя 𝑖=−1 и собрав подобные термины, мы можем переписать это как 𝑧=5−5𝑖5=1−𝑖.
В связи с тем, что умножать и делить комплексные числа таким способом можно довольно долго потребляя, полезно рассмотреть, какой подход будет наиболее эффективным. Это часто включает в себя использование свойств комплексных чисел или замечание факторов, которые мы можем быстро отменить. Следующие два примера продемонстрируют, как мы можем упростить наши вычисления.
Пример 7: комплексный раздел
Упростить (−3+2𝑖)(3+3𝑖)(4+𝑖)(4+4𝑖).
Ответ
При представлении такого выражения хорошо сначала подумать, какой подход
мы должны взяться за ее решение. Мы могли бы расширить скобки в числителе и
знаменатель, а затем умножить числитель и знаменатель на комплекс
сопряжение знаменателя. В качестве альтернативы мы могли бы разделить дробь на две части и попытаться
упростите каждую часть, затем умножьте полученные комплексные числа.
Теперь мы можем умножить и числитель, и знаменатель на комплексно-сопряженное число знаменатель следующим образом: 34(−3+2𝑖)(4+𝑖)=34(−3+2𝑖)(4−𝑖)(4+𝑖)(4−𝑖).
Раскрывая скобки в числителе и знаменателе, имеем 34(−3+2𝑖)(4−𝑖)(4+𝑖)(4−𝑖)=34(−12+3𝑖+8𝑖−2𝑖)(16+4𝑖−4𝑖−𝑖).
Используя 𝑖 =−1 и собирая подобные термины, мы можем переписать это как 34−12+3𝑖+8𝑖−2𝑖(16+4𝑖−4𝑖−𝑖)=34(−10+11𝑖)17.
Наконец, мы можем упростить, чтобы получить 34−12+3𝑖+8𝑖− 2𝑖(16+4𝑖−4𝑖−𝑖)=−1534+3368𝑖.
В ответ на следующий вопрос мы снова рассмотрим пример, в котором применяются свойства
комплексные числа могут упростить вычисления.
Пример 8: Сложные выражения, включающие деление
Упростить 3−4𝑖2+2𝑖+3−4𝑖2−2𝑖.
Ответ
Эту задачу можно решить, выполнив сложное деление на обоих дроби, а затем сложение их результатов. Однако мы можем упростить наши вычисления, сначала заметив, что мы можем вынести 3−4𝑖 из обоих членов. Следовательно, мы можем переписать выражение как
| 3−4𝑖2+2𝑖+3−4𝑖2−2𝑖=(3−4𝑖)12+2𝑖+12−2𝑖. | (1) |
Теперь рассмотрим выражение в скобках; обратите внимание, что знаменатели две дроби представляют собой комплексно-сопряженную пару; то есть выражение имеет вид 1𝑧+1𝑧.
Если мы представим это как одну дробь над общим знаменателем, мы получим 1𝑧+1𝑧=𝑧+𝑧𝑧𝑧.
Используя свойства комплексных сопряженных, мы знаем, что если 𝑧=𝑎+𝑏𝑖, 𝑧𝑧=𝑎+𝑏 и 𝑧+𝑧=2(𝑧)=2𝑎Re. Следовательно, 1𝑧+1𝑧=2𝑎𝑎+𝑏.
Следовательно, 12+2𝑖+12−2𝑖=2×22+2=12.
Подставив это в (1), мы получим 3−4𝑖2+2𝑖+3−4𝑖2−2𝑖=12(3 −4𝑖)=32−2𝑖.
Наконец, давайте рассмотрим пример, в котором нам нужно найти пропущенные значения в уравнение путем деления комплексных чисел.
Пример 9. Решение линейного уравнения с двумя переменными и комплексными коэффициентами
Учитывая, что 𝑦 — действительные числа, определите значение 𝑥 и значение из 𝑦.
Ответ
В этом примере мы хотим определить недостающие значения 𝑥 и 𝑦 в линейном уравнении с двумя переменными с комплексным коэффициенты.
Данное уравнение содержит 3 отдельных сложных деления, два слева и одно справа сторону уравнения. Начнем с упрощения каждого члена, выполнив сложное деление. Это достигается путем умножения числителя и знаменателя на комплексно-сопряженное число знаменателя, что приводит к действительное число в знаменателе после распределения по скобкам.
Для первого члена 𝑥+𝑖𝑦1−3𝑖 мы умножаем
знаменатель и числитель на 1+3𝑖, что является комплексно-сопряженным
знаменателя:
𝑥+𝑖𝑦1−3𝑖=𝑥+𝑖𝑦1−3𝑖×1+3𝑖1+3𝑖=(𝑥+𝑖𝑦)(1+3𝑖)(1−3𝑖)(1+3𝑖).
Распределяя по скобкам в числителе и знаменателе, имеем 𝑥+𝑖𝑦1−3𝑖=𝑥+3𝑥𝑖+𝑦𝑖+3𝑖𝑦1+3𝑖−3𝑖−9𝑖=𝑥+3𝑥𝑖+𝑦𝑖−3𝑦1+9=(𝑥−3𝑦)+ 𝑖(3𝑥+𝑦)10.
Повторение этого процесс для второго члена, 9𝑥−𝑖𝑦1+3𝑖, на этот раз умножив числитель и знаменатель на 1−3𝑖, получаем 9𝑥−𝑖𝑦1+3𝑖=9𝑥−𝑖𝑦1+3𝑖×1−3𝑖1−3𝑖=(9𝑥−𝑖𝑦)(1−3𝑖)(1+3𝑖)(1−3𝑖)=9𝑥−27𝑥𝑖− 𝑦𝑖+3𝑖𝑦1+3𝑖−3𝑖 −9𝑖=9𝑥−27𝑥𝑖−𝑦𝑖−3𝑦1+9=(9𝑥−3𝑦)+𝑖(−27𝑥−𝑦)10.
Наконец, для последнего члена 6+5𝑖4−8𝑖, с правой стороны, умножив знаменатель и числитель на 4+8𝑖, 6+5𝑖4–8𝑖 = 6+5𝑖4–8𝑖 × 4+8𝑖4+8𝑖 = (6+5𝑖) (4+8𝑖) (4–8𝑖) (4+8𝑖) = 24+48𝑖+20𝑖+40𝑖16+32𝑖 — 32𝑖 −64𝑖=24+48𝑖+20𝑖−4016+64=−16+68𝑖80.
Таким образом, данное уравнение принимает вид 𝑥+𝑖𝑦1−3𝑖−9𝑥−𝑖𝑦1+3𝑖=6+5𝑖4−8𝑖(𝑥−3𝑦)+𝑖(3𝑥+𝑦)10−(9𝑥−3𝑦)+𝑖(−27𝑥−𝑦) 10=−16+68𝑖80 (𝑥−3𝑦)−(9𝑥−3𝑦)+𝑖(3𝑥+𝑦)+𝑖(27𝑥+𝑦)10=−16+68𝑖80−8𝑥+𝑖(30𝑥+2𝑦)10=−16+68𝑖80−8𝑥+𝑖(30𝑥+2 𝑦)=− 16+68𝑖8.
Действительные значения 𝑥 и 𝑦 можно найти, приравняв действительную и мнимую части обеих сторон.
Первое приравнивание
настоящие детали у нас есть
−8𝑥=−168𝑥=14.
Теперь мнимые части, 30𝑥+2𝑦=688𝑦=6816−15𝑥=6816−154=12.
Подводя итог, можно сказать, что реальными решениями данного уравнения являются 𝑥=14,𝑦=12.
Давайте резюмируем некоторые ключевые моменты, которые мы рассмотрели в этом объяснении.
Ключевые моменты
- Для деления комплексных чисел используется тот же метод, что и для рационализации знаменатель.
- Чтобы разделить комплексные числа, мы умножаем числитель и знаменатель на комплексное сопряжение знаменателя, а затем раскрываем скобки и упрощаем, используя 𝑖=−1.
- В выражениях, включающих умножение и деление нескольких комплексных чисел, полезно искать общие факторы или можно ли применить некоторые свойства комплексные числа, чтобы упростить наши расчеты.
Разделить комплексные числа | Колледж Алгебра
Результаты обучения
- Определите и запишите комплексно-сопряженное число комплексного числа.
- Деление комплексных чисел.
- Упростите степени [latex]i[/latex].
Деление комплексных чисел
Деление двух комплексных чисел сложнее, чем сложение, вычитание и умножение, потому что мы не можем делить на мнимое число, а это означает, что у любой дроби должен быть действительный знаменатель. Нам нужно найти член, на который мы можем умножить числитель и знаменатель, который исключит мнимую часть знаменателя, чтобы мы получили действительное число в качестве знаменателя. Этот термин называется комплексное сопряжение знаменателя, которое находится при изменении знака мнимой части комплексного числа. Другими словами, комплексное сопряжение [латекс]а+би[/латекс] есть [латекс]а-би[/латекс].
Обратите внимание, что комплексные сопряжения имеют обратную связь: комплексное сопряжение [латекс]а+би[/латекс] равно [латекс]а-би[/латекс], а комплексное сопряжение [латекс]а-би[/ латекс] это [латекс]а+би[/латекс]. Важно отметить, что комплексно-сопряженные пары обладают особым свойством.
Их продукт всегда реален. 92\end{align}[/latex]
Предположим, мы хотим разделить [latex]c+di[/latex] на [latex]a+bi[/latex], где ни [latex]a[/latex], ни [латекс]b[/латекс] равно нулю. Сначала запишем деление в виде дроби, затем найдем комплексно-сопряженную часть знаменателя и умножим.
[латекс]\dfrac{c+di}{a+bi}[/latex], где [латекс]a\ne 0[/латекс] и [латекс]b\ne 0[/латекс].
Умножить числитель и знаменатель на комплексное сопряжение знаменателя.
[латекс]\dfrac{\left(c+di\right)}{\left(a+bi\right)}\cdot \dfrac{\left(a-bi\right)}{\left(a- би \ вправо)} = \ dfrac {\ влево (с + ди \ вправо) \ влево (а-би \ вправо)} {\ влево (а + би \ вправо) \ влево (а-би \ вправо)} [/ латекс] 9{2}}\end{align}[/latex]
A Общее примечание: комплексное сопряжение
Комплексное сопряжение комплексного числа [latex]a+bi[/latex] равно [latex]a-bi [/латекс]. Его находят изменением знака мнимой части комплексного числа. Действительная часть числа остается неизменной.
- Когда комплексное число умножается на его комплексно-сопряженное, результатом является действительное число.
- Когда комплексное число добавляется к его комплексно-сопряженному, результатом является действительное число.
Пример: нахождение комплексно-сопряженных чисел
Найдите комплексно-сопряженные числа каждого числа.
- [латекс]2+i\sqrt{5}[/латекс]
- [латекс]-\frac{1}{2}i[/латекс]
Показать решение
Как: Даны два комплексных числа, разделить одно на другое.
- Запишите задачу на деление в виде дроби.
- Определите комплексное сопряжение знаменателя.
- Умножить числитель и знаменатель дроби на комплексное сопряжение знаменателя. 9{2}-3x[/латекс]. Вычислите [латекс]f\влево(8-i\вправо)[/латекс].
Показать решение
Пример: замена мнимого числа в рациональной функции
Пусть [latex]f\left(x\right)=\dfrac{2+x}{x+3}[/latex].
