Дослідити на парність функцію: Приклади на парність та непарність функцій

Содержание

Приклади на парність та непарність функцій

Продовжуємо цикл публікацій із ЗНО підготовки на властивості елементарних функцій. Сьогодні розберемо приклади на парність та непарність функцій, формули перевірки парності та непарності, далі вивчатимемо періодичність тригонометричних функцій. Завдання досить прості, тому Ви швидко зможете засвоїти основні властивості функцій та алгоритми обчислень подібних завдань.

Розділ 22. Елементарні функції та їх властивості

Приклад 22.12 Указати парну функцію.

Розв’язування: Функція y=f(x) називається парною, якщо y(-x)=y(x).
Перевіримо парність y(x)=4^x, для від’ємних значень маємо , робимо висновок що функція y(x)=4^x не є парною;
y(x)=x, тоді y(-x)=-x ≠y(x) — не є парною;
y(x)= √x, тоді — не є парною;
y(x)=tg(x), тоді y(-x)=tg(-x)=-tg(x)≠y(x) — не є парною;
y(x)=|x|, тоді y(-x)=|-x|=x=y(x) — функція є парною.
Відповідь: y=|x| – Д.

Приклад 22.13 Яка з наведених функцій є непарною?

Розв’язування: Функція y=f(x) називається непарною, якщо y(-x)=-y(x).
Розглянемо y(x)=x+|x|, розпишемо y(-x)=-x+|-x|=-x+|x|≠y(x) — не є непарною;
y(x)=sin²(x), тоді y(-x)=sin²(-x)= sin²(x) |≠y(x) — не є непарною;
, тоді — не є непарною;
, розпишемо — не є непарною;
, тоді — функція є непарною.
Відповідь: – Д.

Приклад 22.14 Функція f(x) — парна, а функція g(x) — непарна. f(7)=-11, g(5)=-2. Обчислити 2f(-7)-3g(-5).

Розв’язування: Оскільки функція f(x) — парна, то f(-x)=f(x), звідси f(-7)=f(7)=-11.
Оскільки функція g(x) — непарна, то g(-x)=-g(x), звідси g(-5)=-g(5)=2.
Обчислюємо значення виразу
2f(-7)-3g(-5)=2•(-11)-3•2=-22-6=-28.
Відповідь: -28 – А.

Приклад 22.15 На рисунку зображено графік функції y=f(x), визначеної на проміжку [-4;4].

Знайти множину всіх значень x, для яких f(x) ≤-2.

Розв’язування: Проведемо пряму y=-2 (паралельно осі Ox), та знайдемо такі значення x, при яких графік функції y=f(x) знаходиться під прямою y=-2

(і на прямій також, бо нерівність нестрога), тобто знайдемо розв’язки нерівності f(x) ≤-2:
x∈[0;3] .
Відповідь: [0;3] – А.

Приклад 22.16 За ескізом графіка y=ax+b вказати знаки параметрів a і b.

Розв’язування: Графіком функції y=ax+b є пряма. Функція зростає: f(x1)>f(x2), якщо x1>x2, або f(x1)<f(x2), якщо x1<x2, тоді a>0 (або якщо пряма утворює гострий кут з додатним напрямком осі Ox).
У завданні функція зростає, тому a>0.
Параметр b вказує на ординату перетину прямої y=ax+b з віссю Oy. На ескізі графіка b=-2<0.
Відповідь: a>0, b<0.

Приклад 22.39 Установити відповідність між функціями (1–4) та їх парністю (А–Д).

1. y=0
2. y=x³+tg(x)
3.y=x³-sin(x)
4. y=x⁵·sin(x)

А. На парність не досліджується
Б. Парна
В. Непарна
Г. Ні парна, ні непарна
Д. Парна і непарна

Розв’язування: Функція y=y(x) парна, якщо y(-x)=y(x) (графік симетричний відносно осі Oy).
Функція y=y(x) непарна, якщо y(-x)=-y(x) (графік симетричний відносно початку координат).
Наведемо допоміжний рисунок, щоб Ви переконалися в правильності міркувань.

1. y=0 — функція і парна, і непарна (особливий випадок) 1 — Д.
Запам’ятайте цей момент, оскільки на цьому рідко наголошують.
На графіку задана функція зображена чорним кольором (вісь Ox).

2. y(x)=x³+tg(x).
y(-x)=(-x)³+tg(-x)=-³-tg(x)=-(x³+tg(x))=-tg(x) — функція непарна 2 — В.
Функція y(x)=x³+tg(x) зображена синім кольором (симетрична відносно початку координат).

3. y(x)=x⁴-sin(x).
y(-x)=(-x)⁴-sin(-x)=x⁴+sin(x)≠±y(x) — функція ні парна, ні непарна 3 — Г.
Функція на графіку y(x)=x³+tg(x) зображена зеленим кольором.

4. y(x)=x⁵·sin(x).
y(-x)=(-x)⁵•sin(-x)=-x⁵•(-sin(x))=x⁵•sin(x)=y(x) — функція парна 4 — Б.
На графіку y(x)=x⁵·sin(x) зображена червоним кольором (симетрична відносно осі Oy).

Приклад 22.52 За якого найбільшого значення параметра a функція буде непарною?
Розв’язування: Функція f(x) непарна, якщо f(-x)=-f(x).
Складаємо рівняння з умови на парність
.
Розв’яжемо логарифмічне рівняння:
відносно параметра a.

a²=1,
a₁=1,
a₂=-1.
a=1 — найбільше значення, за якого функція буде непарною.
Відповідь: 1.

Знання властивостей функцій потрібні для швидкого їх дослідження, що перевіряється в шкільній практиці та продовжують вивчати у ВУЗах. Вступні тести є перехідним етапом, але через обмеженість часу Ви маєте вивчити великий об’єм матеріалу, тому починайти готуватися завчасно.

Область визначення складних кореневих, логарифмічних, тригонометричних функцій
Дослідження функції на монотонність, екстремуми, побудова графіка
Дослідження функції на монотонність, екстремуми, побудова графіка
Паралельне перенесення графіку функції, симетричне відображення, розтяг та стиск

Числові функції.

Їх властивості та графіки

При вивченні множин ми бачили, що можна задати зв’язок між множинами, тобто поставити відповідність між елементами двох множин. Така залежність, при якій кожному елементу з однієї множини (множини Х) ставиться у відповідність єдиний елемент з другої множини (множини Y), називається функцією. Зазначимо, що функція не є взаємно однозначною відповідністю: деякому елементу з множини Y може відповідати декілька елементів з множини X. Найчастіше позначається функція записом f, f(x),y, y(x).

Існує декілька способів задання функції.

Формульний. Наприклад, y=2x+4. Перевагою такого способу є те, що можна знайти значення функції в кожній точці. Недоліком є те, що потрібно час на обчислення, відсутня наочність.

Табличний. Задається таблицею, де прописується пара x,y.Перевагою такого способу є те, що дуже швидко знаходиться значення функції в певних точках. Недоліком є те, що не для всіх чисел задано значення.

x	y
2	5
7	11
15	4

Графічний. Перевагою цього способу є те, що наочно видно залежність між х та у, видно зміну значень. Недоліком є те, що неможливо встановити точного значення функції в певній точці.

Словесний. Застосовується тоді, коли функцію важко задати іншими способами.

Чим характеризується кожна функція? По-перше, можна вказати відповідні множини Х та У. Множина Х називається областю визначення функції і позначається D(y), множина Y називається областю значень функції і позначається E(Y).

Приклад 1.

Задано функцію y=4+x². Знайти область визначення та область значень функції.

Розв’язання. Оскільки замість х ми можемо поставити будь-яке дійсне число, то областю визначення функції є всі дійсні числа. Тобто D(y): x∈R (або x∈(-∞;+∞). Оскільки x

2 може приймати значення від 0 до +∞, то 4+x² може приймати значення від 4 до +∞. Тобто E(y): y∈[4;+∞).

Щоб отримати значення функції в певній точці, достатньо підставити у рівняння функції замість невідомої значення абсциси (х) точки. Відповідно, для того, щоб перевірити, чи належить точка графіку функції, достатньо підставити відповідні значення абсциси та ординати у рівняння. Якщо отримаємо рівність, то точка належить графіку функції, якщо ні — то не належить.

Приклад 2.

Знайти значення функції y=3x²+4x-2 в точці 5.

Розв’язання. у(5)= 3⋅5²+4⋅5-2=3⋅25+20-2=75+20-2=93.

Приклад 3.

Перевірити, чи належать точки (2;12),(3;38) графіку функції y=4x

2+2x-4.

Розв’язання. 1) Підставимо замість х число 2, замість у число 12. Отримаємо 12=4⋅2²+2⋅2-4, тобто 12=16. Рівність не вірна, тому точка (2;12) не належить графіку функції.
2) Підставимо замість х число 3, замість у число 38. Отримаємо 38=4⋅3²+2⋅3-4, тобто 38=38. Рівність вірна, тому точка (3;38) належить графіку функції.

Одним зі способів задання функції є графічний, коли показано залежність між множинами. Це дозволяє швидко охопити картину поведінки функції. Тому доцільно для функції будувати її графік. Отже, графік функції y(x) — множина точок координатної площини з координатами (х,у), де х∈D(y), y — відповідне значення функції при даному значенні х.

Властивості функції.

Якщо більшому значенню аргументу відповідає більше значення функції (якщо x₁<x

2, то y₁<y₂), то така функція називається зростаючою. Якщо ж навпаки, більшому значенню аргументу відповідає менше значення функції (якщо x₁<x₂, то y₁>y₂), то така функція називається спадною. Графік зростаючої функції виглядає як підйом у гору, а спадної — як спуск з гори.

Функція називається парною, якщо для будь-якого х з її області визначення f(-x)=f(x). Якщо значення функції при протилежних значення аргументу співпадає, то така функція називається парною. Прикладом парної функції є y=x² (y(-x)=(-x)²=x²=y(x)). Графік парної функції симетричний відносно осі ординат.

Якщо ж протилежним значенням аргумента відповідають протилежні значення функції, тобто f(-x)=-f(x), то така функція називається непарною.

Функція називається непарною, якщо для будь-якого х з її області визначення f(-x)=-f(x)

Прикладом непарної функції є y=x³ (y(-x)=(-x)³=-x³=-y(x)). Графік непарної функції симетричний відносно початку координат.

Зверніть увагу, що є також функції, які не є ні парними, ні непарними. Прикладом такої функції є y=x²+4х (y(-x)=(-x)²+4⋅(-х)=x²-4х. Таке значення не співпадає ні з y(x), ні з -y(x).

Приклад 4.

Дослідити функції на парність та непарність. 1) y=x⁴+3x²+5; 2) y=x³-2x; 3) y=x²+4x.

Розв’язання. 1) y(-x)=(-x)⁴+3(-x)²+5=x⁴+3x²+5=y(x). Функція парна. 2) y(-x)=(-x)³-2(-x)=-x³+2x=-(x³-2x)=-y(x). Функція непарна. 3) y(-x)=(-x)

2+4(-x)=x²-4x. y(-x) не дорівнює y(x), y(-x) не дорівнює -y(x). Функція ні парна, ні непарна.

Приклад 5.

Дослідити функції на парність та непарність за її графіком.

Розв’язання. 1) Оскільки графік функції симетричний відносно осі ОУ, то функція парна. 2) Оскільки графік функції не симетричний ні відносно осі ОУ, ні відносно початку координат, то функція ні парна, ні непарна. 3) Оскільки графік функції симетричний відносно початку координат, то функція непарна.

Определение функции четности и интуиция, характеристическая функция множества.

Мы определяем $\tilde x\in\mathbb{Z}$ и $\tilde x_i\in\mathbb{Z_2}$ (это битовое значение),

и $\tilde x_i = 1-2x_i$ ясно представлена следующая функция:

\begin{align*} f(x) = \begin{случаи} 1 &\text{если $x$ = 0}\\ -1 &\text{если $x$ = 1} \end{cases}\end{align*}

Когда $x$ (входной бит) равен $0$, функция возвращает $1$, иначе, если $x$ равно $1$, функция возвращает $-1$ .

9{N-1} е (\ тильда x_i), \end{align*}

Заглавная буква «пи» обозначает умножение последовательных значений. Следовательно, мы перемножаем вместе все четности. А поскольку $f(x)$ возвращает либо $1$, либо $-1$, то $P(\tilde x)$ возвращает либо значение $-1$, либо значение $1$. Процесс $P$ является итеративным, и значение $-1$ никогда не изменяется, если последующая четность также не равна $-1$ (тогда она меняет свой знак), эта четность будет переворачиваться столько раз, сколько единиц в таблице. бинарное расширение ($\tilde x$) и сохранение конечного состояния при $i=N-1$. Конечное состояние в основном зависит от количества $1$ в двоичном расширении. Короче говоря, каждый раз, когда $\tilde x_i=1$, произведение будет менять свой знак, но когда $\tilde x_i=0$, произведение никак не повлияет на результат. Эти два ряда действий легко понять, когда $x\cdot -1=-x$ и $x\cdot 1=x$. то есть:

$$+\cdot+ = +$$ $$+\cdot- = -$$ $$-\cdot+ = -$$ $$-\cdot- = +$$

Из приведенных выше рассуждений мы можем вывести некоторые факты:

когда $\tilde x$ имеет нечетное количество $1$ в своем двоичном представлении, $P$ вернет $-1$.
, когда $\tilde x$ имеет четное число $1$ в своем двоичном представлении, $P$ вернет $1$.

Примеры:

$$P(2_{10}) = P(10_2) = -1$$ $$P(13_{10}) = P(1101_2) = -1$$ $$P(27_{10}) = P(11011_2) = 1$$ $$P(60_{10}) = P(111100_2) = 1$$

Другие факты:

Длина бита сама по себе не влияет на четность.

Ответы:

1) Функция, которая возвращает младший (самый правый) бит аргумента.

$$P(00_2) = 1$$ $$P(01_2) = -1$$ $$P(10_2) = -1$$ $$P(11_2) = 1$$

Есть два возможных входа, при которых возвращается $1$: $0$ и $3_{10}$.

2) Функция, возвращающая k-нумерованный бит аргумента, где k меньше n.

Я не уверен, что вы имеете в виду под k-нумерованным битом аргумента. Предполагая, что вы имеете в виду битовую длину аргумента, это не влияет на выходную четность.

3) const f(x) = 1

Функция является четной только тогда, когда $\tilde x = 0$ или в двоичном представлении $\tilde x$ есть четное число $1$.

4) const f(x) = 0

$0=$ паритет $1$

5) «Характеристическая функция множества мощности 5»

Предположим, вы имеете в виду, что паритет $1$ четный, тогда $5$ четный.

6) f(x)=1, только если x имеет нечетное количество единиц при записи в двоичном формате

False, $P(\tilde x)=-1$, если число единиц нечетное.

7) f(x)=1, только если x имеет четное число единиц при записи в двоичном формате

Верно, $P(\tilde x)=1$, если число единиц четное.

Определение, формула, принцип работы и примеры

Что такое паритет пут-колл?

Термин «паритет пут-колл» относится к принципу, определяющему взаимосвязь между ценой европейских опционов пут и колл одного и того же класса. Проще говоря, эта концепция подчеркивает согласованность этих же классов. Опционы пут и колл должны иметь одинаковый базовый актив, цену исполнения и дату экспирации, чтобы быть в одном классе. Паритет пут-колл, применимый только к европейским опционам, можно определить с помощью уравнения.

Основные выводы

Паритет пут-колл показывает взаимосвязь, которая должна существовать между европейскими опционами пут и колл, имеющими одинаковый базовый актив, дату истечения и цену исполнения.
Эта концепция гласит, что цена колл-опциона подразумевает определенную справедливую цену соответствующего пут-опциона с той же ценой исполнения и сроком действия, и наоборот.
Паритет пут-колл не применяется к американским опционам, поскольку вы можете исполнить их до даты истечения срока.
Если соотношение пут-колл нарушается, возникают возможности для арбитража.
Вы можете определить сторону пут-колл, используя формулу C + PV(x) = P + S.

Паритет пут-колл

Понимание четности пут-колл

Как отмечалось выше, паритет пут-колл — это концепция, применимая к европейским опционам. Эти опционы относятся к одному классу, то есть у них есть базовый актив, цена исполнения и дата экспирации. Таким образом, этот принцип не применяется к американским опционам, которые могут быть исполнены в любое время до истечения срока действия.

Паритет пут-колл утверждает, что одновременное владение коротким европейским путом и длинным европейским коллом того же класса принесет такую же прибыль, как и владение одним форвардным контрактом на тот же базовый актив с тем же сроком действия и форвардной ценой, равной страйку опциона. цена.

Если цены опционов пут и колл расходятся так, что это соотношение не сохраняется, существует возможность арбитража. Это означает, что опытные трейдеры теоретически могут получать безрисковую прибыль. Такие возможности редки и недолговечны на ликвидных рынках.

Уравнение, выражающее паритет пут-колл:

С + п В ( Икс ) «=» п + С где: С «=» Цена европейского колл-опциона п В ( Икс ) «=» Текущая стоимость цены исполнения (x), со скидкой от стоимости по истечении срока действия дата по безрисковой ставке п «=» Цена европейского пута С «=» Спотовая цена или текущая рыночная стоимость базового актива \begin{aligned}&C + PV(x) = P + S \\&\textbf{где:} \\&C = \text{Цена европейского колл-опциона} \\&PV(x) = \text{Текущая стоимость от цены исполнения (x),} \\&\text{дисконтировано от значения на момент экспирации} \\&\text{дата по безрисковой ставке} \\ &P = \text{Цена европейского пут} \\&S = \text{Спотовая цена или текущая рыночная стоимость} \\&\text{базового актива} \\\end{aligned} C+PV(x)=P+S, где:C=Цена европейского колл-опционаPV(x)=Текущая стоимость цены исполнения (x), дисконтированная от стоимости на дату экспирации по безрисковой ставкеP=Цена европейский пут=цена спот или текущая рыночная стоимость базового актива

Концепция паритета пут-колл была введена экономистом Хансом Р. Столлом в его статье «Взаимосвязь между ценами опционов пут и колл» в декабре 1969 года, которая была опубликована в The Journal of Finance .

Особые указания

Когда одна сторона уравнения паритета пут-колл больше другой, это представляет собой возможность арбитража. Вы можете продать более дорогую часть уравнения и купить более дешевую, чтобы получить во всех смыслах безрисковую прибыль.

На практике это означает продажу пут, короткую продажу акций, покупку колла и покупку безрискового актива (например, TIPS). На самом деле возможности для арбитража недолговечны и их трудно найти. Кроме того, маржа, которую они предлагают, может быть настолько незначительной, что для того, чтобы воспользоваться ими, потребуется огромный капитал.

Паритет пут-колл и арбитраж

На двух графиках выше ось y- представляет стоимость портфеля, а не прибыль или убыток, потому что мы предполагаем, что трейдеры раздают опционы. Но это не так, и цены европейских опционов пут и колл в конечном итоге регулируются паритетом пут-колл. На теоретическом, совершенно эффективном рынке цены на европейские опционы пут и колл будут регулироваться уравнением, которое мы отметили выше:

С + п В ( Икс ) «=» п + С \begin{выровнено}&C + PV(x) = P + S \\\end{выровнено} C+PV(x)=P+S

Предположим, что безрисковая ставка составляет 4%, а акции TCKR торгуются по 10 долларов. Давайте продолжим игнорировать комиссии за транзакции и предположим, что TCKR не выплачивает дивиденды. Для опционов TCKR со сроком действия один год и ценой исполнения 15 долларов мы имеем:

С + ( 15 ÷ 1,04 ) «=» п + 10 4,42 «=» п − С \begin{выровнено}&C + ( 15 \div 1.04 ) = P + 10 \\&4.42 = P — C \\\end{выровнено} С+(15÷1,04)=Р+104,42=Р-С

На этом гипотетическом рынке путы TCKR должны торговаться с премией в 4,42 доллара к соответствующим коллам. Поскольку TCKR торгуется по цене всего 67% от цены исполнения, бычий колл, кажется, имеет более высокие шансы, что интуитивно понятно. Допустим, это не так, хотя по какой-то причине путы торгуются по 12 долларов, а коллы по 7 долларов.

Допустим, вы покупаете европейский колл-опцион на акции TCKR. Дата экспирации — через год, цена исполнения — 15 долларов, а покупка колла стоит 5 долларов. Этот контракт дает вам право, но не обязательство, купить акции TCKR по истечении срока действия за 15 долларов, какой бы ни была рыночная цена.

Если через год TCKR будет торговаться по 10 долларов, вы не воспользуетесь опционом. Если, с другой стороны, TCKR торгуется по 20 долларов за акцию, вы воспользуетесь опционом, купите TCKR по 15 долларов и безубыточности, поскольку изначально вы заплатили 5 долларов за опцион. Любая сумма TCKR, превышающая 20 долларов США, является чистой прибылью при нулевой комиссии за транзакцию.

7 + 14.42 < 12 + 10 21.42 доверительный звонок < 22 защищенный пут \begin{выровнено}&7 + 14.42 < 12 + 10 \\&21.42 \ \text{фидуциарное требование} < 22 \ \text{защищенное размещение} \\\end{выровнено} 7+14.42<12+1021.42 фидуциарный вызов<22 защищенный пут

Защитный слой

Еще один способ представить паритет пут-колл — сравнить производительность защитного пут-опциона и фидуциарного колл-опциона одного и того же класса.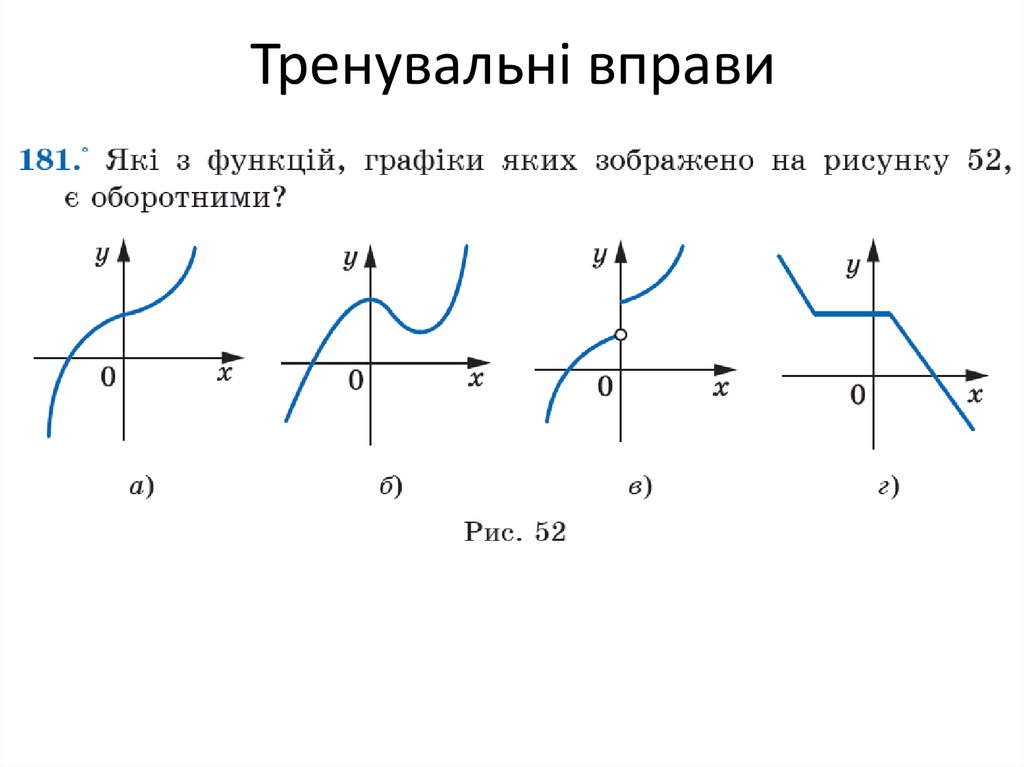 Защитный пут — это длинная позиция по акциям в сочетании с длинным путом, который ограничивает отрицательную сторону владения акциями.

Фидуциарный звонок

Фидуциарный колл — это длинный колл в сочетании с денежными средствами, равными приведенной стоимости (с поправкой на ставку дисконтирования) цены реализации; это гарантирует, что у инвестора будет достаточно денежных средств для исполнения опциона в дату истечения срока действия. Ранее мы говорили, что опционы пут и колл TCKR со страйком $15 и сроком действия в один год торгуются по $5, но давайте на секунду предположим, что они торгуются бесплатно.

Пример паритета пут-колл

Допустим, вы также продаете (или «выписываете» или «коротко») европейский пут-опцион на акции TCKR. Дата экспирации, цена исполнения и стоимость опциона одинаковы. Вы получаете 5 долларов за продажу опциона, и вам не решать, использовать ли опцион или нет, поскольку вы им не владеете. Покупатель приобретает право, но не обязательство, продать вам акции TCKR по цене исполнения. Это означает, что вы обязаны заключить эту сделку, какой бы ни была рыночная цена акций TCKR.

Таким образом, если TCKR торгуется по 10 долларов через год, покупатель продает вам акции по 15 долларов. Вы оба безубыточны — вы уже заработали 5 долларов на продаже опциона пут, восполнив свой дефицит, в то время как покупатель уже потратил 5 долларов на его покупку, поглотив свою прибыль. Если TCKR торгуется по цене 15 долларов или выше, вы зарабатываете 5 долларов и только 5 долларов, поскольку другая сторона не использует опцион. Если TCKR торгуется ниже 10 долларов, вы теряете деньги — до 10 долларов, если TCKR падает до нуля.

Прибыль или убыток по этим позициям для разных цен на акции TCKR выделены на графике непосредственно над этим разделом. Обратите внимание, что если вы добавите прибыль или убыток от длинного колла к короткому путу, вы заработаете или потеряете ровно столько, сколько получили бы, если бы просто подписали форвардный контракт на акции TCKR по цене 15 долларов, срок действия которого истекает через год. Если акции продаются менее чем за 15 долларов, вы теряете деньги. Если они пойдут на большее, вы выиграете. Опять же, этот сценарий игнорирует все комиссии за транзакции.

Почему важен паритет пут-колл?

Паритет пут-колл позволяет рассчитать приблизительную стоимость пут-колла по отношению к другим его компонентам. Если соотношение пут-колл нарушается, что означает, что цены опционов пут и колл расходятся, так что это соотношение не сохраняется, существует возможность арбитража. Хотя такие возможности редки и краткосрочны на ликвидных рынках, опытные трейдеры теоретически могут получать безрисковую прибыль. Кроме того, он предлагает гибкость для создания синтетических позиций.

Какова формула паритета пут-колл?

Паритет пут-колл утверждает, что одновременная покупка и продажа европейского колл-опциона и пут-опциона одного и того же класса (тот же базовый актив, цена исполнения и дата экспирации) идентична покупке базового актива прямо сейчас. Обратное этому соотношению также было бы верно.

Цена опциона «колл» + PV(x) = цена опциона «пут» + текущая цена базового актива

-или-

Текущая цена базового актива = цена опциона «колл» — цена опциона «пут» + PV(x)

где: PV(x) = текущая стоимость цены исполнения (x), дисконтированная от стоимости на дату экспирации по безрисковой ставке

Как оцениваются опционы?

Цена опциона представляет собой сумму его внутренней стоимости, которая представляет собой разницу между текущей ценой базового актива и ценой исполнения опциона, и временной стоимости, которая напрямую связана со временем, оставшимся до истечения срока действия опциона.