Делимое которое нацело делится на какое нибудь число: Как называется делимое к делителю. Деление нацело или без остатка

что такое, чем отличаются друг от друга, как найти, примеры решения

Что такое делители и кратные числа

Определение 1

Деление — математическое действие, которое определяет, сколько раз одно число содержится в другом. Обратной операцией является умножение.

Выделяют следующие компоненты деления:

• делимое;
• делитель;
• частное.

Определение 2

Делимое — число, которое делят на несколько частей.

Делитель — число, которое показывает, на сколько частей нужно разделить делимое.

Частное — число, которое является результатом деления.

a:b =c , где a — делимое, b — делитель, c — частное.

Умножение частного на делитель дает делимое.

Чтобы получить делитель, нужно делимое разделить на частное.

Делимое = частное * делитель

Дельтель = делимое / частное

Пример 1

Например, нужно поровну разделить 16 мандаринов между двумя детьми. Для этого 16:2=8. Таким образом, каждый ребенок получит по 8 мандаринов.

16 в этом примере является делимым, 2 — делителем, 8 — частным. Шестнадцать поделили на две части, по восемь в каждой. Или восемь содержится в 16 два раза. Или 2 содержится в 16 восемь раз. Деление прошло без остатка — нацело. Тогда число 2 является делителем числа 16.

Определение 3

Делителем числа a называется такое число b, на которое a делится нацело.

Пример 2

Например, 9:4=2 (остаток 5).

В примере 9 — делимое, 4 — делитель, 2 — неполное частное, 5 — остаток.

Остаток от деления — число, которое меньше делителя. Образуется при делении с остатком. Значит, в примере 9:4=2 (остаток 5) — число 4 не является делителем числа 9.

Упражнение 

Задание: найдите такую пару делителей числа 144, если один из делителей равен 2.

Объяснение:

Пусть неизвестный делитель равен x. Чтобы найти еще один делитель, если какой-то известен, нужно данное нам число разделить на известный делитель.

Тогда представим решение данной задачи в виде уравнения:

144:x = 2;

x = 144:2;

x=72.

72 — целое число, без остатка.

Проверка:

Произведение делителей должно дать в результате 144:

72*2 = 144 — верно, значит, 72 — корень уравнения и делитель 144.

Ответ: числа 2 и 72 — делители 144.

Определение 4

Число называют кратным, если оно делится на данное число нацело, без остатка.

Пример 3

Например, 15:3 нацело.

15:3=5.

Тогда число 15 является кратным 3.

Пишут: 15 кратно 3.

Слово «кратно» синонимично слову «делится».

Фразу «15 кратно 3» можно в уме заменить на «15 делится на 3 нацело».

Примечание 1

Основные понятия и определения

Определение 5

Делитель — это число, на которое данное число делится нацело. Делитель всегда меньше или равен числу.

Делится нацело = без остатка.

Наименьшим делителем любого числа является единица.

Наибольшим делителем числа является само число.

Делителем нуля будет любое число, но сам 0 делителем не будет.

При делении нуля на любое число получаем 0. А делить на ноль нельзя.

У единицы только один делитель — единица.

Другие числа, кроме 1, имеют не меньше двух делителей.

Определение 6

Кратное — число, которое делится на данное число нацело. Всегда больше или равно числу.

Наименьшее кратное числа является равным самому числу.

Наибольшее кратное подобрать нельзя, потому что ряд натуральных чисел бесконечен. У любого натурального числа бесконечное множество кратных.

Ноль является кратным для любого числа. При умножении на ноль всегда получается ноль.

Когда одно число делится нацело на другое, то первое число — кратное второго, а второе — делитель первого.

Примечание 2

a:b=c, где а — кратное b и c — делитель a

Чем отличаются друг от друга, как найти

Делитель отличается от кратного тем, что:

• делитель — это число, НА которое делится заданное число;
• кратное — это число, которое само ДЕЛИТСЯ НА заданное число.

Чтобы найти делители числа, нужно данное число разложить на множители.

Разложить на множители — представить число в виде произведения целых чисел.

Чтобы проверить, является ли одно число делителем другого, нужно разделить число на данное нам.

Для нахождения кратного числа заданному числу, нужно это число последовательно умножать на натуральные числа. Каждое полученное число будет кратно — будет делиться — заданному.

Делители и кратные связаны между собой. Например, делителем числа 15 является 3 и число, кратное 3, равно 15.

Примеры решения задач

Задача 1

Необходимо найти делители числа 14.

Решить задание можно двумя способами.

Способ 1:

Последовательно делим 14 на натуральные числа от 1 до 14. Помним, что делитель всегда меньше или равен заданному числу.

Выбираем такие числа в качестве делителя, при делении на которые мы не получили остаток: 1, 2, 7, 14.

Ответ: делители числа 14: 1, 2, 7, 14.

Способ 2:

Представим 14 в виде произведения чисел:

14 = 14*1 = 2*7

Делителями будут множители, так как можем разделить 14 нацело на каждый из них.

Ответ: делители 14: 1, 2, 7, 14.

Задача 2

Найдите три числа, кратных 7.

Решение:

Чтобы найти число, кратное данному, нужно это число умножить на любое натуральное число.

7*1 = 7 — семь кратно семи;

7*2=14— 14 кратно 7;

7*3=21— 21 кратно 7.

Ответ: числа, кратные 7: 7, 14, 21.

Задача 3

Самостоятельно проверьте, 225 кратно 3 или нет.

Чтобы проверить, кратно ли одно число другому, нужно разделить числа друг на друга.

225:3=75.

75 — целое число, при делении нет остатка. Тогда 225 кратно 3.

Задача 4

Найдите любое число, делителями которого являются числа 7 и 8.

Самый простой способ, если в задании не оговорены еще какие-либо условия, просто перемножить эти делители:

 7*8=56

Ответ: 56.

ДЕЛЕНИЕ НА 8: НАЦЕЛО И С ОСТАТКОМ

Примеры.

Открыть в полном размере

‹

›

Благодарен вашему журналу за публикацию моего материала о признаке делимости целых чисел на 7 (см. «Наука и жизнь» № 10, 1997 г.). Рискну предложить еще один новый признак делимости, но уже на 8.

Я перелистал много книг по занимательной математике, но такого признака не нашел нигде.

Общепринятый признак делимости на 8 выглядит так: число делится на 8 в том и только в том случае, если его последние три цифры образуют число, делящееся на 8.

Этот способ деления основан на том, что все числа, кратные 1000, делятся на 8 без остатка.

Значит, определение признака делимости на 8 любых многозначных целых чисел сводится в итоге к определению признака делимости на 8 трехзначных чисел.

Трехзначные числа и будем рассматривать.

Б. А. Кордемский сводит делимость уже трехзначных чисел к делимости двузначных (образованных цифрами сотен и десятков): «На 8 делится всякое трехзначное число, у которого двузначное число, образованное цифрами сотен и десятков, сложенное с половиной числа единиц, делится на 4».

Он приводит пример с числом 592. Применяя к нему признак делимости, получаем:

59 + 1 = 60,

где 1 — это 2:2, половина числа единиц.

Число 60 делится на 4, значит, число 592 делится на 8 без остатка.

При данном методе определения остатка от деления надо учитывать, что трехзначные числа, оканчивающиеся нечетной цифрой (1, 3, 5, 7, 9), надо сначала «округлить» в разряде единиц до ближайшей большей или меньшей четной цифры и в конечном результате опять же учесть эту единицу, то есть прибавить ее или отнять.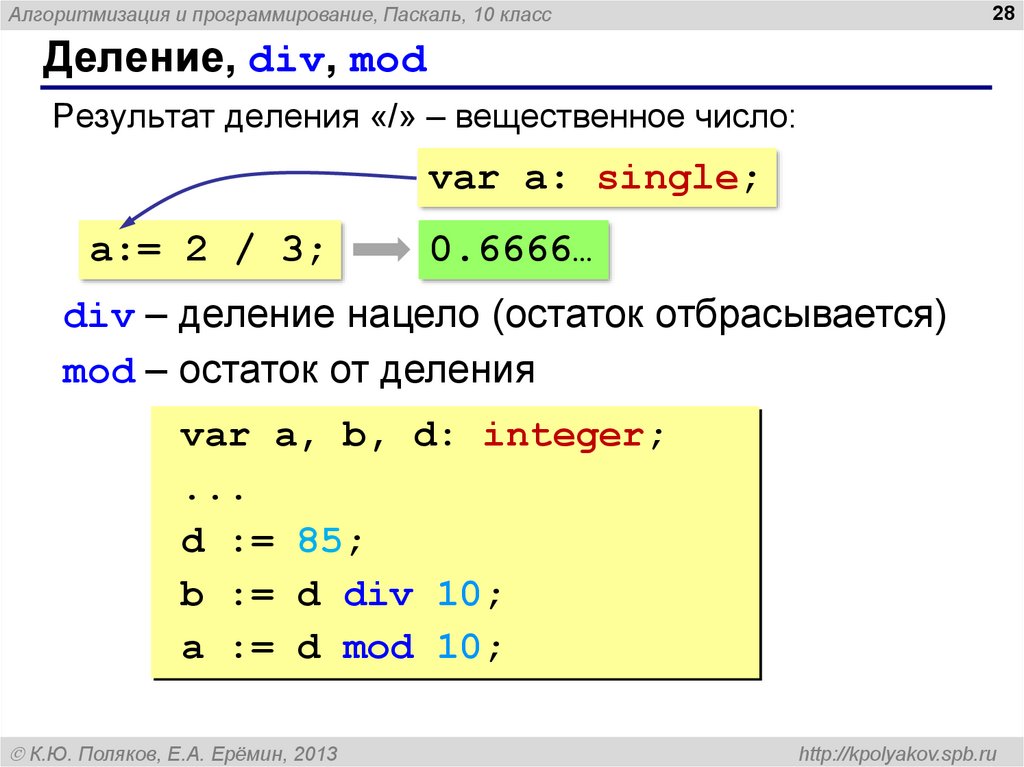

Это первое.

Второе: в некоторых случаях сумма двузначного числа, образованного цифрами сотен и десятков, и половины единиц будет также трехзначным числом, что опять же не совсем удобно. Это будет происходить с рядом чисел в промежутке от 968 до 999.

Однако всех этих неудобств — прибавления (вычитания) 1 и оперирования трехзначными числами — можно избежать.

Вспомним, что четное число сотен — 2, 4, 6, 8 (200, 400, 600, 800) делится на 8 без остатка. Следовательно, у таких, к примеру, чисел, как 059, 237, 461, 632, 844, определить остаток от деления на 8 можно сразу по двузначному числу, составленному из десятков и единиц, то есть по числам 59, 37, 61, 32, 44. Достаточно в уме разделить эти двузначные числа на 8.

Если цифры сотен в трехзначных исходных числах нечетны (1, 3, 5, 7, 9), то опять же делим на 8 двузначные числа, образованные десятками и единицами, но в этом случае прибавляем (или отнимаем) к двузначным числам цифру 4. Этот факт следует из того, что все целые нечетные сотни (100, 300, 500, 700, 900) при делении на 8 дают один остаток — 4.

Для примера возьмем числа 165, 371, 587, 716, 923. «Превратим» их в двузначные числа, прибавляя (можно отнимая) 4:

69, 75, 91, 20, 27.

Делить эти двузначные числа на 8 опять же просто. Остатки от делений и будут остатками от деления на 8 исходных трехзначных чисел.

А как поступить, если трехзначное число 997?

Выше говорилось, что цифру 4 можно не только прибавлять, но и отнимать от двузначного числа. Значит, делить на 8 будем уже число 93: 97- 4 = 93.

Так происходит «избавление» от трехзначных чисел.

Обобщая все вышесказанное, алгоритм упрощенного признака делимости на 8 целых чисел можно записать так: отделяем, отсчитывая справа, три цифры исходного числа; если третья справа цифра четная (0, 2, 4, 6, 8), то делим на 8 только число, образованное двумя крайними правыми цифрами; остаток от этого деления и будет остатком от деления на 8 всего исходного числа; если третья справа цифра в исходном числе нечетная (1, 3, 5, 7, 9), делим на 8 число, образованное двумя крайними правыми цифрами, плюс (минус) 4; остаток от деления этой суммы и даст остаток от деления на 8 всего исходного целого числа.

Как видно, этот признак делимости совсем прост, и для его освоения понадобятся минимальные усилия и знание элементарной арифметики.

Литература

Кордемский Б. А. Математическая смекалка. М., 1991.

Воробьев Н. Н. Признаки делимости. М., 1980.

Гарднер М. Математические досуги. М., 1995.

Делимое

Когда делимое делится на делитель, а частное представляет собой целое число без остатка, говорят, что делимое делится на делитель.

На рисунке ниже показано, что 8 делится на 2, но не на 3. Слева мы видим, что 8 можно без остатка разделить на 4 группы по 2. С другой стороны, 8 нельзя разделить на 3 группы. Только 2 группы могут содержать 3 объекта, а третья группа может содержать только 2 объекта.

Примеры

Определите, являются ли следующие элементы делимыми.

1. 48 ÷ 8:

48 &дел. 8 = 6

48 делится на 8.

2. 32 ÷ 5:

32 &дел.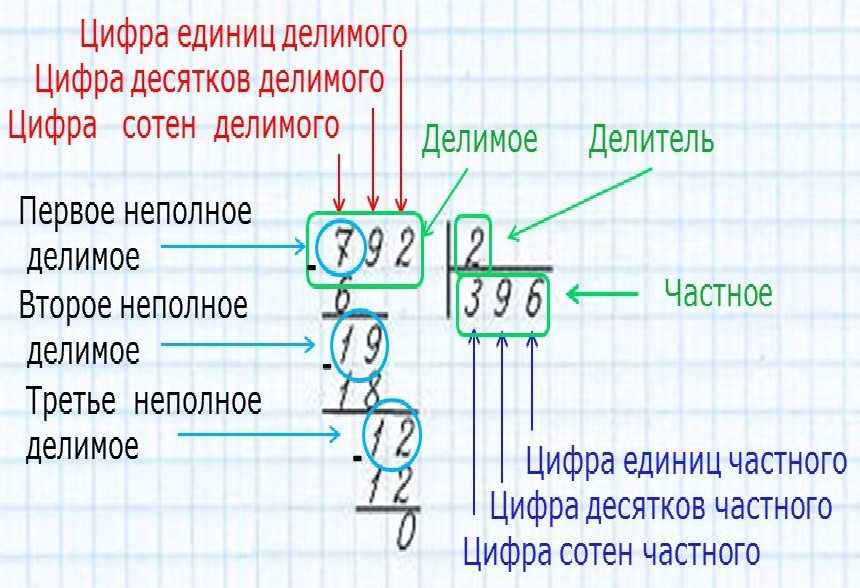 5 = 6 R2

32 не делится на 5.

Определение того, делится ли число на определенное целое путем деления вручную и проверки остатка, может очень быстро стать утомительным, поскольку числа становятся больше. К счастью, есть несколько быстрых тестов, с помощью которых можно проверить, делится ли заданное число на определенные целые числа. В некоторых случаях выполнить деление может быть быстрее, но в других эти тесты могут сэкономить время. Ниже приведены тесты на делимость чисел от 1 до 10.

Признак делимости на 1

Все числа делятся на 1. Независимо от того, что это за число, при делении его на 1 получится одно и то же число.

Признак кратности 2

Если цифра в разряде единиц (последняя цифра) числа четная (0, 2, 4, 6, 8), то число делится на 2.

Пример

Проверить, следующие числа делятся на 2.

1. 5568:

8 делится на 2, поэтому 5568 делится на 2.

2. 527:

7 не делится на 2, поэтому 527 не делится на 2.

Делимость на 3

Найдите сумму всех цифр в числе. Если сумма цифр числа делится на 3, то это число делится на 3.

Пример

Проверить, делятся ли следующие числа на 3.

1. 273:

2 + 7 + 3 = 12

12 делится на 3, поэтому 273 делится на 3.

2. 323:

3 + 2 + 3 = 8

8 не делится на 3, поэтому 323 не делится на 3.

Делимость на 4

Если число, состоящее из двух последних цифр числа, делится на 4, то это число делится на 4.

Пример

Проверить, делятся ли следующие числа на 4.

1. 428:

28 ÷ 4 = 7

28 делится на 4, поэтому 428 делится на 4.

2. 1055:

55 ÷ 4 = 13 R3

55 не делится на 3, поэтому 1055 не делится на 3.

Признак кратности 5

Если последняя цифра в числе 5 или 0, то число делится на 5.

Пример

Проверить, делятся ли следующие числа на 5.

1. 3325:

Последняя цифра числа 3325 — 5, поэтому число 3325 делится на 5.

2. 325270:

Последняя цифра числа 325270 — 0, поэтому число 325270 делится на 5.

3. 4872: 900 03

Последняя цифра в 4872 не равно ни 0, ни 5, поэтому оно не делится на 5.

Признак кратности 6

Если число делится и на 2, и на 3, то оно делится и на 6.

Пример

Проверить, делятся ли следующие числа на 6.

1. 2358:

2358 &дел ; 2 = 1179

2358 &дел; 3 = 786

2358 делится и на 2, и на 3, поэтому оно делится на 6. Обратите внимание, что мы могли бы также использовать тесты на делимость для 2 и 3, а не решать задачу деления; вывод был бы таким же. 8 — четное число, поэтому 2358 делится на 2. 2 + 3 + 5 + 8 = 18, что делится на 3, поэтому 2358 делится на 3.

2. 4528:

4528 ÷ 2 = 2264

4528 &дел; 3 = 1509 R1

4528 делится на 2, но не на 3, поэтому 4528 не делится на 6.

3. 123:

123 ÷ 3 = 41

123 &дел; 2 = 61 R1

123 делится на 3, но не на 2, поэтому 123 не делится на 6. продукт от исходного номера. Если результат делится на 7, то исходное число делится на 7.

Пример

Проверить, делятся ли следующие числа на 7.

1. 567:

7 × 2 = 14

56 — 14 = 42

42 ÷ 7 = 6

42 делится на 7, значит, 567 делится на 7. &дел; 7 = 5 R3

38 не делится на 7, поэтому 548 не делится на 7.

Делимость на 8

Если последние 3 цифры в числе равны 0, число делится на 8. Если последние 3 цифры цифры не равны 0, но число, образованное последними 3 цифрами исходного числа, делится на 8, тогда исходное число делится на 8.

Пример

Проверить, делятся ли следующие числа на 8.

1. 231968:

968 ÷ 8 = 121

968 делится на 8, значит, 231968 делится на 8.

2. 347823000:

делится на 8.

Делимость на 9

Если сумма цифр числа делится на 9, тогда число делится на 9. И наоборот, число, которое дважды делится на 3, делится на 9.

Пример

Проверить, делятся ли следующие числа на 9.

1. 2349:

2 + 3 + 4 + 9 = 18

18 делится на 9, поэтому 2349 делится к 9.

2 405

405 &дел; 3 = 135

135 &дел; 3 = 45

405 делится на 3 дважды, поэтому 405 делится на 9.

Делимость на 10

Если последняя цифра в числе 0, то число делится на 10.

Пример

Проверить, делятся ли на 10 следующие числа. некоторые случаях проверка делимости может быть более утомительной, чем выполнение деления. Показаны только тесты на делимость от 1 до 10, поскольку они относительно просты.

Делитель — определение, формула, свойства, примеры

A делитель — это число, которое делится на другое число. Без делителя мы не можем делить числа. При делении используются четыре важных термина: делимое, делитель, частное и остаток. Деление — это метод равномерного распределения предметов по группам. Число, которое необходимо разделить, называется делимым, а общее количество равных групп, на которые оно должно быть разделено, называется делителем.

Число, которое не учитывается без образования группы, называется «остатком».

1.	Что такое делитель?
2.	Как найти делитель?
3.	Формула делителя
4.	Факты о делителях
5.	Разница между делителем и множителями
6.	Часто задаваемые вопросы о делителях

Что такое делитель?

Делитель делит число на равные группы. Число, которое делится, называется делимым , а число, на которое оно делится, называется делителем

.

Делитель Значение

Число, которое делится на другое число с остатком или без него, называется делителем.

Существуют разные способы записи задачи на деление. На следующем рисунке показаны различные способы выражения деления и показано, как идентифицировать делитель, делимое и частное.

Как найти делитель?

Без делителей деление невозможно. Это означает, что определить делитель довольно просто. Например, если нам нужно разделить число 35 на 5, его можно представить как 35 ÷ 5 = 7. Здесь число 35 — делимое, число 5 — делитель , а число 7 — частное .

Иногда мы знаем значение делимого и частного и нам нужно найти делитель. В этом случае мы используем формула делителя . Давайте узнаем о формуле делителя в следующем разделе.

Формула делителя

Формула делителя формируется для двух ситуаций — с остатком или без остатка:

• Если остаток равен 0, то Делитель = Дивиденд ÷ Частное.
• Если остаток не равен 0, то Делитель = (Дивиденд — Остаток) ÷ Частное

Пример 1: Найдите делитель, если делимое равно 48, а частное равно 4.

Решение: Мы знаем, что делимое = 48, частное = 4. Итак, применим формулу делителя Делитель = Делимое ÷ Частное. Подставляя известные значения в формулу, получаем Делитель = 48 ÷ 4 = 12. Следовательно, делитель = 12.

Пример 2: Найдите делитель, если делимое равно 59, частное 11, а остаток равен 4.

Решение: Мы знаем, что делимое = 59, частное = 11, остаток = 4. Итак, применим формулу делителя Делитель = (Дивиденд — Остаток) ÷ Частное. Подставив известные значения в формулу, получим, Делитель = (59- 4) ÷ 11 = 55 ÷ 11 = 5. Следовательно, делитель = 5.

Факты о делителях

Вот список некоторых фактов, связанных с делителем.

• Если частное равно делимому, то делитель равен 1. Например, 45 ÷ 1 = 45
• Когда делимое и делитель равны в задаче на деление, частное равно 1. Например, 45 ÷ 45 = 1
• Частным называется число, которое получается при делении делимого на делитель, а любое число, оставшееся после деления, называется остатком.
• Остаток всегда меньше делителя.
• Когда остаток равен нулю, это означает, что делитель полностью разделил делимое.
• Если делитель больше делимого, результирующее число будет десятичным числом. Например, 45 ÷ 100 = 0,45·
.

Разница между множителем и делителем

Мы знаем, что делитель — это число, на которое делится делимое. Когда делитель полностью делит делимое и не оставляет остатка, этот делитель также называется множителем этого числа. Таким образом, все делители числа являются делителями, но не всегда все делители должны быть делителями числа.

Пример 1: Множители 8 = 1, 2, 4 и 8. Это означает, что 8 полностью делится на 1, 2, 4, 8. Следовательно, все эти множители в данном случае являются делителями.
Пример 2: Разделите 12 на 5. Если мы разделим 12 на 5, мы получим 2 в качестве частного, а остаток равен 2. Это означает, что 12 ÷ 5 = 2, остаток = 2. В этом случае делитель равен 5, но 12 не делится полностью на 5. Таким образом, 5 не является делителем 12, но является делителем 12, так как дает остаток 2.
Следовательно, все делители являются делителями, но не все делители являются факторами.

Важные советы по делителю

Ниже приведены некоторые важные советы, связанные с делителем, которые мы изучили в этой статье.

• Делитель не может быть равен нулю, потому что при делении числа на ноль результат не определен.
• Задача на деление остается верной, даже если поменять местами частное и делитель.
• Когда ноль делится на любой делитель, в частном всегда получается ноль.

☛Статьи по теме

• Дивизион Формула
• Формула остатка делителя дивиденда
• Деление десятичных дробей

Часто задаваемые вопросы о делителях

Что такое делитель в математике?

Число, на которое делится другое число, называется делителем . Например, когда мы делим 20 на 4, мы получаем 5. Когда мы записываем это как 20 ÷ 4 = 5, здесь 4 — это число, на которое делится число 20. Следовательно, 4 называется делителем.

Является ли число делителем самого себя?

Да, число является делителем самого себя, потому что число может полностью делиться само на себя. Это означает, что частное будет равно 1. Например, 23 ÷ 23 = 1

Что такое делитель в дроби?

Дробь представляется в виде p/q, (где q не равно 0). Здесь знаменатель q является делителем. Например, в дроби 6/2 знаменатель 2 является делителем.

Что такое формула делителя?

Мы используем формулу делителя, когда знаем значение делимого и частного. У нас есть два сценария, чтобы найти делитель.

• Если остаток равен 0, то Делитель = Делимое ÷ Частное.
• Если остаток не равен 0, то Делитель = (Дивиденд — Остаток) ÷ Частное

Чему равен делитель в факте деления 30 ÷ 15 = 2?

Делитель — это число, на которое делится другое число. Здесь 30 делится на 15. Следовательно, 15 — делитель.

В чем разница между делителем и дивидендом?

Делитель делит число на равные группы.

No related posts.