Введение в задачи с параметром: решение уравнений с параметром
На этой странице вы узнаете- Игра в прятки: как значение одной переменной может помочь найти другую?
- Парадокс: как стоять на месте и бежать с любой скоростью одновременно?
- Решаем параметры осторожно: как не совершить ошибку в квадратном уравнении с параметром?
Мы привыкли, что в уравнении коэффициенты не меняются. Но возможно ли из одного уравнения составить бесконечное множество различных его вариантов? Узнаем об этом в статье.
Что такое параметрУтром на термометре было некоторое количество градусов, которое мы обозначим за х. В обед температура воздуха изменилась в несколько раз. Во сколько раз должна была измениться температура воздуха, чтобы на термометре было 20 градусов?
Такие задачи достаточно легко решаются. Если бы изначально было пять градусов, то искомое число было бы равно \(\frac{20}{5} = 4\). А если было 10 градусов, то искомое число было бы равно \(\frac{20}{10} = 2\).
А если было 10 градусов, то искомое число было бы равно \(\frac{20}{10} = 2\).
Но не все так просто. Мы не знаем, какой изначально была температура. Также мы не знаем, во сколько раз она изменилась. То есть мы получили уравнение с двумя неизвестными переменными.
Обозначим вторую переменную a, у нас получится уравнение вида ax=20. Только что введенная нами переменная “a” называется параметр.
Параметр — это условная буква, вместо которой можно подставить число.
То есть параметр — это еще одна переменная, которая может принять несколько значений.
Как решать уравнения с параметром, если у нас целых две (а то и больше) неизвестных переменных? Нужен иной подход, чем при решении обычного уравнения.
Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется.
Мы ищем не единственное значение параметра, а все возможные его значения для заданного условия.
| Игра в прятки: как значение одной переменной может помочь найти другую? Поскольку параметр — переменная в уравнении, которая является коэффициентом, его значение задает и корни уравнения. |
Вернемся к нашей погоде. У нас получилось уравнение ax = 20. Как найти, сколько градусов было изначально? Разделить все уравнение на число a.
\(x = \frac{20}{a}\)
Какие значения может принимать параметр? Любые. Например, при a = 1 x = 20.
При a = 2 x = 10.
При a = 40 x = 0,5
Что, если a=0? Мы получаем уравнение \(x = \frac{20}{0}\), у которого нет решения, поскольку на 0 делить нельзя.
Если мы не будем преобразовывать изначальное уравнение, то получится 0*x=20, то есть уравнение не будет выполняться: какое бы число мы ни умножили на 0, получится 0.
Получается, решение есть при любых значениях a, кроме 0. Таким образом, мы и нашли ответ: при a = 0 решений нет, при a \(\neq\) 0 — x = 20a.
Добавим немного теории. Представим наше уравнение в виде ax = b, где a, b — действительные числа. Рассмотрим несколько случаев.
1) b \(\neq\) 0.
Предположим, Пете необходимо в несколько раз увеличить скорость х, пробежать дистанцию и поставить рекорд. Чтобы поставить рекорд, он должен бежать со скоростью 15 км/ч — это и будет коэффициент b.
Получаем уравнение ax = 15. Как найти начальную скорость Пети? \(x = \frac{15}{a}\).
Такое уравнение мы уже решали выше. Получаем два случая:
- Если a = 0 — решений нет.
- Если a \(\neq\) 0, то изначальная скорость Пети была равна \(x = \frac{15}{a}\).
| Парадокс: как стоять на месте и бежать с любой скоростью одновременно? Когда Пете нужно увеличить скорость в 0 раз, получается парадокс. |
2) b = 0.
Мы получаем уравнение ax = 0. Также разберем два случая значений параметра:
- a = 0. Мы получаем уравнение 0 * x = 0. Какое значение х нужно подставить, чтобы уравнение выполнялось?
Какое бы число мы ни умножили на 0, получим 0. Получаем бесконечное множество решений.
- a \(\neq\) 0. Здесь получается, что равен 0 уже х: \(x = \frac{0}{a} = 0\).
Подведем итог. Как можно решить уравнение вида ax = b?
- Если a = 0, b = 0 — бесконечное множество решений.
- Если a = 0, b \(\neq\) 0 — решений нет.
- Если a \(\neq\) 0, b \(\neq\) 0 — решением будет \(x = \frac{b}{a}\).
Прежде чем приступать к изучению следующего материала, рекомендуем ознакомиться с понятием квадратного уравнения в статье «Линейные, квадратные и кубические уравнения». Также важно ориентироваться в графиках параболы из статьи «Основные элементарные функции».
Квадратное уравнение имеет вид ax2 + bx + c = 0, а графиком функции y = ax2 + bx + c будет парабола.
Как работать с такими уравнениями, если в них присутствует параметр? В первую очередь, важны рассуждения. Любое задание с параметром можно решить, проанализировав функцию.
Решение квадратного уравнения опирается на понятие дискриминанта. В зависимости от его значений может получиться разное количество корней:
- При D > 0 уравнение имеет два корня.
- При D = 0 уравнение имеет один корень.
- При D < 0 уравнение не имеет корней.
Как это проверить на графике? Корни уравнения — это точки, в которых парабола пересекает ось абсцисс, то есть ось х.
Рассмотрим три уравнения.
1) x2 — x — 2 = 0
Решим уравнение с помощью дискриминанта.
D = 12 — 4 * 1 * (-2) = 1 + 8 = 9
Поскольку дискриминант больше 0, то уравнение имеет два корня.
\(x_1 = \frac{1 + 3}{2} = 2\)
\(x_2 = \frac{1 — 3}{2} = -1\)
Проверим с помощью графика функции. Построим параболу и заметим, что она действительно дважды пересекает ось абсцисс, а координаты этих точек равны (−1; 0) и (2; 0) .
2) x2 -4x + 4 = 0
Решим уравнение с помощью дискриминанта.
D = 16 — 4 * 1 * 4 = 16 — 16 = 0
Поскольку дискриминант равен 0, у уравнения всего один корень.
\(x = \frac{4}{2} = 2\)
Проверим на графике. И действительно, парабола касается оси х только один раз в вершине, координаты которой (2; 0).
3) x2 — 5x + 7 = 0
Решим уравнение с помощью дискриминанта.
D = 25 — 4 * 1 * 7 = 25 — 28 = -3
Поскольку дискриминант отрицательный, у уравнения нет корней. И это отлично видно, если посмотреть на график функции: парабола лежит выше оси х и никогда ее не пересечет.
Где можно применить эти знания, решая параметры?
Пример 1. Найдите все значения параметра a, при которых уравнение x2 + (3a + 11)x + 18,25 + a = 0 имеет два различных решения.
Решение. Перед нами квадратное уравнение с коэффициентами b = 3a + 11, c = a + 18,25. В каких случаях это уравнение будет иметь два различных корня?
Квадратное уравнение имеет два корня, если D > 0. Нужно найти все значения параметра, при которых дискриминант будет положительным.
1. Для начала найдем сам дискриминант.
D = (3a + 11)2 — 4 * 1 * (a + 18,25) = 9a2 + 66a + 121 — 4a — 73 = 9a2 + 62a + 48
2. Поскольку дискриминант должен быть больше 0, то получаем неравенство 9a2 + 62a + 48 > 0
3. Решим его «Методом интервалов».
9a2 + 62a + 48 = 0
D = 3844 — 1728 = 2116
\(a_1 = \frac{-62 + 46}{18} = -\frac{16}{18} = -89\)
\(a_2 = \frac{-62 — 46}{18} = -\frac{108}{18} = -6\)
4. Дискриминант будет положительным при \(a \in (-\infty; -6) \cup (-\frac{8}{9}; +\infty)\). Это и будет ответ.
Ответ: \(a \in (-\infty; -6) \cup (-\frac{8}{9}; +\infty)\).
Важно: в уравнении мы указываем не сами решения уравнения, а значения параметра, при которых уравнение имеет два решения.
Пример 2. При каких значениях параметра a уравнение (2a + 1)x2 — ax + 3a + 1 = 0 имеет два различных решения?
Решение. Этот пример похож на предыдущий, однако здесь есть одна важная особенность. Что произойдет с уравнением, если 2a+1 = 0?
Мы получим уравнение 0,5x — 0,5 = 0, то есть линейное уравнение. У уравнения будет всего одно решение, что уже не подходит под условие задачи.
| Решаем параметры осторожно: как не совершить ошибку в квадратном уравнении с параметром? Если перед x2 стоит коэффициент, обязательно проверить, чтобы он не был равен 0. В противном случае уравнение из квадратного превращается в линейное, а это уже совершенно другой алгоритм решений уравнений. |
1. Поскольку по условию должно быть 2 решения, мы получаем, что a \(\neq\) -0,5. 2 + 20a + 4 = 23(a — \frac{2\sqrt{2} — 10}{23})(a — \frac{-2\sqrt{2} — 10}{23})\)
2 + 20a + 4 = 23(a — \frac{2\sqrt{2} — 10}{23})(a — \frac{-2\sqrt{2} — 10}{23})\)
5. Получаем неравенство:
\(23(a — \frac{2\sqrt{2} — 10}{23})(a — \frac{-2\sqrt{2} — 10}{23} < 0\)
6.Тогда \(a \in (\frac{-2\sqrt{2} — 10}{23}; \frac{2\sqrt{2} — 10}{23})\). Вспомним, что a \(\neq\) -0,5, следовательно, мы получаем ответ \(a \in (\frac{-2\sqrt{2} — 10}{23}; -0,5) \cup (-0,5; \frac{2\sqrt{2} — 10}{23})\).
Ответ: \(a \in (\frac{-2\sqrt{2} — 10}{23}; -0,5) \cup (-0,5; \frac{2\sqrt{2} — 10}{23})\)
Теорема ВиетаДискриминант — не единственный способ решить квадратное уравнение. Обратимся к теореме Виета. Если нам дано уравнение ax2 + bx + c = 0, то его корни можно найти с помощью следующей системы:
Теорему Виета удобно использовать, если на корни уравнения наложены дополнительные ограничения.
Пример 3. При каких значениях параметра a корни уравнения x2 — 3ax — a(a — 1) = 0 удовлетворяют условию x1 = 5x2. 2 — 4a = 0 \rightarrow a(9a — 4) = 0 \rightarrow a = 0, a = \frac{4}{9}\)
2 — 4a = 0 \rightarrow a(9a — 4) = 0 \rightarrow a = 0, a = \frac{4}{9}\)
5. Мы нашли значения параметра, при которых выполняется условие. Осталось проверить, чтобы при этих значениях у уравнения было два корня.
a = 0 не подходит, поскольку ограничение \(a \in (-\infty; 0) \cup (\frac{4}{13}; +\infty)\) не включает точку 0.
\(a = \frac{4}{9}\) подходит, поскольку \(\frac{4}{9} > \frac{4}{13}\).
Ответ: \(a = \frac{4}{9}\)
Условия на корни квадратного трехчленаОднако могут встретиться еще более сложные задания с параметрами. Рассмотрим каждый из этих случаев.
1. Корни квадратного трехчлена меньше, чем число N.
Построим параболу. Вспомним, что ветви параболы могут быть направлены или вверх, или вниз.
Если ветви параболы направлены вверх. Отметим на оси х точку N так, чтобы она лежала правее обоих корней уравнения. Так мы зададим условие, что корни уравнения меньше, чем число N.
Представим, что мы идем по холмистой местности, и у нас есть ее карта. Имея перед собой плоскую картинку, мы понимаем, как относительно друг друга располагаются точки в пространстве. Но посмотрев на рельеф сбоку, заметим, что точки имеют разную высоту.
Пусть в точках, где парабола пересекает ось х, будут привалы на экскурсионном маршруте, а в точке N будет смотровая площадка.
Что можно сказать про смотровую площадку на этой карте? Она находится выше, чем привалы, и лежит правее, чем самая низкая точка рельефа.
Рассмотрим эти условия на графике. В точке N значение функции f(x) больше, чем в корнях уравнения. Более того, она лежит правее, чем вершина параболы, то есть ее абсцисса больше абсциссы параболы.
Почему эти условия так важны? Пусть точка N будет лежать левее вершины параболы. Тогда не выполняется условие, что корни меньше, чем N.
В этом случае на нашем экскурсионном маршруте смотровая площадка будет лежать до привалов.
А если значение функции в точке N будет меньше, чем в корнях уравнения? Точка N будет лежать между ними.
В этом случае смотровая площадка окажется между привалами.
Аналогичным способом можно проследить изменение условий при любом положении точки N на графике.
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий:
Что произойдет, если ветви параболы будут направлены вниз? Наш экскурсионный маршрут немного поменяется: появится гора, а не овраг.
Где теперь располагается смотровая площадка? Она будет ниже, чем привалы, и дальше, чем самая высокая точка горы.
Мы можем сделать вывод, что точка N на графике будет лежать правее вершины параболы, а значение функции в ней будет меньше, чем значение функции в корнях уравнения.
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий:
2. Корни квадратного трехчлена больше, чем число N.
Корни квадратного трехчлена больше, чем число N.
Рассуждаем так же, как и в предыдущей функции, однако теперь точка N перемещается левее параболы.
Если ветви параболы направлены вверх, то функция в точке N принимает большее значение, чем в корнях уравнения, а сама точка N будет лежать левее параболы.
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий:
Теперь направим ветви параболы вниз. Значение функции в точке N будет меньше, чем в корнях уравнения.
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий:
С помощью анализа расположения точек на графике функций можно задать условия для любой ситуации, даже если точек будет несколько.
| Алгоритм: как задать любые условия для корней квадратных уравнений с помощью графика? Достаточно начертить примерный график функции и расставить на оси х нужные точки. 1. Определить, куда направлены ветви параболы и задать условие для коэффициента перед x2. |
В итоге должна получиться система, с помощью которой можно решить задачу.
Фактчек- Параметр — это буква a, вместо которой можно подставить число. Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется.
- При решении линейного уравнения ax=b в зависимости от значения коэффициентов может получиться несколько вариантов решений. Если a = 0, b = 0 — бесконечное множество решений. Если a = 0, b \(\neq\) 0 — решений нет.
 Если a \(\neq\) 0, b \(\neq\) 0 — решением будет \(x = \frac{b}{a}\).
Если a \(\neq\) 0, b \(\neq\) 0 — решением будет \(x = \frac{b}{a}\). - При решении квадратного уравнения обязательно проверять коэффициент перед x2. Если коэффициент будет равен 0, то уравнение станет линейным.
- При решении квадратного уравнения важно учитывать значение дискриминанта: если он строго больше 0, то корней у уравнения два, если дискриминант равен 0, то у уравнения один корень, если дискриминант меньше 0, то у уравнения нет корней.
- Решить квадратное уравнение можно и с помощью теоремы Виета.
- Если в задаче даны дополнительные условия на корни уравнения (например, они должны быть больше или меньше определенного числа), то задать их можно с помощью системы. Неравенства в системе можно составить с помощью анализа примерного графика функций.
Задание 1.
Что такое параметр?
- Это буква a, вместо которой можно подставить число.

- Это коэффициент перед x2 в квадратном уравнении.
- Это переменная х.
- Это значение функции в определенной точке.
Задание 2.
Дано уравнение ax = b. Сколько решений оно имеет, если a = 0 и b = 0?
- Решений нет.
- Одно решение.
- Бесконечное множество решений.
- Невозможно определить количество решений.
Задание 3.
При каких значениях дискриминанта уравнение будет иметь корни?
- D > 0
- D = 0
- D < 0
- D \(\neq\) 0
Задание 4.
Корни квадратного уравнения меньше числа А. Где будет лежать вершина параболы относительно точки А?
- Справа.
- Слева.
- Совпадать с точкой А.
- Невозможно определить расположение вершины.
Задание 5.
Меньший корень квадратного уравнения больше числа А, но меньше числа В. Ветви параболы направлены вниз. Чему будет равно значение функции в точке В?
- Значение функции в точке В будет меньше 0.

- Значение функции в точке В будет равно 0.
- Значение функции в точке В будет больше 0.
- Невозможно определить значение функции.
Ответы: 1. — 1 2. — 3 3. — 4 4. — 2 5. — 3.
3-8Функция квадратного корня в Python — Real Python
Смотреть сейчас Это руководство содержит соответствующий видеокурс, созданный командой Real Python.
Вы пытаетесь решить квадратное уравнение? Возможно, вам нужно вычислить длину одной стороны прямоугольного треугольника. Для этих и других типов уравнений функция квадратного корня Python, sqrt() поможет вам быстро и точно рассчитать ваши решения.
К концу этой статьи вы узнаете:
- Что такое квадратный корень
- Как использовать функцию квадратного корня Python,
sqrt() - Когда
sqrt()может быть полезен в реальном мире
Начинаем!
Python Pit Stop: Это руководство представляет собой быстрое и практическое способов найти нужную информацию, чтобы вы быстро вернулись к своему проекту!
Бесплатный бонус: Нажмите здесь, чтобы получить нашу бесплатную памятку по Python, которая покажет вам основы Python 3, такие как работа с типами данных, словарями, списками и функциями Python.
Квадратные корни в математике
В алгебре квадрат , x , является результатом числа, n , умноженного на себя: x = n²
Вы можете вычислять квадраты с помощью Python:
>>>
>>> n = 5 >>> х = п ** 2 >>> х 25
Оператор Python ** используется для вычисления степени числа. В этом случае 5 в квадрате или 5 в степени 2 равно 25.
Таким образом, квадратный корень — это число n , которое при умножении само на себя дает квадрат x .
В этом примере
25 является примером идеальный квадрат . Совершенные квадраты — это квадраты целых чисел:
.>>>
>>> 1 ** 2 1 >>> 2 ** 2 4 >>> 3 ** 2 9
Возможно, вы запомнили некоторые из этих правильных квадратов, когда изучали таблицу умножения на уроке элементарной алгебры.
Если вам дан маленький идеальный квадрат, может быть достаточно просто вычислить или запомнить его квадратный корень. Но для большинства других квадратов этот расчет может стать немного более утомительным. Часто оценка достаточно хороша, когда у вас нет калькулятора.
К счастью, у вас как у разработчика Python есть калькулятор, а именно интерпретатор Python!
Удалить рекламу
Функция квадратного корня Python
Модуль Python math в стандартной библиотеке может помочь вам решить связанные с математикой задачи в коде. Он содержит множество полезных функций, таких как Reостатка() и factorial() . Он также включает функцию квадратного корня Python, sqrt() .
Вы начнете с импорта математика :
>>>
>>> импорт математики
Это все, что нужно! Теперь вы можете использовать math. для вычисления квадратных корней.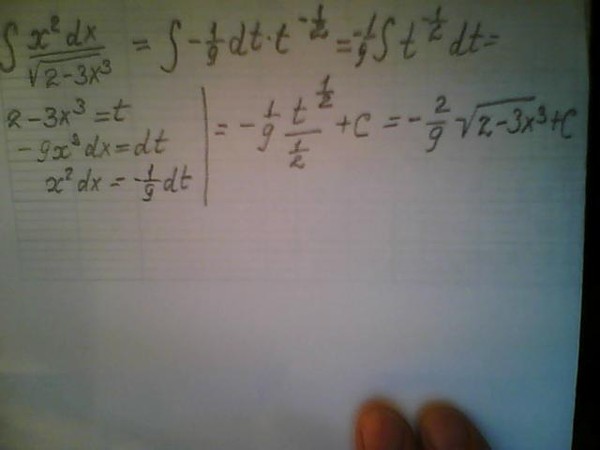 sqrt()
sqrt()
sqrt() имеет простой интерфейс.
Он принимает один параметр, x , который (как вы видели ранее) обозначает квадрат, для которого вы пытаетесь вычислить квадратный корень. В предыдущем примере это будет 25 .
Возвращаемое значение sqrt() — это квадратный корень из x
5.0 . Давайте рассмотрим несколько примеров того, как (и как не следует) использовать sqrt() .
Квадратный корень из положительного числа
Один тип аргумента, который вы можете передать в sqrt() , является положительным числом. Сюда входят типы int и float .
Например, вы можете найти квадратный корень из 9.0913 49 с использованием sqrt() :
>>>
>>> math.sqrt(49) 7,0
Возвращаемое значение — 7,0 (квадратный корень из 49 ) в виде числа с плавающей запятой.
Наряду с целыми числами вы также можете передать значений с плавающей запятой :
>>>
>>> math.sqrt(70.5) 8.396427811873332
Вы можете проверить точность этого квадратного корня, вычислив его обратную величину:
>>>
>>> 8.396427811873332 ** 2 70,5
Квадратный корень из нуля
Даже 0 является допустимым квадратом для передачи в функцию квадратного корня Python:
>>>
>>> math.sqrt(0) 0,0
Хотя вам, вероятно, не придется часто вычислять квадратный корень из нуля, вы можете передавать в функцию sqrt() переменную, значение которой на самом деле вам неизвестно. Итак, хорошо знать, что в таких случаях он может обрабатывать ноль.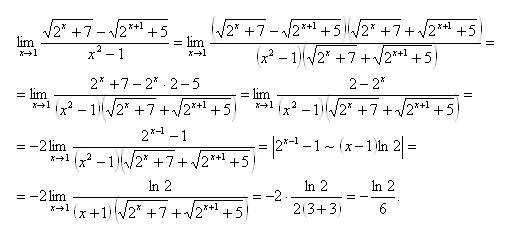
Удалить рекламу
Квадратный корень из отрицательных чисел
Квадрат любого действительного числа не может быть отрицательным. Это связано с тем, что отрицательный продукт возможен только в том случае, если один фактор положительный, а другой отрицательный. Квадрат по определению является произведением числа и самого себя, поэтому отрицательный действительный квадрат невозможен:
>>>
>>> math.sqrt(-25) Traceback (последний последний вызов): Файл "", строка 1, в ValueError: ошибка математического домена
Если вы попытаетесь передать отрицательное число в sqrt() , вы получите ValueError , потому что отрицательные числа не находятся в области возможных действительных квадратов. Вместо этого квадратный корень из отрицательного числа должен быть сложным, что выходит за рамки функции квадратного корня Python.
Квадратные корни в реальном мире
Чтобы увидеть реальное применение функции квадратного корня Python, давайте обратимся к теннису.
Представьте, что Рафаэль Надаль, один из самых быстрых игроков в мире, только что нанес удар справа из дальнего угла, где базовая линия встречается с боковой линией теннисного корта:
Теперь предположим, что его противник контратаковал броском (таким, при котором мяч будет коротким с небольшим импульсом вперед) в противоположный угол, где другая боковая линия встречается с сеткой:
Какое расстояние должен пробежать Надаль, чтобы достать мяч?
По нормативным размерам теннисного корта вы можете определить, что длина базовой линии составляет 27 футов, а боковой линии (с одной стороны сетки) — 39 футов.ноги длинные. Итак, по сути, это сводится к нахождению гипотенузы прямоугольного треугольника:
. Используя ценное уравнение из геометрии, теорему Пифагора, мы знаем, что a² + b² = c² , где a и b — катеты прямоугольного треугольника, а c — гипотенуза.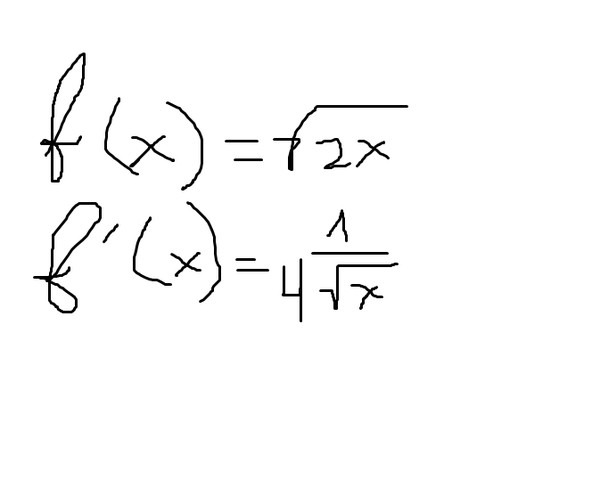
Следовательно, мы можем рассчитать расстояние, которое должен пробежать Надаль, переставив уравнение для решения c :
.Вы можете решить это уравнение, используя функцию квадратного корня Python:
>>>
>>> а = 27 >>> б = 39 >>> math.sqrt(a ** 2 + b ** 2) 47.434164569
Итак, Надаль должен пробежать примерно 47,4 фута (14,5 метра), чтобы дотянуться до мяча и сохранить очко.
Заключение
Поздравляем! Теперь вы знаете все о функции квадратного корня Python.
Вы охватили:
- Краткое введение в квадратные корни
- Все плюсы и минусы функции квадратного корня Python,
кв() - Практическое применение
sqrt()на реальном примере
Умение использовать sqrt() — это только полдела. Понимание того, когда его использовать, — это другое. Теперь вы знаете и то, и другое, так что идите и примените свое новообретенное мастерство в функции квадратного корня Python!
Смотреть сейчас Это руководство содержит связанный с ним видеокурс, созданный командой Real Python.

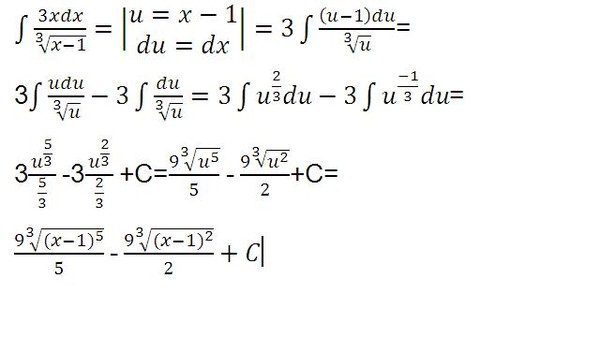 То есть переменные а и х зависят друг от друга так же, как и зависят корни обычного уравнения от его коэффициентов.
То есть переменные а и х зависят друг от друга так же, как и зависят корни обычного уравнения от его коэффициентов. 
 Чтобы составить систему, необходимо:
Чтобы составить систему, необходимо:  Если a \(\neq\) 0, b \(\neq\) 0 — решением будет \(x = \frac{b}{a}\).
Если a \(\neq\) 0, b \(\neq\) 0 — решением будет \(x = \frac{b}{a}\). 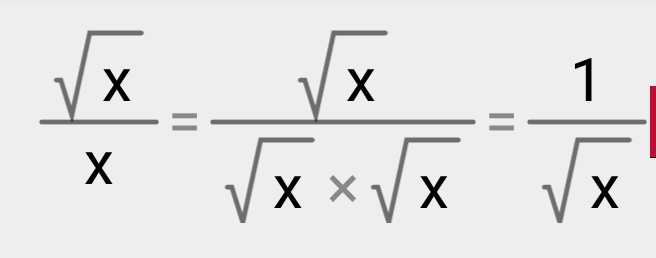
 sqrt(49)
7,0
sqrt(49)
7,0