0b1001 путей решения задачи перевода чисел в римскую запись / Хабр
Привет друзья. Вот вам простенькая задачка. Как бы вы перевели арабские числа в римские используя Python? Правда с одним условием — числа не могут быть больше чем 4000.
Я думаю это должно быть просто, но позвольте я вам покажу вам серию интересных решений и не тривиальных подходов:
«13 шагов» от StefanPochmann
Очень простая идея и при этом самая популярная. Мы делаем таблицу соответствий арабских и римских чисел. Идя по таблице этих соответствий мы уменьшая арабское число и увеличиваем римское.
def checkio(n):
result = ''
for arabic, roman in zip((1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1),
'M CM D CD C XC L XL X IX V IV I'.split()):
result += n // arabic * roman
n %= arabic
print('({}) {} => {}'.format(roman, n, result))
return result
Я добавил функцию print для вас, чтобы решение было понятнее. И вот какой будет вывод:
И вот какой будет вывод:
>>> checkio(177) (M) 177 => (CM) 177 => (D) 177 => (CD) 177 => (C) 77 => C (XC) 77 => C (L) 27 => CL (XL) 27 => CL (X) 7 => CLXX (IX) 7 => CLXX (V) 2 => CLXXV (IV) 2 => CLXXV (I) 0 => CLXXVII 'CLXXVII'
Теперь вы видите, как на каждой итерации меняется римское и арабское числа.
«thous, hunds, tens и ones» от mdeakyne
def checkio(data):
ones = ["","I","II","III","IV","V","VI","VII","VIII","IX"]
tens = ["","X","XX","XXX","XL","L","LX","LXX","LXXX","XC"]
hunds = ["","C","CC","CCC","CD","D","DC","DCC","DCCC","CM"]
thous = ["","M","MM","MMM","MMMM"]
t = thous[data // 1000]
h = hunds[data // 100 % 10]
te = tens[data // 10 % 10]
o = ones[data % 10]
return t+h+te+o
В этом случае у нас уже есть обратное соответствие арабских к римским. При этом нам уже не нужен цикл.
«base.replace» от MaikSchoepe
def checkio(data):
base = "I"*data
base = base.replace("I"*5, "V")
base = base.replace("V"*2, "X")
base = base.replace("X"*5, "L")
base = base.replace("L"*2, "C")
base = base.replace("C"*5, "D")
base = base.replace("D"*2, "M")
base = base.replace("DCCCC", "CM")
base = base.replace("CCCC", "CD")
base = base.replace("LXXXX", "XC")
base = base.replace("XXXX", "XL")
base = base.replace("VIIII", "IX")
base = base.replace("IIII", "IV")
return base
Я верю, что это не самый эффективный способ решения, но один из самых веселых. Он начинается с того, что делает длинную строку из “I”, размером с переданное число. Следующей строй заменяет каждые пять символов “I” на символ “V”. Далее два “V” на “X” и так далее. В конце пути мы получим строку, которую мы искали.
«Enum» от veky
Для того, чтобы понять, как работает следующее решение вам надо знать модуль Enum. Если не знаете — есть отличный шанс погуглить его.
Если не знаете — есть отличный шанс погуглить его.
from enum import Enum
class Roman(Enum):
M = 1000
CM = 900
D = 500
CD = 400
C = 100
XC = 90
L = 50
XL = 40
X = 10
IX = 9
V = 5
IV = 4
I = 1
@classmethod
def encode(cls, n):
for numeral in cls:
rep, n = divmod(n, numeral.value)
yield numeral.name * rep
checkio = lambda n: ''.join(Roman.encode(n))
В целом пример работает так-же как мы видели в первом примере от StefanPochmann, но кое-каким синтаксическим сахором. Таким как Enum и yield
«A derelict battery» от veky
Все эти решения я собрал с CheckiO.
И когда пользователь публикует свое решение на этом ресурсе — он должен выбрать, в какую категорию он хочет его добавить. Есть такая категория как “Creative”, где тебе не надо сильно заморачиваться на тему скорости или как легко твое решение читается.
Это решение как раз из такое категории.
import formatter, functools checkio = functools.partial(formatter.AbstractFormatter.format_roman, None, 'I')
Да, вот и все. Стоит упомянуть, правда, что модуль formater задеприкейтили начиная с версии 3.4 из-за того, что мало кто его использовал. Так что мы скорее всего напишем петицию Гвидо, чтобы оставить этот модуль в Python. Своим ап-вотом за это решение — вы как-бы ставите свою подпись под этой петицией.
«Достаточно элегантно, но не очень по питоновски» от nathan.l.cook
Мы идем дальше и решения становятся тяжелее
def checkio(data):
rom = ['I', 'V', 'X', 'L', 'C', 'D', 'M']
str_data = str(data)
str_data = str_data[::-1]
num_digits = len(str_data)
ans = ""
rom_pointer = 0
for place in range(num_digits):
if str_data[place] in ["0", "1", "2", "3"]:
ans = rom[rom_pointer] * int(str_data[place]) + ans
elif str_data[place] in ["4"]:
ans = rom[rom_pointer] + rom[rom_pointer + 1] + ans
elif str_data[place] in ["5", "6", "7", "8"]:
ans = rom[rom_pointer + 1] + rom[rom_pointer] * (int(str_data[place]) - 5) + ans
elif str_data[place] in ["9"]:
ans = rom[rom_pointer] + rom[rom_pointer + 2] + ans
rom_pointer += 2
return ans
Знаете, когда читаешь чье то решение и первые строки, которые ты видишь это:
str_data = str(data)
str_data = str_data[::-1]
Ты думаешь: “Ок, тут ща точно будет какая-то магия”
«Немного истории от» от veky (или от …)
def checkio(n:int) -> str:
pool = "m2d5c2l5x2v5i"
rep = lambda t: int(pool[t - 1])
def roman(n, j=0, v=1000):
while True:
while n >= v: yield pool[j]; n -= v
if n <= 0: return
k = j + 2; u = v // rep(k)
if rep(k) == 2: k += 2; u //= rep(k)
if n + u >= v: yield pool[k]; n += u
else: j += 2; v //= rep(j)
return "". join(roman(n)).upper()
join(roman(n)).upper()
Вы можете знать автора этого решения по таким книгам как The Art of Computer Programming, Concrete Mathematics, Surreal Numbers и так далее.
«Эта странная римская математика» от LukeSolo
Довольно часто ты встречаешь решения на CheckiO, и при этом ты даже не представляешь, как они работают:
from math import sqrt
alpha = "IVXLCDM"
one = lambda n, s: (n % 5 >> n % 5 // 4 * 2) * alpha[s]
two = lambda n, s: (3 < n) * alpha[s + (3 < n) + (8 < n)]
three = lambda n, s: sqrt(n) == int(sqrt(n)) and ''.join(reversed(s)) or s
go = lambda n, s: three(n, two(n, s) + one(n, s))
def checkio(data, s = 0, conc = ""):
d, m = divmod(data, 10)
text = go(m, s) + conc
return d and checkio(d, s + 2, text) or text
Но я думаю, что вы разберетесь 🙂
Спасибо
В списке используемых материалов я добавил ссылки на решения CheckiO пользователей, которые использовал в этой статье. Перейдя по ним, вы можете прочитать код-ревью других пользователей либо написать свое.
Перейдя по ним, вы можете прочитать код-ревью других пользователей либо написать свое.
Это первый раз, когда я пытаюсь поделится такой вот коллекцией наиболее интересных решений на CheckiO. Дайте мне знать, насколько интересно вам о таком читать и на сколько вам нравится сам формат.
Для создания этой статьи использовались решения пользователей CheckiO:
- “13 шагов” от StefanPochmann
- “thous, hunds, tens и ones” от mdeakyne
- “base.replace” от MaikSchoepe
- “Enum” от veky
- “A derelict battery” от veky
- “Достаточно элегантно, но не очень по питоновски” от nathan.l.cook
- “Немного истории от” от veky (или от …)
- “Эта странная римская математика” от LukeSolo
ПС: Кстати, еще есть категория “Speedy” для решений. И когда ты говоришь, что решение задачи не может быть длиннее чем 4000 символов, то самым быстрым решением для этой задачи будет вот это. По понятным причинам я могу вам показать только ссылку.
По понятным причинам я могу вам показать только ссылку.
римских цифр | Цифры вики
в: Наборы цифр, наборы натуральных цифр
Посмотреть источникРимские цифры — это набор цифр, использовавшихся римлянами для обозначения чисел.
Содержание
- 1 Определение
- 2 больших числа
- 2.1 Апостроф
- 2.2 Винкулум
- 3 В разные базы
Определение
Римские цифры определяются следующими шагами:
- Разделите число на разрядные значения. Пример: 1023 = 1000 + 20 + 3.
- Расположите части от тысяч до единиц. 1000 + 20 + 3.
- Преобразуйте детали в римские цифры в соответствии с этой таблицей:
| Тысячи | Сотни | Десятки | единиц | |
|---|---|---|---|---|
| 1 | М | С | Х | я |
| 2 | мм | СС | ХХ | II |
| 3 | МММ | ССС | ХХХ | III |
| 4 | компакт-диск | XL | IV | |
| 5 | Д | л | В | |
| 6 | округ Колумбия | люкс | VI | |
| 7 | ДКК | ЛХХ | VII | |
| 8 | ДККК | ЛХХХ | VIII | |
| 9 | см | ХС | IX |
Пример: 1000 + 20 + 3 = М + ХХ + III
Следовательно, 1023 = MXXIII.
Большие числа
Согласно 4, 40 и 400, 4000 должно быть 5000-1000. Но римской цифры для 5000 нет. Вот несколько вариантов римских цифр для больших чисел:
Апостроф
Апостроф определяется следующим образом:
|Ↄ равно 500. |ƆƆ равно 5000, а |ƆƆƆ равно 50000. Число Ɔ – это количество нулей после 50, увеличивающее предыдущее число в десять раз.
C|Ɔ равно 1000. CC|ƆƆ равно 10000, а CCC|ƆƆƆ равно 100000. Думайте о C и Ɔ как о скобках. Количество CƆ — это количество нулей после 100, что также увеличивает предыдущее в десять раз.
В этой системе нет ни D, ни M, ни вычитательных определений для больших чисел. поэтому 400 — это CCCC вместо CD. Вы просто повторяете цифры эффективным способом.
4000 — это C|ƆC|ƆC|ƆC|Ɔ (1000+1000+1000+1000).
С помощью апострофа вы можете написать любое число римскими цифрами. Пример: 123456 = 100000 + 20000 + 3000 + 400 + 50 + 6.
100000 = CCC|ƆƆƆ
20000 = CC|ƆƆCC|ƆƆ
3000 = С|ƆС|ƆС|Ɔ
400 = CCCC
50 = Л
6 = VI
Следовательно, 123456 = CCC|ƆƆƆCC|ƆƆCC|ƆƆC|ƆC|ƆC|ƆCCCCLVI
Vinculum
Вместо использования апострофов, которые могут затруднить представление числа, мы можем масштабировать число в 1000 раз, рисуя линию над числом, если результат больше или равен 4000. Следовательно, 3000 будет МММ, а 4000 будет I̅V̅. 5000 — это V̅. 10 000 — это X̅, а 100 000 — это C̅. 1 000 000 – это M̅. Этот вариант намного проще, чем вышеописанный, и поэтому многие предпочитают его.
Следовательно, 3000 будет МММ, а 4000 будет I̅V̅. 5000 — это V̅. 10 000 — это X̅, а 100 000 — это C̅. 1 000 000 – это M̅. Этот вариант намного проще, чем вышеописанный, и поэтому многие предпочитают его.
100000 = C̅
20000 = X̅X̅
3000 = MMM
400 = CD
50 = L
6 = VI
Следовательно, 123456 = C̅X̅X̅MMMCDLVI.
В разные системы счисления
В сообществе аналитиков римские цифры были преобразованы в различные четные системы счисления, поскольку некоторые не предпочитают десятичную систему. Значения букв были скорректированы в соответствии с полномочиями новой базы. Базовые индикаторы, такие как точка Хамфри, до сих пор используются для отличия числа от десятичного.
Ниже приведена таблица значений римских цифр для десятичных и дюжинных, а также других четных оснований b{\displaystyle b}:
| Символ | Значение | Десятичный | Дюжина | ||
|---|---|---|---|---|---|
| Я | 1 | 1 | |||
| В | b2{\ displaystyle {\ frac {b} {2}}} | 5 | 9{3}}1000 | 1000; = 1 728 10 | |
Вычитающие числительные, такие как 4 = IV (в десятичной системе), также применимы к другим основаниям. Они также применяются к цифрам со значением от b4+1{\displaystyle {\frac {b}{4}}+1}до b2−1{\displaystyle {\frac {b}{2}}-1}. как 3b4+1{\displaystyle {\frac {3b}{4}}+1}до 3b2−1{\displaystyle {\frac {3b}{2}}-1}.
Они также применяются к цифрам со значением от b4+1{\displaystyle {\frac {b}{4}}+1}до b2−1{\displaystyle {\frac {b}{2}}-1}. как 3b4+1{\displaystyle {\frac {3b}{4}}+1}до 3b2−1{\displaystyle {\frac {3b}{2}}-1}.
То есть для дюжинных римских цифр 4 пишется как IIV; так как b4 + 1 = 4 {\ displaystyle {\ frac {b} {4}} + 1 = 4}, когда b = 12 {\ displaystyle b = 12}. То же правило применимо к 5 и , записанным как IV;, IIX; и IX; соответственно.
Это будет сложно для больших баз, так как для небольших чисел требуется много символов. Однако это можно решить, определив новые буквы как другие круглые значения. (Например, десятичное число 15 в шестидесятеричных римских цифрах будет представлено как IIIIIIIIIIIIIII, что может быть упрощено как AIIIIII, определяя A как новый символ для десяти.) Пока не было известно никаких предложений по этому поводу.
| Исторические | китайские цифры • египетские цифры • греческие цифры • индийско-арабские цифры • цифры майя • римские цифры |
|---|---|
| Предложения по трансдесятичным системам счисления | Algam • De Vlieger Argam • Система дюжины • Grecset • Heptian Vigesimal • Hillarian «Cadexal» • MBeargam • Recset |
Контент сообщества доступен по лицензии CC-BY-SA, если не указано иное.
Римские цифры
Римские цифры, система счисления в Древнем Риме, используют комбинации букв латинского алфавита для обозначения значений.
Римские цифры не имеют ни понятия числа ноль, ни жесткого понятия разрядного значения . Из-за этого длина символа цифр увеличивается и уменьшается неравномерно по мере увеличения числа.
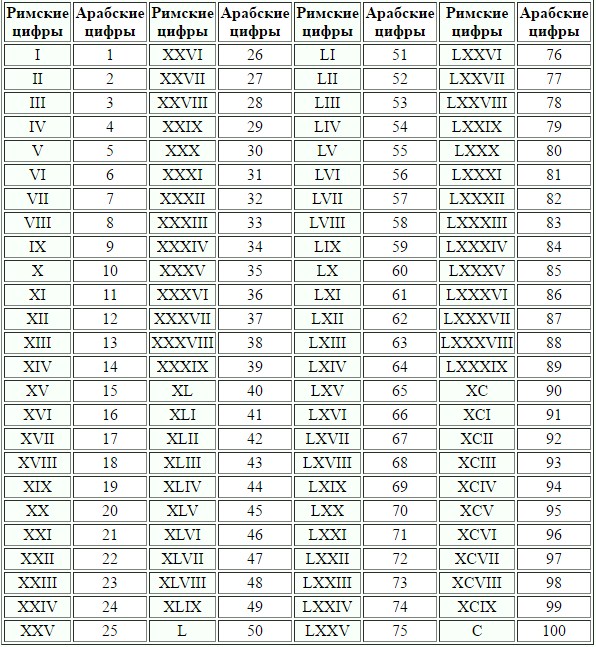
Ниже приведены числа от 1 до 500, отображаемые римскими цифрами. Подробнее о формате чисел можно прочитать здесь
|
|
|
|
|
Ниже приведен график, показывающий, как изменяется длина этих римских цифр. Как вы можете видеть, это очень циклично: длина увеличивается по мере того, как цифра I добавляется поэтапно, а затем уменьшается, когда она проходит кратность пяти, заменяясь символом с более высоким значением.
Как вы можете видеть, это очень циклично: длина увеличивается по мере того, как цифра I добавляется поэтапно, а затем уменьшается, когда она проходит кратность пяти, заменяясь символом с более высоким значением.
Самая длинная римская цифра до 250 — CLXXXVIII, состоящая из девяти символов и представляющая число 188.
Первое число из обязательных десяти цифр — 288, и это CCLXXXVIII
Таблица умножения
Несмотря на отсутствие практического применения, здесь тепловая карта, показывающая длины произведения двух римских цифр. Вверху слева — I x I. Чем светлее цвета, тем короче строки, чем темнее цвета, тем длиннее строки продукта.
Каждый квадрат вправо и вниз увеличивает число на единицу. По понятным причинам диаграмма симметрична относительно ведущей диагонали, но интересно различить гармоники, из-за которых она выглядит так, как будто на графике есть кольца. На графике представлены продукты для 1-50 по каждой оси.
Использование
В наши дни римские цифры используются в основном для украшения и придают изысканность при каждом использовании.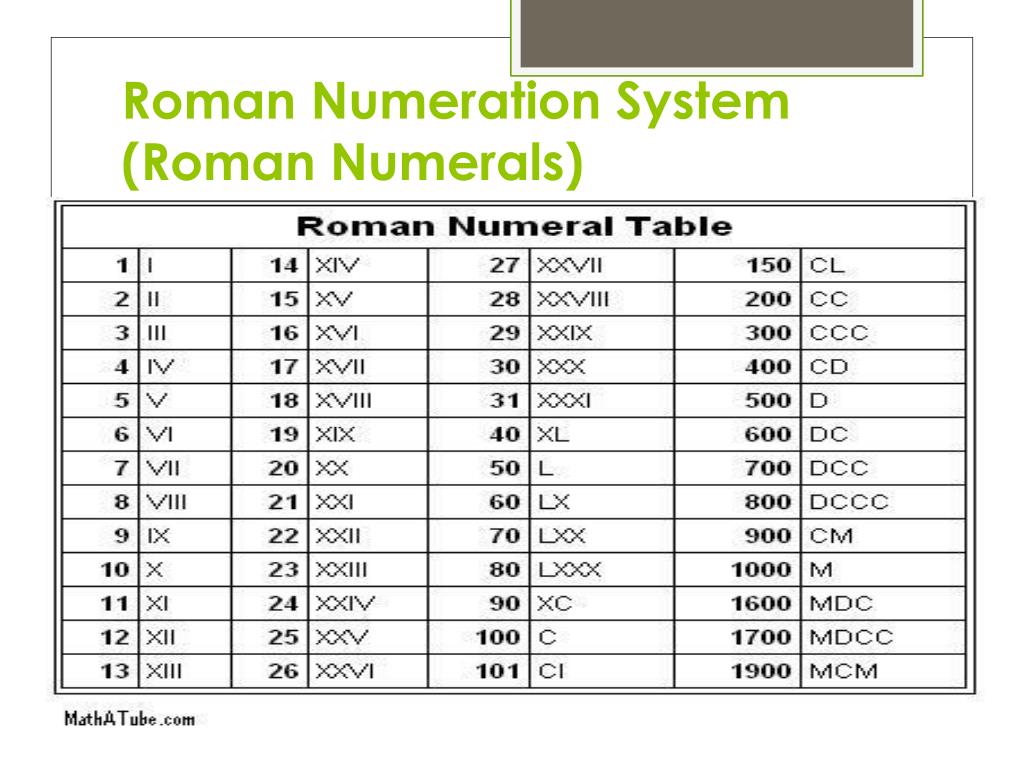

 join(roman(n)).upper()
join(roman(n)).upper()
 0053 CXIV
0053 CXIV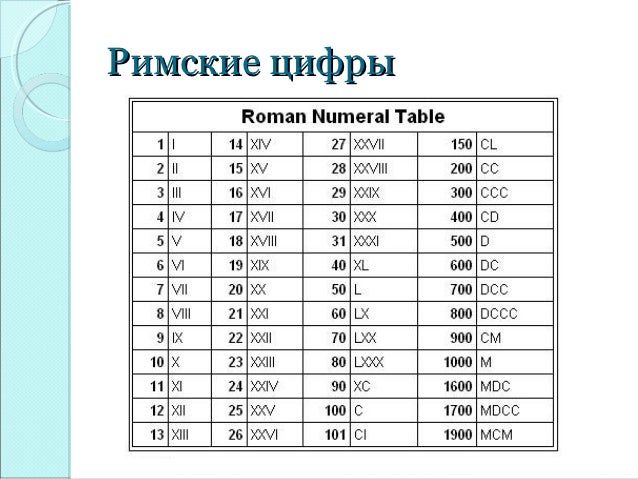 0054
0054