Делитель делимое: Нахождение неизвестного делимого — урок. Математика, 3 класс.

Содержание

Как найти делимое зная делитель и остаток

Содержание

Деление с остатком.
Остаток от деления
Ответ или решение 1
Общее представление о делении целых чисел с остатками
Теорема о делимости целых чисел с остатком
Связь между делимым, делителем, неполным частным и остатком
Деление с остатком целых положительных чисел, примеры
Правило деления с остатком целого положительного числа на целое отрицательное, примеры
Деление с остатком целого отрицательного числа на целое положительное, примеры
Правило деления с остатком целых отрицательных чисел, примеры
Проверка результата деления целых чисел с остатком

Деление с остатком.

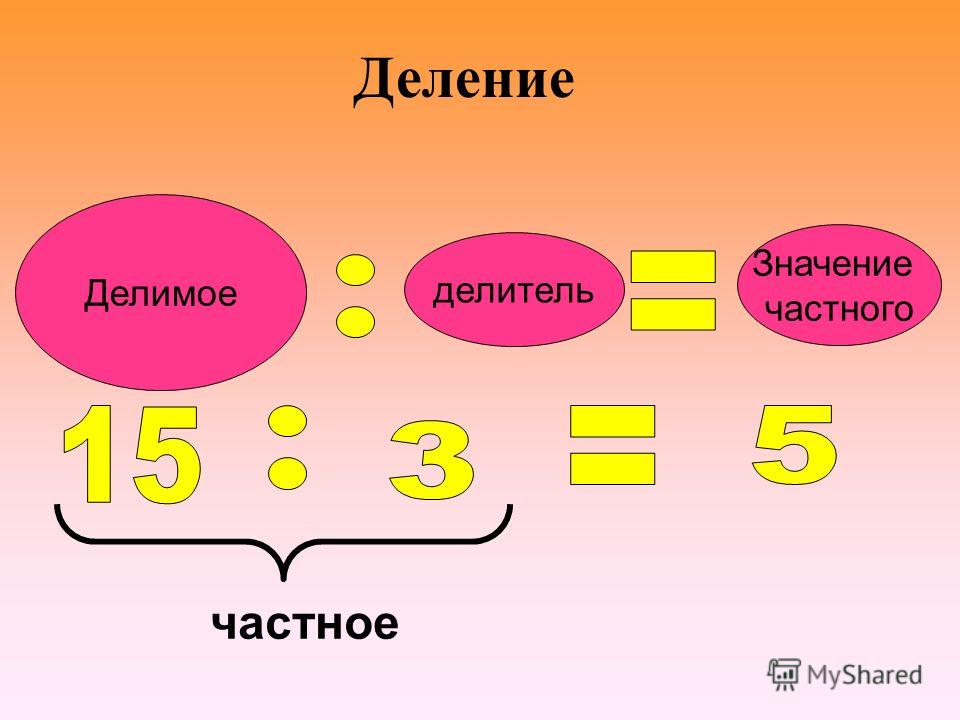
Рассмотрим простой пример:
15:5=3
В этом примере натуральное число 15 мы поделили нацело на 3, без остатка.

Иногда натуральное число полностью поделить нельзя нацело. Например, рассмотрим задачу:
В шкафу лежало 16 игрушек. В группе было пятеро детей. Каждый ребенок взял одинаковое количество игрушек. Сколько игрушек у каждого ребенка?

Решение:
Поделим число 16 на 5 столбиком получим:

Мы знаем, что 16 на 5 не делиться. Ближайшее меньшее число, которое делиться на 5 это 15 и 1 в остатке. Число 15 мы можем расписать как 5⋅3. В итоге (16 – делимое, 5 – делитель, 3 – неполное частное, 1 — остаток). Получили формулу деления с остатком, по которой можно сделать проверку решения.

a=b⋅c+d
a – делимое,
b – делитель,
c – неполное частное,
d – остаток.

Ответ: каждый ребенок возьмет по 3 игрушки и одна игрушка останется.

Остаток от деления

Остаток всегда должен быть меньше делителя.

Если при делении остаток равен нулю, то это значит, что делимое делиться нацело или без остатка на делитель.

Если при делении остаток больше делителя, это значит, что найденное число не самое большое. Существует число большее, которое поделит делимое и остаток будет меньше делителя.

Вопросы по теме “Деление с остатком”:
Остаток может быть больше делителя?
Ответ: нет.

Остаток может быть равен делителю?
Ответ: нет.

Как найти делимое по неполному частному, делителю и остатку?
Ответ: значения неполного частного, делителя и остатка подставляем в формулу и находим делимое. Формула:
a=b⋅c+d
(a – делимое, b – делитель, c – неполное частное, d – остаток.)

Пример №1:

Выполните деление с остатком и сделайте проверку: а) 258:7 б) 1873:8

Решение:
а) Делим столбиком:

258 – делимое,
7 – делитель,
36 – неполное частное,
6 – остаток. Остаток меньше делителя 6 Category: 5 класс, Натуральные числа Leave a comment

Ответ или решение 1

Есть формула выполнения деления, а именно:

Делимое : делитель = частное.

Откуда, делимое — это число, которое делится; делитель — число, на которое нужно делить, частное — результат деления делимого на делитель.

Для того, чтоб найти делитель необходимо делимое разделить на частное. Если же в результате деления получаем остаток, тогда, чтоб найти делитель, необходимо делимое разделить на частное и прибавить остаток.

Статья разбирает понятие деления целых чисел с остатком. Докажем теорему о делимости целых чисел с остатком и просмотрим связи между делимыми и делителями, неполными частными и остатками. Рассмотрим правила, когда производится деление целых чисел с остатками, рассмотрев подробно на примерах. В конце решения выполним проверку.

Общее представление о делении целых чисел с остатками

Деление целых чисел с остатком рассматривается как обобщенное деление с остатком натуральных чисел. Это выполняется потому, что натуральные числа – это составная часть целых.

Деление с остатком произвольного числа говорит о том, что целое число a делится на число b , отличное от нуля. Если b = 0 , тогда не производят деление с остатком.

Также как и деление натуральных чисел с остатком, производится деление целых чисел a и b , при b отличном от нуля, на c и d . В этом случае a и b называют делимым и делителем, а d – остатком деления, с – целое число или неполное частное.

Если считать, что остаток – это целое неотрицательное число, тогда его величина не больше модуля числа b . Запишем таким образом: 0 ≤ d ≤ b . Данная цепочка неравенств используется при сравнении 3 и более количества чисел.

Если с – неполное частное, тогда d – остаток от деления целого числа a на b , кратко можно зафиксировать: a : b = c (ост. d ).

Остаток при делении чисел a на b возможен нулевой, тогда говорят, что a делится на b нацело, то есть без остатка. Деление без остатка считается частным случаем деления.

Если делим ноль на некоторое число, получаем в результате ноль. Остаток деления также будет равен нулю. Это можно проследить из теории о делении нуля на целое число.

Теперь рассмотрим смысл деления целых чисел с остатком.

Известно, что целые положительные числа – натуральные, тогда при делении с остатком получится такой же смысл, как и при делении натуральных чисел с остатком.

При делении целого отрицательного числа а на целое положительное b имеется смысл. Рассмотрим на примере. Представив ситуацию, когда имеем долг предметов в количестве a , которое необходимо погасить b человек. Для этого необходимо каждому внести одинаковый вклад. Чтобы определить величину долга для каждого, необходимо обратить внимание на величину частного с . Остаток d говорит о том, что известно количество предметов после расплаты с долгами.

Рассмотрим на примере с яблоками. Если 2 человека должны 7 яблок. В случае, если посчитать, что каждый должен вернуть по 4 яблока, после полного расчета у них останется 1 яблоко.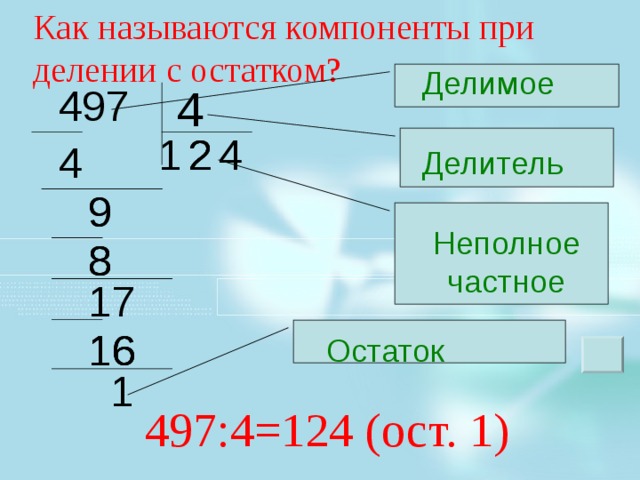 Запишем в виде равенства это: ( − 7 ) : 2 = − 4 ( о с т . 1 ) .

Деление любого числа а на целое не имеет смысла, но возможно как вариант.

Теорема о делимости целых чисел с остатком

Мы выявили, что а – это делимое, тогда b – это делитель, с – неполное частное, а d – остаток. Они между собой связаны. Эту связь покажем при помощи равенства a = b · c + d . Связь между ними характеризуется теоремой делимости с остатком.

Любое целое число может быть представлено только через целое и отличное от нуля число b таким образом: a = b · q + r , где q и r – это некоторые целые числа. Тут имеем 0 ≤ r ≤ b .

Докажем возможность существования a = b · q + r .

Если существуют два числа a и b , причем a делится на b без остатка, тогда из определения следует, что имеется число q , что будет верно равенство a = b · q . Тогда равенство можно считать верным: a = b · q + r при r = 0 .

Если посчитать, что b – целое положительное число, тогда, следует выбрать целое q так, чтобы произведение b · q не было больше значения числа а , а произведение b · ( q + 1 ) было больше, чем a .

Тогда необходимо взять q такое, чтобы данное неравенством b · q a b · ( q + 1 ) было верным. Необходимо вычесть b · q из всех частей выражения. Тогда придем к неравенству такого вида: 0 a − b · q b .

Имеем, что значение выражения a − b · q больше нуля и не больше значения числа b, отсюда следует, что r = a − b · q . Получим, что число а можем представить в виде a = b · q + r .

Теперь необходимо рассмотреть возможность представления a = b · q + r для отрицательных значений b .

Модуль числа получается положительным, тогда получим a = b · q 1 + r , где значение q 1 – некоторое целое число, r – целое число, которое подходит условию 0 ≤ r b . Принимаем q = − q 1 , получим, что a = b · q + r для отрицательных b .

Доказательство единственности

Допустим, что a = b · q + r , q и r являются целыми числами с верным условием 0 ≤ r b , имеется еще одна форма записи в виде a = b · q 1 + r 1 , где q 1 и r 1 являются некоторыми числами, где q 1 ≠ q , 0 ≤ r 1 b .

Когда из левой и правых частей вычитается неравенство, тогда получаем 0 = b · ( q − q 1 ) + r − r 1 , которое равносильно r — r 1 = b · q 1 — q . Так как используется модуль, получим равенство r — r 1 = b · q 1 — q .

Заданное условие говорит о том, что 0 ≤ r b и 0 ≤ r 1 b запишется в виде r — r 1 b . Имеем, что q и q 1 – целые, причем q ≠ q 1 , тогда q 1 — q ≥ 1 . Отсюда имеем, что b · q 1 — q ≥ b . Полученные неравенства r — r 1 b и b · q 1 — q ≥ b указывают на то, что такое равенство в виде r — r 1 = b · q 1 — q невозможно в данном случае.

Отсюда следует, что по-другому число a быть представлено не может, кроме как такой записью a = b · q + r .

Связь между делимым, делителем, неполным частным и остатком

При помощи равенства a = b · c + d можно находить неизвестное делимое a , когда известен делитель b с неполным частным c и остатком d .

Определить делимое, если при деление получим — 21 , неполное частное 5 и остаток 12 .

Необходимо вычислить делимое a при известном делителе b = − 21 , неполным частным с = 5 и остатком d = 12 . Нужно обратиться к равенству a = b · c + d , отсюда получим a = ( − 21 ) · 5 + 12 . При соблюдении порядка выполнения действий умножим — 21 на 5 , после этого получаем ( − 21 ) · 5 + 12 = − 105 + 12 = − 93 .

Ответ: — 93 .

Связь между делителем и неполным частным и остатком можно выразить при помощи равенств: b = ( a − d ) : c , c = ( a − d ) : b и d = a − b · c . С их помощью мы можем вычислить делитель, неполное частное и остаток. Это сводится к постоянному нахождению остатка от деления целого целых чисел a на b с известным делимым, делителем и неполным частным. Применяется формула d = a − b · c . Рассмотрим решение подробно.

Найти остаток от деления целого числа — 19 на целое 3 при известном неполном частном равном — 7 .

Чтобы вычислить остаток от деления, применим формулу вида d = a − b · c . По условию имеются все данные a = − 19 , b = 3 , c = − 7 .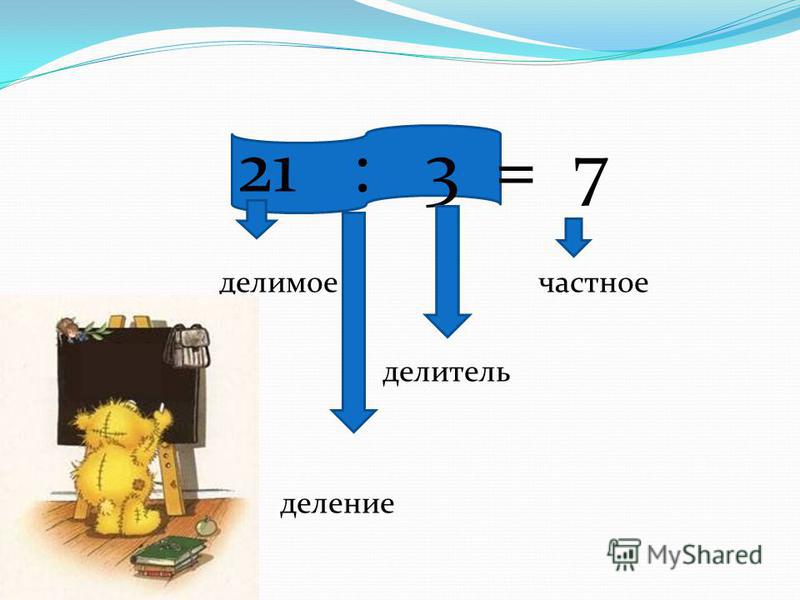

Отсюда получим d = a − b · c = − 19 − 3 · ( − 7 ) = − 19 − ( − 21 ) = − 19 + 21 = 2 (разность − 19 − ( − 21 ) . Данный пример вычислен по правилу вычитания целого отрицательного числа.

Ответ: 2 .

Деление с остатком целых положительных чисел, примеры

Все целые положительные числа являются натуральными. Отсюда следует, что деление выполняется по всем правилам деления с остатком натуральных чисел. Скорость выполнения деления с остатком натуральных чисел важна, так как на нем основано не только деление положительных, но и правила деления целых произвольных.

Самый удобный метод деления – это столбик, так как проще и быстрее получить неполное или просто частное с остатком. Рассмотрим решение более подробно.

Произвести деление 14671 на 54 .

Данное деление необходимо выполнять столбиком:

То есть неполное частное получается равным 271 , а остаток – 37 .

Ответ: 14 671 : 54 = 271 . (ост. 37 )

Правило деления с остатком целого положительного числа на целое отрицательное, примеры

Чтобы выполнить деление с остатком положительного числа на целое отрицательное, необходимо сформулировать правило.

Неполное частное от деления целого положительного a на целое отрицательное b получаем число, которое противоположно неполному частному от деления модулей чисел a на b . Тогда остаток равен остатку при делении a на b .

Отсюда имеем, что неполное частное от деления целого полодительного числа на целое отрицательное число считают целым неположительным числом.

найти модули делимого и делителя;
делить модуль делимого на модуль делителя, тогда получим неполное частное и
остаток;
запишем число противоположное полученному.

Рассмотрим на примере алгоритма деления целого положительного числа на целое отрицательное.

Выполнить деление с остатком 17 на — 5 .

Применим алгоритм деления с остатком целого положительного числа на целое отрицательное. Необходимо разделить 17 на — 5 по модулю. Отсюда получим, что неполное частное равно 3 , а остаток равен 2 .

Получим, что искомое число от деления 17 на — 5 = — 3 с остатком равным 2 .

Ответ: 17 : ( − 5 ) = − 3 (ост. 2 ).

Необходимо разделить 45 на — 15 .

Необходимо разделить числа по модулю. Число 45 делим на 15 , получим частное 3 без остатка. Значит, число 45 делится на 15 без остатка. В ответе получаем — 3 , так как деление производилось по модулю.

45 : ( — 15 ) = 45 : — 15 = — 45 : 15 = — 3

Ответ: 45 : ( − 15 ) = − 3 .

Деление с остатком целого отрицательного числа на целое положительное, примеры

Формулировка правила деления с остатком выглядит следующим образом.

Для того, чтобы получить неполное частное с при делении целого отрицательного a на положительное b , нужно применить противоположное данному числу и вычесть из него 1 , тогда остаток d будет вычисляться по формуле: d = a − b · c .

Исходя из правила можно сделать вывод, что при делении получим целое неотрицательное число. Для точности решения применяют алгоритм деления а на b с остатком:

найти модули делимого и делителя;
делить по модулю;
записать противоположное данному число и вычесть 1 ;
использовать формулу для остатка d = a − b · c .

Рассмотрим на примере решения, где применяется данный алгоритм.

Найти неполное частное и остаток от деления — 17 на 5 .

Делим заданные числа по модулю. Получаем, что при делении частное равно 3 , а остаток 2 . Так как получили 3 , противоположное — 3 . Необходимо отнять 1 .

Искомое значение полчаем равное — 4 .

Чтобы вычислить остаток, необходимо a = − 17 , b = 5 , c = − 4 , тогда d = a − b · c = − 17 − 5 · ( − 4 ) = − 17 − ( − 20 ) = − 17 + 20 = 3 .

Значит, неполным частным от деления является число — 4 с остатком равным 3 .

Ответ: ( − 17 ) : 5 = − 4 (ост. 3 ).

Разделить целое отрицательное число — 1404 на положительное 26 .

Необходимо произвести деление столбиком и по мудулю.

Мы получили деление модулей чисел без остатка. Это значит, что деление выполняется без остатка, а искомое частное = — 54 .

Ответ: ( − 1 404 ) : 26 = − 54 .

Правило деления с остатком целых отрицательных чисел, примеры

Необходимо сформулировать правило деления с остатком целых отрицательных чисел.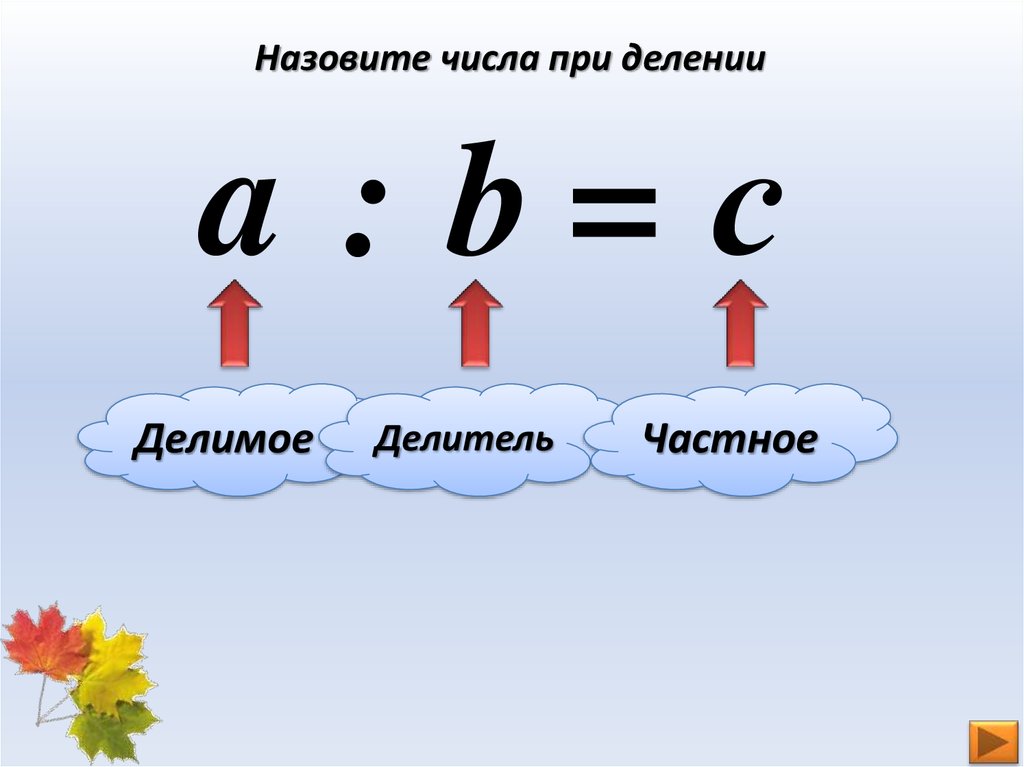

Для получения неполного частного с от деления целого отрицательного числа a на целое отрицательное b , необходимо произвести вычисления по модулю, после чего прибавить 1 , тогда сможем произвести вычисления по формуле d = a − b · c .

Отсюда следует, что неполное частное от деления целых отрицательных чисел будет число положительное.

Сформулируем данное правило в виде алгоритма:

найти модули делимого и делителя;
разделить модуль делимого на модуль делителя с получением неполного частного с
остатком;
прибавление 1 к неполному частному;
вычисление остатка, исходя из формулы d = a − b · c .

Данный алгоритм рассмотрим на примере.

Найти неполное частное и остаток при делении — 17 на — 5 .

Для правильности решения применим алгоритм для деления с остатком. Для начала раздели числа по модулю. Отсюда получим, что неполное частное = 3 , а остаток равен 2 . По правилу необходимо сложить неполное частное и 1 . Получим, что 3 + 1 = 4 . Отсюда получим, что неполное частное от деления заданных чисел равно 4 .

Для вычисления остатка мы применим формулу. По условию имеем, что a = − 17 , b = − 5 , c = 4 , тогда, используя формулу, получим d = a − b · c = − 17 − ( − 5 ) · 4 = − 17 − ( − 20 ) = − 17 + 20 = 3 . Искомый ответ, то есть остаток, равен 3 , а неполное частное равно 4 .

Ответ: ( − 17 ) : ( − 5 ) = 4 (ост. 3 ).

Проверка результата деления целых чисел с остатком

После выполнение деления чисел с остатком необходимо выполнять проверку. Данная проверка подразумевает 2 этапа. Вначале идет проверка остатка d на неотрицательность, выполнение условия 0 ≤ d b . При их выполнении разрешено выполнять 2 этап. Если 1 этап не выполнился, значит вычисления произведены с ошибками. Второй этап состоит из того, что равенство a = b · c + d должно быть верным. Иначе в вычисления имеется ошибка.

Рассмотрим на примерах.

Произведено деление — 521 на — 12 . Частное равно 44 , остаток 7 . Выполнить проверку.

Так как остаток – это число положительное, то его величина является меньше, чем модуль делителя. Делитель равен — 12 , значит, его модуль равен 12 . Можно переходить к следующему пункту проверки.

По условию имеем, что a = − 521 , b = − 12 , c = 44 , d = 7 . Отсюда вычислим b · c + d , где b · c + d = − 12 · 44 + 7 = − 528 + 7 = − 521 . Отсюда следует, что равенство верное. Проверка пройдена.

Выполнить проверку деления ( − 17 ) : 5 = − 3 (ост. − 2 ). Верно ли равенство?

Смысл первого этапа заключается в том, что необходимо проверить деление целых чисел с остатком. Отсюда видно, что действие произведено неверно, так как дан остаток, равный — 2 . Остаток не является отрицательным числом.

Имеем, что второе условие выполненное, но недостаточное для данного случая.

Ответ: нет.

Число — 19 разделили на — 3 . Неполное частное равно 7 , а остаток 1 . Проверить, верно ли выполнено данное вычисление.

Дан остаток, равный 1 . Он положительный. По величине меньше модуля делителя, значит, первый этап выполняется. Перейдем ко второму этапу.

Вычислим значение выражения b · c + d . По условию имеем, что b = − 3 , c = 7 , d = 1 , значит, подставив числовые значения, получим b · c + d = − 3 · 7 + 1 = − 21 + 1 = − 20 . Следует, что a = b · c + d равенство не выполняется, так как в условии дано а = — 19 .

Отсюда следует вывод, что деление произведено с ошибкой.

Конспект урока по математике на тему «Делимое.Делитель» | План-конспект урока по математике (3 класс) на тему:

Министерство образования и науки Челябинской области

Государственное бюджетное образовательное учреждение

«Челябинский педагогический колледж №1»

Технологическая карта урока математики

«Делимое. Делитель»

Выполнила:

студентка 46 гр. Тугумбаева Венера

Проверила: Бубнова Л.А.

Отметка:

Дата:

Челябинск, 2016

Предмет: Математика

Класс: 3 «а»

Тема урока: Делимое. Делитель

Цели урока: познакомить с правилами нахождения делимого и делителя на основе взаимосвязи компонентов действий.

Планируемые результаты:

Предметные: научатся использовать взаимосвязь умножения и деления при вычислениях;

выполнять деление двузначного числа на однозначное;

читать равенства, используя математическую терминологию.

Личностные: выполнять задания творческого и поискового характера;

работать в парах.

Тип урока: открытие новых знаний.

Оборудование: презентация.

Этап урока. Методы и приемы

Время

Содержание урока

Деятельность ученика

УУД

Организационный этап

Словесный: беседа

5 мин

— Приветствие. Проверка осанки.

Устный счет

— найдите разность 72 и 4 (68)

— какое число надо увеличить в 7 раз, чтобы получить 63? (9)

— сколько надо прибавить к 16, чтобы получить 96? (80)

— найдите сумму наибольшего трехзначного числа и 1 (1000)

— во сколько раз 14 меньше, чем 84? (в 6 раз)

Приветствовать учителя

Вычислять

Регулятивные — постановка учебной задачи.

Актуализация опорных знаний

Словесный: беседа

7 мин

— Рассмотрите равенства

24:6=4 6:2=3

24:4=6 3∙2=6

— Прочитайте первое равенство математическим языком. (Делимое 24, делитель 6, частное 4)

— Какого равенства не хватает в первом столбце? (6∙4=24)

— Как его получить из первого равенства? (Делитель 6 надо умножить на частное 4, и получится делимое 24)

— Какого равенства не хватает во втором столбце? (6:3=2)

— Как его получили? (Делимое 6 разделили на частное 3, и получили

делитель 2)

— Как вы думаете, чем мы будем заниматься сегодня на уроке? (Находить неизвестное делимое, если известны частное и делитель; и не известный делитель, если известны делимое и частное)

— Какие математические законы мы будем применять? (Законы о взаимосвязи деления и умножения)

— Какова будет цель нашего урока? (познакомить с правилами нахождения делимого и делителя на основе взаимосвязи компонентов действий)

Рассматривать равенства

Участвовать в беседе

Коммуникативные — высказывать свое мнение при обсуждении задания.

Умение выбирать и использовать в ходе решения изученные свойства арифметических действий.

Изучение новой темы

Практический: работа с учебником

Словесный: устное решение

15 мин

— Рассмотрите фигуры и равенства на странице 16. Подсчитайте площадь (количество клеток) в первом прямоугольнике. (15)

— Чему равна длины прямоугольника? (5 клеток) Ширина? (3 клетки)

— Что нашли выражением 15:5=3? (Ширину прямоугольника)

— Прочитайте равенство, называя компоненты деления. (Делимое 15, делитель 5, частное 3)

— Как можно найти делимое по известным частному и делителю? (Если делитель умножить на частное, то получится делимое 5∙3=15)

— Как можно узнать делитель по известным частному и делимому? (Если делимое разделить на частное, то получится делитель 15:3=5)

— Объясните, как получились равенства во втором столбце?

— Прочитайте выводы в красной рамочке.

— А сейчас решаем с комментированием №1.

Первый столбик. Делимое 40, делитель 8, частное 5.

Делитель умножим на частное получаем делимое.

Делимое разделим на частное получаем делитель.

Второй столбик. Делимое 27, делитель 9, частное 3.

Делитель умножаем на частное получаем делимое.

Делимое разделим на частное получаем делитель.

Второй столбик. Делимое 56, делитель 7, частное 8.

Делитель умножаем на частное получаем делимое.

Делимое разделим на частное получаем делитель.

Четвертый столбик. Делимое 54, делитель 6, частное 9.

Делитель умножаем на частное получаем делимое.

Делимое разделим на частное получаем делитель.

Отвечать на вопросы

Вычислять

Комментировать

Предметные — применять базовые знания для решения конкретной проблемы.

Физминутка

2 мин

Выполнять

Решение частных задач

Практический: решение задач

10 мин

-Прочитайте задачу №2.

— О чем говорится в этой задаче? (Об улитке, о том, которая ползла)

— Что значит «четвертая часть»? (Указанное расстояние повторится 4 раза)

— Поставьте вопрос к задаче. (Какое расстояние нужно проползти улитке до земли?)

— Как узнать расстояние? Какое правило нужно вспомнить? (Правило нахождения числа по его доле)

— Запишите решение и ответ задачи самостоятельно. Кто первым решит, к доске.

3∙4=12(дм) надо проползти улитке.

Ответ: 12 дм

— Прочитайте задачу №3.

— О чем говорится в задаче? (О вишне)

— Какую величину мы будем искать? (Массу)

— Как нам удобнее записать задачу кратко? (С помощью таблицы)

Заполняем таблицу в тетрадях. Один ученик у доски. Как мы назовем столбики? (Масса одного пакета, количество пакетов, общая масса пакетов)

Масса одного пакета	Количество пакетов	Общая масса пакетов
? (одинаковая)	4 шт.	28 кг
	3 шт.	?
	7 шт.	?

— Что надо знать, чтобы найти массу 3 пакетов? 7 пакетов? (Массу одного пакета)

— Как найти массу одного пакета? (28:4=7(кг) масса одного пакета)

— Каким действием мы узнаем массу 3 пакетов? 7 пакетов? (3∙3=9(кг) масса трех пакетов; 7∙3=21(кг) масса семи пакетов)

Итог урока

2 мин

— Как связаны между собой компоненты деления?

— Какое открытие вы сегодня сделали?

— Кто справился со всеми заданиями без ошибок?

— Кому нужна помощь товарищей?

Анализировать свои успехи

Личностные — способность к самооценке на основе критерия успешности учебной деятельности.

Урок 34 «Когда делимое меньше делителя» (1 урок) — МегаЛекции

Предметные задачи:

— знакомство со случаем действия деления с остатком меньшего числа на большее;

— выполнение заданий, в которых применяется правило: если при делении с остатком делимое меньше делителя, то неполное частное равно 0, а остаток равен делимому;

Формирование УУД: Познавательные УУД: применение правила для проверки правильности выполнения задания. Регулятивные: умение определять задачи урока, анализировать достигнутые результаты Коммуникативные: умение излагать своё мнение и аргументировать свою точку зрения, управлять действиями партнёраЛичностные: ориентация на самоанализ и самоконтроль результата, на анализ соответствия результатов требованиям конкретной задачи, на понимание предложений и оценок учителей, товарищей

Пропедевтика: деление с остатком столбиком, если неполное частное в середине записи содержит 0.

Повторение: табличные случаи деления

Методы и приемы организации учебной деятельности учащихся: изучение нового материала по тексту и заданиям учебника. Учебно-методическое обеспечение: У-1, Т-1.

Вводная часть урока

Просим учащихся прочитать тему урока «Когда делимое меньше делителя» и привести примеры частных, в которых делимое меньше делителя.

Выслушиваем ответы учеников, записывая на доске приведённые ими примеры: 2 : 6 5 : 12 и др.

Спрашиваем, возможно ли найти значение частного, если делимое меньше делителя?

Ожидаемый ответ: в этом случае значение частного найти невозможно. Сообщаем ученикам, что на уроке мы всё же научимся делить меньшее число на большее.

Продолжение урока

Задание № 180 (У – 1, с. 60)

Учащиеся читают задание и вспоминают правило: если делитель умножить на неполное частное и к полученному результату прибавить остаток,то в итоге получитсяделимое.

Выясняем, что для равенства 58 = 8 7 + 2 приведён соответствующий ему случай деления с остатком: 58 : 8 = 7 (ост. 2)

Предлагаем ученикам, используя это правило записать соответствующий случай деления с остатком для равенства 12 = 15 0 + 12 (пауза) Ожидаемый ответ: 12 : 15 = 0 (ост. 12).

Подводим итог, если делитель меньше делителя, то неполное частное равно0, а остаток – делимому!

Следовательно, деление меньшего числа на большее возможно!

Задание № 181 (У – 1, с. 60)

Учащиеся читают первую часть задания: раздели с остатком на 10 последовательно следующие числа: 48, 38, 28, 18. Даём время на выполнение задания, проверяем на доске:

48 : 10 = 4 (ост. 8) 38 : 10 = 3 (ост. 8) 28 : 10 = 2 (ост. 8) 18 : 10 = 1 (ост. 8) Спрашиваем, что общего во всех этих случаях и чем они отличаются? Ожидаемый ответ: похожи тем, что во всех случаях остаток равен 8, а отличаются – неполными частными.

Сравниваем остаток в каждом случае с числом в разряде единиц делимого, а неполное частное — с числом в разряде десятков делимого.

Делаем вывод, что при делении на 10 остаток равен числу, стоящему вразряде единиц делимого (48 : 10 = 4 (ост. 8)) а неполное частное равночислу, стоящему в разряде десятков делимого (48 : 10 = 4 (ост. 8))

Спрашиваем, какой должен быть остаток при делении числа 8 на число 10, и какое неполное частное должно получиться в этом случае деления с остатком?

Ожидаемый ответ: остаток равен числу, стоящему в разряде единиц делимого, неполное частное равно числу, стоящему в разряде десятков делимого 8 : 10 = 0 (ост. 8) Проверяем, правильно ли выполнено деление с остатком 8 : 10 = 0 (ост. 8). Записывая на доске равенство 10 0 + 8 = 8, делаем вывод, что деление состатком 8 : 10 = 0 (ост. 8) выполнено правильно.

Задание № 182 (У – 1, с. 60)

Один из учеников вслух читает первую часть задания: какому условию должны удовлетворять делимое и делитель для того, чтобы в результате деления с остатком неполное частное равнялось 0?

Ожидаемый ответ: чтобы в результате деления с остатком неполное частное равнялось 0, делимое должно быть меньше делителя.

Предлагаем ученикам привести три примера случаев деления с остатком, чтобы в результате деления неполное частное равнялось 0?

Записываем на доске под диктовку учеников приведённые примеры:

3 : 6 = 0 (ост. 3), 56 : 100 = 0 (ост. 56), 14 : 60 = 0 (ост. 14) и др.

Спрашиваем, как в рассмотренных случаях остаток связан с делимым? Ожидаемый ответ: остаток равен делимому.

Задание № 183 (У – 1, с. 60)

Учащиеся читают задание и самостоятельно записывают три случая деления с остатком, в каждом из которых делимое равно остатку.

Организуем проверку в условиях парной работы.

Задание № 176 (У – 1, с. 59)

Учащиеся читают задание: запиши по порядку первые шесть натуральных чисел, которые при делении на 7 дают в остатке 1.

Вспоминаем, если делитель умножить на неполное частное и кполученному результату прибавить остаток, то получится делимое. Следовательно, искомые делимые можно найти, если к делимым (7, 14, 21, 28, 35), которые делятся на 7 без остатка прибавить остаток 1. Записываем на доске под диктовку учеников равенства и проверяем правильность выполнения деления с остатком:

7 + 1 = 8 8 : 7 = 1 (ост. 1)

14 + 1 = 15 15 : 7 = 2 (ост. 1)

21 + 1 = 22 22 : 7 = 3 (ост. 1)

28 + 1 = 29 29 : 7 = 4 (ост. 1)

35 + 1 = 36 36 : 7 = 5 (ост. 1)

Дополняем данный ряд чисел числом 1, так как 1 : 7 = 0 (ост. 1) Итак, записанные числа 1, 8, 15, 22, 29, 36 делятся на число 7 и дают в остатке 1.

Задание № 184 (У – 1, с. 61)

Учащиеся читают задание и самостоятельно выполняют деление с остатком.

Даём время на выполнение задания, проверяем на доске:

9 : 10 = 0 (ост. 9) 12 : 24 = 0 (ост. 12) 1 : 100 = 0 (ост. 1)

364 : 387 = 0 (ост. 364) 1000 : 10000 = 0 (ост. 1000)

Обращаем внимание учеников на то, что в каждом из выполненных случаев деления делимое меньше делителя, неполное частное равно 0, а остаток равен делимому.

Ученики читают правило на голубой плашке: если при делении с остаткомделимое меньше делителя, то неполное частное равно 0, а остаток равенделимому и с помощью него проверяют правильность выполнения деления с остатком.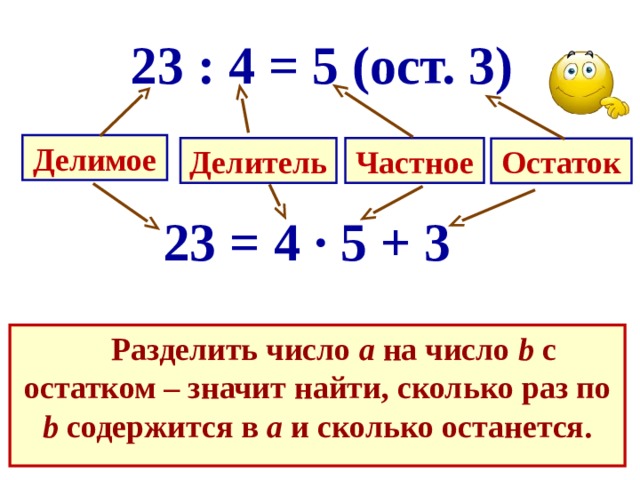

Задание № 185* (У – 1, с. 61)

Учащиеся читают задание: приведи пример двух чисел, которые при делении на 56897 дают в остатке число 1.

Ожидаемый ответ: 1) 56898 : 56897 = 1 (ост. 1) 2) 1 : 56897 = 0 (ост. 1)

Задание № 186 (У – 1, с. 61)

Вспоминаем, что при делении с остатком в случаях, где делимое меньшеделителя, остаток равен делимому.

Записываем на доске пример деления на число 5 с остатком 4 (4 : 5 = 0 (ост. 4))

Оставшиеся случаи деления ученики самостоятельно записывают в тетрадях.

Проверяем устно или на доске: 4 : 6 = 0 (ост. 4) 4 : 7 = 0 (ост. 4) 4 : 8 = 0 (ост. 4) 4 : 9 = 0 (ост. 4) 4 : 10 = 0 (ост. 4)

Задание № 187 (У – 1, с. 61)

Учащиеся самостоятельно читают задание.

Выясняем, что согласно правилу: если при делении с остатком делимое меньше делителя, то неполное частное равно 0, а остаток равен делимому, значит, если остаток равен 9, то делимое в этом случае тоже равно 9. Делаем вывод, что число, которое при делении на любое двузначное число даёт в остатке 9 – это число 9.

Просим учеников привести несколько примеров, доказывающих, что при делении числа 9 на любое двузначное число в остатке получается.

Задание № 188* (У – 1, с. 61)

Учащиеся самостоятельно читают задание и вспоминают, если при делении с остатком делимое меньше делителя, то неполное частное равно 0, а остаток равен делимому, значит, если остаток равен 1, то делимое в этом случаетоже равно 1.

Делаем вывод, что число, которое при делении на все натуральные числа даёт в остатке 1 – это число 1.

Просим учеников самостоятельно записать в тетрадях несколько примеров, некоторые из них записываем на доске под диктовку учеников:

1 : 23 = 0 (ост. 1) 1 : 258 = 0 (ост. 1) 1 : 4300 = 0 (ост. 1)

Задание № 189 (У – 1, с. 61)

Учащиеся читают задание: какими могут быть делимое и делитель, если неполное частное равно 0, а остаток равен 5?

Ожидаемый ответ: если неполное частное равно 0, то делимое должно бытьменьше делителя, а остаток (5) равен делимому. Следовательно, искомое делимое должно быть равно 5, а в качестве делителя можно брать любое натуральное число, которое больше 5.

5 : 34 = 0 (ост. 5) 5 : 28 = 0 (ост. 5) 5 : 763 = 0 (ост. 5)

Задание № 190 (У – 1, с. 61)

Вспоминаем условие, при котором в неполном частном получается 0:

делимое должно быть меньше делителя.

Делаем вывод, что учащиеся должны выписать все натуральные однозначные числа, которые меньше 10: 1, 2, 3, 4, 5, 6, 7, 8, 9. Подводим итог, что при делении каждого из этих чисел на число 10 в неполном частном получится 0. (Например, 5 : 10 = 0 (ост.5))

Спрашиваем, чему равен остаток в каждом таком случае? (остаток равен делимому)

Задание № 94 (Т – 1, с. 50)

Учащиеся читают задачу и выясняют, что задача с известным результатом разностного сравнения.

Просим учеников самостоятельно начертить схему и записать решение задачи (пауза)

Проверяем на доске:

3 м 50 см

? ? 1 м 30 см

1) 3 м 50 см – 1 м 30 см = 2 м 20 см – удвоенное количество ткани второго вида

2) 2м 20 см : 2 = 1 м 10 см – купили ткани второго вида

3) 1 м 10 см + 1 м 30 см = 2 м 40 см – купили ткани первого вида Просим учеников прочитать требование задачи: можно ли сшить костюм из этой ткани, если на брюки нужно 2 м ткани первого вида, а на пиджак – 1 м 20 см ткани второго вида?

Ожидаемый ответ: нельзя, так как на пиджак нужно 1 м 20 см ткани второго вида, а купили 1 м 10 см.

Ученики самостоятельно записывают ответ задачи в тетрадях.

Задание на дом: № 90 — 93 (Т – 1, с. 49)

Воспользуйтесь поиском по сайту:

Отсутствующий делитель/дивиденд — таблица 2 (Горизонтальные вопросы

Этот базовый рабочий лист «Отсутствующий делитель/дивиденд» предназначен для того, чтобы помочь детям практиковать пропущенный делитель/дивиденд для таблицы 2 с вопросами о делении, которые меняются при каждом посещении. Этот математический рабочий лист

С помощью этого генератора математических листов вы можете легко создавать рабочие листы с отсутствующими делителями/дивидендами, которые никогда не бывают одинаковыми и всегда разными, предоставляя вам неограниченный запас математических листов для использования. в классе или дома

Каждый лист математики также имеет необязательный флажок Ключ ответа , который можно установить, если вы хотите напечатать ключ ответа, чтобы сопровождать свой лист математики. И есть шесть различных стилей вопросов на выбор, как указано ниже.

Возможные вопросы на деление в этом листе по математике:

2÷2, 4÷2, 6÷2, 8÷2, 10÷2, 12÷2, 14÷2, 16÷2, 18÷2 , 20÷2, 22÷2, 24÷2

СОВЕТ: Нажмите кнопку Обновить ниже, чтобы получить новый рабочий лист по математике!

MISSING DIVISOR/DIVIDEND

. KEY

9000 29000 2

2 902 =

9000 29000 2

9000 2

9000 29000 29000 2

9000 2 9000

9000 29000 29000 29000 229000

9000 29000 29000 29000 2

0002 ÷

9000 2
9292929292929292929000 29292929000 2929292929000
29292929000
29292929292929000 9000 2
9000 2
÷
2
2
2
=
10
16
÷
2
=
8
2
÷
2
=
1
24
÷
2
=
12
10
÷
2
=
5
22
÷
2
=
11
18
÷
2
=
9
2
÷
2
=
1
12
÷
2
=
6
4
÷
2
=
2
22
÷
2
=
11
4
÷
2
=
2
6
÷
2
=
3
2
÷
2
=
1
© 2009-2022 www.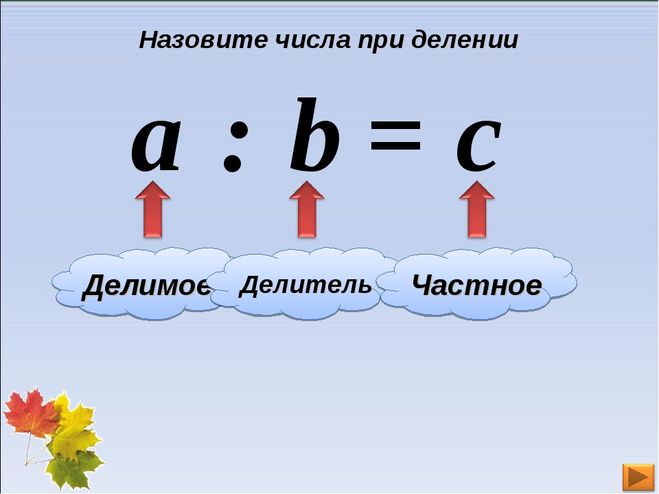 BigActivities.com
По
Адам Хейс
Полная биография
Адам Хейс, доктор философии, CFA, финансовый писатель с более чем 15-летним опытом работы на Уолл-стрит в качестве трейдера деривативов. Помимо своего обширного опыта торговли деривативами, Адам является экспертом в области экономики и поведенческих финансов. Адам получил степень магистра экономики в Новой школе социальных исследований и докторскую степень. из Университета Висконсин-Мэдисон по социологии. Он является обладателем сертификата CFA, а также лицензий FINRA Series 7, 55 и 63. В настоящее время он занимается исследованиями и преподает экономическую социологию и социальные исследования финансов в Еврейском университете в Иерусалиме.
Узнайте о нашем редакционная политика
Обновлено 31 октября 2021 г.
Рассмотрено
Чарльз Поттерс
Рассмотрено Чарльз Поттерс
Полная биография
Чарльз является признанным на национальном уровне специалистом по рынкам капитала и педагогом с более чем 30-летним опытом разработки углубленных программ обучения для начинающих финансовых специалистов. Чарльз преподавал в ряде учреждений, включая Goldman Sachs, Morgan Stanley, Societe Generale и многих других.
Узнайте о нашем Совет финансового контроля
Факт проверен
Кэтрин Бир
Факт проверен Кэтрин Бир
Полная биография
Кэтрин Бир — писатель, редактор и архивариус из Нью-Йорка. У нее большой опыт исследовательской и писательской деятельности, она освещала такие разнообразные темы, как история общественных садов Нью-Йорка и выступление Бейонсе на фестивале Coachella в 2018 году.
Узнайте о нашем редакционная политика
Что такое делитель индекса?
Делитель индекса — это число, выбранное в начале взвешенного по цене индекса фондового рынка, которое применяется к индексу для создания более управляемой стоимости индекса. Когда создается индекс, будь то индекс, взвешенный по цене или рыночной капитализации, цены компонентов индекса складываются вместе, чтобы создать начальное начальное значение индекса. Делитель применяется для приведения кажущегося случайным числа, представляющего собой сумму всех составляющих, к круглому запоминающемуся числу, которое легче запомнить и отслеживать, например 100. После того, как делитель индекса установлен, он не изменяется.
Ключевые выводы
Делитель индекса — это показатель стандартизации, используемый для расчета номинальной стоимости взвешенного по цене рыночного индекса.
Делитель используется для того, чтобы такие события, как дробление акций, специальные дивиденды и обратный выкуп, не оказывали существенного влияния на индекс.
Некоторые делители, такие как тот, который используется для нормализации промышленного индекса Доу-Джонса, регулярно обновляются.
Как работают индексные делители
Делитель индекса дает инвестору или наблюдателю простой способ отслеживать значение индекса с течением времени. Механизм делителя позволяет людям легко отслеживать значение индекса, глядя на частное значения индекса, деленное на делитель индекса. Тем не менее, может потребоваться корректировка делителя, если в индексе произошли существенные изменения, влияющие на его стоимость, например, если участник выходит из индекса или компания выкупает акции или предлагает права.
Существуют различные способы построения индекса. В индексе, взвешенном по цене, к индексу добавляется цена одной акции каждой составляющей. Индивидуальные цены акций всех составляющих, сложенные вместе, создают начальное начальное значение индекса. Если это индекс крупных фармацевтических компаний, то может быть 20 компаний, и цена каждой их акции при суммировании может равняться 476. Это ужасное число, которое нужно помнить. Делитель индекса, равный 4,76, создается для того, чтобы уменьшить отслеживаемое значение индекса до 100. Со временем легче запомнить начальное значение индекса, равное 100, и определить, выросло или упало значение индекса.
Взвешенный индекс рыночной капитализации вычисляет свою стоимость по-другому: берется цена акций составной части и умножается на количество акций в обращении. Полученные значения продуктов всех составляющих затем складываются вместе. После завершения процесса результирующее значение индекса может быть нечетным и запоминающимся числом, например 6873. Этому будет присвоен делитель индекса, например 68,73 или 6,873, чтобы уменьшить отслеживаемое значение индекса до округления 100 или 1000.
Пример делителя индекса
Делитель Доу — это числовое значение, используемое для расчета уровня промышленного индекса Доу-Джонса (DJIA). Индекс Доу-Джонса рассчитывается путем сложения всех цен акций его 30 компонентов и деления суммы на делитель. Однако делитель постоянно корректируется с учетом корпоративных действий, таких как выплата дивидендов и дробление акций.
Если сумма цен 30 составляющих индекса Доу-Джонса составляет 4001, деление этой цифры на делитель Доу-Джонса на 8 февраля 2021 г., равный 0,152, даст индексу уровень 26 322. Используя этот делитель, каждый доллар изменения цены конкретной акции в пределах среднего значения соответствует изменению на 6,5 (или 1 / 0,152) пункта.
Источники статей
Investopedia требует, чтобы авторы использовали первоисточники для поддержки своей работы. К ним относятся официальные документы, правительственные данные, оригинальные отчеты и интервью с отраслевыми экспертами. Мы также при необходимости ссылаемся на оригинальные исследования других авторитетных издателей. Вы можете узнать больше о стандартах, которым мы следуем при создании точного и беспристрастного контента, в нашем редакционная политика.
Бэрронс. «Лаборатория рынка», 8 февраля 2021 г. По состоянию на 28 августа 2021 г.
TOP 8 что такое делимое и делитель ЛУЧШИЙ и НОВЕЙШИЙ
Вы задаетесь вопросом что такое делимое и делитель но в настоящее время нет ответа, поэтому позвольте kienthuctudonghoa.com обобщить и перечислить главные статьи с вопросом. ответьте на вопрос что такое делимое и делитель, что поможет вам получить максимально точный ответ. Следующая статья призвана помочь вам сделать более правильный выбор и получить больше полезной информации
Mục lục
1 1. Делитель, дивиденд, значение частного в математике | Примеры – Byju’s
2 2. Что такое делитель? – Определения, факты и примеры – SplashLearn
3 3. Что такое дивиденды и делители? – Наука
4 4.Дивиденд, делитель, частное и остаток | Свойства деления
5 5.делим, деление, делимое, делитель – Математический словарь для детей
6 6.Дивиденд – определение, формула и важные правила – Веданту
7 7. Что такое дивиденд и что такое делитель? – YouTube
8 8.Что такое дивиденды в математике? – Видео и стенограмма урока – Study.com
1. Делитель, дивиденд, значение частного в математике | Примеры — Byju’s
Автор: Byjus.com
Дата поста: 29 вчера
Рейтинг: 5 (1013 Обзоры)
. Высокий рейтинг: 4
40004 40004 40004 40004 40004 40004 40004 40004 40004 40004 40004 40004 40004 40004 40004 4000444
Итого: Делитель — это целое число, которое делит другое целое число для получения результата. Число, которое делится, называется делимым, а полученный результат — …
См. подробности
2.Что такое делитель? — Определение Факты и пример — Splashlearn
Автор: www.splashlearn.com
Дата поста: 14 вчера
.0015 Низкий рейтинг: 1
Резюме: Делитель — это число, которое полностью или с остатком делится на другое число. Делитель представлен в уравнении деления как: Дивиденд ÷ Делитель …
Подробнее
3.Что такое дивиденды и делители? – Наука
Автор: sciencing.com
Дата публикации: 20 вчера
Рейтинг: 5(413 отзывов)
Высший рейтинг: 3
Низкий рейтинг: 1
Сводка:
Подробнее
4.Дивиденд, делитель, частное и остаток | Свойства подразделения
Автор: www. math-only-math.com
Дата поста: 10 вчера
Оценка: 1 (1610 Обзоры)
Высоко высокий. Низкий рейтинг: 3
Итого: Мы знаем, что делитель означает разделить большую группу объектов на маленькие равные группы. Большая группа называется дивидендом. Число меньших равных групп равно …
Подробнее
5.divide, Division, Division, divisor – Математический словарь для детей
Автор: www.amathsdictionaryforkids.com 29
Дата публикации вчера
Рейтинг: 3(474 отзыва)
Высший рейтинг: 5
Низкий рейтинг: 2
Резюме: число на равные части. • делимое: делимое число. • делитель или множитель: число, на которое делимое точно делится. Примеры:
См. Подробности
6. Dividend — Определение, формула и важные правила — Vedantu
Автор: www. vedantu.com
Дата сообщения: 13 вчера
: 4 ( 13
: 4 ( 13
: 689 отзывов)
Высший рейтинг: 4
Низкий рейтинг: 3
Резюме: Дивиденд Определение · Дивиденд – Дивиденд – это число, которое делится на делитель. · Делитель – число, на которое делится дивиденд, …
Подробнее
7. Что такое дивиденд и что такое делитель? – YouTube
Автор: www.youtube.com
Дата публикации: 1 вчера
Рейтинг: 2(256 отзывов)
Высшая оценка: 3
Низкая оценка: 2
Сводка:
См. подробности 8.10005 — Видео и стенограмма урока — Исследование.
Автор: Исследование.
Дата поста: 30 вчера
Рейтинг: 3 (604 Обзоры)
Высокий рейтинг: 4

.
No related posts.