Правильное дерево решений для правильного выбора
Рассказываем, как правильно использовать дерево решений для машинного обучения, визуализации данных и наглядной демонстрации процесса принятия решений. Пригодится не только аналитикам данных, но и тем, кто хочет найти методику, помогающую более взвешенно принимать решения в жизни и бизнесе.
Статья подготовлена на основе перевода: How to Create a Perfect Decision Tree by Upasana Priyadarshiny.
Основные задачи, которые дерево решений решает в машинном обучении, анализе данных и статистике:
- Классификация — когда нужно отнести объект к конкретной категории, учитывая его признаки.
- Регрессия — использование данных для прогнозирования количественного признака с учетом влияния других признаков.
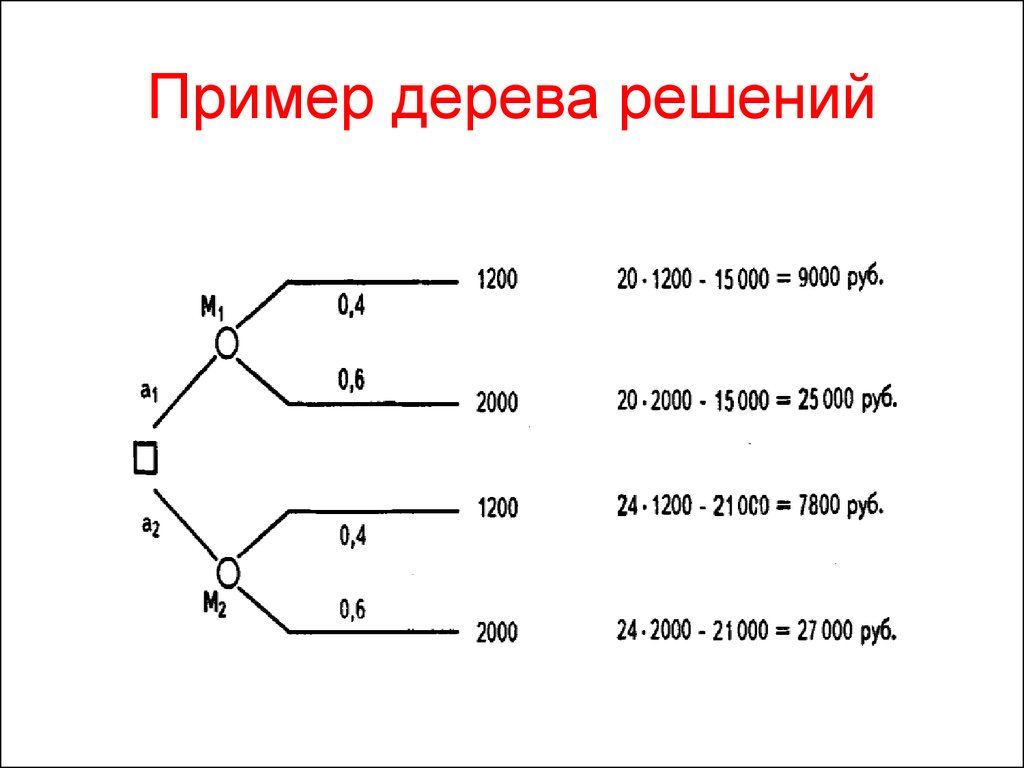
Деревья решений также могут помочь визуализировать процесс принятия решения и сделать правильный выбор в ситуациях, когда результаты одного решения влияют на результаты следующих решений. Попробуем объяснить, как это работает на простых примерах из жизни.
Что такое дерево решений
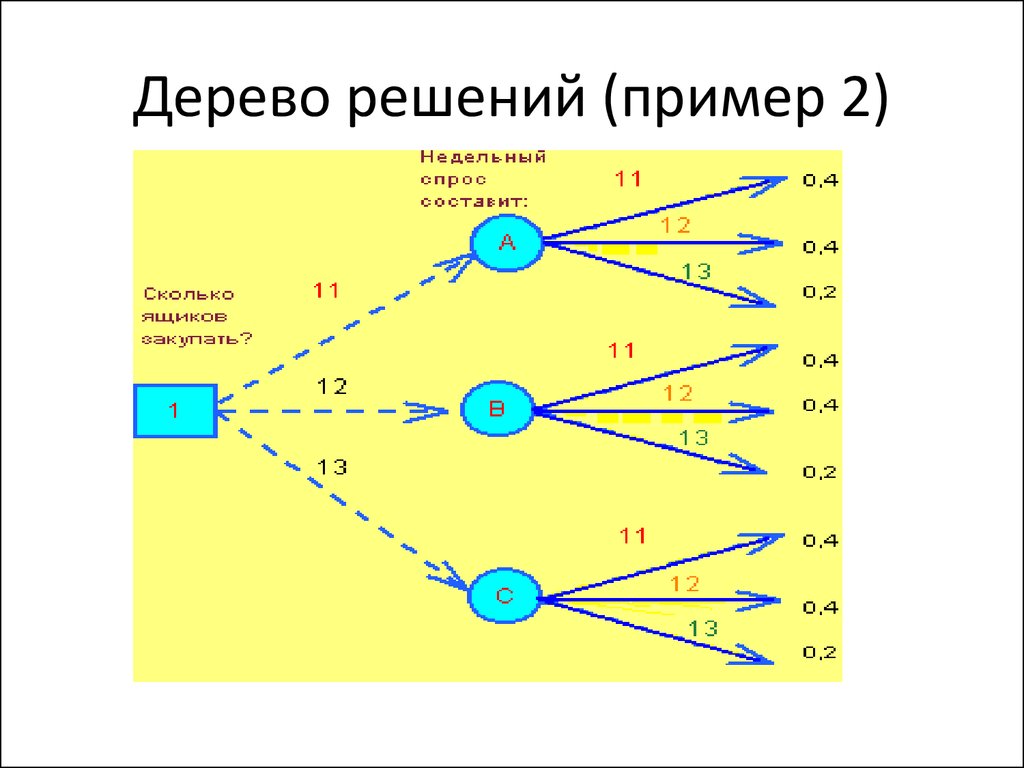
Визуально дерево решений можно представить как карту возможных результатов из ряда взаимосвязанных выборов. Это помогает сопоставить возможные действия, основываясь на их стоимости (затратах), вероятности и выгоде.
Как понятно из названия, для этого используют модель принятия решений в виде дерева. Такие древовидные схемы могут быть полезны и в процессе обсуждения чего-либо, и для составления алгоритма, который математически определяет наилучший выбор.
Обычно дерево решений начинается с одного узла, который разветвляется на возможные результаты. Каждый из них продолжает схему и создает дополнительные узлы, которые продолжают развиваться по тому же признаку. Это придает модели древовидную форму.
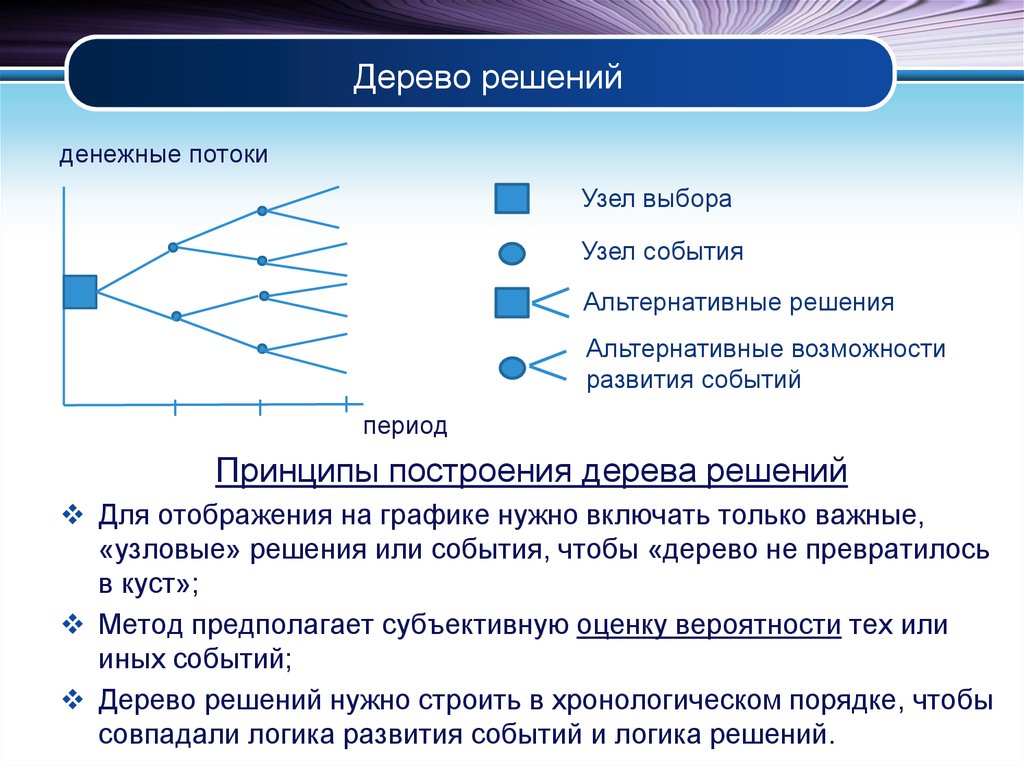
Дерево принятия решения: играть или не играть. Учитывается прогноз погодыВ дереве решений могут быть три разных типа узлов:
- Decision nodes — узлы решения, они показывают решение, которое нужно принять.
- Chance nodes — вероятностные узлы, демонстрируют вероятность определенных результатов.

- End nodes — замыкающие узлы, показывают конечный результат пути решения.
Преимущества и недостатки методики дерева решений
Преимущества метода:
- Деревья решений создаются по понятным правилам, они просты в применении и интерпретации.
- Можно обрабатывать как непрерывные, так и качественные (дискретные) переменные.
- Можно работать с пропусками в данных, деревья решений позволяют заполнить пустое поле наиболее вероятным значением.
- Помогают определить, какие поля больше важны для прогнозирования или классификации.
Недостатки метода:
- Есть вероятность ошибок в задачах классификации с большим количеством классов и относительно небольшим числом примеров для обучения.
- Нестабильность процесса: изменение в одном узле может привести к построению совсем другого дерева, что связано с иерархичностью его структуры.
- Процесс «выращивания» дерева решений может быть довольно затратным с точки зрения вычислений, ведь в каждом узле каждый атрибут должен раскладываться до тех пор, пока не будет найден наилучший вариант решения или разветвления.
 В некоторых алгоритмах используются комбинации полей, в таком случае приходится искать оптимальную комбинацию по «весу» коэффициентов. Алгоритм отсечения (или «обрезки») также дорогостоящий, так как необходимо сформировать и сравнить большое количество потенциальных ветвей.
В некоторых алгоритмах используются комбинации полей, в таком случае приходится искать оптимальную комбинацию по «весу» коэффициентов. Алгоритм отсечения (или «обрезки») также дорогостоящий, так как необходимо сформировать и сравнить большое количество потенциальных ветвей.
Как создать дерево решений
Для примера предлагаем сценарий, в котором группа астрономов изучает планету — нужно выяснить, сможет ли она стать новой Землей.
Существует N решающих факторов, которые нужно тщательно изучить, чтобы принять разумное решение. Этими факторами может быть наличие воды на планете, температурный диапазон, подвержена ли поверхность постоянным штормам, сможет ли выжить флора и фауна в этом климате и еще сотни других параметров.
Задачу будем исследовать через дерево решений.
- Пригодная для обитания температура находится в диапазоне от 0 до 100 градусов Цельсия?
- Есть ли там вода?
- Флора и фауна процветает?
- Подвержена ли поверхность планеты штормам?
Таким образом, у нас получилось завершенное дерево решений.
Правила классификации
Сначала определимся с терминами и их значениями.
Правила классификации — это случаи, в которых учитываются все сценарии, и каждому присваивается переменная класса.
Переменная класса — это конечный результат, к которому приводит наше решение. Переменная класса присваивается каждому конечному, или листовому, узлу.
Вот правила классификации из примера дерева решений про исследование новой планеты:
- Если температура не находится в диапазоне от -0,15 °C до 99,85 °C, то выживание затруднительно.
- Если температура находится в диапазоне от -0,15 °C до 99,85 °C, но нет воды, то выживание затруднительно.
- Если температура находится в диапазоне от -0,15 °C до 99,85 °C, есть вода, но нет флоры и фауны, то выживание затруднительно.
- Если температура находится в диапазоне от -0,15 °C до 99,85 °C, есть вода, есть флора и фауна, поверхность не подвержена штормам, то выживание возможно.

- Если температура находится в диапазоне от -0,15 °C до 99,85 °C, есть вода, есть флора и фауна, но поверхность подвержена штормам, то выживание затруднительно.
Почему сложно построить идеальное дерево решений
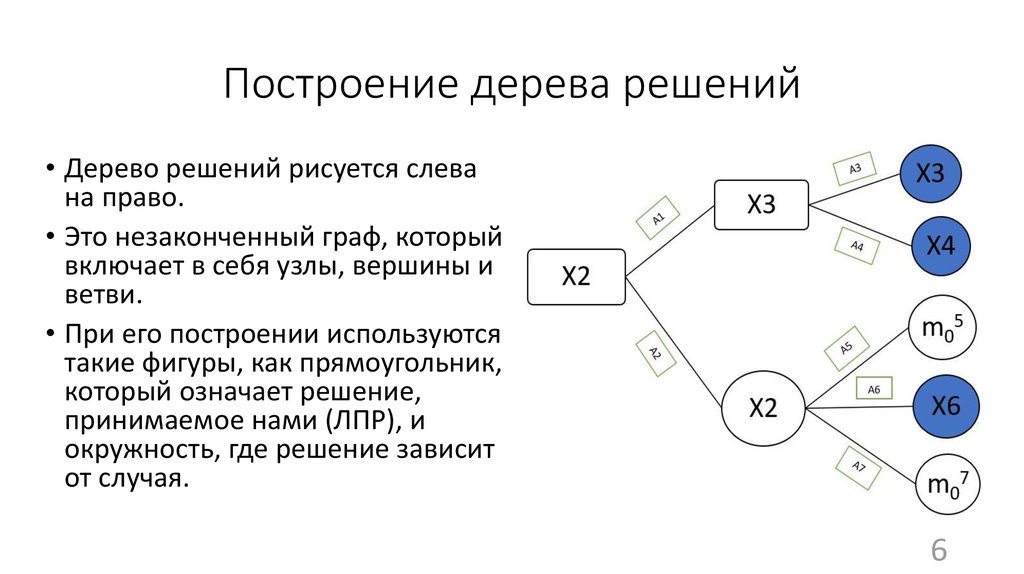
В структуре дерева решений выделяют следующие компоненты:
- Root Node, или корневой узел — тот, с которого начинается дерево, в нашем примере в качестве корня рассматривается фактор «температура».
- Internal Node, или внутренний узел — узлы с одним входящим и двумя или более исходящими соединениями.
- Leaf Node, или листовой узел — это заключительный элемент без исходящих соединений.
Когда создается дерево решений, мы начинаем от корневого узла, проверяем условия тестирования и присваиваем элемент управления одному из исходящих соединений. Затем снова тестируем условия и назначаем следующий узел. Чтобы считать дерево законченным, нужно все условия привести к листовому узлу (Leaf Node). Листовой узел будет содержать все метки класса, которые влияют на «за» и «против» в принятии решения.
Обратите внимание — мы начали с признака «температура», посчитали его корнем. Если выбрать другой признак, то и дерево получится другим. В этом принцип метода — нужно выбрать оптимальный корень и с помощью него выстраивать дерево, решить, какое же дерево нужно для выполнения задачи.
Есть разные способы найти максимально подходящее дерево решений для конкретной ситуации. Ниже расскажем об одном из них.
Как использовать жадный алгоритм для построения дерева решений
Смысл подхода — принцип так называемой жадной максимизации прироста информации. Он основан на концепции эвристического решения проблем — делать оптимальный локальный выбор в каждом узле, так достигая решения, которое с высокой вероятностью будет самым оптимальным.
Упрощенно алгоритм можно объяснить так:
- На каждом узле выбирайте оптимальный способ проверки.
- После разбейте узел на все возможные результаты (внутренние узлы).
- Повторите шаги, пока все условия не приведут к конечным узлам.

Главный вопрос: «Как выбрать начальные условия для проверки?»
. Ответ заключается в значениях энтропии и прироста информации (информационном усилении). Рассказываем, что это и как они влияют на создание нашего дерева:- Энтропия — в дереве решений это означает однородность. Если данные полностью однородны, она равна 0; в противном случае, если данные разделены (50-50%), энтропия равна 1. Проще этот термин можно объяснить так — это то, как много информации, значимой для принятия решения, мы не знаем.
- Прирост информации — величина обратная энтропии, чем выше прирост информации, тем меньше энтропия, меньше неучтенных данных и лучше решение.
Итого — мы выбираем атрибут, который имеет наибольший показатель прироста информации, чтобы пойти на следующий этап разделения. Это помогает выбрать лучшее решение на любом узле.
Смотрите на примере. У нас есть большое количество таких данных:
| Номер | Возраст (Age) | Уровень дохода (Income) | Студент (Student) | Кредитный рейтинг (CR) | Покупка компьютера (Buys Computer) |
| 1 | <30 | низкий (Low) | да | средний (Fair) | да |
| 2 | 30-40 | высокий (High) | нет | прекрасный (Excellent) | да |
| 3 | 40 | высокий (High) | нет | прекрасный (Excellent) | нет |
| 4 | <30 | средний (Medium) | нет | средний (Fair) | нет |
Здесь может быть n деревьев решений, которые формируются из этого набора атрибутов.
Ищем оптимальное решение с жадным алгоритмом
Первый шаг
: создать два условных класса:- «Да», человек может купить компьютер.
- «Нет», возможность отсутствует.
Второй шаг — вычислить значение вероятности для каждого из них.
- Для результата «Да», «buys_computer=yes», формула выглядит так:
- Для результата «Нет», «buys_computer=no», вот так:
$$P(buys = yes) = {9 \over 14}$$
$$P(buys = no) = {5 \over 14}$$
Третий шаг: вычисляем значение энтропии, поместив значения вероятности в формулу.
$$Info(D) = I(9,5) = -{9 \over 14}log_{2}({9 \over 14})-{5 \over 14}log_{2}({5 \over 14})=0,940$$
Это довольно высокий показатель энтропии.
Четвертый шаг: углубляемся и считаем прирост информации для каждого случая, чтобы вычислить подходящий корневой атрибут для дерева решения.
Здесь нужно пояснение. Например, что будет означать показатель прироста информации, если за основу взять атрибут «Возраст»? Эти данные показывают, сколько людей, попадающих в определенную возрастную группу, покупают и не покупают продукт.
Допустим, среди людей в возрасте 30 лет и младше покупают (Да) два человека, не покупают (Нет) три человека. Info(D) рассчитывается для последних трех категорий людей — соответственно, Info(D) будем считать по сумме этих трех диапазонов значений возраста.
В итоге разница между общей энтропией Info(D) и энтропией для возраста Info(D) age (пусть она равна 0,694) будет нужным значением прироста информации. Вот формула:
$$Gain(age)=Info(D)-Info_{age}(D)=0,246$$
Сравним показатели прироста информации для всех атрибутов:
- Возраст = 0,246.
- Доход = 0.029.
- Студент = 0,151.
- Кредитный рейтинг = 0,048.
Получается, что прирост информации для атрибута возраста является самым значимым — значит, стоит использовать его. Аналогично мы сравниваем прирост в информации при каждом разделении, чтобы выяснить, брать этот атрибут или нет.
Аналогично мы сравниваем прирост в информации при каждом разделении, чтобы выяснить, брать этот атрибут или нет.
Таким образом, оптимальное дерево выглядит так:
Правила классификации для этого дерева можно записать следующим образом:
- Если возраст человека меньше 30 лет и он не студент, то не будет покупать компьютер.
- Если возраст человека меньше 30 лет, и он студент, то купит компьютер.
- Если возраст человека составляет от 31 до 40 лет, он, скорее всего, купит компьютер.
- Если человек старше 40 лет и имеет отличный кредитный рейтинг, то не будет покупать компьютер.
- Если возраст человека превышает 40 лет, при среднем кредитном рейтинге он, вероятно, купит компьютер.
Вот мы и достигли оптимального дерева решений. Готово.
Внедрение дерева решений с нуля
Дерево решений с нуляДеревья решений просты и легко объяснимы. Они могут быть легко отображены графически и следовательно, допускают гораздо более простую интерпретацию. Они также являются довольно популярным и успешным оружием, когда речь идет о соревнованиях по машинному обучению (например Kaggle).
Они также являются довольно популярным и успешным оружием, когда речь идет о соревнованиях по машинному обучению (например Kaggle).
Однако простота на первый взгляд не означает, что алгоритм и лежащие в его основе механизмы скучны или даже тривиальны.
В следующих разделах мы собираемся поэтапно реализовать дерево решений для классификации, используя только Python и NumPy. Мы также узнаем о концепциях энтропии и получения информации, которые дают нам средства для оценки возможных расщеплений, что позволяет нам разумно вырастить дерево решений.
Но прежде чем погрузиться непосредственно в детали реализации, давайте установим некоторые базовые интуитивные представления о деревьях решений в целом.
Методы на основе дерева просты и полезны для интерпретации, поскольку лежащие в их основе механизмы считаются очень похожими на процесс принятия решений человеком.
Методы включают стратификацию или сегментацию пространства предикторов на несколько более простых областей. Делая прогноз, мы просто используем среднее значение или режим области, к которой принадлежит новое наблюдение, в качестве значения отклика.
Делая прогноз, мы просто используем среднее значение или режим области, к которой принадлежит новое наблюдение, в качестве значения отклика.
Поскольку правила разделения для сегментирования пространства предикторов лучше всего могут быть описаны древовидной структурой, алгоритм обучения с учителем называется деревом решений.
Деревья решений можно использовать как для задач регрессии, так и для задач классификации.
Упрощенный пример дерева решенийТеперь, когда мы знаем, что такое дерево решений и почему оно может быть полезным, нам нужно знать, как его вырастить?
Грубо говоря, процесс построения дерева решений в основном состоит из двух этапов:
- Разделение пространства предикторов на несколько отдельных непересекающихся областей
- Прогнозирование наиболее распространенной метки класса для области, к которой принадлежит любое новое наблюдение
Как бы просто это ни звучало, возникает один фундаментальный вопрос — как разделить пространство предикторов?
Чтобы разделить пространство предикторов на отдельные области, мы используем бинарное рекурсивное разбиение, которое увеличивает наше дерево решений до тех пор, пока мы не достигнем критерия остановки. Поскольку нам нужен разумный способ решить, какие разбиения полезны, а какие нет, нам также нужна метрика для целей оценки.
Поскольку нам нужен разумный способ решить, какие разбиения полезны, а какие нет, нам также нужна метрика для целей оценки.
В теории информации энтропия описывает средний уровень информации или неопределенности и может быть определена следующим образом:
Мы можем использовать концепцию энтропии для расчета прироста информации в результате возможного разделения.
Предположим, у нас есть набор данных, содержащий разные данные о пациентах. Теперь мы хотим классифицировать каждого пациента как имеющего высокий или низкий риск сердечного приступа. Представьте себе возможное дерево решений, подобное следующему:
Пример дерева решений для расчета прироста информацииЧтобы рассчитать прирост информации разделения (IG), мы просто вычисляем сумму взвешенных энтропий дочерних элементов и вычитаем ее из энтропии родителя.
Давайте проработаем наш пример, чтобы прояснить ситуацию:
Прирост информации, равный 1, был бы наилучшим возможным результатом. Однако в нашем примере расщепление дает информационный прирост примерно 0,395 и следовательно, содержит гораздо больше неопределенности или другими словами, более высокое значение энтропии.
Однако в нашем примере расщепление дает информационный прирост примерно 0,395 и следовательно, содержит гораздо больше неопределенности или другими словами, более высокое значение энтропии.
Вооружившись понятиями энтропии и прироста информации, нам просто нужно оценить все возможные разбиения на текущем этапе роста дерева (жадный подход), выбрать лучший и продолжать рекурсивно расти, пока не достигнем критерия остановки.
Теперь, когда мы рассмотрели все основы, мы можем приступить к реализации алгоритма обучения.
Но прежде чем углубиться непосредственно в детали реализации, мы кратко рассмотрим основные вычислительные этапы алгоритма, чтобы предоставить общий обзор, а также некоторую базовую структуру.
Основной алгоритм можно условно разделить на три шага:
- Инициализация параметров (например, максимальная глубина, минимальное количество выборок на разделение) и создание вспомогательного класса
- Построение дерева решений, включающее бинарное рекурсивное разбиение, оценку каждого возможного разбиения на текущем этапе и продолжение роста дерева до тех пор, пока не будет удовлетворен критерий остановки.

- Создание прогноза, который можно описать как рекурсивный обход дерева и возврат наиболее распространенной метки класса в качестве значения ответа.
Поскольку построение дерева состоит из нескольких шагов, мы будем в значительной степени полагаться на использование вспомогательных функций, чтобы сделать наш код как можно более чистым.
Алгоритм будет реализован в двух классах: основной класс, содержащий сам алгоритм, и вспомогательный класс, определяющий узел. Ниже мы можем взглянуть на скелетные классы, которые можно интерпретировать как своего рода план, помогающий нам в реализации в следующем разделе.
class Node:
def __init__(self, feature=None, threshold=None, left=None, right=None, *, value=None):
pass
def is_leaf(self):
passclass DecisionTree:
def __init__(self, max_depth=100, min_samples_split=2):
pass
def _is_finished(self, depth):
pass
def _entropy(self, y):
pass
def _create_split(self, X, thresh):
pass
def _information_gain(self, X, y, thresh):
pass
def _best_split(self, X, y, features):
pass
def _build_tree(self, X, y, depth=0):
pass
def _traverse_tree(self, x, node):
pass
def fit(self, X, y):
pass
def predict(self, X):
pass
Базовая установка и узел
Давайте начнем нашу реализацию с некоторой базовой уборки. Прежде всего, мы определяем некоторые основные параметры для нашего основного класса, а именно критерии остановки
Прежде всего, мы определяем некоторые основные параметры для нашего основного класса, а именно критерии остановки max_depth, min_samples_split и root node.
class DecisionTree:
def __init__(self, max_depth=100, min_samples_split=2):
self.max_depth = max_depth
self.min_samples_split = min_samples_split
self.root = None
Затем мы определяем небольшой вспомогательный класс, который хранит наши разбиения в узле. Узел содержит информацию о feature, threshold значении, подключенном left и right дочернем элементе, которая будет полезна, когда мы рекурсивно проходим по дереву, чтобы сделать прогноз.
class Node:
def __init__(self, feature=None, threshold=None, left=None, right=None, *, value=None):
self.feature = feature
self.threshold = threshold
self.left = left
self.right = right
self.value = value
def is_leaf(self):
return self. value is not None
value is not None
Построение дерева
Теперь все становится немного сложнее. Таким образом, в дальнейшем мы будем в значительной степени полагаться на использование нескольких вспомогательных методов, чтобы оставаться организованными.
class DecisionTree:
def _is_finished(self, depth):
if (depth >= self.max_depth
or self.n_class_labels == 1
or self.n_samples < self.min_samples_split):
return True
return False
def _build_tree(self, X, y, depth=0):
self.n_samples, self.n_features = X.shape
self.n_class_labels = len(np.unique(y))
# stopping criteria
if self._is_finished(depth):
most_common_Label = np.argmax(np.bincount(y))
return Node(value=most_common_Label)
def fit(self, X, y):
self.root = self._build_tree(X, y)
#...
Мы начинаем процесс построения с вызова метода fit(), который просто вызывает наш основной метод _build_tree().
В основном методе мы просто собираем некоторую информацию о наборе данных (количество выборок, признаков и уникальных меток классов), которая потребуется, чтобы решить, соблюдены ли критерии остановки.
Наш вспомогательный метод _is_finished() используется для оценки критериев остановки. Если, например, осталось меньше выборок, чем минимально необходимое количество выборок на оставшееся разделение, наш метод возвращается True, и процесс построения будет остановлен в этой текущей ветви.
Если наш процесс сборки завершен, мы вычисляем наиболее распространенную метку класса и сохраняем это значение в файле leaf node.
Примечание. Критерий остановки служит стратегией выхода для остановки рекурсивного роста. Без стопорного механизма мы бы создали бесконечный цикл.
class DecisionTree:
#...
def _entropy(self, y):
proportions = np.bincount(y) / len(y)
entropy = -np. sum([p * np.log2(p) for p in proportions if p > 0])
return entropy
def _create_split(self, X, thresh):
left_idx = np.argwhere(X <= thresh).flatten()
right_idx = np.argwhere(X > thresh).flatten()
return left_idx, right_idx
def _information_gain(self, X, y, thresh):
parent_loss = self._entropy(y)
left_idx, right_idx = self._create_split(X, thresh)
n, n_left, n_right = len(y), len(left_idx), len(right_idx)
if n_left == 0 or n_right == 0:
return 0
child_loss = (n_left / n) * self._entropy(y[left_idx]) + (n_right / n) * self._entropy(y[right_idx])
return parent_loss - child_loss
def _best_split(self, X, y, features):
split = {'score':- 1, 'feat': None, 'thresh': None}
for feat in features:
X_feat = X[:, feat]
thresholds = np.unique(X_feat)
for thresh in thresholds:
score = self._information_gain(X_feat, y, thresh)
if score > split['score']:
split['score'] = score
split['feat'] = feat
split['thresh'] = thresh
return split['feat'], split['thresh']
def _build_tree(self, X, y, depth=0):
#.
sum([p * np.log2(p) for p in proportions if p > 0])
return entropy
def _create_split(self, X, thresh):
left_idx = np.argwhere(X <= thresh).flatten()
right_idx = np.argwhere(X > thresh).flatten()
return left_idx, right_idx
def _information_gain(self, X, y, thresh):
parent_loss = self._entropy(y)
left_idx, right_idx = self._create_split(X, thresh)
n, n_left, n_right = len(y), len(left_idx), len(right_idx)
if n_left == 0 or n_right == 0:
return 0
child_loss = (n_left / n) * self._entropy(y[left_idx]) + (n_right / n) * self._entropy(y[right_idx])
return parent_loss - child_loss
def _best_split(self, X, y, features):
split = {'score':- 1, 'feat': None, 'thresh': None}
for feat in features:
X_feat = X[:, feat]
thresholds = np.unique(X_feat)
for thresh in thresholds:
score = self._information_gain(X_feat, y, thresh)
if score > split['score']:
split['score'] = score
split['feat'] = feat
split['thresh'] = thresh
return split['feat'], split['thresh']
def _build_tree(self, X, y, depth=0):
#. ..
# get best split
rnd_feats = np.random.choice(self.n_features, self.n_features, replace=False)
best_feat, best_thresh = self._best_split(X, y, rnd_feats)
..
# get best split
rnd_feats = np.random.choice(self.n_features, self.n_features, replace=False)
best_feat, best_thresh = self._best_split(X, y, rnd_feats)Мы продолжаем расширять наше дерево, вычисляя лучшее разделение на текущем этапе. Чтобы получить наилучшее разделение, мы перебираем все индексы функций и уникальные пороговые значения для расчета прироста информации. В предыдущих разделах мы уже узнали, как рассчитать прирост информации, который в основном говорит нам, сколько неопределенности может быть устранено предлагаемым разделением.
Как только мы получим прирост информации для конкретной комбинации признаков и порогов, мы сравним результат с нашими предыдущими итерациями. Если мы находим лучшее разделение, мы сохраняем связанные параметры в словаре.
После перебора всех комбинаций мы возвращаем лучший признак и порог в виде кортежа.
class DecisionTree:
#...
def _build_tree(self, X, y, depth=0):
#. ..
# grow children recursively
left_idx, right_idx = self._create_split(X[:, best_feat], best_thresh)
left_child = self._build_tree(X[left_idx, :], y[left_idx], depth + 1)
right_child = self._build_tree(X[right_idx, :], y[right_idx], depth + 1)
return Node(best_feat, best_thresh, left_child, right_child)
..
# grow children recursively
left_idx, right_idx = self._create_split(X[:, best_feat], best_thresh)
left_child = self._build_tree(X[left_idx, :], y[left_idx], depth + 1)
right_child = self._build_tree(X[right_idx, :], y[right_idx], depth + 1)
return Node(best_feat, best_thresh, left_child, right_child)
Теперь мы можем закончить наш основной метод, рекурсивно вырастив дочерние элементы. Поэтому мы разделяем данные, используя лучшую функцию и пороговое значение, на левую и правую ветви.
Затем мы вызываем наш основной метод из самого себя (здесь это рекурсивная часть), чтобы начать процесс построения дочерних элементов.
Как только мы удовлетворяем критериям остановки, метод будет рекурсивно возвращать все узлы, что позволит нам построить полноценное дерево решений.
Предсказание — или обход дерева
Мы закончили большую часть тяжелой работы — нам просто нужно создать еще один вспомогательный метод, и все готово.
class DecisionTree:
#. ..
def _traverse_tree(self, x, node):
if node.is_leaf():
return node.value
if x[node.feature] <= node.threshold:
return self._traverse_tree(x, node.left)
return self._traverse_tree(x, node.right)
def predict(self, X):
predictions = [self._traverse_tree(x, self.root) for x in X]
return np.array(predictions)
..
def _traverse_tree(self, x, node):
if node.is_leaf():
return node.value
if x[node.feature] <= node.threshold:
return self._traverse_tree(x, node.left)
return self._traverse_tree(x, node.right)
def predict(self, X):
predictions = [self._traverse_tree(x, self.root) for x in X]
return np.array(predictions)Предсказание можно реализовать путем рекурсивного обхода дерева. Это означает, что для каждой выборки в нашем наборе данных мы сравниваем функцию узла и пороговые значения со значениями текущей выборки и решаем, нужно ли нам повернуть налево или направо.
Как только мы достигаем конечного узла, мы просто возвращаем наиболее распространенную метку класса в качестве нашего прогноза.
И это он! Мы закончили реализацию дерева решений.
Закончив реализацию, нам еще нужно протестировать наш классификатор.
В целях тестирования мы будем использовать набор данных Висконсина с классической бинарной классификацией рака молочной железы. Всего набор данных содержит 30 измерений и 569 выборок.
Всего набор данных содержит 30 измерений и 569 выборок.
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split
from DecisionTree import DecisionTree
def accuracy(y_true, y_pred):
accuracy = np.sum(y_true == y_pred) / len(y_true)
return accuracy
data = datasets.load_breast_cancer()
X, y = data.data, data.target
X_train, X_test, y_train, y_test = train_test_split(
X, y, test_size=0.2, random_state=1
)
clf = DecisionTree(max_depth=10)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
acc = accuracy(y_test, y_pred)
print("Accuracy:", acc)
После импорта набора данных мы можем разделить его на обучающую и тестовую выборки соответственно.
Мы создаем экземпляр нашего классификатора, подгоняем его к обучающим данным и делаем наши прогнозы. Используя нашу вспомогательную функцию, мы получаем точность ~ 95,6%, что позволяет нам подтвердить, что наш алгоритм работает.
1.10. Деревья решений — документация scikit-learn 1.
 1.3
1.3Деревья решений (DT) — это непараметрический контролируемый метод обучения для классификации и регрессии. Цель состоит в том, чтобы создать модель, которая предсказывает значение целевая переменная, изучая простые правила принятия решений, полученные на основе данных Особенности. Дерево можно рассматривать как кусочно-постоянную аппроксимацию.
Например, в приведенном ниже примере деревья решений обучаются на основе данных для аппроксимировать синусоиду набором решающих правил «если-то-иначе». Чем глубже дерево, тем сложнее правила принятия решений и лучше модель.
Некоторые преимущества деревьев решений:
Простота для понимания и интерпретации. Деревья можно визуализировать.
Требуется небольшая подготовка данных. Другие методы часто требуют данных нормализация, необходимо создать фиктивные переменные и пустые значения для удалить. Обратите внимание, однако, что этот модуль не поддерживает отсутствующие ценности.
Стоимость использования дерева (т. е. прогнозирования данных) является логарифмической в количество точек данных, используемых для обучения дерева.
Способен обрабатывать как числовые, так и категориальные данные. Тем не менее, scikit-learn реализация пока не поддерживает категориальные переменные. Другой методы обычно специализируются на анализе наборов данных, которые имеют только один тип переменной. Подробнее об алгоритмах см. Информация.
Возможность решения задач с несколькими выходами.
Использует модель белого ящика. Если данная ситуация наблюдаема в модели, объяснение условия легко объясняется булевой логикой. Напротив, в модели черного ящика (например, в искусственном нейронном сеть), результаты могут быть труднее интерпретировать.
Можно проверить модель с помощью статистических тестов. Это делает это можно объяснить надежность модели.
Работает хорошо, даже если его предположения несколько нарушаются истинная модель, из которой были сгенерированы данные.
К недостаткам деревьев решений относятся:
Изучающие деревья решений могут создавать сверхсложные деревья, которые не хорошо обобщать данные. Это называется переоснащением. Механизмы такие как обрезка, установка минимального количества необходимых образцов на листовом узле или установка максимальной глубины дерева. необходимо, чтобы избежать этой проблемы.
Деревья решений могут быть нестабильными из-за небольших изменений в данные могут привести к созданию совершенно другого дерева. Эта проблема смягчается за счет использования дерева решений в ансамбль.
Прогнозы деревьев решений не являются ни гладкими, ни непрерывными, но кусочно-постоянные приближения, как показано на рисунке выше. Следовательно, они не умеют экстраполировать.
Известно, что задача изучения оптимального дерева решений NP-полным по нескольким аспектам оптимальности и даже для простых концепции.
Следовательно, практические алгоритмы обучения дерева решений основаны на эвристических алгоритмах, таких как жадный алгоритм, где в каждом узле принимаются локально оптимальные решения. Такие алгоритмы не может гарантировать возвращение глобально оптимального дерева решений. Этот можно смягчить, обучив несколько деревьев в обучающем ансамбле, где функции и образцы выбираются случайным образом с заменой.
Существуют концепции, которые трудно выучить, потому что деревья решений не выражайте их легко, например XOR, проблемы с четностью или мультиплексором.
Обучающиеся дерева решений создают деревья с ошибками, если некоторые классы доминируют. Поэтому рекомендуется сбалансировать набор данных перед подгонкой. с деревом решений.
1.10.1. Классификация
DecisionTreeClassifier — это класс, способный выполнять
классификация по набору данных.
Как и другие классификаторы, DecisionTreeClassifier принимает на вход два массива:
массив X, разреженный или плотный, формы (n_samples, n_features) , содержащий
обучающие образцы и массив Y целочисленных значений формы (n_samples,) ,
наличие меток класса для обучающих образцов:
>>> из дерева импорта sklearn >>> Х = [[0, 0], [1, 1]] >>> Y = [0, 1] >>> clf = tree.DecisionTreeClassifier() >>> clf = clf.fit(X, Y)
После подгонки модель можно использовать для прогнозирования класса образцов:
>>> clf.predict([[2., 2.]]) массив ([1])
В случае, если существует несколько классов с одинаковым и самым высоким вероятность, классификатор предскажет класс с наименьшим индексом среди этих классов.
В качестве альтернативы выводу определенного класса вероятность каждого класса можно предсказать, что является долей обучающих выборок класса в лист:
>>> clf.predict_proba([[2., 2.]]) массив([[0., 1.]])
DecisionTreeClassifier поддерживает как двоичные (где
метки [-1, 1]) классификация и мультикласс (где метки
[0, …, K-1]) классификации.
Используя набор данных Iris, мы можем построить дерево следующим образом:
>>> из sklearn.datasets импортировать load_iris >>> из дерева импорта sklearn >>> диафрагма = load_iris() >>> X, y = iris.data, iris.target >>> clf = tree.DecisionTreeClassifier() >>> clf = clf.fit(X, y)
После обучения вы можете построить дерево с помощью функции plot_tree :
>>> tree.plot_tree(clf) [...]
Мы также можем экспортировать дерево в формате Graphviz, используя export_graphviz экспортер. Если вы используете диспетчер пакетов conda, двоичные файлы graphviz
и пакет python можно установить с помощью conda install python-graphviz .
В качестве альтернативы двоичные файлы для graphviz можно загрузить с домашней страницы проекта graphviz,
и оболочка Python, установленная из pypi с пипс установить графвиз .
Ниже приведен пример графического экспорта приведенного выше дерева, обученного на всем
набор данных по радужной оболочке; результаты сохраняются в выходной файл iris.pdf :
>>> импорт графика >>> dot_data = tree.export_graphviz(clf, out_file=Нет) >>> graph = graphviz.Source(dot_data) >>> graph.render("радужная оболочка")
Экспортер export_graphviz также поддерживает различные эстетические
параметры, включая раскраску узлов по их классу (или значению для регрессии) и
используя явные имена переменных и классов, если это необходимо. Ноутбуки Jupyter также
отображать эти графики автоматически:
>>> dot_data = tree.export_graphviz(clf, out_file=Нет, ... feature_names=радужная оболочка.feature_names, ... class_names=iris.target_names, ... заполнено=Истина, округлено=Истина, ... special_characters=Истина) >>> graph = graphviz.Source(dot_data) >>> график
Кроме того, дерево можно также экспортировать в текстовом формате с
функция экспорт_текст . Этот метод не требует установки
внешних библиотек и компактнее:
>>> из sklearn.datasets импортировать load_iris >>> из sklearn.tree импортировать DecisionTreeClassifier >>> из sklearn.tree импортировать export_text >>> диафрагма = load_iris() >>> дерево_решений = класс_дерева_решений(случайное_состояние=0, максимальная_глубина=2) >>> дерево_решений = дерево_решений.fit(iris.data, iris.target) >>> r = export_text(decision_tree, feature_names=радужная оболочка['feature_names']) >>> напечатать(р) |--- ширина лепестка (см) <= 0,80 | |--- класс: 0 |--- ширина лепестка (см) > 0,80 | |--- ширина лепестка (см) <= 1,75 | | |--- класс: 1 | |--- ширина лепестка (см) > 1,75 | | |--- класс: 2
Примеры:
Постройте поверхность решений деревьев решений, обученных на наборе данных радужной оболочки
Понимание структуры дерева решений
1.10.2. Регрессия
Деревья решений также можно применять к задачам регрессии, используя Класс DecisionTreeRegressor .
Как и в настройке классификации, метод подгонки будет принимать в качестве аргументов массивы X и y, только то, что в этом случае ожидается, что y будет иметь значения с плавающей запятой вместо целочисленных значений:
>>> из дерева импорта sklearn >>> Х = [[0, 0], [2, 2]] >>> у = [0,5, 2,5] >>> clf = tree.DecisionTreeRegressor() >>> clf = clf.fit(X, y) >>> clf.predict([[1, 1]]) массив ([0,5])
Примеры:
Регрессия дерева решений
1.10.3. Проблемы с несколькими выходами
Задача с несколькими выходами — это контролируемая задача обучения с несколькими выходами.
чтобы предсказать, то есть когда Y представляет собой двумерный массив формы (n_выборок, n_выходов) .
При отсутствии корреляции между выходами очень простой способ решить
такая задача состоит в том, чтобы построить n независимых моделей, т.е. по одной на каждую
вывод, а затем использовать эти модели для независимого прогнозирования каждого из n
выходы. Однако, поскольку вполне вероятно, что выходные значения, относящиеся к
одни и те же входные данные сами коррелируют друг с другом, зачастую лучший способ — создать единый
модель, способная предсказывать одновременно все n выходов. Во-первых, требуется
меньшее время обучения, так как строится только одна оценка.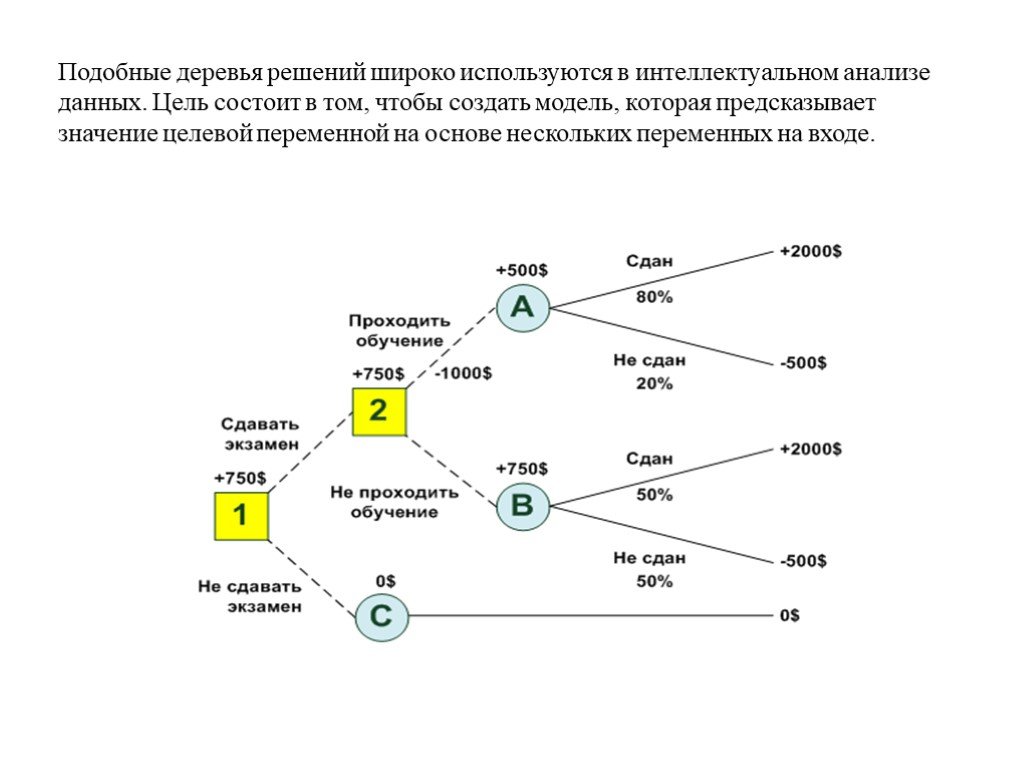 Во-вторых,
точность обобщения результирующей оценки часто может быть увеличена.
Во-вторых,
точность обобщения результирующей оценки часто может быть увеличена.
Что касается деревьев решений, эту стратегию можно легко использовать для поддержки задачи с несколькими выходами. Для этого требуются следующие изменения:
Этот модуль предлагает поддержку задач с несколькими выходами, реализуя этот
стратегия как в DecisionTreeClassifier , так и в DecisionTreeRegressor . Если дерево решений подходит для выходного массива Y
формы (n_samples, n_outputs) , то результирующая оценка будет:
Использование деревьев с несколькими выходами для регрессии продемонстрировано в Регрессия дерева решений с несколькими выходами. В этом примере ввод X — единственное действительное значение, а выходные значения Y — синус и косинус X.
Использование многовыходных деревьев для классификации продемонстрировано в
Завершение грани с многовыходными оценщиками. В этом примере входы
X — пиксели верхней половины граней, а выходные данные Y — пиксели
нижняя половина этих граней.
В этом примере входы
X — пиксели верхней половины граней, а выходные данные Y — пиксели
нижняя половина этих граней.
Примеров:
Регрессия дерева решений с несколькими выходами
Завершение грани с многовыходными оценщиками
Каталожные номера:
М. Дюмон и др., Быстрое мультиклассовое аннотирование изображений со случайными подокнами и несколько выходных рандомизированных деревьев, Международная конференция по Теория и приложения компьютерного зрения 2009
1.10.4. Сложность
В общем случае стоимость времени выполнения для построения сбалансированного бинарного дерева составляет
\(O(n_{samples}n_{features}\log(n_{samples}))\) и время запроса
\(O(\log(n_{выборки}))\). Хотя алгоритм построения дерева пытается
чтобы генерировать сбалансированные деревья, они не всегда будут сбалансированными. Предполагая, что
поддеревья остаются примерно сбалансированными, стоимость в каждом узле состоит из
поиск через \(O(n_{features})\), чтобы найти функцию, которая предлагает
наибольшее снижение критерия примеси, т.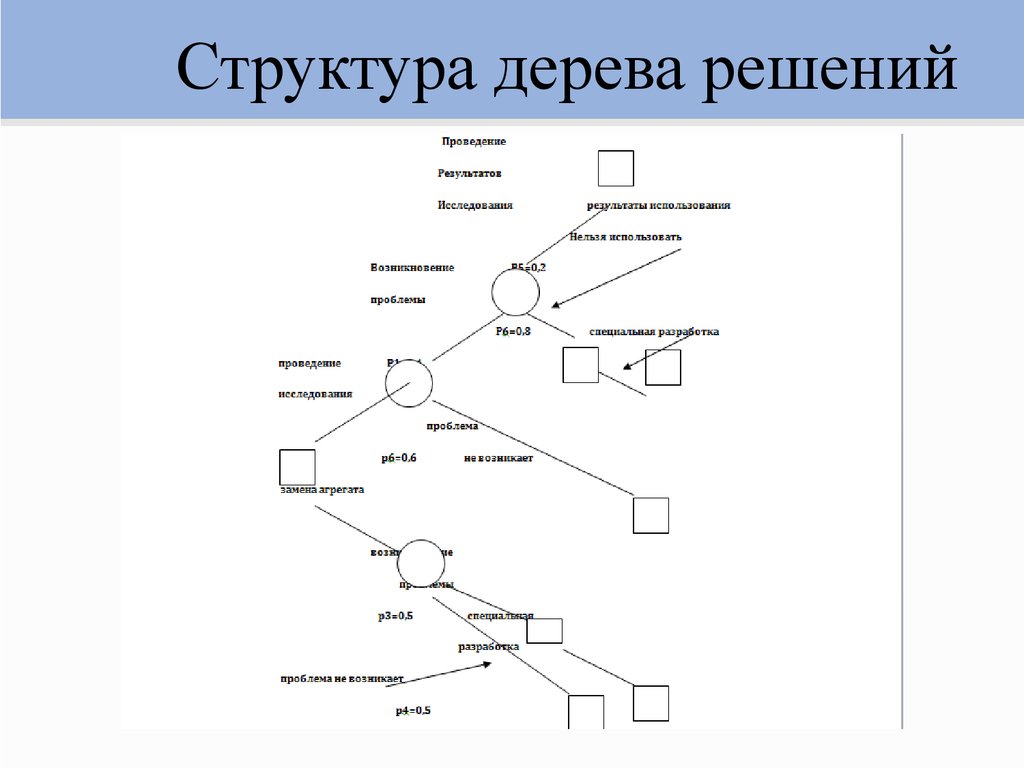 {2}\log(n_{выборки}))\).
{2}\log(n_{выборки}))\).
1.10.5. Советы по практическому использованию
Деревья решений, как правило, подходят для данных с большим количеством признаков. Очень важно получить правильное соотношение выборок к количеству признаков, поскольку дерево с несколькими образцами в многомерном пространстве, скорее всего, переобучится.
Рассмотрите возможность уменьшения размерности (PCA, ICA, или выбор функции) заранее, чтобы дайте вашему дереву больше шансов найти признаки, которые являются дискриминационными.
Понимание структуры дерева решений поможет получить больше информации о том, как дерево решений делает прогнозы, что важно для понимания важных особенностей данных.
Визуализируйте свое дерево во время обучения с помощью экспорта
функция. Используйтеmax_depth=3в качестве начальной глубины дерева, чтобы почувствовать насколько дерево соответствует вашим данным, а затем увеличьте глубину.Помните, что количество выборок, необходимых для заполнения дерева, удваивается за каждый дополнительный уровень, до которого растет дерево. Используйте
max_depthдля управления размер дерева для предотвращения переобучения.Используйте
min_samples_splitилиmin_samples_leaf, чтобы убедиться, что несколько выборки информируют о каждом решении в дереве, контролируя, какие расщепления будут быть на рассмотрении. Очень маленькое число обычно означает, что дерево будет переобучать, тогда как большое число не позволит дереву изучить данные. Пытатьсяmin_samples_leaf=5в качестве начального значения. Если размер выборки варьируется в значительной степени в этих двух параметрах можно использовать число с плавающей запятой в процентах. Покаmin_samples_splitможет создавать сколь угодно маленькие листья,min_samples_leafгарантирует, что каждый лист имеет минимальный размер, избегая листовые узлы с низкой дисперсией и чрезмерным соответствием в задачах регрессии.За классификация с несколькими классами,
min_samples_leaf=1часто является лучшим выбор.Обратите внимание, что
min_samples_splitрассматривает сэмплы напрямую и независимо отsample_weight, если указано (например, узел с m взвешенными выборками по-прежнему рассматривается как имеющий ровно m выборок). Рассмотримmin_weight_fraction_leafилиmin_impurity_decrease, если требуется учет веса выборки при разделении.Сбалансируйте свой набор данных перед тренировкой, чтобы предотвратить смещение дерева к господствующим классам. Балансировка классов может быть выполнена с помощью отбор равного количества образцов из каждого класса или, что предпочтительнее, путем нормализация суммы весов выборки (
sample_weight) для каждого класс на одно и то же значение. Также обратите внимание, что критерии предварительной обрезки, основанные на весе, напримерmin_weight_fraction_leaf, тогда будет менее смещено в сторону доминирующие классы, чем критерии, которые не знают веса выборки, какmin_samples_leaf.Если образцы взвешены, будет проще оптимизировать дерево структура с использованием критерия предварительной обрезки на основе веса, такого как
min_weight_fraction_leaf, которые гарантируют, что конечные узлы содержат не менее часть общей суммы весов выборки.Все деревья решений используют
np.float32массивов внутри. Если обучающие данные не в этом формате, будет сделана копия набора данных.Если входная матрица X очень разреженная, рекомендуется преобразовать ее в разреженную
csc_matrixперед вызовом fit and sparsecsr_matrixперед вызовом предсказывать. Время обучения может быть на несколько порядков меньше для разреженных матричный ввод по сравнению с плотной матрицей, когда функции имеют нулевые значения в большинство образцов.
1.10.6. Алгоритмы дерева: ID3, C4.5, C5.0 и CART
Каковы все различные алгоритмы дерева решений и чем они отличаются друг от друга? Какой из них реализован в scikit-learn?
ID3 (Итеративный дихотомайзер 3) был разработан в 1986 году Россом Куинланом. Алгоритм создает многоходовое дерево, находя для каждого узла (т.е. в
жадным образом) категориальный признак, который даст наибольшую
прирост информации для категориальных целей. Деревья вырастают до своих
максимальный размер, а затем обычно применяется шаг обрезки, чтобы улучшить
способность дерева обобщать невидимые данные.
Алгоритм создает многоходовое дерево, находя для каждого узла (т.е. в
жадным образом) категориальный признак, который даст наибольшую
прирост информации для категориальных целей. Деревья вырастают до своих
максимальный размер, а затем обычно применяется шаг обрезки, чтобы улучшить
способность дерева обобщать невидимые данные.
C4.5 является преемником ID3 и убрал ограничение, должны быть категориальными путем динамического определения дискретного атрибута (на основе числовых переменных), который разбивает непрерывное значение атрибута в дискретный набор интервалов. C4.5 преобразует обученные деревья (т. е. результат алгоритма ID3) в наборы правил «если-то». Затем оценивается точность каждого правила, чтобы определить порядок в которых они должны быть применены. Сокращение выполняется путем удаления правила предварительное условие, если точность правила улучшается без него.
C5.0 — это последняя версия Quinlan, выпущенная под частной лицензией.
Он использует меньше памяти и создает меньшие наборы правил, чем C4.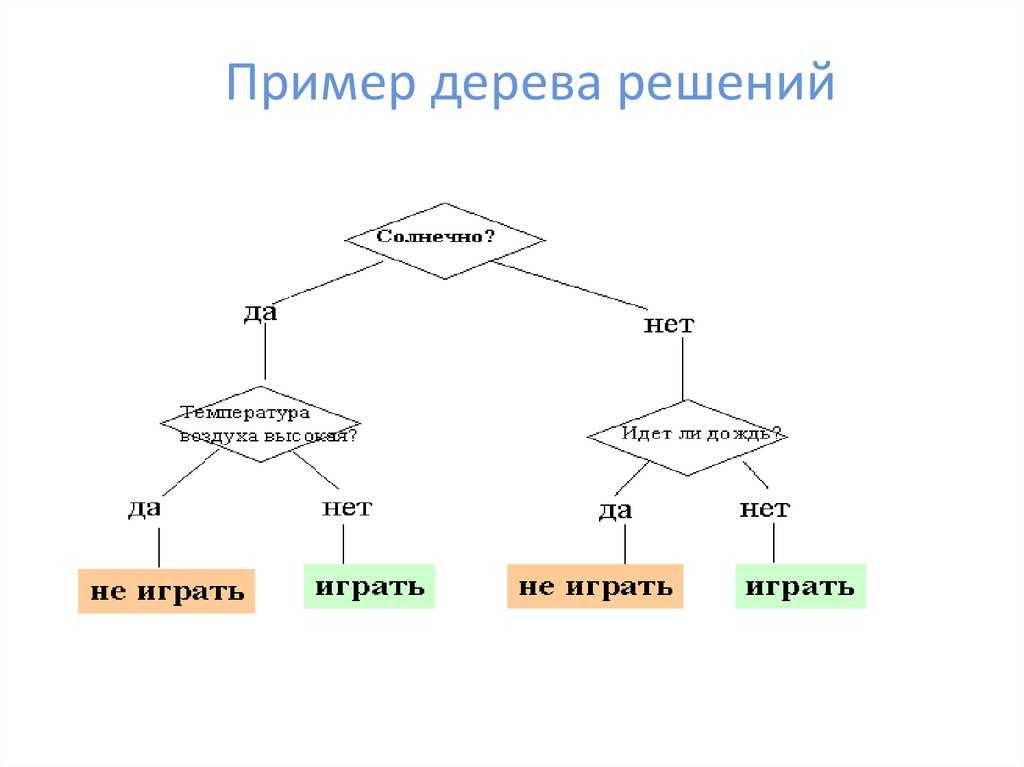 5, в то же время будучи
более точным.
5, в то же время будучи
более точным.
CART (деревья классификации и регрессии) очень похож на C4.5, но отличается тем, что поддерживает числовые целевые переменные (регрессия) и не вычисляет наборы правил. CART строит бинарные деревья, используя функцию и порог, который дает наибольший прирост информации в каждом узле.
scikit-learn использует оптимизированную версию алгоритма CART; Тем не менее Реализация scikit-learn пока не поддерживает категориальные переменные. 9*)\) до достижения максимально допустимой глубины, \(n_m <\min_{выборки}\) или \(n_m = 1\).
1.10.7.1. Критерии классификации
Если целью является результат классификации, принимающий значения 0,1,…,K-1, для узла \(m\) пусть
\[p_{mk} = \frac{1}{n_m} \sum_{y \in Q_m} I(y = k)\]
— доля наблюдений класса k в узле \(m\). Если \(m\) является
терминальный узел, , predict_proba для этого региона установлен в \(p_{mk}\).
Общие меры загрязнения следующие.
Джини:
\[H(Q_m) = \sum_k p_{mk} (1 — p_{mk})\]
Журнал потерь или энтропии:
\[H(Q_m) = — \sum_k p_{mk} \log(p_{mk})\]
Примечание
Критерий энтропии вычисляет энтропию Шеннона возможных классов.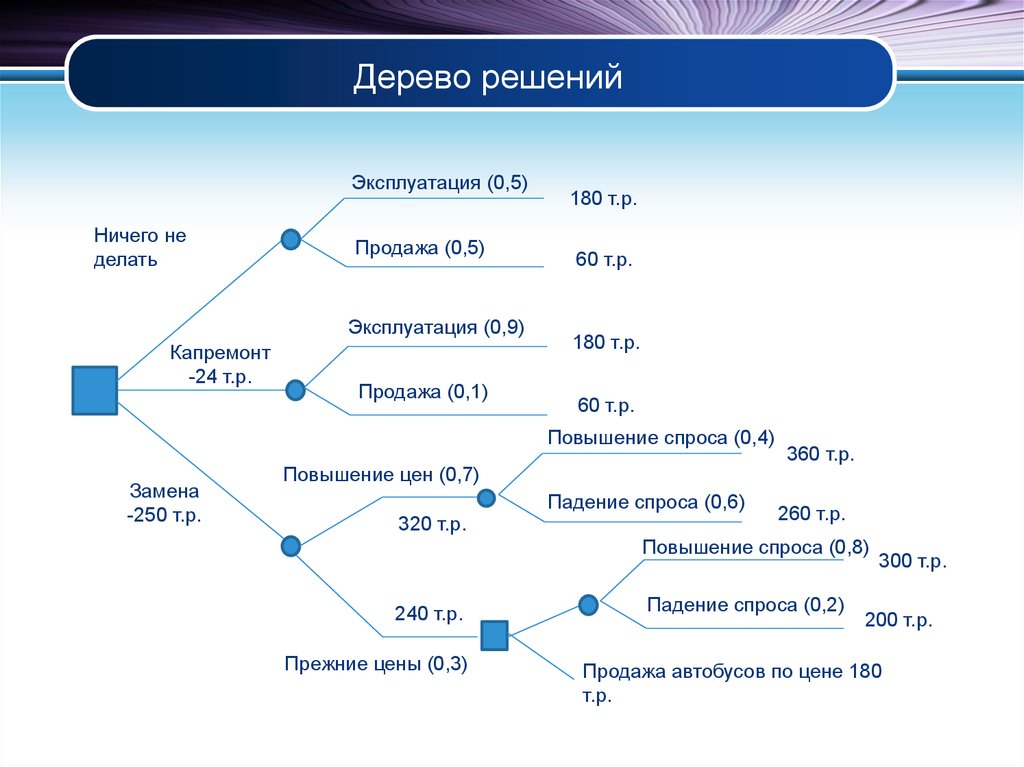 Это
берет частоты класса точек обучающих данных, которые достигли заданного
лист \(m\) как их вероятность. Использование энтропии Шеннона в качестве узла дерева
Критерий разделения эквивалентен минимизации потерь журнала (также известный как
кросс-энтропия и полиномиальное отклонение) между истинными метками \(y_i\)
и вероятностные прогнозы \(T_k(x_i)\) модели дерева \(T\) для класса \(k\).
Это
берет частоты класса точек обучающих данных, которые достигли заданного
лист \(m\) как их вероятность. Использование энтропии Шеннона в качестве узла дерева
Критерий разделения эквивалентен минимизации потерь журнала (также известный как
кросс-энтропия и полиномиальное отклонение) между истинными метками \(y_i\)
и вероятностные прогнозы \(T_k(x_i)\) модели дерева \(T\) для класса \(k\).
Чтобы увидеть это, сначала вспомним, что логарифмическая потеря модели дерева \(T\) вычисляется по набору данных \(D\), определяется следующим образом:
\[\mathrm{LL}(D, T) = -\frac{1}{n} \sum_{(x_i, y_i) \in D} \sum_k I(y_i = k) \log(T_k(x_i))\]
, где \(D\) — обучающий набор данных из \(n\) пар \((x_i, y_i)\).
В дереве классификации предсказанные вероятности классов в листовых узлах постоянны, то есть: для всех \((x_i, y_i) \in Q_m\) имеем: \(T_k(x_i) = p_{mk}\) для каждого класса \(k\).
Это свойство позволяет переписать \(\mathrm{LL}(D, T)\) как сумма энтропий Шеннона, вычисленных для каждого листа \(T\), взвешенного количество точек обучающих данных, достигших каждого листа:
\[\mathrm{LL}(D, T) = \sum_{m \in T} \frac{n_m}{n} H(Q_m)\]
1.
 10.7.2. Критерии регрессии
10.7.2. Критерии регрессииЕсли целью является непрерывное значение, то для узла \(m\) Критерии минимизации при определении мест будущих расколов: Среднее Квадрат ошибки (MSE или ошибка L2), отклонение Пуассона, а также среднее абсолютное значение Ошибка (MAE или ошибка L1). MSE и отклонение Пуассона оба устанавливают прогнозируемое значение конечных узлов к изученному среднему значению \(\bar{y}_m\) узла тогда как MAE устанавливает прогнозируемое значение терминальных узлов в медиану \(медиана(y)_m\). 92\конец{выравнивание}\конец{выравнивание} \]
Полупуассоновское отклонение:
\[H(Q_m) = \frac{1}{n_m} \sum_{y \in Q_m} (y \log\frac{y}{\bar{y}_m} — у + \бар{у}_м)\]
Установка критерия = "poisson" может быть хорошим выбором, если ваша цель — подсчет
или частота (количество на некоторую единицу). В любом случае \(y >= 0\) является
необходимое условие для использования этого критерия. Обратите внимание, что он подходит намного медленнее, чем
критерий МСЭ.
Средняя абсолютная ошибка:
\[ \begin{align}\begin{align}median(y)_m = \underset{y \in Q_m}{\mathrm{median}}(y)\\H(Q_m) = \frac{1}{ n_m} \sum_{y \in Q_m} |y — медиана(y)_m|\end{aligned}\end{align} \]
Обратите внимание, что он подходит намного медленнее, чем критерий MSE.
1.10.8. Отсечение с минимальной стоимостью и сложностью
Обрезка с минимальной стоимостью и сложностью — это алгоритм, используемый для обрезки дерева, чтобы избежать переобучение, описанное в главе 3 [BRE]. Этот алгоритм параметризован на \(\alpha\ge0\), известный как параметр сложности. Сложность Параметр используется для определения показателя сложности затрат, \(R_\alpha(T)\) заданное дерево \(T\):
\[R_\alpha(T) = R(T) + \alpha|\widetilde{T}|\]
, где \(|\widetilde{T}|\) — количество конечных узлов в \(T\) и \(R(T)\)
традиционно определяется как общий коэффициент неправильной классификации терминала
узлы. В качестве альтернативы, scikit-learn использует общую взвешенную примесь выборки
конечные узлы для \(R(T)\). Как показано выше, примесь узла
зависит от критерия. Отсечение с минимальной стоимостью и сложностью находит поддерево
\(T\), который минимизирует \(R_\alpha(T)\).
Как показано выше, примесь узла
зависит от критерия. Отсечение с минимальной стоимостью и сложностью находит поддерево
\(T\), который минимизирует \(R_\alpha(T)\).
Мера сложности стоимости одного узла равна
\(R_\alpha(t)=R(t)+\alpha\). Ветвь \(T_t\) определяется как
дерево, где узел \(t\) является его корнем. В общем, примесь узла
больше суммы примесей его концевых узлов,
\(R(T_t)
Примеры:
Деревья решений после сокращения с сокращением сложности затрат
Каталожные номера:
[БРЕ]
Л. Брейман, Дж. Фридман, Р. Олшен и К. Стоун. Классификация
и деревья регрессии. Уодсворт, Белмонт, Калифорния, 1984 г.
Брейман, Дж. Фридман, Р. Олшен и К. Стоун. Классификация
и деревья регрессии. Уодсворт, Белмонт, Калифорния, 1984 г.
https://en.wikipedia.org/wiki/Decision_tree_learning
https://en.wikipedia.org/wiki/Predictive_analytics
Дж. Р. Куинлан. С4. 5: программы для машинного обучения. Морган Кауфманн, 1993.
Т. Хасти, Р. Тибширани и Дж. Фридман. Элементы статистического Обучение, Springer, 2009.
Что такое диаграмма дерева решений
Дерево решений также можно использовать для построения автоматизированных прогностических моделей, которые могут применяться в машинном обучении, интеллектуальном анализе данных и статистике. Этот метод, известный как обучение дереву решений, учитывает наблюдения за элементом, чтобы предсказать его значение.
В этих деревьях решений узлы представляют данные, а не решения. Этот тип дерева также известен как дерево классификации. Каждая ветвь содержит набор атрибутов или правил классификации, связанных с определенной меткой класса, которая находится в конце ветви.
Эти правила, также известные как правила принятия решений, могут быть выражены в предложении «если-то», где каждое решение или значение данных образуют предложение, например, «если условия 1, 2 и 3 выполнены, то результат x будет результатом с вероятностью y».
Каждый дополнительный фрагмент данных помогает модели более точно предсказать, к какому из конечного набора значений относится рассматриваемый объект. Затем эту информацию можно использовать в качестве входных данных в более крупной модели принятия решений.
Иногда прогнозируемая переменная может быть действительным числом, например, ценой. Деревья решений с непрерывными, бесконечными возможными результатами называются деревьями регрессии.
Для повышения точности иногда несколько деревьев используются вместе в ансамблевых методах:
- Пакетирование создает несколько деревьев путем повторной выборки исходных данных, а затем голосует эти деревья за достижение консенсуса.


 В некоторых алгоритмах используются комбинации полей, в таком случае приходится искать оптимальную комбинацию по «весу» коэффициентов. Алгоритм отсечения (или «обрезки») также дорогостоящий, так как необходимо сформировать и сравнить большое количество потенциальных ветвей.
В некоторых алгоритмах используются комбинации полей, в таком случае приходится искать оптимальную комбинацию по «весу» коэффициентов. Алгоритм отсечения (или «обрезки») также дорогостоящий, так как необходимо сформировать и сравнить большое количество потенциальных ветвей.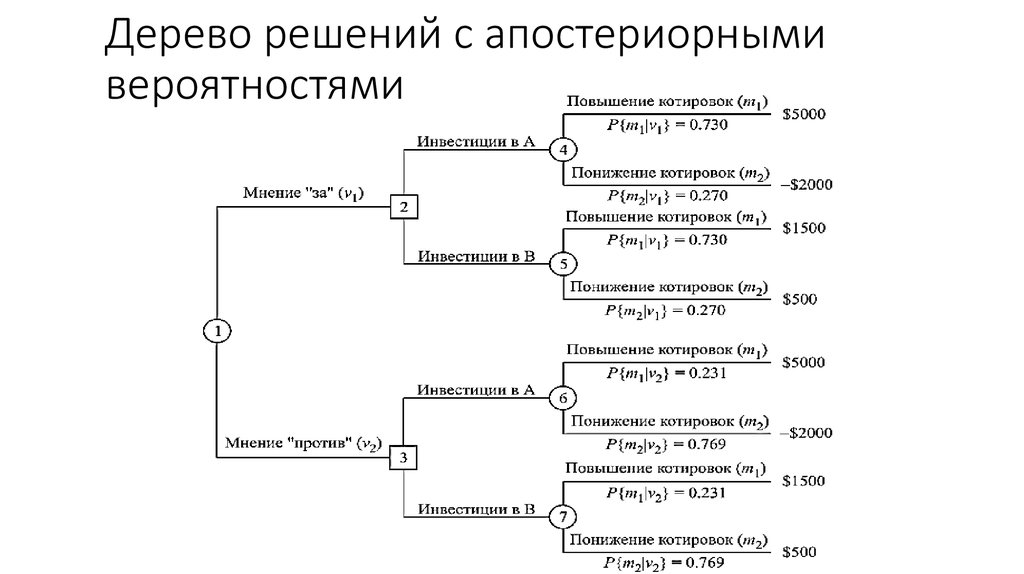

 value is not None
value is not None
 ..
# grow children recursively
left_idx, right_idx = self._create_split(X[:, best_feat], best_thresh)
left_child = self._build_tree(X[left_idx, :], y[left_idx], depth + 1)
right_child = self._build_tree(X[right_idx, :], y[right_idx], depth + 1)
return Node(best_feat, best_thresh, left_child, right_child)
..
# grow children recursively
left_idx, right_idx = self._create_split(X[:, best_feat], best_thresh)
left_child = self._build_tree(X[left_idx, :], y[left_idx], depth + 1)
right_child = self._build_tree(X[right_idx, :], y[right_idx], depth + 1)
return Node(best_feat, best_thresh, left_child, right_child)
 ..
def _traverse_tree(self, x, node):
if node.is_leaf():
return node.value
if x[node.feature] <= node.threshold:
return self._traverse_tree(x, node.left)
return self._traverse_tree(x, node.right)
def predict(self, X):
predictions = [self._traverse_tree(x, self.root) for x in X]
return np.array(predictions)
..
def _traverse_tree(self, x, node):
if node.is_leaf():
return node.value
if x[node.feature] <= node.threshold:
return self._traverse_tree(x, node.left)
return self._traverse_tree(x, node.right)
def predict(self, X):
predictions = [self._traverse_tree(x, self.root) for x in X]
return np.array(predictions)
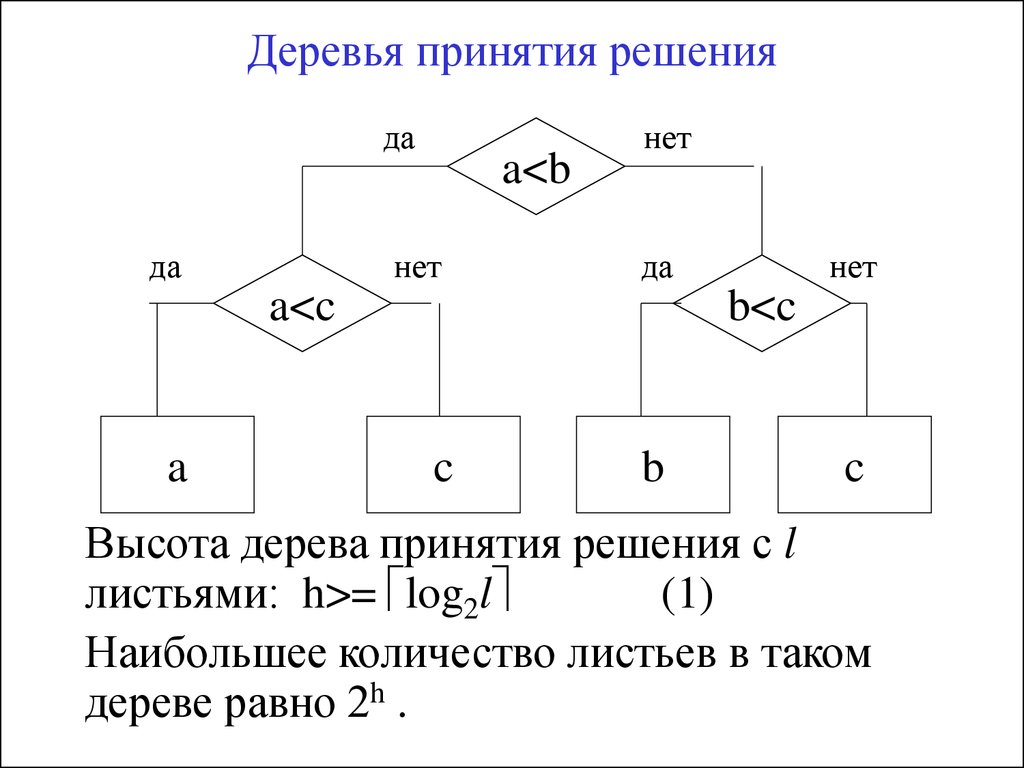 Следовательно, практические алгоритмы обучения дерева решений
основаны на эвристических алгоритмах, таких как жадный алгоритм, где
в каждом узле принимаются локально оптимальные решения. Такие алгоритмы
не может гарантировать возвращение глобально оптимального дерева решений. Этот
можно смягчить, обучив несколько деревьев в обучающем ансамбле,
где функции и образцы выбираются случайным образом с заменой.
Следовательно, практические алгоритмы обучения дерева решений
основаны на эвристических алгоритмах, таких как жадный алгоритм, где
в каждом узле принимаются локально оптимальные решения. Такие алгоритмы
не может гарантировать возвращение глобально оптимального дерева решений. Этот
можно смягчить, обучив несколько деревьев в обучающем ансамбле,
где функции и образцы выбираются случайным образом с заменой. DecisionTreeClassifier()
>>> clf = clf.fit(X, Y)
DecisionTreeClassifier()
>>> clf = clf.fit(X, Y)
 DecisionTreeClassifier()
>>> clf = clf.fit(X, y)
DecisionTreeClassifier()
>>> clf = clf.fit(X, y)
 fit(iris.data, iris.target)
>>> r = export_text(decision_tree, feature_names=радужная оболочка['feature_names'])
>>> напечатать(р)
|--- ширина лепестка (см) <= 0,80
| |--- класс: 0
|--- ширина лепестка (см) > 0,80
| |--- ширина лепестка (см) <= 1,75
| | |--- класс: 1
| |--- ширина лепестка (см) > 1,75
| | |--- класс: 2
fit(iris.data, iris.target)
>>> r = export_text(decision_tree, feature_names=радужная оболочка['feature_names'])
>>> напечатать(р)
|--- ширина лепестка (см) <= 0,80
| |--- класс: 0
|--- ширина лепестка (см) > 0,80
| |--- ширина лепестка (см) <= 1,75
| | |--- класс: 1
| |--- ширина лепестка (см) > 1,75
| | |--- класс: 2
 DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
массив ([0,5])
DecisionTreeRegressor()
>>> clf = clf.fit(X, y)
>>> clf.predict([[1, 1]])
массив ([0,5])
 За
классификация с несколькими классами,
За
классификация с несколькими классами, 
