первый, второй и третий, свойства
Содержание:
- Подобие геометрических фигур
-
Признаки подобия треугольников
- Лемма
- Первый признак: подобие по двум углам
- Второй признак: по двум пропорциональным сторонам и углу между ними
- Третий признак: по трем пропорциональным сторонам
- Примеры задач
- Подобие геометрических фигур
-
Признаки подобия треугольников
- Лемма
- Первый признак: подобие по двум углам
- Второй признак: по двум пропорциональным сторонам и углу между ними
- Третий признак: по трем пропорциональным сторонам
- Примеры задач
Подобие геометрических фигур
Две фигуры называют подобными, если они переводятся друг в друга путем преобразования подобия (расстояния между точками фигур изменяются одно и то же число раз).
Обозначение подобия фигур: \(\sim\), например \(\triangle ABC\sim\triangle KLM\) (треугольник \(ABC\) подобен треугольнику \(KLM\))
Признаки подобия треугольников
Для доказательства признаков подобия нам понадобится следующее утверждение:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Лемма
Прямая, параллельная какой-нибудь стороне треугольника и пересекающая две другие стороны, отсекает от него треугольник, подобный исходному.
Источник: wiki.eduvdom.comПервый признак: подобие по двум углам
Теорема. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Докажем данное утверждение.
Дано: \(\triangle ABC, \triangle A_1B_1C_1, \angle A=\angle A_1, \angle B=\angle B_1\)
Доказать: \(\triangle ABC\sim\triangle A_1B_1C_1\)
Источник: wiki.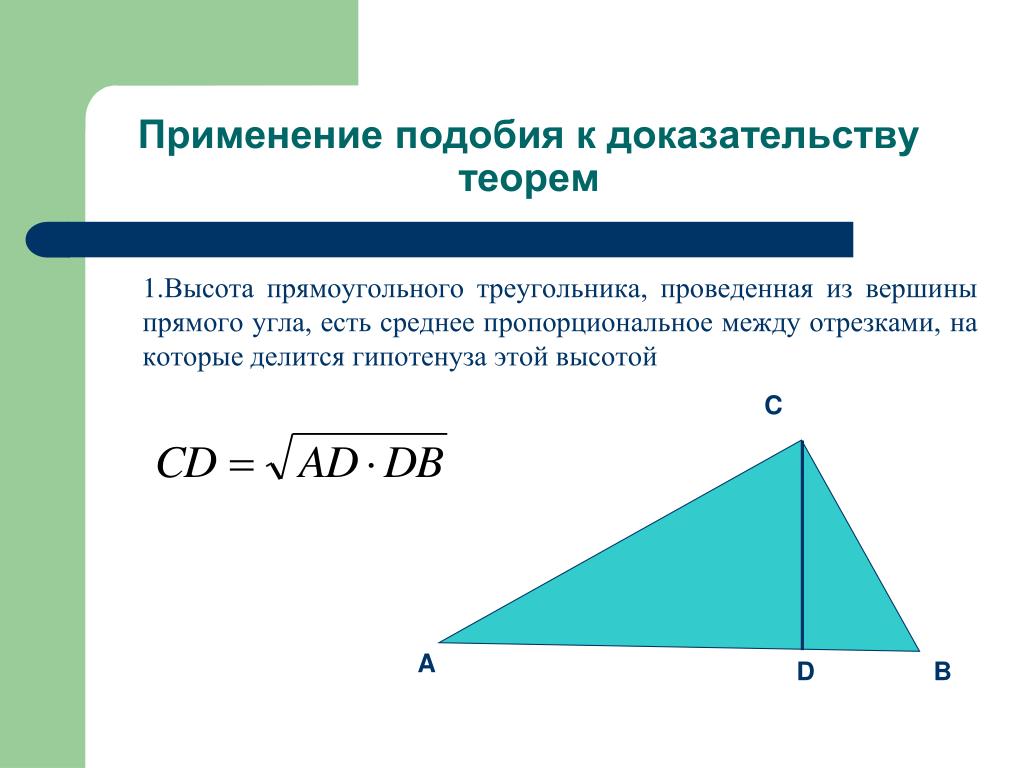
eduvdom.comДоказательство:
Отложим на \(AB\) отрезок \(BA_2\), равный отрезку \(A_1B_1\) и проведем \(A_2C_2\parallel AC\). Рассмотрим \(\triangle A_1B_1C_1\) и \(\triangle A_2BC_2: A_1B_1 = A_2B\) по построению, \(\angle B=\angle B_1\) по условию и \(\angle A_1=\angle A_2\) как соответственные при параллельных прямых. Из леммы следует: \(\triangle A_2BC_2\sim\triangle ABC\), значит,\( \triangle ABC\sim\triangle A_1B_1C_1\).
Второй признак: по двум пропорциональным сторонам и углу между ними
Теорема. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны.
Третий признак: по трем пропорциональным сторонам
Теорема. Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.
Источник: sites.google.comПримеры задач
Задача 1
Через точки \(М\) и \(N\) на сторонах \(АВ\) и \(ВС\) треугольника \(ABC\) соответственно, проведена прямая \(МN\), параллельная стороне \(АС\), \(ВС = 6\), \(МN = 4\) и \(АС = 9\).
Найдите длину \(СN\).
Решение:
Рассмотрим \(\triangle MBN\) и \(\triangle ABC\):
- \(\angle B\) — общий
- \(\angle BMN = \angle BAC\) как соответственные при \(MN\parallel AC\) и секущей \(AB\).
Можем сделать вывод о пропорциональности соответствующих сторон: \(\frac{BN}{BC}=\frac{MN}{AC}=\frac{MB}{AB};\)
Пусть \(NC = x\), тогда \(BN = 6 — x\). Значит справедливо равенство:
\(\frac{6-x}6=\frac49\)
\(9(6-x)=6\times4\)
\(x=\frac{10}3\)
Ответ: \(\frac{10}3\)
Задача 2
Прямая, параллельная основанию треугольника, отсекает от него треугольник и трапецию, площади которых относятся как 4:5 соответственно. Периметр маленького треугольника равен 20 см. Найти периметр данного треугольника.
Источник: egemaximum.ruРешение:
Имеем соотношение: \(\frac{S_{DBE}}{S_{ADEC}}=\frac45,\) значит \(\frac{S_{DBE}}{S_{ABC}}=\frac49\) (т.
2\) (\(k\) — коэффициент подобия), значит \(k=\frac23\), то есть \(\frac{P_{DBE}}{P_{ABC}}=\frac23\), а так как \(P_{DBE}=20\), то выражаем \(P_{ABC}=30.\)
Ответ:30
Насколько полезной была для вас статья?
Рейтинг: 1.50 (Голосов: 6)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Поиск по содержимому
ПОДОБИЕ В ГЕОМЕТРИИ ПОДОБНЫЕ ТРЕУГОЛЬНИКИ
Слайд 1
Описание слайда:
ПОДОБИЕ В ГЕОМЕТРИИ ПОДОБНЫЕ ТРЕУГОЛЬНИКИ
Слайд 2
Описание слайда:
ТЕМА «ПОДОБИЕ» Теоретический материал. Задачи.
Слайд 3
Описание слайда:
ПЛАН
Пропорциональные отрезки.
Свойство биссектрисы треугольника.
Определение подобных треугольников.
Отношение периметров подобных фигур.
Отношение площадей подобных фигур.
Признаки подобия треугольников.
Слайд 4
Описание слайда:
ЗАДАЧИ Разминка. Решение задач. Задачи на признаки подобия. Тест
Слайд 5
Описание слайда:
Пропорциональные отрезки Отношением отрезков называется отношение их длин. Отрезки AB и CD пропорциональны отрезкам A1B1 и C1D1,, если
Слайд 6
Описание слайда:
ПРИМЕР Даны два прямоугольных треугольника
Слайд 7
Описание слайда:
Пропорциональность отрезков
Понятие пропорциональности вводится для любого числа отрезков.
Слайд 8
Описание слайда:
Подобные фигуры Предметы одинаковой формы, но разных размеров
Слайд 9
Описание слайда:
Подобные фигуры В геометрии фигуры одинаковой формы называют подобными фигурами
Слайд 10
Описание слайда:
Подобные треугольники Даны два треугольника AΒC и A1Β1C1, у которых A = A1, Β = Β1, C = C1. Стороны AΒ и A1Β1 , AC и A1C1 , ΒC и Β1C1, лежащие против равных углов, называют сходственными
Слайд 11
Описание слайда:
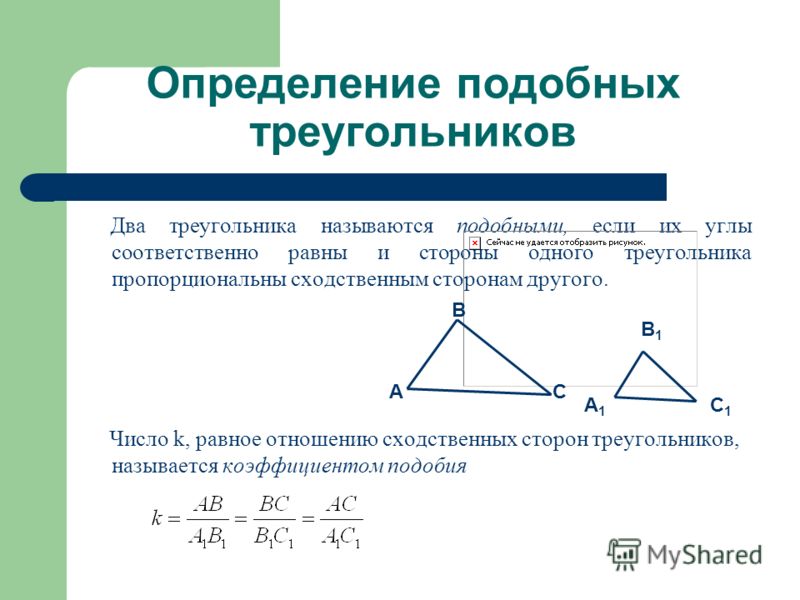
Определение
Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.
Слайд 12
Описание слайда:
Коэффициент подобия Число k , равное отношению сходственных сторон, называется коэффициентом подобия.
Слайд 13
Описание слайда:
Дополнительные свойства Отношение высот подобных треугольников, проведенных к сходственным сторонам, равно коэффициенту подобия. Отношение медиан подобных треугольников, проведенных к сходственным сторонам, равно коэффициенту подобия. Отношение биссектрис подобных треугольников, проведенных к сходственным сторонам, равно коэффициенту подобия.
Слайд 14
Описание слайда:
Отношение периметров
Отношение периметров подобных треугольников равно
коэффициенту подобия.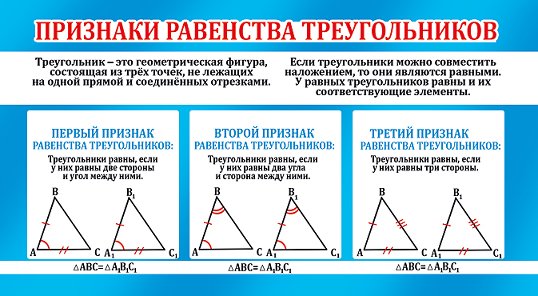
Слайд 15
Описание слайда:
Отношение периметров
Слайд 16
Описание слайда:
Отношение площадей Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
Слайд 17
Описание слайда:
Отношение площадей
Слайд 18
Описание слайда:
Свойство биссектрисы треугольника
Слайд 19
Описание слайда:
Свойство биссектрисы треугольника ΔABD и ΔACD имеют общую высоту AH ΔABD и ΔACD имеют равные углы 1 = 2
Слайд 20
Описание слайда:
Свойство биссектрисы треугольника
Дано: ΔABC
AD – биссектриса
AB = 14 см
BC = 20 см
AC = 21 см
Найти: BD,CD.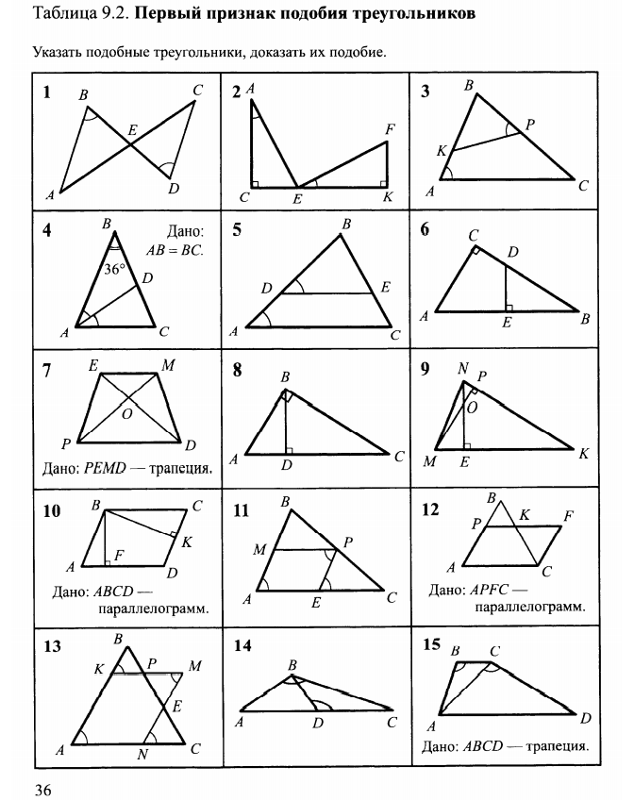
Решение:
Слайд 21
Описание слайда:
Свойство биссектрисы треугольника Решение: Пусть BD = x см, тогда CD = (20 – x) см. По свойству биссектрисы треугольника
Слайд 22
Описание слайда:
Признаки подобия треугольников Первый признак подобия треугольников. (по двум углам) Второй признак подобия треугольников. (по углу и двум пропорциональным сторонам) Третий признак подобия треугольников. (по трем пропорциональным сторонам)
Слайд 23
Описание слайда:
Первый признак подобия треугольников.
Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.
Слайд 24
Описание слайда:
Первый признак подобия треугольников. Дано: ΔABC и ΔA1B1C1, A =A1, B = B. Доказать: ΔABC ~ ΔA1B1C1 Доказательство:
Слайд 25
Описание слайда:
Первый признак подобия треугольников. Доказательство: A = A1, B = B1. C = 180º – A – B, C1 = 180º – A1 – B1. C = C1 Таким образом углы треугольников соответственно равны.
Слайд 26
Описание слайда:
Первый признак подобия треугольников.
Доказательство:
A = A1,
B = B1.
Имеем
Аналогично, рассматривая равенство углов C=C1, A=A1, получим
Итак, сходственные стороны пропорциональны.
Слайд 27
Описание слайда:
Второй признак подобия треугольников. Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.
Слайд 28
Описание слайда:
Второй признак подобия треугольников. Дано: ΔABC и ΔA1B1C1, A =A1, Доказать: ΔABC ~ ΔA1B1C1 Доказательство:
Слайд 29
Описание слайда:
Второй признак подобия треугольников.
Доказательство:
Достаточно доказать, что B = B1.
ΔABC2, 1=A1, 2=B1,
ΔABC2 ~ ΔA1B1C1 по двум углам.
(из подобия).
По условию
AC=AC2.
ΔABC=ΔABC2, т.е. B = B1.
Слайд 30
Описание слайда:
Третий признак подобия треугольников. Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Слайд 31
Описание слайда:
Третий признак подобия треугольников. Дано: ΔABC и ΔA1B1C1, Доказать: ΔABC ~ ΔA1B1C1 Доказательство:
Слайд 32
Описание слайда:
Третий признак подобия треугольников.
Доказательство:
Достаточно доказать, что A=A1
ΔABC2, 1=A1, 2=B1,
ΔABC2 ~ ΔA1B1C1 по двум углам.
Отсюда
По условию
ΔABC=ΔABC2 по трем сторонам, т.
е. A = A1
Слайд 33
Описание слайда:
Разминка 1 Отрезки AB и CD пропорциональны отрезкам MN и PK. Найдите MN, если AB = 3, CD = 4, PK = 2.
Слайд 34
Описание слайда:
Разминка
Слайд 35
Описание слайда:
Разминка
Слайд 36
Описание слайда:
Разминка
Слайд 37
Описание слайда:
Разминка
Слайд 38
Описание слайда:
Решение задач
Слайд 39
Описание слайда:
1 задача
Слайд 40
Описание слайда:
4 задача
Слайд 41
Описание слайда:
7 задача
Слайд 42
Описание слайда:
10 задача
Слайд 43
Описание слайда:
13 задача
Слайд 44
Описание слайда:
2 задача
Слайд 45
Описание слайда:
5 задача
Слайд 46
Описание слайда:
8 задача
Слайд 47
Описание слайда:
11 задача
Слайд 48
Описание слайда:
14 задача
Слайд 49
Описание слайда:
3 задача
Слайд 50
Описание слайда:
6 задача
Слайд 51
Описание слайда:
9 задача
Слайд 52
Описание слайда:
12 задача
Слайд 53
Описание слайда:
15 задача
Слайд 54
Описание слайда:
ЗАДАЧИ
1.
Диагонали трапеции ABCD пересекаются в точке O. Площади треугольников BOC и AOD относятся как 1 : 9. Сумма оснований BC и AD равна 4,8 см. Найдите основания трапеции.
Слайд 55
Описание слайда:
Решение Рассмотрим ΔAOD и ΔBOC: 1=2 (накрест лежащие при AD || BC, и секущей AC; 3=4 (вертикальные) ΔAOD ~ ΔBOC (по двум углам) = k
Слайд 56
Описание слайда:
Решение . k = 3 AD + BC = = 3BC + BC = 4BC AD + BC = 4,8см (по условию) BC = 1,2 см AD = 3,6 см
Слайд 57
Описание слайда:
ЗАДАЧИ
2.
Докажите, что треугольники, изображенные на рисунке, подобны, и выясните взаимное положение прямых CB и DF.
Слайд 58
Описание слайда:
Решение Отсюда ΔABC~ΔDEF по трем пропорциональным сторонам
Слайд 59
Описание слайда:
Решение ΔABC~ΔDEF Соответственно A = E B = F ACB = EDF
Слайд 60
Описание слайда:
ЗАДАЧИ 3. Отрезки AB и CD пересекаются в точке O, причем . Докажите, что CBO = DAO.
Слайд 61
Описание слайда:
Решение
Рассмотрим ΔAOD и ΔCOB
DOA = COB (вертикальные).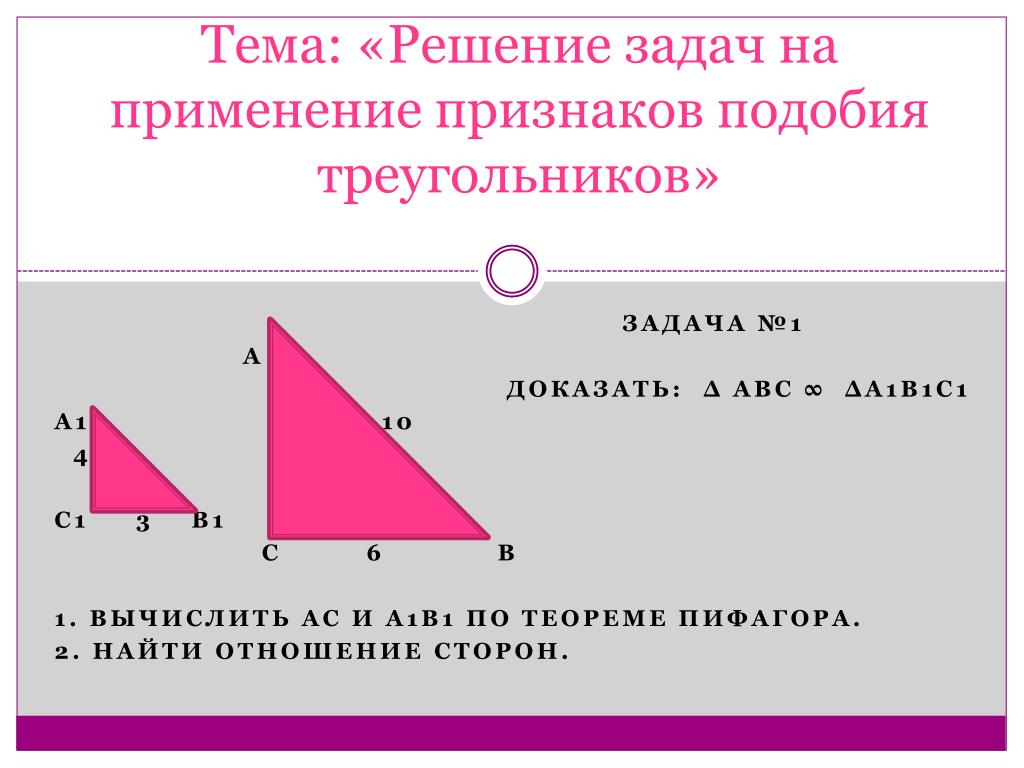
.
ΔAOD ~ ΔCOB по углу и двум пропорциональным сторонам.
CBO = DAO (из подобия).
Слайд 62
Описание слайда:
ЗАДАЧИ 4. В треугольнике ABC AB = 4, BC = 6, AC = 7. Точка E лежит на стороне AB. Внутри треугольника взята точка M так, что MB = 5,25, ME = 4,5, AE = 1. Прямая BM пересекает AC в точке P. Докажите, что ΔAPB равнобедренный.
Слайд 63
Описание слайда:
Решение . Рассмотрим ΔBEM и ΔABC BE = AB − AE = 4 – 1 = 3 BE : AB = 3 : 4 = 0,75 EM : BC = 4,5 : 6 = 0,75 BM : AC = 5,25 : 7 = 0,75, т.е. стороны треугольников пропорциональны
Слайд 64
Описание слайда:
Слайд 65
Описание слайда:
ЗАДАЧИ
5.
Диагональ AC параллелограмма ABCD равна 90.
Середина M стороны AB соединена с вершиной D.
Отрезок MD пересекает AC в точке O.
Найдите отрезки AО и CО.
Слайд 66
Описание слайда:
Решение Рассмотрим ΔAOM и ΔCОD AOM = CОD (вертикальные), MAO = ОCD (накрест лежащие при AB || DC и секущей AC). Отсюда ΔAOM ~ ΔCОD по двум углам.
Слайд 67
Описание слайда:
Решение . AM = ½ AB (по условию) AB = CD (ABCD — параллелограмм), AM : CD = 1 : 2
Слайд 68
Описание слайда:
ТЕСТ
Слайд 69
Описание слайда:
ТЕСТ
1.
По данным рисунка х равен
А) 7
Б) 14
В) 3,5
Г) 14/3
Слайд 70
Описание слайда:
ТЕСТ 2) По данным рисунка периметр ΔABC равен А) 9 Б) 27 В) 36 Г) 18
Слайд 71
Описание слайда:
ТЕСТ 3) По данным рисунка отрезок BC равен А) 3,75 Б) 7,5 В) 5 Г) 4,5
Слайд 72
Описание слайда:
ТЕСТ 4) По данным рисунка площади данных треугольников относятся А) 3 : 1 Б) 9 : 1 В) 6 : 1 Г) 9 : 4
Слайд 73
Описание слайда:
ТЕСТ 5) По данным рисунка прямые AB и DE А) нельзя ответить Б) пересекаются В) параллельны
Слайд 74
Описание слайда:
ТЕСТ
Слайд 75
Описание слайда:
Помощь в управлении презентацией
Как вы используете теорему треугольной пропорциональности каждый день
Как вы используете теорему треугольной пропорциональности каждый день
Шарлотта Тейлор
21 января 2021
онлайн -репетиторство
,
Математика
9000
геометрический закон, согласно которому, когда вы проводите линию, параллельную одной стороне треугольника, она пересекает две другие стороны треугольника и делит их пропорционально.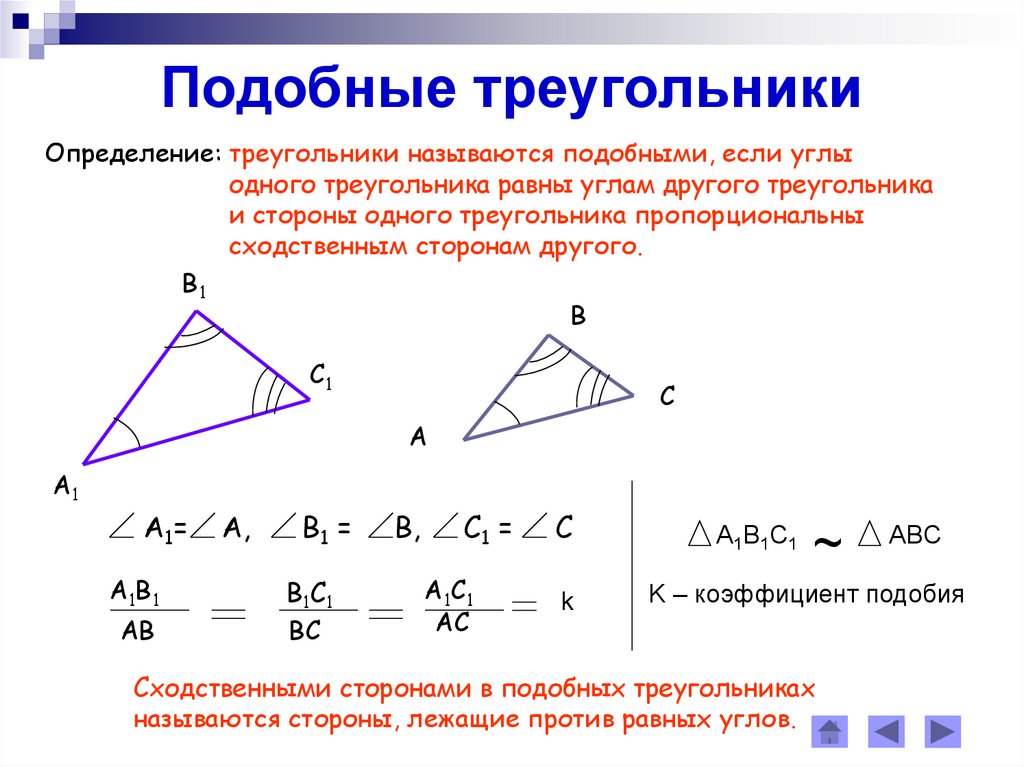
Независимо от того, являются ли они тупыми, остроугольными или прямоугольными треугольниками, эту теорему можно использовать для определения неизвестных длин внутри подобных треугольников.
В приведенной выше модели вы видите стороны треугольника, отмеченные A, B и C. Отрезок перпендикулярной прямой DE пересекает обе стороны B и A, поэтому он является секущей. Поскольку треугольники EDC и ABC разного размера, они не равны. Но поскольку DE параллелен ВА, вы можете постулировать или доказать, что это соответствующие углы. Согласно теореме о треугольной пропорциональности, вы можете определить длину от E до C, используя это соотношение:
Используйте приведенную ниже диаграмму в качестве рабочего листа. Когда вы подставите числа из диаграммы, соотношение будет 8:10=5:?. Затем вы должны использовать дроби, чтобы найти x и найти неизвестную длину:
Теорема пропорциональности треугольника в профессиональном мире
В профессиях, где необходимо построение и формирование нескольких маршрутов, теорема пропорциональности треугольника часто используется для определения длины маршрута.
Например, скажем, инженер хочет построить горную дорогу. Длина от вершины составляет 900 футов и 800 футов соответственно. Инженер определил, что маршрут нужно начинать на высоте 300 футов и 525 футов ниже пика. Используйте теорему о пропорциональности треугольника, чтобы определить длину маршрута:
Использование теоремы в построении
Теорема о пропорциональности треугольника полезна для построения. Например, предположим, что подрядчик строит опорные балки для крыши дома. В верхней части помещения уже применена одна опорная балка, но необходимо соорудить дополнительную. Измерения следующие:
Поскольку мы знаем, что меньшая опорная балка составляет 8 футов, а расстояние от вершины крыши до первой опорной балки равно 7 футам, мы можем использовать теорему пропорциональности треугольника, чтобы выяснить, что нижняя опорная балка должна быть 6,2 фута.
Использование теоремы о пропорциональности треугольника в повседневной жизни
Как часто вам нужно было узнать длину чего-либо, но у вас не было инструментов или знаний для этого? Например, предположим, что вы хотите переставить ковер так, чтобы он был спрятан под секционным диваном и располагался параллельно соседнему ковровому покрытию.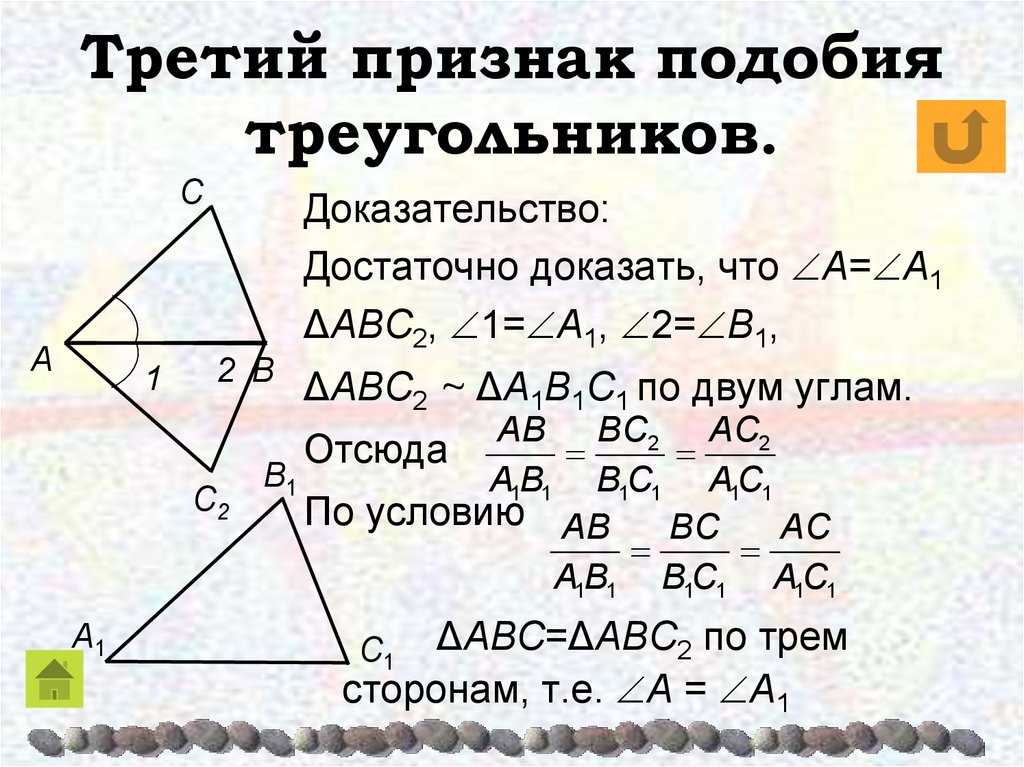
Размеры следующие:
Используя теорему о пропорциональности треугольника, вы получаете соотношение 9:12=4:x. Когда вы решаете для x, в результате должно быть видно 5,3 фута наклонного коврика.
Ваша новая любимая теорема
Используя теорему о пропорциональности треугольника, вы можете узнать, какой длины должны быть объездные дороги и сколько дерева потребуется для изготовления опорных балок. Это правило не только поможет вам в тригонометрии — оно научит вас смотреть на жизнь с более практичной, критической и даже более безопасной точки зрения.
Теорема о треугольной пропорциональности: геометрический трюк, о котором вы даже не подозревали, что он вам нужен
Эта формула выглядит знакомой: A2+B2=C2. Подсказка: это, наверное, самая важная формула в геометрии…
Это теорема Пифагора, формула, используемая для определения неизвестной длины прямоугольного треугольника. При использовании этой теоремы A и B представляют более короткие стороны треугольника, а C представляет гипотенузу или сторону, противоположную прямому углу.
Если вы готовы перейти к более сложной геометрической формуле, у нас есть идеальная формула для вас. Сегодня мы рассмотрим теорему о пропорциональности треугольника. Эта теорема утверждает, что если прямая, параллельная одной стороне треугольника, пересекает две другие стороны, то она пропорционально делит эти стороны. См. модель этой теоремы ниже:
На рисунке выше треугольник ABC пересекается отрезком DE. Поскольку DE параллелен BA, треугольник EDC является уменьшенной копией треугольника ABC. Это один из первых принципов теоремы пропорциональности треугольника. Они не эквивалентны по размеру, но их углы эквивалентны .
Применение теоремы о пропорциональности треугольникаТеорема о пропорциональности треугольника также утверждает, что мы можем найти длину от E до C, используя соотношения. Соотношение CB и CA равно соотношению CD и CE. Или записать математически:
CB:CA=CD:CE
Согласно рисунку выше, длина от точки A до C составляет 11 дюймов, длина от C до D составляет 6 дюймов, а длина от C до B составляет 9 дюймов.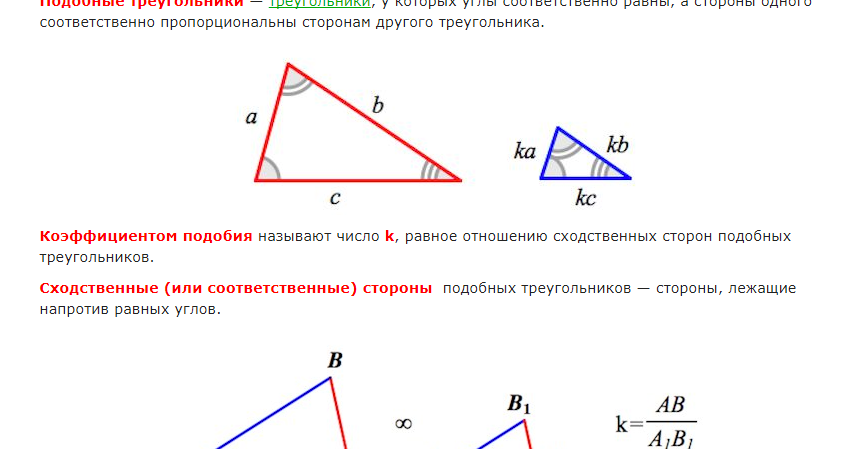
Подставим эти числа в отношение:
9:11=5:x
Используя дроби, вы можете подставить эти числа и найти x:
Теорему о пропорциональности треугольника можно использовать, чтобы найти недостающую длину любой треугольник, если известны три из четырех длин. Давайте посмотрим, как мы можем применить эту теорему к размерам здания или длине маршрута.
Здание с теоремой пропорциональности треугольникаЕсли бы вы построили крышу, вам нужно было бы использовать балки в определенной конфигурации, чтобы поддерживать ее треугольную структуру. Поскольку опорные балки перпендикулярны форме крыши, вы можете использовать теорему пропорциональности треугольника для определения длины этих балок.
См. рисунок ниже. Вы можете видеть, что определены длины большей треугольной конструкции и определена точка для построения опорной балки. Теперь нам нужно узнать длину опорной балки.
Используя уравнение отношения, вы должны найти x, чтобы определить длину балки:
Как видите, эта теорема используется не только на уроках геометрии.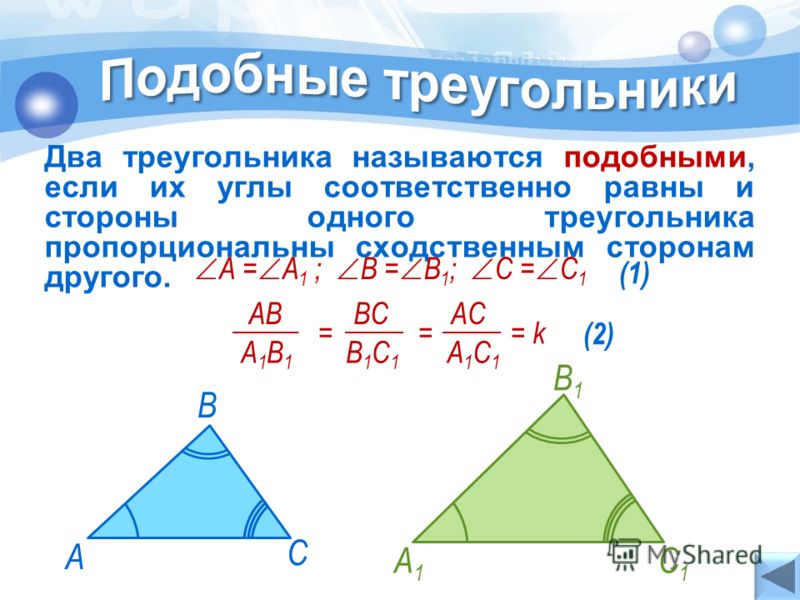
Люди в реальном мире используют это уравнение для многих целей, например, для определения того, сколько материала им понадобится при строительстве треугольных структур.
Другое практическое применение теоремы о пропорциональности треугольника — ее использование для определения длины маршрута. См. рисунок ниже. Скажем, инженер строит дорогу через эту гору. Если земля, на которой образовалась эта гора, плоская, то в идеале инженер построил бы дорогу, параллельную земле.
Длина от подножия одной стороны горы до другой составляет 2000 футов. Расстояние от вершины до подножия составляет 1800 футов. По оценке инженера, дорога должна быть построена на 700 футов ниже вершины горы. горы, но они не знают, какой длины должен быть горный маршрут. Чтобы определить эту длину, мы включим ее в теорему о пропорциональности треугольника:
Из этого примера видно, что эта теорема является инструментом, который инженеры могут использовать для построения маршрутов, будь то через гору или любое другое сооружение треугольной формы.
Применение теоремы в реальной жизни
Думаете, вы не сможете применить эту теорему в повседневной жизни? Подумайте еще раз. Треугольники повсюду. Вафельные рожки, вешалки, палатки, дорожные знаки — все треугольники. И они должны быть определенного размера, чтобы работать должным образом. Вполне вероятно, что теорема о пропорциональности треугольника использовалась при их производстве для обеспечения функциональности
Теперь, когда вы знаете, сколько предметов повседневного обихода было построено с использованием этой теоремы, и как вы можете использовать ее для строительства и построения маршрутов, мы научим вас, как использовать теорему пропорциональности треугольника в походе.
Предположим, вы устанавливаете палатку в походе. Вы хотите установить сетку для хранения бутылок с водой и фонариков, когда вы спите. Размеры палатки смотрите на рисунке ниже. Желтые линии представляют собой размеры внешней палатки, а оранжевые линии представляют собой размеры сетки.
X представляет собой неизвестную длину сети, которую вы строите.
Из рисунка видно, что длина от края палатки до центрального столба составляет 4 фута, а длина от земли до вершины палатки (гипотенузы) составляет 8 футов. определили, что вы хотите, чтобы сеть висела на 3 фута ниже кончика палатки (вдоль стороны гипотенузы). Теперь вы можете использовать теорему о пропорциональности треугольника, чтобы определить длину сети:
Знание теоремы о пропорциональности треугольника позволяет строить трехмерные конструкции, такие как горные дороги, крыши и палатки. Это также упрощает понимание других концепций геометрии треугольника, таких как теорема о конгруэнтности, теорема о неравенстве и теорема об обратной пропорциональности. Понимание этих теорем позволит вам увидеть, как можно использовать геометрические понятия за пределами классной комнаты и применять к более сложным идеям.
Если вам трудно понять такие теоремы, и вы чувствуете, что вам нужна дополнительная помощь, не беспокойтесь.