Читать онлайн «Большая Советская Энциклопедия (ЛО)» — БСЭ БСЭ — RuLit
.
Рис. 1 к ст. Логарифмическая функция.
Рис. 2 к ст. Логарифмическая функция.
Логарифмические таблицы
Логарифми’ческие табли’цы, таблицы логарифмов чисел; применяются для упрощения вычислений. Наиболее распространены таблицы десятичных логарифмов. Т. к. десятичные логарифмы чисел N и 10kN (при k целом) различаются только характеристиками и имеют одинаковые мантиссы (lg10kN = k + lg N), то в таблицах десятичных логарифмов приводятся только мантиссы логарифмов целых чисел. Для отыскания характеристики служат правила: 1) характеристика числа, большего 1, на единицу меньше числа цифр в целой части этого числа (так, lg 20 000 = 4,30103) и 2) характеристика десятичной дроби, меньшей 1, равна взятому со знаком минус числу нулей, предшествующих первой в дроби цифре, отличной от нуля (так, lg 0,0002 = — 4,30103, т.
Существуют таблицы десятичных логарифмов с различным числом знаков мантисс. Наиболее распространены 4-значные и 5-значные таблицы. Иногда употребляют 7-значные таблицы, а в редких случаях — таблицы, позволяющие без большого труда вычислять логарифмы с большим числом знаков. В Л. т. часто приводятся таблицы антилогарифмов — чисел, логарифмы которых суть данные числа, и таблицы так называемых гауссовых логарифмов, служащих для определения логарифмов суммы или разности двух чисел по известным логарифмам этих чисел (без промежуточного нахождения самих чисел). Кроме логарифмов чисел, Л. т. содержат обычно логарифмы тригонометрических величин.
Первые Л. т. были составлены независимо друг от друга Дж. Непером и швейцарским математиком И. Бюрги. Таблицы Непера «Описание удивительной таблицы логарифмов» (1614) и «Устройство удивительной таблицы логарифмов» (1619) содержали 8-значные логарифмы синусов, косинусов и тангенсов для углов от 0° до 90°, следующих через одну минуту.
«Арифметические и геометрические таблицы прогрессий» (1620) Бюрги представляют собой первую таблицу антилогарифмов («чёрные числа») и дают значения чисел, соответствующих равноотстоящим логарифмам («красным числам»). «Красные числа» Бюрги суть логарифмы поделенных на 10 10-значные таблицы от 1 до 100 000 издал голландский математик А. Влакк (1628). Таблицы Влакка легли в основу большинства последующих таблиц, причём их авторы внесли много изменений в структуру Л. т. и поправок в выкладки (у самого Влакка было 173 ошибки, у австрийского математика Г. Вега в 1783 — пять; первые безошибочные таблицы выпустил в 1857 немецкий математик К. Бремикер). В России таблицы логарифмов впервые были изданы в 1703 при участии Л. Ф. Магницкого. Таблицы т. н. гауссовых логарифмов были опубликованы в 1802 итальянским математиком З. Леонелли; К. Ф.Гаусс ввёл (1812) эти логарифмы в общее употребление.
10-значные таблицы от 1 до 100 000 издал голландский математик А. Влакк (1628). Таблицы Влакка легли в основу большинства последующих таблиц, причём их авторы внесли много изменений в структуру Л. т. и поправок в выкладки (у самого Влакка было 173 ошибки, у австрийского математика Г. Вега в 1783 — пять; первые безошибочные таблицы выпустил в 1857 немецкий математик К. Бремикер). В России таблицы логарифмов впервые были изданы в 1703 при участии Л. Ф. Магницкого. Таблицы т. н. гауссовых логарифмов были опубликованы в 1802 итальянским математиком З. Леонелли; К. Ф.Гаусс ввёл (1812) эти логарифмы в общее употребление.
Лит.: Брадис В. М., Четырехзначные математические таблицы, М. — Л., 1928, посл., 44 изд., М., 1973; Милн-Томсон Л.-М., Комри Л.-Дж., Четырехзначные математические таблицы, пер. с англ., М., 1961; Пятизначные таблицы натуральных значений тригонометрических величин, их логарифмов и логарифмов чисел, 6 изд., М., 1972; Вега Г., Таблицы семизначных логарифмов, 4 изд. , М., 1971; Субботин М. Ф., Многозначные таблицы логарифмов, М. — Л., 1940; Десятизначные таблицы логарифмов комплексных чисел…, М., 1952; Таблицы натуральных логарифмов, 2 изд., т. 1—2, М., 1971.
, М., 1971; Субботин М. Ф., Многозначные таблицы логарифмов, М. — Л., 1940; Десятизначные таблицы логарифмов комплексных чисел…, М., 1952; Таблицы натуральных логарифмов, 2 изд., т. 1—2, М., 1971.
Логарифмический приёмник
Логарифми’ческий приёмник
 С ростом входного сигнала диод начинает проводить электрический ток; его внутреннее сопротивление падает и шунтирует сопротивление нагрузки. Общее сопротивление нагрузки изменяется так, что амплитуда на выходе усилителя пропорциональна логарифму амплитуды на входе. Во втором случае при возрастании входного сигнала каскады усилителя, начиная с последнего, поочерёдно выходят из линейного режима и до перехода в режим насыщения (ограничения) обеспечивают получение логарифмической амплитудной характеристики.
С ростом входного сигнала диод начинает проводить электрический ток; его внутреннее сопротивление падает и шунтирует сопротивление нагрузки. Общее сопротивление нагрузки изменяется так, что амплитуда на выходе усилителя пропорциональна логарифму амплитуды на входе. Во втором случае при возрастании входного сигнала каскады усилителя, начиная с последнего, поочерёдно выходят из линейного режима и до перехода в режим насыщения (ограничения) обеспечивают получение логарифмической амплитудной характеристики. Лит.: Волков В. М., Логарифмические усилители на транзисторах, К., 1965.
А. С. Афромеев.
Логарифмически-нормальное распределение
Логарифми’чески-норма’льное распределе’ние, специальный вид распределения вероятностей случайных величин. Если Х имеет нормальное распределение и Y = ех, то Y имеет Л.-н. р., характеризуемое плотностью:
.
Здесь m и s — параметры распределения величины X.
Вещественный десятичный логарифм числа b {displaystyle b} существует, если b > 0 {displaystyle b>0} (комплексный десятичный логарифм существует для всех b ≠ 0 {displaystyle b eq 0} ). Международный стандарт ISO 31-11 обозначает его lg b {displaystyle lg ,b} . Примеры:
lg 1 = 0 ; lg 10 = 1 ; lg 100 = 2 {displaystyle lg ,1=0;,lg ,10=1;,lg ,100=2} lg 1000000 = 6 ; lg 0 , 1 = − 1 ; lg 0,001 = − 3 {displaystyle lg ,1000000=6;,lg ,0{,}1=-1;,lg ,0{,}001=-3} В зарубежной литературе, а также на клавиатуре калькуляторов встречаются и другие обозначения десятичного логарифма: log , Log , Log10 {displaystyle operatorname {log} ,operatorname {Log} ,operatorname {Log10} } , причём следует иметь в виду, что первые 2 варианта могут относиться и к натуральному логарифму.
Алгебраические свойства
В нижеследующей таблице предполагается, что все значения положительны:
Существует очевидное обобщение приведённых формул на случай, когда допускаются отрицательные переменные, например:
lg | x y | = lg ( | x | ) + lg ( | y | ) , {displaystyle lg |xy|=lg(|x|)+lg(|y|),} lg | x y | = lg ( | x | ) − lg ( | y | ) , {displaystyle lg !left|{frac {x}{y}} ight|=lg(|x|)-lg(|y|),}Формула для логарифма произведения без труда обобщается на произвольное количество сомножителей:
lg ( x 1 x 2 … x n ) = lg ( x 1 ) + lg ( x 2 ) + ⋯ + lg ( x n ) {displaystyle lg(x_{1}x_{2}dots x_{n})=lg(x_{1})+lg(x_{2})+dots +lg(x_{n})}Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления. Например, умножение многозначных чисел x , y {displaystyle x,y} с помощью логарифмических таблиц производилось по следующему алгоритму:
Например, умножение многозначных чисел x , y {displaystyle x,y} с помощью логарифмических таблиц производилось по следующему алгоритму:
Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично производились возведение в степень и извлечение корня.
Связь десятичного и натурального логарифмов:
ln x ≈ 2,302 59 lg x ; lg x ≈ 0,434 29 ln x {displaystyle ln xapprox 2{,}30259 lg x;quad lg xapprox 0{,}43429 ln x}Знак логарифма зависит от логарифмируемого числа: если оно больше 1, логарифм положителен, если оно между 0 и 1, то отрицателен. {-2} imes 1{,}2)=-2+lg ,1{,}2approx -2+0{,}079181=-1{,}920819}
{-2} imes 1{,}2)=-2+lg ,1{,}2approx -2+0{,}079181=-1{,}920819}
Чтобы унифицировать действия с положительными и отрицательными логарифмами, у последних целая часть (характеристика) надчёркивалась сверху:
lg 0,012 ≈ − 2 + 0,079 181 = 2 ¯ , 079181 {displaystyle lg ,0{,}012approx -2+0{,}079181={ar {2}}{,}079181}Мантисса логарифма, выбираемая из таблиц, при таком подходе всегда положительна.
Функция десятичного логарифма
Если рассматривать логарифмируемое число как переменную, мы получим функцию десятичного логарифма: y = lg x . {displaystyle y=lg ,x.} Она определена при всех x > 0. {displaystyle x>0. } Область значений: E ( y ) = ( − ∞ ; + ∞ ) {displaystyle E(y)=(-infty ;+infty )} . График этой кривой часто называется логарифмикой.
} Область значений: E ( y ) = ( − ∞ ; + ∞ ) {displaystyle E(y)=(-infty ;+infty )} . График этой кривой часто называется логарифмикой.
Функция монотонно возрастает, непрерывна и дифференцируема всюду, где она определена. Производная для неё даётся формулой:
d d x lg x = lg e x {displaystyle {frac {d}{dx}}lg ,x={frac {lg ,e}{x}}}Ось ординат ( x = 0 ) {displaystyle (x=0)} является вертикальной асимптотой, поскольку:
lim x → 0 + 0 lg x = − ∞ {displaystyle lim _{x o 0+0}lg ,x=-infty }Применение
Логарифмы по основанию 10 до изобретения в 1970-е годы компактных электронных калькуляторов широко применялись для вычислений. Как и любые другие логарифмы, они позволяли многократно упростить и облегчить трудоёмкие расчёты, заменяя умножение на сложение, а деление на вычитание; аналогично упрощались возведение в степень и извлечение корня. Но десятичные логарифмы обладали преимуществом перед логарифмами с иным основанием: целую часть логарифма числа x {displaystyle x} (характеристику логарифма) [ lg x ] {displaystyle [lg x]} легко определить.
Как и любые другие логарифмы, они позволяли многократно упростить и облегчить трудоёмкие расчёты, заменяя умножение на сложение, а деление на вычитание; аналогично упрощались возведение в степень и извлечение корня. Но десятичные логарифмы обладали преимуществом перед логарифмами с иным основанием: целую часть логарифма числа x {displaystyle x} (характеристику логарифма) [ lg x ] {displaystyle [lg x]} легко определить.
- Если x ⩾ 1 {displaystyle xgeqslant 1} , то [ lg x ] {displaystyle [lg x]} на 1 меньше числа цифр в целой части числа x {displaystyle x} . Например, сразу очевидно, что lg 345 {displaystyle lg 345} находится в промежутке ( 2 , 3 ) {displaystyle (2,3)} .

- Если 0 < x < 1 {displaystyle 0<x<1} , то ближайшее к lg x {displaystyle lg x} целое в меньшую сторону равно общему числу нулей в x {displaystyle x} перед первой ненулевой цифрой (включая ноль перед запятой), взятому со знаком минус. Например, lg 0,001 4 {displaystyle lg 0{,}0014} находится в интервале ( − 3 , − 2 ) {displaystyle (-3,-2)} .
Кроме того, при переносе десятичной запятой в числе на n {displaystyle n} разрядов значение десятичного логарифма этого числа изменяется на n . {displaystyle n.} Например:
lg 8314 , 63 = lg 8,314 63 + 3 {displaystyle lg 8314{,}63=lg 8{,}31463+3}Отсюда следует, что для вычисления десятичных логарифмов достаточно составить таблицу логарифмов для чисел в диапазоне от 1 {displaystyle 1} до 10 {displaystyle 10} . Такие таблицы, начиная с XVII века, выпускались большим тиражом и служили незаменимым расчётным инструментом учёных и инженеров.
Такие таблицы, начиная с XVII века, выпускались большим тиражом и служили незаменимым расчётным инструментом учёных и инженеров.
Поскольку применение логарифмов для расчётов с появлением вычислительной техники почти прекратилось, в наши дни десятичный логарифм в значительной степени вытеснен натуральным. Он сохраняется в основном в тех математических моделях, где исторически укоренился — например, при построении логарифмических шкал.
Обратите внимание, что у всех приведенных в таблице чисел n {displaystyle n} одна и та же мантисса M {displaystyle M} , поскольку:
lg ( n ) = lg ( x × 10 C ) = lg ( x ) + lg ( 10 C ) = lg ( x ) + C {displaystyle lg(n)=lg left(x imes 10^{C} ight)=lg(x)+lg left(10^{C} ight)=lg(x)+C} ,где 1 < x < 10 {displaystyle 1<x<10} — значащая часть числа n {displaystyle n} .
История
Первые таблицы десятичных логарифмов опубликовал в 1617 году оксфордский профессор математики Генри Бригс для чисел от 1 до 1000, с восемью (позже — с четырнадцатью) знаками. Поэтому за рубежом десятичные логарифмы часто называют бригсовыми. Но в этих и в последующих изданиях таблиц обнаружились ошибки. Первое безошибочное издание на основе таблиц Георга Веги (1783) появилось только в 1852 году в Берлине (таблицы Бремикера).
В России первые таблицы логарифмов были изданы в 1703 году при участии Л. Ф. Магницкого. В СССР выпускались несколько сборников таблиц логарифмов:

Калькулятор логарифмов
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Дом Карта сайта Мастера преобразования Калькуляторы Закладки О Свяжитесь с нами Политика конфиденциальности Отказ от ответственности | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Изменение формулы основания логарифмов — Krista King Math
Изменение формулы основания логарифмов
Нам проще вычислять логарифмы основания ???10??? или основание ???e???, потому что калькуляторы обычно имеют ???\log??? и ???\лн??? кнопки для них.
Когда база отличается от ???10??? или ???e???, мы можем использовать формулу изменения основания .
???\log_ab=\frac{\log_cb}{\log_ca}???
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Читать далее.
Обратите внимание, что для лога с базой ???a??? и аргумент ???b???, мы можем выбрать любое значение, которое мы хотели бы использовать в качестве новой базы, ???c???. Что действительно полезно, потому что мы можем выбрать новую базу ???10??? или ???e???, если нам удобно.
Как использовать формулу изменения основания для упрощения выражений с логарифмами (логарифмами)
Пройти курс
Хотите узнать больше об Алгебре 2? У меня есть пошаговый курс для этого.
 🙂
🙂Учить больше
Преобразование журнала с другим основанием в журнал с основанием 10
Пример
Оцените логарифм до четырех знаков после запятой.
???\log_54???
Мы можем использовать формулу замены основания.
???\log_ab=\frac{\log_cb}{\log_ca}???
???\log_54=\frac{\log_{10}4}{\log_{10}5}???
Теперь мы можем использовать калькулятор, чтобы вычислить ответ.
???\log_54\приблизительно\фракция{0,6021}{0,6990}???
???\log_54 \приблизительно 0,8614???
Поймите, что мы можем работать и в обратном направлении, прокладывая путь к изменению базовой формулы.
Обратите внимание, что, имея журнал с основанием a и аргументом b, мы можем выбрать любое значение, которое мы хотели бы использовать в качестве нового основания, c.
Пример
Упростите выражение до одного действительного числа без использования калькулятора.
???\frac{\log{625}}{\log{25}}???
Если мы используем формулу замены основания, то можем переписать это выражение в виде ???\log_ab???.
???\log_{25}{625}???
Тогда, используя общую форму логарифмов, мы можем сказать, что значение этого бревна равно ???x???, и, следовательно, 94???
Поскольку основания эквивалентны, это означает, что показатели степени также должны быть эквивалентны, чтобы уравнение было верным.
???2x=4???
???х=2???
Следовательно, значение исходного выражения равно ???2???, или
???\frac{\log{625}}{\log{25}}=2???
Мы также можем решать другие виды экспоненциальных уравнений, используя журналы и формулу изменения основания.
Пример
Используйте журналы для решения уравнения.
9{2x}=30???Теперь мы можем использовать общее правило для журналов, чтобы преобразовать это в логарифмическое уравнение.
???\log_5{30}=2x???
Применим изменение базовой формулы,
???2x=\frac{\log{30}}{\log{5}}???
И тогда мы можем найти переменную.


 Обычный логарифм — это логарифм с основанием 10, также известный как десятичный логарифм или десятичный логарифм. В то время как натуральный логарифм является основанием с математической константой «е», которая приблизительно равна 2,718281828459
Обычный логарифм — это логарифм с основанием 10, также известный как десятичный логарифм или десятичный логарифм. В то время как натуральный логарифм является основанием с математической константой «е», которая приблизительно равна 2,718281828459 ..
..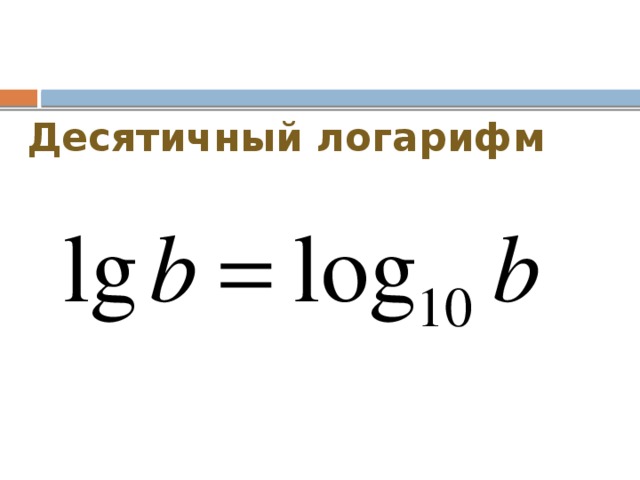 Найдите свой счастливый номер
Найдите свой счастливый номер ..
.. ..
..