Как никогда не путать табличные значения синусов и косинусов? Секрет моей классной…: whatiswhat1 — LiveJournal
- Образование
- Cancel
Вчера помогала сыну разобраться с задачей из ОГЭ по математике и поняла, что он «плавает» в табличных значениях тригонометрических функций. Объяснила ему, как их запомнить так, чтобы больше никогда не ошибиться.
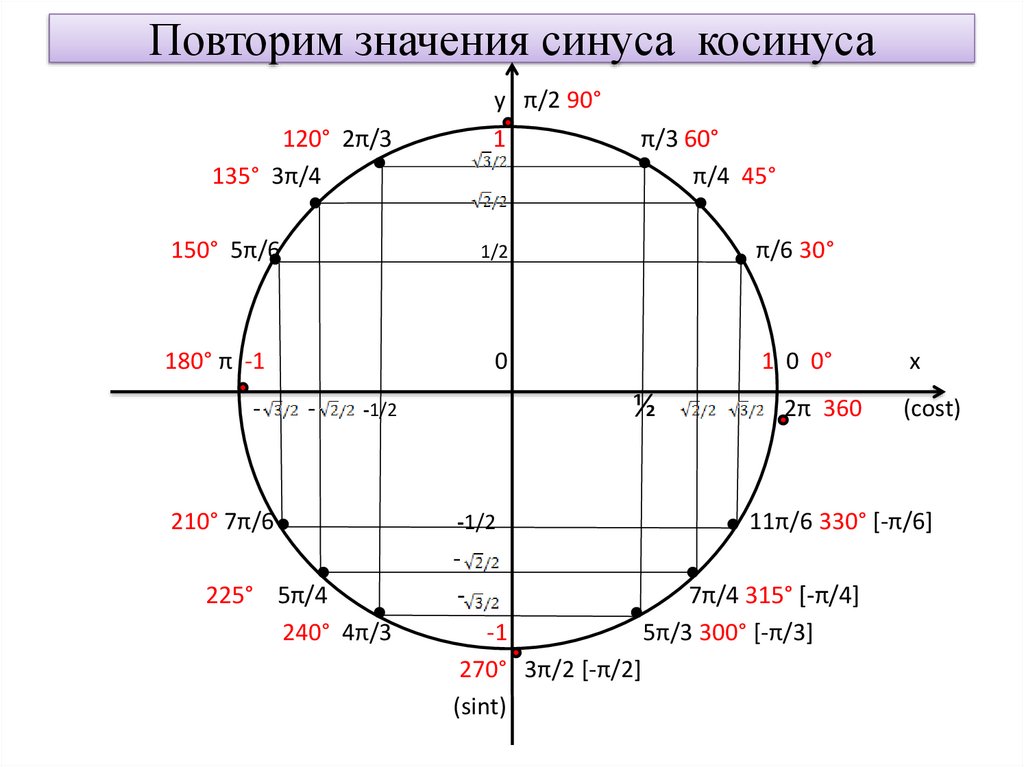
Для начала рисуем единичную окружность, откладываем нужный угол, получаем точку А при пересечении с окружностью.
Вспоминаем, что синус — это ордината точки А (координата по оси OY), а косинус — абсцисса точки А (координата по оси OX).
Наша замечательная классная руководительница, которая вела у нас математику, учила нас запоминать так:
Противоположности притягиваются. Сиииинус (произносим писклявым голоском) — звучит так мяяягко, а с ним в паре орррдинаааата (басом) — звучит жестко… Кооосинус (басом) — звучит твердо, а с ним в паре абсциииисса (пискляво) — звучит мяяягко.
Вот так запомнить — даже во сне уже не перепутаешь. Проверенно!
Обычно ни у кого нет проблем запомнить, что вся эта таблица синусов-косинусов крутится вокруг трех чисел:
Осталось только понять, какое из этих чисел чему соответствует.
На всякий случай вспомним, что корень из одного, это все равно, что один, тогда наши волшебные числа имеют вид:
Ну и тут уж совсем очевидно, что
И теперь, когда нам нужно сообразить, чему, например, равен синус угла в тридцать градусов, мы на полях тетради рисуем маленькую единичную окружность (от руки, разумеется, без всяких линеек и циркулей), откладываем там углы 30, 45, 60.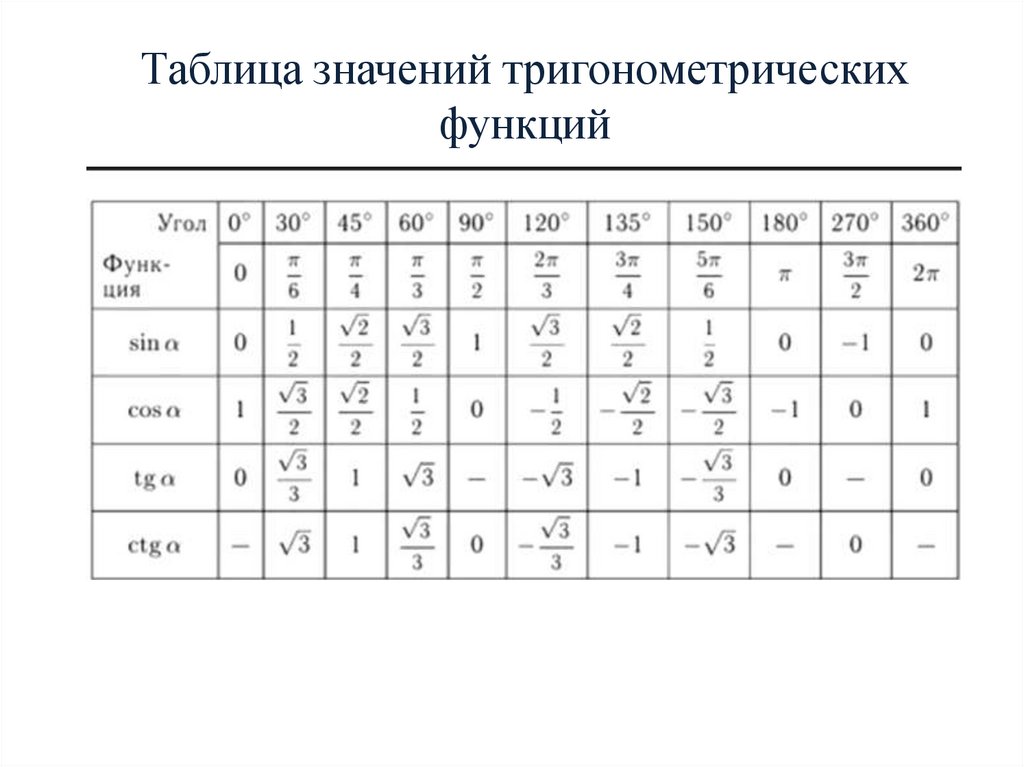
По единичной окружности сразу видно, что синус угла 30 градусов равен синусу угла 150 градусов, потому что ординаты у них одинаковые. А вот косинус 150-ти равен самому большому, но отрицательному числу — минус корень из трех на два…
Так, пользуясь притяжением противоположностей и единичной окружностью, Вы никогда не перепутаете табличные значения синусов и косинусов!
Осталось вспомнить, что тангенс — синус деленный на косинус, а котангенс — наоборот, косинус на синус. И, вспомнив значения синуса и косинуса, легко вычислить тангенс и котангенс.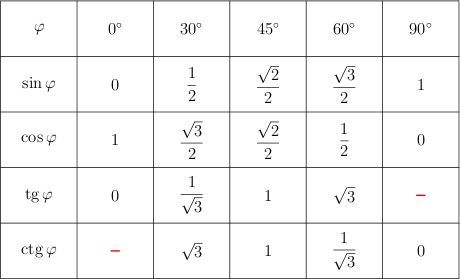 Так что их тоже не забудете.
Так что их тоже не забудете.
Поначалу, я помню, что эти единичные окружности я прямо рисовала в тетради на полях постоянно, чтобы наглядно все было. А потом в этом отпала необходимость: картинка у меня просто возникала перед мысленным взором.
Надеюсь, этот пост кому-нибудь окажется полезным 🙂 Ставьте лайки, и пишите, если нашли неточности…
Читайте также- Оглавление по рубрикам — для Вашего удобства я разбила все статьи на канале по темам.
- Ненужные предметы в школе — учить или не учить
- Высшее образование — самые прагматичные аргументы «за»
- Почему я против TikTok-а. Моя стыдная история
детиматематикаобразованиеучебашкольное образование
Табличное вычисление синуса с использованием линейной интерполяции
Табличное вычисление синуса с использованием линейной интерполяции| [Home] | [Donate!] [Контакты] |
Табличное вычисление синуса с использованием линейной интерполяции
Оглавление
Точность линейной интерполяции при вычислении значений sin
Минимальный размер таблицы синусов для цифрового синтеза сигнала
Точность линейной интерполяции при вычислении значений
sinНа малых участках нелинейную функцию можно приближённо заменить линейной с целью значительного упрощения численных расчётов. Если y1, y2 — значения некоторой функции в достаточно близко расположенных точках x
Если y1, y2 — значения некоторой функции в достаточно близко расположенных точках x
$$
y(x) \approx y1+\frac{y_2-y_1}{x_2-x_1}(x-x_1),
$$
причём в точках x1, x2 формула даёт всегда точные значения y1 и y2.
Такое линейное приближение произвольной функции на отрезке с использованием значений функции на концах этого отрезка и является линейной интерполяцией.
Воспользуемся линейной интерполяцией для вычисления синуса в любой точке, если у нас имеется таблица значений синуса в некоторых точках области [0, 2π) с фиксированным шагом d и оценим допускаемую при этом погрешность. Это, в свою очередь, позволит нам определить максимальный шаг аргумента в таблице синусов, при котором допускаемая погрешность не превысит заданного предельного значения.
Предположим, что нам требуется определить значение функции sin в точке \(\phi\), которая находится между точками \(\phi_0\) и \(\phi_0+d\), для которых в таблице имеются значения синусов. Тогда, пользуясь линейной интерполяцией, получаем: $$ \sin\phi \approx \sin\phi_0+\frac{\sin(\phi_0+d)-\sin\phi_0}d \Delta \phi, \tag 1 $$ где \(\Delta\phi=\phi-\phi_0, 0 \le \Delta\phi \le d\).
Заменяя точное значение функции на интерполированное, мы допускаем ошибку
$$
\Delta s=\sin\phi-\sin\phi_0-\frac{\sin(\phi_0+d)-\sin\phi_0}d \Delta \phi. \tag 2
$$
Из формулы видно, что ошибка обращается в 0 в точках \(\Delta \phi=0\) и \(\Delta \phi=d\) (что вполне естественно, так как в этих точках в качестве интерполированного используется точное табличное значение).
Подставляя найденное значение в (2), получим величину наибольшего отклонения интерполяционного приближения от истинного значения функции sin:
$$
\Delta s(d/2)=\sin\left(\phi_0+\frac d 2\right)-\sin\phi_0-\frac{sin(\phi_0+d)-\sin\phi_0}2.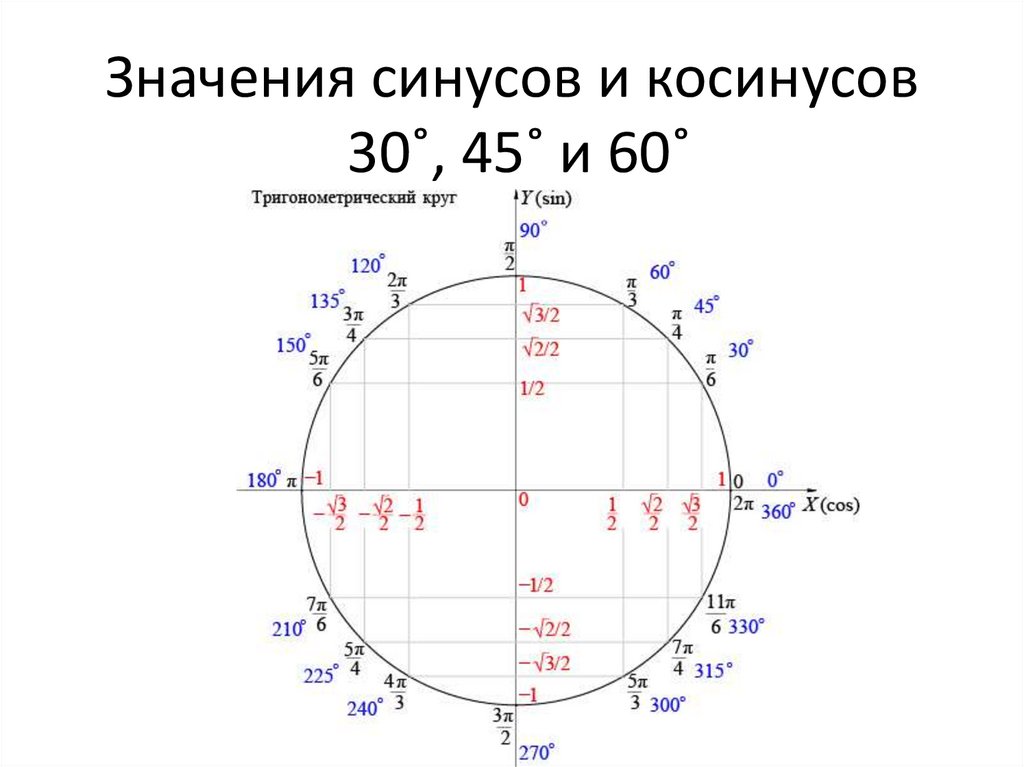 $$
В дальнейшем будем обозначать эту величину просто как \(\Delta s\), так как нас интересует именно наибольшая величина ошибки.
$$
В дальнейшем будем обозначать эту величину просто как \(\Delta s\), так как нас интересует именно наибольшая величина ошибки.
Применяя формулу для разности синусов, получаем: $$ \Delta s=2\cos\frac{2\phi_0+d/2}2 \sin\frac d 4-\frac 1 2 \left(2\cos\frac{2\phi_0+d}2 \sin\frac d 2\right). $$ С учётом того, что \(\sin\frac d 4 \approx \frac d 4, \sin\frac d 2 \approx \frac d 2\), получаем $$ \Delta s \approx \frac d 2 \cos\left(\phi_0+\frac d 4\right)-\frac d 2 \cos\left(\phi_0+\frac d 2\right). $$ Теперь применяем формулу разности косинусов: $$ \cos\alpha-\cos\beta=-2\sin\frac{\alpha+\beta}2 \sin\frac{\alpha-\beta}2, \\ \Delta s \approx \frac d 2 \left(-2\sin\frac{2\phi_0+3d/4}2 \sin\frac{-d/4}2\right)= \\ =d\sin\left(\phi_0+\frac{3d}8\right)\sin\frac d 8. $$
Опять воспользуемся тем, что синус от малого аргумента примерно равен значению аргумента:
$$
\Delta s \approx \frac{d^2}8 \sin\left(\phi_0+\frac{3d}8\right).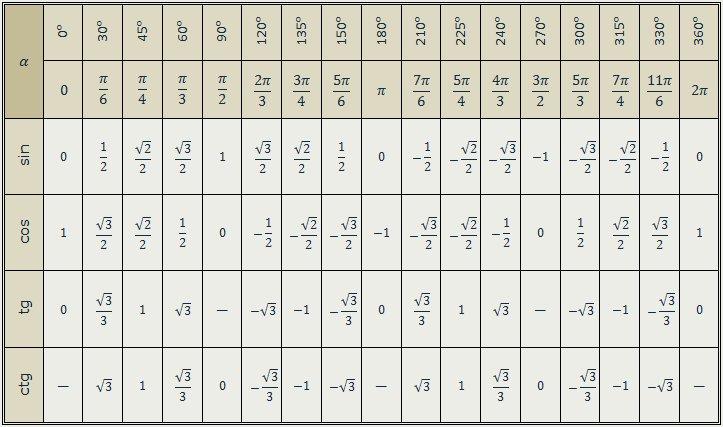 2}8.
$$
2}8.
$$
Если же от нас требуется, чтобы допускаемая погрешность при интерполяции не превышала по абсолютной величине значения \(\Delta s\), то следует выбирать шаг таблицы из условия $$ d \le \sqrt{8\Delta s}. \tag 4 $$ Таблица значений для аргументов из промежутка [0, 2π) будет содержать L элементов, $$ L \ge \frac{2\pi}d, \\ L \ge \frac{2\pi}{\sqrt{8\Delta s}}. \tag 5 $$
Минимальный размер таблицы синусов для цифрового синтеза сигнала
Предположим, что с помощью микроконтроллера и цифро-аналогового преобразователя (DAC) мы осуществляем генерацию синусоидального сигнала. Требуется оценить, какие размеры должна иметь таблица синусов, чтобы ошибка вычислений не превышала заданной величины.
Пусть используемый DAC имеет однополярный выход с напряжением от 0 до VREF. В таком случае нам потребуется иметь постоянное смещение в сигнале, так как наш DAC не способен сформировать сигналы с отрицательными значениями напряжения.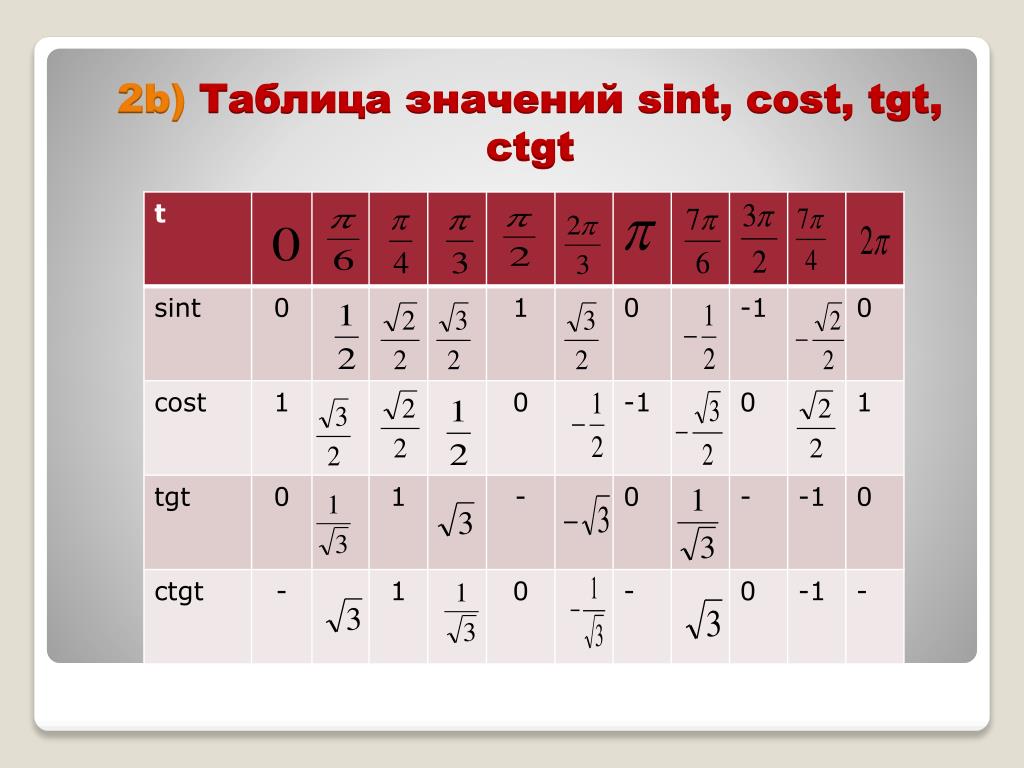 Обозначим постоянное смещение сигнала как a0, амплитуду сигнала a1, сам сигнал будет описываться выражением
$$
u=a_0+a_1\sin\phi, \tag 6
$$
здесь \(\phi\) — фаза сигнала, соответствующая данному моменту времени. В соответствии со свойствами нашего DAC,
$$
a_0-a_1 \ge 0, \\
a_0+a_1 \le V_{REF}.
$$
Отсюда следует, что a1 должно быть в переделах от 0 до VREF/2, а величина a0 может быть задана от a1 до (VREF-a1).
Обозначим постоянное смещение сигнала как a0, амплитуду сигнала a1, сам сигнал будет описываться выражением
$$
u=a_0+a_1\sin\phi, \tag 6
$$
здесь \(\phi\) — фаза сигнала, соответствующая данному моменту времени. В соответствии со свойствами нашего DAC,
$$
a_0-a_1 \ge 0, \\
a_0+a_1 \le V_{REF}.
$$
Отсюда следует, что a1 должно быть в переделах от 0 до VREF/2, а величина a0 может быть задана от a1 до (VREF-a1).
Из (6) видим, что абсолютная ошибка \(\Delta u\), допускаемая при вычислении величины сигнала, при условии что синус вычисляется с ошибкой \(\Delta s\), составляет $$ \Delta u=a_1\Delta s. $$ Нас в первую очередь интересует наибольшая величина ошибки, которая будет при максимальном возможном значении a1=VREF/2: $$ \Delta u=V_{REF}\Delta s/2. \tag 7 $$
Нет смысла добиваться чрезмерно малых значений ошибки вычислений, так как с учётом ограниченной разрядности N преобразователя DAC, напряжение на выходе всё равно будет установлено кратным 1 LSB=VREF/2N. {N/2}. \tag 8
$$
Наиболее простой программная реализация вычислений получается в том случае, если в качестве L выберем ближайшее к (8), большее значение, являющееся степенью 2. Например, генерация синусоиды с использованием 12-разрядного ADC, требует, в соответствии с (8) таблицы синусов из 142 элементов, поэтому выбираем значение L=256=28.
{N/2}. \tag 8
$$
Наиболее простой программная реализация вычислений получается в том случае, если в качестве L выберем ближайшее к (8), большее значение, являющееся степенью 2. Например, генерация синусоиды с использованием 12-разрядного ADC, требует, в соответствии с (8) таблицы синусов из 142 элементов, поэтому выбираем значение L=256=28.
author: hamper; date: 2016-10-25
тригонометрия — Как посчитать синус вручную, без всяких правил, калькулятора и прочего?
Я бы предложил менее известный метод, который прекрасно обобщается на многие другие функции и может быть весьма эффективным, даже когда вам нужно выполнять все вычисления вручную:
Пара $(c,s) = (\cos x , \sin x)$ (в радиан , конечно!) можно интерпретировать как единственное решение обыкновенного дифференциального уравнения
$$
\ frac {\ mathrm {d}} {\ mathrm {d} x} \ begin {pmatrix} c \\ s \ end {pmatrix}
= \begin{pmatrix}-s\\c\end{pmatrix}
$$
с начальным условием $c(0) = 1$, $s(0) = 0$.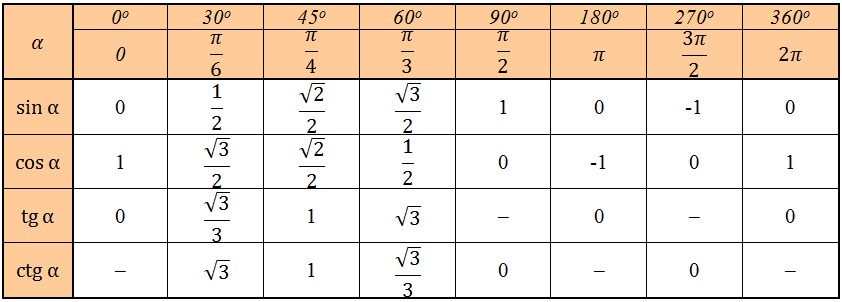 Таким образом, его можно приблизительно решить с помощью решателей Рунге-Кутты. Идея состоит в том, чтобы начать с нуля, а затем шаг за шагом приближаться к целевому значению, эффективно используя разложение Тейлора вокруг каждой точки. Поскольку шаги малы, разложение Тейлора здесь сходится намного быстрее, чем если бы вы напрямую вводили целевое значение. 9\circ) = \sin (\tfrac\pi4)$. Мы знаем, что это должно получиться как $\sqrt2/2$, но давайте посмотрим. Я выберу 0,2 в качестве размера шага по умолчанию. Поехали:
Таким образом, его можно приблизительно решить с помощью решателей Рунге-Кутты. Идея состоит в том, чтобы начать с нуля, а затем шаг за шагом приближаться к целевому значению, эффективно используя разложение Тейлора вокруг каждой точки. Поскольку шаги малы, разложение Тейлора здесь сходится намного быстрее, чем если бы вы напрямую вводили целевое значение. 9\circ) = \sin (\tfrac\pi4)$. Мы знаем, что это должно получиться как $\sqrt2/2$, но давайте посмотрим. Я выберу 0,2 в качестве размера шага по умолчанию. Поехали:
$x_0=0$, $c_0=1$, $s_0=0$
- $$\begin{align} h_1=&0,2 \\ x_1=&0,2 \\ \тильда c_1 =& c_0 — h_1\times s_0 = 1 \\ \тильда s_1 =& s_0 + h_1\times c_0 = 0,2 \\ c_1 =& c_0 — \frac{h_1}2\times (s_0 + \tilde s_1) = 1 — 0,1\times0,2 = 0,98 \\ s_1 =& s_0 + \frac{h_1}2\times (c_0 + \tilde c_1) = 0,2 \end{выравнивание}$$
- $$\begin{выравнивание} h_2=&0,2 \\ x_2=&0,4 \\ \тильда c_2 =& c_1 — h_2\times s_1 = 0,98 — 0,2\times0,2 = 0,94 \\ \тильда s_2 =& s_1 + h_2\times c_1 = 0,2 + 0,2\cdot0,98 = 0,396 \\ c_2 =& c_1 — \frac{h_2}2\times (s_1 + \tilde s_2) = 0,98 — 0,1\times 0,596 = 0,9204 \\ s_2 =& s_1 + \frac{h_2}2\times (c_1 + \tilde c_2) = 0,2 + 0,1\times 1,92 = 0,392 \end{выравнивание}$$
- $$\begin{выравнивание} h_3=&0,2 \\ x_3=&0,6 \\ \тильда c_3 =& \ldots = 0,9204 — 0,2\умножить на 0,392 = 0,842 \\ \тильда s_3 =& \ldots = 0,392 + 0,2\times 0,9204 = 0,5768 \\ c_3 =& \ldots = 0,9204 — 0,1\умножить на 0,9688 = 0,82352 \\ s_3 =& \ldots = 0,392 + 0,1\умножить на 1,7624 = 0,56824 \end{выравнивание}$$
- Хорошо, если бы мы теперь сделали еще один шаг 0,2, мы бы получили 0,8, но $\pi/4 \приблизительно 0,7854$.
 Так что мы сделаем только шаг 0,1. Также я начну округлять здесь после пятого знака после запятой.
$$\begin{выравнивание}
h_4=&0,1 \\ x_4=&0,7
\\ \tilde c_4 =& \ldots = 0,82352 — 0,1\times 0,56824 \приблизительно 0,76670
\\ \тильда s_4 =& \ldots = 0,56824 + 0,1\times 0,82352 \приблизительно 0,65059\\ c_4 =& \ldots = 0,82352 — 0,05\times 1,21883 \приблизительно 0,76258
\\ s_4 =& \ldots = 0,56824 + 0,05\умножить на 1,53339 \приблизительно 0,64491
\end{выравнивание}$$
Так что мы сделаем только шаг 0,1. Также я начну округлять здесь после пятого знака после запятой.
$$\begin{выравнивание}
h_4=&0,1 \\ x_4=&0,7
\\ \tilde c_4 =& \ldots = 0,82352 — 0,1\times 0,56824 \приблизительно 0,76670
\\ \тильда s_4 =& \ldots = 0,56824 + 0,1\times 0,82352 \приблизительно 0,65059\\ c_4 =& \ldots = 0,82352 — 0,05\times 1,21883 \приблизительно 0,76258
\\ s_4 =& \ldots = 0,56824 + 0,05\умножить на 1,53339 \приблизительно 0,64491
\end{выравнивание}$$ - $$\begin{выравнивание}
h_5=&0,08 \\ x_5=&0,78
\\ \tilde c_5 =& \ldots = 0,76258 — 0,08\times 0,64491 \приблизительно 0,71099
\\ \тильда s_5 =& \ldots = 0,64491 + 0,08\умножить на 0,76258 \приблизительно 0,70592
\\ c_5 =& \ldots = 0,76258 — 0,04\умножить на 1,47357 \приблизительно 0,70364
\\ s_5 =& \ldots = 0,64491 + 0,04\умножить на 1,35083 \приблизительно 0,692 \примерно 0,495$. Достаточно близко к $0,5$. Не великий , но также я сделал только пять не таких уж маленьких шагов (поскольку схема Хеуна имеет точность 2-го порядка, уменьшение шагов дало бы действительно заметно лучшую точность) и — это главное преимущество — все они включал только очень простые умножения, потому что я мог выбрать размер шага так, чтобы это было удобно, в отличие от прямой оценки ряда Тейлора.

Это также основная идея метода CORDIC, который уже упоминался в комментариях. Это использует дополнительные свойства синуса и косинуса для достижения большей эффективности, но на самом деле это не нужно. Многие функции, определенные ОДУ, эффективно оцениваются решателем Рунге-Кутты; часто предпочтительнее версия четвертого порядка, которая дает еще лучшую сходимость.
На практике этот метод по-прежнему лучше прямого метода Тейлора только в том случае, если вам нужно несколько значений функции. Тогда это очень хорошо, потому что а) вы составляете таблицу значений по мере продвижения б) вы вычисляете и синус, и косинус, которые затем можно комбинировать, используя свойства симметрии/периодичности.
Видео-вопрос: Распознавание обратной функции синуса из таблицы значений функций
Стенограмма видео
В данных таблицах показаны некоторые значения 𝑓 из 𝑥, 𝑔 из 𝑥 и ℎ из 𝑥. Какой функции соответствует функция sin, обратная 𝑥?
Итак, как сказано в вопросе, у нас есть три таблицы, и они представляют значения 𝑓 из 𝑥, 𝑔 из 𝑥 и ℎ из 𝑥 соответственно.
 Одна из этих функций 𝑓 от 𝑥, 𝑔 от 𝑥 или ℎ от 𝑥 является синус-обратной по отношению к 𝑥, и мы пройдемся по каждому варианту по очереди, чтобы определить, какой именно.
Одна из этих функций 𝑓 от 𝑥, 𝑔 от 𝑥 или ℎ от 𝑥 является синус-обратной по отношению к 𝑥, и мы пройдемся по каждому варианту по очереди, чтобы определить, какой именно.Итак, сначала мы смотрим на таблицу, соответствующую 𝑓 из 𝑥, и спрашиваем: «равно ли 𝑓 из 𝑥 греху, обратному 𝑥?» Что ж, если это так, то грех 𝑓 от 𝑥 равен греху греха, обратному 𝑥, а грех греха, обратному 𝑥, равен 𝑥. Так что на самом деле мы спрашиваем, равен ли грех 𝑓 из 𝑥 𝑥. И мы можем проверить это, используя значения в таблице. Итак, мы смотрим на первую пару значений, где 𝑥 — отрицательный корень три на два, а 𝑓 из 𝑥 — отрицательное 𝜋 на три. И мы запрашиваем эту пару значений, если грех 𝑓 из 𝑥 равен 𝑥. Таким образом, отрицательный грех 𝜋 на три должен быть равен отрицательному корню три на два.
И либо зная кое-что о специальных углах, либо используя наш калькулятор, мы можем убедиться, что это действительно так. Но, конечно, нам нужно, чтобы это было верно для других значений 𝑥 и 𝑓 из 𝑥. Итак, мы смотрим на вторую пару значений, 𝑥 отрицательна наполовину, а 𝑓 из 𝑥 отрицательна 𝜋 на шесть.
 И поэтому мы должны спросить: «равен ли грех отрицательного числа 𝜋 на шесть отрицательной половине?» И, конечно же, это так. Итак, все выглядит хорошо для 𝑓 из 𝑥, но нам нужно проверить все значения. Итак, двигаясь дальше, глядя на следующую пару, мы спрашиваем, равен ли нулевой грех нулю, и, конечно, это так. Итак, переходя к следующей паре значений, мы спрашиваем, равен ли грех 𝜋 на четыре половине, и, конечно же, это не так. Грех 𝜋 на четыре равен корню два из двух, а не половине. А это значит, что для этой пары значений sin 𝑓 of 𝑥 не равен 𝑥. Итак, 𝑓 из 𝑥 не является грехом, обратным 𝑥. Итак, 𝑓 из 𝑥 не является нашим ответом, и мы переходим к рассмотрению 𝑔 из 𝑥.
И поэтому мы должны спросить: «равен ли грех отрицательного числа 𝜋 на шесть отрицательной половине?» И, конечно же, это так. Итак, все выглядит хорошо для 𝑓 из 𝑥, но нам нужно проверить все значения. Итак, двигаясь дальше, глядя на следующую пару, мы спрашиваем, равен ли нулевой грех нулю, и, конечно, это так. Итак, переходя к следующей паре значений, мы спрашиваем, равен ли грех 𝜋 на четыре половине, и, конечно же, это не так. Грех 𝜋 на четыре равен корню два из двух, а не половине. А это значит, что для этой пары значений sin 𝑓 of 𝑥 не равен 𝑥. Итак, 𝑓 из 𝑥 не является грехом, обратным 𝑥. Итак, 𝑓 из 𝑥 не является нашим ответом, и мы переходим к рассмотрению 𝑔 из 𝑥.Таким образом, это точно такой же процесс, но для 𝑔 из 𝑥 вместо 𝑓 из 𝑥. Чтобы узнать, равен ли 𝑔 𝑥 греху, обратному 𝑥, мы спрашиваем, равен ли грех 𝑔 𝑥 𝑥 для всех значений в нашей таблице. Поэтому, рассматривая первую пару значений, мы спрашиваем, равен ли грех отрицательного 𝜋 на шесть отрицательному корню из трех над двумя.


 Сиииинус (произносим писклявым голоском) — звучит так мяяягко, а с ним в паре орррдинаааата (басом) — звучит жестко… Кооосинус (басом) — звучит твердо, а с ним в паре абсциииисса (пискляво) — звучит мяяягко.
Сиииинус (произносим писклявым голоском) — звучит так мяяягко, а с ним в паре орррдинаааата (басом) — звучит жестко… Кооосинус (басом) — звучит твердо, а с ним в паре абсциииисса (пискляво) — звучит мяяягко.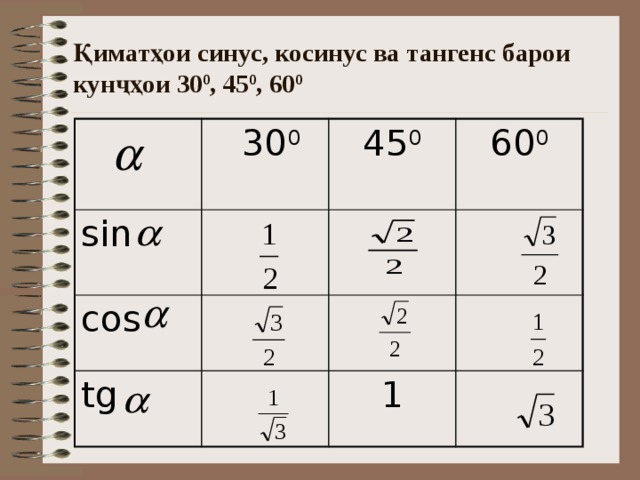 Так что мы сделаем только шаг 0,1. Также я начну округлять здесь после пятого знака после запятой.
$$\begin{выравнивание}
h_4=&0,1 \\ x_4=&0,7
\\ \tilde c_4 =& \ldots = 0,82352 — 0,1\times 0,56824 \приблизительно 0,76670
\\ \тильда s_4 =& \ldots = 0,56824 + 0,1\times 0,82352 \приблизительно 0,65059\\ c_4 =& \ldots = 0,82352 — 0,05\times 1,21883 \приблизительно 0,76258
\\ s_4 =& \ldots = 0,56824 + 0,05\умножить на 1,53339 \приблизительно 0,64491
\end{выравнивание}$$
Так что мы сделаем только шаг 0,1. Также я начну округлять здесь после пятого знака после запятой.
$$\begin{выравнивание}
h_4=&0,1 \\ x_4=&0,7
\\ \tilde c_4 =& \ldots = 0,82352 — 0,1\times 0,56824 \приблизительно 0,76670
\\ \тильда s_4 =& \ldots = 0,56824 + 0,1\times 0,82352 \приблизительно 0,65059\\ c_4 =& \ldots = 0,82352 — 0,05\times 1,21883 \приблизительно 0,76258
\\ s_4 =& \ldots = 0,56824 + 0,05\умножить на 1,53339 \приблизительно 0,64491
\end{выравнивание}$$
 Одна из этих функций 𝑓 от 𝑥, 𝑔 от 𝑥 или ℎ от 𝑥 является синус-обратной по отношению к 𝑥, и мы пройдемся по каждому варианту по очереди, чтобы определить, какой именно.
Одна из этих функций 𝑓 от 𝑥, 𝑔 от 𝑥 или ℎ от 𝑥 является синус-обратной по отношению к 𝑥, и мы пройдемся по каждому варианту по очереди, чтобы определить, какой именно. И поэтому мы должны спросить: «равен ли грех отрицательного числа 𝜋 на шесть отрицательной половине?» И, конечно же, это так. Итак, все выглядит хорошо для 𝑓 из 𝑥, но нам нужно проверить все значения. Итак, двигаясь дальше, глядя на следующую пару, мы спрашиваем, равен ли нулевой грех нулю, и, конечно, это так. Итак, переходя к следующей паре значений, мы спрашиваем, равен ли грех 𝜋 на четыре половине, и, конечно же, это не так. Грех 𝜋 на четыре равен корню два из двух, а не половине. А это значит, что для этой пары значений sin 𝑓 of 𝑥 не равен 𝑥. Итак, 𝑓 из 𝑥 не является грехом, обратным 𝑥. Итак, 𝑓 из 𝑥 не является нашим ответом, и мы переходим к рассмотрению 𝑔 из 𝑥.
И поэтому мы должны спросить: «равен ли грех отрицательного числа 𝜋 на шесть отрицательной половине?» И, конечно же, это так. Итак, все выглядит хорошо для 𝑓 из 𝑥, но нам нужно проверить все значения. Итак, двигаясь дальше, глядя на следующую пару, мы спрашиваем, равен ли нулевой грех нулю, и, конечно, это так. Итак, переходя к следующей паре значений, мы спрашиваем, равен ли грех 𝜋 на четыре половине, и, конечно же, это не так. Грех 𝜋 на четыре равен корню два из двух, а не половине. А это значит, что для этой пары значений sin 𝑓 of 𝑥 не равен 𝑥. Итак, 𝑓 из 𝑥 не является грехом, обратным 𝑥. Итак, 𝑓 из 𝑥 не является нашим ответом, и мы переходим к рассмотрению 𝑔 из 𝑥.