Страница не найдена — ПриМат
По данному адресу ничего не найдено. Попробуйте воспользоваться поиском.
Искать:© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Игорь Любинский (8), Юлия Стерлянко (8), Денис Стехун (8), Валентин Малявко (8), Елизавета Савицкая (8), Олег Шпинарев (7), Александр Базан (7), Анна Чалапчий (7), Константин Берков (7), Кирилл Волков (6), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2), Юлия Стоева (2), Александр Розин (2), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2),
Определитель матрицы 3 x 3 – объяснение и примеры
Определитель – это скалярная величина, полученная в результате определенных операций с элементами матрицы.
С помощью определителей матриц мы можем решить линейную систему уравнений и найти обратную матрицу, если она существует.
Определитель матрицы 3 x 3 представляет собой скалярное значение, которое мы получаем, разбивая матрицу на более мелкие матрицы 2 x 2 и выполняя определенные операции с элементами исходной матрицы.
В этом уроке мы рассмотрим формулу матрицы $3\times 3$ и как найти определитель матрицы $3\times 3$. Мы рассмотрим несколько примеров, а также дадим вам несколько практических задач.
Начнем.
Что такое определитель матрицы?
Напомним, что определитель матрицы — это скалярное значение, полученное в результате определенных операций над матрицей. Мы можем обозначить определитель матрицы $3$ способами.
Рассмотрим матрицу $ 3 \times 3 $, показанную ниже:
$ A = \begin{bmatrix} { a } & { b } & c \\ { d } & { e } & f \\ g & h & i \end {bmatrix} $
Мы можем обозначить его определитель следующими $ 3 $ способами:
Примечание: мы можем использовать обозначения взаимозаменяемо.
Как найти определитель матрицы 3 x 3
Прежде всего, мы можем вычислить определитель только для квадратных матриц! Нет определителей для неквадратных матриц.
Существует формула (точнее, алгоритм) для нахождения определителя любой квадратной матрицы. Но это выходит за рамки данного урока, и мы не будем его здесь рассматривать. Мы уже рассмотрели формулу определителя для матрицы $2\times2$, простейшую. Если вам нужна редакция этого, пожалуйста, нажмите здесь.
Ниже мы рассмотрим формулу для определителя матрицы $3\times3$ и покажем несколько примеров нахождения определителя матрицы $3\times3$.
Определитель матрицы 3 x 3 Формула
Рассмотрим матрицу $ 3 \times 3 $, показанную ниже:
$ A = \begin{bmatrix} { a } & { b } & c \\ { d } & { e } & f \\ g & h & i \end {bmatrix} $
Формула для определителя матрицы $ 3 \times 3 $ показана ниже:
$ det( A ) = | А | = \begin{vmatrix} { a } & { b } & c \\ { d } & { e } & f \\ g & h & i \ end {vmatrix} = a \begin {vmatrix} { e } & f \\ h & i \end {vmatrix} – b \begin{vmatrix} d & f \\ g & i \end {vmatrix} + c \begin{vmatrix} d & e \\ g & h \end {vmatrix} $
Обратите внимание, что мы разбили матрицу $3\x 3$ на более мелкие матрицы $2\x 2$.
Вертикальные черточки за пределами матриц $ 2 \times 2 $ указывают на то, что мы должны взять определитель. Зная определитель $ 2 \times 2 $ матриц, мы можем дополнительно упростить формулу:
$ det(A)=| А | = a(ei-fh) – b(di – fg) + c(dh-eg) $
Вычислим определитель матрицы $3 x 3$ по только что изученной формуле. Рассмотрим матрицу $B$:
$ B = \begin{bmatrix} 1 & 1 & 2 \\ 3 & 1 & 2\\ 3 & 1 & 1 \end {bmatrix} $
Используя формулу, мы можем найти определитель:
$ |В| = a( ei – fh ) – b( di – fg ) + c( dh – eg ) $
$ = 1((1)(1) – (2)(1)) – 1((3)(1 ) – (2)(3)) + 2((3)(1) – (1)(3)) $
$ = 1(-1) – 1(-3) + 2(0) $
$ = -1 + 3 $
$ = 2 $
Определитель матрицы $B$ равен $2$.
Давайте рассмотрим несколько примеров. 9Пример 1 bmatrix} $, найти $ | С | $.
Решение
Матрица $C$ является матрицей $3 \times 3$. Найдем его определитель по формуле. Ниже показано:
$ |C| = a( ei – fh ) – b( di – fg ) + c( dh – eg ) $
$ = 1((1)(4) – (1)(-2)) – (-1)(( -2)(4) – (1)(0)) + 0((-2)(-2) – (1)(0)) $
$ = 1(6) + 1(-8) + 0 (4) 9 долларов0003
$ = -2 $
Определитель матрицы $C$ равен $ -2 $.
Пример 2 & 1 & 4 \end {bmatrix} $
Решение
Мы будем использовать формулу для определителя матрицы $3 \times 3 $ для вычисления определителя матрицы $F$. Показано ниже:
$| Ф | = \begin{vmatrix} 2 & 1 & 2 \\ 1 & 0 & 1 \\ 4 & 1 & 4 \ end {vmatrix} $
$ = 2((0)(4) – (1)(1) ) – 1((1)(4) – (1)(4)) + 2((1)(1) – (0)(4)) $
$ = 2( – 1 ) – 1(0) + 2(1) $
$ = – 2 + 2 $
$ = 0 $
Определитель этой матрицы $ 0 $!
Это особый тип матрицы. Это необратимая матрица , известная как сингулярная матрица . Прочтите эту статью, чтобы узнать больше о сингулярных матрицах!
Пример 3Найти $ m $ по $ \begin{vmatrix} { -2 } & 1 & m \\ { -1 } & 0 & { – 2 } \\ 4 & { – 2 } & 6 \end {vmatrix} = 10 $.
Решение
В этой задаче нам уже дан определитель и нужно найти элемент матрицы $ m $.
Давайте подставим его в формулу и проделаем алгебраические вычисления, чтобы вычислить $m$. Процесс показан ниже:
$ \begin{vmatrix} { – 2 } & 1 & m \\ { – 1 } & 0 & { – 2 } \\ 4 & { – 2 } & 6 \ end {vmatrix} = 10$
$ -2((0)(6) – (-2)(-2)) -1((-1)(6) – (-2)(4)) +m((-1)(- 2) – (0)(4)) = 10 $
$ -2(-4) -1(2) +m(2) = 10 $
$ 8 – 2 + 2m = 10 $
$ 2m = 10 – 8 + 2 $
$ 2m = 4 $
$ m = \frac{ 4 }{ 2 } $
$ m = 2 $
Стоимость m равна $ 2 $.
Теперь ваша очередь попрактиковаться в вопросах!
Практические вопросыНайдите определитель матрицы, показанной ниже:
$ B = \begin{bmatrix} { – \frac{ 1 }{ 2 } } & { – \frac{ 1 }{ 6 } } & 2 \\ 3 & 0 & 1 \\ { – 10 } & { 12 } & -1 \end {bmatrix} $Найти $ z $ по заданному $ \begin{vmatrix} -2 & -1 & \frac{ 1 }{ 4 } \\ 0 & 8 & z \\ 4 & -2 & 12 \end {vmatrix} = 24 $
- Рассмотрим матрицы $ A $ и $ B $, показанные ниже:
$ A = \begin{bmatrix} 0 & 1 & x \\ 4 & { – 2 } & 6 \\ 10 & { – 1 } & { – 4 } \ end {bmatrix} $
$ B = \begin{bmatrix} 1 & x & { – 1 } \\ 6 & 0 & { – 2 } \\ 8 & 20 & { – 2 } \end {bmatrix} $
Если определитель обоих матрицы равны ($|A|=|B|$), узнать значение $x$.
Матрица $ B $ представляет собой квадратную матрицу размера $ 3 x 3 $. Давайте найдем определитель, используя формулу, которую мы изучили в этом уроке.
Процесс нахождения определителя показан ниже:
$ | Б | = a( ei – fh ) – b( di – fg ) + c( dh – eg ) $
$ = -\frac{ 1 }{ 2 }((0)(-1) – (1)(12) ) – (-\frac{ 1 }{ 6 })((3)(-1) – (1)(-10)) + 2((3)(12) – (0)(-10)) $
$ = -\frac{ 1 }{ 2 }(-12) + \frac{ 1 }{ 6 }(7) + 2( 36 ) $
$ = 6 + \frac{ 7 }{ 6 } + 72 $
$ = 79 \frac{ 1 }{ 6 } $
Таким образом, $ | Б | = 79 \frac{ 1 }{ 6 } $.
В этой задаче нам уже дан определитель и нужно найти элемент матрицы, $z$. Давайте подставим его в формулу и проделаем алгебраические вычисления, чтобы вычислить $z$. Процесс показан ниже:
$ \begin{vmatrix} { – 2 } & { – 1 } & \frac{ 1 }{ 4 } \\ 0 & 8 & z \\ 4 & { – 2 } & 12 \ end {vmatrix} = 24 $
$ -2((8)(12) – (z)(-2)) -(-1)((0)(12) – (z)(4)) + \ frac{ 1 }{ 4 }((0)(-2) – (8)(4)) = 24 $
$ -2( 96 + 2z ) +1( – 4z ) + \frac{ 1 }{ 4 }( – 32 ) = 24 $
$ -192 – 4z – 4z – 8 = 24 $
$ -8z = 224 $
$ z = \frac{ 224 }{ – 8 } $
$ z = – 28 $
Значение z равно $ – 28 $.
- Используя формулу для определителя матрицы $3\times 3$, мы можем записать выражения для определителя Матрицы $A$ и Матрицы $B$.
Определитель матрицы $ A $:
$ | А | = \begin{vmatrix} 0 & 1 & x \\ 4 & -2 & 6 \\ 10 & -1 & -4 \end {vmatrix} $
$ | А | = 0((-2)(-4) – (6)(-1)) – 1((4)(-4) – (6)(10)) +x((4)(-1) – ( -2)(10)) $
$ | А | = 0 -1(– 76) + x(16)$
$ | А | = 76 + 16 x $Определитель матрицы $ B $:
$ | Б | = \begin{vmatrix} 1 & x & -1 \\ 6 & 0 & -2 \\ 8 & 20 & -2 \end {vmatrix} $
$ | Б | = 1((0)(-2) – (-2)(20)) – х((6)(-2) – (-2)(8)) -1((6)(20) – (0 )(8)) $
$ | Б | = 1(40) -x(4) -1(120) $
$ | Б | = 40 – 4х – 120$
$ | Б | = -80 – 4x $Поскольку оба определителя равны, мы приравниваем оба выражения и находим $ x $. Алгебраический процесс показан ниже:
$ | А | = | Б | $
$ 76 + 16 x = -80 – 4x $
$ 16x + 4x = – 80 – 76 $
$ 20x = -156 $
$ x = \frac{-156 }{ 20 } $
$ x = – 7\frac{ 4 }{ 5 } $
Значение $ x $ равно $ – 7\frac{ 4 }{ 5 } $.
Как найти определитель матрицы 3×3 (практические задачи)
Здесь мы объясним, как найти определитель матрицы 3×3, используя метод разложения на кофактор или сокращенный метод. Также вы увидите примеры вычислений определителей 3×3 и, наконец, найдете решенные упражнения, чтобы вы могли потренироваться и в совершенстве понять, как вычислять определитель матрицы 3×3.
Содержание
Что такое определитель матрицы 3×3?
Определитель матрицы 3×3 — это матрица третьего порядка, представленная вертикальной чертой на каждой стороне матрицы. Например, если у нас есть следующая матрица:
Определитель квадратной матрицы A представляется следующим образом:
Как вы видели, записать определители матриц 3×3 просто. Теперь давайте посмотрим, как их решить:
Определитель матрицы 3×3: разложение на кофактор
Чтобы найти определитель матрицы размерности 3×3:
- Умножьте элемент a на определитель матрицы 2×2, полученный удалением строки и столбца, в которых находится a.
- Повторите процедуру для элементов b и c.
- Сложите произведение элементов a и c и вычтите произведение элемента b.
Таким образом, вычисление определителя матрицы 3×3 разбивается на определители 2×2. Итак, формула для вычисления определителя матрицы 3×3 выглядит следующим образом:
Этот метод вычисления определителя матрицы 3×3 называется методом разложения кофакторов.
Помните, что для нахождения определителя матрицы 2×2 нужно перемножить элементы на главной диагонали и вычесть произведение элементов на побочной диагонали.
Пример определителя матрицы 3×3
После того, как мы увидели формулу для нахождения определителя матрицы 3×3, давайте посмотрим пример того, как выполнять вычисления:
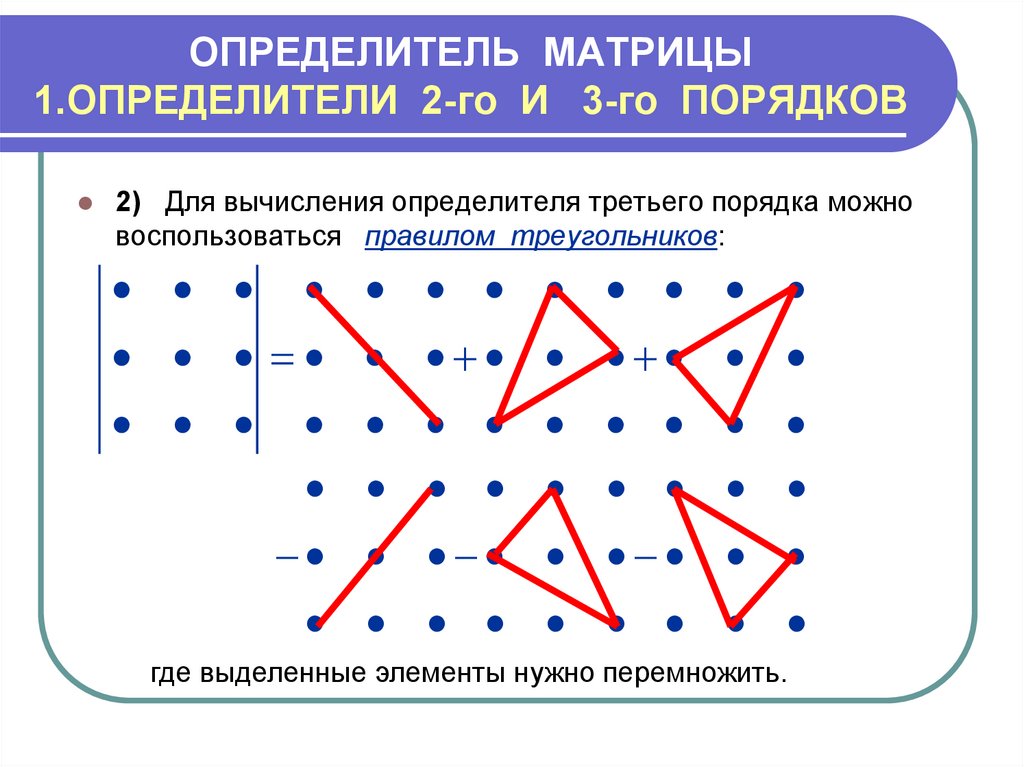
Определитель матрицы 3×3: сокращенный метод
Существует еще один метод вычисления определителя матрицы 3×3, называемый сокращенным методом, правила которого таковы:
- Дублирование первых двух столбцов матрицы справа от его третьего столбца.
- Сложите произведения главных диагоналей, идущих сверху вниз.
- Вычтите произведения главных диагоналей, идущих снизу вверх.
Этот метод представляет собой простой способ найти определитель матрицы 3×3, используя ее диагонали. Более того, этот метод также известен как Правило Сарруса или Схема Сарруса.
Вы можете увидеть, как применять сокращенный метод, в следующем примере:
Сначала мы перепишем первые два столбца справа от матрицы 3×3:
И затем мы сложим произведения основного диагоналей, идущих сверху вниз, и вычесть произведения главных диагоналей, идущих снизу вверх:
Практические задачи на нахождение определителя матрицы 3×3
Задача 1
Найдите определитель следующих 3× 3 матрицы:
См. решение
Определитель матрицы 3×3 можно найти по формуле:
Этот определитель 3×3 было легко вычислить, поскольку в первой строке матрицы находится ноль.
.
Определитель также можно вычислить с помощью сокращенного метода. Дублируем первые два столбца матрицы справа:
Затем применяем правило Сарруса:
Задача 2
Вычислить определитель следующей матрицы порядка 3:
См. решение
Чтобы найти определитель 3×3, мы можем использовать общий метод:
определитель можно найти и сокращенным методом. Сначала перепишем первые два столбца матрицы справа:
А затем применим формулу Сарруса:
Задача 3
Вычислить определитель следующей квадратной матрицы 3×3:
См. решение
Для вычисления определителя 3×3 можно применить стандартную формулу:
Определитель ×3 методом диагоналей. Для этого продублируем первые два столбца матрицы справа:
И, наконец, воспользуемся схемой Сарруса для решения определителя 3 на 3:
Задача 4
Найдите значение x в следующей матрице 3×3, при котором ее определитель равен 0:
См.