Тела вращения 9 класс онлайн-подготовка на Ростелеком Лицей
Тела вращения
Одним из первых величайших изобретений человечества был гончарный круг. С его помощью стало возможным в большом количестве создавать посуду и другие изделия из керамики.
Поскольку гончарный круг во время работы вращается, то в результате его работы получаются изделия особой формы – они симметричны относительно вертикальной оси (см. рис. 1).
Рис. 1. Гончарные изделия симметричны относительно вертикальной оси
Такие тела, что вполне логично, называют телами вращения, ведь их можно получить, вращая плоскую фигуру вокруг некоторой оси.
Известный нам цилиндр можно получить, вращая вокруг вертикальной оси прямоугольник (см. рис. 2).
Рис. 2. Цилиндр получается вращением вокруг вертикальной оси прямоугольника
Конус можно получить, вращая вокруг вертикальной оси равнобедренный (или прямоугольный) треугольник (см. рис. 3).
Рис.
3. Конус получается вращением вокруг вертикальной оси равнобедренного или прямоугольного треугольника
Шар можно получить, вращая вокруг вертикальной оси круг (см. рис. 4).
Рис. 4. Шар получается вращением вокруг вертикальной оси круга
Отличие тел вращения от многогранников
Поскольку объекты, имеющие форму тел вращения, встречаются довольно часто (в строительстве, архитектуре и вообще в быту), мы будем подробно изучать свойства этих тел. В частности, научимся вычислять характеристики их элементов, площадь поверхности и объем таких тел.
Главным отличием тел вращения от многогранников является отсутствие вершин, ребер или граней, т. е. поверхность тел вращения не образована пересечением нескольких плоскостей (см. рис. 5). Именно это различие означает «гладкую» форму тел вращения и «угловатую» форму многогранников. Это, конечно, не строгие математические термины, но они помогают нам легко, «на глаз», различать такие тела.
Рис. 5. Тела вращения отличаются от многогранников отсутствием вершин, ребер или граней
При этом многогранники нам помогут получить и доказать различные свойства тел вращения. Вспомните, что мы приближали окружность правильными многоугольниками (см. рис. 6).
Рис. 6. Приближение окружности правильными многоугольниками
Точно так же можно поступить и с телами вращения – например, призма, в основании которой лежит правильный многоугольник с большим количеством вершин, будет очень похожа на цилиндр, пирамида – на конус (см. рис. 7).
Рис. 7. Приближение призмы (основание – правильный многоугольник) и пирамиды
С шаром чуть сложнее, но его тоже можно приближать различными многогранниками (см. рис. 8).
Рис. 8. Приближение шара
Так, футбольный мяч обычно представляет собой многогранник, гранями которого являются пяти- и шестиугольники (см. рис. 9). И этот многогранник настолько хорошо приближает сферу, что позволяет футболистам играть футбол и даже использовать поговорку: «Мяч круглый».
Рис. 9. Футбольный мяч представляет собой многогранник, гранями которого являются пяти- и шестиугольники
Правильные многогранники
Может возникнуть вопрос – почему с шаром не сделать так же, как с кругом. Почему не взять правильный многогранник и не увеличивать в нем количество граней до тех пор, пока не получится тело, очень похожее на шар?
Оказывается, проблема в том, что правильных многогранников не так много. Если существуют правильные многоугольники с любым количеством вершин, то правильных многогранников существует всего видов. Посмотрим, почему так получается.
Пусть правильный многогранник имеет граней, каждая из которых представляет собой правильный n-угольник. И пусть в каждой вершине сходится ребер, а в многограннике всего вершин и ребер.
Мы можем сказать, что , (в каждой вершине сходится не меньше ребер).
Т. к. каждая грань содержит ребер, то:
( появляется, т. к. каждое ребро принадлежит двум граням (см.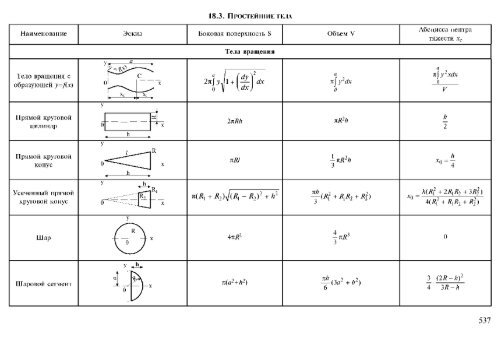
рис. 10), и мы его посчитали раза).
Рис. 10. Каждое ребро принадлежит двум граням
Аналогично, т. к. в каждой вершине сходится ребер, то:
( появляется, т. к. каждое ребро соединяет вершины (см. рис. 11) и мы опять его посчитали раза).
Рис. 11. Каждое ребро соединяет вершины
Вспомним теорему Эйлера для многогранников:
Подставим полученные равенства:
Т. к. правая часть должна быть положительной, то левая часть тоже положительная:
Или:
Если , то:
Значит, либо , либо должно быть равно или .
Пусть , тогда:
Откуда:
Возможные варианты:
1. Если :
Откуда:
Это тетраэдр (см. рис. 12).
Рис. 12. Тетраэдр
2. Если , :
Откуда:
Это октаэдр (см. рис. 13).
Рис. 13. Октаэдр
3. Пусть , :
Откуда:
Это икосаэдр (см.
рис. 14).
Рис. 14. Икосаэдр
4. Пусть :
Откуда:
Т. е. единственный возможный вариант: :
Откуда:
Это куб (см. рис. 15).
Рис. 15. Куб
Осталось рассмотреть два случая: . Поскольку в неравенстве и симметричны, то все случаи будут рассматриваться аналогично. Случаи и мы уже рассмотрели.
5. Единственный новый случай: :
Откуда:
Это додекаэдр (см. рис. 16).
Рис. 16. Додекаэдр
Мы рассмотрели все возможные варианты, других правильных многогранников нет (см. рис. 17).
Рис. 17. Правильные многогранники
Поэтому провести аналогию с приближением окружности правильными многоугольниками для правильных многогранников не получится. Это не значит, что шар нельзя приблизить многогранниками – можно, мы уже приводили пример футбольного мяча. Но эти многогранники не будут правильными.
Цилиндр
Возьмем прямоугольник и будем его вращать вокруг стороны (см.
рис. 18).
Рис. 18. Получение цилиндра вращением прямоугольника вокруг стороны
Сверху и снизу у нас получатся два круга. Их мы будем называть верхним и нижним основаниями цилиндра (см. рис. 19).
Рис. 19. Верхнее и нижнее основания цилиндра
Радиусы этих кругов одинаковы и равны длинам отрезков и . Эти радиусы оснований также будем называть и радиусом самого цилиндра (см. рис. 20).
Рис. 20. Радиус цилиндра
Кроме основания, у нас получилась поверхность, созданная вращением отрезка . Она называется боковой поверхностью цилиндра или просто цилиндрической поверхностью (см. рис. 21).
Рис. 21. Боковая поверхность цилиндра (цилиндрическая поверхность)
Боковая поверхность состоит из вертикальных отрезков, параллельных друг другу. Они называются образующими цилиндра (см. рис. 22). Любая образующая является высотой цилиндра.
Рис. 22. Образующая цилиндра
Какие бывают цилиндры
На самом деле, мы дали определение не произвольного цилиндра, а одного из видов – прямого кругового (см.
рис. 23). Название вполне объяснимое: «прямой», так как образующие перпендикулярны основаниям, «круговой», так как в основании лежат круги.
Рис. 23. Прямой круговой цилиндр
Более общее определение цилиндра такое. Если взять две одинаковые кривые и разместить их в параллельных плоскостях, то вместе с семейством параллельных образующих, которые соединяют точки этих кривых, они образуют цилиндр (см. рис. 24). Само семейство параллельных образующих называется цилиндрической поверхностью (см. рис. 25).
Рис. 24. Образование цилиндра
Рис. 25. Цилиндрическая поверхность
Понятно, что цилиндр может быть прямым (см. рис. 26) или наклонным (см. рис. 27) (в зависимости от угла наклона образующих к плоскости основания).
Рис. 26. Прямой цилиндр
Рис. 27. Наклонный цилиндр
Также вид цилиндра может определяться кривой, которая лежит в основаниях. Например, эллиптический (см. рис. 28). При таком определении призма тоже будет частным случаем цилиндра (см.
рис. 29).
Рис. 28. Эллиптический цилиндр
Рис. 29. Призма как частный случай цилиндра
Но все же в подавляющем большинстве случаев под цилиндром мы будем подразумевать именно прямой круговой цилиндр.
Формулы цилиндра
Как мы уже говорили, цилиндр можно приближать правильной призмой, увеличивая количество вершин в основании последней.
Вспомним, что объем любой призмы равен произведению площади основания на высоту.
Тогда объем цилиндра как предельного случая призмы тоже можно вычислить по этой формуле:
Т. к. основание цилиндра – круг, то площадь основания находится по формуле площади круга:
А объем цилиндра тогда вычисляется по формуле:
Площадь боковой поверхности цилиндра тоже легко находится. Развернем боковую поверхность – получим прямоугольник (см. рис. 30).
Рис. 30. Развертка цилиндрической поверхности
Высота этого прямоугольника равна высоте цилиндра, а длина равна длине окружности основания.
Таким образом, площадь боковой поверхности вычисляется по формуле:
Конус
Можно провести аналогию с приближением цилиндра призмой для конуса: приближать его правильной пирамидой.Но конус также является фигурой вращения.Чтобы его получить, рассмотрим прямоугольный треугольник и начнем его вращать вокруг катета (см. рис. 31).
Рис. 31. Получение конуса вращением прямоугольного треугольника вокруг катета
Катет опишет круг – основание конуса – и будет, соответственно, радиусом конуса (рис. 32).
Рис. 32. Катет является радиусом конуса
А при вращении гипотенузы образуется боковая поверхность конуса, другое название – коническая поверхность (см. рис. 33). Отрезки, из которых состоит коническая поверхность, как и в случае цилиндра, называются образующими.
Рис. 33. Боковая поверхность конуса (коническая поверхность)
Вершина – это вершина конуса, – ось конуса, которая является и высотой (см.
рис. 34).
Рис. 34. Вершина и ось (высота) конуса
Какие бывают конусы
И снова, как и в ситуации с цилиндром, мы дали определение одному из видов конуса – прямому круговому конусу (см. рис. 35).
Рис. 35. Прямой круговой конус
Более общее определение такое. Рассмотрим точку в пространстве и кривую. Соединим выбранную точку со всеми точками этой кривой (см. рис. 36). Семейство этих образующих – коническая поверхность (см. рис. 37). Вместе с частью плоскости, которую ограничивает кривая, коническая поверхность образует конус (см. рис. 38).
Рис. 36. Образование конуса
Рис. 37. Коническая поверхность
Рис. 38. Коническая поверхность образует конус вместе с частью плоскости, которую ограничивает кривая
Понятно, что конус может быть прямым (см. рис. 39) (если у основания есть центр симметрии и вершина конуса проецируется в этот центр симметрии), а может быть наклонным (см. рис. 40).
Рис.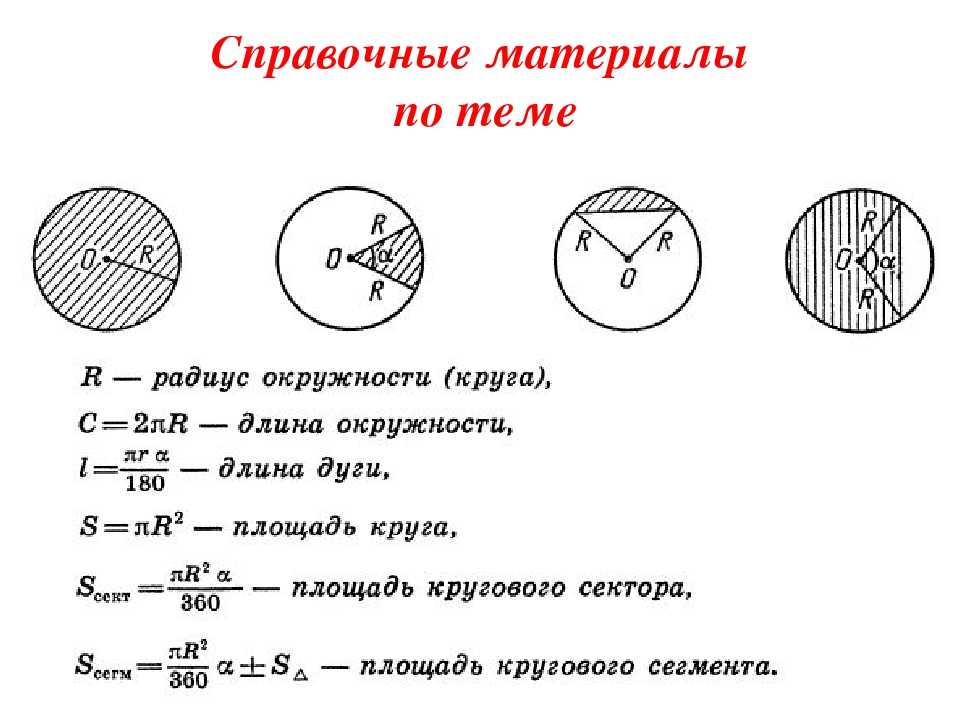
39. Прямой конус
Рис. 40. Наклонный конус
Также ясно, что, в зависимости от кривой в основании, конус может быть круговым, эллиптическим (см. рис. 41) и т. д. Более того, при таком определении даже пирамида является частным случаем конуса (см. рис. 42).
Рис. 41. Эллиптический конус
Рис. 42. Пирамида как частный случай конуса
Но в подавляющем большинстве задач мы будем встречаться именно с прямым круговым конусом.
Формулы конуса
Объем любой пирамиды вычисляется по формуле:
Эту же формулу можно использовать для вычисления объема конуса как предельного случая правильной пирамиды.
Поскольку площадь основания – это площадь круга, то объем конуса вычисляется по формуле:
Развертка конической поверхности представляет собой не прямоугольник, как у цилиндра, а круговой сектор (см. рис. 43).
Рис. 43. Развертка конической поверхности
Вспомним, как вычисляется площадь сектора.
Пусть есть сектор радиуса длиной дуги (см. рис. 44).
Рис. 44. Сектор радиуса длиной дуги
Длина всей окружности равна:
Площадь сектора во столько раз меньше площади целого круга, во сколько длина дуги меньше длины всей окружности:
Рассмотрим конус с образующей и радиусом основания (см. рис. 45).
Рис. 45. Конус с образующей и радиусом основания
Теперь для вычисления боковой поверхности конуса разрежем ее по одной из образующих и развернем. Получим круговой сектор (см. рис. 46).
Рис. 46. Развертка конуса с образующей и радиусом основания
Радиусом сектора является образующая конуса , а длина дуги равна длине окружности основания конуса:
Найдем площадь сектора:
Это и есть формула боковой поверхности конуса:
Посмотрим на еще один предельный случай. Понятно, что у конуса образующая всегда больше радиуса основания . Если ее уменьшать и таким образом приближать к , то высота конуса будет стремиться к нулю.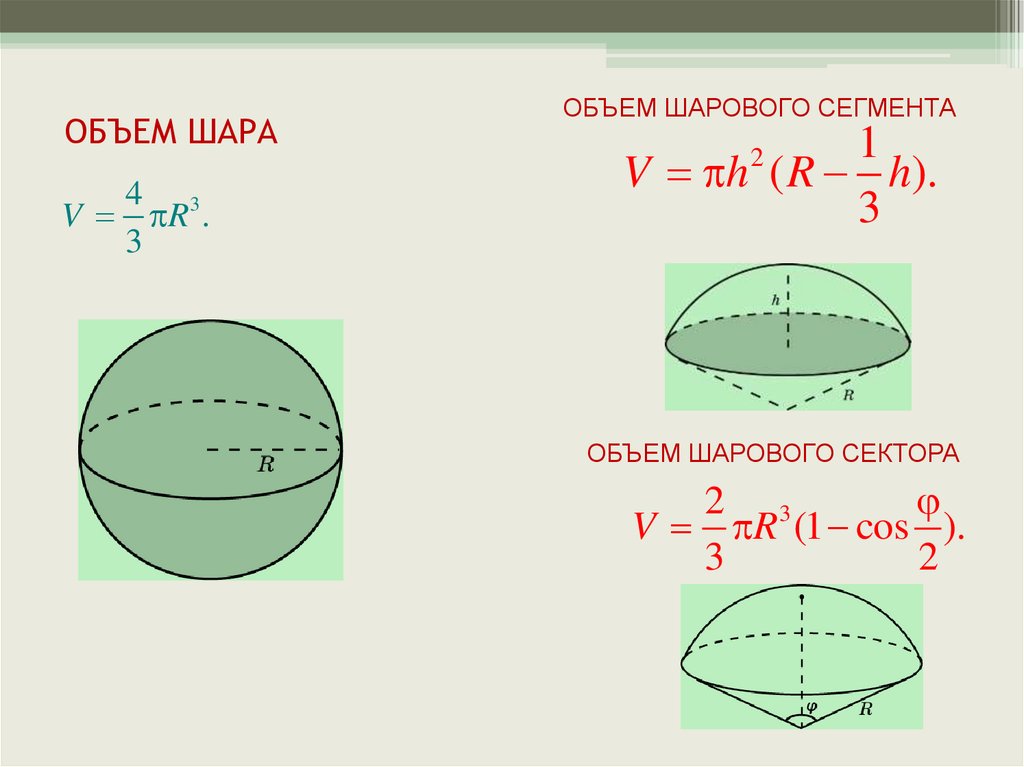
Тогда сама коническая поверхность будет стремиться к кругу, лежащему в основании (см. рис. 47).
Рис. 47. Приближение образующей конуса к радиусу основания
Тогда неудивительно, что формула боковой поверхности конуса при стремлении к превращается в формулу площади круга, лежащего в основании конуса:
Шар
Переходим к рассмотрению третьего тела вращения – шара (см. рис. 48). Шар во многом является трехмерным аналогом круга. Они имеют идентичные определения, которые мы рассмотрим чуть позже.
Рис. 48. Шар
Кроме этого, границы шара и круга имеют отдельные названия. Это достаточно необычно для фигур. Например, граница квадрата так и будет называться – граница или периметр квадрата. Граница же круга называются окружностью, а граница шара называется сферой (см. рис. 49).
Рис. 49. Сфера и окружность
Можно представлять дело ровно наоборот: не окружность – это граница круга, а круг – это часть плоскости, ограниченная окружностью.
Точно так же не сфера – граница шара, а шар – часть пространства, ограниченная сферой.
На самом деле для всех четырех фигур (см. рис. 50) существуют свои строгие независимые определения:
- Окружность – множество точек плоскости, удаленных от данной точки на данное расстояние.
- Круг – множество точек плоскости, удаленных от данной точки не более чем на данное расстояние.
- Сфера – множество точек пространства, удаленных от данной точки на данное расстояние.
- Шар – множество точек пространства, удаленных от данной точки не более чем на данное расстояние.
Рис. 50. Слева направо: окружность, круг, сфера, шар
Почему шар называется фигурой вращения, тоже понятно. Его можно получить вращением круга (или даже достаточно полукруга) вокруг своего диаметра (см. рис. 51).
Рис. 51. Получение шара вращение круга вокруг своего диаметра
Расстояние от любой точки сферы до центра называется радиусом сферы и шара (см.
рис. 52).
Рис. 52. Радиус сферы и шара
Отрезок, соединяющий две точки сферы и проходящий через центр, называется диаметром. Понятно, что, как и в случае круга, диаметр равен двум радиусам.
Объем шара
Вопрос объема и площади поверхности шара (т. е. площади сферы) решается немного сложнее, чем для цилиндра и конуса. Начнем с объема.
Попробуем найти объем шара радиуса . Для удобства оставим только половину шара (см. рис. 53), и если нам удастся найти ее объем, то умножим потом результат на два.
Рис. 53. Половина шара радиуса
Положим полушар на плоскость и рядом поставим цилиндр, высота и радиус которого равны , т. е. высоты у обоих тел одинаковые (см. рис. 54).
Рис. 54. Полушар и цилиндр с равными высотами и радиусами на плоскости
Помните, что более простая фигура ставится рядом с более сложной, чтобы применить принцип Кавальери для сравнения их объемов (Многогранники. Виды многогранников.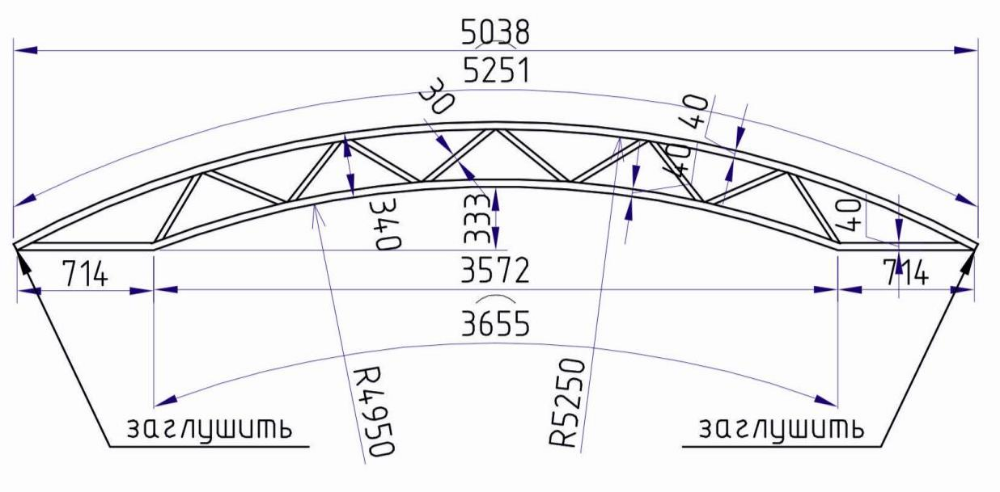
Объём).
Основания у обоих тел – это равные круги радиуса . Но если мы пересечем фигуры плоскостью (см. рис. 55), то равенство площадей пропадает.
Рис. 55. Пересечение полушара и цилиндра плоскостью
Явно сечение у цилиндра больше, чему у половины шара. Найдем площадь сечения половины шара. Пусть расстояние между плоскостями равно (см. рис. 56).
Рис. 56. Расстояние между плоскостями равно
Тогда радиус сечения мы найдем по теореме Пифагора:
Тогда площадь сечения (см. рис. 57):
Рис. 57. Площадь сечения
При этом площадь сечения цилиндра равна:
Значит, чтобы площадь сечения цилиндра стала равна площади сечения половины шара, нужно вычесть из него величину , т. е. круг радиуса .
Внутри круга радиуса построим круг радиуса . Площадь полученного кольца (см. рис. 58):
Т. е. равна площади сечения половины шара.
Рис. 58. Кольцо
Осталось подобрать тело, у которого будут такие сечения.
Нетрудно догадаться, что таким телом будет цилиндр, из которого вырезали перевернутый конус, основание которого совпадает с верхним основанием цилиндра (см. рис. 59).
Рис. 59. Цилиндр, из которого вырезали перевернутый конус, основание которого совпадает с верхним основанием цилиндра
Посмотрим на ситуацию еще раз. Два тела стоят на плоскости . Первое – половина шара радиуса . Второе – цилиндр радиуса и высоты , в котором вырезана полость в виде перевернутого конуса. Радиус основания и высота конуса тоже равны .
Если провести плоскость параллельно плоскости на расстоянии , то мы получим два сечения – круг и кольцо, площади которых одинаковы и равны:
Но тогда, по принципу Кавальери, эти тела имеют равные объемы. Объем сконструированного нами тела равен разности объемов цилиндра и конуса:
Мы нашли объем половины шара. Осталось его умножить на два и получить объем шара:
Площадь поверхности шара
Попробуем теперь определить площадь поверхности шара (площадь сферы).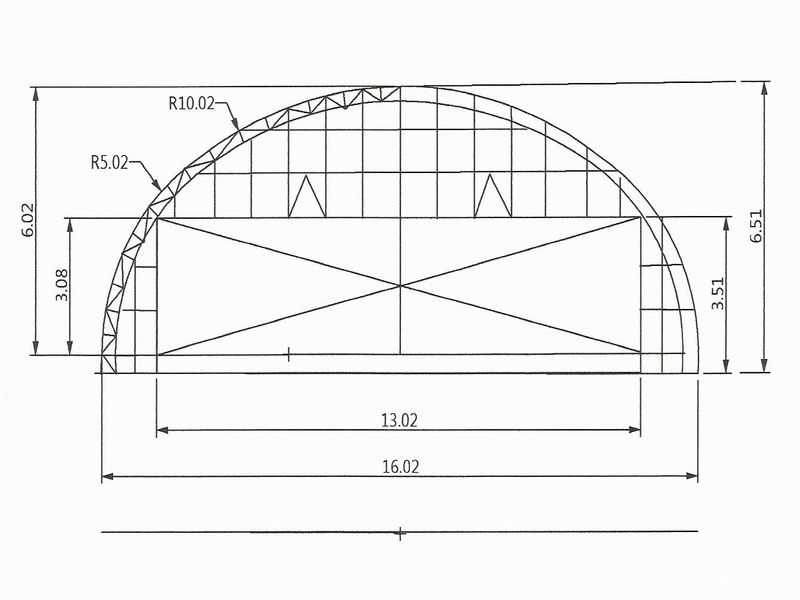
Основная идея будет следующей. Если есть тонкая пленка, то объем такой пленки равен произведению ее площади на толщину:
Если так окажется, что мы знаем объем и толщину пленки, то можем найти ее площадь:
Рассмотрим теперь шар радиуса . Покрасим его слоем краски толщиной (см. рис. 60). Радиус окрашенного шара равен .
Рис. 60. Шар радиуса покрашен слоем краски толщиной
Объем слоя краски можно вычислить как разность объемов окрашенного и неокрашенного шаров:
Найдем площадь слоя краски – разделим объем на :
Если мы говорим о площади поверхности шара радиуса, то это соответствует нашей задаче с краской, толщина слоя которой . Тогда формула приобретает вид:
Это и есть формула площади поверхности шара (площади сферы):
Заключение
1. Цилиндр очень похож на призму и имеет такую же формулу для вычисления объема:
Развертка цилиндрической поверхности – это прямоугольник, ее площадь рассчитывается по формуле:
2.
Конус очень похож на пирамиду и имеет такую же формулу для вычисления объема:
Развертка конической поверхности – это сектор, ее площадь рассчитывается по формуле:
где – образующая конуса.
3. Объем шара рассчитывается по формуле:
Площадь его поверхности, т. е. сферы, рассчитывается по формуле:
Список литературы
- Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 9 класс. Учебник. – М.: «Просвещение», 2017.
- Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия, 9 класс. Учебник. – М.: «Просвещение», 2018.
- Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия, 9 класс. Учебник. – М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал yaklass.ru (Источник)
- Интернет-портал yoclever.org (Источник)
- Интернет-портал math5school.
ru (Источник)
ru (Источник)
Домашнее задание
- Найти объем цилиндра, радиус которого равен , а высота равна радиусу.
- Найти объем конуса, радиус основания которого равен , а высота вдвое больше радиуса основания.
- Объемы двух шаров относятся как . Найти отношение площадей их поверхностей.
Добавление круговой диаграммы — Служба поддержки Майкрософт
Excel
Импорт и анализ данных
Диаграммы
Диаграммы
Добавление круговой диаграммы
Excel для Microsoft 365 Word для Microsoft 365 PowerPoint для Microsoft 365 Excel 2021 Word 2021 PowerPoint 2021 Excel 2019 Word 2019 PowerPoint 2019 Excel 2016 Word 2016 PowerPoint 2016 Excel 2013 Word 2013 PowerPoint 2013 Excel 2010 Word 2010 PowerPoint 2010 Excel 2007 Word 2007 PowerPoint 2007 Еще.
..Меньше
Круговые диаграммы — распространенный способ показать, какую часть от общего количества (например, годового объема продаж) составляют отдельные значения (например, квартальный объем продаж).
Выберите приложение, с которым работаете
(Либо сразу перейдите к сведениям о круговых диаграммах, пропустив описание приложений).
-
Excel
-
PowerPoint
-
Word
-
Данные для круговых диаграмм
-
Другие типы круговых диаграмм
Примечание: Снимки экрана в этой статье относятся к Office 2016.
Если вы используете более раннюю версию Office, интерфейс может немного отличаться, но действия будут теми же.
Excel
-
На листе выделите данные, которые будут использоваться для круговой диаграммы.
Дополнительные сведения об упорядочении данных для круговой диаграммы см. в разделе Данные для круговых диаграмм.
-
На вкладке Вставка нажмите кнопку Вставить круговую или кольцевую диаграмму, а затем выберите нужную диаграмму.
-
Чтобы показать, скрыть или отформатировать такие элементы, как названия осей или подписи данных,щелкните элементов диаграммы .
-
Чтобы быстро изменить цвет или стильдиаграммы, используйте стили .
-
Чтобы отфильтровать или скрыть данные на диаграмме, щелкните «Фильтры диаграммы» .
org/ListItem»>
Щелкните диаграмму, а затем добавьте последние штрихи с помощью значков рядом с диаграммой.
Совет: Вы можете привлечь внимание к отдельным сегментам круговой диаграммы, выдвинув их.
PowerPoint
-
Выберите команду Вставка > Диаграмма > Круговая и выберите нужный тип круговой диаграммы.
Примечание: На маленьком экране кнопка Диаграмма может быть уменьшена:
-
В появившейся электронной таблице замените заполнители собственными данными.
Дополнительные сведения об упорядочении данных для круговой диаграммы см. в разделе Данные для круговых диаграмм.
-
Щелкните диаграмму, а затем добавьте последние штрихи с помощью значков рядом с диаграммой.
-
Чтобы показать, скрыть или отформатировать такие элементы, как названия осей или подписи данных,щелкните
-
Чтобы быстро изменить цвет или стильдиаграммы, используйте стили .
-
Чтобы отфильтровать или скрыть данные на диаграмме, щелкните «Фильтры диаграммы» .
-
org/ListItem»>
По завершении закройте редактор электронных таблиц.
Совет: Вы можете привлечь внимание к отдельным сегментам круговой диаграммы, выдвинув их.
Word
-
На вкладке Вставка нажмите кнопку Диаграмма.
Примечание: На маленьком экране кнопка Диаграмма может быть уменьшена:
-
Нажмите кнопку Круговая и дважды щелкните нужный тип диаграммы.
-
В появившейся электронной таблице замените заполнители собственными данными.
Дополнительные сведения об упорядочении данных для круговой диаграммы см. в разделе Данные для круговых диаграмм.
-
По завершении закройте редактор электронных таблиц.
-
Щелкните диаграмму, а затем добавьте последние штрихи с помощью значков рядом с диаграммой.
-
Чтобы показать, скрыть или отформатировать такие элементы, как названия осей или подписи данных,щелкните элементов диаграммы .
org/ListItem»>
Чтобы быстро изменить цвет или стильдиаграммы, используйте стили .
-
-
Чтобы отфильтровать или скрыть данные на диаграмме, щелкните «Фильтры диаграммы» .
-
Чтобы расположить диаграмму и текст в документе, нажмите кнопку «Параметры разметки» .
Совет: Вы можете привлечь внимание к отдельным сегментам круговой диаграммы, выдвинув их.
Данные для круговых диаграмм
Столбец или строку электронной таблицы можно преобразовать в круговую диаграмму. Каждый сегмент диаграммы (точка данных) показывает размер или процентное отношение этого сегмента ко всей диаграмме.
Круговые диаграммы лучше всего использовать, когда:
-
нужно отобразить только один ряд данных;
-
ряд данных не содержит нулевых и отрицательных значений;
-
ряд данных содержит не более семи категорий — диаграмма из более чем семи сегментов может быть сложной для восприятия.
Совет: Если круговая диаграмма не подходит для ваших данных, попробуйте использовать линейчатую диаграмму, гистограмму или график.
Другие типы круговых диаграмм
Помимо трехмерных круговых диаграмм, вы можете создать круг и линию круговой диаграммы.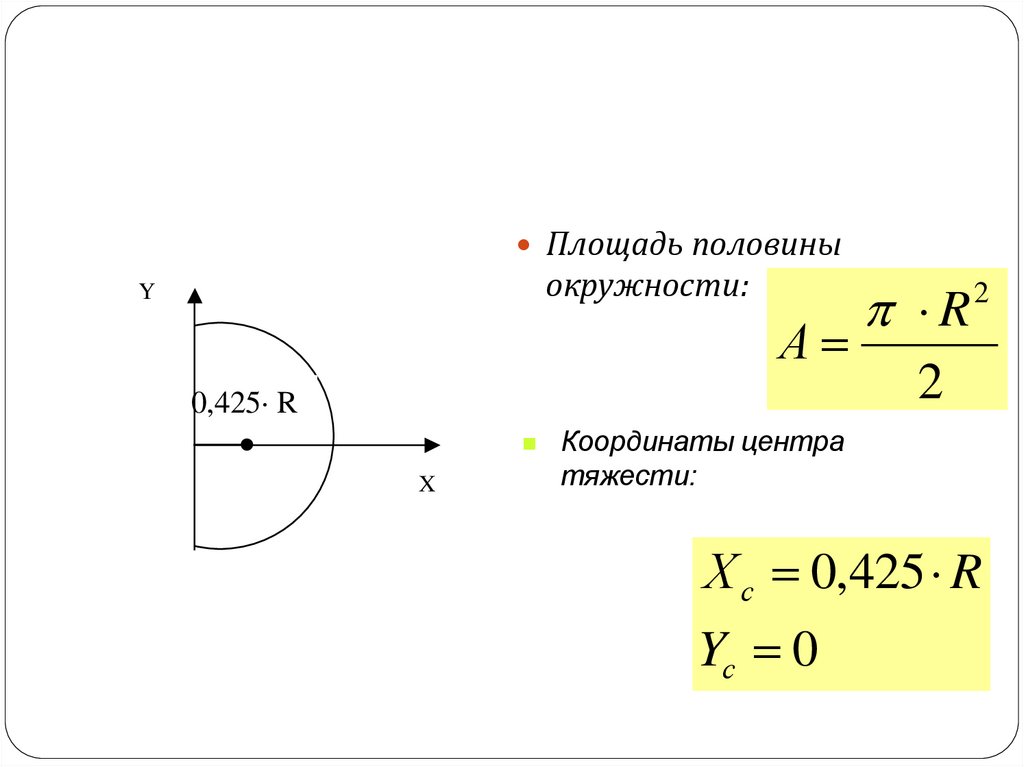
Эти диаграммы отображают меньшие значения во вторичной круговой или линейчатой диаграмме с накоплением, что упрощает их чтение. Чтобы преобразовать диаграмму в один из этих типов, щелкните ее, а затем на вкладке Работа с диаграммами | Конструктор выберите команду Изменить тип диаграммы. Когда откроется коллекция Изменение типа диаграммы, выберите нужный тип.
См. также
Выбор данных для диаграмм в Excel
Создание диаграммы в Excel
Добавление диаграммы в документ Word
Добавление диаграммы в презентацию PowerPoint
Типы диаграмм в Office
Поиск сечений: треугольники и полуокружности
Все ресурсы по исчислению AB
45 практических тестов Вопрос дня Карточки Learn by Concept
Calculus AB Справка » Поиск объема с помощью интеграции » Найдите сечения: треугольники и полуокружности
Найдите объем твердого тела, поперечное сечение которого представляет собой равносторонний треугольник, а основание представляет собой диск радиуса .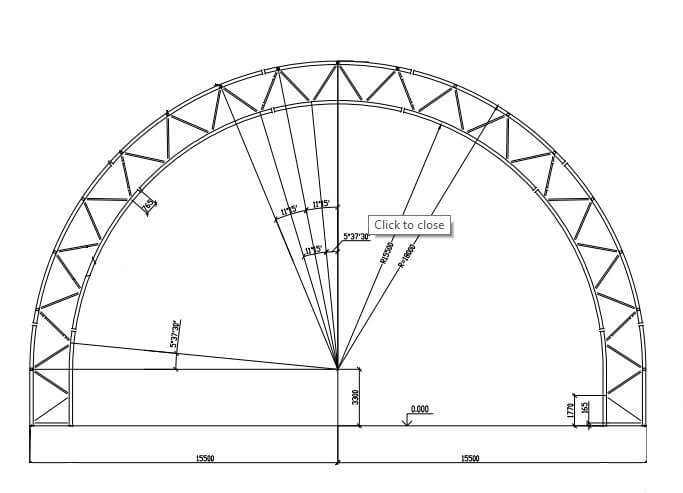
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку диск имеет радиус R, основание определяется по следующей формуле: .
Правильная формула площади равностороннего треугольника выглядит следующим образом:
, где — длина стороны треугольника.
Применяя эту формулу к нашей общей формуле объема , мы получаем следующее: .
Радиус R определяет границы как . Затем можно найти s, поняв, что значение — это расстояние от вершины до низа круга в любой заданной точке вдоль . Следовательно, длина одной стороны равностороннего треугольника равна .
Собрав все вместе, получается следующее:
*Примечание: в задаче не указано, перпендикулярны ли поперечные сечения оси или оси. Поскольку основание представляет собой круг, это не должно изменить результирующий объем.
Единственная разница должна заключаться в использовании или в качестве переменных в правильном выражении.
Сообщить об ошибке
Найдите объем твердого тела, основание которого ограничено окружностью и чьи поперечные сечения представляют собой прямоугольные равнобедренные треугольники, перпендикулярные оси, с одной стороной на основании твердого тела.
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку основание представляет собой окружность радиусом , границы определяются как .
Площадь прямоугольного равнобедренного треугольника можно найти по формуле , где – длина стороны треугольника. Применяя это к нашей общей формуле объема, мы получаем следующее:
Выражение для может быть найдено, если понять, что катет треугольника находится на основании твердого тела.
Значение в два раза больше высоты полукруга .
Собирая все вместе, получаем следующее:
Сообщить об ошибке
Найдите правильное выражение для объема твердого тела, поперечное сечение которого представляет собой равносторонний треугольник, перпендикулярный оси и основание которого ограничено и .
Возможные ответы:
Правильный ответ:
Объяснение:
Во-первых, поперечное сечение, перпендикулярное оси , означает, что выражение должно быть выражено через .
Площадь равностороннего треугольника равна , где длина стороны треугольника. Применяя эту формулу к нашей общей формуле объема (), мы получаем следующее: .
Точками пересечения функций и являются и . Координаты этих точек будут определять границы интеграла, поскольку наше выражение выражено через .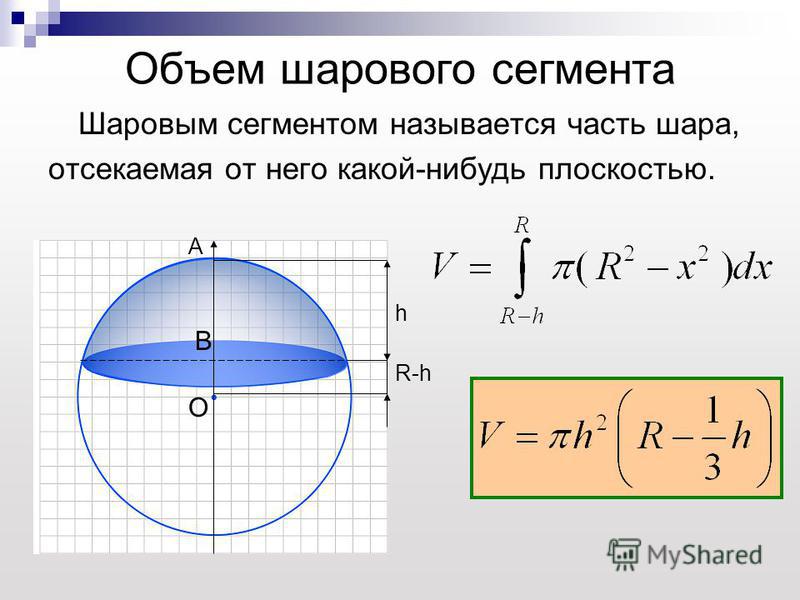
База ограничена и . Переписывая эти функции через , получаются следующие уравнения: и . Так как находится дальше от оси, правильное выражение для длины стороны равно .
Собирая все вместе, получаем следующее:
Сообщить об ошибке
Найдите правильное выражение для объема твердого тела, основание которого ограничено , , и , и чьи поперечные сечения являются прямоугольными равнобедренными треугольниками, перпендикулярно оси, с одной ногой на основании твердого тела.
Возможные ответы:
Правильный ответ:
Объяснение:
Во-первых, поперечное сечение, перпендикулярное оси , означает, что выражение должно быть выражено через . Площадь прямоугольного равнобедренного треугольника можно найти по формуле , где – длина катета треугольника. Применяя это к нашей общей формуле объема, мы получаем следующее:
Точками пересечения функций, определяющих область, являются и .
Координаты этих точек будут определять границы интеграла, поскольку наше выражение выражено через .
База ограничена , и . Поскольку поперечные сечения перпендикулярны оси, катет треугольных поперечных сечений определяется как: .
Собирая все вместе, получаем следующее:
Сообщить об ошибке
Найдите объем твердого тела, поперечное сечение которого равносторонние треугольники, а основание — диск радиуса .
Возможные ответы:
Правильный ответ:
Объяснение:
Так как диск имеет радиус , основание определяется по следующей формуле: .
Правильная формула площади равностороннего треугольника выглядит следующим образом:
, где s — длина стороны треугольника.
Применяя эту формулу к нашей общей формуле объема , мы получаем следующее: .
Радиус определяет границы как . Затем можно найти, поняв, что значение – это расстояние от вершины до низа круга в любой заданной точке вдоль . Следовательно, длина одной стороны равностороннего треугольника равна .
Собрав все вместе, получается следующее:
*Примечание: в задаче не указано, перпендикулярны ли поперечные сечения оси или . Поскольку основание представляет собой круг, это не должно изменить результирующий объем. Единственным отличием должно быть использование или в качестве переменных в правильном выражении.
Сообщить об ошибке
Найдите выражение для объема твердого тела, поперечное сечение которого представляет собой полуокружность, перпендикулярную оси , а основание ограничено и .
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку поперечные сечения перпендикулярны оси , выражение объема будет выражено через .
Площадь полукруга . Применяя эту формулу к нашей общей формуле объема , мы получаем следующее: .
Поскольку область, ограниченная символами и , является основанием твердого тела, точки пересечения этих функций создадут границы для выражения объема. Это точки и . Поскольку выражение выражено в терминах , для границ можно использовать координаты.
Далее необходимо определить выражение для . Поскольку радиус – это половина диаметра полуокружности, а диаметр полукруга – это длина, протянувшаяся между функциями и , выражение для радиуса будет следующим: . Упрощенно это читается.
Сложив все это вместе, мы получим следующее:
Сообщить об ошибке
Найдите объем тела, поперечное сечение которого является полукругом, а основание ограничено кругом .
Возможные ответы:
Правильный ответ:
Объяснение:
База определяется по следующей формуле: .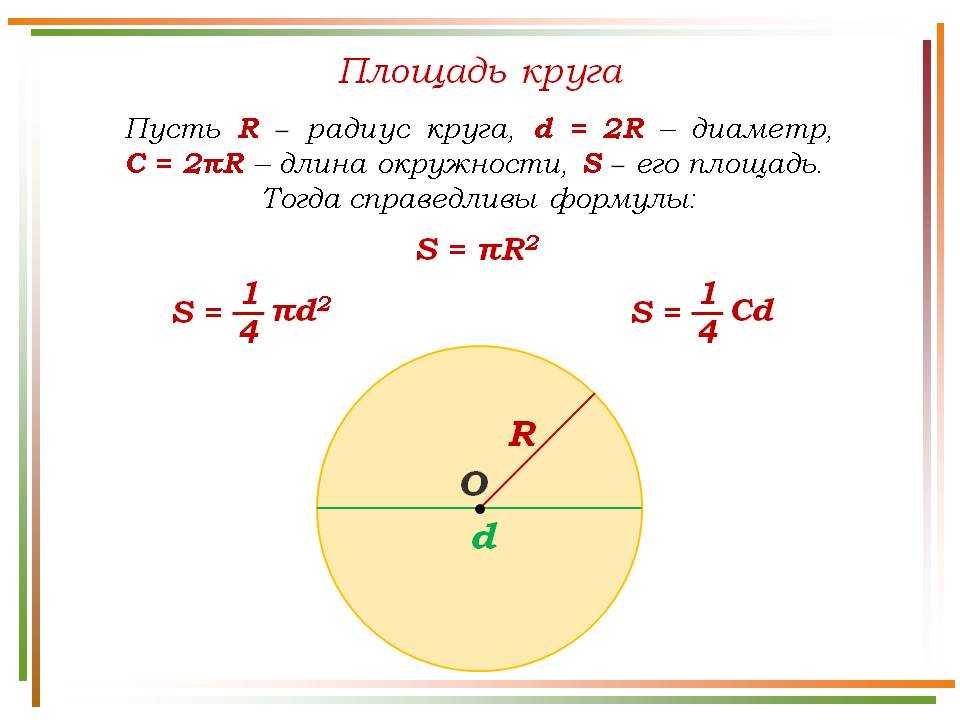
Следовательно, радиус основания равен . Радиус определяет границы как
. Правильная формула для площади полукруга выглядит следующим образом:
, где r — радиус полукруга.
Применяя эту формулу к нашей общей формуле объема , мы получаем следующее: .
Далее необходимо определить выражение для . Радиус равен половине диаметра поперечного сечения полукруга. Значение эквивалентно половине высоты основания или . Следовательно, .
Собрав все вместе, мы находим следующее:
*Примечание: в задаче не указано, перпендикулярны ли поперечные сечения к оси или . Поскольку основание представляет собой круг, это не должно изменить результирующий объем. Единственным отличием должно быть использование или в качестве переменных в правильном выражении.
Сообщить об ошибке
Найдите правильное выражение для объема твердого тела, поперечное сечение которого представляет собой полуокружность, перпендикулярную оси , и чье основание ограничено и .
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку поперечные сечения перпендикулярны оси , выражение объема будет выражено через .
Площадь полукруга . Применяя эту формулу к нашей общей формуле объема , мы получаем следующее: .
Поскольку область, ограниченная символами и , является основанием твердого тела, точки пересечения этих функций создадут границы для выражения объема. Это точки и . Поскольку выражение выражено в терминах , для границ можно использовать координаты.
Далее необходимо определить выражение для . Поскольку радиус – это половина диаметра полуокружности, а диаметр полукруга – это длина, протянувшаяся между функциями и , выражение для радиуса будет следующим: .
Собирая все это вместе, мы находим следующее:
Сообщить об ошибке
Найдите правильное выражение для объема твердого тела, поперечное сечение которого представляет собой полуокружности, перпендикулярные оси , и чье основание ограничено и .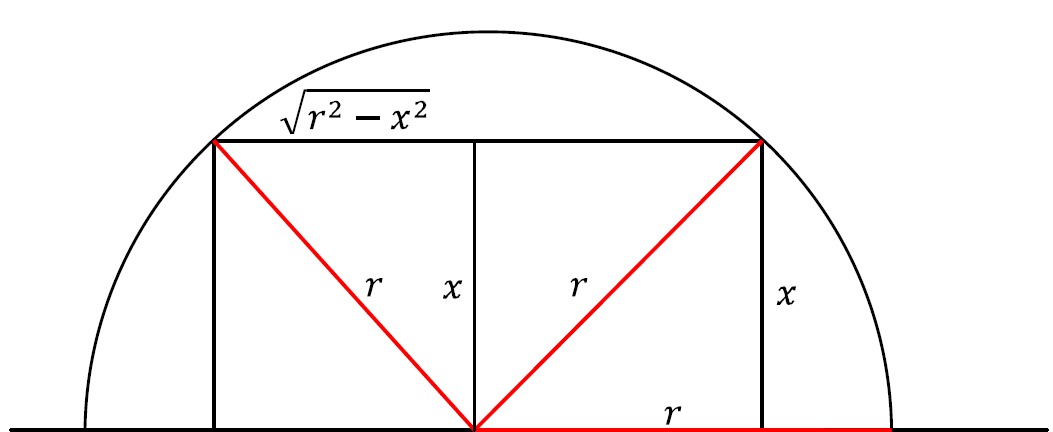
Возможные ответы:
Правильный ответ:
Объяснение:
Поскольку поперечные сечения перпендикулярны оси , выражение объема будет выражено через .
Площадь полукруга . Применяя эту формулу к нашей общей формуле объема , мы получаем следующее: .
Поскольку область, ограниченная и , является основанием твердого тела, точки пересечения этих функций создадут границы для выражения объема. Эти точки и . Поскольку выражение выражено в терминах , для границ можно использовать координаты.
Далее необходимо определить выражение для . Поскольку радиус – это половина диаметра полуокружности, а диаметр полукруга – это длина, протянувшаяся между функциями и , выражение для радиуса будет следующим: . Это можно упростить:
Собрав все это вместе, мы находим следующее:
Сообщить об ошибке
Определите правильное выражение для объема твердого тела, поперечное сечение которого представляет собой полукруги, параллельные оси y, и чье основание ограничено , и .
Возможные ответы:
Правильный ответ:
Объяснение:
Сечения параллельны оси; это еще один способ сказать, что поперечные сечения перпендикулярны оси. Поэтому выражение объема будет через .
Площадь полукруга . Применяя эту формулу к нашей общей формуле объема , мы получаем следующее: .
Поскольку область ограничена , и , основанием является площадь между осью и на интервале . Поскольку выражение выражается в терминах , интервал будет определять границы.
Далее необходимо определить выражение для . Поскольку радиус – это половина диаметра полукруга, а диаметр полукруга – это длина, протянувшаяся между и осью, выражение для радиуса будет следующим: .
Собрав все вместе, мы находим следующее:
Сообщить об ошибке
Уведомление об авторских правах
Все ресурсы Calculus AB
45 Практические тесты Вопрос дня Карточки Learn by Concept
Объем полуцилиндра – формула, примеры, определение
Объем полуцилиндра определяется как количество пространства, занимаемого фигурой в трехмерной плоскости.
Объем полуцилиндра измеряется в кубических единицах, таких как кубические сантиметры (см 3 ), кубические дюймы (в 3 ), кубические футы (футы 3 ), кубические метры (м 3 ) или просто в кубических единицах. Полуцилиндр в математике — это объемная объемная фигура, которая получается при продольном усечении цилиндра. Когда горизонтальный цилиндр разрезается на две равные части, параллельные длине цилиндра, полученные таким образом формы называются полуцилиндрами. Давайте подробно разберем формулу для расчета объема полуцилиндра и частичного цилиндра в следующих разделах.
| 1. | Формула объема полуцилиндра |
| 2. | Как найти объем неполного цилиндра? |
| 3. | Формула площади поверхности полуцилиндра |
| 4. | Часто задаваемые вопросы об объеме полуцилиндра |
Формула объема полуцилиндра
Полуцилиндром в математике называется трехмерная объемная фигура, представляющая собой продольно усеченный цилиндр.
Объем полуцилиндра равен половине всего объема цилиндра. Объем полуцилиндра определяется как объем пространства, занимаемый полуцилиндром. Объем полуцилиндра измеряется в кубических единицах, таких как кубические сантиметры, кубические дюймы, кубические футы, кубические метры и т. д.
Формула для расчета объема полуцилиндра может быть получена как,
Мы знаем, объем цилиндра = площадь основания × высота
⇒ Объем цилиндра = πr 2 × h
где
- r = радиус
- ч = высота
Поскольку объем полуцилиндра = (1/2) × объем цилиндра
⇒ Объем полуцилиндра = (1/2) × πr 2 h
Также диаметр, d = 2 × r
или r = d/2
Таким образом, объем полуцилиндра в единицах диаметра может быть выражен как 92})\)
где,
- r = радиус цилиндра.
- h = высота воды.
- l = длина цилиндра.
Примечание: Функция cos -1 выражается в радианах.
Объем частичного цилиндра будет в кубических единицах. Например, кубические дюймы, кубические футы и кубические метры. Теперь, когда мы научились вычислять объем полуцилиндра, давайте быстро посмотрим, как вычислить площадь его поверхности в следующем разделе.
Формула площади поверхности полуцилиндра
Мы можем рассчитать площадь поверхности полуцилиндра, сложив половину площади криволинейной поверхности цилиндра с площадью двух полукругов и площадью нижнего прямоугольного сечения. Формула площади поверхности полуцилиндра может быть представлена следующим образом:
Общая площадь поверхности полуцилиндра = (1/2) × площадь изогнутой поверхности цилиндра + 2 × площадь полукруга + площадь нижнего прямоугольника.
Общая площадь поверхности полуцилиндра = (1/2) × 2πrh + 2 × (1/2)πr 2 + 2rh
Общая площадь поверхности полуцилиндра = πrh + πr 2 + 2rh
Давайте лучше поймем объем полуцилиндра на нескольких решенных примерах.
Решенные примеры для объема полуцилиндра
Пример 1: Найдите количество кофе, которое может поместиться в чашке, имеющей форму полуцилиндра. Радиус чашки равен 2 дюймам, а высота — 4 дюймам (используйте π = 3,14)
Решение:
Дано:
Радиус (r) = 2 в
Высота (h) = 4 дюймаМы воспользуемся формулой объема полуцилиндра, чтобы найти количество кофе, которое может вместить кружка.
Объем полуцилиндра = (1/2)πr 2 ч кубических единицПодставляя значения в приведенную выше формулу,
Объем полуцилиндра = (1/2) × 3,14 × (2) 2 × (4)Ответ: Объем кофе равен 25,12 в 3 .
Пример 2: У Сэма есть цилиндрическая свеча диаметром 4 дюйма и высотой 10 дюймов. Он хочет разрезать его на два полуцилиндра. Каков будет объем половины свечи? рассчитать объем по формуле полуцилиндра.
(Используйте π = 3,14)Решение:
Дано:
Радиус свечи (r) = 2 в
Высота свечи (h) = 10 вИспользуем формулу объема полуцилиндра,
Объем полуцилиндра = (1/2)πr 2 ч кубических единицПодставляя значения в приведенную выше формулу,
Объем полуцилиндрической свечи, V = (1/2) × 3,14 × (2) 2 × 10Ответ: Объем полуцилиндрической свечи равен 62,8 дюйма 3 .
(Используйте π = 3,14)перейти к слайдуперейти к слайду
Разбивайте сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по объему полуцилиндра
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об объеме полуцилиндра
Каков объем полуцилиндра?
Объем полуцилиндра определяется как общее пространство, занимаемое полуцилиндром в трехмерной плоскости.
Объем полуцилиндра равен половине объема цилиндра.
Как найти объем полуцилиндра?
Объем полуцилиндра можно рассчитать, разделив общий объем цилиндра на 2. Зная радиус и высоту полуцилиндра, мы можем рассчитать его объем по формуле Объем цилиндра = (1 /2)πr 2 ч
где
- r — радиус
- h высота цилиндра
Как найти радиус полуцилиндра, используя объем?
Радиус полуцилиндра можно рассчитать, если известны объем и высота. Чтобы найти радиус в этом случае, мы можем применить формулу объема полуцилиндра, V = (1/2)πr 2 h, где «r» — радиус, а «h» — высота цилиндра, и подставьте известные значения для решения «r».
Как найти высоту полуцилиндра, используя объем
Высота полуцилиндра с использованием объема и радиуса может быть рассчитана по формуле Объем полуцилиндра = (1/2)πr 2 h, где «r» — радиус, а «h » — высота цилиндра. Подставьте данные значения и решите найти недостающее значение высоты полуцилиндра.